Простое объяснение закона Ампера и силы, которую он характеризует
Теория и расчеты Автор: elektrobossСодержание
В этой статье вы узнаете, как формулируется закон Ампера, и какого его применение. А также,что это за феномен – сила Ампера.
Электричество – это достаточно непростая область физики, состоящая из множества законов и явлений, который аккомпанируют движению тока в проводнике.
Сила показывает себя разными способами, вот Вам простой пример: если у нас есть два или больше проводников, по которым проходит электричество, то их тяготение будет направлено друг другу или наоборот.
Понятие силы АмпераЗакон Ампера описывает силу, которая появляется около проводника и соизмерима его длине, силе тока и магнитной индукции, равным образом также косинуса угла между проводником и вектором магнитной индукции. Вследствие этого, получается такая формула: F=BILcosa. Где F – сила Ампера.
Вследствие этого, получается такая формула: F=BILcosa. Где F – сила Ампера.
Ни на что не похоже? Сама формула и ее физический смысл подобен силе Лоренца. Разница только в том, что закон Ампера применяется для проводника в магнитном поле, а Лоренца – на заряженные частицы.
В дифференциальной форме, уравнение будет выглядеть так:
В векторной форме так:
Существует и другая формулировка, которая была открыта Андре Мари Ампером в 1820 году. Она гласит: закон Ампера характеризует силу, воздействующую на проводник в магнитном поле.
Эта величина, как и другие силы в физике, измеряется в Ньютонах (Н).
Поскольку закон Ампера предполагает появление какой-либо силы, то не взирая ни на что, присутствие двух и больше таких сил вызовет их взаимодействие между собой. Каким же образом?
Направление (устремление) силы АмпераСамое важное действие в данном законе это, что при взаимодействии параллельных токов, которые движутся в одном направлении, проводники, располагающиеся рядом, начнут притягиваться.
В случае, если токи будут двигаться в разных направлениях они будут отталкиваться.
Для определения направления прибегают к правилу левой руки. Для этого Вам потребуется разместить раскрытую ладонь левой руки возле проводника таким образом, чтобы в нее входили векторы индукции магнитного поля, а четыре открытых пальца показывали направление движение тока.
Вследствие этого, большой палец укажет, куда устремлены силы Ампера и Лоренца.
Давайте вспомним, как найти направление вектора магнитной индукции… Он находится путем применения правила правой руки: четырьмя пальцами правой руки «обнять» проводник, а большой палец выпрямить под углом 90 градусов таким образом, чтоб он показывал направление тока.
Вследствие этого, четыре согнутых пальца будут изображать круги вокруг токопроводящей нити и указывать, как пробегают линии магнитного поля.
Применение в жизниВ электротехнике закон Ампера «играет» одну из самых важных «ролей». Давайте обсудим случаи его применения на практике. Электропривод — это основа практически каждого предприятия. Для передвижения или доведения до действий всевозможных систем, таких как:
Давайте обсудим случаи его применения на практике. Электропривод — это основа практически каждого предприятия. Для передвижения или доведения до действий всевозможных систем, таких как:
- электромобили;
- трамваи;
- троллейбусы;
- автоматизированные задвижки трубопроводов;
- грузоподъемных механизмов;
- электротранспорта (электровозы на ЖД) и других,
применяются двигатели и электромагнитные исполнительные механизмы.
В результате содействия между обмотками ротора и статора, сила вынуждает двигатель вращаться.
Чтобы заставить обмотки вращаться, их либо переключают с помощью щеточного узла и коллектора в двигателях постоянного тока, либо используют переменный ток.
Свое назначение закон Ампера нашел также в динамиках и громкоговорителях. В них осуществляется движение мембраны, на которой находится обмотка из медной проволоки в магнитном поле постоянного магнита.
Ее действие просматривается при коротких замыканиях на линиях электропередач. Там, под влиянием сверхбольших токов, провода и шины начинают изгибаться.
В рельсотроне в момент выстрела раздвигаются рельсы. Это предопределено уже вышеперечисленными причинами.
Похожие публикации:
Действие магнитного поля на движущуюся заряженную частицу. Сила Лоренца — презентация
Первый слайд презентации: Действие магнитного поля на движущуюся заряженную частицу. Сила Лоренца
План урока:
Выполните тест «магнитное поле-3».
Изучите новый материал и сделайте конспект (его нужно будет сфотографировать и прислать на проверку).
Прорешайте задачи, поставив презентацию на воспроизведение (сначала попробуйте дать ответ, а затем смотрите решение).
Изображение слайда
Слайд 2: Сила Лоренца
Сила Лоренца – сила, действующая со стороны магнитного поля на движущийся заряд. Сила Лоренца равна произведению модуля заряда на скорость движения частицы, магнитную индукцию и синус угла между вектором скорости и вектором магнитной индукции. F=|q|∙ V∙B∙sin α
Изображение слайда
Слайд 3: Вывод формулы силы Лоренца
Изображение слайда
Слайд 4: Направление силы Лоренца
Правило левой руки.
Правило левой руки :
4 пальца левой руки направлены по движению положительного заряда;
Вертикальная составляющая вектора магнитной индукции входит в ладонь;
Большой палец отогнутый на угол 90˚ покажет направление силы Лоренца.
Изображение слайда
Слайд 5: Движение заряженной частицы в однородном магнитном поле. (случай первый)
Вектор магнитной индукции поля перпендикулярен вектору скорости частицы. Как направлена сила Лоренца? Магнитное поле не меняет модуля скорости частицы – меняет только направление движения частицы. Выведем формулы, характеризующие движение частицы в магнитном поле.
Изображение слайда
Слайд 6: Вывод формул, характеризующих движение частицы в магнитном поле
Второй закон Ньютона: (1) Сила Лоренца: (2) Центростремительное ускорение: (3) Из формул (1), (2), (3): После сокращения: (4)
Изображение слайда
Слайд 7: Радиус кривизны траектории и период обращения частицы в магнитном поле
Из формулы получим формулу радиуса кривизны траектории частицы: Найдем период (время одного оборота) обращения частицы в магнитном поле: Таким образом:
Изображение слайда
Слайд 8: Траектория частицы в однородном магнитном поле (вид сверху)
Частица влетает в магнитное поле перпендикулярно силовым линиям.
Изображение слайда
Слайд 9: Решение задач
Изображение слайда
Слайд 10: Задача 18
Протон влетевший в зазор между полюсами электромагнита, имеет горизонтальную скорость, перпендикулярную вектору магнитной индукции, направленного вертикально. Куда направлена действующая на него сила Лоренца? По правилу левой руки: 4 пальца направляются по вектору скорости частицы; вектор магнитной индукции входит в ладонь; большой палец покажет направление силы Ампера. Сила Ампера направлена горизонтально к нам.
Изображение слайда
Слайд 11: Задача 19
Электрон, влетевший в зазор между полюсами электромагнита, имеет горизонтально направленную скорость, перпендикулярную вектору индукции. Куда направлена действующая на него сила Лоренца?
Используя правило левой руки…
Сила Лоренца направлена вертикально вверх.
Куда направлена действующая на него сила Лоренца?
Используя правило левой руки…
Сила Лоренца направлена вертикально вверх.
Изображение слайда
Слайд 12: Задача 20
Как изменится период обращения заряженной частицы в однородном магнитном поле при увеличении ее скорости в 5 раз? Рассматривается нерелятивистский случай. Период обращения частицы в магнитном поле определяется формулой: T=2 π R/V=2 π m/|q|∙B Из этой формулы видно, что период обращения частицы не зависит от ее скорости в магнитном поле.
Изображение слайда
Слайд 13: Задача 21
Нейтрон и протон влетают в однородное магнитное поле перпендикулярно вектору магнитной индукции с одинаковыми скоростями. Чему равно отношение модуля силы, действующей на нейтрон к модулю силы, действующей на протон
В магнитном поле действует сила Лоренца: F=|q|∙V∙B∙sin α
Но сила Лоренца действует только на протон, т. к. нейтрон не имеет заряда.
Отношение сил равно нулю.
к. нейтрон не имеет заряда.
Отношение сил равно нулю.
Изображение слайда
Слайд 14: Задача 22
Электрон и протон влетают в однородное магнитное поле перпендикулярно вектору магнитной индукции с одинаковыми скоростями. Чему равно отношение модулей сил, действующих на них со стороны магнитного поля? На электрон и протон действует сила Лоренца. F=|q|∙ V∙B∙sin α Следовательно, сила, действующая на частицы зависит от величины заряда частиц. Заряды электрона и протона равны, значит, равны и силы, действующие на них. Ответ: отношение сил равно 1.
Изображение слайда
Слайд 15: Задача 23
Электрон и α -частица влетают в однородное магнитное поле перпендикулярно вектору магнитной индукции с одинаковыми скоростями.
Изображение слайда
Слайд 16: Задача 24
Два первоначально покоившихся электрона ускоряются в электрическом поле: первый проходит разность потенциалов U, второй 2 U.Ускорившиеся электроны влетают в магнитное поле перпендикулярно линиям магнитной индукции. Чему равно отношение радиусов кривизны траекторий первого и второго электронов?
В электрическом поле кинетическая энергия электронов приобретается за счет энергии поля: ( mV 2 /2= eU ) => V=√2eU/m ; V ₁~√U, V₂~√2U ; V₁/V₂=1/√2
Радиус кривизны: r= m∙V /|q|∙B ; r~V => r ₁/r₂= V₁/V₂=1/√2. Ответ: 1/√2 или √2/2.
Ответ: 1/√2 или √2/2.
Изображение слайда
Последний слайд презентации: Действие магнитного поля на движущуюся заряженную частицу. Сила Лоренца: Домашнее задание
Тест «Магнитное поле-3» § 6 (11кл). конспект.
Изображение слайда
22.10: Магнитная сила между двумя параллельными проводниками
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 2704
- OpenStax
- OpenStax
Цели обучения
К концу этого раздела вы сможете:
- Описывать эффекты магнитной силы между двумя проводниками.

- Рассчитайте силу между двумя параллельными проводниками.
Можно было бы ожидать, что между проводниками с током действуют значительные силы, поскольку обычные токи создают значительные магнитные поля, а эти поля воздействуют на обычные токи значительными силами. Но вы можете не ожидать, что сила между проводами используется для определяют ампер. Вы также можете удивиться, узнав, что эта сила как-то связана с тем, почему большие автоматические выключатели сгорают, когда они пытаются отключить большие токи.
Силу между двумя длинными прямыми и параллельными проводниками, разделенными расстоянием \(r\), можно найти, применяя то, что мы разработали в предыдущих разделах. На рисунке \(\PageIndex{1}\) показаны провода, их токи, поля, которые они создают, и последующие силы, которые они воздействуют друг на друга. Рассмотрим поле, создаваемое проводом 1, и силу, которую он оказывает на провод 2 (назовем силу \(F_{2}\)). Поле из-за \(I_{1}\) на расстоянии \(r\) равно
\[B_{1} = \frac{\mu_{0}I_{1}}{2\pi r}.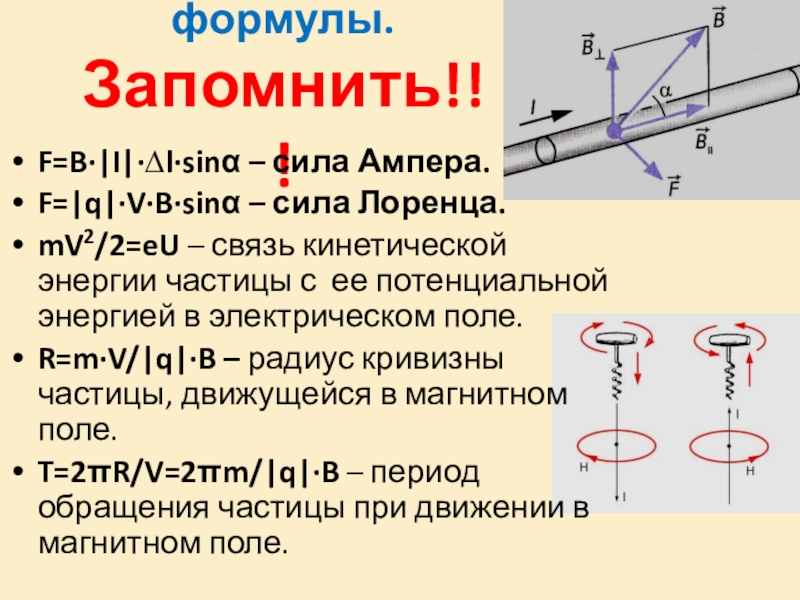 \label{22.11.1}\]
\label{22.11.1}\]
Это поле однородно вдоль провода 2 и перпендикулярно ему, поэтому сила \(F_{2}\), действующая на провод 2, определяется выражением \(F = IlB sin\theta\) с \(sin \theta = 1\): \[F_{2} = I_{2}lB_{1}.\label{22.11.2}\] По третьему закону Ньютона силы на проводах равны по величине, поэтому мы просто пишем \ (F\) для величины \(F_{2}\). (Обратите внимание, что \(F_{1} = -F_{2}\).) Поскольку провода очень длинные, удобно думать в терминах \(F/l\), сила на единицу длины. Подстановка выражения для \(B_{1}\) в последнее уравнение и перестановка членов дает
\[\frac{F}{l} = \frac{\mu_{0}I_{1}I_{2}}{2\pi r}. \label{22.11.3}\]
\label{22.11.3}\]
\(F/l\) сила на единицу длины между двумя параллельными токами \(I_{1}\) и \(I_{2}\), разделенными расстоянием \(r\). Сила притяжения, если токи имеют одинаковое направление, и отталкивания, если они направлены в противоположные стороны.
Эта сила отвечает за пинч-эффект в электрических дугах и плазме. Сила существует независимо от того, есть ли токи в проводах или нет. В электрической дуге, где токи движутся параллельно друг другу, существует притяжение, которое сжимает токи в трубку меньшего размера. В больших автоматических выключателях, таких как те, которые используются в системах распределения электроэнергии по соседству, эффект защемления может концентрировать дугу между пластинами выключателя, пытаясь отключить большой ток, прожечь дыры и даже зажечь оборудование. Другой пример пинч-эффекта можно найти в солнечной плазме, где струи ионизированного материала, такие как солнечные вспышки, формируются под действием магнитных сил. 9{-7} Н/м\) на каждом проводе.
Прямые провода бесконечной длины нецелесообразны, поэтому на практике баланс токов создается с помощью витков провода, разделенных несколькими сантиметрами. Сила измеряется для определения силы тока. Это также дает нам метод измерения кулона. Измеряем заряд, протекающий при токе в один ампер за одну секунду. То есть \(1 C = 1 A \cdot s\). Как для ампера, так и для кулона метод измерения силы между проводниками является наиболее точным на практике.
- Сила между двумя параллельными токами \(I_{1}\) и \(I_{2}\), разделенными расстоянием \(r\), имеет величину на единицу длины, определяемую как \[\frac{F} {l} = \frac{\mu_{0}I_{1}I_{2}}{2\pi r}.\]
- Сила притяжения, если токи имеют одинаковое направление, и отталкивания, если они направлены в противоположные стороны.
Эта страница под названием 22.10: Магнитная сила между двумя параллельными проводниками распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- ОпенСтакс
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Программа OER или Publisher
- ОпенСтакс
- Показать оглавление
- нет
- Теги
- Магнитная сила
- параллельные проводники
- источник@https://openstax.
 org/details/books/college-physics
org/details/books/college-physics
[PDF] Эквивалентность сил Ампера и сил Грассмана
- 96EquivalenceBA,
title={Эквивалентность сил Ампера и Грассмана},
автор={А. К. Т. Ассис и Марсело Буэно},
journal={Транзакции IEEE на Magnetics},
год = {1996},
объем = {32},
страницы={431-436}
}
- А. Ассис, М. Буэно
- Опубликовано 1 19 марта96
- Математика
- IEEE Transactions on Magnetics
Мы рассчитываем силу, действующую на часть одиночной замкнутой цепи из-за оставшейся цепи в четырех различных геометриях, в соответствии с силами Ампера и Грассмана. Все аналитические расчеты выполняются с использованием элементов поверхностного или объемного тока, чтобы избежать расхождений, возникающих при линейных элементах тока нулевого диаметра. Делаем вывод, что при рассмотрении действия замкнутой цепи в целом и использовании только цепей с замкнутыми линиями тока будет иметь место…
Просмотр через Publisher
ifi.
 unicamp.br
unicamp.brДоказательство тождества сил Ампера и сил Грассмана
- М. Буэно, А. Ассис
- 1997 9 0030
- 1998
- 2012
- 2013
- 2016
- 2018
- 2020
- 2021
- 2016
- 1988
- 1987
- 1992
- 1989
- 1990
- 1993
- 1982
Математика
Рассмотрим полоидальный ток, текущий по поверхности проводящий цилиндр длиной l и радиусом a. Мы точно вычисляем силу, действующую на элемент поверхностного тока, принадлежащий этому цилиндру из-за…
Получение силы из индуктивности
- М. Буэно, А. Ассис
Инженерия, физика
Показана правильность расчета силы на токоведущие цепи путем взятия производной коэффициента индуктивности цепей даже в случае одиночной замкнутой цепи,…
Закон Ампера оказался несовместимым с Закон силы Грассмана
- Дж. О. Джонсон
Физика
Часто предпринимались попытки установить связи между различными подходами в электромагнетизме. Такие имена, как Ампер, Кулон, Лоренц, Грассманн, Максвелл и др.
 все связаны с усилиями по…
все связаны с усилиями по…Неэквивалентность магнитостатической потенциальной энергии, соответствующей формулам силы элемента тока Ампера и Грассмана
- Т. Минтир
Физика
Лоренц) текущая формула силы элемента хорошо зарекомендовал себя. Однако при наличии магнитостатической потенциальной энергии, соответствующей этим силам…
Космический корабль «Шпилька Ампера»
- К. Макдональд
Физика
1 Задача В 1822 году Ампер и де Ла Рив [1] провели эксперимент, показанный ниже, в котором проводящая «шпилька» npqr плавала на двух желобах с ртутью, соединенных с двумя…
Аналитическая модель силы Лоренца Между одномерными линейными токами в произвольных относительных положениях и направлениях
- Цубаса Каваи, Т. Инамори, К. Хори
Физика
IEEE Transactions on Magnetics
Мы выводим аналитическую формулу для Сила Лоренца и крутящий момент между Одномерные линейные текущие элементы в произвольных относительных позициях явно, не оставаясь целыми.
 Цепь представлена как…
Цепь представлена как…Законы взаимодействия токов и зарядов и определение магнитного поля
- Тараканов А.
Физика
Различные варианты взаимодействия токовых элементов и движущихся зарядов, записанные в векторной форме, начиная с Ампера теории, считаются. Показано, что с точки зрения…
Экспериментальное исследование необычного индукционного эффекта и его интерпретация как необходимое следствие веберовской электродинамики
- S. Kühn
Physics
Journal of Electrical Engineering
Аннотация Магнитная составляющая силы Лоренца действует исключительно перпендикулярно направлению движения пробного заряда, тогда как электрическая составляющая не зависит от скорости
Расширенное использование закона Кулона в связи с установленными законами электромагнетизма
- J. O. Jonson
Physics
Исторически предполагалось, что компетентность в основном электростатического закона Кулона ограничивается чистым электростатика.
 Как только начали изучать электрические заряды в движении, появились новые своды законов…
Как только начали изучать электрические заряды в движении, появились новые своды законов…Обнаруженное направление силы на постоянном магните, вызванное током смещения в проволочном зазоре, поддерживает веберовскую электродинамику забытая веберовская электродинамика с помощью легко воспроизводимого и простого эксперимента. Для этого сначала теоретически…
Измерение магнитостатической силы токовой цепи на части самой себя
- В. Пеоглос
Физика
Сообщается о результатах эксперимента, предназначенного для измерения силы, действующей токовой цепью на часть самой себя, и для сравнения этого с предсказаниями Био-Савара и Ампера…
Эквивалентность законов сил Ампера и Био-Савара в магнитостатике
- К. Христодулидес
Физика
Эквивалентность законов сил Ампера и Био-Савара в магнитостатике исследуется путем рассмотрения разница в ожидаемых силах по двум законам.
 Условия, при которых эта сила…
Условия, при которых эта сила…Отдача рельсотрона, амперное напряжение и законы электродинамики
- А. Э. Робсон, Дж. Сетиан
Физика
текущие элементы следует предпочесть более знакомым и повсеместно используемым…
Вычисление шестикратных интегралов закона силы Био-Савара-Лоренца в замкнутом контуре
- П. Мойссайдс
Физика
Шестикратные интегралы закона силы Био-Савара-Лоренца рассчитываются для замкнутого контура с использованием процедур ЦЕРН. Рассматриваются различные распределения тока. Теоретические расчеты…
Конечный размер металлического элемента тока
- Н. Грано
Физика
Разница между ньютоновскими и релятивистскими силами
- П. Грано
Физика 90 032
В этой статье обсуждается новый поворот в 148-летнем споре о законе электродинамической силы между законом силы Ампера 1822 года ньютоновской электродинамики и законом Грассмана 1845 года, который стал…
Применение закона силы Ампера к рельсотронным ускорителям
Физика
В этой статье исследуется вопрос о том, где в цепи ускорителя рельсотрона находится место действия силы отдачи.
 Объясняется, что традиционная теория электромагнитного поля и старая теория Ампера…
Объясняется, что традиционная теория электромагнитного поля и старая теория Ампера…Веберовская электродинамика, часть I. Общая теория, эффекты постоянного тока
- Дж. Уэсли
- 1990
Физика
Первоначальная теория действия Вебера на расстоянии, справедливая для медленно меняющихся эффектов, распространяется на поля с запаздыванием во времени, справедливо для быстро меняющихся эффектов, включая радиацию. Новый закон силы…
Строгая количественная проверка сил Био–Савара–Лоренца
- П. Мойссайдс, П. Паппас
- 1986
Физика
В настоящей статье описывается эксперимент, проведенный в Афинском национальном техническом университете, по сравнению теоретических сил Био–Савара–Лоренца с экспериментально измеренными силами, которые…
- 1987
В этой статье механический КПД рельсотрона определяется как сила, ускоряющая комбинацию арматура-снаряд, деленная на общую электродинамическую силу, создаваемую в пушке.


 В случае, если токи будут двигаться в разных направлениях они будут отталкиваться.
В случае, если токи будут двигаться в разных направлениях они будут отталкиваться.
 org/details/books/college-physics
org/details/books/college-physics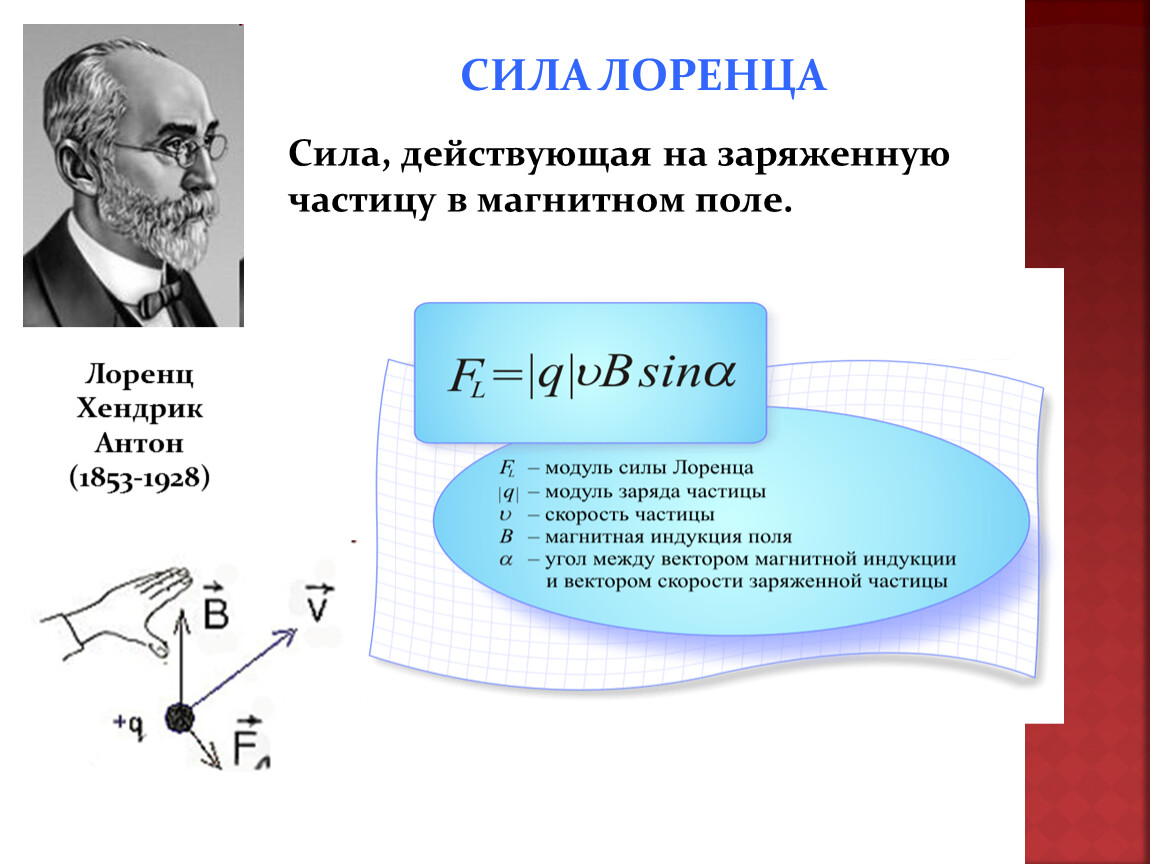 unicamp.br
unicamp.br все связаны с усилиями по…
все связаны с усилиями по… Цепь представлена как…
Цепь представлена как… Как только начали изучать электрические заряды в движении, появились новые своды законов…
Как только начали изучать электрические заряды в движении, появились новые своды законов…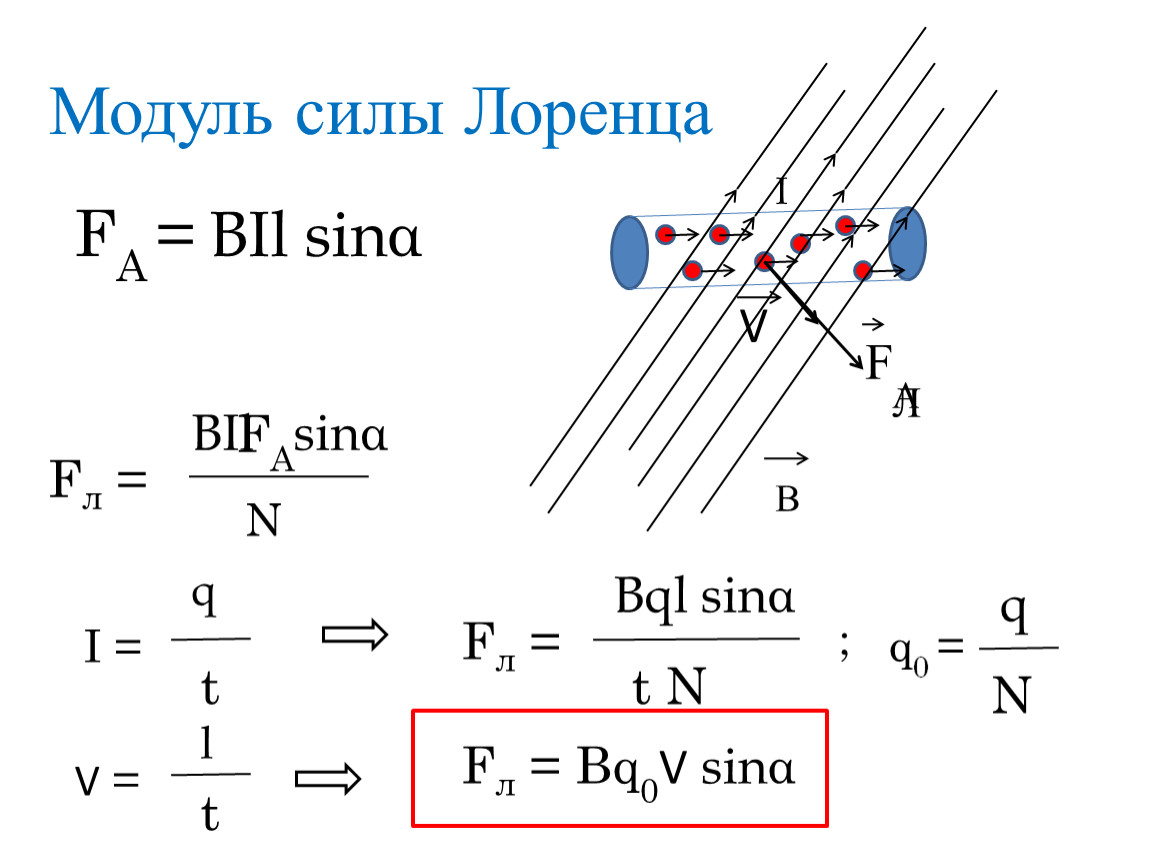 Условия, при которых эта сила…
Условия, при которых эта сила… Объясняется, что традиционная теория электромагнитного поля и старая теория Ампера…
Объясняется, что традиционная теория электромагнитного поля и старая теория Ампера…