Сила Ампера | Магниты и магнитное поле

Мы уже знаем, что на движущуюся заряженную частицу, помещенную в магнитное поле, будет действовать сила, которую называют силой Лоренца. При этом не всегда мы имеем дело с какими-то одинокими частицами, иногда приходится работать с их совокупностью, движущейся в определенном направлении, – электрическим током.

Рассмотрим проводник с током, помещенный в однородное магнитное поле.

Сила, с которой на него будет действовать магнитное поле, называют силой Ампера. Обычно ее обозначают как \vec{F_А}. По идее, она является частным случаем силы Лоренца, а свое собственное название получила в связи с тем, что была открыта и изучена раньше. Давайте попробуем, используя это, сказать, как можно найти величину силы Ампера и ее направление.

Вспомним формулу, по которой находят модуль силы Лоренца:

F_л=qvB\sin\alpha

Теперь представим, что нас интересует не весь проводник с током, а только его кусочек длиной l.

В таком случае скорость, с которой движутся электроны на данном участке, можно вычислить следующим образом:

v=\dfrac{l}{t}

Попробуем воспользоваться этим, чтобы преобразовать выражение для расчета силы Лоренца в выражение для расчета силы Ампера:

F_А=q×\dfrac{l}{t}×B×\sin\alpha

F_А=\dfrac{q}{t}×l×B×\sin\alpha

\boxed{F_А=IlB\sin\alpha}

Какой угол теперь следует брать в качестве угла \alpha? Технически это угол между вектором магнитной индукции и вектором \vec{l}, характеризующим расположение проводника с током в пространстве. По направлению он совпадает с направлением, в котором течет ток.

Давайте применим полученную формулу на практике.

Пусть сила тока равна 3 амперам, а модуль магнитной индукции – 1 тесле. Участок проводника, для которого нужно определить величину воздействия со стороны магнитного поля, равен 1 метру.

Учитывая, что проводник с током располагается перпендикулярно линиям магнитного поля, найдем силу, действующую на него:

F_А=IlB\sin\alpha

F_А=IlB

F_А=3\,А×1\,м×1\,Тл

F_А=3\,Н

Осталось разобраться с направлением силы Ампера. Тут есть забавный момент.

Надеюсь, вы еще помните, что при определении направления силы Лоренца, частным случаем которой и является сила Ампера, нужно различать две ситуации – с отрицательно заряженной частицей мы имеем дело или с положительно заряженной? После этого нужно применить соответственно либо правило правой руки, либо правило левой руки.

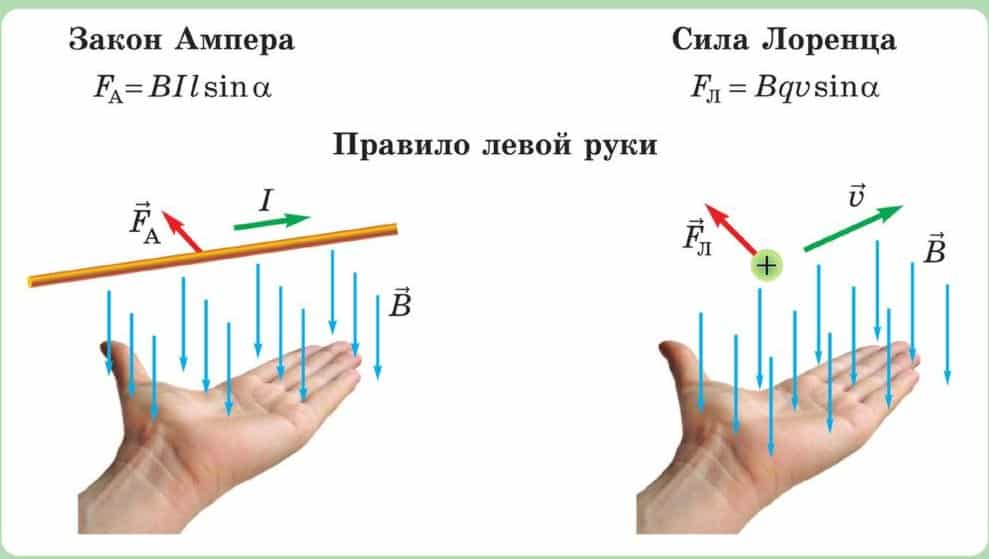
В нашем случае речь идет о движении электронов по проводнику.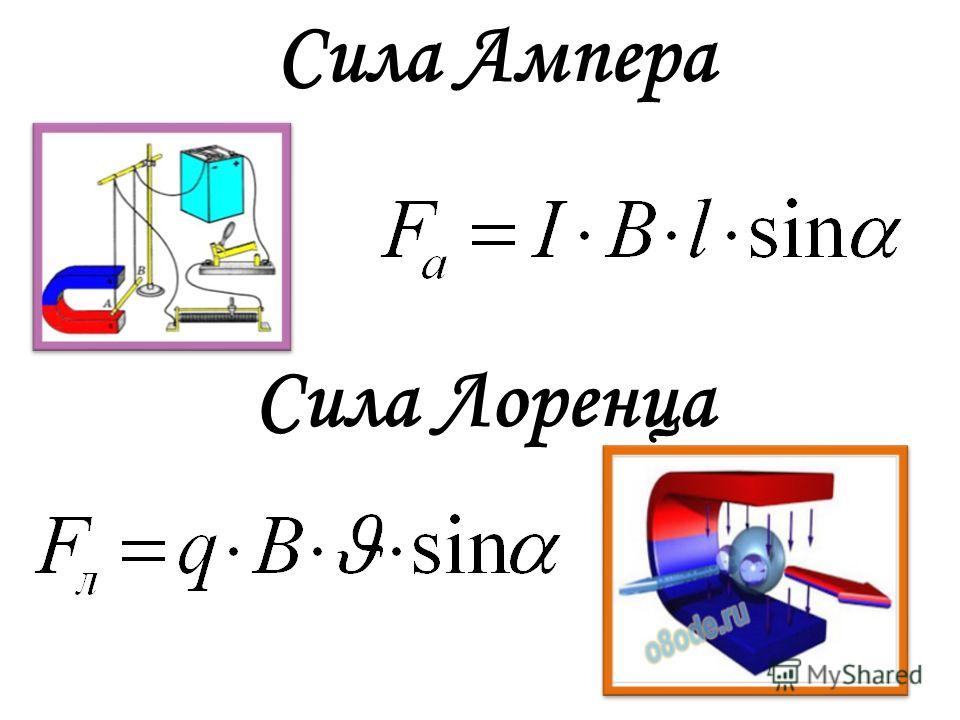 Вроде бы, нужна правая рука. Но нет, нужна левая. Исторически получилось так, что за направление тока считают направление, противоположное тому, в котором движутся электроны. Другими словами, предполагается, что по проводнику движутся положительно заряженные частицы. Поэтому нужно использовать правило левой руки. Ох уж эта физика!

Еще раз взглянем на нашу картинку. Векторы магнитной индукции направлены от нас, четыре пальцы следует направить в сторону протекания тока, тогда большой палец, отогнутый на 90 градусов, покажет направление силы Ампера.

20.Сила Ампера. Сила Лоренца

Сила, действующая на участок проводника, пропорциональна силе тока I, длине Δl этого участка и синусу угла α между направлениями тока и вектора магнитной индукции: F ~ IΔl sin α.

Эта сила называется силой Ампера. Она достигает максимального по модулю значения Fmax, когда проводник с током ориентирован перпендикулярно линиям магнитной индукции.

F = I·L·B·sina

I — сила тока в проводнике;

B — модуль вектора индукции магнитного поля;

L — длина проводника, находящегося в магнитном поле;

a — угол между вектором магнитного поля инаправлением тока в проводнике.

Сила Ампера, действующая на отрезок проводника длиной Δl с силой тока I, находящийся в магнитном поле B, F = IBΔl sin α

может быть выражена через силы, действующие на отдельные носители заряда.

Пусть концентрация носителей свободного заряда в проводнике есть n, а q – заряд носителя. Тогда произведение n q υ S, где υ – модуль скорости упорядоченного движения носителей по проводнику, а S – площадь поперечного сечения проводника, равно току, текущему по проводнику: I = q n υ S. Выражение для силы Ампера можно записать в виде: F = q n S Δl υB sin α. Так как полное число N носителей свободного заряда в проводнике длиной Δl и сечением S равно n S Δl, то сила, действующая на одну заряженную частицу, равна FЛ = q υ B sin α. Эту силу называют

силой Лоренца. Угол α в этом выражении равен углу между скоростью и вектором магнитной индукции Направление силы Лоренца, действующей на положительно заряженную частицу, так же, как и направление силы Ампера, может быть найдено по правилу левой руки или по правилу буравчика.

По реакции на внешнее магнитное поле и характеру внутреннего магнитного упорядочения все вещества в природе можно подразделить на пять групп:

• диамагнетики,

• парамагнетики,

• ферромагнетики,

• антиферромагнетики

• ферримагнетики.

Перечисленным видам магнетиков соответствуют пять различных видов магнитного состояния вещества: диамагнетизм, парамагнетизм, ферромагнетизм, антиферромагнетизм и ферримагнетизм.

К диамагнетикам относят вещества, у которых магнитная восприимчивость отрицательна и не зависит от напряженности внешнего магнитного поля.

К парамагнетикам относят вещества с положительной магнитной восприимчивостью, не зависящей от напряженности внешнего магнитного поля.

К ферромагнетикам относят вещества с большой положительной магнитной восприимчивостью (до 106), которая сильно зависит от напряженности магнитного поля и температуры.

Антиферромагнетиками являются вещества, в которых ниже некоторой температуры спонтанно возникает антипараллельная ориентация элементарных магнитных моментов одинаковых атомов или ионов кристаллической решетки.

При нагревании антиферромагнетик испытывает фазовый переход в парамагнитное состояние.

К ферримагнетикам относят вещества, магнитные свойства которых обусловлены нескомпенсированным антиферромагнетизмом. Подобно ферромагнетикам они обладают высокой магнитной восприимчивостью, которая существенно зависит от напряженности магнитного поля и температуры. Наряду с этим ферримагнетики характеризуются и рядом существенных отличий от ферромагнитных материалов.

Свойствами ферримагнетиков обладают некоторые упорядоченные металлические сплавы, но, главным образом,- различные оксидные соединения, среди которых наибольший практический интерес представляют ферриты.

2\vec{F_{12}}$$

Где $i_2d\vec{\ell_2}$ и $i_1d\vec{\ell_1}$ — текущие элементы проводов. А круговой закон таков: $$\oint \vec B\cdot d\vec l=\mu_oI_{net}$$

Мой вопрос: какой закон был написан первым? Извлекает ли Ампер закон замыкания из приведенного выше уравнения силы? Является ли математическая форма уравнения магнитного поля исходной формой, которую написал Ампер, или она пришла позже других ученых, и если да, то какова исходная формулировка.

• электромагнетизм
• магнитные поля
• история

$\endgroup$

2

$\begingroup$

Насколько я знаю, Ампер пытался объяснить силу между проводниками по формуле, которую вы написали. Господствующим понятием того времени было действие на расстоянии, успешное как для гравитации, так и для электростатики.

Даже магнитные силы он объяснял как равнодействующую сил между микротоками в материалах.

Представление о магнитном поле, передающем силу между проводами, со временем возобладало, возможно, потому, что микротоки были слишком умозрительны, а железные пломбы Фарадея слишком убедительно доказывали существование магнитного поля.

$\endgroup$

0

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

сил Ампера и Лоренца | Semantic Scholar

• DOI: 10.1016/0375-9601(85)90590-0
• Идентификатор корпуса: 123446131

 @article{Graneau1985AmpereAL,
  title={силы Ампера и Лоренца},
  автор={Питер Грано},
  журнал = {буквы по физике А},
  год = {1985},
  объем = {107},
  страницы = {235-237}
} 

• P. Graneau
• Опубликовано 4 февраля 1985 г.
• Физика
• Физические буквы A

View Via Publisher

О разнице между Lorentz и Ampere Force Law Физика

1989

Автор рассматривает эквивалентность или различие двух возможных законов силы в магнитостатике для взаимодействующих частиц: законов силы Ампера и Лоренца. Он показывает, что эти двое…

Эквивалентность законов силы Ампера и Био-Савара в магнитостатике

• К. Христодулидес

• Физика

• 1987

Рассмотрение различия силы Ампера и Савара в биостатической эквивалентности в законах магнитостатики и

в силах, предсказанных двумя законами. Условия, при которых эта сила…

Закон Ампера оказался несовместимым с законом силы Грассмана

• Дж. О. Джонсон

• Физика

• 2012

Часто предпринимались попытки установить связи между различными подходами в электромагнетизме. Такие имена, как Ампер, Кулон, Лоренц, Грассманн, Максвелл и др. все связаны с усилиями по…

О формах закона силы для элементов тока

• Ж. Стрнад

• Физика

• 1989

0035

• Дж. О. Джонсон

• Физика

• 2010

В этой статье описывается, как закон силы Ампера использовался для объяснения экспериментальных результатов экспериментов на Амперовом мосту. Подробный вывод, основанный на статье Уэсли, готовится…

Электродинамика Вебера, часть I. Общая теория, эффекты постоянного тока Теория, действительная для медленно меняющихся эффектов, распространяется на поля с запаздыванием во времени, верная для быстро меняющихся эффектов, включая излучение. Новый закон силы…

Расширенное использование закона Кулона по отношению к установленным законам электромагнетизма

• J. O. Jonson

• Физика

• 2016

Исторически компетенция

была ограничена чисто электростатическим законом Кулона Как только стали изучать электрические заряды в движении, появились новые своды законов…

По принципу Маха

• А. Ассис

• Физика

• 1989

Мы предлагаем постулат, что результирующая сила, действующая на любое тело, равна нулю. С помощью этого постулата и с помощью веберовского закона силы тяготения мы получаем уравнения движения и заключаем, что все… 2009

Обзор применения третьего закона Ньютона в физике

• P. Cornille

• Physics, Education

• 1999

SHOWING 1-8 OF 8 REFERENCES

Identity of the Ampere and Biot-Savart electromagnetic force laws

• D. Jolly

• Physics

• 1985

Совместимость законов силы Ампера и Лоренца с концепцией виртуальной работы , как и в конструкции рельсотронов, необходимо сделать выбор между тремя доступными формулами, которые имеют…

First indication of Ampere tension in solid electric conductors

• P. Graneau

• Physics

• 1983

The original Ampère force and Biot-Savart and Lorentz forces

• P. Pappas

• Physics

• 1983

Резюме Целью данной статьи является представление результатов очень простого эксперимента, подтверждающего исходную силу Ампера и однозначно опровергающего силу относительности Био-Савара или ее…

История теорий эфира и электричества

• Эдмунд Тейлор Уиттакер

• Физика, образование

• 1910

Рынок: Физики, заинтересованные непрофессионалы и историки науки.