Механическое напряжение — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 13 мая 2017; проверки требуют 3 правки. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 13 мая 2017; проверки требуют 3 правки. У этого термина существуют и другие значения, см. Напряжение.

Механическое напряжение — мера внутренних сил, возникающих в деформируемом теле под влиянием различных факторов. Механическое напряжение в точке тела определяется как отношение внутренней силы к единице площади в данной точке рассматриваемого сечения.

Напряжения являются результатом взаимодействия частиц тела при его нагружении. Внешние силы стремятся изменить взаимное расположение частиц, а возникающие при этом напряжения препятствуют смещению частиц, ограничивая его в большинстве случаев некоторой малой величиной.

Q=FS{\displaystyle Q={\frac {F}{S}}}

Q — механическое напряжение.

F — сила, возникшая в теле при деформации.

S — площадь.

Различают две составляющие вектора механического напряжения:

• Нормальное механическое напряжение — приложено на единичную площадку сечения, по нормали к сечению (обозначается σ{\displaystyle \sigma }).
• Касательное (тангенциальное) механическое напряжение — приложено на единичную площадку сечения, в плоскости сечения по касательной (обозначается τ{\displaystyle \tau }).

Совокупность напряжений, действующих по различным площадкам, проведенным через данную точку, называется напряженным состоянием в точке.

В Международной системе единиц (СИ) механическое напряжение измеряется в паскалях.

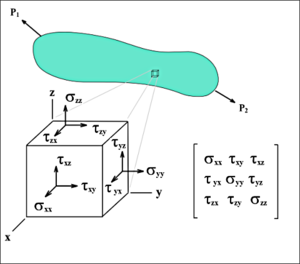Полный тензор механического напряжения элементарного объёма тела. Буквой σ обозначены нормальные механические напряжения, а касательные буквой τ.

Более строго механическое напряжение — тензорная величина. Компоненты тензора напряжений σij{\displaystyle \sigma _{ij}} равны отношению компоненты силы ΔFi{\displaystyle \Delta F_{i}}, действующей на элементарную площадку ΔS{\displaystyle \Delta S}, к её площади:

σij=ΔFiΔSj.{\displaystyle \sigma _{ij}={\frac {\Delta F_{i}}{\Delta S_{j}}}.}

Здесь под ΔSj{\displaystyle \Delta S_{j}} понимаются компоненты вектора, образованного из нормали к элементарной площадке n→{\displaystyle {\vec {n}}} и её площади ΔS{\displaystyle \Delta S}:

ΔS→=n→ΔS.{\displaystyle \Delta {\vec {S}}={\vec {n}}\Delta S.}

Таким образом сила, действующая на некий объём V, равна интегралу тензора напряжения на границе этого объёма по поверхности этого объёма S{\displaystyle S} (в отсутствие объёмных сил):

Fi=∮S⁡σijdSj{\displaystyle F_{i}=\oint _{S}\sigma _{ij}dS_{j}}

Единица измерения напряжения, теория и онлайн калькуляторы

Определение и единица измерения напряжения

Определение

Напряжением ($U$) на участке цепи называют величину, равную отношению суммарной работы ($A$), при перемещении заряда, к величине этого заряда ($q$):

\[U=\frac{A}{q}\left(1\right).\]

В Международной системе единиц (СИ) вольт — единица измерения напряжения. Обозначается буквой В. Эта единица измерения была названа в честь итальянского ученого А. Вольты (Он изобрел известный вольтов столб — это была первая электрическая батарея). Один вольт — единица измерения напряжения, равная работе в один джоуль над зарядом в 1 кулон при перемещении заряда из одной точки в другую:

\[1В=\frac{1\ Дж}{1\ Кл}.\]

Иногда используют другое определение вольта, при этом говорят, что один вольт — это электрическое напряжение, которое взывает в цепи постоянный ток, имеющий силу в 1 ампер при мощности один ватт:

\[1В=\frac{1\ Вт}{1\ А}.\]

Вольт является производной единицей измерения в системе СИ. Через основные единицы вольт можно выразить, используя его определение, например:

\[\left[U\right]=В=\frac{\ Дж}{\ Кл}=\frac{{\rm Н}\cdot {\rm м}}{{\rm А}\cdot {\rm с}}=\frac{{\rm кг}\cdot {\rm м}\cdot {\rm м}}{{\rm А}\cdot {\rm с}\cdot {{\rm с}}^{{\rm 2}}}=\frac{{\rm кг}\cdot {{\rm м}}^{{\rm 2}}}{{\rm А}\cdot {{\rm с}}^{{\rm 3}}}.\]

С вольтом используют любые стандартные приставки системы СИ, применяемые для формирования кратных и дольных единиц. Например:

\[1\ кВ={10}^3В;;1мкВ={10}^{-6}В\ \dots \]

В системе СГС (сантиметр, грамм, секунда) единицы потенциала — единица измерения напряжения. Между вольтами и единицами измерения потенциала имеется следующее соотношение:

\[1В=\frac{1}{300}\ ед.\ потенциала.\]

Вольт — единица измерения напряжения и эффект Джозефсона

В 1990 году была проведена стандартизация вольта в измерениях, при этом использовался нестационарный эффект Джозефсона. При пропускании через контакт Джозефсона тока больше критического, падение напряжения на контакте и сила тока через него помимо постоянной составляющей будет обладать переменной компонентой (говорят, что контакт излучает электромагнитные волны). Частота ($\nu $) этой составляющей определяется из фундаментального выражения:

\[h\nu =2q_eU\ \left(2\right),\]

где $h$ — постоянная Планка; $q_e$ — элементарный заряд. Данный эффект можно наблюдать и измерять при размещении контакта во внешнем электромагнитном поле высокой частоты. Если частота внешнего поля совпадает (или кратна) с частотой электромагнитного излучения, то появляется резонанс. Вольт — амперная характеристика для средних величин тока и напряжения является ступенчатой кривой. Ширина «ступенек» (ступеньки Шапиро) в направлении оси напряжений составляет величину $\frac{h\nu }{2q_e}$. Данные ступеньки позволяют измерять частоту внешнего поля вместо слабого эл

Электрическое напряжение — это… Что такое Электрическое напряжение?

У этого термина существуют и другие значения, см. Напряжение.

Электри́ческое напряже́ние между точками A и B электрической цепи или электрического поля — физическая величина, значение которой равно отношению работы электрического поля, совершаемой при переносе пробного электрического заряда из точки A в точку B, к величине пробного заряда.

При этом считается, что перенос пробного заряда не изменяет распределения зарядов на источниках поля (по определению пробного заряда). В потенциальном электрическом поле эта работа не зависит от пути, по которому перемещается заряд. В этом случае электрическое напряжение между двумя точками совпадает с разностью потенциалов между ними.

Альтернативное определение —

— интеграл от проекции поля эффективной напряжённости поля (включающего сторонние поля) на расстояние между точками A и B вдоль заданной траектории, идущей из точки A в точку B. В электростатическом поле значение этого интеграла не зависит от пути интегрирования и совпадает с разностью потенциалов.

Единицей измерения напряжения в системе СИ является вольт.

Напряжение в цепях постоянного тока

Напряжение в цепи постоянного тока определяется так же, как и в электростатике.

Напряжение в цепях переменного тока

Для описания цепей переменного тока применяются следующие понятия:

Мгновенное напряжение

Мгновенное напряжение есть разность потенциалов между двумя точками, измеренная в данный момент времени. Оно является функцией времени:

Амплитудное значение напряжения

Амплитуда напряжения есть максимальное по модулю значение мгновенного напряжения за весь период колебаний:

Для гармонических (синусоидальных) колебаний напряжения мгновенное значение напряжения выражается как:

Для сети переменного синусоидального напряжения со среднеквадратичным значением 220 В амплитудное равно приблизительно 311,127 В.

Амплитудное напряжение можно измерить с помощью осциллографа.

Среднее значение напряжения

Среднее значение напряжения (постоянная составляющая напряжения) определяется за весь период колебаний, как:

Для чистой синусоиды среднее значение напряжения равно нулю.

Среднеквадратичное значение напряжения

Среднеквадратичное значение (устаревшее наименование: действующее, эффективное) наиболее удобно для практических расчётов, так как на линейной активной нагрузке оно совершает ту же работу (например, лампа накаливания имеет ту же яркость свечения, нагревательный элемент выделяет столько же тепла), что и равное ему постоянное напряжение:

Для синусоидального напряжения справедливо равенство:

В технике и быту при использовании переменного тока под термином «напряжение» имеется в виду именно эта величина, и все вольтметры проградуированы исходя из её определения. Однако конструктивно большинство приборов фактически измеряют не среднеквадратичное, а средневыпрямленное (см. ниже) значение напряжения, поэтому для несинусоидального сигнала их показания могут отличаться от истинного значения.

Средневыпрямленное значение напряжения

Средневыпрямленное значение есть среднее значение модуля напряжения:

Для синусоидального напряжения справедливо равенство:

На практике используется редко, однако большинство вольтметров переменного тока (те, в которых ток перед измерением выпрямляется) фактически измеряют именно эту величину, хотя их шкала и проградуирована по среднеквадратичным значениям.

Напряжение в цепях трёхфазного тока

В цепях трёхфазного тока различают фазное и линейное напряжения. Под фазным напряжением понимают среднеквадратичное значение напряжения на каждой из фаз нагрузки, а под линейным — напряжение между подводящими фазными проводами. При соединении нагрузки в треугольник фазное напряжение равно линейному, а при соединении в звезду (при симметричной нагрузке или при глухозаземлённой нейтрали) линейное напряжение в раз больше фазного.

На практике напряжение трёхфазной сети обозначают дробью, в знаменателе которой стоит линейное напряжение, а в числителе — фазное при соединении в звезду (или, что то же самое, потенциал каждой из линий относительно земли). Так, в России наиболее распространены сети с напряжением 220/380 В; также иногда используются сети 127/220 В и 380/660 В.

Стандарты

Объект	Тип напряжения	Значение (на вводе потребителя)	Значение (на выходе источника)
Электрокардиограмма	Импульсное	1-2 мВ	—
Телевизионная антенна	Переменное высокочастотное	1-100 мВ	—
Батарейка AA («пальчиковая»)	Постоянное	1,5 В	—
Литиевая батарейка	Постоянное	3 В — 1,8 В (в исполнении пальчиковой батарейки , на примере Varta Professional Lithium, AA)	—
Управляющие сигналы компьютерных компонентов	Импульсное	3,5 В, 5 В	—
Батарейка типа 6F22 («Крона»)	Постоянное	9 В	—
Силовое питание компьютерных компонентов	Постоянное	12 В	—
Электрооборудование автомобиля	Постоянное	12/24 В	—
Блок питания ноутбука и жидкокристаллических мониторов	Постоянное	19 В	—
Сеть «безопасного» пониженного напряжения для работы в опасных условиях	Переменное	36-42 В	—
Напряжение наиболее стабильного горения свечи Яблочкова	Постоянное	55 В	—
Напряжение в телефонной линии (при опущенной трубке)	Постоянное	60 В	—
Напряжение в электросети Японии	Переменное трёхфазное	100/172 В	—
Напряжение в домашних электросетях США	Переменное трёхфазное	120 В / 240 В (сплит-фаза)	—
Напряжение в электросети России	Переменное трёхфазное	220/380 В	230/400 В
Разряд электрического ската	Постоянное	до 200—250 В	—
Контактная сеть трамвая и троллейбуса	Постоянное	550 В	600 В
Разряд электрического угря	Постоянное	до 650 В	—
Контактная сеть метрополитена	Постоянное	750 В	825 В
Контактная сеть электрифицированной железной дороги (Россия, постоянный ток)	Постоянное	3 кВ	3,3 кВ
Распределительная воздушная линия электропередачи небольшой мощности	Переменное трёхфазное	6-20 кВ	6,6-22 кВ
Генераторы электростанций, мощные электродвигатели	Переменное трёхфазное	10-35 кВ	—
Анод кинескопа	Постоянное	7-30 кВ	—
Статическое электричество	Постоянное	1-100 кВ	—
Свеча зажигания автомобиля	Импульсное	10-25 кВ	—
Контактная сеть электрифицированной железной дороги (Россия, переменный ток)	Переменное	25 кВ	27,5 кВ
Пробой воздуха на расстоянии 1 см		10-20 кВ	—
Катушка Румкорфа	Импульсное	до 50 кВ	—
Пробой трансформаторного масла на расстоянии 1 см		100-200 кВ	—
Воздушная линия электропередачи большой мощности	Переменное трёхфазное	35 кВ, 110 кВ, 220 кВ, 330 кВ	38 кВ, 120 кВ, 240 кВ, 360 кВ
Электрофорная машина	Постоянное	50-500 кВ	—
Воздушная линия электропередачи сверхвысокого напряжения (межсистемные)	Переменное трёхфазное	500 кВ, 750 кВ, 1150 кВ	545 кВ, 800 кВ, 1250 кВ
Трансформатор Тесла	Импульсное высокочастотное	до нескольких МВ	—
Генератор Ван де Граафа	Постоянное	до 7 МВ	—
Грозовое облако	Постоянное	От 2 до 10 ГВ	—

См. также

Ссылки

определение, формула, единицы измерения :: SYL.ru

Степень изменения формы тела при деформации зависит не только от природы вещества, но и такой физической величиной, как механическое напряжение. Если рассматривать атомную кристаллическую решетку такого вещества, можно отметить постоянное взаимодействие молекул друг с другом. Это состояние напрямую влияет на величину механического напряжения.

Что такое деформация? Виды деформации

Явление, при котором происходит изменение формы тела под действием какой-либо внешней силы, называется деформацией. Ее природа заключается в движении молекул вещества или целых слоев кристаллической решетки, что приводит к возникновению так называемых дефектов. Степень деформирования зависит от многих факторов, среди которых мы рассмотрим механическое напряжение.

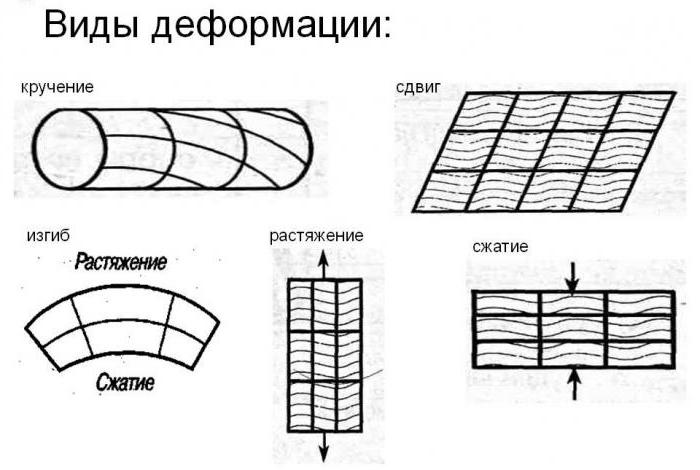
Выделяют несколько видов изменения формы тела:

1. Деформация растяжения, когда внешняя сила воздействует вдоль всего тела. Имеет прикладное значение при изготовлении веревок, тросов и строительных материалов;
2. Деформация сжатия. В этом случае вектор действия внешней силы совпадает с продольной осью тела, однако он направлен в сторону центра этого тела. Применяется этот вид деформирования при изготовлении металла и строительных материалов для придания им прочности;
3. Деформация сдвига возникает под действием внешней силы, которая направлена перпендикулярно продольной оси и вызывает движение различных плоскостей тела относительно друг друга;
4. Деформация изгиба характеризуется искривлением главной оси тела, например, когда имеется две точки опоры. Сила, которую может выдержать тот или иной предмет, а также механическое напряжение играют большую роль при создании строительных материалов;
5. Деформация кручения возникает при повороте тела вокруг его продольной оси. Этот вид деформации можно наглядно продемонстрировать на пружинке, которая после прекращения воздействия внешней силы восстановит свою форму.

Упругая и пластическая деформация

Механическое напряжение, которое зависит от природы вещества, влияет на способность тела восстанавливать свою первоначальную форму после возникновения дефекта в кристаллической решетке. По этому признаку выделяют упругую и пластическую деформацию.

При пластической деформации тело после воздействия внешней силы не способно восстановить прежнюю форму. Например, пластилин при надавливании на него пальцем сохраняет образовавшуюся ямку.

Упругая деформация характерна для тех веществ, которые способны восстанавливать свою первоначальную форму после воздействия на них внешней силы. Примером может служить та же пружина, которая при любом описанном выше виде деформации возвращается в первоначальное состояние.

Механическое напряжение: формула и определение

Величина механического напряжения характеризуется внутренними силами молекул, которые направлены против давления и деформации тела, на единицу площади.

Различают два вида напряжения:

1. Нормальное напряжение приложено на единицу площади сечения, параллельного главной оси тела.
2. Касательное механическое напряжение приложено на единицу площади сечения любой другой плоскости сечения.

Для математического вычисления механического напряжения используется формула: Q=F/S.

Единицы механического напряжения

Величина Q в СИ измеряется в паскалях (Па) и зависит от внутренней силы сопротивления деформации, а также площади тела. Сейчас можно встретить и другие единицы измерения механического напряжения. Среди них атмосфера, торр, бар, физическая и техническая атмосфера, метр водяного столба, миллиметр (дюйм) ртутного столба, фунт-сила на квадратный дюйм и т. д.

СГС — Википедия

СГС (сантиметр-грамм-секунда) — система единиц измерения, которая широко использовалась до принятия Международной системы единиц (СИ). Другое название — абсолютная физическая система единиц^{[К 1]}.

В рамках СГС существуют три независимые размерности — длина (сантиметр), масса (грамм) и время (секунда) — все остальные сводятся к ним путём умножения, деления и возведения в степень (возможно, дробную). Кроме трёх основных единиц измерения, в СГС существует ряд дополнительных единиц измерения, которые являются производными от основных. Некоторые физические константы получаются безразмерными. Есть несколько вариантов СГС, отличающихся выбором электрических и магнитных единиц измерения и величиной констант в различных законах электромагнетизма (СГСЭ, СГСМ, Гауссова система единиц).

СГС отличается от СИ не только выбором конкретных единиц измерения. Из-за того, что в СИ были дополнительно введены основные единицы для электромагнитных физических величин, которых не было в СГС, некоторые единицы имеют другие размерности. Из-за этого некоторые физические законы в этих системах записываются по-разному (например, закон Кулона). Отличие заключается в коэффициентах, большинство из которых — размерные. Поэтому, если в формулы, записанные в СГС, просто подставить единицы измерения СИ, то будут получены неправильные результаты. Это же относится и к разным разновидностям СГС — в СГСЭ, СГСМ и Гауссовой системе единиц одни и те же формулы могут записываться по-разному.

В формулах СГС отсутствуют нефизические коэффициенты, необходимые в СИ (например, электрическая постоянная в законе Кулона), и, в Гауссовой разновидности, все четыре вектора электрических и магнитных полей E, D, B и H имеют одинаковые размерности, в соответствии с их физическим смыслом, поэтому СГС считается более удобной для теоретических исследований^{[К 2]}.

В научных работах, как правило, выбор той или иной системы определяется более преемственностью обозначений и прозрачностью физического смысла, чем удобством измерений.

Для облегчения работы в СГС в электродинамике были приняты дополнительно системы СГСЭ (абсолютная электростатическая система) и СГСМ (абсолютная электромагнитная система), а также гауссова. В каждой из этих систем электромагнитные законы записываются по-разному (с разными коэффициентами пропорциональности).

Закон Кулона: F=kCq⋅q′d2{\displaystyle F=k_{\rm {C}}{\frac {q\cdot q’}{d^{2}}}}

Сила Ампера: dFdL=2kAII′d{\displaystyle {\frac {dF}{dL}}=2k_{\rm {A}}{\frac {I\,I’}{d}}}

При этом обязательно^[4]kA=kCc2{\displaystyle k_{\mathrm {A} }={\frac {k_{\mathrm {C} }}{c^{2}}}}

Сила Лоренца: F=αLqv×B{\displaystyle \mathbf {F} =\alpha _{\rm {L}}q\;\mathbf {v} \times \mathbf {B} }

Вектор магнитной индукции: dB=αBIdl×r^r2{\displaystyle d\mathbf {B} =\alpha _{\rm {B}}{\frac {Id\mathbf {l} \times \mathbf {\hat {r}} }{r^{2}}}}

При этом обязательно^[4]αLαB=kA{\displaystyle \alpha _{\mathrm {L} }\alpha _{\mathrm {B} }=k_{\mathrm {A} }}

Закон Фарадея: E=−αLdΦBdt{\displaystyle {\mathcal {E}}=-\alpha _{\mathrm {L} }{{d\Phi _{B}} \over dt}}

Уравнения Максвелла^[4]:

∇→⋅E→=4πkCρ∇→⋅B→=0∇→×E→=−αL∂B→∂t∇→×B→=4παBj→+αBkC∂E→∂t{\displaystyle {\begin{array}{ccl}{\vec {\nabla }}\cdot {\vec {E}}&=&4\pi k_{\rm {C}}\rho \\{\vec {\nabla }}\cdot {\vec {B}}&=&0\\{\vec {\nabla }}\times {\vec {E}}&=&\displaystyle {-\alpha _{\rm {L}}{\frac {\partial {\vec {B}}}{\partial t}}}\\{\vec {\nabla }}\times {\vec {B}}&=&\displaystyle {4\pi \alpha _{\rm {B}}{\vec {j}}+{\frac {\alpha _{\rm {B}}}{k_{\rm {C}}}}{\frac {\partial {\vec {E}}}{\partial t}}}\end{array}}}

В среде:

D=ϵ0E+λP{\displaystyle \mathbf {D} =\epsilon _{0}\mathbf {E} +\lambda \mathbf {P} }

H=B/μ0−λ′M{\displaystyle \mathbf {H} =\mathbf {B} /\mu _{0}-\lambda ‘\mathbf {M} }

∇⋅P=4πϵ0kCλρb{\displaystyle \nabla \cdot \mathbf {P} ={\frac {4\pi \epsilon _{0}k_{\mathrm {C} }}{\lambda }}\rho _{b}}

∇×M=4παBλ′μ0jb−λαBλ′μ0ϵ0kC∂P∂t{\displaystyle \nabla \times \mathbf {M} ={\frac {4\pi \alpha _{\mathrm {B} }}{\lambda ‘\mu _{0}}}\mathbf {j} _{b}-{\frac {\lambda \alpha _{\mathrm {B} }}{\lambda ‘\mu _{0}\epsilon _{0}k_{\mathrm {C} }}}{\frac {\partial \mathbf {P} }{\partial t}}}

При этом λ{\displaystyle \lambda } и λ′{\displaystyle \lambda ‘} обычно выбираются равными 4πkCϵ0{\displaystyle 4\pi k_{\mathrm {C} }\epsilon _{0}}

∇→⋅D→=4πϵ0kCρf∇→⋅B→=0∇→×E→=−αL∂B→∂t∇→×H→=4παBμ0j→f+αBμ0ϵ0kC∂D→∂t{\displaystyle {\begin{array}{ccl}{\vec {\nabla }}\cdot {\vec {D}}&=&4\pi \epsilon _{0}k_{\rm {C}}\rho _{f}\\{\vec {\nabla }}\cdot {\vec {B}}&=&0\\{\vec {\nabla }}\times {\vec {E}}&=&\displaystyle {-\alpha _{\rm {L}}{\frac {\partial {\vec {B}}}{\partial t}}}\\{\vec {\nabla }}\times {\vec {H}}&=&\displaystyle {{\frac {4\pi \alpha _{\rm {B}}}{\mu _{0}}}{\vec {j}}_{f}+{\frac {\alpha _{\rm {B}}}{\mu _{0}\epsilon _{0}k_{\mathrm {C} }}}{\frac {\partial {\vec {D}}}{\partial t}}}\end{array}}}

СГСМ[править | править код]

В СГСМ магнитная постоянная µ₀ безразмерна и равна 1, а электрическая постоянная ε₀ = 1/с² (размерность: с²/см²). В этой системе нефизические коэффициенты отсутствуют в формуле закона Ампера для силы, действующей на единицу длины l каждого из двух бесконечно длинных параллельных прямолинейных токов в вакууме: F = 2I₁I₂l/d, где d — расстояние между токами. В результате единица силы тока должна быть выбрана как квадратный корень из единицы силы (дина^1/2). Из выбранной таким образом единицы силы тока (иногда называемой абампером, размерность: см^1/2г^1/2с⁻¹) выводятся определения производных единиц (заряда, напряжения, сопротивления и т. п.).

Все величины этой системы отличаются от единиц СИ в 10 в целой степени раз, за исключением напряженности магнитного поля: 1 А/м = 4π 10^-3Э

СГСЭ[править | править код]

В СГСЭ электрическая постоянная ε₀ безразмерна и равна 1, магнитная постоянная µ₀ = 1/с² (размерность: с²/см²), где c — скорость света в вакууме, фундаментальная физическая постоянная. В этой системе закон Кулона в вакууме записывается без дополнительных коэффициентов: F = Q₁Q₂/r², в результате единица заряда должна быть выбрана как квадратный корень из единицы силы (дина^1/2), умноженный на единицу расстояния (сантиметр). Из выбранной таким образом единицы заряда (называемой статкулоном, размерность: см^3/2г^1/2с⁻¹) выводятся определения производных единиц (напряжения, силы тока, сопротивления и т. п.).

Все величины этой системы отличаются от единиц СГСМ в c в целой степени раз.

СГС симметричная, или Гауссова система единиц[править | править код]

В симметричной СГС (называемой также смешанной СГС или Гауссовой системой единиц) магнитные единицы (магнитная индукция, магнитный поток, магнитный дипольный момент, напряженность магнитного поля) равны единицам системы СГСМ, электрические (включая индуктивность) — единицам системы СГСЭ. Магнитная и электрическая постоянные в этой системе единичные и безразмерные: µ₀ = 1, ε₀ = 1.

А также в этой системе (помимо уравнений Максвелла) изменяются уравнения, описывающие катушку индуктивности и трансформатор:

U=Φ˙c;Φ=LIc{\displaystyle U={\frac {\dot {\Phi }}{c}};\,\,\,\,\,\,\,\Phi =L{\frac {I}{c}}}

Электромагнитные величины в различных системах СГС[править | править код]

Основной источник: ^[6]

Приведённые ниже множители для преобразования единиц основываются на точных значениях электрической и магнитной постоянных в СИ, действовавших до изменений СИ 2018—2019 годов. В редакции СИ, действующей с 2019 года, электрическая и магнитная постоянная практически сохранили своё численное значение, но стали экспериментально определяемыми величинами, известными с определённой погрешностью (в девятом знаке после запятой). Вместе с электрической и магнитной постоянными погрешность приобрели и множители для преобразования единиц между СИ и вариантами СГС^[7].

Понимать это следует так: 1 A = (10⁻¹) абА, и т. д.

Система мер, основанная на сантиметре, грамме и секунде, была предложена немецким ученым Гауссом в 1832. В 1874 Максвелл и Томсон усовершенствовали систему, добавив в неё электромагнитные единицы измерения.

Величины многих единиц системы СГС были признаны неудобными для практического использования, и вскоре она была заменена системой, основанной на метре, килограмме и секунде (МКС). СГС продолжали использовать параллельно с МКС, в основном в научных исследованиях.

После принятия в 1960 системы СИ СГС почти вышла из употребления в инженерных приложениях, однако продолжает широко использоваться, например, в теоретической физике и астрофизике из-за более простого вида законов электромагнетизма.

Из трёх дополнительных систем наибольшее распространение получила система СГС симметричная.

• Абсолютные системы единиц // Большая Советская энциклопедия (в 30 т.) / А. М. Прохоров (гл. ред.). — 3-е изд. — М.: Сов. энциклопедия, 1969(70). — Т. I. — С. 35. — 608 с.

Комментарии

1. ↑ В настоящее время термин «абсолютная» в качестве характеристики систем единиц не употребляется и считается устаревшим^[1][2].
2. ↑ По мнению Д. В. Сивухина «в этом отношении система СИ не более логична, чем, скажем, система, в которой длина, ширина и высота предмета измеряются не только различными единицами, но и имеют разные размерности»^[3].

Источники

1. ↑ Чертов А. Г. Единицы физических величин. — М.: «Высшая школа», 1977. — С. 19. — 287 с.
2. ↑ Деньгуб В. М., Смирнов В. Г. Единицы величин. Словарь-справочник. — М.: Издательство стандартов, 1990. — С. 19. — 240 с. — ISBN 5-7050-0118-5.
3. ↑ Сивухин Д. В. О международной системе физических величин (рус.) // Успехи физических наук. — М.:: Наука, 1979. — Т. 129, № 2. — С. 335—338.
4. ↑ ^{1 2 3 4 5 6 7 8} Jackson, John David. Classical Electrodynamics (неопр.). — 3rd. — New York: Wiley, 1999. — С. 775—784. — ISBN 0-471-30932-X.
5. ↑ После изменений СИ 2018—2019 года это не точное, а приближённое значение.
6. ↑ ^{1 2} Cardarelli, F. Encyclopaedia of Scientific Units, Weights and Measures: Their SI Equivalences and Origins (англ.). — 2nd. — Springer, 2004. — P. 20—25. — ISBN 1-85233-682-X.
7. ↑ Ronald B. Goldfarb. Electromagnetic Units, the Giorgi System, and the Revised International System of Units // IEEE Magnetics Letters. — 2018. — Vol. 9. — P. 1—5. — DOI:10.1109/LMAG.2018.2868654.

Напряжённость магнитного поля — Википедия

Материал из Википедии — свободной энциклопедии

Напряжённость магни́тного по́ля — векторная физическая величина, равная разности вектора магнитной индукции B и вектора намагниченности M. Обычно обозначается символом Н.

В Международной системе единиц (СИ):

H=1μ0B−M,{\displaystyle \mathbf {H} ={\frac {1}{\mu _{0}}}\mathbf {B} -\mathbf {M} ,}

где μ0{\displaystyle \mu _{0}} — магнитная постоянная.

В системе СГС:

H=B−4πM.{\displaystyle \mathbf {H} =\mathbf {B} -4\pi \mathbf {M} .}

В простейшем случае изотропной (по магнитным свойствам) среды и в приближении достаточно низких частот, намагниченность M зависит линейно от приложенного магнитного поля с индукцией B:

M=αB.{\displaystyle \mathbf {M} =\alpha \mathbf {B} .}

Однако исторически принято эту линейную зависимость описывать не коэффициентом α{\displaystyle \alpha }, а использовать связанные величины — магнитную восприимчивость χ{\displaystyle \chi } или магнитную проницаемость μ{\displaystyle \mu }:

M=χ1+4πχB=μ−14πμB.{\displaystyle \mathbf {M} ={\frac {\chi }{1+4\pi \chi }}\mathbf {B} ={\frac {\mu -1}{4\pi \mu }}\mathbf {B} .}

В системе СГС напряжённость магнитного поля измеряется в эрстедах (Э), в системе СИ — в амперах на метр (А/м). В технике эрстед постепенно вытесняется единицей СИ — ампером на метр.

1 Э = 1000/(4π) А/м ≈ 79,5775 А/м.

1 А/м = 4π/1000 Э ≈ 0,01256637 Э.

В вакууме (или в отсутствие среды, способной к магнитной поляризации, а также в случаях, когда последняя пренебрежима) напряжённость магнитного поля (Н) совпадает с вектором магнитной индукции (B) с точностью до коэффициента, равного 1 в СГС и μ0{\displaystyle \mu _{0}} в СИ.

В магнетиках (магнитных средах) напряжённость магнитного поля имеет физический смысл «внешнего» поля, то есть совпадает (быть может, в зависимости от принятых единиц измерения, с точностью до постоянного коэффициента, как, например, в системе СИ, что общего смысла не меняет) с таким вектором магнитной индукции, какой «был бы, если магнетика не было».

Например, если поле создаётся катушкой с током, в которую вставлен железный сердечник, то напряжённость магнитного поля H внутри сердечника совпадает (в СГС точно, а в СИ — с точностью до постоянного размерного коэффициента) с вектором магнитной индукции B₀ поля, которое было бы создано этой катушкой при отсутствии сердечника. B₀ в принципе может быть рассчитан исходя из геометрии катушки и тока в ней, без всякой дополнительной информации о материале сердечника и его магнитных свойствах.

При этом надо иметь в виду, что более фундаментальной характеристикой магнитного поля является вектор магнитной индукции B. Именно он определяет силу действия магнитного поля на движущиеся заряженные частицы и токи, а также может быть непосредственно измерен, в то время как напряжённость магнитного поля H можно рассматривать скорее как вспомогательную величину (хотя рассчитать её, по крайней мере, в статическом случае, проще, в чём состоит её ценность: ведь H создает так называемые свободные токи, которые сравнительно легко непосредственно измерить, а трудно измеримые связанные токи — то есть токи молекулярные и т. п. — учитывать не надо).

Правда, в обычно используемое выражение для энергии магнитного поля (в среде) B и H входят почти равноправно, но надо иметь в виду, что в эту энергию включена и энергия, затраченная на поляризацию среды, а не только энергия собственно поля^[1]. Энергия магнитного поля как такового выражается только через фундаментальную величину B. Тем не менее видно, что величина H феноменологическая и тут весьма удобна.

1. ↑ Для иллюстрации раскроем выражение для плотности энергии поля в среде wsubst{\displaystyle w_{subst}} в случае линейной связи намагниченности от напряженности магнитного поля M=χH.{\displaystyle \mathbf {M} =\chi \mathbf {H} .} В системе СИwsubst=12H⋅B=12(1μ0B−M)⋅B=12μ0B2−12M⋅B,{\displaystyle w_{subst}={\frac {1}{2}}\mathbf {H} \cdot \mathbf {B} ={\frac {1}{2}}({\frac {1}{\mu _{0}}}\mathbf {B} -\mathbf {M} )\cdot \mathbf {B} ={\frac {1}{2\mu _{0}}}\mathbf {B} ^{2}-{\frac {1}{2}}\mathbf {M} \cdot \mathbf {B} ,}где первый член — энергия магнитного поля, второй — энергия взаимодействия поля со средой (например, с магнитными диполями парамагнетика).

• Иродов И. Е. Основные законы электромагнетизма. — 2-е, стереотипное. — Москва: Высшая школа, 1991.

Механическое напряжение — это… Что такое Механическое напряжение?

У этого термина существуют и другие значения, см. Напряжение.

Механическое напряжение — это мера внутренних сил, возникающих в деформируемом теле под влиянием различных факторов. Механическое напряжение в точке тела определяется как отношение внутренней силы к единице площади в данной точке рассматриваемого сечения.

Напряжения являются результатом взаимодействия частиц тела при его нагружении. Внешние силы стремятся изменить взаимное расположение частиц, а возникающие при этом напряжения препятствуют смещению частиц, ограничивая его в большинстве случаев некоторой малой величиной.

Q — механическое напряжение.

F — сила, возникшая в теле при деформации.

S — площадь.

Различают две составляющие вектора механического напряжения:

• Нормальное механическое напряжение — приложено на единичную площадку сечения, по нормали к сечению (обозначается ).
• Касательное механическое напряжение — приложено на единичную площадку сечения, в плоскости сечения по касательной (обозначается ).

Совокупность напряжений, действующих по различным площадкам, проведенным через данную точку, называется напряженным состоянием в точке.

В системе СИ механическое напряжение измеряется в паскалях.

Тензор механического напряжения

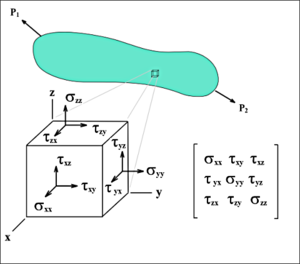Полный тензор механического напряжения элементарного объёма тела. Буквой σ обозначены нормальные механические напряжения, а касательные буквой τ.

Более строго механическое напряжение — тензорная величина. Компоненты тензора напряжений равны отношению компоненты силы , действующей на элементарную площадку к её площади:

Здесь под понимаются компоненты вектора, образованного из нормали к элементарной площадке и её площади :

Таким образом сила, действующая на некий объём V равна интегралу тензора напряжения на границе этого объёма по поверхности этого объёма (в отсутствие объёмных сил):

См. также