Двоичный код. Виды и длина двоичного кода. Обратный двоичный код

Двоичный код представляет собой форму записи информации в виде единиц и нулей. Такая система исчисления является позиционной с основанием 2. На сегодняшний день двоичный код (таблица, представленная немного ниже, содержит некоторые примеры записи чисел) используется во всех без исключения цифровых устройствах. Его популярность объясняется высокой надежность и простотой данной формы записи. Двоичная арифметика весьма проста, соответственно, ее легко реализовать и на аппаратном уровне. Цифровые электронные компоненты (или как их еще называют – логические) весьма надежны, так как они оперируют в работе всего двумя состояниями: логической единицы (есть ток) и логического нуля (нет тока). Тем самым они выгодно отличаются от аналоговых компонентов, работа которых основана на переходных процессах.

Как составляется двоичная форма записи?

Давайте разберемся, каким образом формируется такой ключ. Один разряд двоичного кода может содержать всего два состояния: ноль и единицу (0 и 1). При использовании двух разрядов появляется возможность записать четыре значения: 00, 01, 10, 11. Трехразрядная запись содержит восемь состояний: 000, 001 … 110, 111. В результате получаем, что длина двоичного кода зависит от числа разрядов. Это выражение можно записать с помощью следующей формулы: N =2m, где: m – это количество разрядов, а N – число комбинаций.

Виды двоичных кодов

В микропроцессорах такие ключи применяются для записи разнообразной обрабатываемой информации. Разрядность двоичного кода может существенно превышать разрядность процессора и его встроенной памяти. В таких случаях длинные числа занимают несколько ячеек запоминающего устройства и обрабатываются с помощью нескольких команд. При этом все сектора памяти, которые выделены под многобайтный двоичный код, рассматриваются в качестве одного числа.

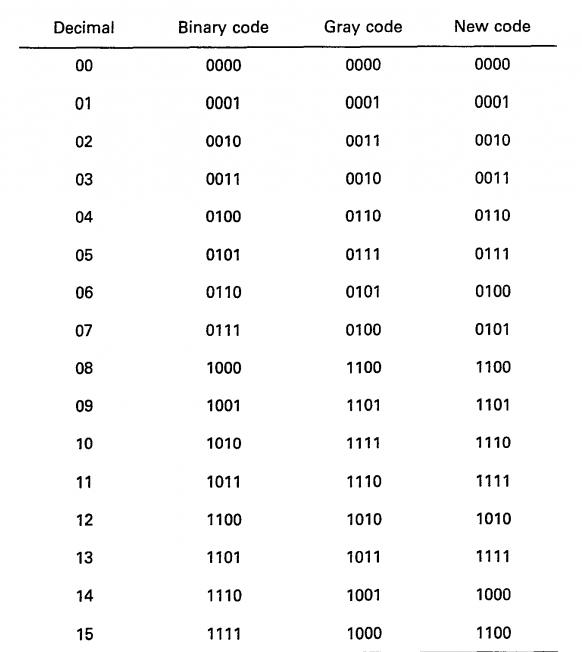В зависимости от необходимости предоставления той или иной информации, различают следующие виды ключей:

• беззнаковые;
• прямые целыезнаковые коды;
• знаковые обратные;
• знаковые дополнительные;
• код Грея;
• код Грея-Экспресс.;
• дробные коды.

Рассмотрим более детально каждый из них.

Беззнаковый двоичный код

Давайте разберемся, что же представляет собой такой вид записи. В целых беззнаковых кодах каждый разряд (двоичный) представляет степень цифры два. При этом наименьшее число, которое можно записать в такой форме, равно нулю, а максимальное можно представить следующей формулой: М=2^п-1. Эти два числа полностью определяют диапазон ключа, которым можно выразить такой двоичный код. Давайте рассмотрим возможности упомянутой формы записи. При использовании данного вида беззнакового ключа, состоящего из восьми разрядов, диапазон возможных чисел составит от 0 до 255. Шестнадцатиразрядный код будет иметь диапазон от 0 до 65535. В восьмиразрядных процессорах для хранения и записи таких чисел используют два сектора памяти, которые располагаются в соседних адресатах. Работу с такими ключами обеспечивают специальные команды.

Прямые целые знаковые коды

В данном виде двоичных ключей старший разряд используется для записи знака числа. Нуль соответствует плюсу, а единица — минусу. В результате введения данного разряда диапазон закодированных чисел смещается в отрицательную сторону. Получается, что восьмиразрядный знаковый целый двоичный ключ может записать числа в диапазоне от -127 до +127. Шестнадцатиразрядный – в диапазоне от -32767 до +32767. В восьмиразрядных микропроцессорах для хранения подобных кодов используют два соседних сектора.

Недостатком такой формы записи является то, что знаковые и цифровые разряды ключа необходимо обрабатывать раздельно. Алгоритмы программ, работающих с этими кодами, получаются очень сложными. Для изменения и выделения знаковых разрядов необходимо применять механизмы маскировки этого символа, что способствует резкому увеличению размеров программного обеспечения и уменьшению его быстродействия. С целью устранения данного недостатка был введен новый вид ключа – обратный двоичный код.

Знаковый обратный ключ

Данная форма записи отличается от прямых кодов только тем, что отрицательное число в ней получается путем инвертирования всех разрядов ключа. При этом цифровые и знаковые разряды идентичны. Благодаря этому, алгоритмы работы с таким видом кодов существенно упрощаются. Однако обратный ключ требует специальный алгоритм для распознавания символа первого разряда, вычисления абсолютной величины числа. А также восстановления знака результирующего значения. Более того, в обратном и прямом кодах числа для записи нуля используют два ключа. Несмотря на то что это значение не имеет положительного или отрицательного знака.

Знаковый дополнительный код двоичного числа

Данный вид записи не имеет перечисленных недостатков предыдущих ключей. Такие коды позволяют проводить непосредственное суммирование как положительных, так и отрицательных чисел. При этом не проводится анализ знакового разряда. Все это стало возможным благодаря тому факту, что дополнительные числа представляют собой естественное кольцо символов, а не искусственные образования, такие как прямые и обратные ключи. Более того, важным фактором является, то что произвести вычисления дополнений в двоичных кодах чрезвычайно просто. Для этого достаточно к обратному ключу добавить единицу. При использовании данного вида знакового кода, состоящего из восьми разрядов, диапазон возможных чисел составит от -128 до +127. Шестнадцатиразрядный ключ будет иметь диапазон от -32768 до +32767. В восьмиразрядных процессорах для хранения таких чисел также используют два соседних сектора.

Двоичный дополнительный код интересен наблюдаемым эффектом, который называют явлением распространения знака. Давайте разберемся, что это значит. Данный эффект заключается в том, что в процессе преобразования однобайтового значения в двухбайтовое достаточно каждому биту старшего байта назначить значения знаковых битов младшего байта. Получается, что для хранения знакового символа числа можно воспользоваться старшими битами. При этом значение ключа совершенно не изменяется.

Код Грея

Данная форма записи, по сути, является одношаговым ключом. То есть в процессе перехода от одного значения к другому меняется всего лишь один бит информации. При этом погрешность при считывании данных приводит к переходу от одного положения к другому с незначительным смещением по времени. Однако получение совершенно неверного результата углового положения при таком процессе полностью исключается. Достоинством такого кода является его способность зеркально отображать информацию. Например, инвертируя старшие биты, можно просто менять направление отсчета. Это происходит благодаря управляющему входу Complement. При этом выдаваемое значение может быть как возрастающим, так и спадающим при одном физическом направлении вращения оси. Так как информация, записанная в ключе Грея, имеет исключительно кодированный характер, который не несет реальных числовых данных, то перед дальнейшей работой требуется предварительно преобразовать его в обычную бинарную форму записи. Осуществляется это с помощью специального преобразователя – декодера Грей-Бинар. Данное устройство легко реализуется на элементарных логических элементах как аппаратным, так и программным способом.

Код Грея-Экспресс

Стандартный одношаговый ключ Грей подходит для решений, которые представлены в виде чисел, возведенных в степень два. В случаях, где необходимо реализовывать иные решения, из такой формы записи вырезают и используют только средний участок. В результате сохраняется одношаговость ключа. Однако в таком коде началом числового диапазона не является нуль. Он смещается на заданное значение. В процессе обработки данных от генерируемых импульсов отнимают половину разницы между начальным и редуцированным разрешением.

Представление дробного числа в двоичном ключе с фиксированной запятой

В процессе работы приходится оперировать не только целыми цифрами, но и дробными. Такие числа можно записывать с помощью прямых, обратных и дополнительных кодов. Принцип построения упомянутых ключей такой же, как и у целых. До сих пор мы считали, что двоичная запятая должна находиться справа от младшего разряда. Но это не так. Она может располагаться и слева от старшего разряда (в таком случае в качестве переменной можно записывать исключительно дробные числа), и посередине переменной (можно записывать смешанные значения).

Представление двоичного кода с плавающей запятой

Такая форма применяется для записи больших чисел, либо наоборот — очень малых. В качестве примера можно привести межзвездные расстояния или размеры атомов и электронов. При вычислении таких значений пришлось бы применять двоичный код с очень большой разрядностью. Однако нам нет необходимости учитывать космические расстояние с точностью до миллиметра. Поэтому форма записи с фиксированной запятой в данном случае неэффективна. Для отображения таких кодов используется алгебраическая форма. То есть число записывается как мантисса, умноженная на десять в степени, отображающей нужный порядок числа. Следует знать, что мантисса не должна быть больше единицы, а после запятой не должен записываться ноль.

Это интересно

Считается, что двоичное исчисление было изобретено в начале 18-го века математиком из Германии Готфридом Лейбницем. Однако, как недавно открыли ученые, задолго до этого аборигены полинезийского острова Мангареву использовали данный вид арифметики. Несмотря на то что колонизация практически полностью уничтожила оригинальные системы исчисления, ученые восстановили сложные двоичные и десятичные виды счета. Кроме того, ученый Когнитивист Нуньес утверждает, что кодирование двоичным кодом применялось в древнем Китае еще в 9-м веке до н. э. Другие древние цивилизации, например, индейцы майя, также использовали сложные комбинации десятичных и бинарных систем для отслеживания временных интервалов и астрономических явлений.

Двоичный код — это… Что такое Двоичный код?

Слово «Wikipedia» закодированное двоичным ASCII-кодом.

Двоичный код — это способ представления данных в одном разряде в виде комбинации двух знаков, обычно обозначаемых цифрами 0 и 1. Разряд в этом случае называется двоичным разрядом.
В случае обозначения цифрами «0» и «1», возможные состояния двоичного разряда наделяются качественным соотношением «1» > «0» и количественными значениями чисел «0» и «1».

Двоичный код может быть непозиционным и позиционным.

Из комбинаторики известно, что, в случае непозиционного кода, количество комбинаций (кодов) n-разрядного кода является числом сочетаний с повторениями, равно биномиальному коэффициенту:

, [возможных состояний (кодов)], где:

— количество элементов в данном множестве различных элементов (количество возможных состояний, цифр, кодов в разряде),
— количество элементов в наборе (количество разрядов).
В двоичной системе кодирования (n=2) количество

возможных состояний (кодов) равно :

, [возможных состояний (кодов)], т.е.

описывается линейной функцией:

, [возможных состояний (кодов)], где

— количество двоичных разрядов (дворов, битов).
Например, в одном 8-ми битном байте (k=8) количество возможных состояний (кодов) равно:

, [возможных состояний (кодов)].

В случае позиционного кода, число комбинаций (кодов) n-разрядного двоичного кода равно числу размещений с повторениями:

, где

 — число разрядов двоичного кода.

Используя два двоичных разряда можно закодировать четыре различные комбинации: 00 01 10 11, три двоичных разряда — восемь: 000 001 010 011 100 101 110 111, и так далее.

При увеличении разрядности позиционного двоичного кода на 1, количество различных комбинаций в позиционном двоичном коде удваивается.

Двоичные коды являются комбинациями двух элементов и не являются двоичной системой счисления, но используются в ней как основа. Двоичный код также может использоваться для кодирования чисел в системах счисления с любым другим основанием. Пример: в двоично-десятичном кодировании (BCD) используется двоичный код для кодирования чисел в десятичной системе счисления.
При кодировании алфавитноцифровых символов (знаков) двоичному коду не приписываются весовые коэффициенты, как это делается в системах счисления, в которых двоичный код используется для представления чисел, а используется только порядковый номер кода из множества размещений с повторениями.

В системах счисления n-разрядный двоичный код, (n-1)-разрядный двоичный код, (n-2)-разрядный двоичный код и т. д. могут отображать одно и то же число. Например, 0001, 001, 01, 1 — одно и то же число — «1» в двоичных кодах с разным числом разрядов — n.

В этом разделе не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. Вы можете отредактировать эту статью, добавив ссылки на авторитетные источники. Эта отметка установлена 12 мая 2011.

Таблица двоичных кодов

числовое (буквенное) значение	двоичный код
0	0000
1	0001
2	0010
3	0011
4	0100
5	0101
6	0110
7	0111
8	1000
9	1001
A	1010
B	1011
C	1100
D	1101
E	1110
F	1111

Пример «доисторического» использования кодов

Инки имели свою счётную систему кипу, которая физически представляла собой верёвочные сплетения и узелки. Генри Эртан обнаружил, что в узелках заложен некий код, более всего похожий на двоичную систему счисления.^[1]

Примечания

См. также

Лекция на тему «Машинные коды двоичного числа»

Машинные коды двоичного числа

В ЭВМ в целях упрощения выполнения арифметических операций применяют специальные коды для представления чисел. При помощи этих кодов упрощается определение знака результата операции. Операция вычитания (или алгебраического сложения) чисел сводится к арифметическому сложению кодов, облегчается выработка признаков переполнения разрядной сетки. В результате упрощаются устройства ЭВМ, выполняющие арифметические операции.

Для представления чисел со знаком в ЭВМ применяют прямой, обратный и дополнительный коды.

Общая идея построения кодов такова. Код трактуется как число без знака, а диапазон представляемых кодами чисел без знака разбивается на два поддиапазона. Один из них представляет положительные числа, другой – отрицательные. Разбиение выполняется таким образом, чтобы принадлежность к поддиапазону определялась максимально просто.

Наиболее распространенным и удобным является формирование кодов таким образом, чтобы значение старшего разряда указывало на знак представляемых чисел, т.е. использование такого кодирования позволяет говорить о старшем разряде как о знаковом (бит знака) и об остальных как о цифровых разрядах кода.

Прямой код

Прямой код – это представление числа в двоичной системе счисления, при котором первый (старший) разряд отводится под знак числа. Если число положительное, то в левый разряд записывается 0; если число отрицательное, то в левый разряд записывается 1.

Таким образом, в двоичной системе счисления, используя прямой код, в восьмиразрядной ячейке (байте) можно записать семиразрядное число. Например:

        0 0001101–положительное число                                                   1 0001101 – отрицательное число

Количество значений, которые можно поместить в семиразрядной ячейке со знаком в дополнительном разряде равно 256. Это совпадает с количеством значений, которые можно поместить в восьмиразрядную ячейку без указания знака. Однако диапазон значений уже другой, ему принадлежат значения от -128 до 127 включительно (при переводе в десятичную систему счисления).

При этом в вычислительной технике прямой код используется почти исключительно для представления положительных чисел.

Обратный код

В обратном коде (ОК), также как и в прямом коде, для обозначения знака положительного числа используется бит, равный нулю, и знака отрицательного – единице.

Обратный код положительного двоичного числа совпадает с его прямым кодом. Обратный код отрицательного двоичного числа содержит единицу в знаковом разряде, формируется дополнением модуля исходного числа нулями до самого старшего разряда модуля, а затем поразрядной заменой всех нулей числа на единицу и всех единиц на нули. Обратный перевод осуществляется в той же последовательности.

 

 

 

 

 

 

Пример. Записать обратный код чисел  и 

Решение:

                                  

                                                               

Работа с обратным кодом вызывает ряд трудностей. В частности, возникают два нуля: положительный и отрицательный, т.е. в прямом коде (в котором представлены положительные числа) имеет место , а в обратном коде (в котором представлены отрицательные числа) .

Для отрицательных чисел используется так называемый дополнительный код. Это связано с удобством выполнения операций над числами электронными устройствами компьютера.

Дополнительный код

В дополнительном коде, также как и прямом, первый разряд отводится для представления знака числа. Прямой код используется для представления положительных чисел, а дополнительный – для представления отрицательных. Поэтому, если в первом разряде находится 1, то мы имеем дело с дополнительным кодом и с отрицательным числом.

Все остальные разряды числа в дополнительном коде сначала инвертируются, т.е. заменяются противоположными (0 на 1, а 1 на 0). Например, если 1 0001100 – это прямой код числа, то при формировании его дополнительного кода, сначала надо заменить нули на единицы, а единицы на нули, кроме первого разряда. Получаем 1 1110011. Но это еще не окончательный вид дополнительного кода числа.

Далее следует прибавить единицу к получившемуся инверсией числу:

1 1110011 + 1 = 1 1110100

В итоге и получается число, которое принято называть дополнительным кодом числа.

Причина, по которой используется дополнительный код числа для представления отрицательных чисел, связана с тем, что так проще выполнять математические операции. Например, у нас два числа, представленных в прямом коде. Одно число положительное, другое – отрицательное и эти числа нужно сложить. Однако просто сложить их нельзя. Сначала компьютер должен определить, что это за числа. Выяснив, что одно число отрицательное, ему следует заменить операцию сложения операцией вычитания. Потом, машина должна определить, какое число больше по модулю, чтобы выяснить знак результата и определиться с тем, что из чего вычитать. В итоге, получается сложный алгоритм. Куда проще складывать числа, если отрицательные преобразованы в дополнительный код. Это можно увидеть на примерах ниже.

 

 

Операция сложения положительного числа и отрицательного числа, представленного в прямом коде

1. Прямой код числа 5: 0 000 0101
   Прямой код числа -7: 1 000 0111
2. Два исходных числа сравниваются. В разряд знака результата записывается знак большего исходного числа.
3. Если числа имеют разные знаки, то вместо операции сложения используется операция вычитания из большего по модулю значения меньшего. При этом первый (знаковый) разряд в операции не участвует.
4. _ 000 0111
5.   000 0101
6. ————-
7.   000 0010
8. После выполнения операции учитывается первый разряд. Результат операции 1 000 0010, или -2₁₀.

Операция сложения положительного числа и отрицательного числа, представленного в дополнительном коде

1. Прямой код числа 5: 0 000 0101
   Прямой код числа -7: 1 000 0111
2. Формирование дополнительного кода числа -7.
   Прямой код : 1 000 0111
   Инверсия : 1 111 1000
   Добавление единицы: 1 111 1001
3. Операция сложения.
4.   0 000 0101
5. + 1 111 1001
6.   —————
7.   1 111 1110
8. Проверка результата путем преобразования к прямому коду.
   Дополнительный код: 1 111 1110
   Вычитание единицы : 1 111 1101
   Инверсия : 1 000 0010 (или -2₁₀)

 

Двоичные коды Гоппы — Википедия

В математике и информатике двоичный код Гоппы — код коррекции ошибок (ECC), который принадлежит к классу общих кодов Гоппы. Первоначально был описан Валерием Денисовичем Гоппа. В сравнении с недвоичными вариантами, бинарная структура дает ему несколько математических преимуществ, а также лучше подходит для общего использования в компьютерах и телекоммуникациях. Двоичные коды Гоппы обладают интересными свойствами, полезными для криптографии в криптосистемах, подобных McElise и аналогичных.^[1]

Двоичный код Гоппы определяется как полином g(x){\displaystyle g(x)} в степени t{\displaystyle t} над конечным полем GF(2m){\displaystyle GF(2^{m})} без конечного числа нулей, и последовательность L{\displaystyle L} из n{\displaystyle n} различных элементов GF(2m){\displaystyle GF(2^{m})} которые не являются корнями или полиномами.

∀i,j∈{0,…,n−1}:Li∈GF(2m)∧(Li=Lj⟹i=j)∧g(Li)≠0{\displaystyle \forall i,j\in \{0,\ldots ,n-1\}:L_{i}\in GF(2^{m})\land (L_{i}=L_{j}\implies i=j)\land g(L_{i})\neq 0}

Ключи принадлежат ядру функции, формируя подпространство {0,1}n{\displaystyle \{0,1\}^{n}}:

Γ(g,L)={c∈{0,1}n|∑i=0n−1cix−Li≡0modg(x)}{\displaystyle \Gamma (g,L)=\left\{c\in \{0,1\}^{n}\left|\sum _{i=0}^{n-1}{\frac {c_{i}}{x-L_{i}}}\equiv 0\mod g(x)\right.\right\}}

Код определен, как пара (g,L){\displaystyle (g,L)} с минимальной длиной 2t+1{\displaystyle 2t+1}, таким образом, он может исправить t=⌊(2t+1)−12⌋{\displaystyle t=\left\lfloor {\frac {(2t+1)-1}{2}}\right\rfloor } ошибок в слове длиной n−mt{\displaystyle n-mt} используя ключи размером n{\displaystyle n}. Он также обладает удобной матрицей контроля четности H{\displaystyle H} в виде:

H=VD=(111⋯1L01L11L21⋯Ln−11L02L12L22⋯Ln−12⋮⋮⋮⋱⋮L0t−1L1t−1L2t−1⋯Ln−1t−1)(1g(L0)1g(L1)1g(L2)⋱1g(Ln−1)){\displaystyle H=VD={\begin{pmatrix}1&1&1&\cdots &1\\L_{0}^{1}&L_{1}^{1}&L_{2}^{1}&\cdots &L_{n-1}^{1}\\L_{0}^{2}&L_{1}^{2}&L_{2}^{2}&\cdots &L_{n-1}^{2}\\\vdots &\vdots &\vdots &\ddots &\vdots \\L_{0}^{t-1}&L_{1}^{t-1}&L_{2}^{t-1}&\cdots &L_{n-1}^{t-1}\end{pmatrix}}{\begin{pmatrix}{\frac {1}{g(L_{0})}}&&&&\\&{\frac {1}{g(L_{1})}}&&&\\&&{\frac {1}{g(L_{2})}}&&\\&&&\ddots &\\&&&&{\frac {1}{g(L_{n-1})}}\end{pmatrix}}}

Обратите внимание, что эта форма матрицы контроля четности состоит из определителя Вандермонда V{\displaystyle V} и диагональной матрицы D{\displaystyle D}, имеет форму, схожую с проверочными матрицами альтернативных кодов, таким образом, в этой форме могут использоваться альтернативные декодеры. Такие декодеры обычно обеспечивают только ограниченную возможность исправления ошибок (чаще всего t/2{\displaystyle t/2}).

Для практических целей, матрица проверки на четность двоичного кода Гоппы обычно преобразуется к более в более удобную для изпользования компьютером двоичную форму с помощью конструкции трассировки, которая преобразует t{\displaystyle t}-на-n{\displaystyle n} матрицу над GF(2m){\displaystyle GF(2^{m})} в двоичную матрицу mt{\displaystyle mt}-на-n{\displaystyle n} разделив полиномиальные коэффициенты GF(2m){\displaystyle GF(2^{m})} на m{\displaystyle m} последовательных рядов.

Обычно, декодирование двоичного кода Гоппы производится алгоритмом Паттерсона, который способен эффективно исправлять ошибки(он исправлет все t{\displaystyle t} обнаруженные ошибки), и который так же достаточно прост в реализации.

Алгоритм Паттерсона преобразует синдром в вектор ошибок. Предполагается, что синдром двоичного слова c=(c0,…,cn−1){\displaystyle c=(c_{0},\dots ,c_{n-1})} , примет вид:

s(x)≡∑i=0n−1cix−Limodg(x){\displaystyle s(x)\equiv \sum _{i=0}^{n-1}{\frac {c_{i}}{x-L_{i}}}\mod g(x)}

Альтернативная форма матрицы контроля четности основана на формуле для s(x){\displaystyle s(x)}, и может быть использована для создания такого синдрома с простым произведением матриц.

Далее алгоритм производит расчет v(x)≡s(x)−1−xmodg(x){\displaystyle v(x)\equiv {\sqrt {s(x)^{-1}-x}}\mod g(x)}. Это не удается, когда s(x)≡0{\displaystyle s(x)\equiv 0}, но это тот случай, когда входное слово является ключом, поэтому исправление ошибок не требуется.

Используя расширенный алгоритм Евклида v(x){\displaystyle v(x)}сводится к полиномам a(x){\displaystyle a(x)} и b(x){\displaystyle b(x)}, так, что a(x)≡b(x)⋅v(x)modg(x){\displaystyle a(x)\equiv b(x)\cdot v(x)\mod g(x)}, при этом deg⁡(a)≤⌊t/2⌋{\displaystyle \deg(a)\leq \lfloor t/2\rfloor } и deg⁡(b)≤⌊(t−1)/2⌋{\displaystyle \deg(b)\leq \lfloor (t-1)/2\rfloor }.

Наконец, полином определяющий расположение ошибок, вычисляется как σ(x)=a(x)2+x⋅b(x)2{\displaystyle \sigma (x)=a(x)^{2}+x\cdot b(x)^{2}}. Обратите внимание, что в двоичном случае для исправления ошибок достаточно их найти, так как существует только одно отличное значение.

Если исходный ключ был декодирован и e=(e0,e1,…,en−1){\displaystyle e=(e_{0},e_{1},\dots ,e_{n-1})}- двоичный вектор ошибок, то

σ(x)=∏i=0n−1ei(x−Li){\displaystyle \sigma (x)=\prod _{i=0}^{n-1}e_{i}(x-L_{i})}

Разложение на множители или оценка всех корней σ(x){\displaystyle \sigma (x)} дает достаточно информации, чтобы восстановить вектор ошибок и исправить их.

Двоичные коды Гоппы, рассматриваемые как особый случай кодов Гоппы, обладают интересным свойством — они исправляют все deg⁡(g){\displaystyle \deg(g)} ошибок, в то время как троичные и прочие коды исправляют только deg⁡(g)/2{\displaystyle \deg(g)/2}. Асимптотически такая способность к исправлению ошибок соответствует известной границе Гильберта — Варшамова.

Благодаря высокой способности исправления ошибок, с учетом высокой скорости кодирования и сложной формы матрицы проверки на четность (которую обычно трудно отличить от случайной двоичной матрицы того же ранга) двоичные коды Гоппы используются в нескольких постквантовых криптосистемах, в частности в криптосистеме McEliece. и криптосистеме Нидеррейтера.

.

1. ↑ Elwyn R. Berlekamp, Goppa Codes, IEEE Transactions on information theory, Vol. IT-19, No. 5 — 1c
   

Двоичный код — Карта знаний

• Двои́чный код — это способ представления данных в виде кода, в котором каждый разряд принимает одно из двух возможных значений, обычно обозначаемых цифрами 0 и 1. Разряд в этом случае называется двоичным разрядом.

  В случае обозначения цифрами «0» и «1», возможные состояния двоичного разряда наделяются качественным соотношением «1» > «0» и количественными значениями чисел «0» и «1».

  Двоичный код может быть непозиционным и позиционным. Позиционный двоичный код лежит в основе двоичной системы счисления, широко распространенной в современной цифровой технике.

Источник: Википедия

Связанные понятия

Обратный код (англ. ones’ complement) — метод вычислительной математики, позволяющий вычесть одно число из другого, используя только операцию сложения над натуральными числами. Ранее метод использовался в механических калькуляторах (арифмометрах). Многие ранние компьютеры, включая CDC 6600, LINC, PDP-1 и UNIVAC 1107, использовали обратный код. Большинство современных компьютеров используют дополнительный код. Двоичная система счисления — позиционная система счисления с основанием 2. Благодаря непосредственной реализации в цифровых электронных схемах на логических вентилях, двоичная система используется практически во всех современных компьютерах и прочих вычислительных электронных устройствах. Двоично-десятичный код (англ. binary-coded decimal), BCD, 8421-BCD — форма записи рациональных чисел, когда каждый десятичный разряд числа записывается в виде его четырёхбитного двоичного кода. Прямой код — способ представления двоичных чисел с фиксированной запятой в компьютерной арифметике. Главным образом используется для записи неотрицательных чисел. В случае использования прямого кода для чисел как положительных, так и отрицательных, то есть чисел, запись которых подразумевает возможность использования знака минус (знаковых чисел), хранимые цифровые разряды числа дополняются знаковым разрядом.

Упоминания в литературе

Этот путь заключался в использовании двоичного кода. При двоичном коде все числа записываются с помощью двух знаков – 0 и 1. В двоичном коде нулю соответствует 0, единице – 1, а вот число «2» в двоичном коде пишется как «10». «3» выражается «11», «4» – это 100 и т. д. Поскольку в цифровом описании мы имеем дело с двоичным представлением, полученные значения необходимо воспроизвести в виде двоичного кода. При этом происходит усечение значений параметра до ближайшего допустимого значения (рис. 3.1). Степень числа «два», при которой мы получим нужное число допустимых значений параметра, называется глубиной, или уровнем квантования, или разрядностью слова данных. Уважаемый читатель, не спешите пугаться обилию незнакомых терминов. Разберем несколько примеров. Крайним может быть случай, когда для описания выделен один бит. Тогда параметр может принимать 21 = 2 значения: 0 и 1. Изображение, описанное подобным образом, будет состоять из черных и белых точек. Если, допустим, уровень квантования равен 8, то для описания выделено 8 бит (1 байт), и параметр может принимать 28 = 256 значений, при уровне квантования 10 получим 1024 допустимых значения и т. д. На рис 3.1 имеем 8 допустимых значений (от 0 до 7), соответственно, уровень квантования равен трем. Концепция технологии COM для семейства операционных систем Windows заключается в построении программ из компонент, которые состоят из объектов, представляющих собой непосредственно исполняемый двоичный код. Важнейший признак «компонентности» – исполняемую программу можно собирать из отдельных частей без операций сборки (модуля). Запуск программы самотестирования. Сразу же после включения компьютера начинает свою работу одна из главных подпрограмм BIOS – POST (Poweron self-test; самотестирование при включении). Она выполняет начальное тестирование всех компонентов компьютера. Если в процессе тестирования ошибок не обнаружено, начинается выполнение следующей подпрограммы BIOS. Если обнаружен какой-либо конфликт, POST сразу же сообщает об этом пользователю тремя способами: звуковыми сообщениями, текстовыми сообщениями и двоичными кодами в специальный программный порт.

Связанные понятия (продолжение)

Дополнительный код (англ. two’s complement, иногда twos-complement) — наиболее распространённый способ представления отрицательных целых чисел в компьютерах. Он позволяет заменить операцию вычитания на операцию сложения и сделать операции сложения и вычитания одинаковыми для знаковых и беззнаковых чисел, чем упрощает архитектуру ЭВМ. В англоязычной литературе обратный код называют первым дополнением, а дополнительный код называют вторым дополнением. Позиционная систе́ма счисле́ния (позиционная нумерация) — система счисления, в которой значение каждого числового знака (цифры) в записи числа зависит от его позиции (разряда). Троичный компьютер — компьютер, построенный на двоичных и троичных логических элементах и узлах , работающий в двоичной и троичной системе счисления по законам двоичной и троичной логики с применением двоичных и троичных алгоритмов. Код Хэ́мминга — вероятно, наиболее известный из первых самоконтролирующихся и самокорректирующихся кодов. Построен применительно к двоичной системе счисления. Позволяет исправлять одиночную ошибку (ошибка в одном бите) и находить двойную. Полусумма́тор — комбинационная логическая схема, имеющая два входа и два выхода (двухразрядный сумматор, бинарный сумматор). Полусумматор позволяет вычислять сумму A+B, где A и B — это разряды (биты) обычно двоичного числа, при этом результатом будут два бита S и C, где S — это бит суммы по модулю 2, а C — бит переноса. Код — взаимно однозначное отображение конечного упорядоченного множества символов, принадлежащих некоторому конечному алфавиту, на иное, не обязательно упорядоченное, как правило более обширное множество символов для кодирования передачи, хранения или преобразования информации. Бит (русское обозначение: бит; международное: bit; от англ. binary digit — двоичное число; также игра слов: англ. bit — кусочек, частица) — единица измерения количества информации. 1 бит информации — символ или сигнал, который может принимать два значения: включено или выключено, да или нет, высокий или низкий, заряженный или незаряженный; в двоичной системе исчисления это 1 (единица) или 0 (ноль). Число с плавающей запятой (или число с плавающей точкой) — форма представления вещественных (действительных) чисел, в которой число хранится в форме мантиссы и показателя степени. При этом число с плавающей запятой имеет фиксированную относительную точность и изменяющуюся абсолютную. Используемое наиболее часто представление утверждено в стандарте IEEE 754. Реализация математических операций с числами с плавающей запятой в вычислительных системах может быть как аппаратная, так и программная. Компьютер для операций с математическими функциями (в отличие от обычного компьютера) оперирует с функциями на аппаратном уровне (то есть без программирования этих операций). Перенос и заём в арифметике — приёмы, применяемые в арифметических алгоритмах позиционных систем счисления при выполнении операций сложения и вычитания соответственно, а также (в составе тех же сложения и вычитания) и иных арифметичких операций. Перенос можно понимать как выделение умножения на основание системы счисления в отдельное слагаемое, с последующей перегруппировкой слагаемых. Систе́ма счисле́ния (англ. numeral system или system of numeration) — символический метод записи чисел, представление чисел с помощью письменных знаков. Экспоненциальный код Голомба порядка k — это универсальный код, параметризованный целым числом k. Разработан Соломоном Голомбом. Для кодирования неотрицательного числа в экспоненциальный код Голомба порядка k можно использовать следующий метод… Целое, целочисленный тип данных (англ. Integer), в информатике — один из простейших и самых распространённых типов данных в языках программирования. Служит для представления целых чисел. «Се́тунь» — малая ЭВМ на основе троичной логики, разработанная в вычислительном центре Московского государственного университета в 1959 году. Код Гре́я — двоичный код, иначе зеркальный код, он же код с отражением, в котором две «соседние» (в упорядоченном, то есть лексикографическом, наборе) кодовые комбинации различаются только цифрой в одном двоичном разряде. Иными словами, расстояние Хэмминга между соседними кодовыми комбинациями равно 1. Циклическое число — целое число, циклические перестановки цифр которого являются произведениями этого числа на последовательные числа. Наиболее известный пример такого числа — 142857… Цифрово́й компара́тор или компара́тор ко́дов логическое устройство с двумя словарными входами, на которые подаются два разных двоичных слова равной в битах длины и обычно с тремя двоичными выходами, на которые выдаётся признак сравнения входных слов, — первое слово больше второго, меньше или слова равны. При этом выходы «больше», «меньше» имеют смысл, если входные слова кодируют числа в том или ином машинном представлении. В математике деление на два, деление пополам — это математическая операция, частный случай деления. Древние египтяне отличали деление на два от деления на другие числа, поскольку их алгоритм умножения использовал деление на два как один из промежуточных этапов. В XVI веке некоторые математики предложили рассматривать деление на два как операцию, отличающуюся от деления на другие числа. В современном программировании также иногда выделяют деление именно на два. Аффинный шифр — это частный случай более общего моноалфавитного шифра подстановки. К шифрам подстановки относятся также шифр Цезаря, ROT13 и Атбаш. Поскольку аффинный шифр легко дешифровать, он обладает слабыми криптографическими свойствами. Целочисленная последовательность называется полной последовательностью, если любое положительное целое число может быть выражено в виде суммы значений из последовательности, при этом каждое значение можно использовать только один раз. Двоичный (бинарный) файл — в широком смысле: последовательность произвольных байтов. Название связано с тем, что байты состоят из бит, то есть двоичных (англ. binary) цифр. Длинная арифметика — выполняемые с помощью вычислительной машины арифметические операции (сложение, вычитание, умножение, деление, возведение в степень, элементарные функции) над числами, разрядность которых превышает длину машинного слова данной вычислительной машины. Эти операции реализуются не аппаратно, а программно, с использованием базовых аппаратных средств работы с числами меньших порядков. Частный случай — арифметика произвольной точности — относится к арифметике, в которой длина чисел ограничена… Сумма́тор — в кибернетике — устройство, преобразующее информационные сигналы (аналоговые или цифровые) в сигнал, эквивалентный сумме этих сигналов; устройство, производящее операцию сложения. Логарифмическая система счисления (LNS) — это арифметическая система, иногда используемая для представления вещественных чисел в компьютере и в цифровых аппаратных средствах, особенно в цифровой обработке сигналов. Октет в информатике — восемь двоичных разрядов. В русском языке октет обычно называют байтом. Октет может принимать 256 возможных состояний (кодов, значений, комбинаций битов (нулей и единиц)). Симметри́чные криптосисте́мы (также симметричное шифрование, симметричные шифры) (англ. symmetric-key algorithm) — способ шифрования, в котором для шифрования и расшифровывания применяется один и тот же криптографический ключ. До изобретения схемы асимметричного шифрования единственным существовавшим способом являлось симметричное шифрование. Ключ алгоритма должен сохраняться в тайне обеими сторонами, осуществляться меры по защите доступа к каналу, на всем пути следования криптограммы, или сторонами… Алгоритм умножения Бута это алгоритм умножения, который позволяет перемножить два двоичных числа в дополнительном коде. Алгоритм был разработан Эндрю Дональдом Бутом в 1951 при проведении исследований в области кристаллографии в колледже им. Дж. Бирбека в Блумсбери (Лондон). Бут пользовался настольными вычислителями, которые выполняли операцию сдвига быстрее, чем операцию сложения, и создал алгоритм для увеличения скорости их работы. Алгоритм Бута представляет интерес при изучении архитектуры компьютера… Хеширование (англ. hashing – «превращать в фарш», «мешанина») — преобразование массива входных данных произвольной длины в (выходную) битовую строку установленной длины, выполняемое определённым алгоритмом. Функция, воплощающая алгоритм и выполняющая преобразование, называется «хеш-функцией» или «функцией свёртки». Исходные данные называются входным массивом, «ключом» или «сообщением». Результат преобразования (выходные данные) называется «хешем», «хеш-кодом», «хеш-суммой», «сводкой сообщения». Код Левенштейна — это универсальный код, позволяющий кодировать неотрицательные целые числа. Он был придуман Владимиром Левенштейном. Двоичный алгоритм поиска подстроки (также bitap algorithm, shift-or algorithm) — алгоритм поиска подстроки, использующий тот факт, что в современных компьютерах битовый сдвиг и побитовое ИЛИ являются атомарными операциями. По сути, это примитивный алгоритм поиска с небольшой оптимизацией, благодаря которой за одну операцию производится до 32 сравнений одновременно (или до 64, в зависимости от разрядности машины). Легко переделывается на приблизительный поиск. Циклический код — линейный, блочный код, обладающий свойством цикличности, то есть каждая циклическая перестановка кодового слова также является кодовым словом. Используется для преобразования информации для защиты её от ошибок (см. Обнаружение и исправление ошибок). Циклический избыточный код (англ. Cyclic redundancy check, CRC) — алгоритм нахождения контрольной суммы, предназначенный для проверки целостности данных. CRC является практическим приложением помехоустойчивого кодирования, основанным на определённых математических свойствах циклического кода. В теории информации теорема Шеннона об источнике шифрования (или теорема бесшумного шифрования) устанавливает предел максимального сжатия данных и числовое значение энтропии Шеннона. Пото́чный или Пото́ковый шифр — это симметричный шифр, в котором каждый символ открытого текста преобразуется в символ шифрованного текста в зависимости не только от используемого ключа, но и от его расположения в потоке открытого текста. Поточный шифр реализует другой подход к симметричному шифрованию, нежели блочные шифры. Веду́щие нули́ в записи числа при помощи позиционной системы счисления — последовательность из одного или более нулей, занимающая старшие разряды. Понятие ведущих нулей возникает при использовании представлений чисел, имеющих фиксированное количество разрядов. В остальных случаях, как правило, ведущие нули не пишутся. Криптосистема Накаша — Штерна (англ. Naccache — Stern cryptosystem)— криптографический алгоритм с открытым ключом, основывающийся на вычислительной сложности задачи дискретного логарифмирования. В отличии от RSA, гомоморфен по сложению и вычитанию, а не по умножению… Блочный шифр «Кузнечик» (входит в стандарт ГОСТ Р 34.12-2015) — симметричный алгоритм блочного шифрования с размером блока 128 бит и длиной ключа 256 бит и использующий для генерации раундовых ключей сеть Фейстеля. Би́товое поле (англ. bit field) в программировании — некоторое количество бит, расположенных последовательно в памяти, значение которых процессор не способен прочитать из-за особенностей аппаратной реализации. Ниббл (англ. nibble, nybble), полубайт, тетрада или гексадецит (hexadecit — hexadecimal digit) — единица измерения информации, равная четырём двоичным разрядам (битам), удобна тем, что представима одной шестнадцатеричной цифрой, то есть является одним шестнадцатеричным разрядом. Переменная размера «ниббл» может принимать 24=16 различных значений. В русском языке используется синоним «тетрада». ГОСТ Р 34.11-94 — устаревший российский криптографический стандарт вычисления хеш-функции.

Двоичный код — Википедия. Что такое Двоичный код

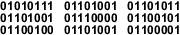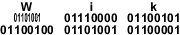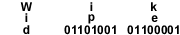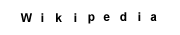Слово «Wikipedia», закодированное двоичным ASCII-кодом.

Двои́чный код — это способ представления данных в виде кода, в котором каждый разряд принимает одно из двух возможных значений, обычно обозначаемых цифрами 0 и 1. Разряд в этом случае называется двоичным разрядом.

В случае обозначения цифрами «0» и «1», возможные состояния двоичного разряда наделяются качественным соотношением «1» > «0» и количественными значениями чисел «0» и «1».

Двоичный код может быть непозиционным и позиционным. Позиционный двоичный код лежит в основе двоичной системы счисления, широко распространенной в современной цифровой технике.

Описание

Из комбинаторики известно, что, в случае непозиционного кода, количество комбинаций (кодов) n-разрядного кода является числом сочетаний с повторениями, равно биномиальному коэффициенту:

(n+k−1k)=(−1)k(−nk)=(n+k−1)!k!(n−1)!{\displaystyle {n+k-1 \choose k}=(-1)^{k}{-n \choose k}={\frac {\left(n+k-1\right)!}{k!\left(n-1\right)!}}}, [возможных состояний (кодов)], где:

n{\displaystyle n} — количество элементов в данном множестве различных элементов (количество возможных состояний, цифр, кодов в разряде),
k{\displaystyle k} — количество элементов в наборе (количество разрядов).
В двоичной системе кодирования (n=2) количество возможных состояний (кодов) равно :

(n+k−1)!k!(n−1)!=(2+k−1)!k!(2−1)!=(k+1)!k!1!=k+1{\displaystyle {\frac {\left(n+k-1\right)!}{k!\left(n-1\right)!}}={\frac {\left(2+k-1\right)!}{k!\left(2-1\right)!}}={\frac {\left(k+1\right)!}{k!1!}}=k+1}, [возможных состояний (кодов)], то есть

описывается линейной функцией:

Nkp(k)=k+1{\displaystyle N_{kp}(k)=k+1}, [возможных состояний (кодов)], где

k{\displaystyle k} — количество двоичных разрядов.
Например, в одном 8-ми битном байте (k=8) количество возможных состояний (кодов) равно:

Nkp(k)=k+1=8+1=9{\displaystyle N_{kp}(k)=k+1=8+1=9}, [возможных состояний (кодов)].

В случае позиционного кода, число комбинаций (кодов) k-разрядного двоичного кода равно числу размещений с повторениями:

Np(k)=A¯(2,k)=A¯2k=2k{\displaystyle N_{p}(k)={\bar {A}}(2,k)={\bar {A}}_{2}^{k}=2^{k}}, где

 k{\displaystyle \ k} — число разрядов двоичного кода.

Используя два двоичных разряда можно закодировать четыре различные комбинации: 00 01 10 11, три двоичных разряда — восемь: 000 001 010 011 100 101 110 111, и так далее.
При увеличении разрядности позиционного двоичного кода на 1, количество различных комбинаций в позиционном двоичном коде удваивается.

Двоичные коды являются комбинациями двух элементов и не являются двоичной системой счисления, но используются в ней как основа. Двоичный код также может использоваться для кодирования чисел в системах счисления с любым другим основанием. Пример: в двоично-десятичном кодировании (BCD) используется двоичный код для кодирования чисел в десятичной системе счисления.
При кодировании алфавитноцифровых символов (знаков) двоичному коду не приписываются весовые коэффициенты, как это делается в системах счисления, в которых двоичный код используется для представления чисел, а используется только порядковый номер кода из множества размещений с повторениями.

В системах счисления k-разрядный двоичный код, (k-1)-разрядный двоичный код, (k-2)-разрядный двоичный код и т. д. могут отображать одно и то же число. Например, 0001, 001, 01, 1 — одно и то же число — «1» в двоичных кодах с разным числом разрядов — k.

Примеры двоичных чисел

В таблице показаны первые 16 двоичных чисел и их соответствие десятичным и шестнадцатиричным числам.

Десятичное число	Шестнадцатеричное число	Двоичное число
0	0	0000
1	1	0001
2	2	0010
3	3	0011
4	4	0100
5	5	0101
6	6	0110
7	7	0111
8	8	1000
9	9	1001
10	A	1010
11	B	1011
12	C	1100
13	D	1101
14	E	1110
15	F	1111

Пример «доисторического» использования кодов

Инки имели свою счётную систему кипу, которая физически представляла собой верёвочные сплетения и узелки. Генри Эртан обнаружил, что в узелках заложен некий код, более всего похожий на двоичную систему счисления^[1].

См. также

Примечания

двоичный шифр — со всех языков на русский

См. также в других словарях:

• Шифр Хилла — полиграммный шифр подстановки, основанный на линейной алгебре. Лестер С. Хилл изобрел этот шифр в 1929, и это был первый шифр, который позволял на практике (хотя и с трудом) оперировать более чем с тремя символами за раз. Последующее обсуждение… …   Википедия

• Поточный шифр — это симметричный шифр, в котором каждый символ открытого текста преобразуется в символ шифрованного текста в зависимости не только от используемого ключа, но и от его расположения в потоке открытого текста. Поточный шифр реализует другой подход к …   Википедия

• История криптографии — Основная статья: Криптография История криптографии насчитывает около 4 тысяч лет. В качестве основного критерия периодизации криптографии возможно использовать технологические характеристики используемых методов шифрования. Первый период… …   Википедия

• Задача о ранце в криптографии — (англ. Knapsack problem)  это задача, на основе которой американские криптографы Ральф Меркл (англ.) и Мартин Хеллман разработали первый алгоритм шифрования с открытым ключом. Он носит название криптосистема Меркла Хеллмана. Для… …   Википедия

• Сеть Фейстеля — (конструкция Фейстеля)  один из методов построения блочных шифров. Сеть представляет собой определённую многократно повторяющуюся (итерированную) структуру, называющуюся ячейкой Фейстеля. При переходе от одной ячейки к другой меняется ключ,… …   Википедия

• NUSH — Создатель: Анатолий Лебедев, Алексей Волчков Создан: 1999 г. Опубликован: 2000 г. Размер ключа: 128, 192, 256 бит Размер блока: 64, 128, 256 бит Число раундов: 36, 68, 132 NUSH («Наш»)  блочный …   Википедия

• Шифратор (электроника) — У этого термина существуют и другие значения, см. Шифратор. Шифратор (кодер)  (англ. encoder) логическое устройство, выполняющее логическую функцию (операцию)  преобразование позиционного n разрядного кода в m разрядный двоичный,… …   Википедия

• Двоичная система счисления — Эта статья или раздел нуждается в переработке. Пожалуйста, улучшите статью в соответствии с правилами написания статей …   Википедия

• Квантовая криптография — Квантовая криптография  метод защиты коммуникаций, основанный на принципах квантовой физики. В отличие от традиционной криптографии, которая использует математические методы, чтобы обеспечить секретность информации, квантовая криптография… …   Википедия

• Л (кириллица) — Буква кириллицы Л Кириллица А Б В …   Википедия

• Фридман, Уильям Фредерик — Уильям Фредерик Фридман William Frederick Friedman …   Википедия