Шестнадцатиричные числа | это… Что такое Шестнадцатиричные числа?
Толкование
- Шестнадцатиричные числа
Шестнадцатеричная система счисления (шестнадцатеричные числа) — позиционная система счисления по целочисленному основанию 16. Обычно в качестве шестнадцатеричных цифр используются десятичные цифры от 0 до 9 и латинские буквы от A до F для обозначения цифр от 10 до 15.
Содержание
- 1 Применение
- 2 Способы записи
- 2.1 В математике
- 2.2 В языках программирования
- 3 Перевод чисел из одной системы счисления в другую
- 3.1 Перевод чисел из шестнадцатеричной системы в десятичную
- 3.2 Перевод чисел из двоичной системы в шестнадцатеричную
- 3.3 Таблица перевода чисел
- 4 См.
 также
также - 5 Ссылки
Применение
Широко используется в низкоуровневом программировании и вообще в компьютерной документации, поскольку в современных компьютерах минимальной единицей памяти является 8-битный байт, значения которого удобно записывать двумя шестнадцатеричными цифрами. Такое использование началось с системы IBM/360, где вся документация использовала шестнадцатеричную систему, в то время как в документации других компьютерных систем того времени (даже с 8-битными символами, как, например, БЭСМ-6) использовали восьмеричную систему.
В стандарте Юникода номер символа принято записывать в шестнадцатеричном виде, используя не менее 4 цифр (при необходимости — с ведущими нулями).
Способы записи
В математике
В математике систему счисления принято писать в подстрочном знаке. Например, десятичное число 1443 можно записать как 1443
В языках программирования
В разных языках программирования для записи шестнадцатеричных чисел используют различный синтаксис:
- В Ада и
- В Си и языках схожего синтаксиса, например, в
- В некоторых ассемблерах используют букву «h», которую ставят после числа.
 Например, «5A3h». При этом, если число начинается не с десятичной цифры, впереди ставится «0» (ноль): «0FFh» (25510)
Например, «5A3h». При этом, если число начинается не с десятичной цифры, впереди ставится «0» (ноль): «0FFh» (25510) - Другие ассемблеры (AT&T, Motorola), а также Паскаль и некоторые версии Бэйсика используют префикс «$». Например, «$5A3».
- Некоторые иные платформы, например ZX Spectrum в своих ассемблерах (MASM, TASM, ALASM, GENS и т.д.) использовали запись #5A3, обычно выровненную до одного или двух байт: #05A3.
- Другие версии Бэйсика используют для указания шестнадцатеричных цифр сочетание «&h». Например, «&h5A3».
- В Unix-подобных операционных системах (и многих языках программирования, имеющих корни в Unix/linux) непечатные символы при выводе/вводе кодируются как \xCC, где CC — шестнадцатеричный код символа.
Перевод чисел из одной системы счисления в другую
Перевод чисел из шестнадцатеричной системы в десятичную
Для перевода шестнадцатеричного числа в десятичное необходимо это число представить в виде суммы произведений степеней основания шестнадцатеричной системы счисления на соответствующие цифры в разрядах шестнадцатеричного числа.

Например, требуется перевести шестнадцатеричное число 5A3 в десятичное. В этом числе 3 цифры. В соответствии с вышеуказанным правилом представим его в виде суммы степеней с основанием 16:
5A316=5·162+10·161+3·160
=5·256+10·16+3·1=1280+160+3=144310Перевод чисел из двоичной системы в шестнадцатеричную
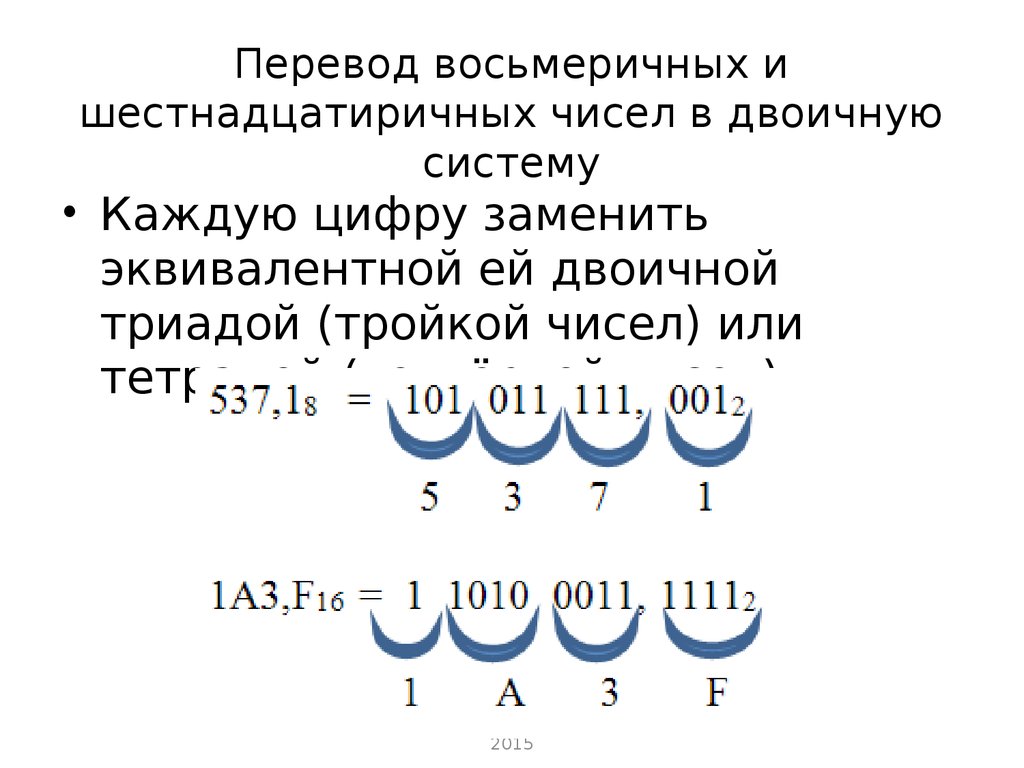
Для перевода многозначного двоичного числа в шестнадцатеричную систему нужно разбить его на тетрады справа налево и заменить каждую тетраду соответствующей шестнадцатеричной цифрой.
Например:
101101000112=0101 1010 0011=5A316 Таблица перевода чисел
0hex = 0dec = 0oct 0 0 0 0 1hex = 1dec = 1oct 0 0 0 1 2hex = = 2oct 0 0 1 0 3hex = 3dec = 3oct 0 0 1 1 4hex = 4dec = 4oct 0 1 0 0 5hex = 5dec = 5oct 0 1 0 1 = 6dec = 6oct 0 1 1 0 7hex = 7dec = 7oct 0 1 1 1 8hex = 8dec = 10oct 1 0 0 0 9hex = 9dec = 11oct 1 0 0 1 Ahex = 10dec = 12oct 1 0 1 0 Bhex = 11dec = 13oct 1 0 1 1 Chex = 12dec = 14oct 1 1 0 0 Dhex = 13dec = 15oct 1 1 0 1 Ehex = 14dec = 16oct 1 1 1 0 Fhex = 15dec = 17oct 1 1 1 1 См.
 также
также- Система счисления
- Двоичные приставки
- Шестнадцатеричный редактор
Ссылки
- Шестнадцатеричные числа и операции с ними
- Таблица порядков двоичных, шестнадцатеричных и десятичных чисел
- Онлайн калькулятор для перевода чисел из одной системы счисления в другую
Wikimedia Foundation. 2010.
Нужна курсовая?
- Шестнадцать
- Шестнадцатиричная система исчисления
Полезное
Шестнадцатиричные числа | это… Что такое Шестнадцатиричные числа?
Толкование
- Шестнадцатиричные числа
Шестнадцатеричная система счисления (шестнадцатеричные числа) — позиционная система счисления по целочисленному основанию 16. Обычно в качестве

Содержание
- 1 Применение
- 2 Способы записи
- 2.1 В математике
- 2.2 В языках программирования
- 3 Перевод чисел из одной системы счисления в другую
- 3.1 Перевод чисел из шестнадцатеричной системы в десятичную
- 3.2 Перевод чисел из двоичной системы в шестнадцатеричную
- 3.3 Таблица перевода чисел
- 4 См. также
- 5 Ссылки
Применение
Широко используется в низкоуровневом программировании и вообще в компьютерной документации, поскольку в современных компьютерах минимальной единицей памяти является 8-битный байт, значения которого удобно записывать двумя шестнадцатеричными цифрами. Такое использование началось с системы IBM/360, где вся документация использовала шестнадцатеричную систему, в то время как в документации других компьютерных систем того времени (даже с 8-битными символами, как, например, БЭСМ-6) использовали восьмеричную систему.

В стандарте Юникода номер символа принято записывать в шестнадцатеричном виде, используя не менее 4 цифр (при необходимости — с ведущими нулями).
Способы записи
В математике
В математике систему счисления принято писать в подстрочном знаке. Например, десятичное число 1443 можно записать как 144310 или как 5A316.
В языках программирования
В разных языках программирования для записи шестнадцатеричных чисел используют различный синтаксис:
- В Ада и
- В Си и языках схожего синтаксиса, например, в
- В некоторых ассемблерах используют букву «h», которую ставят после числа. Например, «5A3h». При этом, если число начинается не с десятичной цифры, впереди ставится «0» (ноль): «0FFh» (25510)
- Другие ассемблеры (AT&T, Motorola), а также Паскаль и некоторые версии Бэйсика используют префикс «$». Например, «$5A3».
- Некоторые иные платформы, например ZX Spectrum в своих ассемблерах (MASM, TASM, ALASM, GENS и т.
 д.) использовали запись #5A3, обычно выровненную до одного или двух байт: #05A3.
д.) использовали запись #5A3, обычно выровненную до одного или двух байт: #05A3. - Другие версии Бэйсика используют для указания шестнадцатеричных цифр сочетание «&h». Например, «&h5A3».
- В Unix-подобных операционных системах (и многих языках программирования, имеющих корни в Unix/linux) непечатные символы при выводе/вводе кодируются как \xCC, где CC — шестнадцатеричный код символа.
Перевод чисел из одной системы счисления в другую
Перевод чисел из шестнадцатеричной системы в десятичную
Для перевода шестнадцатеричного числа в десятичное необходимо это число представить в виде суммы произведений степеней основания шестнадцатеричной системы счисления на соответствующие цифры в разрядах шестнадцатеричного числа.
Например, требуется перевести шестнадцатеричное число 5A3 в десятичное. В этом числе 3 цифры. В соответствии с вышеуказанным правилом представим его в виде суммы степеней с основанием 16:
5A316=5·162+10·161+3·160
=5·256+10·16+3·1=1280+160+3=144310Перевод чисел из двоичной системы в шестнадцатеричную
Для перевода многозначного двоичного числа в шестнадцатеричную систему нужно разбить его на тетрады справа налево и заменить каждую тетраду соответствующей шестнадцатеричной цифрой.

Например:
101101000112=0101 1010 0011=5A316 Таблица перевода чисел
0hex = 0dec = 0oct 0 0 0 0 1hex = 1dec = 1oct 0 0 0 1 2hex = 2dec = 2oct 0 0 1 0 3hex = 3dec = 3oct 0 0 1 1 4hex = 4dec = 4oct 0 1 0 0 5hex = 5dec = 5oct 0 1 0 1 6hex = 6dec = 6oct 0 1 1 0 7hex = 7dec = 7oct 0 1 1 1 8hex = 8dec = 10oct 1 0 0 0 9hex = 9dec = 11oct 1 0 0 1 Ahex = 10dec = 12oct 1 0 1 0 Bhex = 11dec = 13oct 1 0 1 1 Chex = 12dec = 14oct 1 1 0 0 Dhex = 13dec = 15oct 1 1 0 1 Ehex = 14dec = 16oct 1 1 1 0 Fhex = 15dec = 17oct 1 1 1 1 См.
 также
также- Система счисления
- Двоичные приставки
- Шестнадцатеричный редактор
Ссылки
- Шестнадцатеричные числа и операции с ними
- Таблица порядков двоичных, шестнадцатеричных и десятичных чисел
- Онлайн калькулятор для перевода чисел из одной системы счисления в другую
Wikimedia Foundation. 2010.
Нужен реферат?
- Шестнадцать
- Шестнадцатиричная система исчисления
Полезное
Шестнадцатеричные числа
Шестнадцатеричные числаШестнадцатеричная система счисления
Шестнадцатеричная (с основанием 16) система счисления работает так же, как и десятичная. (основание 10) система счисления, за исключением того, что она основана на шестнадцати вместо десяти. работа с десятичной системой знакома.
Ниже представлено 4-значное число с основанием 10 5826, указывающее, как значение
числа получается из значений его 4 цифр.
Всем известно, что число 5826 означает пять тысяч восемьсот двадцать шесть. Но только потому, что их учили, что 1, 10, 100 и 1000 являются частью вычисление , хотя они никогда не пишутся как . Все, что есть на самом деле всего написано двадцать один (5 и 8 и 2 и 6). Только интерпретация что люди поставляют, что является чисто умственным и неписаным, информирует о том, что написано с предполагаемым значением.
Шестнадцатеричное число работает таким же образом. Каждая цифра «взвешивается» «множитель» со всеми результатами, сложенными вместе. Множители в обе системы являются степенями системной базы (10 или 16). Полномочия числа 10 1, 10, 100, 1000 и т. д., а числа 16 — 1, 16, 256, 409.6 и т.д. Так же цифры «5826», используемые в базе 16, представляют собой значение, рассчитанное следующим образом:
Хотя цифры одинаковые (5826), значения получаются совершенно разными, потому что база и ее «значения множителя» различны.
Вы увидите шестнадцатеричные числа, некоторые из цифр которых являются буквами вместо
числа. Это потому, что количество цифр, необходимых для любой системы счисления,
база номера. Таким образом, для основания 2 требуется 2 цифры, для основания 10 требуется 10, а для основания
16 нужно 16. База 2 имеет 0 и 1. База 10 имеет от 0 до 9. База 16 заимствует 0
хотя 9, но нужно еще 6. Для них мы могли бы придумать некоторые символы. Однако,
для удобства мы используем первые 6 букв алфавита (от A до F)
вместо. Когда у нас заканчиваются цифры на 9, мы используем А в качестве следующей цифры. Итак, А
представляет значение 10. B следует за ним и представляет 11. Шестнадцатеричные цифры
и значение, которое они обозначают:
Это потому, что количество цифр, необходимых для любой системы счисления,
база номера. Таким образом, для основания 2 требуется 2 цифры, для основания 10 требуется 10, а для основания
16 нужно 16. База 2 имеет 0 и 1. База 10 имеет от 0 до 9. База 16 заимствует 0
хотя 9, но нужно еще 6. Для них мы могли бы придумать некоторые символы. Однако,
для удобства мы используем первые 6 букв алфавита (от A до F)
вместо. Когда у нас заканчиваются цифры на 9, мы используем А в качестве следующей цифры. Итак, А
представляет значение 10. B следует за ним и представляет 11. Шестнадцатеричные цифры
и значение, которое они обозначают:
| Шестнадцатеричная цифра | Значение |
0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 8 |
| 9 | 9 |
| А | 10 |
| Б | 11 |
| С | 12 |
| Д | 13 |
| Е | 14 |
| Ф | 15 |
Вот вывод значения другого 4-значного шестнадцатеричного числа, но этот использует некоторые из старших цифр AF:
Максимальное число, которое вы можете сосчитать с заданным количеством цифр (в любом числе
системы) — это число, в котором каждая цифра содержит максимальное значение в
система счисления (1 по основанию 2, или 9 по основанию 10, или F по основанию 16). Итак, самый большой
число, которое вы можете представить с помощью 4 цифр в базе 16:
Итак, самый большой
число, которое вы можете представить с помощью 4 цифр в базе 16:
Чтобы считать больше, вам потребуется использовать больше цифр. следующее число — 10000 в шестнадцатеричном формате или 65536 в десятичном. Это известное значение в информатике и называется «64К».
Шестнадцатеричные числа
Хотя числа обрабатываются внутри компьютера как двоичные, это не означает, что мы должны всегда представлять эти числа как двоичные для людей.
Почему мы используем шестнадцатеричное число
Какой из следующих номеров легче запомнить?
- 1010 0101
- А5
Если вы думаете, что A5 легче и удобнее запоминать и использовать, то теперь вы понимаете, почему некоторые двоичные файлы представлены в шестнадцатеричном формате. A5 на самом деле то же значение, что и 1010 0101 ; однако он представлен как шестнадцатеричный, а не двоичный.
Мы часто видим, что шестнадцатеричные числа используются для представления двоичных чисел для:
- Цвета. Их часто представляют как интенсивность красного, зеленого и синего света, каждый из которых может быть представлен двумя шестнадцатеричными цифрами. Смотрите наши Представление данных курс для получения дополнительной информации.
- MAC-адресов, используемых в сети. Дополнительную информацию см. в нашем курсе Введение в компьютерные сети .
- Адреса памяти: конкретное место в памяти, в котором хранится часть данных. Они часто важны в сообщениях об ошибках.
Шестнадцатеричная система счисления с основанием 16 : она использует 16 цифр. Итак, если бы у нас было существо с 16 пальцами, они бы считали его в шестнадцатеричной системе счисления следующим образом:
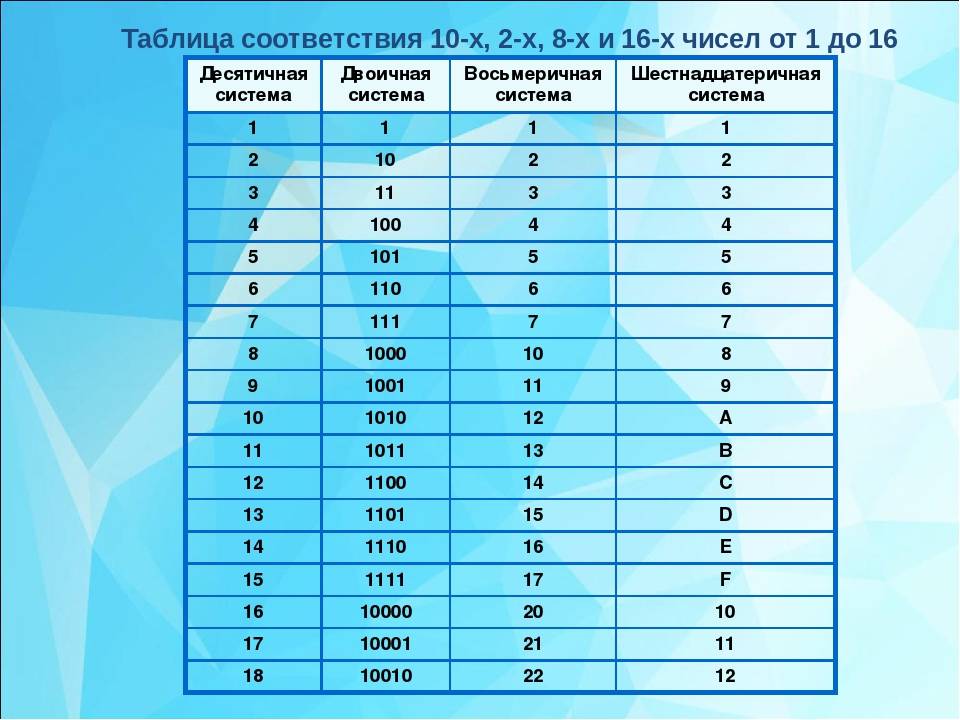
В этой таблице показаны эквивалентные десятичные, двоичные и шестнадцатеричные значения:
| Денарий | Двоичный | Шестигранник |
|---|---|---|
| 0 | 0000 | 0 |
| 1 | 0001 | 1 |
| 2 | 0010 | 2 |
| 3 | 0011 | 3 |
| 4 | 0100 | 4 |
| 5 | 0101 | 5 |
| 6 | 0110 | 6 |
| 7 | 0111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| 10 | 1010 | А |
| 11 | 1011 | Б |
| 12 | 1100 | С |
| 13 | 1101 | Д |
| 14 | 1110 | Е |
| 15 | 1111 | Ф |
Шестнадцатеричное число обычно используется в вычислениях, поскольку оно может представлять байт данных всего двумя символами (вместо восьми). Каждый шестнадцатеричный символ представляет половину байта, также называемого полубайтом.
Каждый шестнадцатеричный символ представляет половину байта, также называемого полубайтом.
- Итак, шестнадцатеричный 7D эквивалентен двоичному 0111 1101.
Аналогично, двоичное число 0001 1010 преобразуется в шестнадцатеричное следующим образом:
- 0001 — это двоичное представление 1 (которое одинаково в десятичной и шестнадцатеричной системе счисления).
- 1010 — это двоичное представление десятичного числа 10, которое представлено в шестнадцатеричном виде как A.
- Итак, двоичное число 0001 1010 эквивалентно шестнадцатеричному 1А.
Преобразование шестнадцатеричных чисел в десятичные с помощью двоичных чисел
Вы уже знаете, как преобразовывать двоичные числа в десятичные, а поскольку вы только что научились преобразовывать шестнадцатеричные числа в двоичные, вы также можете преобразовать их в десятичные.
Например, число A9 в шестнадцатеричном виде равно 1010 1001 в двоичном формате. И мы можем преобразовать это в денарии, используя таблицу, которую мы использовали ранее:
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|
| 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 |
128 + 32 + 8 + 1 = 169
Преобразование шестнадцатеричного числа непосредственно в десятичное
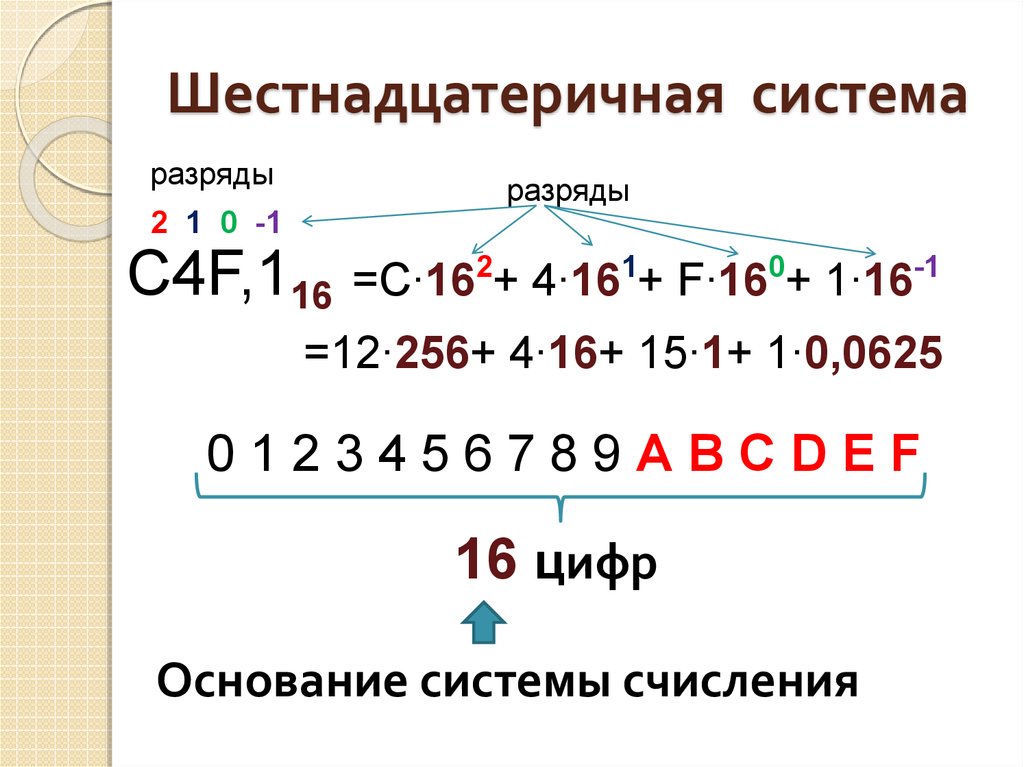
Мы также можем преобразовать шестнадцатеричное число непосредственно в десятичное, подумав о разрядных значениях.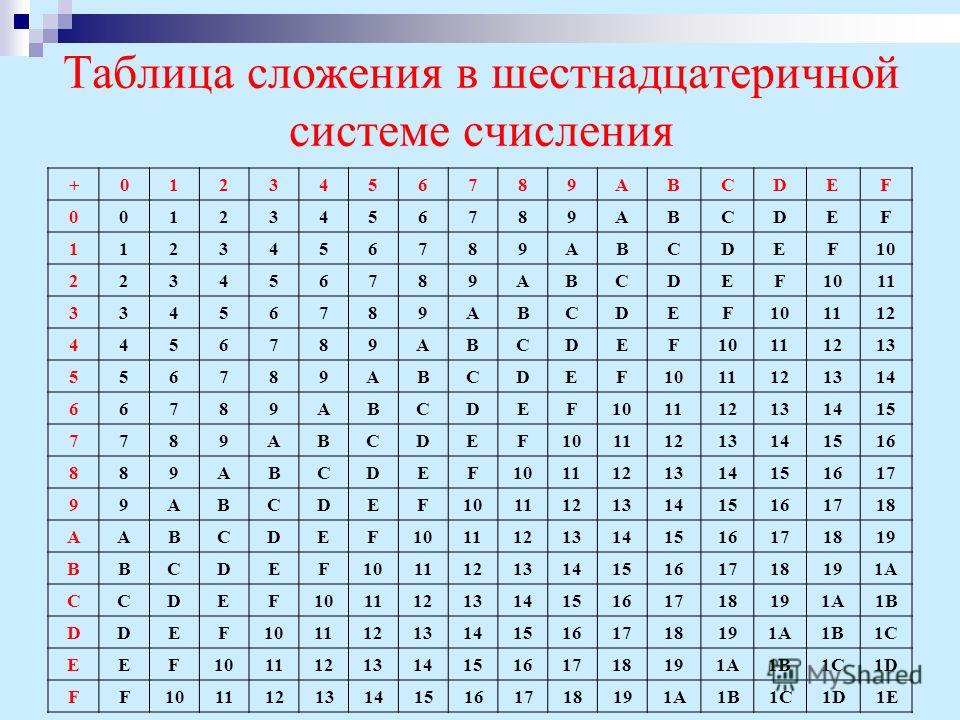 Вы знаете, что разрядность десятичных чисел работает следующим образом:
Вы знаете, что разрядность десятичных чисел работает следующим образом:
1089 = (1 × 1000) + (0 × 100) + (8 × 10) + (9 × 1)
| Базовые 10 разрядов | 1000 (10³) | 100 (10²) | 10 (10¹) | 1 (10⁰) |
|---|---|---|---|---|
| Денарная стоимость | 1 | 0 | 8 | 9 |
Шестнадцатеричный код работает очень похоже, с основанием 16 вместо 10. Преобразуем шестнадцатеричное число A9 в десятичное:
| Базовые 16 разрядов | 16 (16¹) | 1 (16⁰) |
|---|---|---|
| Шестнадцатеричное значение | А | 9 |
- Из приведенной выше таблицы мы знаем, что шестнадцатеричная цифра А представляет десятичную цифру, а шестнадцатеричная цифра 9.представляет собой денарий 9.
- Как и в 1089, на позиции 1 стоит 9: (9 × 1).
- На позиции 16 стоит цифра 10: (10 × 16).



 также
также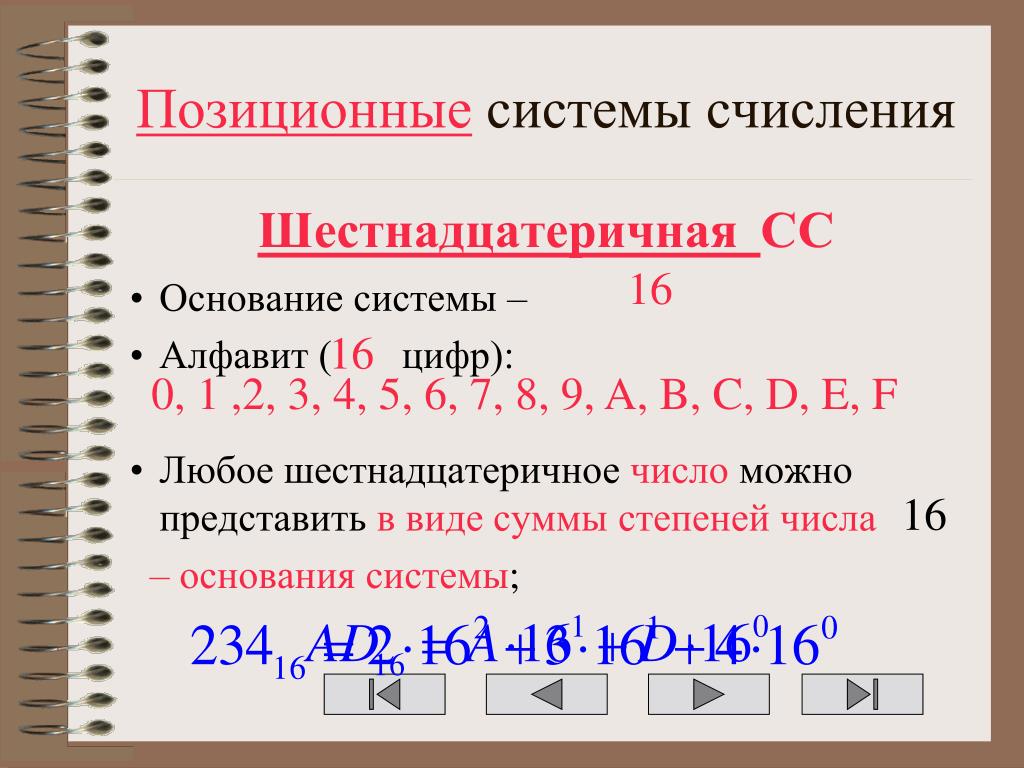 Например, «5A3h». При этом, если число начинается не с десятичной цифры, впереди ставится «0» (ноль): «0FFh» (25510)
Например, «5A3h». При этом, если число начинается не с десятичной цифры, впереди ставится «0» (ноль): «0FFh» (25510)
 также
также
 д.) использовали запись #5A3, обычно выровненную до одного или двух байт: #05A3.
д.) использовали запись #5A3, обычно выровненную до одного или двух байт: #05A3.
 также
также