Как перевести из шестнадцатиричной в двоичную

Системы счисления (Теория)

Сегодня разберём теоретический аспект работы с различными системами счисления. Основными системами счисления являются: двоичная, восьмеричная, десятичная (наша родная) и шестнадцатиричная.

Перевод чисел из двоичной системы в шестнадцатиричную систему счисления.

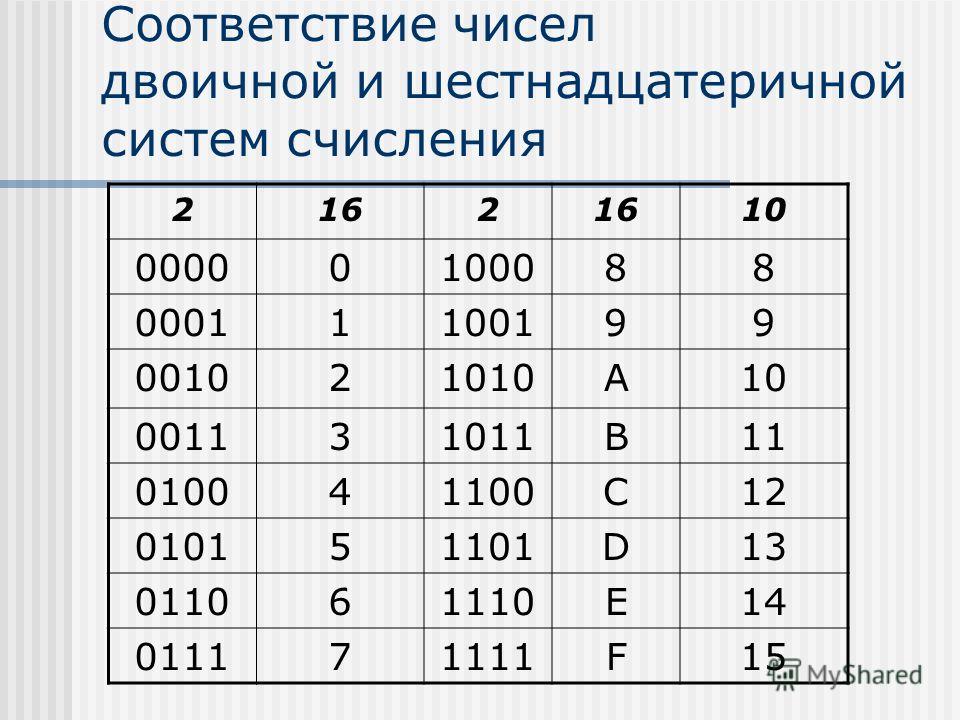
Для начала нужно написать себе в черновик следующую таблицу:

Давайте рассмотрим данную таблицу. В первом столбце идут числа от 0 до 15 в нашей родной десятичной системе счисления. Во втором столбце идут числа так же от 0 до 15, но уже в двоичной системе, а в третьем тоже от 0 до 15 в шестнадцатиричной системе счисления.

Написать числа от 0 до 15 в нашей родной десятичной системе не у кого затруднений не вызовет.

Числа в двоичной же системе лучше всего написать по следующему правилу: в младшем разряде чередуем ноль и единицу, в следующем разряде чередование нулей и единиц происходит в два раза медленнее (два нуля, две единицы, два нуля и т. д.), в следующем разряде ещё в два раза медленнее чередование (4 нуля, 4 единицы и т.д.) и наконец 8 нулей и 8 единиц — в самом старшем разряде.

В шестнадцатиричной системе счисления помимо наших привычных символов от 0 до 9 придуманы символы A, B, С, D, E, F, и из этих 16 символов (от 0 до 15) составляется любое число, так же как в нашей системе составляется любое число из десяти цифр (от 0 до 9).Соответственно, чтобы посчитать от 0 до 15 — нужно перебрать все символы, которые имеются в шестнадцатиричной системе (от 0 до F).

Теперь рассмотрим, как с помощью данной таблицы переводить из двоичной системы в шестнадцатиричную. Переведём число 100101000 из двоичной системы в шестнадцатиричную.

Чтобы выполнить данную задачу, необходимо разбить наше двоичное число по 4 цифры начиная с правого края, и каждую 4-ку цифр нужно найти в нашей таблице: 1000 — это будет 8, 0010 — 2, 0001 -это 1. В старшем разряде у нас осталась одна единица, мы её дополнили 3-мя нулями.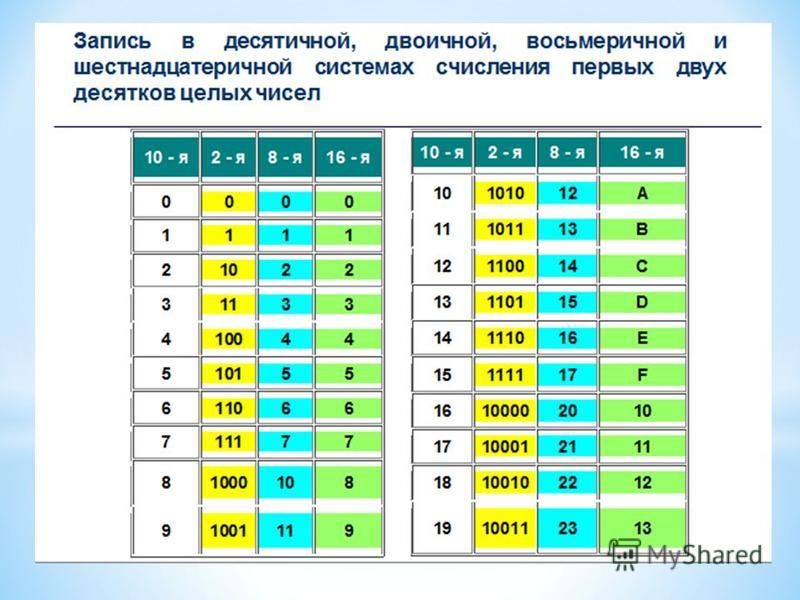

Значит число 100101000₂ в двоичной системе счисления будет 128₁₆ в шестнадцатиричной.

Перевод чисел из двоичной системы в восьмеричную

систему счисления.

Из двоичной системы в восьмеричную систему X₂ -> X₈ переводим точно так же, только теперь из таблицы берём не по четыре цифры, а по три цифры.

Таким образом, число 1001111001₂ в двоичной системе будет равно 1171₈ в восьмеричной системе.

Перевод чисел из шестнадцатиричной системы в двоичную

систему счисления.

Делаем точно так же, как и при переводе чисел из двоичной в шестнадцатиричную, но в обратном порядке. По таблице смотрим: D — 1101, F — 1111, 4 — 0100. Получается число 010011111101. Слева нули мы отбрасываем 10011111101.

Перевод чисел из восьмеричной системы в двоичную

систему счисления.

Поступаем, как мы поступали ранее. Разбиваем каждую цифру восьмеричной системы по 3 цифры двоичной системы, используя таблицу, которая приведена в начале статьи. Нули слева откидываем.

Перевод чисел из двоичной системы в десятичную

систему счисления.

Берём цифры двоичного числа, начиная с младшего разряда (т.е. справа), и начинаем умножать на двойку в соответствующей степени. Степень начинается с нуля и с каждым разом увеличивается на 1. Все эти произведения суммируем.

После вычисления получаем число в десятичной системе:

Результат 11010011₂ -> 211₁₀

Перевод чисел из десятичной системы в двоичную

систему счисления.

Рассмотрим, как перевести из десятичной системы в двоичную. Возьмём число 213.

Перевод чисел из шестнадцатиричной системы в восьмеричную систему

счисления и обратно.

Переведём число A10 из шестнадцатиричной системы в восьмеричную A10₁₆ -> X₈.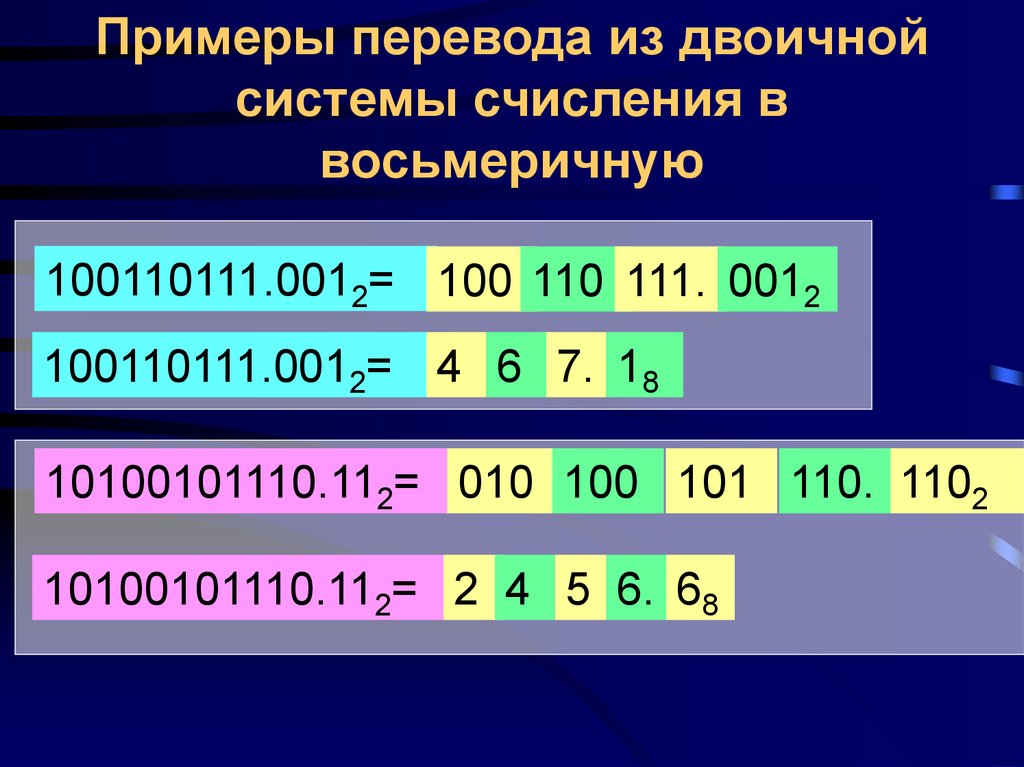

Разбиваем каждую цифру шестнадцатиричного кода по 4-ри цифры двоичного кода из таблицы в начале статьи (Т.е. переводим число в двоичную систему). Полученное число разбиваем по три цифры — и собираем число уже в восьмеричной системе — как показано на рисунке. Обратно переводим аналогично, только в обратном порядке.

Перевод чисел из шестнадцатиричной системы в десятичную

систему счисления.

Переведём число 5B3 из шестнадцатиричной системы в десятичную систему счисления 5B3₁₆ -> X₁₀.

Действуем точно также, как при переводе из двоичной системы в десятичную, только умножаем цифры на 16 в соответствующей степени. Буквы превращаем в десятичные числа из таблицы. Начинаем, как всегда, справа, т.е. с младшего разряда.

Перевод чисел из десятичной системы в шестнадцатиричную

систему счисления.

Переведём число 203 из десятичной системы в шестнадцатиричную систему счисления 203₁₀ -> X₁₆

Делим число на 16 до тех пор пока не получится число от 1 до 15. Записываем остатки в обратном порядке. Числа от 10 до 15 превращаем в буквы.

Перевод чисел из восьмеричной системы в десятичную

систему счисления.

Переведём число 347 из восьмеричной системы в десятичную систему счисления 347₈ -> X₁₀

Делаем аналогично предыдущим примерам, только теперь умножаем на 8 в соответствующей степени.

Перевод чисел из шестнадцатеричной системы счисления в двоичную

Перевод чисел из шестнадцатеричной системы счисления в двоичную — это преобразование чисел шестнадцатеричной системы счисления в числа двоичной системы счисления.

Содержание

[править] Алгоритм

Цифры исходного числа шестнадцатеричной системы счисления заменяются (слева направо) на соответствующие (по таблице тетрад) тетрады (четвёрки цифр двоичной системы счисления). Незначащие нули первой (самой левой) тетрады опускаются (отбрасываются).

[править] Таблица тетрад

• Заметим, что возможны другие способы перевода чисел: 16→4→2 и 16→10→2.

[править] Пример перевода 16→2

[править] Другие алгоритмы:

; ; ; ; ; ; ; ; ; ; ; ; ;
• перевод чисел из шестнадцатеричной системы счисления в двоичную; ; .

Персональные инструменты

Пространства имён

• Статья
• Обсуждение

Варианты

Просмотры

• Читать
• Правка
• История

Действия

Поиск

Навигация

Инструменты

• Последнее изменение этой страницы: 09:27, 24 ноября 2019.
• К этой странице обращались 6909 раз.

Текст страницы доступен по условиям лицензии GNU Free Documentation License. Материалы могут быть скопированы при условии указания активной ссылки на источник копирования в теле статьи (на той же странице). В отдельных случаях могут действовать условия лицензии Creative Commons Attribution-ShareAlike (CC BY-SA 3.0), информацию об этом можно просмотреть на странице обсуждения или в истории правок. В частности, условия лицензии CC BY-SA 3.0 действуют в отношении статей, перенесенных из Википедии (указание на факт переноса всегда есть в истории правок статьи или на ее странице обсуждения).

В текстах упоминаются организации, признанные на территории Российской Федерации террористическими и/или в отношении которых судом принято вступившее в законную силу решение о запрете деятельности. В том числе:

Признаны террористическими организациями: «Исламское государство» (другие названия: «Исламское Государство Ирака и Сирии», «Исламское Государство Ирака и Леванта», «Исламское Государство Ирака и Шама»), «Высший военный Маджлисуль Шура Объединенных сил моджахедов Кавказа», «Конгресс народов Ичкерии и Дагестана», «База» («Аль-Каида»), «Братья-мусульмане» («Аль-Ихван аль-Муслимун»), «Движение Талибан», «Имарат Кавказ» («Кавказский Эмират»), Джебхат ан-Нусра (Фронт победы) (другие названия: «Джабха аль-Нусра ли-Ахль аш-Шам» (Фронт поддержки Великой Сирии), Всероссийское общественное движение «Народное ополчение имени К. Минина и Д. Пожарского», Международное религиозное объединение «АУМ Синрике» (AumShinrikyo, AUM, Aleph) — см. полный список.

Деятельность запрещена по решению суда: Межрегиональная общественная организация «Национал-большевистская партия», Межрегиональная общественная организация «Движение против нелегальной иммиграции», Украинская организация «Правый сектор», Украинская организация «Украинская национальная ассамблея — Украинская народная самооборона» (УНА — УНСО), Украинская организация «Украинская повстанческая армия» (УПА), Украинская организация «Тризуб им. Степана Бандеры», Украинская организация «Братство», Межрегиональное общественное объединение — организация «Народная Социальная Инициатива» (другие названия: «Народная Социалистическая Инициатива», «Национальная Социальная Инициатива», «Национальная Социалистическая Инициатива»), Межрегиональное общественное объединение «Этнополитическое объединение „Русские“», Общероссийская политическая партия «ВОЛЯ», Общественное объединение «Меджлис крымскотатарского народа», Религиозная организация «Управленческий центр Свидетелей Иеговы в России» и входящие в ее структуру местные религиозные организации, Межрегиональное общественное движение «Артподготовка» — см. полный список.

Перевод из шестнадцатеричной системы счисления в двоичную

Для перевода чисел из шестнадцатеричной системы в двоичную, воспользуемся соответствующим алгоритмом. Важно заметить, что алгоритм перевода целых и дробных чисел будет отличаться.

Алгоритм перевода шестнадцатеричных чисел в двоичную систему счисления

1. Перевести шестнадцатеричное число число в двоичную систему счисления;
2. Полученное шестнадцатеричное число перевести в двоичную систему.

Подробно о переводе из шестнадцатеричной в десятичную систему смотрите на этой странице, о переводе из десятичной в двоичную — здесь. Для целостного понимания, разберем несколько примеров, но для начала вспомним алфавиты двоичной, десятичной и шестнадцатеричной систем счисления:

Перевод целого шестнадцатеричного числа в двоичную систему счисления

Пример 1: перевести число F16 из шестнадцатеричной в двоичную систему.

Как было сказано выше, необходимо сначала перевести число в десятичное, а полученный ответ в двоичный код.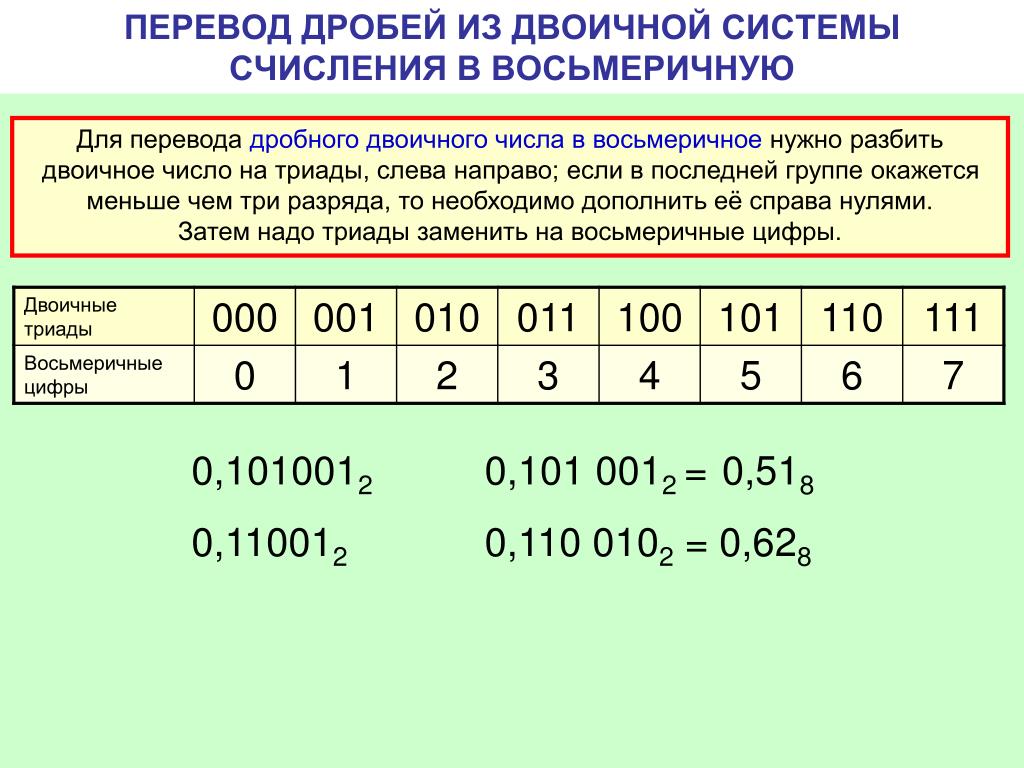 Решение будет выглядеть следующим образом:

Для перевода шестнадцатеричного числа F16 в десятичную систему, воспользуемся формулой:

F16₁₆=F ∙ 16 2 + 1 ∙ 16 1 + 6 ∙ 16 0 = 15 ∙ 256 + 1 ∙ 16 + 6 ∙ 1 = 3840 + 16 + 6 = 3862₁₀

Полученное число 3862 переведем из десятичной системы счисления в двоичную. Для этого, осуществим последовательное деление на 2, до тех пор пока остаток не будет меньше чем 2.

Полученные остатки записываем в обратном порядке, таким образом:

Перевод дробного шестнадцатеричного числа в двоичную систему счисления

Пример 2: перевести 1F.625 из шестнадцатеричной в двоичную систему счисления.

Общий смысл алгоритма перевода дробного числа, аналогичен алгоритму перевода целого, т.е. вначале переводим в десятичную, а затем в двоичную:

1. Для перевода числа 1F.625 в десятичную систему воспользуемся формулой:

1F.625₁₆=1 ∙ 16 1 + F ∙ 16 0 + 6 ∙ 16 -1 + 2 ∙ 16 -2 + 5 ∙ 16 -3 = 1 ∙ 16 + 15 ∙ 1 + 6 ∙ 0. 0625 + 2 ∙ 0.00390625 + 5 ∙ 0.000244140625 = 16 + 15 + 0.375 + 0.0078125 + 0.001220703125 = 31.384033203125₁₀

Обратите внимание! Формула перевода дробного числа в десятичную систему, очень похожа на формулу перевода целого, однако немного отличается.

2. Полученное число 31.384033203125 переведем из десятичной системы счисления в двоичную. Т.к. полученное число содержит дробную часть, нам потребуется перевести вначале целую часть, а затем дробную. Таким образом необходимо:

1. Перевести 31 в двоичную систему;
2. Перевести 0.384033203125 в двоичную систему;

2.1 Для того, чтобы перевести число 31 из десятичной системы счисления в двоичную, необходимо осуществить последовательное деление на 2, до тех пор пока остаток не будет меньше чем 2.

Полученные остатки записываем в обратном порядке, таким образом:

2.2 Для перевода десятичной дроби 0.384033203125 в двоичную систему, необходимо выполнить последовательное умножение дроби на 2, до тех пор, пока дробная часть не станет равной 0 или пока не будет достигнута заданная точность вычисления.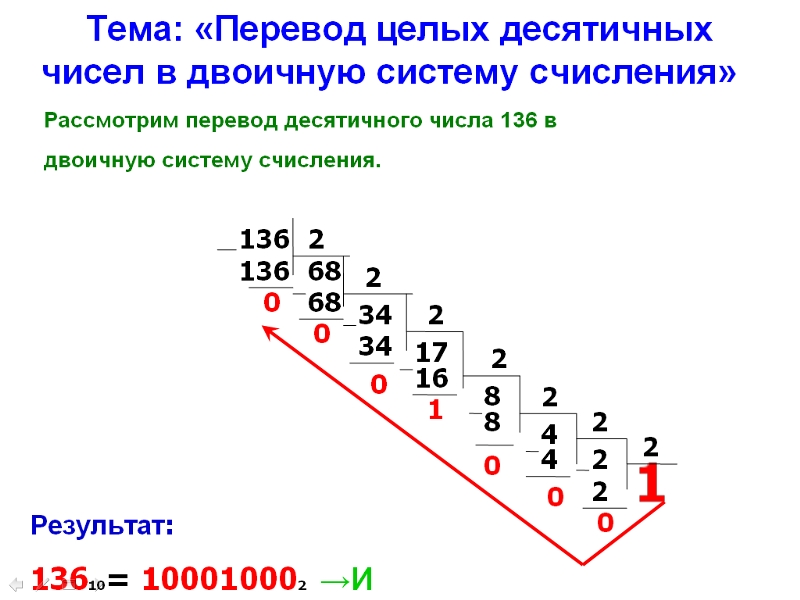 Получаем:

0.384033203125 ∙ 2 = 0.76806640625 (0)
0.76806640625 ∙ 2 = 1.5361328125 (1)
0.5361328125 ∙ 2 = 1.072265625 (1)
0.072265625 ∙ 2 = 0.14453125 (0)
0.14453125 ∙ 2 = 0.2890625 (0)
0.2890625 ∙ 2 = 0.578125 (0)
0.578125 ∙ 2 = 1.15625 (1)
0.15625 ∙ 2 = 0.3125 (0)
0.3125 ∙ 2 = 0.625 (0)
0.625 ∙ 2 = 1.25 (1)
0.25 ∙ 2 = 0.5 (0)

Шестнадцатеричное число в двоичное — значение, таблица преобразования, примеры, часто задаваемые вопросы

Преобразование шестнадцатеричного числа в двоичное выполняется для получения двоичного эквивалента шестнадцатеричного числа. Система счисления бывает четырех типов, а именно: двоичная система счисления, восьмеричная система счисления, десятичная система счисления и шестнадцатеричная система счисления. Каждая из этих систем счисления имеет свое собственное основное число, которое помогает в процессе преобразования. Шестнадцатеричное преобразование в двоичное выполняется по их соответствующим базовым числам.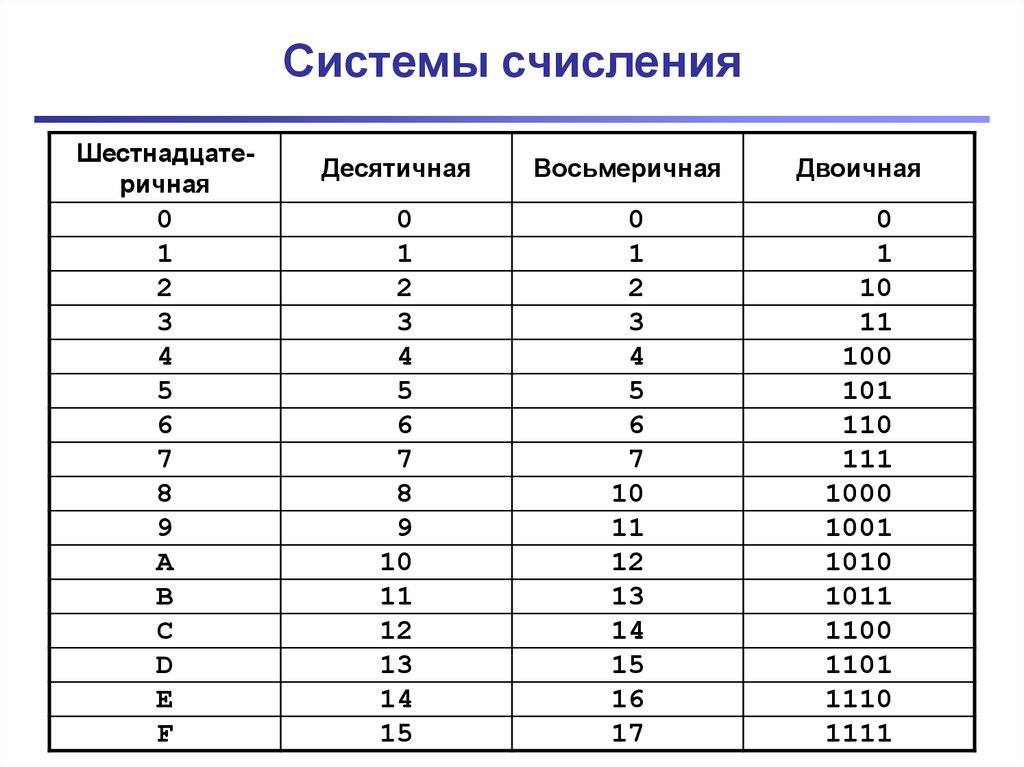 Давайте узнаем больше о том, как преобразовать шестнадцатеричные числа в двоичные числа.

1.	Что такое преобразование шестнадцатеричных чисел в двоичные?
2.	шагов для преобразования шестнадцатеричной системы счисления в двоичную
3.	Преобразование шестнадцатеричных чисел в двоичные с десятичной точкой
4.	Часто задаваемые вопросы о преобразовании шестнадцатеричных чисел в двоичные

Что такое преобразование шестнадцатеричной системы в двоичную?

Преобразование шестнадцатеричных чисел в двоичные — это процесс преобразования шестнадцатеричного числа с основанием 16 в двоичное число с основанием 2. Преобразование шестнадцатеричных чисел в двоичные важно, поскольку компьютеры понимают только двоичный язык. Следовательно, все другие типы систем счисления также преобразуются в двоичные числа.

Преобразование шестнадцатеричного в двоичное не может быть выполнено напрямую. Шестнадцатеричное число должно быть преобразовано в десятичное число, а затем преобразовано в двоичное число. Прежде чем мы перейдем к этапам преобразования, давайте посмотрим, что такое шестнадцатеричные и двоичные числа.

Шестнадцатеричная система счисления

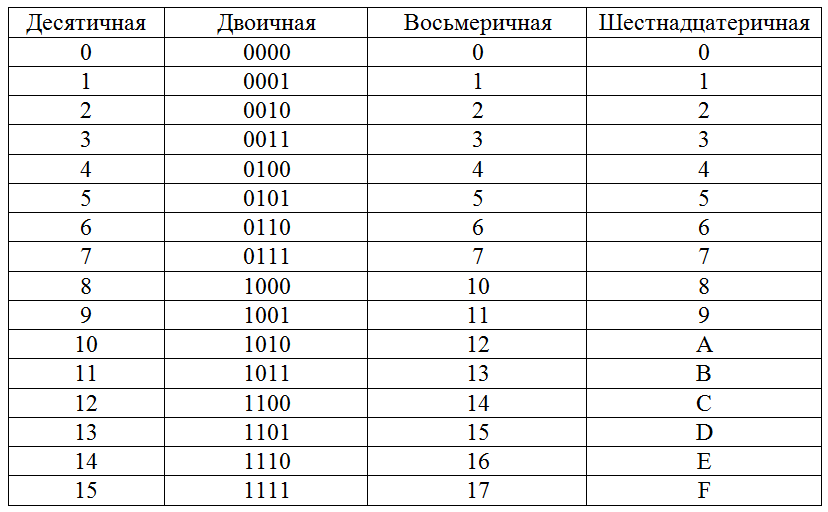
Шестнадцатеричная система счисления имеет базовое число 16 и использует шестнадцать цифр/алфавитов: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 и A, B, C, D, E, F. Здесь A-F шестнадцатеричной системы счисления означают соответственно числа 10-15 десятичной системы счисления. Эта система используется в компьютерах для сокращения больших строк двоичной системы. Самая большая одиночная цифра — F (на 1 меньше основания 16). Каждая цифра в шестнадцатеричной системе счисления представляет степень основания (16). Например: \(7B4_{16}, 9F_{16}, 3B1A_{16}\) — некоторые примеры чисел в шестнадцатеричной системе счисления.

Двоичная система счисления

Двоичная система счисления использует только две цифры: 0 и 1 с базовым числом 2.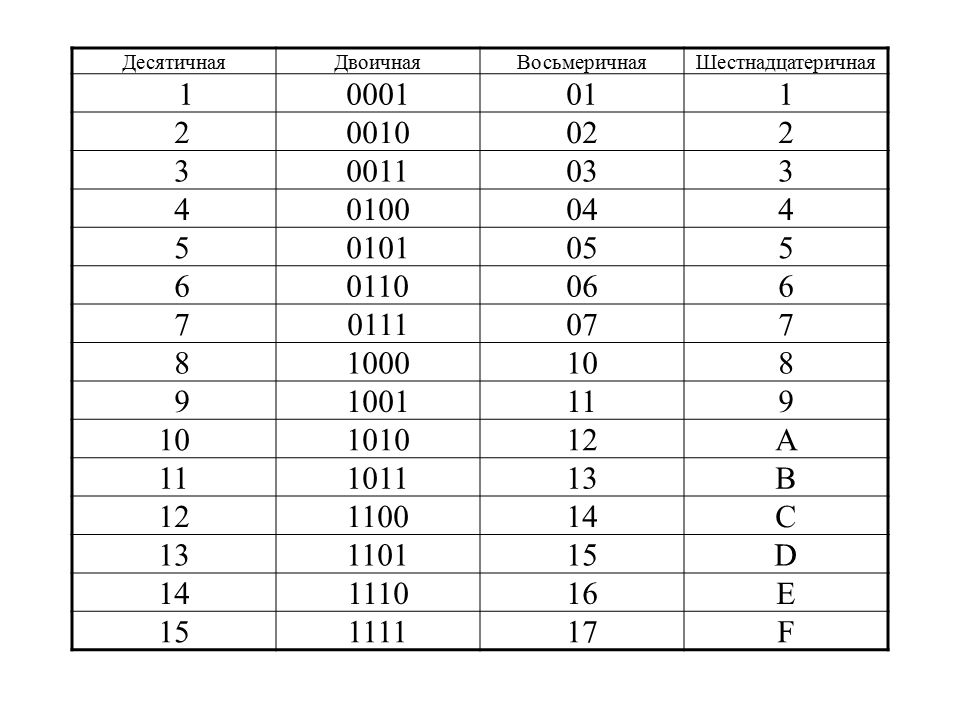

Цифры 0 и 1 называются битами, а 8 битов вместе составляют байт. Данные в компьютерах хранятся в виде битов и байтов. Двоичная система счисления не работает с другими числами, такими как 2,3,4,5 и так далее. Например: \(10001_2, 111101_2, 1010101_2 \) — некоторые примеры чисел в двоичной системе счисления.

шагов для преобразования шестнадцатеричной системы в двоичную

Чтобы преобразовать шестнадцатеричное число в двоичное, нам нужно сначала преобразовать шестнадцатеричное число в десятичное число, чтобы, наконец, преобразовать его в двоичное число. Один из наиболее важных аспектов, который следует помнить, заключается в том, что каждое шестнадцатеричное число дает 4 двоичных цифры. Преобразование шестнадцатеричного в двоичное может происходить двумя способами. Во-первых, после преобразования шестнадцатеричного числа в десятичное число мы преобразуем десятичное число, используя процесс деления для получения двоичного числа. Во-вторых, мы можем напрямую использовать таблицу преобразования шестнадцатеричной в десятичную в двоичную.

Давайте посмотрим на шаги обоих методов.

Метод 1: преобразование шестнадцатеричных чисел в десятичные и двоичные (без таблицы преобразования)

Этот метод требует как умножения, так и деления чисел с использованием соответствующих базовых чисел. Шестнадцатеричное основание числа равно 16, основание десятичного числа равно 10, а основание двоичного числа равно 2. Давайте рассмотрим шаги:

• Шаг 1: Запишите шестнадцатеричное число и найдите его эквивалентное десятичное число. .
• Шаг 2: Чтобы найти десятичный эквивалент, мы умножаем каждую цифру на 16 ^n-1 , где цифра находится на n-й позиции.
• Шаг 3: После умножения чисел сложите произведение этих чисел, чтобы получить десятичное число.
• Шаг 4: Чтобы преобразовать десятичное число в двоичное, мы делим десятичное число на 2, отбрасывая остаток и деля частное на 2, пока не получим ноль.
• Шаг 5: Когда частное равно нулю, мы упорядочиваем остаток снизу вверх, т. е. в обратном порядке, чтобы получить двоичное число.

Давайте рассмотрим пример для лучшего понимания. Преобразование шестнадцатеричного \((100)_{16}\) в двоичное.

Шаг 1 + 2: преобразовать \((100)_{16}\) в десятичное число, умножив каждую цифру на 16 ^n-1 . Умножьте

\((100)_{16}\) = 1 × 16 ^(3-1) + 0 × 16 ^(2-1) + 0 × 16 ^(1-1)

\((100)_{16}\) = 1 × 16 ² + 0 × 16 ¹ + 0 × 16 ⁰

Шаг 3: Умножьте числа и добавьте произведение, чтобы получить десятичное число.

\((100)_{16}\) = 1 × 256 + 0 × 16 + 0 × 1

\((100)_{16}\) = 256 + 0 + 0

\((100 )_{16}\) = 256

Следовательно, \((100)_{16}\) = \((256)_{10}\)

Шаг 4: Преобразование десятичного числа \((256) _{10}\) в двоичное число путем деления числа на 2 до тех пор, пока частное не станет равным нулю.

Следовательно, \((256)_{10}\) = \((100000000)_{2}\)

Шаг 5: После получения двоичного файла выполняется преобразование.

Следовательно, \((100)_{16}\) = \((100000000)_{2}\).

Метод 2: Преобразование шестнадцатеричного в десятичное в двоичное (с таблицей преобразования)

Этот метод является прямой процедурой, просто взглянув на таблицу диалога, мы можем преобразовать шестнадцатеричное в двоичное. Шаги довольно просты, давайте посмотрим на них:

• Шаг 1: Запишите шестнадцатеричное число
.
• Шаг 2: Найдите эквивалентное десятичное число каждой из цифр, взглянув на таблицу преобразования.
• Шаг 2: Получив десятичное число, просмотрев ту же таблицу, мы можем преобразовать его в двоичное.
• Шаг 3: Объедините все двоичные числа, чтобы получить окончательное двоичное число.

Давайте рассмотрим пример для лучшего понимания. Преобразование шестнадцатеричного \((E5B)_{16}\) в двоичное.

Шаг 1: У нас есть шестнадцатеричное число как \((E5B)_{16}\).

Шаг 2: Глядя на таблицу преобразования, найдите эквивалент каждой цифры.

E = \((14)_{10}\) , 5 = \((5)_{10}\) , B = \((11)_{10}\)

Шаг 3: После получается десятичное число каждой цифры, глядя на таблицу преобразования, преобразуйте каждое десятичное число в двоичное.

\((14)_{10}\) = \((1110)_{2}\)

\((5)_{10}\) = \((0101)_{2}\)

\((11)_{10}\) = \((1011)_{2}\)

Шаг 4: Объедините все двоичные числа, чтобы получить окончательное число.

Следовательно, \((E5B)_{16}\) = \((111001011011)_{2}\).

Преобразование шестнадцатеричных чисел в двоичные с десятичной точкой

Чтобы преобразовать шестнадцатеричное число в двоичное, мы используем метод, аналогичный тому, что использовался в предыдущем разделе. Мы используем таблицу преобразования для преобразования шестнадцатеричных чисел в двоичные. При преобразовании с десятичной запятой мы используем те же шаги, но не учитываем нули, расположенные в самой правой части, поскольку они называются конечными нулями. Давайте посмотрим на пример, преобразуем \((0. C48)_{16}\) в двоичный файл.

Шаг 1: У нас есть шестнадцатеричный вид \((0.C48)_{16}\).

Шаг 2: Глядя на таблицу преобразования, найдите эквивалент каждой цифры. Ноль в расчет не берем.

C = \((12)_{10}\) , 4 = \((4)_{10}\) , 8 = \((8)_{10}\)

Шаг 3: После получается десятичное число каждой цифры, глядя на таблицу преобразования, преобразуйте каждое десятичное число в двоичное.

\((12)_{10}\) = \((1100)_{2}\)

\((4)_{10}\) = \((0100)_{2}\)

\((8)_{10}\) = \((1000)_{2}\)

Шаг 4: Объедините все двоичные числа, чтобы получить окончательное число. Ноль перед десятичным числом будет записан вместе с последним двоичным числом.

Следовательно, \((0.C48)_{16}\) = \((110001001000)_{2}\).

Связанные темы

Вот несколько интересных тем, связанных с преобразованием шестнадцатеричных чисел в двоичные, взгляните.

• Двоично-десятичный калькулятор
• Калькулятор преобразования десятичной системы в двоичную
• Преобразование десятичной дроби в двоичную формулу

Часто задаваемые вопросы о преобразовании шестнадцатеричных чисел в двоичные

Что такое преобразование шестнадцатеричной системы в двоичную?

Преобразование шестнадцатеричных чисел в двоичные помогает получить двоичный эквивалент шестнадцатеричной цифры. Двоичная и шестнадцатеричная системы счисления имеют свои собственные базовые числа, которые помогают в процессе преобразования. Базовое число шестнадцатеричного числа равно 16, а базовое число двоичного числа равно 2. Чтобы преобразовать шестнадцатеричное число в двоичное, нам нужно преобразовать шестнадцатеричные цифры в десятичные, чтобы, наконец, преобразовать их в двоичные.

Как преобразовать шестнадцатеричное число в двоичное?

Преобразование шестнадцатеричных чисел в двоичные осуществляется двумя разными способами. Первый метод заключается в преобразовании шестнадцатеричной цифры в десятичную путем умножения каждой цифры на 16 ^n-1 и сложения их вместе. Далее преобразуйте десятичное число в двоичное, разделив десятичное число на 2, пока частное не станет равным нулю. Как только цель достигнута, двоичное число получается путем записи остатка снизу вверх. Второй метод выполняется напрямую с помощью таблицы преобразования.

Как преобразовать шестнадцатеричное число в двоичное с десятичной точкой?

Преобразование шестнадцатеричного в двоичное с десятичной точкой выполняется простым способом с помощью таблицы преобразования. Вот шаги:

• Напишите шестнадцатеричные цифры.
• Преобразуйте каждую цифру в эквивалентное десятичное число с помощью таблицы преобразования.
• После получения десятичного числа найдите двоичный эквивалент каждого десятичного числа.
• После получения каждого двоичного числа запишите их все вместе, чтобы получить окончательное двоичное число.

Что такое 9C в двоичном формате?

Чтобы найти двоичное число в шестнадцатеричном формате, нам нужно сначала преобразовать шестнадцатеричное число в десятичное, а затем в двоичное. Итак, шестнадцатеричная 9С при преобразовании в десятичную записывается как:

9 = 9 и С = 12, глядя на таблицу преобразования.

9 × 16 ¹ + 12 × 16 ⁰ = 144 + 12 = 156.

\(9C_16\) = \(156_10\).

Следовательно, двоичное значение равно \(9C_16\) = \(10011100_2\).

Что такое шестнадцатеричный FF в двоичном формате?

Чтобы преобразовать шестнадцатеричный FF в двоичный, мы сначала преобразуем его в десятичный, а затем в двоичный.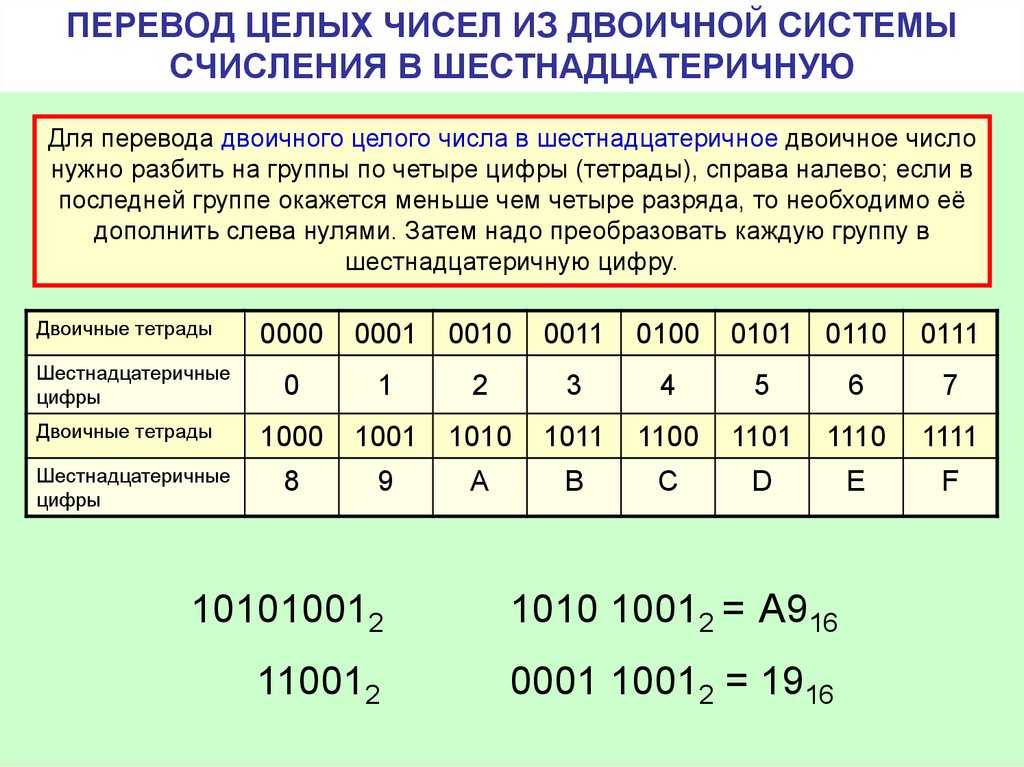 Вот шаги:

FF в десятичном виде записывается как F = \(15_10\) и F = \(15_10\).

Преобразование десятичного числа в двоичное, \(15_10\) = \((1111)_{2}\) и \(15_10\) = \((1111)_{2}\)

Следовательно, \(FF_16\) ) = \((11111111)_{2}\).

Какое основание используется для преобразования шестнадцатеричных чисел в двоичные?

Чтобы преобразовать шестнадцатеричное число в двоичное, мы сначала преобразуем шестнадцатеричное число в десятичное число, используя базовое число 16, которое является базовым числом шестнадцатеричного числа. Как только десятичное число получено, мы используем основание двоичной системы счисления, то есть 2, для преобразования десятичного числа в двоичное. Следовательно, шестнадцатеричный код преобразуется в двоичный.

ПРЕОБРАЗОВАТЕЛЬ ШЕСТНАДЦАТЕРИЧНЫХ В ДВОИЧНЫЕ (ШАГАМИ)

Введите шестнадцатеричное число.

RESULT

( A46.09 ) ₂ = ( 101001000110. 00001001 ) ₈

DESCRIPTIONS

1010A0100401106.0000010019

Чтобы преобразовать шестнадцатеричное число в двоичное, мы записываем 4-битный двоичный эквивалент каждой шестнадцатеричной цифры в том же порядке.

( A46.09 ) ₂ = ( 101001000110.00001001 ) ₈

. Другая информация

.

Нажмите здесь, чтобы увидеть восьмеричный эквивалент A46.09

Скачать решение

Скопировано в буфер обмена

Скопировать текст

© MadforMath

Посмотреть решение

2 → 8 2 → 16 8 → 2 8 → 16 16 → 2 16 → 8

ПРЕОБРАЗОВАНИЕ ШЕСТНАДЦАТЕРИЧНОГО В ДВОИЧНОЕ

Чтобы преобразовать шестнадцатеричное число в двоичное, мы записываем 4-битный двоичный эквивалент каждой шестнадцатеричной цифры в том же порядке.

4-битные двоичные эквиваленты шестнадцатеричных цифр показаны ниже.

Шестнадцатеричный	4-битный двоичный код
0	0000
1	0001
2	0010
3	0011
4	0100
5	0101
6	0110
7	0111
8	1000
9	1001
А	1010
Б	1011
С	1100
Д	1101
Е	1110
Ф	1111

ЧТО ТАКОЕ ШЕСТНАДЦАТЕРИЧНОЕ В ДВОИЧНОЕ ПРЕОБРАЗОВАТЕЛЬ?

Преобразователь шестнадцатеричных чисел в двоичные,

• Вычисляет двоичный эквивалент введенного шестнадцатеричного числа,
• Графически иллюстрирует преобразование и
• Пошаговое описание решения.

КАК ИСПОЛЬЗОВАТЬ ПРЕОБРАЗОВАТЕЛЬ ШЕСТНАДЦАТЕРИЧНЫХ В ДВОИЧНЫЕ?

Преобразователь шестнадцатеричного кода в двоичный можно использовать двумя способами.

• ПОЛЬЗОВАТЕЛЬСКИЕ ВВОДЫ

  Вы можете ввести шестнадцатеричное число в поле ввода и нажать кнопку « ПРЕОБРАЗОВАТЬ ». Результат и пояснения появляются под калькулятором

• СЛУЧАЙНЫЕ ВВОДЫ

  Вы можете щелкнуть ЗНАЧОК УМЕР рядом с полем ввода. Если вы используете это свойство, случайное шестнадцатеричное число генерируется и автоматически вводится в калькулятор. Вы можете увидеть результат и пояснения под калькулятором. Вы можете создавать свои собственные примеры и практиковаться в использовании этого свойства.

• ОЧИСТКА ПОЛЯ ВВОДА

  Чтобы проверить двоичные эквиваленты других шестнадцатеричных чисел, вы можете очистить поле ввода, нажав кнопку ОЧИСТИТЬ под полем ввода.