Шестнадцатеричная система счисления.
Шестнадцатеричная система счисления имеет набор цифр {0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F} и основание степени (p) – 16.
Количественный эквивалент некоторого целого n-значного шестнадцатеричного числа f45ed23c равен:
15*167+4*166+5*165+14*164+13*163+2*162+3*161+12*160.
Приведем соответствие двоичных чисел и их десятичных и шестнадцатеричных эквивалентов.
Десятичное число | Двоичная тетрада | Шестнадцатеричное число |
0 | 0000 | 0 |
1 | 0001 | 1 |
2 | 0010 | 2 |
3 | 0011 | 3 |
4 | 0100 | 4 |
5 | 0101 | 5 |
6 | 0110 | 6 |
7 | 0111 | 7 |
8 | 1000 | 8 |
9 | 1001 | 9 |
10 | 1010 | A |
11 | 1011 | B |
12 | 1100 | C |
13 | 1101 | D |
14 | 1110 | E |
15 | 1111 | F |
16 | 10000 | 10 |
Поначалу запомнить
эти соотношения сложно, поэтому полезно
иметь под руками некоторую справочную
информацию.
Приведенная таблица содержит
представления десятичных чисел из
диапазона 0-16 в двоичной и шестнадцатеричной
системах счисления. Ее удобно использовать
для взаимного преобразования чисел в
рассмотренных трех системах счисления.
Шестнадцатеричная система счисления
при вычислениях несколько сложнее, чем
двоичная, в частности, в том, что касается
правил переносов в старшие разряды.
Главное здесь запомнить следующее
равенство – (1+F=10)
Перевод чисел из одной системы счисления в другую
Одного знания о существовании разных систем счисления мало. Для того, чтобы в полной мере использовать их в своей практической работе при программировании, необходимо научиться выполнять взаимное преобразование чисел между тремя системами счисления.
Перевод в десятичную систему счисления
Перевод в десятичную
систему счисления является самым
простым. Обычно его производят с помощью
так называемого алгоритма замещения,
суть которого заключается в следующем:
сначала в десятичную систему счисления
переводится основание степени p,
а затем – цифры исходного числа.
Перевод в двоичную систему счисления Перевод из десятичной системы счисления
Перевод числа в двоичную систему счисления из десятичной выполняется по следующему алгоритму:
Резделить десятичное число A на 2. Запомнить частное q и остаток a.
Если в результате шага 1 частное q не равно 0, то принять его за новое делимое и отметить остаток a, который будет очередной значащей цифрой, и вернуться к шагу 1, на котором в качестве нового делимого участвует полученное на шаге 2 частное.
Если в результате шага 1 частное q равно 0, алгоритм прекращается. Выписать остатки в порядке, обратном их получению. Получится двоичный эквивалент исходного числа.
Переведем в двоичную систему счисления число 247.
1 шаг.
Делим 247 на 2. Результат 123 остаток 1.
2 шаг.
Делим 123 на 2.
Результат 61 остаток 1.
3 шаг.
4 шаг.
Делим 30 на 2. Результат 15 остаток 0.
5 шаг.
Делим 15 на 2. Результат 7 остаток 1.
6 шаг.
Делим 7 на 2. Результат 3 остаток 1.
7 шаг.
Делим 3 на 2. Результат 1 остаток 1.
8 шаг.
Делим 1 на 2. Результат 0, есть остаток. (1)
Получаем следующее двоичное чсисло: 11110111.
Перевод из восьмеричной и шестнадцатеричной систем счисления в двоичную с помощью таблиц — Информатика, информационные технологии
csaa Комментарии к записи Перевод из восьмеричной и шестнадцатеричной систем счисления в двоичную с помощью таблиц отключены
Перевод целых чисел из десятичной системы в любую другую позиционную систему счисления
При переводе целого десятичного числа в систему с основанием q его необходимо последовательно делить на q до тех пор, пока не останется остаток, меньший или равный q–1.
Число в системе с основанием q записывается как последовательность остатков от деления, записанных в обратном порядке, начиная с последнего.
Пример: Перевести число 75 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:
Перевод правильных десятичных дробей в любую другую позиционную систему счисления
При переводе правильной десятичной дроби в систему счисления с основанием q необходимо сначала саму дробь, а затем дробные части всех последующих произведений последовательно умножать на q, отделяя после каждого умножения целую часть произведения. Число в новой системе счисления записывается как последовательность полученных целых частей произведения.
Умножение производится до тех поp, пока дробная часть произведения не станет равной нулю. Это значит, что сделан точный перевод. В противном случае перевод осуществляется до заданной точности. Достаточно того количества цифр в результате, которое поместится в ячейку.
Пример: Перевести число 0,35 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:
Ответ:
0,35(10)=0,01011(2)=0,263(8)=0,59(16)
Перевод из восьмеричной и шестнадцатеричной систем счисления в двоичную с помощью таблиц
Двоичная система, удобная для компьютеров, для человека неудобна из-за ее громоздкости и непривычной записи.
Перевод чисел из десятичной системы в двоичную и наоборот выполняет машина. Однако, чтобы профессионально использовать компьютер, следует научиться понимать слово машины. Для этого и разработаны восьмеричная и шестнадцатеричная системы.
Числа в этих системах читаются почти так же легко, как десятичные, требуют соответственно в три (восьмеричная) и в четыре (шестнадцатеричная) раза меньше разрядов, чем в двоичной системе (ведь числа 8 и 16 – соответственно, третья и четвертая степени числа 2).
Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему очень прост: достаточно каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) или тетрадой (четверкой цифр).
Все двоичные числа записаны в четырёхзначном виде (там, где знаков меньше четырёх, слева добавлены нули). Проделаем следующее: каждую цифру в шестнадцатеричном числе 15FC заменим на соответствующую ей в таблице четвёрку двоичных знаков. Т.е., перекодируем число 15FC по таблице в двоичную форму.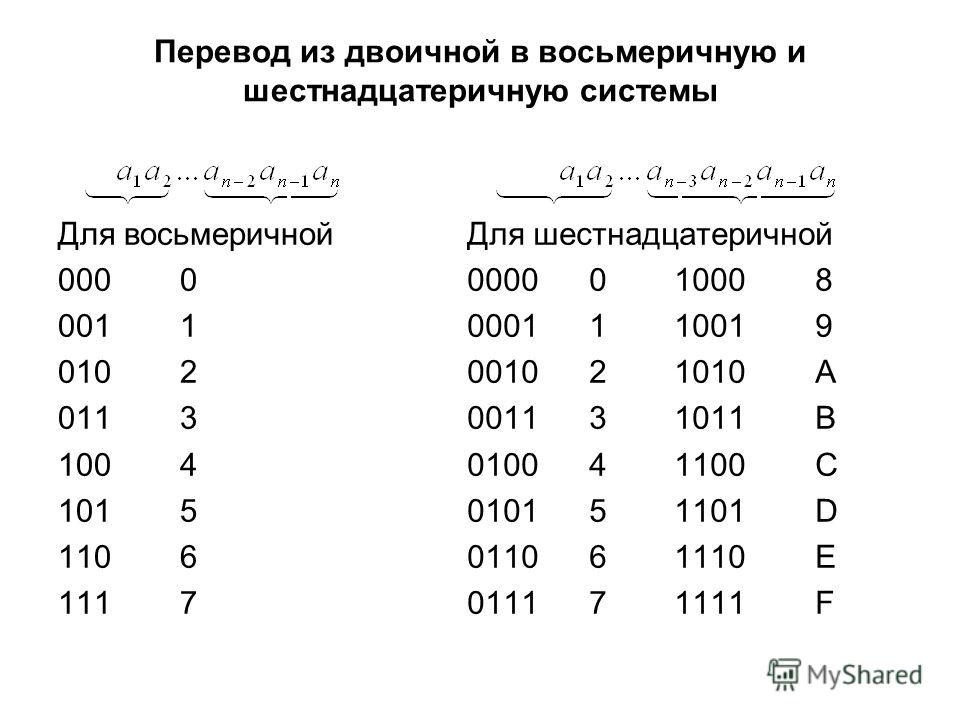
Получается:
0001 0101 1111 1100.
Если отбросить нули справа (в любой системе счисления они не влияют на значение целого числа), то получим искомое двоичное число.
| десятичная | восьмеричная | двоичная | шестнадцатеричная | двоичная |
| — | — | |||
| — | — | |||
| — | — | — | А(10) | |
| — | — | — | B(11) | |
| — | — | — | C(12) | |
| — | — | — | D(13) | |
| — | — | — | E(14) | |
| — | — | — | F(15) |
Перевод в двоично-десятичную систему (ДДК — двоично-десятичное кодирование)
Для перевода из десятичной системы в ДДК, каждая цифра десятичной системы записывается в виде четырех разрядов двоичной системы.
Пример: 351(10)=0011 0101 0001(2-10)
Преобразуем теперь двоично-десятичное число 1000 0000 0111 0010 в его десятичный эквивалент. Каждая группа из 4 бит прямо преобразуется в ее десятичный эквивалент, и тогда получаем 1000 0000 0111 0010ДДК=807210.
| десятичное | ДДК=(2-10) |
Статьи к прочтению:
- Первый звонок: андреа лопес
- Подбор литературы и составление списка использованных источников
Таблица триад и тетрад. Системы счисления.
Похожие статьи:
Перевод двоичных чисел в восьмеричную и шестнадцатеричную системы счисления
Перевод двоичного числа в восьмеричную и шестнадцатеричную системы осуществляется также просто: двоичное число разбивается вправо и влево от точки,…
Для перевода восьмеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной триадой.
Пример.Число перевести в двоичную систему счисления. Для перевода шестнадцатеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей…
Шестнадцатеричный — SparkFun Learn
- Главная
- Учебники
- Шестнадцатеричный
≡ Страниц
Авторы: Джимблом
Избранное Любимый 32
Дышите спокойно! Мы избавились от сложных преобразований. Мы используем шестнадцатеричный код в электротехнике и вычислительной технике, потому что его невероятно легко преобразовывать в двоичный код и из него — язык компьютеров, состоящий из нулей и единиц.
Преобразование между шестнадцатеричным и двоичным числами легко, потому что каждая цифра шестнадцатеричного числа «сопоставляется» с четырьмя битами (бит представляет собой отдельную двоичную цифру) двоичного значения.
Таким образом, байт — восемь двоичных цифр — всегда может быть представлен как
Преобразование двоичного формата в шестнадцатеричный
Начнем с преобразования первых 16 шестнадцатеричных значений в двоичные.
| Decimal | Hex | Binary | … | Decimal | Hex | Binary |
|---|---|---|---|---|---|---|
| 00 | 0 | 0000 | 08 | 8 | 1000 | |
| 01 | 1 | 0001 | 09 | 9 | ||
| 02 | 2 | 0010 | 10 | A | 1010 | |
| 03 | 3 | 0011 | 11 | B | 1011 | |
| 04 | 4 | 0100 | 12 | C | 1100 | |
| 05 | 5 | 0101 | 13 | D | 1101 | |
| 06 | 6 | 0110 | 14 | E | 1110 | |
| 07 | 7 | 0111 | 15 | F | 1111 |
По мере того, как вы будете расти и продолжать использовать шестнадцатеричный и двоичный код, эти 16 значений станут запоминаться.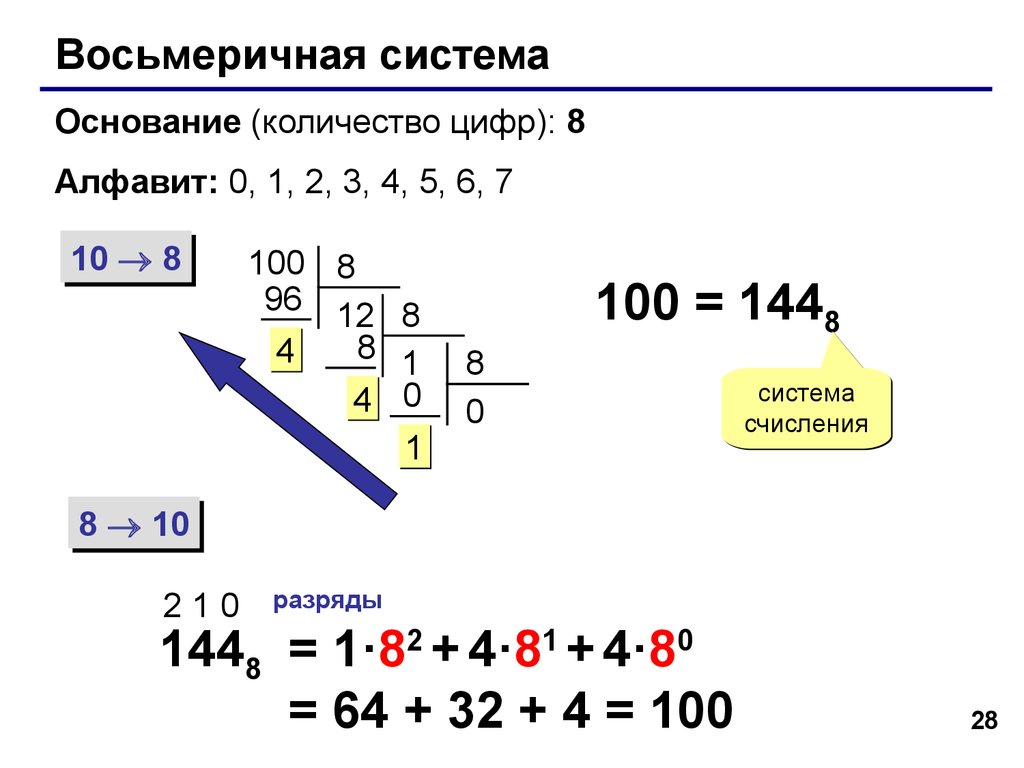
Для преобразования между двоичным и шестнадцатеричным числом мы хотим воспользоваться тем фактом, что четыре двоичных разряда (бита) отображаются в один шестнадцатеричный разряд. Выполните следующие действия для преобразования двоичного формата в шестнадцатеричный.
- Разделить двоичное значение на группы по четыре , начиная с самой правой стороны.
- Для каждой группы из четырех цифр обратитесь к приведенной выше таблице, чтобы найти соответствующее шестнадцатеричное значение, и
Вот оно! Давайте попробуем.
Двоичный код в шестнадцатеричный Пример: преобразование 0b101111010100001
Для начала начните с правого края двоичного числа и отсортируйте 1 и 0 в группы по четыре:
| Отсортировано двоичных цифр: | 0101 | 1110 | 1010 | 0001 |
|---|
Теперь проконсультируйтесь с нашим большим Table-O’-Sixteen, чтобы преобразовать группы с четвертью в Hex Digit:
Барнальные бинарные цифры.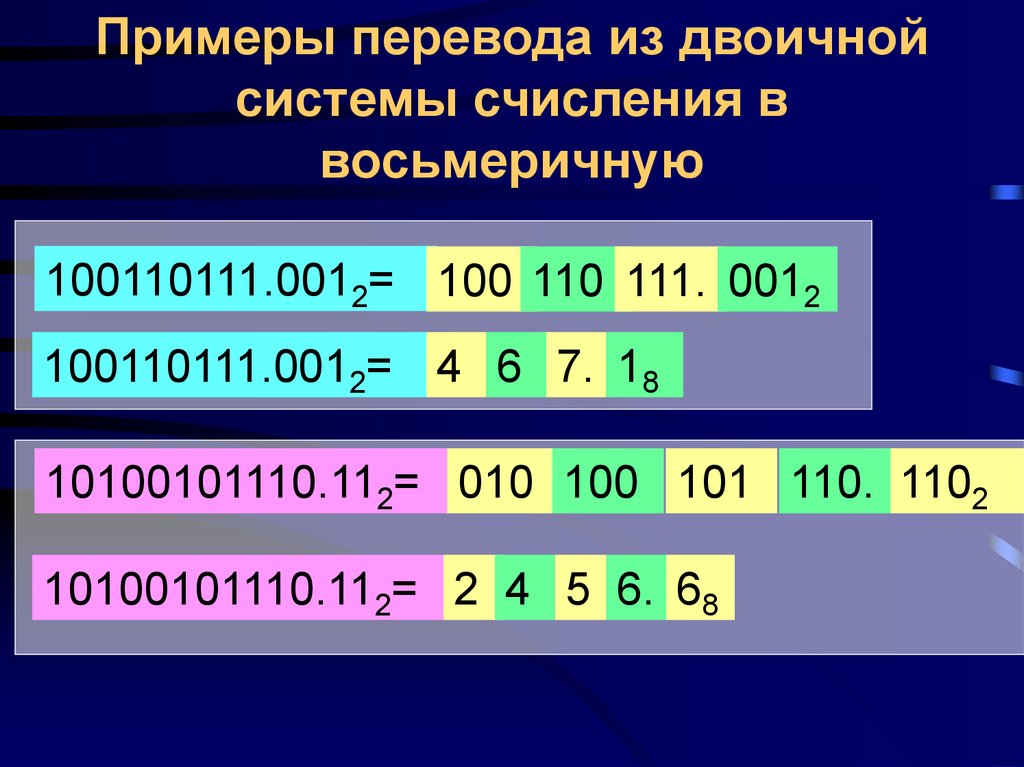 | 133...1332.||||
|---|---|---|---|---|
| 1110 | 1010 | 0001 | ||
| HEX Эквиваленты: | 5 | E | A | 1 | A | D | B | E | E | F |
Then convert each hex digit into four bits:
| Hex Digits Sorted: | D | E | A | D | B | E | E | F |
|---|---|---|---|---|---|---|---|---|
| Hex Digits Sorted: | 1101 | 1110 | 1010 | 1101 | 1011 | 1110 | 1110 | 1111 |
Другими словами, 0xDEADBEEF = 0b11011110101011011011111011101111.
Это много 1 и 0.
Использование шестнадцатеричного представления и идентификации байтов
Приведенные выше примеры демонстрируют одну из величайших возможностей шестнадцатеричного представления: легко представляет значения байтов . Нам часто проще работать с Hex, потому что значения короче и лучше запоминаются, чем длинная строка из 1 и 0.
Например, приведенная выше карта регистров взята из LSM9DS0 (изящный, 9датчик глубины резкости). В нем перечислены адреса регистров, которые используются для управления датчиком, как в шестнадцатеричном, так и в двоичном формате. Если вы хотите получить доступ к регистру CTRL_REG2_G, гораздо проще запомнить 0x21, чем 0b010001, а обнаружить опечатку в шестнадцатеричном значении гораздо проще, чем в двоичном. По этой причине мы гораздо чаще будем использовать шестнадцатеричные значения в нашем коде, чем их двоичные эквиваленты.
python — преобразовать шестнадцатеричный код в двоичный
Преобразовать шестнадцатеричный код в двоичный
У меня ABC123EFFF.
Я хочу иметь 001010101111000001001000111110111111111111 (т.е. двоичный репр. с, скажем, 42 цифрами и ведущими нулями).
Краткий ответ:
Новые f-строки в Python 3.6 позволяют вам сделать это, используя очень лаконичный синтаксис:
>>> f'{0xABC123EFFF:0>42b}'
'001010101111000001001000111110111111111111'
или, чтобы разбить это на семантику:
>>> number, pad, rjust, size, kind = 0xABC123EFFF, '0', '>', 42, 'b'
>>> f'{номер:{pad}{rjust}{размер}{вид}}'
'001010101111000001001000111110111111111111'
Длинный ответ:
На самом деле вы говорите, что у вас есть значение в шестнадцатеричном представлении, и вы хотите представить эквивалентное значение в двоичном формате.
Значение эквивалентности является целым числом. Но вы можете начать со строки, а для просмотра в двоичном виде вы должны закончить строкой.
Преобразование шестнадцатеричного в двоичное, 42 цифры и ведущие нули?
У нас есть несколько прямых способов достичь этой цели без хаков с использованием слайсов.
Во-первых, прежде чем мы сможем выполнять какие-либо бинарные манипуляции, преобразовать в int (я предполагаю, что это в строковом формате, а не как литерал):
>>> целое число = int('ABC123EFFF', 16)
> >> целое
737679765503
в качестве альтернативы мы могли бы использовать целочисленный литерал, выраженный в шестнадцатеричной форме:
>>> integer = 0xABC123EFFF >>> целое 737679765503
Теперь нам нужно выразить наше целое число в двоичном представлении.
Используйте встроенную функцию, формат
Затем перейдите к формату :
>>> формат (целое число, '0> 42b') '001010101111000001001000111110111111111111'
Используется мини-язык спецификации форматирования.
Чтобы разобрать это, вот его грамматическая форма:
[[fill]align][sign][#][0][width][][.precision][type]
Чтобы превратить это в спецификацию для наших нужд, мы просто исключаем то, что нам не нужно:
>>> spec = '{fill}{align}{width}{type}'. format(fill=' 0', выравнивание='>', ширина=42, тип='b')
>>> спец.
'0>42b'
format(fill=' 0', выравнивание='>', ширина=42, тип='b')
>>> спец.
'0>42b'
и просто передайте это в формат
>>> bin_representation = format(integer, spec) >>> bin_representation '001010101111000001001000111110111111111111' >>> печать (bin_representation) 001010101111000001001000111110111111111111
Форматирование строки (шаблон) с помощью
str.format Мы можем использовать это в строке, используя метод str.format :
>>> 'вот двоичная форма: {0:{spec}}' .format(целое, спец=спецификация)
'вот двоичная форма: 001010101111000001001000111110111111111111'
Или просто поместите спецификацию прямо в исходную строку:
>>> 'вот двоичная форма: {0:0>42b}'.format(integer)
'вот двоичная форма: 001010101111000001001000111110111111111111'
Форматирование строк с новыми f-строками
Продемонстрируем новые f-строки. Они используют одни и те же правила форматирования мини-языка:
>>> целое число = 0xABC123EFFF
>>> длина = 42
>>> f'{целое число:0>{длина}b}'
'001010101111000001001000111110111111111111'
Теперь давайте поместим эту функциональность в функцию для повторного использования:
def bin_format(integer, length):
вернуть f'{целое число:0>{длина}b}'
А теперь:
>>> bin_format (0xABC123EFFF, 42) '001010101111000001001000111110111111111111'
В сторону
Если вы просто хотите закодировать данные в виде строки байтов в памяти или на диске, вы можете использовать метод int.
