Двоично-шестнадцатеричная таблица
2-ная | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 |
16-ная | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
2-ная | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1111 | |
16-ная | 8 | 9 | A | B | C | D | E | F |
2-ная | 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
8-ная | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Задания
1. | Переведите в десятичную систему счисления: | |||
| ||||
2. | Сравните два числа: | |||
|
|
Слайд
1.26
Использование калькулятора Windows
Число 999 в десятичной, шестнадцатеричной и двоичной системах.
Слайд
1.28
Вычисления в двоичной системе счисления
Следующим
важнейшим достижением информатики
является возможность выполнения
компьютером арифметических и логических
действий над числами и кодами символов
алфавита.
Арифметические действия:
Арифметические действия, выполняемые в двоичной системе, подчиняются тем же правилам, что и в десятичной системе. Только в двоичной системе перенос единиц в старший разряд возникает чаще, чем в десятичной. Вот как выглядит таблица сложения в двоичной системе:
0 + 0 = 0 0 + 1 = 1
1 + 0 = 1 1 + 1 = 0 (перенос в старший разряд)
Таблица умножения для двоичных чисел еще проще:
0 * 0 = 0 0 * 1 = 0 1 * 0 = 0 1 * 1 = 1
Рассмотрим
подробнее, как происходит процесс
умножения двоичных чисел. Пусть надо
умножить число 1101 на 101 (оба числа в
двоичной системе счисления). Машина
делает это следующим образом: она берет
число 1101 и, если первый элемент второго
множителя равен 1, то она заносит его в
сумму. Затем сдвигает число 1101 влево на
одну позицию, получая тем самым 11010, и
если, второй элемент второго множителя
равен единице, то тоже заносит его в
сумму. Если элемент второго множителя
равен нулю, то сумма не изменяется.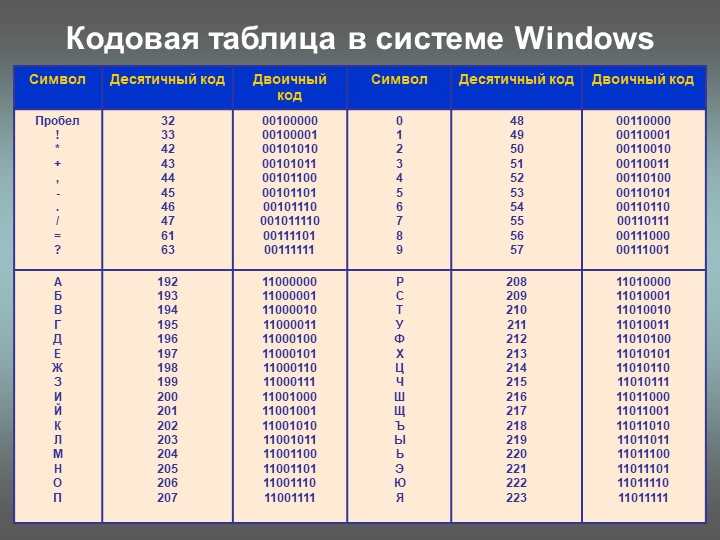
Двоичное деление основано на методе, знакомом вам по десятичному делению, т. е. сводится к выполнению операций умножения и вычитания. Выполнение основной процедуры — выбор числа, кратного делителю и предназначенного для уменьшения делимого, здесь проще, так как таким числом могут быть только либо 0, либо сам делитель.
А
Слайд
1.29
Слайд
1.30
лгебра логики
Логические действия компьютера основаны на применении Алгебры Логики.
Алгебра логики (алгебра высказываний) — раздел математической логики, в котором изучаются логические операции над высказываниями. Высказывания могут быть истинными, ложными или содержащими истину и ложь в разных соотношениях.
Определения
Базовыми элементами, которыми оперирует алгебра логики, являются высказывания. Высказывания строятся над множеством {B, , , , 0, 1}, где B — непустое множество, над элементами которого определены три операции:
отрицание
конъюнкция (бинарная),
дизъюнкция (бинарная),
а
также константы —
логический ноль 0 и логическая единица 1.
ИНВЕРСИЯ (Логическое отрицание) — если исходное выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное выражение ложно, то результат отрицания будет истинным/ Данная операция означает, что к исходному логическому выражению добавляется частица
Конъю́нкция (от лат. conjunctio союз, связь) — логическая операция, по своему применению максимально приближённая к союзу «и». Синонимы: логи́ческое «И», логи́ческое умноже́ние, иногда просто «И».
Конъюнкция может быть бинарной операцией, то есть, иметь два операнда, тернарной операцией, т.е. иметь три операнда или n-арной операцией, т.е. иметь n операндов. Чаще всего встречаются следующие варианты инфиксной записи:
.
Дизъю́нкция —
(лат.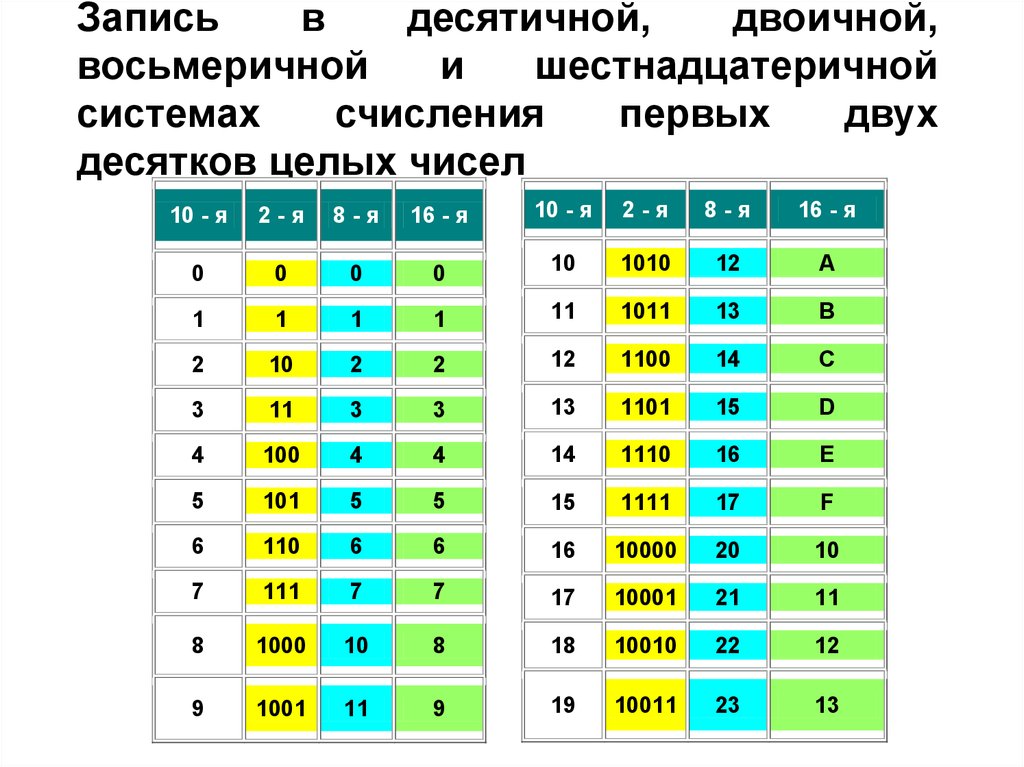
Дизъюнкция может быть бинарной операцией, то есть, иметь два операнда, тернарной операцией, то есть иметь три операнда или n-арной операцией, то есть иметь n операндов. Запись может быть префиксной — знак операции стоит перед операндами (польская запись), инфиксной — знак операции стоит между операндами или
Как
правило, в математических выражениях Ложь отождествляется с логическим нулём, а Истина —
с логической единицей, а операции
отрицания (НЕ), конъюнкции (И) и дизъюнкции
(ИЛИ) определяются в привычном нам
понимании.
Опираясь
на этот математический инструментарий, логика
высказываний изучает высказывания и
Логика высказываний послужила основным математическим инструментом при создании компьютеров. Она легко преобразуется в битовую логику: истинность высказывания обозначается одним битом (0 — ЛОЖЬ, 1 — ИСТИНА).
Инверсия (перестановка)
В комбинаторикеперестановка— этоупорядоченный наборчисел обычно трактуемый какбиекцияна множестве , которая числуiставит соответствиеi-й элемент из набора. Числоnпри этом называетсяпорядкомперестановки.
Т
Слайд
1.31
аблица истинности
Под
«логической функцией» в данном случае
понимается функция, у которой значения
переменных (параметров функции) и
значение самой функции выражают
логическую истинность. Например, в
двузначной логике они могут принимать
значения «истина» либо «ложь» (
либо
,
либо
).
Например, в
двузначной логике они могут принимать
значения «истина» либо «ложь» (
либо
,
либо
).
Табличное задание функций встречается не только в логике, но для логических функций таблицы оказались особенно удобными, и с начала XX века за ними закрепилось это специальное название. Особенно часто таблицы истинности применяются в булевой алгебре и в аналогичных системах многозначной логики.
Логические операции и таблицы истинности
A | неА |
0 | 1 |
1 | 0 |
Не A .NOT. A
Логическое отрицание: ИНВЕРСИЯ — если исходное выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное выражение ложно, то результат отрицания будет истинным/ Данная операция означает, что к исходному логическому выражению добавляется частицаНЕили словаНЕВЕРНО, ЧТО…
. NOT. Отсутствовал
на занятии (0) = Посетил (1)
NOT. Отсутствовал
на занятии (0) = Посетил (1)
.NOT. Сдал экзамен (1) = Отчислен (0)
Слайд
1.32
A | B | F |
1 | 1 | 1 |
1 | 0 | 0 |
0 | 1 | 0 |
0 | 0 | 0 |
F = A & B F = A .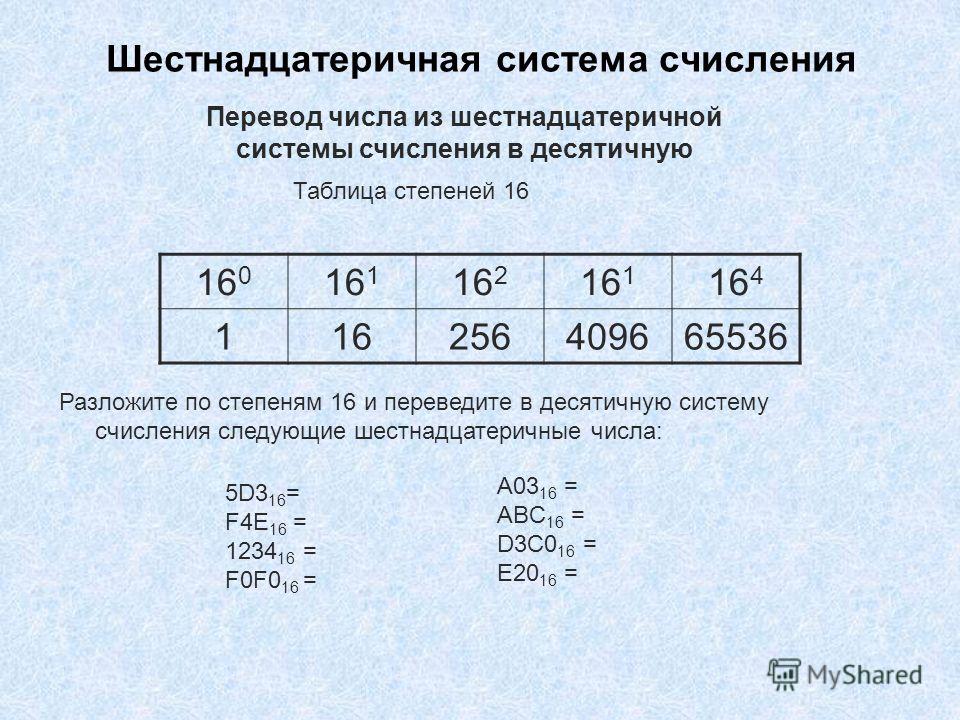 AND. B
AND. B
Логическое умножение КОНЪЮНКЦИЯ — это новое сложное выражение будет истинным только тогда, когда истинны оба исходных простых выражения. Конъюнкция определяет соединение двух логических выражений с помощью союзаИ.
Выход на сессию (1) .AND. Сдал экзамен (1) = Переведен на следующий семестр (1)
Выход на сессию (1) .AND. Не сдал экзамен (0) = Отчислен (0)
Не выход на сессию (0) .AND. Не сдал экзамен (0) = Отчислен (0)
A | B | F |
1 | 1 | 1 |
1 | 0 | 1 |
0 | 1 | 1 |
0 | 0 | 0 |
Слайд
1. 33
33
F = A + B F = A .OR. B
Логическое сложение – ДИЗЪЮНКЦИЯ— это новое сложное выражение будет истинным тогда и только тогда, когда истинно хотя бы одно из исходных (простых) выражений. Дизъюнкция определяет соединение двух логических выражений с помощью союзаИЛИ
Вышел на сессию (1) .AND. Сдал экзамен (1) = Переведен на следующий семестр (1)
Выход на сессию (1) .AND. Не сдал экзамен (0)= Отчислен (0)
С
Слайд
1.34
ПАСИБО ЗА ВНИМАНИЕ!
A | B | F |
1 | 1 | 1 |
1 | 0 | 0 |
0 | 1 | 1 |
0 | 0 | 1 |
Логическое
следование: ИМПЛИКАЦИЯ—
связывает два простых логических
выражения, из которых первое является
условием (А), а второе (В)– следствием
из этого условия. Результатом ИМПЛИКАЦИИ
является ЛОЖЬ только тогда, когда условие
А истинно, а следствие В ложно. Обозначается
символом «следовательно»
и выражается словамиЕСЛИ … ,
ТО …
Результатом ИМПЛИКАЦИИ
является ЛОЖЬ только тогда, когда условие
А истинно, а следствие В ложно. Обозначается
символом «следовательно»
и выражается словамиЕСЛИ … ,
ТО …
A | B | F |
1 | 1 | 1 |
1 | 0 | 0 |
0 | 1 | 0 |
0 | 0 | 1 |
Л Слайд 1. 34
34
Построение таблиц истинности для сложных выражений:
Количество строк= 2n+ две строки для заголовка (n — количество простых высказываний)
Количество столбцов= количество переменных + количество логических операций
При построении таблицы надо учитывать все возможные сочетания логических значений 0 и 1 исходных выражений. Затем – определить порядок действий и составить таблицу с учетом таблиц истинности основных логических операций.
ПРИМЕР:составить таблицу истинности сложного логического выражения D = неA & ( B+C )
А,В, С — три простых высказывания, поэтому :
количество строк= 23+2 = 10 (n=3, т. к. на входе три элеманта А, В,
С)
к. на входе три элеманта А, В,
С)
количество столбцов :
1) А
2) В
3) С
4) не A это инверсия А (обозначим Е)
5) B + C это операция
6) D = неA & ( B+C ), т.е. D = E & F это операция конъюнкции дизъюнкции (обозначим F)
1 | 2 | 3 | 4 | 5 | 6 |
А | В | С | E = не А (не 1) | F = В+С (2+3) | D = E&F (4*5) |
1 | 1 | 1 | 0 | 1 | 0 |
1 | 1 | 0 | 0 | 1 | 0 |
1 | 0 | 1 | 0 | 1 | 0 |
1 | 0 | 0 | 0 | 0 | 0 |
0 | 1 | 1 | 1 | 1 | 1 |
0 | 1 | 0 | 1 | 1 | 1 |
0 | 0 | 1 | 1 | 1 | 1 |
0 | 0 | 0 | 1 | 0 | 0 |
Вычисления выполняемые компьютером
Информация в вычислительной машине
представляется в двоичном коде (0 и 1),
(да, нет), (вкл. , выкл.). 0 и 1 — это 1 бит
информации или 1 двоичный разряд. 1 байт
— это 8 бит (8 двоичных разрядов). В
компьютере 1 байт является наименьшей
единицей информации, что соответствует
одному знаку в командной строке (цифре,
букве, специальному символу или пробелу).
, выкл.). 0 и 1 — это 1 бит
информации или 1 двоичный разряд. 1 байт
— это 8 бит (8 двоичных разрядов). В
компьютере 1 байт является наименьшей
единицей информации, что соответствует
одному знаку в командной строке (цифре,
букве, специальному символу или пробелу).
Дистанционный репетитор — онлайн-репетиторы России и зарубежья
КАК ПРОХОДЯТ
ОНЛАЙН-ЗАНЯТИЯ?
Ученик и учитель видят и слышат
друг друга, совместно пишут на
виртуальной доске, не выходя из
дома!
КАК ВЫБРАТЬ репетитора
Выбрать репетитора самостоятельно
ИЛИ
Позвонить и Вам поможет специалист
8 (800) 333 58 91
* Звонок является бесплатным на территории РФ
** Время приема звонков с 10 до 22 по МСК
ПОДАТЬ ЗАЯВКУ
Россия +7Украина +380Австралия +61Белоруссия +375Великобритания +44Израиль +972Канада, США +1Китай +86Швейцария +41
Выбранные репетиторы
Заполните форму, и мы быстро и бесплатно подберем Вам дистанционного репетитора по Вашим пожеланиям.
Менеджер свяжется с Вами в течение 15 минут и порекомендует специалиста.
Отправляя форму, Вы принимаете Условия использования и даёте Согласие на обработку персональных данных
Вы также можете воспользоваться
расширенной формой подачи заявки
Как оплачивать и СКОЛЬКО ЭТО СТОИТ
от
800 до 5000 ₽
за 60 мин.
и зависит
ОТ ОПЫТА и
квалификации
репетитора
ОТ ПОСТАВЛЕННЫХ ЦЕЛЕЙ ОБУЧЕНИЯ
(например, подготовка к олимпиадам, ДВИ стоит дороже, чем подготовка к ЕГЭ)
ОТ ПРЕДМЕТА (например, услуги репетиторовиностранных языков дороже)
Оплата непосредственно репетитору, удобным для Вас способом
Почему я выбираю DisTTutor
БЫСТРЫЙ ПОДБОР
РЕПЕТИТОРА И
ИНДИВИДУАЛЬНЫЙ ПОДХОД
ОПТИМАЛЬНОЕ
СООТНОШЕНИЕ ЦЕНЫ И
КАЧЕСТВА
ПРОВЕРЕНЫ ДОКУМЕНТЫ ОБ ОБРАЗОВАНИИ У ВСЕХ РЕПЕТИТОРОВ
НАДЕЖНОСТЬ И ОПЫТ.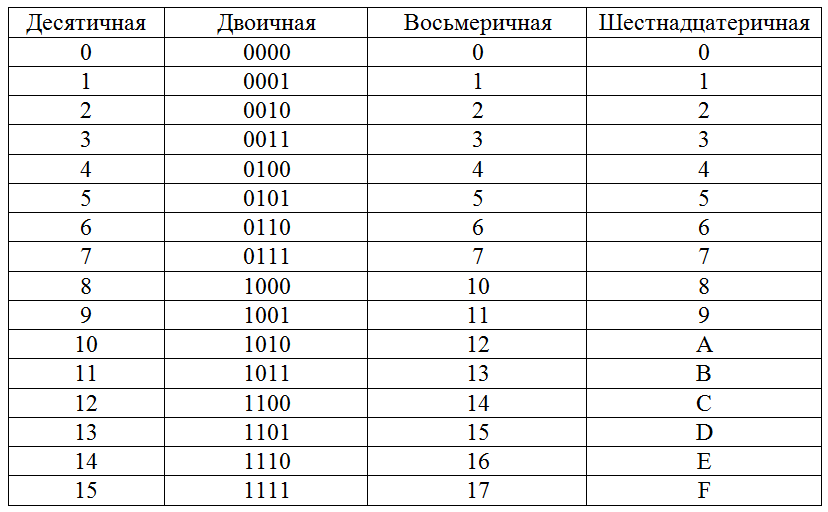
DisTTutor на рынке с 2008 года.
ПРОВЕДЕНИЕ БЕСПЛАТНОГО, ПРОБНОГО УРОКА
ЗАМЕНА РЕПЕТИТОРА, ЕСЛИ ЭТО НЕОБХОДИМО
376025 УЧЕНИКОВ ИЗ РАЗНЫХ СТРАН МИРА
уже сделали свой выбор
И вот, что УЧЕНИКИ ГОВОРЯТ
о наших репетиторах
Владимир Александрович Кузьмин
«
Тренинг у Кузьмина В. А. проходил в экстремальных условиях. Мой модем совершенно не держал соединение. За время часового тренинга связь прерывалась практически постоянно. Ясно, что в таких условиях чрезвычайно непросто чему-то учить.
Однако Владимир Александрович проявил удивительную выдержку и терпение. Неоднократно он перезванивал мне на сотовый телефон, чтобы дать пояснения или комментарии.
Ценой больших усилий нам удалось рассмотреть три программы: ConceptDraw MINDMAP Professional Ru, GeoGebra и Ultra Flash Video FLV Converter. Владимир Александрович открыл мне курс на платформе dist-tutor.info и научил подключать и настраивать Виртуальный кабинет, порекомендовав изучать возможности этого ресурса, чтобы постепенно уходить от использования Skype.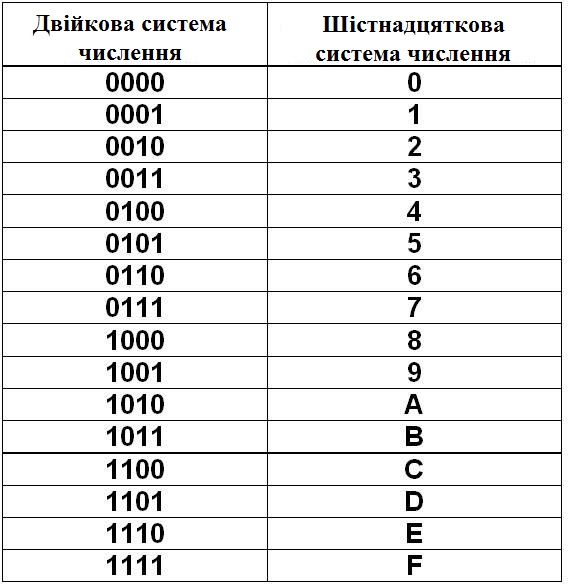 В итоге, занятие мне очень понравилось! Спокойное объяснение материала, дружелюбный настрой, подбадривание дистанционного ученика даже в самых непростых ситуациях — вот далеко не полный перечень качеств Владимира Александровича как дистанционного педагога. Мне следует учиться у такого замечательного репетитора!
В итоге, занятие мне очень понравилось! Спокойное объяснение материала, дружелюбный настрой, подбадривание дистанционного ученика даже в самых непростых ситуациях — вот далеко не полный перечень качеств Владимира Александровича как дистанционного педагога. Мне следует учиться у такого замечательного репетитора!
«
Вячеслав Юрьевич Матыкин
Чулпан Равилевна Насырова
«
Я очень довольна репетитором по химии. Очень хороший подход к ученику,внятно объясняет. У меня появились сдвиги, стала получать хорошие оценки по химии. Очень хороший преподаватель. Всем , кто хочет изучать химию, советую только её !!!
«
Алина Крякина
Надежда Васильевна Токарева
«
Мы занимались с Надеждой Васильевной по математике 5 класса. Занятия проходили в удобное для обоих сторон время. Если необходимо было дополнительно позаниматься во внеурочное время, Надежда Васильевна всегда шла навстречу. Ей можно было позванить, чтобы просто задать вопрос по непонятной задачке из домашнего задания.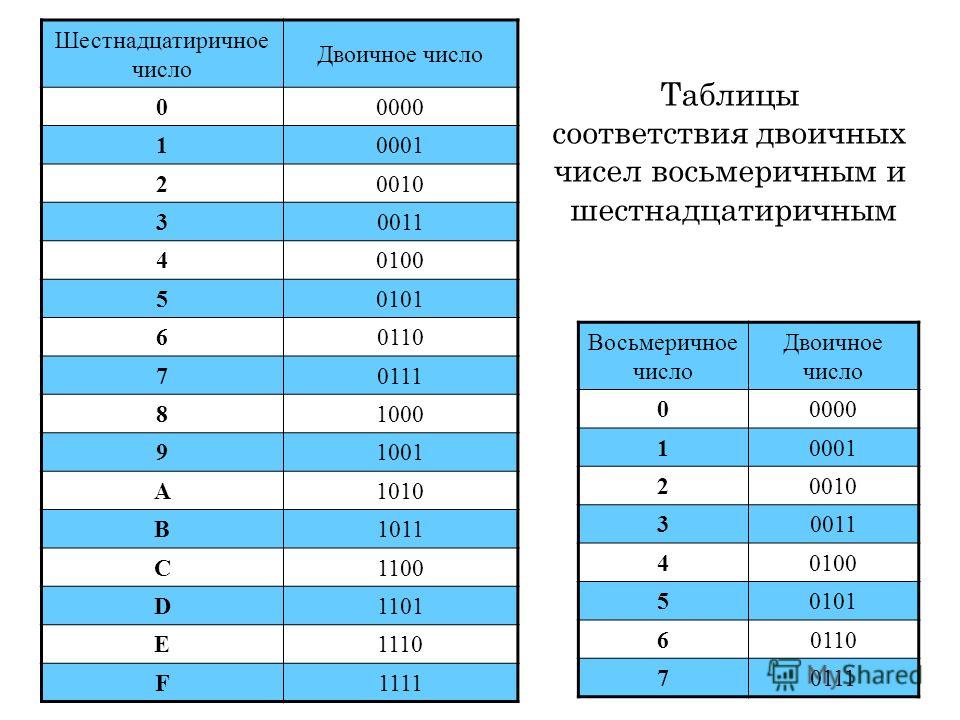 Моя дочь существенно подняла свой уровень знаний по математике и начала демонстрировать хорошие оценки. Мы очень благодарны Надежде Васильевне за помощь в этом учебном году, надеемся на продолжение отношений осенью.
Моя дочь существенно подняла свой уровень знаний по математике и начала демонстрировать хорошие оценки. Мы очень благодарны Надежде Васильевне за помощь в этом учебном году, надеемся на продолжение отношений осенью.
«
Эльмира Есеноманова
Ольга Александровна Мухаметзянова
«
Подготовку к ЕГЭ по русскому языку мой сын начал с 10 класса. Ольга Александровна грамотный педагог, пунктуальный, ответственный человек. Она всегда старается построить занятие так, чтобы оно прошло максимально плодотворно и интересно. Нас абсолютно все устраивает в работе педагога. Сотрудничество приносит отличные результаты, и мы его продолжаем. Спасибо.
«
Оксана Александровна
Клиентам
- Репетиторы по математике
- Репетиторы по русскому языку
- Репетиторы по химии
- Репетиторы по биологии
- Репетиторы английского языка
- Репетиторы немецкого языка
Репетиторам
- Регистрация
- Публичная оферта
- Библиотека
- Бан-лист репетиторов
Партнеры
- ChemSchool
-
PREPY.
 RU
RU
- Class
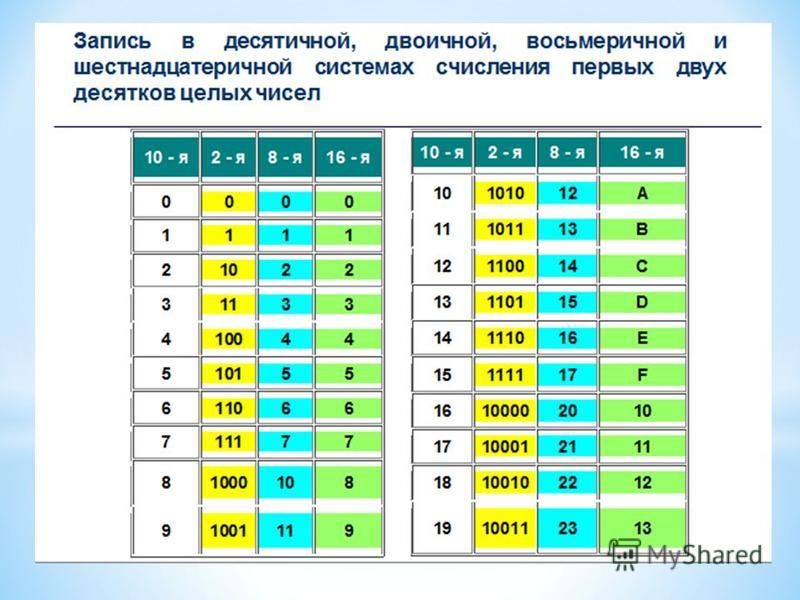
Таблица преобразования десятичных чисел в шестнадцатеричные
Таблица преобразования десятичных чисел в шестнадцатеричныеПреобразование десятичного числа в шестнадцатеричное
В этой таблице показаны десятичные числа и их шестнадцатеричные эквиваленты. Цвета выражаются в формате html с использованием шестнадцатеричных значений для красного, синего и зеленого.
расположены парами. Например, десятичное число «0», имеющее шестнадцатеричное значение «00», имеет
значение цвета равно нулю. Теперь, если мы припишем красную, синюю и зеленую части цвета
с этим значением мы получаем «000000», что в терминах html означает черный цвет. Это делает
совершенном смысле, поскольку черный существует только из-за отсутствия цвета. Многие графические редакторы выражают атрибуты цвета с помощью десятичных значений. диаграмма преобразования позволит вам узнать шестнадцатеричный эквивалент, чтобы вы могли визуализировать цвета правильно в html документе. Таблица состоит из нескольких столбцов с десятичным значением и его шестнадцатеричным эквивалентом. | |||
| дек | Шестнадцатеричный | декабрь | Шестнадцатеричный | декабрь | Шестнадцатеричный | декабрь | Шестнадцатеричный | декабрь | Шестнадцатеричный | декабрь | Шестнадцатеричный | декабрь | Шестнадцатеричный | декабрь | Шестнадцатеричный | |||||||
| 0 | 00 | 32 | 20 | 64 | 40 | 96 | 60 | 128 | 80 | 160 | а0 | 192 | с0 | 224 | е0 | |||||||
| 1 | 01 | 33 | 21 | 65 | 41 | 97 | 61 | 129 | 81 | 161 | а1 | 193 | с1 | 225 | е1 | |||||||
| 2 | 02 | 34 | 22 | 66 | 42 | 98 | 62 | 130 | 82 | 162 | а2 | 194 | с2 | 226 | е2 | |||||||
| 3 | 03 | 35 | 23 | 67 | 43 | 99 | 63 | 131 | 83 | 163 | а3 | 195 | с3 | 227 | е3 | |||||||
| 4 | 04 | 36 | 24 | 68 | 44 | 100 | 64 | 132 | 84 | 164 | а4 | 196 | с4 | 228 | е4 | |||||||
| 5 | 05 | 37 | 25 | 69 | 45 | 101 | 65 | 133 | 85 | 165 | а5 | 197 | с5 | 229 | е5 | |||||||
| 6 | 06 | 38 | 26 | 70 | 46 | 102 | 66 | 134 | 86 | 166 | а6 | 198 | с6 | 230 | е6 | |||||||
| 7 | 07 | 39 | 27 | 71 | 47 | 103 | 67 | 135 | 87 | 167 | а7 | 199 | с7 | 231 | е7 | |||||||
| 8 | 08 | 40 | 28 | 72 | 48 | 104 | 68 | 136 | 88 | 168 | а8 | 200 | с8 | 232 | е8 | |||||||
| 9 | 09 | 41 | 29 | 73 | 49 | 105 | 69 | 137 | 89 | 169 | а9 | 201 | с9 | 233 | е9 | |||||||
| 10 | 0а | 42 | 2а | 74 | 4а | 106 | 6а | 138 | 8а | 170 | аа | 202 | примерно | 234 | Шт. | |||||||
| 11 | 0б | 43 | 2б | 75 | 4б | 107 | 6б | 139 | 8б | 171 | аб | 203 | кб | 235 | иб | |||||||
| 12 | 0с | 44 | 2с | 76 | 4с | 108 | 6с | 140 | 8с | 172 | ак | 204 | куб.см | 236 | эк | |||||||
| 13 | 0д | 45 | 2д | 77 | 4д | 109 | 6д | 141 | 8д | 173 | объявление | 205 | компакт-диск | 237 | изд | |||||||
| 14 | 0е | 46 | 2е | 78 | 4е | 110 | 6e | 142 | 8e | 174 | 206 | 238 | ее | |||||||||
| 15 | 0f | 47 | 2ф | 79 | 4ф | 111 | 6ф | 143 | 8ф | 175 | и | 207 | в сравнении с | 239 | и | |||||||
| 16 | 10 | 48 | 30 | 80 | 50 | 112 | 70 | 144 | 90 | 176 | б0 | 208 | д0 | 240 | ф0 | |||||||
| 17 | 11 | 49 | 31 | 81 | 51 | 113 | 71 | 145 | 91 | 177 | б1 | 209 | д1 | 241 | ф1 | |||||||
| 18 | 12 | 50 | 32 | 82 | 52 | 114 | 72 | 146 | 92 | 178 | б2 | 210 | д2 | 242 | ф2 | |||||||
| 19 | 13 | 51 | 33 | 83 | 53 | 115 | 73 | 147 | 93 | 179 | б3 | 211 | д3 | 243 | ф3 | |||||||
| 20 | 14 | 52 | 34 | 84 | 54 | 116 | 74 | 148 | 94 | 180 | б4 | 212 | д4 | 244 | ф4 | |||||||
| 21 | 15 | 53 | 35 | 85 | 55 | 117 | 75 | 149 | 95 | 181 | б5 | 213 | д5 | 245 | ф5 | |||||||
| 22 | 16 | 54 | 36 | 86 | 56 | 118 | 76 | 150 | 96 | 182 | б6 | 214 | д6 | 246 | ф6 | |||||||
| 23 | 17 | 55 | 37 | 87 | 57 | 119 | 77 | 151 | 97 | 183 | б7 | 215 | д7 | 247 | ф7 | |||||||
| 24 | 18 | 56 | 38 | 88 | 58 | 120 | 78 | 152 | 98 | 184 | б8 | 216 | д8 | 248 | ф8 | |||||||
| 25 | 19 | 57 | 39 | 89 | 59 | 121 | 79 | 153 | 99 | 185 | б9 | 217 | д9 | 249 | ф9 | |||||||
| 26 | 1а | 58 | 3а | 90 | 5а | 122 | 7а | 154 | 9а | 186 | ба | 218 | да | 250 | ФА | |||||||
| 27 | 1б | 59 | 3б | 91 | 5б | 123 | 7б | 155 | 9б | 187 | бб | 219 | дб | 251 | фб | |||||||
| 28 | 1с | 60 | 3с | 92 | 5с | 124 | 7с | 156 | 9с | 188 | до н.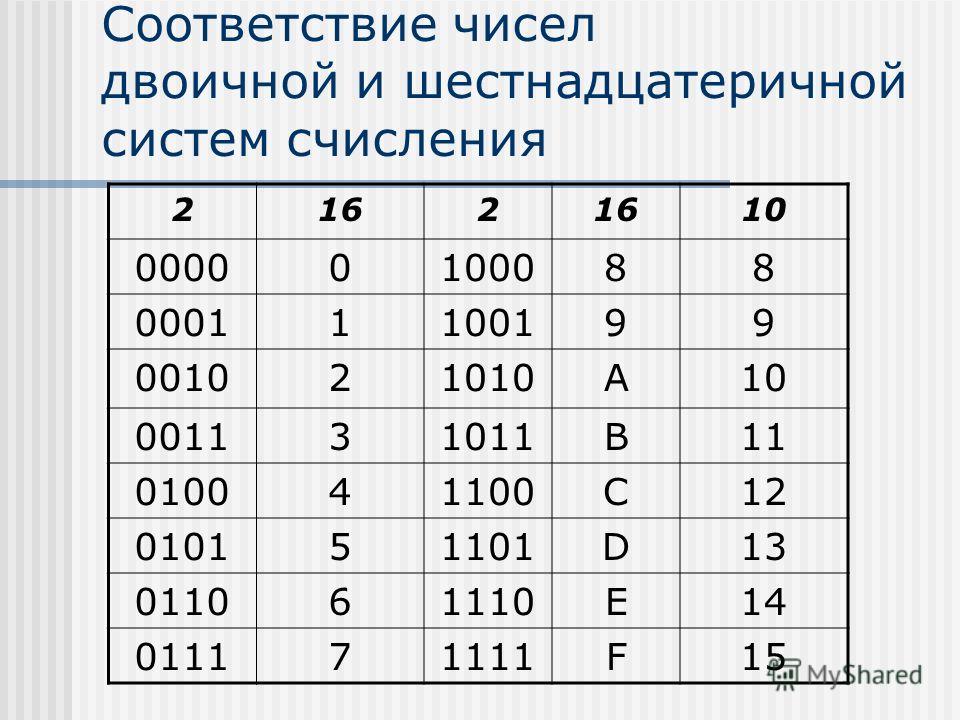 э. э. | 220 | постоянный ток | 252 | фк | |||||||
| 29 | 1д | 61 | 3д | 93 | 5д | 125 | 7д | 157 | 9д | 189 | бд | 221 | дд | 253 | фд | |||||||
| 30 | 1e | 62 | 3е | 94 | 5e | 126 | 7e | 158 | 9е | 190 | будет | 222 | из | 254 | и | |||||||
| 31 | 1ф | 63 | 3f | 95 | 5ф | 127 | 7f | 159 | 9ф | 191 | бф | 223 | дф | 255 | и далее | |||||||
| Декабрь | Шестнадцатеричный | декабрь | Шестнадцатеричный | декабрь | Шестнадцатеричный | декабрь | Шестнадцатеричный | декабрь | Шестнадцатеричный | декабрь | Шестнадцатеричный | декабрь | Шестнадцатеричный | декабрь | Шестнадцатеричный | |||||||
|
Лучше всего просматривать при разрешении экрана 1024 x 768 с помощью Internet Explorer 5.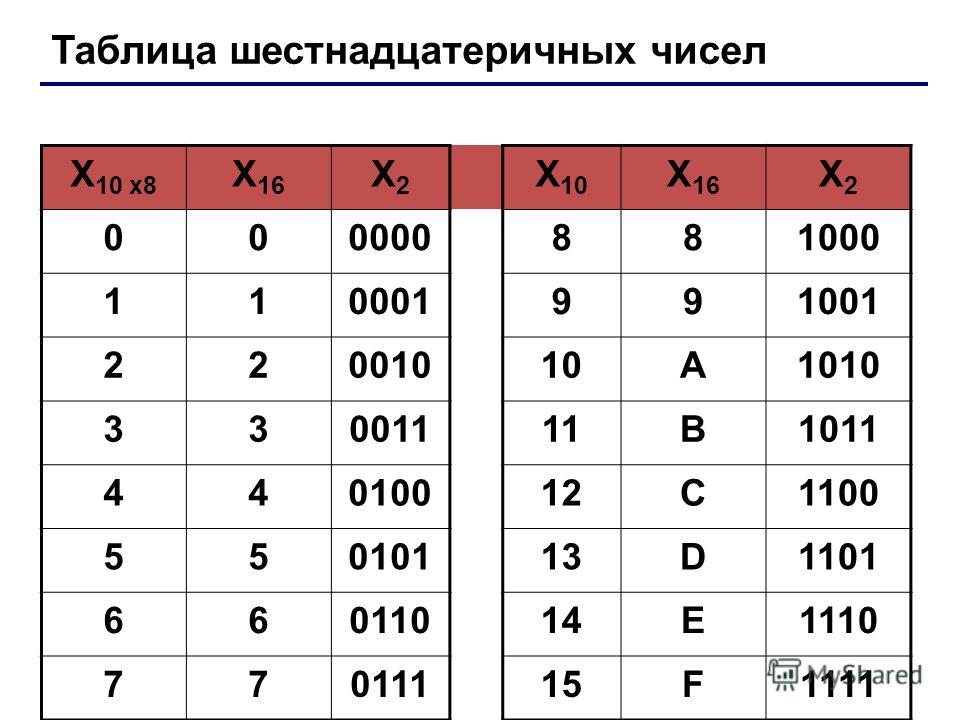 |



 RU
RU
 И наоборот, если бы мы были
чтобы выбрать максимальное значение цвета «ff» для каждого из красных, синих и зеленых элементов, что дает нам
шестнадцатеричное значение цвета «ffffff», это даст нам белый цвет.
И наоборот, если бы мы были
чтобы выбрать максимальное значение цвета «ff» для каждого из красных, синих и зеленых элементов, что дает нам
шестнадцатеричное значение цвета «ffffff», это даст нам белый цвет.