Шестнадцатеричная система счисления.

Шестнадцатеричная система счисления имеет набор цифр {0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F} и основание степени (p) – 16.

Количественный эквивалент некоторого целого n-значного шестнадцатеричного числа f45ed23c равен:

15*16⁷+4*16⁶+5*16⁵+14*16⁴+13*16³+2*16²+3*16¹+12*16⁰.

Приведем соответствие двоичных чисел и их десятичных и шестнадцатеричных эквивалентов.

Десятичное число	Двоичная тетрада	Шестнадцатеричное число
0	0000	0
1	0001	1
2	0010	2
3	0011	3
4	0100	4
5	0101	5
6	0110	6
7	0111	7
8	1000	8
9	1001	9
10	1010	A
11	1011	B
12	1100	C
13	1101	D
14	1110	E
15	1111	F
16	10000	10

Поначалу запомнить эти соотношения сложно, поэтому полезно иметь под руками некоторую справочную информацию. Приведенная таблица содержит представления десятичных чисел из диапазона 0-16 в двоичной и шестнадцатеричной системах счисления. Ее удобно использовать для взаимного преобразования чисел в рассмотренных трех системах счисления. Шестнадцатеричная система счисления при вычислениях несколько сложнее, чем двоичная, в частности, в том, что касается правил переносов в старшие разряды. Главное здесь запомнить следующее равенство – (1+F=10)

16.

Перевод чисел из одной системы счисления в другую

Одного знания о существовании разных систем счисления мало. Для того, чтобы в полной мере использовать их в своей практической работе при программировании, необходимо научиться выполнять взаимное преобразование чисел между тремя системами счисления.

Перевод в десятичную систему счисления

Перевод в десятичную систему счисления является самым простым. Обычно его производят с помощью так называемого алгоритма замещения, суть которого заключается в следующем: сначала в десятичную систему счисления переводится основание степени p, а затем – цифры исходного числа.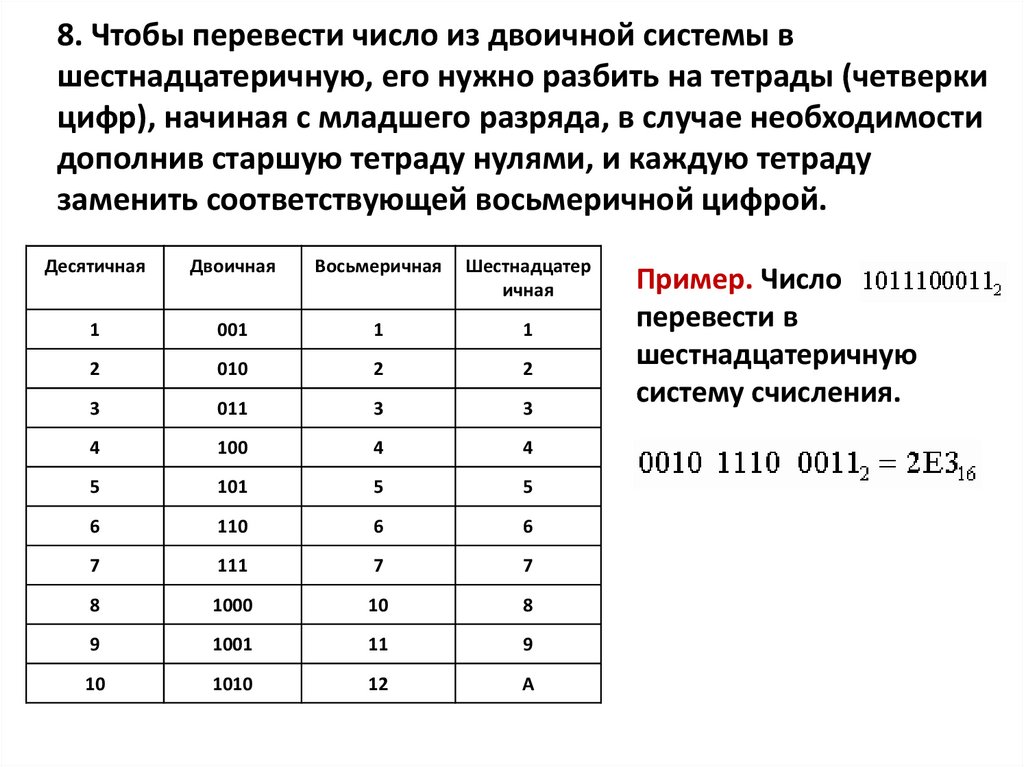

Результаты подставляются в формулу (1). Полученная сумма и будет искомым результатом.

Перевод в двоичную систему счисления Перевод из десятичной системы счисления

Перевод числа в двоичную систему счисления из десятичной выполняется по следующему алгоритму:

1. Резделить десятичное число A на 2. Запомнить частное q и остаток a.

2. Если в результате шага 1 частное q не равно 0, то принять его за новое делимое и отметить остаток a, который будет очередной значащей цифрой, и вернуться к шагу 1, на котором в качестве нового делимого участвует полученное на шаге 2 частное.

3. Если в результате шага 1 частное q равно 0, алгоритм прекращается. Выписать остатки в порядке, обратном их получению. Получится двоичный эквивалент исходного числа.

Переведем в двоичную систему счисления число 247.

1 шаг.

Делим 247 на 2. Результат 123 остаток 1.

2 шаг.

Делим 123 на 2. Результат 61 остаток 1.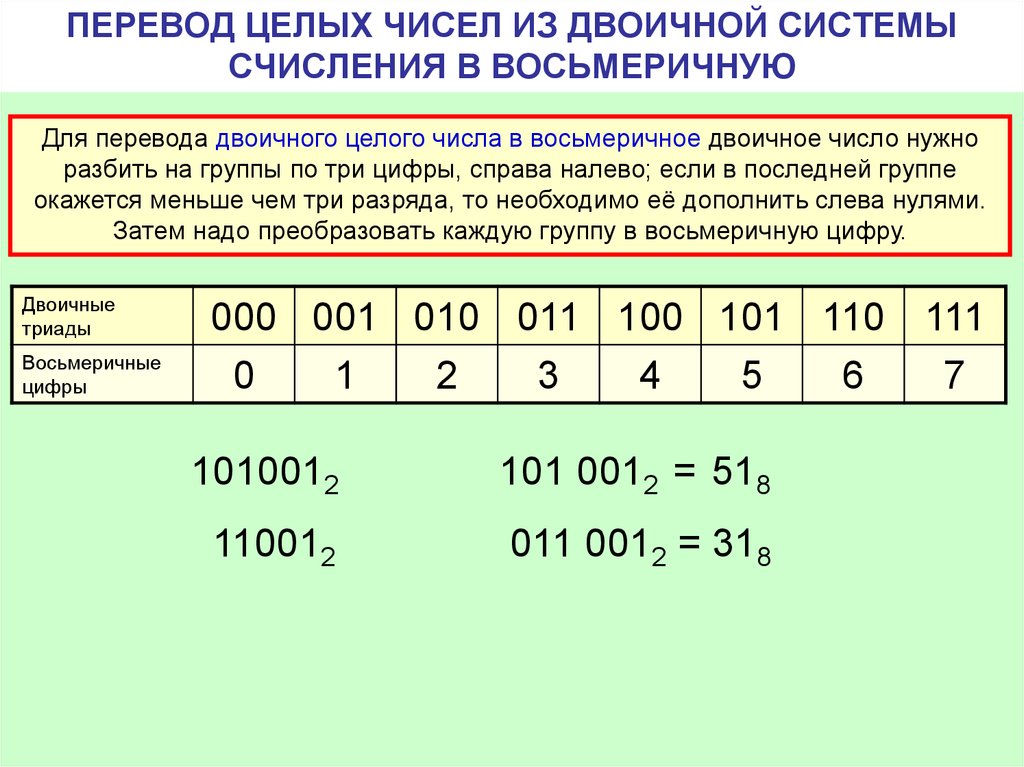

3 шаг.

Делим 61 на 2. Результат 30 остаток 1.

4 шаг.

Делим 30 на 2. Результат 15 остаток 0.

5 шаг.

Делим 15 на 2. Результат 7 остаток 1.

6 шаг.

Делим 7 на 2. Результат 3 остаток 1.

7 шаг.

Делим 3 на 2. Результат 1 остаток 1.

8 шаг.

Делим 1 на 2. Результат 0, есть остаток. (1)

Получаем следующее двоичное чсисло: 11110111.

§10. Шестнадцатеричная система счисления | Перевод чисел

Планирование уроков на учебный год (по учебнику К.Ю. Полякова, Е.А. Еремина, базовый уровень)

Главная | Информатика и информационно-коммуникационные технологии | Планирование уроков и материалы к урокам | 8 классы | Планирование уроков на учебный год (по учебнику К.Ю. Полякова, Е.А. Еремина, базовый уровень) | §10. Шестнадцатеричная система счисления

Содержание урока

Перевод чисел

Связь с двоичной системой счисления

Алгоритм перевода шестнадцатеричного числа в двоичную систему счисления

Алгоритм перевода двоичного числа в шестнадцатеричную систему счисления

Арифметические действия

Применение шестнадцатеричной системы

Выводы. Интеллект-карта

Вопросы и задания

Ключевые слова:

• шестнадцатеричная система 
• перевод чисел	
• связь с двоичной системой
• сложение
• вычитание

Шестнадцатеричная система (позиционная система с основанием 16) широко используется для записи адресов и содержимого ячеек памяти компьютера. Её алфавит содержит 16 цифр. Вместе с 10 арабскими цифрами от 0 до 9 используются первые буквы латинского алфавита:

А = 10, В = 11, С = 12, D = 13, Е = 14 и F = 15.

Какие числа записаны в шестнадцатеричной системе неверно: 34AF5₁₆, 5BG6₁₆, 9FF61₁₆, ADh33₁₆? Как вы рассуждали?

Перевод чисел

Для перевода чисел из десятичной системы в шестнадцатеричную используют алгоритм деления на 16 и выписывания остатков. Важно не забыть, что все остатки, большие 9, заменяются на буквы:

Переведите в шестнадцатеричную систему счисления числа 31, 91, 126, 172.

Запись некоторого числа в шестнадцатеричной системе счисления заканчивается на 0. Что можно сказать о свойствах этого числа?

Запись некоторого числа в шестнадцатеричной системе счисления заканчивается на 3. Что можно сказать о свойствах этого числа?

Платон перевёл некоторое число из десятичной системы в шестнадцатеричную, полученная запись содержит 2 цифры. Какое это могло быть число (назовите наименьшее и наибольшее возможные значения)?

Для перевода числа из шестнадцатеричной системы в десятичную значение каждой цифры умножают на 16 в степени, равной её разряду, и полученные значения складывают:

Переведите числа 12₁₆, 57₁₆, 79₁₆, АВ₁₆, DD₁₆, EF₁₆ в десятичную систему счисления.

Не выполняя перевода чисел в другие системы счисления, выясните, может ли число 225 быть записано в шестнадцатеричной системе как 11F₁₆. Как вы рассуждали?

Следующая страница Связь с двоичной системой счисления

Cкачать материалы урока

Online Hex to String Converter Tool

Обратите внимание: все пробелы и двоеточия (:) в шестнадцатеричной строке будут удалены.

Нужно преобразовать текст в шестнадцатеричный формат?

Шестнадцатеричная система счисления используется для удобного представления двоичных значений в компьютерном программировании и цифровой электронике. Большинство языков программирования, таких как Java, ASP.NET, C++, Fortran и т. д., имеют встроенные функции, которые конвертируют в шестнадцатеричный формат и из него.

Что такое шестнадцатеричное число?

Большинство людей знакомы с десятичной системой счисления с основанием 10 (все возможные числа можно записать с помощью 10 цифр: 0,1,2,3,4,5,6,7,8,9) . Имея всего 10 цифр, дополнительные цифры необходимо использовать через определенные промежутки времени, чтобы правильно записать число. Например, в числе 423 004 используется вдвое больше цифр, чем в числе 961.

Шестнадцатеричная система с основанием 16 была создана для имитации некоторых свойств обычной десятичной системы. Общая разница в том, что для обозначения значения числа доступно 16 цифр вместо 10 цифр.

В шестнадцатеричной системе используются 16 символов: 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E и F. Таким образом, вместо десятичного символа из 10, шестнадцатеричная использует A, и так далее, и так далее, пока мы не дойдем до десятичного числа 15, которое обозначается как F. Как и в десятичной системе, после того, как было использовано основание из 16 символов, добавляется соответствующая дополнительная цифра. и порядок чисел начинается заново. Другими словами, после F мы начинаем с 10 и так далее. Чтобы лучше понять взаимосвязь между десятичной и шестнадцатеричной системами счисления, ознакомьтесь с таблицей ниже.

Как инструмент преобразования шестнадцатеричного текста в текст используется в программировании?

Шестнадцатеричная кодировка используется программистами для улучшения читаемости байтов, которые используются для связи с компьютерами. Существует ряд преимуществ использования шестнадцатеричного кодирования, в том числе доступная более высокая плотность информации, поскольку шестнадцатеричное кодирование эффективно сокращает 8 цифр двоичного кода до 2 шестнадцатеричных цифр.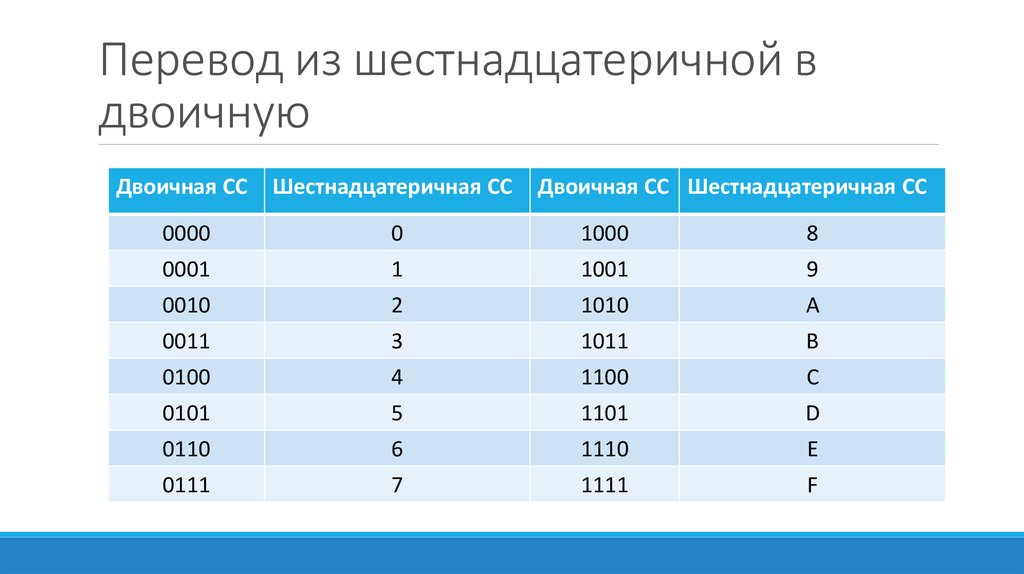 Таким образом, 2 шестнадцатеричных цифры выражают любое число от 0 до 255, то есть тот же набор чисел, что и 8 цифр в двоичном формате.

Преобразование текста в шестнадцатеричное кодирование по сравнению с кодировкой Base 64

Хотя кодирование в шестнадцатеричном формате является популярной стратегией кодирования, используемой программистами, шестнадцатеричное кодирование значительно увеличивает объем используемого хранилища, что снижает эффективность вашего взаимодействия с компьютером. Если место для хранения является проблемой, в качестве альтернативы рекомендуется кодирование в Base 64.

Для чего используется шестнадцатеричное кодирование?

Причины использования шестнадцатеричного кодирования в основном те же, что и для кодирования Base64 — оно используется, когда вы хотите отправить или сохранить 8-битные данные на носителе, который принимает только 6 или 7 бит. Шестнадцатеричное кодирование выполняется путем преобразования 8-битных данных в 2 шестнадцатеричных символа. Шестнадцатеричные символы затем сохраняются как двухбайтовые строковые представления символов.

Часто для облегчения чтения закодированных данных используется какой-либо разделитель. С 8 битами, преобразованными в три символа, и каждый символ хранится как 1-4 байта, вы можете использовать до 12 байтов (или даже больше в некоторых случаях) для каждого байта информации.

Опять же, не используйте шестнадцатеричное кодирование, если вам не хватает места для хранения. Однако кодировка довольно легко читается, поэтому, если удобочитаемость для человека является проблемой, то шестнадцатеричная кодировка, вероятно, является лучшим выбором, чем кодировка base64.

Использование бесплатного инструмента для кодирования шестнадцатеричного кода

Приведенный выше переводчик шестнадцатеричного кода в текст очень прост в использовании. Введите или вставьте шестнадцатеричное число, которое вы хотите преобразовать в текст, а затем нажмите «Преобразовать» под областью вставки.

Закодированная строка появится в поле ниже, откуда ее можно легко скопировать. Для вашего удобства и эффективности мы рекомендуем добавить этот инструмент в закладки для использования в будущем.

String Functions также создала бесплатный онлайн-инструмент для обратного преобразования строки в шестнадцатеричный формат. Попробуйте сегодня!

Политика конфиденциальности Карта сайта

Ключевые слова: шестнадцатеричное декодирование строкового текста, инструмент, онлайн-инструмент, конвертер символов в шестнадцатеричный.

Преобразование двоичных и шестнадцатеричных чисел

Преобразование чисел из двоичных в шестнадцатеричные не очень сложно, и чем больше вы будете этим заниматься, а чем больше вы будете работать с микроконтроллерами и цифровой электроникой, тем проще он автоматически распознает шаблоны.

Преобразование двоичных чисел в шестнадцатеричные

Как и раньше, начнем с числа 42, B00101010. Помните, что одна шестнадцатеричная цифра может содержать значение четырех двоичных цифр, поэтому разбейте это двоичное значение на два равных размера 4 и 4 и проверьте каждое по очереди: B00101010 становится 0010 и 1010. Я не выдумываю, это называется «верхний полубайт», а второй четырехбитный фрагмент называется «нижний полубайт». Байты, кусочки и биты…. не заводи меня. В любом случае, поскольку четырехбитное число может принимать значения только от 0 до 15, это значительно упрощает выполнение задачи.

0010: эквивалент десятичного числа 2. Десятичное число 2 равно 2 в шестнадцатеричном формате.
1010: эквивалент десятичного числа 10. Десятичное число 10 — это A в шестнадцатеричном формате.

Теперь вы просто объединяете куски вместе 0010 = 2 и 1010 = A, таким образом, у вас есть 0x2A. Когда я смотрю на откусывания, в моей голове я начинаю слева направо и иду «нет восьми, нет четырех, двойка, нет единицы, равно двум» и «восемь, нет четырех, двойка, ни одной, восемь и два равно десяти». Затем, когда я перехожу от десятичного к шестнадцатеричному, это очень просто, потому что это прямое отображение, которое не будет превышать одну шестнадцатеричную позицию. Единственная сложная часть — это запомнить шаблон A = 10, B = 11, C = 12, D = 13, E = 14, F = 15, и это просто вопрос знакомства и практики. Вы освоите это.

Вот еще один пример использования B11010001…

1101: эквивалент десятичного числа 13. Десятичное число 13 — это D в шестнадцатеричном формате.
0001: эквивалент десятичной 1. Десятичная 1 — это 1 в шестнадцатеричном формате.

1101 = D и 0001 = 1, так что в сумме получается 0xD1.

Вот несколько практических задач…

Преобразование B10010011 в шестнадцатеричное… (нажмите здесь, чтобы увидеть описание решения)

Наведите курсор, чтобы прочитать ответ0071 (нажмите здесь, чтобы прочитать описание решения)

Наведите курсор, чтобы прочитать ответ

Преобразовать B11101011 в шестнадцатеричный… (нажмите здесь, чтобы прочитать описание решения)

Наведите указатель мыши, чтобы прочитать ответ to Binary

Переход в обратном направлении осуществляется по очень похожей схеме: разбить значение на отдельные фрагменты, преобразовать фрагменты в десятичные числа, преобразовать десятичные числа в двоичные. Опять же, поскольку мы разбиваем его на верхний и нижний фрагменты, это очень упрощает работу. Если мы хотим преобразовать 0x1B в двоичный формат, мы разобьем его на две части 1 и B, а затем преобразуем каждую из них.

1: эквивалент десятичной 1. Десятичная 1 — это 0001 в двоичном виде.
B: эквивалент десятичного числа 11. Десятичное число 11 равно 1011 в двоичном формате.

Соедините две части двоичного кода вместе, и вы получите 0x1B = B00011011.

Вот еще один пример с использованием 0xCE…

C: эквивалентно десятичному числу 12. Десятичное число 12 равно 1100 в двоичном виде.
E: эквивалентно десятичному числу 14. Десятичное число 14 равно 1110 в двоичном формате.

Соедините две части двоичного кода вместе, и вы получите 0xCE = B11001110.

И снова несколько практических задач…

Преобразовать 0xD8 в двоичный файл… (нажмите здесь для описания решения)

Наведите курсор, чтобы прочитать ответ

Преобразуйте 0x53 в двоичный файл. .. описание решения)

Наведите курсор, чтобы прочитать ответ

Преобразовать 0x9F в двоичный файл… (нажмите здесь, чтобы прочитать описание решения)

Наведите курсор, чтобы прочитать ответ

Я делаю , а не , смотрю на 0x2A или 0xD1, и мой мозг просто читает это как «О, привет, это 42» или «Ага, 209, как я и ожидал». Мне все еще нужно сделать мысленное преобразование для большинства значений. Однако по мере того, как вы будете более глубоко работать с микроконтроллерами, шаблоны станут очень очевидными, а конкретные шестнадцатеричные числа будут иметь важное значение. Например, буквы всегда выше цифр, поэтому, даже если вы понятия не имеете, каково десятичное значение 0xD1 по сравнению с 0x2A, вы можете увидеть, как расположены буквы по сравнению с числами: то, что начинается с «D», должно быть больше. чем то, что начинается с 2. 0xFF и 0x00, начнет занимать особое место в вашем сердце, потому что первое заполняет 8-битное значение, полное единиц, а другое заполняет то же самое значение, полное нулей.