Перевод в шестнадцатеричную систему счисления

Пример 1. Перевести число 56,567₁₀ в шестнадцатеричное представление.

Решение получаем через калькулятор. Переводим целую часть числа (56).

Целая часть от деления	Остаток от деления
56 div 16 = 3	56 mod 16 = 8 (56 — 3*16)
3 div 16 = 0	3 mod 16 = 3	0 div 16 = 0	0 mod 16 = 0

Остаток от деления записываем в обратном порядке. Получаем число в 16-ой системе счисления: 038
56 = 038₁₆

Для перевода дробной части числа последовательно умножаем дробную часть на основание 16. В результате каждый раз записываем целую часть произведения.
0.567*16 = 9.072 (целая часть 9)
0.072*16 = 1.152 (целая часть 1)
0.152*16 = 2.432 (целая часть 2)
0.432*16 = 6.912 (целая часть 6)
Получаем число в 16-ой системе счисления: 9126

0. 567 = 9126₁₆

Таким образом, число 56,567 в шестнадцатеричной системе счисления записывается как 38,9126.

Пример 2. Перевести число 0101110,011 в шестнадцатеричное представление.
Переводим целую часть числа. Для этого разделим исходный код на группы по 4 разряда.
0101110₂ = 0010 1110 ₂
Затем заменяем каждую группу на код из таблицы.

Двоичная СС	Шестнадцатеричная СС
0000	0
0001	1
0010	2
0011	3
0100	4
0101	5
0110	6
0111	7
1000	8
1001	9
1010	A
1011	B
1100	C
1101	D
1110	E
1111	F

Получаем число: 0010 1110 ₂ = 2E₁₆

Переводим дробную часть числа.

Для этого разделим исходный код на группы по 4 разряда.
011₂ = 0110₂
Затем заменяем каждую группу на код из таблицы.
Получаем число: 0110₂ = 6₁₆

Пример 3. Перевести число 456,54₈ в шестнадцатеричное представление.
Переводим целую часть числа. Заменяем каждый разряд на код из таблицы.

Двоичная СС	Восьмеричная СС
000	0
001	1
010	2
011	3
100	4
101	5
110	6
111	7

Получаем число: 456₈ = 100101110₂

Переводим дробную часть числа.
Получаем число: 54₈ = 101100₂
Переводим целую часть числа. Для этого разделим исходный код на группы по 4 разряда.
100101110₂ = 0001 0010 1110 ₂
Затем заменяем каждую группу на код из таблицы.
Получаем число: 0001 0010 1110 ₂ = 12E

16

Переводим дробную часть числа. Для этого разделим исходный код на группы по 4 разряда.
101100₂ = 1011 0000₂
Затем заменяем каждую группу на код из таблицы.
Получаем число: 1011 0000₂ = B0₁₆

Перейти к онлайн решению своей задачи

Шестнадцатиричная система счисления | это… Что такое Шестнадцатиричная система счисления?

ТолкованиеПеревод

Шестнадцатиричная система счисления

Шестнадцатеричная система счисления (шестнадцатеричные числа) — позиционная система счисления по целочисленному основанию 16.

Обычно в качестве шестнадцатеричных цифр используются десятичные цифры от 0 до 9 и латинские буквы от A до F для обозначения цифр от 10 до 15.

Содержание 1 Применение 2 Способы записи 2.1 В математике 2.2 В языках программирования 3 Перевод чисел из одной системы счисления в другую 3.1 Перевод чисел из шестнадцатеричной системы в десятичную 3.2 Перевод чисел из двоичной системы в шестнадцатеричную 3.3 Таблица перевода чисел 4 См. также 5 Ссылки

Применение

Широко используется в низкоуровневом программировании и вообще в компьютерной документации, поскольку в современных компьютерах минимальной единицей памяти является 8-битный байт, значения которого удобно записывать двумя шестнадцатеричными цифрами. Такое использование началось с системы IBM/360, где вся документация использовала шестнадцатеричную систему, в то время как в документации других компьютерных систем того времени (даже с 8-битными символами, как, например, БЭСМ-6) использовали восьмеричную систему.

В стандарте Юникода номер символа принято записывать в шестнадцатеричном виде, используя не менее 4 цифр (при необходимости — с ведущими нулями).

Способы записи

В математике

В математике систему счисления принято писать в подстрочном знаке. Например, десятичное число 1443 можно записать как 1443₁₀ или как 5A3₁₆.

В языках программирования

В разных языках программирования для записи шестнадцатеричных чисел используют различный синтаксис:

• В Ада и
• В Си и языках схожего синтаксиса, например, в
• В некоторых ассемблерах используют букву «h», которую ставят после числа. Например, «5A3h». При этом, если число начинается не с десятичной цифры, впереди ставится «0» (ноль): «0FFh» (255₁₀)
• Другие ассемблеры (AT&T, Motorola), а также Паскаль и некоторые версии Бэйсика используют префикс «$». Например, «$5A3».
• Некоторые иные платформы, например ZX Spectrum в своих ассемблерах (MASM, TASM, ALASM, GENS и т. д.) использовали запись #5A3, обычно выровненную до одного или двух байт: #05A3.
• Другие версии Бэйсика используют для указания шестнадцатеричных цифр сочетание «&h». Например, «&h5A3».
• В Unix-подобных операционных системах (и многих языках программирования, имеющих корни в Unix/linux) непечатные символы при выводе/вводе кодируются как \xCC, где CC — шестнадцатеричный код символа.

Перевод чисел из одной системы счисления в другую

Перевод чисел из шестнадцатеричной системы в десятичную

Для перевода шестнадцатеричного числа в десятичное необходимо это число представить в виде суммы произведений степеней основания шестнадцатеричной системы счисления на соответствующие цифры в разрядах шестнадцатеричного числа.

Например, требуется перевести шестнадцатеричное число 5A3 в десятичное. В этом числе 3 цифры. В соответствии с вышеуказанным правилом представим его в виде суммы степеней с основанием 16:

5A3₁₆=5·16²+10·16¹+3·16⁰
=5·256+10·16+3·1=1280+160+3=1443₁₀

Перевод чисел из двоичной системы в шестнадцатеричную

Для перевода многозначного двоичного числа в шестнадцатеричную систему нужно разбить его на тетрады справа налево и заменить каждую тетраду соответствующей шестнадцатеричной цифрой.

Например:

10110100011₂=0101 1010 0011=5A3₁₆

Таблица перевода чисел

	0hex	=	0dec	=	0oct		0	0	0	0
	1hex	=	1dec	=	1oct		0	0	0	1
	2hex	=	2dec	=	2oct		0	0	1	0
	3hex	=	3dec	=	3oct		0	0	1	1
	4hex	=	4dec	=	4oct		0	1	0	0
	5hex	=	5dec	=	5oct		0	1	0	1
	6hex	=	6dec	=	6oct		0	1	1	0
	7hex	=	7dec	=	7oct		0	1	1	1
	8hex	=	8dec	=	10oct		1	0	0	0
	9hex	=	9dec	=	11oct		1	0	0	1
	Ahex	=	10dec	=	12oct		1	0	1	0
	Bhex	=	11dec	=	13oct		1	0	1	1
	Chex	=	12dec	=	14oct		1	1	0	0
	Dhex	=	13dec	=	15oct		1	1	0	1
	Ehex	=	14dec	=	16oct		1	1	1	0
	Fhex	=	15dec	=	17oct		1	1	1	1

См.

также

• Система счисления
• Двоичные приставки
• Шестнадцатеричный редактор

Ссылки

• Шестнадцатеричные числа и операции с ними
• Таблица порядков двоичных, шестнадцатеричных и десятичных чисел
• Онлайн калькулятор для перевода чисел из одной системы счисления в другую

Wikimedia Foundation. 2010.

Игры ⚽ Поможем написать курсовую

• Шестиконечная звезда
• Шестнадцатеричные числа

Полезное

Конвертер

шестнадцатеричных чисел в десятичные | Calculator-App

Шестнадцатеричный калькулятор обычно используется для сложения, вычитания, деления и умножения любых двух шестнадцатеричных чисел.

Что такое шестнадцатеричное число?

Шестнадцатеричная система счисления — это 16-базовая система счисления, в которой используются шестнадцать символов от 0 до 9 и буквы A, B, C, D, E, F. Здесь A, B, C, D, E и F представляют десятичное число 10. до 15. Шестнадцатеричный на основе четырехбитного двоичного кодирования.

9Калькулятор 0011 hex to decimal выполняет три вычисления: шестнадцатеричный расчет, преобразование шестнадцатеричного и преобразование десятичного. Во-первых, вы можете выполнять шестнадцатеричное сложение, вычитание, деление и умножение. Во-вторых, используйте этот шестнадцатеричный калькулятор для преобразования шестнадцатеричного значения в десятичное. Наконец, преобразуйте десятичные значения в шестнадцатеричные значения, используя этот онлайн-калькулятор шестнадцатеричных чисел.

См. также: Калькулятор стандартного отклонения

Объяснение шестнадцатеричной системы счисления.

Система счисления с основанием 16, состоящая из чисел {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, a, b, c, d, e, f}.

Десятичная система счисления

Система счисления с основанием 10, состоящая из чисел {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}.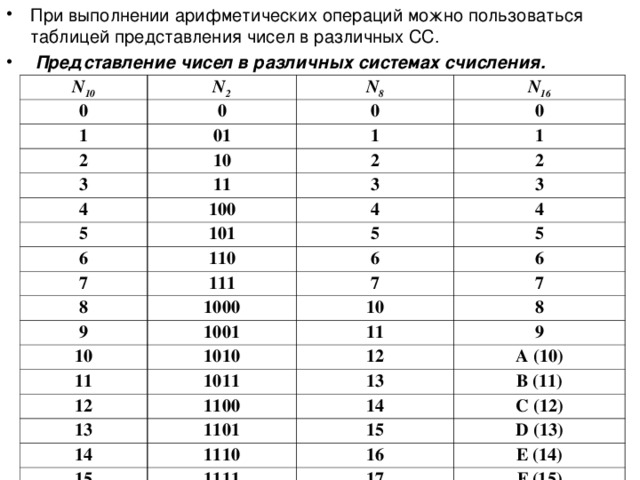

1.Hex to Decimal

В обычных десятичных числах цифры умножаются на 10.

Каждая цифра 137 умножается на соответствующую степень 10:

9 137 1 1_{0042 2 +3×10 ¹ +7×10 ⁰ = 100+30+7}

В отличие от обычных чисел, шестнадцатеричные числа читаются как степень 16, а не степень 10.

Умножьте каждую цифру числа шестнадцатеричное число с соответствующей степенью 16.

Зачем утруждать себя, когда у вас есть наш волшебный преобразователь в шестнадцатеричное число. Просто добавьте значение и рассчитайте.

2. Десятичное число в шестнадцатеричное

Приведенная ниже таблица поможет вам преобразовать десятичные числа в шестнадцатеричные числа.

Десятичный номер

0 1 2 3 4 5 6 7 8 9 11 12 13 14 15

Эквивалентный шестнадцатеричный

1. Разделите число на 16.
2. Получить целое частное для следующей итерации.
3. Остаток шестнадцатеричной цифры.
4. Как только частное достигнет 0, повторите шаги.

Короче говоря, десятичный калькулятор в шестнадцатеричный сделает ваше преобразование очень простым за считанные секунды без каких-либо забот.

Пример #1

Преобразовать 756210 в шестнадцатеричный вид:

Деление на 16	Частное (целое число)	Остаток (десятичный)	Остаток (шестнадцатеричный)	Цифра #
7562/16	472	10	А	0
472/16	29	8	8	1
29/16	1	13	Д	2
1/16	0	1	1	3

Итак, ответ: 756210 = 1D8A16

Этот шестнадцатеричный калькулятор дает вам точный шестнадцатеричный расчет. Вы можете просто выполнять сложение, вычитание и многое другое, используя наш шестнадцатеричный калькулятор сложения , шестнадцатеричный калькулятор вычитания.

Для получения дополнительных калькуляторов вы также можете попробовать Калькулятор перекрестного произведения и Калькулятор дисперсии.

Онлайн-калькулятор дополнения до двух и конвертер системы счисления

Требуется Javascript

Для этой страницы требуется Javascript. Либо вы включаете его в настройках своего браузера, либо переходите по ссылке на более старую версию (на немецком языке), работающую с простым HTTP:

Калькулятор системы счисления (без Javascript)

Это маленькое Javascript-приложение преобразует произвольные большие числа в их десятичные, шестнадцатеричные, двоичные или восьмеричные аналоги, а также вычисляет их дополнение до единицы и до двух. Введите значение в поля сверху, нажмите Enter и прочитайте результат из всех остальных значений.

Ввод:
Декабрь
Шестигранник
Корзина
окт

	Беззнаковый
	Дек	Шестнадцатер
16
32
64
п
	Дополнение
		Hex	Bin	Oct
8
16
32
64
п
	Дополнение до двух
	Декабрь	Шестнадцатеричный	Корзина	Октябрь
8
16
32
64
п

Этот калькулятор также существует в виде приложения Bit Fiddle для Windows и macOS.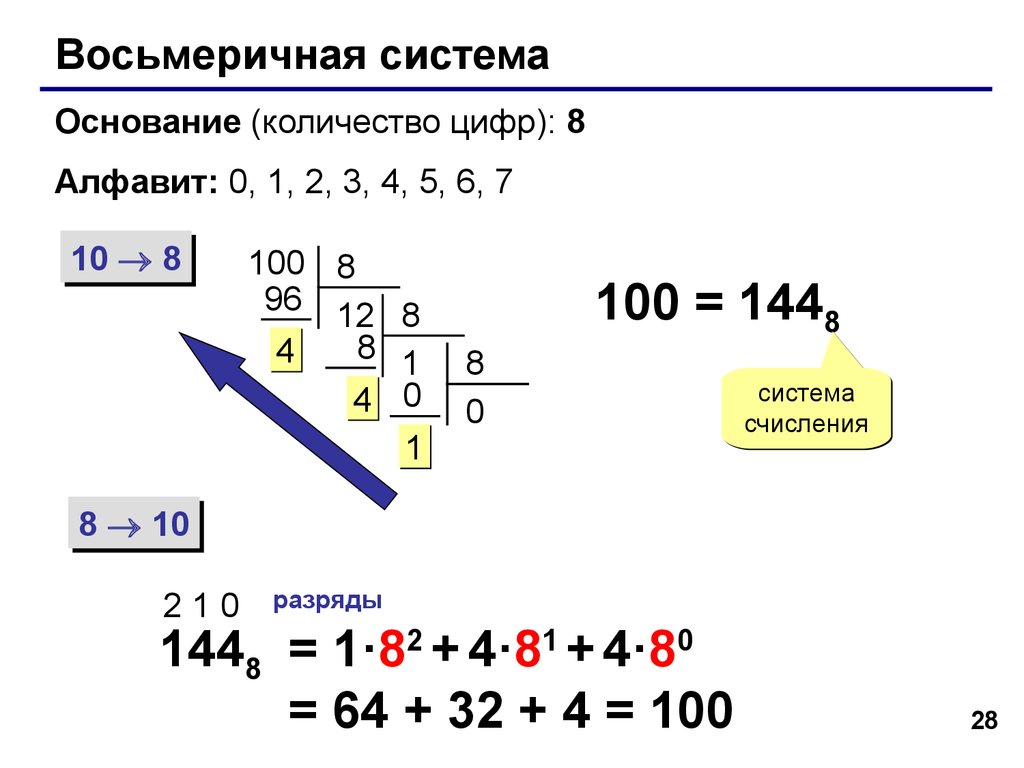

Результирующие значения представлены в битах разного размера, тогда как значение ограничивается определенным числом младших значащих битов. Результат в 9.0393 n Биты регулируют свой размер в соответствии с размером значения, поэтому всегда отображается полное значение без ограничения, но с минимальным количеством битов, необходимых для беззнакового варианта.

Можно ввести следующие символы:

Дек 0,1,2,3,4,5,6,7,8,9
Шестнадцатеричный 0,1,2,3,4,5,6,7,8,9,a,b,c,d,e,f,A,B,C,D,E,F
Ячейка 0,1
0,1,2,3,4,5,6,7 октября 

Все остальные символы будут просто пропущены . Таким образом, можно вводить числа в различных форматах (например, шестнадцатеричные с префиксом 9).0407 0x ) без проблем. Будьте осторожны с десятичной точкой! Эта точка также не будет обнаружена, то есть значение, подобное 123,456, будет интерпретировано как 123456. Вывод значений всегда будет содержать автоматически генерируемые разделительные символы для улучшения отображения в браузере и повышения удобочитаемости.

При отображении десятичных значений будет использоваться отрицательный знак, чтобы показать дополнение до двух при интерпретации как отрицательное число. Осторожно: результат дополнения не обязательно должен быть отрицательным вариантом введенного значения, так как из-за зажима избыточных битов значения отличаются несопоставимо. Отображение десятичного значения дополнения до единицы по умолчанию отключено, поскольку дополнение до единицы имеет смысл только в современных компьютерах для двоичных, шестнадцатеричных или восьмеричных чисел. Если кому интересно, код для отображения этих значений закомментирован в исходном коде.

Размер вводимых значений ограничен только возможностями Javascript.

Как программа выполняет вычисления?

Приложение работает на основе массивов. Любые входные значения сначала будут преобразованы в их двоичное представление, а биты сохранены в массиве. Поскольку массив может быть произвольно большим, можно вводить произвольно большие значения.