Перевод из шестнадцатеричной в двоичную систему счисления, калькулятор
Осуществить перевод числа из шестнадцатеричной системы счисления в двоичную можно тремя способами.
Способ 1:
Перевести сначала в десятичную систему счисления, затем из нее в конечную.
Способ 2:
- Каждый разряд шестнадцатеричного числа, начиная с высшего делим на 2, записываем остаток и делим снова до тех пор, пока в результате не будет нуля. Каждый раз записываем остаток. Буквеные разряды шестнадцатеричного числа заменяем соответствующими числовыми значениями: A — 10, B — 11, C — 12, D — 13, E — 14, F — 15.
- Записываем полученные остатки в обратном порядке, получая двоичное число.
- Если полученное двоичное число имеет менее четырех разрядов (то есть на если предыдущем шаге получили менее четырех остатков), то дополняем нулями слева до четырех разрядов.
- Повторяем предыдущие шаги для каждого следующего разряда, таким образом получаем несколько групп по 4 разряда двоичного числа.

- Записываем все вместе по порядку, отбрасываем нули слева при их наличии, получаем искомую двоичную запись числа.
Возьмем число 8E16.
- Делим на 2 каждый разряд, начиная с высшего, получаем остатки:
8 / 2 = 4, остаток 0
4 / 2 = 2, остаток 0
2 / 2 = 1, остаток 0
1 / 2 = 0, остаток 1
- Записываем остатки в обратном порядке: 1000
- Дополнять нулями не нужно, т.к. полученное число имеет 4 разряда.
- Повторяем для каждого следующего разряда:
E / 2 = 14 / 2 = 7, остаток 0
3 / 2 = 1, остаток 1
1 / 2 = 0, остаток 1
Получаем 1110
- Записываем все вместе (1000)(1110), получаем двоичное число 100011102
Способ 3:
Используем таблицу тетрад:
| Цифра | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Тетрада | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
Каждую цифру исходного числа заменяется на соответствующие тетрады. Ведущие нули самой первой тетрады отбрасываются.
Ведущие нули самой первой тетрады отбрасываются.
D816 = (1101) (1000) = 110110002
Смотрите также
- Перевод из двоичной в десятичную
- Перевод из двоичной в восьмеричную
- Перевод из двоичной в шестнадцатеричную
- Перевод из десятичной в двоичную
- Перевод из десятичной в восьмеричную
- Перевод из десятичной в шестнадцатеричную
- Перевод из восьмеричной в двоичную
- Перевод из восьмеричной в десятичную
- Перевод из шестнадцатеричной в десятичную
Шестнадцатеричная система счисления
Основание
этой системы счисления p равно шестнадцати.
Эту систему счисления можно считать
ещё одним вариантом записи двоичного
числа. В этой системе счисления
используется шестнадцать цифр. Здесь
уже не хватает десяти цифр, поэтому
приходится придумать недостающие шесть
цифр.
Для обозначения этих цифр можно воспользоваться первыми буквами латинского алфавита. При записи шестнадцатеричного числа неважно буквы верхнего или нижнего регистра будут использоваться в качестве цифр. В качестве цифр в шестнадцатеричной системе используются символы 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
Так как здесь появляются новые цифры, то приведём таблицу соответствия этих цифр десятичным значениям.
Таблица 6. Таблица соответствия шестнадцатеричных цифр десятичным значениям
Шестнадцатеричная цифра | Десятичный эквивалент | Шестнадцатеричная цифра | Десятичный эквивалент |
0 | 0 | 8 | 8 |
1 | 9 | 9 | |
2 | 2 | A | 10 |
3 | 3 | B | 11 |
4 | 4 | C | 12 |
5 | 5 | D | 13 |
6 | 6 | E | 14 |
7 | 7 | F | 15 |
Число
в этой системе счисления записывается
как сумма единиц, чисел шестнадцать,
двести пятьдесят шесть и так далее.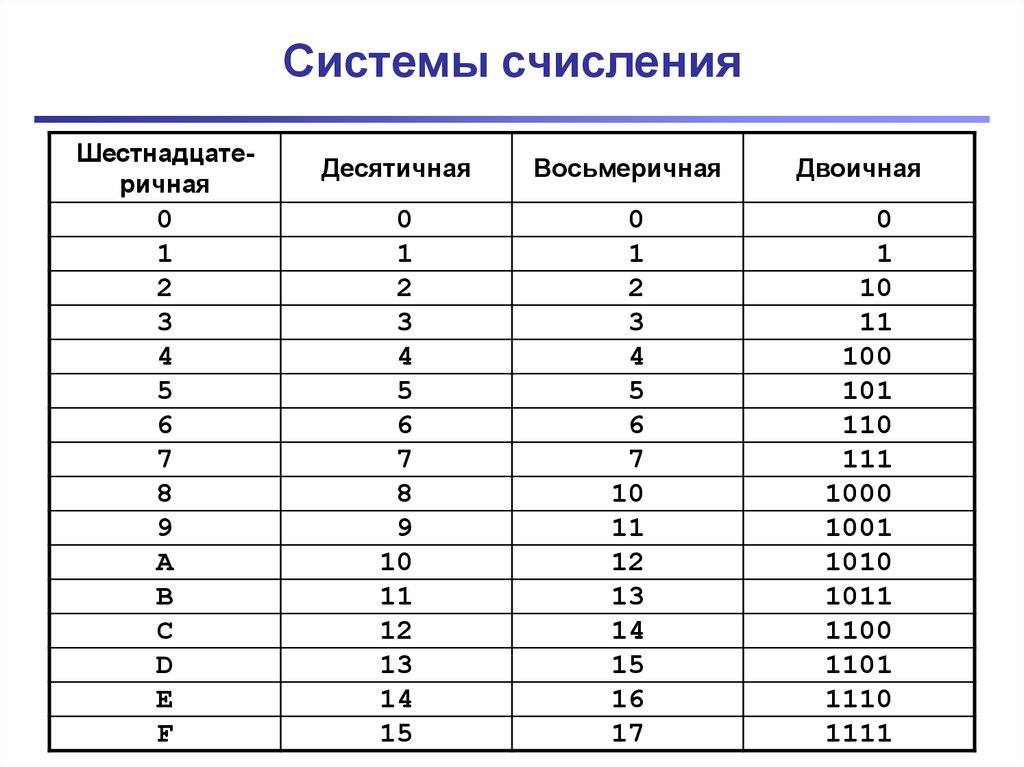 То
есть веса соседних разрядов различаются
в шестнадцать раз. Точно также записываются
и числа, меньшие единицы. В этом случае
разряды числа будут называться как
шестнадцатые, двести пятьдесят шестые
и так далее доли единицы.
То
есть веса соседних разрядов различаются
в шестнадцать раз. Точно также записываются
и числа, меньшие единицы. В этом случае
разряды числа будут называться как
шестнадцатые, двести пятьдесят шестые
и так далее доли единицы.
Рассмотрим пример записи шестнадцатеричного числа:
A16=2AF,C416=2*162+10*161+15*160+12*16-1+4*16 -2=
=51210+16010+1510+1210/1610+410/25410
Из
приведённых примеров записи чисел в
различных системах счисления вполне
очевидно, что для записи одного и того
же числа с одинаковой точностью в разных
системах счисления требуется различное
количество разрядов.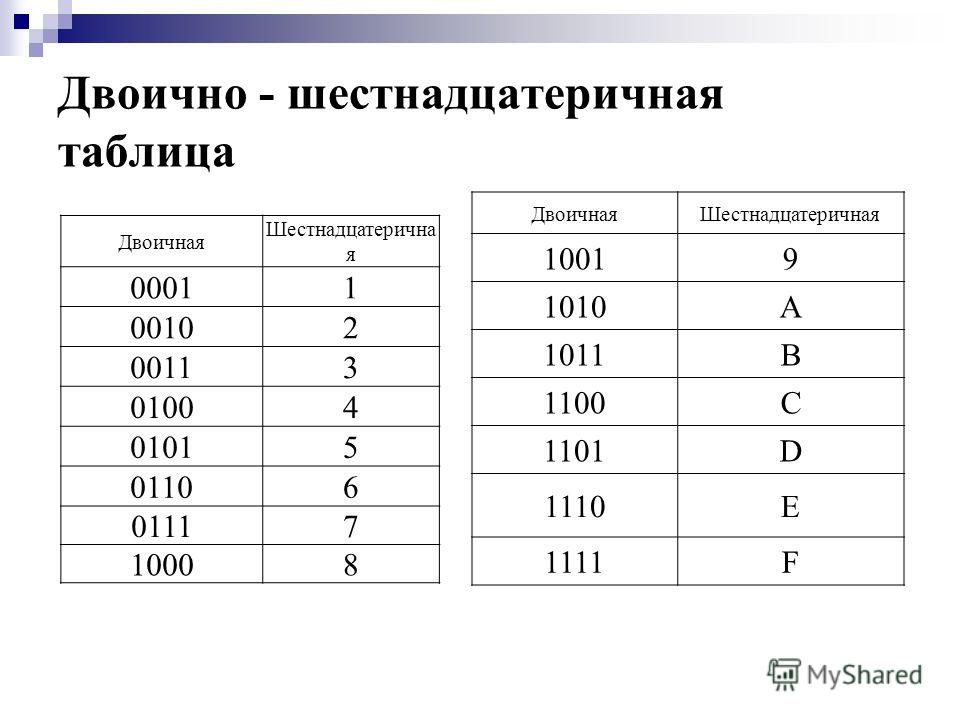 Чем больше основание
системы счисления, тем меньшее количество
разрядов требуется для записи одного
и того же числа.
Чем больше основание
системы счисления, тем меньшее количество
разрядов требуется для записи одного
и того же числа.
Достаточно часто требуется уметь переводить число из одной системы счисления в другую. Давайте научимся выполнять такое действие. Преобразование целых чисел и правильных дробей выполняется по разным правилам. В действительном числе преобразование целой и дробной части производят по отдельности.
Для перевода необходимо исходное число разделить на основание новой системы счисления до получения целого остатка, который является младшим разрядом числа в новой системе счисления (единицы). Полученное частное снова делим на основание системы и так до тех пор, пока частное не станет меньше основания новой системы счисления. Все операции выполняются в исходной системе счисления.
Рассмотрим для примера перевод числа из десятичной системы счисления в двоичную систему счисления.
Возьмём десятичное
число А10 =
124 и поделим его на основание двоичной
системы, то есть число 2.
В результате первого деления получим разряд единиц (самый младший разряд). В результате второго деления получим разряд двоек. Деление продолжаем, пока результат деления больше двух. В конце операции преобразования мы получили двоичное число 11111002.
Теперь то же самое число переведём в восьмеричную систему счисления. Для этого число 12410 разделим на число 8:
Как
мы видим, остаток от первого деления
равен 4. То есть младший разряд восьмеричного
числа содержит цифру 4. Остаток от второго
деления равен 7. то есть второй разряд
восьмеричного числа – это цифра 7.
Старший разряд получился равным 1. То
есть в результате многократного деления
мы получили восьмеричное число 174
Проверим, не ошиблись ли мы в процессе преобразования? Для этого преобразуем получившееся двоичное число в десятичную систему по обычной формуле разложения:
1×82+7×81+4×80=6410+5610+410=124
;А
можно ли осуществить перевод из
восьмеричной системы счисления в
двоичную делением? Можно! Но деление
нужно произвести по правилам восьмеричной
арифметики.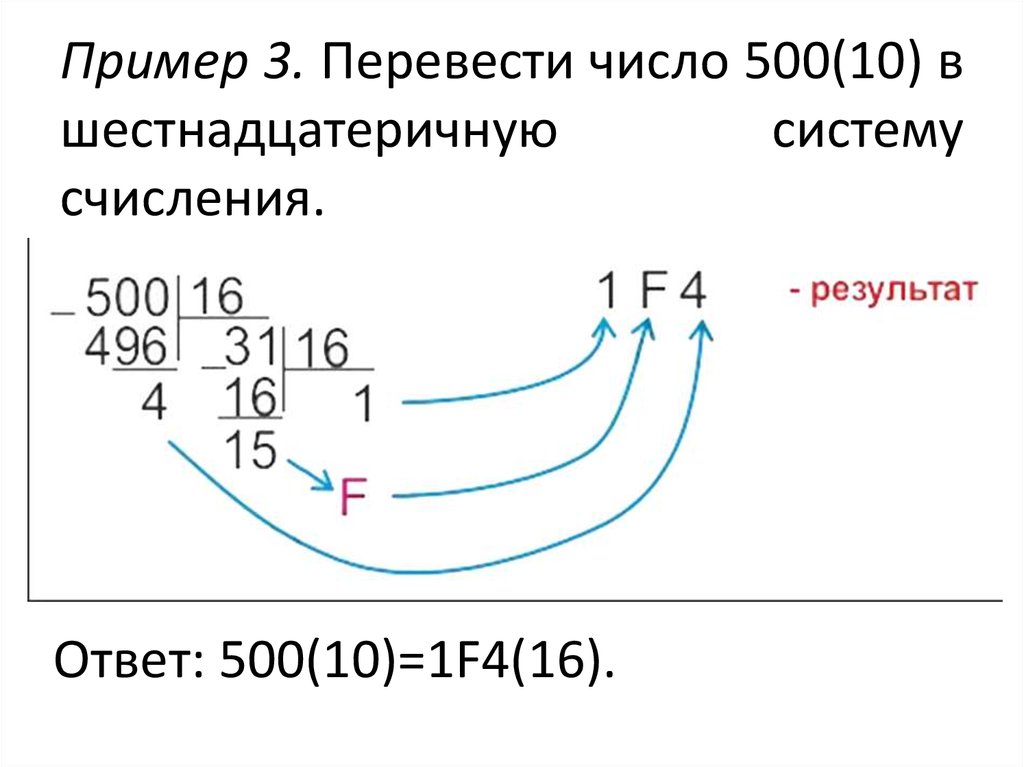 Правила работы в восьмеричной
системе счисления мы рассмотрим в
следующей главе. Тем не менее, для полноты
материала, рассмотрим пример перевода
в двоичную форму полученного ранее
восьмеричного числа 1748.
Разделим его на основание новой системы
счисления 2.
Правила работы в восьмеричной
системе счисления мы рассмотрим в
следующей главе. Тем не менее, для полноты
материала, рассмотрим пример перевода
в двоичную форму полученного ранее
восьмеричного числа 1748.
Разделим его на основание новой системы
счисления 2.
Как мы убедились выполнять деление в восьмеричной системе очень неудобно, ведь подсознательно мы делим в десятичной системе счисления. Давайте обратим внимание на то, что число 8 является степенью числа 2. То есть можно считать восьмеричную систему счисления просто более короткой записью двоичного числа. Это означает, что для представления восьмеричной цифры можно использовать три двоичных бита (8=23). Давайте составим таблицу соответствия. Она приведена в таблице 1.
Таблица 1. Таблица соответствия восьмеричных цифр и двоичного кода
Двоичный код | Восьмеричная цифра | Десятичный эквивалент |
000 | 0 | 0 |
001 | 1 | 1 |
010 | 2 | 2 |
011 | 3 | 3 |
100 | 4 | 4 |
101 | 5 | 5 |
110 | 6 | 6 |
111 | 7 | 7 |
Используя
эту таблицу можно просто заменить каждую
восьмеричную цифру тремя двоичными
битами. Три двоичных бита обычно называют
триадой или трибитом. Теперь давайте
переведём восьмеричное число 1748 в
двоичную форму при помощи таблицы 7:
Три двоичных бита обычно называют
триадой или трибитом. Теперь давайте
переведём восьмеричное число 1748 в
двоичную форму при помощи таблицы 7:
Аналогично можно выполнить перевод числа из двоичной системы в восьмеричную. Для этого двоичное число разбивают на триады относительно крайнего правого разряда (или двоичной запятой) и, используя таблицу 7, каждой триаде ставят в соответствие восьмеричную цифру.
Аналогичным образом можно выполнить перевод числа из шестнадцатеричной формы в двоичную и обратно. В этом случае для представления шестнадцатеричной цифры потребуется четыре двоичных разряда. Четыре двоичных разряда обычно называют тетрадой. Иногда при переводе иностранных книг используется термин нибл.
Давайте
составим таблицу соответствия двоичных
тетрад и шестнадцатеричных цифр. Для
этого мы будем просто прибавлять единицу
к значению предыдущей строки в каждом
столбце таблицы, в соответствии с
используемой в этом столбце системой
счисления.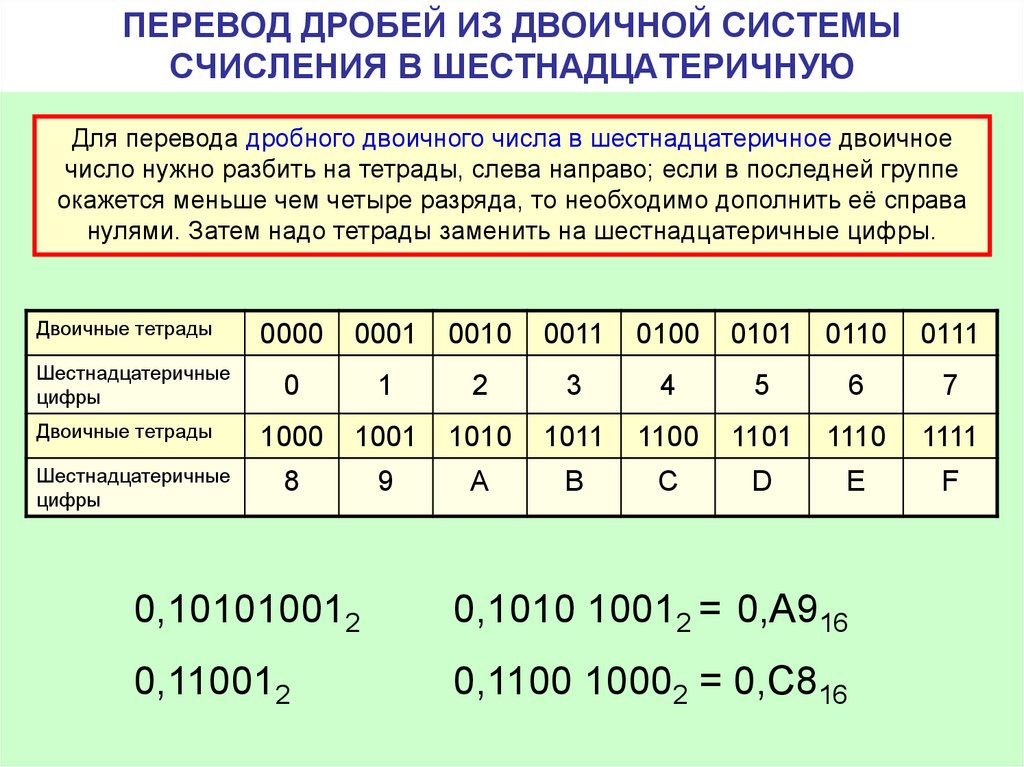 Результат приведён в таблице 2.
Результат приведён в таблице 2.
В качестве примера использования таблицы 2 переведем шестнадцатеричное число 7С16 в двоичную форму представления:
Таблица 2. Таблица соответствия шестнадцатеричных цифр и двоичного кода
Двоичный код | Восьмеричная цифра | Десятичный эквивалент |
0000 | 0 | 0 |
0001 | 1 | 1 |
0010 | 2 | 2 |
0011 | 3 | 3 |
0100 | 4 | 4 |
0101 | 5 | 5 |
0110 | 6 | 6 |
0111 | 7 | 7 |
1000 | 8 | 8 |
1001 | 9 | 9 |
1010 | a | a |
1011 | b | b |
1100 | c | c |
1101 | d | d |
1110 | e | e |
1111 | f | f |
Пример
преобразования двоичного числа в
восьмеричную и шестнадцатеричную форму
приведён на рисунке 1.
Рисунок 1. Пример преобразования двоичного числа в 8-ричную и 16-ричную форму.
На этом рисунке внизу выделены двоичные тетрады и соответствующие им шестнадцатеричные цифры. Их соответствие можно проверить при помощи таблицы 2. Сверху выделены триады и соответствующие им восьмеричные цифры. Старшая триада получилась неполной. Её нужно дополнить старшими незначащими нулями для того, чтобы можно было бы воспользоваться таблицей 1.
F То, чего вы (вероятно) не знали о шестнадцатеричной системе счисления
Шестнадцатеричная система счисления, или основание 16, Сноска 1 десятилетиями использовалась в качестве компьютерного языка. Но многое из того, что было написано о развитии термина шестнадцатеричной и связанной с ней самой системы счисления, неверно. В этой короткой статье мы углубимся в историю термина, системы счисления и ее обозначения, чтобы предложить более полную (и точную!) историю шестнадцатеричной системы счисления и развеять некоторые мифы, возникшие на этом пути. Итак, вот F или пятнадцать вещей, которые вы (вероятно) не знали о шестнадцатеричном формате:
Итак, вот F или пятнадцать вещей, которые вы (вероятно) не знали о шестнадцатеричном формате:
1
Первая аттестация Oxford English Dictionary из шестигранных дат из рассылки в январе 1954 года, в котором использовалось слово для описания миниацкого, Стонетта 2 . что его можно «управлять шестнадцатеричным числом» [2, с. 6]. На самом деле это слово может быть датировано 1950 годом, когда оно использовалось для обозначения обозначения, используемого для ввода чисел и инструкций в восточный автоматический компьютер стандартов (SEAC), разработанный и построенный Национальным бюро стандартов, правительственным учреждением США. базируется в Мэриленде [1, с. 123]. Сноска 3 . Однако часто высказываемое утверждение, что IBM придумала в шестнадцатеричном формате (см., например, [6, стр. 118]), неверно.
2
Шестнадцатеричные цифры, выбранные Национальным бюро стандартов, представляли собой западно-арабские цифры 0–9 и латинские буквы A–F, и с тех пор они остаются стандартными. Это не всем понравилось. В 1968 году Брюс Алан Мартин [13, с. 658] жаловался, что «[с] нелепым выбором букв A, B, C, D, E, F в качестве шестнадцатеричных числовых символов, усугубляющих и без того неприятные проблемы различения восьмеричных (или шестнадцатеричных) чисел от десятичных чисел (или имен переменных) , настало время пересмотреть наши числовые символы». С этой целью он набросал пятнадцать новых символов для ненулевых цифр шестнадцатеричной системы счисления:
Это не всем понравилось. В 1968 году Брюс Алан Мартин [13, с. 658] жаловался, что «[с] нелепым выбором букв A, B, C, D, E, F в качестве шестнадцатеричных числовых символов, усугубляющих и без того неприятные проблемы различения восьмеричных (или шестнадцатеричных) чисел от десятичных чисел (или имен переменных) , настало время пересмотреть наши числовые символы». С этой целью он набросал пятнадцать новых символов для ненулевых цифр шестнадцатеричной системы счисления:
Однако предложение Мартина о замене цифр 0–9 и A–F ни к чему не привело, или .
3
Вдохновение для выбора Национальным бюро стандартов A–F в качестве шести дополнительных цифр могло быть получено из книги Джозефа Боудена Special Topics in Theoretical Arithmetic (1936), в которой он предположил, что [ , п. 50] Сноска 4
[i]Если мы хотим использовать основание больше десяти, мы можем вместо использования новых символов использовать буквы для дополнительных цифр. Таким образом, с 2 5 для основания мы можем считать следующим образом:
Таким образом, с 2 5 для основания мы можем считать следующим образом:
1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, G, H, K, L, M, N, P, Q, R, S, T, U, V, W, X, Y, 10.
Боуден также рассмотрел достоинства основания 16, которое он назвал сексуальным числом , а этот термин он, по-видимому, позаимствовал у Роберта Морриса Пирса, который использовал его в 1898 году. 9] выбрал строчные латинские буквы a, b, c, d, e, f. С целью предоставления информации, которая могла бы поддержать попытку отойти от десятичной системы общественного пользования, он показал, как работают стандартные арифметические операции в системах счисления 8, 10, 12 и 16.
4
In Искусство компьютерного программирования , Дональд Кнут [8, с. 202] отмечает, что преобладающий сегодня термин для основания 16, шестнадцатеричное , представляет собой «смесь греческих и латинских основ», Сноска 6 , а именно греческое ἕξ ( hex , «шесть») и латинское decem ( «10»).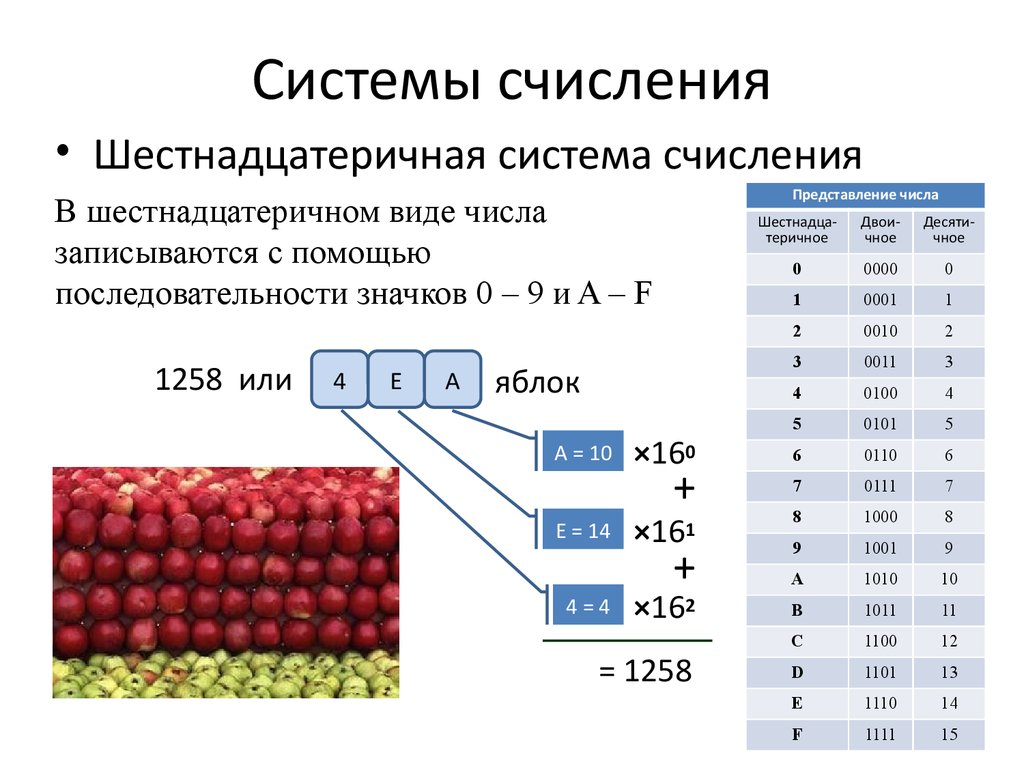 Это все равно, что смешать английские и немецкие корни, чтобы получить sixzehn или sechsteen . Конечно, результат все еще можно понять, и некоторые гибриды (такие как телевидение) стали повсеместными, но греческие и латинские корни, как правило, лучше хранить отдельно, так как объединение их словарей увеличивает распространенность омографов (т. правописание), из-за чего гораздо сложнее понять, что означает чеканка; например, только допустив их разделение, можно быть уверенным, что педология есть изучение (λόγος · логос ) почвы ( π έδον · pédon ), не ноги ( pedes ).
Это все равно, что смешать английские и немецкие корни, чтобы получить sixzehn или sechsteen . Конечно, результат все еще можно понять, и некоторые гибриды (такие как телевидение) стали повсеместными, но греческие и латинские корни, как правило, лучше хранить отдельно, так как объединение их словарей увеличивает распространенность омографов (т. правописание), из-за чего гораздо сложнее понять, что означает чеканка; например, только допустив их разделение, можно быть уверенным, что педология есть изучение (λόγος · логос ) почвы ( π έδον · pédon ), не ноги ( pedes ).
5
Кнут [8, с. 202] также утверждает, что «более подходящими терминами были бы «сениденарный», «восстановительный» или даже «шестнадцатеричный». . Это ложное число на , вероятно, происходит из-за неправильного деления числа 9.0005 шестидесятеричный (термин, используемый для обозначения основания 60; буквально «относящийся к шестидесяти») как шестидесятеричный .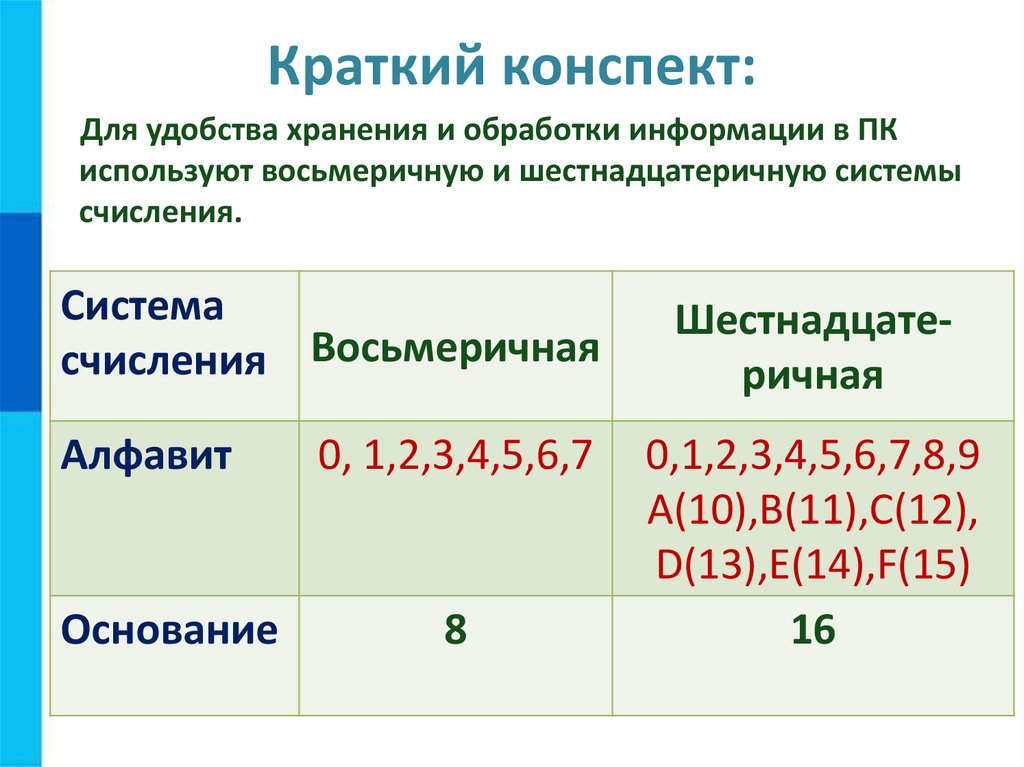 Footnote 7 Искаженный термин шестнадцатеричный впервые появился в 1895 году в словаре Уильяма Дуайта Уитни The Century Dictionary [24, p. 5535]. Сноска 8 К сожалению, искажение уже укоренилось: в книге по этимологии математических терминов Шварцман [18, стр. 5, 105] ошибочно принимает шестнадцатеричное за этимологически правильную альтернативу 9.0005 шестнадцатеричный .
Footnote 7 Искаженный термин шестнадцатеричный впервые появился в 1895 году в словаре Уильяма Дуайта Уитни The Century Dictionary [24, p. 5535]. Сноска 8 К сожалению, искажение уже укоренилось: в книге по этимологии математических терминов Шварцман [18, стр. 5, 105] ошибочно принимает шестнадцатеричное за этимологически правильную альтернативу 9.0005 шестнадцатеричный .
6
Согласно Кнуту [8, с. 201], первым, кто использовал основание 16, был шведско-американский инженер Джон Уильям Нистром (1825–1885). Это неверно, как мы увидим. Но Нистром был, по крайней мере, очень ярым сторонником основания 16, которое он очень подробно изложил в книге, опубликованной в 1862 году, и в серии статей, опубликованных годом позже. Сноска 9 Он предложил заменить знакомую десятичную систему системой с основанием 16, которую он назвал 9.0005 тон . Название не имеет ничего общего с музыкой; скорее, в системе Нистрома число 10 (то есть 16 в десятичной системе) произвольно названо тонн . Фактически Нистром [14, с. 16–17] придумал новые названия для всех чисел, выраженных в его тональной системе; например, 0 — нолл, 9 — ко, 100 — сан, 1000 — милль, 1000000 — санбонг и т. д. Для тональной записи он предложил [14, с. 15] следующие символы: Footnote 10
Фактически Нистром [14, с. 16–17] придумал новые названия для всех чисел, выраженных в его тональной системе; например, 0 — нолл, 9 — ко, 100 — сан, 1000 — милль, 1000000 — санбонг и т. д. Для тональной записи он предложил [14, с. 15] следующие символы: Footnote 10
Нистром был настолько очарован своей тональной системой, что не только предложил новые единицы измерения веса и меры, но и изобрел циферблат часов, который делил день на шестнадцать часов. Он даже предложил разделить год на 16 месяцев примерно по 23 дня в каждом, причем каждый месяц имел собственное новое название (первыми тремя были Ануарий, Дебрян и Тимандр). Footnote 11 Помимо числа 16, допускающего более удобное двоичное деление (т. е. деление на 2), чем число 10, Нистром [14, с. 23] также предпочитал 16-ю системе счисления по основанию 10, потому что первая требует «меньшего количества цифр для выражения большого числа».
7
Однако в 1867 г. У. Б. Тейлор из Патентного ведомства США рассмотрел предложение Нистрома и пришел к выводу, что 16-кратное основание не намного экономичнее 10-кратного, как утверждал Нистром. Тейлор [22, с. 120] продемонстрировал, что, когда дело дошло до выражения очень больших чисел, таких как «количество песчинок, необходимое для образования земного шара размером с нашу Землю», около 659 г.квинтиллион, Сноска 12 порядковая система (предпочтительный термин Тейлора для основания 16) была едва ли более удобной, чем десятичная, поскольку в то время как десятичная система потребовала бы 33 цифры для выражения такого большого числа, порядковая система по-прежнему требовала бы 28: незначительно», по мнению Тейлора. Не завоевав поддержки своей тональной системы, Нистром позже отказался от своих усилий по ее продвижению, вместо этого рекомендуя публичное принятие дуоденальной (то есть двенадцатеричной или двенадцатиричной) системы [16, с.
У. Б. Тейлор из Патентного ведомства США рассмотрел предложение Нистрома и пришел к выводу, что 16-кратное основание не намного экономичнее 10-кратного, как утверждал Нистром. Тейлор [22, с. 120] продемонстрировал, что, когда дело дошло до выражения очень больших чисел, таких как «количество песчинок, необходимое для образования земного шара размером с нашу Землю», около 659 г.квинтиллион, Сноска 12 порядковая система (предпочтительный термин Тейлора для основания 16) была едва ли более удобной, чем десятичная, поскольку в то время как десятичная система потребовала бы 33 цифры для выражения такого большого числа, порядковая система по-прежнему требовала бы 28: незначительно», по мнению Тейлора. Не завоевав поддержки своей тональной системы, Нистром позже отказался от своих усилий по ее продвижению, вместо этого рекомендуя публичное принятие дуоденальной (то есть двенадцатеричной или двенадцатиричной) системы [16, с.
8
Нистром не заявлял, что основание 16 является его собственным изобретением. Он писал, что король Швеции Карл XII (1682–1718) рассматривал возможность введения в Швеции системы с основанием 16, но его возражение против вытекающего из этого требования новых символов для дополнительных цифр заставило его предпочесть восьмеричную (с основанием 8) систему. вместо этого [15, с. 263–264]. Однако Нистром не представил никаких доказательств своего утверждения, и оно опровергается свидетельством очевидца Эмануэля Сведенборга (1668–1772), в котором описывается интерес Карла XII к восьмеричной системе и даже к основанию 64, но не к основанию 16 [21].
Он писал, что король Швеции Карл XII (1682–1718) рассматривал возможность введения в Швеции системы с основанием 16, но его возражение против вытекающего из этого требования новых символов для дополнительных цифр заставило его предпочесть восьмеричную (с основанием 8) систему. вместо этого [15, с. 263–264]. Однако Нистром не представил никаких доказательств своего утверждения, и оно опровергается свидетельством очевидца Эмануэля Сведенборга (1668–1772), в котором описывается интерес Карла XII к восьмеричной системе и даже к основанию 64, но не к основанию 16 [21].
9
Нистром был, по крайней мере, прав в том, что он не был изобретателем базы 16, даже если он не был прав в том, кто до него дошел. Почти двумя десятилетиями ранее, в 1845 году, английский школьный учитель и математик Томас Райт Хилл (1763–1851) предложил систему счисления с основанием 16 в докладе, зачитанном на собрании Британской ассоциации содействия развитию науки в Кембридже, Англия. Статья была опубликована посмертно как «Система числовой номенклатуры и обозначений, основанная на принципах абстрактной полезности» [7, с. 63–85]. Хилл называл свою систему с основанием 16 числом 9.0005 полудесятичный . Латинское слово для шестнадцати — sedecim (что дает английское sedecim ), но оно также может быть записано как sexdecim , так что выбор термина Хиллом этимологически верен.
Статья была опубликована посмертно как «Система числовой номенклатуры и обозначений, основанная на принципах абстрактной полезности» [7, с. 63–85]. Хилл называл свою систему с основанием 16 числом 9.0005 полудесятичный . Латинское слово для шестнадцати — sedecim (что дает английское sedecim ), но оно также может быть записано как sexdecim , так что выбор термина Хиллом этимологически верен.
A
Хилл [7, с. 69] черпал свое вдохновение из различного использования термина камень в графстве Йоркшир, Англия, для обозначения веса в 16 фунтов, а не в 14 фунтов, как в других местах Британии. Хилл отметил, что практика Йоркшира допускает более удобное деление пополам, что предполагает, что преимущества можно получить, приняв основание 16 в более широком смысле. Вместо того, чтобы определить шестнадцать различных цифр для своей десятичной системы счисления, Хилл [7, с. 78] придумал девять элементов, которые можно комбинировать, чтобы сформировать любое положительное или отрицательное значение в секс-десятичной системе счисления:
На основе этих элементов Хилл сгенерировал отличительные имена для всех положительных и отрицательных шестнадцатеричных значений; например, dĭn = +1, dĭkōn = +16 (поскольку ĭ или 1 стоит на месте 16, а k перед 9 ō 900), разделитель 6 0 ō 900 dĭdōkōn = +256 (поскольку х , или 1, стоит на месте 256, а d и k перед каждым ō ), действует как 9 разделителей мест0005 kĭn = −1, kĭkōn = −16 и т. д., где ō может предшествовать либо d , либо k , в зависимости от предпочтений в произношении, поскольку на + или − это не влияет.
д., где ō может предшествовать либо d , либо k , в зависимости от предпочтений в произношении, поскольку на + или − это не влияет.
Б
Холм [7, с. 74] считал, что шестнадцатеричная система до сих пор не нашла сторонников, заявив: «Насколько мне известно, его число [т. е. 16] до сих пор публично не рекомендовалось». Хилл был прав в том, что секс-десятеричная система раньше публично не рекомендовалась, но это не значит, что он был первым, кто ее придумал. Фактически, основание 16 было изобретено в семнадцатом веке эрудитом Готфридом Вильгельмом Лейбницем (1646–1716), который хорошо известен рядом других математических нововведений, таких как исчисление и двоичная система. Первоначально термин Лейбница для основания 16 был равен 9.0005 десятеричный . В своем первом сочинении по основанию 16 Лейбниц [9] разработал, как преобразовать десятичное число 1679, представляющее год его изобретения, в десятеричное счисление.
C
Лейбниц экспериментировал с различными формами записи десятеричных чисел. В своей первой работе на эту тему [9] он использовал латинские буквы m, n, p, q, r и s для шести дополнительных цифр, прежде чем отказаться от них в пользу шести аретинских слогов ut, re, mi, фа, соль и ля, Сноска 13 сокращено Лейбницем до u, r, m, f, s и ℓ. Объединив эти слоги с немецкими словами, обозначающими числа, он создал совершенно новый набор терминов для значений, выраженных в десятеричной системе счисления. Например, utzehn , комбинация слога ut , означающего десять, и немецкого слова zehn , которое традиционно означало десять, но было перепрофилировано Лейбницем для обозначения шестнадцати, было термином Лейбница для обозначения десятичного числа. 26 выражено в десятеричной системе счисления (1u в системе обозначений Лейбница).
D
Лейбниц [10] также экспериментировал с различными формами обозначения основания 16. В другом раннем сочинении, в котором он назвал систему счисления сидячей , Сноска 14 , он сложил точки и тире, используя точка для каждого 0 бита и тире для каждого 1 бита, со старшим битом вверху и младшим битом внизу:
В другом раннем сочинении, в котором он назвал систему счисления сидячей , Сноска 14 , он сложил точки и тире, используя точка для каждого 0 бита и тире для каждого 1 бита, со старшим битом вверху и младшим битом внизу:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| • | – | – • | — — | – • • | – • – | – – • | – – – | – • • • | – • • – | – • – • | – • – – | – – • • | – – • – | – – – • | – – – – | – • |
Система счисления Лейбница с точками и тире напоминает систему счисления древних майя (с основанием 20, или виценарную), в которой, кроме специального символа «ракушка» для нуля, используются только два символа, точка (для 1) и черта (для 5), со стопками точек и полос, используемых для формирования чисел до 19, и вертикальной позиционной системой для представления еще более высоких чисел [3, с. 764]. Однако нет никаких доказательств того, что Лейбниц знал майя, поэтому сходство, безусловно, является случайным.
764]. Однако нет никаких доказательств того, что Лейбниц знал майя, поэтому сходство, безусловно, является случайным.
E
В 1682 году или около того Лейбниц [11] набросал еще одну форму оседлых обозначений на обратной стороне конверта. На этот раз он начинает с вогнутого полукруга для обозначения 0 и вогнутого вниз полукруга для обозначения 1, а затем модифицирует эти символы, чтобы получить остальные цифры:
Делая выводы из своих описаний (или инструкций), Лейбниц основывал каждую цифру на латинские буквы, как одиночные, так и соединенные, причем некоторые из них были «двухвостыми», т. е. вытянутыми за хвост ( cauda на латыни) с обеих сторон, а другие «антехвостые», то есть удлиненные хвостом только с левой стороны.
F
Вероятно, в своей последней работе по 16-кратному счислению Лейбниц [12] нарисовал таблицу, показывающую десятичные числа от 0 до 40, представленные в каждом основании от 2 до 16. В этой таблице Лейбниц использовал строчные латинские буквы a, b, c, d, e и f для шести дополнительных цифр его сидячего набора символов, первый и единственный раз, когда он это сделал. Это предвосхитило, а не повлияло на современное соглашение об использовании A, B, C, D, E и F для шести дополнительных цифр, поскольку работы Лейбница о малоподвижном образе жизни только сейчас начинают публиковаться [20].
В этой таблице Лейбниц использовал строчные латинские буквы a, b, c, d, e и f для шести дополнительных цифр его сидячего набора символов, первый и единственный раз, когда он это сделал. Это предвосхитило, а не повлияло на современное соглашение об использовании A, B, C, D, E и F для шести дополнительных цифр, поскольку работы Лейбница о малоподвижном образе жизни только сейчас начинают публиковаться [20].
Примечания
Под «основанием 16» мы подразумеваем позиционную систему счисления, использующую 16 в качестве основания. Таким образом, мы исключаем практику деления целых величин на шестнадцать дробных частей без позиции. Такие практики зафиксированы, например, в тамильской литературе и Древнем Риме. О них см. [19] и [23, с. 336].
Словарь Merriam-Webster также дает 1954 год как год , шестнадцатеричный , который был впервые использован, предположительно по той же причине.
«>В 1903 г. Боуден [4, с. 26] цитируется страница 9 из книги Пирса, на которой сексиденальных занимает видное место. К сожалению, при этом Боуден увековечил ошибку Пирса: i в сексиденальном — это интерфикс, т. е. короткий звук (обычно гласный), не имеющий значения, вставленный между частями слова в сложном слове для облегчения произношения. Греко-латинские заимствования изобилуют интерфиксами, но есть и слова, секс («шесть») — один из них, правильно составляющий без интерфикса. В английском языке на самом деле нет интерфиксов, но в нем есть несколько схожих явлений, таких как и , которые становятся и перед гласной, и то, как некоторые люди произносят , рисуя , как если бы оно писалось как , рисование .
Собственно, корни.
«>Этимология записи отмечает, что это слово «Prop. *sexdecimal », звездочка, указывающая на то, что форма не засвидетельствована (из-за неполных знаний этого лексикографа).
Нистром [14, с. 3] впервые предложил свою систему с основанием 16 на собрании Международной ассоциации по получению единой десятичной системы весов, мер и монет, состоявшемся в Брэдфорде, Англия, 11 октября 1859 г..
Обратите внимание, что «старые цифры в Тональной Системе несут [ sic ] старое значение (кроме 9) один за другим» [14, с. 17], так что приведенный выше порядок не ошибочен.
Другими были Гостус, Сувенарий, Билиан, Ратамбер, Месудий, Никтоарий, Колумбиан, Хусамбер, Викториус, Ламбориус, Полиан, Филандер и Тонбориус.

Здесь Тейлор дает квинтиллион его значения по длинной шкале (1 000 000 5 = 10 30 ). Эквивалентное число в короткой шкале будет 659 нониллионов.
Они превратились в сольфа, который Джули Эндрюс декламирует в песне «Do-Re-Mi» в The Sound of Music .
Читая эту короткую статью, вы не могли не заметить необычное изобилие имен для основания 16. Мы привели восемь, и вполне вероятно, что использовались и другие формы. Мы уже приводили причины, по которым шестнадцатеричное число , шестидесятеричный и шестидесятеричный вызывают возражения, в то время как тональный совершенно идиосинкразичен. Но как насчет остальных четырех — порядкового числа , шестнадцатеричного числа , порядкового числа и порядкового числа ? Каждый из них так же хорош, как и другие? Или есть какое-то обоснованное основание, по которому можно отдать предпочтение? Sedecimal и sexdecimal каждое происходит от одного из двух вариантов написания латинского слова для кардинального числительного шестнадцать с английским суффиксом — al добавлено для образования прилагательного; они одинаково действительны, но формы без x встречаются чаще, как на английском, так и на латинице.
 Sedenary и senidenary в конечном счете происходят, соответственно, от sedeni и senideni , латинских дистрибутивных числительных, значение которых наиболее естественно выражается в английском языке такими фразами, как «шестнадцать за один раз» или «в шестнадцать». ” Из этих двух классов прилагательных те, которые образованы от дистрибутивных числительных, предпочтительнее, чем производные от количественных числительных, потому что смысл дистрибутивов лучше соответствует системе, в которой количество, выражаемое каждой последующей позицией, увеличивается на кратное основанию (в этом случае, на 16 за раз), а также потому, что эти прилагательные являются промежуточным производным от предварительно сформированных латинских прилагательных, которые заканчиваются на — arius (в данном случае sedenarius и senidenarius ). Наконец, между столь же безупречными сидячими и сидячими выбирать особо не из чего; стоит только отметить, что senideni предшествовали sedeni .
Sedenary и senidenary в конечном счете происходят, соответственно, от sedeni и senideni , латинских дистрибутивных числительных, значение которых наиболее естественно выражается в английском языке такими фразами, как «шестнадцать за один раз» или «в шестнадцать». ” Из этих двух классов прилагательных те, которые образованы от дистрибутивных числительных, предпочтительнее, чем производные от количественных числительных, потому что смысл дистрибутивов лучше соответствует системе, в которой количество, выражаемое каждой последующей позицией, увеличивается на кратное основанию (в этом случае, на 16 за раз), а также потому, что эти прилагательные являются промежуточным производным от предварительно сформированных латинских прилагательных, которые заканчиваются на — arius (в данном случае sedenarius и senidenarius ). Наконец, между столь же безупречными сидячими и сидячими выбирать особо не из чего; стоит только отметить, что senideni предшествовали sedeni .
В 1988 году название агентства было изменено на Национальный институт стандартов и технологий.
В исходном латинском sexagesimus («шестидесятый»), ‑agesimus — «‑десятая» часть; соответственно латиница сексадецим похож на английский sixtiteen .
Ссылки
Аноним. SEAC — Национальное бюро стандартов Восточного автоматического компьютера. Национальное бюро стандартов Бюллетень технических новостей 34: 9 (1950), 121–125. Доступно по адресу https://jovial.com/documents/SEAC.pdf.
Аноним. Миниак. Информационный бюллетень цифровых компьютеров 6: 1 (1954), 6. Доступно по адресу https://nsarchive.gwu.edu/sites/default/files/documents/5008299/Office-of-Naval-Research-Mathematical-Science.pdf.
Джеймс К. Бидуэлл. Арифметика майя. Учитель математики 60:7 (1967), 762–768. Доступно по адресу https://www.jstor.org/stable/27957685.
Джозеф Боуден. Элементы теории целых чисел . Макмиллан, 1903 г. Доступно по адресу https://archive.org/details/elementsoftheory00bowd.
Джозеф Боуден.
 Специальные разделы теоретической арифметики . Джозеф Боуден, 1936 г. Доступно по адресу https://hdl.handle.net/2027/uc1.$b543512.
Специальные разделы теоретической арифметики . Джозеф Боуден, 1936 г. Доступно по адресу https://hdl.handle.net/2027/uc1.$b543512.Ян Гилленбок. Энциклопедия исторической метрологии, весов и мер , том. 1. Биркхойзер, 2018.
Томас Райт Хилл. Выдержки из бумаг покойного Томаса Райта Хилла, эсквайра. Ф.Р.А.С. Джон В. Паркер и сын, 1860 г. Доступно на https://archive.org/details/selectionsfromhi00hilluoft.
Дональд Э. Кнут. Искусство компьютерного программирования. Том 2 : Получисловые алгоритмы , третье издание. Addison-Wesley, 1988.
Готфрид Вильгельм Лейбниц. Секретарная прогрессия. Неопубликованная рукопись с маркой LH 35, 13, 3 Bl. 23, принадлежит Библиотеке Готфрида Вильгельма Лейбница — Niedersächsische Landesbibliothek, Ганновер, 1679 г..
Готфрид Вильгельм Лейбниц.
 Progressio binaria est pro theoria, sedenaria pro praxi. Неопубликованная рукопись с маркой LH 35, 3 B 17 Bl. 4 r , принадлежит Библиотеке Готфрида Вильгельма Лейбница – Niedersächsische Landesbibliothek, Ганновер, 1679.
Progressio binaria est pro theoria, sedenaria pro praxi. Неопубликованная рукопись с маркой LH 35, 3 B 17 Bl. 4 r , принадлежит Библиотеке Готфрида Вильгельма Лейбница – Niedersächsische Landesbibliothek, Ганновер, 1679.Готфрид Вильгельм Лейбниц. Рукопись без названия. Неопубликованная рукопись с маркой LH 35, 3 B 5 Bl. 77, принадлежит Библиотеке Готфрида Вильгельма Лейбница – Niedersächsische Landesbibliothek, Ганновер, 1682 г.
Готфрид Вильгельм Лейбниц. Рукопись без названия. Неопубликованная рукопись с маркой LH 35, 3 B 11 Bl. 11 v , принадлежит Библиотеке Готфрида Вильгельма Лейбница – Niedersächsische Landesbibliothek, Ганновер, 1703.
Брюс А. Мартин. О двоичной записи. Сообщения ACM 11:10 (1968), 658. Доступно на https://dl.acm.org/doi/pdf/10.1145/364096.364107.
Джон В. Нистром. Проект новой системы арифметики, веса, меры и монет, которую предлагается назвать тональной системой, с шестнадцатью по основанию .
 JB Lippincott & Co., 1862. Доступно на https://books.google.com/books?id=aNYGAAAAYAAJ.
JB Lippincott & Co., 1862. Доступно на https://books.google.com/books?id=aNYGAAAAYAAJ.Джон В. Нистром. О новой системе арифметики и метрологии, называемой тональной системой. Журнал Института Франклина 76 (1863), 263–275, 337–348, 402–407. Доступно на https://archive.org/details/journalfranklini76fran.
Джон В. Нистром. Новый трактат об элементах механики, устанавливающий строгую точность в значении динамических терминов, с приложением по дуоденальной арифметике и метрологии . Портер и Коутс, 1875 г. Доступно по адресу https://books.google.com/books?id=eUYOAAAAAYAAJ.
Роберт М. Пирс. Задачи числа и меры . Роберт М. Пирс, 1898 г. Доступно по адресу https://gdz.sub.uni-goettingen.de/id/PPN603882684.
Стивен Шварцман. Слова математики: этимологический словарь математических терминов, используемых в английском языке .
 Издательство Кембриджского университета, 1996.
Издательство Кембриджского университета, 1996.С. Шринивасан, Дж. В. М. Джозеф и П. Харикумар. Расшифровка индусского письма: метод подобия в действии. Текущая наука 103: 3 (2012), 268–281. Доступно по адресу https://www.jstor.org/stable/24085030.
Ллойд Стрикленд и Гарри Льюис. Лейбниц о двоичном коде: изобретение компьютерной арифметики . MIT Press, 2022.
Эмануэль Сведенборг. Любопытные мемуары г-на Эмануэля Сведенборга о Карле XII. Швеции. Журнал джентльмена и историческая хроника 24 (1754), 423–424. Д. Генри и Р. Кейв у ворот Святого Иоанна. Доступно по адресу https://www.google.com/books?id=WKwUAAAAQAAJ.
У. Б. Тейлор. Доклад об улучшенной системе счисления. В Годовом отчете попечительского совета Смитсоновского института , показывающем операции, расходы и состояние учреждения за 1867 год , стр.
 119–120. Государственная типография, 1867 г. Доступно по адресу https://archive.org/details/annualreportofbo1867smith.
119–120. Государственная типография, 1867 г. Доступно по адресу https://archive.org/details/annualreportofbo1867smith.Роберт Б. Ульрих. Роман Деревообработка . Издательство Йельского университета, 2007.
. Google Scholar
Уильям Дуайт Уитни. Словарь века: энциклопедический словарь английского языка, Том VII. The Century Co., 1895 г. Доступно по ссылке https://archive.org/details/centiciona07whit.
Ссылки на скачивание
Благодарности
Мы хотели бы поблагодарить анонимного рецензента за полезные комментарии к предыдущей версии этой статьи. Ллойд Стриклэнд также благодарен Gerda Henkel Stiftung, Дюссельдорф, за предоставление исследовательской стипендии (AZ 46/V/21), которая сделала возможной эту статью.
Информация о авторе
Авторы и принадлежность
Департамент истории, политики и философии, Манчестерский столичный университет, Geoffrey Manton Build
Owain Daniel Jones
Авторы
- Lloyd Strickland
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Академия
- Owain Daniel Jones
Посмотреть публикации автора
Вы также можете искать этого автора в PubMed Google Scholar
Автор, ответственный за корреспонденцию
Ллойд Стрикленд.
Дополнительная информация
Примечание издателя
Springer Nature остается нейтральной в отношении юрисдикционных претензий в опубликованных картах и институциональной принадлежности.
Права и разрешения
Открытый доступ Эта статья находится под лицензией Creative Commons Attribution 4.0 International License, которая разрешает использование, совместное использование, адаптацию, распространение и воспроизведение на любом носителе или в любом формате при условии, что вы укажете автора(ов) оригинала. и источник, предоставьте ссылку на лицензию Creative Commons и укажите, были ли внесены изменения. Изображения или другие сторонние материалы в этой статье включены в лицензию Creative Commons на статью, если иное не указано в кредитной строке материала. Если материал не включен в лицензию Creative Commons статьи, а ваше предполагаемое использование не разрешено законом или выходит за рамки разрешенного использования, вам необходимо получить разрешение непосредственно от правообладателя. Чтобы просмотреть копию этой лицензии, посетите http://creativecommons.org/licenses/by/4.0/.
Чтобы просмотреть копию этой лицензии, посетите http://creativecommons.org/licenses/by/4.0/.
Перепечатки и разрешения
Об этой статье
Шестнадцатеричная система счисления (определение, преобразование и примеры)
Двоичная система счисления является естественным выбором для систем с двумя состояниями. Но в этой системе числа имеют тенденцию становиться короткими, а довольно длинными. Следовательно, чтобы уменьшить длину данного числа, довольно часто используется шестнадцатеричная система счисления. Шестнадцатеричная система счисления имеет основание 16, то есть состоит из 16 цифр и символов. Он использует цифры от 0 до 9плюс буквы A, B, C, D, E и F. Поскольку числовые цифры и алфавиты используются для представления цифр в шестнадцатеричной системе счисления, это буквенно-цифровая система счисления . В таблице 44.3 показано соотношение между шестнадцатеричным, десятичным и двоичным форматами. Важно отметить, что шестнадцатеричные (сокращение от шестнадцатеричных) цифры от A до F эквивалентны десятичным значениям от 10 до 15.
Из таблицы 44.3 видно, что имеется 16 комбинаций 4-битных двоичных чисел и наборов 4-битные двоичные числа можно вводить в компьютер в виде шестнадцатеричных (шестнадцатеричных) цифр. Эти числа должны быть преобразованы в двоичные представления с использованием схем преобразования шестнадцатеричных чисел в двоичные, прежде чем они смогут быть обработаны цифровыми схемами. Эта система широко используется в микропроцессорной работе.
Счет в шестнадцатеричной системе счисления:Как мы будем считать в шестнадцатеричной системе счисления, когда дойдем до F ? Просто начните с другого столбца и продолжайте следующим образом:
С двумя шестнадцатеричными цифрами мы можем сосчитать до FF 16 , что равно 255 10 . Для подсчета сверх этого требуются три шестнадцатеричных цифры. Например, 100 16 равно 256 10 , 101 16 равно 257 10 и так далее. Максимальное трехзначное шестнадцатеричное число — FFF 16 , что равно 4095 10 .
Шестнадцатеричное число можно преобразовать в его десятичный эквивалент, умножив каждую шестнадцатеричную цифру на ее вес, а затем взяв сумму этих произведений. Веса шестнадцатеричных чисел являются возрастающими степенями 16 (справа налево). Для четырехзначного шестнадцатеричного числа веса следующие:
Для иллюстрации рассмотрим несколько примеров.
Пример 44.41: Найдите десятичный эквивалент шестнадцатеричного числа 1A53.
Решение:
Пример 44.42: Преобразовать (FF3B) 16 в эквивалентное десятичное число.
Решение:
Преобразование десятичного числа в шестнадцатеричное:
Повторное деление десятичного числа на 16 даст эквивалентное шестнадцатеричное число, образованное остатком от каждого деления. Это похоже на повторное деление на 2 для десятичного преобразования в двоичное и повторное деление на 8 для десятичного преобразования в восьмеричное. Следующие примеры иллюстрируют процедуру.
Это похоже на повторное деление на 2 для десятичного преобразования в двоичное и повторное деление на 8 для десятичного преобразования в восьмеричное. Следующие примеры иллюстрируют процедуру.
Example 44.44: Convert the following number: (374.37) 10 = ( ) 16
Solution:
Hexadecimal-To-Binary Conversion:
Hex числа могут быть преобразованы в эквивалентные двоичные числа путем замены каждой шестнадцатеричной цифры ее эквивалентным 4-битным двоичным числом. Эта процедура проиллюстрирована ниже.
Пример 44.46: Выполните следующее преобразование: (1684) 16– () 2
Решение:
Пример 44,47: Преобразование следующего числа (A6B.F5) 16 → (?) 2 .
Решение: Преобразовывая каждую шестнадцатеричную цифру в двоичное число бит, мы имеем
Двоично-шестнадцатеричное преобразование:
Преобразование из двоичного в шестнадцатеричное — это просто обратный процесс выше. Двоичное число группируется в группы по 4 бита, начиная с LSB и продвигаясь к MSB для целой части, а затем каждая группа из четырех бит заменяется ее шестнадцатеричным представлением. Нули добавляются по мере необходимости для завершения 4-битной группы.
Двоичное число группируется в группы по 4 бита, начиная с LSB и продвигаясь к MSB для целой части, а затем каждая группа из четырех бит заменяется ее шестнадцатеричным представлением. Нули добавляются по мере необходимости для завершения 4-битной группы.
Для дробной части описанная выше процедура повторяется, начиная с бита, следующего за двоичной точкой, и продвигаясь вправо.
Пример 44.49: Преобразовать длинное двоичное число 1001001101010001 в восьмеричное и шестнадцатеричное.
Решение: (1001001101010001) 2
Преобразование из шестнадцатеричного в восьмеричное и наоборот.
Шестнадцатеричные числа могут быть преобразованы в эквивалентные восьмеричные числа, а восьмеричные числа могут быть преобразованы в эквивалентные шестнадцатеричные числа путем преобразования шестнадцатеричного/восьмеричного числа в эквивалентное двоичное, а затем в восьмеричное/шестнадцатеричное соответственно.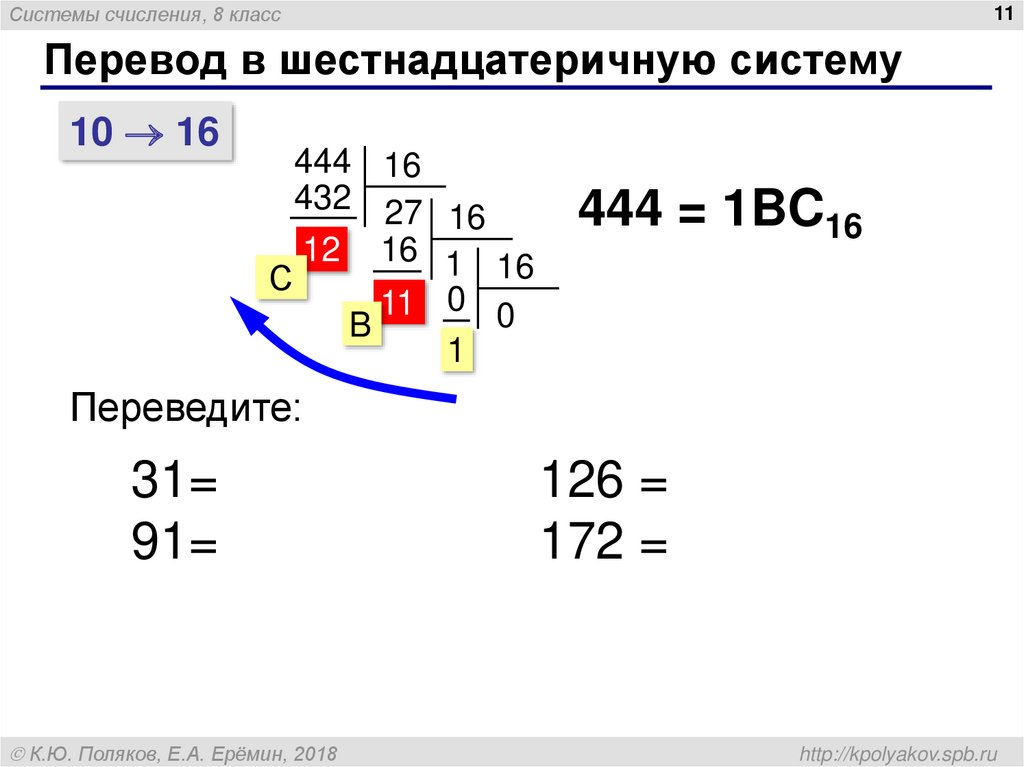




 Sedenary и senidenary в конечном счете происходят, соответственно, от sedeni и senideni , латинских дистрибутивных числительных, значение которых наиболее естественно выражается в английском языке такими фразами, как «шестнадцать за один раз» или «в шестнадцать». ” Из этих двух классов прилагательных те, которые образованы от дистрибутивных числительных, предпочтительнее, чем производные от количественных числительных, потому что смысл дистрибутивов лучше соответствует системе, в которой количество, выражаемое каждой последующей позицией, увеличивается на кратное основанию (в этом случае, на 16 за раз), а также потому, что эти прилагательные являются промежуточным производным от предварительно сформированных латинских прилагательных, которые заканчиваются на — arius (в данном случае sedenarius и senidenarius ). Наконец, между столь же безупречными сидячими и сидячими выбирать особо не из чего; стоит только отметить, что senideni предшествовали sedeni .
Sedenary и senidenary в конечном счете происходят, соответственно, от sedeni и senideni , латинских дистрибутивных числительных, значение которых наиболее естественно выражается в английском языке такими фразами, как «шестнадцать за один раз» или «в шестнадцать». ” Из этих двух классов прилагательных те, которые образованы от дистрибутивных числительных, предпочтительнее, чем производные от количественных числительных, потому что смысл дистрибутивов лучше соответствует системе, в которой количество, выражаемое каждой последующей позицией, увеличивается на кратное основанию (в этом случае, на 16 за раз), а также потому, что эти прилагательные являются промежуточным производным от предварительно сформированных латинских прилагательных, которые заканчиваются на — arius (в данном случае sedenarius и senidenarius ). Наконец, между столь же безупречными сидячими и сидячими выбирать особо не из чего; стоит только отметить, что senideni предшествовали sedeni .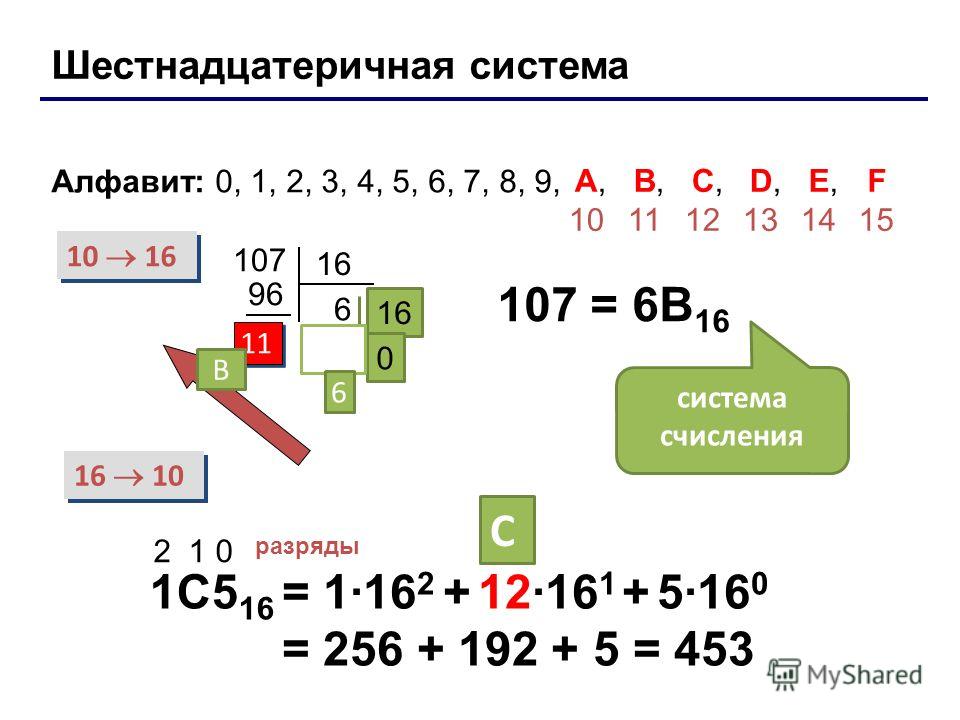
 Специальные разделы теоретической арифметики . Джозеф Боуден, 1936 г. Доступно по адресу https://hdl.handle.net/2027/uc1.$b543512.
Специальные разделы теоретической арифметики . Джозеф Боуден, 1936 г. Доступно по адресу https://hdl.handle.net/2027/uc1.$b543512.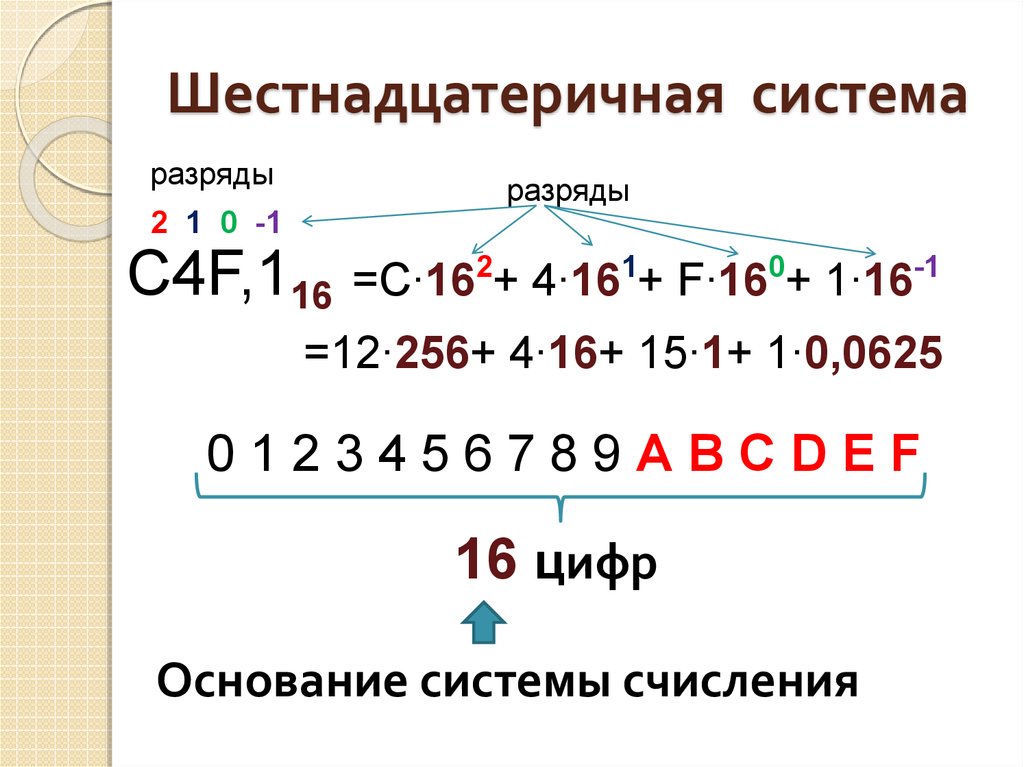 Progressio binaria est pro theoria, sedenaria pro praxi. Неопубликованная рукопись с маркой LH 35, 3 B 17 Bl. 4 r , принадлежит Библиотеке Готфрида Вильгельма Лейбница – Niedersächsische Landesbibliothek, Ганновер, 1679.
Progressio binaria est pro theoria, sedenaria pro praxi. Неопубликованная рукопись с маркой LH 35, 3 B 17 Bl. 4 r , принадлежит Библиотеке Готфрида Вильгельма Лейбница – Niedersächsische Landesbibliothek, Ганновер, 1679. JB Lippincott & Co., 1862. Доступно на https://books.google.com/books?id=aNYGAAAAYAAJ.
JB Lippincott & Co., 1862. Доступно на https://books.google.com/books?id=aNYGAAAAYAAJ. Издательство Кембриджского университета, 1996.
Издательство Кембриджского университета, 1996. 119–120. Государственная типография, 1867 г. Доступно по адресу https://archive.org/details/annualreportofbo1867smith.
119–120. Государственная типография, 1867 г. Доступно по адресу https://archive.org/details/annualreportofbo1867smith.