Перевод двоичных чисел в шестнадцатеричную систему счисления

Если нужно преобразовать двоичное число в шестнадцатеричное, то снача­ла оно переводится в десятичную систему счисления. Затем десятичное число преобразовывается в шестнадцатеричное так, как описано в разд. 8.5.3. Этот метод надежен, однако трудоемок. Имеется значительно более простой спо­соб преобразования.

Между двоичной и шестнадцатеричной системами счисления имеется тесная связь. Все числа с основанием 16 могут также быть записаны как числа с основанием 2 (16° = 2°, 16‘ = 2⁴, 16² = 2⁸ и т. д.). Если составить уже известную таблицу пересчета для двоичных чисел, то окажется, что содер­жимое каждого четвертого столбца в двоичной системе соответствует по величине содержимому столбца шестнадцатеричной системы (рис. 8.20).

Любое четырехразрядное двоичное число может быть представлено 1 ше­стнадцатеричным числом.

С одним четырехразрядным двоичным числом можно вести счет от 0 до 15, значит, всего суще­ствуют 16 тетрад. Каждая тетрада соответствует ше­стнадцатеричной цифре (рис. 8.21).

Двоичные числа с разрядностью больше четы­рех представляются несколькими шестнадцатерич­ными цифрами, каждая из которых представляет четыре двоичных разряда. Если последняя группа слева содержит меньше, чем четыре разряда, то ее нужно дополнить нулями до четырех разрядов.

Группа из четырех двоичных цифр представляет одно шестнадцатеричное число.

Пример——————————————————————————————

Посредством таблиц пересчета (рис. 8.22) можно проверить результат. Результат верен.

В вещественных двоичных числах с запятой нужно образовывать тетра­ды справа и слева от запятой.

Пример——————————————————————————————

Проверка с помощью таблиц пересчета на рис. 8.23 показывает, что найденный результат верен.

Шестнадцатеричная система счисления часто используется, чтобы более наглядно представить длинное двоичное число.

Например, 32-разрядное двоичное число можно записать восемью шест­надцатеричными цифрами.

Пример——————————————————————————————

Перевод шестнадцатеричных чисел в двоичную систему счисления

Так как нам уже знакомо преобразование двоичных чисел в шестнадцате­ричные, то обратное преобразование не представляет трудности.

Каждая шестнадцатеричная цифра представляется 4 двоичными разрядами.

При помощи таблицы на рис. 8.21 преобразование шестнадцатеричных чисел в двоичные производится очень быстро. Для каждой шестнадцате­ричной цифры пишут соответствующие ей четыре двоичных разряда.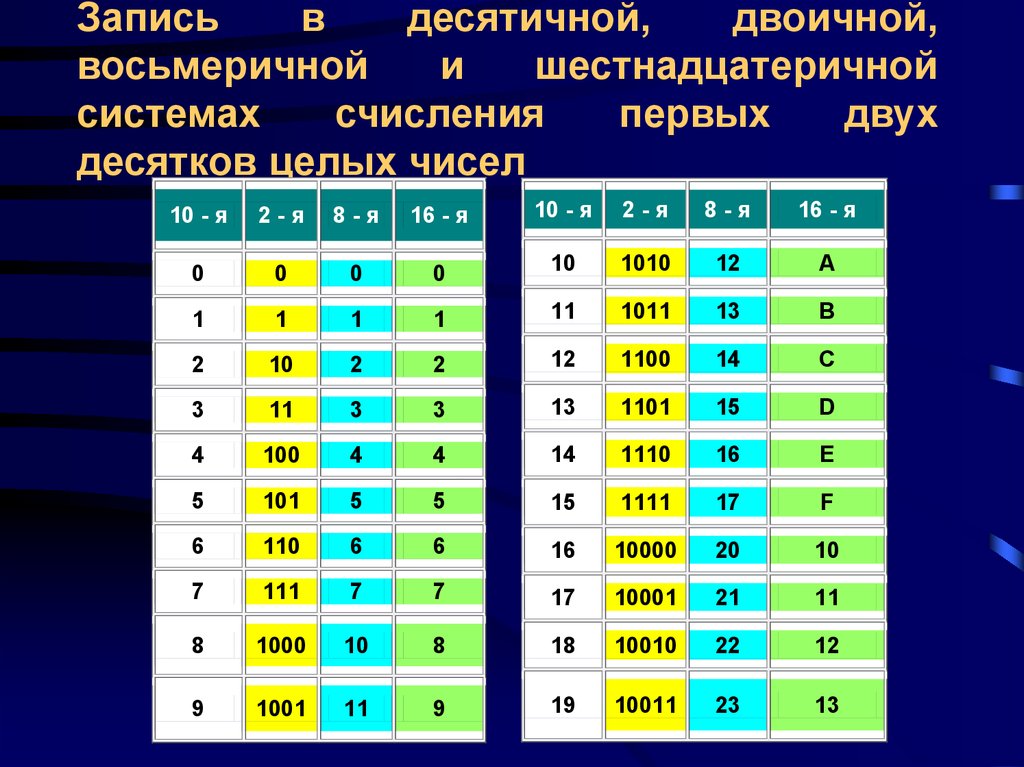

Пример——————————————————————————————

Восьмеричная система счисления (Octal)

Структура восьмеричной системы счисления

Восьмеричная система счисления, как и шестнадцатеричная, является по­зиционной системой счисления.

Каждый разряд восьмеричного числа является множителем степени 8.

Структура восьмеричной системы счисления показана на рис. 8.24. В разряде, который умножается на 8° = 1, можно считать до 7. Только начиная с 8 можно использовать второй разряд. Значит, вместе с нулем нужны 8 цифр. В восьмеричной системе счисления используются цифры, известные из десятичной системы.

В восьмеричной системе счисления используют 8 цифр.

На рис. 8.25 показано соответствие восьмеричных цифр десятичным числам от 0 до 7. Чтобы избежать путаницы между десятичными и восьме­ричными числами, записывают индекс в скобках. Индекс 8 обозначает восьмеричную систему счисления, индекс 10 — десятичную систему.

Пример——————————————————————————————

2583₍₁₀₎ — 5027₍₈₎

Преобразование шестнадцатеричного в двоичный — онлайн и бесплатно

Преобразование шестнадцатеричного в двоичный — онлайн и бесплатно

Легко конвертировать шестнадцатеричные единицы в двоичное число

В шестнадцатеричном формате используются следующие символы: 123456789ABCDEF.

Двоичный:

Как преобразовать шестнадцатеричный формат в двоичный

Шаг 1

Введите или вставьте свой номер в шестнадцатеричном формате в первое поле.

Шаг 2

Нажмите кнопку, чтобы преобразовать числовой формат в другой

Шаг 3

Теперь вы можете скопировать или скачать полученное число в двоичном формате.

Что такое шестнадцатеричный и двоичный

Шестнадцатеричная система счисления, как и восьмеричная, широко используется в информатике из-за простоты перевода в нее двоичных чисел. В случае шестнадцатеричной записи числа более компактны. Цифры от 0 до 9 и первые шесть латинских букв — A, B, C, D, E, F используются как алфавит шестнадцатеричной системы счисления. При преобразовании в десятичную систему буквы заменяются числами 10, 11, 12, 13, 14, 15 соответственно … Записывая числа в восьмеричной системе, мы получаем довольно компактные выражения, но в шестнадцатеричной системе мы получаем выражения более компактные. Первые десять цифр из шестнадцати шестнадцатеричных цифр представляют собой стандартный интервал от 0 до 9, следующие шесть цифр выражаются с использованием первых букв латинского алфавита: A, B, C, D, E, F.

Перевод из шестнадцатеричной системы в в двоичной системе и в обратном направлении выполняется аналогичный процесс для восьмеричной системы.

Двоичная система счисления напрямую связана с математической теорией чисел. Необходимость изучения этой темы обусловлена тем, что в нашей современной жизни сложно обойтись без компьютера, и все числа в памяти компьютера представлены в двоичной системе счисления. Эта тема способствует фундаментальному математическому школьному образованию. Когда есть необходимость в числовых вычислениях, используются различные системы счисления, от вычислений в начальной школе на бумаге до вычислений на суперкомпьютерах. Двоичная система счисления — это позиционная система счисления, то есть существует зависимость от положения цифры в записи числа. Для записи числа в двоичной системе счисления используются две цифры 0 и 1. Чтобы определить, в какой системе счисления записано число, ниже справа от числа поставьте цифру, которая называется основанием системы счисления.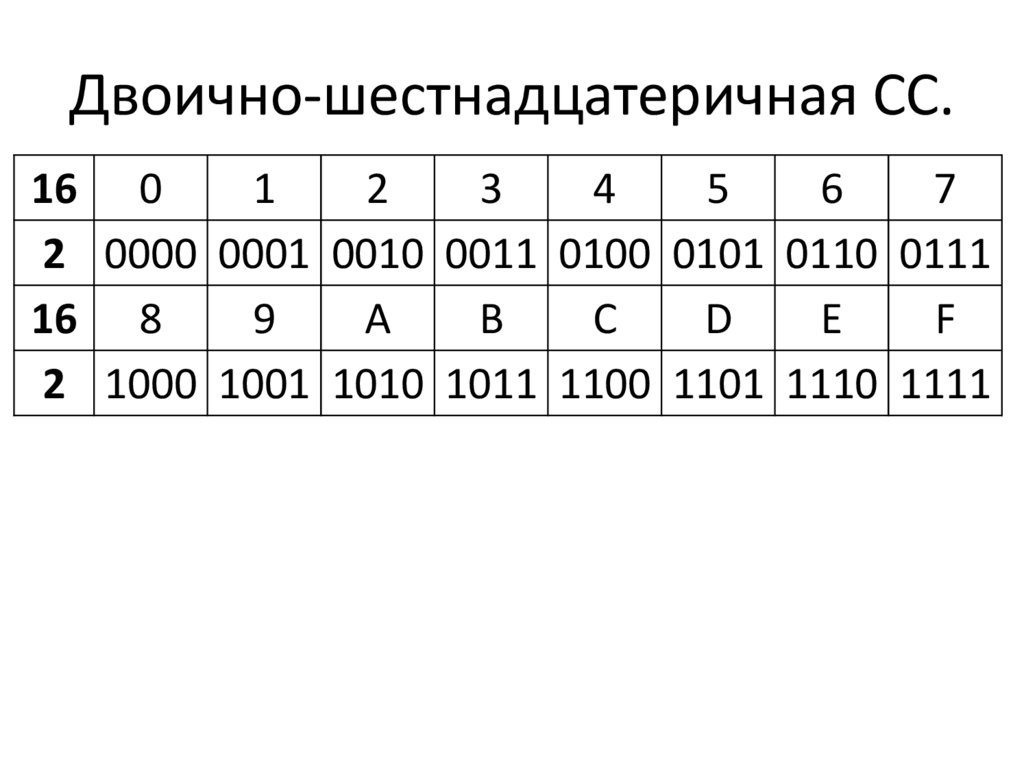

Был ли вам полезен AnyTextEditor?

Привет. Мы очень старались создать удобный сайт, которым будем пользоваться сами. Если вам понравился какой-либо из наших инструментов и редакторов, добавьте его в свои закладки, потому что он будет вам полезен не раз. И не забудьте поделиться в социальных сетях. Мы будем лучше для вас.

Преобразование шестнадцатеричной системы счисления в двоичную

Шестнадцатеричные системы счисления помогают компьютерам обрабатывать большие объемы данных, с которыми они должны работать. Шестнадцатеричные системы счисления — это числовая система с основанием 16. Различные комбинации 16 основных цифр используются после 9 в десятичной системе. Понимание преобразования между шестнадцатеричными и двоичными числами жизненно важно в области цифровой электроники, так же как понимание преобразования рупий в доллары или долларов в евро в физическом мире. Прежде чем понять эти преобразования, давайте попробуем ознакомиться с двоичной и шестнадцатеричной системами счисления.

 

Двоичная система счисления

Двоичная система счисления — это система счисления с основанием 2. В этой системе счисления есть только два числа — 0 и 1. Мы используем некоторые комбинации этих двух цифр для создания всей двоичной системы счисления. Таким образом, (0) ₁₀ (десятичное число) представлено как (00) ₂

в двоичном виде, а (1) ₁₀ равно 01. Следующие числа 10,11 и т. д.

 

соответствующее двоичное представление любой десятичной цифры путем непрерывного деления цифры на 2 до тех пор, пока частное не станет равным 0. Например, 24 в двоичном представлении можно найти с помощью:

 

 \[\frac {24}{2}\] = 12; напоминание = 0

 

 \[\frac {12}{2}\] = 6; напоминание = 0

 

 \[\frac {6}{2}\] = 3; напоминание = 0

 

 \[\frac {3}{2}\] = 1; напоминание = 1

 

 \[\frac {1}{2}\] = 0; напоминание = 1

 

Следовательно, (24) ₁₀ = (11000) ₂

 

Мы можем даже представлять числа с десятичной точкой, такие как 0,205 и 1,234, в двоичной системе.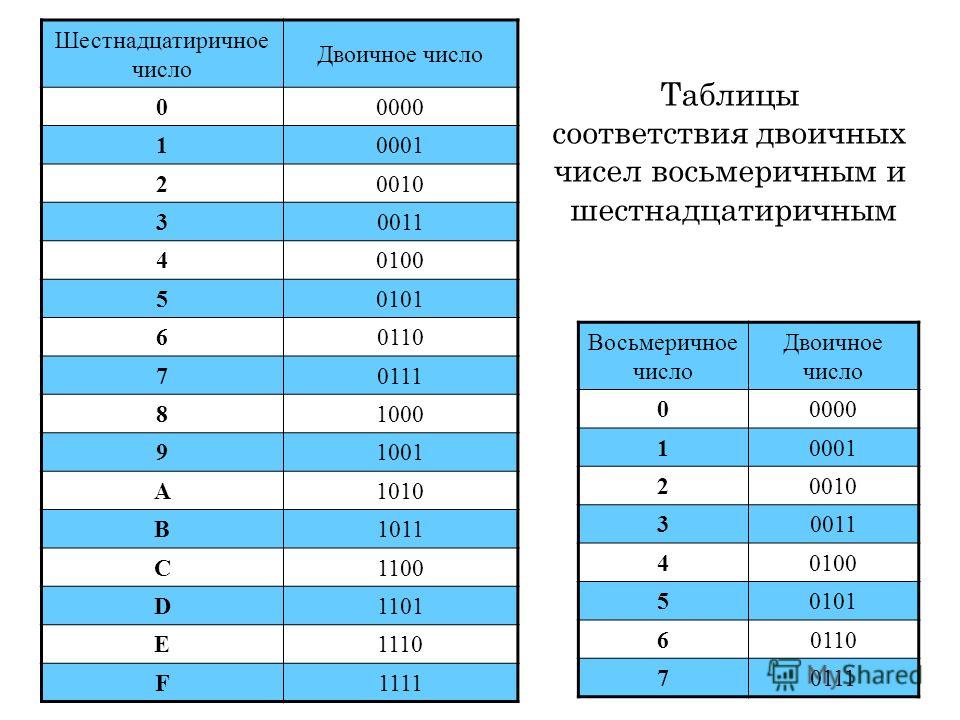 В этом случае вместо деления на 2 мы умножаем числа после запятой на 2, пока числа после запятой не станут равными 0. Например, чтобы представить 0,25 в двоичной системе,

 

Возьмите 0,25 из 0,25 и умножьте на 2.

 

0,25*2=0,50; Число до запятой = 0;

 

0,50*2 = 1,00; Число до запятой = 1;

 

Отсюда (0,25) ₁₀ = (0,01) ₂

Некоторые десятичные числа в двоичном представлении0084

0

0000

1

0001

2

0010

3

0011

4

0100

5

0101

6

0110

7

0111

8

1000

9

1001

10

1010

11

1011

12

1100

9008 13

13 9003 13

0003

1101

14

1110

15

1111

 

Hexadecimal Numbers

The hexadecimal number system is a numerical system of основание 16.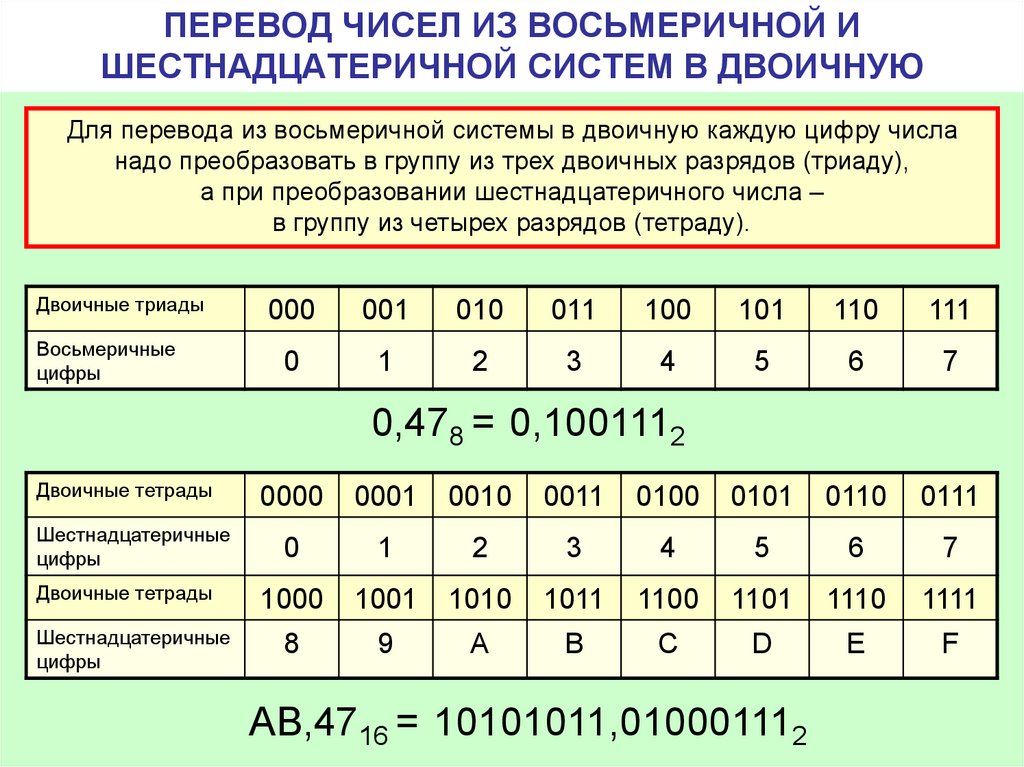 Здесь так же, как мы используем 10,11,12 и т. д. после 9 в десятичной системе счисления, мы используем различные комбинации 16 основных цифр шестнадцатеричной системы счисления. Посмотрим на представление десятичных чисел в шестнадцатеричной системе счисления.

110003

44444444444449

Decimal Digit	Hexadecimal Digit
0	0
1	1
2	2
3	3
4	4 44 0089
5	5
6	6
7	7
8	8
9
10	A
11	B9003	B9003
0089
12	C
13	D
14	E
15	F

 

Это основные шестнадцатеричные числа.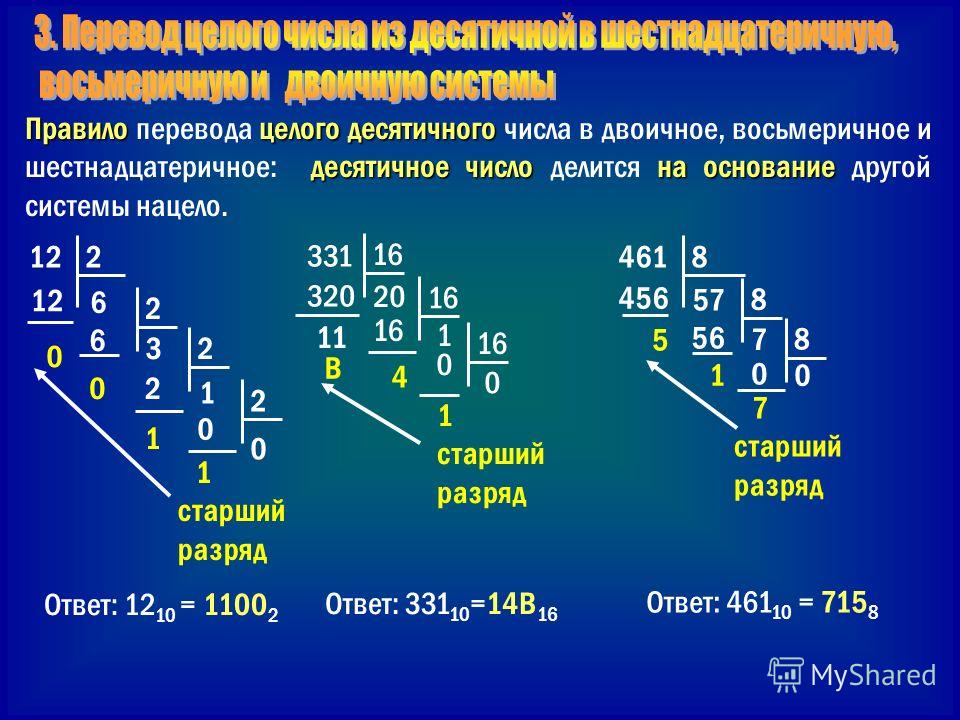 Любое десятичное число можно преобразовать в шестнадцатеричное, разделив число на 16, а затем следуя аналогичному алгоритму, как показано выше.

Преобразование шестнадцатеричного числа в двоичное

Сначала посмотрим, как преобразовать целое число из шестнадцатеричного в двоичное.

 

Предположим, у нас есть число E9A; Чтобы найти соответствующее двоичное число, мы записываем каждую шестнадцатеричную цифру с соответствующим двоичным числом. Из приведенной выше таблицы мы знаем, что

• E равно 14 в десятичном представлении и 14 равно 1110 в двоичном представлении.

• 9 равно 9 в десятичном представлении и 1000 в двоичном.

• A — это A в десятичном формате и 111 в двоичном формате.

Отсюда (E9A) ¹⁶ = 111010011010

 

Теперь давайте посмотрим, как преобразовать шестнадцатеричное число с десятичной точкой в ​​двоичное. Преобразовать 0.A39 в двоичный формат.

 

Здесь действуют те же правила, что и выше, за исключением того, что в этом случае мы избегаем крайних правых нулей. Они называются конечными нулями.

 

То есть (0.A38) ¹⁶ = (0,101000111) ₂

 

Будет очень полезно иметь таблицу преобразования шестнадцатеричных чисел в двоичные. Этого можно добиться, объединив приведенные выше таблицы.

Hexadecimal to Binary Table

9999939399999393

15

0081

1111

Decimal Digit	Hexadecimal Digit	Binary Digit
0	0	0000
1	1	0001
2	2	0010
3	3	0011
4	4	0100
5	5	01019003	01019003
0101 9003	01019.
6	6	0110
7	7	0111
8	8	1000
9		1001
10	A	1111199	A	1111111840003
11	B	1011
12	C	1100
13	D	1101
14	E	1110
15	F	F 9003

 

Мы рассмотрели основную идею двоичной и шестнадцатеричной систем счисления и преобразование «шестнадцатеричной системы счисления в двоичную».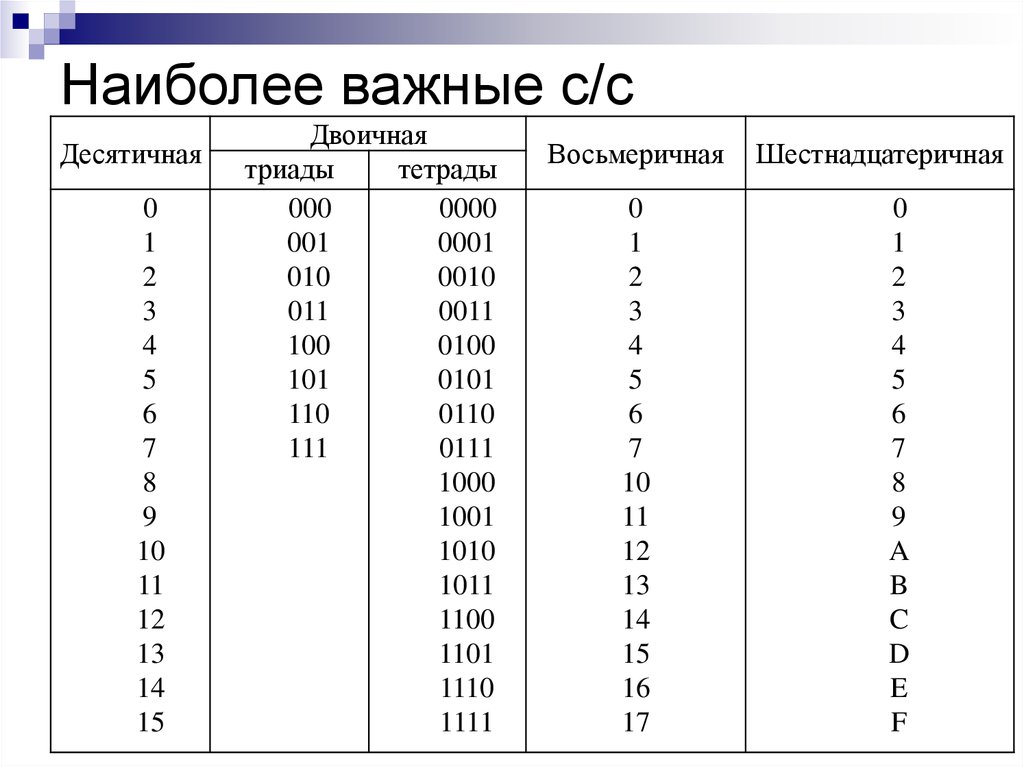 Попробуем обобщить правила:

• Пишите аккуратно шестнадцатеричное число.

• Под каждой цифрой напишите соответствующую десятичную цифру.

• Под каждым десятичным слагаемым напишите соответствующую двоичную цифру.

• Соедините вместе все цифры без пробелов между ними.

• Перепишите ответ, исключив начальные и конечные нули. Мы получили окончательный ответ.

Примеры преобразования шестнадцатеричных (Hex) чисел в двоичную систему

Пример 1. Преобразование шестнадцатеричного числа A2B16 в эквивалентное ему двоичное число.

Шаги: Сначала преобразуйте шестнадцатеричное число в эквивалентное ему десятичное число, как показано ниже:

A2B ₁₆ = (A*16 ² ) + (2*16 ¹ ) + (B*16 ⁰ )

= (A*256)+(2*16)+(B*1)

= (10*256)+32+11

= 2560+43

= 2603 (эквивалентное десятичное число)

Теперь мы преобразуем это десятичное число в двоичную форму:

Примем базовое значение 2, делим 2603 до тех пор, пока не получим частное, равное нулю.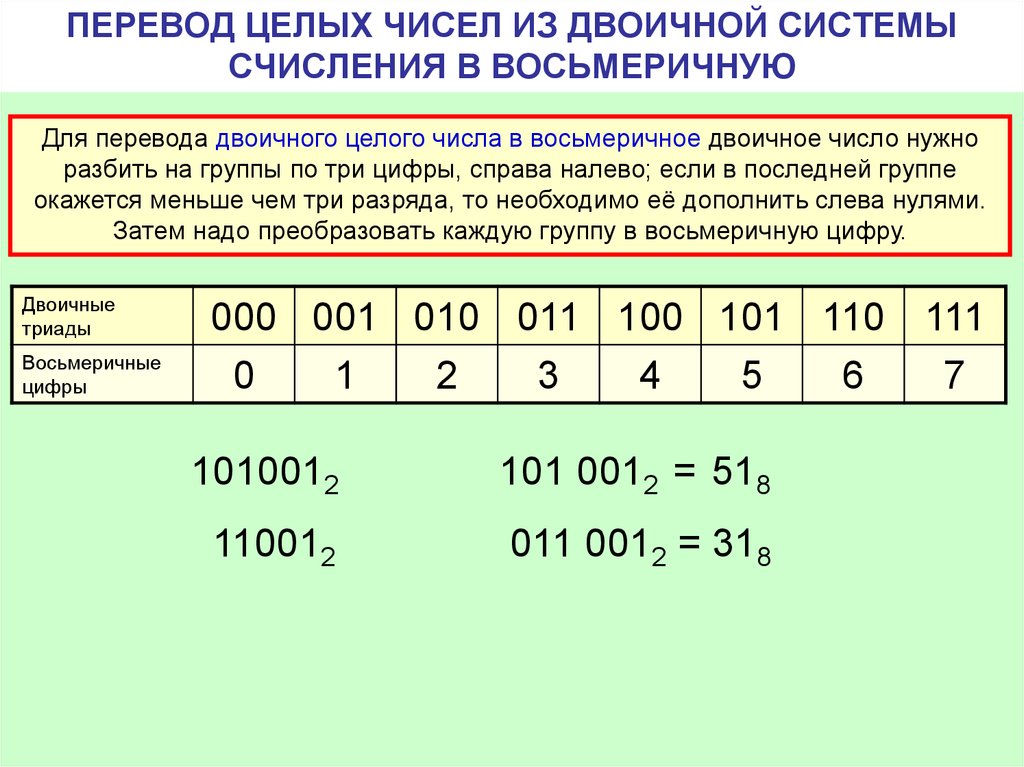

Полученный набор частных запишем справа налево как 101000101011 ₂

Пример 2: Преобразование шестнадцатеричного числа E16 в эквивалентное ему двоичное число.

Шаги: Сначала мы преобразуем данное шестнадцатеричное число в эквивалентное ему десятичное число, как показано ниже:

E16= E*16 ⁰

=E*1

=E

=14 (Полученное десятичное числовое значение из приведенной выше таблицы)

Теперь мы преобразуем это десятичное число в его двоичный эквивалент

Это можно сделать, разделив число 14 на 2, пока не будет получено частное, равное нулю.

Уникальный набор частных выводится и записывается справа налево.

Это должно быть представлено как 1110 ²

Следовательно, двоичный эквивалент шестнадцатеричного E16 равен 1110 ²

Пример 3: Чтобы преобразовать шестнадцатеричное число 3016 в его двоичный эквивалент.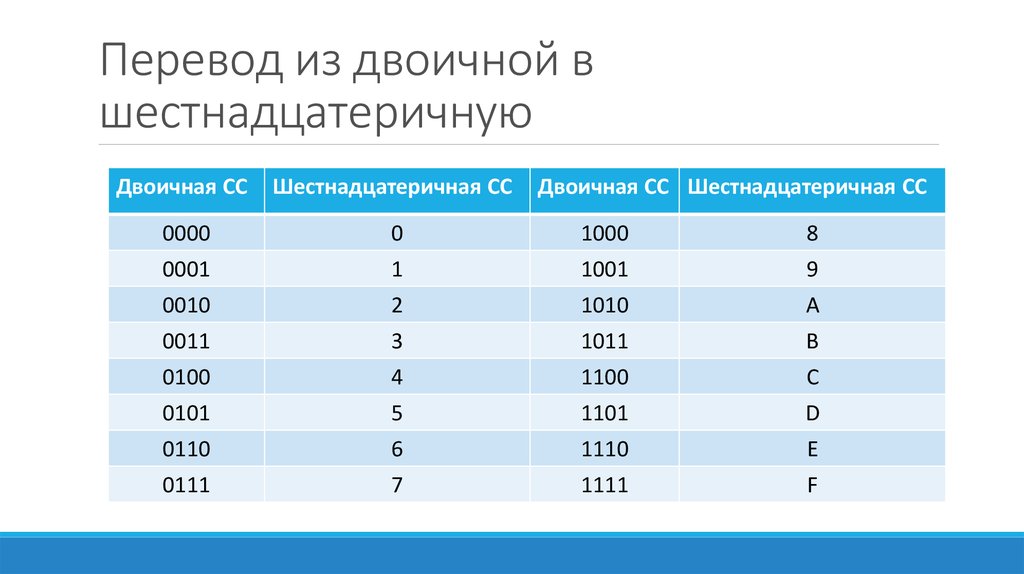

Шаги: Чтобы получить двоичное значение для данного шестнадцатеричного числа, мы выполняем указанные шаги в следующем порядке:

 

Сначала мы получаем десятичное значение данного шестнадцатеричного числа как

30 ₁₆ = (3*16 ¹ )+ (0*16 ⁰ )

= 48+ 0

= 48 (десятичное значение 30 ₁₆ )

= 48 (десятичное значение 30 ₁₆ )

 

Теперь на следующем шаге мы можем преобразовать десятичное число в двоичное, разделив значение на 2 так, чтобы окончательное частное, полученное в конце, было равно нулю. Полученное двоичное число равно 110000 ₂ .

 

Следовательно, двоичный эквивалент шестнадцатеричного 30 ₁₆ это 110000 ₂

Использование двоичной системы

Ниже приведены наиболее важные области применения двоичной системы в современном мире:

• Все мы знаем о важности компьютеров и компьютерных систем в нашей работе и социальной структуре. Будет интересно узнать, что все компьютерные системы полностью зависят от двоичной системы счисления для хранения, поиска, обработки данных и, по существу, всех операций машинного уровня.

• В системах связи сигналы «оцифровываются» посредством двоичной системы.

Чтобы узнать больше о двоичной и шестнадцатеричной системах счисления, войдите в Веданту. Найдите лучшие идеи от ведущих экспертов в области математики и узнайте, как преобразовать шестнадцатеричную систему в двоичную или наоборот. Получите разъяснение своих сомнений от экспертов на живых сеансах, зарегистрировавшись в этом онлайн-учебном домене.

Шестнадцатеричное в десятичное и двоичное

В сетевой вселенной мы используем двоичные, десятичные и шестнадцатеричные значения. Два хороших примера, где мы используем шестнадцатеричные значения, — это MAC-адреса и адреса IPv6.

Специально для IPv6-адресов полезно понимать, как можно производить вычисления из шестнадцатеричной системы в двоичную и десятичную или наоборот.

В десятичной системе мы считаем от 0 до 10, в шестнадцатеричной системе мы считаем от 0 до F. Вот пример:

Десятичный	Шестнадцатеричный
1	1
2	2
3	3
4	4
5	5
6	6
7	7
8	8
9	9
10	А
11	Б
12	С
13	Д
14	Е
15	Ф

Не так уж и плохо, верно? Теперь, если вы хотите перейти от двоичного к шестнадцатеричному, вам нужно освоить один прием. Допустим, у вас есть десятичное число 255 в двоичном виде:

128	64	32	16	8	4	2	1
1	1	1	1	1	1	1	1

Если вы хотите преобразовать это в шестнадцатеричное, вам нужно разрезать 8 бит на две части по 4 бита (4 бита также известны как полубайт ).

Первый полубайт:

1

1

1

1

Второй полубайт:

1

1

1

1

Теперь преобразуйте эти полубайты из двоичного в десятичный:

8	4	2	1
1	1	1	1

Оба полубайта выглядят одинаково: 8 + 4 + 2 + 1 = 15

Теперь взгляните на диаграмму преобразования десятичной системы в шестнадцатеричную, и вы увидите, что 15 в десятичной системе равно «F» в шестнадцатеричной.

Таким образом, шестнадцатеричное значение = FF. Обычно вы видите шестнадцатеричные значения, записанные как 0xFF. Если вы видите «0x», значит, это шестнадцатеричное значение.

Давайте попробуем другое десятичное значение и пересчитаем его в шестнадцатеричное, например 118. Сначала мы преобразуем 118 в двоичное:

128	64	32	16	8	4	2	1
0	1	1	1	0	1	1	0

64 + 32 + 16 + 4 + 2 = 118

Разделим наши 8 бит на две части и вот что мы получим:

Первая часть:

1

1

1

Второй полубайт:

0

1

1

0

Теперь давайте преобразуем эти полубайты из двоичного в десятичный:

8	4	2	1
0	1	1	1

Первый полубайт будет 4 + 2 + 1 = 7. Десятичное значение 7 совпадает с шестнадцатеричным.

8	4	2	1
0	1	1	0

Второй полубайт будет 4+2 = 6. Десятичное значение 6 такое же, как и в шестнадцатеричном формате.

Наше шестнадцатеричное значение будет 0x76. Давайте попробуем еще один!

Допустим, у нас есть десятичное значение 206. В двоичном виде это выглядит так:

128	64	32	16	8	4	2	1
1	1	0	0	1	1	1	0

128 + 64 + 8 + 4 + 2 = 206.

Мы разбиваем наши 8 бит на два кулака, и это то, что мы получаем:

Первый Nibble:

481

1

44449

1

1

1

0

0

Второй полубайт:

1

1

1

0

Теперь давайте преобразуем эти полубайты из двоичного в десятичный:

8	4	2	1
1	1	0	0

Первый полубайт будет 8 + 4 = 12.