Шестнадцатеричные числа | это… Что такое Шестнадцатеричные числа?
ТолкованиеПеревод
- Шестнадцатеричные числа
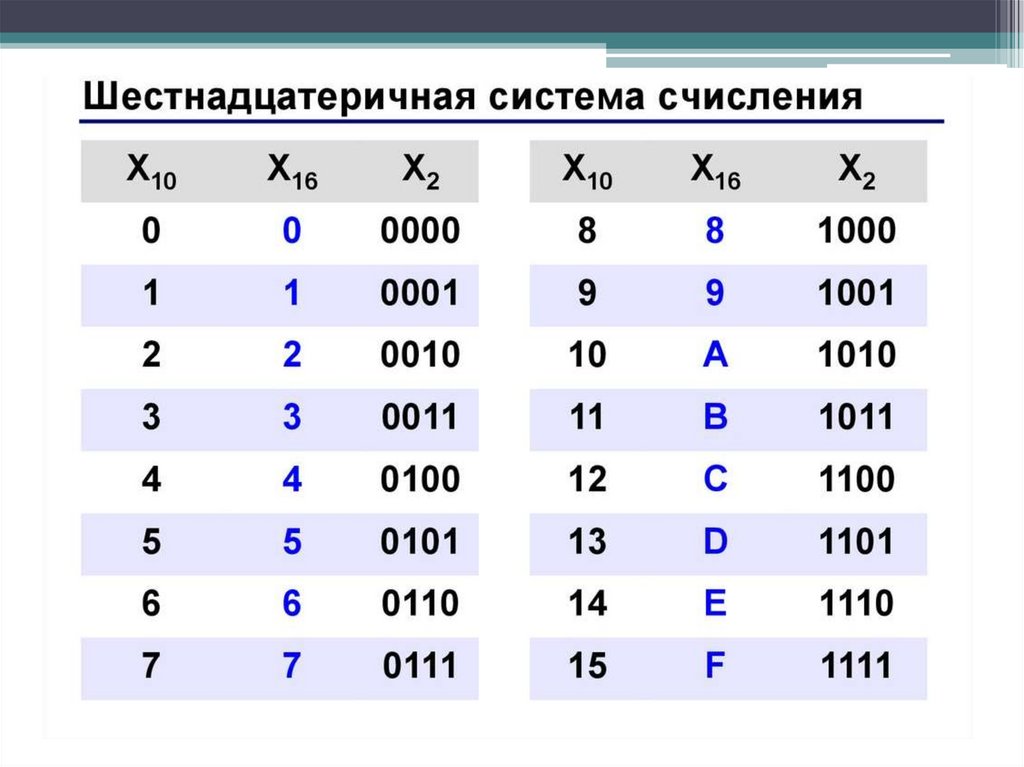
Шестнадцатеричная система счисления (шестнадцатеричные числа) — позиционная система счисления по целочисленному основанию 16. Обычно в качестве шестнадцатеричных цифр используются десятичные цифры от 0 до 9 и латинские буквы от A до F для обозначения цифр от 10 до 15.
Содержание
- 1 Применение
- 2 Способы записи
- 2.1 В математике
- 2.2 В языках программирования
- 3 Перевод чисел из одной системы счисления в другую
- 3.1 Перевод чисел из шестнадцатеричной системы в десятичную
- 3.2 Перевод чисел из двоичной системы в шестнадцатеричную
- 3.3 Таблица перевода чисел
- 4 См.
 также
также - 5 Ссылки
Применение
Широко используется в низкоуровневом программировании и вообще в компьютерной документации, поскольку в современных компьютерах минимальной единицей памяти является 8-битный байт, значения которого удобно записывать двумя шестнадцатеричными цифрами. Такое использование началось с системы IBM/360, где вся документация использовала шестнадцатеричную систему, в то время как в документации других компьютерных систем того времени (даже с 8-битными символами, как, например, БЭСМ-6) использовали восьмеричную систему.
В стандарте Юникода номер символа принято записывать в шестнадцатеричном виде, используя не менее 4 цифр (при необходимости — с ведущими нулями).
Способы записи
В математике
В математике систему счисления принято писать в подстрочном знаке. Например, десятичное число 1443 можно записать как 1443
В языках программирования
В разных языках программирования для записи шестнадцатеричных чисел используют различный синтаксис:
- В Ада и
- В Си и языках схожего синтаксиса, например, в
- В некоторых ассемблерах используют букву «h», которую ставят после числа.
 Например, «5A3h». При этом, если число начинается не с десятичной цифры, впереди ставится «0» (ноль): «0FFh» (25510)
Например, «5A3h». При этом, если число начинается не с десятичной цифры, впереди ставится «0» (ноль): «0FFh» (25510) - Другие ассемблеры (AT&T, Motorola), а также Паскаль и некоторые версии Бэйсика используют префикс «$». Например, «$5A3».
- Некоторые иные платформы, например ZX Spectrum в своих ассемблерах (MASM, TASM, ALASM, GENS и т.д.) использовали запись #5A3, обычно выровненную до одного или двух байт: #05A3.
- Другие версии Бэйсика используют для указания шестнадцатеричных цифр сочетание «&h». Например, «&h5A3».
- В Unix-подобных операционных системах (и многих языках программирования, имеющих корни в Unix/linux) непечатные символы при выводе/вводе кодируются как \xCC, где CC — шестнадцатеричный код символа.
Перевод чисел из одной системы счисления в другую
Перевод чисел из шестнадцатеричной системы в десятичную
Для перевода шестнадцатеричного числа в десятичное необходимо это число представить в виде суммы произведений степеней основания шестнадцатеричной системы счисления на соответствующие цифры в разрядах шестнадцатеричного числа.

Например, требуется перевести шестнадцатеричное число 5A3 в десятичное. В этом числе 3 цифры. В соответствии с вышеуказанным правилом представим его в виде суммы степеней с основанием 16:
5A316=5·162+10·161+3·160
=5·256+10·16+3·1=1280+160+3=144310Перевод чисел из двоичной системы в шестнадцатеричную
Для перевода многозначного двоичного числа в шестнадцатеричную систему нужно разбить его на тетрады справа налево и заменить каждую тетраду соответствующей шестнадцатеричной цифрой.
Например:
101101000112=0101 1010 0011=5A316 Таблица перевода чисел
0hex = 0dec = 0oct 0 0 0 0 1hex = 1dec = 1oct 0 0 0 1 2 = 2dec = 2oct 0 0 1 0 3hex = 3dec = 3oct 0 0 1 1 4hex = 4dec = 4oct 0 1 0 0 5hex = 5dec = 5oct 0 1 0 6hex = 6dec = 6oct 0 1 1 0 7hex = 7dec = 7oct 0 1 1 1 8hex = 8dec = 10oct 1 0 0 0 9hex = 9dec = 1 0 0 1 Ahex = 10dec = 12oct 1 0 1 0 Bhex = 11dec = 13oct 1 0 1 1 Chex = 12dec = 14oct 1 1 0 0 Dhex = 13dec = 15oct 1 1 0 1 Ehex = 14dec = 16oct 1 1 1 0 Fhex = 15dec = 17oct 1 1 1 1 См.
 также
также- Система счисления
- Двоичные приставки
- Шестнадцатеричный редактор
Ссылки
- Шестнадцатеричные числа и операции с ними
- Таблица порядков двоичных, шестнадцатеричных и десятичных чисел
- Онлайн калькулятор для перевода чисел из одной системы счисления в другую
Wikimedia Foundation. 2010.
Игры ⚽ Нужно сделать НИР?
- Шестнадцатиричная система счисления
- Шестнадцать
Полезное
Восьмеричная система счисления. Шестнадцатеричная система счисления. Правило перевода целых десятичных чисел в систему счисления с основанием
Для начала вспомним, что такое позиционная система счисления.
Позиционная система счисления – это система счисления, в которой количественный эквивалент цифры зависит от её положения (позиции) в записи числа.
На этом уроке мы с вами
познакомимся с восьмеричной и шестнадцатеричной системами счисления, узнаем
правила перевода из восьмеричной и шестнадцатеричной систем счисления в
десятичную и наоборот. Также изучим правило перевода целых десятичных чисел в
систему счисления с основание q.
Также изучим правило перевода целых десятичных чисел в
систему счисления с основание q.
Начнём с восьмеричной системы счисления.
Восьмеричная система счисления – это позиционная система счисления с основанием 8. В алфавит восьмеричной системы счисления входят цифры от 0 до 7 включительно.
Мы с вами уже узнали, как записывается развёрнутая форма записи числа. Она выглядит следующим образом:
Из этой формулы можно вывести развёрнутую форму записи целого восьмеричного числа:
Посмотрим, как это выглядит на примере. Нам дано следующее число: 41538. Давайте распишем его по формуле. Ставим равно. Для начала проставим над цифрами степени для восьмёрки справа налево, начиная с нуля.
После равно пишем первую
цифру 4 и умножаем её на 83. Ставим плюс. Далее запишем вторую цифру
1, умноженную на 82. Снова ставим плюс. Записываем цифру 5 и
умножаем её на 81.
Мы с вами расписали исходное число в развёрнутой форме целого восьмеричного числа.
Правило для перевода из восьмеричной системы счисления в десятичную очень простое. Достаточно расписать число в развёрнутой форме записи, а затем вычислить значение получившегося выражения.
Давайте переведём наше число из восьмеричной системы счисления в десятичную. Оно уже у нас расписано в развёрнутой записи. Нам осталось сосчитать. Обратимся к математике и распишем степени числа восемь.
Теперь осталось всё посчитать. Ставим равно.
Мы получили число 2 155. Это число представлено в десятичной системе счисления.
А теперь давайте переведём число 125 из десятичной системы счисления в восьмеричную.
Это правило похоже на перевод из десятичной в двоичную систему счисления, но в данном случае мы будем делить на число 8.
Само правило
звучит следующим образом: для перевода целого десятичного числа в восьмеричную
систему счисления следует последовательно выполнять деление данного числа и
получаемых целых частных на 8 до тех пор, пока не получим частное, равное 0.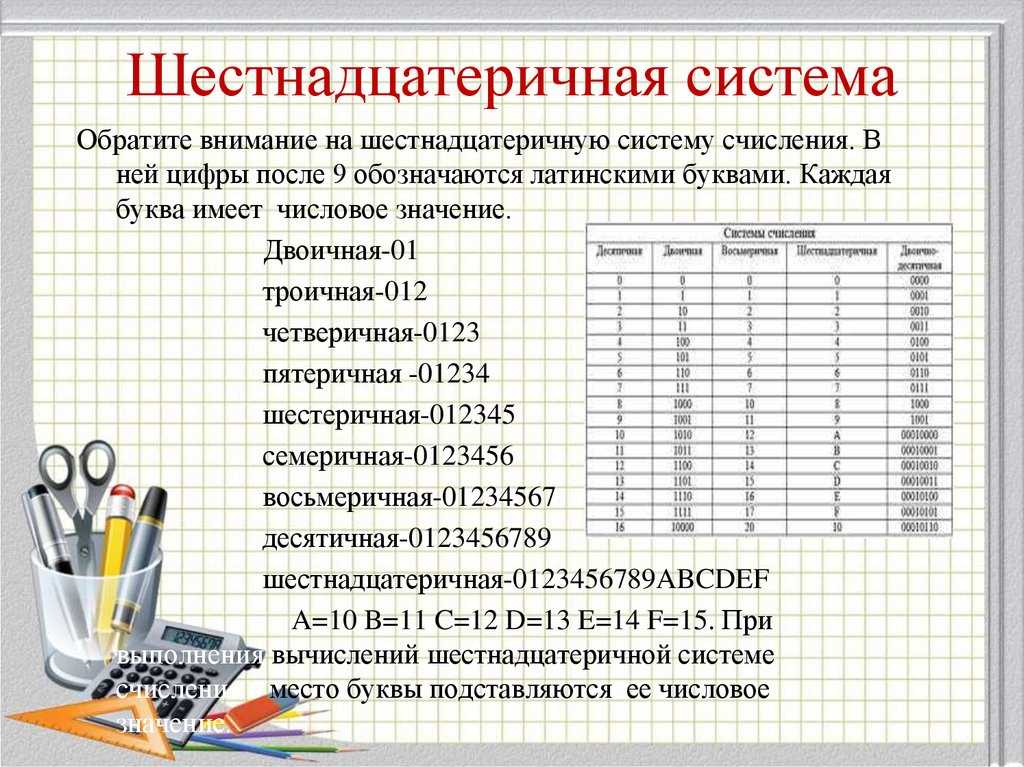 В
результате нужно записать в одну строку, справа налево все остатки, начиная с
последнего.
В
результате нужно записать в одну строку, справа налево все остатки, начиная с
последнего.
Переведём наше число. Делим его на 8. Получим 15, а в остатке 5. Обведём остаток в кружок.
Теперь число 15 делим на 8. Получим 1. В остатке 7. Снова обведём это число.
1 больше 0. Значит делим число 1 на 8. Получим 0. А в остатке 1. Обводим наш остаток.
Теперь осталось после равно записать все остатки справа налево.
12510 = 1758
Мы перевели число 125 в восьмеричную систему счисления.
А теперь давайте узнаем, что такое шестнадцатеричная система счисления.
Шестнадцатеричная система счисления – это позиционная система счисления с основанием 16. В алфавит этой системы входят цифры от 0 до 9 и буквы А, B, C, D, Е, F. Эти буквы обозначают в десятичной системе числа от 10 до 15 соответственно.
Для представление целого шестнадцатеричного числа в развёрнутой форме записи нужно использовать следующую формулу:
Распишем предоставленное
шестнадцатеричное число A6E
в развёрнутой форме.
Ставим знак равно. Снова проставим степени для шестнадцати над цифрами нашего числа справа налево.
Пишем букву А и умножаем её на 162. Ставим плюс. Пишем цифру 6, умноженную на 161 и прибавляем букву Е, умноженную на 160.
Для перевода целого шестнадцатеричного числа в десятичную систему счисления нужно перейти к его развёрнутой записи, заменить буквы на соответствующие им цифры в десятичной системе счисления и вычислить значение получившегося выражения.
Наше число уже записано в развёрнутой форме. Нам осталось заменить буквы на соответствующие им десятичной системе числа и сосчитать. Ставим равно. Буква А соответствует числу 10 в десятичной системе счисления. Запишем число 10 и умножаем его на 162.
Ставим плюс и перепишем число 6, умноженное на 161.
Снова ставим плюс. Букве
Е соответствует число 14 в десятичной системе счисления.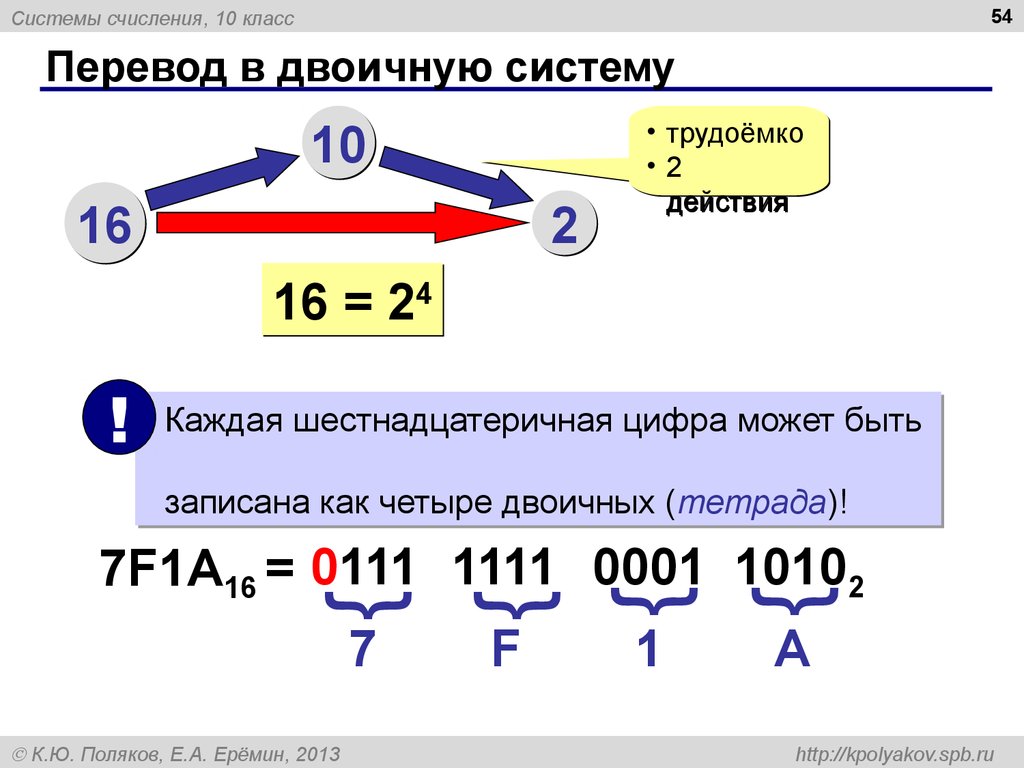 Пишем число 14,
умноженное на 160.
Ставим равно.
Пишем число 14,
умноженное на 160.
Ставим равно.
Прежде, чем всё это сосчитать снова обратимся к математике и распишем степени числа шестнадцать.
162 = 256.
162 ·10 = 2 560
Ставим плюс.
161 = 16.
161 · 6 = 96.
Снова ставим плюс.
160 = 1.
160 · 14 = 14.
Ставим равно.
Мы получили 2 670 в десятичной системе счисления.
Для перевода целого десятичного числа в шестнадцатеричную систему счисления следует последовательно выполнять деление данного числа и получаемых целых частных на 16 до тех пор, пока не получим частное, равное 0. В результате нужно записать в одну строку, справа налево все остатки, начиная с последнего, при необходимости, заменяя цифры на соответствующие им буквы в шестнадцатеричной системе счисления.
Переведём число 350 в
шестнадцатеричную систему счисления.
Делим наше число на 16, получим 21, остаток 14. Выделим его.
Делим 21 на 16. Получим 1 и 5 в остатке. Обводим наш остаток.
1 больше 0. Делим 1 на 16, получим 0 и 1 в остатке. И снова выделяем остаток 1.
Теперь запишем все числа справа налево. Записываем следующие цифры: 1, 5.
35010 = 15.
Так как в шестнадцатеричной системе счисления числу 14 соответствует буква Е, то пишем её после 5.
35010 = 15E16.
Мы с вами перевели число 350 в шестнадцатеричную систему счисления.
Вы, наверное, заметили, что все правила перевода целого десятичного числа в любую систему счислению с другим основанием похожи.
Давайте изучим общее правило перевода целых десятичных чисел в любую систему счисления с основание q.
Для того, чтобы перевести целое десятичное число в систему счисления с основанием q нужно:
1. Последовательно
выполнять деление данного числа и получаемых целых частных на основание новой
системы счисления до тех пор, пока не получим частное, равное нулю.
Последовательно
выполнять деление данного числа и получаемых целых частных на основание новой
системы счисления до тех пор, пока не получим частное, равное нулю.
2. Полученные остатки, которые являются цифрами числа в новой системе счисления, привести в соответствии с алфавитом новой системы счисления.
3. Составить число в новой системе счисления, записывая его, начиная с последнего полученного остатка.
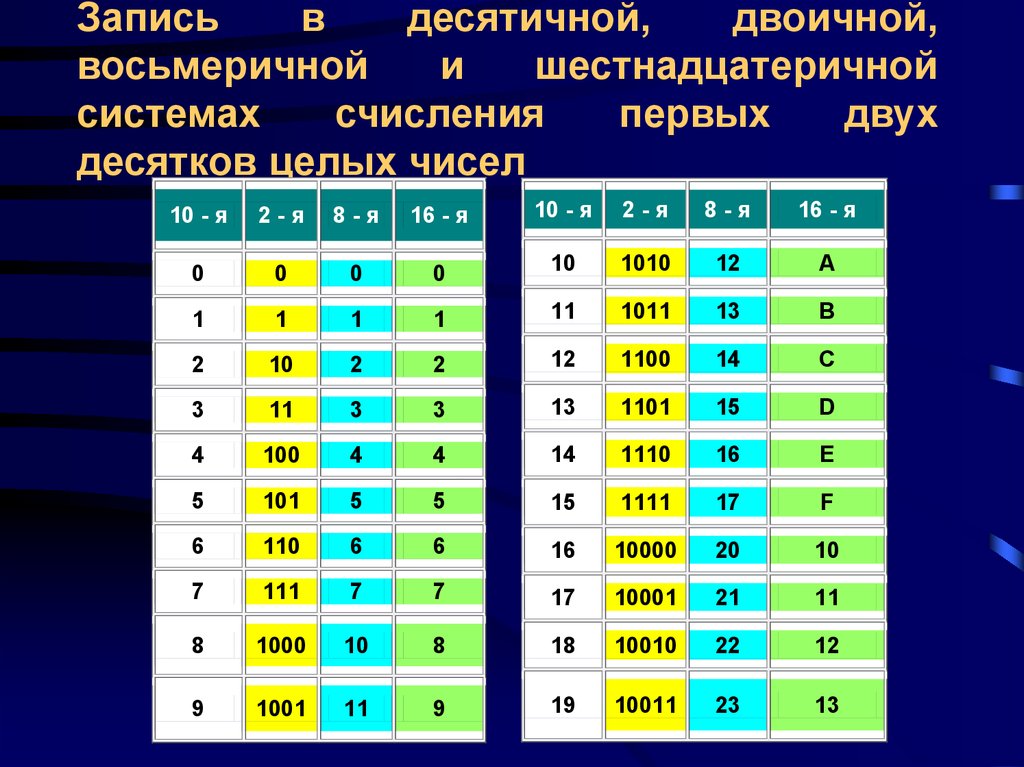
Вам предоставлена таблица соответствия десятичных, двоичных, восьмеричных и шестнадцатеричных чисел от 0 до 20. Числа от 0 до 20 подразумевают собой десятичную систему счисления.
А теперь давайте выполним задание.
Переведём одно и то же число 247 в двоичную, восьмеричную и шестнадцатеричную системы счисления и сравним получившиеся числа.
Для начала переведём из
десятичной в двоичную систему счисления. Для этого будем использовать таблицу,
так как число большое. В ней будет две строки. В первую строку первого столбца
запишем наше число.
Делим его на 2. Получим 123 и 1 в остатке. 123 запишем во вторую ячейку первой строки, а 1 – в первую ячейку второй строки.
Далее 123 разделить на 2 и получим 61 и 1 в остатке. 61 запишем после числа 123, а остаток один под число 123.
Далее 61 : 2 = 30 и остаток – 1. Запишем их в таблицу.
30 : 2 = 15, а остаток равен 0. Снова запишем их в таблицу в соответствующие ячейки.
При делении 15 на 2 получим 7 и 1 в остатке. Снова заполняем таблицу.
Далее 7 : 2 = 3 и 1 в остатке. Запишем в соответствующие ячейки наши числа.
3 :2 = 1 и 1 в остатке. Занесём данные в таблицу.
И делим 1 на 2, получим 0 и 1 в остатке. 0 писать не будет. Занесём только наш остаток в ячейку.
А теперь соберём все наши цифры в число в двоичной системе. Записываем их поочерёдно справа налево.
24710 = 111101112.
А сейчас переходим к
переводу в восьмеричную систему счисления числа 247.
Делим 247 на 8. Получим 30 и 7 в остатке. Обведём остаток от деления.
Далее 30 делим на 8, получим 3 и 6 в остатке. Выделяем остаток.
3 делим на 8, получаем 0 и 3 в остатке. Обводим остаток.
Теперь запишем все остатки справа налево и получим число в восьмеричной системе счисления.
24710 = 3678.
Нам осталось перевести наше число в шестнадцатеричную систему счисления. Делим 247 на 16. Получим 15 и 7 в остатке. Обведём остаток.
Теперь делим 15 на 16, получим 0. А остаток от деления равен 15. Выделим его.
А сейчас запишем наши цифры справа налево в соответствии с алфавитом шестнадцатеричной системы счисления. Число 15 — это буква F в этой системе счисления. Ставим её на первое место. А затем пишем число 7.
24710 = F716
Задание выполнено. Давайте сравним все наши получившиеся числа.
Как можем видеть – все
они одинаковые, но записаны разными цифрами, потому что они представлены в
различных системах счисления. Это можно увидеть, если обратить внимание на
основания чисел.
Это можно увидеть, если обратить внимание на
основания чисел.
А теперь пришла пора довести итоги урока. Сегодня мы узнали, что такое восьмеричная и шестнадцатеричная системы счисления, какие действия нужно выполнить для перевода целого десятичного числа в систему счисления с основанием q.
Также мы сегодня научились переводить числа из восьмеричной и шестнадцатеричной систем счисления в десятичную и наоборот.
Что такое шестнадцатеричная нумерация?
К
- Рахул Авати
Шестнадцатеричная система счисления с основанием 16. Она может использоваться для представления больших чисел с меньшим количеством цифр.
В этой системе имеется 16 символов или возможных числовых значений от 0 до 9, за которыми следуют шесть буквенных символов — A, B, C, D, E и F. Эти символы используются для представления десятичных значений от 10 до 15 в одиночном разряде. биты.
Эти символы используются для представления десятичных значений от 10 до 15 в одиночном разряде. биты.
Шестнадцатеричная, также известная как Base 16 или hex, — это одна из четырех систем счисления. Остальные три — десятичные (по основанию 10), двоичные (по основанию 2) и восьмеричные (по основанию 10).
Вот как выглядят десятичная и шестнадцатеричная системы для цифр от 0 до 15.
Десятичный | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
Шестнадцатеричный | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | А | Б | С | Д | Е | Ф |
Шестнадцатеричная система содержит 16 последовательных чисел в качестве основных единиц, включая 0. Первые девять чисел (от 0 до 9) — это те же самые числа, которые обычно используются в десятичной системе. Следующие шесть двузначных чисел (от 10 до 15) представлены буквами от A до F. Вот как в шестнадцатеричной системе используются числа от 0 до 9.и заглавные буквы от A до F для обозначения эквивалентного десятичного числа.
Первые девять чисел (от 0 до 9) — это те же самые числа, которые обычно используются в десятичной системе. Следующие шесть двузначных чисел (от 10 до 15) представлены буквами от A до F. Вот как в шестнадцатеричной системе используются числа от 0 до 9.и заглавные буквы от A до F для обозначения эквивалентного десятичного числа.
В этой системе нумерации каждая позиция цифры в 16 раз значительнее, чем цифра в предыдущей позиции. Шестнадцатеричный номер начинается с младшей значащей цифры справа. Числовое значение этого числа вычисляется путем умножения каждой цифры на значение ее позиции и последующего сложения произведений. Вот почему шестнадцатеричное число — это позиционное или взвешенное число 9.Система 0182.
Необходимость шестнадцатеричных чисел В вычислительных системах двоичные строковые эквиваленты больших десятичных чисел могут стать довольно длинными. Когда речь идет о 16- или 32-битных числах, становится трудно читать и записывать их без ошибок. Эти проблемы можно решить, разбив двоичные числа на группы по четыре бита, т. е. используя шестнадцатеричную систему счисления.
Эти проблемы можно решить, разбив двоичные числа на группы по четыре бита, т. е. используя шестнадцатеричную систему счисления.
Формат шестнадцатеричных чисел более компактен, чем двоичные числа, поскольку они могут представлять большие двоичные числа с меньшим количеством цифр. В результате их легче понять, чем длинные двоичные строки из 1 и 0.
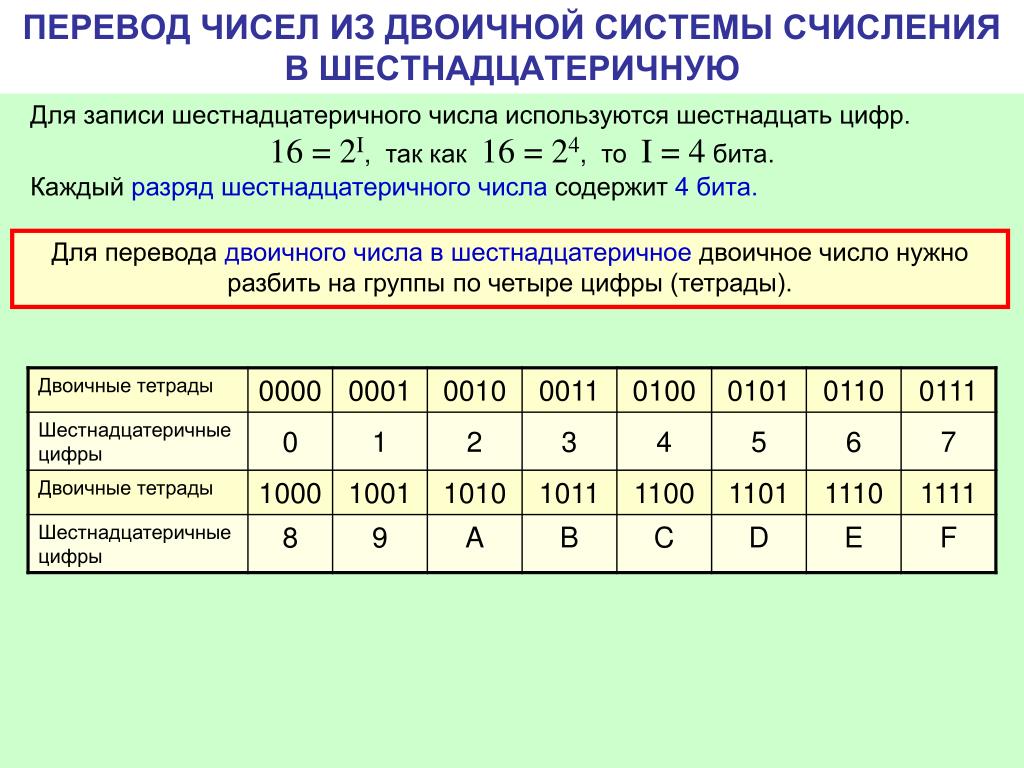
Представление шестнадцатеричных чиселВ шестнадцатеричном формате четыре цифры двоичного числа могут быть представлены одной шестнадцатеричной цифрой. Разделение двоичного числа на 4-битные наборы означает, что каждый набор может иметь возможное значение от 0000 до 1111, допуская 16 комбинаций чисел от 0 до 15. При базовом значении 16 максимальное значение цифры равно 15.
Легко преобразовать двоичное число в шестнадцатеричное и наоборот. Вот как эти числа представлены в каждой системе:
Шестнадцатеричный номер | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
4-битное двоичное число | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 |
Шестнадцатеричный номер | 8 | 9 | А | Б | С | Д | Е | Ф |
4-битное двоичное число | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
Кроме того, цифры слева от шестнадцатеричной точки имеют веса 16 0 , 16 1 , 16 2 и так далее. Точно так же позиции справа имеют веса 16 -1 , 16 -2 и т. д.
Точно так же позиции справа имеют веса 16 -1 , 16 -2 и т. д.
Пример
Для представления десятичного числа 512 в шестнадцатеричном виде:
Десятичное значение = 512
512 = 2×16 2 +0x16 1 +0x160=200
Шестнадцатеричное значение = 200
Преобразование двоичных и десятичных чисел в шестнадцатеричные- Преобразование двоичного кода в шестнадцатеричный
Для преобразования двоичных чисел в шестнадцатеричные четыре двоичные цифры должны быть преобразованы или преобразованы в одну шестнадцатеричную цифру. Вот как работает преобразование:
- Разделить двоичное значение на группы по четыре, начиная с крайней правой цифры.
- Сопоставьте каждую группу из четырех с соответствующим шестнадцатеричным значением.

- Представляет исходное двоичное число в шестнадцатеричном формате.
Пример
Вот как преобразовать двоичное число 1011010101100001 в шестнадцатеричную форму:
Шаг 1: Разделите двоичное значение на группы по четыре.
1011 | 0101 | 0110 | 0001 |
Шаг 2: Замените каждый набор шестнадцатеричным значением.
1011 | 0101 | 0110 | 0001 |
Б | 5 | 6 | 1 |
Шаг 3: Представьте двоичный файл в шестнадцатеричном виде
1011010101100001 2 = B561 16
- Преобразование десятичного числа в шестнадцатеричное
Процесс преобразования десятичного числа в шестнадцатеричное прост, хотя шагов больше:
- Разделить десятичное число на 16.

- Запишите остаток в шестнадцатеричной форме.
- Разделить результат на 16.
- Повторяйте шаги 2 и 3, пока результат не будет равен 0,
Полученное шестнадцатеричное значение представляет собой последовательность остатков от последнего к первому.
Пример
Вот как преобразовать десятичное число 1128 в шестнадцатеричное:
Шаг 1: Разделите 1128 на 16, чтобы получить результат 70 и остаток 8.
Шаг 2: Разделите результат (70) на 16, чтобы получить новый результат 4 и остаток 6.
Шаг 3: Разделите результат (4) на 16, чтобы получить результат 0 и остаток 4.
Шаг 4: Представьте шестнадцатеричное число как последовательность остатков от последнего к первому.
1128 10 = 468 16
Шестнадцатеричные идентификаторы Шестнадцатеричные числа обычно имеют префикс или суффикс с идентификаторами, чтобы избежать путаницы при чтении или записи и упростить отличить шестнадцатеричные числа от десятичных чисел. Некоторые распространенные шестнадцатеричные идентификаторы включают:
Некоторые распространенные шестнадцатеричные идентификаторы включают:
| Идентификатор | Применение | Пример |
% | Обычно используется в URL-адресах для указания символов, таких как пробелы | %2 |
# | Используется в языке HTML в качестве ссылки на цвет | #RR5687 |
0ч | Используется в программируемых графических калькуляторах | 0h7D |
\х | Используется в HTML, XML и других языках для выражения кодов управления символами | \x08: Возврат \x1B: Выход |
0x | Используется в UNIX и программировании на языке C | 0x54EF |
Также доступны другие идентификаторы; однако они обычно ограничены конкретными языками программирования и не могут использоваться взаимозаменяемо с другими языками.
Шестнадцатеричная система счисления особенно полезна в компьютерном программировании и микропроцессорах. Разработчики используют его для описания цветов на веб-страницах, описания областей памяти для каждого байта, указания определенных символов и многого другого. Шестнадцатеричные числа также используются в микроконтроллерах для упрощения обработки данных и манипулирования ими. Другими возможными приложениями являются наука о данных и аналитика, машинное обучение и искусственный интеллект.
Шестнадцатеричные преимущества и недостатки Шестнадцатеричные числа компактны и занимают меньше памяти, поэтому в компьютерных системах можно хранить больше чисел. Их небольшой размер также упрощает обработку ввода-вывода по сравнению с другими форматами нумерации. Поскольку легко преобразовать шестнадцатеричное число в двоичное и наоборот, система широко используется в компьютерном программировании. Также полезно представлять адреса памяти компьютера.
Также полезно представлять адреса памяти компьютера.
Одним из недостатков шестнадцатеричной системы счисления является сложность выполнения сложных математических операций, таких как умножение и деление. Шестнадцатеричные числа также труднее читать и записывать по сравнению с десятичными числами.
See also: Shared Key Authentication , Blowfish , network packet , big-endian and little-endian , globally unique identifier , universally unique идентификатор
Последнее обновление: июнь 2022 г.
Продолжить чтение о шестнадцатеричном формате- Объяснение двоичных и шестнадцатеричных чисел для разработчиков
- Используйте эти надстройки PowerShell, чтобы улучшить свой опыт
- Обработка данных с дискретизацией признаков, стандартизация
- Почему 8 примитивных типов данных Java не являются объектами
- Блокчейн: неизменяемый реестр для замены базы данных
распознавание изображений
Распознавание изображений в контексте машинного зрения — это способность программного обеспечения идентифицировать объекты, места, людей, надписи и действия на цифровых изображениях.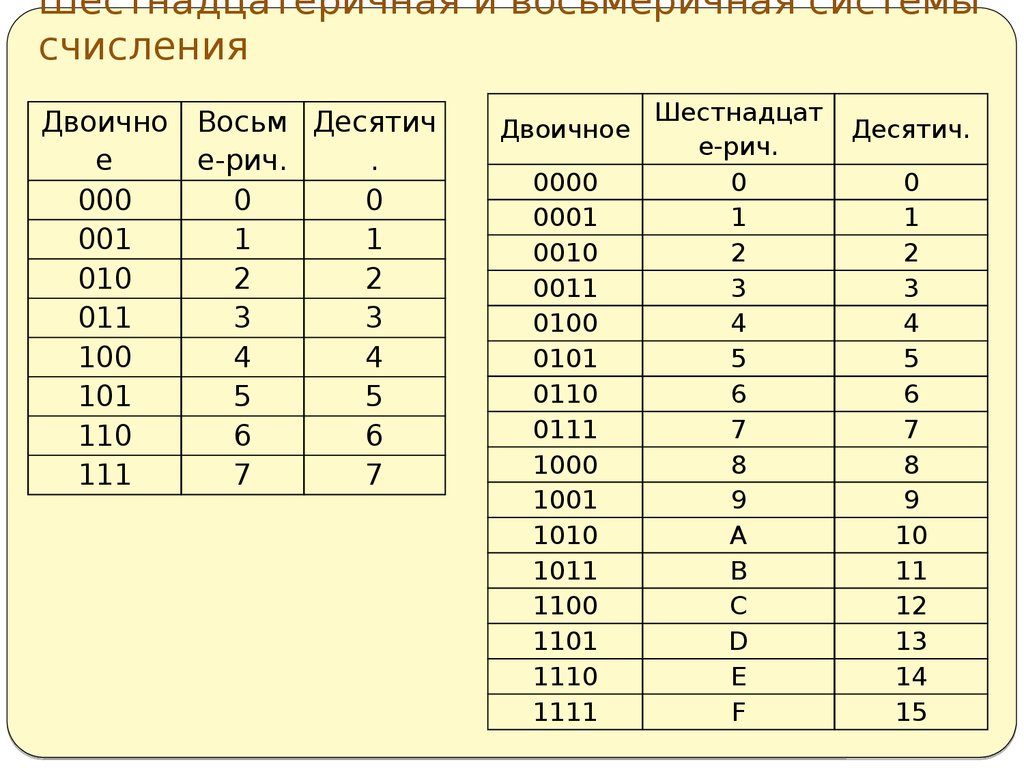
Сеть
- WAN (глобальная сеть)
Глобальная вычислительная сеть (WAN) — это географически распределенная частная телекоммуникационная сеть, которая соединяет между собой несколько локальных …
- SD-ветка
SD-филиал — это единая автоматизированная централизованно управляемая программно-ориентированная платформа, которая заменяет или дополняет существующий филиал …
- сетевой протокол
Сетевой протокол — это набор установленных правил, которые определяют, как форматировать, отправлять и получать данные, чтобы компьютерная сеть …
Безопасность
- Альянс облачной безопасности (CSA)
Альянс по безопасности облачных вычислений (CSA) — это некоммерческая организация, которая продвигает исследования передовых методов защиты облачных …
- квантовое превосходство
Квантовое превосходство — это экспериментальная демонстрация доминирования и преимущества квантового компьютера над классическими компьютерами с помощью .
 ..
.. - антивирусное программное обеспечение (антивирусная программа)
Антивирусное программное обеспечение (антивирусная программа) — программа обеспечения безопасности, предназначенная для предотвращения, обнаружения, поиска и удаления вирусов и других…
ИТ-директор
- сделка
В вычислениях транзакция представляет собой набор связанных задач, рассматриваемых как одно действие.
- бережливое управление
Бережливое управление — это подход к управлению организацией, который поддерживает концепцию постоянного совершенствования, долгосрочного …
- идентификатор устройства (идентификация устройства)
Идентификатор устройства (идентификация устройства) — это анонимная строка цифр и букв, которая однозначно идентифицирует мобильное устройство, такое как …
HRSoftware
- кадровый резерв
Кадровый резерв — это база данных кандидатов на работу, которые могут удовлетворить немедленные и долгосрочные потребности организации.

- разнообразие, равенство и инклюзивность (DEI)
Разнообразие, равенство и инклюзивность — термин, используемый для описания политики и программ, которые способствуют представительству и …
- пассивный кандидат
Пассивный кандидат (пассивный кандидат на работу) — это любой работник, который не ищет работу активно.
Служба поддержки клиентов
- лид, квалифицированный продуктом (PQL)
Лид, квалифицированный по продукту (PQL), — это физическое или юридическое лицо, которое получило выгоду от использования продукта в результате бесплатного …
- квалифицированный маркетолог лид (MQL)
Квалифицированный маркетолог (MQL) — это посетитель веб-сайта, уровень вовлеченности которого указывает на то, что он может стать клиентом.
- успех клиента
Успех клиента — это стратегия, направленная на то, чтобы продукция компании соответствовала потребностям клиента.

Шестнадцатеричная система: Объяснение системы счисления
В то время как десятичная система и ее десять цифр глубоко укоренились в нашей повседневной жизни, информатика и обработка данных в значительной степени зависят от двоичной системы, или двоичного кода . Двоичная система позволяет представлять сложные ситуации всего двумя состояниями: 0 и 1. Однако большие двоичные числа быстро запутываются. Здесь может помочь шестнадцатеричная система . Информация, выраженная с помощью восьми цифр в двоичной системе, может быть выражена с помощью всего двух шестнадцатеричных чисел.
Содержание
- Что такое шестнадцатеричная система?
- Для чего используется шестнадцатеричная система?
- шестнадцатеричная система: как это написать
- Связь между шестнадцатеричными числами и двоичными числами
- Шестнадцатеричная таблица для преобразования в десятичные и бинарные номера
- с помощью шестнадцатеричных номеров
- .
 менее чем за 1 доллар в первый год.
менее чем за 1 доллар в первый год.Зачем ждать? Получите свое любимое доменное имя сегодня!
Соответствующий адрес электронной почты
Сертификат SSL
Поддержка 24/7/365
Что такое шестнадцатеричная система?
Слово шестнадцатеричное состоит из терминов шестнадцатеричное и десятичное . Hexa происходит от греческого и означает «шесть», тогда как decem — это латинское слово, означающее «десять». Шестнадцатеричная система, таким образом, является системой позиционных значений, которая представляет числа с использованием основания 16. Это означает, что шестнадцатеричная система использует 16 различных цифр. Другими словами, существует 16 возможных цифр, в отличие от двух в двоичной системе (0 и 1) и десяти в десятичной системе (от 0 до 9).). Но какова цель системы?
Для чего используется шестнадцатеричная система?
Шестнадцатеричная система используется в компьютерных технологиях и делает большие числа и длинные битовые последовательности более удобочитаемыми.
 Они группируются в разделы по четыре бита, а затем преобразуются в шестнадцатеричные числа. В результате длинная последовательность единиц и нулей превращается в более короткие шестнадцатеричные числа, которые, в свою очередь, можно разделить на группы по два или четыре. Таким образом, шестнадцатеричные числа больше 9.0373 компактный способ представления битовых последовательностей. Система используется, например, для адресов источника и получателя в интернет-протоколах (IP), в кодах ASCII или для описания цветовых кодов в веб-дизайне с помощью языка таблиц стилей CSS.
Они группируются в разделы по четыре бита, а затем преобразуются в шестнадцатеричные числа. В результате длинная последовательность единиц и нулей превращается в более короткие шестнадцатеричные числа, которые, в свою очередь, можно разделить на группы по два или четыре. Таким образом, шестнадцатеричные числа больше 9.0373 компактный способ представления битовых последовательностей. Система используется, например, для адресов источника и получателя в интернет-протоколах (IP), в кодах ASCII или для описания цветовых кодов в веб-дизайне с помощью языка таблиц стилей CSS.Шестнадцатеричная система: как писать
Как упоминалось выше, шестнадцатеричная система использует 16 цифр. Здесь мы сталкиваемся с потенциальной проблемой. В нашем традиционном способе записи чисел мы используем десятичные числа 10, 11, 12, 13, 14 и 15, которые состоят из двух символов, сложенных вместе. Поэтому, если бы вы использовали число 10 в шестнадцатеричной системе счисления, было бы неясно, что вы имеете в виду.

Чтобы избежать этой проблемы, буквы от A до F используются для представления чисел от десяти до 15 в шестнадцатеричной системе счисления. Таким образом, числа от 0 до 9 и от A до F используются для представления эквивалентов двоичных и десятичных чисел. Существуют различные обозначения, позволяющие отличить шестнадцатеричные числа от десятичных:
- 73 16
- 73 hex
- 73h
- 73H
- 73H
- 0x73
- $73
- #73
- «73
- X’73’
The prefix 0x and the suffix h are especially common in programming, and the dollar prefix $ is часто используется в некоторых семействах процессоров на языке ассемблера. используйте группы из трех цифр, чтобы сделать большие числа вроде миллионов, миллиардов и триллионов более читабельны. То же самое и с цифровыми системами. Чтобы упростить чтение битовых последовательностей, таких как 1111010111001111 2 , их обычно делят на группы по четыре.
 Итак, наш пример будет выглядеть так: 1111 0101 1100 1111 2 . Читать становится еще легче, когда двоичные числа преобразуются в шестнадцатеричную систему.
Итак, наш пример будет выглядеть так: 1111 0101 1100 1111 2 . Читать становится еще легче, когда двоичные числа преобразуются в шестнадцатеричную систему.Поскольку шестнадцать — это четвертая степень двойки (2 4 ), существует прямая связь между числами два и шестнадцать: одна шестнадцатеричная цифра соответствует четыре двоичных цифры . Это означает, что вы можете представить четырьмя цифрами из двоичного числа с помощью одной шестнадцатеричной цифры . Это делает преобразование между двоичными и шестнадцатеричными числами относительно простым, и большие двоичные числа могут быть записаны в шестнадцатеричной системе с меньшим количеством цифр.
Шестнадцатеричная таблица для преобразования в десятичные и двоичные числа
Шестнадцатеричная система более сложна, чем двоичная и десятичная системы, и часто используется в связи с адресами памяти. Двоичные числа делятся на группы по четыре бита, и каждая группа битов имеет значение от «0000» до «1111».
 Это приводит к 16 различным комбинациям чисел от 0 до 15. Обратите внимание, что «0» также является допустимой цифрой.
Это приводит к 16 различным комбинациям чисел от 0 до 15. Обратите внимание, что «0» также является допустимой цифрой.Decimal number
4 bit binary number
Hexadecimal number
0
0000
0
1
0001
1
2
0010
2
0010
2
0010
2
0010
2
0010
2
0010
2 0010
2 0010
0014 3
0011
3
4
0100
4
5
0101
5
6
0110
6
7
0111
7
8
1000
8
9
1001
9
10
1010
A
11
1011
B
12
1100
C
13
1101
D
14
1110
E
15
1111
F
16
0001 0000
10 (1+0)
17
0001 0001
11 (1+1)
18
0001 0010
12 (1+2)
19
0001 0011
13 (1+3)
20
0001 0100
14 (1+4)

. номерная последовательность 1111 0101 1100 1111 2 в шестнадцатеричной системе будет выглядеть так: F5CF . Это число намного легче читать, чем длинную последовательность битов. Шестнадцатеричная система может быть использована для записи цифрового кода с меньшим количеством цифр и, таким образом, меньше шансов сделать ошибку . Преобразование шестнадцатеричных чисел обратно в двоичные можно сделать так же просто, используя ту же шестнадцатеричную таблицу, что и выше.
Чтобы было понятно, что число является шестнадцатеричным числом, мы можем записать его следующим образом: F5CF 16 , $F5CF или #F5CF . Последнее обозначение, также называемое хеш-значением, используется для цифрового цветового кодирования, поскольку дизайнеры и разработчики используют шестнадцатеричные цвета в веб-дизайне. Шестнадцатеричные цвета представлены шестизначной комбинацией цифр и букв, определяемой смесью красного, зеленого и синего цветов (RGB).
 #000000 обозначает черный цвет, а #FFFFFF — белый.
#000000 обозначает черный цвет, а #FFFFFF — белый.Счет с шестнадцатеричными числами
Теперь вы знаете, как преобразовывать двоичные числа в шестнадцатеричные числа. Если вы работаете с более чем четырьмя двоичными цифрами, просто начните сначала или продолжите со следующего набора из четырех битов. С двумя шестнадцатеричными цифрами вы можете считать до FF, что соответствует десятичному числу 255.
Добавление дополнительных шестнадцатеричных цифр для преобразования двоичного числа в шестнадцатеричное очень просто, если у вас есть четыре, восемь, двенадцать или шестнадцать цифр. Но вы также можете добавить «0» или «00» слева от старшего бита, даже если количество двоичных разрядов больше не кратно четырем. Например, 110010110110011 2 — это четырнадцатибитное двоичное число, которое слишком велико для трех шестнадцатеричных цифр, но слишком мало для четырех.
Решение состоит в добавлении дополнительных нулей к левому концу числа, пока не будет получен полный набор четырехбитных двоичных чисел.



 также
также Например, «5A3h». При этом, если число начинается не с десятичной цифры, впереди ставится «0» (ноль): «0FFh» (25510)
Например, «5A3h». При этом, если число начинается не с десятичной цифры, впереди ставится «0» (ноль): «0FFh» (25510)
 также
также

 ..
..
 менее чем за 1 доллар в первый год.
менее чем за 1 доллар в первый год. Они группируются в разделы по четыре бита, а затем преобразуются в шестнадцатеричные числа. В результате длинная последовательность единиц и нулей превращается в более короткие шестнадцатеричные числа, которые, в свою очередь, можно разделить на группы по два или четыре. Таким образом, шестнадцатеричные числа больше 9.0373 компактный способ представления битовых последовательностей. Система используется, например, для адресов источника и получателя в интернет-протоколах (IP), в кодах ASCII или для описания цветовых кодов в веб-дизайне с помощью языка таблиц стилей CSS.
Они группируются в разделы по четыре бита, а затем преобразуются в шестнадцатеричные числа. В результате длинная последовательность единиц и нулей превращается в более короткие шестнадцатеричные числа, которые, в свою очередь, можно разделить на группы по два или четыре. Таким образом, шестнадцатеричные числа больше 9.0373 компактный способ представления битовых последовательностей. Система используется, например, для адресов источника и получателя в интернет-протоколах (IP), в кодах ASCII или для описания цветовых кодов в веб-дизайне с помощью языка таблиц стилей CSS.
 Итак, наш пример будет выглядеть так: 1111 0101 1100 1111 2 . Читать становится еще легче, когда двоичные числа преобразуются в шестнадцатеричную систему.
Итак, наш пример будет выглядеть так: 1111 0101 1100 1111 2 . Читать становится еще легче, когда двоичные числа преобразуются в шестнадцатеричную систему.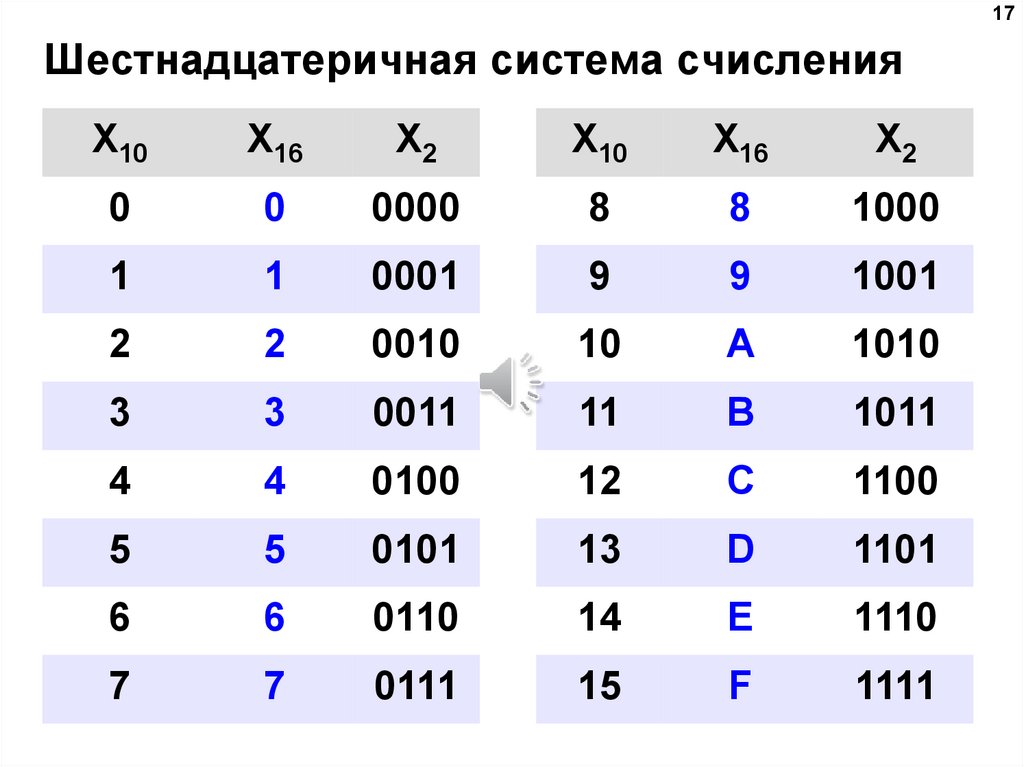 Это приводит к 16 различным комбинациям чисел от 0 до 15. Обратите внимание, что «0» также является допустимой цифрой.
Это приводит к 16 различным комбинациям чисел от 0 до 15. Обратите внимание, что «0» также является допустимой цифрой.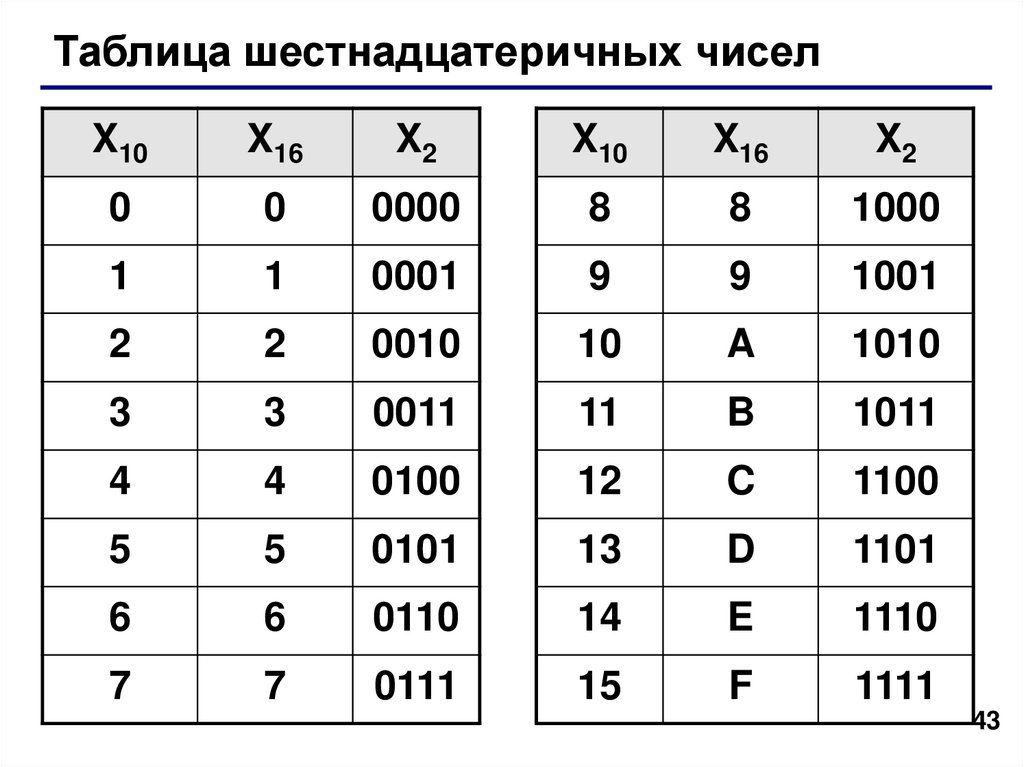
 #000000 обозначает черный цвет, а #FFFFFF — белый.
#000000 обозначает черный цвет, а #FFFFFF — белый.