Что такое двоичный и шестнадцатеричный коды?

В этой статье объясним вам что такое двоичный и шестнадцатеричный коды.

Приобретая знания в средней школе, потом в институте, мы учимся математике и другим наукам в десятеричной системе исчисления. Вся наша обыденная жизнь связана только с ней. Время, деньги, разные физические величины представляются нами только в виде цифр от нуля до девяти.

Ранее, в статье «Введение в информатику. Алгоритмы», я кратко пояснил, что любая цифровая техника от простейшего устройства автоматики до компьютера оперирует всего двумя логическими состояниями «ноль» и «единица». Информация хранится в ячейках памяти, которые могут быть «долговременными», а могут быть оперативными – «кратковременными». К долговременным относятся постоянные запоминающие устройства (ПЗУ) на микросхемах, магнитных лентах и дисках не требующие во время хранения информации питающего напряжения (флеш-карта, дискета, или жёсткий диск компьютера). Оперативные ячейки памяти хранят информацию в течение времени, необходимого для проведения вычислений и требуют постоянного питающего напряжения (оперативное запоминающее устройство компьютера, кэш-память микропроцессора). Минимальная ячейка памяти способна хранить единицу информации — один бит, который может принимать значение равное нулю, либо единице. Восемь битов – это уже байт. Если один бит информации может принимать два значения — от 0 до 1, то сочетание нулей и единиц одного байта может принимать 256 значений — от 0 до 255.

Говорят: компьютер имеет 64-х разрядную шину данных. Это означает, что одновременно его информационная шина способна передавать 64 бита информации от одного функционального узла (устройства) компьютера к другому. 64 / 8 бит = 8 байт . Нет смысла говорить о том какой это большой, или маленький объём информации, ведь всё в мире относительно. Следующая единица информации это килобайт – одна тысяча байт. Далее мегабайт – один миллион байт. Далее терабайт – один миллиард байт.

Мой первый компьютер в 1990 году имел оперативную память равную 16 килобайт, а в качестве ПЗУ использовалась магнитофонная кассета, на которой файлы размером больше 20 килобайт записывать не рекомендовалось (сбоили), на всю кассету помещалось не более 400 килобайт. В 1997-м году у меня был компьютер с оперативной памятью 16 мегабайт и 4-х гигабайтным жёстким диском, в 2002-м году — компьютер с оперативной памятью 256 мегабайт и 80-ти гигабайтным жёстким диском, а в 2014-м году у меня компьютер с оперативной памятью 4 гигабайт и жёстким диском (ПЗУ) в один терабайт. Время бежит вперёд, техника тоже прогрессирует. Скоро и эти объёмы памяти будут смешными.

Вернёмся к битам и байтам и определимся что такое двоичный код. Один байт – это 8 бит. Биты в байте располагаются в следующем порядке:

Как и в десятичной системе исчисления, в двоичной системе также принято делить числа на разряды. В десятичном представлении чисел принято писать слева направо — старшие разряды, потом младшие. Взглянув на число, по количеству символов, мы сначала определяем, к какому порядку число относится (единицы, десятки, сотни и т.д.). Потом посмотрев на впереди стоящую цифру, определяем размерность старших разрядов. Потом последовательно переходим на младшие числа (разряды). Это удобно для нашего восприятия. В двоичной системе абсолютно всё также, старший бит (разряд) располагается слева, правее располагается бит (разряд) по младше, и т.д. до самого младшего — первого.

А теперь попробуем понять определение из учебника информатики:

«За единицу количества информации принимается такое количество информации, которое содержится в информационном сообщении, уменьшающем неопределённость знания в 2 раза. Такая единица названа битом»

Бит – это единица информации. Информационное сообщение может состоять из одного бита, двух битов, трёх битов и т.д. до бесконечности.

Один бит информации может принимать 2 значения: 0, или 1. Второй бит информации также может принимать 2 значения: 0, или 1. Но когда биты объединены в одно сообщение, то это сообщение может иметь 4 различных значения – комбинаций состояния битов (значение равное 0, 1, 2 или 3). Третий бит информации также может принимать 2 значения: 0, или 1. В сумме три отдельных бита могут принимать 6 значений, но объединённые в одно информационное сообщение, в зависимости от состояния битов (комбинаций нулей и единиц), само сообщение может принимать 8 различных значений (от 0 до 7). Четвертый бит информации также может принимать 2 значения: 0, или 1. В сумме четыре отдельных бита могут принимать 8 значений, но объединённые в одно информационное сообщение, в зависимости от состояния битов (комбинаций нулей и единиц), само сообщение может принимать 16 значений (от 0 до 15).

Обратите внимание, что добавление каждого нового бита увеличивает варианты состояний (информации) в 2 раза. Как было написано ранее, один бит хранит информацию от 0 до 1 (два логических состояния). Если мы будем использовать 2 бита, то мы увеличим размерность хранящейся информации вдвое – от 0 до 3 (четыре логических состояния). Если мы будем использовать 3 бита, то размерность информации увеличится ещё в два раза – от 0 до 7 (восемь логических состояний). Используя 4 бита, мы увеличиваем размерность информации ещё в два раза – от 0 до 15 (шестнадцать логических состояний). Использование каждого последующего бита увеличивает размерность информации вдвое. Поэтому на многих схемах разрядность битов подписывают 1, 2, 4, 8, 16, 32, 64, и т.д. умножая на 2. Для объяснения описанного, приведена таблица для 4-х разрядов (полубайта):

Чтобы записать любое десятичное число в двоичной системе, или наоборот перевести из двоичной в десятичную, можно воспользоваться следующей табличкой:

Эта табличка используется для размерностей чисел в пределах 2-х байт – от 0 до 65 535. Если Вам необходимо пересчитывать более крупные числа, тогда можете продолжить табличку самостоятельно, учитывая закономерность, что каждый следующий бит, имеет разрядность в два раза больше предыдущего.

 

Например: Вы хотите определить, как будет выглядеть двоичный код числа 12 345. Берём табличку, добавляем ещё одну строку, назовём её «Состояние битов» и начнём вычислять:

Вычисление производится от старшего бита, старшего байта.

Находим в таблице старший бит (разрядность которого максимальна), но меньше, или равна этому числу. В нашем случае восьмой бит старшего байта имеет разрядность 32 768, это больше числа 12 345, поэтому ставим в табличку 8-го бита «0», тоже самое произойдёт и с 7-м битом. Разрядность 6-го бита 8 192 меньше числа 12 345, поэтому ставим в табличку «1».

После этого делаем вычисление — от искомого числа отнимаем значение 6-го бита: 12 345 – 8 192 = 4 153. Проверяем разрядность следующего пятого бита: 4 096 меньше значения 4 153, тогда ставим «1», и повторяем отнимание: 4 153 – 4 096 = 57. Мы получили число 57. Разрядность 1-4 бита старшего байта и 7-8 бита младшего байта больше числа 57, поэтому ставим в табличку этих битов значения «0». Разрядность 6-го бита – 32 меньше числа 57, поэтому ставим в табличку цифру 1 и производим очередное отнимание: 57 – 32 = 25.

Проверяем разрядность 5-го бита – 16 меньше числа 25, поэтому ставим в табличку цифру 1 и производим очередное отнимание: 25 – 16 = 9.

Проверяем разрядность 4-го бита – 8 меньше числа 9, поэтому ставим в табличку цифру 1 и производим очередное отнимание: 9 – 8 = 1. Разрядность 3-го и 2-го бита младшего байта больше числа 1, поэтому ставим в табличку этих битов значения «0». Разрядность 1-го бита младшего байта равна числу 1, поэтому ставим в табличку этого бита значение «1».

Итак, мы получили двоичный код числа 12 345, который выглядит: 00110000 00111001.

Теперь наоборот, из двоичного кода получим десятичное число. Это намного проще.

Например: у нас имеется двоичное двухбайтное число: 10101010 10101010. Запишем его в нашу таблицу под соответствующие биты:

Нам остается теперь только сложить разрядности всех битов, значение которых равно единице: 2 + 8 + 32 + 128 + 512 + 2 048 + 8 192 + 32 768 = 43 690.

---

Что же такое шестнадцатеричный код? Это представление двоичного кода десятичными символами и буквами, необходимое разработчику программ для сокращённой записи двоичного кода. Компьютер на нём не работает, люди вычислений не делают. Четыре бита которые в двоичном коде имеют четыре цифры-символа, в шестнадцатеричном коде обозначаются всего лишь одним символом, один байт – двумя символами, два байта – четырьмя символами и т.д. по четыре бита на символ. Таким образом, один байт обозначается двумя символами шестнадцатеричного кода.

Соответствие символов шестнадцатеричного кода двоичному коду приведено в таблице:

Например: десятичное число 12 345, которое мы преобразовали ранее в двоичный код 00110000 00111001, в шестнадцатеричной форме выглядит: 30 39.

Двоичное число 10101010 10101010, которое мы преобразовали ранее в десятичное 43 690, в шестнадцатеричной форме выглядит так: АА АА.

Некоторые недоучки могут сказать: «Как, ведь компьютер только и работает, что в шестнадцатеричном коде!» Ничего подобного. По проводнику адресной шины компьютера, или шины данных может идти «единичка» в виде напряжения, или «нолик» в виде отсутствия напряжения. Это двоичный код. Но в неё никак не загнать символы шестнадцатеричного кода. Это, в отличие от наличия, или отсутствия напряжения, которое можно «потрогать языком» как на батарейке, всего лишь символы, без специальных программ понятные только человеку, а не машине.

Шестнадцатеричный код в настоящее время успешно используется в написании алгоритмов для микроконтроллеров, поэтому тот, кто активно занимается микроконтроллерами, должен знать шестнадцатеричный код. Я уж не говорю об ассемблере.

---

На первом своём компьютере, я писал маленькие программки в Ассемблере, вперемешку с Бейсиком, переводя в шестнадцатеричный код, после чего сохранял на внешнем носителе – магнитофоне, и лишь потом смотрел, что же получилось. Ассемблер – это язык программирования, который максимально близок к машинному коду ЭВМ. Для его перевода в «цифру», достаточно наименования команд программирования заменить на шестнадцатеричный код, который с помощью прошитого ПЗУ автоматически переводится в двоичный код. В настоящее время программы пишут на языках высокого уровня, которые сам компьютер не понимает без программ интерпретаторов, компиляторов и прочих других «буферных» программ и подпрограмм, которые в свою очередь перекладывают программы в шестнадцатеричный код, а потом аппаратными средствами – в двоичный код. Это является фактором, значительно снижающим быстродействие выполнения программ, так как компьютер выполняет «дополнительные» операции требующие затраты времени, но развитие компьютерной техники в настоящее время с её высокими скоростями обработки информации и обмена позволяет это делать. Как пример, приведу свой сайт, который вы сейчас читаете.

Все странички своего сайта я пишу в xml-овских тегах, с лёгкостью понятных для любых браузеров интернет-пользователей. Мои страницы занимают мизерный объём памяти и быстро открываются. Задержки могут возникать только в моменты обращения к серверу с открытием рисунков и рекламных тизеров. А многие другие владельцы сайтов пишут свои странички, используя шаблоны WordPress. При том же объёме информации, что и у меня, объём их страниц и время открывания браузером значительно больше. В данном случае, WordPress выполняя роль программы-компилятора замедляет работу. Кроме того, он может создавать «ненужные» теги и символы, которые не только замедляют работу браузеров, но и увеличивают размер файлов. Впрочем, если у вас «быстрый» интернет и «быстроходная машина», этого замедления вы и не заметите. Абсолютно также с замедлением работают все программы от операционных систем, до компьютерных игр. А побеждает по скорости та, которая в результате компиляции ближе к машинным кодам — преобразована с языка программирования высокого уровня в машинные коды с минимальными «ненужными» командами.

Не берусь судить о том, понятно ли я изложил суть темы статьи, но думаю, что в ней с достаточной полнотой даны понятия двоичного и шестнадцатеричного кодов.

HEX, DEC, BIN должны быть понятны кодеру.

Три системы счисления.

Практическое программирование на ассемблере требует понимания системы счисления. Систем счисления существует бесконечное множество. Наиболее знакомая для нас — десятичная система счисления. Римская нумерация циферблата часов демонстрирует нам двенадцатеричную систему счисления. Программистам на ассемблере необходимо освоить три системы счисления : десятичную, двоичную и шестнадцатеричную.

Машина «думает» байтами. Байт состоит из 8 бит. Бит может содержать одно значение: 0 или 1. Так что в принципе, неплохо иметь представление и о восьмеричной системе счисления.Однако машинный код отображается в различных редакторах в виде шестнадцатеричного значения — оно более удобно для восприятия, так что всё же остановимся на трёх обязательно необходимых программисту системах счисления.

Двоичная система счисления — основа мироздания.

Вы помните Даосский символ Инь и Янь? Он состоит из двух цветов, из двух понятий: чёрного и белого, мужского и женского, единицы и нуля. Согласно Даосской философии весь мир сформирован именно с помощью двух противоположных

и вместе с тем неразделимых понятий. Просто поражает гениальность древних мудрецов. С помощью единиц и нулей человек создаёт множество цифровых миров. Год от года они становятся всё более реалистичными. Интересно, догадывается

ли герой компьютерной игры, что весь его мир состоит всего из двух цифр или это только мы такие прозорливые :)?

Десятичная система счисления.

Двоичная система счисления аппретирует только двумя цифрами: Единицей

и Нулём (Инь и Янь). Привычная для нас система счисления — десятеричная. Если все цифры до десяти состоят из различных одиночных символов (от нуля до девятки), то десять отображается уже двумя символами — единицей и нулём, расположенных

в определённой последовательности (10 — единица перед нулём).

Шестнадцатеричная система счисления.

В шестнадцатеричной системе счисления одним символом отображаются числа от нуля до шестнадцати. Чтобы не сочинять новых отображений цифр,
решили использовать буквы латинского  алфавита: A, B, C, D, E, F.

Для большей понятности  — внизу приведена таблица соответствия цифр трём системам счисления.

DEC BIN HEX Десятичная Двоичная Шестнадцатиричная 0 0 0 1 1 1 2 10 2 3 11 3 4 100 4 5 101 5 6 110 6 7 111 7 8 1000 8 9 1001 9 10 1010 A 11 1011 B 12 1100 C 13 1101 D 14 1110 E 15 1111 F 16 10000 10 17 10001 11 18 10010 12 ….

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22

DEC         BIN         HEX Десятичная  Двоичная    Шестнадцатиричная 0 0 0 1 1 1 2 10 2 3 11 3 4 100 4 5 101 5 6 110 6 7 111 7 8 1000 8 9 1001 9 10 1010 A 11 1011 B 12 1100 C 13 1101 D 14 1110 E 15 1111 F 16 10000 10 17 10001 11 18 10010 12 ….

Запоминать соответствия цифр нет необходимости. В состав Windows любой версии входит программа «калькулятор» — calc.exe. Запустите её, переключитесь в программистский вид (Вид->Программист или Alt+3) и да пребудет с вами сила!

Калькулятор программиста: HEX, DEC, OCT, BIN.

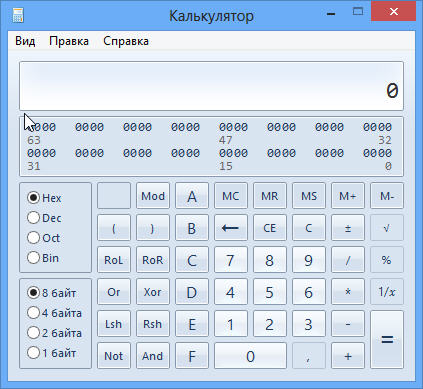
Три системы счисления — практическое использование.

Три системы счисления широко используются в программировании и отладке уже созданных программ.

Шестнадцатеричный (HEX) код удобен для современных процессоров, которые фактически развиваются на основе 16-ти разрядного процессора для персональных компьютеров Intel i8086. В исходных текстах программ практически всех языков программирования цифра обозначает по умолчанию число в десятичной системе счисления (DEC).

Десятичная система счисления более удобна (хотя и не всегда) при написании кода программ, шестнадцатеричная — неотъемлемая часть отладки, взлома, реверсивного программирования.

Двоичная система счисления (BIN) используется в основном при расстановке флагов определённых стилей объектов Windows (стили окон), но об этом попозже. Рассматривая 16 битное число в виде двоичного мы получаем великолепную возможность получить крохотный по размеру набор 16 флагов, где 1 — флаг установлен 0 — флаг снят (например, шестнадцатеричное число 4 000 соответствует двоичному 0100 0000 0000 0000 — установлен второй флаг, остальные сняты; шестнадцатеричное число 3000 соответствует двоичному числу 0011 0000 0000 0000 — установлены третий и четвёртый флаги, остальные сняты ).

Если мы хотим обозначить принадлежность числа к 16-тиричной системе счисления, то:
1. Ассемблер — добавляем к числу постфикс h (H), например: 100h = 256, 10H=16. Иногда для понимания того, что мы< >имеем дело с числом, в качестве префикса сотавят 0 (ноль).

2. Си (С++) к числу добавляется суфикс 0x (0X).

Например: 0x100 = 100h = 0100h = 256, 0x10 = 10H = 010H = 16

Хакерский редактор Hacker Viewer (Hiew) .

Для визуального восприятия шестнадцатиричного кода воспользуемся замечательным простым, но достаточно функциональным DOS редактором Hacker Viewer (Hiew). Вы найдёте его в папке D:\UTILS\HIEW\ (я надеюсь, что наш архив программ DOS-1.rar уже скачан и DOSBox установлен и запущен).

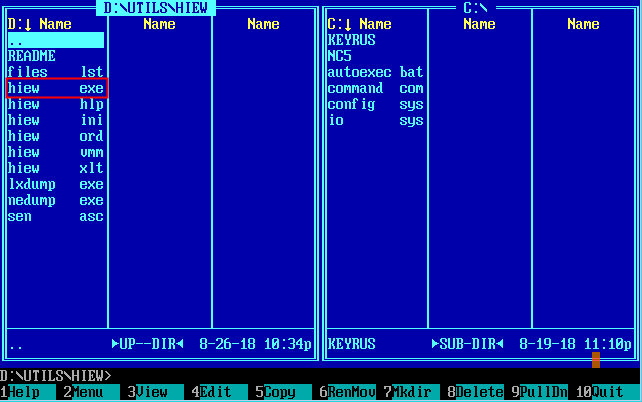Запускаем HIEW (Hacker Viewer).

Инструкцию по пользованию Hiew для хакеров от Криса Касперского вы найдёте в папочке readme. Пользоваться редактором просто и удобно.

Откроем с помощью Hiew нашу программу PRG.COM (выбор файлов — F9). При помощи F4 выбираем режим отображения информации HEX (как вы уже знаете, шестнадцатеричный режим). Можете с помощью F4 или Enter по переключаться между режимами отображения.

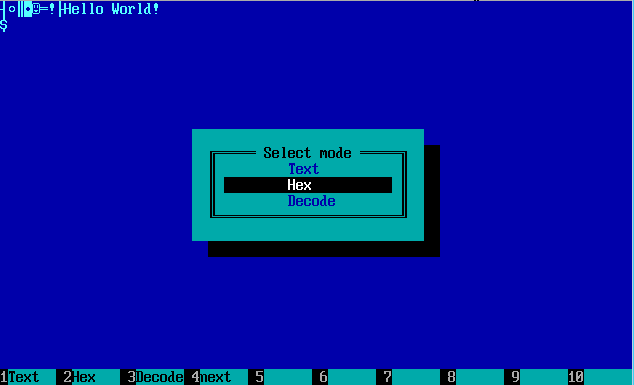Переключение режимов отображения в Hacker Viewer.

Обратите внимание на положение Decode (декодирование). Вам это ни о чём не говорит? Да, да, да в Hiew имеется встроенный дизассемблер и даже ассемблер! Можно внести изменения в ассемблерный код, не выходя из редактора и сохранить изменения.

Исполняемый файл останется рабочим — гениальная программа с поразительными возможностями для своего времени!

Подобное отображение HEX системы счисления вы увидите практически во всех отладочных программах и просмотрщиках файлов.
Перемещайте курсор с помощью клавиш стрелок на клавиатуре. Вверху вы заметите изменение цифры указателя (pointer).

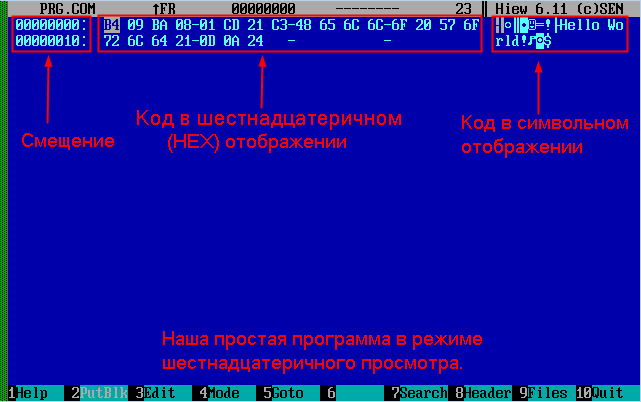Наша первая программа в шестнадцатеричном виде.

Указатель является одним из основополагающих понятий в системе программирования. Основы понимания работы с указателем рассмотрим попозже.

Шестнадцатеричные числа — это… Что такое Шестнадцатеричные числа?



Шестнадцатеричные числа

Шестнадцатеричная система счисления (шестнадцатеричные числа) — позиционная система счисления по целочисленному основанию 16. Обычно в качестве шестнадцатеричных цифр используются десятичные цифры от 0 до 9 и латинские буквы от A до F для обозначения цифр от 10 до 15.

Применение

Широко используется в низкоуровневом программировании и вообще в компьютерной документации, поскольку в современных компьютерах минимальной единицей памяти является 8-битный байт, значения которого удобно записывать двумя шестнадцатеричными цифрами. Такое использование началось с системы IBM/360, где вся документация использовала шестнадцатеричную систему, в то время как в документации других компьютерных систем того времени (даже с 8-битными символами, как, например, БЭСМ-6) использовали восьмеричную систему.

В стандарте Юникода номер символа принято записывать в шестнадцатеричном виде, используя не менее 4 цифр (при необходимости — с ведущими нулями).

Способы записи

В математике

В математике систему счисления принято писать в подстрочном знаке. Например, десятичное число 1443 можно записать как 1443₁₀ или как 5A3

16.

В языках программирования

В разных языках программирования для записи шестнадцатеричных чисел используют различный синтаксис:

• В Ада и
• В Си и языках схожего синтаксиса, например, в
• В некоторых ассемблерах используют букву «h», которую ставят после числа. Например, «5A3h». При этом, если число начинается не с десятичной цифры, впереди ставится «0» (ноль): «0FFh» (255₁₀)
• Другие ассемблеры (AT&T, Motorola), а также Паскаль и некоторые версии Бэйсика используют префикс «$». Например, «$5A3».
• Некоторые иные платформы, например ZX Spectrum в своих ассемблерах (MASM, TASM, ALASM, GENS и т.д.) использовали запись #5A3, обычно выровненную до одного или двух байт: #05A3.
• Другие версии Бэйсика используют для указания шестнадцатеричных цифр сочетание «&h». Например, «&h5A3».
• В Unix-подобных операционных системах (и многих языках программирования, имеющих корни в Unix/linux) непечатные символы при выводе/вводе кодируются как \xCC, где CC — шестнадцатеричный код символа.

Перевод чисел из одной системы счисления в другую

Перевод чисел из шестнадцатеричной системы в десятичную

Для перевода шестнадцатеричного числа в десятичное необходимо это число представить в виде суммы произведений степеней основания шестнадцатеричной системы счисления на соответствующие цифры в разрядах шестнадцатеричного числа.

Например, требуется перевести шестнадцатеричное число 5A3 в десятичное. В этом числе 3 цифры. В соответствии с вышеуказанным правилом представим его в виде суммы степеней с основанием 16:

5A3₁₆=5·16²+10·16¹+3·16⁰
=5·256+10·16+3·1=1280+160+3=1443₁₀

Перевод чисел из двоичной системы в шестнадцатеричную

Для перевода многозначного двоичного числа в шестнадцатеричную систему нужно разбить его на тетрады справа налево и заменить каждую тетраду соответствующей шестнадцатеричной цифрой.

Например:

10110100011₂=0101 1010 0011=5A3₁₆

Таблица перевода чисел

	0hex	=	0dec	=	0oct		0	0	0	0
	1hex	=	1dec	=	1oct		0	0	0	1
	2hex	=	2dec	=	2oct		0	0	1	0
	3hex	=	3dec	=	3oct		0	0	1	1
	4hex	=	4dec	=	4oct		0	1	0	0
	5hex	=	5dec	=	5oct		0	1	0	1
	6hex	=	6dec	=	6oct		0	1	1	0
	7hex	=	7dec	=	7oct		0	1	1	1
	8hex	=	8dec	=	10oct		1	0	0	0
	9hex	=	9dec	=	11oct		1	0	0	1
	Ahex	=	10dec	=	12oct		1	0	1	0
	Bhex	=	11dec	=	13oct		1	0	1	1
	Chex	=	12dec	=	14oct		1	1	0	0
	Dhex	=	13dec	=	15oct		1	1	0	1
	Ehex	=	14dec	=	16oct		1	1	1	0
	Fhex	=	15dec	=	17oct		1	1	1	1

См. также

Ссылки

Wikimedia Foundation. 2010.

• Шестнадцатиричная система счисления
• Шестнадцать

Смотреть что такое «Шестнадцатеричные числа» в других словарях:

• Шестнадцатиричные числа — Шестнадцатеричная система счисления (шестнадцатеричные числа) позиционная система счисления по целочисленному основанию 16. Обычно в качестве шестнадцатеричных цифр используются десятичные цифры от 0 до 9 и латинские буквы от A до F для… …   Википедия

• Hexspeak — Эта статья содержит незавершённый перевод с иностранного языка. Вы можете помочь проекту, переведя её до конца. Если вы знаете, на каком языке написан фрагмент, укажите его в этом шаблоне …   Википедия

• Шестнадцатеричная система счисления — Системы счисления в культуре Индо арабская система счисления Арабская Индийские Тамильская Бирманская Кхмерская Лаоская Монгольская Тайская Восточноазиатские системы счисления Китайская Японская Сучжоу Корейская Вьетнамская Счётные палочки… …   Википедия

• Шестнадцатеричная система — счисления (шестнадцатеричные числа) позиционная система счисления по целочисленному основанию 16. Обычно в качестве шестнадцатеричных цифр используются десятичные цифры от 0 до 9 и латинские буквы от A до F для обозначения цифр от 10 до 15.… …   Википедия

• Шестнадцатиричная система счисления — Шестнадцатеричная система счисления (шестнадцатеричные числа) позиционная система счисления по целочисленному основанию 16. Обычно в качестве шестнадцатеричных цифр используются десятичные цифры от 0 до 9 и латинские буквы от A до F для… …   Википедия

• Шестнадцатиричная система исчисления — Шестнадцатеричная система счисления (шестнадцатеричные числа) позиционная система счисления по целочисленному основанию 16. Обычно в качестве шестнадцатеричных цифр используются десятичные цифры от 0 до 9 и латинские буквы от A до F для… …   Википедия

• Монитор (интерактивная программа) — У этого термина существуют и другие значения, см. Монитор. Монитор компьютера Apple II Монитор  интерактивная программа в компьютерах, особенно 1970 х годов, позволяющая осуществлять управление компьютером на низком уровне: просмотр… …   Википедия

• HIMEM.SYS — HIMEM.SYS  драйвер дополнительной (extended memory) и HMA памяти для операционной системы MS DOS, обеспечивающий поддержку дополнительной памяти (extended или expanded). HIMEM.SYS был введён в состав операционной MS DOS 5.0 для возможности… …   Википедия

• Еггогология — Электроника МК 52 с сообщением «ERROR» (из за специфического отображения буквы r зачастую читалось как «ЕГГОГ») Еггогология& …   Википедия

• ЕГГОГ — Электроника МК 52 с сообщением ERROR (из за специфического отображения буквы r зачастую читалось как «ЕГГОГ» Еггогология изучение скрытых возможностей микрокалькуляторов. Содержание 1 Происхождение …   Википедия

Что такое шестнадцатиричная система цифр?

1234567890abcdef — применялась в профессиональных компьютерах, которые используются на телевидении и обрабатывают видеопоток на лету, в прямом эфире и синтезаторах. Когда скорости процессоров были ещё маленькие, эта система имела огромное преимущество перед двоичным кодом. Сейчас разница уже не так заметна. Если двоичный код это: либо сигнал есть, либо его нет, то шестнадцатиричный код имеет разную тональность для каждого значения. Как разница между импульсным и тоновым набором номера в телефоне. В тоновом режиме номер набирается быстрее. Не так ли? Соответственно и BIOS там прописывался другими значениями от 001 до 0FF. Кстати, слово OFF — как конец работы пошло именно из этой системы.

0 1 2 3 4 5 6 7 8 9 A B C D E F — вот…

система исчисления точнее.. . вот десятиричная, это всем привычная от 0 до 9, после 9 начинается следующий десяток, а в шестнадцатиричной от 0 до F(16), потом начинается новый скажем так «шестнадцатисяток»… во как

Система счисления, в которой десятичные числа 10, 11, 12, 13, 14, 15 являются цифрами и представляются как латинские буквы A, B, C, D, E, F. Обычно число, записанное в такой системе помечают постфиксом «h», например 40960d = A000h (h = (hex) = hexadeximal (шестнадцатеричный)).

Все правильно, только не из-за скорости процессора, а из-за того-что в реальном режиме(MS-DOS) Регистор состоял только из верхнего и нижнего и занимал 2 байта , те 16 битов. Вот и стали использовать шестнадцатиричную систему исчесления! С этим связано еще много разных фактов в програмировании, eg 1КБ = 1024 Б и т.п.

форма самой компактной записи компьютерных данных — в ней 1 байт всегда кодируется двумя символами — от 00 до FF. в то время как в десятичной записи потребуется три символа (000 — 255) а в двоичной — восемь (00000000 — 11111111). повторюсь — это только форма записи, сами данные в компьютере остаются двоичными. и никакой связи между шестнадцатиричной записью и скоростью или разрядностью процессора — нет. любое число можно записать в любой системе счисления.

Обычная система называется десятичной, в ней 10 цифр, от 0 до 9. Когда идёт счёт и доходит до 9, то цифры заканчиваются. Поэтому заводится новый разряд и следующее число записывается, как 10. Когда заканчиваются все комбинации из двух цифр (число 99), то заводится ещё один разряд и получается 100. И так далее.<br><br>В 16-ричной системе к десяти обычным цифрам добавляются ещё 6, которые записываются в виде первых 6 букв латинского алфавита, то есть, ABCDEF.<br><br>В результате, на числе десять цифры не заканчиваются, оно записывается как A. Цифры заканчиваются на числе пятнадцать, которое записывается, как F. Поэтому следующее число, шестнадцать, записывается, как 10. <br><br>Вообще, в любой Н-ричной системе счисления число Н записывается как 10. В двоичной ситеме, например, 10 обозначает число два. <br><br>Последнее двузначное 16-ричное число — это FF. Оно равно 255 (на десятичном языке). <br><br>Удобство 16-ричной системы заключаются в следующем. <br><br>Компьютеры работают в двоичной системе (цифры 0 и 1). Но в этой системе все числа получаются очень длинными. Например, число 134 запишется, как 10000110. Оказывается, если разбить двоичное число на четвёрки разрядов, то есть тут у нас будет 1000 и 0110 и перевести каждую из этих четвёрок в 16 ричную систему (8 и 6), то вместе получится правильное представление числа (86) в 16-ричной системе.<br><br>То есть, 16-ричная система — это способ компактной записи двоичных чисел.

Удобная запись чисел в информатике и цифровой технике

Шестнадцатеричное кодирование. Шестнадцатеричная нумерация и адресация

Шестнадцатеричная система счисления (также — шестнадцатеричный код) является позиционной системой счисления с целочисленным основанием 16. Иногда в литературе также используется термин hex (произносится «хекс», сокращение от англ. hexadecimal). Цифрами данной системы счисления принято использовать арабские цифры 0—9, а также первые символы латинского алфавита A—F. Буквы соответствуют следующим десятичным значениями:

• * A —10;
• * B —11;
• * C —12;
• * D —13;
• * E — 14;
• * F — 15.

Таким образом, десять арабских цифр вкупе с шестью латинскими буквами и составляют шестнадцать цифр системы.

Кстати, на нашем сайте вы можете перевести любой текст в десятичный, шестнадцатеричный, двоичный код воспользовавшись Калькулятором кодов онлайн .

Применение . Шестнадцатеричный код широко применяется в низкоуровневом программировании, а также в различных компьютерных справочных документах. Популярность системы обоснована архитектурными решениями современных компьютеров: в них в качестве минимальной единицы информации установлен байт (состоящий из восьми бит) — а значение байта удобно записывать с помощью двух шестнадцатеричных цифр. Значение байта может ранжироваться с #00 до #FF (от 0 до 255 в десятичной записи) — другими словами, используя шестнадцатеричный код , можно записать любое состояние байта, при этом не остаётся «лишних» не используемых в записи цифр.

В кодировке Юникод для записи номера символа используется четыре шестнадцатеричных цифры. Запись цвета стандарта RGB (Red, Green, Blue — красный, зелёный, синий) также часто использует шестнадцатеричный код (например, #FF0000 — запись ярко-красного цвета).

Способ записи шестнадцатеричного кода.

Математический способ записи . В математической записи основание системы записывают в десятичном виде в нижнем индексе справа от числа. Десятичную запись числа 3032 можно записать как 3032 10 , в шестнадцатеричной системе данное число будет иметь запись BD8 16 .

В синтаксисе языков программирования . Синтаксис различных языков программирования по-разному устанавливает формат записи числа, использующего шестнадцатеричный код :

* В синтаксисе некоторых разновидностей языка ассемблера используется латинская буква «h», которая ставится справа от числа, например: 20Dh. Если число начинается с латинской буквы, то перед ним ставится ноль, например: 0A0Bh. Это сделано для того, чтобы отличать от констант значения, использующие шестнадцатеричный код ;

* В прочих разновидностях ассемблера, а также в Pascal (и его разновидностях, таких как Delphi) и некоторых диалектах Basic, применяют префикс «$»: $A15;

* В языке разметки HTML, а также в каскадных файлах CSS, для указания цвета в формате RGB с шестнадцатеричной системой записи, используется префикс «#»: #00DC00.

Как перевести шестнадцатеричный код в другую систему?

Перевод из шестнадцатеричной системы в десятичную. Для совершения операции перевода из шестнадцатеричной системы в десятичную, требуется представить исходное число как сумму произведений цифр в разрядах шестнадцатеричного числа на степень основания.

Двоичная СС	шестнадцатеричная СС

Например, требуется выполнить перевод шестнадцатеричного числа A14: в нём три цифры. Используя правило, запишем его в виде суммы степеней с основанием 16:

A14 16 = 10.16 2 + 1.16 1 + 4.16 0 = 10.256 + 1.16 + 4.1 = 2560 + 16 + 4 = 2580 10

Перевод чисел из двоичной в шестнадцатеричную систему и наоборот.

Для перевода используется таблица тетрад. Чтобы выполнить перевод числа из двоичной в десятичную систему, необходимо произвести разбиение его на отдельные тетрады справа налево, после чего, используя таблицу, выполнить замену каждой тетрады на соответствующую шестнадцатеричную цифру. При этом, если количество цифр не кратно четырём, то необходимо добавить соответствующее количество нулей справа от числа, для того, чтобы общее число двоичных цифр стало кратно четырём.

Таблица тетрад для перевода.

Для перевода из шестнадцатеричной системы в двоичную, необходимо выполнить обратную операцию: выполнить замену каждой цифры на тетраду из таблицы.

Двоичная СС	Восьмеричная СС

Пример перевода из шестнадцатеричной системы в двоичную : A5E 16 = 1010 0101 1110 = 101001011110 2

Пример перевода из двоичной системы в шестнадцатеричную : 111100111 2 = 0001 1110 0111 = 1E7 16

В этом примере количество цифр в исходном двоичном числе не было равным четырём (9), поэтому были добавлены незначащие нули — общее число цифр стало 12.

Автоматический перевод . Быстрый перевод из шестнадцатеричной системы счисления в одну из трёх популярных систем (двоичную, восьмеричную и десятичную), как и обратный перевод, можно выполнить, используя стандартный калькулятор из комплекта поставки ОС Windows. Откройте калькулятор, выберите в меню Вид -> Программист. В данном режиме можно устанавливать систему счисления, используемую в данный момент (с