Шестнадцатеричная и двоичная системы счисления

Многие пользователи компьютеров понимают, что компьютер работает в двоичной системе счисления. Традиционно состояния двоичной системы представляются цифрами 0 и 1, хотя, если говорить более точнее, каждое состояние обозначает наличие или отсутствие сигнала, т. е. правильнее будет назвать состояния  «выключено» и «включено», либо «нет» и «да». Состоянию «выключено» или «нет» соответствует цифра 0, а состоянию «включено» или «да» цифра 1. Простым пользователям обычно нет необходимости полностью понимать устройство компьютера, однако двоичная система счисления дает о себе знать в виде различных ограничений основанных на степени двойки. Более компактный вариант двоичной системы называют шестнадцатеричной. Число шестнадцать является четвертой степенью числа два. Из этого следует, что можно достаточно просто переводить длинных двоичные последовательностей из нулей и единиц в короткие шестнадцатеричные. Для этого достаточно разбить двоичную последовательность на группы по четыре разряда (цифры) начиная с младшего разряда (справа) и заменить каждую группу на соответствующее шестнадцатеричное значение.

Шестнадцатеричную систему принято использовать для удобства восприятия двоичных данных, так как переводы из шестнадцатеричной системы в двоичную и обратно осуществляются простой заменой строк. Компьютер работает исключительно с двоичными последовательностями, а шестнадцатеричная запись этой последовательности в четыре раза компактнее, так как у этой системы основание 16 (2¹⁶), а двоичной 2. Двоичная последовательность может быть достаточно громоздкой. Например, запись числа 513 требует десять двоичных разрядов (1000000001), а в шестнадцатеричной только три (201). Тем не менее, для представления любых шестнадцатеричных чисел требуется шестнадцать разных символов, а не десять, которые используются в привычной нам десятичной системе счисления. Первые десять символов это символы в интервале от 0 по 9, остальные это буквы латинского алфавита в интервале от A по F. Буквы обычно (но не всегда) пишут в верхнем регистре (заглавные) в шестнадцатеричной записи числа. Первые десять символов (от 0 по 9) записываются аналогично цифрам в десятичной системе счисления и соответствуют им. Буквы в интервале от A по F соответствуют значениям в интервале от 10 до 15.

Рассмотрим соответствие чисел от 0 по 15 шестнадцатеричной и двоичной системам счисления.

Десятичная запись	Шестнадцатеричная запись	Двоичная запись
0	0	0000
1	1	0001
2	2	0010
3	3	0011
4	4	0100
5	5	0101
6	6	0110
7	7	0111
8	8	1000
9	9	1001
10	A	1010
11	B	1011
12	C	1100
13	D	1101
14	E	1110
15	F	1111

Записи 10, 11 и т. д. в десятичной, двоичной и шестнадцатеричной системах не соответствуют друг другу. Рассмотрим небольшой пример. Пусть у нас имеется шестнадцатеричное число число 1A5E. для перевода в двоичную запись достаточно просто заменить шестнадцатеричные разряды на соответствующие двоичные группы. Получится 0001 1010 0101 1110. Если убрать незначащие нули перед числом и записать его без разделителей получим 1101001011110. Для обратного перевода разделим число на группы по четыре разряда начиная с младшего (с правой стороны), а также для удобства добавим незначащие нули в старшей группе до 4 разрядов. Получим 0001 1010 0101 1110. Заменим группы на соответствующие шестнадцатеричные значения, получим 1A5E.

Для перевода шестнадцатеричного числа в десятичное представление можно воспользоваться схемой по которой мы записываем десятичные числа. В десятичном числе каждый разряд обозначает соответствующую степень числа десять начиная с нулевой с возрастанием справа налево. Например, десятичное число 123 обозначает 1*10² + 2*10¹ + 3*10⁰. Аналогичным методом переведем число 1A5E в десятичную систему счисления. В шестнадцатеричной системе счисления, также как и в десятичной каждый разряд обозначает соответствующую степень числа шестнадцать начиная с нулевой с возрастанием справа налево. Символы 1 и 5 в шестнадцатеричной системе счисления соответствуют значениям 1 и 5 в десятичной, а символы A и E — 10 и 14. Тогда 1A5E можно представить в десятичной системе счисления как 1*16

3 + 10*16² + 5*16¹ + 14*16⁰ = 6750. Однако для оценки шестнадцатеричных чисел вовсе не обязательно переводить их в десятичные. Правила сравнения, сложения и умножения в этой системе такие же как и в десятичной, главное не забывать, что каждый разряд может содержать значения от 0 до 15. Для более быстрого перевода числе между система счисления можно воспользоваться стандартным калькулятором в Windows, для этого достаточно в расширенном режиме калькулятора выбрать систему счисления, ввести в ней число и выбрать нужную систему счисления, в которой следует отобразить результат.

Так как шестнадцатеричные числа, состоящие только из чисел, легко спутать с десятичными, их обычно помечают так, чтобы было ясно, что используется именно шестнадцатеричная запись. Шестнадцатеричные записи обычно помечают либо добавлением в конец строчной буквы „h”, либо приставки „0x” перед записью числа. Таким образом шестнадцатеричное число 1A5E  может быть записано как 1A5Eh или 0x1A5E, где „h” на конце или „0x” в начале обозначают, что используется шестнадцатеричная запись.

Шестнадцатеричные числа

Шестнадцатеричные числа в основании системы счисления имеют 16 символов, это числа от 0 до 9 и буквы английского алфавита от А до F:

16-ричное	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
10-ричное	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15

Шестнадцатеричные числа всегда используются при отображении адресов и ссылок на память. Большие значения также можно выразить с помощью шестнадцатеричных чисел, используя всего несколько цифр, причем эти цифры легко преобразовать в двоичные значения. Шестнадцатеричные значения используются при написании программ для MASM и TASM. Для выделения шестнадцатеричных чисел используется буква «h» в конце числа. Например, 45h является шестнадцатеричным числом, тогда как 45 – десятичным.

Преобразование двоичных чисел в шестнадцатеричные

В таблице 2 показано соответствие двоичных чисел шестнадцатеричным цифрам. Большое двоичное число можно легко выразить с помощью шестнадцатеричных цифр.

Таблица 2. Соответствие двоичных и шестнадцатеричных чисел

Двоичное	Шестнадцетеричное	Двоичное	Шестнадцетеричное
0000	0	1000	8
0001	1	1001	9
0010	2	1010	A
0011	3	1011	B
0100	4	1100	C
0101	5	1101	D
0110	6	1110	E
0111	7	1111	F

Например, двоичное число 10101011100101111000011011100101 может быть легко представлено шестнадцатеричным значением АВ9786Е5:

А	В	9	7	8	6	Е	5
1010	1011	1001	0111	1000	0110	1110	0101

Преобразовывать шестнадцатеричное число в двоичное также очень легко, поскольку существует взаимно-однозначное соответствие между шестнадцатеричной цифрой и четырьмя двоичными разрядами. Например:

8А2640=	1000	1010	0010	0110	0100	0000
	8	А	2	6	4	0

Несколько примеров:

0AF6h = 0000101011110110

D58Ch = 1101010110001100

F13Bh = 1111000100111011

Преобразование шестнадцатеричныx чисел в десятичные

Каждая позиция цифры в шестнадцатеричном числе соответствует степени числа 16. Например:

24C2h = 2*16³+4*16²+12*16¹+2*16⁰ = 8192+1024+192+2 = 9410

Преобразование десятичных чисел в шестнадцатеричные

Последовательное деление на 16. Необходимо осуществить первое деление, после чего необходимо с полученным частным снова произвести деление, а полученный результат снова разделить на 16 и т. д. Остаток от каждого деления будет очередной шестнадцатеричной цифрой. Пример:

Десятичное число 12 268:

15 268 / 16 = 954, остаток 4

954 / 16 = 59, остаток 10 (А)

59 / 16 = 3, остаток 11 (В)

3 / 16 = 0, остаток 3

——————————————————

Шестнадцетеричное: 3ВА4

Числа со знаком

Двоичные числа могут быть как со знаком (signed), так и без знака (unsigned). Числа без знака используют все восемь битов для получения значения. Например, 11111111=255. Проссумировав значения всех битов, получим максимально возможное значение, которое может хранить байт без знака (255). Для слова без знака это значение будет составулять 65 535.

Перевод чисел в позиционных системах счисления. 10-й класс

Цели:

Образовательные: изучение и усвоение нового материала: восьмеричная и шестнадцатеричная системы счисления;

изучение и усвоение нового материала: перевод чисел в восьмеричную и шестнадцатеричную системы счисления и наоборот.

Воспитательные:

• повышение мотивации учащихся путем использования нестандартных задач;
• обеспечение сознательного усвоения материала.

Развивающие:

• развитие мышления при помощи задач;
• совершенствование умственной деятельности с привлечением устного счета.

Опорные понятия:

• язык,
• алфавит,
• система счисления,
• позиционная и непозиционная системы,
• основание системы.

Задачи учителя:

• познакомить с восьмеричной и шестнадцатеричной системами счисления;
• научить переводу чисел в восьмеричную и шестнадцатеричную системы счисления и наоборот.

План урока:

1. Организационный момент. Объявление темы урока.
2. Повторение пройденного материала.
3. Объяснение нового материала.
4. Физпауза.
5. Объяснение нового материала.
6. Проверочная работа (на усмотрение учителя).
7. Решение примеров.
8. Подведение итогов урока.
9. Домашнее задание.

ПРОВЕДЕНИЕ УРОКА

1. Организационный момент.

2. Повторение (устный опрос).

а) Что называется знаком?

б) Что называется символом?

в) Что называется алфавитом?

г) Какие вы знаете алфавиты?

д) Какие вы знаете наборы знаков, для которых нет какого-то порядка?

е) Назовите наборы, состоящие из двух знаков.

ж) Какие технические коды возникли с появлением электрического тока?

3. Объяснение нового материала.

Системы счисления, родственные двоичной

При работе с компьютерами приходится иметь дело с двоичными числами, поскольку двоичные числа заложены в конструкцию компьютера. Двоичная система удобна для компьютера, но неудобна для человека – числа получаются очень длинными и их трудно записывать и запоминать. Конечно, можно перевести двоичное число в десятичную систему и записать его в таком виде, а потом, когда оно понадобится, перевести его обратно, но все эти переводы очень трудоемки. Поэтому в современных компьютерах помимо двоичной системы счисления применяют и другие, более компактные по длине чисел системы – восьмеричная и шестнадцатеричная. Перевод из родственной системы в двоичную и обратно может быть мгновенно выполнен в уме.

Восьмеричная система счисления

В этой системе 8 цифр: 0, 1, 2, 3, 4, 5, 6, 7, сама восьмерка (как и двойка в двоичной системе) записывается совокупностью цифр “один” и “ноль” (10О, где буква О – обозначает восьмеричную систему счисления). Цифра 1, записанная в самом младшем разряде, означает – как и в десятичном числе – просто единицу. Та же цифра 1 в следующем разряде означает 8, в следующем – 64 и т.д. Число 100₈ есть не что иное, как 64₁₀, а число 611₈ равно 6*64₁₀ + 1*8₁₀ + 1 = 393₁₀.

Примеры:

1) 502О = 5*8² + 0*8¹ + 2*8⁰ = 5*64 + 0 +2 = 320 + 2 = 322D;

2) 3602О =3*8³ + 6*8² + 0*8¹ + 2*8⁰ = 3*512 + 6*64 + 0*8 + 2*1 = 1536 + 384 + 0 + 2 = 1922D

Для замены десятичного целого числа на равное ему восьмеричное число используется алгоритм последовательного деления этого числа на 8.

Примеры: записать число 317 и 1922 в восьмеричной системе счисления.

Итак, имеем: 317D = 475О; 1922D = 3602О.

Рассмотрим правило замены двоичного числа на равное ему восьмеричное, предварительно рассмотрев таблицу, в которой каждой восьмеричной цифре поставлено в соответствие трехзначное двоичное число:

Восьмеричная цифра	Двоичное число	Восьмеричная цифра	Двоичное число
0	000	4	100
1	001	5	101
2	010	6	110
3	011	7	111

(Можно предложить учащимся самим предложить заполнить данную таблицу).

Удобство применения восьмеричной системы при работе с машинно-ориентированной информацией заключается в том, что переход от восьмеричной записи числа к двоичной осуществляется очень просто:

Каждую цифру восьмеричной записи следует заменить ее двоичным представлением (соответствующей двоичной триадой, т.е. трехразрядным числом).

Например:

Достаточно прост и обратный переход от двоичного представления какого-либо числа к восьмеричному:

Для этого в двоичной записи числа нужно выделить триаду (влево и вправо от запятой) и заменить каждую триаду соответствующей восьмеричной цифрой. В случае необходимости неполные триады дополняются нулями.

Например:

 

Задание.

1) Переведите число 611₈ в двоичную систему.
 

2) Переведите двоичные числа в восьмеричные.
111 111 111₂ = 777₈, 11 111 101 001₂= 3751₈

4. Физпауза.

5. Объяснение нового материала.

Шестнадцатеричная система счисления

Запись числа в 8-ричной системе достаточна компактна, но еще компактнее она получается в 16-ричной системе. В этой системе счисления данные (например, содержимое ячеек памяти – это 8-разрядные двоичные числа) представляются уже в виде двухразрядных чисел, а адреса – в виде максимум четырехразрядных. Для первых 10 из 16 шестнадцатеричных цифр используют привычные цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, а для остальных 6 цифр используют первые буквы латинского алфавита:

A – 10,  D – 13,

B – 11,  E – 14,

C – 12,  F – 15.

Цифра 1, записанная в самом младшем разряде, означает просто единицу. Та же цифра 1 в следующем разряде означает 16₁₀, в следующем – 256₁₀ и т.д. Цифра F, записанная в самом младшем разряде, означает 15₁₀, в следующем разряде – 15₁₀*16₁₀ и т.д. Число 100₁₆ есть не что иное, как 256₁₀, а число AF0₁₆ равно 10₁₀*16²₁₀ + 15₁₀*16₁₀ = 2800₁₀.

Часто нижний индекс 16 опускают, например, вместо BAD₁₆ пишут просто BAD и это не приводит к ПЛОХИМ последствиям, поскольку в каждый момент понятно, о чем говорится – о числе или об английском слове bad (плохой).

Переход от шестнадцатеричной записи числа к двоичной осуществляется:

Каждую цифру шестнадцатеричной записи следует заменять соответствующей ей двоичной тетрадой. Неполные тетрады дополняются нулями. Разбивку производят для целой части числа – справа налево, а дробной – слева направо от запятой. Каждую из этих тетрад (групп) обозначают соответствующим символом:

Десятичные цифры	16-ричная запись	Двоичная запись	Десятичные цифры	16-ричная запись	Двоичная запись
0	0	0000	8	8	1000
1	1	0001	9	9	1001
2	2	0010	10	A	1010
3	3	0011	11	B	1011
4	4	0100	12	C	1100
5	5	0101	13	D	1101
6	6	0110	14	E	1110
7	7	0111	15	F	1111

Примеры:

Вопрос: Что обозначает буква “Н” после чисел?

Подведем итоги
Системы счисления, применяемые в ЭВМ

Система счисления	Основание	Алфавит	Примеры соответствия десятичным числам
Десятичная	10	0,1,2,3,4,5,6,7,8,9
Двоичная	8	1,0	A=11011; A=27
Восьмеричная	16	0,1,2,3,4,5,6,7	A=23; A=19
Шестнадцатеричная	2	0,1,2,3,4,5,6,7,8,9, A,B,C,D,E,F	A=2B; A=43

Можно предложить эту таблицу составить самим учащимся.

6. Проверочная работа ( проводить на этом или на следующем уроке – на усмотрение учителя).

Перед вами рисунок геометрической фигуры, в углах которой разбросаны кружочки с парами букв. Здесь зашифрована известная русская поговорка. Попытайтесь прочесть ее, двигаясь с помощью двоичных цифр в определенной последовательности.

Ответ: Что посеешь, то и пожнешь.

7. Решение примеров.

1) Перевести число 15FC₁₆ в двоичную систему.

2) Перевести двоичное число 110111101011101111 в шестнадцатеричную систему.

3) Представьте следующие десятичные числа в виде позиционной записи:

576
1924
12,5

4) Имеются позиционные записи десятичных чисел. Чему равны сами числа?

8*10² + 5*10¹ + 3*10⁰ + 7*10^-1 + 6*10^-2 (853,76)

0*10⁴ + 1*10³ + 8*10² + 4*10¹ + 0*10⁰ + 0*10^-1 + 9*10^-2(01840,09=1840,09)

9*10⁵ + 4*10³ + 3*10⁰ + 4*10^-2 + 4*10^-3 (904003,044)

5) Переведите в двоичную запись десятичные числа:

17 ; 49; 63

6) Переведите в десятичную запись двоичные числа:

1001
1101
10101

8. Домашнее задание

1. Примеры, которые не успели решить на уроке.

2. Следующие двоичные числа расположите в порядке возрастания: 1001, 111, 100001, 010, 1101, 100, 110000, 10001.

Шестнадцатеричные цифры, преобразование шестнадцатеричного числа в десятичное

Умение преобразовывать шестнадцатеричные числа может быть полезно не только программистам, но и дизайнерам, ведь триада RRGGBB есть не что иное, как «машинные» компоненты для красного, зелёного и синего соответственно — от 0 до 255 каждое. Конечно, графические редакторы содержат палитры со встроенными преобразователями, а стандартный калькулятор операционной системы умеет справляться с этой задачей, но порой гораздо удобнее самому «накинуть +14» к требуемой компоненте, а не запускать сторонние программы.

Прежде, чем я покажу, как (легко) можно переводить числа из шестнадцатеричной системы и более привычную для нас, необходимы дополнительные мероприятия. Все мы в школе учили таблицу умножения, и можем убедиться, что данный навык остался (хотя некоторые им в повседневной жизни не пользуются). Теперь же потребуется немного углубить знания, выучив её вплоть до 16 × 16.

И последнее: я убеждён, что рядовому пользователю эти навыки не понадобятся с вероятностью 99.…%. В общем, вы предупреждены .

Таблица умножение от 11 до 16

11 11 × 2 = 22 11 × 3 = 33 11 × 4 = 44 11 × 5 = 55 11 × 6 = 66 11 × 7 = 77 11 × 8 = 88 11 × 9 = 99 11 × 10 = 110 11 × 11 = 121 11 × 12 = 132 11 × 13 = 143 11 × 14 = 154 11 × 15 = 165 11 × 16 = 176	12 12 × 2 = 24 12 × 3 = 36 12 × 4 = 48 12 × 5 = 60 12 × 6 = 72 12 × 7 = 84 12 × 8 = 96 12 × 9 = 108 12 × 10 = 120 12 × 11 = 132 12 × 12 = 144 12 × 13 = 156 12 × 14 = 168 12 × 15 = 180 12 × 16 = 192	13 13 × 2 = 26 13 × 3 = 39 13 × 4 = 52 13 × 5 = 65 13 × 6 = 78 13 × 7 = 91 13 × 8 = 104 13 × 9 = 117 13 × 10 = 130 13 × 11 = 143 13 × 12 = 156 13 × 13 = 169 13 × 14 = 182 13 × 15 = 195 13 × 16 = 208
14 14 × 2 = 28 14 × 3 = 42 14 × 4 = 56 14 × 5 = 70 14 × 6 = 84 14 × 7 = 98 14 × 8 = 112 14 × 9 = 126 14 × 10 = 140 14 × 11 = 154 14 × 12 = 168 14 × 13 = 182 14 × 14 = 196 14 × 15 = 210 14 × 16 = 224	15 15 × 2 = 30 15 × 3 = 45 15 × 4 = 60 15 × 5 = 75 15 × 6 = 90 15 × 7 = 105 15 × 8 = 120 15 × 9 = 135 15 × 10 = 150 15 × 11 = 165 15 × 12 = 180 15 × 13 = 195 15 × 14 = 210 15 × 15 = 225 15 × 16 = 240	16 16 × 2 = 32 16 × 3 = 48 16 × 4 = 64 16 × 5 = 80 16 × 6 = 96 16 × 7 = 112 16 × 8 = 128 16 × 9 = 144 16 × 10 = 160 16 × 11 = 176 16 × 12 = 192 16 × 13 = 208 16 × 14 = 224 16 × 15 = 240 16 × 16 = 256

Следующим шагом необходимо соотнести десятичные числа от 10 до 15 с шестнадцатеричными цифрами от A до F.

Таблица соответствия шестнадцатеричных цифр

HEX (шестнадцатеричная)	DEC (десятичная)
0	0
1	1
2	2
3	3
4	4
5	5
6	6
7	7
8	8
9	9
A	10
B	11
C	12
D	13
E	14
F	15

А теперь вспомним поразрядное умножение из предыдущей статьи, для цифры 7. Здесь будет лишь поправка на другую систему счисления (не на 10, как там, а на 16).

Обычно в компьютерной литературе, для однозначного указания основания системы счисления, применяется следующая нотация:
— шестнадцатеричное число — 0x100 (256 в десятичной, признак — 0x в начале)
— десятичное число — 100 (наша, человеческая, система счисления)
— восьмеричное число — 0100 (64 в десятичной, признак — ведущий ноль)
— двоичное число — 0b100 (4 в десятичной, признак — 0b в начале)

Преобразование шестнадцатеричного числа в десятичное

Для начала, небольшой рисунок:

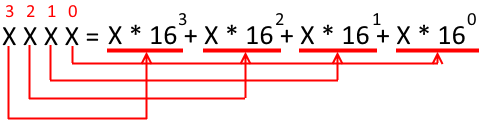
Для преобразования требуется каждую цифру числа умножить на «разряд», в котором оно находится. Из курса начальной школы мы помним, что позиции, занимаемые в числовой строке, называются (справа налево) единицы, десятки, сотни и т. д. Здесь почти то же самое, но с поправкой на систему счисления. Каждый следующий разряд — это +1 степень текущей системы счисления. Любое число в степени ноль — это ноль, в степени 1 — самом число, в степени 2 (квадрат) — число, умноженное само на себя и т. д.

Для наглядности привожу пример. Допустим, возьмём шестнадцатеричное число 0x1F8. Нам требуется перевести его в десятичную систему, поэтому запишем (0x — это признак основания!):

1F8₁₆ = 1₁₆ × 16² + F₁₆ × 16¹ + 8₁₆ × 16⁰ = 1 × 256 + 15 × 16 + 8 × 1 = 256 + 240 + 8 = 504

Обе таблички нам пригодились: благодаря второй мы переводим числа из шестнадцатеричной системы в десятичную, благодаря первой — легко перемножаем «больше» числа.

Небольшое отступление

А знаете ли вы, что у нас сейчас могла бы использоваться двенадцатеричная система счисления, используемая ещё шумерцами? По одной и версий, этому способствовало количество фаланг пальцев руки. Взгляните на рисунок:

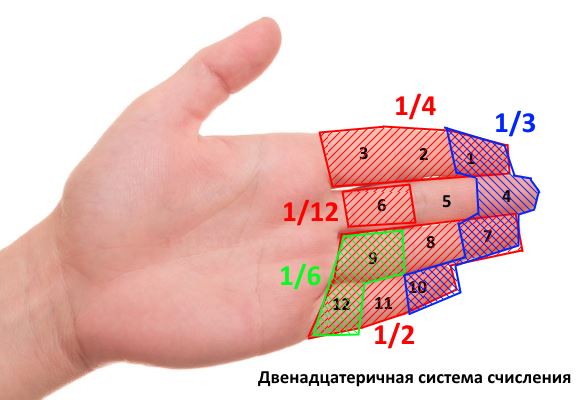
Скорее всего, вам сложно это представить. Но, взглянув на это под другим углом, можем убедиться, что выбор был бы очень хорош, ведь 12 делится без остатка на 2, 3, 4, 6 (в то время, как 10 можно разделить лишь на 2 и 5). Естественно, умножения и деления на степень числа 12 были так же просты, как сейчас аналогичные операции для степени числа 10.

Выучив эти таблицы, любой человек легко сможет переводить компьютерные байты в привычные числа. При желании, как следует потренировавшись и «расширив объём» краткосрочной памяти, станут доступны и более сложные варианты. Но, как уже говорилось чуть ранее, манипуляции с байтами мало кому нужны, не говоря о чём-то большем.

Автор публикации

2 065

не в сети 3 часа

x64 (aka andi)

Комментарии: 2888Публикации: 405Регистрация: 02-04-2009 Загрузка…