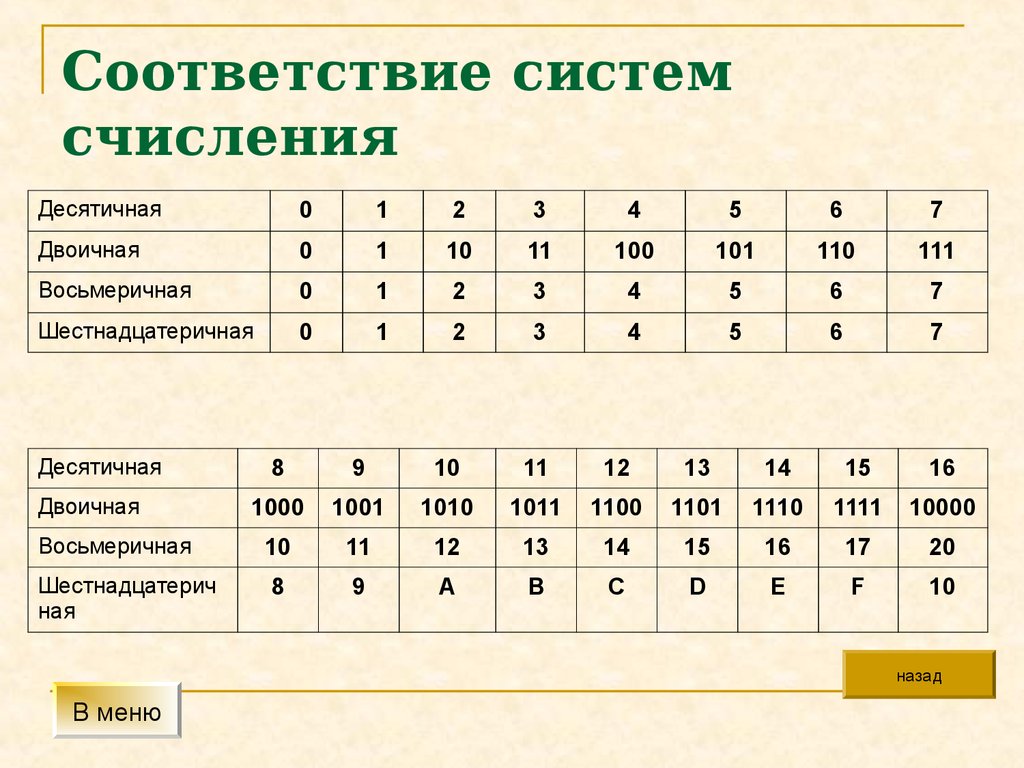
Шестеричная система счисления

Содержание:
Что такое шестеричная система счисления
Как перевести целое десятичное число в шестеричную систему счисления
Как перевести десятичную дробь в шестеричную систему счисления
Как перевести число из шестеричной системы счисления в десятичную
Как перевести дробное шестеричное число в десятичное
Таблица значений десятичных чисел от 0 до 100 в шестеричной системе счисления

Шестеричная система счисления, является позиционной системой счисления, то есть имеется зависимость от позиции цифры в записи числа. Для записи числа в шестеричной системе счисления используется шесть цифр 0, 1, 2, 3, 4 и 5. Для определения в какой системе счисления записано число, внизу, справа от числа ставят цифру, которая называется основанием системы счисления. Например, 3353₆ или 215₆

Если вам необходимо перевести число любой системы счисления в другую систему счисления, воспользуйтесь калькулятором систем счисления с подробным решением онлайн.

Как перевести целое десятичное число в шестеричную систему счисления

Для того, чтобы перевести целое десятичное число в шестеричную систему счисления нужно десятичное число делить на 6 до тех пор, пока неполное частное не будет равно нулю. В результате будет получено число из остатков деления записанное справа налево.

Например, переведем число 115₁₀ в шестеричную систему счисления:

115 : 6 = 19 остаток: 1
19 : 6 = 3 остаток: 1
3 : 6 = 0 остаток: 3

115₁₀ = 311₆

Как перевести десятичную дробь в шестеричную систему счисления

Для того чтобы перевести десятичную дробь в шестеричную систему счисления необходимо сначала перевести целую часть десятичной дроби в шестеричную систему счисления, а затем дробную часть, последовательно умножать на 6, до тех пор, пока в дробной части произведения не получиться ноль (результатом произведения будет целое число) или не будет достигнуто необходимое количество знаков после запятой. Если в результате умножения целая часть не равна нулю, тогда необходимо заменить значение целой части на ноль. В результате будет получено число из целых частей произведений, записанное слева направо.

Например, переведем десятичное число 95.36₁₀ в шестеричную систему счисления:

Переведем целую часть

95 : 6 = 15 остаток: 5
15 : 6 = 2 остаток: 3
2 : 6 = 0 остаток: 2

95₁₀ = 235₆

Переведем дробную часть

0.36 · 6 = 2.16
0.16 · 6 = 0.96
0.96 · 6 = 5.76
0.76 · 6 = 4.56
0.56 · 6 = 3.36
0.36 · 6 = 2.16
0.16 · 6 = 0.96
0.96 · 6 = 5.76
0.76 · 6 = 4.56
0.56 · 6 = 3.36

0.36₁₀ = 0.2054320543

6
95.36₁₀ = 235.2054320543₆

Шестеричные дроби, как и десятичные могут быть как конечными, так и бесконечными. Не всегда конечная десятичная дробь может быть представлена конечной шестеричной. В данном примере получается бесконечная периодическая шестеричная дробь, поэтому умножение на 6 можно производить бесконечное число раз и все равно дробная часть частного не будет равна нулю. В данном случае десятичная дробь 95.36 не может быть точно представлена в шестеричной системе счисления. К примеру, дробь 2.5

10 может быть представлена в двоичной системе счисления в виде конечной 2.5₁₀ = 2.3₂.

Как перевести число из шестеричной системы счисления в десятичную

Для того, чтобы перевести число из шестеричной системы счисления в десятичную систему счисления, необходимо записать позиции каждой цифры в числе с права на лево начиная с нуля. Каждая позиция цифры будет степенью числа 6, так как система счисления 6-ичная. Необходимо последовательно умножить каждое число на 6 в степени соответствующей позиции числа и затем сложить с последующим произведением следующего числа в степени соответствующей его позиции.

Например, переведем число 50421₆ в десятичную систему счисления:

Позиция в числе	4	3	2	1	0
Число	5	0	4	2	1

50421₆ = 5 ⋅ 6⁴ + 0 ⋅ 6³ + 4 ⋅ 6² + 2 ⋅ 6¹ + 1 ⋅ 6⁰ = 6637₁₀

Как перевести дробное шестеричное число в десятичное

Для того, чтобы перевести дробное шестеричное число в десятичное, необходимо записать дробное шестеричное число, убрав точку и затем сверху расставить индексы. Индексы в дробной части числа начинаются от -1 и продолжаются на уменьшение вправо, индексы в целой части начинаются с 0 и ставятся с права на лево по возрастанию. Каждая позиция цифры (индекс) будет степенью числа 6, так как система счисления 6-ичная. Необходимо последовательно умножить каждое число на 6 в степени соответствующей позиции числа и затем сложить с последующим произведением следующего числа в степени соответствующей его позиции.

Например, переведем дробное шестеричное число 13.53₆ в десятичное:

Позиция в числе	1	0	-1	-2
Число	1	3	5	3

13.53₆ = 1 ⋅ 6¹ + 3 ⋅ 6⁰ + 5 ⋅ 6^-1 + 3 ⋅ 6^-2 = 9.9166666666666666666666666669₁₀

Таблица значений десятичных чисел от 0 до 100 в шестеричной системе счисления

Значение числа в десятичной системе счисления	Значение числа в шестеричной системе счисления
010	06
110	16
210	26
310	36
410	46
510	56
610	106
710	116
810	126
910	136
1010	146
1110	156
1210	206
1310	216
1410	226
1510	236
1610	246
1710	256
1810	306
1910	316
2010	326
2110	336
2210	346
2310	356
2410	406
2510	416
2610	426
2710	436
2810	446
2910	456
3010	506
3110	516
3210	526
3310	536
3410	546
3510	556
3610	1006
3710	1016
3810	1026
3910	1036
4010	1046
4110	1056
4210	1106
4310	1116
4410	1126
4510	1136
4610	1146
4710	1156
4810	1206
4910	1216
5010	1226

Значение числа в десятичной системе счисления	Значение числа в шестеричной системе счисления
5110	1236
5210	1246
5310	1256
5410	1306
5510	1316
5610	1326
5710	1336
5810	1346
5910	1356
6010	1406
6110	1416
6210	1426
6310	1436
6410	1446
6510	1456
6610	1506
6710	1516
6810	1526
6910	1536
7010	1546
7110	1556
7210	2006
7310	2016
7410	2026
7510	2036
7610	2046
7710	2056
7810	2106
7910	2116
8010	2126
8110	2136
8210	2146
8310	2156
8410	2206
8510	2216
8610	2226
8710	2236
8810	2246
8910	2256
9010	2306
9110	2316
9210	2326
9310	2336
9410	2346
9510	2356
9610	2406
9710	2416
9810	2426
9910	2436
10010	2446

Шестеричная система счисления — Что вижу

На русских счетах есть особый ряд из четырёх костяшек. Выше находятся рубли, ниже два ряда копеек (Существует ещё вариант с тремя рядами снизу. Он помогает считать тысячные, но это только для математиков). Особый ряд нужен для подсчёта четвертинок. Число десять легко поделить пополам — для этого служат чёрные костяшки в середине ряда, но уже деление на четыре части требует манипуляций на двух рядах. Про деление на три лучше и не вспоминать, оно в десятичной системе записывается бесконечным числом цифр, а значит не может быть сделано на счётах.

В этот момент популяризаторы математики тяжело вздыхают: «Как жаль, что у человека на руке пять пальцев, а не шесть. Сложись иначе и мы бы считали не десятками, а дюжинами». Действительно, дюжина существенно удобнее в быту, поскольку легко делится на два, на три и на четыре. Она, конечно, не делится на пять, но деление на пять частей довольно редкий случай в торговле или в разрезании листа бумаги на открытки.

Надо заметить, что пять пальцев действительно повлияли на традиционные системы счёта.

Возьмём к примеру русский язык: один дом, два дом(А), три дом (А), четыре дом (А), но: пять дом(ОВ).

Римская запись чисел колебалась между пятью и десятью: I,II,III,IIII (IV — сокращённая на одну черту запись), V. Потом комбинации V и I, затем X. Продолжая дальше мы встречаем десять пятёрок L и десять десяток C. Пять пятёрок римляне пропустили, а зря.

Похожая система была и у индейцев майя, которые комбинировали единицы точки и пятёрки чёрточки:

Сегодня, пока я лежал в кресле стоматолога и пытался занять себя чем-нибудь полезным, мне в голову пришла мысль, что счёт шестёрками на пальцах даже более естественен, чем счёт пятёрками.

Подумайте об обычной десятичной записи: у нас есть цифры от 0 до 9, а второй разряд мы используем для записи первого числа (10), для которого у нет своей цифры.

Теперь следите за руками. Вот естественная запись чисел от нуля до шести

Дальше всё продолжается в том же духе. Вот семь, одиннадцать и искомая дюжина.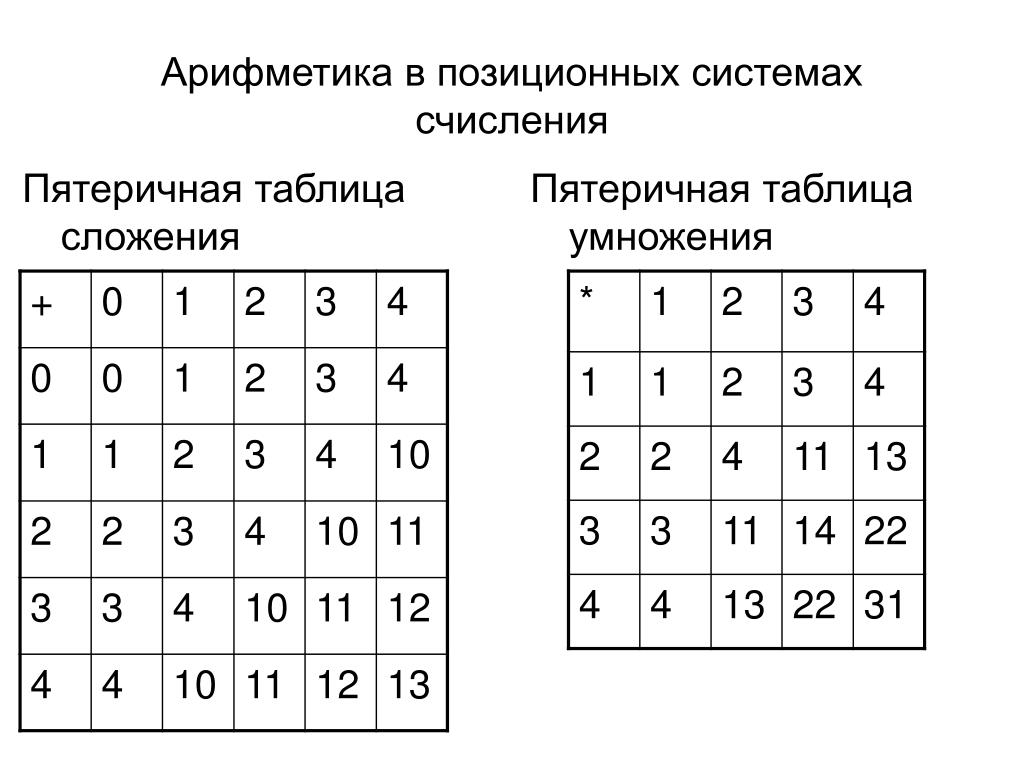

Если вы попробуете выполнить на пальцах сложение и вычитание, то обнаружите, что они происходят естественнее, чем если бы мы откладывали на левой руке традиционные пятёрки.

Предположим, что нам надо прибавить к пяти единицу. При счёте пятёрками мы показываем на левой руке один палец (полная пятёрка), сжимаем правую руку в кулак, а потом открываем на ней же один палец. При счёте шестёрками, мы открываем палец на левой руке, сжимаем правую в кулак и … всё! Получается, что при счёте шестёрками нам надо выполнить на одну операцию меньше, а значит меньше шанс ошибиться. С вычитанием та же история — одним загибанием пальца меньше.

Если бы у французских математиков, вводивших революционную метрическую систему мер было бы чуть больше воображения, то наполеоновская Европа перешла бы на двенадцатеричную систему мер, а дальше к ней с удовольствием подтянулись бы и англоговорящие страны, поскольку в шиллинге 12 пенсов, в футе 12 дюймов и это естественно!

В комментариях подсказали про ещё один (десятичный) вариант «Кафрский счёт»

Что такое шестнадцатеричная нумерация?

По

• Рахул Авати

Что такое шестнадцатеричный формат?

Шестнадцатеричная система счисления с основанием 16. Она может использоваться для представления больших чисел с меньшим количеством цифр.

В этой системе имеется 16 символов или возможных числовых значений от 0 до 9, за которыми следуют шесть буквенных символов — A, B, C, D, E и F. Эти символы используются для представления десятичных значений от 10 до 15 в одиночном разряде. биты.

Сравнение двоичной, десятичной и шестнадцатеричной нумерации

Шестнадцатеричное объяснение

Шестнадцатеричная, также известная как Base 16 или hex, — это одна из четырех систем счисления. Остальные три — десятичные (по основанию 10), двоичные (по основанию 2) и восьмеричные (по основанию 10).

Вот как выглядят десятичная и шестнадцатеричная системы для цифр от 0 до 15.

Десятичный	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Шестнадцатеричный	0	1	2	3	4	5	6	7	8	9	А	Б	С	Д	Е	Ф

Шестнадцатеричная система содержит 16 последовательных чисел в качестве основных единиц, включая 0. Первые девять чисел (от 0 до 9) — это те же самые числа, которые обычно используются в десятичной системе. Следующие шесть двузначных чисел (от 10 до 15) представлены буквами от A до F. Вот как в шестнадцатеричной системе используются числа от 0 до 9.и заглавные буквы от A до F для обозначения эквивалентного десятичного числа.

В этой системе нумерации каждая позиция цифры в 16 раз значительнее, чем цифра в предыдущей позиции. Шестнадцатеричный номер начинается с младшей значащей цифры справа. Числовое значение этого числа вычисляется путем умножения каждой цифры на значение ее позиции и последующего сложения произведений. Вот почему шестнадцатеричное число — это позиционное или взвешенное число 9.Система 0182.

Необходимость шестнадцатеричных чисел

В вычислительных системах двоичные строковые эквиваленты больших десятичных чисел могут стать довольно длинными. Когда речь идет о 16- или 32-битных числах, становится трудно читать и записывать их без ошибок.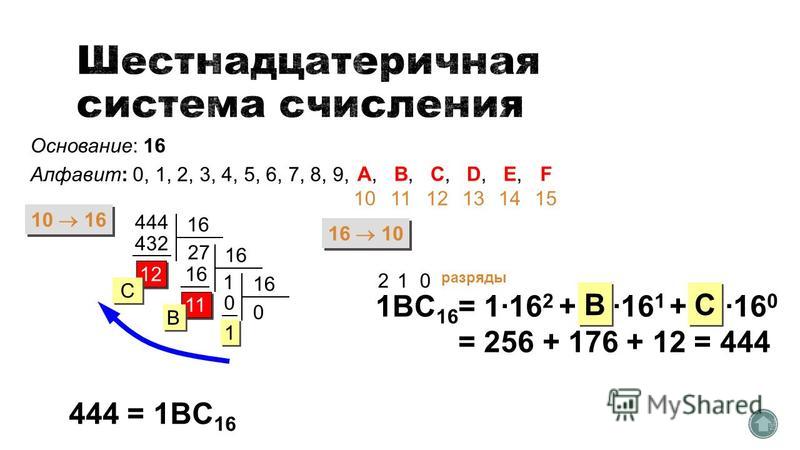 Эти проблемы можно решить, разбив двоичные числа на группы по четыре бита, т. е. используя шестнадцатеричную систему счисления.

Формат шестнадцатеричных чисел более компактен, чем двоичные числа, поскольку они могут представлять большие двоичные числа с меньшим количеством цифр. В результате их легче понять, чем длинные двоичные строки из 1 и 0.

Представление шестнадцатеричных чисел

В шестнадцатеричном формате четыре цифры двоичного числа могут быть представлены одной шестнадцатеричной цифрой. Разделение двоичного числа на 4-битные наборы означает, что каждый набор может иметь возможное значение от 0000 до 1111, допуская 16 комбинаций чисел от 0 до 15. При базовом значении 16 максимальное значение цифры равно 15.

Легко преобразовать двоичное число в шестнадцатеричное и наоборот. Вот как эти числа представлены в каждой системе:

Шестнадцатеричный номер	0	1	2	3	4	5	6	7
4-битное двоичное число	0000	0001	0010	0011	0100	0101	0110	0111

Шестнадцатеричный номер	8	9	А	Б	С	Д	Е	Ф
4-битное двоичное число	1000	1001	1010	1011	1100	1101	1110	1111

Кроме того, цифры слева от шестнадцатеричной точки имеют веса 16 ⁰ , 16 ¹ , 16 ² и так далее. Точно так же позиции справа имеют веса 16 ^-1 , 16 ^-2 и т. д.

Пример

Для представления десятичного числа 512 в шестнадцатеричном виде:

Десятичное значение = 512

512 = 2×16 ² +0x16 ¹ +0x160=200

Шестнадцатеричное значение = 200

Преобразование двоичных и десятичных чисел в шестнадцатеричные

1. Преобразование двоичного кода в шестнадцатеричный

Для преобразования двоичных чисел в шестнадцатеричные четыре двоичные цифры должны быть преобразованы или преобразованы в одну шестнадцатеричную цифру. Вот как работает преобразование:

1. Разделить двоичное значение на группы по четыре, начиная с крайней правой цифры.
2. Сопоставьте каждую группу из четырех с соответствующим шестнадцатеричным значением.
3. Представляет исходное двоичное число в шестнадцатеричном формате.

Пример

Вот как преобразовать двоичное число 1011010101100001 в шестнадцатеричную форму:

Шаг 1: Разделите двоичное значение на группы по четыре.

1011

0101

0110

0001

Шаг 2: Замените каждый набор шестнадцатеричным значением.

1011	0101	0110	0001
Б	5	6	1

Шаг 3: Представьте двоичный файл в шестнадцатеричном виде

1011010101100001 ₂ = B561 ₁₆

1. Преобразование десятичного числа в шестнадцатеричное

Процесс преобразования десятичного числа в шестнадцатеричное прост, хотя шагов больше:

1. Разделить десятичное число на 16.
2. Запишите остаток в шестнадцатеричной форме.
3. Разделить результат на 16.
4. Повторяйте шаги 2 и 3, пока результат не будет равен 0,

Полученное шестнадцатеричное значение представляет собой последовательность остатков от последнего к первому.

Пример

Вот как преобразовать десятичное число 1128 в шестнадцатеричное:

Шаг 1: Разделите 1128 на 16, чтобы получить результат 70 и остаток 8.

Шаг 2: Разделите результат (70) на 16, чтобы получить новый результат 4 и остаток 6.

Шаг 3: Разделите результат (4) на 16, чтобы получить результат 0 и остаток 4.

Шаг 4: Представьте шестнадцатеричное число как последовательность остатков от последнего к первому.

1128 ₁₀ = 468 ₁₆

Шестнадцатеричные идентификаторы

Шестнадцатеричные числа обычно имеют префикс или суффикс с идентификаторами, чтобы избежать путаницы при чтении или записи и упростить отличить шестнадцатеричные числа от десятичных чисел. Некоторые распространенные шестнадцатеричные идентификаторы включают:

.

Идентификатор	Применение	Пример
%	Обычно используется в URL-адресах для указания символов, таких как пробелы	%2
#	Используется в языке HTML в качестве ссылки на цвет	#RR5687
0ч	Используется в программируемых графических калькуляторах	0h7D
\х	Используется в HTML, XML и других языках для выражения кодов управления символами	\x08: Возврат \x1B: Выход
0x	Используется в UNIX и программировании на языке C	0x54EF

Также доступны другие идентификаторы; однако они обычно ограничены конкретными языками программирования и не могут использоваться взаимозаменяемо с другими языками.

Шестнадцатеричные приложения

Шестнадцатеричная система счисления особенно полезна в компьютерном программировании и микропроцессорах. Разработчики используют его для описания цветов на веб-страницах, описания областей памяти для каждого байта, указания определенных символов и многого другого. Шестнадцатеричные числа также используются в микроконтроллерах для упрощения обработки данных и манипулирования ими. Другими возможными приложениями являются наука о данных и аналитика, машинное обучение и искусственный интеллект.

Шестнадцатеричные преимущества и недостатки Шестнадцатеричные числа

компактны и занимают меньше памяти, поэтому в компьютерных системах можно хранить больше чисел. Их небольшой размер также упрощает обработку ввода-вывода по сравнению с другими форматами нумерации. Поскольку легко преобразовать шестнадцатеричное число в двоичное и наоборот, система широко используется в компьютерном программировании. Также полезно представлять адреса памяти компьютера.

Одним из недостатков шестнадцатеричной системы счисления является сложность выполнения сложных математических операций, таких как умножение и деление. Шестнадцатеричные числа также труднее читать и записывать по сравнению с десятичными числами.

See also: Shared Key Authentication , Blowfish , network packet , big-endian and little-endian , globally unique identifier , universally unique идентификатор

Последнее обновление: июнь 2022 г.

Продолжить чтение о шестнадцатеричном формате

• Объяснение двоичных и шестнадцатеричных чисел для разработчиков

• Используйте эти надстройки PowerShell, чтобы улучшить свой опыт

• Обработка данных с дискретизацией признаков, стандартизация

• Почему 8 примитивных типов данных Java не являются объектами

• Блокчейн: неизменяемый реестр для замены базы данных

цифровое рабочее пространство

Цифровое рабочее пространство — это интегрированная технологическая структура, которая централизует управление корпоративными приложениями, данными и конечными точками, позволяя сотрудникам сотрудничать и работать удаленно.

• вариант использования
• отладка
• Общий свод знаний (CBK)
• CIDR (бесклассовая междоменная маршрутизация или суперсеть)
• Кило, мега, гига, тера, пета, экза, зетта и все такое
• съемный носитель
• Gmail
• курсор
• Тестирование API
• пагинация
• Битли
• резервное копирование на основе образа
• стоимость взаимодействия (CPE)
набор инструментов программного обеспечения
• прозрачность
• автокоррекция
• роботизированная хирургия (роботизированная хирургия)
• распределенная файловая система (DFS)
• ценообразование на основе использования
• цифровое рабочее пространство

ПоискСеть

• CIDR (бесклассовая междоменная маршрутизация или суперсеть)

  CIDR (бесклассовая междоменная маршрутизация или суперсеть) — это метод назначения IP-адресов, повышающий эффективность . ..

• пропускная способность

  Пропускная способность — это мера того, сколько единиц информации система может обработать за заданный промежуток времени.

• формирование трафика

  Формирование трафика, также известное как формирование пакетов, представляет собой метод управления перегрузкой, который регулирует передачу данных по сети путем задержки…

ПоискБезопасность

• Общий свод знаний (CBK)

  В области безопасности Общий свод знаний (CBK) представляет собой всеобъемлющую структуру всех соответствующих тем, которые необходимы специалисту по безопасности…

• опустошение буфера

  Опустошение буфера, также известное как опустошение буфера или перезапись буфера, возникает, когда буфер — временное удерживающее пространство …

• единый вход (SSO)

  Единый вход (SSO) — это служба аутентификации сеанса и пользователя, которая позволяет пользователю использовать один набор учетных данных для входа — для . ..

ПоискCIO

• ориентир

  Контрольный показатель — это стандарт или точка отсчета, которые люди могут использовать для измерения чего-либо еще.

• пространственные вычисления

  Пространственные вычисления широко характеризуют процессы и инструменты, используемые для захвата, обработки и взаимодействия с трехмерными данными.

• организационные цели

  Организационные цели — это стратегические задачи, которые руководство компании устанавливает для описания ожидаемых результатов и руководства …

SearchHRSoftware

• Поиск талантов

  Привлечение талантов — это стратегический процесс, который работодатели используют для анализа своих долгосрочных потребностей в талантах в контексте бизнеса …

• удержание сотрудников

  Удержание сотрудников — организационная цель сохранения продуктивных и талантливых работников и снижения текучести кадров за счет стимулирования . ..

• гибридная рабочая модель

  Гибридная модель работы — это структура рабочей силы, включающая сотрудников, работающих удаленно, и тех, кто работает на месте, в офисе компании…

SearchCustomerExperience

• стоимость взаимодействия (CPE)

  Цена за взаимодействие (CPE) — это модель ценообразования рекламы, при которой команды цифрового маркетинга и рекламодатели платят за рекламу только тогда, когда …

• B2C (Business2Consumer или Business-to-Consumer)

  B2C — сокращение от Business-to-Consumer — это модель розничной торговли, в которой продукты поступают непосредственно от предприятия к конечному пользователю, который …

• CRM (управление взаимоотношениями с клиентами) аналитика

  Аналитика CRM (управление взаимоотношениями с клиентами) включает в себя все программы, которые анализируют данные о клиентах и ​​представляют. ..

404: Страница не найдена

Страница, которую вы пытались открыть по этому адресу, похоже, не существует. Обычно это результат плохой или устаревшей ссылки. Мы приносим свои извинения за доставленные неудобства.

Что я могу сделать сейчас?

Если вы впервые посещаете TechTarget, добро пожаловать! Извините за обстоятельства, при которых мы встречаемся. Вот куда вы можете пойти отсюда:

Поиск

• Узнайте последние новости.
• Наша домашняя страница содержит самую свежую информацию о Java-разработке.
• Наша страница «О нас» содержит дополнительную информацию о сайте, на котором вы находитесь, TheServerSide.com.
• Если вам нужно, свяжитесь с нами, мы будем рады услышать от вас.

Поиск по категории

SearchAppArchitecture

• 10 учебных курсов для подготовки к сертификации по микросервисам

  Хотя получить сертификат по архитектуре микросервисов не всегда просто, существует множество курсов, которые вы можете пройти, чтобы . ..

• Признаки антипаттерна «Золотой молот» и 5 способов его избежать

  Антипаттерн «Золотой молот» может подкрасться к команде разработчиков, но есть способы его обнаружить. Изучайте знаки, а также некоторые…

• Почему контрактное тестирование может быть необходимо для микросервисов

  Разработчики сталкиваются с многочисленными трудностями, пытаясь выполнить традиционное сквозное интеграционное тестирование микросервисов. Контракт…

ПоискПОКачество

• Amazon продвигает инструменты CodeWhisperer, AI и ML

  AWS выпустила обновления для ряда инструментов и сервисов ИИ, среди которых были улучшения в системе кодирования CodeWhisperer и …

• Небольшие проекты с открытым исходным кодом представляют значительные риски для безопасности

  Инициативы по обеспечению безопасности с открытым исходным кодом могут предотвратить крупномасштабные уязвимости, такие как Log4j, но небольшие проекты создают риски без. ..

• Увольнения разработчиков программного обеспечения и приостановка найма растут

  Поскольку технологические компании затягивают пояса, разработчики должны подготовиться к более жесткому рынку труда, обновляя резюме и расширяя вакансию …

SearchCloudComputing

• Сравните Azure Key Vault и секреты Kubernetes

  Секреты требуют определенного уровня обслуживания, такого как хранение, доставка и управление. Сравните услуги по этим критериям и узнайте…

• AWS присоединяется к Microsoft в обеспечении прозрачности цепочки поставок

  AWS обнаружил, что основной причиной, по которой компаниям сложно управлять цепочками поставок, является отсутствие прозрачности в сложных …

• Предварительный просмотр программы AWS re:Invent 2022

  Благодаря тому, что в этом году AWS re:Invent 2022 предлагает очные и виртуальные варианты, участники могут выбирать из ряда интерактивных . ..

ПоискБезопасность

• Lockbit 3.0 содержит код программы-вымогателя BlackMatter и червоточины

  LockBit 3.0 или «LockBit Black» включает функции защиты от отладки, возможность удаления файлов теневого копирования тома и …

• Ошибки Exchange Server вызвали многолетние проблемы с безопасностью

  Четыре известных набора уязвимостей безопасности в Microsoft Exchange Server, обнаруженные исследователем Оранж Цай, установлены…

• Риск и повторение: Твиттер, Илон Маск и проблемы безопасности

  В этом выпуске подкаста обсуждаются проблемы безопасности Twitter после приобретения Илона Маска в прошлом месяце, а также возможные данные…

ПоискAWS

• AWS Control Tower стремится упростить управление несколькими учетными записями

  Многие организации изо всех сил пытаются управлять своей огромной коллекцией учетных записей AWS, но Control Tower может помочь.