Сглаживающие фильтры: устройство, описание, схемы, диаграммы
Выпрямленное напряжение имеет существенные пульсации, поэтому широко используют сглаживающие фильтры − устройства, уменьшающие эти пульсации. Важнейшим параметром сглаживающего фильтра является коэффициент сглаживания S. По определению S = ε1 / ε2, причем ε1 и ε2 определяют как коэффициенты пульсаций на входе и выходе фильтра соответственно.
Для емкостного фильтра, у которого вход и выход фактически совпадают, под ε1 понимают коэффициент пульсаций до подключения фильтра, а под ε2 — коэффициент пульсаций после его подключения. Коэффициент сглаживания показывает, во сколько раз фильтр уменьшает пульсации. На выходе фильтра напряжение оказывается хорошо сглаженным, а коэффициент пульсаций может иметь значения в диапазоне 0,001 …. 0,00003.
Васильев Дмитрий Петрович
Профессор электротехники СПбГПУ
Задать вопрос
Простейшим фильтром является емкостной фильтр (С-фильтр).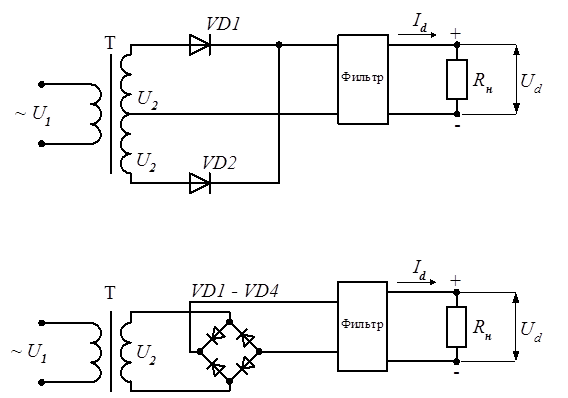 Рассмотрим его работу на примере однофазного однополупериодного выпрямителя (рис. 2.78). Емкостной фильтр подключают параллельно нагрузке (рис. 2.78, а).
Рассмотрим его работу на примере однофазного однополупериодного выпрямителя (рис. 2.78). Емкостной фильтр подключают параллельно нагрузке (рис. 2.78, а).
На отрезке времени t1 … t2диод открыт и конденсатор заряжается (рис. 2.78, б).
На отрезке t2 … t3диод закрыт, источник входного напряжения отключен от конденсатора и нагрузки. Разряд конденсатора характеризуется экспонентой с постоянной времени t = RhC. ток через диод протекает только часть полупериода (отрезок t1 … t2). Чем короче отрезок t1 … t2, тем больше амплитуда тока диода при заданном среднем токе нагрузки.
Абрамян Евгений Павлович
Доцент кафедры электротехники СПбГПУ
Задать вопрос
Если емкость С очень велика, то отрезок t1 … t2 оказывается очень малым, а амплитуда тока диода очень большой, и диод может выйти из строя. Такой фильтр широко используется в маломощных выпрямителях; в мощных выпрямителях он используется редко, так как режим работы диода и соответствующих электрических цепей (к примеру, обмоток трансформатора) достаточно тяжел.
В качестве фильтра можно использовать и индуктивность. Легко доказать, что индуктивный фильтр (L-фильтр) практически не дает полезного эффекта в однофазном однополупериодном выпрямителе. Рассмотрим работу индуктивного фильтра на примере однофазного мостового выпрямителя. Индуктивный фильтр включают последовательно с нагрузкой (рис. 2.79, а). Часто используют катушку индуктивности (реактор) на магнитном сердечнике с зазором.
Предположим, что постоянная времени T, определяемая выражением T= L/Rh, достаточно велика (как это обычно бывает на практике). Тогда ток нагрузки оказывается практически постоянным (рис. 2.79, б).
Такой фильтр широко используется в выпрямителях, особенно мощных. Режим работы диодов (и соответствующих электрических цепей) не является тяжелым.
Н а практике используют также следующие типы фильтров (рис. 2.80): индуктивно-емкостной или Г-образный LC-фильтр (а), Г-образный RС-фильтр (б), П-образный LС-фильтр (в), П-образный RС-фильтр (г).
Обычно Г- и П-образные RC-фильтры применяются только в маломощных схемах, так как они потребляют значительную долю энергии. На практике применяют и другие, более сложные фильтры.
Внешние характеристики выпрямителей с фильтрами.
Внешняя характеристика— это зависимость среднего значения выходного напряжения (напряжения на нагрузке) от среднего значения выходного тока (тока нагрузки). При увеличении выходного тока выходное напряжение уменьшается из-за увеличения падения напряжения на обмотках трансформатора, диодах, подводящих проводах, элементах фильтра.
Рассмотрим типичные внешние характеристики (рис. 2.81), которые получают, изменяя сопротивление нагрузки, подключенное к выходу фильтра.
Наклон внешней характеристики при том или ином токе 1ср характеризуют выходным сопротивлением Rвыx, которое определяется выражением Rвыx = | dUср/dIср|Iср − заданный
Чем меньше величина Rвыx, тем меньше выходное напряжение зависит от выходного тока, что обычно и требуется.
Как следует из рис. 2.81, выпрямитель с RC-фильтром характеризуется повышенным выходным сопротивлением. Здесь отрицательную роль играет резистор фильтра.
Особенности сглаживающих фильтров, их схемы и пример расчета — Help for engineer
Особенности сглаживающих фильтров, их схемы и пример расчета
Для чего нужны сглаживающие фильтры?
Способ получения постоянного тока из переменного синусоидального (идеализированный вид) при использовании одно или двух полупериодного выпрямителя имеет ряд недостатков, о которых мы и поговорим далее.
Главным недостатком такого выпрямителя является пульсирующее напряжение. Избавление от пульсаций напряжения, их сглаживание – необходимое условие для корректной работы многих электрических приборов, особенно это касается радиоаппаратуры, где такой вид напряжения вносит хорошо заметные помехи. Так называемые, сглаживающие фильтры применяют для устранения пульсаций выходного тока и напряжения.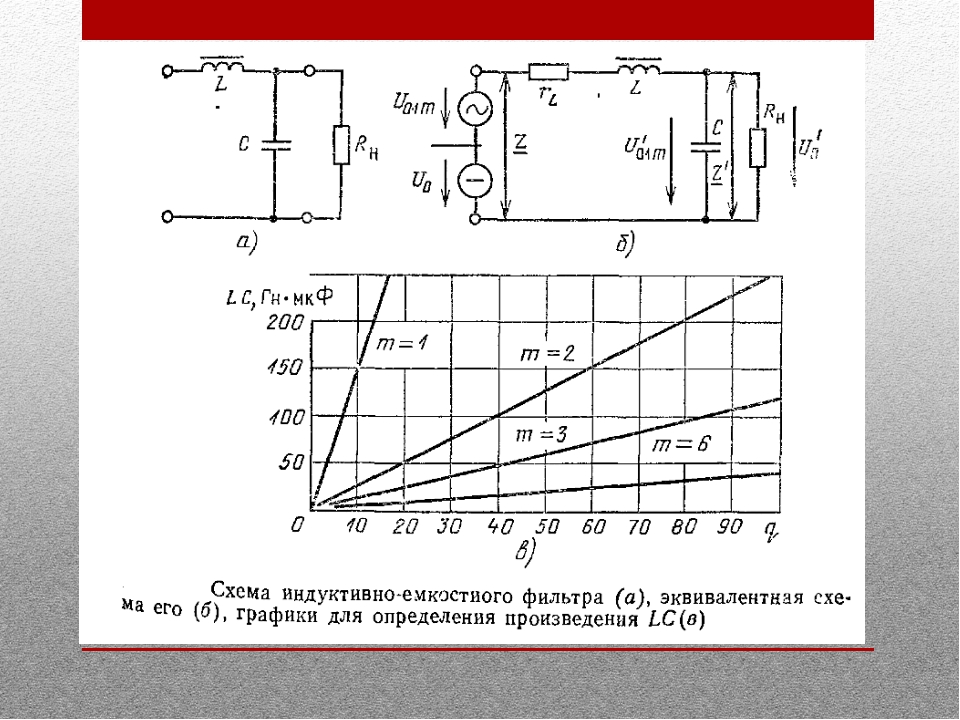
| Емкостной | Индуктивный | Г-образный |
Так же используют различные комбинации выше перечисленных фильтров для достижения необходимого качества напряжения.
Как работает С-фильтр?
Принцип работы сглаживающих фильтров основывается на свойствах конденсатора и катушки индуктивности. Они выполняют роль резервуара энергии. Как известно, напряжение на конденсаторе не может измениться мгновенно, а на индуктивности ток не может мгновенно возрасти или исчезнуть. Эти свойства и положены в основу работы сглаживающих фильтров, рассмотрим это на примерах.
Схема С-фильтра (емкостной)
На рисунке выше, к первичной обмотке трансформатора подводиться переменное напряжение U, ко вторичной обмотке подсоединена нагрузка R Роль выпрямителя в представленной схеме играет диод, как работает полупроводниковый диод, Вы можете прочесть здесь. Конденсатор С – фильтрующий элемент.
Роль выпрямителя в представленной схеме играет диод, как работает полупроводниковый диод, Вы можете прочесть здесь. Конденсатор С – фильтрующий элемент.
Вид выходных тока и напряжения на С-фильтре
Действия диода во вторичной цепи трансформатора описывает серая, пульсирующая кривая. Если быть точным, диод обрезал отрицательную часть переменного напряжения, он пропускает только положительную волну, а при приложении отрицательного напряжения – запирается. Конденсатор С, как уже говорилось раннее – резервуар энергии. Когда диод открыт и ток протекает через нагрузку, то конденсатор (подсоединен параллельно) заряжается до величины напряжения в цепи. А когда диод закрыт (отрицательная волна синусоиды), благодаря наличию емкости, уровень напряжения не может резко снизиться. Конденсатор постепенно разряжается через нагрузку, таким образом, сглаживая огромные скачки уровня напряжения. Разряжается он до следующей положительной волны, а точнее, когда напряжение на катоде диода превысит напряжение на конденсаторе.
Если в качестве выпрямителя применять диодный мост, то выходные ток и напряжения приобретут следующий вид:
Благодаря тому, что диодный мост работает и при положительном, и при отрицательном напряжении — пульсность увеличилась в два раза.
Обратите внимание на вид тока (синий), из-за наличия конденсатора ток имеет резкий скачок, что в свою очередь не есть хорошо для любого электроприбора. На помощь в сложившейся ситуации приходит катушка индуктивности.
Роль индуктивности в сглаживании
Схема Г-образного фильтра (L+C)
 Результат действия катушки L можете наблюдать на представленном ниже изображении. Благодаря катушке, изменение значения тока происходит более плавно. Первую волну можете не принимать во внимание, при пуске происходят различные переходные процессы, которые и вызывают подобные вещи.
Результат действия катушки L можете наблюдать на представленном ниже изображении. Благодаря катушке, изменение значения тока происходит более плавно. Первую волну можете не принимать во внимание, при пуске происходят различные переходные процессы, которые и вызывают подобные вещи.Разница в применении диодного моста и диода
1. Диодный мост работает постоянно (при положительной и отрицательной волне), что увеличивает пульсность выходного напряжения. Соответственно, для получения одного и того же значения напряжения, конденсатор в мостовой схеме нужен меньшей емкости, так как может себе «позволить» разряжаться быстрее.
2. При применении одного диода, имеет место момент времени, когда диод заперт и напряжение между его катодом и анодом равно двухкратному напряжению цепи (на катоде положительное значение благодаря конденсатору, а на аноде отрицательная полуволна, достигшая пика). По этому при выборе диода для выпрямителя, необходимо учесть, что его импульсное обратное напряжение должно превышать 2 значения рабочего напряжения.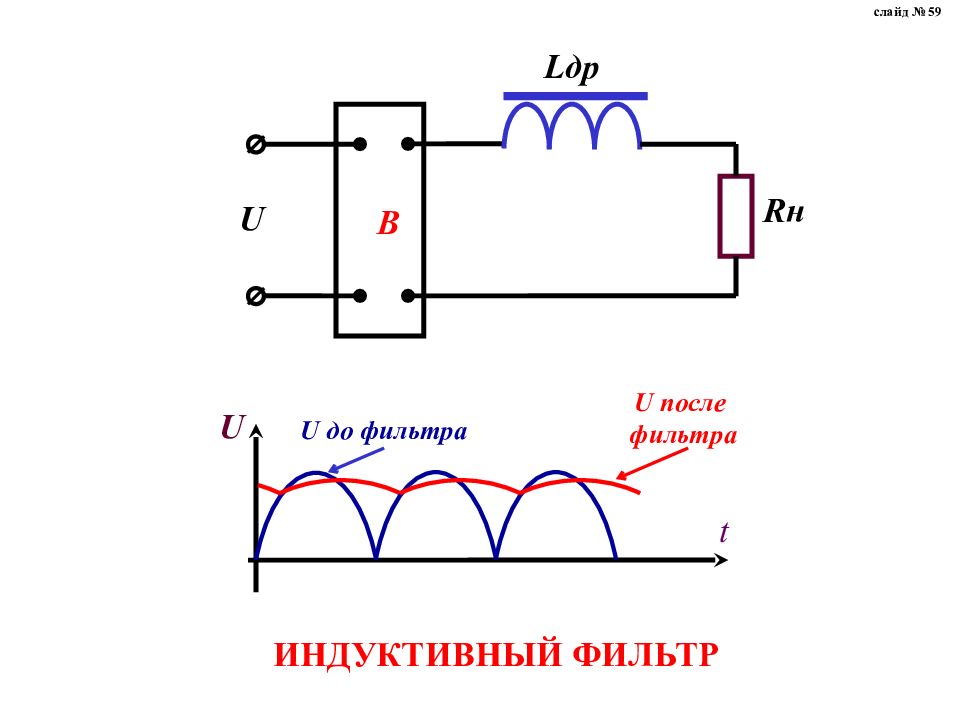
3. Не нужно забывать про свойства полупроводниковых диодов. Ведь при прохождении p-n перехода существует падение напряжения, которое обязательно необходимо учитывать при подборе сглаживающего фильтра. Здесь выигрывает простой диод над диодным мостом. Потому что у него напряжение снижается лишь на одном элементе, а в мостовой схеме, ток в один момент времени протекает по двум полупроводникам. Этот эффект нагляден на рисунках ниже:
Влияние малой нагрузки на эффективность сглаживания
Активное сопротивление катушки индуктивности находится по формуле:
Для конденсатора:
Эффективность индуктивного и емкостного фильтров повышается при соблюдении следующих условий:
Исходя из этого, при очень малой нагрузке (сопротивления потребителя) невозможно будет использовать конденсаторный сглаживающий фильтр.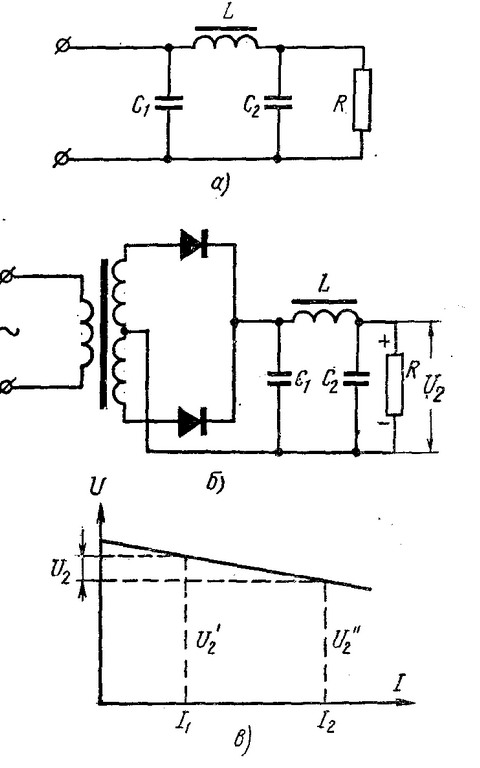
Вид выпрямленного напряжения при малой нагрузке (рисунок ниже):
| — выпрямление диодом; | ||
| — мостовая схема. |
Расчет конденсаторного фильтра
Пример. Допустим, у нас есть источник переменного напряжения U=12 B (действующее значение), в то время как его амплитуда будет равна 17 В. Подробнее о значениях переменного напряжения и их зависимостях читайте по ссылке. Сопротивление нагрузки Rн=300Ом. Выпрямление будем производить одним диодом, а С-фильтр — сглаживающий элемент цепи.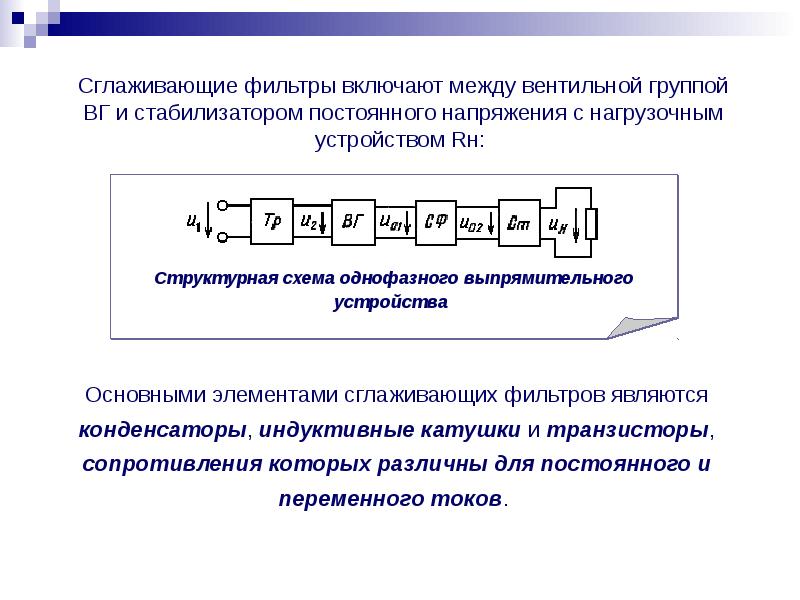
Первым делом, необходимо учесть падение напряжения на диоде, в модели выбран диод, у которого этот параметр равен 0,8 В (для мостовой схемы падение будет равно 0,8 В+0,8 В=1,6 В).
Выходное напряжение будет иметь амплитуду:
Таким образом, 16,2В – максимально возможное напряжение на выходе выпрямителя при бесконечной емкости, но в жизни значение будет, естественно, меньшим.
Емкость фильтра находим из условия:
Откуда следует, что
Для хорошей работы фильтра выбираем емкость конденсатора не менее чем в 10 раз больше расчетного значения. Для примера я выбрал 5,3*10-4Ф.
Рассчитанная ёмкость при заданных входных параметрах даст следующий результат на выходе:
Недостаточно прав для комментирования
Как работает сглаживающий фильтр (конденсатор)
Применение диодных выпрямителей позволяет производить преобразование переменного напряжения в постоянное.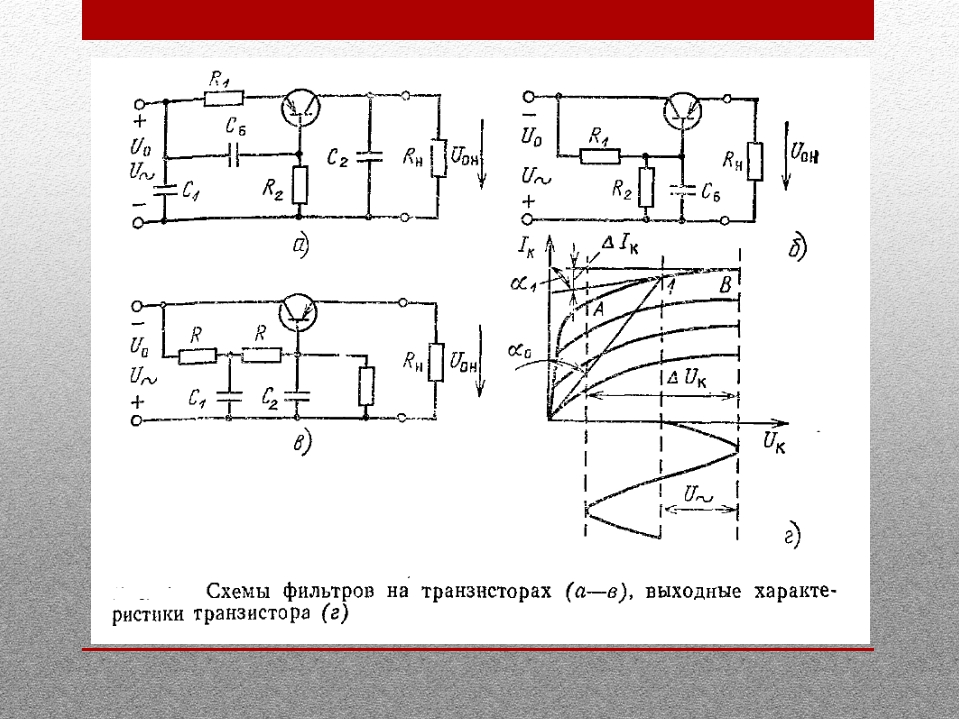 Но у такого метода преобразования есть существенный недостаток – значительные пульсации выпрямленного напряжения. Эти пульсации возникают от того, что форма кривой переменного напряжения близка к синусоидальной и выпрямленное напряжение имеет от неё определённую зависимость.
Но у такого метода преобразования есть существенный недостаток – значительные пульсации выпрямленного напряжения. Эти пульсации возникают от того, что форма кривой переменного напряжения близка к синусоидальной и выпрямленное напряжение имеет от неё определённую зависимость.
| Рисунок 1. Работа ёмкостного фильтра при однофазном однополупериодном выпрямлении. |
Для сглаживания пульсаций постоянного напряжения в качестве фильтра часто применяют сглаживающий конденсатор, подключаемый параллельно нагрузке. Во время роста напряжения по кривой синусоиды происходит не только питание нагрузки, но и заряд конденсатора. После достижения напряжения максимального (амплитудного) значения начинается спад. При этом, пока напряжение на выходе выпрямителя падает, конденсатор начинает разряжаться на нагрузку, таким образом в некоторой степени поддерживая напряжение на ней.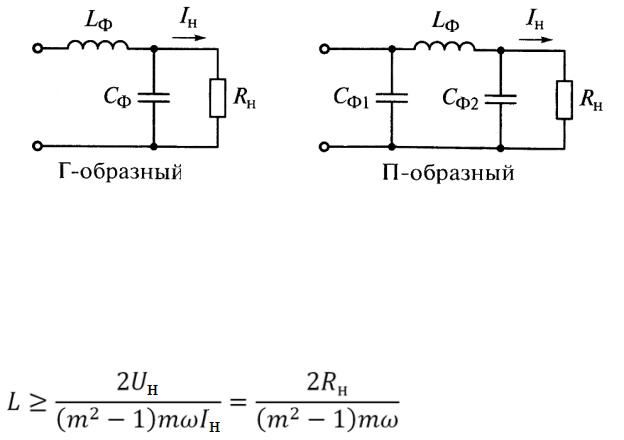 Так происходит сглаживание пульсаций напряжения на выходе выпрямителя.
Так происходит сглаживание пульсаций напряжения на выходе выпрямителя.
Для примеров рассмотрим базовые схемы выпрямителей. На рисунке 1 верхняя диаграмма отображает напряжение питающей сети. Ниже показана схема однополупериодного однофазного выпрямителя и соответствующая ей диаграмма выпрямленного напряжения на нагрузке. Внизу представлена схема выпрямителя с ёмкостным фильтром C1 и соответствующая ей диаграмма выпрямленного напряжения на нагрузке.
По аналогии приведены сравнительные схемы и диаграммы и для других вариантов на рисунках 2, 3 и 4.
Рисунок 2. Фильтр в двухполупериодном выпрямителе. | Рисунок 3. Фильтр в однополупериодном 3-фазном выпрямителе. | Рисунок 4. Фильтр в двухполупериодном 3-фазном выпрямителе. |
сглаживающие и ЭМП-фильтры для импульсных преобразователей
Входные ЭМП-фильтры
Входные и выходные фильтры — необходимая составляющая практически любой электронной системы, в состав которой входят импульсные преобразователи или быстродействующие компоненты. И хотя входные ЭМП-фильтры и выходные сглаживающие фильтры служат разным целям, их конфигурация в ряде случаев может быть схожа.
И хотя входные ЭМП-фильтры и выходные сглаживающие фильтры служат разным целям, их конфигурация в ряде случаев может быть схожа.
Основное назначение входных фильтров заключается в защите от электромагнитных помех (ЭМП), генерируемых преобразователем, а также защита от возможных помех со стороны сети. Во многих случаях наилучшим выбором является покупной ЭМП-фильтр, в котором предусмотрена фильтрация дифференциальных и синфазных помех. Эти фильтры устанавливаются между питающей сетью и AC/DC-преобразователем. В состав фильтров входят магнитосвязанные дроссели и емкости. В общем случае схема такого фильтра представлена на рис. 1.
Рис. 1. Схема синфазного и дифференциального ЭМП-фильтра
В этом ЭМП-фильтре последовательно включены два фильтра. Ближний к сети ЭМП-фильтр дифференциальных помех состоит из конденсаторов CY5, CY6, CX2 и магнитосвязанного двухобмоточного дросселя LDM. Последовательно с ним установлен ЭМП-фильтр дифференциальных помех, в состав которого входят конденсаторы CY3, CY4, CX1 и магнитосвязанный двухобмоточный дроссель LCM.
Как видно из рисунка, ЭМП-фильтры синфазных и дифференциальных помех имеют схожую конфигурацию за исключением расположения начала и конца обмоток дросселей LDM и LCM. Различие объясняется следующим образом. Токи дифференциальных помех в фазе и нейтрали протекают в разных направлениях, а токи синфазных помех в фазе и нейтрали текут в одном направлении и замыкаются через корпус или заземление. Таким образом, в обоих дросселях магнитные потоки, создаваемые двумя обмотками, складываются. Следовательно, индуктивность дросселя возрастает, и ЭМП-фильтр работает как классический LC-фильтр.
Описанные выше ЭМП-фильтры, как правило, устанавливаются в линиях сетевого напряжения 220 В на входе AC/DC-преобразователя. ЭМПфильтры производятся многими известными на российском рынке электроники компаниями, среди которых Murata, Epcos, Würth Elektronik и многие другие.
Автор настоятельно рекомендует использовать покупные фильтры и не пытаться изготавливать их самостоятельно из дискретных компонентов.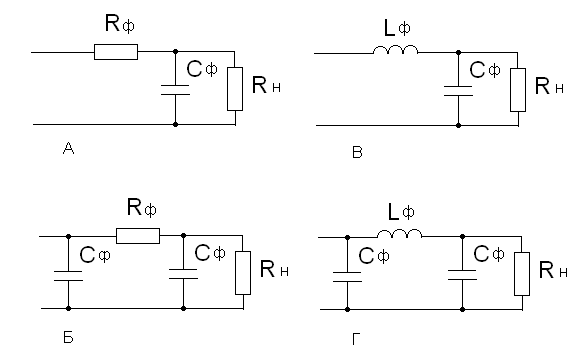 Не следует использовать ЭМП-фильтры для цепей переменного тока в цепях постоянного тока. Постоянный ток создаст подмагничивание дросселей фильтра, а всплески токов помех приводят к насыщению сердечника дросселя, что влечет за собой уменьшение их индуктивности и, следовательно, фильтрующих свойств.
Не следует использовать ЭМП-фильтры для цепей переменного тока в цепях постоянного тока. Постоянный ток создаст подмагничивание дросселей фильтра, а всплески токов помех приводят к насыщению сердечника дросселя, что влечет за собой уменьшение их индуктивности и, следовательно, фильтрующих свойств.
Однако не всегда можно использовать готовые ЭМП-фильтры. Например, в распределенных системах питания в цепях постоянного тока после шинного преобразователя или перед ним может понадобиться установить ЭМП-фильтр перед PoL-преобразователем. В этом случае, скорее всего, придется создать такой фильтр на дискретных компонентах, особенно если невелика мощность преобразователя, перед которым устанавливается фильтр.
Примером может служить LC-фильтр, показанный на рис. 2. Поскольку фильтр описывается уравнением 2‑го порядка и представляет собой хорошо известное колебательное звено, мы лишь приведем окончательные соотношения.
Рис. 2. ЭМП-фильтр LC-типа
Собственная частота колебательного звена определяется из соотношения (1):
ω0 = 1/√LC. (1)
(1)
Величина демпфирования определяется из соотношения (2):
β = (R/2) × (√C/L). (2)
В схеме на рис. 2 отсутствует резистор R в явном виде, поэтому такой фильтр называется недемпфированным, но это не значит, что R = 0 и любое входное воздействие порождает в фильтре незатухающие колебания. Величина R складывается из омического сопротивления дросселя RDC, эквивалентного последовательного сопротивления конденсатора (ESR) и сопротивления проводников. Передаточная характеристика этого фильтра показана на рис. 3.
Рис. 3. Передаточная характеристика LC-фильтра
Как видно из этого рисунка, чем меньше степень демпфирования β, тем ярче выражен резонансный пик в частотной области. Также при условии β<1, чем меньше β, тем более явно выражен колебательный переходный процесс во временной области. В последнем случае вполне уместен афоризм «лучшее – враг хорошего». Известны случаи, когда из-за использования в шинах постоянного тока высококачественных конденсаторов с очень малым ESR возникали колебания напряжения на шине именно из-за малой величины ESR, т.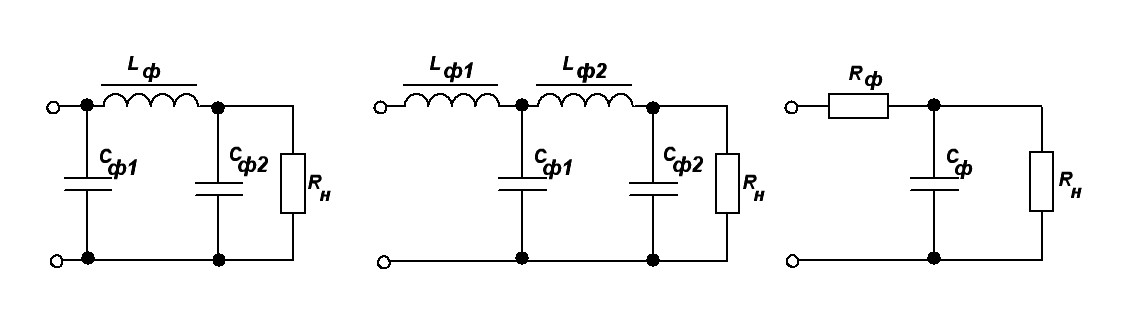 к. при сокращении ESR уменьшалась степень демпфирования и возрастала колебательность переходного процесса.
к. при сокращении ESR уменьшалась степень демпфирования и возрастала колебательность переходного процесса.
Следует учесть еще одно обстоятельство: ЭМП-фильтр будет работать так, как рассчитано, лишь в том случае, если его выходной импеданс существенно меньше, чем входной импеданс преобразователя. В противном случае подключение к выходу фильтра преобразователя заметно исказит характеристики фильтра. И фильтр может исказить работу преобразователя.
Входную цепь преобразователя в общем случае можно представить в виде последовательной RLC-цепочки. Таким образом, у частотной характеристики импеданса появится экстремум в виде минимума. Чтобы устранить взаимовлияние ЭМП-фильтра и преобразователя, желательно, чтобы выходной импеданс преобразователя был на порядок меньше входного импеданса ЭМП-фильтра.
На рис. 4 приведен пример частотной зависимости импедансов ЭМП-фильтра и преобразователя. Из этого рисунка, а также из приведенных выше соображений ясно, что величина демпфирования не должна быть слишком малой.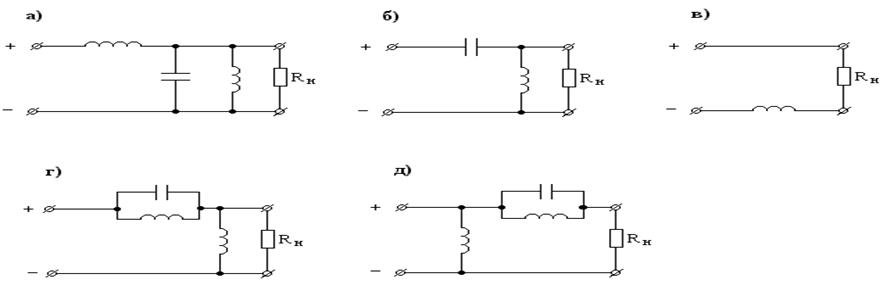 С другой стороны, чрезмерное увеличение β устранит колебательность, переходный процесс станет апериодическим и затянется во времени. Как правило, оптимальное значение β следует выбирать в пределах 0,5–1,0.
С другой стороны, чрезмерное увеличение β устранит колебательность, переходный процесс станет апериодическим и затянется во времени. Как правило, оптимальное значение β следует выбирать в пределах 0,5–1,0.
Рис. 4. Частотные зависимости импедансов ЭМП-фильтра и преобразователя
При недемпфированном фильтре (рис. 2) значение R в соотношении (2) в основном определяется суммой RDC + ESR, но этой величины недостаточно, чтобы увеличить β до 0,7–1,0. Следовательно, требуется ввести дополнительное сопротивление. Наилучший вариант введения демпфирующей цепочки показан на рис. 5. Цепочка Z3 состоит из последовательно соединенных резистора Rd и конденсатора Cd. Последний блокирует постоянное напряжение и предотвращает дополнительную потерю мощности на резисторе Rd. Коэффициент демпфирования ЭМП-фильтра с демпфирующей цепочкой описывается выражением (3):
βd = (n/n + 1) [(Rd/2) × (√C/L)], (3)
где n = Cd/C.
Рис. 5. Демпфированный LC-фильтр
Из практических соображений величина n должна находиться в пределах 4–7 единиц. На рис. 6 показана частотная зависимость импедансов демпфированного и недемпфированного фильтров. Резонансный пик демпфированного ЭМП-фильтра существенно меньше, чем у недемпфированного. Демпфирующую цепочку можно составить из последовательной RL-цепочки и подсоединить ее параллельно индуктивности фильтра, но это не самое лучшее, на наш взгляд, решение, т. к. увеличивается мощность рассеяния на резисторе.
Рис. 6. Частотные зависимости импедансов демпфированного и недемпфированного LC-фильтра
Если последовательно включить несколько LC-фильтров, увеличится крутизна спада АЧХ ЭМП-фильтра в области ω>ω0, и улучшится фильтрация помех, но, как представляется автору, такое решение не имеет смысла. Габариты решения заметно возрастут, а увеличение крутизны спада АЧХ фильтра не принесет практической выгоды. Рабочая частота PoL-преобразователей в настоящее время находится в диапазоне примерно 1–2 МГц.
Рабочая частота PoL-преобразователей в настоящее время находится в диапазоне примерно 1–2 МГц.
С учетом требований стандартов частота среза ЭМП-фильтра должна находиться в пределах нескольких кГц. Если выбрать величину β ≈ 1, то ослабление на частоте 1 МГц составит 50–60 дБ, что вполне достаточно для подавления помех. Если все же потребуется более значительное ослабление, возможно, следует подумать не о применении двухкаскадного ЭМП-фильтра, а проанализировать систему питания и принять иные меры к уменьшению помех.
Выходные сглаживающие фильтры
В качестве сглаживающих выходных фильтров используются те же LC-фильтры, которые были рассмотрены выше. Однако в данном случае такие фильтры не удастся заменить покупными, и их всякий раз приходится рассчитывать разработчику. Выходной сглаживающий фильтр позволяет снизить пульсации выходного напряжения до единиц мВ или даже нескольких сотен мкВ. Уменьшение амплитуды пульсаций до десятков мкВ едва ли возможно, даже если увеличить число каскадов выходного фильтра.
Уменьшению пульсаций помешают паразитные составляющие компонентов фильтра и проводников печатной платы. Кроме того, из-за джиттера частоты коммутации в спектре выходного напряжения могут возникать низкочастотные составляющие вплоть до нескольких Гц. Их, конечно, невозможно подавить сглаживающим фильтром. Таким образом, если требуется ограничить пульсации выходного напряжения вплоть до мкВ, после сглаживающего фильтра в цепь питания устанавливается LDO-регулятор.
Рис. 7. Сглаживающий фильтр на выходе повышающего преобразователя
Рассмотрим наиболее распространенную конфигурацию сглаживающего фильтра – π-фильтр (или П-фильтр). Схема его включения в цепь повышающего преобразователя приведена на рис. 7 [1]. Резонансная частота этого фильтра определяется из выражения (4).
В отличие от ЭМП-фильтра, сглаживающий фильтр входит в состав контура обратной связи, поэтому частота среза фильтра не должна быть меньше 10–20% частоты коммутации. В противном случае уменьшается устойчивость системы из-за запаздывания в петле обратной связи, что приводит к затягиванию переходных процессов, а также к ухудшению устойчивости из-за уменьшения запаса по фазе. Как и в случае с ЭМП-фильтрами, в сглаживающий фильтр необходимо ввести демпфирующую цепочку. На рис. 7 показаны три возможных варианта цепочек демпфирования.
Вариант демпфирования 1 с введением резистора RFILT представляется самым простым и экономичным, но введение этого резистора ослабляет эффективность фильтра. Кроме того, уменьшается импеданс параллельной RL-цепочки фильтра. Вариант демпфирования 2 наиболее эффективен, т. к. эта цепочка улучшает характеристику фильтра, но увеличивает стоимость из-за использования керамического конденсатора. На первый взгляд может показаться, что вариант демпфирования 3 – самый эффективный. Однако в этом случае требуется наибольшая емкость конденсатора. Следовательно, возрастает стоимость решения. К тому же, поскольку введение этой цепочки уменьшит полосу пропускания петли обратной связи, этот вариант следует исключить из рассмотрения.
Для высокочастотных преобразователей с малым выходным током имеется еще один нетривиальный вариант сглаживающего фильтра — вместо дросселя в фильтре используется резистор. Рассмотрим простой пример, где в качестве выходного фильтра PoL-преобразователя с частотой коммутации 2 МГц и выходным током 20 мА применяется RC-фильтр. Пусть сопротивление резистора равно 10 Ом, а емкость конденсатора — 1 мкФ. Частота среза этого фильтра составит около 16 кГц; учитывая ослабление 20 дБ/декаду, получим, что пульсации с частотой 2 МГц ослабляются более чем в 100 раз. Однако придется смириться с падением напряжения 200 мВ на резисторе.
Заметим, что расчет фильтров носит приблизительный характер и расчетные параметры обязательно должны проверяться путем макетирования фильтра совместно с преобразователем. На величину емкости фильтра влияет напряжение заряда, частота пульсации тока, температура емкости. Индуктивность дросселя фильтра нелинейно зависит от тока. Кроме того, на характеристики фильтра будет влиять и преобразователь. Эти изменения невозможно учесть в практических расчетах. Помощь при разработке фильтра оказывают фирменные САПР для расчета фильтров. Например, схему расчета сглаживающего фильтра можно найти в [1]. Для расчета ЭМП-фильтра можно воспользоваться средствами [2].
Выбор компонентов фильтра
При выборе компонентов фильтра следует иметь в виду, что собственная резонансная частота (SFR) конденсатов и дросселей должна заметно превосходить частоту среза фильтра. Поскольку нормативные требования, предъявляемые к кондуктивным помехам, распространяются на частоты до 30 МГц, SFR компонентов фильтра должны быть выше 30 МГц. Например, если SFR выбранного керамического конденсатора меньше 30 МГц, следует заменить этот конденсатор несколькими параллельно включенными конденсаторами с емкостью меньшей величины.
Несколько сложнее обстоят дела с выбором дросселя. В этом случае также уместно вспомнить известный афоризм — «наши недостатки — продолжение наших достоинств». Достоинства дросселей были описаны выше. К сожалению, имеются и недостатки: в любом дросселе помимо основного магнитного поля, замыкающегося в сердечнике, всегда есть поле рассеяния, которое, по сути, является генератором помех.
В значительной степени избавиться от этих помех можно, используя экранированные дроссели. Однако проблема заключается в том, что у этих дросселей меньше ток насыщения Isat, поэтому при увеличении тока пульсации индуктивность дросселя падает и фильтр теряет эффективность. Как часто бывает, ситуацию отчасти разрешается с помощью компромисса. Некоторые производители выпускают полуэкранированные дроссели.
На рис. 8 [3] показана зависимость индуктивности от тока для экранированных, неэкранированных и полуэкранированных индукторов производства компании Würth Elektronik. Видно, что полуэкранированные дроссели серии WE-LQS значительно улучшают ситуацию с током насыщения, но приходится мириться с тем, что излучаемые ими помехи несколько больше, чем экранированными дросселями. Если такое решение недопустимо, придется выбрать экранированный дроссель большего габарита.
Рис. 8. Зависимость индуктивности от тока для экранированных, неэкранированных и полуэкранированных индукторов производства компании Würth Elektronik
На принципиальной электрической схеме следует указать начало обмотки (на корпусе дросселя оно отмечено точкой). Начало обмотки должно быть подключено к источнику пульсирующего напряжения. В этом случае в начале обмотки располагается точка с наибольшим значением dV/dt, а начало обмотки примыкает непосредственно к сердечнику. Следовательно, при многослойной обмотке верхние слои играют роль экрана. Заметим, что при правильном подключении ослабляется главным образом вектор напряженности электрического поля E, напряженность магнитного поля H практически не зависит от подключения начала обмотки.
Крутые переключения силовых ключей порождают звон, частота которого зависит от паразитных индуктивностей и емкостей силового каскада. Избавиться от них практически невозможно. Частота звона находится в диапазоне от сотен МГц до единиц ГГц. Из-за поверхностного эффекта в проводниках этот звон вносит малый вклад в кондуктивные помехи на шинах питания, но он является источником нежелательных радиопомех. Поскольку частота звона чаще всего превышает SFR конденсаторов фильтра, ослабить звон можно только с помощью дросселя, а точнее – сердечника дросселя: именно потери в сердечнике, а не индуктивность дросселя помогут ослабить звон. Потери в сердечнике зависят от материала. Ослабление высокочастотной составляющей для различных материалов показано на рис. 9 для дросселей Würth Elektronik.
Рис. 9. Ослабление высокочастотной составляющей для различных материалов
Литература- Designing second stage output filters for switching power supplies//www.analog.com.
- WEBENCH Design Center//www.ti.com.
- Several parameters such as ripple current, switching frequency, rise & fall time of a switching device are important//powersystemsdesign.com.
Выпрямители: Основные виды сглаживающих фильтров и особенности их применения в выпрямителях
Режим работы выпрямителя в значительной степени определяется типом фильтра, включенного на его выходе. В маломощных выпрямителях, питающихся от однофазной сети переменного тока, применяются простейшие емкостные фильтры, в выпрямителях средней и большой мощности — Г-образные \(LC\), \(RC\) и П-образные \(CLC\) и \(CRC\) фильтры.
Основным параметром сглаживающих фильтров является коэффициент сглаживания \((q)\), который определяется как отношение коэффициента пульсаций на входе фильтра к коэффициенту пульсаций на его выходе (на нагрузке).
Емкостный фильтр является наиболее простым из всех видов сглаживающих фильтров. Он состоит из конденсатора, включаемого параллельно нагрузке. Анализ работы данного фильтра проведен при описании однофазного однополупериодного выпрямителя. Коэффициент пульсаций напряжения на выходе выпрямителя с емкостным фильтром может быть найден по формуле:
\( K_п \approx \cfrac{1}{2 \cdot m \cdot f \cdot R_н \cdot C}\),
где \(m\) зависит от схемы выпрямителя:
\(m = 1\) для однофазного однополупериодного выпрямителя,
\(m = 2\) для однофазного двухполупериодного и мостового выпрямителей),
\(f\) — частота входного переменного напряжения.
Из приведенной формулы видно, что коэффициент пульсаций на выходе выпрямителя с емкостным фильтром обратно пропорционален емкости применяемого конденсатора и величине сопротивления нагрузки. Поэтому применение такого фильтра рационально только при достаточно больших значениях этих величин. По мере совершенствования технологии изготовления конденсаторов большой емкости рассматриваемый тип фильтра вследствие своей простоты и эффективности находит все большее применение.
Индуктивно-емкостные фильтры (Г-образные \(LC\) и П-образные \(CLC\)) широко применяются при повышенных токах нагрузки, поскольку падение напряжения на них можно сделать сравнительно небольшим. Коэффициент полезного действия у таких фильтров достаточно высокий. К недостаткам индуктивно-емкостных фильтров относятся: большие габаритные размеры и масса, повышенный уровень электромагнитного излучения от элементов фильтра, сравнительно высокая стоимость и трудоемкость изготовления.
Наиболее широко используется Г-образный индуктивно-емкостный фильтр (рис. 3.4‑13).
Рис.2 — 1) m \omega} \)
П-образный \(CLC\) фильтр отличается от описанного Г-образного \(LC\) фильтра наличием еще одной емкости, включаемой на входе фильтра (на рис. 3.4-13 конденсатор \(C_0\), показан пунктиром). Расчет таких фильтров производят в два этапа, сначала рассчитывают емкость конденсатора \(C_0\), исходя из допустимой величины пульсации напряжения на нем, затем по приведенным выше формулам рассчитывают Г-образное звено. Наибольший коэффициент сглаживания в П-образном фильтре достигается при \(C_0 = C_1\).
При выборе конденсаторов фильтра необходимо следить за тем, чтобы они были рассчитаны на напряжение на 15…20% превышающее напряжение холостого хода выпрямителя при максимальном напряжении сети (чтобы учесть перенапряжения, возникающие при включении выпрямителя). Необходимо также, чтобы амплитуда переменной составляющей напряжения на них не превышала предельно допустимого значения.
Резистивно-емкостные фильтры целесообразно применять при малых токах нагрузки (менее 10…15 мА) и небольших требуемых коэффициентах сглаживания. Достоинства этих фильтров — малые габариты и масса, низкая стоимость. Недостаток — сравнительно большое падение напряжения на фильтре (что снижает КПД устройства выпрямления в целом).
Простейший Г-образный \(RC\) фильтр (рис. 3.4-14) состоит из балластного резистора (\(R_ф\)) и конденсатора (C_1). Коэффициент сглаживания такого фильтра вычисляется по формуле:
\( q = m \omega C \cfrac{R_н R_ф}{R_н + R_ф}\),
где m зависит от схемы выпрямителя:
(\(m = 1\) для однофазного однополупериодного выпрямителя,
\(m = 2\) для однофазного двухполупериодного и мостового выпрямителей).
Рис. 3.4-14. Схема резистивно-емкостного сглаживающего фильтра
Сопротивление фильтра (\(R_ф\)) выбирают из условия допустимого падения напряжения на фильтре или исходя из заданного КПД (\(h\)) по формуле \(R_ф = R_н (1 – h)/h \). Оптимальным считается КПД порядка 0,6…0,8.
Расчет П-образного резистивно-емкостного фильтра (его схема включает дополнительный конденсатор \(C_0\), показанный на рис. 3.4-14 пунктиром) производится, как и в случае П-образного \(CLC\) фильтра, в два этапа после разделения этого фильтра на емкостный (\(C_0\)) и Г-образный \(LC_1\) фильтр.
Комбинированные фильтры применяются при необходимости получения больших коэффициентов сглаживания на выходе выпрямителя. Они представляют собой последовательное включение нескольких фильтров. При этом могут использоваться как однотипные, так и разнотипные звенья. При каскадном включении \(LC\) фильтров можно считать, что суммарный коэффициент сглаживания (\(q_\Sigma\)) равен произведению коэффициентов сглаживания составляющих фильтр звеньев: \(q_\Sigma = q_1 \cdot q_2 \cdot q_3 … \) . Для нахождения оптимального числа звеньев (\(n_{опт}\)) такого фильтра при заданном \(q_\Sigma\) можно воспользоваться формулой:
\(n_{опт} = \cfrac{\large | \normalsize \ln{1/q_\Sigma} \large | \normalsize}{2} \).
Высокий коэффициент сглаживания и хороший КПД могут также обеспечить разнообразные фильтры на транзисторах.
| < Предыдущая | Следующая > |
|---|
Тема: Сглаживающие фильтры. План. Активно-индуктивный (R-L) сглаживающий фильтр
15.4. СГЛАЖИВАЮЩИЕ ФИЛЬТРЫ
15.4. СГЛАЖИВАЮЩИЕ ФИЛЬТРЫ Сглаживающие фильтры предназначены для уменьшения пульсаций выпрямленного напряжения. Их основным параметром является коэффициент сглаживания равный отношению коэффициента пульсаций
ПодробнееЛекция 8 ВЫПРЯМИТЕЛИ (ПРОДОЛЖЕНИЕ) План
75 Лекция 8 ВЫПРЯМИТЕЛИ (ПРОДОЛЖЕНИЕ) План 1. Введение 2. Однополупериодный управляемый выпрямитель 3. Двухполупериодные управляемые выпрямители 4. Сглаживающие фильтры 5. Потери и КПД выпрямителей 6.
ПодробнееЛекция 2 ЦЕПИ С ДИОДАМИ И ИХ ПРИМЕНЕНИЕ
109 Лекция ЦЕПИ С ДИОДАМИ И ИХ ПРИМЕНЕНИЕ План 1. Анализ цепей с диодами.. Источники вторичного электропитания. 3. Выпрямители. 4. Сглаживающие фильтры. 5. Стабилизаторы напряжения. 6. Выводы. 1. Анализ
Подробнее1. Назначение и устройство выпрямителей
Тема 16. Выпрямители 1. Назначение и устройство выпрямителей Выпрямители это устройства, служащие для преобразования переменного тока в постоянный. На рис. 1 представлена структурная схема выпрямителя,
ПодробнееЛабораторная работа 5.3
Лабораторная работа 5.3 ИССЛЕДОВАНИЕ ДВУХПОЛУПЕРИОДНОГО ВЫПРЯМИТЕЛЯ 5.3.1. Выпрямители Выпрямители служат для преобразования переменного напряжения питающей сети в постоянное. Основное назначение выпрямителя
ПодробнееПРИНЦИП РАБОТЫ ЭЛЕКТРОННОГО ВЫПРЯМИТЕЛЯ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Государственное образовательное учреждение высшего профессионального образования «Оренбургский государственный
Подробнее«Электронный дроссель» Евгений Карпов
«Электронный дроссель» Евгений Карпов В статье рассмотрены особенности работы электронного силового фильтра и возможность его использования в звуковоспроизводящей аппаратуре. Побудительным мотивом написания
ПодробнееМожно показать также, что
Индуктивно-связанные цепи «на ладони» Магнитная связь между двумя катушками появляется, если их потоки взаимно пронизывают витки (часть витков) друг друга. Потокосцеплением называется произведение потока
ПодробнееЛекция 7 ВЫПРЯМИТЕЛИ
Лекция 7 ВЫПРЯМИТЕЛИ План 1. Источники вторичного электропитания 2. Однополупериодный выпрямитель 3. Двухполупериодные выпрямители 4. Трехфазные выпрямители 67 1. Источники вторичного электропитания Источники
Подробнее1.1 Усилители мощности (выходные каскады)
Лекция 7 Тема: Специальные усилители 1.1 Усилители мощности (выходные каскады) Каскады усиления мощности обычно являются выходными (оконечными) каскадами, к которым подключается внешняя нагрузка, и предназначены
ПодробнееРисунок 1 Частотная характеристика УПТ
Лекция 8 Тема 8 Специальные усилители Усилители постоянного тока Усилителями постоянного тока (УПТ) или усилителями медленно изменяющихся сигналов называются усилители, которые способны усиливать электрические
ПодробнееЛекция 9 СТАБИЛИЗАТОРЫ НАПРЯЖЕНИЯ
84 Лекция 9 СТАБИЛИЗАТОРЫ НАПРЯЖЕНИЯ План 1. Введение 2. Параметрические стабилизаторы 3. Компенсационные стабилизаторы 4. Интегральные стабилизаторы напряжения 5. Выводы 1. Введение Для работы электронных
ПодробнееВход Усилитель. Обратная связь
Лекция 5 Тема 5 Обратная связь в усилителях Обратной связью () называют передачу части энергии усиливаемого сигнала из выходной цепи усилителя во входную. На рисунке 4 показана структурная схема усилителя
ПодробнееИМПУЛЬСНЫЕ РЕГУЛЯТОРЫ НАПРЯЖЕНИЯ
95 Лекция 0 ИМПУЛЬСНЫЕ РЕГУЛЯТОРЫ НАПРЯЖЕНИЯ План. Введение. Понижающие импульсные регуляторы 3. Повышающие импульсные регуляторы 4. Инвертирующий импульсный регулятор 5. Потери и КПД импульсных регуляторов
Подробнее1.1 Усилители мощности (выходные каскады)
Лекция 9 Тема 9 Выходные каскады 1.1 Усилители мощности (выходные каскады) Каскады усиления мощности обычно являются выходными (оконечными) каскадами, к которым подключается внешняя нагрузка, и предназначены
ПодробнееЛекция 12 ИНВЕРТОРЫ. План
5 Лекция 2 ИНВЕРТОРЫ План. Введение 2. Двухтактный инвертор 3. Мостовой инвертор 4. Способы формирования напряжения синусоидальной формы 5. Трехфазные инверторы 6. Выводы. Введение Инверторы устройства,
ПодробнееЛабораторная работа 3
Лабораторная работа 3 Определение статических — параметров биполярных транзисторов по характеристикам Цель работы: Научиться работать со справочными материалами и определять статические параметры транзистора
ПодробнееРаздел 2. Усиление слабых сигналов.
Раздел 2. Усиление слабых сигналов. Глава 4. Принципы построения усилительных схем 4.1. Схемы подачи питания и стабилизации Постоянные токи и напряжения в цепях УЭ, соответствующие состоянию покоя, т.е.
ПодробнееБлоки питания лазеров
Елена Морозова, Алексей Разин Блоки питания лазеров Краткий конспект лекций по дисциплине «Лазерная техника» Томск 202 Лекция Элементная база блоков питания и простейшие схемы на их основе Любой лазер
Подробнееidt sin tdt 0,32I T R R R R
Лабораторная работа 1 Выпрямитель переменного тока Цель: изучение работы однополупериодного и двухполупериодного выпрямителей и их характеристик. Выпрямителем называется устройство для преобразования напряжения
ПодробнееРезонанс «на ладони».
Резонанс «на ладони». Резонансом называется режим пассивного двухполюсника, содержащего индуктивные и ёмкостные элементы, при котором его реактивное сопротивление равно нулю. Условие возникновения резонанса
ПодробнееЭлектрические машины
Согласно учебному плану направления 241000.62 (18.03.02) «Энерго- и ресурсосберегающие процессы в химической технологии, нефтехимии и биотехнологии», профиль «Охрана окружающей среды и рациональное использование
ПодробнееДисциплина «Микроэлектроника. Часть 2.»
Дисциплина «Микроэлектроника. Часть 2.» ТЕМА 5: «Интегральные стабилизаторы напряжения.» Легостаев Николай Степанович, профессор кафедры «Промышленная электроника» Содержание 1. Особенности интегральных
Подробнее1. Пассивные RC цепи
. Пассивные цепи Введение В задачах рассматриваются вопросы расчета амплитудно-частотных, фазочастотных и переходных характеристик в пассивных — цепях. Для расчета названных характеристик необходимо знать
ПодробнееГлава 5. УСИЛИТЕЛИ ПЕРЕМЕННОГО НАПРЯЖЕНИЯ
Глава 5. УСИЛИТЕЛИ ПЕРЕМЕННОГО НАПРЯЖЕНИЯ 5.1. ПРИНЦИП УСИЛЕНИЯ ПЕРЕМЕННОГО НАПРЯЖЕНИЯ Назначение и классификация усилителей. Усилители переменного напряжения являются наиболее распространенным типом электронных
ПодробнееВыпрямители синусоидального тока
1 Лекции профессора Полевского В.И. Выпрямители синусоидального тока Вольтамперная характеристика электропреобразовательного диода На рис. 1.1. представлена вольтамперная характеристика (ВАХ) электропреобразовательного
ПодробнееТема 4.2. Цепи переменного тока
Тема 4.. Цепи переменного тока Вопросы темы.. Цепь переменного тока с индуктивностью.. Цепь переменного тока с индуктивностью и активным сопротивлением. 3. Цепь переменного тока с ёмкостью. 4. Цепь переменного
ПодробнееЛАБОРАТОРНАЯ РАБОТА 7
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «УФИМСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЯНОЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» Кафедра прикладной химии
ПодробнееЭлектрические фильтры. План
I. Понятие электрического фильтра II. Классификация фильтров III. Расчет фильтров Электрические фильтры План I.Электрическим фильтром называется четырехполюсник, устанавливаемый между источником питания
ПодробнееТЕМА 6 ЭЛЕКТРОННЫЕ УСИЛИТЕЛИ.
ТЕМА 6 ЭЛЕКТРОННЫЕ УСИЛИТЕЛИ. Электронный усилитель — устройство, преобразующее маломощный электрический сигнал на входе в сигнал большей мощности на выходе с минимальными искажениями формы. По функциональному
ПодробнееТема 1. Линейные цепи постоянного тока.
МЕТОДИЧЕСКОЕ УКАЗАНИЕ 2 системы и технологии» Тема 1. Линейные цепи постоянного тока. 1. Основные понятия: электрическая цепь, элементы электрической цепи, участок электрической цепи. 2. Классификация
ПодробнееГлава 5. Дифференциальные усилители
Глава 5. Дифференциальные усилители 5. Дифференциальные усилители Дифференциальный усилитель это симметричный усилитель с двумя входами и двумя выходами, использующийся для усиления разности напряжений
ПодробнееСглаживающий фильтр СФ, СФ-15, СФ-25, СФ-42, СФ-63, СФ-104 в Москве
Сглаживающий фильтр СФ
Сглаживающие фильтры – это фильтры, которые во время работы пропускают с малым ослаблением постоянную величину с большим ослаблением переменную величину.
Сглаживающие фильтры выпрямителя производят для сглаживания колебаний выпрямленного напряженияв механических устройствах, где необходимо контролировать уровень пульсации.
Принцип работы
Во время заряда реактивных величин от диодного выпрямителя, это происходит за счет действия полуволны напряжения, и их разряд на нагрузку во время отсутствия напряжения
Существуют следующие виды сглаживающих фильтров: емкостные, Г-образные, Т-образные и П-образные.
Исполнение сглаживающего фильтра
- Сглаживающий фильтр типа СФ-15;
- Сглаживающий фильтр типа СФ-25;
- Сглаживающий фильтр типа СФ-42;
- Сглаживающий фильтр типа СФ-63;
- Сглаживающий фильтр типа СФ-104.
Основным отличием между исполнением фильтра является номинальной ток и номинальное напряжение.
Схемы сглаживающих фильтров
Емкостный сглаживающий фильтр
Т-образный фильтр
Г-образный фильтр
П-образный фильтр
К основному параметру сглаживающего фильтра (СФ) можно отнести коэффициент фильтрации (q) (отношение коэффициент пульсации на входе (Кп. вх) фильтра к этому же коэффициенту на выходе (Кп. вых)).
Техническая характеристика
- Номинальный ток на входе – от 15А, 25А, 42А, 63А, 104А (в зависимости от исполнения фильтра)
- Номинальное напряжение на входе – 20В, 24В, 48В
- Частота сети – 50-300Гц
- Коэффициент пульсаций выходного тока– 3%
- Допустимое входное напряжение – 320
Расчет сглаживающего фильтра
q = Kп. вх/ Kп. вых
Обращаем внимание, что исполнение корпуса изготавливается согласно техническим заданиям заказчиков.
Сглаживающий фильтр создает уровень колебаний согласно требований ГОСТ Р 51164-98.
Smoothing Filter — обзор
9.7 Влияние сглаживания на временные ряды
Как обсуждалось в разделе 4.5, сглаживание данных — это линейный процесс формы, d smooth = Gd obs . Сглаживание также является типом фильтрации, что можно увидеть, исследуя форму ядра данных, G (уравнение 4.16), которое является Теплицем. Столбцы G определяют сглаживающий фильтр , s . Обычно мы хотим, чтобы сглаживание было симметричным, чтобы сглаженные данные, d i smooth , вычислялись через средневзвешенное значение наблюдаемых данных, d j obs , как для его слева и справа от i (где j> i соответствует будущему, а j соответствует прошлому).Фильтр s i , следовательно, не причинный с коэффициентами, которые симметричны относительно текущей стоимости ( i = 1). Коэффициенты необходимо суммировать до единицы, чтобы сохранить общую амплитуду данных. Эти черты проиллюстрированы в трехточечном сглаживающем фильтре (см. Уравнение 4.15):
(9.21) s = [s0, s1, s2] T = [¼, ½, T] undefinedT
Он использует настоящее (элемент, i ), прошлое (элемент, i — 1) и будущее (элемент, i + 1) d obs для расчета d i сглаженный :
( 9.22) сглаженные данные = средневзвешенное значение наблюдаемых данныхordismooth = di − 1obs + ½diobs + ¼di + 1obs
Пока фильтр имеет конечную длину, L , мы можем рассматривать вывод как задержанный относительно ввода, и сама операция фильтрации является причинной:
(9.23) сглажено и задержано = ¼diobs + ½di − 1obs + ¼di − 2obs
В этом случае задержка составляет одну выборку. В общем, задержка составляет ( л — 1) / 2 отсчета. Длина L контролирует плавность фильтра, при этом большие L s соответствуют большим степеням сглаживания (Рисунок 9.9).
Рисунок 9.9. Сглаживание гидрографа реки Нойз. (A) Наблюдаемые данные. (B) Наблюдаемые данные сглажены симметричным трехточечным треугольным фильтром. (C) Наблюдаемые сглаженные данные с симметричным треугольным фильтром из 21 точки. Для наглядности нанесены только первые 500 дней. MatLab скрипт eda09_07.
Вышеупомянутый фильтр имеет треугольную форму, так как он линейно увеличивается до своего центрального значения, а затем линейно снижается. Он весит центральную систему данных больше, чем ее соседи. Это контрастирует с унифицированным фильтром , который имеет постоянные коэффициенты L , каждый из которых имеет амплитуду, L — 1 .Он одинаково взвешивает все данные L . Возможны и многие другие формы. Важным вопросом является оптимальная форма сглаживающего фильтра, s .
Один из способов понять выбор фильтра — изучить его влияние на автокорреляционную функцию сглаженного временного ряда. Интуитивно мы ожидаем, что сглаживание расширяет автокорреляцию, потому что оно позволяет меньше различать временные ряды между выборками. Это поведение можно проверить, вычислив автокорреляцию сглаженных временных рядов
(9.24) {s (t) * d (t)} ⋆ {s (t) * d (t)} = s (−t) * d (−t) * s (t) * d (t) = {s (t) ⋆s (t)} * {d (t) ⋆d (t)}
Таким образом, автокорреляция сглаженного временного ряда — это автокорреляция исходного временного ряда, свернутого с автокорреляцией сглаживающего фильтра. Автокорреляционная функция сглаживающего фильтра — это широкая функция. При свертке с функцией автокорреляции данных он сглаживает и расширяет их. Фильтры разной формы имеют функции автокорреляции с разной степенью широты.Каждый результат дает сглаженные данные, имеющие несколько иную форму автокорреляционной функции.
Другой способ понять влияние фильтра — изучить его влияние на спектральную плотность мощности сглаженного временного ряда. Идея сглаживания состоит в том, чтобы подавить высокочастотные колебания данных, оставив низкие частоты неизменными. Одним из показателей качества фильтра является равномерность подавления. С этой точки зрения фильтры, которые равномерно подавляют высокие частоты, лучше фильтров, которые подавляют их неравномерно.
Поведение фильтра можно понять с помощью теоремы о свертке (раздел 6.11), которая утверждает, что преобразование Фурье свертки является продуктом преобразований. Таким образом, преобразование Фурье сглаженных данных составляет всего лишь
(9,25) d ~ smoothhed (ω) = s ~ (ω) d ~ obs (ω)
То есть преобразование сглаженных данных является преобразованием наблюдаемые данные, умноженные на преобразование фильтра. Таким образом, влияние фильтра можно понять, исследуя его амплитудную спектральную плотность, | s ~ (ω) |.
Однородный или товарный вагон , фильтр с шириной T и амплитудой T — 1 проще всего анализировать:
(9,26) с ~ (ω) = 1T∫ T / 2T / 2exp (−iωt) dt = 2T∫0T / 2cos (ωt) dt = 2Tundefinedsin (ωt) ω | 0T / 2 = sincωT2π
Здесь мы использовали правило: exp ( −iωt ) = cos ( ωt ) + i sin ( ωt ) и определение sin c ( x ) = sin ( πx ) / ( πx ).Функция косинуса симметрична относительно начала координат, поэтому ее интеграл на интервале (−½ T , + ½ T ) вдвое больше, чем на интервале (0, + ½ T ). Синусоидальная функция антисимметрична, поэтому ее интеграл на интервале (−½ T , 0) отменяет ее интеграл на интервале (0, + ½ T ). Хотя функция sinc (рисунок 9.10) уменьшается с частотой, она происходит неравномерно, с множеством боковых лепестков , вдоль оси частоты. Он не гасит плавно высокие частоты и, с этой точки зрения, является плохим фильтром.
Рисунок 9.10. Амплитудная спектральная плотность равномерных сглаживающих фильтров (A) Фильтр длины, L = 3. (B) Фильтр длины, L = 21. MatLab script eda09_08.
Фильтр, основанный на нормальной кривой, не будет иметь боковых лепестков (рисунок 9.11), как преобразование Фурье нормальной кривой с дисперсией, σ t 2 , во времени это нормальная кривая с дисперсией, σ ω 2 = σ t −2 , по частоте (Уравнение 6.27). Это лучший фильтр с точки зрения плавного и равномерного демпфирования высоких частот. Однако нормальный фильтр бесконечен по длине и на практике должен быть усечен, что приводит к появлению небольших боковых лепестков. Обратите внимание, что эффективная ширина фильтра зависит не только от его длины, L , но и от его формы. Величина 2 σ t является хорошей мерой его эффективной ширины, где σ t 2 — его изменение во времени.Так, например, нормальный фильтр с σ, t = 6,05 отсчетов имеет примерно такую же эффективную ширину, что и однородный фильтр с L = 21, который имеет дисперсию около 6 2 (сравните рисунки 9.10 и 9.11).
Рисунок 9.11. Амплитудная спектральная плотность обычных сглаживающих фильтров. (A) Фильтр с дисперсией, равной дисперсии равномерного фильтра с длиной L = 3. (B) Фильтр с дисперсией, равной дисперсии равномерного фильтра с длиной L = 21. MatLab скрипт eda09_09.
Сглаживающий фильтр — SubSurfWiki
Фильтры — это простые математические операторы, которые при свертке с каротажными данными, сейсмическими данными или данными интерпретации подчеркивают одни аспекты данных и не выделяют другие. Например, обычным шагом в интерпретации сейсмического горизонта является применение фильтра, который уменьшает высокие пространственные частоты в данных, которые в основном связаны с шумом, и подчеркивает более низкие частоты. Это сглаживающий фильтр .
В этой статье описывается общий метод, а также приводятся некоторые конкретные примеры фильтров сглаживания и их результатов.
Линейные фильтры
Примеры линейных ядер.На любом цифровом изображении или сейсмическом горизонте линейные фильтры работают путем свертки с движущимся окном, называемым ядром. Входной пиксель находится в центре ядра. Ненулевая часть ядра называется опорой фильтра. Большинство фильтров имеют квадратную опору, хотя некоторые из них имеют прямоугольную или круглую форму.Здесь показаны некоторые примеры ядер.
Линейные фильтры работают одинаково с каждым входным пикселем, применяя одинаковые веса к одним и тем же пикселям в опоре. Следовательно, они очень быстрые, но не чувствительны к характеру данных, сглаживая все одинаково. Это их самая большая слабость для геофизических приложений, поскольку, скажем, разломы и границы канала сглаживаются вместе с шумом и артефактами захвата.
Примеры включают средний и гауссов фильтры.
Нелинейные фильтры
Лезвия важны для человеческого восприятия, и обычно желательно сохранить их резкость. Многие нелинейные фильтры сохраняют края, поэтому они важны для обработки изображений. Я думаю, что они относительно мало используются переводчиками.
Нелинейные фильтры сохраняют края, потому что они адаптивны. Не каждый пиксель в опоре влияет на результат. Пиксели, которые действительно вносят вклад, выбираются по некоторому статистическому критерию, обычно это связано с тем, насколько пиксели похожи друг на друга или на входной пиксель.Преимущество этого состоит в том, что зашумленные пиксели вносят меньший вклад в выходной пиксель, а края сохраняются или даже улучшаются.
Примеры включают:
Выбор фильтра
Следующая таблица взята из Hall (2007 [1] ). + указывает на хорошую пригодность, а ++ указывает на отличную пригодность.
| Тип | Случайный шум | Колючий шум | Края сохранены | Комментариев:||
|---|---|---|---|---|---|
| Среднее | линейный | + | Gaussian — лучший выбор | ||
| Гауссовский | линейный | + | Меньше подвержены скачкам, чем среднее | ||
| Консервативный | Нелинейное | + | + | Удаляет только очень редкие шипы | |
| Среднее усеченное | Нелинейное | ++ | ++ | Лучше всего, если края отсутствуют или не нужны | |
| Режим | Нелинейное | + | + | + | Используйте только для дискретных атрибутов или атрибутов класса |
| Медиана | Нелинейное | ++ | ++ | + | Хороший универсал |
| СНН | Нелинейное | ++ | ++ | ++ | Лучший универсал |
| Кувахара | Нелинейное | + | ++ | ++ | Улучшает края, но сначала использует медианный фильтр |
Список литературы
- ↑ Холл, М. (2007).Smooth operator: сглаживание сейсмических горизонтов и атрибутов. The Leading Edge 26 (1), январь 2007 г., стр. 16-20. DOI: 10.1190 / 1.2431821
сглаживающих фильтров
сглаживающих фильтров| Сглаживающие фильтры используются для улучшения зашумленных изображений (за счет размытия). Этот фильтр генерирует среднее значение по области изображения 3 x 3. Технику еще называют движущихся окно усреднения . |
Пример сглаживания
Изображение справа представляет собой сглаженную версию изображения слева.Красный, зеленый, и синие компоненты отфильтровывали отдельно.
Текстовый файл с описанием используемого фильтра имел следующее содержание:
3 х 3 равновзвешенных размер 3 3 1 1 1 1 1 1 1 1 1 9
Желаемые свойства для сглаживающих фильтров
- Постоянная область изображения не должна изменяться.
Это выполняется, если сумма коэффициентов в фильтре равна единице.
Это выполняется, если фильтр не содержит отрицательных элементов
Предпочтительный нечетный размер фильтра
Фильтры с нечетными числами строк и столбцов предпочтительны, потому что существует уникальное центральное положение
| Фильтры с четными числами строк и столбцов могут быть встроены в нечетный размер матрица. |
| Удаление нулевых строк и столбцов делает фильтр более эффективным, но его интерпретация сейчас неоднозначна.Вышеупомянутый фильтр 3 x 3 можно записать четырьмя способами: и изготовить такой же фильтр 2 x 2. |
Линейные комбинации отфильтрованных изображений
Линейные комбинации отфильтрованных изображений (включая исходное изображение) могут использоваться для варьировать конечный эффект.
Линейная интерполяция между двумя изображениями называется альфа-смешением .
Фильтры можно смешивать, а не результирующие изображения, потому что свертка операция линейная .
Пример смешанного фильтра
Повторная свертка
Повторяющиеся свертки могут быть сгруппированы по закону ассоциативности .
Пример
Съемные фильтры
Разделимые фильтры могут быть представлены как произведение векторов строк и столбцов в виде показано ниже.
Эту конструкцию можно понимать как матричное произведение, свертку или как внешнюю произведение двух векторов.
[1 n 1] фильтры
| Фильтр [1 2 1] может быть построен на основе относительных размеров областей, показанных на желтый справа. Конечным эффектом является равномерный вес на 2 x 2 пикселя. область. |
Биномиальные фильтры
Биномиальные фильтры генерируются путем применения биномиального разложения.
Каждый член разложения (с p = q = 1/2) соответствует элементу в фильтре.Например, одномерный фильтр четвертого порядка дает
Двумерные фильтры получают путем взятия внешнего продукта одномерного векторы, как описано ранее.
Пример фильтра (4-й порядок)
Поддерживает Джон Лумис, последнее обновление 14 июня 1997 г.
python — Как правильно сгладить кривую?
На этот вопрос уже дан исчерпывающий ответ, поэтому я думаю, что анализ предложенных методов во время выполнения был бы интересен (во всяком случае, это было для меня).Я также посмотрю на поведение методов в центре и по краям зашумленного набора данных.
| время выполнения в сек | время выполнения в с
метод | список Python | массив numpy
-------------------- | -------------- | ------------
регрессия ядра | 23.93405 | 22,75967
низкий | 0,61351 | 0,61524
наивный средний | 0,02485 | 0,02326
другие * | 0,00150 | 0,00150
fft | 0,00021 | 0,00021
numpy convolve | 0.00017 | 0,00015
* savgol с разными функциями подгонки и некоторыми методами numpy
Регрессия ядра плохо масштабируется, Lowess немного быстрее, но оба дают плавные кривые. Savgol — средний по скорости, он может давать как скачкообразные, так и плавные результаты, в зависимости от степени полинома. БПФ работает очень быстро, но работает только с периодическими данными.
Методы скользящего среднего с numpy быстрее, но, очевидно, создают график с шагами в нем.
Я создал 1000 точек данных в форме кривой греха:
размер = 1000
х = нп.linspace (0, 4 * np.pi, размер)
y = np.sin (x) + np.random.random (размер) * 0,2
data = {"x": x, "y": y}
Я передаю их в функцию для измерения времени выполнения и построения графика соответствия:
def test_func (f, label): # f: дескриптор функции одного из методов сглаживания
начало = время ()
для i в диапазоне (5):
arr = f (данные ["y"], 20)
print (f "{label: 26s} - время: {time () - start: 8.5f}")
plt.plot (данные ["x"], arr, "-", label = label)
Я тестировал множество различных функций сглаживания. arr — это массив значений y для сглаживания, а span — параметр сглаживания. Чем ниже, тем лучше соответствие будет исходным данным, чем выше, тем более гладкой будет результирующая кривая.
def smooth_data_convolve_my_average (arr, span):
re = np.convolve (arr, np.ones (span * 2 + 1) / (span * 2 + 1), mode = "same")
# Часть "my_average": сужает окно усреднения на той стороне, которая
# выходит за пределы данных, сохраняет другую сторону того же размера, что и заданный
# по "диапазону"
re [0] = np.средний (прибл [: промежуток])
для i в диапазоне (1, span + 1):
re [i] = np.average (arr [: i + span])
re [-i] = np.average (arr [-i - span:])
возвратиться
def smooth_data_np_average (arr, span): # мой оригинальный, наивный подход
return [np.average (arr [val - span: val + span + 1]) для val в диапазоне (len (arr))]
def smooth_data_np_convolve (arr, диапазон):
return np.convolve (arr, np.ones (span * 2 + 1) / (span * 2 + 1), mode = "same")
def smooth_data_np_cumsum_my_average (arr, span):
cumsum_vec = нп.кончает (обр.)
moving_average = (cumsum_vec [2 * промежуток:] - cumsum_vec [: - 2 * промежуток]) / (2 * промежуток)
# Снова часть "my_average". Немного отличается от предыдущего, потому что
# Скользящее среднее из cumsum короче входного и требует дополнения
спереди, сзади = [np.average (arr [: span])], []
для i в диапазоне (1, промежуток):
front.append (np.average (arr [: i + span]))
back.insert (0, np.average (arr [-i - span:]))
back.insert (0, np.average (arr [-2 * span:]))
return np.concatenate ((спереди, moving_average, назад))
def smooth_data_lowess (arr, диапазон):
х = нп.linspace (0, 1, len (обр))
return sm.nonparametric.lowess (arr, x, frac = (5 * span / len (arr)), return_sorted = False)
def smooth_data_kernel_regression (arr, диапазон):
# Параметр сглаживания "span" игнорируется. Если ты знаешь как
# включите это с регрессией ядра, пожалуйста, прокомментируйте ниже.
kr = KernelReg (arr, np.linspace (0, 1, len (arr)), 'c')
return kr.fit () [0]
def smooth_data_savgol_0 (arr, диапазон):
вернуть savgol_filter (arr, span * 2 + 1, 0)
def smooth_data_savgol_1 (прибл, промежуток):
вернуть savgol_filter (arr, span * 2 + 1, 1)
def smooth_data_savgol_2 (прибл, промежуток):
вернуть savgol_filter (arr, span * 2 + 1, 2)
def smooth_data_fft (arr, span): # масштабирование "span" открыто для предложений
w = fftpack.rfft (прибл)
спектр = w ** 2
cutoff_idx = спектр <(спектр.max () * (1 - np.exp (-span / 2000)))
w [cutoff_idx] = 0
вернуть fftpack.irfft (w)
Скорость
Время выполнения более 1000 элементов, протестировано на списке Python, а также на массиве numpy для хранения значений.
метод | список Python | массив numpy
-------------------- | ------------- | ------------
регрессия ядра | 23.93405 с | 22.75967 с
низкий | 0,61351 с | 0.61524 с
набухший средний | 0,02485 с | 0,02326 с
savgol 2 | 0,00186 с | 0,00196 с
savgol 1 | 0,00157 с | 0,00161 с
савгол 0 | 0,00155 с | 0,00151 с
numpy convolve + me | 0,00121 с | 0,00115 с
numpy cumsum + me | 0,00114 с | 0,00105 с
fft | 0,00021 с | 0,00021 с
numpy convolve | 0,00017 с | 0,00015 с
В частности, регрессия ядра очень медленно вычисляет более 1k элементов, lowess также не работает, когда набор данных становится намного больше. numpy convolve и fft особенно быстры. Я не исследовал поведение во время выполнения (O (n)) при увеличении или уменьшении размера выборки.
Поведение кромки
Я разделю эту часть на две части, чтобы изображение было понятным.
Методы на основе Numpy + savgol 0 :
Эти методы вычисляют среднее значение данных, график не сглаживается. Все они (за исключением numpy.cumsum ) приводят к одному и тому же графику, когда окно, которое используется для вычисления среднего, не касается края данных.Несоответствие numpy.cumsum , скорее всего, связано с ошибкой «на единицу» в размере окна.
Если метод должен работать с меньшим объемом данных, то поведение ребер различно:
-
savgol 0: продолжается с константой до края данных (savgol 1иsavgol 2заканчиваются линией и параболой соответственно) -
среднее число: останавливается, когда окно достигает левой стороны данных и заполняет эти места в массиве с помощьюNan, то же поведение, что и методmy_averageс правой стороны -
numpy convolve: довольно точно следует за данными.Я подозреваю, что размер окна уменьшается симметрично, когда одна сторона окна достигает края данных -
my_average/me: мой собственный метод, который я реализовал, потому что меня не устраивали другие. Просто сжимает часть окна, которая выходит за пределы данных до края данных, но сохраняет исходный размер окна с другой стороны, заданный с интервалом
Сложные методы:
Все эти методы хорошо подходят к данным. савголь 1 заканчивается линией, савголь 2 параболой.
Поведение кривой
Для демонстрации поведения различных методов в середине данных.
Различные фильтры savgol и average дают грубую линию, lowess , fft и регрессия ядра дают гладкую подгонку. lowess , кажется, срезает углы при изменении данных.
У меня есть данные журнала Raspberry Pi для развлечения, и визуализация оказалась небольшой проблемой.Все точки данных, за исключением использования ОЗУ и трафика Ethernet, записываются только дискретными шагами и / или изначально зашумлены. Например, датчик температуры выдает только целые градусы, но разница между последовательными измерениями составляет до двух градусов. Такой график рассеяния не дает никакой полезной информации. Поэтому для визуализации данных мне понадобился какой-то метод, который не требует слишком больших вычислительных затрат и позволяет получить скользящее среднее. Я также хотел приятного поведения на границах данных, так как это особенно влияет на последнюю информацию при просмотре данных в реальном времени.Я остановился на методе numpy convolve с my_average , чтобы улучшить поведение края.
Сглаживающие фильтры
- itk-DiscreteGaussianImage
Этот фильтр вычисляет свертку входного изображения с гауссовым ядром. Одномерная функция Гаусса дискретизируется на ядре свертки. Размер ядра увеличивается до тех пор, пока не будет достаточно дискретных точек в гауссиане, чтобы гарантировать, что максимальная ошибка, заданная пользователем, не будет превышена.Использование: itk-DiscreteGaussianImage inputImageFile outputImageFile Размер [гауссовская дисперсия] [максимальная ширина ядра]
Ниже представлено изображение и отфильтрованная версия с дисперсией = 30, шириной = 0,5.
- itk-BinomialBlurImage
Этот фильтр вычисляет среднее значение ближайшего соседа по каждому измерению. Процесс повторяется несколько раз, как указано пользователем. Большое количество итераций приблизит свертку с гауссианой.
Использование: itk-BinomialBlurImage inputImageFile outputImageFile повторений измерений
Ниже показано исходное изображение и изображение, отфильтрованное 1, 2 и 5 раз:
- itk-RecursiveGaussianImage Этот классический метод сглаживания изображения с помощью ядра Гаусса является медленным, когда стандартное отклонение Гаусса велико.2 фильтра.
Использование: itk-RecursiveGaussianImage inputImageFile outputImageFile Dimension sigma
Ниже представлено исходное изображение, отфильтрованное с помощью sigma = 1,3,5:
itk-GradientAnisotropicDiffusionImage
Anisotropic diffusion - это нелинейный сглаживающий фильтр. Он создает сглаженное по Гауссу изображение, которое является решением уравнения теплопроводности, с переменной проводимостью для ограничения сглаживания по краям. Для этого конкретного фильтра член проводимости является функцией величины градиента изображения в каждой точке.Для этого фильтра требуются 3 параметра: количество итераций, которые необходимо выполнить, временной шаг и параметр проводимости, используемый при вычислении эволюции набора уровней. Типичные значения: количество итераций = 5, временной шаг = 0,25 для 2D, 0,125 для 3D.
Использование: itk-GradientAnisotropicDiffusionImage inputImageFile outputImageFile Размер num_iterations временной шаг проводимости
Ниже приведено исходное изображение и изображение с проводимостью = 1,0 и 5,0; временной шаг = 0,125, итераций = 5:
- itk-CurvatureAnisotropicDiffusionImage
Этот фильтр выполняет анизотрипическую диффузию на изображении с использованием модифицированного уравнения диффузии кривизны (MCDE).MCDE не проявляет улучшающих кромок свойств классической анизотропной диффузии.
Использование: itk-CurvatureAnisotropicDiffusionImage inputImageFile outputImageFile Размер num_iterations временной шаг проводимости
Ниже приведено исходное изображение и изображение с проводимостью = 1,0 и 5,0; временной шаг = 0,125, итераций = 5:
- itk-CurvatureFlowImage
Этот фильтр выполняет сглаживание с сохранением границ, аналогичное классической анизотропной диффузии. Фильтр использует формирование набора уровней, при котором контуры изоинтенсивности в изображении рассматриваются как наборы уровней, а пиксели определенной интенсивности образуют один набор уровней.Затем функция установки уровня развивается под управлением уравнения диффузии.
Использование: itk-CurvatureFlowImage inputImageFile outputImage Размер файла num_iterations timestep
Ниже приведено исходное изображение и изображение с временным шагом = 0,125, итерациями = 5:
- itk-MinMaxCurvatureFlowImage
Это вариант фильтра кривизны потока, описанного выше. Диффузия включается или выключается в зависимости от масштаба шума, который нужно удалить.Масштаб определяется определяемой пользователем окрестностью для каждого пикселя, задаваемой значением радиуса.
Использование: itk-MinMaxCurvatureFlowImage inputImageFile outputImageFile Размер num_iterations Радиус временного шага
Ниже представлено исходное изображение и изображение с радиусом = 1, временным шагом = 0,125, итерациями = 5 и 20:
- itk-BateralImage
Этот фильтр выполняет сглаживание с использованием окрестностей как домена, так и диапазона. Для сглаживания используются два гауссовых ядра: одно в области изображения, а другое - в области изображения.В результате получается изображение, которое сглаживается в однородных областях, но с сохранением краев. Результаты аналогичны анизотропному диффузионному фильтру, но реализация является неитеративной. Требуются два параметра: для каждого измерения в пространстве используется набор значений сигмы. Второе значение сигмы используется для сглаживания диапазона изображения.
Использование: itk-BateralImage inputImageFile outputImageFile Dimension domainSigmas rangeSigma
Ниже приведено исходное изображение и изображение, отфильтрованное со всеми значениями сигмы, установленными на 5.0:
itk-rgbGradientAnisotropicDiffusionImage
Этот фильтр реализует N-мерную версию классического квадрата анизотропной диффузии Перона-Малика для векторных изображений. Перона и Малик представили альтернативу линейной фильтрации - анизотропную диффузию. Сглаженное по Гауссу изображение - это единственный временной интервал решения уравнения теплопроводности. В анизотропной диффузии для этого уравнения используется член переменной проводимости, который зависит от структуры изображения.Идея здесь состоит в том, чтобы ограничить сглаживание по краям, чтобы изображения оставались резкими по краям, а остальная часть изображения сглаживалась. Подход векторной анизотропной диффузии может быть применен к цветным изображениям. Каждый компонент RGB распространяется независимо. Этот фильтр требует тех же параметров, что и другие градиентные анизотропные диффузионные фильтры:
Использование: itk-rgbGradientAnisotropicDiffusionImage inputImageFile outputImage Размер файла num_iterations timestep
Эти изображения ниже увеличены вдвое, чтобы показать диффузию после 20 временных шагов size = 0.05:
itk-VectorCurvatureAnisotropicDiffusionImage
Этот фильтр выполняет анизотрипную диффузию на векторном изображении с использованием модифицированного уравнения диффузии кривизны. Компоненты вектора, в данном случае компоненты RGB, распространяются независимо друг от друга.
Использование: itk-VectorCurvatureAnisotropicDiffusionImage inputImageFile outputImage Размер файла num_iterations timestep
Приведенные ниже изображения увеличены в два раза, чтобы показать диффузию после 20 временных шагов size = 0.05:
OpenCV: сглаживание изображений
целей
Learn to:
- Размытие изображений с помощью различных фильтров нижних частот
- Применение настраиваемых фильтров к изображениям (2D-свертка)
2D-свертка (фильтрация изображений)
Как и в случае одномерных сигналов, изображения также можно фильтровать с помощью различных фильтров нижних частот (LPF), фильтров верхних частот (HPF) и т. Д. LPF помогает удалять шум, размытие изображений и т. Д. Фильтры HPF помогают находить края в изображениях.
OpenCV предоставляет функцию cv.filter2D () для свертки ядра с изображением. В качестве примера мы попробуем применить фильтр усреднения к изображению. Ядро усредняющего фильтра 5x5 будет выглядеть следующим образом:
\ [K = \ frac {1} {25} \ begin {bmatrix} 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 \ end {bmatrix} \]
Операция работает следующим образом: оставьте это ядро над пикселем, добавьте все 25 пикселей ниже этого ядра, возьмите среднее значение и замените центральный пиксель новым средним значением.Эта операция продолжается для всех пикселей изображения. Попробуйте этот код и проверьте результат:
import numpy as np
import cv2 as cv
from matplotlib import pyplot as plt
kernel = np.ones ((5,5), np.float32) / 25
plt.subplot (121), plt.imshow (img), plt.title ('Исходный')
plt.xticks ([]), plt.yticks ([])
plt.subplot (122), plt. imshow (dst), plt.title ('Усреднение')
plt.xticks ([]), plt.yticks ([])
plt.show ()
Результат:
изображение
Размытие изображения (сглаживание изображения)
Размытие изображения достигается за счет свертки изображения с помощью ядра фильтра нижних частот. Это полезно для удаления шума. Фактически он удаляет высокочастотный контент (например, шум, края) из изображения. Таким образом, края в этой операции немного размыты (есть также методы размытия, которые не размывают края). OpenCV предоставляет четыре основных типа методов размытия.
1. Среднее значение
Это делается путем свертки изображения с помощью нормализованного блочного фильтра.Он просто берет среднее значение всех пикселей под областью ядра и заменяет центральный элемент. Это делается функцией cv.blur () или cv.boxFilter () . Дополнительную информацию о ядре смотрите в документации. Мы должны указать ширину и высоту ядра. Нормализованный прямоугольный фильтр 3x3 будет выглядеть следующим образом:
\ [K = \ frac {1} {9} \ begin {bmatrix} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \ end {bmatrix} \]
- Примечание
- Если вы не хотите использовать нормализованный прямоугольный фильтр, используйте cv.boxFilter () . Передайте функции аргумент normalize = False.
Посмотрите пример демонстрации ниже с ядром размером 5x5:
import cv2 as cv
import numpy as np
from matplotlib import pyplot as plt
plt.subplot (121), plt.imshow (img) , plt.title ('Оригинал')
plt.xticks ([]), plt.yticks ([])
plt.subplot (122), plt.imshow (размытие), plt.title ('Blurred')
plt.xticks ([]), plt.yticks ([])
plt.show ()
Результат:
изображение
2.Размытие по Гауссу
В этом методе вместо прямоугольного фильтра используется гауссово ядро. Это делается с помощью функции cv.GaussianBlur () . Мы должны указать ширину и высоту ядра, которые должны быть положительными и нечетными. Мы также должны указать стандартное отклонение в направлениях X и Y, sigmaX и sigmaY соответственно. Если указан только sigmaX, sigmaY считается таким же, как sigmaX. Если оба даны как нули, они рассчитываются исходя из размера ядра. Размытие по Гауссу очень эффективно для удаления гауссовского шума с изображения.
Если хотите, вы можете создать ядро Гаусса с помощью функции cv.getGaussianKernel () .
Приведенный выше код можно изменить для размытия по Гауссу:
Результат:
изображение
3. Медианное размытие
Здесь функция cv.medianBlur () берет медианное значение всех пикселей в области ядра, а центральный элемент заменяется этим медианным значением. Это очень эффективно против шума с солью и перцем на изображении.Интересно, что в вышеупомянутых фильтрах центральный элемент - это вновь вычисленное значение, которое может быть значением пикселя в изображении или новым значением. Но при медианном размытии центральный элемент всегда заменяется некоторым значением пикселя в изображении. Это эффективно снижает шум. Размер его ядра должен быть положительным нечетным целым числом.
В этой демонстрации я добавил 50% шума к нашему исходному изображению и применил медианное размытие. Проверить результат:
Результат:
изображение
4.Двусторонняя фильтрация
cv.bilateralFilter () очень эффективно удаляет шум, сохраняя при этом края острыми. Но работа медленнее по сравнению с другими фильтрами. Мы уже видели, что фильтр Гаусса берет окрестности вокруг пикселя и находит его средневзвешенное значение по Гауссу. Этот фильтр Гаусса является функцией только пространства, то есть при фильтрации учитываются соседние пиксели. При этом не учитывается, имеют ли пиксели почти одинаковую интенсивность. Он не учитывает, является ли пиксель краевым пикселем или нет.Таким образом, он также размывает края, чего мы не хотим делать.
Двусторонняя фильтрация также использует фильтр Гаусса в пространстве, но еще один фильтр Гаусса, который является функцией разности пикселей. Функция Гаусса пространства гарантирует, что только близлежащие пиксели рассматриваются для размытия, а функция Гаусса разницы интенсивности гарантирует, что только те пиксели, интенсивность которых аналогична центральному пикселю, рассматриваются для размытия. Таким образом, он сохраняет края, поскольку пиксели по краям будут иметь большое изменение интенсивности.
В приведенном ниже примере показано использование двустороннего фильтра (подробные сведения об аргументах см. В документации).
Результат:
изображение
Видите, текстура на поверхности исчезла, но края остались.
Дополнительные ресурсы
- Подробная информация о двусторонней фильтрации
Упражнения
Пространственная фильтрация и ее типы
Пространственная фильтрация и ее типы
Пространственная фильтрация Метод используется непосредственно на пикселях изображения.Обычно считается, что маска добавляется по размеру, чтобы у нее был определенный центральный пиксель. Эта маска перемещается по изображению таким образом, чтобы центр маски пересекал все пиксели изображения.
Классификация на основе линейности:
Есть два типа:
1. Линейный пространственный фильтр 2. Нелинейный пространственный фильтр
Общая классификация:
Сглаживающий пространственный фильтр: Сглаживающий фильтр используется для размытия и уменьшения шума в изображении.Размытие - это этапы предварительной обработки для удаления мелких деталей, а шумоподавление достигается за счет размытия.
Типы сглаживающих пространственных фильтров:
1. Линейный фильтр (средний фильтр) 2. Фильтр статистики порядка (нелинейный)
Они объясняются ниже.
- Средний фильтр:
Линейный пространственный фильтр - это просто среднее значение пикселей, содержащихся в окрестности маски фильтра.Идея заключается в замене значения каждого пикселя изображения на среднее значение уровней серого в окрестности, определяемой маской фильтра.Типы среднего фильтра:
- (i) Усредняющий фильтр: Используется для уменьшения детализации изображения. Все коэффициенты равны.
- (ii) Фильтр взвешенного усреднения: В этом случае пиксели умножаются на разные коэффициенты. Центральный пиксель умножается на большее значение, чем средний фильтр.
- Фильтр статистики порядка:
Он основан на упорядочении пикселей, содержащихся в области изображения, охваченной фильтром.Он заменяет значение центрального пикселя значением, определенным результатом ранжирования. Края лучше сохраняются при такой фильтрации.Типы фильтра статистики заказов:
- (i) Минимальный фильтр: Фильтр 0-го процентиля является минимальным фильтром. Значение центра заменяется наименьшим значением в окне.
- (ii) Максимальный фильтр: Фильтр 100-го процентиля - это максимальный фильтр. Значение центра заменяется самым большим значением в окне.
- (iii) Медианный фильтр: Учитывается каждый пиксель изображения. Первые соседние пиксели сортируются, и исходные значения пикселя заменяются медианой списка.
Пространственный фильтр повышения резкости: Он также известен как производный фильтр. Цель пространственного фильтра повышения резкости прямо противоположна пространственному фильтру сглаживания. Его основной упор делается на устранение размытости и выделение краев. Он основан на производной первого и второго порядка.
Производная первого порядка:
- Должен быть равен нулю в плоских сегментах.
- Должен быть ненулевым в начале шага уровня серого.
- На пандусах должно быть ненулевое значение.
Производная первого порядка в 1-D определяется как:
f '= f (x + 1) - f (x)
Производная второго порядка:
- Должен быть равен нулю на плоских участках.
- Должен быть равен нулю в начале и в конце пандуса.
- Должен быть равен нулю вдоль пандусов.


