1.2. Законы Кирхгофа
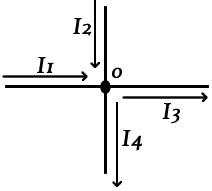
Первый закон Кирхгофа: алгебраическая сумма всех токов, втекающих в любой узел, равна нулю. Токи, втекающие в узел, условно принимаются положительными, а вытекающие из него — отрицательными (или наоборот). Если, например, в узел втекает ток II, а вытекают токи 12 и 13, то первый закон Кирхгофа может быть записан в виде выражения: 11-12-13=0.
Второй закон Кирхгофа: алгебраическая сумма ЭДС любого замкнутого контура равна алгебраической сумме падений напряжений на всех участках контура.
При применении второго закона Кирхгофа необходимо учитывать знаки ЭДС и выбранное направление токов на всех участках контура. Направление обхода контура выбирается произвольным; при записи левой части равенства ЭДС, направления которых совпадают с выбранным направлением обхода независимо от направления протекающего через них тока, принимаются положительными, а ЭДС обратного направления принимаются отрицательными. При записи правой части равенства со знаком плюс берутся падения напряжения на тех участках, в которых положительное направление тока совпадает с направлением обхода независимо от направления ЭДС на этих участках, и со знаком минус — на участках, в которых положительное направление тока противоположно направлению обхода.
Общая методика применения законов Кирхгофа для расчета сложных многоконтурных цепей такова. Устанавливается число неизвестных токов, которое равно числу ветвей р. Для каждой ветви задается положительное направление тока. Число независимых уравнений, составляемых по первому закону Кирхгофа, равно числу узлов q (точек соединения не менее чем трех проводников) минус единица, т.е.д-1. Число независимых уравнений, составляемых по второму закону Кирхгофа, равно числу контуров n=p-q+\. Общее число уравнений, составляемых по первому и второму законам Кирхгофа, равно числу неизвестных токов р. Решение этой системы уравнений и дает значения искомых токов.
Для иллюстрации изложенной методики рассмотрим многоконтурную цепь постоянного тока на рис. 5.4. В этой цепи всего три узла: А, В и С (q =3), следовательно, число независимых уравнений, составляемых по первому закону Кирхгофа, будет на единицу меньше, т.е. два. При числе ветвей цепи р=5 число контуров п=5-3+1=3, следовательно, по второму закону Кирхгофа можно составить три взаимно независимых уравнения. Таким образом, общее число независимых уравнений, составляемых по первому и второму законам Кирхгофа, будет равно числу неизвестных токов в пяти ветвях схемы.
Выберем положительные направления токов, которые на схеме обозначены соответствующим включением амперметров. Например, ток II течет справа налево и втекает в узел А (положительное направление тока), поскольку отрицательная клемма, отмеченная утолщенной черной линией, находится слева и ток через амперметр будет течь справа налеро. Ток 12 вытекает из узла А, поскольку ток через одноименный амперметр будет течь сверху вниз (к отрицательному зажиму, расположенному на нижней грани иконки) и т.д.
Составим систему уравнений Кирхгофа:
для узла А 11-12+13-15=0;
для узла В -11-13-14=0;
для контура ABFA E1+E2=I1-R1-I3-R3;
для контура АВСА E3=-I3-R3+I4-R4+I5-R5;
для контура ADCA E2=I2-R2+I5-R5.
После подстановки в полученные уравнения числовых значений они приобретают следующий вид:
11-12+13-15=0;
11-13-14=0;
6-11-10-13=20;
-10-13+2,5-14+15-15=5;
5-12+15-15=70. Решая полученную систему уравнений, будем иметь: 11=5 А; 12=8 А; 13=1 А;
14=- 6 А; 15=2 А, что соответствует показаниям приборов. Отрицательный знак для тока 14 означает, что истинное направление этого тока противоположно принятому.
Контрольные вопросы и задания
1. Сформулируйте первый и второй законы Кирхгофа. Чем отличается второй закон Кирхгофа от закона Ома для полной цепи?
2. Проведите расчеты по определению токов в ветвях с использованием законов Кирхгофа для цепей на рис. 5.5. После подключения к схемам необходимых измерительных приборов проведите их моделирование. Сравните полученные данные с результатами расчетов.
Законы Кирхгофа

В цепях, состоящих из последовательно соединенных источника и приемника энергии, соотношения между током, ЭДС и сопротивлением всей цепи или , между напряжением и сопротивлением на каком-либо участке цепи определяется законом Ома.
На практике в цепях, токи, от какой-либо точки, идут по разным путям.
Точки, где сходятся несколько проводников, называются узлами, а участки цепи, соединяющие два соседних узла, ветвями.
В замкнутой электрической цепи ни в одной ее точке не могут скапливаться электрические заряды так, как это вызвало бы изменение потенциалов точек цепи. Поэтому электрические заряды притекающие к какому-либо узлу в единицу времени, равны зарядам, утекающим от этого узла за ту же единицу.
В узле А цепь разветвляется на четыре ветви, которые сходятся в узел В.
Обозначим токи в неразветвленной части цепи — I, а в ветвях соответственно
I1
, I2, I3, I4.У этих токов в такой цепи будет соотношение:
I = I1+I2+I3+I4;
равна сумме токов, уходящих от этого узла.

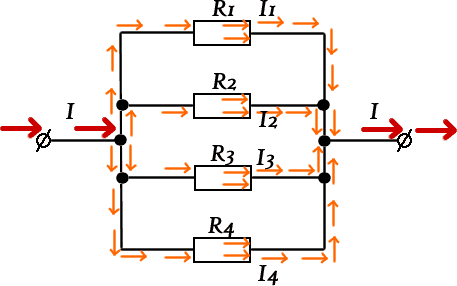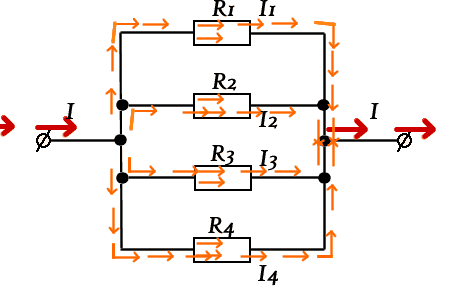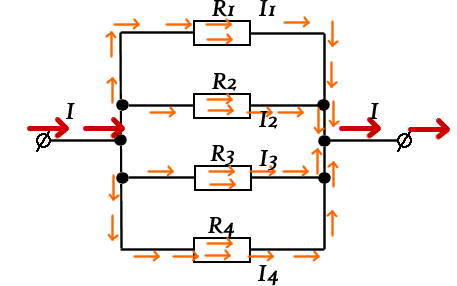
При параллельном соединении резисторов ток проходит по четырем направлениям, что уменьшает общее сопротивление или увеличивает общую проводимость цепи, которая равна сумме проводимостей ветвей.
Обозначим силу тока в неразветвленной ветви буквой I.
Силу тока в отдельных ветвях соответственно I1, I2, I3 и I4
Напряжение между точками A и B — U.
Общее сопротивление между этими точками — R.
По закону Ома напишем:
I = U/R; I1 = U/R1; I2 = U/R2; I3 = U/R3; I4 = U/R4;
Согласно первому закону Кирхгофа:
I = I1+I2+I3+I4; или U/R = U/R1+U/R2+U/R3+U/R4.
Сократив обе части полученного выражения на U получим:
1/R = 1/R1+1/R2+1/R3+1/R4, что и требовалось доказать.
Cоотношение для любого числа параллельно соединенных резисторов.
R1 и R2, то можно написать равенство:
1/R =1/R1+1/R2;
Из этого равенства найдем сопротивление R, которым можно заменить два параллельно соединенных резистора:

Полученное выражение имеет большое практическое применение.
Благодаря этому закону производятся расчёты электрических цепей.
Второй закон Кирхгофа
В замкнутом контуре электрической цепи сумма всех эдс равна
сумме падения напряжения в сопротивлениях того же контура.
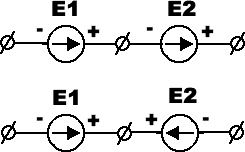
E1 + E2 + E3 +…+ En = I1R1 + I2R2 + I3R3 +…+ InRn.При составлении уравнений выбирают направление обхода цепи и произвольно задаются направлениями токов.Если в электрической цепи включены два источника энергии, эдс которых совпадают по направлению, т. е. согласно изо1, то эдс всей цепи равна сумме эдс этих источников,
т. е.
E = E1+E2.Если же в цепь включено два источника, эдс которых имеют противоположные направления, т. е. включены встречно изо2, то общая эдс цепи равна разности эдс этих источников
Е = Е1—Е2.
Благодаря этим законам производятся расчёты электрических цепей.
Существует несколько методов расчёта, один из них «Метод узловых напряжений»
Скачать можно здесь
(Подробно и доходчиво в видеокурсе «В мир электричества — как в первый раз!»)
Правила Кирхгофа — Википедия. Что такое Правила Кирхгофа
Пра́вила Кирхго́фа (часто в литературе ошибочно называются Зако́нами Кирхго́фа) — соотношения, которые выполняются между токами и напряжениями на участках любой электрической цепи. Правила Кирхгофа позволяют рассчитывать любые электрические цепи постоянного, переменного и квазистационарного тока[1]. Имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения многих задач в теории электрических цепей и практических расчётов сложных электрических цепей. Применение правил Кирхгофа к линейной электрической цепи позволяет получить систему линейных уравнений относительно токов или напряжений, и соответственно, найти значения токов на всех ветвях цепи и все межузловые напряжения.
Сформулированы Густавом Кирхгофом в 1845 году[2].
Название «Правила» корректнее потому, что эти правила не являются фундаментальными законами природы, а вытекают из фундаментальных законов сохранения заряда и безвихревости электростатического поля (третье уравнение Максвелла при неизменном магнитном поле). Эти правила не следует путать с ещё двумя законами Кирхгофа в химии и физике.
Формулировка правил
Определения
Для формулировки правил Кирхгофа вводятся понятия узел, ветвь и контур электрической цепи. Ветвью называют участок электрической цепи с одним и тем же током, например, на рис. отрезок, обозначенный R1, I1 есть ветвь. Узлом называют точку соединения трех и более ветвей (на рис. обозначены жирными точками). Контур — замкнутый путь, проходящий через несколько ветвей и узлов разветвлённой электрической цепи. Термин замкнутый путь означает, что, начав с некоторого узла цепи и однократно пройдя по нескольким ветвям и узлам, можно вернуться в исходный узел. Ветви и узлы, проходимые при таком обходе, принято называть принадлежащими данному контуру. При этом нужно иметь в виду, что ветвь и узел могут принадлежать одновременно нескольким контурам.
В терминах данных определений правила Кирхгофа формулируются следующим образом.
Первое правило
Сколько тока втекает в узел, столько из него и вытекает.i2 + i3 = i1 + i4
Первое правило Кирхгофа гласит, что алгебраическая сумма токов ветвей, сходящихся в каждом узле любой цепи, равна нулю. При этом направленный к узлу ток принято считать положительным, а направленный от узла — отрицательным: Алгебраическая сумма токов, направленных к узлу, равна сумме направленных от узла.
- ∑ j = 1 n I j = 0. {\displaystyle \sum \limits _{j=1}^{n}I_{j}=0.}
Иными словами, сколько тока втекает в узел, столько из него и вытекает. Это правило следует из фундаментального закона сохранения заряда.
Второе правило
Второе правило Кирхгофа (правило напряжений Кирхгофа) гласит, что алгебраическая сумма напряжений на резистивных элементах замкнутого контура равна алгебраической сумме ЭДС, входящих в этот контур. Если в контуре нет источников ЭДС (идеализированных генераторов напряжения), то суммарное падение напряжений равно нулю:
- для постоянных напряжений ∑ k = 1 n E k = ∑ k = 1 m U k = ∑ k = 1 m R k I k ; {\displaystyle \sum _{k=1}^{n}E_{k}=\sum _{k=1}^{m}U_{k}=\sum _{k=1}^{m}R_{k}I_{k};}
- для переменных напряжений ∑ k = 1 n e k = ∑ k = 1 m u k = ∑ k = 1 m R k i k + ∑ k = 1 m u L k + ∑ k = 1 m u C k . {\displaystyle \sum _{k=1}^{n}e_{k}=\sum _{k=1}^{m}u_{k}=\sum _{k=1}^{m}R_{k}i_{k}+\sum _{k=1}^{m}u_{L\,k}+\sum _{k=1}^{m}u_{C\,k}.}
Это правило вытекает из 3-го уравнения Максвелла, в частном случае стационарного магнитного поля.
Иными словами, при полном обходе контура потенциал, изменяясь, возвращается к исходному значению. Частным случаем второго правила для цепи, состоящей из одного контура, является закон Ома для этой цепи. При составлении уравнения напряжений для контура нужно выбрать положительное направление обхода контура. При этом падение напряжения на ветви считают положительным, если направление обхода данной ветви совпадает с ранее выбранным направлением тока ветви, и отрицательным — в противном случае (см. далее).
Правила Кирхгофа справедливы для линейных и нелинейных линеаризованных цепей при любом характере изменения во времени токов и напряжений.
Особенности составления уравнений для расчёта токов и напряжений
Если цепь содержит p {\displaystyle p} узлов, то она описывается p − 1 {\displaystyle p-1} уравнениями токов. Это правило может применяться и для других физических явлений (к примеру, система трубопроводов жидкости или газа с насосами), где выполняется закон сохранения частиц среды и потока этих частиц.
Если цепь содержит m {\displaystyle m} ветвей, из которых содержат источники тока ветви в количестве m i {\displaystyle m_{i}} , то она описывается m − m i − ( p − 1 ) {\displaystyle m-m_{i}-(p-1)} уравнениями напряжений.
- Правила Кирхгофа, записанные для p − 1 {\displaystyle p-1} узлов или m − ( p − 1 ) {\displaystyle m-(p-1)} контуров цепи, дают полную систему линейных уравнений, которая позволяет найти все токи и все напряжения.
- Перед тем, как составить уравнения, нужно произвольно выбрать:
- положительные направления токов в ветвях и обозначить их на схеме, при этом не обязательно следить, чтобы в узле направления токов были и втекающими, и вытекающими, окончательное решение системы уравнений всё равно даст правильные знаки токов узла;
- положительные направления обхода контуров для составления уравнений по второму закону, с целью единообразия рекомендуется для всех контуров положительные направления обхода выбирать одинаковыми (напр.: по часовой стрелке).
- Если направление тока совпадает с направлением обхода контура (которое выбирается произвольно), падение напряжения считается положительным, в противном случае — отрицательным.
- При записи линейно независимых уравнений по второму правилу Кирхгофа стремятся, чтобы в каждый новый контур, для которого составляют уравнение, входила хотя бы одна новая ветвь, не вошедшая в предыдущие контуры, для которых уже записаны уравнения по второму закону (достаточное, но не необходимое условие).
- В сложных непланарных графах электрических цепей человеку трудно увидеть независимые контуры и узлы, каждый независимый контур (узел) при составлении системы уравнений порождает ещё 1 линейное уравнение в определяющей задачу системе линейных уравнений. Подсчёт количества независимых контуров и их явное указание в конкретном графе развит в теории графов.
Пример
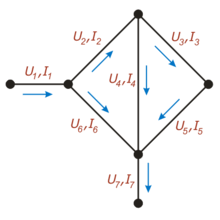 На этом рисунке для каждой ветви обозначен протекающий по ней ток (буквой «I») и напряжение между соединяемыми ею узлами (буквой «U»)
На этом рисунке для каждой ветви обозначен протекающий по ней ток (буквой «I») и напряжение между соединяемыми ею узлами (буквой «U»)Количество узлов: 3.
p − 1 = 2 {\displaystyle p-1=2}
Количество ветвей (в замкнутых контурах): 4. Количество ветвей, содержащих источник тока: 0.
m − m i − ( p − 1 ) = 2 {\displaystyle m-m_{i}-(p-1)=2}
Количество контуров: 2.
Для приведённой на рисунке цепи, в соответствии с первым правилом, выполняются следующие соотношения:
- { I 1 − I 2 − I 6 = 0 I 2 − I 4 − I 3 = 0 {\displaystyle {\begin{cases}I_{1}-I_{2}-I_{6}=0\\I_{2}-I_{4}-I_{3}=0\end{cases}}}
Обратите внимание, что для каждого узла должно быть выбрано положительное направление, например, здесь токи, втекающие в узел, считаются положительными, а вытекающие — отрицательными.
Решение полученной линейной системы алгебраических уравнений позволяет определить все токи узлов и ветвей, такой подход к анализу цепи принято называть методом контурных токов.
В соответствии со вторым правилом, справедливы соотношения:
- { U 2 + U 4 − U 6 = 0 U 3 + U 5 − U 4 = 0 {\displaystyle {\begin{cases}U_{2}+U_{4}-U_{6}=0\\U_{3}+U_{5}-U_{4}=0\end{cases}}}
Полученные системы уравнений полностью описывают анализируемую цепь, и их решения определяют все токи и все напряжения ветвей. Такой подход к анализу цепи принято называть методом узловых потенциалов.
О значении для электротехники
Правила Кирхгофа имеют прикладной характер и позволяют наряду и в сочетании с другими приёмами и способами (метод эквивалентного генератора, принцип суперпозиции, способ составления потенциальной диаграммы) решать задачи электротехники. Правила Кирхгофа нашли широкое применение благодаря простоте формулировки уравнений и возможности их решения стандартными способами линейной алгебры (методом Крамера, методом Гаусса и др.).
Закон излучения Кирхгофа
Закон излучения Кирхгофа гласит — отношение излучательной способности любого тела к его поглощательной способности одинаково для всех тел при данной температуре для данной частоты для равновесного излучения и не зависит от их формы, химического состава и проч.
Закон Кирхгофа в химии
Закон Кирхгофа гласит — температурный коэффициент теплового эффекта химической реакции равен изменению теплоёмкости системы в ходе реакции.
Примечания
Литература
- Матвеев А. Н. Электричество и магнетизм : учебное пособие. — М.: Высшая школа, 1983. — 463 с.
- Калашников С. Г. Электричество : учебное пособие. — М.: Физматлит, 2003. — 625 с.
- Бессонов Л. А. Теоретические основы электротехники. Электрические цепи. — 11-е издание. — М.: Гардарики, 2007.
- Герасимов В. Г., Кузнецов Э. В., Николаева О. В. Электротехника и электроника. Кн. 1. Электрические и магнитные цепи. — М.: Энергоатомиздат, 1996. — 288 с. — ISBN 5-283-05005-X.
Законы Кирхгофа. Законы Кирхгофа являются одной из форм закона сохранения энергии и потому относятся к фундаментальным законам природы
Законы Кирхгофа являются одной из форм закона сохранения энергии и потому относятся к фундаментальным законам природы.
Первый закон Кирхгофа является следствием принципа непрерывности электрического тока, в соответствии с которым суммарный поток зарядов через любую замкнутую поверхность равен нулю, т.е. количество зарядов выходящих через эту поверхность должно быть равно количеству входящих зарядов. Основание этого принципа очевидно, т.к. при нарушении его электрические заряды внутри поверхности должны были бы либо исчезать, либо возникать без видимых причин.
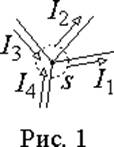 Если заряды перемещаются внутри проводников, то они образуют в них электрический ток. Величина электрического тока может измениться только в узле цепи, т.к. связи считаются идеальными проводниками. Поэтому, если окружить узел произвольной поверхностью s (рис. 1), то потоки зарядов через эту поверхность будут тождественны токам в проводниках образующих узел и
Если заряды перемещаются внутри проводников, то они образуют в них электрический ток. Величина электрического тока может измениться только в узле цепи, т.к. связи считаются идеальными проводниками. Поэтому, если окружить узел произвольной поверхностью s (рис. 1), то потоки зарядов через эту поверхность будут тождественны токам в проводниках образующих узел и
суммарный ток в узле должен быть равным нулю.
Для математической записи этого закона нужно принять систему обозначений направлений токов по отношению к рассматриваемому узлу. Можно считать токи направленные к узлу положительными, а от узла отрицательными. Тогда для узла рис. 1 уравнение Кирхгофа будет иметь вид I3+I4—I1—I2 = 0 или I3+I4=I1+I2 .
Обобщая сказанное на произвольное число ветвей сходящихся в узле, можно сформулировать первый закон Кирхгофа следующим образом:
- алгебраическая сумма токов в любом узле электрической цепи равна нулю
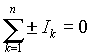
| (1) |
или
- в любом узле сумма токов направленных к узлу равна сумме токов направленных от узла
 , где p+q=n. , где p+q=n.
| (2) |
Очевидно, что обе формулировки равноценны и выбор формы записи уравнений может быть произвольным. Существенным является только соглашение о знаках токов для данной цепи, т.е. в пределах описания одной электрической цепи нельзя для разных узлов использовать разные знаки для токов направленных к узлам или от узлов.
При составлении уравнений по первому закону Кирхгофа направления токов в ветвях электрической цепи выбирают обычно произвольно. При этом необязательно даже стремиться, чтобы во всех узлах цепи присутствовали токи разных направлений. Может получиться так, что в каком-либо узле все токи сходящихся в нем ветвей будут направлены к узлу или от узла, нарушая тем самым принцип непрерывности. В этом случае в процессе определения токов один или несколько из них окажутся отрицательными, что будет свидетельствовать о протекании их в направлении противоположном принятому.
ЗАДАЧА 1
Второй закон Кирхгофа связан с понятием потенциала электрического поля, как работы, совершаемой при перемещении единичного точечного заряда в пространстве. Если такое перемещение совершается по замкнутому контуру, то суммарная работа при возвращении в исходную точку будет равна нулю. В противном случае путем обхода контура можно было бы получать положительную энергию, нарушая закон ее сохранения.
Каждый узел или точка электрической цепи обладает собственным потенциалом и, перемещаясь вдоль замкнутого контура, мы совершаем работу, которая при возврате в исходную точку будет равна нулю. Это свойство потенциального электрического поля и описывает второй закон Кирхгофа в применении к электрической цепи.
Он также как и первый закон формулируется в двух вариантах, связанных с тем, что падение напряжения на источнике ЭДС численно равно электродвижущей силе, но имеет противоположный знак. Поэтому, если какая либо ветвь содержит сопротивление и источник ЭДС, направление которой согласно с направлением тока, то при обходе контура эти два слагаемых падения напряжения будут учитываться с разными знаками. Если же падение напряжения на источнике ЭДС учесть в другой части уравнения, то его знак будет соответствовать знаку напряжения на сопротивлении.
Сформулируем оба варианта второго закона Кирхгофа, т.к. они принципиально равноценны:
- алгебраическая сумма падений напряжения вдоль любого замкнутого контура электрической цепи равна нулю

| (3) |
Примечание: знак + выбирается перед падением напряжения на резисторе, если направление протекания тока через него и направление обхода контура совпадают; для падений напряжения на источниках ЭДС знак + выбирается, если направление обхода контура и направление действия ЭДС встречны независимо от направления протекания тока;
- алгебраическая сумма ЭДС вдоль любого замкнутого контура равна алгебраической сумме падений напряжения на резисторах в этом контуре
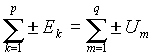 , где p+q=n , где p+q=n
| (4) |
Примечание: знак + для ЭДС выбирается в том случае, если направление ее действия совпадает с направлением обхода контура, а для напряжений на резисторах знак + выбирается, если в них совпадают направление протекания тока и направление обхода.
Здесь также как и в первом законе оба варианта корректны, но на практике удобнее использовать второй вариант, т.к. в нем проще определить знаки слагаемых.
ЗАДАЧА 2
С помощью законов Кирхгофа для любой электрической цепи можно составить независимую систему уравнений и определить любые неизвестные параметры, если число их не превышает число уравнений. Для выполнения условий независимости эти уравнения должны составляться по определенным правилам.
Общее число уравнений N в системе равно числу ветвей Nв минус число ветвей, содержащих источники тока NJ , т.е. N = Nв — NJ .
Наиболее простыми по выражениям являются уравнения по первому закону Кирхгофа, однако их число N1не может быть больше числа узлов Nу минус один.
Недостающие уравнения составляются по второму закону Кирхгофа, т.е.
| N1 = Nу -1 ; | (5) |
| N2 = N — N1 = Nв — NJ — N1. | (6) |
Сформулируем алгоритм составления системы уравнений по законам Кирхгофа :
- определить число узлов и ветвей цепи Nу и Nв;
- определить число уравнений по первому и второму законам N1 и N2.;
- для всех ветвей (кроме ветвей с источниками тока) произвольно задать
направления протекания токов; - для всех узлов, кроме одного, выбранного произвольно, составить уравнения по первому закону Кирхгофа;
- произвольно выбрать на схеме электрической цепи замкнутые контуры таким образом, чтобы они отличались друг от друга по крайней мере одной ветвью и чтобы все ветви, кроме ветвей с источниками тока, входили по крайней мере в один контур;
- произвольно выбрать для каждого контура направление обхода и составить уравнения по второму закону Кирхгофа, включая в правую часть уравнения ЭДС действующие в контуре, а в левую падения напряжения на резисторах. Примечание: Знак ЭДС выбирают положительным, если направление ее действия совпадает с направлением обхода независимо от направления тока; а знак падения напряжения на резисторе принимают положительным, если направление тока в нем совпадает с направлением обхода.
Рассмотрим этот алгоритм на примере рис 2.
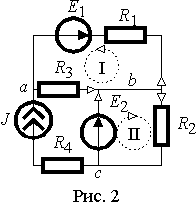 Здесь светлыми стрелками обозначены выбранные произвольно направления токов в ветвях цепи. Ток в ветви с R4 не выбирается произвольно, т.к. в этой ветви он определяется действием источником тока.
Здесь светлыми стрелками обозначены выбранные произвольно направления токов в ветвях цепи. Ток в ветви с R4 не выбирается произвольно, т.к. в этой ветви он определяется действием источником тока.
Число ветвей цепи равно 5, а т.к. одна из них содержит источник тока, то общее число уравнений Кирхгофа равно четырем.
Число узлов цепи равно трем (a, b и c), поэтому число уравнений по первому закону Кирхгофа равно двум и их можно составлять для любой пары из этих трех узлов. Пусть это будут узлы a и b, тогда
| a) J + IE1 = J + IR1 = IR3 Û J + IR1 — IR3 = 0 | (7) |
| b) IR3 + IE2 = IR1 + IR2 Û IR3 + IE2 — IR1 — IR2 = 0 | (8) |
По второму закону Кирхгофа нужно составить два уравнения. Выберем два контура I и II так, чтобы все ветви, кроме ветви с источником тока попали по крайней мере в один из них, и зададим произвольно направление обхода как показано стрелками. Тогда
| I) —E1 = IR1R1 + IR3R3 | (9) |
| II) E2 = IR2R2 | (10) |
При выборе контуров и составлении уравнений все ветви с источниками тока должны быть исключены, т.е. контуры обхода не должны включать ветви с источниками тока. Это не означает что для контуров с источниками тока нарушается второй закон Кирхгофа. Просто при необходимости определения падения напряжения на источнике тока или на других элементах ветви с источником тока это можно сделать после решения системы уравнений. Например, на рис. 2 можно создать замкнутый контур из элементов R3, R4 , J и E2, и для него будет справедливым уравнение
IR3R3+ E2+JR4 + UJ = 0 ,
где UJ — падение напряжения на источнике тока J.
Из сказанного выше очевидно, что законы Кирхгофа необязательно использовать в виде систем уравнений. Они справедливы всегда для любого узла и для любого замкнутого контура любой электрической цепи.
ЗАДАЧА 3
Современные средства математического анализа позволяют легко получить результат решения составленной выше системы уравнений, если она записана в матричной форме A´X=B. Это можно сделать, например, для токов в качестве неизвестных.
Каждая строка матрицы A должна соответствовать одному из уравнений (7)-(10). Поэтому в строки матрицы A нужно включить все коэффициенты при токах соответствующего уравнения, в той последовательности, в какой эти токи включены в координаты вектора неизвестных величин. Если какой-либо ток отсутствует в уравнении, то в качестве элемента матрицы нужно указать нуль. Для включения в матрицу уравнения по первому закону Кирхгофа удобнее записывать в форме (1) с нулевой правой частью, однако, для уравнения (7) нужно перенести ток источника J в правую часть, т.к. он не входит в число неизвестных.
Вектор неизвестных токов X представляет собой столбец, в который включены неизвестные токи в произвольной последовательности.
Вектор B представляет собой столбец, координатами которого являются источники электрической энергии, действующие в цепи (правая часть уравнений (7)-(10)). Порядок включения их в столбец должен соответствовать порядку записи уравнений в строки матрицы A .
Составим матричное уравнение для схемы рис. 2, используя полученные ранее уравнения (7)-(8) и (9)-(10).

Здесь для упрощения восприятия строки записи помечены указателями на тот узел или контур, которому они соответствуют.
Правила Кирхгофа — это… Что такое Правила Кирхгофа?
Правила Кирхгофа (часто, в литературе, называются не совсем корректно Зако́ны Кирхго́фа) — соотношения, которые выполняются между токами и напряжениями на участках любой электрической цепи. Правила Кирхгофа позволяют рассчитывать любые электрические цепи постоянного, переменного и квазистационарного тока.[1] Имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения многих задач в теории электрических цепей и практических расчётов сложных электрических цепей. Применение правил Кирхгофа к линейной электрической цепи позволяет получить систему линейных уравнений относительно токов или напряжений, и соответственно, найти значение токов на всех ветвях цепи и все межузловые напряжения. Сформулированы Густавом Кирхгофом в 1845 году. Название «Правила» корректнее потому, что эти правила не являются фундаментальными законами Природы, а вытекают из фундаментальных законов сохранения заряда и безвихревости электростатического поля (3-е уравнение Максвелла при неизменном магнитном поле). Эти правила не следует путать с ещё двумя законами Кирхгофа в химии и физике.
Формулировка правил
Определения
Для формулировки правил Кирхгофа, вводятся понятия узел, ветвь и контур электрической цепи. Ветвью называют любой двухполюсник, входящий в цепь, например, на рис. отрезок, обозначенный U1, I1 есть ветвь. Узлом называют точку соединения двух и более ветвей (на рис. обозначены жирными точками). Контур — замкнутые циклы из ветвей. Термин замкнутый цикл означает, что начав с некоторого узла цепи и пройдя по нескольким ветвям и узлам однократно можно вернуться в исходный узел. Ветви и узлы, проходимые при таком обходе, принято называть принадлежащими данному контуру. При этом нужно иметь в виду, что каждая ветвь и узел может одновременно принадлежать нескольким контурам.
В терминах данных определений правила Кирхгофа формулируются следующим образом.
Первое правило
Сколько тока втекает в узел, столько из него и вытекает. i2 + i3 = i1 + i4Первое правило Кирхгофа (правило токов Кирхгофа) гласит, что алгебраическая сумма токов в каждом узле любой цепи равна нулю. При этом втекающий в узел ток принято считать положительным, а вытекающий — отрицательным:
Иными словами, сколько тока втекает в узел, столько из него и вытекает. Это правило следует из фундаментального закона сохранения заряда.
Второе правило
Второе правило Кирхгофа (правило напряжений Кирхгофа) гласит, что алгебраическая сумма падений напряжений на всех ветвях, принадлежащих любому замкнутому контуру цепи, равна алгебраической сумме ЭДС ветвей этого контура. Если в контуре нет источников ЭДС (идеализированных генераторов напряжения), то суммарное падение напряжений равно нулю:
- для постоянных напряжений
- для переменных напряжений
Это правило вытекает из 3-го уравнения Максвелла, в частном случае стационарного магнитного поля.
Иными словами, при полном обходе контура потенциал, изменяясь, возвращается к исходному значению. Частным случаем второго правила для цепи, состоящей из одного контура, является закон Ома для этой цепи. При составлении уравнения напряжений для контура нужно выбрать положительное направление обхода контура. При этом падение напряжения на ветви считают положительным, если направление обхода данной ветви совпадает с ранее выбранным направлением тока ветви, и отрицательным — в противном случае (см. далее).
Правила Кирхгофа справедливы для линейных и нелинейных линеаризованных цепей при любом характере изменения во времени токов и напряжений.
- Пример
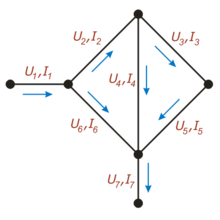 На этом рисунке для каждого проводника обозначен протекающий по нему ток (буквой «I») и напряжение между соединяемыми им узлами (буквой «U»)
На этом рисунке для каждого проводника обозначен протекающий по нему ток (буквой «I») и напряжение между соединяемыми им узлами (буквой «U»)Например, для приведённой на рисунке цепи, в соответствии с первым правилом выполняются следующие соотношения:
Обратите внимание, что для каждого узла должно быть выбрано положительное направление, например здесь, токи, втекающие в узел, считаются положительными, а вытекающие — отрицательными.
Решение полученной линейной системы алгебраических уравнений позволяет определить все токи узлов и ветвей, такой подход к анализу цепи принято называть методом контурных токов.
В соответствии со вторым правилом, справедливы соотношения:
Снова, полученная система уравнений, полностью описывает анализируемую цепь и её решение определяет все токи и все напряжения ветвей, такой подход к анализу цепи принято называть методом узловых потенциалов.
Особенности составления уравнений для расчёта токов и напряжений
Если цепь содержит узлов, то она описывается уравнениями токов. Это правило может применяться и для других физических явлений (к примеру, система трубопроводов жидкости или газа с насосами), где выполняется закон сохранения частиц среды и потока этих частиц.
Если цепь содержит ветвей, из которых содержат источники тока ветви в количестве , то она описывается уравнениями напряжений.
- Правила Кирхгофа, записанные для узлов или контуров цепи, дают полную систему линейных уравнений, которая позволяет найти все токи и все напряжения.
- Перед тем, как составить уравнения, нужно произвольно выбрать:
- положительные направления токов в ветвях и обозначить их на схеме, при этом не обязательно следить, чтобы в узле направления токов были и втекающими и вытекающими, окончательное решение системы уравнений всё равно даст правильные знаки токов узла;
- положительные направления обхода контуров для составления уравнений по второму закону, с целью единообразия рекомендуется для всех контуров положительные направления обхода выбирать одинаковыми (напр.: по часовой стрелке).
- Если направление тока совпадает с направлением обхода контура (которое выбирается произвольно), падение напряжения считается положительным, в противном случае — отрицательным.
- При записи линейно независимых уравнений по второму правилу Кирхгофа, стремятся, чтобы в каждый новый контур, для которого составляют уравнение, входила хотя бы одна новая ветвь, не вошедшая в предыдущие контуры, для которых уже записаны уравнения по второму закону (достаточное, но не необходимое условие).
- В сложных непланарных графах электрических цепей человеку трудно увидеть независимые контуры и узлы, каждый независимый контур (узел) при составлении системы уравнений порождает ещё 1 линейное уравнение, в определяющей задачу системе линейных уравнений. Подсчёт количества независимых контуров и их явное указание в конкретном графе развит в теории графов.
О значении для электротехники
Правила Кирхгофа имеют прикладной характер и позволяют наряду и в сочетании с другими приёмами и способами (метод эквивалентного генератора, принцип суперпозиции, способ составления потенциальной диаграммы) решать задачи электротехники. Правила Кирхгофа нашли широкое применение благодаря простоте формулировки уравнений и возможности их решения стандартными способами линейной алгебры (методом Крамера, методом Гаусса и др.).
Закон излучения Кирхгофа
Закон излучения Кирхгофа гласит — отношение излучательной способности любого тела к его поглощательной способности одинаково для всех тел при данной температуре для данной частоты для равновесного излучения и не зависит от их формы, химического состава и проч.
Закон Кирхгофа в химии
Закон Кирхгофа гласит — температурный коэффициент теплового эффекта химической реакции равен изменению теплоёмкости системы в ходе реакции.
Примечания
Литература
- Матвеев А. Н. Электричество и магнетизм. — Учебное пособие. — М.: Высшая школа, 1983. — 463 с.
- Калашников С. Г. Электричество. — Учебное пособие. — М.: Физматлит, 2003. — 625 с.
- Бессонов Л. А. Теоретические основы электротехники. Электрические цепи. — 11-е издание. — М.: Гардарики, 2007.
Законы Кирхгофа — Закон Кирхгофа о токе и напряжении Кирхгофа
Первый закон Кирхгофа Второй закон Кирхгофа Решенный пример Кирхгофа
Законы схем Кирхгофа лежат в основе анализа схем. С помощью этих законов и уравнения для отдельных компонентов (резистора, конденсатора и катушки индуктивности) у нас есть основной инструмент для начала анализа схем. В этой статье мы обсудим закон Кирхгофа по току и напряжению и то, как использовать их в анализе цепей.
История о Густаве Роберте Кирхгофе
Густав Роберт Кирхгоф (1824-1887)Густав Роберт Кирхгоф, немецкий физик, родился 12 марта 1824 года в Кенигсберге, Пруссия. Его первой исследовательской темой была электропроводность. Это исследование привело к тому, что Кирхгоф сформулировал законы замкнутых электрических цепей в 1845 году. Эти законы в конечном итоге были названы в честь Кирхгофа и теперь известны как законы Кирхгофа по напряжению и току. Поскольку эти законы применимы ко всем электрическим цепям, понимание их основ имеет первостепенное значение для понимания того, как функционирует электронная цепь.Хотя эти законы увековечили Кирхгофа в области электротехники, у него есть и другие открытия. Он был первым, кто подтвердил, что электрический импульс распространяется со скоростью света. Кроме того, Кирхгоф внес большой вклад в изучение спектроскопии и продвинул исследования излучения черного тела.
Что такое закон Кирхгофа?
В 1845 году немецкий физик Густав Кирхгоф разработал пару законов, касающихся сохранения тока и энергии в электрических цепях.Эти два закона широко известны как закон Кирхгофа по напряжению и току. Эти законы помогают в вычислении электрического сопротивления сложной сети или импеданса в случае переменного тока и тока, протекающего в разных потоках сети. В следующем разделе давайте посмотрим, что утверждают эти законы.
Что утверждают законы Кирхгофа?
- Действующий закон Кирхгофа известен под несколькими названиями: Первый закон Кирхгофа и Правило перекрестка Кирхгофа. Согласно правилу соединения, в цепи сумма токов в соединении равна сумме токов вне соединения.
- Закон Кирхгофа о напряжении известен под несколькими названиями: Второй закон Кирхгофа и Правило петли Кирхгофа. Согласно правилу контура, сумма напряжений вокруг замкнутого контура равна нулю.
Первый закон Кирхгофа
Согласно действующему закону Кирхгофа,
Полный ток, входящий в соединение или узел, равен заряду, выходящему из узла, поскольку заряд не теряется.
Другими словами, алгебраическая сумма каждого тока, входящего в узел и выходящего из него, должна быть нулевой.Это свойство закона Кирхгофа обычно называется сохранением заряда, где I (выход) + I (вход) = 0.
Подробнее: Первый закон Кирхгофа
На приведенном выше рисунке токи I 1 , I 2 и I 3 , входящие в узел, считаются положительными, аналогично токи I 4 и I 5 , выходящие из узлов, считаются отрицательными по значениям. . Это можно выразить в виде уравнения:
I 1 + I 2 + I 3 — I 4 — I 5 = 0
Термин «узел» относится к стыку или соединению двух или более токоведущих маршрутов, таких как кабели и другие компоненты.Текущий закон Кирхгофа также может применяться для анализа параллельных цепей.
Второй закон Кирхгофа
Согласно Закону Кирхгофа о напряжении,
Напряжение вокруг контура равно сумме всех падений напряжения в том же контуре для любой замкнутой сети, а также равно нулю.
Другими словами, алгебраическая сумма каждого напряжения в контуре должна быть равна нулю, и это свойство закона Кирхгофа называется сохранением энергии.
Подробнее: Второй закон Кирхгофа
Когда вы начинаете с любой точки петли и продолжаете движение в том же направлении, обратите внимание на падение напряжения во всех направлениях, будь то отрицательное или положительное, и вернитесь в ту же точку.Важно сохранять направление против часовой стрелки или по часовой стрелке; иначе конечное значение напряжения не будет равно нулю. Закон напряжения также может применяться при анализе последовательных цепей.
При анализе цепей переменного или постоянного тока на основе законов Кирхгофа для цепей необходимо четко понимать всю терминологию и определения, которые описывают компоненты цепи, такие как пути, узлы, ячейки
.Вывод второго закона Кирхгофа, решенные примеры, применения и ограничения
Закон Кирхгофа или законы цепей состоит из двух математических уравнений равенства, которые имеют дело с сопротивлением, током и напряжением в сосредоточенной элементарной модели электрических цепей. Законы фундаментальны для теории цепей. Они количественно определяют, как токи и напряжения изменяются в контуре цепи. Густав Роберт Кирхгоф, немецкий физик, внес вклад в фундаментальное понимание электрических цепей.
Каковы законы Кирхгофа?
Есть два закона, а именно:
- Второй закон Кирхгофа , также известный как закон напряжения Кирхгофа (KVL), гласит, что сумма всех напряжений вокруг замкнутого контура в любой цепи должна быть равна нулю. Это снова является следствием сохранения заряда, а также сохранения энергии.
Здесь, в этой короткой статье, мы обсудим второй закон Кирхгофа.
Закон Кирхгофа о напряжении
Второй закон Кирхгофа или закон напряжения гласит, что
Чистая электродвижущая сила вокруг замкнутого контура равна сумме падений потенциала вокруг контура
Это называется правилом петли Кирхгофа, которое является результатом действия консервативного электростатического поля.
Следовательно,
- Если заряд движется по замкнутому контуру в цепи, он должен набрать столько же энергии, сколько и потерять.
- Сказанное выше можно резюмировать как выигрыш в энергии за счет заряда = соответствующие потери энергии через сопротивления
- Математически полное напряжение в замкнутом контуре цепи выражается как \ (\ sum V = 0 \).
На рисунке ниже показано, что полное напряжение в замкнутом контуре должно быть нулевым.
Этот закон регулирует падение напряжения на разных ветвях электрической цепи.Рассмотрим одну точку замкнутого контура в электрической цепи. Если кто-то пойдет в другую точку аналогичного кольца, он или она обнаружит, что потенциал этого второго аспекта может быть не совсем таким, как первый.
На случай, если он или она продолжит отправляться в какую-то уникальную точку на петле, и он или она может обнаружить некий необычный потенциал в этой новой области. Если он или она пойдет дальше по замкнутому циклу, в конечном итоге он или она достигнет основной точки, с которой было начато путешествие.
Это означает, что он или она возвращается в аналогичную потенциальную точку после пересечения различных уровней напряжения. Можно снова сказать, что выигрыш в электрической энергии за счет заряда равен соответствующим потерям энергии через сопротивления.
Связанная статья:
Решение схемы с использованием второго закона Кирхгофа
- Первый и самый важный шаг — нарисовать замкнутый контур в цепи.После этого нарисуйте направление потока тока.
- Очень важно определить наше соглашение о знаках

- Используя первый закон Кирхгофа, в точках B и A мы получаем \ (I_ {1} + I_ {2} = I_ {3} \)
- Используя вышеуказанное соглашение и Второй закон Кирхгофа
Из цикла 1 имеем:
\ (10 = R_ {1} * I_ {1} + R_ {3} * I_ {3} \)
\ (= 10I_ {1} + 40I_ {3} \)
\ (1 = I_ {1} + 4I_ {3} \)
Из цикла 2 имеем:
\ (20 = R_ {2} * I_ {2} + R_ {3} * I_ {3} \)
\ (20I_ {2} + 40I_ {3} \)
\ (1 = I_ {2} + 2I_ {3} \)
Из цикла 3 имеем:
\ (10-20 = 10I_ {1} -20I_ {2} \)
\ (1 = -I_ {1} + 2I_ {2} \)
- Используя Первый закон Кирхгофа \ (I_ {1} + I_ {2} = I_ {3} \)
Уравнение сводится к следующему (из цикла 1):
\ (1 = 5I_ {1} + 4I_ {2} \)
Уравнение сводится к следующему (из цикла 2):
\ (1 = 2I_ {1} + 3I_ {2} \)
- Это приводит к следующему уравнению: \ (I_ {1} = — \ frac {1} {3} I_ {2} \)
- Из последних трех уравнений получаем \ (1 = \ frac {1} {3} I_ {2} + 2I_ {2} \) \ (I_ {2} = 0.429A \) \ (I_ {1} = 0,143A \) \ (I_ {3} = 0,286A \)
Преимущества и ограничения закона Кирхгофа
Преимущества законов:
- Упрощает расчет неизвестных напряжений и токов
- Анализ и упрощение сложных замкнутых цепей становится управляемым
Законы Кирхгофа работают в предположении, что в замкнутом контуре нет флуктуирующих магнитных полей. Электрические поля и электродвижущая сила могут быть инд.
.Законы схем Кирхгофа — Простая английская Википедия, бесплатная энциклопедия
В 1845 году немецкий физик Густав Кирхгоф описал два закона об электрических схемах. Эти законы являются обобщением закона Ома. Законы Кирхгофа для схем очень полезны при решении схемных задач.
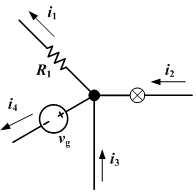
Ток, входящий в любой переход, равен току, выходящему из этого перехода. i 1 + i 4 = i 2 + i 3
Текущий закон Кирхгофа также известен как первый закон Кирхгофа и закон соединения Кирхгофа.Этот закон гласит, что «сумма тока в переходе равна сумме тока вне соединения». Это то же самое, что и закон Кирхгофа. В переходе действует закон сохранения суммы электрического заряда. Если входящее значение тока — это i2 и i3, этот ток разделяется на ток i1 и i4. Тогда уравнение (i1 + i4 = i2 + i3) выполняется. Правый рисунок дает пример. Первый закон Кирхгофа состоит в том, что заряд не разрушается и не создается в точке соединения.Это основано на законе сохранения электрического заряда.
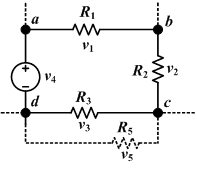 Сумма всех напряжений вокруг контура равна нулю. v 1 + v 2 + v 3 + v 4 = 0
Сумма всех напряжений вокруг контура равна нулю. v 1 + v 2 + v 3 + v 4 = 0Закон напряжения Кирхгофа также известен как второй закон Кирхгофа, закон замкнутой цепи и закон петли Кирхгофа.
Алгебраическая сумма разностей напряжений (потенциалов) в любом контуре должна равняться нулю (эта схема является замкнутой). Любую сложную схему можно разделить на множество замкнутых схем.Этот закон означает, что в цепи есть электрическая ячейка и электрическое сопротивление. Электрический элемент придает заряду электродвижущую силу, а затем электрическое сопротивление рассеивает эту силу. Но в электрическом сопротивлении, если направление противоположно направлению тока, это электрическое сопротивление добавляет электродвижущую силу. Этот второй закон Кирхгофа основан на законе сохранения потенциальной энергии.
.правил Кирхгофа | физика | Britannica
Правила Кирхгофа , два утверждения о многопетлевых электрических цепях, которые воплощают в себе законы сохранения электрического заряда и энергии и которые используются для определения значения электрического тока в каждой ветви цепи.
Подробнее по этой теме
электричество: законы электрических цепей Кирхгофа
Для определения значений токов в цепях можно использовать два простых соотношения.Они пригодятся даже в довольно сложных ситуациях, таких как …
Первое правило, теорема о переходах, гласит, что сумма токов в конкретном переходе в цепи равна сумме токов, исходящих из того же перехода. Электрический заряд сохраняется: он не появляется и не исчезает внезапно; он не накапливается в одном месте и не истончается в другом.
Второе правило, уравнение контура, утверждает, что вокруг каждого контура в электрической цепи сумма ЭДС (электродвижущих сил или напряжений источников энергии, таких как батареи и генераторы) равна сумме падений потенциала, или напряжения на каждом из сопротивлений в одном контуре.Вся энергия, передаваемая источниками энергии заряженным частицам, переносящим ток, просто эквивалентна энергии, теряемой носителями заряда при полезной работе и рассеивании тепла вокруг каждого контура цепи.
На основе двух правил Кирхгофа можно написать достаточное количество уравнений, включающих каждый из токов, так что их значения могут быть определены алгебраическим решением.
Britannica Premium: удовлетворение растущих потребностей искателей знаний. Получите 30% подписки сегодня.Подпишись сейчасПравила Кирхгофа также применимы к сложным цепям переменного тока и с модификациями сложных магнитных цепей.
.