1.2. Закон Био–Савара–Лапласа. Принцип суперпозиции в магнетизме

Био и Савар провели в 1820 г. исследование магнитных полей токов различной формы. Они установили, что магнитная индукция во всех случаях пропорциональна силе тока, создающего магнитное поле. Лаплас проанализировал экспериментальные данные, полученные Био и Саваром, и нашел, что магнитное поле тока I любой конфигурации может быть вычислено как векторная сумма (суперпозиция) полей, создаваемых отдельными элементарными участками тока.

Длинакаждого участка тока настолько мала, что его можно считать прямым отрезком, расстояние от которого до точки наблюдения много больше. Удобно ввести понятие элемента токагде направление векторасовпадает с направлением токаI, а его модуль равен (рис. 6).

Для индукции магнитного поля , создаваемого элементом токав точке, находящейся на расстоянииr от него (рис. 6), Лаплас вывел формулу, справедливую для вакуума:

.

(1.1)

Формула закона Био–Савара–Лапласа (1.1) написана в системе СИ, в которой постоянная называется магнитной постоянной.

Уже отмечалось, что в магнетизме, как и в электричестве, имеет место принцип суперпозиции полей, т. е. индукция магнитного поля, создаваемого системой токов, в данной точке пространства равна векторной сумме индукций магнитных полей, создаваемых в этой точке каждым из токов в отдельности:

(1.2)

На рис. 7 приведен пример построения вектора магнитной индукциив поле двух параллельных и противоположных по направлению токови :

1.3. Применение закона Био–Савара–Лапласа. Магнитное поле прямого тока

Рассмотрим отрезок прямого тока. Элемент тока создает магнитное поле, индукция которого в точке

А (рис. 8) по закону Био–Савара–Лапласа находится по формуле:

, (1.3)

где – угол между направлением тока и вектором, характеризующим положение точкиА относительно

На рис.  9 представлен фрагмент рис. 8. Опустив перпендикуляр из точки С на сторону ОА, получим два прямоугольных треугольника. Из треугольника ODC следует, что СD =, а из треугольникаCDA следует, что CD=.

Учитывая, что ибесконечно малые величины, получим

. (1.4)

После подстановки (1.4) в (1.3) получим:

.

Из рис. 8 следует, что , гдеb – расстояние от прямого тока до рассматриваемой точки А. Следовательно,

.

По принципу суперпозиции . В точкеА все от различных элементов отрезка прямого тока имеют одинаковое направление. Величина магнитной индукции в точкеА равна алгебраической сумме от всех элементов прямого тока:

I

.

Таким образом, для индукции магнитного поля отрезка прямого тока конечной длины (рис.

 10) получаем формулу

. (1.5)

В случае бесконечно длинного прямого проводника с током ,. Следовательно,Отсюда следует, что индукция магнитного поля бесконечно длинного прямогопроводника с током находится по формуле

. (1.6)

1.4. Применение закона Био–Савара–Лапласа. Магнитное поле кругового тока

Рассмотрим проводник в форме окружности радиуса R, по которому протекает ток I (рис. 11). Разобьем круговой ток на элементы тока , каждый из которых создает в центре кругового тока (точкаО) магнитное поле . По закону Био–Савара–Лапласа (1.1), с учетом, что , магнитная индукция, создаваемая элементом тока в точке

О, определяется формулой

.

По принципу суперпозиции. В точкеО все от разных элементов кругового тока имеют одинаковое направление. Следовательно,

.

Таким образом, для индукции магнитного поля в центре кругового тока получаем

. (1.7)

Рассмотрим магнитное поле, создаваемое круговым током в других точках на оси z (рис. 12).

Л

z

юбая пара равных по величине элементов тока (), расположенная симметрично относительно осиz, создает в точках на оси магнитное поле: (). Векторв соответствии с законом Био–Савара–Лапласа направлен перпендикулярно плоскости, содержащей вектораи . Вектор направлен перпендикулярно плоскости, содержащей вектораи . Вектора иобразуют ромб, диагональ которого представляет вектор, направленный вдоль осиОz.

Как следует из рис. 12,

.

Учитывая, что , по закону Био–Савара–Лапласа

.

Так как ,, получаем

.

По принципу суперпозиции результирующий вектор также направлен вдоль осиz, поэтому

.

Окончательное выражение для индукции в точках на оси кругового тока имеет вид

.

Занятие 13 закон био – савара – лапласа

Учебная цель: добиться понимания физической сущности закона Био — Савара — Лапласа, принципа суперпозиции для магнитного поля элементов тока и научиться применять их для расчета магнитных полей проводников с током.

Литература

Основная: Детлаф А.А., Яворский Б.М. Курс физики. – М.: Высшая школа, 1989. – Гл. 22, § 22.1, 22.2, 22.3.

Дополнительная: Савельев И.В. Курс общей физики. – М.: Наука, 1989. – Т. 2, гл. 6, § 39 — 42.

Контрольные вопросы для подготовки к занятию

1. Сформулируйте, запишите математическое выражение закона Био — Савара — Лапласа и поясните его.

2. По какому правилу определяется направление вектора магнитной индукции (напряженности) элемента тока?

3.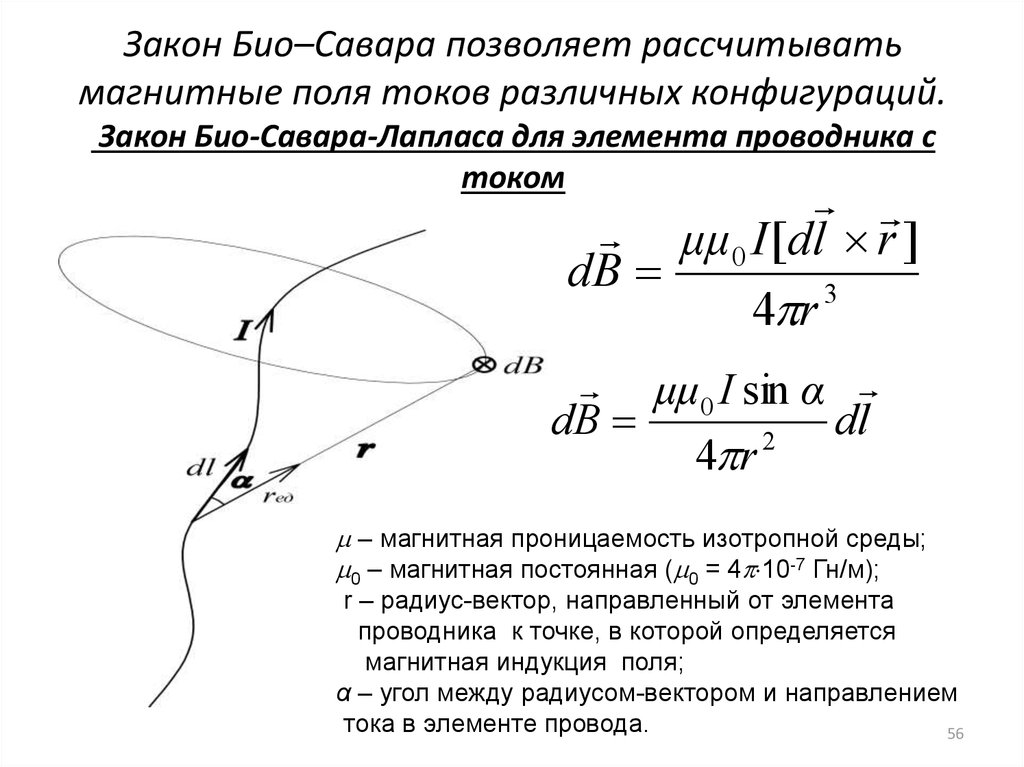 Запишите выражение закона Био — Савара — Лапласа для напряженности магнитного поля элемента тока.

4. Сформулируйте и поясните принцип суперпозиции магнитных полей.

5. Как рассчитывается величина индукции (напряженности) магнитного поля в случае, если направление индукции (напряженности) элементов тока данного проводника одинаковы?

6. Сформулируйте, запишите выражение и поясните закон полного тока (теорему о циркуляции напряженности магнитного поля).

7. Сформулируйте и объясните правило выбора знаков токов, охватываемых данным контуром.

8. По какой формуле рассчитывается индукция (напряженность) магнитного поля:

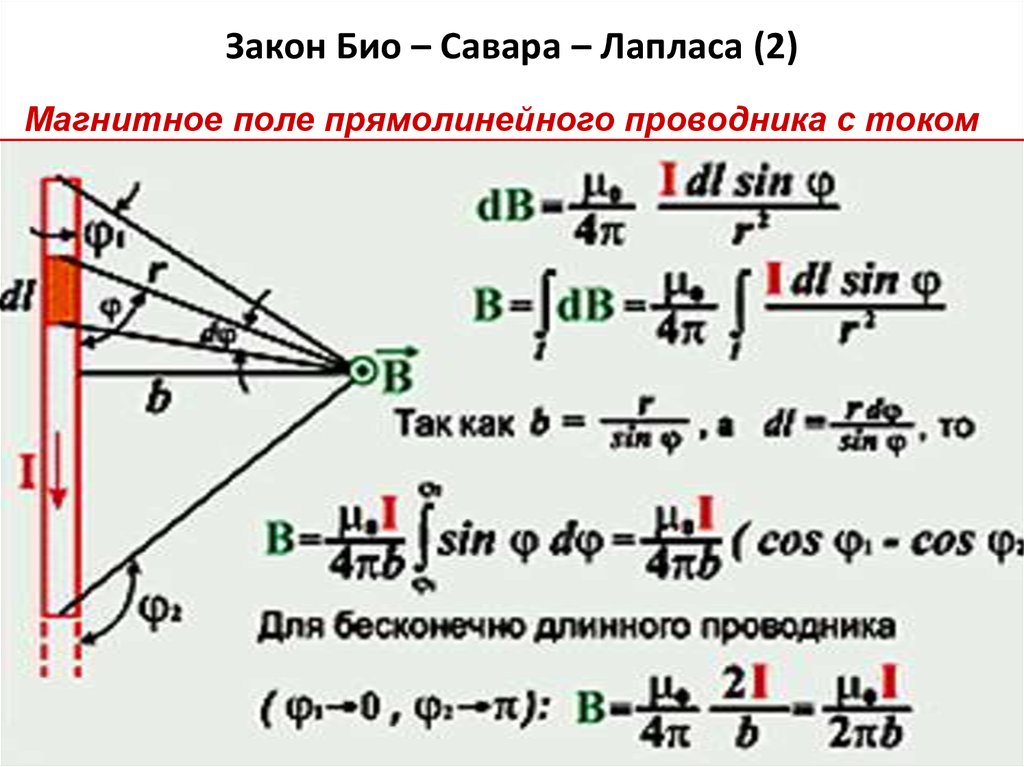
— прямого проводника конечной длины с током на расстоянии r от его оси;

— бесконечно длинного проводника;

— в центре прямоугольного проводника с током;

— на оси кругового витка радиусом R с током I ?

9. Запишите выражение индукции (напряженности) магнитного поля соленоида и поясните его.

10. Что называется длинным соленоидом (нормальной катушкой), каким является его поле?

11. Запишите выражение для индукции (напряженность) магнитного поля в произвольной точке соленоида конечной длины с током I.

Краткие теоретические сведения и основные формулы

Закон Био – Савара – Лапласа позволяет определить величину и направление магнитной индукции в любой точке магнитного поля, создаваемого бесконечно малым элементом проводника с током I – элементом тока (I dl).

Согласно этому закону, элемент проводника dl с током I (рис. 13.1) создает в некоторой точке С магнитное поле, индукция которого dB пропорциональна длине dl, силе тока I, синусу угла  между направлением тока и радиус-вектором точкиС и обратно пропорциональна квадрату расстояния , т. е.

,

где — магнитная постоянная; — безразмерная величина, характеризующая магнитные свойства среды и называемая магнитной проницаемостью среды.

Рис. 13.1

В векторной форме закон Био — Савара — Лапласа имеет вид

. (13.1)

Направление определяется по правилу векторного произведения, или по правилу обхвата правой руки. Вектор направлен перпендику­лярно к плоскости, в которой лежат векторыи, таким образом, что из конца вектораповоротдо совмещения спо кратчайшему пу­ти виден происходящим против часовой стрелки.

Наглядно правило векторного произведения на практике заменяется правилом

обхвата правой руки: отставленный под прямым углом боль­шой палец правой руки направляют по направлению тока в проводнике, концы загнутых четырех пальцев, охватывающих проводник с током, по­мещенных в заданную точку магнитного поля, покажут направление вектора в этой точке.

Учитывая, что векторы магнитной индукции и напряженности связа­ны соотношением

или , (13.2)

для напряженности законБио — Савара — Лапласа примет вид

. (13.3)

Величина вектора равна

. (13.4)

Для магнитных полей, так же как и для электростатических, соблюда­ется принцип суперпозиции: при наложении нескольких магнитных по­лей, имеющих магнитные индукции ,,,…,, магнитная индукция ре­зультирующего поля равна геометрической сумме магнитных индукций складываемых полей:

.

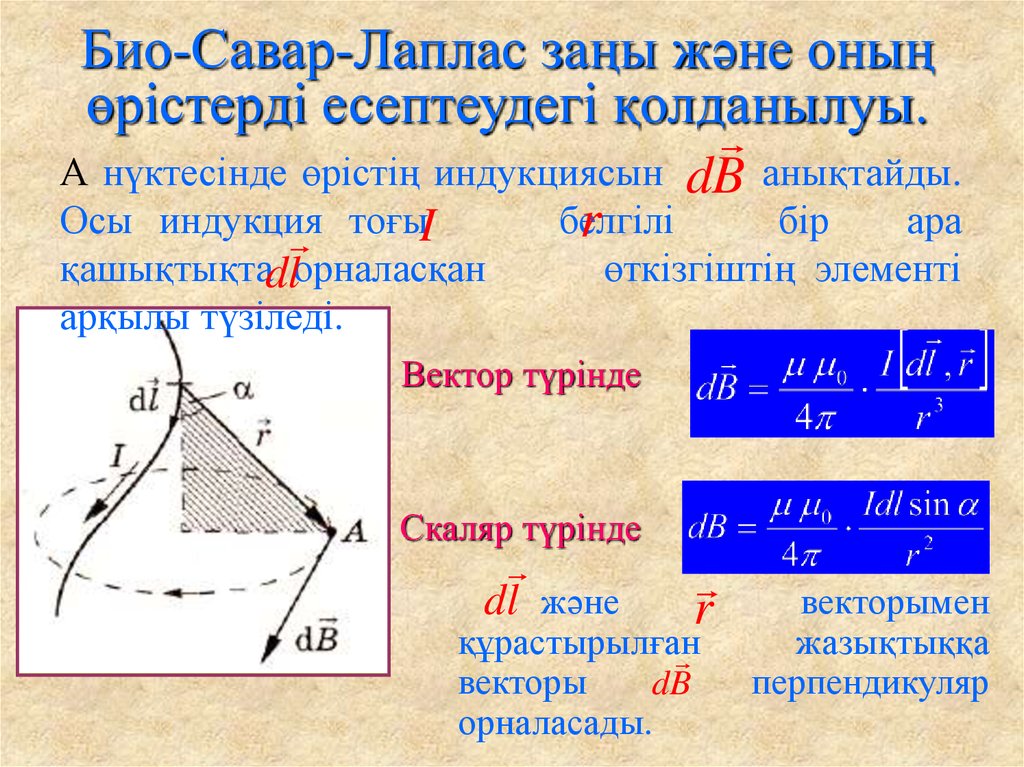
Закон Био — Савара — Лапласа (13.1) и (13.3) представлен в виде диф­ференциального уравнения для магнитной индукции и напряженности, создаваемых небольшим участком проводника . Для вычисления полной магнитной индукции или напряженностимагнитного поля,создаваемого в точке с током , идущим по проводнику конечной длинынадо гео­метрически суммировать элементарные индукции (напряженности), создаваемые всеми элементами тока :

, .

Если индукция магнитного поля от всех элементов токанаправлены вдоль одной прямой, то геометрическое суммирование сводится к алгебраическому суммированию, т.е. к интегрированию:

; (13.5)

. (13.6)

Знак (l) показывает, что интегрирование производится по всей длине l проводника.

12.1 Закон Био-Савара – University Physics Volume 2

Глава 12. Источники магнитных полей

Цели обучения

К концу этого раздела вы сможете:

• Объяснять, как получить магнитное поле из произвольного тока в отрезке линии
• Расчет магнитного поля по закону Био-Савара в определенных геометрических формах, таких как ток в линии и ток в дуге окружности

Мы видели, что масса создает гравитационное поле и также взаимодействует с этим полем. Заряд создает электрическое поле и также взаимодействует с этим полем.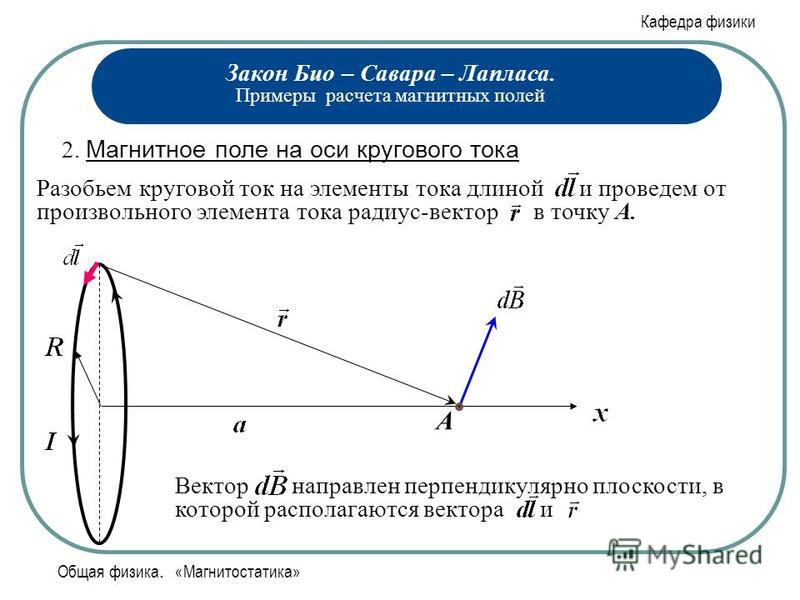 Поскольку движущийся заряд (то есть ток) взаимодействует с магнитным полем, можно было бы ожидать, что он также создает это поле — и так оно и есть.

Уравнение, используемое для расчета магнитного поля, создаваемого током, известно как закон Био-Савара. Это эмпирический закон, названный в честь двух ученых, которые исследовали взаимодействие между прямым проводником с током и постоянным магнитом. Этот закон позволяет вычислить величину и направление магнитного поля, создаваемого током в проводе. 9{\ text {−7}} \ text {T} \ cdot \ text {м / А} [/ латекс]

в системе СИ. Бесконечно малый отрезок провода [латекс]d\stackrel{\to }{\textbf{l}}[/латекс] направлен в том же направлении, что и ток I (предполагается положительным), r — расстояние от [латекс ]d\stackrel{\to }{\textbf{l}}[/latex] в P , а [latex]\hat{\textbf{r}}[/latex] – единичный вектор, указывающий из [latex] d\stackrel{\to }{\textbf{l}}[/latex] до P , как показано на рисунке.

Направление [latex]d\stackrel{\to }{\textbf{B}}[/latex] определяется путем применения правила правой руки к векторному произведению [latex]d\stackrel{\to }{\ textbf{l}}\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}\hat{\textbf{r}}.[/latex] Величина [ латекс] d \ stackrel {\ to } {\ textbf {B}} [/ латекс] равен 9{2}}[/латекс]

, где [латекс]\тета[/латекс] — угол между [латекс]d\stackrel{\to }{\textbf{l}}[/латекс] и [латекс]\шляпа{\textbf{r}}. [/latex] Обратите внимание, что если [латекс]\тета = 0,[/латекс], то [латекс]d\stackrel{\to }{\textbf{B}}=\stackrel{\to }{\textbf{0} }.[/latex] Поле, создаваемое текущим элементом [latex]Id\stackrel{\to }{\textbf{l}}[/latex], не имеет компонентов, параллельных [latex]d\stackrel{\to }{ \textbf{l}}.[/латекс]

Магнитное поле из-за конечной длины провода с током находится путем интегрирования уравнения 12.3 вдоль провода, что дает нам обычную форму закона Био-Савара. 9{2}}.[/латекс]

Поскольку это векторный интеграл, вклады от различных текущих элементов могут не указывать в одном и том же направлении. Следовательно, интеграл часто трудно вычислить даже для довольно простых геометрий. Следующая стратегия может быть полезной.

Стратегия решения проблем: Решение задач Био-Савара

Для решения задач закона Био-Савара полезны следующие шаги:

1. Определите, что закон Био-Савара является выбранным методом для решения данной проблемы. Если в задаче на сравнение [latex]\stackrel{\to }{\textbf{B}}[/latex] и [latex]d\stackrel{\to }{\textbf{l}} есть симметрия,[/latex ] Закон Ампера может быть предпочтительным методом для решения вопроса.
2. Нарисуйте текущую длину элемента [latex]d\stackrel{\to }{\textbf{l}}[/latex] и единичный вектор [latex]\hat{\textbf{r}},[/latex], отметив, что [latex]d\stackrel{\to }{\textbf{l}}[/latex] указывает в направлении текущего элемента, а [latex]\hat{\textbf{r}}[/latex] указывает на текущий элемент к точке, где требуется поле.
3. Вычислить векторное произведение [латекс]d\stackrel{\to }{\textbf{l}}\phantom{\rule{0. 2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}\ hat{\textbf{r}}.[/latex] Результирующий вектор задает направление магнитного поля в соответствии с законом Био-Савара.
4. Используйте уравнение 12.4 и подставьте все заданные величины в выражение, чтобы найти магнитное поле. Обратите внимание, что все переменные, которые остаются постоянными по всей длине провода, могут быть исключены из интегрирования.
5. Используйте правило правой руки, чтобы проверить направление магнитного поля, создаваемого током, или запишите направление магнитного поля, если в предыдущей части была найдена только величина.

Пример

Расчет магнитных полей коротких сегментов тока

По короткому проводу длиной 1,0 см течет ток силой 2,0 А в вертикальном направлении (рис. 12.3). Остальная часть провода экранирована, поэтому она не добавляется к магнитному полю, создаваемому проводом. Рассчитайте магнитное поле в точке P , которая находится на расстоянии 1 метра от провода в направлении x .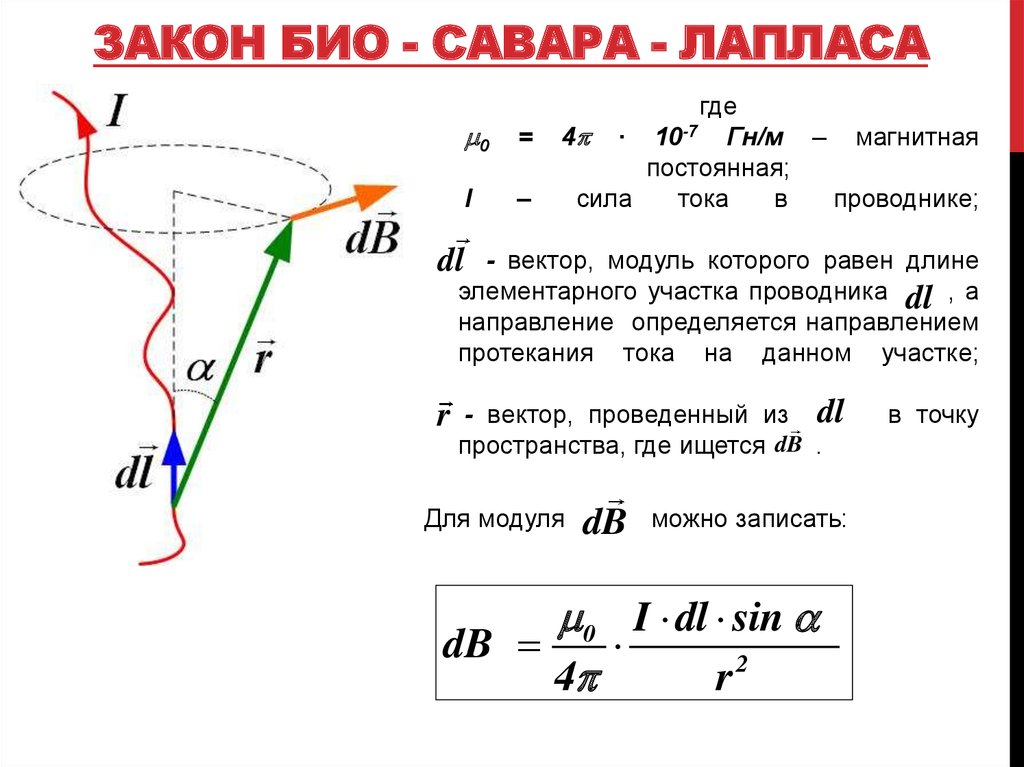

Рисунок 12.3  Небольшой отрезок линии несет ток I в вертикальном направлении. Чему равно магнитное поле на расстоянии x от сегмента?

Стратегия

Мы можем определить магнитное поле в точке P , используя закон Био-Савара. Поскольку текущий отрезок намного меньше, чем расстояние x , мы можем исключить интеграл из выражения. Интегрирование преобразуется обратно в суммирование, но только для малых dl , которые мы теперь запишем как [latex]\text{Δ}l.[/latex] Другой способ думать об этом состоит в том, что каждое из значений радиуса равно почти одинаково, независимо от того, где находится текущий элемент на отрезке, если [latex]\text{Δ}l[/latex] мал по сравнению с 9{-9}\text{T}.[/latex]

По правилу правой руки и закону Био-Савара поле направлено внутрь страницы.

Значение

Это приближение подходит только в том случае, если длина сегмента линии очень мала по сравнению с расстоянием от текущего элемента до точки.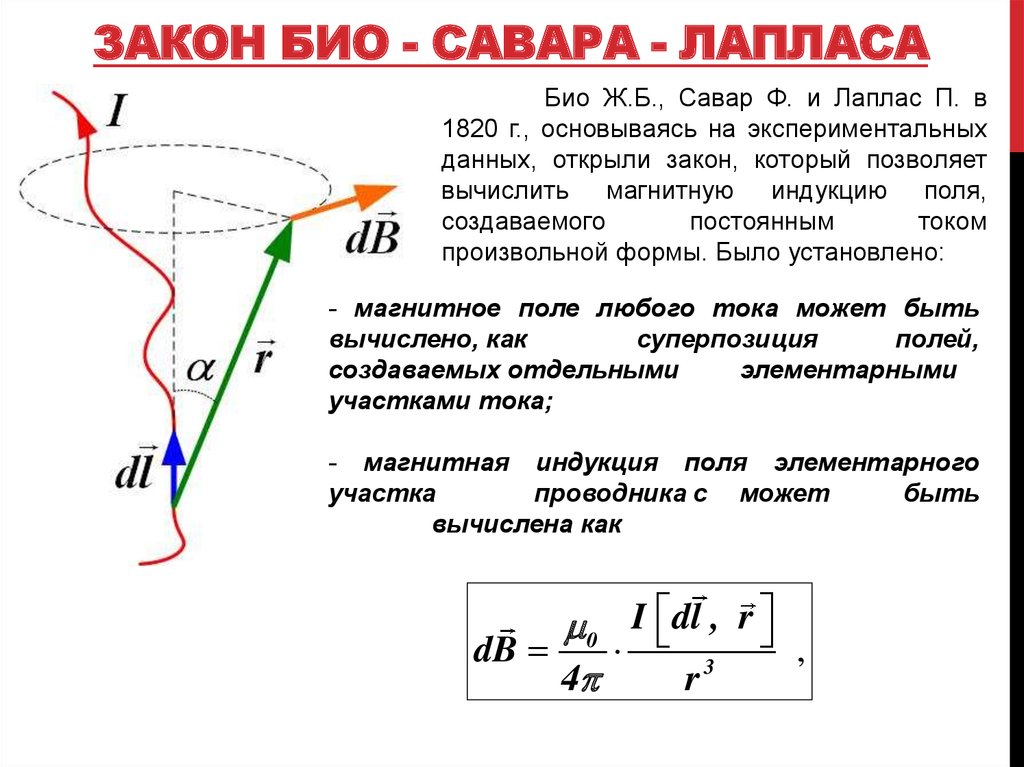 В противном случае для расчета магнитного поля необходимо использовать интегральную форму закона Био-Савара по всему отрезку прямой.

Проверьте свое понимание

Используя пример 12.1, на каком расстоянии будет P должны быть для измерения магнитного поля половину данного ответа?

Show Solution

1,41 м

Пример

Расчет магнитного поля дуги окружности из проволоки

По проводу течет ток I по дуге окружности радиусом R , проходящей под произвольным углом [латекс]\тета[/латекс] (рис. 12.4) . Рассчитайте магнитное поле в центре этой дуги в точке P .

Рисунок 12.4  Сегмент провода, по которому течет ток I. Путь [латекс]d\stackrel{\to }{\textbf{l}}[/латекс] и радиальное направление [латекс]\шляпа{\текстбф{г} }[/latex].

Стратегия

Мы можем определить магнитное поле в точке P , используя закон Био-Савара. Направления радиала и длины пути всегда находятся под прямым углом, поэтому перекрестное произведение превращается в умножение.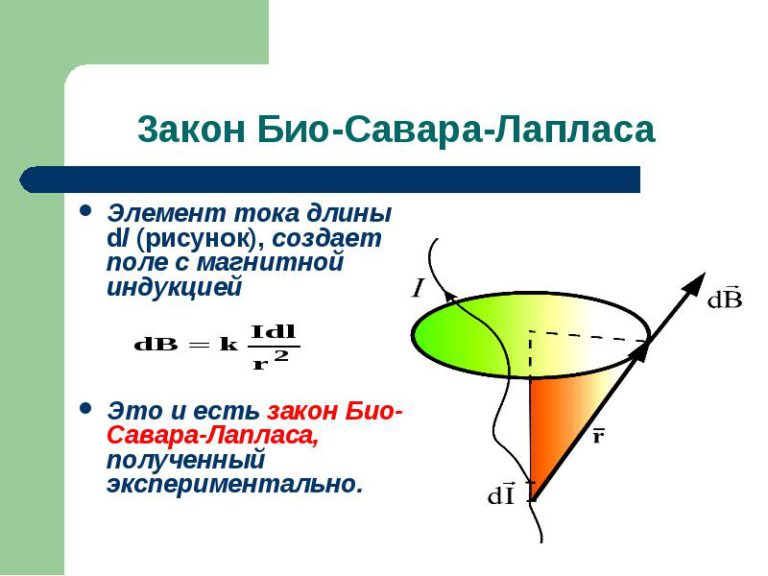 {2}}.[/latex]

Ток и радиус можно вытащить из интеграла, потому что они одинаковы независимо от того, где мы находимся на пути. Остается только интеграл по углу

[латекс] B = \ frac {{\ mu } _ {0} I} {4 \ pi r} \ underset {\ text {wire}} {\ int} d \ theta .[/latex]

Угол меняется на проводе от 0 до [латекс]\тета[/латекс]; следовательно, результат

[латекс] B=\frac{{\mu}_{0}I\theta}{4\pi r}.[/latex]

Значение

Направление магнитного поля в точке P определяется по правилу правой руки, как показано в предыдущей главе. Если на диаграмме наряду с дугой есть другие провода, и вас просят найти результирующее магнитное поле, найдите каждый вклад от провода или дуги и сложите результаты путем суперпозиции векторов. Обязательно обратите внимание на направление каждого вклада. Также обратите внимание, что в симметричной ситуации, такой как прямой или круглый провод, вклады с противоположных сторон точки P компенсируют друг друга.

Проверьте свое понимание

Проволочная петля образует полный круг радиусом R и током I . Какова величина магнитного поля в центре?

Показать раствор

[латекс]\frac{{\mu }_{0}I}{2R}[/латекс]

Резюме

• Магнитное поле, создаваемое проводом с током, находится по закону Био-Савара.
• Текущий элемент [latex]Id\stackrel{\to }{\textbf{l}}[/latex] создает магнитное поле на расстоянии р прочь.

Концептуальные вопросы

Каковы преимущества и недостатки закона Био-Савара для расчета магнитных полей?

Показать решение

Преимущество закона Био-Савара в том, что он работает с любым магнитным полем, создаваемым токовой петлей. Недостатком является то, что это может занять много времени.

Опишите магнитное поле, создаваемое током в двух проводах, подключенных к двум клеммам источника ЭДС и плотно скрученных друг вокруг друга.

Как определить, бесконечен ли провод?

Показать решение

Если бы вы подошли к началу отрезка и вычислили угол [латекс]\тета[/латекс], равный примерно [латекс]0\текст{°}[/латекс], то провод можно считать бесконечным. Это суждение основано также на точности, которая вам нужна в результате.

Одинаковые токи проходят по двум кольцевым петлям; однако одна петля имеет вдвое больший диаметр, чем другая петля. Сравните магнитные поля, создаваемые петлями в центре каждой петли.

Проблемы

По показанному проводу протекает ток силой 10 А. Какова величина магнитного поля, создаваемого отрезком провода диаметром 0,5 мм, измеренная в точке А (а) и точке В (б)?

Десять ампер проходят через квадратную петлю, каждая сторона которой имеет длину 20 см. В каждом углу петли находится отрезок длиной 0,01 см, который соединяет более длинные провода, как показано на рисунке. Вычислите величину магнитного поля в центре петли.

Показать решение 9{-8}\text{T}[/латекс]

Чему равно магнитное поле в точке P из-за тока I в показанном проводе?

На прилагаемом рисунке показана токовая петля, состоящая из двух концентрических дуг окружности и двух перпендикулярных радиальных линий.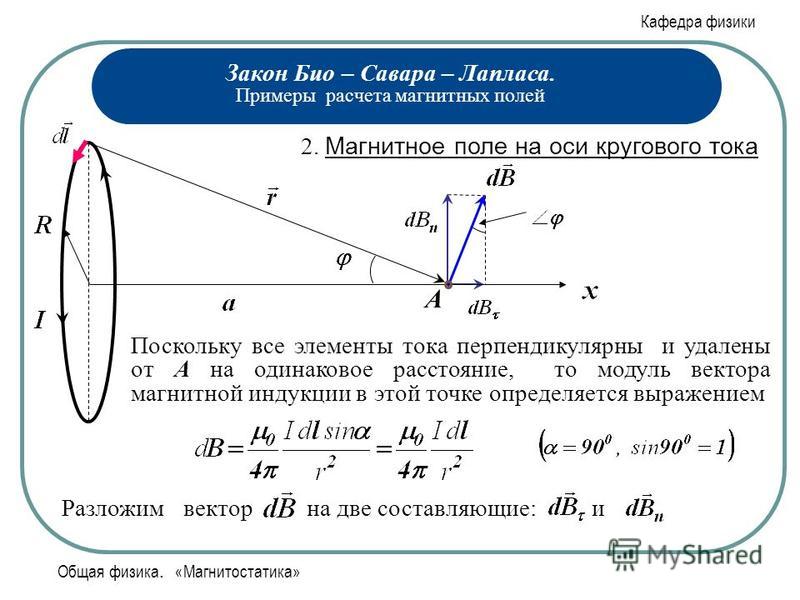 Определить магнитное поле в точке P.

Показать решение

[латекс]B=\frac{{\mu }_{o}I}{8}\left(\frac{1}{a}-\ phantom{\rule{0.05em}{0ex}}\frac{1}{b}\right)[/latex] со страницы

Найдите магнитное поле в центре С прямоугольной проволочной петли, показанной на прилагаемом рисунке.

Два длинных провода, один из которых имеет полукруглый изгиб радиусом R , расположены, как показано на прилагаемом рисунке. Если по обоим проводам течет ток I , на каком расстоянии друг от друга должны быть их параллельные участки, чтобы суммарное магнитное поле в точке P было равно нулю? Ток в прямом проводе течет вверх или вниз?

Показать решение

[latex]a=\frac{2R}{\pi }[/latex]; ток в проводе справа должен течь вверх по странице.

Глоссарий

Закон Био-Савара

уравнение, определяющее магнитное поле в точке, создаваемое проводом с током

проницаемость свободного пространства

[латекс]{\mu }_{0},[/латекс] мера способности материала, в данном случае свободного пространства, поддерживать магнитное поле

Лицензии и авторские права

Закон Био-Савара. Автор : Колледж OpenStax. Расположен по адресу : https://openstax.org/books/university-physics-volume-2/pages/12-1-the-biot-savart-law. Лицензия : CC BY: Attribution . Условия лицензии : Скачать бесплатно по адресу https://openstax.org/books/university-physics-volume-2/pages/1-introduction

ठोस अवस्था नोट्स | Химия класс 12 Глава 1 Примечания на хинди

विषय-सूची

पदाा की अवस अवस अवस अवस अवस अवस अवस अवस अवस अवस अवस अवस अवस अवस अवस अवस अवस आयन) प प प प प प प प संवृत संवृत क क क क क क थ थ थ Как संवृतчего ज wher ण थшли. रहते हैं। एवं इन पदार्थों के कण अपने अक्ष पर ही दोलन करते हह (твердое состояние на хинди) ठोस पदार्थ का आकार व आयतन निश्चित रहता है।

ठोस अवस्था

ठोस अवस्था के लक्षण

• इनका दшить
• इनके बीच अंतराण्विक बल लघु परास वाले होते ैत
• इनके बीच प्रबल अंतराण्विक बल होते हैं।
• यह असंपीड्य तथा कठोर होते हैं।
• इनके अवयवी कणों की स्थिति निश्चित होती है।
• ठोस के अवयवी कण केवल अपने अक्ष पर ही कंपन क।॰ ह॰ ही

ठोस अवस्था के उदाहरण

• NaCl, KCl, MgCl ₂ आदि ठोस में सं सं000 इक इक आयतन हैं।। हैं हैं हैं हैं हैं हैं हैं हैं
• О ₂ , CO ₂ , H ₂ आदि आण्विक ठोस में संरचनात्मक इकाई अणु हैं।।।।।।।।।।।। हैं हैं हैं हैं हैं
• डायमंड एवं गшить 9033

ठोस अवस्था के गुण

ठोस पद|
(1) विद्युतीय गुण
(2) चुंबकीय गुण

1.

विद्युतीय गुण

(i) चालक — वह ठोस पद पद000 (i) चालक — वह पद पद जिनमें विद विद विद000
(ii) विद्युतरोधी — वह ठोस पदार्थ जिनमें विद्युत धारा प्रवाहित नहीं होती उन उन्हें और विद्युतरोधी कहते हैं।।।।।।।।।।
(ii) अर्धचालक — वह ठोस पद पद पद पद जिनमें विद विद्युत ध ध ध एवं कुछ प выполнительный

2. चुंबकीय गुण

(i) प्रतिचुंबकीय — वे ठोस पद पद000 (i) प्रतिचुंबकीय — वे ठोस पद पद जो चुंबकीय क्षेत्षेतравия द्वारा दुर्बल ूप से पшить होते हैं उन उन उनхов पшить पद पद हैं प प हैं होते हैं उन्व प्हें प्हेंравив
(ii) अनुचुंबकीय — वे ठोस पदार्थ जो चुंबकीय क्षेत्रों द ударя
(ii) लौहचुंबकीय — वे ठोस पदार्थ जो चुंबकीय क्षेत्रों द्वारा प्रबल ूप आक आका होते उन उन्हें लौहचुंबकीय पद पद कहते हैं हैं।।।।।।।।।।।।।।। हैं हैं हैं हैं हैं हैं हैं हैं।।। आक आक।।।।।।।।।।।।। हैं हैं हैं हैं हैं हैं हैं हैं हैं हैं हैं हैं।।।।।।।।।

ХИМИЯ КЛАСС 12 ГЛАВА 1 Примечания на хинди

रसायन विज्ञान कक्षा 12 इसलिए हमने लेख में इस प प को पू पू000 कव नहीं है बल बल प सभी सभी महत महत महत महत महत महत महत महत महत महत महत महत त त त त आप को में आस आस हो औ आप बो न को समझने समझने में आस हो।।।।।।।।।।।।। सभी लेखों के लिंक नीचे दिए गए हैं। पढ़ें…

• क्रिस्टलीय तथा अकшить
• क्रिस्टलीय ठोस का वर्गीकरण | Закрыть
• .