Задачи по квантовой механике. Том 2
Задачи по квантовой механике. Том 2
ОглавлениеIII. Частицы со спиномЗадача 130. Собственные векторы матриц Паули Задача 131. Алгебра спиновых матриц Задача 132. Трансформационные свойства спиноров Задача 133. Электрон со спином в центральном поле Задача 134. Квадрупольный момент при наличии спина Задача 135.  Среднее значение магнитного момента Среднее значение магнитного моментаЗадача 136. Тонкая структура Задача 137. Плоские волны для частиц со спином 1/2 Задача 138. Спиновый резонанс для свободного электрона Б. Двух- и трехчастичные задачи Задача 139. Спиновые функции двух частиц Задача 140. Центральное взаимодействие между нуклонами, зависящее от спина Задача 142. Собственные функции оператора полного момента двух частиц, обладающих спином Задача 143. Тензорные силы Задача 144. Дейтрон с тензорным взаимодействием Задача 145. Электрический квадрупольный и магнитный днпольный моменты дейтрона Задача 146. Спиновые функции трех частиц Задача 147. Рассеяние нейтронов молекулярным водородом IV. Многочастичные задачи Задача 148. Две отталкивающиеся частицы на окружности Задача 149. Трехатомная линейная молекула Задача 150. Движение центра масс Задача 151. Теорема вириала Задача 152. Определитель Слэтера  Определитель Слэтера и обменное взаимодействие Определитель Слэтера и обменное взаимодействиеЗадача 154. Два атомных электрона в основном состоянии Задача 155. Возбужденные состояния атома гелия Задача 156. Возбужденные S-состояния атома гелия Задача 157. Основное состояние атома лития Задача 158. Обменные поправки к основному состоянию атома лития Задача 159. Электрическая восприимчивость Задача 160. Диамагнитная восприимчивость неона Задача 161. Силы Ван-дер-Ваальса Задача 162. Обменное вырождение при наличии возбуждения Задача 163. Нейтральная молекула водорода Задача 164. Рассеяние одинаковых частиц Задача 166. Неупругое рассеяние Б. Очень большое число частиц. Квантовая статистика Задача 167. Электронный газ в металле Задача 168. Парамагнитная восприимчивость металла Задача 169. Холодная эмиссия без учета сил электростатического изображения Задача 170. Холодная эмиссия с учетом сил электростатического изображения Задача 171.  Белый карлик Белый карликЗадача 172. Приближение Томаса — Ферми Задача 173. Поправка Амальди для нейтрального атома Задача 174. Энергия атома в модели Томаса — Ферми Задача 175. Теорема вириала для модели атома Томаса-Ферми Задача 177. Вариационный метод для модели атома Томаса — Ферми Задача 178. Влияние экранировки на K-электроны V. Нестационарные задачи Задача 179. Двухуровневая система под действием не зависящего от времени возмущения Задача 180. Действие периодического возмущения на двухуровневую систему Задача 181. Теория возмущений Дирака Задача 182. Периодическое возмущение и резонанс Задача 183. Золотое правило для рассеяния Задача 184. Борновское рассеяние в импульсном представлении Задача 185. Кулоновское возбуждение атома Задача 186. Фотоэффект Задача 187. Дисперсия света. Силы осцилляторов Задача 188. Спин-флип в магнитной резонансной системе Задача 189.  Квадрирование уравнения Дирака Квадрирование уравнения ДиракаЗадача 190. Плоские волны Дирака с положительной энергией Задача 191. Трансформационные свойства дираковских спиноров Задача 192. Лоренцевы коварианты Задача 193. Пространственная инверсия Задача 194. Зарядовое сопряжение Задача 195. Состояния со смешанной спиральностью Задача 196. Среднее значение спина Задача 197. Алгебраические свойства волнового спинора Дирака Задача 198. Плотность тока в алгебраической формулировке Задача 199. Ток проводимости и ток поляризации Задача 201. Центральные силы в теории Дирака Задача 202. Проблема Кеплера в теории Дирака Задача 203. Тонкая структура энергетических уровней атома водорода Задача 204. Проблема Кеплера. Радиальные функции при положительных энергиях Задача 205. Разложение дираковской плоской волны по состояниям с определенным моментом Задача 206. Рассеяние в поле центральных сил Задача 208. 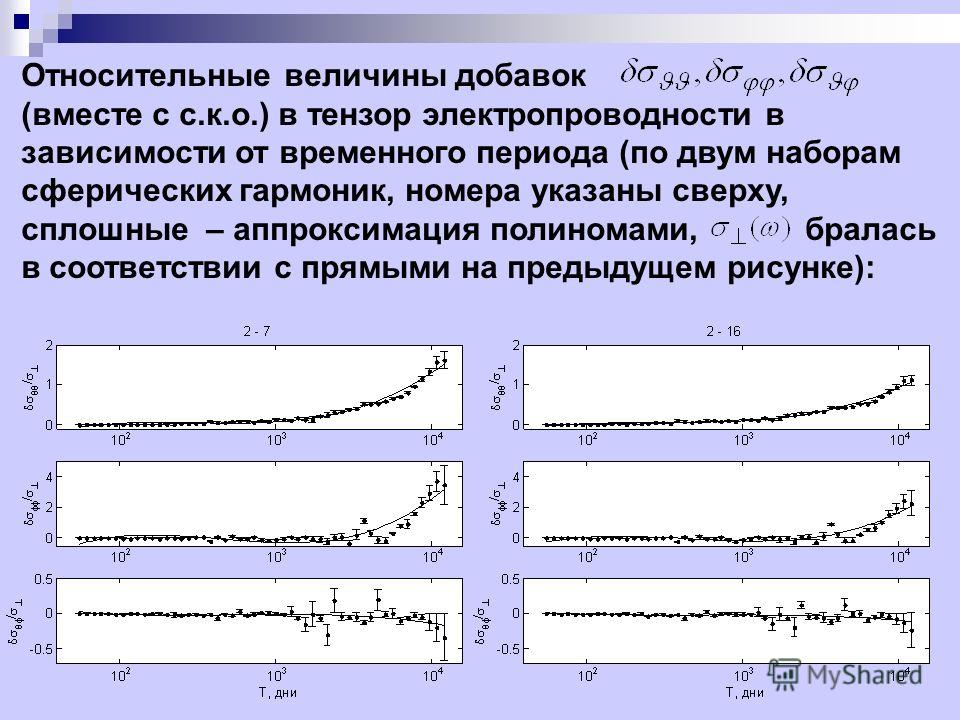 Наклонное падение плоской волны на прямоугольную потенциальную ступеньку Наклонное падение плоской волны на прямоугольную потенциальную ступенькуЗадача 209. Отражение от прямоугольной потенциальной ступеньки при наклонном падении Задача 210. Квантование шредингеровского волнового поля Задача 211. Рассеяние в борновском приближении Задача 212. Квантование классического поля излучения Задача 213. Вероятность переходов с излучением одного фотона Задача 214. Угловое распределение излучения Задача 215. Полная вероятность перехода Задача 216. Правила отбора для дипольного излучения Задача 217. Интенсивности линий лаймановской серии Задача 218. Эффект Комптона Задача 219. Тормозное излучение Математическое приложение Криволинейные координаты Г-функция Функции Лежандра Сферические гармоники Гипергеометрическая функция Некоторые функции, определяемые интегралами |
Помогите решить / разобраться (М)
Сообщения без ответов | Активные темы | Избранное
Правила форума
Посмотреть правила форума
| madschumacher |
| |||
28/04/16 |
| |||
| ||||
| amon |
| |||
04/09/14 |
| |||
| ||||
| madschumacher |
| |||
28/04/16 |
| |||
| ||||
| Metford |
| |||
06/04/13 |
| |||
| ||||
| madschumacher |
| |||
28/04/16 |
| |||
| ||||
| Metford |
| |||
06/04/13 |
| |||
| ||||
| amon |
| |||
04/09/14 |
| |||
| ||||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 7 ] |
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
| Найти: |
сферических гармоник | Brilliant Math & Science Wiki
Содержание
- Построение по уравнению Лапласа
- Физические приложения
- Рекомендации
Сферические гармоники построены как собственные функции угловой части лапласиана в трех измерениях, также называемые лапласианом на сфере. 2\). 92} &= -\ell (\ell+1) Y(\theta, \phi),
\end{выравнивание}
\]
2\). 92} &= -\ell (\ell+1) Y(\theta, \phi),
\end{выравнивание}
\]
где \(\ell(\ell+1)\) — некоторая константа, называемая константой разделения , записанная в наиболее удобной форме. Умножение верхнего уравнения на \(Y(\theta,\phi)\) с обеих сторон, нижнего уравнения на \(R(r)\) с обеих сторон и добавление двух значений восстановит исходное трехмерное уравнение Лапласа. в сферических координатах; постоянная разделения получается путем признания того, что исходное уравнение Лапласа описывает два уравнения на собственные значения противоположных знаков. 9{\ell}.\]
Примечательно, что эта формула корректно определена и отлична от нуля только для \(\ell \geq 0\) и \(m\) целых чисел, таких что \(|m| \leq \ell\) . Формально эти условия на \(m\) и \(\ell\) можно вывести, потребовав периодичности решений относительно \(\theta\) и \(\phi\).
Общие решения для каждой линейно независимой \(Y(\theta, \phi)\) представляют собой сферические гармоники с константой нормализации, умножающей решение, как описано до сих пор, чтобы сделать независимые сферические гармоники ортонормированными: 92 \ell (\ell + 1), \quad L_z = \hbar m. \]
\]
Можно сделать вывод, что сферические гармоники в решении для волновой функции электрона в атоме водорода определяют угловой момент электрона. В квантовой механике константы \(\ell\) и \(m\) называются азимутальным квантовым числом и магнитным квантовым числом из-за их связи с вращением и того, как энергия электрона в ненулевой \(m \) изменения состояния в магнитном поле.
(Да, Да) (Да нет) (Нет да) (Нет, нет) 9{\ell}\) — некоторый набор коэффициентов, зависящий от граничных условий. Обратите внимание, что первый член внутри сумм — это просто ряд Лорана по \(r\), описывающий все возможные степени \(r\) до порядка \(\ell\).
Проводящая сфера радиуса \(R\) со слоем заряда \(Q\), распределенным по ее поверхности, имеет электрический потенциал на поверхности сферы, равный
\[V = \frac{1}{4\pi \epsilon_0} \frac{Q}{R} \sin \theta \cos \theta \cos (\phi).
\] 93} \sin \theta \cos \theta \cos \phi, \\r
Что из следующего дает поверхностную плотность заряда на поверхности сферы?
\(\)
Примечание: Напомним, что изменение электрического поля по обе стороны проводника равно \(\frac{\sigma}{\epsilon_0},\), где \(\sigma\) равно плотность поверхностного заряда.Физика черных дыр
Сферические гармоники также обычно полезны для расширения решений в физических условиях со сферической симметрией. Одним интересным примером сферической симметрии, где полезно разложение по сферическим гармоникам, является случай с черной дырой Шварцшильда. Возмущения безмассового комплексного скалярного поля \(\Phi\) вне черной дыры Шварцшильда с массой \(M\) удовлетворяют версии уравнения Лапласа, обобщенной для искривленного пространства-времени: 9{-i\omega t} \sum_{\ell ,m} \frac{\Psi (r)}{r} Y_{\ell m} (\theta, \phi).\]
Это разложение обычно выполняется в рамках анализа мод \(\omega\), описывающих эволюцию возмущения \(\Phi\), названных квазинормальными модами [3].
Возможность расширения в основе сферических гармоник необходима для выделения радиальной зависимости, которая в конечном итоге ограничивает моды \(\omega\).
[1] Изображение с https://en.wikipedia.org/wiki/Spherical_harmonics#/media/File:Spherical_Harmonics.png по лицензии Creative Commons для повторного использования и модификации.
[2] Гриффитс, Дэвид Дж. Введение в квантовую механику . Второе издание. Pearson: Upper Saddle River, NJ, 2006.
[3] E. Berti, V. Cardoso, and A.O. Старинец. Квазинормальные моды черных дыр и черных бран . http://arxiv.org/pdf/0905.2975v2.pdf.
Цитировать как: Сферические гармоники. Brilliant.org . Извлекаются из https://brilliant.org/wiki/spherical-harmonics/
Сферические гармоники — Химия LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 64932
Сферические гармоники — это группа функций, используемых в математике и физических науках для решения задач в таких дисциплинах, как геометрия, уравнения в частных производных и теория групп.
Общая нормализованная сферическая гармоника изображена ниже: 92 \psi = 0 \]
Эти гармоники классифицируются как сферические из-за того, что они являются решением угловой части уравнения Лапласа в сферической системе координат. Работа Лапласа включала изучение гравитационных потенциалов, и Кельвин использовал их в сотрудничестве с Питером Тейтом для написания учебника. В 20 веке Эрвин Шредингер и Вольфганг Паули опубликовали в 1926 году статьи с подробным описанием того, как решить «простую» систему атомов водорода. Сейчас, еще девяносто лет спустя, точные решения для атома водорода все еще используются для анализа многоэлектронных атомов и даже целых молекул. Большая часть современной физической химии основана на структуре, которая была создана этими квантово-механическими трактовками природы. 9{|m|}(\cos\theta)\), который называется полиномом Лежандра . Детали того, откуда берутся эти многочлены, здесь в значительной степени излишни, чтобы мы не сказали, что это набор решений -секундного дифференциального уравнения, который формируется в результате попытки решить уравнение Лапласа.
Неудивительно, что это уравнение называется «уравнением Лежандра», и оно содержит преобразование \(\cos\theta = x\). Как показывает выше общая функция, для сферической гармоники, где \(l = m = 0\), член в квадратных скобках превращается в простую константу. Экспонента равна единице, и мы говорим, что: 9{0}(\theta,\phi) = \sqrt{ \dfrac{1}{4\pi} }\]
Не полностью показано, что происходит с полиномом Лежандра, присоединенным к нашему выражению в квадратных скобках. В простом \(l = m = 0\) случае он исчезает.
Не случайно в этой статье обсуждается как квантовая механика, так и две переменные, \(l\) и \(m\). Это именно квантовое число углового момента и магнитное квантовое число, соответственно, которые упоминаются на уроках общей химии. Если мы рассмотрим спектроскопическую запись, квантовое число углового момента, равное нулю, предполагает, что мы имеем 9o\]
Расширенное описание
Мы описали эти функции как набор решений дифференциального уравнения, но мы также можем взглянуть на сферические гармоники с точки зрения операторов и области линейной алгебры.
2\) и (2) тот факт, что сферические гармоники действуют как собственный базис для данного векторного пространства. 92}{2I}\]
для \(I\), равного моменту инерции представляемой системы. Это линейный оператор (следует правилам аддитивности и однородности). Точнее, эрмитов. Это означает, что когда он используется в задаче на собственные значения, все собственные значения будут действительными, а собственные функции будут ортогональными.
В нотации Дирака ортогональность означает, что скалярное произведение любых двух различных собственных функций будет равно нулю:
\[\langle \psi_{i} | \psi_{j} \rangle = 0\]
Принимая во внимание тот факт, что эти функции также часто нормируются, мы можем записать классическое соотношение между собственными функциями квантово-механического оператора, используя кусочную функцию: дельту Кронекера.
\[\langle \psi_{i} | \psi_{j} \rangle = \delta_{ij} \, for \, \delta_{ij} = \begin{case} 0 & i \neq j \ 1 & i = j \end{case} \]
Это соотношение также применимо к множеству решений сферической гармоники, поэтому мы можем записать соотношение ортонормированности для каждого квантового числа: 9{n} \rangle = \delta_{lk}\delta_{mn}\]
Пример \(\PageIndex{2}\): Симметрия
Оператор контроля четности иногда обозначается буквой «P», но будет называться как \(\Pi\) здесь, чтобы не путать его с оператором импульса.
Когда этот эрмитов оператор применяется к функции, знаки всех переменных внутри функции меняются местами. Этот оператор дает нам простой способ определить симметрию функции, на которую он действует.
Напомним, что четные функции появляются как \(f(x) = f(-x)\), а нечетные функции появляются как \(f(-x) = -f(x)\). Сочетание этого с \(\Pi\) дает условия: 9{\inf} (EVEN)(НЕЧЕТНЫЕ)(EVEN)d\tau \]
Опять же, сложная проблема зондирования сводится к очень простому анализу. Используя интегральные свойства, мы видим, что это равно нулю для любого четного-\(l\).
Напоминание о том, почему собственный вектор (синий) особенный. Из https://en.Wikipedia.org/wiki/Eigenvalues_and_eigenvectors.
Наконец, сферические гармоники образуют полный набор и как таковые могут служить основой для данного (гильбертова) пространства. Это означает, что любая сферическая функция может быть записана как линейная комбинация этих базисных функций (поскольку базис по определению охватывает пространство непрерывных сферических функций): 9{m}(\theta,\phi) \]
Хотя любой конкретный базис может действовать таким образом, тот факт, что сферические гармоники могут делать это, показывает хорошую связь между этими функциями и рядом Фурье, базисным набором синусов.
и косинусы. Сферические гармоники считаются многомерными аналогами этих комбинаций Фурье и невероятно полезны в приложениях, связанных с частотными областями. За последние несколько лет, с развитием компьютерной графики и рендеринга, моделирование систем динамического освещения привело к новому использованию этих функций.
Пример \(\PageIndex{3}\)
Для выполнения каких-либо серьезных вычислений с большой суммой сферических гармоник нам необходимо иметь возможность генерировать их с помощью компьютера в режиме реального времени (особенно для реального времени). графические системы). Это требует использования либо рекуррентных соотношений, либо производящих функций. В то время как в самом верху этой страницы находится общая формула для наших функций, полиномы Лежандра все еще не определены. Перечислены два основных оператора, необходимых для этого примера: 9{i\phi} \]
В качестве примечания, существует ряд различных соотношений, которые можно использовать для создания сферических гармоник или полиномов Лежандра.
Часто эффективные компьютерные алгоритмы имеют гораздо более длинные полиномиальные члены, чем короткие операторы на основе производных из начала этой задачи.
В заключение мы должны более подробно рассмотреть два рекурсивных соотношения полиномов Лежандра вместе. Поскольку производные четных функций дают нечетные функции и наоборот, мы замечаем, что для нашего первого уравнения четное значение \(l\) подразумевает четное число производных, а это дает еще одну четную функцию. Когда мы подставим это во второе соотношение, нам придется иметь дело с производными \(|m|\) нашей функции \(P_{l}\). Нам, однако, повезло, так как в сферических гармонических функциях есть отдельная составляющая, полностью зависящая от знака \(m\). Таким образом, любые изменения четности полинома Лежандра (для создания связанной функции Лежандра) будут отменены изменением знака \(m\) в азимутальной составляющей. Четность зависит только от \(l\)! 9{м}\).
Ссылки
- Подробная информация об истории S.



 08.2016, 13:14
08.2016, 13:14 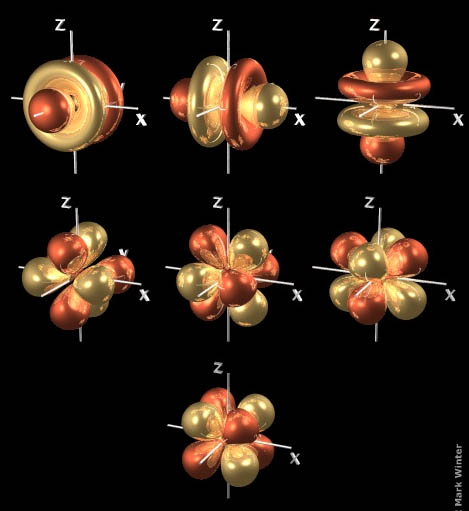 08.2016, 14:29
08.2016, 14:29  08.2016, 15:07
08.2016, 15:07  08.2016, 15:19
08.2016, 15:19  В качестве пространства представления выбираются дифференцируемые функции трёх вещественных переменных, причём достаточно ограничиться теми, которые заданы на сфере (при любых вращениях сфера переходит сама в себя).
В качестве пространства представления выбираются дифференцируемые функции трёх вещественных переменных, причём достаточно ограничиться теми, которые заданы на сфере (при любых вращениях сфера переходит сама в себя). Больше деталей у Ландау или, например, у Хамермеша.
Больше деталей у Ландау или, например, у Хамермеша. В Ландавшица 3 я как раз сразу и полез и видимо не туда. Хотелось именно словами сказанную фразу.
В Ландавшица 3 я как раз сразу и полез и видимо не туда. Хотелось именно словами сказанную фразу.
 Неприводимые представления, допустим, можно строить как представления группы вращений, только не используя аппарат групп Ли. Базисные функции — однородные полиномы, и их надо придумать так, что бы при преобразованиях из они преобразовывались друг через друга. То, что получится будет аналогом сферических функций. Места, где такие «тетраэдрические» или «кубические» функции были бы выписаны регулярно я не знаю. Кое-что можно отыскать в известной книжке Бира и Пикуса «Симметрия и деформационные эффекты в полупроводниках». Названия пугаться не надо, группы и — стандартные группы симметрии полупроводниковых кристаллов, и про них там много чего полезного написано.
Неприводимые представления, допустим, можно строить как представления группы вращений, только не используя аппарат групп Ли. Базисные функции — однородные полиномы, и их надо придумать так, что бы при преобразованиях из они преобразовывались друг через друга. То, что получится будет аналогом сферических функций. Места, где такие «тетраэдрические» или «кубические» функции были бы выписаны регулярно я не знаю. Кое-что можно отыскать в известной книжке Бира и Пикуса «Симметрия и деформационные эффекты в полупроводниках». Названия пугаться не надо, группы и — стандартные группы симметрии полупроводниковых кристаллов, и про них там много чего полезного написано. \] 93} \sin \theta \cos \theta \cos \phi, \\r
\] 93} \sin \theta \cos \theta \cos \phi, \\r Возможность расширения в основе сферических гармоник необходима для выделения радиальной зависимости, которая в конечном итоге ограничивает моды \(\omega\).
Возможность расширения в основе сферических гармоник необходима для выделения радиальной зависимости, которая в конечном итоге ограничивает моды \(\omega\). Общая нормализованная сферическая гармоника изображена ниже: 92 \psi = 0 \]
Общая нормализованная сферическая гармоника изображена ниже: 92 \psi = 0 \] Неудивительно, что это уравнение называется «уравнением Лежандра», и оно содержит преобразование \(\cos\theta = x\). Как показывает выше общая функция, для сферической гармоники, где \(l = m = 0\), член в квадратных скобках превращается в простую константу. Экспонента равна единице, и мы говорим, что: 9{0}(\theta,\phi) = \sqrt{ \dfrac{1}{4\pi} }\]
Неудивительно, что это уравнение называется «уравнением Лежандра», и оно содержит преобразование \(\cos\theta = x\). Как показывает выше общая функция, для сферической гармоники, где \(l = m = 0\), член в квадратных скобках превращается в простую константу. Экспонента равна единице, и мы говорим, что: 9{0}(\theta,\phi) = \sqrt{ \dfrac{1}{4\pi} }\] 2\) и (2) тот факт, что сферические гармоники действуют как собственный базис для данного векторного пространства. 92}{2I}\]
2\) и (2) тот факт, что сферические гармоники действуют как собственный базис для данного векторного пространства. 92}{2I}\] Когда этот эрмитов оператор применяется к функции, знаки всех переменных внутри функции меняются местами. Этот оператор дает нам простой способ определить симметрию функции, на которую он действует.
Когда этот эрмитов оператор применяется к функции, знаки всех переменных внутри функции меняются местами. Этот оператор дает нам простой способ определить симметрию функции, на которую он действует. и косинусы. Сферические гармоники считаются многомерными аналогами этих комбинаций Фурье и невероятно полезны в приложениях, связанных с частотными областями. За последние несколько лет, с развитием компьютерной графики и рендеринга, моделирование систем динамического освещения привело к новому использованию этих функций.
и косинусы. Сферические гармоники считаются многомерными аналогами этих комбинаций Фурье и невероятно полезны в приложениях, связанных с частотными областями. За последние несколько лет, с развитием компьютерной графики и рендеринга, моделирование систем динамического освещения привело к новому использованию этих функций. Часто эффективные компьютерные алгоритмы имеют гораздо более длинные полиномиальные члены, чем короткие операторы на основе производных из начала этой задачи.
Часто эффективные компьютерные алгоритмы имеют гораздо более длинные полиномиальные члены, чем короткие операторы на основе производных из начала этой задачи.