Сферические функции — Википедия
Материал из Википедии — свободной энциклопедии
Сферические функции представляют собой угловую часть семейства ортогональных решений уравнения Лапласа, записанную в сферических координатах. Они широко используются для изучения физических явлений в пространственных областях, ограниченных сферическими поверхностями и при решении физических задач, обладающих сферической симметрией. Сферические функции имеют большое значение в теории дифференциальных уравнений в частных производных и теоретической физике, в частности в задачах расчёта электронных орбиталей в атоме, гравитационного поля геоида, магнитного поля планет и интенсивности реликтового излучения.
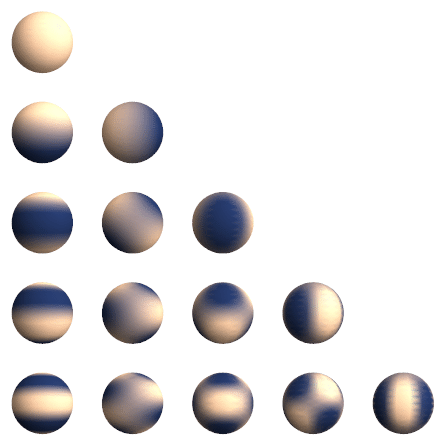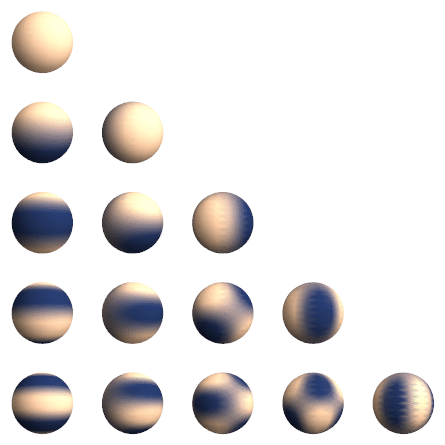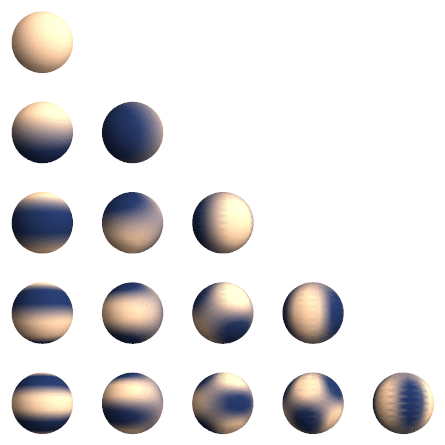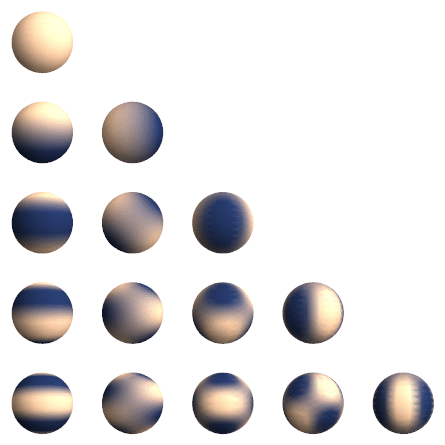
Вещественные сферические функции Ylm, l=0…4 (сверху вниз), m=0…4 (слева направо). Функции отрицательного порядка Yl-m повёрнуты вокруг оси Z на 90/m
Сферические функции являются собственными функциями оператора Лапласа в сферической системе координат (обозначение Ylm(θ,φ){\displaystyle Y_{l}^{m}(\theta ,\varphi )}). Они образуют ортонормированную систему в пространстве функций на двумерной сфере:
- ⟨Ylm;Ylm⟩=∬|Ylm|2sinθdθdφ=1{\displaystyle \langle Y_{l}^{m};Y_{l}^{m}\rangle =\iint |Y_{l}^{m}|^{2}\sin {\theta }\,d\theta \,d\varphi =1}
- ⟨Ylm;Yl′m′⟩=∫02π∫0πYl′m′∗Ylmsinθdθdφ=δll′δmm′{\displaystyle \langle Y_{l}^{m};Y_{l’}^{m’}\rangle =\int \limits _{0}^{2\pi }\int \limits _{0}^{\pi }Y_{l’}^{m’*}Y_{l}^{m}\sin {\theta }\,d\theta \,d\varphi =\delta _{ll’}\delta _{mm’}},
где * обозначает комплексное сопряжение, δll′{\displaystyle \delta _{ll’}} — символ Кронекера.
Сферические функции имеют вид
- Ylm=12πeimφΘlm(θ){\displaystyle Y_{l}^{m}={\frac {1}{\sqrt {2\pi }}}e^{im\varphi }\Theta _{lm}(\theta )},
где функции Θlm(θ){\displaystyle \Theta _{lm}(\theta )} являются решениями уравнения
- 1sinθddθ(sinθdΘlmdθ)−m2sin2θΘlm+l(l+1)Θlm=0{\displaystyle {\frac {1}{\sin {\theta }}}{\frac {d}{d\theta }}\left(\sin {\theta }{\frac {d\Theta _{lm}}{d\theta }}\right)-{\frac {m^{2}}{\sin ^{2}{\theta }}}\Theta _{lm}+l(l+1)\Theta _{l}^{m}=0}
и имеют вид
- Θlm=2l+12(l−m)!(l+m)!Plm(cosθ){\displaystyle \Theta _{l}^{m}={\sqrt {{\frac {2l+1}{2}}{\frac {(l-m)!}{(l+m)!}}}}P_{l}^{m}(\cos \theta )}
Здесь Plm(cosθ){\displaystyle P_{l}^{m}(\cos \theta )} — присоединённые многочлены Лежандра, а m!{\displaystyle m!} — факториал.
Присоединенные многочлены Лежандра с отрицательным m{\displaystyle m} здесь вводятся как
- Pℓ−m(x)=(−1)m(ℓ−m)!(ℓ+m)!Pℓm(x){\displaystyle P_{\ell }^{-m}(x)=(-1)^{m}{\frac {(\ell -m)!}{(\ell +m)!}}P_{\ell }^{m}(x)}
Решение уравнения Лапласа в сферических координатах есть так называемая шаровая функция, получаемая умножением сферической функции на решение радиального уравнения.
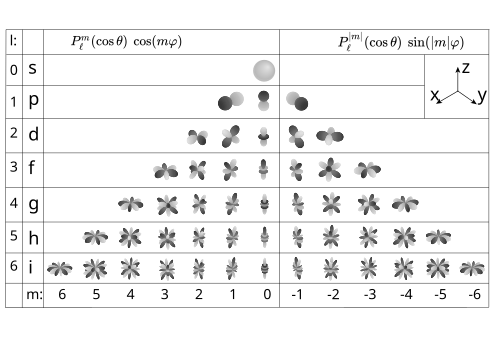 Вещественные сферические функции до шестого порядка
Вещественные сферические функции до шестого порядкаДля сферических функций форма зависимости от угла φ{\displaystyle \varphi } — комплексная экспонента. Используя Формулу Эйлера, можно ввести вещественные сферические функции. Иногда их удобнее использовать в связи с тем, что вещественные функции могут быть наглядно показаны на иллюстрациях, в отличие от комплексных.
- Yℓm={i2(Yℓm−(−1)mYℓ−m) m<0Yℓ0 m=012(Yℓ−m+(−1)mYℓm) m>0.={2(−1)mIm[Yℓ|m|] m<0Yℓ0 m=02(−1)mRe[Yℓm] m>0.{\displaystyle {\begin{aligned}Y_{\ell m}&={\begin{cases}\displaystyle {i \over {\sqrt {2}}}\left(Y_{\ell }^{m}-(-1)^{m}\,Y_{\ell }^{-m}\right)&{\text{ }}\ m<0\\\displaystyle Y_{\ell }^{0}&{\text{ }}\ m=0\\\displaystyle {1 \over {\sqrt {2}}}\left(Y_{\ell }^{-m}+(-1)^{m}\,Y_{\ell }^{m}\right)&{\text{ }}\ m>0.\end{cases}}\\&={\begin{cases}\displaystyle {\sqrt {2}}\,(-1)^{m}\,\operatorname {Im} [{Y_{\ell }^{|m|}}]&{\text{ }}\ m<0\\\displaystyle Y_{\ell }^{0}&{\text{ }}\ m=0\\\displaystyle {\sqrt {2}}\,(-1)^{m}\,\operatorname {Re} [{Y_{\ell }^{m}}]&{\text{ }}\ m>0.\end{cases}}\end{aligned}}}
Обратное преобразование:
- Yℓm={12(Yℓ|m|−iYℓ,−|m|) m<0Yℓ0 m=0(−1)m2(Yℓ|m|+iYℓ,−|m|) m>0.{\displaystyle Y_{\ell }^{m}={\begin{cases}\displaystyle {1 \over {\sqrt {2}}}\left(Y_{\ell |m|}-iY_{\ell ,-|m|}\right)&{\text{ }}\ m<0\\\displaystyle Y_{\ell 0}&{\text{ }}\ m=0\\\displaystyle {(-1)^{m} \over {\sqrt {2}}}\left(Y_{\ell |m|}+iY_{\ell ,-|m|}\right)&{\text{ }}\ m>0.\end{cases}}}
Иногда вещественные сферические функции называют зональными, тессеральными и секториальными.[1]. Функции с m > 0 зависят от угла как косинус, а с m < 0 — как синус.
Yℓm={(−1)m22ℓ+14π(ℓ−|m|)!(ℓ+|m|)! Pℓ|m|(cosθ) sin(|m|φ) m<02ℓ+14π Pℓm(cosθ) m=0(−1)m22ℓ+14π(ℓ−m)!(ℓ+m)! Pℓm(cosθ) cos(mφ) m>0.{\displaystyle Y_{\ell m}={\begin{cases}\displaystyle (-1)^{m}{\sqrt {2}}{\sqrt {{2\ell +1 \over 4\pi }{(\ell -|m|)! \over (\ell +|m|)!}}}\ P_{\ell }^{|m|}(\cos \theta )\ \sin(|m|\varphi )&{\mbox{ }}m<0\\\displaystyle {\sqrt {2\ell +1 \over 4\pi }}\ P_{\ell }^{m}(\cos \theta )&{\mbox{ }}m=0\\\displaystyle (-1)^{m}{\sqrt {2}}{\sqrt {{2\ell +1 \over 4\pi }{(\ell -m)! \over (\ell +m)!}}}\ P_{\ell }^{m}(\cos \theta )\ \cos(m\varphi )&{\mbox{ }}m>0\,.\end{cases}}}
 Поворот вещественной сферической функции с m=0 и l=3. Коэффициенты не равны D-матрицам Вигнера, поскольку показаны вещественные функции, но могут быть получены при переразложении по комплексным функциям
Поворот вещественной сферической функции с m=0 и l=3. Коэффициенты не равны D-матрицам Вигнера, поскольку показаны вещественные функции, но могут быть получены при переразложении по комплексным функциямРассмотрим поворот системы координат R{\displaystyle {\mathcal {R}}}, на Углы Эйлера α,β,γ,{\displaystyle \alpha ,\beta ,\gamma ,} который преобрaзует единичный вектор r{\displaystyle \mathbf {r} } в вектор r′{\displaystyle {\mathbf {r} }’}. При этом углы θ′,φ′{\displaystyle \theta ‘,\varphi ‘} вектора r′{\displaystyle {\mathbf {r} }’} в новой системе координат выражаются через углы в старой системе координат следующим образом
- cosθ′=cosθcosβ+sinθsinβcos(φ−α){\displaystyle \cos \theta ^{\prime }=\cos \theta \cos \beta +\sin \theta \sin \beta \cos(\varphi -\alpha )}
- ctg(φ′+γ)=ctg(φ−α)cosβ−ctgθsinβsin(φ−α){\displaystyle \operatorname {ctg} \left(\varphi ^{\prime }+\gamma \right)=\operatorname {ctg} (\varphi -\alpha )\cos \beta -{\frac {\operatorname {ctg} \theta \sin \beta }{\sin(\varphi -\alpha )}}}
В новой системе координат сферическая функция с индексами ℓ{\displaystyle \ell } и m{\displaystyle m} будет представима в виде линейной комбинации всех функций с тем же номером ℓ{\displaystyle \ell } и различными m{\displaystyle m}. Коэффициентами в линейной комбинации являются комплексно- сопряженные D-матрицы Вигнера[2]
- D^(α,β,γ)Ylm(θ,φ)=Yℓm(θ′,φ′)=∑m′=−ℓℓ[Dmm′(ℓ)(α,β,γ)]∗Yℓm′(θ,φ),{\displaystyle {\hat {D}}(\alpha ,\beta ,\gamma )Y_{l}^{m}(\theta ,\varphi )=Y_{\ell }^{m}(\theta ‘,\varphi ‘)=\sum _{m’=-\ell }^{\ell }[D_{mm’}^{(\ell )}(\alpha ,\beta ,\gamma )]^{*}Y_{\ell }^{m’}(\theta ,\varphi ),}
Сферические функции с номером ℓ{\displaystyle \ell } образуют базис неприводимого представления размерности (2ℓ+1){\displaystyle (2\ell +1)} группы вращений SO(3).
Разложение плоской волны по сферическим функциям[править | править код]
Комплексная экспонента может быть представлена в виде разложения по сферическим функциям
- eik⋅r=4π∑l=0∞iljl(kr)∑m=−llYlm∗(r|r|)Ylm(k|k|){\displaystyle e^{i\mathbf {k} \cdot \mathbf {r} }=4\pi \sum _{l=0}^{\infty }i^{l}j_{l}(kr)\sum _{m=-l}^{l}Y_{l}^{m*}\left({\frac {\mathbf {r} }{|r|}}\right)Y_{l}^{m}\left({\frac {\mathbf {k} }{|k|}}\right)}
Здесь jn(x)=π2xJn+12(x){\displaystyle j_{n}(x)={\sqrt {\frac {\pi }{2x}}}J_{n+{\frac {1}{2}}}(x)} — сферическая функция Бесселя
Список сферических функций — Википедия
Материал из Википедии — свободной энциклопедии
Эта статья — список ортонормированных сферических функций, которые используют фазу Кондона-Шортли вплоть до степени l=10. Некоторые из этих формул приведены в декартовых координатах. Связь между x, y, z, и r, θ{\displaystyle \theta }, φ{\displaystyle \varphi } определяется по следующим образом:
- x=rsinθcosφy=rsinθsinφz=rcosθ{\displaystyle {\begin{aligned}x&=r\sin \theta \cos \varphi \\y&=r\sin \theta \sin \varphi \\z&=r\cos \theta \end{aligned}}}
- Y00(θ,φ)=121π{\displaystyle Y_{0}^{0}(\theta ,\varphi )={1 \over 2}{\sqrt {1 \over \pi }}}
Вещественные сферические функции с l = 0[править | править код]
- s=Y00=121π{\displaystyle s=Y_{0}^{0}={\frac {1}{2}}{\sqrt {\frac {1}{\pi }}}}
- Y1−1(θ,φ)=1232π⋅e−iφ⋅sinθ=1232π⋅(x−iy)rY10(θ,φ)=123π⋅cosθ=123π⋅zrY11(θ,φ)=−1232π⋅eiφ⋅sinθ=−1232π⋅(x+iy)r{\displaystyle {\begin{aligned}Y_{1}^{-1}(\theta ,\varphi )&={1 \over 2}{\sqrt {3 \over 2\pi }}\cdot e^{-i\varphi }\cdot \sin \theta \quad ={1 \over 2}{\sqrt {3 \over 2\pi }}\cdot {(x-iy) \over r}\\Y_{1}^{0}(\theta ,\varphi )&={1 \over 2}{\sqrt {3 \over \pi }}\cdot \cos \theta \quad \quad ={1 \over 2}{\sqrt {3 \over \pi }}\cdot {z \over r}\\Y_{1}^{1}(\theta ,\varphi )&={-1 \over 2}{\sqrt {3 \over 2\pi }}\cdot e^{i\varphi }\cdot \sin \theta \quad ={-1 \over 2}{\sqrt {3 \over 2\pi }}\cdot {(x+iy) \over r}\end{aligned}}}
Вещественные сферические функции с l = 1[править | править код]
- px=12(Y1−1−Y11)=34π⋅xrpy=i12(Y1−1+Y11)=34π⋅yrpz=Y10=34π⋅zr{\displaystyle {\begin{aligned}p_{x}&={\sqrt {\frac {1}{2}}}\left(Y_{1}^{-1}-Y_{1}^{1}\right)={\sqrt {\frac {3}{4\pi }}}\cdot {\frac {x}{r}}\\p_{y}&=i{\sqrt {\frac {1}{2}}}\left(Y_{1}^{-1}+Y_{1}^{1}\right)={\sqrt {\frac {3}{4\pi }}}\cdot {\frac {y}{r}}\\p_{z}&=Y_{1}^{0}={\sqrt {\frac {3}{4\pi }}}\cdot {\frac {z}{r}}\end{aligned}}}
m < 0
- Y2−2(θ,φ)=14152π⋅e−2iφ⋅sin2θ=14152π⋅(x−iy)2r2{\displaystyle Y_{2}^{-2}(\theta ,\varphi )={1 \over 4}{\sqrt {15 \over 2\pi }}\cdot e^{-2i\varphi }\cdot \sin ^{2}\theta \quad ={1 \over 4}{\sqrt {15 \over 2\pi }}\cdot {(x-iy)^{2} \over r^{2}}}
- Y2−1(θ,φ)=12152π⋅e−iφ⋅sinθ⋅cosθ=12152π⋅(x−iy)zr2{\displaystyle Y_{2}^{-1}(\theta ,\varphi )={1 \over 2}{\sqrt {15 \over 2\pi }}\cdot e^{-i\varphi }\cdot \sin \theta \cdot \cos \theta \quad ={1 \over 2}{\sqrt {15 \over 2\pi }}\cdot {(x-iy)z \over r^{2}}}
m ⩾ 0
- Y20(θ,φ)=145π⋅(3cos2θ−1)=145π⋅(2z2−x2−y2)r2{\displaystyle Y_{2}^{0}(\theta ,\varphi )={1 \over 4}{\sqrt {5 \over \pi }}\cdot (3\cos ^{2}\theta -1)\quad ={1 \over 4}{\sqrt {5 \over \pi }}\cdot {(2z^{2}-x^{2}-y^{2}) \over r^{2}}}
- Y21(θ,φ)=−12152π⋅eiφ⋅sinθ⋅cosθ=−12152π⋅(x+iy)zr2{\displaystyle Y_{2}^{1}(\theta ,\varphi )={-1 \over 2}{\sqrt {15 \over 2\pi }}\cdot e^{i\varphi }\cdot \sin \theta \cdot \cos \theta \quad ={-1 \over 2}{\sqrt {15 \over 2\pi }}\cdot {(x+iy)z \over r^{2}}}
- Y22(θ,φ)=14152π⋅e2iφ⋅sin2θ=14152π⋅(x+iy)2r2{\displaystyle Y_{2}^{2}(\theta ,\varphi )={1 \over 4}{\sqrt {15 \over 2\pi }}\cdot e^{2i\varphi }\cdot \sin ^{2}\theta \quad ={1 \over 4}{\sqrt {15 \over 2\pi }}\cdot {(x+iy)^{2} \over r^{2}}}
Вещественные сферические функции
m < 0
- Y3−3(θ,φ)=1835π⋅e−3iφ⋅sin3θ=1835π⋅(x−iy)3r3{\displaystyle Y_{3}^{-3}(\theta ,\varphi )={1 \over 8}{\sqrt {35 \over \pi }}\cdot e^{-3i\varphi }\cdot \sin ^{3}\theta \quad ={1 \over 8}{\sqrt {35 \over \pi }}\cdot {(x-iy)^{3} \over r^{3}}}
- Y3−2(θ,φ)=141052π⋅e−2iφ⋅sin2θ⋅cosθ=141052π⋅(x−iy)2zr3{\displaystyle Y_{3}^{-2}(\theta ,\varphi )={1 \over 4}{\sqrt {105 \over 2\pi }}\cdot e^{-2i\varphi }\cdot \sin ^{2}\theta \cdot \cos \theta \quad ={1 \over 4}{\sqrt {105 \over 2\pi }}\cdot {(x-iy)^{2}z \over r^{3}}}
- Y3−1(θ,φ)=1821π⋅e−iφ⋅sinθ⋅(5cos2θ−1)=1821π⋅(x−iy)(4z2−x2−y2)r3{\displaystyle Y_{3}^{-1}(\theta ,\varphi )={1 \over 8}{\sqrt {21 \over \pi }}\cdot e^{-i\varphi }\cdot \sin \theta \cdot (5\cos ^{2}\theta -1)\quad ={1 \over 8}{\sqrt {21 \over \pi }}\cdot {(x-iy)(4z^{2}-x^{2}-y^{2}) \over r^{3}}}
m ⩾ 0
- Y30(θ,φ)=147π⋅(5cos3θ−3cosθ)=147π⋅z(2z2−3×2−3y2)r3{\displaystyle Y_{3}^{0}(\theta ,\varphi )={1 \over 4}{\sqrt {7 \over \pi }}\cdot (5\cos ^{3}\theta -3\cos \theta )\quad ={1 \over 4}{\sqrt {7 \over \pi }}\cdot {z(2z^{2}-3x^{2}-3y^{2}) \over r^{3}}}
- Y31(θ,φ)=−1821π⋅eiφ⋅sinθ⋅(5cos2θ−1)=−1821π⋅(x+iy)(4z2−x2−y2)r3{\displaystyle Y_{3}^{1}(\theta ,\varphi )={-1 \over 8}{\sqrt {21 \over \pi }}\cdot e^{i\varphi }\cdot \sin \theta \cdot (5\cos ^{2}\theta -1)\quad ={-1 \over 8}{\sqrt {21 \over \pi }}\cdot {(x+iy)(4z^{2}-x^{2}-y^{2}) \over r^{3}}}
- Y32(θ,φ)=141052π⋅e2iφ⋅sin2θ⋅cosθ=141052π⋅(x+iy)2zr3{\displaystyle Y_{3}^{2}(\theta ,\varphi )={1 \over 4}{\sqrt {105 \over 2\pi }}\cdot e^{2i\varphi }\cdot \sin ^{2}\theta \cdot \cos \theta \quad ={1 \over 4}{\sqrt {105 \over 2\pi }}\cdot {(x+iy)^{2}z \over r^{3}}}
- Y33(θ,φ)=−1835π⋅e3iφ⋅sin3θ=−1835π⋅(x+iy)3r3{\displaystyle Y_{3}^{3}(\theta ,\varphi )={-1 \over 8}{\sqrt {35 \over \pi }}\cdot e^{3i\varphi }\cdot \sin ^{3}\theta \quad ={-1 \over 8}{\sqrt {35 \over \pi }}\cdot {(x+iy)^{3} \over r^{3}}}
Вещественные сферические функции
m < 0
- Y4−4(θ,φ)=316352π⋅e−4iφ⋅sin4θ=316352π⋅(x−iy)4r4{\displaystyle Y_{4}^{-4}(\theta ,\varphi )={3 \over 16}{\sqrt {35 \over 2\pi }}\cdot e^{-4i\varphi }\cdot \sin ^{4}\theta ={\frac {3}{16}}{\sqrt {\frac {35}{2\pi }}}\cdot {\frac {(x-iy)^{4}}{r^{4}}}}
- Y4−3(θ,φ)=3835π⋅e−3iφ⋅sin3θ⋅cosθ=3835π⋅(x−iy)3zr4{\displaystyle Y_{4}^{-3}(\theta ,\varphi )={3 \over 8}{\sqrt {35 \over \pi }}\cdot e^{-3i\varphi }\cdot \sin ^{3}\theta \cdot \cos \theta ={\frac {3}{8}}{\sqrt {\frac {35}{\pi }}}\cdot {\frac {(x-iy)^{3}z}{r^{4}}}}
- Y4−2(θ,φ)=3852π⋅e−2iφ⋅sin2θ⋅(7cos2θ−1)=3852π⋅(x−iy)2⋅(7z2−r2)r4{\displaystyle Y_{4}^{-2}(\theta ,\varphi )={3 \over 8}{\sqrt {5 \over 2\pi }}\cdot e^{-2i\varphi }\cdot \sin ^{2}\theta \cdot (7\cos ^{2}\theta -1)={\frac {3}{8}}{\sqrt {\frac {5}{2\pi }}}\cdot {\frac {(x-iy)^{2}\cdot (7z^{2}-r^{2})}{r^{4}}}}
- Y4−1(θ,φ)=385π⋅e−iφ⋅sinθ⋅(7cos3θ−3cosθ)=385π⋅(x−iy)⋅z⋅(7z2−3r2)r4{\displaystyle Y_{4}^{-1}(\theta ,\varphi )={3 \over 8}{\sqrt {5 \over \pi }}\cdot e^{-i\varphi }\cdot \sin \theta \cdot (7\cos ^{3}\theta -3\cos \theta )={\frac {3}{8}}{\sqrt {\frac {5}{\pi }}}\cdot {\frac {(x-iy)\cdot z\cdot (7z^{2}-3r^{2})}{r^{4}}}}
m ⩾ 0
- Y40(θ,φ)=3161π⋅(35cos4θ−30cos2θ+3)=3161π⋅(35z4−30z
Таблица сферических гармоник — Table of spherical harmonics
Это таблица ортонормированных сферических гармоник , которые используют Кондон-Шортли фазу до степени = 10. Некоторые из этих формул дают «декартово» версию. Это предполагает , х , у , г , и г связаны и через обычную сферическую к трансформации декартовых координат: ℓ{\ Displaystyle \ ell_p}θ{\ Displaystyle \ Theta}φ{\ Displaystyle \ varphi \}
- {Иксзнак равноргрехθсозφYзнак равноргрехθгрехφZзнак равнорсозθ{\ Displaystyle {\ начинается {случаев} х & = г \ грех \ Theta \ соз \ varphi \\ у & = г \ ет \ Theta \ греха \ varphi \\ г & = г \ соз \ тета \ конечных {случаев}}}
Сферические гармоники
ℓ{\ Displaystyle \ ell_p} = 0
- Y00(θ,φ)знак равно121π{\ Displaystyle Y_ {0} ^ {0} (\ Theta, \ varphi) = {1 \ более 2} {\ SQRT {1 \ над \ пи}}}
ℓ{\ Displaystyle \ ell_p} = 1
- Y1-1(θ,φ)знак равно1232π⋅е-яφ⋅грехθзнак равно1232π⋅(Икс-яY)рY10(θ,φ)знак равно123π⋅созθзнак равно123π⋅ZрY11(θ,φ)знак равно-1232π⋅еяφ⋅грехθзнак равно-1232π⋅(Икс+яY)р{\ Displaystyle {\ начинаются {выровнены} Y_ {1} ^ {- 1} (\ Theta, \ varphi) & = && {1 \ более 2} {\ SQRT {3 \ над 2 \ пи}} \ CDOT е ^ {-i \ varphi} \ CDOT \ грех \ тета = && && {1 \ более 2} {\ SQRT {3 \ над 2 \ пи}} \ CDOT {(х-гу) \ по г} \\ Y_ {1 } ^ {0} (\ Theta, \ varphi) & = && {1 \ более 2} {\ SQRT {3 \ над \ пи}} \ CDOT \ соз \ тета && = && {1 \ более 2} {\ SQRT {3 \ над \ пи}} \ CD {г \ над г} \\ y_ {1} ^ {1} (\ Theta, \ varphi) & = & — & {1 \ более 2} {\ SQRT {3 \ более 2 \ пи}} \ CDOT е ^ {я \ varphi} \ CDOT \ грех \ тета = && && {1 \ более 2} {\ SQRT {3 \ над 2 \ пи}} \ CDOT {(х + гу) \ над г} \ {конец выровнен}}}
ℓ{\ Displaystyle \ ell_p} = 2
- Y2-2(θ,φ)знак равно14152π⋅е-2яφ⋅грех2θзнак равно14152π⋅(Икс-яY)2р2Y2-1(θ,φ)знак равно12152π⋅е-яφ⋅грехθ⋅созθзнак равно12152π⋅(Икс-яY)Zр2Y20(θ,φ)знак равно145π⋅(3соз2θ-1)знак равно145π⋅(2Z2-Икс2-Y2)р2Y21(θ,φ)знак равно-12152π⋅еяφ⋅грехθ⋅созθзнак равно-12152π⋅(Икс+яY)Zр2Y22(θ,φ)знак равно14152π⋅е2яφ⋅грех2θзнак равно14152π⋅(Икс+яY)2р2{\ Displaystyle {\ начинаются {выровнены} Y_ {2} ^ {- 2} (\ Theta, \ varphi) & = && {1 \ более 4} {\ SQRT {15 \ более 2 \ пи}} \ CDOT е ^ {-2i \ varphi} \ CDOT \ грех ^ {2} \ тета \ четырехъядерных && = && {1 \ более 4} {\ SQRT {15 \ более 2 \ пи}} \ CDOT {(х-гу) ^ {2 } \ по г ^ {2}} & \\ Y_ {2} ^ {- 1} (\ Theta, \ varphi) & = && {1 \ более 2} {\ {15 квадратный корень \ более 2 \ пи}} \ CDOT е ^ {- я \ varphi} \ CDOT \ грешить \ Theta \ CDOT \ соз \ Theta \ четверной && = && {1 \ более 2} {\ SQRT {15 \ над 2 \ пи}} \ CDOT {(х- гу) г \ по г ^ {2}} & \\ Y_ {2} ^ {0} (\ Theta, \ varphi) & = && {1 \ более 4} {\ SQRT {5 \ над \ пи}} \ CDOT (3 \ соз ^ {2} \ тета-1) \ четырехъядерных && = && {1 \ более 4} {\ SQRT {5 \ над \ пи}} \ CDOT {(2z ^ {2} -x ^ {2 } -y ^ {2}) \ по г ^ {2}} & \\ Y_ {2} ^ {1} (\ Theta, \ varphi) & = & — & {1 \ более 2} {\ SQRT {15 \ над 2 \ пи}} \ CDOT е ^ {я \ varphi} \ CDOT \ грешить \ Theta \ CDOT \ соз \ Theta \ четверной && = && {1 \ более 2} {\ SQRT {15 \ над 2 \ пи}} \ CDOT {(х + гу) г \ по г ^ {2}} & \\ Y_ {2} ^ {2} (\ Theta, \ varphi) & = && {1 \ более 4} {\ SQRT {15 \ более 2 \ пи}} \ CDOT е ^ {2i \ varphi} \ CDOT \ грех ^ {2} \ тета \ четырехъядерных && = && {1 \ более 4} {\ SQRT {15 \ более 2 \ пи} } \ CDOT {(х + гу) ^ {2} \ по г ^ {2}} & \ {конец выровнен}}}
ℓ{\ Displaystyle \ ell_p} = 3
- Y3-3(θ,φ)знак равно1835π⋅е-3яφ⋅грех3θзнак равно1835π⋅(Икс-яY)3р3Y3-2(θ,φ)знак равно141052π⋅е-2яφ⋅грех2θ⋅созθзнак равно141052π⋅(Икс-яY)2Zр3Y3-1(θ,φ)знак равно1821π⋅е-яφ⋅грехθ⋅(5соз2θ-1)знак равно1821π⋅(Икс-яY)(4Z2-Икс2-Y2)р3Y30(θ,φ)знак равно147π⋅(5соз3θ-3созθ)знак равно147π⋅Z(2Z2-3Икс2-3Y2)р3Y31(θ,φ)знак равно-1821π⋅еяφ⋅грехθ⋅(5соз2θ-1)знак равно-1821π⋅(Икс+яY)(4Z2-Икс2-Y2)р3Y32(θ,φ)знак равно141052π⋅е2яφ⋅грех2θ⋅созθзнак равно141052π⋅(Икс+яY)2Zр3Y33(θ,φ)знак равно-1835π⋅е3яφ⋅грех3θзнак равно-1835π⋅(Икс+яY)3р3{\ Displaystyle {\ начинаются {выровнены} Y_ {3} ^ {- 3} (\ Theta, \ varphi) & = && {1 \ более 8} {\ SQRT {35 \ над \ пи}} \ CDOT е ^ { -3i \ varphi} \ CDOT \ грех ^ {3} \ тета \ четырехъядерных && = && {1 \ более 8} {\ SQRT {35 \ над \ пи}} \ CDOT {(х-гу) ^ {3} \ по г ^ {3}} & \\ Y_ {3} ^ {- 2} (\ Theta, \ varphi) & = && {1 \ более 4} {\ {105 квадратный корень \ над 2 \ пи}} \ CDOT е ^ {- 2i \ varphi} \ CDOT \ грех ^ {2} \ тета \ CDOT \ соз \ тета \ четырехъядерных && = && {1 \ более 4} {\ SQRT {105 \ более 2 \ пи}} \ CDOT {( х-гу) ^ {2} г \ по г ^ {3}} & \\ Y_ {3} ^ {- 1} (\ Theta, \ varphi) & = && {1 \ более 8} {\ SQRT {21 \ над \ пи}} \ CDOT е ^ {- я \ varphi} \ CDOT \ грех \ тета \ CDOT (5 \ соз ^ {2} \ тета-1) \ четырехъядерных && = && {1 \ более 8} {\ SQRT {21 \ над \ пи}} \ CDOT {(х-гу) (4z ^ {2} -x ^ {2} -y ^ {2}) \ по г ^ {3}} & \\ Y_ {3 } ^ {0} (\ Theta, \ varphi) & = && {1 \ более 4} {\ SQRT {7 \ над \ пи}} \ CDOT (5 \ соз ^ {3} \ тета -3 \ соз \ тета ) \ четырехъядерных && = && {1 \ более 4} {\ SQRT {7 \ над \ пи}} \ CDOT {г (2z ^ {2} -3x ^ {2} -3y ^ {2}) \ по г ^ {3}} & \\ Y_ {3} ^ {1} (\ Theta, \ varphi) & = & — & {1 \ более 8} {\ SQRT {21 \ над \ пи}} \ CDOT е ^ {я \ varphi} \ CDOT \ грех \ тета \ CDOT (5 \ соз ^ {2} \ тета-1) \ четырехъядерных && = && {- 1 \ более 8} { \ SQRT {21 \ над \ пи}} \ CDOT {(х + гу) (4z ^ {2} -x ^ {2} -y ^ {2}) \ по г ^ {3}} & {\\ Y_ 3} ^ {2} (\ Theta, \ varphi) & = && {1 \ более 4} {\ SQRT {105 \ более 2 \ пи}} \ CDOT е ^ {2i \ varphi} \ CDOT \ грех ^ {2 } \ тета \ CDOT \ соз \ тета \ четырехъядерных && = && {1 \ более 4} {\ SQRT {105 \ более 2 \ пи}} \ CDOT {(х + гу) ^ {2} г \ по г ^ { 3}} & \\ Y_ {3} ^ {3} (\ Theta, \ varphi) & = & — & {1 \ более 8} {\ SQRT {35 \ над \ пи}} \ CDOT е ^ {3i \ varphi} \ CDOT \ грех ^ {3} \ тета \ четырехъядерных && = && {- 1 \ более 8} {\ SQRT {35 \ над \ пи}} \ CDOT {(х + гу) ^ {3} \ по г ^ {3}} & \ {конец выровнен}}}
ℓ{\ Displaystyle \ ell_p} = 4
- Y4-4(θ,φ)знак равно316352π⋅е-4яφ⋅грех4θзнак равно316352π⋅(Икс-яY)4р4Y4-3(θ,φ)знак равно3835π⋅е-3яφ⋅грех3θ⋅созθзнак равно3835π⋅(Икс-яY)3Zр4Y4-2(θ,φ)знак равно3852π⋅е-2яφ⋅грех2θ⋅(7соз2θ-1)знак равно3852π⋅(Икс-яY)2⋅(7Z2-р2)р4Y4-1(θ,φ)знак равно385π⋅е-яφ⋅грехθ⋅(7соз3θ-3созθ)знак равно385π⋅(Икс-яY)⋅Z⋅(7Z2-3р2)р4Y40(θ,φ)знак равно3161π⋅(35соз4θ-30соз2θ+3)знак равно3161π⋅(35Z4-30Z2р2+3р4)р4Y41(θ,φ)знак равно-385π⋅еяφ⋅грехθ⋅(7соз3θ-3созθ)знак равно-385π⋅(Икс+яY)⋅Z⋅(7Z2-3р2)р4Y42(θ,φ)знак равно3852π⋅е2яφ⋅грех2θ⋅(7соз2θ-1)знак равно3852π⋅(Икс+яY)2⋅(7Z2-р2)р4Y43(θ,φ)знак равно-3835π⋅е3яφ⋅грех3θ⋅созθзнак равно-3835π⋅(Икс+яY)3Zр4Y44(θ,φ)знак равно316352π⋅е4яφ⋅грех4θзнак равно316352π⋅(Икс+яY)4р4{\ Displaystyle {\ начинаются {выровнены} Y_ {4} ^ {- 4} (\ Theta, \ varphi) & = {3 \ над 16} {\ SQRT {35 \ более 2 \ пи}} \ CDOT е ^ { -4i \ varphi} \ CDOT \ грех ^ {4} \ тета = {\ гидроразрыва {3} {16}} {\ SQRT {\ гидроразрыва {35} {2 \ пи}}} \ CDOT {\ гидроразрыва {(х -iy) ^ {4}} {г ^ {4}}} \\ Y_ {4} ^ {- 3} (\ Theta, \ varphi) & = {3 \ более 8} {\ SQRT {35 \ над \ пи}} \ CDOT х ^ {- 3i \ varphi} \ CDOT \ грех ^ {3} \ Theta \ CD \ соз \ Theta = {\ гидроразрыва {3} {8}} {\ SQRT {\ гидроразрыва {35} { \ пи}}} \ CDOT {\ гидроразрыва {(х-гу) ^ {3} г} {г ^ {4}}} \\ Y_ {4} ^ {- 2} (\ Theta, \ varphi) & = {3 \ более 8} {\ SQRT {5 \ более 2 \ пи}} \ CDOT е ^ {- 2i \ varphi} \ CDOT \ грех ^ {2} \ тета \ CDOT (7 \ соз ^ {2} \ тета -1) = {\ гидроразрыва {3} {8}} {\ SQRT {\ гидроразрыва {5} {2 \ пи}}} \ CDOT {\ гидроразрыва {(х-гу) ^ {2} \ CDOT (7z ^ {2} -r ^ {2})} {г ^ {4}}} \\ Y_ {4} ^ {- 1} (\ Theta, \ varphi) & = {3 \ более 8} {\ SQRT {5 \ над \ пи}} \ CDOT е ^ {- я \ varphi} \ CDOT \ грех \ Theta \ CDOT (7 \ соз ^ {3} \ тета -3 \ соз \ тета) = {\ гидроразрыва {3} {8 }} {\ SQRT {\ гидроразрыв {5} {\ Pi}}} \ CDOT {\ гидроразрыв {(х-гу) \ CD г \ CD (7z ^ {2} -3R ^ {2})} {г ^ {4}}} \\ Y_ {4} ^ {0} (\ Theta, \ varphi) & = {3 \ над 16} {\ SQRT {1 \ над \ пи}} \ CDOT (35 \ соз ^ {4 } \ тета -30 \ соз ^ {2} \ Theta +3) = {\ Гидроразрыва {3} {16}} {\ SQRT {\ гидроразрыва {1} {\ Pi}}} \ CDOT {\ гидроразрыва {(35Z ^ {4} -30z ^ {2} г ^ {2} + 3r ^ {4})} {г ^ {4}}} \\ Y_ {4} ^ {1} (\ Theta, \ varphi) & = {- 3 \ более 8} {\ SQRT {5 \ над \ пи} } \ CDOT е ^ {я \ varphi} \ CDOT \ грех \ Theta \ CDOT (7 \ соз ^ {3} \ тета -3 \ соз \ тета) = {\ гидроразрыва {-3} {8}} {\ SQRT {\ гидроразрыва {5} {\ Pi}}} \ CDOT {\ гидроразрыв {(х + гу) \ CD г \ CD (7z ^ {2} -3R ^ {2})} {г ^ {4}}} \\ Y_ {4} ^ {2} (\ Theta, \ varphi) & = {3 \ более 8} {\ SQRT {5 \ более 2 \ пи}} \ CDOT е ^ {2i \ varphi} \ CDOT \ грех ^ {2} \ тета \ CDOT (7 \ соз ^ {2} \ тета-1) = {\ гидроразрыва {3} {8}} {\ SQRT {\ гидроразрыва {5} {2 \ пи}}} \ CDOT {\ гидроразрыва {(х + гу) ^ {2} \ CDOT (7z ^ {2} -r ^ {2})} {г ^ {4}}} \\ Y_ {4} ^ {3} (\ тета , \ varphi) & = {- 3 \ более 8} {\ SQRT {35 \ над \ пи}} \ CDOT е ^ {3i \ varphi} \ CDOT \ грех ^ {3} \ тета \ CDOT \ соз \ тета = {\ гидроразрыва {-3} {8}} {\ SQRT {\ гидроразрыва {35} {\ Pi}}} \ CDOT {\ гидроразрыва {(х + гу) ^ {3} г} {г ^ {4}} } \\ Y_ {4} ^ {4} (\ Theta, \ varphi) & = {3 \ над 16} {\ SQRT {35 \ более 2 \ пи}} \ CDOT е ^ {4i \ varphi} \ CDOT \ грех ^ {4} \ тета = {\ гидроразрыва {3} {16}} {\ SQRT {\ гидроразрыва {35} {2 \ пи}}} \ CDOT {\ гидроразрыва {(х + гу) ^ {4}} {г ^ {4}}} \ {конец выровнен}}}
ℓ{\ Displaystyle \ ell_p} = 5
- Y5-5(θ,φ)знак равно33277π⋅е-5яφ⋅грех5θY5-4(θ,φ)знак равно3163852π⋅е-4яφ⋅грех4θ⋅созθY5-3(θ,φ)знак равно132385π⋅е-3яφ⋅грех3θ⋅(9соз2θ-1)Y5-2(θ,φ)знак равно1811552π⋅е-2яφ⋅грех2θ⋅(3соз3θ-созθ)Y5-1(θ,φ)знак равно1161652π⋅е-яφ⋅грехθ⋅(21соз4θ-14соз2θ+1)Y50(θ,φ)знак равно11611π⋅(63соз5θ-70соз3θ+15созθ)Y51(θ,φ)знак равно-1161652π⋅еяφ⋅грехθ⋅(21соз4θ-14соз2θ+1)Y52(θ,φ)знак равно1811552π⋅е2яφ⋅грех2θ⋅(3соз3θ-созθ)Y53(θ,φ)знак равно-132385π⋅е3яφ⋅грех3θ⋅(9соз2θ-1)Y54(θ,φ)знак равно3163852π⋅е4яφ⋅грех4θ⋅созθY55(θ,φ)знак равно-33277π⋅е5яφ⋅грех5θ{\ Displaystyle {\ начинаются {выровнены} Y_ {5} ^ {- 5} (\ Theta, \ varphi) & = {3 \ над 32} {\ SQRT {77 \ над \ пи}} \ CDOT е ^ {- 5i \ varphi} \ CDOT \ грех ^ {5} \ \\ тета Y_ {5} ^ {- 4} (\ Theta, \ varphi) & = {3 \ над 16} {\ SQRT {385 \ более 2 \ пи }} \ CDOT е ^ {- 4i \ varphi} \ CDOT \ грех ^ {4} \ тета \ CDOT \ соз \ \\ тета Y_ {5} ^ {- 3} (\ Theta, \ varphi) & = {1 \ более 32} {\ SQRT {385 \ над \ пи}} \ CDOT е ^ {- 3i \ varphi} \ CDOT \ грех ^ {3} \ тета \ CDOT (9 \ соз ^ {2} \ тета-1) \\ Y_ {5} ^ {- 2} (\ Theta, \ varphi) & = {1 \ более 8} {\ SQRT {+1155 \ более 2 \ пи}} \ CDOT е ^ {- 2i \ varphi} \ CDOT \ грех ^ {2} \ тета \ CDOT (3 \ соз ^ {3} \ тета — \ соз \ тета) \\ Y_ {5} ^ {- 1} (\ Theta, \ varphi) & = {1 \ над 16} {\ SQRT {165 \ над 2 \ пи}} \ CDOT е ^ {- я \ varphi} \ CDOT \ грех \ Theta \ CDOT (21 \ соз ^ {4} \ тета -14 \ соз ^ {2} \ тета + 1) \\ Y_ {5} ^ {0} (\ Theta, \ varphi) & = {1 \ старше 16} {\ SQRT {11 \ над \ пи}} \ CDOT (63 \ соз ^ {5 } \ тета -70 \ соз ^ {3} \ тета + 15 \ соз \ тета) \\ Y_ {5} ^ {1} (\ Theta, \ varphi) & = {- 1 \ старше 16} {\ SQRT { 165 \ более 2 \ пи}} \ CDOT е ^ {я \ varphi} \ CDOT \ грех \ Theta \ CDOT (21 \ соз ^ {4} \ тета -14 \ соз ^ {2} \ тета + 1) \\ Y_ {5} ^ {2 } (\ Theta, \ varphi) & = {1 \ более 8} {\ SQRT {1155 \ над 2 \ пи}} \ CDOT е ^ {2i \ varphi} \ CDOT \ грех ^ {2} \ тета \ CDOT ( 3 \ соз ^ {3} \ тета — \ соз \ тета) \\ Y_ {5} ^ {3} (\ Theta, \ varphi) & = {- 1 \ более 32} {\ SQRT {385 \ \ над пи }} \ CDOT е ^ {3i \ varphi} \ CDOT \ грех ^ {3} \ тета \ CDOT (9 \ соз ^ {2} \ тета-1) \\ Y_ {5} ^ {4} (\ тета, \ varphi) & = {3 \ над 16} {\ SQRT {385 \ более 2 \ пи}} \ CDOT е ^ {4i \ varphi} \ CDOT \ грех ^ {4} \ тета \ CDOT \ соз \ \\ тета Y_ {5} ^ {5} (\ Theta, \ varphi) & = {- 3 \ над 32} {\ SQRT {77 \ над \ пи}} \ CDOT е ^ {5i \ varphi} \ CDOT \ грех ^ { 5} \ тета \ {конец выровнен}}}
ℓ{\ Displaystyle \ ell_p} = 6
- Y6-6(θ,φ)знак равно1643003π⋅е-6яφ⋅грех6θY6-5(θ,φ)знак равно3321001π⋅е-5яφ⋅грех5θ⋅созθY6-4(θ,φ)знак равно332912π⋅е-4яφ⋅грех4θ⋅(11соз2θ-1)Y6-3(θ,φ)знак равно1321365π⋅е-3яφ⋅грех3θ⋅(11соз3θ-3созθ)Y6-2(θ,φ)знак равно1641365π⋅е-2яφ⋅грех2θ⋅(33соз4θ-18соз2θ+1)Y6-1(θ,φ)знак равно1162732π⋅е-яφ⋅грехθ⋅(33соз5θ-30соз3θ+5созθ)Y60(θ,φ)знак равно13213π⋅(231соз6θ-315соз4θ+105соз2θ-5)Y61(θ,φ)знак равно-1162732π⋅еяφ⋅грехθ⋅(33соз5θ-30соз3θ+5созθ)Y62(θ,φ)знак равно1641365π⋅е2яφ⋅грех2θ⋅(33соз4θ-18соз2θ+1)Y63(θ,φ)знак равно-1321365π⋅е3яφ⋅грех3θ⋅(11соз3θ-3созθ)Y64(θ,φ)знак равно332912π⋅е4яφ⋅грех4θ⋅(11соз2θ-1)Y65(θ,φ)знак равно-3321001π⋅е5яφ⋅грех5θ⋅созθY66(θ,φ)знак равно1643003π⋅е6яφ⋅грех6θ{\ Displaystyle {\ начинаются {выровнены} Y_ {6} ^ {- 6} (\ Theta, \ varphi) & = {1 \ над 64} {\ SQRT {3003 \ над \ пи}} \ CDOT е ^ {- 6i \ varphi} \ CDOT \ грех ^ {6} \ \\ тета Y_ {6} ^ {- 5} (\ Theta, \ varphi) & = {3 \ над 32} {\ SQRT {1001 \ над \ пи} } \ CDOT е ^ {- 5i \ varphi} \ CDOT \ грех ^ {5} \ тета \ CDOT \ соз \ \\ тета Y_ {6} ^ {- 4} (\ Theta, \ varphi) & = {3 \ более чем 32} {\ SQRT {91 \ более 2 \ пи}} \ CDOT е ^ {- 4i \ varphi} \ CDOT \ грех ^ {4} \ \ тета CDOT (11 \ соз ^ {2} \ тета-1) \\ Y_ {6} ^ {- 3} (\ Theta, \ varphi) & = {1 \ над 32} {\ SQRT {+1365 \ над \ пи}} \ CDOT е ^ {- 3i \ varphi} \ CDOT \ грех ^ {3} \ тета \ CDOT (11 \ соз ^ {3} \ тета -3 \ соз \ тета) \\ Y_ {6} ^ {- 2} (\ Theta, \ varphi) & = {1 \ над 64} {\ SQRT {1365 \ над \ пи}} \ CDOT е ^ {- 2i \ varphi} \ CDOT \ грех ^ {2} \ тета \ CDOT (33 \ соз ^ {4} \ тета -18 \ соз ^ {2} \ тета + 1) \\ Y_ {6} ^ {- 1} (\ Theta, \ varphi) & = {1 \ старше 16} {\ SQRT {273 \ более 2 \ пи}} \ CDOT е ^ {-i \ varphi} \ CDOT \ грех \ Theta \ CDOT (33 \ соз ^ {5} \ тета -30 \ соз ^ {3} \ тета + 5 \ соз \ тета) \\ Y_ {6} {0 ^ } (\ Theta, \ varphi) & = {1 \ над 32} {\ SQRT {13 \ над \ пи}} \ CDOT (231 \ соз ^ {6} \ тета -315 \ соз ^ {4} \ тета + 105 \ соз ^ {2} \ тета -5) \\ Y_ {6} ^ {1} (\ Theta, \ varphi) & = — {1 \ старше 16} {\ SQRT {273 \ над 2 \ пи}} \ CDOT е ^ {я \ varphi} \ CDOT \ грех \ Theta \ CDOT (33 \ соз ^ {5} \ тета -30 \ соз ^ {3} \ тета + 5 \ соз \ тета) \\ Y_ {6} ^ {2} (\ Theta, \ varphi) & = {1 \ старше 64} {\ SQRT {1365 \ над \ пи}} \ CDOT е ^ {2i \ varphi} \ CDOT \ грех ^ {2} \ тета \ CDOT (33 \ соз ^ {4} \ тета -18 \ соз ^ {2} \ тета + 1) \\ Y_ {6} ^ {3} (\ Theta, \ varphi) & = — {1 \} более 32 {\ SQRT {+1365 \ над \ пи}} \ CDOT е ^ {3i \ varphi} \ CDOT \ грех ^ {3} \ тета \ CDOT (11 \ соз ^ {3} -3 тета \ соз \ тета \) \ \ Y_ {6} ^ {4} (\ Theta, \ varphi) & = {3 \ над 32} {\ SQRT {91 \ более 2 \ пи}} \ CDOT е ^ {4i \ varphi} \ CDOT \ грех ^ {4} \ тета \ CDOT (11 \ соз ^ {2} \ тета-1) \\ Y_ {6} ^ {5} (\ Theta, \ varphi) & = — {3 \ над 32} {\ SQRT { +1001 \ над \ пи}} \ CDOT е ^ {5i \ varphi} \ CDOT \ грех ^ {5} \ тета \ CDOT \ соз \ \\ тета Y_ {6} ^ {6} (\ Theta, \ varphi) & = {1 \ над 64} {\ SQRT {3003 \ над \ пи}} \ CDOT е ^ {6i \ varphi} \ CDOT \ грех ^ {6} \ тета \ {конец выровнен}}}
ℓ{\ Displaystyle \ ell_p} = 7
- Y7-7(θ,φ)знак равно3647152π⋅е-7яφ⋅грех7θY7-6(θ,φ)знак равно3645005π⋅е-6яφ⋅грех6θ⋅созθY7-5(θ,φ)знак равно3643852π⋅е-5яφ⋅грех5θ⋅(13соз2θ-1)Y7-4(θ,φ)знак равно3323852π⋅е-4яφ⋅грех4θ⋅(13соз3θ-3созθ)Y7-3(θ,φ)знак равно364352π⋅е-3яφ⋅грех3θ⋅(143соз4θ-66соз2θ+3)Y7-2(θ,φ)знак равно36435π⋅е-2яφ⋅грех2θ⋅(143соз5θ-110соз3θ+15созθ)Y7-1(θ,φ)знак равно1641052π⋅е-яφ⋅грехθ⋅(429соз6θ-495соз4θ+135соз2θ-5)Y70(θ,φ)знак равно13215π⋅(429соз7θ-693соз5θ+315соз3θ-35созθ)Y71(θ,φ)знак равно-1641052π⋅еяφ⋅грехθ⋅(429соз6θ-495соз4θ+135соз2θ-5)Y72(θ,φ)знак равно36435π⋅е2яφ⋅грех2θ⋅(143соз
Рассеяние света сферической частицей — Википедия

Рассеяние све́та сфери́ческой части́цей (Рассеяние Ми) — классическая задача электродинамики, решённая в 1908 году Густавом Ми для сферической частицы произвольного размера[1].
Задача рассматривает рассеяние электромагнитной волны, имеющей напряжённость электрического поля
- E=E0eik⋅r−iωt,{\displaystyle \mathbf {E} =\mathbf {E} _{0}e^{i\mathbf {k} \cdot \mathbf {r} -i\omega t},}
где ω — частота, k — волновой вектор, а E0 — амплитуда волны, на сферической частице с радиусом R и диэлектрической проницаемостью ε.
Решение задачи находится с помощью разложения электромагнитного поля на векторные сферические гармоники.
Рассеяние зависит от соотношения размеров частицы и длины волны света в материале частицы. Рэлеевское рассеяние является частным случаем рассеяния Ми для случая, когда частица намного меньше длины волны . В этом случае внешняя электромагнитная волна поляризует частицу, возбуждая в ней переменный дипольный момент. Дипольный момент, колеблющийся в такт с частотой внешней волны, переизлучает свет с характерной для дипольного момента диаграммой направленности. Если можно пренебречь частотной зависимостью диэлектрической проницаемости частицы, интенсивность рассеяния зависит от частоты в четвертой степени, что приводит к сильному рассеянию коротких волн. В рассеянном белом свете преобладает голубой оттенок, а в нерассеянном — красный.
В случае близости размеров частицы к длине волны света диаграмма направленности рассеяния становится сложной. Проявляется интерференция волн, отражённых от различных участков поверхности частицы. Интенсивность рассеянного под определенным углом света зависит от того, сколько раз волна укладывается на диаметре частицы, поэтому она сильно зависит от размеров частицы. Когда в размеры частицы укладывается несколько длин волны, чередование максимумов и минимумов в диаграмме направленности становится настолько частым, что при падении белого света на, например, коллоидный раствор, наблюдатель увидит белый рассеянный свет. В итоге вещество с большим количеством таких частиц становится непрозрачным. В этом причина белого цвета облаков на небе, белого цвета молока и т. д. Раствор коллоидных частиц может быть окрашен в том случае, когда вещество частиц избирательно поглощает свет в определенном спектральном диапазоне.
Если размеры сферы намного больше длины волны света, то поверхность сферы будет вести себя как плоская поверхность. Происходит преломление и отражение света, которые описываются формулами Френеля.
Рассеяние плоской волны сферической частицей[править | править код]
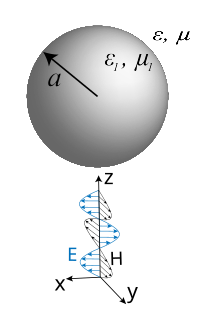 Рассеяние плоской волны, падающей вдоль оси z на сферической наночастице радиусом a
Рассеяние плоской волны, падающей вдоль оси z на сферической наночастице радиусом aЗадача рассеяния сферической наночастицей решается точно независимо от размера частицы. Будем рассматривать рассеяние плоской волной, распространяющейся вдоль оси z, поляризованной по x. Диэлектрическая и магнитная проницаемости частицы ε1{\displaystyle \varepsilon _{1}} и μ1{\displaystyle \mu _{1}}, а среды — ε{\displaystyle \varepsilon } и μ{\displaystyle \mu } соответственно. Для того, чтобы решить задачу рассеяния[2], выпишем сначала решения векторного уравнения Гельмгольца в сферических координатах, поскольку поля внутри и снаружи частицы должны ему удовлетворять. Уравнение Гельмгольца:
- ∇2E+k2E=0, ∇2H+k2H=0{\displaystyle \nabla ^{2}\mathbf {E} +{k}^{2}\mathbf {E} =0,\ \ \ \ \nabla ^{2}\mathbf {H} +{k}^{2}\mathbf {H} =0}
кроме уравнения Гельмгольца, поля должны ещё удовлетворять условиям ∇⋅E=∇⋅H=0{\displaystyle \nabla \cdot \mathbf {E} =\nabla \cdot \mathbf {H} =0} и ∇×E=iωμH{\displaystyle \nabla \times \mathbf {E} =i\omega \mu \mathbf {H} }, ∇×H=−iωεE{\displaystyle \nabla \times \mathbf {H} =-i\omega \varepsilon \mathbf {E} }. Всеми необходимыми свойствами обладают векторные сферические гармоники, введенные следующим образом:
- Moemn=∇×(rψoemn){\displaystyle \mathbf {M} _{^{e}_{o}mn}=\nabla \times \left(\mathbf {r} \psi _{^{e}_{o}mn}\right)} — магнитные гармоники
- Noemn=∇×Moemnk{\displaystyle \mathbf {N} _{^{e}_{o}mn}={\frac {\nabla \times \mathbf {M} _{^{e}_{o}mn}}{\mathbf {k} }}} — электрические гармоники
где
- ψemn=cosmφPnm(cosϑ)zn(kr){\displaystyle {\psi _{emn}=\cos m\varphi P_{n}^{m}(\cos \vartheta )z_{n}({k}r)}}
- ψomn=sinmφPnm(cosϑ)zn(kr){\displaystyle {\psi _{omn}=\sin m\varphi P_{n}^{m}(\cos \vartheta )z_{n}({k}r)}}
и Pnm(cosθ){\displaystyle P_{n}^{m}(\cos \theta )} — присоединенные полиномы Лежандра, а zn(kr){\displaystyle z_{n}({k}r)} — любая из сферических функций Бесселя.
Далее необходимо разложить падающую плоскую волну по векторным сферическим гармоникам.
- Einc=E0eikrcosθex=E0∑n=1∞in2n+1n(n+1)(Mo1n(1)(k,r)−iNe1n(1)(k,r)){\displaystyle \mathbf {E} _{inc}=E_{0}e^{ikr\cos \theta }\mathbf {e} _{x}=E_{0}\sum _{n=1}^{\infty }i^{n}{\frac {2n+1}{n(n+1)}}\left(\mathbf {M} _{o1n}^{(1)}(k,\mathbf {r} )-i\mathbf {N} _{e1n}^{(1)}(k,\mathbf {r} )\right)}
- Hinc=−kωμE0∑n=1∞in2n+1n(n+1)(Me1n(1)(k,r)+iNo1n(1)(k,r)){\displaystyle \mathbf {H} _{inc}={\frac {-k}{\omega \mu }}E_{0}\sum _{n=1}^{\infty }i^{n}{\frac {2n+1}{n(n+1)}}\left(\mathbf {M} _{e1n}^{(1)}(k,\mathbf {r} )+i\mathbf {N} _{o1n}^{(1)}(k,\mathbf {r} )\right)}
здесь верхний индекс (1){\displaystyle (1)} означает, что в радиальной части функций ψoemn{\displaystyle \psi _{^{e}_{o}mn}} — сферические фунции Бесселя.
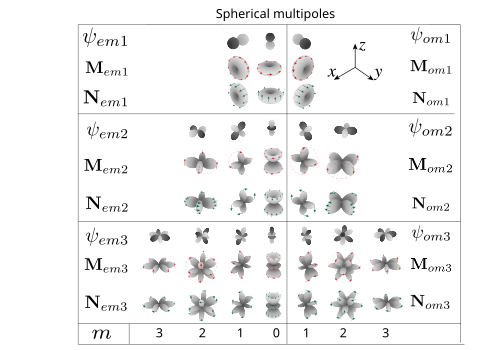 Угловая часть магнитных и электрических векторных сферических гармоник. Красными и зелеными стрелками показаны направления векторного поля. Первые три порядка — диполи, квадруполи и октуполи.
Угловая часть магнитных и электрических векторных сферических гармоник. Красными и зелеными стрелками показаны направления векторного поля. Первые три порядка — диполи, квадруполи и октуполи.Коэффициенты разложения получаются при взятии интегралов вида
- ∫02π∫0πEinc⋅Moemn(1)sinθdθdφ∫02π∫0π|Moemn(1)|2sinθdθdφ{\displaystyle {\frac {\int _{0}^{2\pi }\int _{0}^{\pi }\mathbf {E} _{inc}\cdot \mathbf {M} _{^{e}_{o}mn}^{(1)}\sin \theta d\theta d\varphi }{\int _{0}^{2\pi }\int _{0}^{\pi }|\mathbf {M} _{^{e}_{o}mn}^{(1)}|^{2}\sin \theta d\theta d\varphi }}}
при этом все коэффициенты при m≠1{\displaystyle m\neq 1} обнуляются, поскольку обнуляется интеграл по углу φ{\displaystyle \varphi } в числителе.
Затем накладываются
1) граничные условия на границе между шаром и окружающей средой (которые позволяют связать коэффициенты разложения падающего, внутреннего, и рассеянного полей),
2) условие ограниченности решения в начале координат(поэтому в радиальной части производящих функций ψoemn{\displaystyle \psi _{^{e}_{o}mn}} для внутреннего поля выбираются сферические функции Бесселя),
3) для рассеянного поля асимптотика на бесконечности соответствует расходящееся сферической волне(в связи с этим для рассеянного поля в радиальной части производящих функций ψoemn{\displaystyle \psi _{^{e}_{o}mn}} выбираются сферические функции Ханкеля первого рода).
Рассеянные поля записываются в виде разложения по векторным гармоникам как
- Es=∑n=1∞En(ianNe1n(3)(k,r)−bnMo1n(3)(k,r)){\displaystyle \mathbf {E} _{s}=\sum _{n=1}^{\infty }E_{n}\left(ia_{n}\mathbf {N} _{e1n}^{(3)}(k,\mathbf {r} )-b_{n}\mathbf {M} _{o1n}^{(3)}(k,\mathbf {r} )\right)}
- Hs=kωμ∑n=1∞En(anMe1n(3)(k,r)+ibnNo1n(3)(k,r)){\displaystyle \mathbf {H} _{s}={\frac {k}{\omega \mu }}\sum _{n=1}^{\infty }E_{n}\left(a_{n}\mathbf {M} _{e1n}^{(3)}(k,\mathbf {r} )+ib_{n}\mathbf {N} _{o1n}^{(3)}(k,\mathbf {r} )\right)}
здесь верхний индекс (3){\displaystyle (3)} означает, что в радиальной части функций ψoemn{\displaystyle \psi _{^{e}_{o}mn}} — сферические фунции Ханкеля,
а внутренние:
- E1=∑n=1∞En(−idnNe1n(1)(k1,r)+cnMo1n(1)(k1,r)){\displaystyle \mathbf {E} _{1}=\sum _{n=1}^{\infty }E_{n}\left(-id_{n}\mathbf {N} _{e1n}^{(1)}(k_{1},\mathbf {r} )+c_{n}\mathbf {M} _{o1n}^{(1)}(k_{1},\mathbf {r} )\right)}
- h2=−k1ωμ1∑n=1∞En(dnMe1n(1)(k1,r)+icnNo1n(1)(k1,r)){\displaystyle \mathbf {H} _{1}={\frac {-k_{1}}{\omega \mu _{1}}}\sum _{n=1}^{\infty }E_{n}\left(d_{n}\mathbf {M} _{e1n}^{(1)}(k_{1},\mathbf {r} )+ic_{n}\mathbf {N} _{o1n}^{(1)}(k_{1},\mathbf {r} )\right)}
k=ωcn{\displaystyle k={\frac {\omega }{c}}n}- волновой вектор снаружи частицы, k1=ωcn1{\displaystyle k_{1}={\frac {\omega }{c}}{n_{1}}} — волновой вектор в среде из материала частицы, n{\displaystyle n} и n1{\displaystyle n_{1}} — показатели преломления среды и частицы, После применения граничных условий получаются выражения для коэффициентов:
- cn(ω)=μ1[ρhn(ρ)]′jn(ρ)−μ1[ρjn(ρ)]′hn(ρ)μ1[ρhn(ρ)]′jn(ρ1)−μ[ρ1jn(ρ1)]′hn(ρ){\displaystyle c_{n}(\omega )={\frac {\mu _{1}\left[\rho h_{n}(\rho )\right]’j_{n}(\rho )-\mu _{1}\left[\rho j_{n}(\rho )\right]’h_{n}(\rho )}{\mu _{1}\left[\rho h_{n}(\rho )\right]’j_{n}(\rho _{1})-\mu \left[\rho _{1}j_{n}(\rho _{1})\right]’h_{n}(\rho )}}}
- dn(ω)=μ1n1n[ρhn(ρ)]′jn(ρ)−μ1n1n[ρjn(ρ)]′hn(ρ)μn12[ρhn(ρ)]′jn(ρ1)−μ1n2[ρ1jn(ρ1)]′hn(ρ),{\displaystyle d_{n}(\omega )={\frac {\mu _{1}n_{1}n\left[\rho h_{n}(\rho )\right]’j_{n}(\rho )-\mu _{1}n_{1}n\left[\rho j_{n}(\rho )\right]’h_{n}(\rho )}{\mu n_{1}^{2}\left[\rho h_{n}(\rho )\right]’j_{n}(\rho _{1})-\mu _{1}n^{2}\left[\rho _{1}j_{n}(\rho _{1})\right]’h_{n}(\rho )}},}
- bn(ω)=μ1[ρjn(ρ)]′jn(ρ1)−μ[ρ1jn(ρ1)]′jn(ρ)μ1[ρhn(ρ)]′jn(ρ1)−μ[ρ1jn(ρ1)]′hn(ρ){\displaystyle b_{n}(\omega )={\frac {\mu _{1}\left[\rho j_{n}(\rho )\right]’j_{n}(\rho _{1})-\mu \left[\rho _{1}j_{n}(\rho _{1})\right]’j_{n}(\rho )}{\mu _{1}\left[\rho h_{n}(\rho )\right]’j_{n}(\rho _{1})-\mu \left[\rho _{1}j_{n}(\rho _{1})\right]’h_{n}(\rho )}}}
- an(ω)=μn12[ρjn(ρ)]′jn(ρ1)−μ1n2[ρ1jn(ρ1)]′jn(ρ)μn12[ρhn(ρ)]′jn(ρ1)−μ1n2[ρ1jn(ρ1)]′hn(ρ),{\displaystyle a_{n}(\omega )={\frac {\mu n_{1}^{2}\left[\rho j_{n}(\rho )\right]’j_{n}(\rho _{1})-\mu _{1}n^{2}\left[\rho _{1}j_{n}(\rho _{1})\right]’j_{n}(\rho )}{\mu n_{1}^{2}\left[\rho h_{n}(\rho )\right]’j_{n}(\rho _{1})-\mu _{1}n^{2}\left[\rho _{1}j_{n}(\rho _{1})\right]’h_{n}(\rho )}},}
Здесь ρ=ka{\displaystyle \rho =ka}, ρ1=k1a{\displaystyle \rho _{1}=k_{1}a}, где a{\displaystyle a} — радиус наночастицы, jn{\displaystyle j_{n}} и hn{\displaystyle h_{n}} — сферические функции Бесселя и Ханкеля первого рода соответственно.
Сечения рассеяния и экстинкции[править | править код]
Сечения рассеяния и экстинкции могут быть получены интегрированием соответствующих функций электрического и магнитного полей по внешней сфере большого радиуса.[2] Из-за свойств ортогональности векторных сферических гармоник, получается простая связь коэффициентов Ми и сечений. Сечение рассеяния:
- Csca=2πk2∑n=1∞(2n+1)(|an|2+|bn|2){\displaystyle C_{sca}={\frac {2\pi }{k^{2}}}\sum _{n=1}^{\infty }(2n+1)(|a_{n}|^{2}+|b_{n}|^{2})}
сечение экстинкции:
- Cext=2πk2∑n=1∞(2n+1)ℜ(an+bn){\displaystyle C_{ext}={\frac {2\pi }{k^{2}}}\sum _{n=1}^{\infty }(2n+1)\Re (a_{n}+b_{n})}
Применение к субволновым частицам[править | править код]
Если в материале рассеивающего шара укладывается несколько длин волн, то рассеянные поля обладают некоторыми особенностями. Далее речь будет идти о виде электрического поля, поскольку магнитное поле получается из него взятием ротора.
Все коэффициенты Ми зависят от частоты и имеют максимумы, когда знаменатель близок к нулю (точное равенство нулю достигается для комплексных частот). При этом возможны ситуации, когда в рассеянии значительно доминирует вклад одной конкретной гармоники. Тогда на больших расстояниях от частицы диаграмма направленности рассеянного поля будет похожа на соответствующую диаграмму направленности угловой части векторных сферических гармоник. Гармоники Noem1{\displaystyle \mathbf {N} _{^{e}_{o}m1}} соответствуют электрическим диполям (если в разложении электрического поля доминирует вклад этой гармоники, то поле похоже на поле электрического диполя), Moem1{\displaystyle \mathbf {M} _{^{e}_{o}m1}} соответствуют электрическому полю магнитного диполя, Noem2{\displaystyle \mathbf {N} _{^{e}_{o}m2}} и Moem2{\displaystyle \mathbf {M} _{^{e}_{o}m2}} — электрический и магнитный квадруполи, Noem3{\displaystyle \mathbf {N} _{^{e}_{o}m3}} и Moem3{\displaystyle \mathbf {M} _{^{e}_{o}m3}} — октуполи, и так далее. Максимумы коэффициентов рассеяния (а также смена их фазы на π{\displaystyle \pi }) называются мультипольными резонансами.
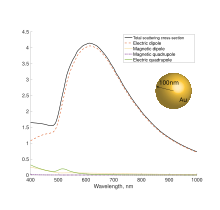 Мультипольное разложение зависимости сечения рассеяния золотым шаром радиусом 100 нм от длины падающей плоской волны.
Мультипольное разложение зависимости сечения рассеяния золотым шаром радиусом 100 нм от длины падающей плоской волны. 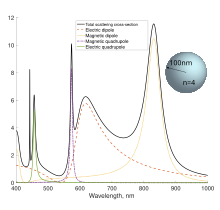 Мультипольное разложение зависимости сечения рассеяния шаром с показателем преломления n=4 радиусом 100 нм от длины падающей плоской волны.
Мультипольное разложение зависимости сечения рассеяния шаром с показателем преломления n=4 радиусом 100 нм от длины падающей плоской волны. 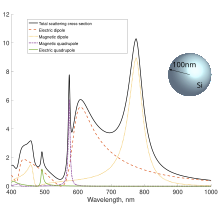 Мультипольное разложение зависимости сечения рассеяния кремниевым шаром радиусом 100 нм от длины падающей плоской волны.
Мультипольное разложение зависимости сечения рассеяния кремниевым шаром радиусом 100 нм от длины падающей плоской волны.
Вид зависимости сечения рассеянния от длины волны и вклад конкретных резонансов сильно зависит от материала частицы. Так, например, для золотой частицы радиусом 100нм в оптическом диапазоне преобладает вклад электрического диполя в рассеяние, а для кремниевой есть ярко выраженные магнитный дипольный и квадрупольный резонансы. Для металлических частиц пик, видимый в сечении рассеяния, также называют локализованным плазмонным резонансом.
В пределе малых частиц или больших длин волн в сечении рассеяния доминирует электрический дипольный вклад.
Другие направления падающей плоской волны[править | править код]
В случае x-поляризованной плоской волны, падающей вдоль z, разложения всех полей содержали только гармоники с m=1, но для произвольной падающей волны это не так[3]. Для повернутой плоской волны коэффициенты разложения можно получить, например, используя то, что при поворотах векторные сферические гармоники преобразуются друг через друга определенным образом. При этом рассеянное поле будет раскладываться уже по всем возможным гармоникам:
- Es=∑n=1∞∑m=0nE0(DMemnMemn(3)(k,r)+DMomnMomn(3)(k,r)+DNemnNemn(3)(k,r)+DNomnNomn(3)(k,r)){\displaystyle \mathbf {E} _{s}=\sum _{n=1}^{\infty }\sum _{m=0}^{n}E_{0}(D_{Memn}\mathbf {M} _{emn}^{(3)}(k,\mathbf {r} )+D_{Momn}\mathbf {M} _{omn}^{(3)}(k,\mathbf {r} )+D_{Nemn}\mathbf {N} _{emn}^{(3)}(k,\mathbf {r} )+D_{Nomn}\mathbf {N} _{omn}^{(3)}(k,\mathbf {r} ))}
Тогда сечение рассеяния будет выражаться через коэффициенты следующим образом:
- Csca=2ππa2k2∑n=1∞n(n+1)(2n+1)×[∑m=1n(n+m)!(n−m)!(|DMemn|2+|DMomn|2+|DNemn|2+|DNomn|2)+2|DMe0n|2+2|DNe0n
Сферические гармоники Википедия
Сферические функции представляют собой угловую часть семейства ортогональных решений уравнения Лапласа, записанную в сферических координатах. Они широко используются для изучения физических явлений в пространственных областях, ограниченных сферическими поверхностями и при решении физических задач, обладающих сферической симметрией. Сферические функции имеют большое значение в теории дифференциальных уравнений в частных производных и теоретической физике, в частности в задачах расчёта электронных орбиталей в атоме, гравитационного поля геоида, магнитного поля планет и интенсивности реликтового излучения.
Определение
Вещественные сферические функции Ylm, l=0…4 (сверху вниз), m=0…4 (слева направо). Функции отрицательного порядка Yl-m повёрнуты вокруг оси Z на 90/m градусов относительно функций положительного порядка.
Сферические функции являются собственными функциями оператора Лапласа в сферической системе координат (обозначение Ylm(θ,φ){\displaystyle Y_{l}^{m}(\theta ,\varphi )}). Они образуют ортонормированную систему в пространстве функций на двумерной сфере:
- ⟨Ylm;Ylm⟩=∬|Ylm|2sinθdθdφ=1{\displaystyle \langle Y_{l}^{m};Y_{l}^{m}\rangle =\iint |Y_{l}^{m}|^{2}\sin {\theta }\,d\theta \,d\varphi =1}
- ⟨Ylm;Yl′m′⟩=∫02π∫0πYl′m′∗Ylmsinθdθdφ=δll′δmm′{\displaystyle \langle Y_{l}^{m};Y_{l’}^{m’}\rangle =\int \limits _{0}^{2\pi }\int \limits _{0}^{\pi }Y_{l’}^{m’*}Y_{l}^{m}\sin {\theta }\,d\theta \,d\varphi =\delta _{ll’}\delta _{mm’}},
где * обозначает комплексное сопряжение, δll′{\displaystyle \delta _{ll’}} — символ Кронекера.
Сферические функции имеют вид
- Ylm=12πeimφΘlm(θ){\displaystyle Y_{l}^{m}={\frac {1}{\sqrt {2\pi }}}e^{im\varphi }\Theta _{lm}(\theta )},
где функции Θlm(θ){\displaystyle \Theta _{lm}(\theta )} являются решениями уравнения
- 1sinθddθ(sinθdΘlmdθ)−m2sin2θΘlm+l(l+1)Θlm=0{\displaystyle {\frac {1}{\sin {\theta }}}{\frac {d}{d\theta }}\left(\sin {\theta }{\frac {d\Theta _{lm}}{d\theta }}\right)-{\frac {m^{2}}{\sin ^{2}{\theta }}}\Theta _{lm}+l(l+1)\Theta _{l}^{m}=0}
и имеют вид
- Θlm=2l+12(l−m)!(l+m)!Plm(cosθ){\displaystyle \Theta _{l}^{m}={\sqrt {{\frac {2l+1}{2}}{\frac {(l-m)!}{(l+m)!}}}}P_{l}^{m}(\cos \theta )}
Здесь Plm(cosθ){\displaystyle P_{l}^{m}(\cos \theta )} — присоединённые многочлены Лежандра, а m!{\displaystyle m!} — факториал.
Присоединенные многочлены Лежандра с отрицательным m{\displaystyle m} здесь вводятся как
- Pℓ−m(x)=(−1)m(ℓ−m)!(ℓ+m)!Pℓm(x){\displaystyle P_{\ell }^{-m}(x)=(-1)^{m}{\frac {(\ell -m)!}{(\ell +m)!}}P_{\ell }^{m}(x)}
Решение уравнения Лапласа в сферических координатах есть так называемая шаровая функция, получаемая умножением сферической функции на решение радиального уравнения.
Вещественная форма
Вещественные сферические функции до шестого порядкаДля сферических функций форма зависимости от угла φ{\displaystyle \varphi } — комплексная экспонента. Используя Формулу Эйлера, можно ввести вещественные сферические функции. Иногда их удобнее использовать в связи с тем, что вещественные функции могут быть наглядно показаны на иллюстрациях, в отличие от комплексных.
- Yℓm={i2(Yℓm−(−1)mYℓ−m) m<0Yℓ0 m=012(Yℓ−m+(−1)mYℓm) m>0.={2(−1)mIm[Yℓ|m|] m<0Yℓ0 m=02(−1)mRe[Yℓm] m>0.{\displaystyle {\begin{aligned}Y_{\ell m}&={\begin{cases}\displaystyle {i \over {\sqrt {2}}}\left(Y_{\ell }^{m}-(-1)^{m}\,Y_{\ell }^{-m}\right)&{\text{ }}\ m<0\\\displaystyle Y_{\ell }^{0}&{\text{ }}\ m=0\\\displaystyle {1 \over {\sqrt {2}}}\left(Y_{\ell }^{-m}+(-1)^{m}\,Y_{\ell }^{m}\right)&{\text{ }}\ m>0.\end{cases}}\\&={\begin{cases}\displaystyle {\sqrt {2}}\,(-1)^{m}\,\operatorname {Im} [{Y_{\ell }^{|m|}}]&{\text{ }}\ m<0\\\displaystyle Y_{\ell }^{0}&{\text{ }}\ m=0\\\displaystyle {\sqrt {2}}\,(-1)^{m}\,\operatorname {Re} [{Y_{\ell }^{m}}]&{\text{ }}\ m>0.\end{cases}}\end{aligned}}}
Обратное преобразование:
- Yℓm={12(Yℓ|m|−iYℓ,−|m|) m<0Yℓ0 m=0(−1)m2(Yℓ|m|+iYℓ,−|m|) m>0.{\displaystyle Y_{\ell }^{m}={\begin{cases}\displaystyle {1 \over {\sqrt {2}}}\left(Y_{\ell |m|}-iY_{\ell ,-|m|}\right)&{\text{ }}\ m<0\\\displaystyle Y_{\ell 0}&{\text{ }}\ m=0\\\displaystyle {(-1)^{m} \over {\sqrt {2}}}\left(Y_{\ell |m|}+iY_{\ell ,-|m|}\right)&{\text{ }}\ m>0.\end{cases}}}
Иногда вещественные сферические функции называют зональными, тессеральными и секториальными.[1]. Функции с m > 0 зависят от угла как косинус, а с m < 0 — как синус.
Yℓm={(−1)m22ℓ+14π(ℓ−|m|)!(ℓ+|m|)! Pℓ|m|(cosθ) sin(|m|φ) m<02ℓ+14π Pℓm(cosθ) m=0(−1)m22ℓ+14π(ℓ−m)!(ℓ+m)! Pℓm(cosθ) cos(mφ) m>0.{\displaystyle Y_{\ell m}={\begin{cases}\displaystyle (-1)^{m}{\sqrt {2}}{\sqrt {{2\ell +1 \over 4\pi }{(\ell -|m|)! \over (\ell +|m|)!}}}\ P_{\ell }^{|m|}(\cos \theta )\ \sin(|m|\varphi )&{\mbox{ }}m<0\\\displaystyle {\sqrt {2\ell +1 \over 4\pi }}\ P_{\ell }^{m}(\cos \theta )&{\mbox{ }}m=0\\\displaystyle (-1)^{m}{\sqrt {2}}{\sqrt {{2\ell +1 \over 4\pi }{(\ell -m)! \over (\ell +m)!}}}\ P_{\ell }^{m}(\cos \theta )\ \cos(m\varphi )&{\mbox{ }}m>0\,.\end{cases}}}
Повороты
Поворот вещественной сферической функции с m=0 и l=3. Коэффициенты не равны D-матрицам Вигнера, поскольку показаны вещественные функции, но могут быть получены при переразложении по комплексным функциямРассмотрим поворот системы координат R{\displaystyle {\mathcal {R}}}, на Углы Эйлера α,β,γ,{\displaystyle \alpha ,\beta ,\gamma ,} который преобрaзует единичный вектор r{\displaystyle \mathbf {r} } в вектор r′{\displaystyle {\mathbf {r} }’}. При этом углы θ′,φ′{\displaystyle \theta ‘,\varphi ‘} вектора r′{\displaystyle {\mathbf {r} }’} в новой системе координат выражаются через углы в старой системе координат следующим образом
- cosθ′=cosθcosβ+sinθsinβcos(φ−α){\displaystyle \cos \theta ^{\prime }=\cos \theta \cos \beta +\sin \theta \sin \beta \cos(\varphi -\alpha )}
- ctg(φ′+γ)=ctg(φ−α)cosβ−ctgθsinβsin(φ−α){\displaystyle \operatorname {ctg} \left(\varphi ^{\prime }+\gamma \right)=\operatorname {ctg} (\varphi -\alpha )\cos \beta -{\frac {\operatorname {ctg} \theta \sin \beta }{\sin(\varphi -\alpha )}}}
В новой системе координат сферическая функция с индексами ℓ{\displaystyle \ell } и m{\displaystyle m} будет представима в виде линейной комбинации всех функций с тем же номером ℓ{\displaystyle \ell } и различными m{\displaystyle m}. Коэффициентами в линейной комбинации являются комплексно- сопряженные D-матрицы Вигнера[2]
- D^(α,β,γ)Ylm(θ,φ)=Yℓm(θ′,φ′)=∑m′=−ℓℓ[Dmm′(ℓ)(α,β,γ)]∗Yℓm′(θ,φ),{\displaystyle {\hat {D}}(\alpha ,\beta ,\gamma )Y_{l}^{m}(\theta ,\varphi )=Y_{\ell }^{m}(\theta ‘,\varphi ‘)=\sum _{m’=-\ell }^{\ell }[D_{mm’}^{(\ell )}(\alpha ,\beta ,\gamma )]^{*}Y_{\ell }^{m’}(\theta ,\varphi ),}
Сферические функции с номером ℓ{\displaystyle \ell } образуют базис неприводимого представления размерности (2ℓ+1){\displaystyle (2\ell +1)} группы вращений SO(3).
Разложение плоской волны по сферическим функциям
Комплексная экспонента может быть представлена в виде разложения по сферическим функциям
- eik⋅r=4π∑l=0∞iljl(kr)∑m=−llYlm∗(r|r|)Ylm(k|k|){\displaystyle e^{i\mathbf {k} \cdot \mathbf {r} }=4\pi \sum _{l=0}^{\infty }i^{l}j_{l}(kr)\sum _{m=-l}^{l}Y_{l}^{m*}\left({\frac {\mathbf {r} }{|r|}}\right)Y_{l}^{m}\left({\frac {\mathbf {k} }{|k|}}\right)}
Здесь jn(x)=π2xJn+12(x){\displaystyle j_{n}(x)={\sqrt {\frac {\pi }{2x}}}J_{n+{\frac {1}{2}}}(x)} — сферическая функция Бесселя
См. также
Примечания
Литература
Приложения
Ссылки
Зональные сферические гармоники — Zonal spherical harmonics
В математическом исследовании вращательной симметрии , то зональные сферические гармоники специальные сферические гармоники , которые инвариантны относительно поворота на определенную фиксированную ось. В зональных сферических функциях являются широким распространением понятия зональных сферических гармоник для обеспечения более общей группа симметрии .
На двумерной сфере, уникальная зональная сферическая гармоника степени л, инвариантных относительно вращений фиксируя северный полюс представлен в сферических координатах
- Z(ℓ)(θ,φ)знак равнопℓ(созθ){\ Displaystyle Z ^ {(\ ell_p)} (\ Theta, \ фи) = Р _ {\ ell_p} (\ \ соз тета)}
где P ℓ является полином Лежандра степени л. Общем зональная сферическая гармоника степени л обозначается , где х представляет собой точку на сфере , представляющей фиксированную ось, а у является переменной функции. Это может быть получено путем вращения основной гармоники зональнойZИкс(ℓ)(Y){\ Displaystyle Z _ {\ mathbf {х}} ^ {(\ ell_p)} (\ mathbf {у})}Z(ℓ)(θ,φ),{\ Displaystyle Z ^ {(\ ell_p)} (\ тета, \ фи).}
В п — мерном евклидовом пространстве, зональные сферические гармоники определяются следующим образом . Пусть й точка на ( п -1) -сфере. Определить , являются двойным представлением линейного функционала ZИкс(ℓ){\ Displaystyle Z _ {\ mathbf {х}} ^ {(\ ell_p)}}
- п↦п(Икс){\ Displaystyle Р \ mapsto Р (\ mathbf {х})}
в конечномерном гильбертовом пространстве Н л сферических гармоник степени л. Другими словами, следующее воспроизводя свойство имеет место:
- Y(Икс)знак равно∫SN-1ZИкс(ℓ)(Y)Y(Y)dΩ(Y){\ Displaystyle У (\ mathbf {х}) = \ Int _ {S ^ {N-1}} Z _ {\ mathbf {х}} ^ {(\ ell_p)} (\ mathbf {у}) У (\ mathbf {у}) \, д \ Omega (у)}
для всех Y ∈ H л . Интеграл берется по инвариантной вероятностной меры.
Отношения с гармоническими потенциалами
Зональные гармоники естественно появляются как коэффициенты ядра Пуассона для единичного шара в R п : для й и у единичных векторов,
- 1ωN-11-р2|Икс-рY|Nзнак равноΣКзнак равно0∞рКZИкс(К)(Y),{\ Displaystyle {\ гидроразрыва {1} {\ Omega _ {п-1}}} {\ гидроразрыва {1-г ^ {2}} {| \ mathbf {х} -r \ mathbf {у} | {^ п }}} = \ сумма _ {к = 0} ^ {\ infty} ^ г {к} Z _ {\ mathbf {х}} ^ {(к)} (\ mathbf {у}),}
где это площадь поверхности (N-1) мерной сферы. Они также связаны с ядром Ньютона с помощью ωN-1{\ Displaystyle \ омега _ {п-1}}
- 1|Икс-Y|N-2знак равноΣКзнак равно0∞сN,К|Икс|К|Y|N+К-2ZИкс/|Икс|(К)(Y/|Y|){\ Displaystyle {\ гидроразрыва {1} {| \ mathbf {х} — \ mathbf {у} | ^ {п-2}}} = \ сумма _ {к = 0} ^ {\ infty} c_ {п, к } {\ гидроразрыва {| \ mathbf {х} | ^ {к}} {| \ mathbf {у} | ^ {п + к-2}}} Z _ {\ mathbf {х} / | \ mathbf {х} | } ^ {(к)} (\ mathbf {у} / | \ mathbf {у} |)}
где х , у ∈ R п и константы Ĉ п , к задаются
- сN,Кзнак равно1ωN-12К+N-2(N-2),{\ Displaystyle C_ {п, к} = {\ гидроразрыва {1} {\ Omega _ {п-1}}} {\ гидроразрыва {2k + п-2} {(п-2)}}.}
Коэффициенты ряда Тейлора ядра Ньютона (с подходящей нормировкой) в точности ультрасферических полиномы . Таким образом, зональные сферические гармоники могут быть выражены следующим образом . Если α = ( п — 2) / 2, то
- ZИкс(ℓ)(Y)знак равноN+2ℓ-2N-2Сℓ(α)(Икс⋅Y){\ Displaystyle Z _ {\ mathbf {х}} ^ {(\ ell_p)} (\ mathbf {у}) = {\ гидроразрыва {п + 2 \ ell_p -2} {п-2}} C _ {\ ell_p} ^ {(\ альфа)} (\ mathbf {х} \ CDOT \ mathbf {у})}
где с п , ℓ константа выше и является ультрасферическим многочленом степени л. Сℓ(α){\ Displaystyle C _ {\ ell_p} ^ {(\ альфа)}}
свойства
- Зональные сферические гармоники вращательно инвариантные, т.е.
- ZрИкс(ℓ)(рY)знак равноZИкс(ℓ)(Y){\ Displaystyle Z_ {Р \ mathbf {х}} ^ {(\ ell_p)} (R \ mathbf {у}) = Z _ {\ mathbf {х}} ^ {(\ ell_p)} (\ mathbf {у}) }
- для каждого ортогонального преобразования R . И наоборот, любая функция ƒ ( х , у ) на S п -1 × S н -1 , которая является сферической гармонической в у при каждом фиксированном х , и что удовлетворяет этому инвариантность свойств, является постоянным кратным степени л зональной гармоники.
- ZИкс(ℓ)(Y)знак равноΣКзнак равно1dYК(Икс)YК(Y)¯,{\ Displaystyle Z _ {\ mathbf {х}} ^ {(\ ell_p)} (\ mathbf {у}) = \ сумма _ {к = 1} ^ {d} Y_ {K} (\ mathbf {х}) { \ Overline {Y_ {K} (\ mathbf {у})}}.}
- Оценка при х = у дает
- ZИкс(ℓ)(Икс)знак равноωN-1-1тусклыйЧАСℓ,{\ Displaystyle Z _ {\ mathbf {х}} ^ {(\ ell_p)} (\ mathbf {х}) = \ омега _ {п-1} ^ {- 1} \ тусклый \ mathbf {H} _ {\ ell_p }.}
Рекомендации
<img src=»https://en.wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>Сферические гармоники Википедия
Сферические функции представляют собой угловую часть семейства ортогональных решений уравнения Лапласа, записанную в сферических координатах. Они широко используются для изучения физических явлений в пространственных областях, ограниченных сферическими поверхностями и при решении физических задач, обладающих сферической симметрией. Сферические функции имеют большое значение в теории дифференциальных уравнений в частных производных и теоретической физике, в частности в задачах расчёта электронных орбиталей в атоме, гравитационного поля геоида, магнитного поля планет и интенсивности реликтового излучения.
Определение[ | ]
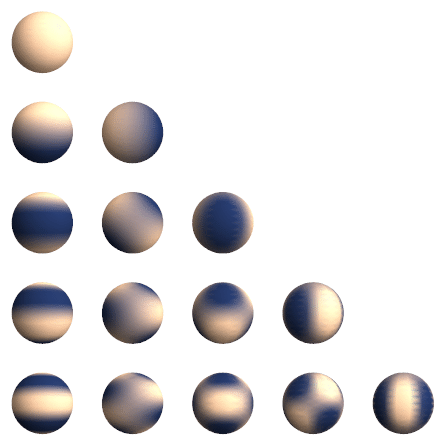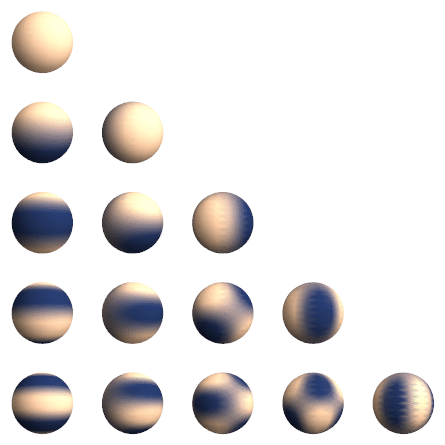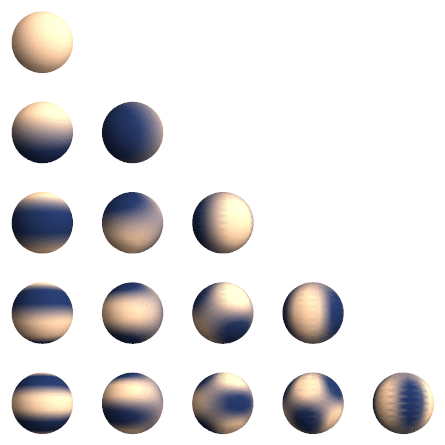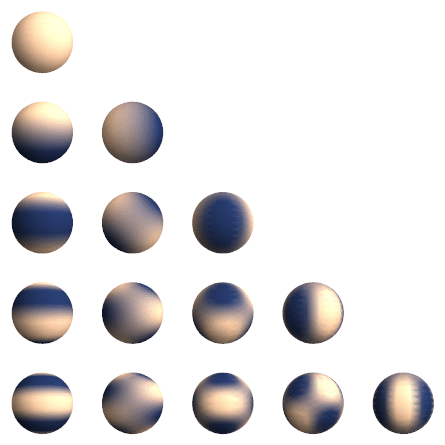
Вещественные сферические функции Ylm, l=0…4 (сверху вниз), m=0…4 (слева направо). Функции отрицательного порядка Yl-m повёрнуты вокруг оси Z на 90/m градусов относительно функций положительного порядка.
Сферические функции являются собственными функциями оператора Лапласа в сферической системе координат (обозначение Ylm(θ,φ){\displaystyle Y_{l}^{m}(\theta ,\varphi )}). Они образуют ортонормированную систему в пространстве функций на двумерной сфере:
- ⟨Ylm;Ylm⟩=∬|Ylm|2sinθdθdφ=1{\displaystyle \langle Y_{l}^{m};Y_{l}^{m}\rangle =\iint |Y_{l}^{m}|^{2}\sin {\theta }\,d\theta \,d\varphi =1}
- ⟨Ylm;Yl′m′⟩=∫02π∫0πYl′m′∗Ylmsinθdθdφ=δll′δmm′{

