1 вариант 1.На рисунке изображена электрическая цепь электромагнита. Какой магнитный полюс будет наверху? | 2 вариант 1.На рисунке изображена электрическая цепь электромагнита. Указано положение северного полюса. Определите заряд верхней клеммы источника тока. | ||
2.Прямолинейный проводник длиной 0,2 м, по которому течёт ток 2 А, находится в однородном магнитном поле с индукцией 0,6 Тл и расположен перпендикулярно вектору В. Каков модуль силы, действующей на проводник со стороны магнитного поля? | 2.Прямолинейный проводник длиной 50 см, по которому течёт ток 2 А, находится в однородном магнитном поле с индукцией 0,1 Тл. Каков угол между проводником и вектором магнитной индукции, если сила Ампера равна 0,05 Н? | ||
3. 3 раза, а индукцию магнитного поля увеличить в 3 раза? | 3. Прямолинейный проводник длины 𝒍 c током I помещён в однородное магнитном поле параллельно линиям индукции В. Как изменится сила Ампера, действующая на проводник, если его длину увеличить в 3 раза, а индукцию магнитного поля уменьшить в 3 раза? | ||
4.Определите направление силы Ампера, действующей на проводник. | 5.Протон влетает в магнитное поле. Определите направление силы Лоренца, действующей на протон. | 4.Определите направление силы Ампера, действующей на проводник. | 5.Электрон влетает в магнитное поле. Определите направление силы Лоренца, действующей на электрон. |
6. | 6.Электрон движется по окружности радиусом 2 см в однородном магнитном поле, имея импульс 6,4·10-23 кг· м/с. Определите модуль магнитной индукции поля. | ||
1 вариант 1.На рисунке изображена электрическая цепь электромагнита. Какой магнитный полюс будет наверху? | 2 вариант 1.На рисунке изображена электрическая цепь электромагнита. Указано положение северного полюса. Определите заряд верхней клеммы источника тока. | ||
2.Прямолинейный проводник длиной 0,2 м, по которому течёт ток 2 А, находится в однородном магнитном поле с индукцией 0,6 Тл и расположен перпендикулярно вектору В. Каков модуль силы, действующей на проводник со стороны магнитного поля? | 2. | ||
3. Прямолинейный проводник длины 𝒍 c током I помещён в однородное магнитное поле перпендикулярно линиям индукции В. Как изменится сила Ампера, действующая на проводник, если его длину уменьшить в 3 раза, а индукцию магнитного поля увеличить в 3 раза? | 3. Прямолинейный проводник длины 𝒍 c током I помещён в однородное магнитном поле параллельно линиям индукции В. Как изменится сила Ампера, действующая на проводник, если его длину увеличить в 3 раза, а индукцию магнитного поля уменьшить в 3 раза? | ||
4.Определите направление силы Ампера, действующей на проводник. | 5.Протон влетает в магнитное поле. Определите направление силы Лоренца, действующей на протон. | 4.Определите направление силы Ампера, действующей на проводник. | 5.Электрон влетает в магнитное поле. Определите направление силы Лоренца, действующей на электрон. |
6.Электрон влетает в однородное магнитное поле с индукцией1,26 мТл перпендикулярно силовым линиям со скоростью 10 Мм/с. Определите радиус окружности, по которой будет двигаться электрон? | 6.Электрон движется по окружности радиусом 2 см в однородном магнитном поле, имея импульс 6,4·10-23 кг· м/с. Определите модуль магнитной индукции поля. | ||
самостоятельная работа по теме «Сила Ампера. Сила Лоренца» 9 класс
Главная / Старшие классы / Физика
Скачать
106 КБ, 1457873.doc Автор: Солдатенко Галина Николаевна, 2 Мар 2016
самостоятельная работа по теме «Сила Ампера. Сила Лоренца» 9 класс состоит из 8 вариантов. Пять заданий в кадом варианте.
Сила Лоренца» 9 класс состоит из 8 вариантов. Пять заданий в кадом варианте.
Автор: Солдатенко Галина Николаевна
Похожие материалы
| Тип | Название материала | Автор | Опубликован |
|---|---|---|---|
| документ | самостоятельная работа по теме «Сила Ампера. Сила Лоренца» 9 класс | 2 Мар 2016 | |
| документ | урок в 9 классе по теме «Сила Ампера. Сила Лоренца»» Конспект урока «Сила Ампера. Сила Лоренца.»9 класс | Дружаева Светлана Васильевна | 21 Мар 2015 |
| презентация | Презентация к уроку в 9,11 классе «Действие магнитного поля на проводник с током. Сила Ампера. Сила Лоренца» Сила Ампера. Сила Лоренца» | Желнова Наталья Васильевна | 21 Мар 2015 |
| документ | Самостоятельная работа по физике 7 класс по теме: «Сила трения» | Уваров Сергей Александрович | 21 Мар 2015 |
| документ | Самостоятельная работа по физике 8 класс по теме: «Электрический ток. Сила тока.» | Уваров Сергей Александрович | 21 Мар 2015 |
| документ | Самостоятельная работа по физике 7 класс по теме «Сила» к учебнику Н.С. Пурышевой | Зайцева Ирина Николаевна | 21 Мар 2015 |
| презентация | Презентация к уроку по теме «Сила Лоренца» | Ахметова Нязиля Джафяровна | 5 Ноя 2015 |
| презентация, документ | Урок физики в 9 классе «Сила Ампера» | Анашкина Ирина Владимировна | 31 Мар 2015 |
| документ | «Методический анализ ошибки». (по теме «Сила Ампера») (по теме «Сила Ампера») | Романовская Галина Александровна | 21 Мар 2015 |
| документ | Самостоятельная работа по теме «Архимедова сила. Плавание тел» | Гредасова Елена Петровна | 19 Мар 2016 |
| документ | Разработка урока физики в 11 классе по теме: «Сила Лоренца» | Хвостова Елена Владимировна | 21 Мар 2015 |
| презентация, документ | Разработка урока в 11 классе по теме «Сила Лоренца» | Шилова Лариса Петровна | 21 Мар 2015 |
| документ | 7 кл- Самостоятельная работа по теме «Сила. Сила тяжести. Вес тела. Сила упругости» Сила тяжести. Вес тела. Сила упругости» | Фасхутдинова Лилия Ирековна | 21 Мар 2015 |
| презентация, документ | «Преобразование электрической энергии в механическую. Сила Ампера» | Матвиевский Андрей Александрович | 21 Мар 2015 |
| документ | самостоятельная работа по теме «Неметаллы» 9 класс | Хаттунен Галина Алексеевна | 21 Мар 2015 |
| документ | Самостоятельная работа по теме «Окружность» (9 класс) | Павлова Татьяна Сергеевна | 21 Ноя 2015 |
| документ | Технологическая карта урока физики по теме «Сила. | Шемена Валентина Викторовна | 7 Ноя 2015 |
| презентация | Презентация по теме «Архимедова сила» | Мучкаева Галина Ивановна | 9 Апр 2015 |
| презентация | тест по теме «Сила. Сила тяжести» | Рассказова Юлия Николаевна | 6 Дек 2015 |
| документ | Самостоятельная работа по физике для 7 класса на тему «Сила» к учебнику Н.С. Пурышевой | Зайцева Ирина Николаевна | 21 Мар 2015 |
| документ | Самостоятельная работа по физике в 7 классе «Архимедова сила» | Сафронова Елена Геннадьевна | |
| документ | Контрольная работа по теме: «Архимедова сила» 7 класс | Свиридова Татьяна Александровна | 1 Апр 2015 |
| разное | Урок по теме «Сила трения» 7 класс | Никитина Марина Борисовна | 21 Мар 2015 |
| презентация, документ | Урок по теме «Сила трения», 7 класс | Платова Людмила Юльяновна | 21 Мар 2015 |
| презентация, документ | Урок по теме»Архимедова сила», 7 класс. | Вахрушев Максим Юрьевич | 21 Мар 2015 |
| документ | урок по теме «Сила трения» 7 класс | Алексеенко Валентина Анатольевна | 21 Мар 2015 |
| презентация | презентация по теме» Сила трения» 7 класс | Шевякова Наталия Валерьевна | 21 Мар 2015 |
| документ | Тест по теме «Сила» 7 класс | Маликова Гильминур Нигматчановна | 14 Фев 2016 |
| документ | Самостоятельная работа по теме «Движение» по геометрии 9 класс. | Новосельская Оксана Анатольевна | 21 Мар 2015 |
| разное | Самостоятельная работа по физике по теме «Импульс. Закон сохранения импульса» (9 класс) — MS Office Excel. | Шамарина Татьяна Николаевна | 21 Мар 2015 |
| документ | Самостоятельная работа по биологии по теме «Строение клетки» 9 класс | Лисицына Светлана Александровна | 31 Мар 2015 |
| документ | Самостоятельная работа по геометрии по теме «Длина окружности. Площадь круга»,9 класс | Россамахина Ирина Юрьевна | 31 Мар 2015 |
| документ | самостоятельная работа по алгебре 9 класс по теме «Квадратичные неравенства» | Исакова Екатерина Александровна | 1 Апр 2015 |
| документ | Самостоятельная работа по алгебре 9 класс по теме «Рациональные неравенства» | Ольга Михайловна Щербакова | 18 Окт 2015 |
| документ | Самостоятельная работа по геометрии 9 класс по теме «Векторы» | Ольга Михайловна Щербакова | 13 Дек 2015 |
| презентация | Презентация для 11 класса «Модуль вектора магнитной индукции. Сила Ампера.» Сила Ампера.» | Молочко Лидия Николаевна | 21 Мар 2015 |
| документ | Самостоятельная работа по теме «Закон сохранения импульса» 9 класс | Шохина Елена Николаевна | 21 Мар 2015 |
| документ | Самостоятельная работа по теме «Основные конструкции языка программирования Паскаль.» 9 класс | Коробова Татьяна Михайловна | 21 Мар 2015 |
| документ | Самостоятельная работа по теме «Числовые функции» (9 класс) | Ермак Елена Юрьевна | 30 Янв 2016 |
| документ | самостоятельная работа по теме «Галогены.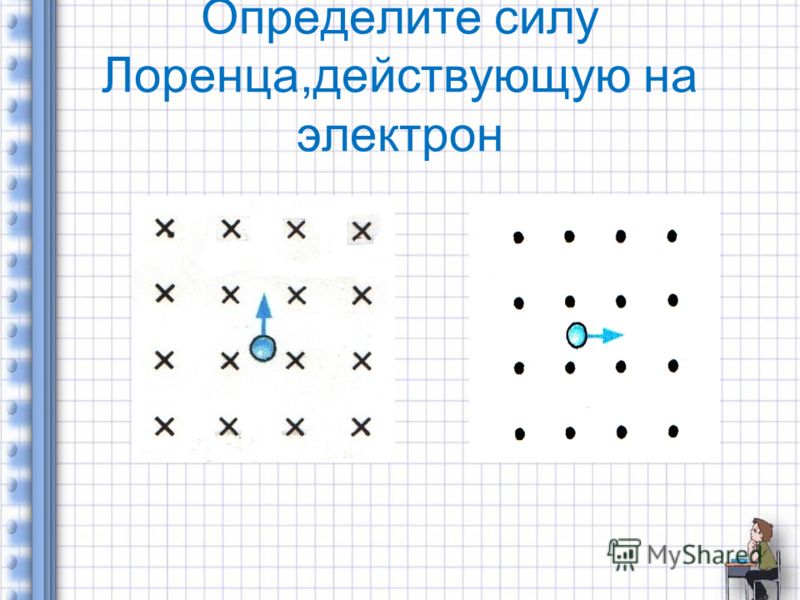 Соединения галогенов» 9 класс Соединения галогенов» 9 класс | Файзулина Анастасия Андреевна | 19 Мар 2016 |
— Почему силовая система Лоренца независима?
Задавать вопрос
спросил
Изменено 2 года, 7 месяцев назад
Просмотрено 1к раз
$\begingroup$
Недавно я начал изучать магнетизм и наткнулся на утверждение в своей книге, которое меня смутило. Оно гласило:
Магнитная сила зависит от системы координат, электрическая сила зависит от системы координат, но сила Лоренца не зависит от системы координат
Я могу понять, что магнитная сила зависит от системы отсчета, так как это сила, зависящая от скорости, а скорость зависит от системы отсчета, в которой она измеряется. Однако я не могу понять, почему электрическая сила зависит от системы отсчета. в неинерциальной системе отсчета или в движущейся инерциальной системе электрическая сила становится магнитной силой, когда покоящийся заряд движется относительно этой системы отсчета?
Однако я не могу понять, почему электрическая сила зависит от системы отсчета. в неинерциальной системе отсчета или в движущейся инерциальной системе электрическая сила становится магнитной силой, когда покоящийся заряд движется относительно этой системы отсчета?
Кроме того, то, что сила Лоренца не зависит от системы отсчета, заставляет меня думать, что некоторые компоненты, возникающие из-за смещения системы отсчета, компенсируют друг друга, делая результирующую силу Лоренца одинаковой. Однако я не могу получить полную картину.
Может ли кто-нибудь объяснить мне причину этого, не используя сложную математику/теорию относительности? Какая интуиция стоит за этим?
- электромагнетизм
- специальная теория относительности
- магнитные поля
- электрические поля
- инерциальные системы
$\endgroup$
4
$\begingroup$
3-вектор силы Лоренца не зависит от системы отсчета только при преобразовании Галилея.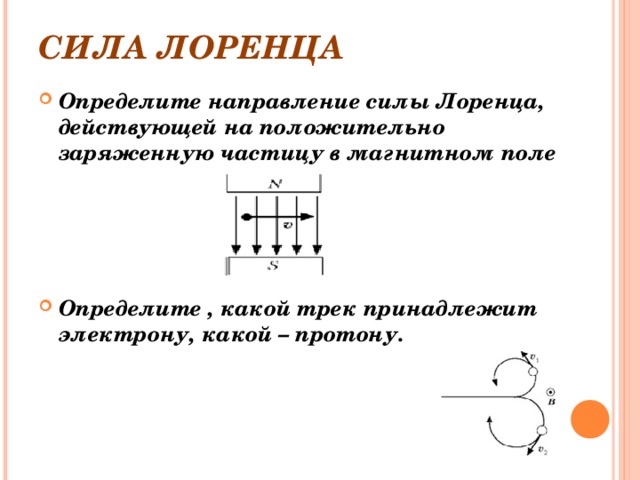 Например, предположим, что вы переводите в новый кадр, перемещающийся на $\mathbf{V}_{o}$ относительно исходного кадра, тогда преобразованные векторы будут:
$$
\начать{выравнивать}
\mathbf{E}’ & = \mathbf{E} + \mathbf{V}_{o} \times \mathbf{B} \tag{0a} \\
\mathbf{B}’ & = \mathbf{B} \tag{0b} \\
\mathbf{v}’ & = \mathbf{v} — \mathbf{V}_{o} \tag{0c}
\end{выравнивание}
$$
Если мы затем поместим их в силу Лоренца, мы найдем:
$$
\начать{выравнивать}
\mathbf{F}’ & = q \left[ \mathbf{E}’ + \mathbf{v}’ \times \mathbf{B}’ \right] \tag{1a} \\
& = q \left[ \left( \mathbf{E} + \mathbf{V}_{o} \times \mathbf{B} \right) + \left( \mathbf{v} — \mathbf{V}_ {o} \right) \times \mathbf{B} \right] \tag{1b} \\
& = q \left[ \mathbf{E} + \mathbf{v} \times \mathbf{B} \right] \tag{1c}
\end{выравнивание}
$$ 9{2} }{ \gamma + 1 } \frac{ \mathbf{V}_{o} }{c } \left( \frac{ \mathbf{V}_{o} }{c } \cdot \mathbf{ B} \справа) \tag{2b}
\end{выравнивание}
$$
в то время как 3-векторная скорость преобразуется в соответствии со сложением скоростей, а $\gamma$ является фактором Лоренца.
Например, предположим, что вы переводите в новый кадр, перемещающийся на $\mathbf{V}_{o}$ относительно исходного кадра, тогда преобразованные векторы будут:
$$
\начать{выравнивать}
\mathbf{E}’ & = \mathbf{E} + \mathbf{V}_{o} \times \mathbf{B} \tag{0a} \\
\mathbf{B}’ & = \mathbf{B} \tag{0b} \\
\mathbf{v}’ & = \mathbf{v} — \mathbf{V}_{o} \tag{0c}
\end{выравнивание}
$$
Если мы затем поместим их в силу Лоренца, мы найдем:
$$
\начать{выравнивать}
\mathbf{F}’ & = q \left[ \mathbf{E}’ + \mathbf{v}’ \times \mathbf{B}’ \right] \tag{1a} \\
& = q \left[ \left( \mathbf{E} + \mathbf{V}_{o} \times \mathbf{B} \right) + \left( \mathbf{v} — \mathbf{V}_ {o} \right) \times \mathbf{B} \right] \tag{1b} \\
& = q \left[ \mathbf{E} + \mathbf{v} \times \mathbf{B} \right] \tag{1c}
\end{выравнивание}
$$ 9{2} }{ \gamma + 1 } \frac{ \mathbf{V}_{o} }{c } \left( \frac{ \mathbf{V}_{o} }{c } \cdot \mathbf{ B} \справа) \tag{2b}
\end{выравнивание}
$$
в то время как 3-векторная скорость преобразуется в соответствии со сложением скоростей, а $\gamma$ является фактором Лоренца. {2} }$ в этом термине.
{2} }$ в этом термине.
$\endgroup$
$\begingroup$
Законы, управляющие электромагнитными явлениями, не инвариантны при преобразовании Галилея, вместо этого они инвариантны при преобразовании Лоренца.
Как только это будет установлено, мы сможем ответить на ваш вопрос: магнитные поля и электрические поля (а также магнитная сила и электрическая сила) действительно зависят от системы отсчета, если вы измените систему отсчета с помощью преобразования Лоренца . Однако комбинированный эффект электрического и магнитного полей (а также сила Лоренца) является , а не зависимым от системы координат при преобразовании Лоренца . Вот почему мы любим говорить о электромагнитных полях , а не об электрическом и магнитном полях по отдельности.
Теперь вопрос: почему мы используем преобразование Лоренца вместо стандартного преобразования Галилея? Что ж, как я упоминал выше, законы электромагнетизма не инвариантны относительно преобразования Галилея; это означает, что у нас возникнут проблемы, если мы не согласимся использовать преобразование Лоренца.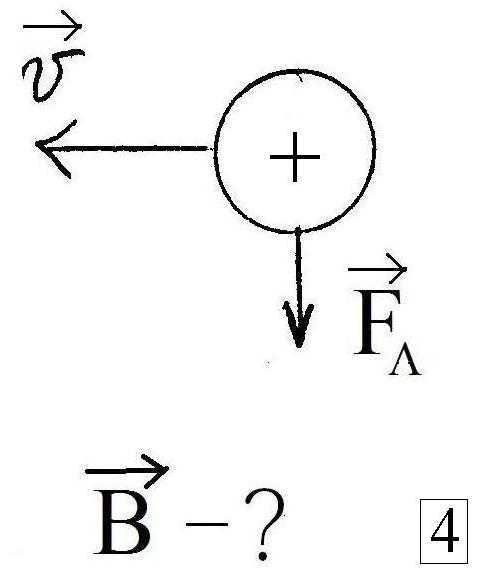 Например, : законы электромагнетизма предсказывают, что скорость света должна быть постоянной в каждой системе отсчета, но это очевидно абсурдно при преобразовании Галилея.
Например, : законы электромагнетизма предсказывают, что скорость света должна быть постоянной в каждой системе отсчета, но это очевидно абсурдно при преобразовании Галилея.
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
электромагнетизм.
 Работа, совершаемая магнитной силой
Работа, совершаемая магнитной силойспросил
Изменено 5 лет, 4 месяца назад
Просмотрено 7к раз
$\begingroup$
Магнитная часть силы Лоренца действует перпендикулярно скорости заряда и, следовательно, совершает над ней нулевую работу. Можем ли мы экстраполировать это утверждение, чтобы сказать, что такая природа силы по существу делает ее соответствующую работу независимой от выбора пути и, следовательно, что магнитная сила консервативна?
- электромагнетизм
- силы
- энергосбережение
- терминология
- работа
$\endgroup$
6
$\begingroup$
Не совсем, потому что магнитная сила зависит от скорости, а не только от положения, так что вы не можете экстраполировать, зная, что интеграл по пути равен нулю, к выводу, что сила есть градиент потенциала.
Что вы можете сделать, так это сделать аналог потенциального аргумента для компонентов импульса, так что магнитное поле представляет собой ротор векторного потенциала. Этот аргумент может быть физически выдвинут в пользу сохранения импульса вокруг пространственно-временной петли, во многом подобно тому, как сохранение энергии следует из интеграла силы вдоль пространственной петли.
Это объясняется здесь: Порождают ли статическое электрическое поле и закон сохранения импульса связь между $E$, $t$ и некоторым путем $s$?
$\endgroup$
$\begingroup$
Работа, совершаемая суммарной магнитной силой, равна нулю. Но одна из его составляющих может быть не нулевой. Как мы видели, когда блок проскальзывает под углом на наклонной плоскости, его нормаль равна нулю, но его горизонтальная составляющая помогает ему двигаться.
$\endgroup$
$\begingroup$
Что ж, работа равна нулю независимо от того, какой путь вы выберете, так что в этом смысле магнитная сила (тривиально) консервативна.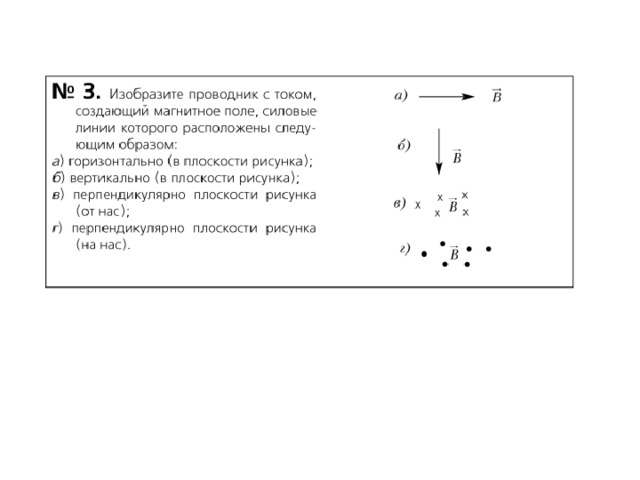
$\endgroup$
1
$\begingroup$
Работа, совершаемая магнитной силой, действительно равна нулю.
$F_m=q[V \times B]$
$dW=q[V \times B].dr =q[V\times B]Vdt=0$ 9B dW=0$$
Работа, совершаемая магнитной силой, не зависит от пути [и равна нулю для всех таких путей]
Однако мы можем иметь следующее интересное соображение:
Пусть $V=V_1+V_2$
[Можно выбрать $V_1$ и $V_2 $ так, чтобы $V_1,V_2$ и $B$ не лежали в одной плоскости]
$dW=0=q[(V_1+V_2)\times B](V_1 +V_2)dt$
$=q[V_1 \times B]V_1+q[V_1 \times B]V_2+q[V_2 \times B]V_1+q[V_2 \times B]V_2$
$0=q [V_1 \times B]V_2+q[V_2 \times B]V_1$
Величины $q[V_1 \times B]V_2 $ и $q[V_2 \times B]V_1$ не могут быть равны нулю по отдельности[учитывая, что $V_1,V_2$ и $B$ не лежат в одной и той же плоскости по нашему выбору], хотя их сумма равна нулю. Мы могли бы подумать об использовании любого из них для какой-то технологической цели.
Мы могли бы подумать об использовании любого из них для какой-то технологической цели.
$\endgroup$
$\begingroup$
Отсюда: http://en.wikipedia.org/wiki/Conservative_force
Многие силы (особенно те, которые зависят от скорости) не являются силовыми полями. В этих случаях три вышеуказанных условия математически не эквивалентны. Например, магнитная сила удовлетворяет условию 2 (поскольку работа, совершаемая магнитным полем над заряженной частицей, всегда равна нулю), но не удовлетворяет условию 3, а условие 1 даже не определено (сила не является векторным полем, поэтому нельзя оценить его завиток). Соответственно, одни авторы классифицируют магнитную силу как консервативную[3], а другие нет[4]. Магнитная сила — необычный случай; большинство сил, зависящих от скорости, таких как трение, не удовлетворяют ни одному из трех условий и, следовательно, однозначно неконсервативны.


 Прямолинейный проводник длины 𝒍 c током I помещён в однородное магнитное поле перпендикулярно линиям индукции В. Как изменится сила Ампера, действующая на проводник, если его длину уменьшить в
Прямолинейный проводник длины 𝒍 c током I помещён в однородное магнитное поле перпендикулярно линиям индукции В. Как изменится сила Ампера, действующая на проводник, если его длину уменьшить в Электрон влетает в однородное магнитное поле с индукцией1,26 мТл перпендикулярно силовым линиям со скоростью 10 Мм/с. Определите радиус окружности, по которой будет двигаться электрон?
Электрон влетает в однородное магнитное поле с индукцией1,26 мТл перпендикулярно силовым линиям со скоростью 10 Мм/с. Определите радиус окружности, по которой будет двигаться электрон?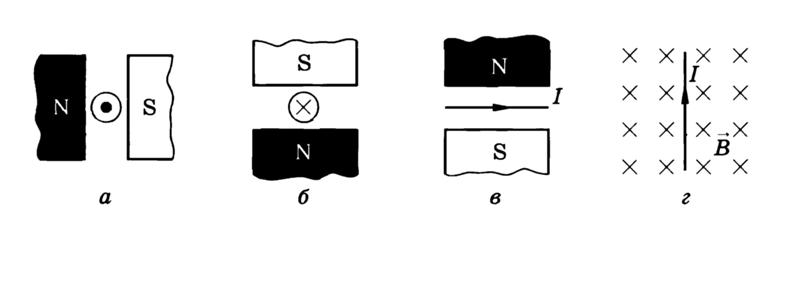 Прямолинейный проводник длиной 50 см, по которому течёт ток 2 А, находится в однородном магнитном поле с индукцией 0,1 Тл. Каков угол между проводником и вектором магнитной индукции, если сила Ампера равна 0,05 Н?
Прямолинейный проводник длиной 50 см, по которому течёт ток 2 А, находится в однородном магнитном поле с индукцией 0,1 Тл. Каков угол между проводником и вектором магнитной индукции, если сила Ампера равна 0,05 Н?
