Ответы@Mail.Ru: Что такое полюс электродвигателя?

Как это у АД нет полюсов? А работает он на внутреннем сгорании, что ли? Понятие полюс АД является величиной расчетной. У асинхронного двигателя число пар полюсов определяется р = (60*f) / n1 или для частоты f = 50 Герц число полюсов соответствует синхронной частоте АД: •2 полюса = ~ 3000 об/мин •4 полюса = ~ 1500 об/мин •6 полюсов = ~ 1000 об/мин •8 полюсов = ~ 750 об/мин Конструктивно число полюсов АД формируется исключительно схемой обмотки статора — числом пазов в статоре и количеством слоев в пазе. У трехфазного АД число пазов в статоре всегда кратно 6. Визуально для трехфазного двигателя число пар полюсов определяется так — достаточно подсчитать число пазов на статоре, поделить на три (фазы) , затем на 2 (пары полюсов) и на число катушечных групп (количества обмоток соединенных последовательно и параллельно — для этого необходимо знать схему обмотки) . У двигателей с состредоточенными обмотками все наглядно. Переключение схем обмоток позволяет изменять число пар полюсов и соответственно скорость двигателя. В последние годы разработаны схемы обмоток, дающие возможность путем переключения катушечных групп изменять числа полюсов и в отношении, отличном от 1:2, с сохранением достаточно высокого обмоточного коэффициента для обеих частот вращения и числа выводных концов обмотки (не более шести) . Особенность этих схем заключается в специфической компоновке катушечных групп из разновитковых катушек, при которой изменение точек подсоединения обмотки к питающей сети приводит не только к изменению полярности отдельных катушечных групп, но и к переключению групп между фазами или даже к отключению отдельных катушек. При переключениях изменяется и амплитуда МДС обмотки при разных числах полюсов, поэтому такой метод построения схем называют полюсно-амплитудной модуляцией (ПАМ) . Для трехскоростных и четырехскоростных асинхронных двигателей используют оба принципа изменения числа полюсов: устанавливают две независимые обмотки, каждая из которых (в четырехскоростных) или одна из них (в трехскоростных двигателях) выполняется полюснопереключаемой.

у ад нет полюсов

<a rel=»nofollow» href=»http://www.electricalschool.info/maschiny/477-ustrojjstvo-jelektrodvigatelja.html» target=»_blank» >Здесь</a>

какие там полюса?

У любого магнита есть пара полюсов. Благодаря электромагнитной индукции АД и работает. Естественно, на каждой фазе возникает пара полюсов- S и N. При увеличении пар полюсов на одной фазе, кратно уменьшается количество оборотов двигателя.

Описание параметра «Количество и тип полюсов»

Согласно ГОСТ Р 51327.1-2010  по числу полюсов и путей тока классифицируют следующие типы устройств:

1p+N — двухполюсный АВДТ с одним защищенным от сверхтоков полюсом;

2p — двухполюсный АВДТ с двумя защищенными от сверхтоков полюсами;

3p — трехполюсный АВДТ с тремя защищенными от сверхтоков полюсами;

3p+N — четырехполюсный АВДТ с тремя защищенными от сверхтоков полюсами;

4p — четырехполюсный АВДТ с четырьмя защищенными от сверхтоков полюсами.

Полюс, который не является защищенным от сверхтоков может быть «незащищенным» полюсом или «полюсом, коммутирующим нейтраль».

 

Стороны света — Википедия

В географии сторона горизонта — одно из четырёх основных направлений (север, юг, запад, восток).

Направления север и юг определяются полюсами Земли, а восток и запад (связанных с вращением планеты вокруг своей оси) — видимым восходом и закатом небесных светил. С древности человек определял примерное южное направление — по положению солнца в зените, восточное — по месту его восхода, а западное — по месту заката; северное направление (в Северном полушарии) определяли по Полярной звезде. На современных географических картах северная сторона обычно находится сверху: в этом случае юг находится снизу, запад — слева, а восток — справа. На старинных, а порой и современных картах, могли располагать вверху юг или восток.

Карты звёздного неба, как правило, изображают так, что небесный свод (небесная сфера) располагается видимой, в отличие от карт земной поверхности, не под, а над наблюдателем. При этом для наблюдателя, смотрящего в направление небесного экватора, впереди будет юг, сзади — север, слева — восток и справа — запад.

При ориентации человека в пространстве также используется принцип четырёх сторон: «впереди», «позади», «слева», «справа». В этом случае направления не фиксированы и выбираются уже относительно самого человека.

Принцип четырёхсторонней ориентации на поверхности был важной вехой в познании человеком окружающего мира. Овеществлён в кресте.

Принцип четырёхкратности отражён в фольклоре, обычаях, религиозных обрядах многих народов, в том числе и славянских:

• «пойти на все четыре стороны»;
• трипольские четырёхчастные жертвенники были точно ориентированы своими четырьмя крестовинами по сторонам света, даже если это направление расходилось с ориентировкой стен дома и т. д.

Кроме разбиения круга на четыре направления — север, юг, запад, восток — по мере развития задач ориентирования вводились дополнительные разбиения с промежуточными направлениями: северо-запад, северо-восток, юго-запад, юго-восток; всего направлений стало восемь. Позже вводились следующие промежуточные разбиения: северо-северо-запад, запад-северо-запад и т. д. с доведением числа направлений до 16. После ещё одного разбиения на промежуточные направления этот процесс завершился с вводом 32 румбов.

Цвета, символизирующие стороны света[править | править код]

Традиционная окраска магнитной стрелки компаса, указывающей на север, красная.

Для обозначения сторон света часто используют 4 латинские буквы: N, S, E, W, (что соответствует первым буквам названий сторон света в английском языке — North, South, East, West) или С, Ю, В, З (что соответствует первым буквам названий сторон света в русском языке — Север, Юг, Восток, Запад).

Помимо этого, в истории российской морской навигации длительное время чаще всего применялись немецкие названия сторон света (также и по сей день используются) — Nord, Süd, Ost, West (Норд, Зюд, Ост, Вест).

Это объясняется, скорее всего, тем, что в Петровскую эпоху — начало XVIII столетия, когда шло зарождение морского флота Российской империи, многие термины в русский язык пришли, как известно, из голландского языка, а там стороны света имеют следующие названия, во многом созвучные родственным им немецким: N — noord (норд), O — oost (ост), Z — zuid (зюйд), W — west (вест).

Понятие полюсов и нулей в передаточных функциях

Добавлено 24 декабря 2019 в 23:34

Сохранить или поделиться

Данная статья объясняет, что такое полюсы и нули, и обсуждает, как полюсы и нули передаточной функции связаны с поведением схем аналоговых фильтров относительно амплитуды и фазы.

В предыдущей статье я представил два стандартных способа представления передаточной функции в s-области для RC фильтра нижних частот первого порядка. Давайте кратко рассмотрим некоторые важные концепции.

• Передаточная функция математически выражает поведение фильтра в частотной области при передаче сигнала от входа к выходу.
• Мы можем написать передаточную функцию относительно переменной s, которая представляет собой комплексную частоту, и мы можем заменить s на jω, когда нам нужно вычислить амплитуду и сдвиг фазы на конкретной частоте.
• Нормированная форма передаточной функции похожа на шаблон, который помогает нам быстро определять определяющие характеристики фильтра.
• Математическое манипулирование нормированной передаточной функцией первого порядка позволяет нам продемонстрировать, что частота среза фильтра – это частота, на которой амплитуда уменьшается на 3 дБ, а фаза сдвигается на –45°.

Полюсы и нули

Предположим, что у нас есть передаточная функция, в которой переменная s появляется как в числителе, так и в знаменателе. В этой ситуации, по крайней мере, одно значение s приведет к тому, что числитель будет равен нулю, и, по крайней мере, одно значение s приведет к тому, что знаменатель будет равен нулю. Значение, при котором числитель равен нулю, является нулем передаточной функции, а значение, которое приводит к нулю в знаменателе, является полюсом передаточной функции.

Давайте рассмотрим следующий пример:

\[T(s)=\frac{Ks}{s+\omega _{0}}\]

В этой системе мы имеем ноль при s = 0 и полюс при s = –ω₀.

Полюсы и нули являются определяющими характеристиками фильтра. Если вы знаете расположение полюсов и нулей, то у вас много информации о том, как система будет реагировать на сигналы с разными входными частотами.

Влияние полюсов и нулей

Диаграмма Боде (логарифмическая амплитудно-частотная характеристика, АЧХ) обеспечивает простую визуализацию взаимосвязи между полюсом или нулем и поведением системы при передаче сигнала от входа к выходу.

Частота полюса соответствует угловой частоте, при которой наклон кривой АЧХ уменьшается на 20 дБ/декада, а ноль соответствует угловой частоте, при которой наклон увеличивается на 20 дБ/декада. В следующем примере амплитудно-частотная характеристика представляет собой аппроксимацию амплитудного отклика системы, которая имеет полюс при 10² радиана в секунду (рад/с) и ноль при 10⁴ рад/с.

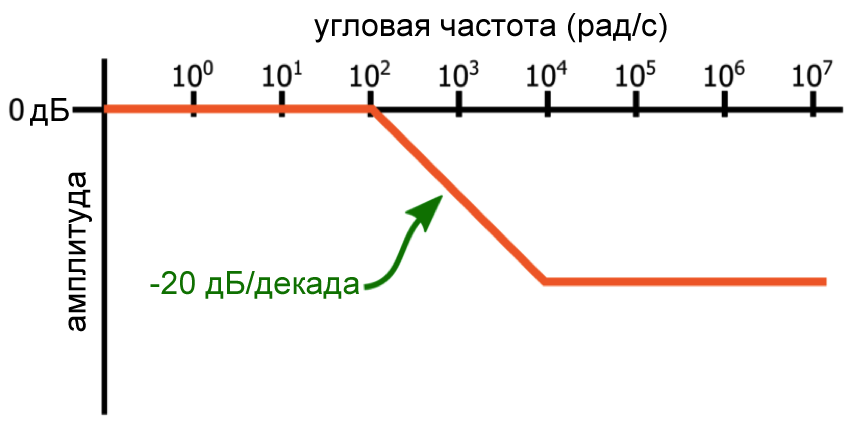Рисунок 1 – Полюс и ноль на логарифмической амплитудно-частотной характеристике

Влияние на фазу

В предыдущей статье мы видели, что математическим источником фазо-частотной характеристики фильтра нижних частот является функция арктангенса. Если мы используем функцию арктангенса (точнее, функцию отрицательного арктангенса), чтобы сгенерировать график зависимости фазы (в градусах) от частоты в логарифмическом масштабе, мы получим следующий график:

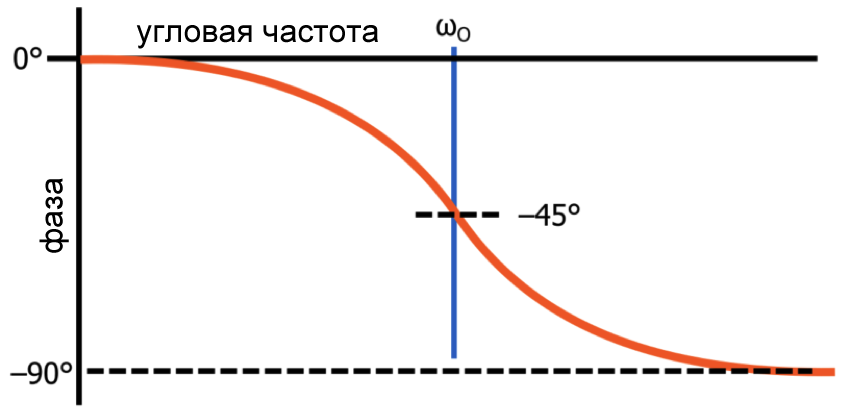Рисунок 2 – Фазо-частотная характеристика ФНЧ первого порядка

Аппроксимация логарифмической фазо-частотной характеристики для сдвига фазы, генерируемого полюсом, представляет собой прямую линию, представляющую сдвиг фазы -90°. Эта линия центрируется на частоте полюса и имеет наклон –45 градусов на декаду, что означает, что наклонная линия начинается за одну декаду до частоты полюса и заканчивается через одну декаду после частоты полюса. Влияние нуля будет таким же, за исключением того, что линия имеет положительный наклон, поэтому итоговый сдвиг фазы составляет +90°.

В следующем примере представлена система, которая имеет полюс при 10² рад/с и ноль при 10⁵ рад/с.

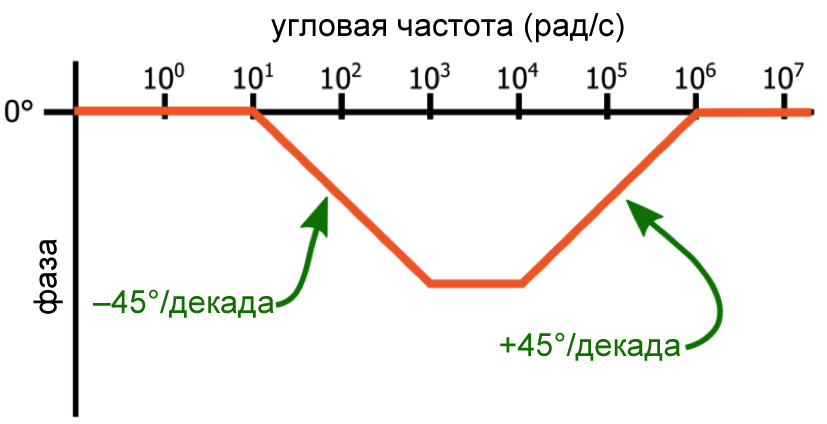Рисунок 3 – Полюс и ноль на логарифмической фазо-частотной характеристике

Скрытый ноль

Если вы читали предыдущую статью, вы знаете, что передаточная функция фильтра нижних частот может быть записана следующим образом:

\[T(s)=\frac{a_0}{s+\omega_0}\]

У этой системы есть ноль? Если мы применим определение, данное ранее в этой статье, мы сделаем вывод, что его нет – переменная s не появляется в числителе, и поэтому никакое значение s не приведет к тому, что числитель станет равным нулю.

Однако оказывается, что у нее на самом деле есть ноль, и чтобы понять почему, нам нужно рассмотреть более обобщенное определение полюсов и нулей передаточной функции: ноль (z от «zero») возникает при значении s, которое заставляет передаточную функцию уменьшаться до нуля, а полюс (p от «pole») возникает при значении s, которое заставляет передаточную функцию стремиться к бесконечности:

\[\lim_{s\rightarrow z}T(s)=0\]

\[\lim_{s\rightarrow p}T(s)=∞\]

Имеет ли фильтр нижних частот первого порядка значение s, которое приводит к T(s) → 0? Да, это так, а именно, s = ∞. Таким образом, система фильтра нижних частот первого порядка имеет полюс в точке ω₀ и ноль в точке ω = ∞.

Я попытаюсь дать физическую интерпретацию нуля при ω = ∞: это указывает на то, что фильтр не может «всегда» продолжать увеличивать ослабление (где «всегда» относится к частоте, а не ко времени). Если вам удастся создать входной сигнал, частота которого продолжает увеличиваться до тех пор, пока она не «достигнет» бесконечности рад/с, то ноль при s = ∞ заставит фильтр прекратить увеличивать ослабление, т.е. наклон амплитудно-частотной характеристики увеличится с –20 дБ/декада до 0 дБ/декада.

Заключение

Мы изучили основные теоретические и практические аспекты полюсов и нулей передаточной функции и увидели, что можем создать прямую связь между частотами полюса и нуля фильтра и его амплитудно-частотной и фазо-частотной характеристиками. В следующей статье мы рассмотрим передаточную функцию фильтра верхних частот первого порядка.

Оригинал статьи:

Теги

АЧХ (амплитудно-частотная характеристика)Передаточная функцияФильтрФНЧ (фильтр нижних частот)ФЧХ (фазо-частотная характеристика)Частота среза

Сохранить или поделиться

НЕБЕСНЫЕ КООРДИНАТЫ • Большая российская энциклопедия

НЕБЕ́СНЫЕ КООРДИНА́ТЫ, чис­ла, опи­сы­ваю­щие по­ло­же­ние све­ти­ла на не­бес­ной сфе­ре. Как пра­ви­ло, ис­поль­зу­ют сфе­рич. сис­те­мы ко­ор­ди­нат, в ко­то­рых по­ло­же­ние на за­дан­ной сфе­ре опи­сы­ва­ет­ся дву­мя уг­ло­вы­ми ве­ли­чи­на­ми. Ес­ли рас­стоя­ния до све­тил из­вест­ны, то при­ме­ни­мы так­же де­кар­то­вы сис­те­мы ко­ор­ди­нат, но обыч­но вме­сто рас­стоя­ния ука­зы­ва­ет­ся па­рал­лакс не­бес­но­го све­ти­ла. При вы­со­ко­точ­ных из­ме­ре­ни­ях тре­бу­ет­ся учи­ты­вать эф­фек­ты об­щей тео­рии от­но­си­тель­но­сти. В этом слу­чае по­ло­же­ние све­ти­ла опи­сы­ва­ет­ся от­но­си­тель­но сис­тем от­счёта, яв­ляю­щих­ся со­во­куп­но­стью ко­ор­ди­нат­ных осей и шка­лы вре­ме­ни (вре­мя рас­смат­ри­ва­ет­ся как чет­вёр­тая ко­ор­ди­на­та не­бес­но­го те­ла).

В за­ви­си­мо­сти от вы­бо­ра на­ча­ла от­счё­та раз­ли­ча­ют сле­дую­щие сис­те­мы Н. к.: то­по­цен­три­че­ские (на­блю­да­тель на­хо­дит­ся на по­верх­но­сти Зем­ли), гео­цен­три­че­ские (на­блю­да­тель – в цен­тре масс Зем­ли), ба­ри­цен­три­че­ские (на­блю­да­тель – в цен­тре масс Сол­неч­ной сис­те­мы) и объ­ек­то­цен­три­че­ские (на­блю­да­тель – в цен­тре масс пла­не­ты, спут­ни­ка и т. п.). Со­от­вет­ст­вен­но в ка­ж­дой сис­теме оп­ре­де­ля­ют­ся шка­лы вре­ме­ни, т. е. вре­мен­нáя ко­ор­ди­на­та. Ма­те­ма­тич. оп­ре­де­ле­ние сис­тем Н. к. и свя­зи ме­ж­ду ни­ми, а так­же оп­ре­де­ле­ние шкал вре­ме­ни и со­от­но­ше­ний ме­ж­ду ни­ми яв­ля­ет­ся за­да­чей сфе­ри­че­ской ас­тро­но­мии. Реа­ли­за­ция сис­тем ко­ор­ди­нат, т. е. при­вяз­ка их к вы­бран­ным не­бес­ным те­лам, – за­да­ча ас­т­ро­мет­рии.

Для оп­ре­де­ле­ния сис­те­мы ко­ор­ди­нат не­об­хо­ди­мо за­дать её на­ча­ло (как пра­ви­ло, это по­ло­же­ние на­блю­да­те­ля) и на­прав­ле­ние осей. За­тем вы­би­ра­ет­ся осн. плос­кость сис­те­мы, про­хо­дя­щая че­рез на­ча­ло ко­ор­ди­нат. От осн. плос­ко­сти от­счи­ты­ва­ет­ся од­на из сфе­рич. ко­ор­ди­нат. Сис­те­мы ко­ор­ди­нат, при­ме­няе­мые в ас­тро­но­мии, по­лу­чи­ли на­зва­ния по осн. плос­ко­сти сис­те­мы: го­ри­зон­таль­ная, эк­ва­то­ри­аль­ная, эк­лип­ти­че­ская и га­лак­ти­че­ская.

Горизонтальная система координат

Системы небесных координат: а – горизонтальная, б – экваториальная, в – эклиптическая, г – галактическая. N, S, W, E – точки севера, юга, запада, востока; Z – зенит…

Вы­бран­ным на­прав­ле­ни­ем в этой сис­те­ме яв­ля­ет­ся на­прав­ле­ние от­вес­ной ли­нии; осн. плос­кость сис­те­мы пер­пен­ди­ку­ляр­на от­вес­ной ли­нии. Н. к. све­ти­ла в этой сис­те­ме яв­ля­ют­ся зе­нит­ное рас­стоя­ние $z$ и ази­мут $A$ (рис., а). Вме­сто $z$ час­то ис­поль­зу­ет­ся др. ко­ор­ди­на­та: вы­со­та $h$ све­ти­ла над го­ри­зон­том, при­чём $z+h=90°$. Ес­ли све­ти­ло на­хо­дит­ся над го­ри­зон­том, то его зе­нит­ное рас­стоя­ние из­ме­ня­ет­ся от 0° (све­ти­ло в зе­ни­те) до 90° (све­ти­ло в плос­ко­сти го­ри­зон­та). Ес­ли $z>90°$ ($h<0°$), то го­во­рят, что све­ти­ло на­хо­дит­ся под го­ри­зон­том; в этом слу­чае оно, как пра­ви­ло, не­ви­ди­мо для на­блю­да­те­ля.

Под ази­му­том в ас­тро­но­мии по­ни­ма­ет­ся дву­гран­ный угол ме­ж­ду вер­ти­каль­ным кру­гом, про­хо­дя­щим че­рез точ­ки се­ве­ра $N$ и юга $S$ (не­бес­ным ме­ри­диа­ном), и вер­ти­ка­лом све­ти­ла. Ази­мут мо­жет от­счи­ты­вать­ся от точ­ки юга $S$ в на­прав­ле­нии на за­пад $W$ (по ча­со­вой стрел­ке) от 0° до 360° или от точ­ки се­ве­ра $N$ на вос­ток $E$ от 0° до 360°; ино­гда ази­мут из­ме­ря­ет­ся в пре­де­лах от –180° до 180°.

Экваториальная система координат

Осн. плос­кость сис­те­мы – плос­кость не­бес­но­го эк­ва­то­ра, пер­пен­ди­ку­ляр­ная оси вра­ще­ния Зем­ли. Н. к. све­ти­ла в этой сис­те­ме яв­ля­ют­ся скло­не­ние $δ$ и пря­мое вос­хо­ж­де­ние $α$ (рис., б).

Скло­не­ние $δ$ от­счи­ты­ва­ет­ся от плос­ко­сти не­бес­но­го эк­ва­то­ра; $δ$ по­ло­жи­тель­но, ес­ли све­ти­ло на­хо­дит­ся в Сев. по­лу­ша­рии не­бес­ной сфе­ры, и от­ри­ца­тель­но, ес­ли – в Юж­ном, т. е. из­ме­ня­ет­ся в пре­де­лах от –90° до 90°. Ино­гда вме­сто скло­не­ния ис­поль­зу­ет­ся по­ляр­ное рас­стоя­ние $p$, ко­то­рое от­счи­ты­ва­ет­ся от сев. по­лю­са ми­ра $P_N$ и из­ме­ня­ет­ся в пре­де­лах от 0° до 180°, при­чём $p + \delta$ = 90°.

Вы­бор на­ча­ла от­счё­та пря­мых вос­хо­ж­де­ний про­из­во­лен, т. к. в плос­ко­сти не­бес­ного эк­ва­то­ра нет ни­ка­ко­го вы­де­лен­но­го на­прав­ле­ния. Пря­мое вос­хо­ж­де­ние от­счи­ты­ва­ет­ся от точ­ки ве­сен­не­го рав­но­ден­ст­вия ♈ про­тив ча­со­вой стрел­ки, ес­ли смот­реть с сев. по­лю­са ми­ра, и из­ме­ня­ет­ся в пре­де­лах от 0^h до 24^h или от 0° до 360°.

В 1998 Ме­ж­ду­нар. ас­тро­но­мич. сою­зом в ос­но­ву оп­ре­де­ле­ния Н. к. све­ти­ла был по­ло­жен ка­та­лог вне­га­лак­тич. ра­дио­ис­точ­ни­ков. За на­ча­ло от­счё­та пря­мых вос­хо­ж­де­ний взя­та точ­ка, близ­кая к ди­на­мич. рав­но­ден­ст­вию на эпо­ху J2000,0 (это сде­ла­но под­гон­кой пря­мо­го вос­хож­де­ния ква­за­ра 3C273B к зна­че­нию в сис­те­ме фун­дам. ка­та­ло­га FK5). При та­ком оп­ре­де­ле­нии точ­ка ве­сен­не­го рав­но­ден­ст­вия уже не при­вя­за­на к по­ло­же­нию эк­лип­ти­ки; её ста­биль­ность в про­стран­ст­ве объ­яс­ня­ет­ся от­сут­ст­ви­ем соб­ст­вен­но­го дви­же­ния ква­за­ров (из-за их уда­лён­но­сти).

В ка­че­ст­ве вто­рой ко­ор­ди­на­ты в этой сис­те­ме мо­жет ис­поль­зо­вать­ся ча­со­вой угол $t$, от­счи­ты­вае­мый от наи­выс­шей точ­ки $B$ не­бес­но­го эк­ва­то­ра по ча­со­вой стрел­ке, ес­ли смот­реть с сев. по­лю­са ми­ра, и из­ме­няю­щий­ся в тех же пре­де­лах, что и $α$. Сис­те­ма ко­ор­ди­нат, за­да­вае­мая ча­со­вым уг­лом и скло­не­ни­ем, яв­ля­ет­ся ле­вой.

Эклиптическая система координат

Эту сис­те­му ко­ор­ди­нат ис­поль­зу­ют, как пра­ви­ло, при изу­че­нии дви­же­ния тел Сол­неч­ной сис­те­мы, т. к. плос­ко­сти ор­бит боль­шин­ст­ва тел Сол­неч­ной сис­те­мы на­кло­не­ны к плос­ко­сти эк­лип­ти­ки под ма­лы­ми уг­ла­ми. Осн. кру­га­ми в эк­лип­тич. сис­те­ме ко­ор­ди­нат (рис., в) яв­ля­ют­ся плос­кость эк­лип­ти­ки и круг ши­ро­ты (боль­шой круг не­бес­ной сфе­ры, про­хо­дя­щий че­рез северный $П_N$ и южный $П_S$ по­лю­сы эк­лип­ти­ки и све­ти­ло). Н. к. све­ти­ла в этой сис­те­ме яв­ля­ют­ся эк­лип­тич. ши­ро­та и дол­го­та. Эк­лип­тич. ши­ро­та $β$ – это ду­га кру­га ши­ро­ты, от­счи­ты­вае­мая от плос­ко­сти эк­лип­ти­ки до све­ти­ла; она по­ло­жи­тель­на в Се­вер­ном и от­ри­ца­тель­на в Юж. по­лу­ша­рии не­бесной сфе­ры: $–90°⩽β⩽90°$. Эк­лип­тич. дол­го­та $λ$ – это дву­гран­ный угол ме­ж­ду боль­шим кру­гом, про­хо­дя­щим че­рез по­лю­сы эк­лип­ти­ки и точ­ку ве­сен­не­го рав­но­ден­ст­вия, и кру­гом ши­ро­ты. Дол­го­та от­счи­ты­ва­ет­ся от точ­ки ве­сен­не­го рав­но­ден­ст­вия про­тив ча­со­вой стрел­ки, ес­ли смот­реть с сев. по­лю­са эк­лип­ти­ки: $0°⩽λ⩽360°$.

Галактическая система координат

Эта сис­те­ма ко­ор­ди­нат час­то ис­поль­зу­ет­ся в за­да­чах звёзд­ной ди­на­ми­ки. За осн. плос­кость сис­те­мы при­ня­та плос­кость га­лак­тич. дис­ка; её по­ло­же­ние за­да­ёт­ся ко­ор­ди­на­та­ми од­но­го из по­лю­сов га­лак­ти­ки. В на­стоя­щее вре­мя га­лак­тич. сис­те­ма ко­ор­ди­нат оп­ре­де­ля­ет­ся по дан­ным, по­лу­чен­ным кос­мич. мис­си­ей Hipparcos (Ев­роп. кос­мич. агент­ст­во, 1989–93), по­зво­лив­шей оп­ре­де­лить ас­т­ро­мет­рич. па­ра­мет­ры 118 тыс. звёзд. Сев. по­люс Га­лак­ти­ки $G_N$ (рис., г) на эпо­ху J2000,0 име­ет сле­дую­щие эк­ва­то­ри­аль­ные ко­орди­на­ты: $α=192,85948°$, $δ=27,12825°$; диа­мет­раль­но про­ти­во­по­лож­ная точ­ка не­бес­ной сфе­ры счи­та­ет­ся юж. по­лю­сом Га­лак­ти­ки. Боль­шой круг, пер­пен­ди­ку­ляр­ный ли­нии, со­еди­няю­щей по­лю­сы, на­зы­ва­ет­ся га­лак­тич. эк­ва­то­ром. Боль­шой круг, про­хо­дя­щий че­рез све­ти­ло и по­лю­сы Га­лак­ти­ки, на­зы­ва­ет­ся кру­гом га­лак­тич. ши­ро­ты. Ду­га это­го кру­га от эк­ва­то­ра до све­ти­ла на­зы­ва­ет­ся га­лак­тич. ши­ро­той $b$ све­ти­ла. Га­лак­тич. ши­ро­та по­ло­жи­тель­на в Сев. по­лу­ша­рии (со­дер­жа­щем точ­ку $G_N$) и от­ри­ца­тель­на в Юж­ном: $–90°⩽b⩽90°$. Га­лак­тич. дол­го­та $l$ ра­нее от­счи­ты­ва­лась от точ­ки пе­ре­се­че­ния га­лак­тич. и не­бес­но­го эк­ва­то­ров ♌ , пря­мое вос­хо­ж­де­ние ко­то­рой рав­ня­лось $18^h50^m$. Ны­не га­лак­тич. дол­го­та от­счи­ты­ва­ет­ся от на­прав­ле­ния на центр Га­лак­ти­ки (на­прав­ле­ние х на рис., г), ко­то­рое оп­ре­де­ля­ет­ся че­рез га­лак­тич. дол­го­ту вос­хо­дя­ще­го уз­ла га­лак­тич. эк­ва­то­ра, рав­ную $l_♌=32,93192°$. Га­лак­тич. дол­го­та от­счи­ты­ва­ет­ся от 0° до 360° про­тив ча­со­вой стрел­ки, ес­ли смот­реть с сев. по­лю­са Га­лак­ти­ки.

Объектоцентрические системы координат

Эти сис­те­мы ис­поль­зу­ют при про­ве­де­нии на­блю­де­ний с др. пла­не­ты, с бор­та кос­мич. ап­па­ра­та или лю­бо­го др. те­ла. Осн. плос­кость сис­те­мы и её по­лю­сы свя­зы­ва­ют с тем те­лом, с ко­то­ро­го про­во­дят­ся на­блю­де­ния. Как пра­ви­ло, это плос­кость ор­би­ты или плос­кость эк­ва­то­ра (пер­пен­ди­ку­ляр­ная оси вра­ще­ния те­ла). Сис­те­ма ко­ор­ди­нат мо­жет так­же за­да­вать­ся ося­ми сис­те­мы ста­би­ли­за­ции кос­мич. ап­па­ра­та. Од­на из ко­ор­ди­нат, напр. ор­ди­на­та, есть ду­га боль­шо­го кру­га (кру­га ор­ди­нат), про­хо­дя­ще­го че­рез по­лю­сы сис­те­мы и све­ти­ло, от осн. плос­ко­сти до све­ти­ла. Вто­рая ко­ор­ди­на­та (абс­цис­са) – это дву­гран­ный угол ме­ж­ду боль­шим кру­гом, про­хо­дя­щим че­рез по­лю­сы сис­те­мы и точ­ку на­ча­ла от­счё­та абс­цисс, и кру­гом ор­ди­нат. Вы­бор на­ча­ла от­счё­та абс­цисс в прин­ци­пе про­из­во­лен и про­из­во­дит­ся с учё­том удоб­ст­ва об­ра­бот­ки на­блю­де­ний.

Основные точки и линии Небесной сферы

1. 3енит и горизонт. Отвесная линия, проходящая через глаз наблюдателя, пересекает небесную сферу в точке зенита. Зенит есть наивысшая точка над головой наблюдателя. Плоскость, перпендикулярная к отвесной линии, называется горизонтальной плоскостью.

Математическим горизонтом называется линия пересечения небесной сферы с горизонтальной плоскостью, проходящей через центр небесной сферы. Плоскость горизонта можно определить при помощи уровня. Видимый же горизонт ограничен линией, по которой, как нам кажется, небо «сходится» с Землей.

2. Полюсы и ось мира. Присматриваясь к ночному небу, мы замечаем, что звезды в течение суток описывают тем большие круги, чем дальше от Полярной звезды они находятся. Полярная звезда в течение суток описывает очень небольшой кружок и всегда видна почти на одной и той же высоте над горизонтом, в северной стороне неба. На рисунке 5 показано изменение в течение суток положения Большой Медведицы относительно горизонта и неизменность положения Полярной звезды. Попробуйте сами убедиться в том, что это так.

На рисунке 12 показано суточное вращение небесной сферы. Снимок получен так: фотоаппарат, установленный «на бесконечность», направили на Полярную звезду и хорошо укрепили. Оставив аппарат с открытым затвором в этом положении на один час, проявили снимок. На фотографической пластинке (негативе) обнаружились черные следы звезд (на позитиве — светлые). Все они имеют вид концентрических дуг. В центре их лежит центр вращения небесной сферы.

Рисунок 12 — Фотография полярной области неба, полученная неподвижным аппаратом за один час.

Центр вращения южного полушария неба находится в точке, противоположной центру вращения северного небесного полушария. Но ведь в центре небесной сферы находится наш глаз. Следовательно, небесная сфера вращается как одно целое вокруг некоторой оси, проходящей через наш глаз. Ось суточного вращения небесной сферы называется осью мира.

Точки пересечения небесной сферы с осью мира называются полюсами мира. Полярная звезда расположена вблизи северного полюса мира (на расстоянии около 1°). Южный полюс мира находится в южном полушарии небесной сферы. Вблизи него никакой яркой звезды нет.

3. Небесный экватор. Плоскость, перпендикулярная к оси мира и проходящая через центр небесной сферы, называется плоскостью небесного экватора, а линия пересечения ее с небесной сферой — небесным экватором.

Небесный экватор делит небесную сферу на два полушария — северное и южное. Мы видим, что ось мира, полюсы мира и небесный экватор аналогичны оси, полюсам и экватору Земли. Да это и естественно, так как перечисленные названия связаны с видимым вращением небесной сферы, а оно само есть следствие действительного вращения земного шара.

4. Небесный меридиан и полуденная линия. Плоскостью небесного меридиана называется плоскость, проходящая через точку зенита, центр небесной сферы и полюс мира. Пересекаясь с небесной сферой, эта плоскость образует линию небесного меридиана. Вертикальная плоскость, проходящая через Полярную звезду и через наблюдателя, приблизительно будет плоскостью меридиана. В любом месте Земли плоскость небесного меридиана совпадает с плоскостью географического меридиана этого же места.

Полуденной линией называется линия пересечения плоскостей меридиана и горизонта. Эта линия названа так потому, что в полдень тени от вертикальных предметов падают как раз по этому направлению. Практически полуденную линию можно проводить на Земле или на горизонтальной плоскости, отмечая в полдень направление тени от вертикального стержня.

5. Точки горизонта. Горизонт пересекается с небесным меридианом в точках севера N и юга S, а с небесным экватором — в точках востока Е и запада W. Если мы встанем лицом к полюсу мира (к Полярной звезде), то на горизонте прямо под ним будем иметь точку севера, за спиной — точку юга, справа — точку востока и слева — точку запада. Помня это, мы всегда сможем ориентироваться на местности.

Чтобы яснее представить себе все, что было здесь сказано, изобразим небесную сферу на чертеже (Рисунок 13).

Рисунок 13 — Основные точки и линии небесной сферы.

На этом чертеже С — центр небесной сферы, в котором находится глаз наблюдателя, ZCZ’ — отвесная линия, Z — зенит, Z’ — надир (противоположная зениту точка небесной сферы),

РР — ось мира, Р — северный полюс мира, Р’ — южный полюс мира, EAWQ — небесный экватор, плоскость которого перпендикулярна к оси мира, ESWN — горизонт, S — точка юга, N — точка севера, Е — точка востока и W — точка запада. Легко понять, что над горизонтом видна ровно половина небесной сферы и половина небесного экватора, а также то, что в точках Е и W (отстоящих от точек S и N на 90°) горизонт и экватор, пересекаясь, делят друг друга пополам.

Линия NS есть полуденная линия, а большой круг NPZASP’ — небесный меридиан.

Необходимо научиться чертить небесную сферу. Угол между осью мира и плоскостью горизонта на чертеже можно брать каким угодно. Как мы потом увидим, этот угол зависит от местонахождения наблюдателя на земном шаре.

Введенные в этом параграфе определения необходимы для практических применений астрономии.

6. Линии небесной сферы и Земля. Наблюдателю, находящемуся на Земле в какой-либо точке С (Рисунок 14), кажется, что звездное небо вращается вокруг оси, проходящей через него самого и параллельной оси вращения Земли. Ось вращения небесной сферы СР мы назвали осью мира и теперь видим, что она для всякого наблюдателя параллельна оси вращения Земли. Для наблюдателей, находящихся на полюсах Земли, ось вращения Земли и ось мира совпадают.

Ось вращения Земли и параллельная ей ось мира направлены к Полярной звезде, поскольку Полярная звезда находится от нас очень далеко и направления на нее для всех наблюдателей на Земле практически параллельны друг другу.

Плоскость небесного экватора CEAW, перпендикулярная к оси мира, параллельна плоскости земного экватора. Для наблюдателя, находящегося на экваторе Земли, эти плоскости совпадают.

Если считать Землю шаром, то отвесная линия CZ является продолжением радиуса Земли ОС, проведенного из ее центра в точку, где находится наблюдатель. Поэтому плоскость горизонта, проходящая через центр небесной сферы (через точку С), является плоскостью, касательной к земному шару в точке С. Плоскости небесного и географического меридианов совпадают.

Рисунок 14 — Соотношение между линиями и плоскостями небесной сферы и Земли.

Наблюдатель вращается вместе с Землей, а с ним и его небесная сфера. Поэтому горизонт в равное время суток проходит через разные части звездного неба. Разные светила будут и в зените. Небесный экватор скользит в своей плоскости, а ось мира остается параллельной самой себе. Звезды, занимая неизменное положение относительно друг друга и экватора, движутся в плоскостях, параллельных плоскости небесного экватора.

Небесная сфера — Википедия

Небе́сная сфе́ра — воображаемая сфера произвольного радиуса, на которую проецируются небесные тела: служит для решения различных астрометрических задач. За центр небесной сферы принимают глаз наблюдателя; при этом наблюдатель может находиться как на поверхности Земли, так и в других точках пространства (например, он может быть отнесён к центру Земли). Для наземного наблюдателя вращение небесной сферы воспроизводит суточное движение светил на небе.

Каждому небесному светилу соответствует точка небесной сферы, в которой её пересекает прямая, соединяющая центр сферы с центром светила. При изучении положений и видимых движений светил на небесной сфере выбирают ту или иную систему сферических координат. Расчёты положений светил на небесной сфере производятся с помощью небесной механики и сферической тригонометрии и составляют предмет сферической астрономии.

Представление о небесной сфере возникло в глубокой древности; в основу его легло зрительное впечатление о существовании куполообразного небесного свода. Это впечатление связано с тем, что в результате огромной удалённости небесных светил человеческий глаз не в состоянии оценить различия в расстояниях до них, и они представляются одинаково удалёнными. У древних народов это ассоциировалось с наличием реальной сферы, ограничивающей весь мир и несущей на своей поверхности многочисленные звёзды. Таким образом, в их представлении небесная сфера была важнейшим элементом Вселенной. С развитием научных знаний такой взгляд на небесную сферу отпал. Однако заложенная в древности геометрия небесной сферы в результате развития и совершенствования получила современный вид, в котором и используется в астрометрии.

Отвесная линия и связанные с ней понятия[править | править код]

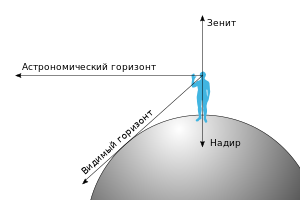Диаграмма, показывающая соотношение зенита, надира и горизонта (в различных определениях). Заметим, что зенит противоположен надиру.

Отве́сная ли́ния (или вертика́льная ли́ния) — прямая, проходящая через центр небесной сферы и совпадающая с направлением нити отвеса в месте наблюдения. Отвесная линия пересекается с поверхностью небесной сферы в двух точках — зените над головой наблюдателя и надире под ногами наблюдателя.

Истинный (математический, или астрономический) горизонт — большой круг небесной сферы, плоскость которого перпендикулярна к отвесной линии. Истинный горизонт делит поверхность небесной сферы на две полусферы: видимую полусферу с вершиной в зените и невидимую полусферу с вершиной в надире. Истинный горизонт не совпадает с видимым горизонтом вследствие приподнятости точки наблюдения над земной поверхностью, а также по причине искривления лучей света в атмосфере.

Круг высоты, или вертикал, светила — большой полукруг небесной сферы, проходящий через светило, зенит и надир. Альмукантара́т (араб. «круг равных высот») — малый круг небесной сферы, плоскость которого параллельна плоскости математического горизонта. Круги высоты и альмукантараты образуют координатную сетку, задающую горизонтальные координаты светила.

Суточное вращение небесной сферы и связанные с ним понятия[править | править код]

Ось мира — воображаемая линия, проходящая через центр мира, вокруг которой происходит вращение небесной сферы. Ось мира пересекается с поверхностью небесной сферы в двух точках — северном полюсе мира и южном полюсе мира. Вращение небесной сферы происходит против часовой стрелки вокруг северного полюса, если смотреть на небесную сферу изнутри.

Небесный экватор — большой круг небесной сферы, плоскость которого перпендикулярна оси мира и проходит через центр небесной сферы. Небесный экватор делит небесную сферу на два полушария: северное и южное.

Круг склонения светила — большой круг небесной сферы, проходящий через полюсы мира и данное светило.

Суточная параллель — малый круг небесной сферы, плоскость которого параллельна плоскости небесного экватора. Видимые суточные движения светил совершаются по суточным параллелям. Круги склонения и суточные параллели образуют на небесной сфере координатную сетку, задающую экваториальные координаты светила.

Термины, рождаемые в пересечениях понятий «Отвесная линия» и «Вращение небесной сферы»[править | править код]

Небесный экватор пересекается с математическим горизонтом в точке востока и точке запада. Точкой востока называется та, в которой точки вращающейся небесной сферы восходят из-за горизонта. Полукруг высоты, проходящий через точку востока, называется первым вертикалом.

Небесный меридиан — большой круг небесной сферы, плоскость которого проходит через отвесную линию и ось мира. Небесный меридиан делит поверхность небесной сферы на два полушария: восточное полушарие и западное полушарие.

Полуденная линия — линия пересечения плоскости небесного меридиана и плоскости математического горизонта. Полуденная линия и небесный меридиан пересекают математический горизонт в двух точках: точке севера и точке юга. Точкой севера называется та, которая ближе к северному полюсу мира.

Годовое движение Солнца по небесной сфере и связанные с ним понятия[править | править код]

P,P’ — полюсы мира, T,T’ — точки равноденствия, E,C — точки солнцестояния, П,П’ — полюса эклиптики, PP’ — ось мира, ПП’ — ось эклиптики, ATQT’- небесный экватор, ETCT’ — эклиптика

Эклиптика — большой круг небесной сферы, по которому происходит видимое годовое движение Солнца. Плоскость эклиптики пересекается с плоскостью небесного экватора под углом ε = 23°26′.

Две точки, в которых эклиптика пересекается с небесным экватором, называются точками равноденствия. В точке весеннего равноденствия Солнце в своём годовом движении переходит из южного полушария небесной сферы в северное; в точке осеннего равноденствия — из северного полушария в южное. Прямая, проходящая через эти две точки, называется линией равноденствий^[1]. Две точки эклиптики, отстоящие от точек равноденствия на 90° и тем самым максимально удалённые от небесного экватора, называются точками солнцестояния. Точка летнего солнцестояния находится в северном полушарии, точка зимнего солнцестояния — в южном полушарии. Эти четыре точки обозначаются символами зодиака, соответствующими созвездиям, в которых они находились во времена Гиппарха^[2] (в результате предварения равноденствий эти точки сместились и ныне находятся в других созвездиях): весеннего равноденствия — знаком Овна (♈), осеннего равноденствия — знаком Весов (♎), зимнего солнцестояния — знаком Козерога (♑), летнего солнцестояния — знаком Рака (♋)^[3].

Ось эклиптики — диаметр небесной сферы, перпендикулярный плоскости эклиптики. Ось эклиптики пересекается с поверхностью небесной сферы в двух точках — северном полюсе эклиптики, лежащем в северном полушарии, и южном полюсе эклиптики, лежащем в южном полушарии. Северный полюс эклиптики имеет экваториальные координаты R.A. = 18^h00^m, Dec = +66°33′, и находится в созвездии Дракона, а южный полюс — R.A. = 6^h00^m, Dec = −66°33′ в созвездии Золотой Рыбы.

Круг эклиптической широты, или просто круг широты — большой полукруг небесной сферы, проходящий через полюсы эклиптики.