Импульс. RC и RL цепи
Всем доброго времени суток. Сегодняшний мой пост начинает серию статей про импульсные устройства. Такие устройства предназначены для формирования и преобразования электрических сигналов, имеющих характер импульсов и перепадов напряжений. К импульсным устройствам относятся все цифровые микросхемы и некоторые аналоговые, например, микросхемы генераторов и компараторов. Ранее я рассматривал один из основных элементов импульсных устройств – транзистор, работающий в ключевом режиме.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Формы импульса (слева направо): прямоугольная, трапецеидальная, пилообразная, экспоненциальная.
В радиоэлектронике используются импульсы самых разнообразных форм, но наиболее распространённые это: прямоугольные, трапецеидальные, пилообразные и экспоненциальные формы импульсов. Форма любого импульса характеризуется следующими основными параметрами:
- амплитуда (максимальное значение) импульса, U
- начальное значение импульса, U0;
- длительность импульса, tи;
- длительность переднего фронта (или просто фронта) импульса, tф;
- длительность заднего фронта (или среза) импульса, tс;
- длительность вершины импульса, tв;
- снижение вершины импульса, Δu;
- крутизна фронта импульса (скорость изменения напряжения при формировании переднего или заднего фронта).

В случае использовании периодичности повторяющихся импульсов имеют большое значение такие параметры, как скважность импульсов (ξ или S), коэффициент заполнения импульсов (η или D), частота повторения импульсов (f) и период повторения импульсов (T). Данные параметры имеют следующие соотношения между собой
Форма реального импульса
Временные параметры импульса (tи, tф, tс, tв) имеют точное значение только в случае идеального импульса, а в реальности лишь в некоторой степени имеют приближённое значение. Поэтому временные параметры отсчитываются от некоторых приближённых величин, которые в достаточной для практики точности имеют значения 0,05 и 0,95. Поясню на примере формы реального импульса, изображённого выше: при определении длительности фронта (t В случае длительности среза, соответственно, начало – 0,95*Um, а окончание – 0,05*Um.
В случае длительности среза, соответственно, начало – 0,95*Um, а окончание – 0,05*Um.
Переходный процесс
Рассмотрение импульсных устройств и схем не возможно без представлении о переходном процессе. Он возникает в цепях при различных коммутациях, то есть при включении или выключении элементов схемы, источников напряжения, при коротких замыканиях отдельных цепей и т.д. Переходный процесс объясняется тем, что энергия электромагнитных полей, связанных с цепью, в разные промежутки времени неодинакова, а резкое изменение энергии невозможно из-за ограниченной мощности источников питания.
Исходя из вышесказанного, можно сделать вывод, что напряжение на ёмкости и ток в индуктивность не могут изменяться скачкообразно, так как данные параметры определяют энергию электрического поля конденсатора и магнитного поля катушки индуктивности.
Таким образом, можно сделать вывод, что при рассмотрении импульсных схем наибольшее внимание необходимо обратить на цепи, представляющие собой комбинации резисторов и конденсаторов или резисторов и катушек индуктивностей (RC- и RL-цепей).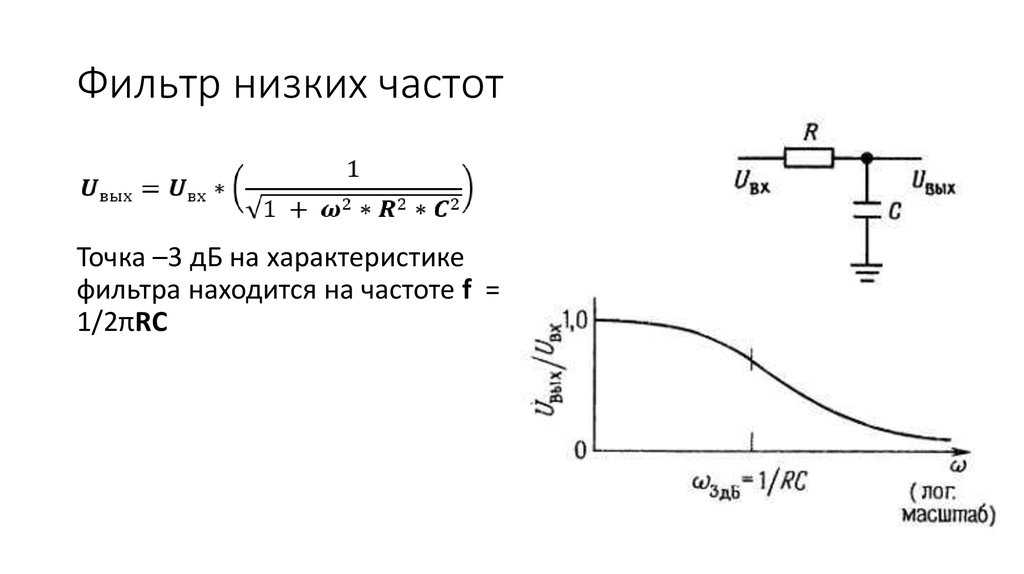 Такие цепи применяются непосредственно для формирования импульсов, а также являются важнейшими элементами релаксационных генераторов, триггеров и других устройств. Поэтому ниже рассмотрим основные свойства элементарных RC- и RL-цепей, а также изменение формы импульсов при прохождении через эти цепи.
Такие цепи применяются непосредственно для формирования импульсов, а также являются важнейшими элементами релаксационных генераторов, триггеров и других устройств. Поэтому ниже рассмотрим основные свойства элементарных RC- и RL-цепей, а также изменение формы импульсов при прохождении через эти цепи.
Влияние RC- и RL-цепей на импульсы различной формы
Несмотря на то, что формы электрических импульсов довольно разнообразны, их можно представить в виде суммы элементарных (типовых) напряжений трёх форм: скачкообразного, линейно изменяющегося и экспоненциального. Поэтому рассмотрим воздействие различных форм напряжений на RC- и RL-цепи.
Изображение RC- и RL-цепей.
Элементарные формы напряжения (сверху вниз): ступенчатое, линейно-изменяющееся, экспоненциальное.
Ступенчатое изменение напряжения. При подключении RC-цепи к источнику постоянного напряжения uвх = Е = const, напряжения на конденсаторе и резисторе будет изменяться по экспоненциальному закону:
где е – математическая постоянная, е = 2,72;
t – время, с;
τ – постоянная времени, с. {- \frac{t}{\tau_{1}}})[/math]
{- \frac{t}{\tau_{1}}})[/math]
Временные диаграммы для uR представлены ниже при различных значениях q. При больших значениях q, то есть постоянной времени цепи τ, формы напряжений uR близки к формам, соответствующим ступенчатому изменению входного напряжения. При уменьшении τ, кроме сокращения длительности спада напряжения uR, уменьшается и максимальное значение uR.
Временные диаграммы напряжений на резисторе RC-цепи при различных значениях
q = τ/τ1.
Формулы и временные диаграммы для напряжений на выходе RL-цепи оказываются такими же, как и для RC-цепи.
Дифференцирующие цепи
Довольно часто в электронике вообще, а в импульсной в частности требуется преобразовать один вид импульсов в другой (например, прямоугольный преобразовать в треугольный). Для этой цели используют различные схемы, в основе которых простейшие RC- и RL-цепи. Такие цепи называются дифференцирующими и интернирующими цепями.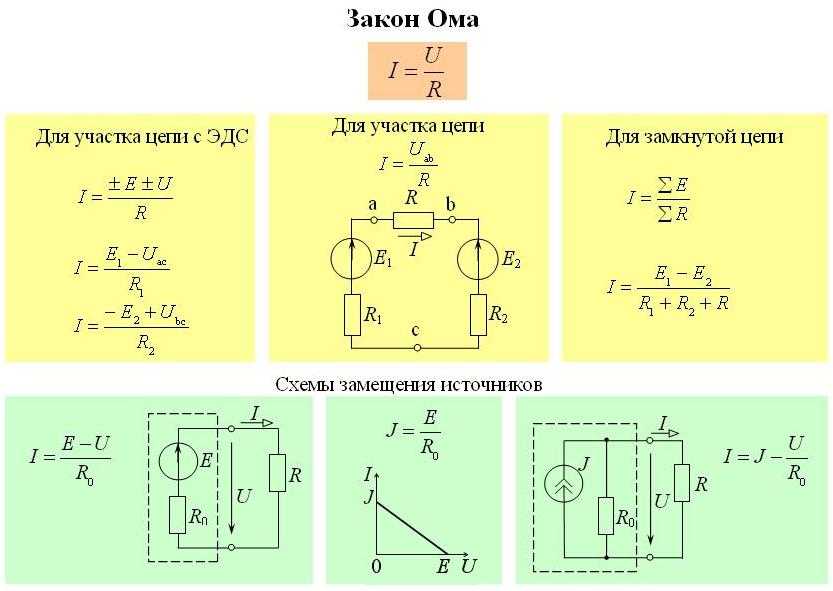 Для начала рассмотрим дифференцирующие цепи, которые показаны на изображении ниже.
Для начала рассмотрим дифференцирующие цепи, которые показаны на изображении ниже.
Своё название дифференцирующие цепи получили от того, что напряжение на выходе такой цепи пропорционально производной входного напряжения, а нахождение производной в математике называется дифференцирование. В случае RC-цепи напряжение снимается с резистора, а в случае RL-цепи – с индуктивности.
Простейшие .
В настоящее время большинство дифференцирующих цепей основаны на RC-цепях, поэтому будем рассматривать их, но все основные выкладки соответствуют также и RL-цепям.
Рассмотрим, как дифференцирующая цепь будет реагировать на прямоугольный импульс. Прямоугольный импульс представляет собой как бы два скачка напряжения. Реакцию RC-цепи на скачкообразное изменение напряжения рассматривалась выше, а в случае прямоугольного импульса выходное напряжение с дифференцирующей цепи будет в виде двух коротких импульсов различной полярности, длительность которых соответствует 3τ = 3RC и 3τ = 3L/R, в случае RL-цепи.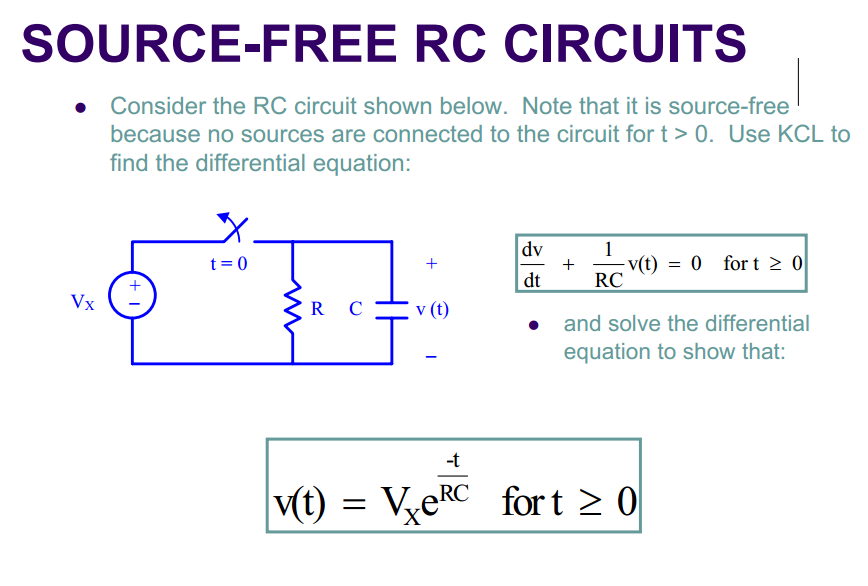
Реакция дифференцирующей цепи на прямоугольный импульс.
Из величины и формы выходного напряжения можно сделать вывод, что дифференциальные цепи вполне могут применяться для уменьшения длительности импульсов, что довольно часто применяется на практике и ранее такие цепи иногда называли укорачивающими.
Интегрирующие цепи
Интегрирующие цепи, так же как и дифференцирующие строят на основе RC- и RL-цепей, отличие заключается в том, откуда снимают выходное напряжение.
Простейшие RC и RL интегрирующие цепи.
Своё название интегрирующие цепи получили от того, что выходное напряжение, снимаемое с их выхода пропорционально интегралу от входного напряжения. Рассмотрим реакцию интегрирующей цепи на прямоугольный импульс напряжения. Напомню, что прямоугольный импульс, по сути, является напряжением, которое изменяется ступенчато два раза. В результате первого скачка напряжения конденсатор начинает заряжаться до тех пор, пока напряжение на входе не изменится, после этого начнётся разряд конденсатора по экспоненциальному закону.
Реакция интегрирующей цепи на прямоугольный импульс.
Не трудно заметить, что длительность импульса на выходе интегрирующей цепи несколько больше, чем длительность импульса на входе. Эту особенность нередко используют для увеличения длительности импульса, и такие цепи ранее называли расширяющими.
Теория это хорошо, но необходимо отрабатывать это всё практически ПОПРОБЫВАТЬ МОЖНО ЗДЕСЬ
1.4 Исследование интегрирующей RL-цепи. Исследование переходных процессов и анализ частотных характеристик элементарных звеньев радиотехнических цепей
Исследование переходных процессов и анализ частотных характеристик элементарных звеньев радиотехнических цепей
дипломная работа
Начертим принципиальную схему интегрирующей RL-цепи в программе MC9 (рисунок 1.16)
Рисунок 1.16 — Принципиальная схема интегрирующей RL-цепи
Определим постоянную времени нашей RL-цепи:
Вычислим коэффициент передачи по напряжению интегрирующей RL-цепи:
В этой формуле К — коэффициент передачи по напряжению, зависящий от частоты щ, Uout — напряжение на выходе цепи, Uin — напряжение на входе цепи, I — ток в цепи, j — мнимая единица, щ — круговая частота, R-сопротивление резистора, L — индуктивность катушки.
Произведем расчет АЧХ интегрирующей RL-цепи. Преобразуем коэффициент передачи:
Вычислим АЧХ как модуль коэффициента передачи:
В программе MathCAD построим АЧХ интегрирующей RL-цепи (рисунок 1.17). На рисунке 1.18 изображена АЧХ той же интегрирующей RL-цепи, построенная в программе МС9.
|K|
f, Гц
Рисунок 1.17 — АЧХ интегрирующей RL-цепи, построенная в программе MathCAD
|K|
f, Гц
Рисунок 1.18 — АЧХ интегрирующей RL-цепи, построенная в программе МС9
По этим двум рисункам видно, что графики, изображенные на них, тождественны. Из этого следует, что расчет АЧХ выполнен верно.
Выполним расчет ФЧХ дифференцирующей RL-цепи. Для этого найдем зависимость угла коэффициента передачи от частоты:
На рисунке 1.19 изображен график ФЧХ RL-цепи, построенный в программе MathCAD,а на рисунке 1.20 — в программе МС9. Видим, что графики совпадают. Это свидетельствует о том, что расчет ФЧХ выполнен верно.
ц°
f, Гц
Рисунок 1. 19 — ФЧХ интегрирующей RL-цепи, построенная в программе MathCAD
19 — ФЧХ интегрирующей RL-цепи, построенная в программе MathCAD
ц°
f, Гц
Рисунок 1.20 — ФЧХ интегрирующей RL-цепи, построенная в программе MC9
Вывод: интегрирующая RL-цепь не пропускает сигнал на высоких частотах (АЧХ там стремится к нулю), но пропускает на низких (АЧХ там стремится к 1). При малой частоте сдвиг по фазе между выходным и входным сигналом стремится к 0 градусам. При большой частоте — к -90.
Делись добром 😉
Автоматическая система регулирования с П-регулятором
8. Исследование устойчивости АСР
Исследование замкнутых АСР на устойчивость предполагает получение ответов на следующие вопросы. Является ли система с рассчитанным регулятором устойчивой, то есть…
Анализ режимов автоматического управления
1.5 Исследование устойчивости САУ
Устойчивость — это свойство системы возвращаться в исходный или близкий к нему установившийся режим после всякого выхода из него в результате какого-либо воздействия.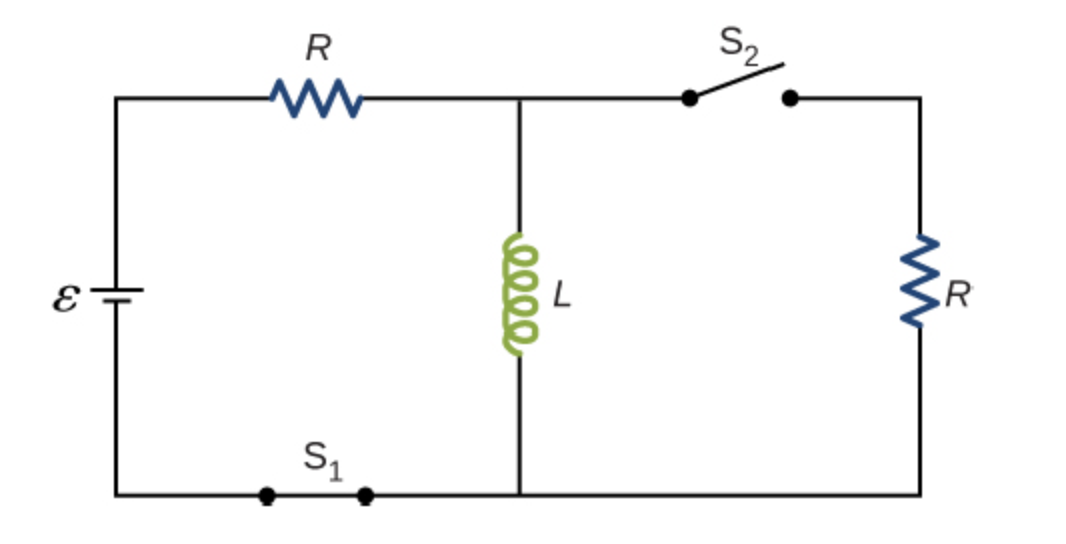 Критерий устойчивости Рауса-Гурвица.
Это алгебраический критерий…
Критерий устойчивости Рауса-Гурвица.
Это алгебраический критерий…
Исследование двухконтурной системы автоматического регулирования
4.1 Исследование астатической двукратно интегрирующей САР по управляющему воздействию
В соответствии с принципом оптимизации структурной схемы САР, настроенная по симметричному оптимуму, имеет вид (рис. 13). Рис. 13 Структурная схема астатической САР в общем виде Передаточная функция регулятора внешнего контура Так же…
Исследование переходных процессов и анализ частотных характеристик элементарных звеньев радиотехнических цепей
1.1 Исследование дифференцирующей RC-цепи
Начертим принципиальную схему дифференцирующей RC-цепи в программе MC9 (рисунок 1.1). Рисунок 1.1 — Принципиальная схема дифференцирующей RC-цепи Определим постоянную времени нашей RC-цепи: В этой формуле ф — постоянная времени RC-цепи…
Исследование переходных процессов и анализ частотных характеристик элементарных звеньев радиотехнических цепей
1.
 2 Исследование интегрирующей RC-цепи
2 Исследование интегрирующей RC-цепиНачертим принципиальную схему интегрирующей RC-цепи в программе MC9 (рисунок 1.6). Рисунок 1.6 — Принципиальная схема интегрирующей RC-цепи Постоянная времени нашей RC-цепи будет вычисляться по той же формуле, какую мы использовали в пункте 1.1…
Исследование переходных процессов и анализ частотных характеристик элементарных звеньев радиотехнических цепей
2.2 Переходные процессы в интегрирующей RC-цепи
Представим принципиальную схему интегрирующей RC-цепи в программе MS-10 (Рисунок 2.8) Рисунок 2.8 — Принципиальная схема интегрирующей RC-цепи, выполненная в программе MS-10 Произведем расчет переходных процессов…
Исследование переходных процессов и анализ частотных характеристик элементарных звеньев радиотехнических цепей
2.4 Переходные процессы в интегрирующей RL-цепи
Начертим принципиальную схему интегрирующей RL-цепи в программе MS-10 (Рисунок 2.22):
Рисунок 2.22 — Принципиальная схема интегрирующей RL-цепи, выполненная в программе MS-10
Постоянная времени этой RL-цепи была рассчитана ранее в пункте 1.
Преобразователи напряжение-ток
4. Исследование ПНТ
«Соберите» упрощённую схему ПНТ, приведённую на рисунке 2а. Упрощение этой схемы обусловлено применением идеальных источников тока, что существенно не повлияет на изучение принципа её работы…
Разработка системы управления
8. Исследование устойчивости СУ
В Схемное Окно поставили 2 блока «В память» и провели к ним линии связи, представленные на рисунке 15. Рисунок 15 — Структурная схема с блоками «В память» В меню «Анализ» выбрали пункт «Частотный анализ…
Разработка цифровой системы автоматического управления технологической установкой
9. Аналитическое исследование
Получив дискретную передаточную функцию объекта и регулятора, проведём аналитическое исследование…
Схемные функции и частотные характеристики линейной электрической цепи
3. Исследование нагрузки
…
Схемные функции и частотные характеристики линейных электрических цепей
3. Исследование нагрузки
. ..
..
Схемные функции и частотные характеристики линейных электрических цепей
3. Исследование нагрузки
Рассчитаем параметры нагрузки на резонансной частоте ; ; для вычисления добротности, нужно схему преобразовать в эквивалентную схему, где сопротивление шунта и емкость соединены последовательно. 0=100; Rш=1000; rвн=9,901; добротность (R=10): =5…
Устройство стабилизации скорости перемещения схвата промробота
1.4 Исследование САР на устойчивость
Рисунок 1.7 — Переходная характеристика соединения САР устойчива, т.к. переходная характеристика сходящаяся…
Устройство формирования управляющих сигналов
1. Расчет в общем виде АЧХ и ФЧХ скорректированного дифференцирующего устройства (r-L-c цепи). Расчет параметров r-L-c цепи согласно требованиям технического задания.
Составим уравнения Кирхгоффа для r-L-c-цепочки в комплексной форме (рис. 17):
Рис.17 К расчету дифференцирующей rc-цепочки комплексным методом
Комплексный коэффициент передачи напряжения может быть найден, как отношение комплексных амплитуд. ..
..
Переходные процессы в электрических цепях при формировании и преобразовании импульсов — МегаЛекции
Простейший переходной процесс в цепи, содержащей резистор R и конденсатор C (рисунок 1.1), возникает при подключении ее к источнику постоянной ЭДС.
Рисунок 1.1 – Дифференцирующая RC цепь
При этом входное воздействие имеет вид:
при
(1)
при
Уравнение потенциалов для такой цепи:
(2)
где
(3)
(4)
т.е.
(5)
Производя дифференцирование (5) с учетом (1) получим:
Отсюда, произведя разделение переменных и интегрируя, получим выражение для мгновенного значения тока в цепи:
(6)
Подстановка начальных условий в (2) и (4) даст , поэтому:
(7)
В формулах (6) и (7) τ есть постоянная времени цепи:
(8)
Рисунок 1. 2 – Графики изменения тока и напряжения
2 – Графики изменения тока и напряжения
Графики показывают, что перепады входного сигнала воспроизводятся цепью без искажений, однако потом и напряжение и ток в цепи постепенно уменьшаются. Таким образом, если на вход такой цепи подать прямоугольный импульс длительностью t u, то если τ << t u , выходной сигнал будет иметь вид двух остроконечных разнополярных импульсов, отстоящих один от другого на время t
Форма выходного сигнала говорит о том, что рассматриваемая цепь может приближенно выполнять операцию дифференцирования — именно поэтому цепь такого типа называют дифференцирующей или укорачивающей.
В случае если tu < τ, то искажения в выходном сигнале будут менее значительными: они будут проявляться в виде спада плоской части импульса. Величина таких искажений оценивается коэффициентом спада плоской части импульса
(9)
Если tu << τ, то можно ограничиться лишь линейными членами в этой формуле, что дает:
(10)
Рисунок 1.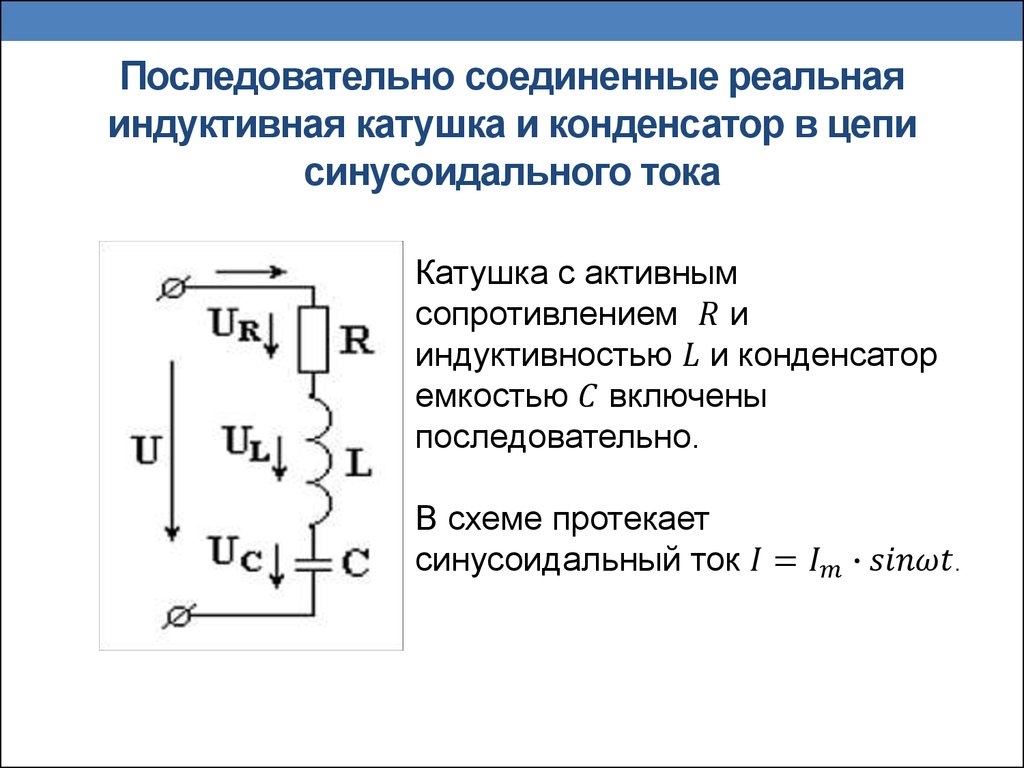
Эффект дифференцирования входного сигнала может быть получен и при использовании цепи, составленной из резистора R и катушки индуктивности L (рисунок 1.3). Переходной процесс в такой цепи описывается уравнением:
(11)
где — ;
.
Решая уравнения, получаем:
(12)
(13)
где — постоянная времени.
В RL цепи так же, как и в RC цепи, при уменьшении постоянной времени повышается точность выполнения операции дифференцирования.
Таким образом, рассмотренные цепи типа RL и RC могут быть использованы для дифференцирования или укорочения импульсов малой длительности. Однако наиболее часто
Рисунок 1.4 – Интегрирующая RC цепь
Рассмотрим цепь, состоящую из резистора R и конденсатора C, включенную как показано на рисунке 1. 4.
4.
Выходное напряжение такой цепи может быть посчитано по формуле:
(14)
Рисунок 1.5 – Графики изменения тока и выходного напряжения
Кривые показывают, что при подаче на вход такой цепи мгновенного перепада напряжения, выходное напряжение нарастает постепенно.
Время, за которое выходное напряжение изменяется в заданном пределе, называется временем установления.
Так, время изменения выходного напряжения в пределах от 0 до 0,95 от максимального значения, равно:
(15)
Время изменения выходного напряжения от 0 до 0,9 максимального значения, равно:
(16)
Время изменения выходного напряжения от 0,1 до 0,9 максимального значения, равно:
(17)
Если выбрать τ и tu из условия τ >> tu, то выходное напряжение будет изменяться практически линейно, однако величина его через промежуток времени, равный tu будет незначительной. Таким образом, рассматриваемая цепь при соблюдении условия τ >> tu выполняет приближенно операцию интегрирования. Именно поэтому эта цепь получила название интегрирующей цепи.
Именно поэтому эта цепь получила название интегрирующей цепи.
Интегрирующая цепь может быть построена путем использования свойств индуктивности, напряжение на которой связано с протекающим током i уравнением . Интегрирование этого уравнения дает:
(18)
Чтобы операция интегрирования выполнялась, возможно, точнее, необходимо выполнение условия:
Следует заметить, что на практике цепи RL и LR применяются значительно реже, чем цепи RC и CR. Это объясняется как сложностью выполнения индуктивностей и их габаритами, так и влиянием цепей нагрузки.
Рассмотрим влияние цепей нагрузки на работу линейных цепей. Нагрузку для не очень высоких частот можно считать состоящей из соединенных параллельно активного сопротивления RHи конденсатора CH. Очевидно, что емкостная составляющая сопротивления нагрузки будет сказываться лишь при высоких частотах или формулировании перепадов напряжений.
а – Интегрирующая RC цепь б – Дифференцирующая RC цепь
в – Дифференцирующая RL цепь г – Интегрирующая RL цепь
Рисунок 1. 6 – RC и RL цепи с подключенной нагрузкой
6 – RC и RL цепи с подключенной нагрузкой
На рисунках 1.6а) – 1.6г) показаны рассматриваемые цепи с подключенной к ним нагрузкой.
Как видно из рисунка 1.6а) подключение нагрузки образует схему реостатного делителя, шунтированного емкостью.
Данную цепь можно свести к интегрирующей с постоянной времени:
(19)
и подключенной к источнику сигнала, величина которого:
(20)
Как следует из приведенных зависимостей, цепь на рисунке 1.6б) имеет меньшую постоянную времени и может обеспечить меньшую величину выходного напряжения.
На рисунках 1.6в) и 1.6г) показаны RL цепи с подключенной к ним нагрузкой. Как видно из рисунков, подключение нагрузки приводит к образованию колебательных контуров.
Для цепи на рисунке 1.6в) образуется параллельный колебательный контур, а для цепи рисунка 1.6г) – последовательный. При этом режим работы цепей существенно меняется. Прямоугольные импульсы напряжения, подаваемые на RL – цепи вызывают в них режим ударного возбуждения колебаний.
Подключение осциллографа для исследования цепей неизбежно приводит к шунтированию их входной емкостью осциллографа, т.е. к образованию схем типа 1.6в) и 1.6г).
Читайте также:
Воспользуйтесь поиском по сайту:
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Оценка эффективности инструментов коммуникационной политики: Внешние коммуникации — обмен информацией между организацией и её внешней средой… Проблема типологии научных революций: Глобальные научные революции и типы научной рациональности… Марксистская теория происхождения государства: По мнению Маркса и Энгельса, в основе развития общества, происходящих в нем изменений лежит. Интересное: Уполаживание и террасирование склонов: Если глубина оврага более 5 м необходимо устройство берм. Варианты использования оврагов для градостроительных целей… Аура как энергетическое поле: многослойную ауру человека можно представить себе подобным… Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
Цель работы: изучение свойств интегрирующих и дифференцирующих RC— и RL-цепей и способов их применения совместно с цифровыми элементами в схемах формирования импульсов.
Общие сведения Интегрирующие и дифференцирующие цепи находят широкое применение как компоненты более сложных цепей, так и в качестве упрощенных моделей реально наблюдаемых в электрических цепях процессов. Например, интегрирующая цепь часто используется как модель линейного усилителя с ограниченной полосой пропускания. Более просты в использовании RC-цепи, поскольку индуктивности не считаются технологичными компонентами, а конденсаторы легко реализуются и выпускаются на практически любые значения емкости. Рассмотрим RC-цепи в первую очередь. RC-цепь в нашем случае представляет последовательное включение всего двух деталей: резистора R и конденсатора C. Интегрирующая и дифференцирующая цепи отличаются лишь тем, что в интегрирующей цепи выходной сигнал снимается с конденсатора, а в дифференцирующей – с резистора (рис. 7.1). Обратим внимание на поведение изучаемых цепей при воздействии ступенчатого сигнала и на частотные свойства при воздействии гармонического сигнала. Первый случай представляет интерес при использовании RC-це-пей совместно с логическими элементами для решения задач формирования импульсов требуемой длительности или реализации элемента задержки цифрового сигнала на заданный интервал времени. В этом случае моделью входного сигнала является сигнал вида x(t) = E1(t), который равен нулю при t <0, равен E при t ³ 0. Поведение схемы определяется путем решения дифференциального уравнения первого порядка. Приведем решение в окончательном виде и ограничимся описанием поведения каждой схемы с учетом того факта, что напряжение на конденсаторе в процессе коммутации не может мгновенно измениться, т.е. конденсатор старается сохранить свое исходное состояние, хранимый на нем до момента коммутации заряд. а) б) в) г) д) е)
Рис.
Предположим для интегрирующей цепи (см. рис. 7.1,а), что в исходном состоянии напряжение на конденсаторе равно нулю. При воздействии на вход «input» ступенчатого сигнала с амплитудой E напряжение на конденсаторе сохраняется равным нулю, т.е. ток через резистор оказывается максимально большим и равным E / R. Все входное напряжение окажется приложенным к резистору. В процессе заряда конденсатора растет напряжение на выходе «output», соответственно, уменьшается напряжение на резисторе, следовательно, уменьшается ток заряда конденсатора, что уменьшает скорость изменения выходного напряжения. Ток заряда конденсатора течет по цепи: источник напряжения E, резистор, конденсатор. В процессе роста выходного напряжения оно приближается к установившемуся значению, равному входному напряжению величиной E. Когда на выходе интегрирующей цепи установится уровень напряжения с высокой степенью точности равный E и входное напряжение мгновенно (с большой скоростью) падает до нуля, то конденсатор сохраняет свой начальный уровень напряжения и получает возможность разряжаться по цепи: конденсатор, резистор. Нулевое напряжение на входе равносильно замыканию входной цепи. Направление тока окажется в данном случае противоположно направлению тока заряда конденсатора при подаче напряжения E. Временные диаграммы работы интегрирующей цепи при воздействии импульса с длительностью, значительно большей постоянной времени, показаны на рис. 7.1,в. Если же постоянная времени значительно больше периода входных импульсов, то выходное напряжение будет колебаться в небольших пределах относительно уровня среднего значения входного импульсного сигнала (см. рис. 7.1,д). При воздействии гармонического сигнала на интегрирующую цепь определяют граничную частоту цепи fгр как частоту, на которой значение коэффициента передачи уменьшается в раз, т.е. составляет величину, примерно равную 0,707 при исходном коэффициенте передачи на нулевой частоте, равном единице. При f = fгр справедливо равенство R = xc. С ростом частоты значением реактивного сопротивления xc в знаменателе по сравнению с сопротивлением резистора R можно пренебречь, что и объясняет поведение коэффициента передачи на высоких частотах. Если к выходу цепи подключается нагрузка, то при анализе поведения выходного сигнала необходимо учитывать влияние этой нагрузки. Предположим для дифференцирующей цепи (см. рис. 7.1,б), что в исходном состоянии напряжение на конденсаторе равно нулю. При воздействии на вход «input» ступенчатого сигнала с амплитудой E напряжение на конденсаторе сохраняется равным нулю, т.е. ток через резистор оказывается максимально большим и равным E/R. Все входное напряжение окажется приложенным к резистору, т.е. в начальный момент времени на выходе будет наблюдаться максимально большое напряжение, равное E. В процессе заряда конденсатора растет напряжение на нем и, соответственно, уменьшается напряжение на резисторе, т. При изменении напряжения на входе, когда оно упадет до нуля, конденсатор окажется подключен к выходному резистору, причем обкладка с положительным зарядом окажется соединена с общим проводом, а на выходе образуется отрицательное напряжение с амплитудой, в начальный момент времени равной E. Со временем уровень отрицательного напряжения будет уменьшаться до нуля, поскольку в резисторе будет рассеиваться накопленная на конденсаторе электрическая энергия. Поведение выходного сигнала при этом описывается выражением uR = — Ee –t/t . За нулевой момент времени принимается момент изменения напряжения на входе от величины E к нулю. Временные диаграммы работы дифференцирующей цепи при воздействии импульса с длительностью, значительно большей постоянной времени, показаны на рис. 7.1,г. Если же постоянная времени значительно больше периода входных импульсов, то выходное напряжение окажется смещенным относительно входного напряжения таким образом, что среднее значение выходного напряжения будет равно нулю (см. рис. 7.1,д). При этом наблюдаются искажения формы исходных прямоугольных импульсов, что является проявлением дифференцирующих свойств цепи. Для гармонического сигнала определяют граничную частоту передачи дифференцирующей цепи, на которой с ростом частоты коэффициент передачи цепи увеличивается до уровня 0.707. Дальнейшее увеличение частоты входного гармонического сигнала увеличивает коэффициент передачи в пределе до единицы. Интегрирующая и дифференцирующая RL-цепи предложены на рис. 7.2. Их поведение подобно поведению RC —цепей при условии, что постоянная времени определяется выражением t = L / R.
а) б)
Рис. 7.2. Интегрирующая (а) и дифференцирующая (б) RL-цепи Порядок выполнения работы
Работа со стендом 1. Изучение свойств RC-цепей при импульсных сигналах и некоторые практические применения этих цепей. 1.1. Соберите на стенде интегрирующую RC-цепь с параметрами, предложенными в табл. 7.1.
Таблица 7.1
Рассчитайте постоянную времени tи изучите реакцию цепи на импульсный сигнал с генератора, формирующего импульсы с частотами F(»1…2 мГц), F2, F4, F8, F16. 1.2. Подключите к выходу интегрирующей цепи инвертор, контролируя форму выходного сигнала цепи осциллографом. Постройте идеализированные временные диаграммы выходных сигналов генератора и инвертора с учетом измеренных времен задержки по обоим фронтам. 1.3. Подключите параллельно резистору интегрирующей цепи германиевый диод. Зафиксируйте изменения в сигналах схемы и объясните их. 1.4.* Подключите выходы генератора и инвертора к элементу, выполняющему функцию И-НЕ (y = x1& x2). 1.5. Соберите на стенде дифференцирующую цепь с параметрами, приведенными в табл. 7.1. Определите ее поведение при воздействии импульсных сигналов и измерьте длительности формируемых импульсов. 1.6. Нагрузите дифференцирующую цепь на инвертор, изобразите временные диаграммы работы схемы и измерьте длительность выходного импульса. Сравните длительность импульса с величиной постоянной времени. Обратите внимание на поведение отрицательного импульса с выхода цепи при подключении входа инвертора. Объясните его поведение. Зарисуйте полученную схему. 1.7. В схеме предыдущего пункта переключите тот выход резистора, который подключен к общему проводу, на выход источника положительного напряжения E1. Объясните наблюдаемые поведения сигналов во всех точках схемы, постройте временные диаграммы и измерьте длительность импульса на выходе инвертора. Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим… Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций… Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого… Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)… |
Экспериментальное исследование дифференцирующих и интегрирующих свойств RС-цепи
Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
Амурский Государственный Университет
(ГОУ ВПО «АмГУ»)
Кафедра: АПП и Э
Лабораторная работа по ТОЭ № 16 а
На тему: Исследование дифференцирующих и интегрирующих цепей
Выполнил студент 542 г.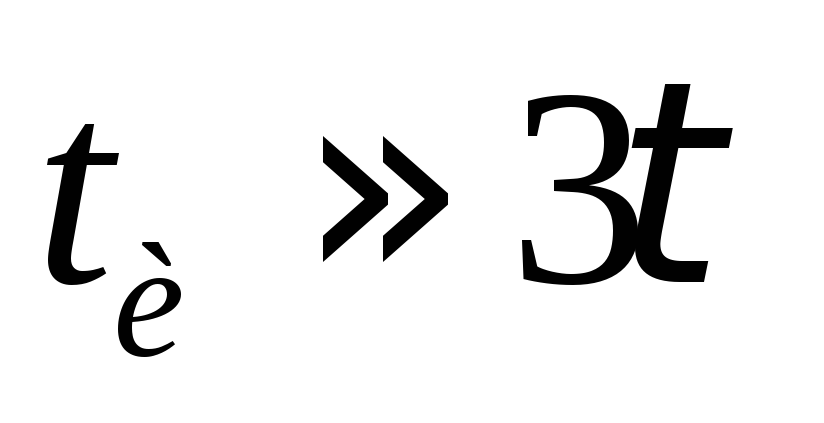 Н.Г. Поткин
Н.Г. Поткин
Преподаватель Т.В. Карпова
Благовещенск 2007
ЛАБОРАТОРНАЯ РАБОТА № 16 а
ИССЛЕДОВАНИЕ ДИФФЕРЕНЦИРУЮЩИХ И ИНТЕГРИРУЮЩИХ
ЦЕПЕЙ
I. ЦЕЛЬ РАБОТЫ.
Экспериментальное исследование дифференцирующих и интегрирующих свойствRС – цепи.
П. КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ.
Простейшая апериодическая цепь RC (или RL) может выполнять линейные операции преобразования сигналов путем дифференцирования или интегрирования.
I) Дифференцирующая цепь. Напряжение на выходе цепи пропорционально производной от входного напряжения:
Рис.1
Передаточная функция цепи
При условии ωτ<<1 может быть заменена приближенным значением:
где τ = RС —
постоянная времени цепи.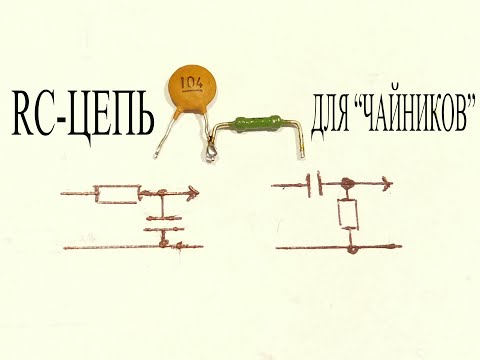
Следовательно, напряжение на выходе то естьRС — цепь в области частот ω<<1/ τ осуществляется приближенное дифференцирование входного сигнала:
Постоянная времени RС — цепи, а следовательно, её параметры, рассчитываются с учетом ширины спектра входного сигнала. Если на вход дифференцирующей цепи подавать прямоугольные импульсы длительностью tи, то значение постоянной времени выбирается из условия
Цепь при таком условии укорачивает и обостряет импульсы, так как за время действия импульсов конденсатор успевает перезарядиться. Временные диаграммы напряжений дифференцирующей цепи приведены на рис.2
Рис.2
На интервале времени t2-t3 конденсатор, заряженный до напряжения U и во время действия импульса, разряжается на резистор через источник питания.
Для
получения выходных импульсов одной полярности к выходу дифференцирующей цепи
подключают диод. Остроконечные импульсы, полученные на выходе цепи, могут
использоваться в качестве запускающих импульсов последующих узлов в момент
начала (или окончания) импульса прямоугольной формы.
2) Интегрирующая цепь. Напряжение на выходе цепи пропорционально интегралу от входного напряжения
Рис.3
Передаточная функция цепи:
При условии ωτ>>1 может быть заменена приближенным выражением где т =RС — постоянная времени цепи.
Следовательно, напряжение на выходе то естьRС — цепь в области частот ω » 1 /τ осуществляет приближенное интегрирование входного сигнала:
Постоянная времени RС — цепи, а следовательно, и её параметры, рассчитываются с учетом ширины спектра входного сигнала.
Если на вход интегрирующей цепи подавать прямоугольные импульсы длительностью tи, то значение постоянной времени выбирается из условия:
Временная диаграмма напряжений интегрирующей цепи при Т »tи+3τ приведены на рис.4
Если входное напряжение снимать с R, тоU2≈U1, а цепь называется проходной.
III. ПОДГОТОВКА К РАБОТЕ
1)
На вход дифференцирующей цепи с конденсатором С = 0,1 мкФ подается напряжение u1=5sin 314 t В.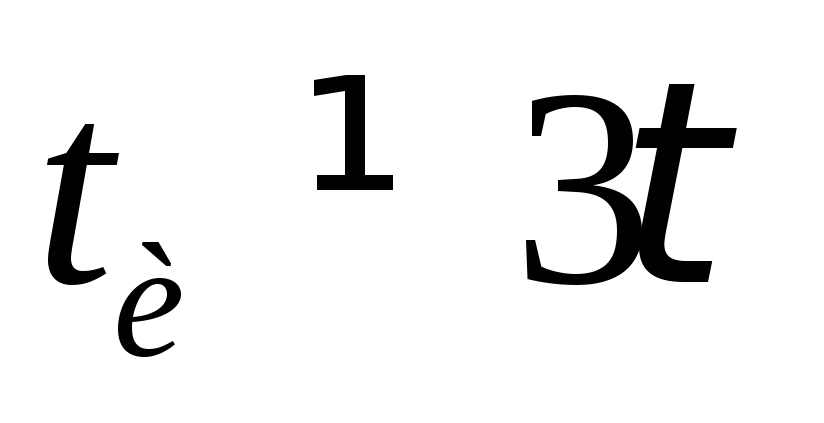 Рассчитать
сопротивление резистора R, которое в 100 раз меньше
емкостного сопротивления и записать мгновенное значение
выходного напряжения. Построить временные диаграммы входного и выходного
напряжений.
Рассчитать
сопротивление резистора R, которое в 100 раз меньше
емкостного сопротивления и записать мгновенное значение
выходного напряжения. Построить временные диаграммы входного и выходного
напряжений.
Найти постоянную времени полученной цепи, подобрать длительность периода и подсчитать частоту входного напряжения из условия
Примечание. Значение С задается преподавателем.
2) На вход интегрирующей цепи с конденсатором С = 0,1 мкФ подается напряжение u1=5sin 314 t В. Рассчитать сопротивление резистораR, которое в 100 раз больше емкостного сопротивления и записать мгновенное значение выходного напряжения. Построить временные диаграммы входного и выходного напряжений.
Найти постоянную времени полученной цепи, подобрать длительность периода и подсчитать частоту входного напряжения из условия
IV) ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1.
Собрать RС — цепь с
конденсатором заданной емкости и магазином сопротивлений. В качестве источника взять
генератор, который генерирует периодическое, напряжение различных форм.
Осциллограммы наблюдаются с помощью двухканального осциллографа. Схема цепи имеет
вид:
В качестве источника взять
генератор, который генерирует периодическое, напряжение различных форм.
Осциллограммы наблюдаются с помощью двухканального осциллографа. Схема цепи имеет
вид:
2. Установить значение R, рассчитанное для дифференцирующей цепи, по дать на вход синусоидальное напряжение заданной амплитуды и зарисовать осциллограммы входного u1(t) и выходного u2(t) напряжений.
3. Подать на вход дифференцирующей цепи напряжение П — образной формы. Зарисовать изображения напряжений на входе и выходе.
4. Проделать те же опыты, что в п.п.2 и 3, для интегрирующей цепи с рас считанными выше параметрами.
5. Исследовать с помощью осциллографа влияние R (или С) на точность дифференцирования и интегрирования сигналов.
Ответы на контрольные вопросы:
1. При каких условиях RС-цепь можно считать дифференцирующей (интегрирующей)?
Для интегрирующей цепи в интервале
времени, для которого Ri>>uC можно считать, что ивх≈iRт. е.
напряжение на выходе схемы пропорционально интегралу от напряжения на ее входе,
если длительность интервала интегрирования много меньше τ. При
синусоидальном входном напряжении необходимо выполнение условия UR>> UC или RI >> XCI т.е. ωRC>>1.
Интегрирование будет тем точнее, чем больше постоянная времени τ по
сравнению с периодом входного напряжения Т.
е.
напряжение на выходе схемы пропорционально интегралу от напряжения на ее входе,
если длительность интервала интегрирования много меньше τ. При
синусоидальном входном напряжении необходимо выполнение условия UR>> UC или RI >> XCI т.е. ωRC>>1.
Интегрирование будет тем точнее, чем больше постоянная времени τ по
сравнению с периодом входного напряжения Т.
Для дифференцирующей цепи в интервале времени, для которого Ri<<uC можно считать, что uвх≈uC, т.е. напряжение на выходе схемы пропорционально производной напряжения на ее входе, если длительность сигнала много больше τ.
При
синусоидальном входном напряжении необходимо выполнение условия UR<<UC
или RI<<XCI, т.е. ωRC<<1.
и 2πτ<< Т .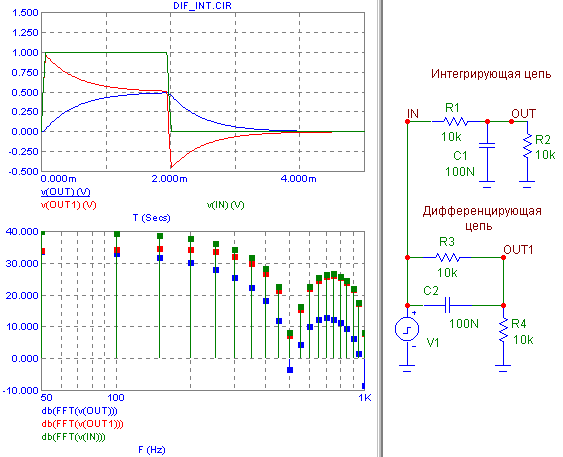 Дифференцирование будет тем точнее, чем меньше
постоянная времени т по сравнению с периодом входного напряжения Т.
Дифференцирование будет тем точнее, чем меньше
постоянная времени т по сравнению с периодом входного напряжения Т.
2. Почему в дифференцирующей цепи при наличии на входе однополярных импульсов напряжение на резисторе представляет собой импульсы положительной и отрицательной полярности?
Постоянная времени RС — цепи, а следовательно, её параметры рассчитываются с учетом ширины спектра входного сигнала. Если на вход дифференцирующей цепи подавать прямоугольные импульсы длительностью tu, то значение постоянной времени выбирается из условия τ<<tu.
Цепь при таком условии укорачивает и обостряет импульсы, так как за время действия импульсов конденсатор успевает перезарядиться. Временные диаграммы напряжений дифференцирующей цепи приведены на рис. 2.
На интервале времени t2-t3 конденсатор, заряженный до напряжения
U во время действия импульса, разряжается на резистор через источник питания.
3. RС — цепи в
качестве дифференцирующих и интегрирующих получили большее распространение по сравнению
с RL — цепями.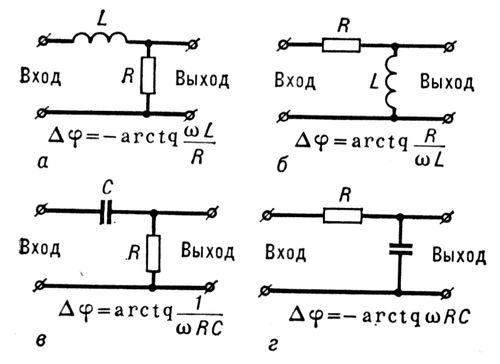 Почему?
Почему?
RС — цепи в качестве дифференцирующих и интегрирующих получили большее распространение по сравнению с RL — цепями, потому что практически их проще реализовать: они обладают меньшими габаритами, массой и более удобна для регулирования.
4. Каково назначение дифференцирующих и интегрирующих цепей?
Простейшая апериодическая цепь RC (RL) может выполнять линейные операции преобразования сигналов путем дифференцирования или интегрирования.
Задание 2.1 Дифференцирование прямоугольных импульсов RL-цепью
Амплитуда Um=4,9В. Амплитуда положительных импульсов Um+=2В, отрицательныхUm— =1,9В. Длительность положительнаяτn+=26, отрицательная τn— =26. τ=L/R Lmin=25 мГн R3=6,8 к τ =25×10-3 =3,5×10-6с=3,5 мкс 6,8 ×103 Lmax=75 мГн τ =75×10-3 =11×10-6с=11мкс 6,8 ×103 Вывод: Можно сделать вывод о том, что после прохождения через дифференцирующую цепочку в формировании выходного сигнала в большей степени участвуют высокие частоты, отвечающие за резкий фронт прямоугольных импульсов.
Задание 2.2 Дифференцирование прямоугольных импульсов RL-цепью
Амплитуда Um=8В. Амплитуда положительных импульсов Um+=4В, отрицательных Um— =4В. Длительность положительная τn+=26, отрицательная τn— =26. τ=R1×C2 R1=2 к C2=240 рF(240×10-12) τ=2×103×240×10-12=480×10-9с
С2 Нормальная цепь
С3 Переходная цепь
Вывод: дифференцирующая RL-цепь не пропускает сигнал на низких частотах (АЧХ там стремится к нулю), но пропускает на высоких (АЧХ там стремится к 1). При малой частоте сдвиг по фазе между выходным и входным сигналом стремится к 90 градусам. При большой частоте — к 0.
Экспериментальные данные: Задание 2.3. Исследование частотной зависимости коэффициента передачи дифференцирующих цепей С3
С2
Задание 3. С4. Амплитуда Un=3,3В Длительность τn=50 мкс Длительность переднего фронта τф=10 мкс и заднего фронта τзф=20 мкс τ= R5×C4 R5=100 к C4=560рF(560×10-12) τ=100×103×560×10-12=560×10-7с
С5 Амплитуда Un=4,3В Длительность τn= 60 мкс Длительность переднего фронта τф=22 мкс и заднего фронта τзф=22 мкс τ= R5×C4 R5=100 к C4=560рF(560×10-12) τ=100×103×560×10-12=560×10-7с
С6 Амплитуда Un=4,2В Длительность τn= 30 мкс Длительность переднего фронта τф= 15 мкс и заднего фронта τзф= 20 мкс τ= R5×C4 R5=150 к C4=560рF(560×10-12) τ=100×103×560×10-12=560×10-7с
С4
С5
С6
Вывод:интегрирующая RC-цепь не пропускает сигнал на высоких частотах (АЧХ там стремится к нулю), но пропускает на низких (АЧХ там стремится к 1).
Задание 3.2. Получение частотной зависимости коэффициента передачи интегрирующей RC-цепи С4
С5
С6
Интегрирование однотональных АМВЧ пульсирующего сигнала Сложной RC-цепью R5 min
R5 max
R10 min
R 10 max
Вывод:С помощью RL и RC цепей можно производить интегрирование входного сигнала, чаще всего для этого используется RC цепь.
Интегрирование однотонального АМВЧ пульсируюшего сигнала RL-цепью Схема имитирующая работу (Подключаем ёмкость)
с О2-24
Вывод:Функционально линейные устройства формирования и преобразования электрических сигналовпри рассмотрении интегрирующие цепи, применяемые для интегрирования сигналов, и иногда для расширения (увеличения длительности) импульсов и дифференцирующие (укорачивающие) цепи, применяемые для дифференцирования сигналов, а также для укорочения импульсов (получения импульсов заданной длительности). Важнейшее свойство линейных устройств заключается в их способности накапливать и отдавать энергию в емкостных и индуктивных элементах и этим преобразовывать входные сигналы во временное изменение интервалов на выходе. Это свойство лежит в основе работы генераторов, устройств подавления импульсных помех, возникающих в процессе прохождения электрического сигнала через цепи с различной временной задержкой. Типовые разделительные фильтры даже с ровной суммарной АЧХ нередко являются причиной возникновения фазовых искажений, влияние которых на форму выходного сигнала особенно проявляется вблизи частоты раздела fp. показаны изменения, которые претерпевает сигнал в виде симметричных прямоугольных импульсов длительностью, примерно равной 1/fp, пройдя через разделительный фильтр с нелинейной суммарной ФЧХ. Если на частоте раздела средне- и высокочастотной полос эти искажения допустимы, так как мало сказываются на качестве звучания, то в области частот раздела средне- и низкочастотной полос их желательно устранить, поскольку именно здесь сосредоточены наибольшие среднестатические уровни реального сигнала, и к тому же чувствительность слуха максимальна.
Для неискаженной передачи сигналов импульсного характера, кроме ровной суммарной АЧХ, необходимо обеспечить одинаковую временную задержку составляющих сигнала при прохождении через разделительный фильтр.
|
Интеграторы — Формирование волны — Основы электроники
Формирование волны
Интегратор (RC или RL) используется в качестве сети формирования сигналов, например. в связь, радиолокационные системы и компьютеры. К интеграторам часто применяется прямоугольная волна. Гармоническое содержание прямоугольная волна состоит из нечетных кратных основной частоты. Поэтому значимых гармоник (те, которые влияют на контур) будет присутствовать в 50 или 60 раз больше основной частоты в волне.
Интеграторы RC
Конденсатор будет предлагать реактивное сопротивление ( X C ) другого амплитуда каждой из гармоник
Это означает, что падение напряжения на конденсаторе для каждой гармоники
присутствующая частота не будет одинаковой. Для низких частот конденсатор
будет оказывать большое сопротивление, обеспечивая большое падение напряжения на
конденсатор. Для высоких частот реактивное сопротивление конденсатора будет
чрезвычайно мало, вызывая небольшое падение напряжения на конденсаторе. Это
ничем не отличается от фильтров нижних и верхних частот (дискриминаторов)
представлены позже. Если составляющая напряжения гармоники не развивается
через реактивное сопротивление конденсатора, оно будет развиваться через
резистор, если мы соблюдаем закон напряжения Кирхгофа. Гармоническая амплитуда
и соотношение фаз на конденсаторе не такое, как у
ввод исходной частоты; следовательно, идеальной прямоугольной волны не будет.
производится на конденсаторе. Вы должны помнить, что предлагаемое реактивное сопротивление
частота каждой гармоники вызовет изменение как амплитуды, так и фазы
частоты каждой отдельной гармоники по отношению к
актуальная ссылка. Величина изменения фазы и амплитуды, происходящая в
конденсатор зависит от X C конденсатора. Значение
также следует учитывать сопротивление, предлагаемое резистором.
здесь; это часть коэффициента развития напряжения в сети.
Для высоких частот реактивное сопротивление конденсатора будет
чрезвычайно мало, вызывая небольшое падение напряжения на конденсаторе. Это
ничем не отличается от фильтров нижних и верхних частот (дискриминаторов)
представлены позже. Если составляющая напряжения гармоники не развивается
через реактивное сопротивление конденсатора, оно будет развиваться через
резистор, если мы соблюдаем закон напряжения Кирхгофа. Гармоническая амплитуда
и соотношение фаз на конденсаторе не такое, как у
ввод исходной частоты; следовательно, идеальной прямоугольной волны не будет.
производится на конденсаторе. Вы должны помнить, что предлагаемое реактивное сопротивление
частота каждой гармоники вызовет изменение как амплитуды, так и фазы
частоты каждой отдельной гармоники по отношению к
актуальная ссылка. Величина изменения фазы и амплитуды, происходящая в
конденсатор зависит от X C конденсатора. Значение
также следует учитывать сопротивление, предлагаемое резистором.
здесь; это часть коэффициента развития напряжения в сети.
Схема частичного интегрирования.
Схема на рисунке выше поможет показать отношения R и X C более четко. Прямоугольная волна, приложенная к цепи
составляет 100 вольт пик на частоте 1 килогерц. Нечетные гармоники будут 3
килогерц, 5 килогерц, 7 килогерц и т. д. В таблице ниже приведены значения X C и R предлагаются для нескольких
гармоник и указывает приблизительное значение частоты среза
( X C = R ). Из таблицы ясно видно, что отсечка
частота лежит между пятой и седьмой гармониками. Между этими двумя
значений, емкостное реактивное сопротивление будет равно сопротивлению. Поэтому для всех
Гармонические частоты выше пятой, большая часть выходного напряжения будет
не проявляться на выходном конденсаторе. Скорее, большая часть вывода будет
разработан через Р . Отсутствие высших гармоник приводит к
передний фронт сигнала, развивающегося на конденсаторе, должен быть скруглен. Пример этого эффекта показан на рисунке ниже. Если значение
емкость увеличивается, реактивные сопротивления каждой частоте гармоники будут
далее уменьшилось. Это означает, что будет развиваться еще меньше гармоник.
через конденсатор.
Пример этого эффекта показан на рисунке ниже. Если значение
емкость увеличивается, реактивные сопротивления каждой частоте гармоники будут
далее уменьшилось. Это означает, что будет развиваться еще меньше гармоник.
через конденсатор.
| Гармоника | X C (кОм) | Ч (кОм) |
|---|---|---|
| Фундаментальный | 159 | 25 |
| 3-й | 53 | 25 |
| 5-й | 31,8 | 25 |
| 7-й | 22,7 | 25 |
| 9-й | 17,7 | 25 |
| 11-й | 14,5 | 25 |
Частичная интеграция.
Гармоники, не развивающиеся эффективно на конденсаторе, должны быть развиты
через резистор, чтобы удовлетворять закону напряжения Кирхгофа. Обратите внимание на узор
осциллограммы напряжения на резисторе и конденсаторе. Если формы волны
как на резисторе, так и на конденсаторе были добавлены графически, в результате
будет точной копией входной прямоугольной волны.
Когда емкость достаточно увеличена, полная интеграция входа сигнал имеет место на выходе через конденсатор. Пример полного интегрирование показано на рисунке ниже (форма сигнала v C ). Этот эффект может быть вызван значительным уменьшением значения емкостной реактивное сопротивление. Тот же эффект будет иметь место при увеличении значения сопротивление. Интегрирование происходит в RC-цепи, когда на выходе через конденсатор.
Интеграция.
Величина интегрирования зависит от значений R и C .
Величина интегрирования может также зависеть от постоянной времени
схема. Постоянная времени цепи должна быть не менее 10 раз
больше , чем длительность входного импульса для интегрирования.
Значение 10 является приблизительным. Когда постоянная времени цепи
в 10 и более раз превышает значение длительности входного импульса, схема
говорят, что оно имеет большую постоянную времени. Когда постоянная времени велика,
конденсатор не имеет возможности мгновенно заряжаться до значения
приложенное напряжение.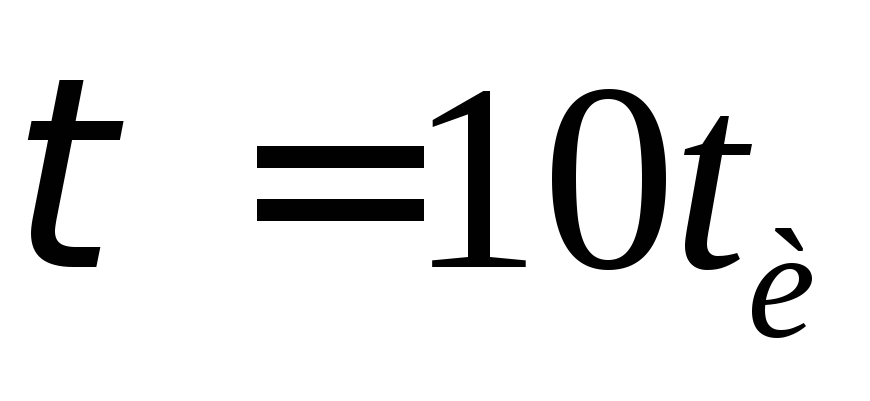 Таким образом, получается длинная, наклонная, интегрированная
форма волны.
Таким образом, получается длинная, наклонная, интегрированная
форма волны.
RL Интеграторы
Цепь RL также может использоваться как интегрирующая схема. интегрированный Форма сигнала может быть получена из последовательной цепи RL, взяв выходной сигнал через резистор. Характеристики индуктора таковы, что при первый момент времени, когда приложено напряжение, через индуктивность минимальна, а напряжение на ней максимально. Следовательно, значение падения напряжения на последовательном резисторе в этот первый момент должно быть 0 вольт, потому что ток через него не течет. По прошествии времени, ток начинает течь по цепи и на ней возникает напряжение резистор. Поскольку цепь имеет большую постоянную времени, напряжение на резистор делает , а не реагируют на быстрые изменения в напряжение входной прямоугольной волны. Таким образом, условия интегрирования в цепи RL — это постоянная времени с выходным сигналом через резистор. Эти условия показаны на рисунке ниже.
Форма сигнала интегратора RL.
Анализ сигналов интегратора
Если RC- или RL-цепь имеет постоянную времени в 10 раз больше, чем длительность входного импульса, схемы способны к интегрированию. Давайте вычислить и отобразить фактическую форму волны, которая от большой постоянной времени (в 10 раз больше длительности импульса), короткой постоянной времени (1/10 длительности импульса) и средняя постоянная времени (эта постоянная времени между длинным и коротким). Чтобы точно построить значения для конденсатора выходное напряжение, мы будем использовать универсальную диаграмму постоянной времени, показанную на рисунок ниже.
Универсальная таблица постоянной времени.
Вы уже знаете, что заряд конденсатора соответствует форме кривой, показанной на рис.
рисунок выше. Эту кривую можно использовать для определения величины напряжения
через любой компонент в последовательной RC-цепи. Пока постоянная времени
или известна дробная часть постоянной времени, напряжение на
компонент может быть определен.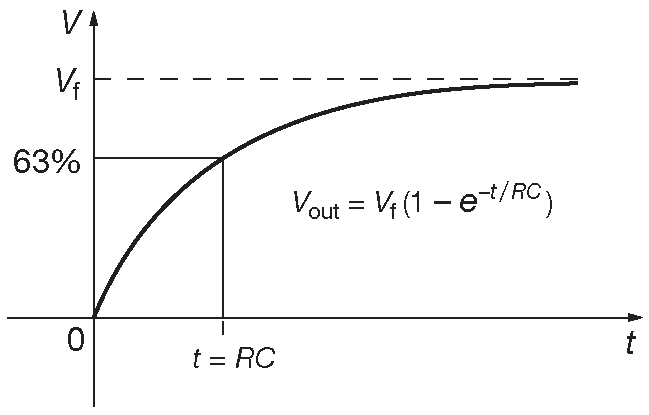
Краткосрочный интегратор с постоянной выдержкой времени
Цепь RC-интегратора.
На рисунке выше 100-микросекундный импульс с амплитудой 100 вольт применяется к цепи. Схема состоит из 0,01 мкФ конденсатор и переменный резистор R . Применяемая прямоугольная волна представляет собой чистая прямоугольная волна. Сопротивление переменного резистора установлено равным 1000 Ом. Постоянная времени цепи определяется уравнением:
Подставляем значения:
Поскольку постоянная времени цепи составляет 10 мкс, а импульс
длительность 100 мкс, постоянная времени короткая (1/10 импульса
продолжительность). Конденсатор заряжается экспоненциально через резистор. В 5
постоянных времени, конденсатор для всех практических целей будет полностью
заряжен. При первой постоянной времени конденсатор заряжается до 63,2 вольта,
на втором 86,5 вольт, на третьем 95 вольт, на четвертом 98 вольт,
и, наконец, в конце пятой постоянной времени (50 микросекунд) конденсатор
почти полностью заряжен.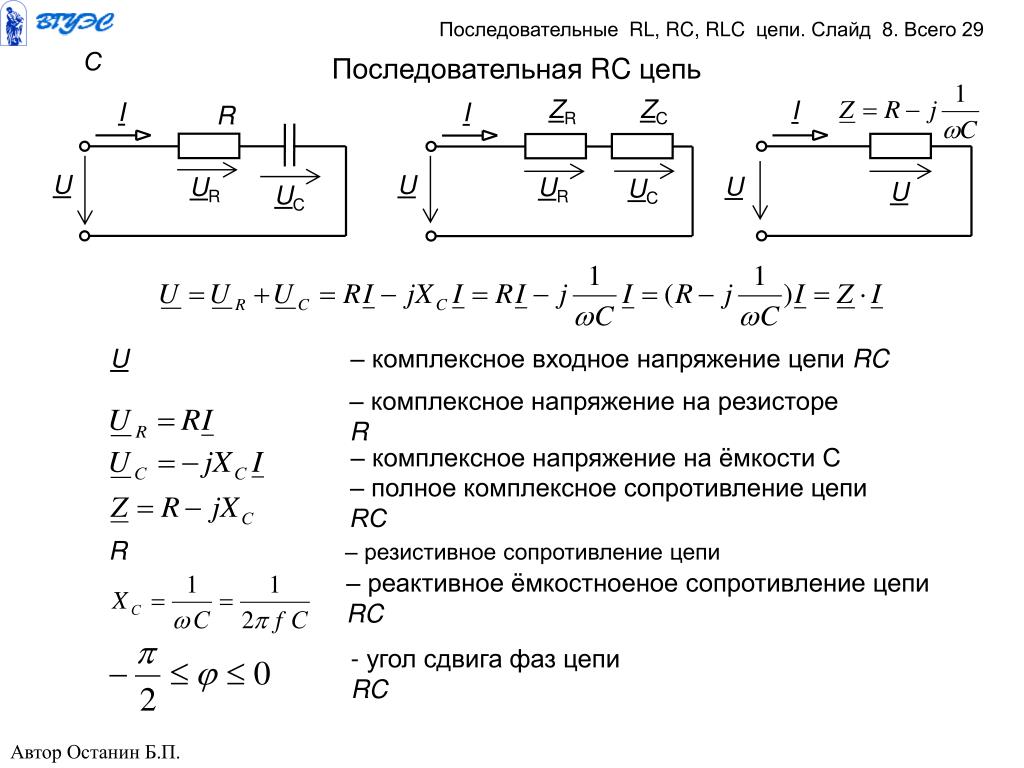 Это показано на рисунке ниже.
Это показано на рисунке ниже.
Прямоугольная волна применяется к короткому интегратору с постоянной времени.
Обратите внимание, что передний фронт прямоугольной волны на конденсаторе равен округлый. Если бы постоянная времени была сделана очень короткой, закругленный край стал бы квадратным.
Средний интегратор с постоянной времени
Постоянную времени на рисунке выше можно изменить, увеличив значение переменного резистора на 10000 Ом. Тогда постоянная времени будет равна до 100 микросекунд.
Эта постоянная времени известна как средняя постоянная времени. Его значение находится между
экстремальные диапазоны коротких и длинных постоянных времени. В этом случае его
значение оказывается в точности равным длительности входного импульса,
100 микросекунд. Показана форма выходного сигнала после нескольких постоянных времени.
на рисунке ниже. Длинный, наклонный рост и падение напряжения вызваны
неспособность конденсатора быстро заряжаться и разряжаться через
Последовательное сопротивление 10 000 Ом.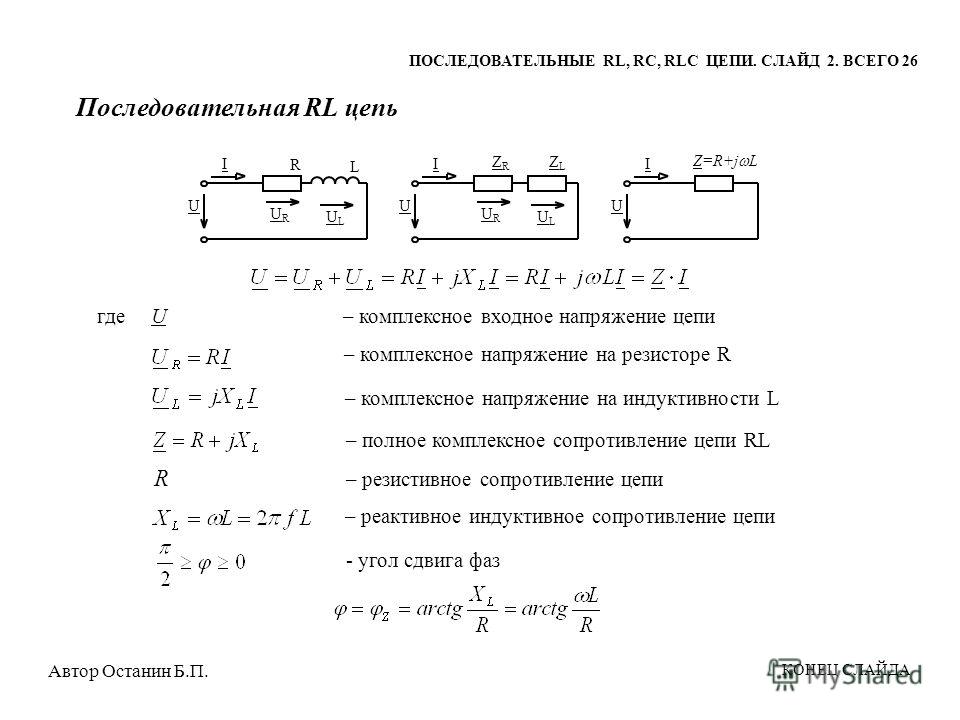
Средний интегратор с постоянной времени.
В первый момент времени к среде с постоянной времени приложено 100 вольт.
схема. В этой схеме 1 τ в точности равно длительности входного
пульс. Через 1 τ конденсатор зарядился до 63,2 процента входного напряжения.
(100 вольт). Следовательно, в конце 1 τ (100 мкс) напряжение
на конденсаторе равно 63,2 вольта. Однако, как только 100 микросекунд
истекло, и первоначальный заряд конденсатора поднялся до 63,2 вольта,
входное напряжение внезапно падает до 0. Оно остается там в течение 100 микросекунд.
Теперь конденсатор будет разряжаться в течение 100 микросекунд. С момента выписки
время составляет 100 микросекунд (1 τ ), конденсатор разрядится на 63,2%
его общий заряд 63,2 вольта, значение 23,3 вольта. Во время следующего
100 микросекунд, входное напряжение увеличится с 0 до 100 вольт
мгновенно. Конденсатор снова будет заряжаться в течение 100 микросекунд (1 τ ).
Напряжение, доступное для этого заряда, представляет собой разницу между напряжением
подается и заряд на конденсаторе (100 — 23,3 вольта), или 76,7 вольта.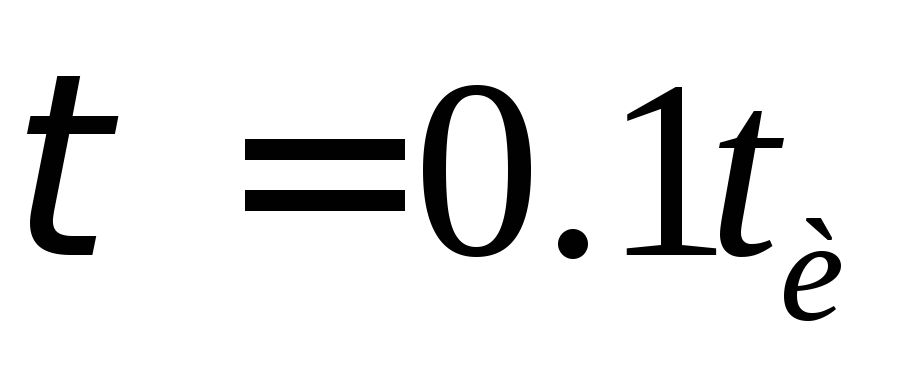 Так как конденсатор сможет заряжаться только за 1 τ , он будет заряжаться до
63,2 процента от 76,7 вольт, или 48,4 вольта. Общий заряд на
конденсатор в конце 300 мкс будет 23,3 + 48,4 вольта, или 71,7 вольта.
Так как конденсатор сможет заряжаться только за 1 τ , он будет заряжаться до
63,2 процента от 76,7 вольт, или 48,4 вольта. Общий заряд на
конденсатор в конце 300 мкс будет 23,3 + 48,4 вольта, или 71,7 вольта.
Обратите внимание, что напряжение конденсатора в конце 300 микросекунд больше, чем напряжение конденсатора в конце 100 мкс. Напряжение в конце 100 микросекунд составляет 63,2 вольта, а напряжение на конденсаторе в конце 300 микросекунд — это 71,7 вольта, увеличение на 8,5 вольта.
Форма выходного сигнала на этом графике ( v C ) — форма сигнала, будет производиться после многих циклов подачи сигнала на интегратор. конденсатор будет заряжаться и разряжаться постепенно, пока, наконец, заряжает и разряжает выше и ниже уровня 50 вольт. Уровень 50 вольт управляется максимальной амплитудой симметричного входного импульса, среднее значение которого составляет 50 вольт.
Интегратор с длительной постоянной времени
Если сопротивление в RC-интеграторе увеличить до 100 000 Ом, время
постоянная схемы составит 1000 мкс. Эта постоянная времени
10-кратная длительность импульса входного импульса. Следовательно, это
цепь с длительной постоянной выдержкой времени.
Эта постоянная времени
10-кратная длительность импульса входного импульса. Следовательно, это
цепь с длительной постоянной выдержкой времени.
Форма выходного сигнала на конденсаторе показана на рисунке. ниже. Форма выходного сигнала характеризуется длинным, наклонным нарастание и падение напряжения на конденсаторе.
Прямоугольная волна применительно к интегратору с большой постоянной времени.
В первый момент времени на большую постоянную времени подается 100 вольт.
схема. Величина заряда конденсатора в конце первых 100
микросекунды входного сигнала можно найти с помощью
Таблица универсальной постоянной времени. Предположим, что линия
проецируется вверх от точки базовой линии, соответствующей 0,1 т .
Линия будет пересекать кривую в точке, которая представляет собой процент напряжения
через конденсатор в конце первых 100 микросекунд. С момента применения
напряжение 100 вольт, заряд на конденсаторе в конце первого
100 микросекунд будут примерно 9,5 вольт. В конце первого
100 микросекунд, входной сигнал внезапно упадет до 0, а конденсатор
начнет разряжаться. Он сможет разряжаться за 100 микросекунд.
Следовательно, конденсатор разрядится на 90,5 процента накопленного
9,5 вольт (0,095 × 9,5 = 0,90 вольт). Разряд
0,90 вольта приведут к остаточному заряду на конденсаторе 8,6 вольт.
По истечении 200 микросекунд входной сигнал снова резко возрастет до
значение 100 вольт. Конденсатор сможет заряжаться до 9,5 процентов
разности (100 — 8,6 = 91,4 вольта). Это также может быть представлено как
значение 8,7 вольта плюс начальные 8,6 вольта. Это приводит к общему
заряд на конденсаторе (в конце первых 300 мкс)
8,7 + 8,6 = 17,3 вольта.
В конце первого
100 микросекунд, входной сигнал внезапно упадет до 0, а конденсатор
начнет разряжаться. Он сможет разряжаться за 100 микросекунд.
Следовательно, конденсатор разрядится на 90,5 процента накопленного
9,5 вольт (0,095 × 9,5 = 0,90 вольт). Разряд
0,90 вольта приведут к остаточному заряду на конденсаторе 8,6 вольт.
По истечении 200 микросекунд входной сигнал снова резко возрастет до
значение 100 вольт. Конденсатор сможет заряжаться до 9,5 процентов
разности (100 — 8,6 = 91,4 вольта). Это также может быть представлено как
значение 8,7 вольта плюс начальные 8,6 вольта. Это приводит к общему
заряд на конденсаторе (в конце первых 300 мкс)
8,7 + 8,6 = 17,3 вольта.
Обратите внимание, что напряжение конденсатора в конце первых 300 микросекунд равно больше, чем напряжение конденсатора в конце первых 100 микросекунд. Напряжение в конце первых 100 микросекунд составляет 9,5 вольт; конденсатор напряжение в конце первых 300 мкс составляет 17,3 вольта, увеличение 7,8 вольта.
Конденсатор заряжается и разряжается поэтапно до тех пор, пока
наконец, конденсатор заряжается и разряжается выше и ниже уровня 50 вольт.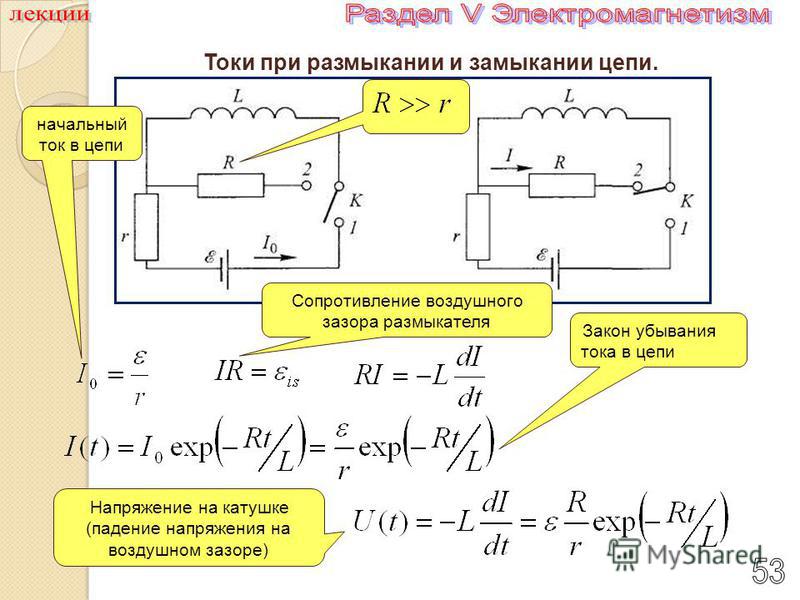 Уровень 50 вольт контролируется максимальной амплитудой прямоугольного сигнала.
входной импульс, среднее значение которого составляет 50 вольт.
Уровень 50 вольт контролируется максимальной амплитудой прямоугольного сигнала.
входной импульс, среднее значение которого составляет 50 вольт.
Что такое интегратор RL? – Book Vea
Содержание
Что такое интегратор RL?
Подобно интегратору RC, интегратор RL представляет собой схему, аппроксимирующую математический процесс интегрирования. При эквивалентных условиях осциллограммы выглядят как интегратор RC. Для цепи RL u03c4 L/R. Базовая схема интегратора RL представляет собой резистор, включенный последовательно с катушкой индуктивности и источником.
Для чего используется цепь RL?
Цепи RL используются в Системы связи, передатчики радиоволн, схемы генераторов, усилители РЧ, схемы фильтрации, схемы с переменной настройкой, усиление тока и напряжения и т. д.
Является ли схема RL дифференциатором?
Формулы для дифференциатора RL Дифференциатор работает как формирователь импульсов. Элемент RL генерирует импульсное переменное напряжение на выходе схемы из прямоугольного напряжения на входе схемы.
Что такое радиоуправляемый интегратор?
RC-интегратор представляет собой последовательно соединенную RC-сеть, которая выдает выходной сигнал, соответствующий математическому процессу интегрирования.
Какова цель RL?
RL Настой используется для снабжения организма дополнительной водой и электролитами (солью). Он используется, когда пациент не может пить достаточное количество жидкости или когда необходимы дополнительные жидкости после какой-либо операции или травмы.
Что такое RL в усилителе?
1 (а). Конденсатор CB используется для связи входного сигнала с входным портом усилителя, а конденсатор CC используется для связи выхода усилителя с портом 9.0005 Нагрузочный резистор RL.
Что такое электротехника RL?
Цепь резистора-индуктора (цепь RL), или фильтр RL, или сеть RL — это электрическая цепь, состоящая из резисторов и катушек индуктивности, приводимая в действие источником напряжения или тока.
Где используются цепи RC и RL?
RC-цепи используются в схемах синхронизации, вспышках фотокамер, кардиостимуляторах и т. д. RC- и RL-цепи используются для фильтрации определенных частот и допускают определенные частоты, форму волны и синхронизацию.
Что такое схема серии RL?
RL-цепь (также известная как RL-фильтр или RL-сеть) определяется как электрическая цепь, состоящая из пассивных элементов цепи резистора (R) и катушки индуктивности (L), соединенных вместе, приводимая в действие источником напряжения или Источник тока.
Что такое дифференциатор RL?
24. Дифференциатор RLДифференциатор RL также представляет собой схему, которая аппроксимирует математический процесс дифференцирования. Он может производить выходные данные, которые представляют собой скорость изменения входных данных при определенных условиях. Базовая схема дифференциатора RL представляет собой катушку индуктивности, последовательно соединенную с резистором и истоком.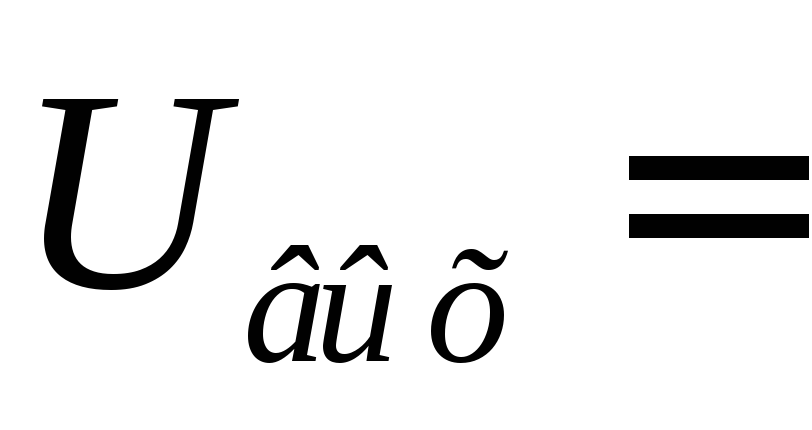
Когда цепь RL используется в качестве выходного сигнала дифференциатора?
В дифференцирующей цепи RL выходное напряжение снимается через резистор.
Что такое дифференциальные цепи?
В электронике дифференциатором является схема, спроектированная таким образом, что выход схемы приблизительно прямо пропорционален скорости изменения (производной по времени) входа. Настоящий дифференциатор не может быть физически реализован, потому что он имеет бесконечный коэффициент усиления на бесконечной частоте.
Что означает цепь RL?
Цепи RL (резисторно-индукторная цепь), также называемые RL-сетью или RL-фильтром, представляют собой тип цепи, включающей комбинацию катушек индуктивности и резисторов и обычно приводимый в действие каким-либо источником питания. Таким образом, в цепи RL индуктор и резистор соединены либо параллельно, либо последовательно друг с другом.
Для чего используется интегратор?
Интегратор в приложениях измерения и управления — это элемент, выходной сигнал которого является интегралом по времени его входного сигнала.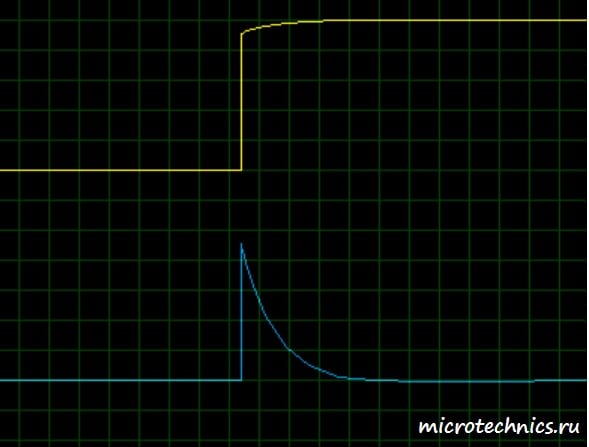 Он накапливает входное количество в течение определенного времени для получения репрезентативного результата. Интеграция является важной частью многих инженерных и научных приложений.
Он накапливает входное количество в течение определенного времени для получения репрезентативного результата. Интеграция является важной частью многих инженерных и научных приложений.
Для чего нужен дифференциатор RC?
RC Резюме дифференциатора Схема дифференциатора используется для создания запускающих или пиковых импульсов для приложений схемы синхронизации. Когда на эту RC-цепь подается ступенчатая прямоугольная волна, на выходе получается волна совершенно другой формы.
Для чего используется RC-цепь?
RC-цепь имеет тысячи применений и является очень важной схемой для изучения. Его можно использовать не только для синхронизации цепей , но и для фильтрации нежелательных частот в цепи и в источниках питания, например, для вашего компьютера, чтобы помочь преобразовать переменное напряжение в постоянное напряжение
Каково назначение цепи RL?
Использование цепи RL Используется в качестве фильтра верхних частот или фильтра нижних частот. Используется в дросселях ламповых ламп Используется для фильтрации сигналов малой мощности и накопления энергии в виде потенциальной магнитной энергии
Используется в дросселях ламповых ламп Используется для фильтрации сигналов малой мощности и накопления энергии в виде потенциальной магнитной энергии
Где используется RL-цепь?
Использование цепи RL Для подачи питания постоянного тока на радиочастотные усилители, где дроссель используется для пропускания постоянного тока смещения и блокирования возврата РЧ обратно в источник питания.
Что такое система RL?
Обучение с подкреплением (RL) — это область машинного обучения, связанная с тем, как интеллектуальные агенты должны действовать в окружающей среде, чтобы максимизировать понятие кумулятивного вознаграждения. Обучение с подкреплением — это одна из трех основных парадигм машинного обучения, наряду с обучением с учителем и обучением без учителя.
Для чего используются RC- и RL-цепи?
Цепи RC и RL используются для обеспечения фильтрации, формирования сигналов и синхронизации. Чаще всего используется конденсатор.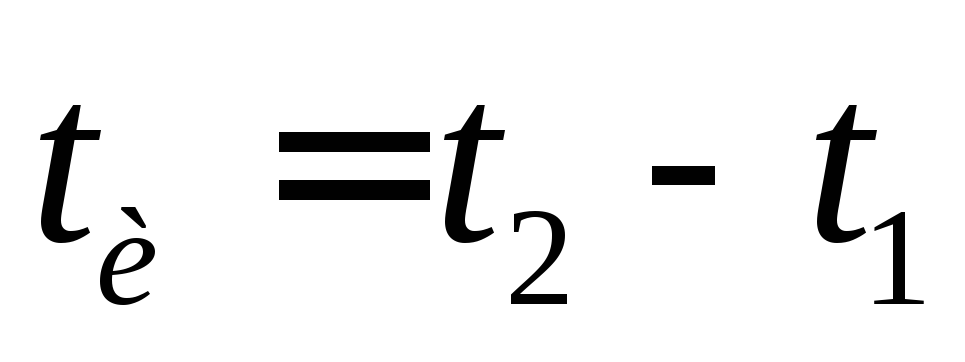 Конденсаторы меньше и экономичнее катушек индуктивности и не имеют сильных магнитных полей. Последовательная RC-цепочка содержит источник напряжения с последовательно соединенными резистором и конденсатором.
Конденсаторы меньше и экономичнее катушек индуктивности и не имеют сильных магнитных полей. Последовательная RC-цепочка содержит источник напряжения с последовательно соединенными резистором и конденсатором.
Что такое RL в транзисторе?
RL Настой используется для снабжения организма дополнительной водой и электролитами (солью). Он используется, когда пациент не может пить достаточное количество жидкости или когда необходимы дополнительные жидкости после какой-либо операции или травмы.
Какова формула RL?
Поскольку сопротивление нагрузки ( R L ) соединено последовательно с коллектором, коэффициент усиления по току схемы транзистора с общим эмиттером довольно велик, поскольку он равен отношению Ic/Ib. Коэффициент усиления по току транзистора обозначается греческим символом бета (u03b2).
Что такое RO в усилителе?
Эти уравнения показывают, что последовательная RL-цепь имеет постоянную времени, обычно обозначаемую как u03c4 L/R и представляющую собой время, за которое напряжение на компоненте либо падает (на катушке индуктивности), либо возрастает (на резисторе) с точностью до 1 /e его конечного значения.
Что означает RL в электротехнике?
цепь резистора-индуктора
Что такое RL в цепи переменного тока?
RL Настой используется для снабжения организма дополнительной водой и электролитами (солью). Он используется, когда пациент не может пить достаточное количество жидкости или когда необходимы дополнительные жидкости после какой-либо операции или травмы.
Естественная реакция RL — Интуиция
Мы разрабатываем интуицию для естественной реакции цепи резистор-индуктор $(\text{RL})$.
Формальный вывод описан в следующей статье, естественный ответ RL — вывод
Автор Вилли Макаллистер.
Содержимое
- Настройка
- Начальные условия
- Что происходит спустя долгое время?
- Что происходит между ними?
Естественный отклик цепи — это то, что цепь делает «естественно», когда у нее есть некоторая внутренняя энергия, и мы позволяем ей рассеиваться.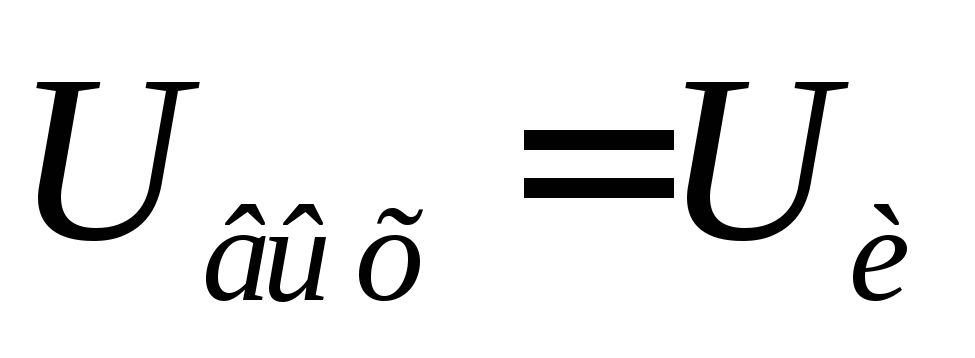 Это самое основное поведение схемы.
Это самое основное поведение схемы.
Почему мы изучаем естественную реакцию $\text{RL}$? Потому что он появляется каждый раз, когда провод включается в цепь. Если провод сформирован в катушку, мы называем это катушкой индуктивности. Даже если он не скручен, каждый провод и каждая дорожка на печатной плате имеют небольшую индуктивность, которая может иметь значение. Золотые провода в интегральной схеме имеют достаточную индуктивность, чтобы играть важную роль в очень быстрых схемах. Вокруг всегда есть индуктивность и всегда рядом сопротивление.
Настройка
Чтобы заставить схему $\text{RL}$ что-то делать, мы вызываем внешнего помощника для создания тока в катушке индуктивности. Затем отключаем внешнюю цепь, отступаем назад и смотрим, что происходит.
С правой стороны у нас есть катушка индуктивности $\text L$ и резистор $\text R$. Это схема, которую мы хотим изучить. Слева находится наш «внешний помощник», состоящий из источника тока $\text I$, резистора $\text R0$ и переключателя в замкнутом положении.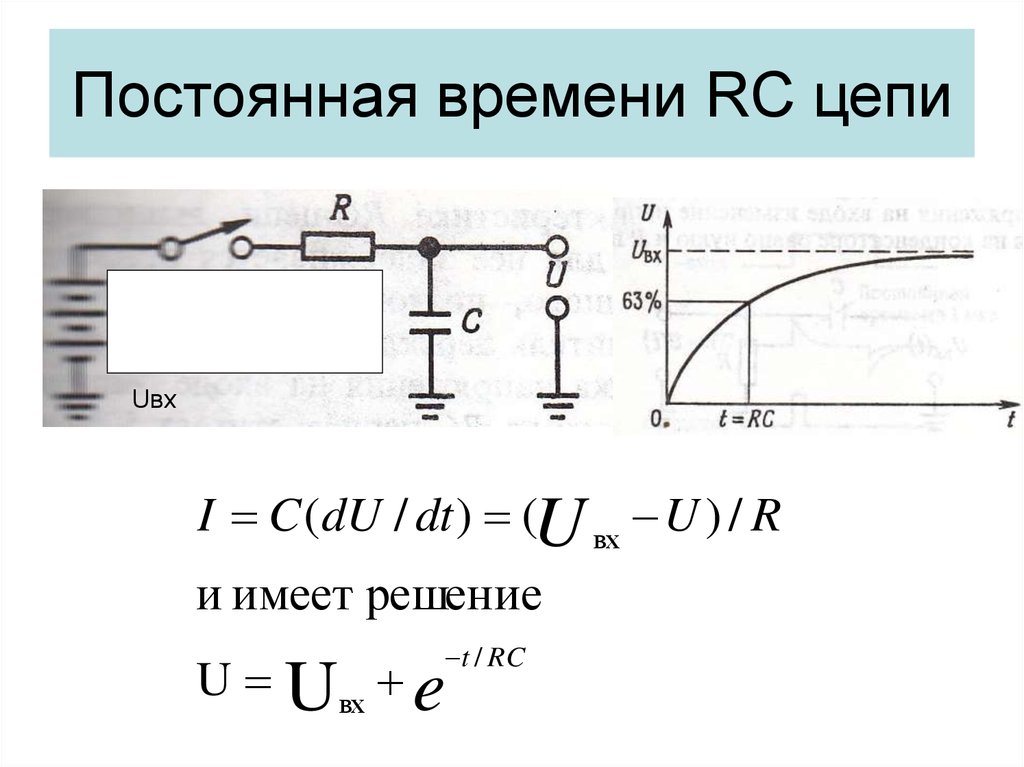
Предположим, что переключатель был замкнут в течение длительного времени. Синяя петля показывает, как протекает ток в этой цепи,
Откуда мы знаем, что весь ток протекает только через катушку индуктивности и не течет ни по одному из резисторов? Уравнение индуктора говорит нам об этом:
$v = \text{L}\,\dfrac{di}{dt}$
Производная по времени является мерой того, как значение изменяется.
Производная по времени от константы всегда равна $0$.
Поскольку ток от источника постоянный, в записи производной мы говорим:
$\dfrac{di}{dt} = \dfrac{d}{dt}\text I_0 = 0$.
Если мы подставим это значение в уравнение индуктора, мы получим
$v = \text L\,\dfrac{di}{dt}=\text L \cdot 0$
$v = 0$
Итак напряжение на катушке индуктивности (и, следовательно, на обоих резисторах) равно $0$. Закон Ома говорит нам, что резистор с напряжением $0$ вольт имеет ток $0$. Следовательно, весь $\text I_0$ должен проходить через индуктор.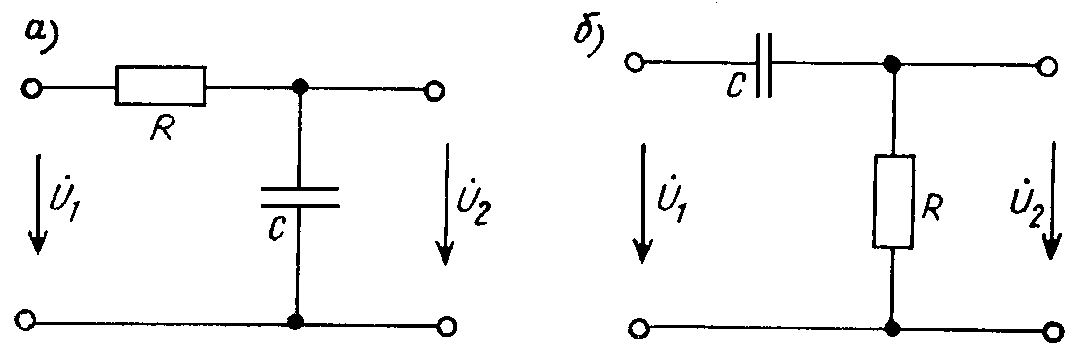
Когда ток в катушке индуктивности постоянный (также известный как DC или нулевая частота), на ней $0$ вольт, как в идеальном проводе. В этих условиях индуктор выглядит как короткое замыкание.
Резюме: Перед размыканием переключателя
Ток в катушке индуктивности равен $\text I_0$.
Напряжение на катушке индуктивности и резисторе $0$ вольт.
Начальные условия
Мы знаем, что происходит, когда переключатель замкнут. Следующим шагом является нахождение $i$ и $v$ всего после , когда переключатель размыкается. Они называются начальными условиями . Размыкание переключателя — это резкое изменение цепи. Что происходит с током и напряжением? Они остаются прежними? Переходят ли они к какому-то новому значению? Мы должны разобраться.
Переключатель размыкается в момент времени $t = 0$. Вспомогательная схема $\text I$ и $\text R0$ отключается от секции $\text{RL}$. В итоге у нас есть два отдельных пути для тока:
На вспомогательной стороне ток от источника течет через $\text R0$.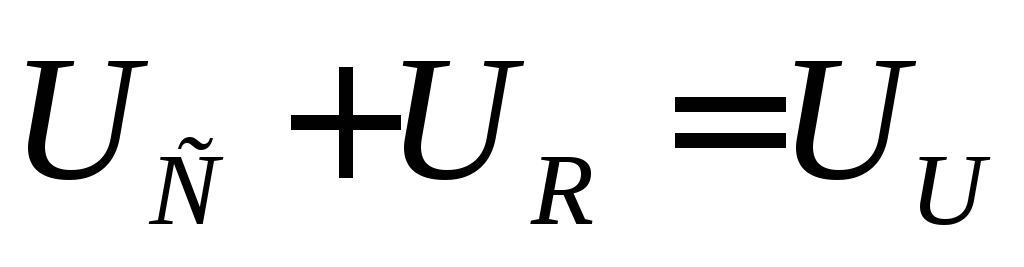
Со стороны $\text{RL}$ ток в $\text L$ протекает через $\text R$.
Вспомогательная схема сделала свое дело и впредь не будем на нее обращать внимание.
Зачем нужен R0?После размыкания переключателя $\text R0$ обеспечивает путь для тока от текущего источника. Нехорошо просить источник тока управлять разомкнутой цепью. Идеальный источник тока создает бесконечное напряжение, если пытается направить ток в разомкнутую цепь. Если вы смоделируете эту схему без $\text R0$, симулятор будет очень недоволен. (По той же причине никогда не следует закорачивать идеальный источник напряжения, чтобы избежать бесконечного тока.) 9+$, что происходит с током индуктора? Это останавливается? Это продолжается? Это меняется?
Вот самое интересное свойство катушки индуктивности,
Ток в катушке индуктивности не может изменяться мгновенно.
почему? Ток, подаваемый в индуктор, вызывает накопление энергии в магнитном поле, окружающем индуктор. Если ток прекращается, накопленная энергия не исчезает и не уходит куда-то еще за нулевое время. Накопленная магнитная энергия возвращается в цепь, продолжая проталкивать ток индуктора. 9-)$.
Накопленная магнитная энергия возвращается в цепь, продолжая проталкивать ток индуктора. 9-)$.
Это поведение предсказывается уравнением индуктора,
$v = \text L\,\dfrac{di}{dt}$
Если ток изменяется мгновенно, это подразумевает конечное изменение тока, $di = \Delta i$, происходящее за нулевое время, $dt = 0$. Производная тока равна $di/dt = \Delta i/0$ или бесконечно. Уравнение индуктора предсказывает, что на индукторе будет бесконечное напряжение. Бесконечного напряжения не бывает. Здесь имеет как некоторый конечный интервал времени $\Delta t$, позволяющий рассеять энергию.
механическая аналогияЭнергия, запасенная в магнитном поле индуктора, аналогична импульсу, запасенному в массе. Если вы попытаетесь остановить движущуюся массу, ее импульс не рассеется мгновенно. Вы не можете остановить движущуюся массу в одно мгновение. Мы говорим: импульс стремится поддерживать движение массы.
Отличным примером движущейся массы является велосипедное колесо. Поднимите переднее колесо велосипеда с земли и хорошенько крутите его. Теперь схватите его рукой и постарайтесь мгновенно остановить. Ваша рука получает сильный толчок, и колесо не останавливается сразу. В прялке хранится много энергии. 9-) = \text I_0$
Поднимите переднее колесо велосипеда с земли и хорошенько крутите его. Теперь схватите его рукой и постарайтесь мгновенно остановить. Ваша рука получает сильный толчок, и колесо не останавливается сразу. В прялке хранится много энергии. 9-) = \text I_0$
Это начальное условие для тока $\text{RL}$.
Начальное напряжение
Что происходит с напряжением, когда выключатель размыкается? Внезапно в $\text R$ возникает ток, поэтому напряжение резко подскакивает до $v = \text I_0\,\text R$.
Ток дросселя не может изменяться внезапно, но его напряжение может совершать резкие скачки.
Напряжение индуктора может измениться в одно мгновениеКатушка индуктивности не имеет проблем, если ее напряжение изменяется мгновенно. Если вы заставите напряжение подскочить с $1$ до $10\,\text V$ уравнение $i$-$v$ говорит, что наклон тока, $di/dt$, увеличится в $10$. Ток индуктора может изменить наклон; он просто не может резко перейти к новому значению.
В механической аналогии напряжение аналогично силе. Ничто не мешает вам внезапно изменить силу нажатия на велосипедное колесо, когда вы его раскручиваете.
Ничто не мешает вам внезапно изменить силу нажатия на велосипедное колесо, когда вы его раскручиваете.
Мы поразмышляли над событием переключения.
Что происходит спустя долгое время?
Прежде чем мы рассмотрим, что происходит после события переключения, давайте сначала подумаем о том, что происходит в долгосрочной перспективе. Если мы ждем долгое время, магнитная энергия в катушке индуктивности проявляется в виде тока, который в конечном итоге преобразуется резистором в тепло. Когда вся энергия превратится в тепло, $i$ будет равно $0$, а $v$ будет равно $0$. это конечное состояние нашей схемы.
$i(t)$ и $v(t)$ выглядят так с добавленным долговременным откликом,
Что происходит между ними?
Теперь мы заполняем то, что происходит между $t=0$ и «много времени спустя». Давайте сделаем предположение. Вероятно, есть какая-то плавная кривая, соединяющая два сегмента. Я предполагаю, что скорость изменения может быть выше в начале, когда ток высок.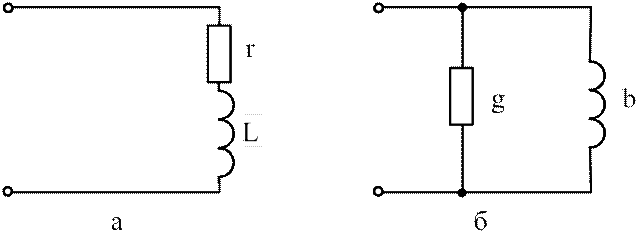 Это означает, что рассеиваемая мощность в резисторе высока, поэтому энергия рассеивается быстрее. Руководствуясь этой интуицией, мы рисуем предсказанные кривые для тока и напряжения,
Это означает, что рассеиваемая мощность в резисторе высока, поэтому энергия рассеивается быстрее. Руководствуясь этой интуицией, мы рисуем предсказанные кривые для тока и напряжения,
Итог
Это окажется довольно хорошим предположением для естественного ответа $\text{RL}$. Просто своей интуицией мы разобрались, где он начинается и заканчивается, и оценили, как выглядят ток и напряжение при переходе. Мы не совсем уверены, насколько быстро снижаются кривые или как долго на самом деле длится «долгое время».
Формальный вывод в следующей статье, естественный ответ RL — вывод.
RC и RL
Ваш браузер не поддерживает апплеты Java
ПЕРЕХОДНЫЕ РЕАКЦИИ RC И RL
Конденсаторы сопротивляются изменениям в Напряжение. Катушки индуктивности противодействуют изменениям тока.
Постоянная времени в
Конденсаторная цепь представляет собой произведение сопротивления и емкости. Т = RC.
постоянная времени цепи индуктора — это индуктивность, деленная на
сопротивление. Т = Л/П.
Т = Л/П.
Постоянная времени – это время требуется для изменения на 63,2 % напряжения на конденсаторе или тока через индуктор.
Постоянные времени позволяют исследование переходных характеристик в последовательных RC и RL цепях.
Преходящая реакция – это временное состояние, связанное с изменением напряжения или тока, существующее только пока не будет достигнуто установившееся значение напряжения или тока.
Переходные реакции связаны с несинусоидальными формами напряжения и тока (например, квадратной, прямоугольной и треугольной формы), а также при включенном источнике постоянного тока и выключенный.
Влияние индуктивности и емкость на несинусоидальных сигналах должна вызывать изменение формы сигнала.
Цепи RC и RL используются для обеспечивают фильтрацию, формирование волны и синхронизацию.
Конденсатор чаще всего
использовал. Конденсаторы меньше и экономичнее катушек индуктивности и не имеют
сильные магнитные поля.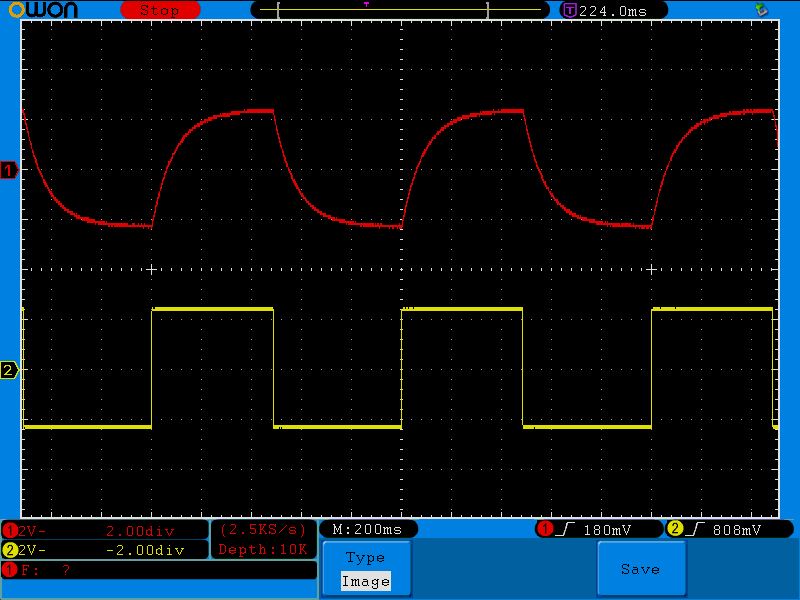
ЦИКЛЫ ЗАРЯДА И РАЗРЯДА RC
Цикл заряда
Цепь серии RC содержит источник напряжения с последовательно соединенными резистором и конденсатором. Переключатель обеспечивает заряд или разряд.
t0 – время, когда переключатель сначала закрывается. t1 – время, когда конденсатор достигает полного заряда или увольнять. Время полной зарядки или разрядки конденсатора равно пяти постоянные времени.
Напряжение источника мгновенно увеличивается от нуля до максимума и остается на этом уровне.
Ток цепи мгновенно увеличивается до максимума, а затем постепенно уменьшается по мере заряда конденсатора. Когда конденсатор полностью заряжен током при нуле и остается нулем.
Напряжение на резистор мгновенно возрастает до максимума, а затем постепенно падает.
Напряжение на конденсатор постепенно увеличивается до максимума.
Цикл разрядки
При переводе переключателя в
В положении разряда напряжение источника мгновенно падает до нуля.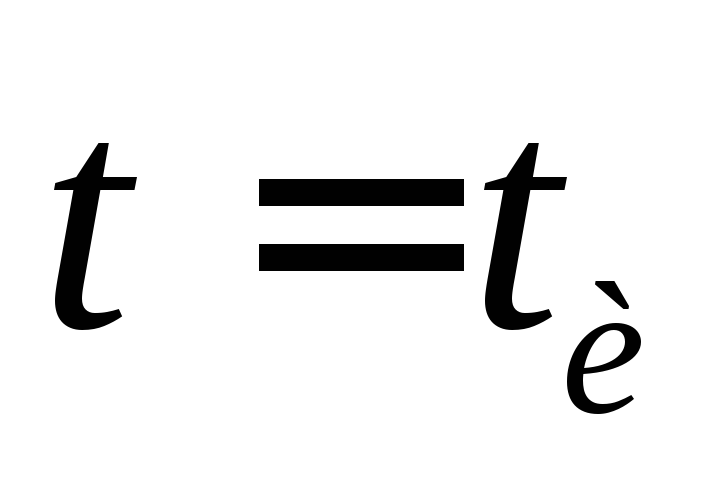 Разряд
ток мгновенно достигает максимума, а затем постепенно снижается. Резистор
напряжение моментально достигает максимума. Напряжение постепенно снижается до нуля.
напряжение на конденсаторе также постепенно уменьшается, пока не достигнет нуля.
Разряд
ток мгновенно достигает максимума, а затем постепенно снижается. Резистор
напряжение моментально достигает максимума. Напряжение постепенно снижается до нуля.
напряжение на конденсаторе также постепенно уменьшается, пока не достигнет нуля.
Высокий емкостный разряд Текущий
Схема может быть настроена для обеспечения высокого тока разряда на мгновение во времени. Это обычно используется для съемки со вспышкой.
ПОСТОЯННАЯ ВРЕМЕНИ RC
Время, необходимое для зарядки конденсатора до 63,2 % или разряд до 36,8 % от максимального напряжения является постоянной времени. T = RC R находится в ом C в фарадах.
После пяти постоянных времени напряжение составляет 99,3 %, т.е. обычно считается полностью заряженным.
МОм x мкФ = с
кОм x мкФ = мс
МОм x пФ = us
ДИАГРАММА ПОСТОЯННОЙ ВРЕМЕНИ
Диаграмма может использоваться для определения значения напряжения или тока.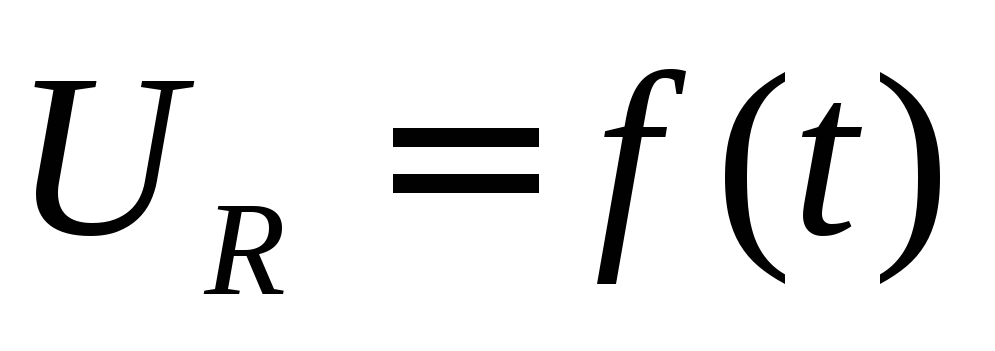 на любое количество времени.
на любое количество времени.
RC ЭКСПОНЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Уравнения зарядки конденсатора
Напряжение конденсатора
Ток конденсатора
Напряжение зарядки Время
Уравнения разрядки конденсатора
Напряжение конденсатора
Ток конденсатора
Напряжение разрядки Время
ПОСТОЯННАЯ ВРЕМЕНИ Л/П
т = л/р
Высокое напряжение возникает, когда цепь RL разомкнута
Когда цепь разомкнута магнитное поле катушки индуктивности схлопывается. Коллапсирующее магнитное поле будет индуцировать высокое напряжение. Диоды часто используются в цепях индуктивности, таких как реле. чтобы предотвратить повреждение компонентов схемы этим высоким напряжением.
L / R ЭКСПОНЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Уравнение тока индуктора
Уравнение напряжения индуктора
ДЛИННЫЙ, СРЕДНИЙ И КОРОТКИЙ ПОСТОЯННЫЕ ВРЕМЕНИ
RC-цепи используются больше
чаще, чем цепи RL.
Длительная постоянная времени
Средняя постоянная времени
Кратковременная постоянная
ИНТЕГРАТОР ДУ
ДИФФЕРЕНЦИАТОР RC
Анализ параллельной цепи RL с использованием дифференциального уравнения
Параллельная цепь RL первого порядка имеет один резистор (или группу резисторов) и один индуктор. Цепи первого порядка можно анализировать с помощью дифференциальных уравнений первого порядка. Анализируя схему первого порядка, вы можете понять ее синхронизацию и задержки.Анализ такой параллельной RL-цепи, как показанная здесь, следует тому же процессу, что и анализ последовательной RC-цепи. Так что, если вы знакомы с этой процедурой, это должно быть на одном дыхании.
Если в вашей параллельной цепи RL индуктор соединен с сетью резисторов, а не с одним резистором, вы можете использовать тот же подход для анализа цепи. Но сначала вам нужно найти аналог Norton, сократив сеть резисторов до одного резистора, подключенного параллельно с одним источником тока.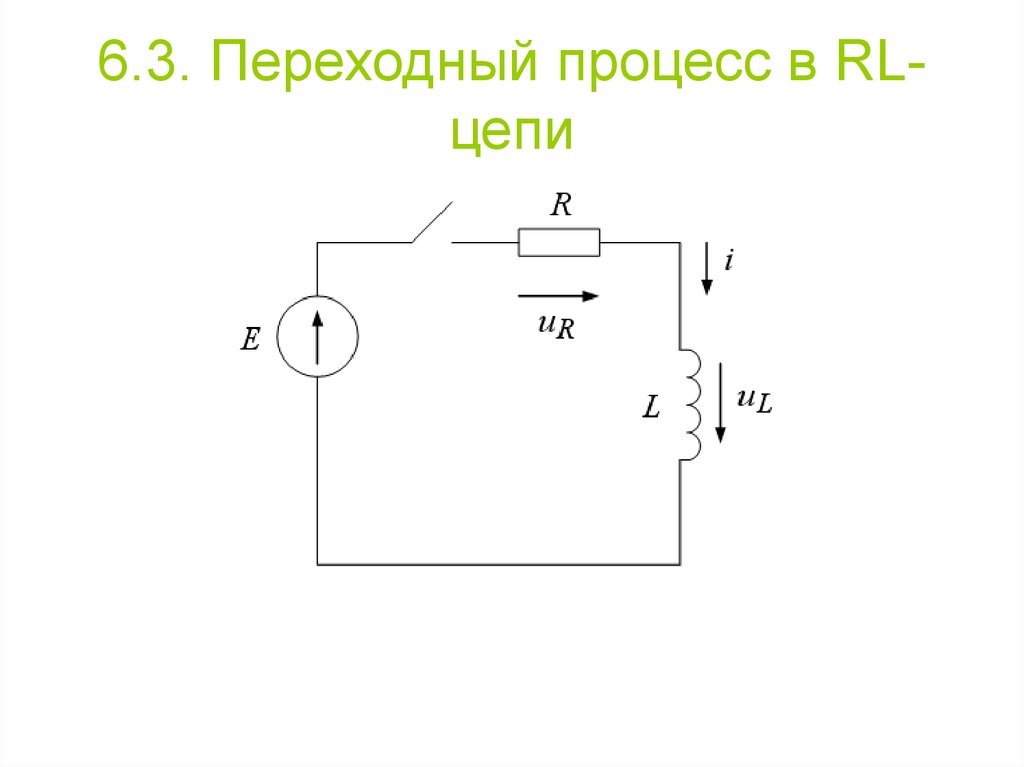
Пуск с простой параллельной цепью RL
Поскольку в примере резистор и катушка индуктивности соединены параллельно, они должны иметь одинаковое напряжение v(t) . Ток резистора i R (t) основан на законе Ома: индуктивность.Для создания напряжения на катушке индуктивности необходим переменный ток. Если ток индуктора не меняется, напряжение на индукторе отсутствует, что означает короткое замыкание.
Теперь подставьте v(t) = Ldi(t)/dt в закон Ома, потому что у вас одинаковое напряжение на резисторе и катушке индуктивности: . Используйте KCL в узле A схемы примера, чтобы получить i N (t) = i R (t) =i(t) .Подставьте i R (t) в уравнение KCL, чтобы получить
Параллельная цепь RL является цепью первого порядка, поскольку она описывается дифференциальным уравнением первого порядка, где неизвестной переменной является ток катушки индуктивности i(t) . Цепь, содержащая одну эквивалентную катушку индуктивности и эквивалентный резистор, является схемой первого порядка.
Цепь, содержащая одну эквивалентную катушку индуктивности и эквивалентный резистор, является схемой первого порядка.
Зная ток катушки индуктивности, вы можете определить магнитную энергию, хранящуюся в катушке индуктивности.
Обычно ток катушки индуктивности называют переменной состояния, поскольку ток катушки индуктивности описывает поведение схемы.
Рассчитать реакцию при нулевом входе для параллельной цепи RL
Вот как параллельная схема RL разделяется на две проблемы: отклик с нулевым входом и отклик с нулевым состоянием. Здесь вы начнете с анализа ответа с нулевым входом.Для упрощения вы устанавливаете источник входного сигнала (или функцию форсирования) равным 0: i N (t) = 0 ампер. Это означает отсутствие входного тока навсегда — большой жирный ноль. Дифференциальное уравнение первого порядка сводится к
Для входного источника без тока ток дросселя i Z I называется реакцией нулевого входа . На цепь не действуют никакие внешние силы, за исключением ее начального состояния (или тока индуктора в данном случае). Выходной сигнал обусловлен некоторым начальным током катушки индуктивности I 0 в момент времени t = 0,
На цепь не действуют никакие внешние силы, за исключением ее начального состояния (или тока индуктора в данном случае). Выходной сигнал обусловлен некоторым начальным током катушки индуктивности I 0 в момент времени t = 0,
Вы делаете обоснованное предположение о решении (естественная экспоненциальная функция!) и сначала подставляете свое предположение в RL дифференциальное уравнение порядка. Предположим, что ток индуктора и решение равны
i ZI (t) = Be ктЭто разумное предположение, потому что производная экспоненты по времени также является экспонентой. Как хороший друг, экспоненциальная функция не подведет вас при решении этих дифференциальных уравнений.
Вы определяете константы B и k далее. Подставьте свое предположение i ZI (t) = Be кт в дифференциальное уравнение:
Замена I ZI (T) с BE KT , а выполнение математики дает вам следующее:
Вы имеете характеристическое равное после того, как Be .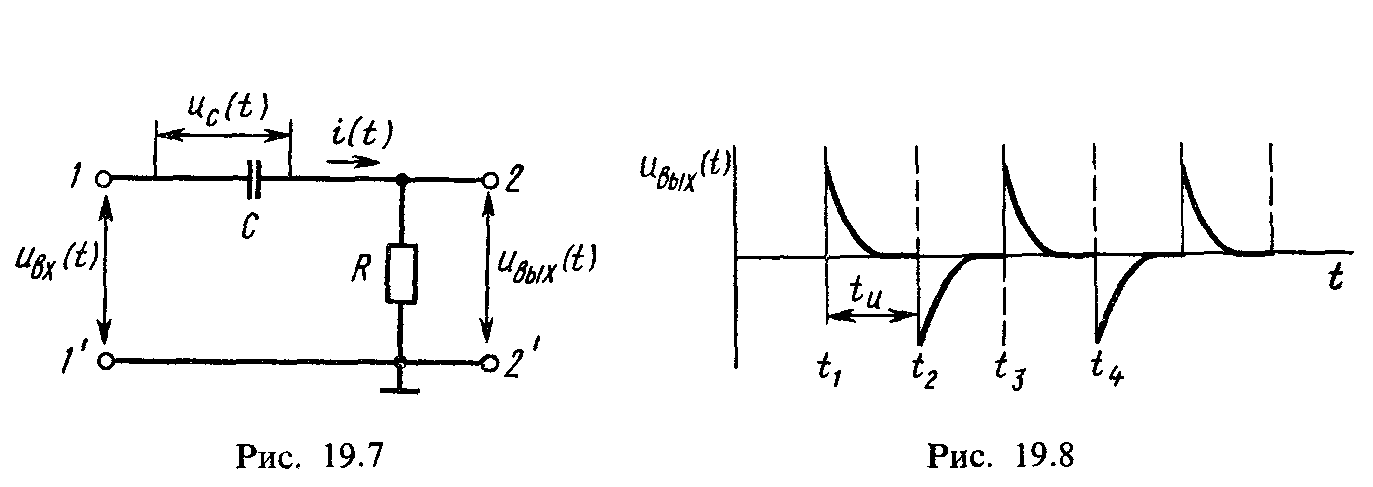 :
:
Характеристическое уравнение дает вам алгебраическую задачу для решения константы k :
Используйте k = –R/L и начальный ток дросселя I 0 AT T = 0. Это подразумевает, что B = I 0 , поэтому ответ с нулевым входом I ZI (T) ZI (T) : Tome : Tome : T) : T) : T) : T) : T) : T) : T) : T) : T) : T) : Tome : Tom. : Tome Zi
Постоянная L/R называется постоянной времени . Постоянная времени обеспечивает меру того, сколько времени требуется току индуктора, чтобы перейти к 0 или перейти из одного состояния в другое.
Для дальнейшего анализа параллельной схемы RL необходимо рассчитать отклик схемы в нулевом состоянии, а затем добавить этот результат к отклику при нулевом входе, чтобы найти общий отклик схемы.
Об этой статье
Эта статья взята из книги:
- Анализ цепей для чайников,
Об авторе книги:
Джон М. Сантьяго-младший, доктор наук, служил в ВВС США (USAF). ) в течение 26 лет. В течение этого времени он занимал различные руководящие должности в области управления техническими программами, разработки приобретений и поддержки исследований в области эксплуатации. Находясь в Европе, он руководил более чем 40 международными научными и инженерными конференциями/семинарами.
Эту статью можно найти в категории:
- Схема,
Разница между RC и RL схемами (со сравнительной таблицей)
Основное различие между RC-цепями и RL-цепями заключается в том, что RC-цепь хранит энергию в виде электрического поля , а RL-цепь хранит энергию в виде магнитного поля.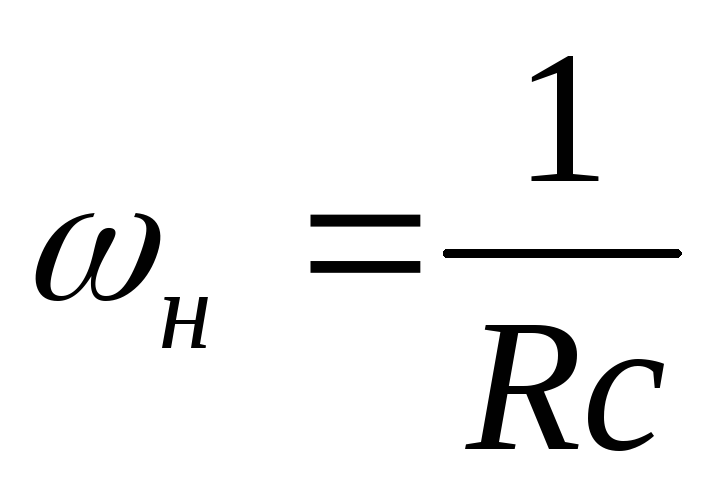
Резистивно-емкостная цепь образована последовательным подключением резистора к конденсатору, а для зарядки конденсатора предусмотрен источник питания. Цепь RL формируется путем соединения сопротивления с катушкой индуктивности, а для подачи тока на катушку индуктивности предусмотрен источник питания.
Еще одно существенное различие между RC- и RL-цепями заключается в том, что RC-цепь первоначально оказывает нулевое сопротивление току, протекающему через нее, а когда конденсатор полностью заряжен, она оказывает бесконечное сопротивление току. В то время как цепь RL первоначально противостоит току, протекающему через нее, но когда достигается установившееся состояние, она обеспечивает нулевое сопротивление току через катушку.
Между цепями RC и RL существует еще одно важное различие; мы обсудим все это с помощью сравнительной таблицы. Но перед этим давайте ознакомимся с содержанием этой статьи.
Тема: Цепи RC и RL
- Сравнительная таблица
- Определение
- Ключевые отличия
- Заключение
Сравнительная таблица
| Параметры | RC-цепь | RL-цепь |
|---|---|---|
| Определение | RC-цепь представляет собой последовательное соединение сопротивления и емкости, эта цепь хранит энергию в виде электрического поля. | Цепь RL представляет собой последовательную комбинацию сопротивления и индуктивности, которая накапливает энергию в виде магнитной энергии. |
| Рассеиваемая мощность | Высокая рассеиваемая мощность | Низкая рассеиваемая мощность |
| Фильтрация сигналов | Подходит для фильтрации сигналов малой мощности. | Подходит для фильтрации сигналов высокой мощности. |
| Размер и стоимость | Небольшой размер, легкий вес и дешевизна. | Катушки индуктивности имеют большие размеры, поэтому схемы RL громоздкие и дорогие. |
| Шум | RC-цепь генерирует низкий уровень шума или незначительный шум. | Цепь RL состоит из катушек индуктивности, которые создают магнитное поле, создающее гистерезис и шум в цепи. |
Определение
RC-цепь (сопротивление – емкостная цепь)
RC-цепь включает зарядку конденсатора посредством внешнего источника питания.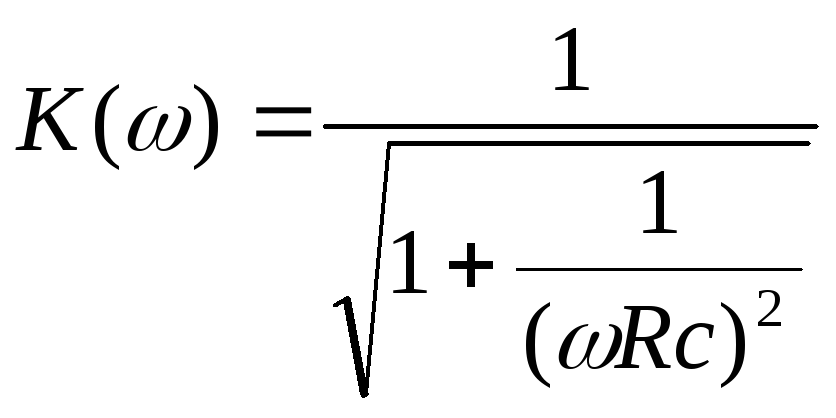 Первоначально, когда переключатель замкнут, сопротивление RC-цепи равно нулю. Это связано с тем, что конденсатор разряжен, через некоторое время, когда конденсатор полностью заряжен, поскольку больше напряжения не требуется, сопротивление, предлагаемое RC-цепью, бесконечно.
Первоначально, когда переключатель замкнут, сопротивление RC-цепи равно нулю. Это связано с тем, что конденсатор разряжен, через некоторое время, когда конденсатор полностью заряжен, поскольку больше напряжения не требуется, сопротивление, предлагаемое RC-цепью, бесконечно.
Изменение заряда при внешнем напряжении показано на диаграмме ниже.
Из приведенной выше диаграммы видно, что заряд увеличивается с увеличением напряжения. Чтобы понять емкость, нам нужно проанализировать приведенную выше диаграмму. Наклон приведенного выше графика представляет значение емкости.
Площадь на приведенном выше графике представляет собой энергию, хранящуюся в форме электрического поля. Это связано с тем, что параллельные пластины конденсатора накапливают заряд, и он преобразуется в электростатическую энергию.
Математически ток, протекающий через RC-цепь, можно рассчитать с помощью закона напряжения и тока Кирхгофа. Энергия, запасенная в виде электрического поля, может быть выражена через заряд и напряжение. С помощью приведенного ниже уравнения вы можете лучше понять RC-цепь.
С помощью приведенного ниже уравнения вы можете лучше понять RC-цепь.
Цепь RL (цепь сопротивления – индуктивности)
Цепь RL состоит из сопротивления и индуктивности, соединенных последовательно с источником питания. Ток от источника напряжения первоначально испытывает бесконечное сопротивление, когда переключатель замкнут. Как только цепь RL достигает устойчивого состояния, сопротивление катушки индуктивности начинает уменьшаться, и в какой-то момент значение сопротивления цепи RL становится равным нулю.
Поток, связанный с катушкой индуктора, создает вокруг нее магнитное поле. Кроме того, поток изменяется в зависимости от тока, протекающего через катушку. Изменение потока в зависимости от тока показано ниже с помощью графика.
Наклон графика отображает значение индуктивности, а площадь, охватываемая графиком, определяет энергию, запасенную в виде магнитного поля.
Чтобы лучше понять это, вы можете обратиться к приведенному ниже уравнению. Эти уравнения показывают связь между током, индуктивностью и внешним напряжением с помощью закона Кирхгофа. Энергия, хранящаяся в виде магнитного поля, может быть выражена через поток и ток.
Эти уравнения показывают связь между током, индуктивностью и внешним напряжением с помощью закона Кирхгофа. Энергия, хранящаяся в виде магнитного поля, может быть выражена через поток и ток.
Основные различия между RC и RL цепями
- RC и RL цепи хранят энергию, но RC цепь хранит энергию в виде электрического поля. В то время как цепь RL запасает энергию в виде магнитного поля.
- RC-цепи экономичны, поскольку конденсаторы дешевы и доступны в изобилии, а катушки индуктивности дороги, что делает RL-цепи дорогими.
- Катушки индуктивности имеют более широкие допуски по сравнению с резисторами, поэтому RL-схема имеет высокие допуски.
- Катушка индуктивности создает магнитное поле, создающее помехи в цепи. Это приводит к плохой работе цепи RL, когда шумовой сигнал становится высоким. Проблема шума может быть уменьшена с помощью RC-цепи, поскольку конденсатор не создает магнитного поля.
Заключение
Цепи RL и RC являются основой различных электронных схем.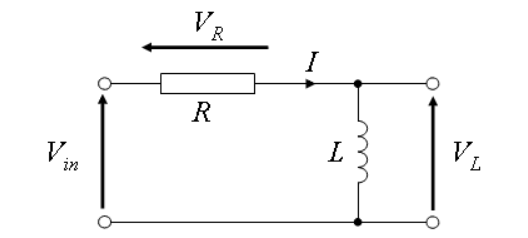



 ..
..
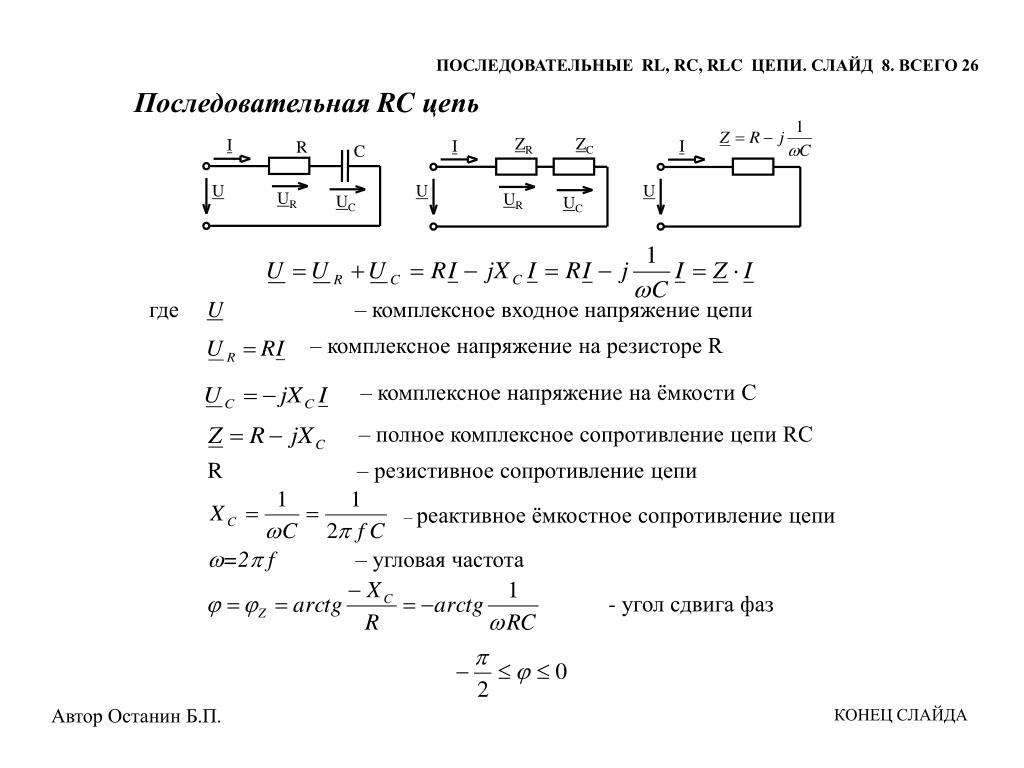

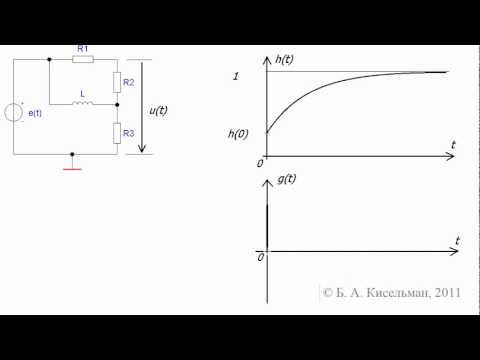 7.1. Интегрирующая (а) и дифференцирующая (б) RC-цепи
7.1. Интегрирующая (а) и дифференцирующая (б) RC-цепи 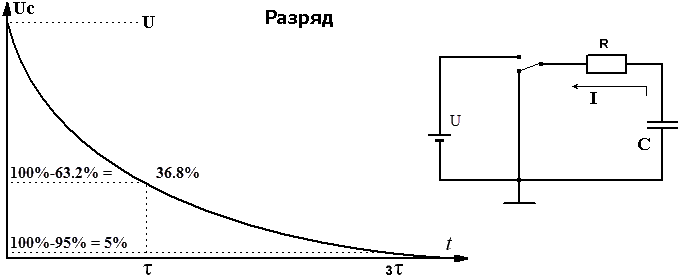 Скорость роста выходного напряжения определяется величиной постоянной времени, равной для RC-цепи . Выходное напряжение изменится за время до уровня, примерно равного 95 % от установившегося напряжения E. Выходное напряжение достигнет уровня за время примерно . Таким образом, время задержки импульсного сигнала равно = = 0,7t. В процессе заряда конденсатора выходное напряжение интегрирующей цепи меняется в соответствии с предложенным выражением: uc = E(1– e –t/t).
Скорость роста выходного напряжения определяется величиной постоянной времени, равной для RC-цепи . Выходное напряжение изменится за время до уровня, примерно равного 95 % от установившегося напряжения E. Выходное напряжение достигнет уровня за время примерно . Таким образом, время задержки импульсного сигнала равно = = 0,7t. В процессе заряда конденсатора выходное напряжение интегрирующей цепи меняется в соответствии с предложенным выражением: uc = E(1– e –t/t).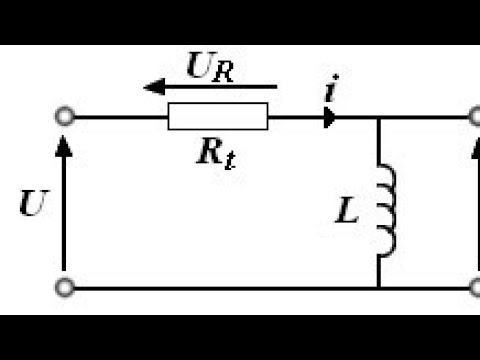 Благодаря этому и полярность падения напряжения на резисторе будет противоположной первоначальному значению при подаче напряжения E на вход. Поведение выходного напряжения определится из выражения u c = Ee –t/t.
Благодаря этому и полярность падения напряжения на резисторе будет противоположной первоначальному значению при подаче напряжения E на вход. Поведение выходного напряжения определится из выражения u c = Ee –t/t. Если выражать изменение коэффициента в логарифмическом масштабе, то это соответствует уменьшению на 3 дБ. Значение граничной частоты вычисляется из следующего выражения: fгр= 1/2pRC. С ростом частоты коэффициент передачи интегрирующей цепи падает со скоростью 20 дБ на декаду, т.е. на частоте 10 fгр коэффициент передачи будет равен 0,1, а на частоте 100 fгр коэффициент передачи уменьшится до 0,01. Такое поведение цепи определяется коэффициентом передачи, который учитывает реактивное сопротивление конденсатора xc = 1/2pfC : .
Если выражать изменение коэффициента в логарифмическом масштабе, то это соответствует уменьшению на 3 дБ. Значение граничной частоты вычисляется из следующего выражения: fгр= 1/2pRC. С ростом частоты коэффициент передачи интегрирующей цепи падает со скоростью 20 дБ на декаду, т.е. на частоте 10 fгр коэффициент передачи будет равен 0,1, а на частоте 100 fгр коэффициент передачи уменьшится до 0,01. Такое поведение цепи определяется коэффициентом передачи, который учитывает реактивное сопротивление конденсатора xc = 1/2pfC : . Например, при подключении к выходу интегрирующей цепи резистора с сопротивлением R2 постоянная времени изменится и станет равной произведению , выходное напряжение устанавливается при этом к уровню . Если к выходу подключается нелинейная нагрузка, то анализ поведения цепи целесообразно попытаться разбить на этапы, на каждом из которых с достаточной степенью точности приемлема некоторая линейная модель схемы. Это позволяет выполнить анализ поэтапно.
Например, при подключении к выходу интегрирующей цепи резистора с сопротивлением R2 постоянная времени изменится и станет равной произведению , выходное напряжение устанавливается при этом к уровню . Если к выходу подключается нелинейная нагрузка, то анализ поведения цепи целесообразно попытаться разбить на этапы, на каждом из которых с достаточной степенью точности приемлема некоторая линейная модель схемы. Это позволяет выполнить анализ поэтапно.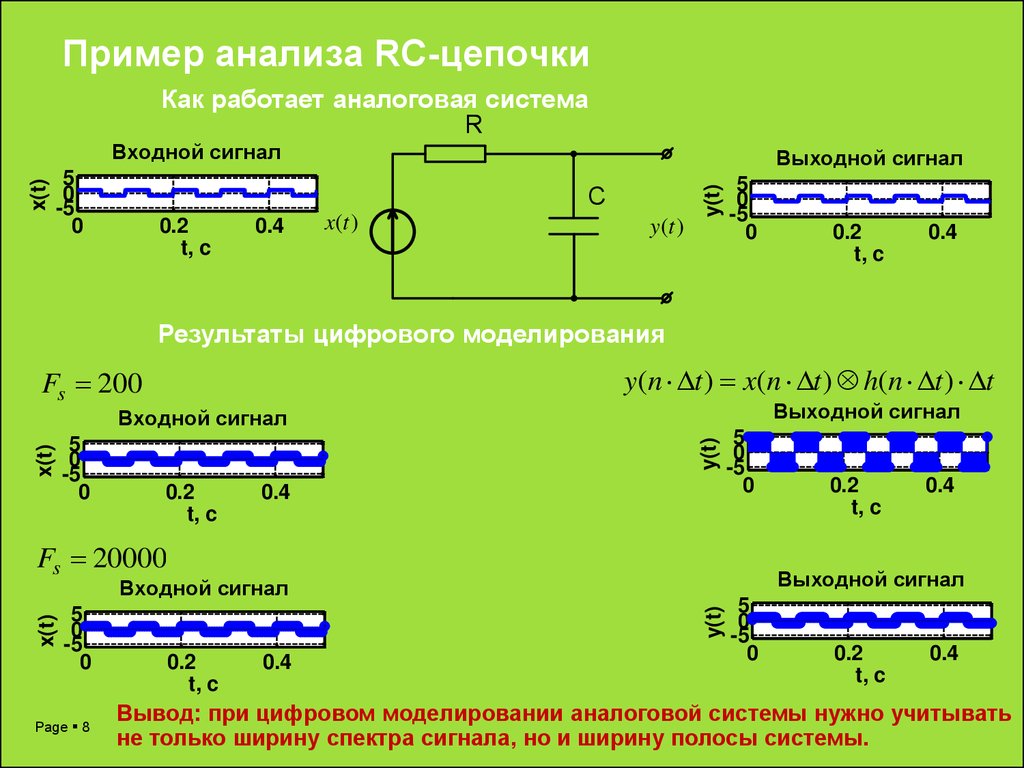 е. на выходе. Выходное напряжение подчиняется выражению uR = Ee –t/t. Конденсатор в конечном итоге окажется заряжен до уров-
е. на выходе. Выходное напряжение подчиняется выражению uR = Ee –t/t. Конденсатор в конечном итоге окажется заряжен до уров-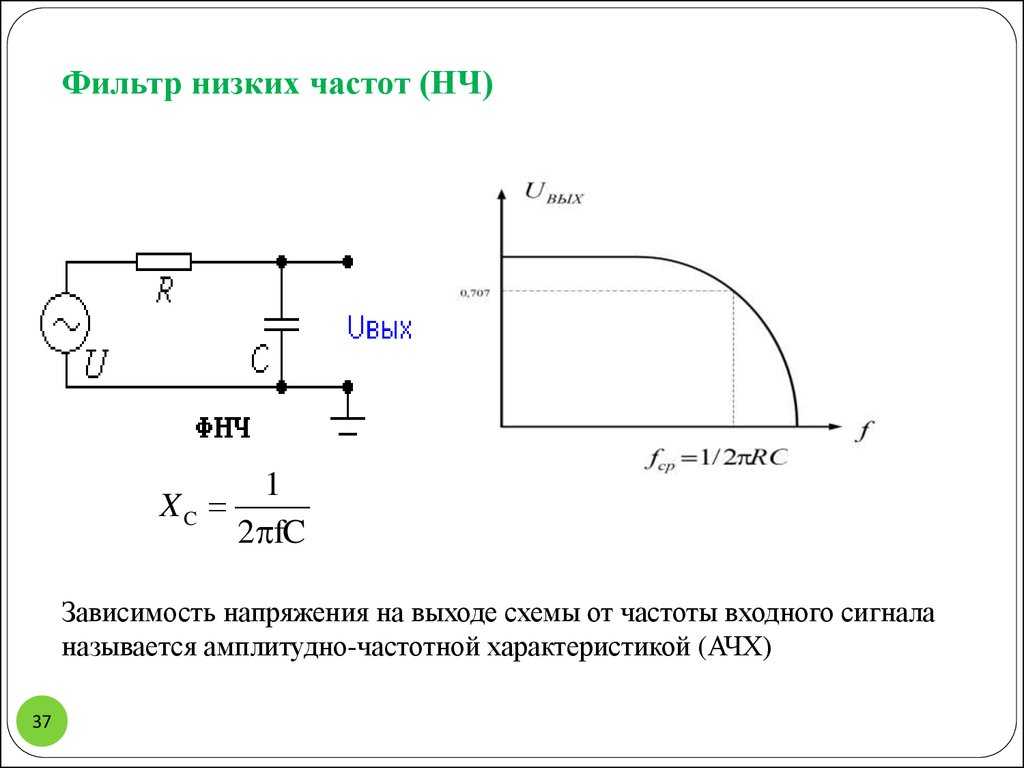

 При этом выберите частоту с таким периодом T, чтобы было справедливо неравенство: T > 6t. Во время эксперимента необходимо измерить время задержки интегрирующей цепи по каждому фронту, постоянную времени полученной цепи. Сравните измеренное значение постоянной времени с расчетным и объясните расхождения. Сравните измеренные по фронтам времена задержки с расчетными значениями и объясните результат. При объяснении результатов учтите влияние входной паразитной емкости осциллографа.
При этом выберите частоту с таким периодом T, чтобы было справедливо неравенство: T > 6t. Во время эксперимента необходимо измерить время задержки интегрирующей цепи по каждому фронту, постоянную времени полученной цепи. Сравните измеренное значение постоянной времени с расчетным и объясните расхождения. Сравните измеренные по фронтам времена задержки с расчетными значениями и объясните результат. При объяснении результатов учтите влияние входной паразитной емкости осциллографа.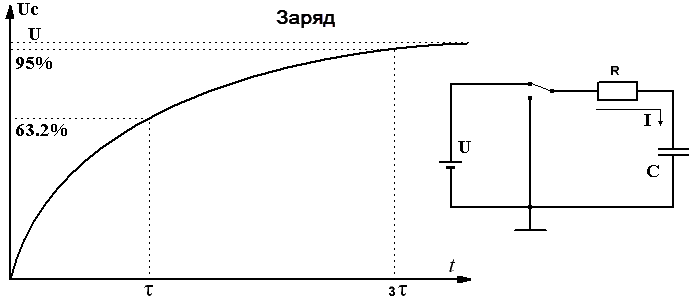 Постройте временные диаграммы входных и выходного сигналов и измерьте длительность выходного импульса и задержку его относительно фронта входного сигнала.
Постройте временные диаграммы входных и выходного сигналов и измерьте длительность выходного импульса и задержку его относительно фронта входного сигнала.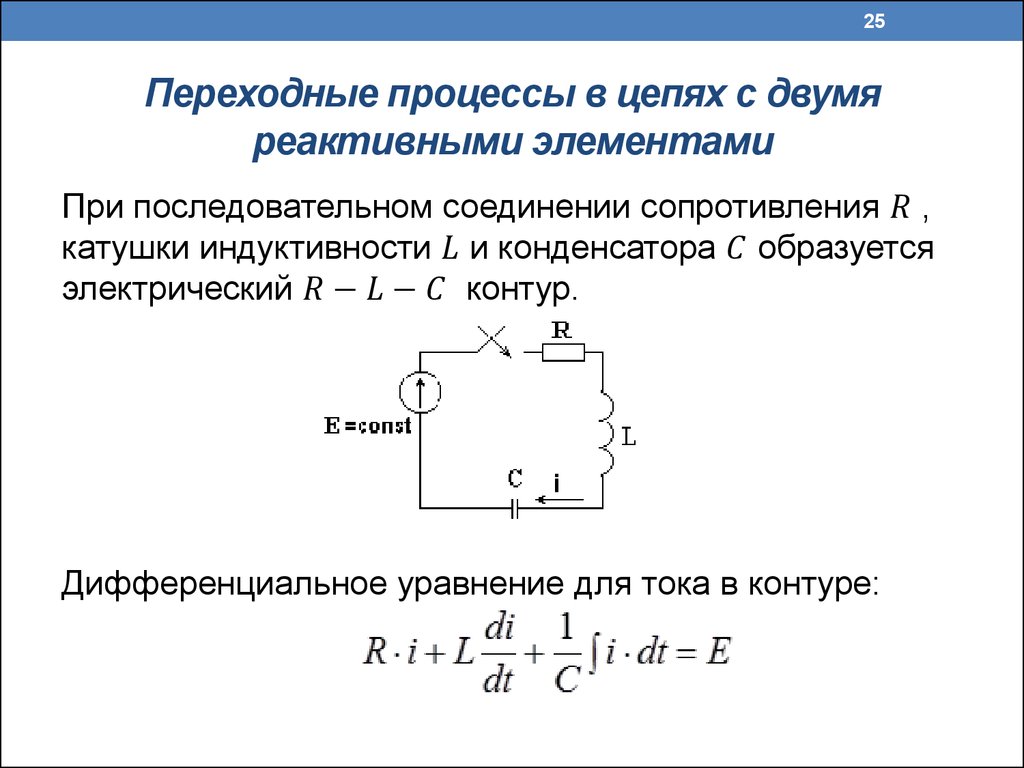 Зарисуйте полученную схему.
Зарисуйте полученную схему.

 1 Интегрирование сигналов простой RC цепью
1 Интегрирование сигналов простой RC цепью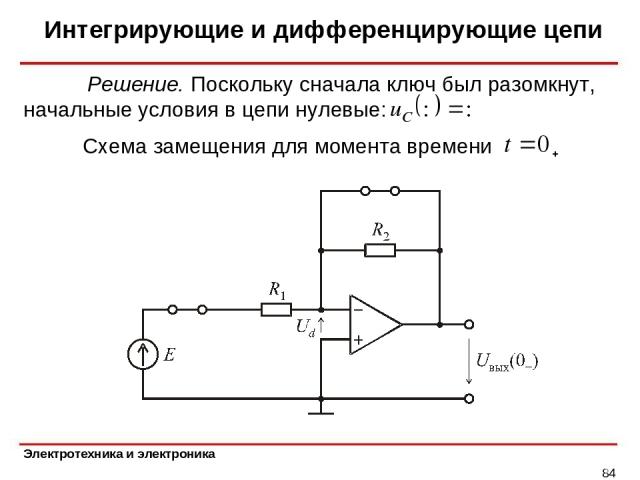 При малой частоте сдвиг по фазе между выходным и входным сигналом стремится к 0 градусам. При большой частоте — к -90.
При малой частоте сдвиг по фазе между выходным и входным сигналом стремится к 0 градусам. При большой частоте — к -90.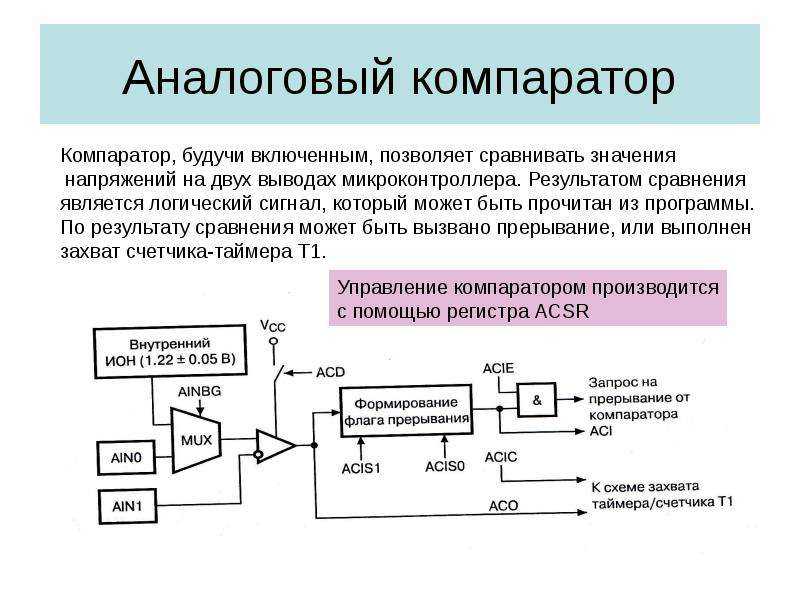 Выходной сигнал пропорционален интегралу от входного.
Выходной сигнал пропорционален интегралу от входного.
 Форма выходного импульсного сигнала для фильтра с линейной суммарной.
Форма выходного импульсного сигнала для фильтра с линейной суммарной.