Дифференцирующая rl-цепь

Дифференцирующая RL-цепь показана на рис 2-33 б, выходное напряжение снимается с индуктивностьюL. В этом случае при рассмотрении процессов в цепи при дифференцировании прямоугольного импульса следует воспользоваться первым законом коммутации. Все рассуждения аналогичны тем, какие были при рассмотренииRC- цепей.

Следует отметить, что RL-цепи используются режеRC-цепей, так как конструктивно сложнее.

В связи с тем, что электрический фильтр является четырехполюсником, то для описания его используют коэффициент передачи(), с помощью которого можно определять диапазон пропускных частот. (рис 13-36).В том случае, если, то электрический импульс с высокой частотой будет пропускаться электрическим фильтром. Если, то электрический сигнал с низкой частотой будет подавляться.

Рис 13-36. Амплитудно-частотная характеристика ФВЧ.

Рассмотрим АЧХ интегрирующей RCцепи, изображённом на рис.

2-39а

Частный коэффициент передачи интегрирующей цепи равен

Если приравнять к 1/, то получают нижнюю границу полосы пропускания интегрирующейRC-цепи,

и это объясняет, что интегрирующая RCцепь не пропускает высокочастотных составляющих спектров входных сигналов. Также фильтры ещё называют сглаживающими или низкочастотными фильтрами

Интегрирующие цепи(фнч) (фильтр высоких частот)

Сигнал на выходе интегрирующей цепи пропорционален интегралу входного сигнала .

Схемы реальных интегрирующих цепей показаны на рис 13-37 а и 13-37 б. Коэффициент пропорциональности К в уравнении есть величина, обратная времени цепи(). Для цепиRC=RC, для цепиRL=L/R.

Рис 13-37. Схемы интегрирующих цепей.

Интегрирующая rc-цепь.

Эта цепь является также четырехполюсником.

В интегрирующий RC-цепи выходной сигнал (импульс напряжения) снимается с конденсатораC, то есть(смотри рис 13-37 а).

Рассмотрим, какую форму будет иметь сигнал на выходе, если интегрируемый сигнал (входной импульс) будет прямоугольной формы. При этом сначала, положим, что длительность входного импульса (смотри рис 13-38).

Рис 13-38. Интегрируемый сигнал (а) и сигнал на выходе интегрирующей RC-цепи (б),.

В момент включения цепи () напряжение на выходе в силу второго закона коммутации будет равно 0, а затем конденсатор будет заряжаться и напряжение на нем будет возрастать по экспоненциальному закону.

По истечению времени действия импульсов конденсатор полностью зарядится и в момент временинапряжение на нем достигнет. С этого момента действие импульса на цель прекращается, конденсатор начинает разряжаться по экспоненциальному законуи через время, равное, напряжение на нем спадет до 0.

Если , амплитуда и форма импульсов на выходе будут другими. Такие импульсы

Показаны на рис 2-39 б для случая, когда ,на рис 13-39 в для случая когдаи нас рис13-39 г.

Рис 13-39. Изменение формы импульса на выходе интегрирующей цепи в зависимости от соотношения между и.

Из формул и рис 13-39 следует, что в случае, если постоянная времени цепи , амплитуда выходного сигнала (импульса) будет меньше амплитуды входного сигнала. И она будет тем меньше, чем больше.

Для обеспечения более точного интегрирования постоянная времени цепи выбирается такой величины, чтобы она была значительно больше длительности интегрируемого импульса. При этом учитывается уменьшение амплитуды. Наиболее точное интегрирование, как и дифференцирование, можно осуществить с помощью операционных усилителей.

Импульс. RC и RL цепи

Всем доброго времени суток. Сегодняшний мой пост начинает серию статей про импульсные устройства. Такие устройства предназначены для формирования и преобразования электрических сигналов, имеющих характер импульсов и перепадов напряжений. К импульсным устройствам относятся все цифровые микросхемы и некоторые аналоговые, например, микросхемы генераторов и компараторов. Ранее я рассматривал один из основных элементов импульсных устройств – транзистор, работающий в ключевом режиме.

Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.

Формы импульса (слева направо): прямоугольная, трапецеидальная, пилообразная, экспоненциальная.

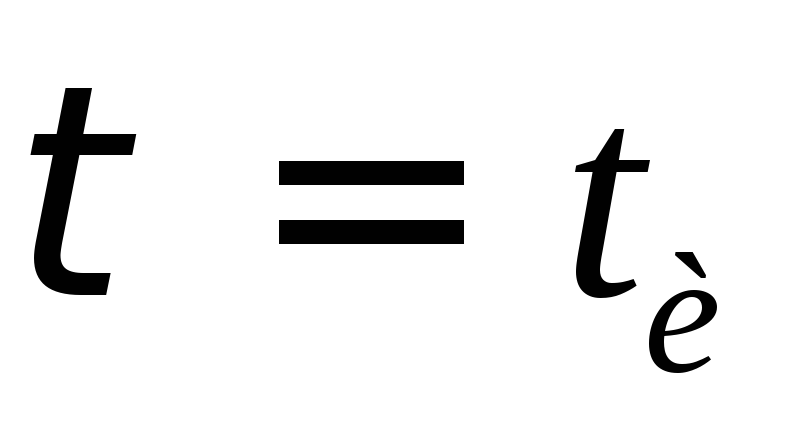
В радиоэлектронике используются импульсы самых разнообразных форм, но наиболее распространённые это: прямоугольные, трапецеидальные, пилообразные и экспоненциальные формы импульсов. Форма любого импульса характеризуется следующими основными параметрами:

• амплитуда (максимальное значение) импульса, U_m;
• начальное значение импульса, U₀;
• длительность импульса, t_и;
• длительность переднего фронта (или просто фронта) импульса, t_ф;
• длительность заднего фронта (или среза) импульса, t_с;
• длительность вершины импульса, t_в;
• снижение вершины импульса, Δu;
• крутизна фронта импульса (скорость изменения напряжения при формировании переднего или заднего фронта).

В случае использовании периодичности повторяющихся импульсов имеют большое значение такие параметры, как скважность импульсов (ξ или S), коэффициент заполнения импульсов (η или D), частота повторения импульсов (f) и период повторения импульсов (T).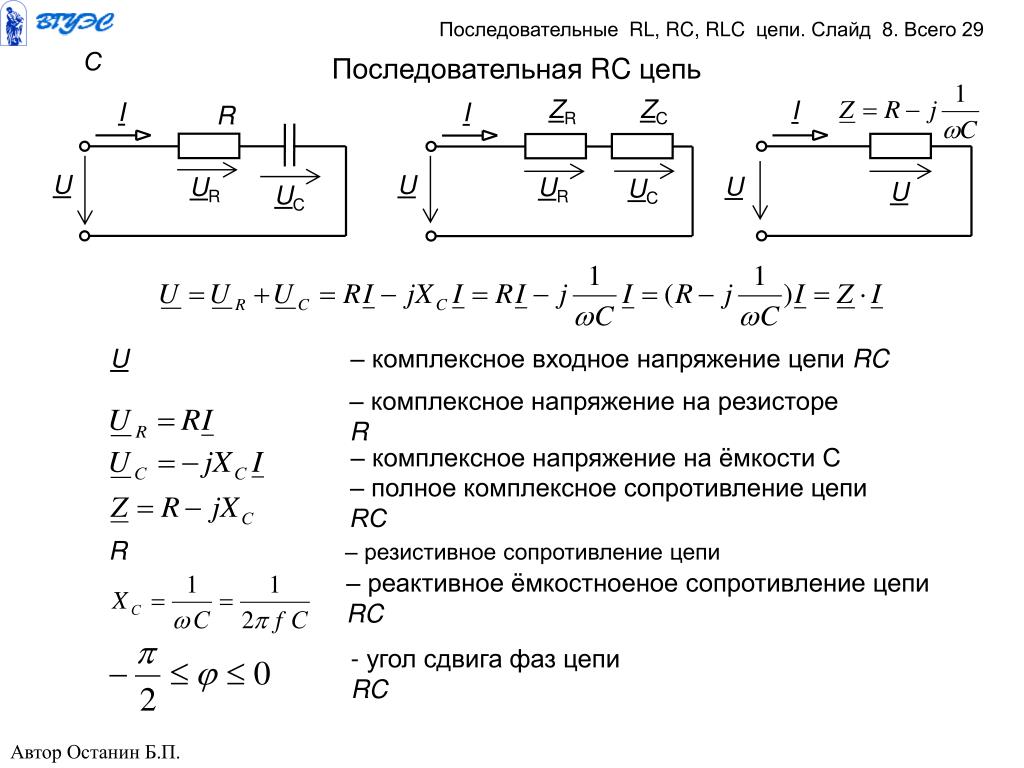 Данные параметры имеют следующие соотношения между собой

Форма реального импульса

Временные параметры импульса (t_и, t_ф, t_с, t_в) имеют точное значение только в случае идеального импульса, а в реальности лишь в некоторой степени имеют приближённое значение. Поэтому временные параметры отсчитываются от некоторых приближённых величин, которые в достаточной для практики точности имеют значения 0,05 и 0,95. Поясню на примере формы реального импульса, изображённого выше: при определении длительности фронта (t

ф) импульса, за начало фронта принимают значение 0,05*U_m, а за окончание фронта – 0,95*U_m. В случае длительности среза, соответственно, начало – 0,95*U_m, а окончание – 0,05*U_m.

Переходный процесс

Рассмотрение импульсных устройств и схем не возможно без представлении о переходном процессе. Он возникает в цепях при различных коммутациях, то есть при включении или выключении элементов схемы, источников напряжения, при коротких замыканиях отдельных цепей и т. д. Переходный процесс объясняется тем, что энергия электромагнитных полей, связанных с цепью, в разные промежутки времени неодинакова, а резкое изменение энергии невозможно из-за ограниченной мощности источников питания.

Исходя из вышесказанного, можно сделать вывод, что напряжение на ёмкости и ток в индуктивность не могут изменяться скачкообразно, так как данные параметры определяют энергию электрического поля конденсатора и магнитного поля катушки индуктивности.

Таким образом, можно сделать вывод, что при рассмотрении импульсных схем наибольшее внимание необходимо обратить на цепи, представляющие собой комбинации резисторов и конденсаторов или резисторов и катушек индуктивностей (RC- и RL-цепей). Такие цепи применяются непосредственно для формирования импульсов, а также являются важнейшими элементами релаксационных генераторов, триггеров и других устройств. Поэтому ниже рассмотрим основные свойства элементарных RC- и RL-цепей, а также изменение формы импульсов при прохождении через эти цепи.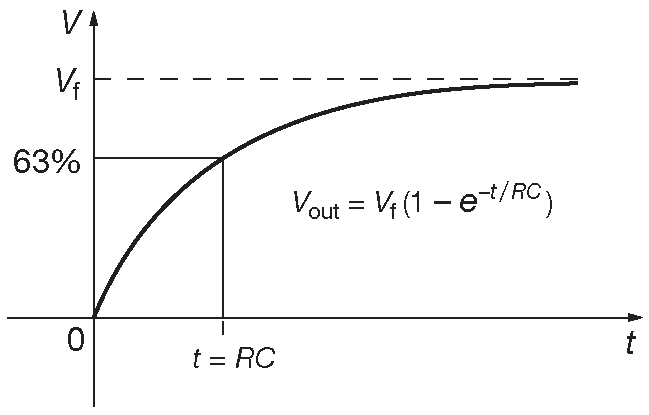

Влияние RC- и RL-цепей на импульсы различной формы

Несмотря на то, что формы электрических импульсов довольно разнообразны, их можно представить в виде суммы элементарных (типовых) напряжений трёх форм: скачкообразного, линейно изменяющегося и экспоненциального. Поэтому рассмотрим воздействие различных форм напряжений на RC- и RL-цепи.

Изображение RC- и RL-цепей.

Элементарные формы напряжения (сверху вниз): ступенчатое, линейно-изменяющееся, экспоненциальное.

Ступенчатое изменение напряжения. При подключении RC-цепи к источнику постоянного напряжения u_вх = Е = const, напряжения на конденсаторе и резисторе будет изменяться по экспоненциальному закону:

где е – математическая постоянная, е = 2,72;
t – время, с;
τ – постоянная времени, с.

τ = RC.

С определением напряжения всё понятно, но в практике чаще возникает вопрос о времени установления напряжения. Например, необходимо вычислить время за которое на конденсаторе установится напряжение равное u_С = 0,95 Е. Простым преобразованием формулы напряжения получим

Аналогично при подключении RL-цепи к источнику постоянного напряжения u_вх = Е = const

где τ – постоянная времени, с. τ = L/R.

Линейно изменяющееся напряжение. При подключении RC-цепи к источнику линейно изменяющегося напряжения u_ВХ = kt, напряжения на резисторе и конденсаторе будут изменяться согласно следующей формуле

Для RL-цепи подключённой к источнику с линейно изменяющимся напряжением u_ВХ = kt, напряжения на элементах соответственно будут такими

 

Временные диаграммы напряжений при линейно изменяющемся напряжении в RC- и RL-цепях.

Экспоненциально изменяющееся напряжение. При подключении RC-цепи к источнику экспоненциально изменяющегося напряжения

напряжения на резисторе и конденсаторе будут изменяться согласно следующей формуле

где q = τ/τ₁.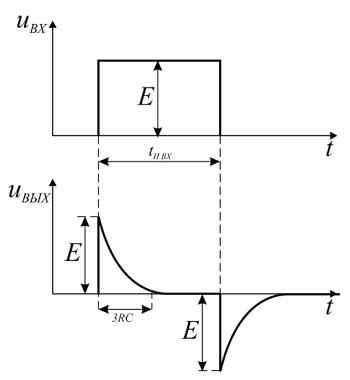

Соответственно напряжение на конденсаторе будет равно разности напряжений источника и напряжения на резисторе

Временные диаграммы для u_R представлены ниже при различных значениях q. При больших значениях q, то есть постоянной времени цепи τ, формы напряжений u_R близки к формам, соответствующим ступенчатому изменению входного напряжения. При уменьшении τ, кроме сокращения длительности спада напряжения u_R, уменьшается и максимальное значение u

R.

Временные диаграммы напряжений на резисторе RC-цепи при различных значениях
q = τ/τ₁.

Формулы и временные диаграммы для напряжений на выходе RL-цепи оказываются такими же, как и для RC-цепи.

Дифференцирующие цепи

Довольно часто в электронике вообще, а в импульсной в частности требуется преобразовать один вид импульсов в другой (например, прямоугольный преобразовать в треугольный). Для этой цели используют различные схемы, в основе которых простейшие RC- и RL-цепи. Такие цепи называются дифференцирующими и интернирующими цепями. Для начала рассмотрим дифференцирующие цепи, которые показаны на изображении ниже.

Своё название дифференцирующие цепи получили от того, что напряжение на выходе такой цепи пропорционально производной входного напряжения, а нахождение производной в математике называется дифференцирование. В случае RC-цепи напряжение снимается с резистора, а в случае RL-цепи – с индуктивности.

Простейшие .

В настоящее время большинство дифференцирующих цепей основаны на RC-цепях, поэтому будем рассматривать их, но все основные выкладки соответствуют также и RL-цепям.

Рассмотрим, как дифференцирующая цепь будет реагировать на прямоугольный импульс. Прямоугольный импульс представляет собой как бы два скачка напряжения. Реакцию RC-цепи на скачкообразное изменение напряжения рассматривалась выше, а в случае прямоугольного импульса выходное напряжение с дифференцирующей цепи будет в виде двух коротких импульсов различной полярности, длительность которых соответствует 3τ = 3RC и 3τ = 3L/R, в случае RL-цепи.

Реакция дифференцирующей цепи на прямоугольный импульс.

Из величины и формы выходного напряжения можно сделать вывод, что дифференциальные цепи вполне могут применяться для уменьшения длительности импульсов, что довольно часто применяется на практике и ранее такие цепи иногда называли укорачивающими.

Интегрирующие цепи

Интегрирующие цепи, так же как и дифференцирующие строят на основе RC- и RL-цепей, отличие заключается в том, откуда снимают выходное напряжение.

Простейшие RC и RL интегрирующие цепи.

Своё название интегрирующие цепи получили от того, что выходное напряжение, снимаемое с их выхода пропорционально интегралу от входного напряжения. Рассмотрим реакцию интегрирующей цепи на прямоугольный импульс напряжения. Напомню, что прямоугольный импульс, по сути, является напряжением, которое изменяется ступенчато два раза. В результате первого скачка напряжения конденсатор начинает заряжаться до тех пор, пока напряжение на входе не изменится, после этого начнётся разряд конденсатора по экспоненциальному закону.

Реакция интегрирующей цепи на прямоугольный импульс.

Не трудно заметить, что длительность импульса на выходе интегрирующей цепи несколько больше, чем длительность импульса на входе. Эту особенность нередко используют для увеличения длительности импульса, и такие цепи ранее называли расширяющими.

Теория это хорошо, но необходимо отрабатывать это всё практически ПОПРОБЫВАТЬ МОЖНО ЗДЕСЬ

Интеграторы — Формирование волны — Основы электроники

Формирование волны

Интегратор (RC или RL) используется в качестве сети формирования сигналов, например. в связь, радиолокационные системы и компьютеры. К интеграторам часто применяется прямоугольная волна. Гармоническое содержание прямоугольная волна состоит из нечетных кратных основной частоты. Поэтому значимых гармоник (те, которые влияют на контур) будет присутствовать в 50 или 60 раз больше основной частоты в волне.

Интеграторы RC

Конденсатор будет предлагать реактивное сопротивление ( X _C ) другого амплитуда каждой из гармоник

Это означает, что падение напряжения на конденсаторе для каждой гармоники присутствующая частота не будет одинаковой. Для низких частот конденсатор будет оказывать большое сопротивление, обеспечивая большое падение напряжения на конденсатор. Для высоких частот реактивное сопротивление конденсатора будет чрезвычайно мало, вызывая небольшое падение напряжения на конденсаторе. Это ничем не отличается от фильтров нижних и верхних частот (дискриминаторов) представлены позже. Если составляющая напряжения гармоники не развивается через реактивное сопротивление конденсатора, оно будет развиваться через резистор, если мы соблюдаем закон напряжения Кирхгофа. Гармоническая амплитуда и соотношение фаз на конденсаторе не такое, как у ввод исходной частоты; следовательно, идеальной прямоугольной волны не будет. производится на конденсаторе. Вы должны помнить, что предлагаемое реактивное сопротивление частота каждой гармоники вызовет изменение как амплитуды, так и фазы частоты каждой отдельной гармоники по отношению к актуальная ссылка. Величина изменения фазы и амплитуды, происходящая в конденсатор зависит от X _C конденсатора.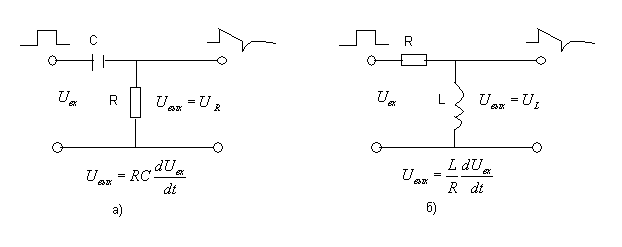 Значение также следует учитывать сопротивление, предлагаемое резистором. здесь; это часть коэффициента развития напряжения в сети.

Схема частичного интегрирования.

Схема на рисунке выше поможет показать отношения R и X _C более четко. Прямоугольная волна, приложенная к цепи составляет 100 вольт пик на частоте 1 килогерц. Нечетные гармоники будут 3 килогерц, 5 килогерц, 7 килогерц и т. д. В таблице ниже приведены значения X _C и R предлагаются для нескольких гармоник и указывает приблизительное значение частоты среза ( X _C = R ). Из таблицы ясно видно, что отсечка частота лежит между пятой и седьмой гармониками. Между этими двумя значений, емкостное реактивное сопротивление будет равно сопротивлению. Поэтому для всех Гармонические частоты выше пятой, большая часть выходного напряжения будет не проявляться на выходном конденсаторе. Скорее, большая часть вывода будет разработан через Р .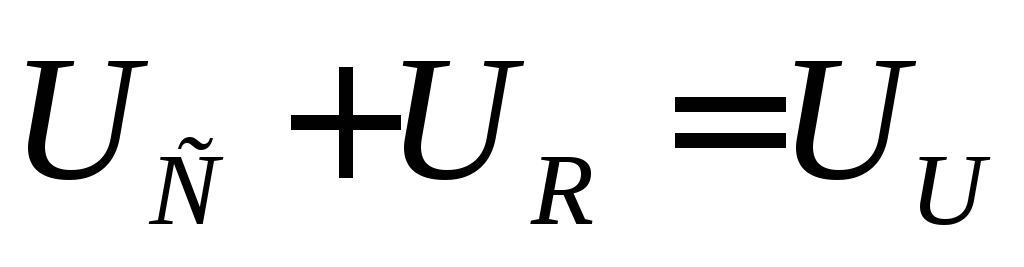 Отсутствие высших гармоник приводит к передний фронт сигнала, развивающегося на конденсаторе, должен быть скруглен. Пример этого эффекта показан на рисунке ниже. Если значение емкость увеличивается, реактивные сопротивления каждой частоте гармоники будут далее уменьшилось. Это означает, что будет развиваться еще меньше гармоник. через конденсатор.

Гармоника	X C (кОм)	Ч (кОм)
Фундаментальный	159	25
3-й	53	25
5-й	31,8	25
7-й	22,7	25
9-й	17,7	25
11-й	14,5	25

Частичная интеграция.

Гармоники, не развивающиеся эффективно на конденсаторе, должны быть развиты через резистор, чтобы удовлетворять закону напряжения Кирхгофа. Обратите внимание на узор осциллограммы напряжения на резисторе и конденсаторе. Если формы волны как на резисторе, так и на конденсаторе были добавлены графически, в результате будет точной копией входной прямоугольной волны.

Когда емкость достаточно увеличена, полная интеграция входа сигнал имеет место на выходе через конденсатор. Пример полного интегрирование показано на рисунке ниже (форма сигнала v _C ). Этот эффект может быть вызван значительным уменьшением значения емкостной реактивное сопротивление. Тот же эффект будет иметь место при увеличении значения сопротивление. Интегрирование происходит в RC-цепи, когда на выходе через конденсатор.

Интеграция.

Величина интегрирования зависит от значений R и C . Величина интегрирования может также зависеть от постоянной времени схема. Постоянная времени цепи должна быть не менее 10 раз больше , чем длительность входного импульса для интегрирования. Значение 10 является приблизительным.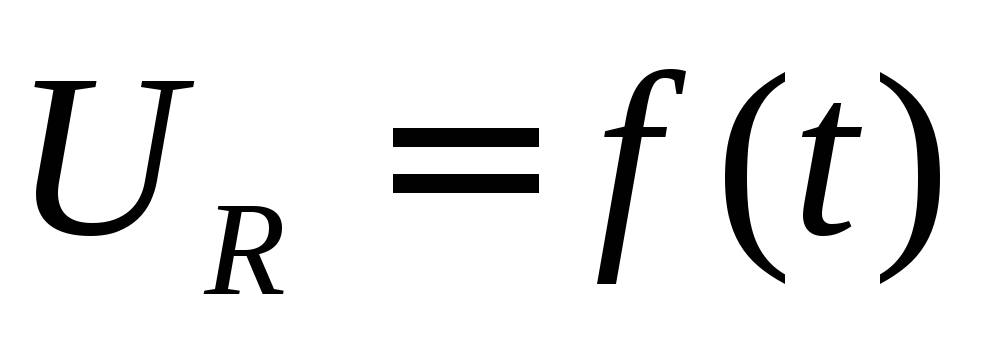 Когда постоянная времени цепи в 10 и более раз превышает значение длительности входного импульса, схема говорят, что оно имеет большую постоянную времени. Когда постоянная времени велика, конденсатор не имеет возможности мгновенно заряжаться до значения приложенное напряжение. Таким образом, получается длинная, наклонная, интегрированная форма волны.

RL Интеграторы

Цепь RL также может использоваться как интегрирующая схема. интегрированный Форма сигнала может быть получена из последовательной цепи RL, взяв выходной сигнал через резистор. Характеристики индуктора таковы, что при первый момент времени, когда приложено напряжение, через индуктивность минимальна, а напряжение на ней максимально. Поэтому, значение падения напряжения на последовательном резисторе в этот первый момент должно быть 0 вольт, потому что ток через него не течет. По прошествии времени, ток начинает течь по цепи и на ней возникает напряжение резистор. Поскольку цепь имеет большую постоянную времени, напряжение на резистор делает , а не реагируют на быстрые изменения в напряжение входной прямоугольной волны. Таким образом, условия интегрирования в цепи RL — это постоянная времени с выходным сигналом через резистор. Эти условия показаны на рисунке ниже.

Форма сигнала интегратора RL.

Анализ сигналов интегратора

Если RC- или RL-цепь имеет постоянную времени в 10 раз больше, чем длительность входного импульса, схемы способны к интегрированию. Давайте вычислить и отобразить фактическую форму волны, которая от большой постоянной времени (в 10 раз больше длительности импульса), короткой постоянной времени (1/10 длительности импульса) и средняя постоянная времени (эта постоянная времени между длинным и коротким). Чтобы точно построить значения для конденсатора выходное напряжение, мы будем использовать универсальную диаграмму постоянной времени, показанную на рисунок ниже.

Универсальная таблица постоянной времени.

Вы уже знаете, что заряд конденсатора соответствует форме кривой, показанной на рис. рисунок выше. Эту кривую можно использовать для определения величины напряжения через любой компонент в последовательной RC-цепи. Пока постоянная времени или известна дробная часть постоянной времени, напряжение на компонент может быть определен.

Краткосрочный интегратор с постоянной выдержкой времени

Цепь RC-интегратора.

На рисунке выше 100-микросекундный импульс с амплитудой 100 вольт применяется к цепи. Схема состоит из 0,01 мкФ конденсатор и переменный резистор R . Применяемая прямоугольная волна представляет собой чистая прямоугольная волна. Сопротивление переменного резистора установлено равным 1000 Ом. Постоянная времени цепи определяется уравнением:

Подставляем значения:

Поскольку постоянная времени цепи составляет 10 мкс, а импульс длительность 100 мкс, постоянная времени короткая (1/10 импульса продолжительность). Конденсатор заряжается экспоненциально через резистор. В 5 постоянных времени, конденсатор для всех практических целей будет полностью заряжен. При первой постоянной времени конденсатор заряжается до 63,2 вольта, на втором 86,5 вольт, на третьем 95 вольт, на четвертом 98 вольт, и, наконец, в конце пятой постоянной времени (50 микросекунд) конденсатор почти полностью заряжен. Это показано на рисунке ниже.

Прямоугольная волна применяется к короткому интегратору с постоянной времени.

Обратите внимание, что передний фронт прямоугольной волны на конденсаторе равен округлый. Если бы постоянная времени была сделана очень короткой, закругленный край стал бы квадратным.

Средний интегратор с постоянной времени

Постоянную времени на рисунке выше можно изменить, увеличив значение переменного резистора на 10000 Ом. Тогда постоянная времени будет равна до 100 микросекунд.

Эта постоянная времени известна как средняя постоянная времени. Его значение находится между экстремальные диапазоны коротких и длинных постоянных времени. В этом случае его значение оказывается в точности равным длительности входного импульса, 100 микросекунд. Показана форма выходного сигнала после нескольких постоянных времени. на рисунке ниже. Длинный, наклонный рост и падение напряжения вызваны неспособность конденсатора быстро заряжаться и разряжаться через Последовательное сопротивление 10 000 Ом.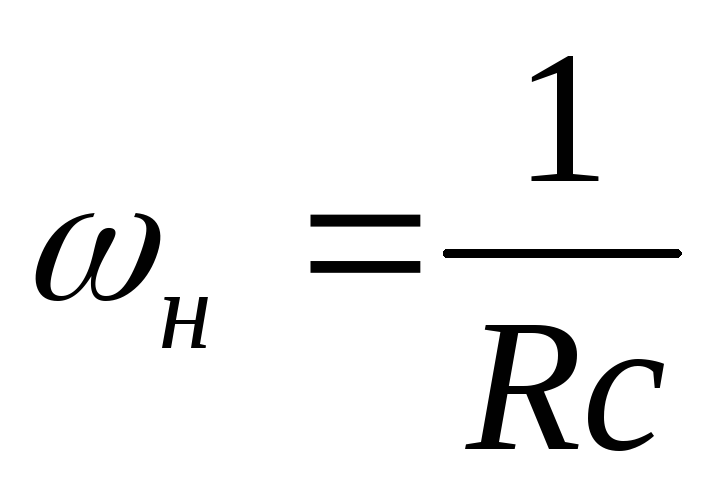

Средний интегратор с постоянной времени.

В первый момент времени к среде с постоянной времени приложено 100 вольт. схема. В этой схеме 1 τ в точности равно длительности входного пульс. Через 1 τ конденсатор зарядился до 63,2 процента входного напряжения. (100 вольт). Следовательно, в конце 1 τ (100 мкс) напряжение на конденсаторе равно 63,2 вольта. Однако, как только 100 микросекунд истекло, и первоначальный заряд конденсатора поднялся до 63,2 вольта, входное напряжение внезапно падает до 0. Оно остается там в течение 100 микросекунд. Теперь конденсатор будет разряжаться в течение 100 микросекунд. С момента выписки время составляет 100 микросекунд (1 τ ), конденсатор разрядится на 63,2% его общий заряд 63,2 вольта, значение 23,3 вольта. Во время следующего 100 микросекунд, входное напряжение увеличится с 0 до 100 вольт мгновенно. Конденсатор снова будет заряжаться в течение 100 микросекунд (1 τ ). Напряжение, доступное для этого заряда, представляет собой разницу между напряжением подается и заряд на конденсаторе (100 — 23,3 вольта), или 76,7 вольта.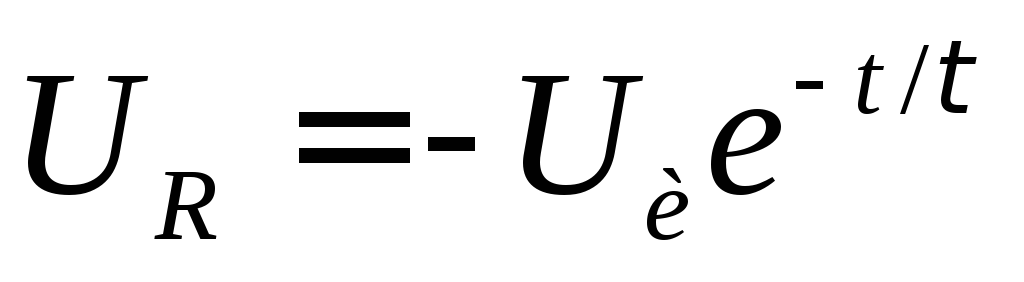 Так как конденсатор сможет заряжаться только за 1 τ , он будет заряжаться до 63,2 процента от 76,7 вольт, или 48,4 вольта. Общий заряд на конденсатор в конце 300 мкс будет 23,3 + 48,4 вольта, или 71,7 вольта.

Обратите внимание, что напряжение конденсатора в конце 300 микросекунд больше, чем напряжение конденсатора в конце 100 мкс. Напряжение в конце 100 микросекунд составляет 63,2 вольта, а напряжение на конденсаторе в конце 300 микросекунд — это 71,7 вольта, увеличение на 8,5 вольта.

Форма выходного сигнала на этом графике ( v _C ) — форма сигнала, будет производиться после многих циклов подачи сигнала на интегратор. конденсатор будет заряжаться и разряжаться постепенно, пока, наконец, заряжает и разряжает выше и ниже уровня 50 вольт. Уровень 50 вольт управляется максимальной амплитудой симметричного входного импульса, среднее значение которого составляет 50 вольт.

Интегратор с длительной постоянной времени

Если сопротивление в RC-интеграторе увеличить до 100 000 Ом, время постоянная схемы составит 1000 мкс. Эта постоянная времени 10-кратная длительность импульса входного импульса. Следовательно, это цепь с длительной постоянной выдержкой времени.

Форма выходного сигнала на конденсаторе показана на рисунке. ниже. Форма выходного сигнала характеризуется длинным, наклонным нарастание и падение напряжения на конденсаторе.

Прямоугольная волна применительно к интегратору с большой постоянной времени.

В первый момент времени на большую постоянную времени подается 100 вольт. схема. Величина заряда конденсатора в конце первых 100 микросекунды входного сигнала можно найти с помощью Таблица универсальной постоянной времени. Предположим, что линия проецируется вверх от точки базовой линии, соответствующей 0,1 т . Линия будет пересекать кривую в точке, которая представляет собой процент напряжения через конденсатор в конце первых 100 микросекунд. С момента применения напряжение 100 вольт, заряд на конденсаторе в конце первого 100 микросекунд будут примерно 9,5 вольт.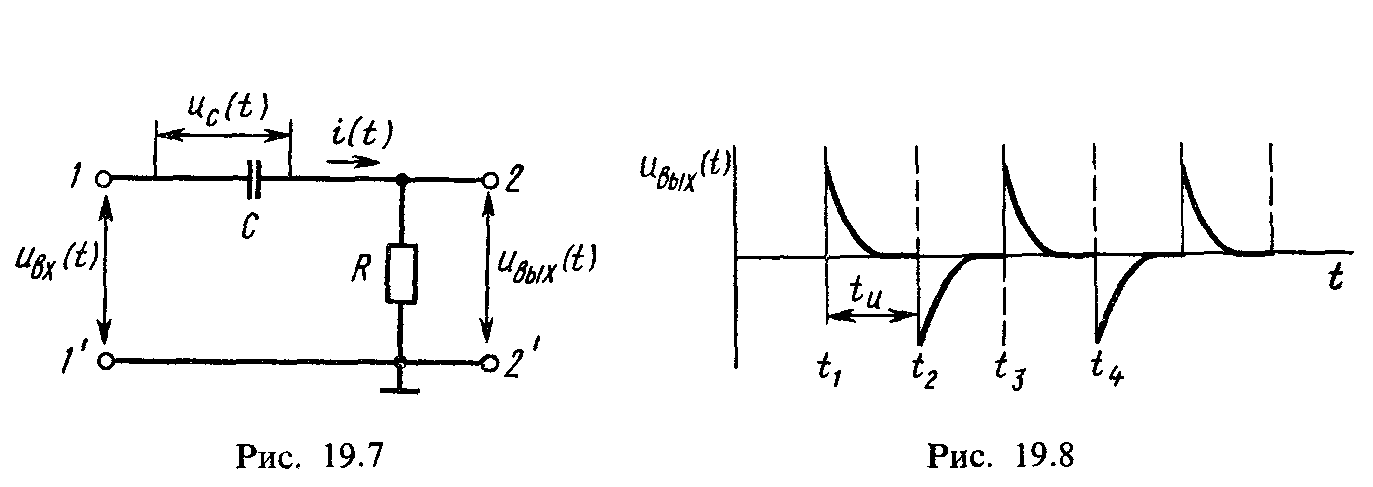 В конце первого 100 микросекунд, входной сигнал внезапно упадет до 0, а конденсатор начнет разряжаться. Он сможет разряжаться за 100 микросекунд. Следовательно, конденсатор разрядится на 90,5 процента накопленного 9,5 вольт (0,095 × 9,5 = 0,90 вольт). Разряд 0,90 вольта приведут к остаточному заряду на конденсаторе 8,6 вольт. По истечении 200 микросекунд входной сигнал снова резко возрастет до значение 100 вольт. Конденсатор сможет заряжаться до 9,5 процентов разности (100 — 8,6 = 91,4 вольта). Это также может быть представлено как значение 8,7 вольта плюс начальные 8,6 вольта. Это приводит к общему заряд на конденсаторе (в конце первых 300 мкс) 8,7 + 8,6 = 17,3 вольта.

Обратите внимание, что напряжение конденсатора в конце первых 300 микросекунд равно больше, чем напряжение конденсатора в конце первых 100 микросекунд. Напряжение в конце первых 100 микросекунд составляет 9,5 вольт; конденсатор напряжение в конце первых 300 мкс составляет 17,3 вольта, увеличение 7,8 вольта.

Конденсатор заряжается и разряжается поэтапно до тех пор, пока наконец, конденсатор заряжается и разряжается выше и ниже уровня 50 вольт. Уровень 50 вольт контролируется максимальной амплитудой прямоугольного сигнала. входной импульс, среднее значение которого составляет 50 вольт.

Integrated Publishing — ваш источник военных спецификаций и образовательных публикаций

Администрация — Навыки, процедуры, обязанности и т. д. военного персонала

Продвижение — Военный карьерный рост книги и т. д.

Аэрограф/метеорология — Метеорология основы, физика атмосферы, атмосферные явления и др.
Руководства по аэрографии и метеорологии военно-морского флота

Автомобилестроение/Механика — Руководства по техническому обслуживанию автомобилей, механика дизельных и бензиновых двигателей, руководства по автомобильным деталям, руководства по деталям дизельных двигателей, руководства по деталям бензиновых двигателей и т. д.
Автомобильные аксессуары | Перевозчик, персонал | Дизельные генераторы | Механика двигателя | Фильтры | Пожарные машины и оборудование | Топливные насосы и хранение | Газотурбинные генераторы | Генераторы | Обогреватели | HMMWV (Хаммер/Хамви) | и т. д…

Авиация — Принципы полетов, авиастроение, авиационная техника, авиационные силовые установки, справочники по авиационным частям, справочники по авиационным частям и т. д.
Руководства по авиации ВМФ | Авиационные аксессуары | Общее техническое обслуживание авиации | Руководства по эксплуатации вертолетов AH-Apache | Руководства по эксплуатации вертолетов серии CH | Руководства по эксплуатации вертолетов Chinook | и т.д…

Боевой — Служебная винтовка, пистолет меткая стрельба, боевые маневры, органическое вспомогательное вооружение и т. д.
Химико-биологические, маски и оборудование | Одежда и индивидуальное снаряжение | Боевая инженерная машина | и т.д…

Строительство — Техническое администрирование, планирование, оценка, планирование, планирование проекта, бетон, кирпичная кладка, тяжелый строительство и др.
Руководства по строительству военно-морского флота | Совокупность | Асфальт | Битумный корпус распределителя | Мосты | Ведро, Раскладушка | Бульдозеры | Компрессоры | Обработчик контейнеров | дробилка | Самосвалы | Землеройные машины | Экскаваторы | и т. д…

Дайвинг — Руководства по водолазным работам и спасению различного снаряжения.

Чертежник — Основы, методы, составление чертежей, эскизов и т. д.

Электроника — Руководства по обслуживанию электроники для базового ремонта и основ. Руководства по компонентам компьютеров, руководства по электронным компонентам, руководства по электрическим компонентам и т. д.
Кондиционер | Усилители | Антенны и мачты | Аудио | Батареи | Компьютерное оборудование | Электротехника (NEETS) (самая популярная) | техник по электронике | Электрооборудование | Электронное общее испытательное оборудование | Электронные счетчики | и т.д…

Машиностроение — Основы и методы черчения, составление проекций и эскизов, деревянное и легкокаркасное строительство и т. д.
Военно-морское машиностроение | Армейская программа исследований прибрежных бухт | и т. д…

Еда и кулинария — Руководства по рецептам и оборудованию для приготовления пищи.

Логистика — Логистические данные для миллионов различных деталей.

Математика — Арифметика, элементарная алгебра, предварительное исчисление, введение в вероятность и т. д.

Медицинские книги — Анатомия, физиология, пациент уход, средства первой помощи, фармация, токсикология и т. д.
Медицинские руководства военно-морского флота | Агентство регистрации токсичных веществ и заболеваний

Военные спецификации — Государственные спецификации MIL и другие сопутствующие материалы

Музыка — Мажор и минор масштабные действия, диатонические и недиатонические мелодии, паттерны такта, и т.д.

Основы ядра — Теории ядерной энергии, химия, физика и т.