Влияние RC- и RL-цепей на импульсы различной формы

⇐ ПредыдущаяСтр 3 из 16Следующая ⇒

Несмотря на то, что формы электрических импульсов довольно разнообразны, их можно представить в виде суммы элементарных (типовых) напряжений трёх форм: скачкообразного, линейно изменяющегося и экспоненциального. Поэтому рассмотрим воздействие различных форм напряжений на RC- и RL-цепи.

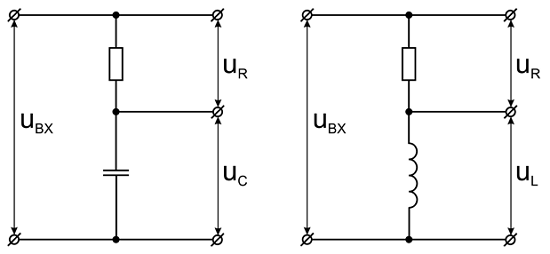
Изображение RC- и RL-цепей.

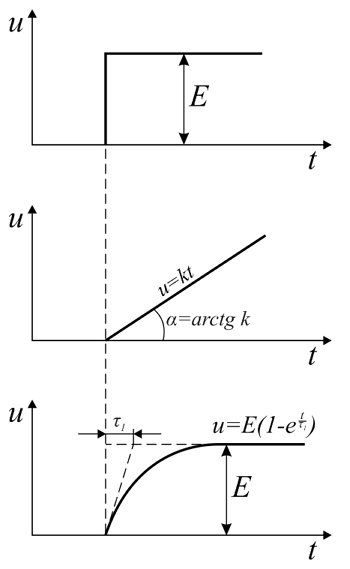
Элементарные формы напряжения (сверху вниз): ступенчатое, линейно-изменяющееся, экспоненциальное.

Ступенчатое изменение напряжения. При подключении RC-цепи к источнику постоянного напряжения u_вх = Е = const, напряжения на конденсаторе и резисторе будет изменяться по экспоненциальному закону:

 

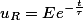
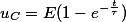
где е – математическая постоянная, е = 2,72;
t – время, с;
τ – постоянная времени, с. τ = RC.

С определением напряжения всё понятно, но в практике чаще возникает вопрос о времени установления напряжения. Например, необходимо вычислить время за которое на конденсаторе установится напряжение равное u_С = 0,95 Е. Простым преобразованием формулы напряжения получим

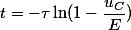
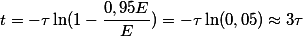
Аналогично при подключении RL-цепи к источнику постоянного напряжения u_вх = Е = const

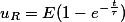
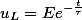
где τ – постоянная времени, с. τ = L/R.

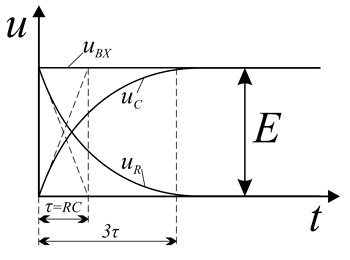
Линейно изменяющееся напряжение. При подключении RC-цепи к источнику линейно изменяющегося напряжения u_ВХ = kt, напряжения на резисторе и конденсаторе будут изменяться согласно следующей формуле

 

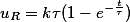
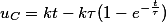
Для RL-цепи подключённой к источнику с линейно изменяющимся напряжением u_ВХ = kt, напряжения на элементах соответственно будут такими

 

 

 

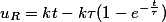
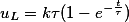
Временные диаграммы напряжений при линейно изменяющемся напряжении в RC- и RL-цепях.

Экспоненциально изменяющееся напряжение. При подключении RC-цепи к источнику экспоненциально изменяющегося напряжения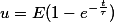

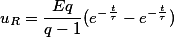
, напряжения на резисторе и конденсаторе будут изменяться согласно следующей формуле

где q = τ/τ₁.

Соответственно напряжение на конденсаторе будет равно разности напряжений источника и напряжения на резисторе

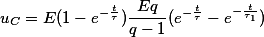
Временные диаграммы для u_R представлены ниже при различных значениях q. При больших значениях q, то есть постоянной времени цепи τ, формы напряжений u

R близки к формам, соответствующим ступенчатому изменению входного напряжения. При уменьшении τ, кроме сокращения длительности спада напряжения u_R, уменьшается и максимальное значение u_R.

 

Временные диаграммы напряжений на резисторе RC-цепи при различных значениях
q = τ/τ₁.

Формулы и временные диаграммы для напряжений на выходе RL-цепи оказываются такими же, как и для RC-цепи.

Дифференцирующие цепи

Довольно часто в электронике вообще, а в импульсной в частности требуется преобразовать один вид импульсов в другой (например, прямоугольный преобразовать в треугольный). Для этой цели используют различные схемы, в основе которых простейшие RC- и RL-цепи. Такие цепи называются дифференцирующими и интернирующими цепями. Для начала рассмотрим дифференцирующие цепи, которые показаны на изображении ниже.

Своё название дифференцирующие цепи получили от того, что напряжение на выходе такой цепи пропорционально производной входного напряжения, а нахождение производной в математике называется дифференцирование. В случае RC-цепи напряжение снимается с резистора, а в случае RL-цепи – с индуктивности.

Простейшие .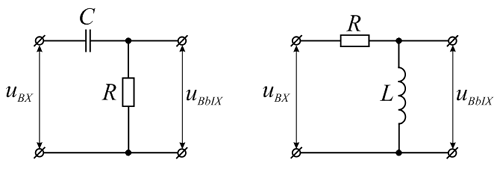

В настоящее время большинство дифференцирующих цепей основаны на RC-цепях, поэтому будем рассматривать их, но все основные выкладки соответствуют также и RL-цепям.

Рассмотрим, как дифференцирующая цепь будет реагировать на прямоугольный импульс. Прямоугольный импульс представляет собой как бы два скачка напряжения. Реакцию RC-цепи на скачкообразное изменение напряжения рассматривалась выше, а в случае прямоугольного импульса выходное напряжение с дифференцирующей цепи будет в виде двух коротких импульсов различной полярности, длительность которых соответствует 3τ = 3RC и 3τ = 3L/R, в случае RL-цепи.

 

Реакция дифференцирующей цепи на прямоугольный импульс.

Из величины и формы выходного напряжения можно сделать вывод, что дифференциальные цепи вполне могут применяться для уменьшения длительности импульсов, что довольно часто применяется на практике и ранее такие цепи иногда называли укорачивающими.

Интегрирующие цепи

Интегрирующие цепи, так же как и дифференцирующие строят на основе RC- и RL-цепей, отличие заключается в том, откуда снимают выходное напряжение.

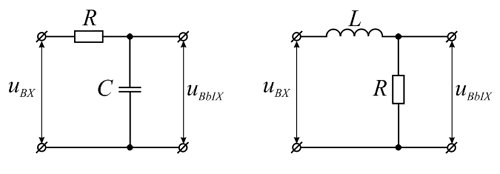
Простейшие RC и RL интегрирующие цепи.

Своё название интегрирующие цепи получили от того, что выходное напряжение, снимаемое с их выхода пропорционально интегралу от входного напряжения. Рассмотрим реакцию интегрирующей цепи на прямоугольный импульс напряжения. Напомню, что прямоугольный импульс, по сути, является напряжением, которое изменяется ступенчато два раза. В результате первого скачка напряжения конденсатор начинает заряжаться до тех пор, пока напряжение на входе не изменится, после этого начнётся разряд конденсатора по экспоненциальному закону.

 

Реакция интегрирующей цепи на прямоугольный импульс.

Не трудно заметить, что длительность импульса на выходе интегрирующей цепи несколько больше, чем длительность импульса на входе. Эту особенность нередко используют для увеличения длительности импульса, и такие цепи ранее называли расширяющими.

№5 Транзисторы, их основные типы, свойства, характеристики.

Транзи́стор (англ. transistor) — радиоэлектронный компонент из полупроводниковогоматериала, обычно с тремя выводами, позволяющий входным сигналам управлять током в электрической цепи. Обычно используется для усиления, генерирования и преобразования электрических сигналов. На принципиальных схемах обозначается «VT» или «Q«.

Управление током в выходной цепи осуществляется за счёт изменения входного напряжения или тока. Небольшое изменение входных величин может приводить к существенно большему изменению выходного напряжения и тока. Это усилительное свойство транзисторов используется в аналоговой технике (аналоговые ТВ, радио, связь и т. п.).

В настоящее время в аналоговой технике доминируют биполярные транзисторы (БТ) (международный термин — BJT, bipolar junction transistor). Другой важнейшей отраслью электроники является цифровая техника (логика, память, процессоры, компьютеры, цифровая связь и т. п.), где, напротив, биполярные транзисторы почти полностью вытеснены полевыми.

Вся современная цифровая техника построена, в основном, на полевых МОП (металл-оксид-полупроводник)-транзисторах (МОПТ), как более экономичных, по сравнению с БТ, элементах. Иногда их называют МДП (металл-диэлектрик-полупроводник)- транзисторы.

 

 

Классификация транзисторов

Рекомендуемые страницы:

3.8. Дифференцирующие и интегрирующие цепи

3.8. Дифференцирующие и интегрирующие цепи

Рассмотрим RC-цепь, изображенную на рис. 3.20,а. Пусть на входе этой цепи действует напряжение u1(t).

Рис. 3.20. Дифференцирующие RC-(а) и RL-(б) цепи.

Тогда для этой цепи справедливо соотношение

и с учетом преобразований будем иметь

                                                       (3.114)

 

Если для данного сигнала выбрать постоянную времени цепи τ=RC настолько большим, что вкладом второго члена правой части (3.114) можно пренебречь, то переменная составляющая напряжения uR≈u1. Это значит, что при больших постоянных времени напряжение на сопротивлении R повторяет входное напряжение. Такую цепь применяют тогда, когда необходимо передать изменения сигнала без передачи постоянной составляющей.

При очень малых значениях τ в (3.114) можно пренебречь первым слагаемым. Тогда

                                                               (3.115)

т. е. при малых постоянных времени τ RC-цепь (рис. 3.20,а) осуществляет дифференцирование входного сигнала, поэтому такую цепь называют дифференцирующей RC-цепью.

Аналогичными свойствами обладает и RL-цепь (рис. 3.20,б).

Рис. 3.21. Частотные (а) и переходная (б) характеристики дифференцирующих цепей.

Сигналы при прохождении через RС- и RL-цепи называют быстрыми, если

,

или медленными, если

.

Отсюда следует, что рассмотренная RC-цепь дифференцирует медленные и пропускает без искажения быстрые сигналы.

Для гармонической э. д. с. аналогичный результат легко получить, вычисляя коэффициент передачи цепи (рис. 3.20,а) как коэффициент передачи делителя напряжения со стационарными сопротивлениямиR и XC=1/ωC:

                                       (3.116)

При малых τ, а именно когда τ<<1/ω, выражение (3.116) преобразуется в

.

При этом фаза выходного напряжения (аргумент K) равна π/2. Сдвиг гармонического сигнала по фазе на π/2 эквивалентен его дифференцированию. При τ>>1/ω коэффициент передачи K≈1.

В общем случае модуль коэффициента передачи (3.116), или частотная характеристика цепи (рис. 3.20,а):

                                                               (3.118)

а аргумент K, или фазовая характеристика этой цепи:

                                                                       (3.119)

Эти зависимости показаны на рис. 3.21,а.

Такими же характеристиками обладает RL-цепь на рис. 3.20,б с постоянной времени τ=L/R.

Если в качестве выходного сигнала взять единичный скачок напряжения , то интегрированием уравнения (3.114) можно получить переходную характеристику дифференцирующей цепи, или временную зависимость выходного сигнала при единичном скачке напряжения на входе:

                                                                       (3.120)

График переходной характеристики показан на рис. 3.21,б.

Рис. 3.22. Интегрииующие RC-(а) и LC-(б) цепи.

Рассмотрим RC-цепь, изображенную на рис. 3.22,а. Она описывается уравнением

или

                                                               (3.121)

При малых τ=RC (для «медленных» сигналов) uC≈u1. Для «быстрых» сигналов напряжение u1 интегрируется:

                                                                       (3.122)

Поэтому RC-цепь, выходное напряжение которого снимается с емкости C называют интегрирующей цепью.

Коэффициент передачи интегрирующей цепи определяется выражением

                                       (3.123)

При ω<<1/τ                K≈1.

Частотная и фазовая характеристики описываются соответственно выражениями

                                                               (3.124)

                                                               (3.125)

Рис. 3.23. Частотные (а) и переходная (б) характеристики интегрирующих цепей.

и изображены на рис. 3.23,а. Переходная характеристика (рис. 3.23,б) получается интегрированием (3.121) при :

                                                               (3.126)

При равных постоянных времени такими же свойствами обладает RL-цепь, изображенная на рис. 3.22,б.

ИССЛЕДОВАНИЕ ДИФФЕРЕНЦИРУЮЩИХ И ИНТЕГРИРУЮЩИХ ЦЕПЕЙ

⇐ ПредыдущаяСтр 6 из 7Следующая ⇒

Цель работы

1.1 Изучить свойства дифференцирующих и интегрирующих цепей.

1.2 Экспериментальное определение формы сигналов на выходе дифференцирующих и интегрирующих цепей при различном воздействии.

1.3 Исследование активных дифференцирующих и интегрирующих цепей.

 

2 Домашнее задание

2.1 Изучить по [9.1] дифференцирующие и интегрирующие цепи.

2.2 Подготовить ответы на вопросы самопроверки.

2.3 Подготовить бланк отчета (см. раздел 6).

2.4 Рассчитать величину резистивного сопротивления R_диф, чтобы цепь (рисунок 10.1) была дифференцирующей, если частота повторения сигналов f = 2 кГц; значение емкости конденсатора равно номеру записи учащегося в учебном журнале (в нФ). Значение R_диф занести в таблицу 10.1.

 

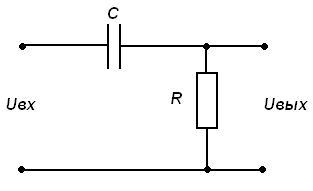
Рисунок 10.1 – Дифференцирующая цепь

 

2.5 Рассчитать величину резистивного сопротивления R_инт, чтобы цепь (рисунок 10.2) была интегрирующей, если частота повторения сигналов f = 2 кГц; значение емкости конденсатора С = 29 нФ. Значение R_инт занести в таблицу 10.2.

 

 

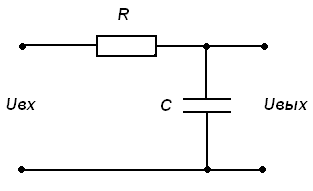
Рисунок 10.2 – Интегрирующая цепь

 

Вопросы для самопроверки

3.1 Что называется дифференцирующей цепью?

3.2 Что называется интегрирующей цепью?

3.3 Какими пассивными элементами можно реализовать дифференцирующую цепь?

3.4 Какими пассивными элементами можно реализовать интегрирующую цепь?

3.5 При каких условиях цепь RC дифференцирует?

3.6 При каких условиях цепь RC интегрирует?

3.7 Приведите схему активной дифференцирующей цепи.

3.8 Приведите схему активной интегрирующей цепи.

3.9 Укажите достоинства активных дифференцирующих и интегрирующих цепей по сравнению с пассивными цепями.

3.10 Приведите график дифференцирования прямоугольного импульса.

3.11 Приведите график интегрирования прямоугольного импульса.

3.12 Какие цепи называют укорачивающими и удлиняющими? Почему?

3.13 Приведите график дифференцирования сигнала треугольной формы.

 

Аппаратное и программное обеспечение

4.1 Рабочая станция локальной сети (персональный компьютер).

4.2 Графический манипулятор мышь.

4.3 Программа Electronics Workbench 5.0.

 

Порядок выполнения работы

5.1 Проверка подготовки учащихся к лабораторной работе по вопросам самопроверки.

5.2 Получить инструктаж по технике безопасности.

ВНИМАНИЕ! Аккуратно обращайтесь с персональным компьютером и его периферийными устройствами. Соблюдайте требования эргономики. Проверьте наличие заземления устройств.

5.3 Запустить программу Electronics Workbench 5.0.

5.4 Собрать схему проведения исследований (рисунок 10.3). Соединить выход генератора с конденсатором. Для их соединения необходимо нажать левую клавишу манипулятора мышь в точке соединения в момент появления стрелки. Удерживая клавишу, перемещать манипулятор мышь по коврику. Отпустить клавишу необходимо в момент появления другой точки в нужном месте соединения. Появляющаяся линия – подтверждение правильности соединения. Аналогично включить остальные элементы схемы.

5.4.1 Установить значение емкости конденсатора согласно п. 2.4 данной лабораторной работы и значение резистивного сопротивления R, которое было рассчитано в домашнем задании. Чтобы установить значение элемента, надо два раза щелкнуть левой клавишей манипулятора мышь на изображение элемента и поменять его значение в раскрывшемся окне, с помощью манипулятора мышь. Нажать «OK», окно закроется, значение элемента изменится.

 

 

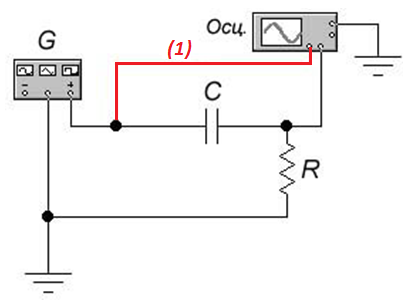
В данной схеме используются:

G – генератор сигнала – (генерирует сигналы различной частоты и длительности синусоидальной, треугольной и прямоугольной форм).

Осц. – осциллограф – для наблюдения формы сигналов на входе и выходе.

 

Рисунок 10.3 – Схема исследования пассивной

дифференцирующей цепи

 

5.4.2 Чтобы наблюдать одновременно импульсы на входе и выходе цепи, надо соединить выход генератора со вторым каналом осциллографа. Эту линию соединения (на рисунке 10.3 – линия (1)) выделить другим цветом, для этого два раза щёлкнуть левой клавишей манипулятора мышь на линию и в раскрывшемся окне выбрать другой цвет. Нажать «OK», окно закроется, цвет линии поменяется.

5.5 Исследовать пассивную дифференцирующую цепь:

5.5.1 Щелкнуть два раза на изображение генератора. Установить режим генерации синусоидальных импульсов, нажав на изображение синусоидальных импульсов в раскрывшемся окне лицевой панели генератора.

5.5.2 Установить частоту (frequency) 2 кГц, амплитуду (amplitude) 5 В, длительность импульса (duty cycle) 50% от периода, постоянную составляющую (offset) сигнала на выходе генератора равную нулю, изменяя эти данные в окошках напротив параметров в раскрывшемся окне лицевой панели генератора.

5.5.3 Включить режим анализа схемы, щелкнув манипулятором мышь на изображение выключателя 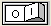, расположенного в правом верхнем углу панели инструментов.

5.5.4 Щелкнуть два раза на изображение осциллографа, наблюдать временные диаграммы сигналов на экране осциллографа.

5.5.5 Щелкнуть на изображение Expand лицевой панели осциллографа. Наблюдать временные диаграммы входного и выходного сигналов на расширенном экране.

5.5.6 Нажать манипулятором мышь надпись Pause на панели инструментов, остановив анализ построения программой временных диаграмм или отключить формирование сигналов, нажав левой клавишей манипулятора мышь на изображение выключателя в правом верхнем углу окна.

5.5.7 Щелчками манипулятора мышь установить на лицевой панели осциллографа переключателем «Время на деление» (Time base) – время, соответствующее наблюдению двух или трех периодов колебания.

5.5.8 Установить переключателем «Вольт на деление» (V/div) удобный для наблюдения масштаб по оси амплитуд. Зарисовать входной и выходной импульсы в отчет.

5.5.9 Измерить напряжение на входе (U_вх) и на выходе (U_вых), для чего установить манипулятор мышь на красном треугольнике 1 и, нажав клавишу манипулятора, перемещать визирную линию на максимальное значение входного сигнала. Записать значение VA1 (U_вх) в таблицу 10.1. Аналогично измерить максимальное значение выходного сигнала. Записать значение VB1 (U_вых) в таблицу 10.1. По этим значениям рассчитать коэффициент передачи цепи (К):.

K = U_вых/U_вх

5.5.10 На лицевой панели генератора установить режим генерации треугольных импульсов. Повторить пп. 5.5.1–5.5.9.

5.5.11 На лицевой панели генератора установить режим генерации прямоугольных импульсов и постоянную составляющую (offset) сигнала на выходе генератора равной амплитуде импульса (см. п. 5.5.2). Повторить пп. 5.5.1–5.5.9.

5.5.12 Для сигнала прямоугольной формы измерить длительность входного и выходного сигналов: для этого воспользоваться визирными линиями. На правом табло осциллографа отображаются значения разностей между соответствующими координатами первой и второй линии: T2-T1. Данные длительности входного и выходного сигналов занести в таблицу 10.1.

 

Таблица 10.1 – Таблица экспериментальных данных исследования дифференцирующих цепей

 

Класс цепи	Форма входного сигнала	По расчету п. 2.4	Получено в эксперименте
Rдиф, Ом	Uвх, В	Uвых, В	К	tимпвх, мкс	tимпвых, мкс
Дифференцирующая цепь RC	Синусоидальная					-	-
Треугольная				-	-
Прямоугольная
Активная дифференцирующая цепь ARC	Синусоидальная					-	-
Треугольная				-	-
Прямоугольная

 

5.6 Исследовать пассивную интегрирующую RC цепь.

5.6.1 Собрать схему, приведенную на рисунке 10.4.

 

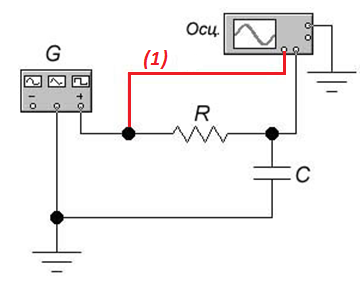
Рисунок 10.4 – Схема исследования пассивной интегрирующей цепи

 

5.6.2 Установить значение резистивного сопротивления R, которое было рассчитано в домашнем задании (п. 2.5). Значение емкости конденсатора С = 29 нФ.

5.6.3 Установить частоту (frequency) 2 кГц, амплитуду (amplitude) 5 В, длительность импульса (duty cycle) 50% от периода, постоянную составляющую (offset) сигнала на выходе генератора равную нулю, изменяя эти данные в окошках напротив параметров в раскрывшемся окне лицевой панели генератора.

5.6.4 Подавать на цепь последовательно три вида напряжений (синусоидальное, треугольное, прямоугольное). Зарисовать осциллограммы сигналов на входе и выходе. Для каждого сигнала измерять значение входного и выходного напряжений, рассчитать коэффициент передачи цепи (К), для сигнала прямоугольной формы измерить длительность входного и выходного сигналов. Результаты измерений и вычислений занести в таблицу 10.2.

 

 

Таблица 10.2 – Таблица экспериментальных данных исследования интегрирующих цепей

 

Класс цепи	Форма входного сигнала	По расчету п. 2.5	Получено в эксперименте
Rинт, кОм	Uвх, В	Uвых, В	К	tимпвх, мкс	tимпвых, мкс
Интегрирующая цепь RC	Синусоидальная					-	-
Треугольная				-	-
Прямоугольная
Активная интегрирующая цепь ARC	Синусоидальная					-	-
Треугольная				-	-
Прямоугольная

 

5.7 Исследовать активную дифференцирующую цепь.

5.7.1 Собрать схему, приведенную на рисунке 10.5. Установить R1= 300 Ом. Это сопротивление необходимо для нейтрализации влияния индуктивности соединительных проводов; C = 29 нФ; R2 = 4 кОм.

5.7.2 Щелкнуть два раза на изображение генератора. Установить режим генерации синусоидальных колебаний, нажав на изображение синусоидальных колебаний в раскрывшемся окне лицевой панели генератора.

 

Рисунок 10.5 – Схема исследования активной

дифференцирующей цепи

 

5.7.3 Установить частоту (frequency) 2 кГц, амплитуду (amplitude) 1 В и длительность импульса (duty cycle) 50% от периода, постоянную составляющую (offset) равной нулю (при исследовании сигналов синусоидальной и треугольной формы), изменяя эти данные в окошках напротив параметров в раскрывшемся окне лицевой панели генератора. При подаче прямоугольных импульсов установить постоянную составляющую (offset) сигнала на выходе генератора равной единице.

5.7.4 Подавать на цепь последовательно три вида напряжений (синусоидальное, треугольное, прямоугольное). Для каждого сигнала измерять значение входного и выходного напряжений, рассчитать коэффициент передачи цепи (К), для сигнала прямоугольной формы измерить длительность входного и выходного сигналов. Результаты измерений и вычислений занести в таблицу 10.1.

5.8 Исследовать активную интегрирующую цепь.

5.8.1 Собрать схему, приведенную на рисунке 10.6. Установить C = 29 нФ, R = 200 Ом.

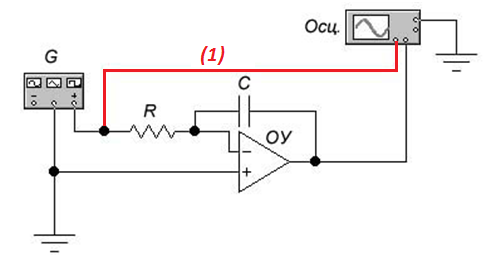
Рисунок 10.6 – Схема исследования активной интегрирующей цепи

 

5.8.2 Установить частоту (frequency) 2 кГц, амплитуду (amplitude) 1 В и длительность импульса (duty cycle) 50% от периода, постоянную составляющую (offset) равной нулю, изменяя эти данные в окошках напротив параметров в раскрывшемся окне лицевой панели генератора.

5.8.3 При исследовании синусоидальных и треугольных колебаний на панели осциллографа выбрать режим AC, для прямоугольных колебаний – DC. Режим АС предназначен для наблюдения только сигналов переменного тока (в этом режиме на входе усилителя включается разделительный конденсатор, не пропускающий постоянную составляющую). В режиме DC (включен по умолчанию) можно проводить осциллографические измерения как постоянного, так и переменного тока.

5.8.4 Подавать на цепь последовательно три вида напряжений (синусоидальное, треугольное, прямоугольное). Для каждого сигнала измерять значение входного и выходного напряжений, рассчитать коэффициент передачи цепи (К), для сигнала прямоугольной формы измерить длительность входного и выходного сигналов. Результаты измерений и вычислений занести в таблицу 10.2.

5.9 Показать результаты выполнения работы преподавателю.

5.10 Выключить оборудование.

5.11 Составить отчет по работе.

 

Содержание отчета

6.1 Наименование и цель работы.

6.2 Решение задачи по п. 2.4, 2.5.

6.3 Схемы исследований (рисунки 10.3, 10.4, 10.5, 10.6).

6.4 Осциллограммы входных и выходных сигналов.

6.5 Заполненные таблицы 10.1; 10.2.

6.6 Ответы на контрольные вопросы (по заданию преподавателя).

6.7 Выводы по работе.

 

7 Контрольные вопросы

7.1 Нарисовать дифференцирующую RL цепь.

7.2 Рассчитать R, чтобы цепь RL была дифференцирующей, если L = 44 мГн; f = 2 кГц.

7.3 Нарисовать интегрирующую RL цепь.

7.4 Рассчитать R, чтобы цепь RL была интегрирующей, если L = 44 мГн, f = 2 кГц.

 

Содержание зачета

Учащийся должен знать ответы на контрольные вопросы. Должен уметь проводить измерения, предусмотренные заданием на работу, анализировать результаты измерений.

 

Литература

9.1 Добротворский, И. Н. Теория электрических цепей / И. Н. Добротворский. – M.: Радио и связь, 1989. – С. 400 – 410.

9.2 Карлащук, В. И. Электронная лаборатория на IBM PC / В. И. Карлащук. – М.: Солон-Р, 1999. – С. 73 – 76.

Лабораторная работа № 11

Рекомендуемые страницы:

Интегрирующие цепи

В случае, когда выходное звено RC-цепи — емкость (рис. 2,а), цепь называют интегрирующей. Она описы­вается уравнением

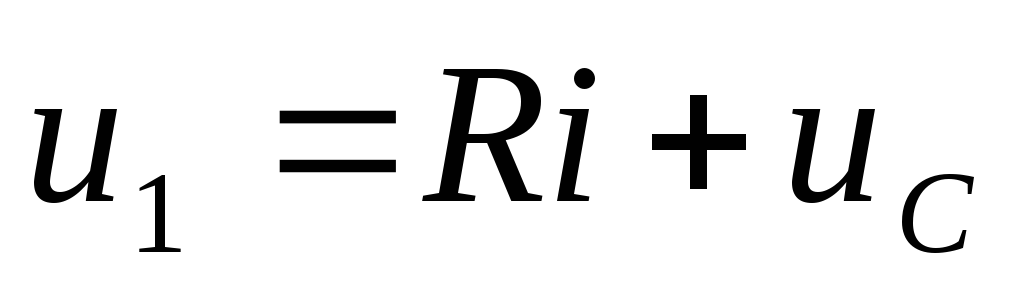
или

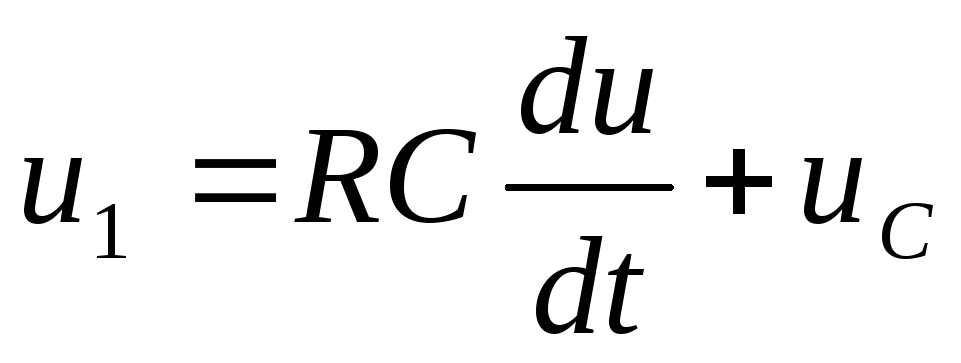. (8)

При малых  = RC (для «медленных» сигналов) 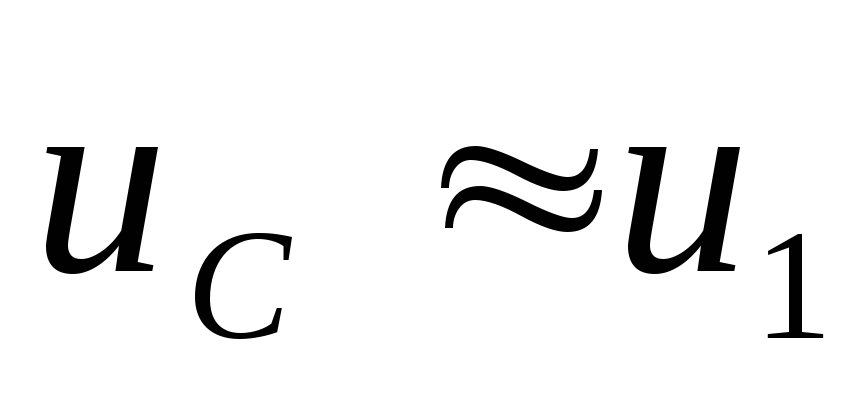. Для «быстрых» сигналов напряжениеи₁ интегри­руется:

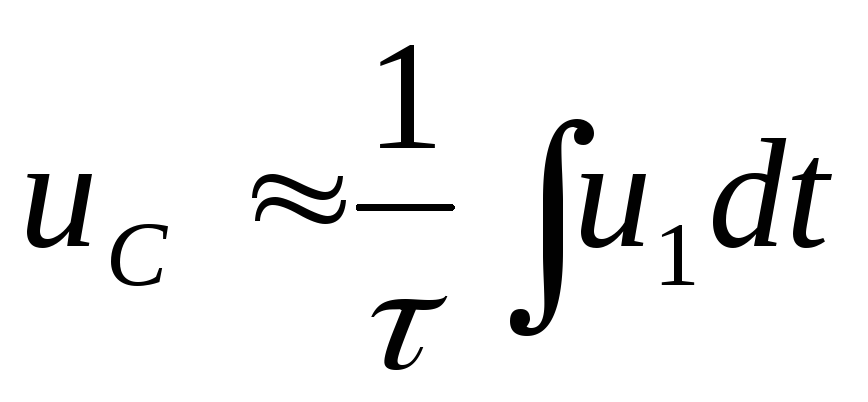. (9)

Коэффициент передачи интегрирующей цепи

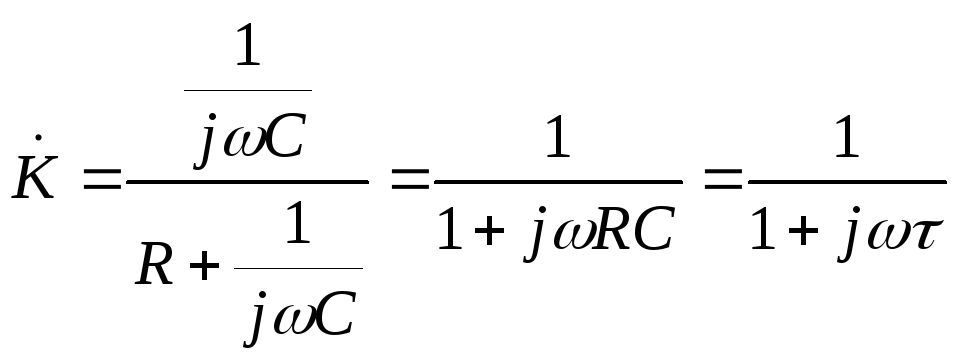. (10)

При <<1/ .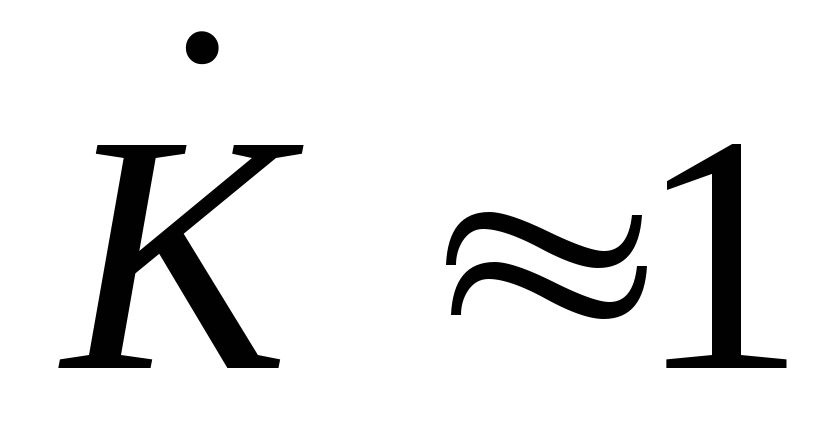

Частотная и фазовая характеристики описываются соответственно

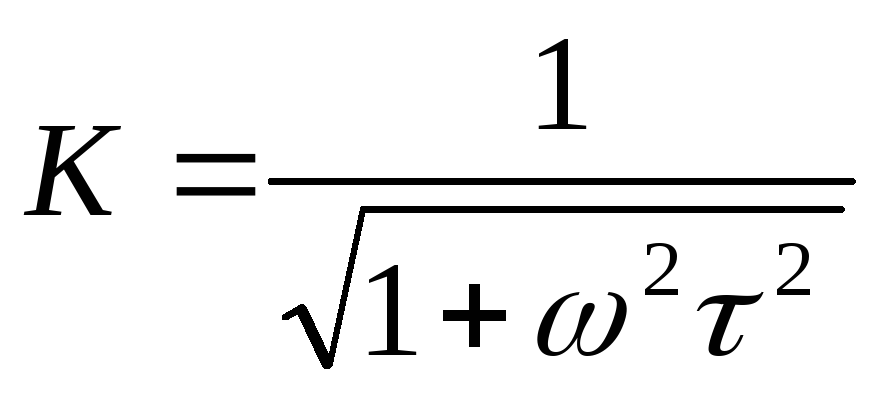; (11)

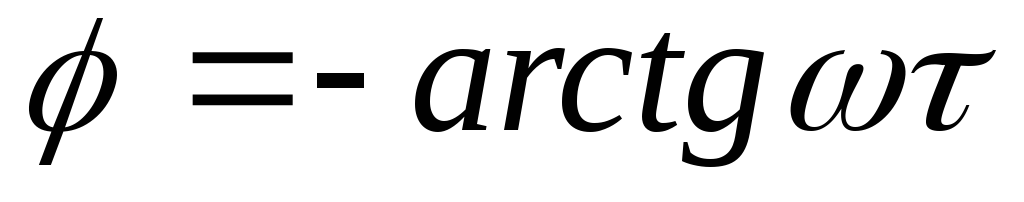(12)

и изображены на рис.2,в. Переходная характеристика (рис.2,г) получается интегрированием (8) при :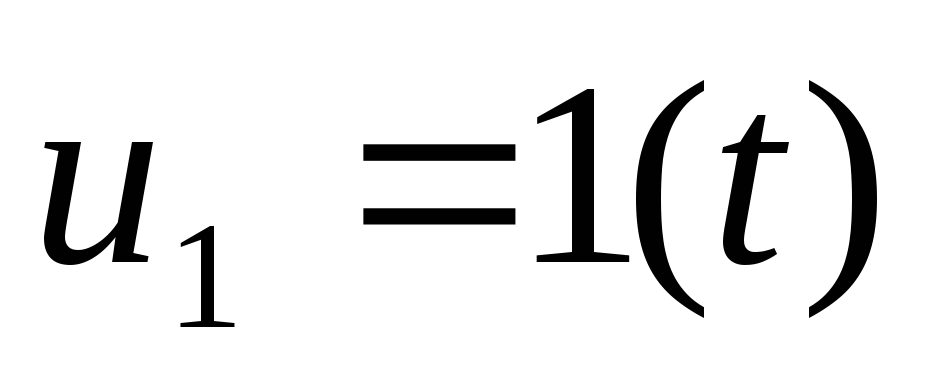

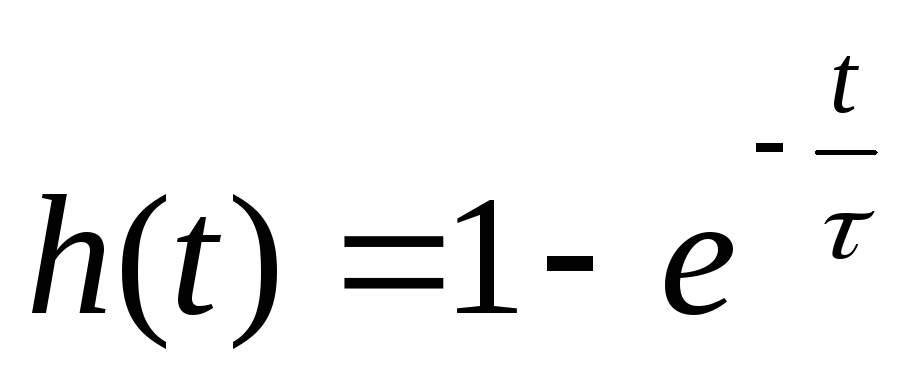(13)

При равных постоянных времени такими же свойствами обладает RL-цепь с сопротивлением на выходе (рис.2,б).

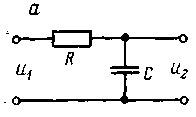
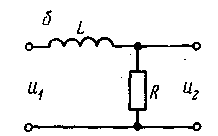
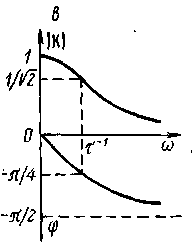
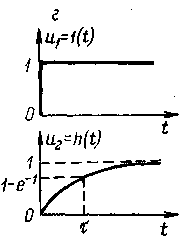
Рис. 2

Порядок выполнения работы

1. Изучите частотные и переходные характеристики дифференцирующих и интегрирующих RC-цепей (R = 470 кОм; С₁ = 0,15 мкФ, С₂ = 6800 пФ, С₃ = 240 пФ, С₄ = 68 пФ) и (R=200 кОм; С₅=0.001мкФ, С₆=0.025 мкФ, С₇=0.05мкФ, С₈=0,5мкФ) соответственно.

   1. Вычислите постоянную времени  и граничную частоту f₁ = 1/2.

   2. Запустите программу Electronics Workbench и откройте файл lab21.ewb, в котором находится схема, показанная на рис.3.

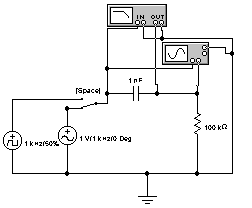
Рис.3

1. При постоянной амплитуде напряжения U_вх на входе RC-цепи, измерьте по осциллографу U_вых для емкостей С₁, С₂, С₃, С₄. Зарисовать эпюры амплитудно-частотной характеристики. Вычислите для этих частот модуль коэффициента передачи цепи К = U_вых/U_вх.

2. Для оценки изменения характера прямоугольного импульса подключите ко входу RC-цепи источник импульсного сигнала, нажав клавишу «Space» («пробел»). Зарисовать эпюры выходного напряжения для емкостей С₁, С₂, С₃, С₄. Из полученной характеристики определите постоянную времени , равную интервалу времени, в течении которого выходное напряжение изменяется в е раз.

3. Проведите измерение амплитудно-частотной и фазово-частотной характеристики по измерителю АЧХ.

4. Сравните измеренные характеристики с вычисленными.

1. Откройте файл lab22.ewb и проделайте такие же измерения для интегрирующей RC-цепи со значениями параметров R=200 кОм; С₅=0.001мкФ, С₆=0.025 мкФ, С₇=0.05мкФ, С₄=0,5мкФ.

Рекомендуемый библиографический список

1. Ефимчик М. К., Шушкевич С. С. Основы радиоэлектроники. Минск. 1981 г.

2. Карлащук В. И. Электронная лаборатория на IBM PC. М. «Солон-Р». 2000 г.

3. Балычев А.Л., Лямин П.М., Тулиев Е.С. Электронные приборы. М.: ЛАЙТ ЛТД, 2000 г.

4. Жеребцов И.П. Основы электроники. Л., «Энергоатомиздат». Ленинградское отделение, 1990 г.

5. Батушев В.А. Электронные приборы М.: «Высшая школа», 1980 г.

6. Бочаров Д.И. Электронные приборы. М.: «Энергия», 1979 г.

Лабораторная работа № 3 Резонансный контур

Цель работы: изучение основных свойств резонансного контура, определение его параметров.

Порядок выполнения работы

1. Определите основные характеристики последовательного резонансного контура.

1.1 Запустите программу Electronics Workbench (Ewb) и откройте файл lab31.ewb, в котором находится схема для исследования последовательного колебательного контура (рис.1).

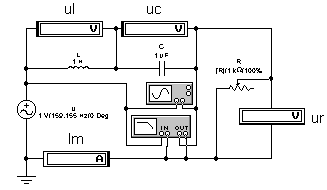
Рис. 1

В цепи, изображенной на рис.1., при равенстве индуктивного и емкостного сопротивлений наблюдается явление резонанса напряжений. При заданных значениях X_L и X_c резонанс наступает при частоте

.

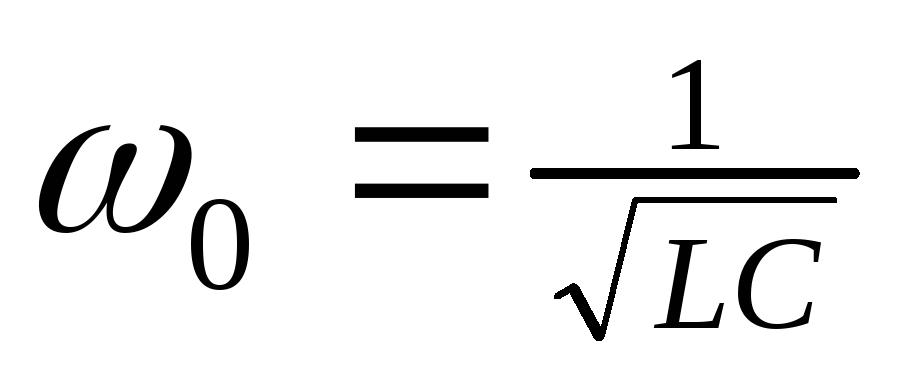При резонансе напряжений ток цепи определяется только сопротивлением резистора R и совпадает по фазе с входным напряжением. Напряжения на индуктивной катушке и конденсаторе равны и могут превышать входное напряжение в Q раз, где Q – добротность контура, равная

.

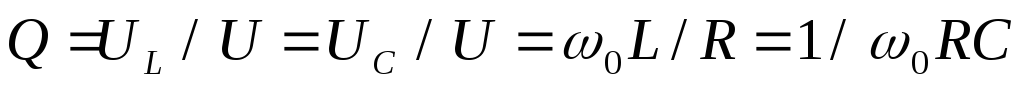Добротность контура может быть записана как отношение характеристического (волнового) сопротивления контура W / R, где

.

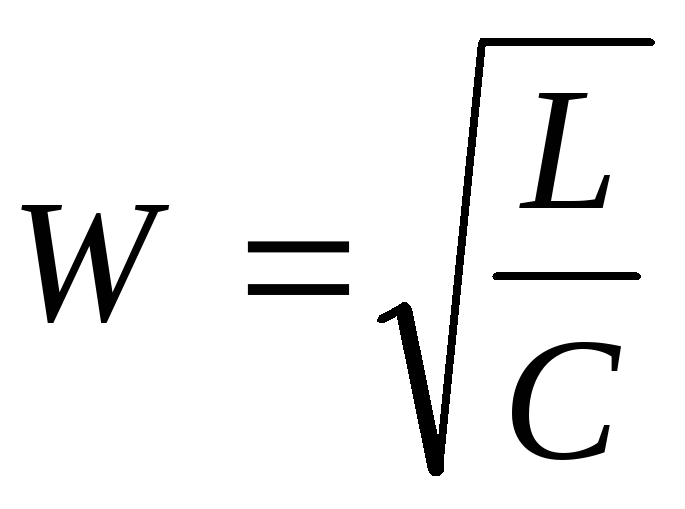Параметр W имеет размерность сопротивления и называется характеристическим сопротивлением контура.

Кривые зависимости действующих значений тока контура, напряжений на участках R, L, C от частоты являются его частотными характеристиками.

В схеме, приведенной на рис.1, для указанных на ней параметров резонанс наблюдается при частоте 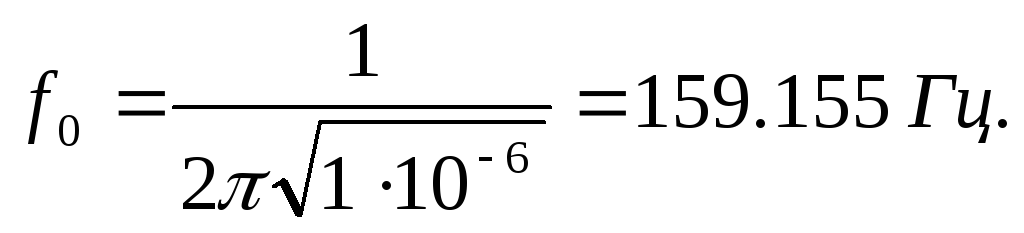Волновое сопротивление W= 10001=1000 Ом, добротность контура Q=W/R = 1.

Значение тока в цепи при резонансе I = U / R = 1/1000 = 1 мА, падение напряжения на индуктивности и емкости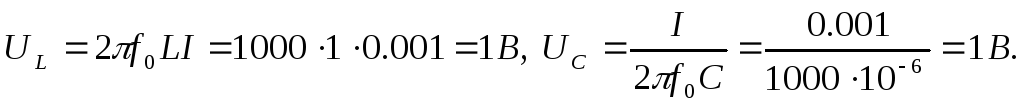

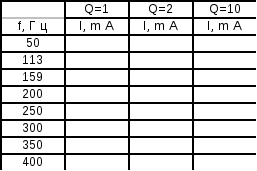
1.2. Изменяйте частоту источника ЭДС в диапазоне, указанном в табл.1 (особый интерес представляет резонансная частота 159.155 Гц), и записывайте показания приборов в табл.1.

Таблица 1. Таблица 2

1.3. Убедитесь, что при резонансе напряжений угол сдвига фаз между током и напряжением равен нулю. Для этого откройте экран осциллографа двойным щелчком мыши.

1.4 По данным табл.1 постройте зависимости I(f), UL(f), Uc(f) на одном графике.

1.5 Повторите опыт еще для двух значений сопротивления резистора (R=500 Ом и R=100 Ом) и измерьте значения тока контура .Запишите показания амперметра в табл.2.

1.6. По данным табл.2 постройте на одном графике зависимости тока от частоты при трех значениях добротности контура Q.

1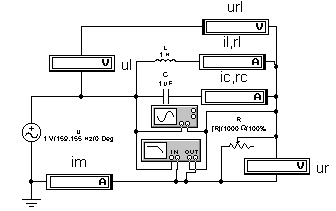

Рис. 2

.7.Выясните зависимость частотных характеристик от добротности контура.

2. Определите основные характеристики параллельного колебательного контура.

2.1. Откройте файл lab32.ewb, содержащий схему для исследования параллельного колебательного контура (рис.2).

В цепи, изображенной на рис.2., при равенстве индуктивного и емкостного сопротивлений наблюдается явление резонанса токов. Параллельный колебательный контур является основным элементом большинства частотно-избирательных устройств.

Собственно колебательный контур состоит из двух параллельно включенных ветвей: индуктивной с сопротивлением потерь в виде внутреннего сопротивления R_l амперметра I_l и емкостной с сопротивлением потерь в виде внутреннего сопротивления R_c амперметра I_c. Эти сопротивления могут изменятся и для рассматриваемой схемы установлены равными 1 Ом для обоих амперметров. К контуру подключены измерительные приборы: вольтметры U_l, U_rl, U_rпредназначены для измерения падения напряжения соответственно на индуктивности L, на сопротивлении потерь R_l и на резисторе R.

Для параллельного колебательного контура вводится параметр, который равен сопротивлению контура на резонансной частоте и называется резонансным сопротивлением R_р, определяемым по формуле:

R_р=(₀^.L)²/R_s=1/[R_s(₀^.C)²],

где R_s=R_l+R_c — суммарное сопротивление потерь контура.

Соотношение между подводимым к контуру током I_m и током в контуре I_k на резонансной частоте определяется выражением:

I_k=Q^.I_m, где Q — добротность контура, равная ₀^.L/R_s=1/(₀^.R_s^.C).

Для схемы на рис.2. R_р=(1000^.1)²/2=500000 Ом; Q=(1000^.1)/2=500. Подводимый к контуру ток и ток контура: I_m=U/(R_р+R)=1/(500000+1000)=1,996 мкА;

I_k=1,996^.500=998 мкА.

2.2. Проведите измерение амплитудно-частотной и фазово-частотной характеристики по измерителю АЧХ и ФЧХ (Bode Plotter).

2.3. Проведите моделирование при сопротивлении потерь R_l = R_c = 8ом.

2.5. Рассчитайте амплитудно-частотную и фазо-частотную характеристики колебательного контура и сравните полученные результаты с данными моделирования.

1.4 Исследование интегрирующей RL-цепи. Исследование переходных процессов и анализ частотных характеристик элементарных звеньев радиотехнических цепей

Похожие главы из других работ:

Автоматическая система регулирования с П-регулятором

8. Исследование устойчивости АСР

Исследование замкнутых АСР на устойчивость предполагает получение ответов на следующие вопросы. Является ли система с рассчитанным регулятором устойчивой, то есть…

Анализ режимов автоматического управления

1.5 Исследование устойчивости САУ

Устойчивость — это свойство системы возвращаться в исходный или близкий к нему установившийся режим после всякого выхода из него в результате какого-либо воздействия. Критерий устойчивости Рауса-Гурвица. Это алгебраический критерий…

Исследование двухконтурной системы автоматического регулирования

4.1 Исследование астатической двукратно интегрирующей САР по управляющему воздействию

В соответствии с принципом оптимизации структурной схемы САР, настроенная по симметричному оптимуму, имеет вид (рис. 13). Рис. 13 Структурная схема астатической САР в общем виде Передаточная функция регулятора внешнего контура Так же…

Исследование переходных процессов и анализ частотных характеристик элементарных звеньев радиотехнических цепей

1.1 Исследование дифференцирующей RC-цепи

Начертим принципиальную схему дифференцирующей RC-цепи в программе MC9 (рисунок 1.1). Рисунок 1.1 — Принципиальная схема дифференцирующей RC-цепи Определим постоянную времени нашей RC-цепи: В этой формуле ф — постоянная времени RC-цепи…

Исследование переходных процессов и анализ частотных характеристик элементарных звеньев радиотехнических цепей

1.2 Исследование интегрирующей RC-цепи

Начертим принципиальную схему интегрирующей RC-цепи в программе MC9 (рисунок 1.6). Рисунок 1.6 — Принципиальная схема интегрирующей RC-цепи Постоянная времени нашей RC-цепи будет вычисляться по той же формуле, какую мы использовали в пункте 1.1…

Исследование переходных процессов и анализ частотных характеристик элементарных звеньев радиотехнических цепей

2.2 Переходные процессы в интегрирующей RC-цепи

Представим принципиальную схему интегрирующей RC-цепи в программе MS-10 (Рисунок 2.8) Рисунок 2.8 — Принципиальная схема интегрирующей RC-цепи, выполненная в программе MS-10 Произведем расчет переходных процессов…

Исследование переходных процессов и анализ частотных характеристик элементарных звеньев радиотехнических цепей

2.4 Переходные процессы в интегрирующей RL-цепи

Начертим принципиальную схему интегрирующей RL-цепи в программе MS-10 (Рисунок 2.22): Рисунок 2.22 — Принципиальная схема интегрирующей RL-цепи, выполненная в программе MS-10 Постоянная времени этой RL-цепи была рассчитана ранее в пункте 1.4…

Преобразователи напряжение-ток

4. Исследование ПНТ

«Соберите» упрощённую схему ПНТ, приведённую на рисунке 2а. Упрощение этой схемы обусловлено применением идеальных источников тока, что существенно не повлияет на изучение принципа её работы…

Разработка системы управления

8. Исследование устойчивости СУ

В Схемное Окно поставили 2 блока «В память» и провели к ним линии связи, представленные на рисунке 15. Рисунок 15 — Структурная схема с блоками «В память» В меню «Анализ» выбрали пункт «Частотный анализ…

Разработка цифровой системы автоматического управления технологической установкой

9. Аналитическое исследование

Получив дискретную передаточную функцию объекта и регулятора, проведём аналитическое исследование…

Схемные функции и частотные характеристики линейной электрической цепи

3. Исследование нагрузки

…

Схемные функции и частотные характеристики линейных электрических цепей

3. Исследование нагрузки

…

Схемные функции и частотные характеристики линейных электрических цепей

3. Исследование нагрузки

Рассчитаем параметры нагрузки на резонансной частоте ; ; для вычисления добротности, нужно схему преобразовать в эквивалентную схему, где сопротивление шунта и емкость соединены последовательно. 0=100; Rш=1000; rвн=9,901; добротность (R=10): =5…

Устройство стабилизации скорости перемещения схвата промробота

1.4 Исследование САР на устойчивость

Рисунок 1.7 — Переходная характеристика соединения САР устойчива, т.к. переходная характеристика сходящаяся…

Устройство формирования управляющих сигналов

1. Расчет в общем виде АЧХ и ФЧХ скорректированного дифференцирующего устройства (r-L-c цепи). Расчет параметров r-L-c цепи согласно требованиям технического задания.

Составим уравнения Кирхгоффа для r-L-c-цепочки в комплексной форме (рис. 17): Рис.17 К расчету дифференцирующей rc-цепочки комплексным методом Комплексный коэффициент передачи напряжения может быть найден, как отношение комплексных амплитуд…