Блок 1 механическое движение волны звук законы ньютона силы кинематика прямолинейного движения
Блок 1. Механическое движение. Волны. Звук. Законы Ньютона. Силы.
КИНЕМАТИКА ПРЯМОЛИНЕЙНОГО ДВИЖЕНИЯ
Движение в Природе. Механическое движение – изменение пространственного положения тела относительно других тел с течением времени. Кинематика даёт математическое описание движения тел.
Материальная точка как физическая модель – это тело, размерами которого можно пренебречь.
Тело отсчёта – тело, относительно которого рассматривается движение.
Система отсчёта – это совокупность тела отсчёта и связанной с ним системы координат и часов.
Траектория – линия вдоль которой движется тело.
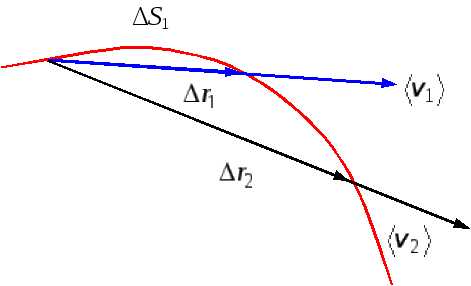
Перемещение показывает на какое расстояние и в каком направлении смещается тело за данное время. Перемещение – вектор, проведённый из начального положения материальной точки в конечное.
Результирующее перемещение равно векторной сумме последовательных перемещений.
Путь – длина участка траектории, пройденного материальной точкой за данный промежуток времени.
Путь равен модулю перемещения только при прямолинейном движении в одном направлении.
Скорость
Средняя скорость равна отношению пройденного пути ко времени, за которое этот путь пройден. V = S/ t
Мгновенная скорость – средняя скорость за бесконечно малый интервал времени. Мгновенная скорость направлена так же, как и перемещение в данный момент времени.
Ускорениехарактеризует изменение скорости.
Ускорение показывает, как изменяется скорость за единицу времени.
Ускорение – векторная физическая величина, равная отношению изменения скорости к промежутку времени, за которое это изменение произошло. а = (V – V0)/t
Вектор ускорения при прямолинейном движении параллелен или антипараллелен вектору скорости.
П рямолинейное равноускоренное движение. а = (V – V0)/t; a – const.
рямолинейное равноускоренное движение. а = (V – V0)/t; a – const.
Скорость при прямолинейном равнопеременном движении V = V0 + at.
График зависимости скорости при равнопеременном движении представляет собой прямую линию. Если скорость не меняется, то эта линия параллельна оси времени.
Свободное падение – это движение тела в гравитационном поле Земли с постоянным
ускорением g = 9,8 м/сек2. Время движения вверх и время падения равны. Скорость бросания равна конечной скорости падения.
П


 еремещение при равнопеременном движении
еремещение при равнопеременном движении

Перемещение всегда равно площади фигуры ограниченной графиком скорости и осью времени.
Уравнение движения. x= x0+ Sх, гдеxиx0 — конечная и начальная координаты Sх – проекция перемещения.
К РИВОЛИНЕЙНОЕ ДВИЖЕНИЕ.
РИВОЛИНЕЙНОЕ ДВИЖЕНИЕ.
Примеры криволинейного движения: равномерное и неравномерное движение по окружности (когда на тело действует перпендикулярная сила), движение по параболе (баллистическое движение, когда скорость тела направлена под углом к горизонту), колебания маятника, или груза на пружине.
Р
 авномерное движение тела по окружности – периодическое движение с постоянной по модулю скоростью.Путь по дуге. Перемещение по хорде. Скорость направлена по касательной. Ускорение к центру окружностиЦентростремительное ускорение a = υ2 /R. Скорость равна отношению пройденного пути ко времени. υ = S/t = 2 πR /Tгде 2 πR – путь, пройденный за один поворот, Т — период – время одного полного поворота. Частота – число поворотов в единицу времени ν = 1/Т .
авномерное движение тела по окружности – периодическое движение с постоянной по модулю скоростью.Путь по дуге. Перемещение по хорде. Скорость направлена по касательной. Ускорение к центру окружностиЦентростремительное ускорение a = υ2 /R. Скорость равна отношению пройденного пути ко времени. υ = S/t = 2 πR /Tгде 2 πR – путь, пройденный за один поворот, Т — период – время одного полного поворота. Частота – число поворотов в единицу времени ν = 1/Т .
Координата вращающейся точки находится по уравнениюx = Rcos φ, где R – радиус окружности при движении тела по окружности, а φ – угол поворота радиуса, соединяющего тело с началом отсчёта (центром окружности).
2 . Колебательное движение является периодическим и
. Колебательное движение является периодическим и
описывается такими же законами, что и движение по окружности. Классическими колебательными системами, способными совершать свободные колебания, являются математический маятник и груз на пружине. Колебания, совершаемые благодаря начальному запасу энергии, называются свободными. Колебания, происходящие под действием внешней периодической силы, называются вынужденными.
Если частота внешней периодической силы совпадает с частотой свободных колебаний, то наступает резонанс – явление резкого возрастания амплитуды вынужденных колебаний при совпадении частоты свободных колебаний с частотой внешней периодической силы. Резонанс является причиной разрушения зданий, мостов, обрыва проводов, поломки двигателей и т.д.
При колебаниях происходят изменения энергии – потенциальная переходит в кинетическую и обратно. Но, если колебания незатухающие, то полная механическая энергия остаётся неизменной E = mv2/2 + mgh = mv2 max/2 = mghmax
Координата колеблющейся точки находится по уравнениюx = Rcos φ, где R – длина маятника, или максимальная
координата (амплитуда) при колебаниях, а φ – угол отклонения маятника – фаза колебания. Колебания, в которых
и зменение координаты от времени описываются синусоидой, или косинусоидой называются гармоническими.
зменение координаты от времени описываются синусоидой, или косинусоидой называются гармоническими.
Период колебаний маятника определяется по формуле где l – длина нити.

Период колебаний груза на пружине по формуле , где m – масса груза, а k — жёсткость пружины.
Д
 вижение по параболе (баллистическое движение)
вижение по параболе (баллистическое движение)
Происходит под действием силы тяжести. Ускорение во всех точках траектории направлено, как и сила тяжести, вертикально вниз. Скорость во всех точках траектории направлена по касательной.
В верхней точке траектории скорость направлена горизонтально.
По законам баллистики движутся снаряды, пули, брошенные под углом к горизонту тела.
ЗАКОНЫ НЬЮТОНА.
Высказывания Галилея. «Нет действия, нет изменения скорости. Есть действие, есть изменение скорости. Каждому действие есть противодействие.»
И нерция – явление сохранения скорости тел при отсутствии действия со стороны других тел.
нерция – явление сохранения скорости тел при отсутствии действия со стороны других тел.
Первый закон Ньютона: «Тело сохраняет состояние покоя или равномерного
прямолинейного движения, пока на него не действуют другие тела».
Сила – физическая величина, характеризующая действие одного тела на другое, в результате которого возникает ускорение, или деформация. Чем больше сила, тем больше ускорение. F = ma. Измеряется в Ньютонах Н
Инертность – свойство тел сопротивляться изменению скорости.
 Масса – мера инертности. m = Vρ. Измеряется в кг ρ – плотность тела (масса в 1 м3)
Масса – мера инертности. m = Vρ. Измеряется в кг ρ – плотность тела (масса в 1 м3)
Зависимость изменения скорости от массы. Чем больше масса, тем меньше изменение скорости.
Равнодействующая сила равна векторной сумме всех, действующих на тело сил.
Второй закон Ньютона: «В инерциальной системе отсчёта ускорение тела прямо
пропорционально равнодействующей силе и обратно пропорционально массе тела». 
Третий закон Ньютона: «Силы, с которыми два тела действуют друг на друга, равны по модулю,
противоположны по направлении и действуют вдоль прямой, соединяющей эти тела».
Эти силы направлены вдоль прямой, соединяющей центры тел, они всегда одной природы
СИЛЫ.
Сила упругости – сила, возникающая при деформации и направлена противоположно смещению частиц при деформации. Fупр= — kx, х – деформация тела, k – жёсткость, которая определяется упругими свойствами тела.
Сила нормального давления – сила упругости, действующая на тело со стороны опоры, перпендикулярно её поверхности.
Сила натяжения – сила упругости, действующая на тело со стороны нити или пружины.
Закон Гука: Сила упругости, возникающая при деформации, пропорциональна деформации и направлена в сторону, противоположную деформации. Fупр= — kx
Сила трения покоя – сила, препятствующая возникновению движения одного тела по поверхности другого. (Она всегда по модулю равна силе, приложенной к телу, но противоположна ей по направлению). Максимальная сила трения покоя равна силе трения скольжения.
Сила трения скольжения – сила, возникающая при движении и направленная в сторону, противоположную движению. Она прямо пропорциональна силе нормального давления Fmp = μN. μ – коэффициент трения, который зависит от качества обработки соприкасающихся поверхностей и материала, из которого они изготовлены
Вес тела – сила, с которой тело действует на опору или подвес.
— вес тела в случае горизонтального движения на горизонтальной опоре P = mg;
движение вниз с ускорением P = m(g-a), без ускорения P = mg.
Невесомость. Вес тела равен нулю, когда тело свободно падает, т.е. на него действует только сила тяжести.
Перегрузки. Вес тела возрастает в несколько раз.
5. Закон всемирного тяготения: все тела во Вселенной притягиваются друг к другу с силой прямо пропорциональной массам этих тел и обратно пропорциональной квадрату расстояния между ними. Эта сила называется силой всемирного тяготенияF = G M m/R2 G = 6,67 ∙ 10-11 Нм2/кг2 – гравитационная постоянная, которая показывает, с какой силой два тела массой по 1 кг притягиваются друг к другу на расстоянии 1 м.
6. Сила тяжести – сила, с которой Земля притягивает к себе тела. На Земле и на различных планетах
Fm =mg, где g – ускорение свободного падения на планете
Для преодоления силы тяжести телу необходимо сообщить скорости:
7,8 км/сек – 1-я космическая скорость (тело становится спутником Земли).
11,2 км/сек – 2-я космическая скорость (тело становится спутником Солнца).
42 км/сек – 3-я космическая скорость (тело покидает Солнечную систему).
ВОЛНЫ. ЗВУК.
К
 олеблющееся тело вовлекает в колебательный процесс частицы окружающей среды. В среде возникает механическая волна – возмущение, распространяющееся в упругой среде. При этом происходит передача энергии без переноса вещества. Существую продольные и поперечные волны. Их вид определяется направлением колебания частиц среды.
олеблющееся тело вовлекает в колебательный процесс частицы окружающей среды. В среде возникает механическая волна – возмущение, распространяющееся в упругой среде. При этом происходит передача энергии без переноса вещества. Существую продольные и поперечные волны. Их вид определяется направлением колебания частиц среды.
Продольная волна (частицы колеблются вдоль распространения возмущения) – возникает во всех средах.
П оперечная волна (частицы колеблются перпендикулярно распространению возмущения) – возникает в твёрдых средах и на поверхности жидкости.
оперечная волна (частицы колеблются перпендикулярно распространению возмущения) – возникает в твёрдых средах и на поверхности жидкости.
Скорость механической волны – скорость распространения возмущения в среде.
Длина волны – расстояние, на которое распространяется волна за время, равное периоду колебаний её источника (расстояние между двумя соседними гребнями)λ =υT = / ν, где λ- длина волны,υ – скорость, Т – период. На графике Т = 8 сек. Амплитуда хмах=0,5 м
2. Звук. Всякое звучащее тело колеблется, но не всякое колеблющееся тело звучит. Частота звуковых колебаний 20 – 20000 Гц. Эти колебания создают в упругой среде звуковые волны, которые вызывают у человека слуховые ощущения. Ниже 20Гц – инфразвуки, выше 20000 – ультразвуки.
Звуковая волна является продольной волной, поэтому распространяется во всех упругих средах. Самая большая скорость распространения звука в твёрдых телах, самая маленькая – в газах. Причина – упругие свойства среды.
Высота звука определяется частотой. Тембр звука определяется наличием обертонов.
Громкость звука определяется амплитудой колебаний давлений в звуковой волне. Порог слышимости – при 1 кГц 10-5Па . Болевой порог – 10 Па. Звуковые волны отражаются от препятствий. Это явление называется ЭХО. Используется в эхолотах – приборах для определения глубины. Время движения до дна и обратно t = 2S/vзв
Обычно в эхолотах используется ультразвук.
. Решение задач
Решение задач
1 . Найти путь и перемещение часовой стрелки за 3,6,12 часов.
S1= R
S2= 2R





2
S3= 0 – перемещение,

S1= πR /2, S2 = πR, S3 = 2πR – путь.
2. Самолёт пролетел первую треть пути со скоростью 1100км/час, а оставшийся путь со скоростью 800км/час. Найти среднюю скорость его полёта.
Методика решения задач на расчёт средней скорости – вводится величина, о которой ничего неизвестно, по этой величине составляется уравнение, затем эта величина выражается через известные величины.

 Решение. t = t1 + t2 , t = S/V, t1 = S/3V1 , t2 = 2S/3V2 ,
Решение. t = t1 + t2 , t = S/V, t1 = S/3V1 , t2 = 2S/3V2 ,
3. По графику зависимости скорости от времени найти параметры движения и написать уравнение движения.
Р ешение. Рисунок 1. Vo = 6м/с , a = (V – Vo)/t = (12 – 6) /6 = 1м/с2
ешение. Рисунок 1. Vo = 6м/с , a = (V – Vo)/t = (12 – 6) /6 = 1м/с2
x = xo +Vot + at2/2, x = 6t + t2/2,
Рисунок 2. самостоятельно.
4 . По уравнению движения х = t + 2 t2 найти параметры движения и построить график зависимости скорости, координаты и ускорения от времени. Ответ: х0 = 0, V0 = 1м/с, а = 4 м/с2. Выражение для скорости V = 1 +4t
. По уравнению движения х = t + 2 t2 найти параметры движения и построить график зависимости скорости, координаты и ускорения от времени. Ответ: х0 = 0, V0 = 1м/с, а = 4 м/с2. Выражение для скорости V = 1 +4t
5 По уравнению движения найти параметры движения, записать закон
По уравнению движения найти параметры движения, записать закон
изменения скорости и построить график зависимости скорости от времени:
а) х = t — 0,5 t2,б)х = 2t + t2
а) Vo = 1м/с , a = — 1м/с2, V = 1 – t.
б — самостоятельно
6. Дано уравнение движения катера x = 8t – 0,5t2и теплохода x = – 10t .
Найти начальные скорости и ускорения каждого тела. Написать закон изменения скорости для каждого и построить графики зависимости скорости от времени


 7.. По графику зависимости скорости от времени найти параметры движения и написать уравнение движения. Найти перемещение за 3 сек.
7.. По графику зависимости скорости от времени найти параметры движения и написать уравнение движения. Найти перемещение за 3 сек.
8 Автомобиль движется со скоростью72км/час. Найти его ускорение и тормозной путь перед светофором , если время торможения 4 сек. Решение по алгоритму.
9 . На рисунке указано направление скорости движущегося тела и силы, действующей на него.
. На рисунке указано направление скорости движущегося тела и силы, действующей на него.
1. Укажите направление ускорения тела.
2. По какой траектории движется тело? Почему?
 3. Когда тело будет находиться в состоянии невесомости:
3. Когда тело будет находиться в состоянии невесомости:
на подъёме, на спуске, в верхней точке траектории.
10. Автомобиль массой 2 тонны проходит по выпуклому мосту, имеющему радиус кривизны 40 м. ср скоростью 36 км /час. С какой силой автомобиль давит на мост в его середине.? С какой скоростью должен двигаться автомобиль, чтобы в середине моста водитель оказался в состоянии невесомости?
Решение: mg — N = ma. a = v2/R, P = N. При невесомости вес тела равен 0, следовательно иN = 0
11. Мяч массой 200г брошен вертикально вверх со скоростью 20 м/с.
A. Найти максимальную высоту и время подъёма.
 B. С какой скоростью и через сколько секунд мяч упадёт на землю?
B. С какой скоростью и через сколько секунд мяч упадёт на землю?
C. Найти силу тяжести и вес мяча в верхней точке траектории.
12. Спутник массой 600 кг движется на высоте 1600 км над поверхностью Земли со скоростью 8 км/с. Радиус Земли 6400 км.
A. С какой силой притягивается спутник к Земле?
B. Что произойдёт с орбитой спутника, если скорость спутника увеличить до 9 км/с?
C. Чему равен вес спутника во время полёта
13. Лодка качается на волнах, длина которых 5 м. Каждые 4 секунды лодка
поднимается на гребне.
Найти: A. Период и частоту колебаний.
B. Скорость волны.
C. Изменится ли расстояние от лодки до берега при отсутствии ветра?
14. Плот качается на волнах, длина которых 6 м. Наблюдатель видит как плот каждые 5 секунд поднимается на гребне.
 Найти: A. Период и частоту колебаний. Скорость волны.
Найти: A. Период и частоту колебаний. Скорость волны.
B. Изменится ли расстояние от плота до берега при отсутствии ветра?
1
t c
5. A) По графику зависимости найти смещения маятника от времени определите амплитуду, период, и частоту колебаний.B) Какие колебания представлены на графике?
16. Волны, создаваемые винтом корабля, набегают на берег через каждые 5 с. Корабль находится в 50 м. от берега и волна проходит расстояние от корабля до берега за 10 с.
Найти: A. Частоту и период колебаний волн.
B. Скорость волны
C. Приблизится ли корабль к берегу. Ветра нет.
Формулы кинематики и динамики
Скорость
V = S/ t – средняя скорость,
V = V0+ at – мгновенная скорость при равноускоренном движении.
Vср = (V + V0)/2 — средняя скорость при равноускоренном движении.
Ускорение a = (V–V0)/t – ускорение при равноускоренном движении.
П
 еремещениеS = Vt – при равномерном движении,
еремещениеS = Vt – при равномерном движении,
При равноускоренном движении:


Уравнение движения x= x0+ Sх
Законы равноускоренного движения (vo = 0)
1. L1: L2 :L3 :L4 … = 1:3:5:7:9… L1, L2, L3, L4 – пути, проходимые телом за равные последовательные промежутки времени (за первую, вторую, третью, и т. д. секунду).
2.S1 : S2 : S3 : S4 : S5 = 1:4:9:16:25… – пути, проходимые телом за одну, две, три, четыре и так далее секунд.
Свободное падение
Используются те же формулы, что и при равноускоренном движении, только ускорение постоянно и равно 9,8 м/с2
Движение по окружности
L = 2πR – длина окружности,
V = 2πR/T – линейная скорость при движении по окружности,
Т – период, т. е. время одного оборота.
ν = 1/T – частота, т.е. число оборотов в 1 сек.
a =V2/R – центростремительное ускорение.
x = Rcos φ координата колеблющегося тела, или тела, движущегося по окружности
— равнодействующая сила.

— ньютоновская сила
Fm =mg— сила тяжести
Fтр = μN— сила трения
Fупр= — kx — сила упругости
F = G M m/R2 – сила всемирного тяготения
x = Rcos φ – уравнение гармонических колебаний
λ = υT = υ/ ν — длина волны. υ – скорость, T — период
Период колебаний математического маятника
П ериод колебаний груза на пружине
ериод колебаний груза на пружине
Результирующее перемещение — Большая Энциклопедия Нефти и Газа, статья, страница 2
Результирующее перемещение
Cтраница 2
Если В перемещается в новое положение С, то результирующее перемещение может быть получено движением точки Л в положение С. [16]
Если складываемые перемещения происходят вдоль одной прямой, то результирующее перемещение равно алгебраической сумме складываемых перемещений. Отсюда вытекает и графический способ сложения колебаний, которым мы будем сейчас пользоваться. [17]
На рис. 375, я и б показано, что результирующее перемещение тела не зависит от последовательности, в которой осуществляются составляющие перемещения: Перемещение треугольника из положения ABC в положение AiB d ( рис. 375, б) можно осуществить путем поворота его вокруг оси, проходящей через точку А, до положения АВ С, в первую очередь, и поступательного перемещения вместе с полюсом А из положения АВ С ь положение AiB i — во вторую очередь. [18]
Работа силы на совокупности последовательных перемещений равна работе силы на результирующем перемещении. [19]
Если точка совершила последовательно два перемещения АВ и ВС, то ее результирующим перемещением будет АС. Из рис. 11 видно, что в случае, когда складываемые перемещения имеют одинаковое направление ( рис. 11, а), направление результирующего перемещения совпадает с направлением слагаемых, а модуль результирующего перемещения равен сумме модулей слагаемых. Если же складываемые перемещения направлены в противоположные стороны ( рис. 11, б и в), направление результирующего перемещения совпадает с направлением того из слагаемых, у которого модуль больше. [21]
Он обладает тем свойством, что его звенья имеют угловые движения, а результирующее перемещение конца манипулятора происходит в прямоугольной системе координат. [23]
Так как на рычаг 4 действуют измерительная мембрана 1 и сильфоны измерения производной, то результирующее перемещение рычага происходит под действием двух составляющих: пропорциональной и дифференциальной. Поэтому перемещение затвора регулирующего органа ПД-регулятора пропорционально отклонению и скорости отклонения регулируемого параметра от заданного значения. [24]
Перемещения поршней сервомоторов 24 и 28 суммируются рычагом 27, поэтому рейка 8 топливного насоса получает результирующее перемещение под действием обоих импульсов регулятора. [25]
В кинематике имеет место закон независимости движений: если материальная точка одновременно участвует в нескольких движениях, то результирующее перемещение точки равно векторной сумме перемещений, совершаемых ею в каждом из движений. [26]
Если выполнить теперь сначала данное перемещение с осью В, а затем — данное перемещение с осью А, то результирующее перемещение будет равносильно двум последовательным транспозициям относительно осей D и D2 и будет поэтому иметь своей осью С2 общий перпендикуляр к этим двум прямым. [29]
Если данные перемещения представляют собой поступательные перемещения, то прямые Д, Д, Z2 будут параллельны между собой, и
Страницы: 1 2 3 4
Результирующее перемещение — Большая Энциклопедия Нефти и Газа, статья, страница 1
Результирующее перемещение
Cтраница 1
Результирующее перемещение двух данных вращений будет в то же время и результирующим перемещений двух транспозиций относительно осей DJ и D2; оно не может быть вращением, так как оси обеих транспозиций не лежат в одной плоскости. [1]
Результирующее перемещение тела, участвующего одновременно в двух перемещениях, направленных под углом друг к другу, определяется по величине и направлению замыкающей стороной треугольника ( или диагональю параллелограмма), построенного на этих перемещениях. [2]
Показать, что результирующее перемещение твердого т ча не пииеит от порядка, в котором следуют одно за другим составляющие его поступательное перемещение и вращение. [3]
Показать, что результирующее перемещение твердого тела не зависит от порядка, в котором следуют одно за другим составляющие его поступательное перемещение и вращение. [4]
Конечно, разделение
Легко видеть, что результирующее перемещение равно векторной сумме первоначальных. Поступательное перемещение является, следовательно, вектором. Этот вектор мы можем построить в любой точке твердого тела, так как для всех них он одинаков, другими словами: вектор, изображающий поступательное перемещение твердого тела, может быть в твердом теле любым образом перемещен. [6]
В самом деле, пусть результирующим перемещением данного вращения около оси SI и транспозиции относительно другой данной осп 51s служит транспозиция относительно некоторой оси L. SI ( две последовательные транспозиции относительно одной и той же оси Se дают тождество), будет и результирующим перемещением двух последовательных транспозиций относительно L и Se. [7]
Под произведением двух перемещений пространства понимают результирующее перемещение. Совокупность всех перемещений образует относительно этого произведения группу. Эта группа называется евклидовой группой. [8]
Аналогично этому в формулах для составляющих результирующего перемещения
Любое число винтовых перемещений имеет своим результирующим перемещением одно винтовое перемещение. [11]
Второе перемещение можно при этом получить как результирующее перемещение транспозиции относительно оси D2 и транспозиции относительно некоторой новой оси D8, пересекающей D под прямым углом. [12]
Если речь идет о поступательных перемещениях, то результирующее перемещение также будет поступательным перемещением. [13]
Работа постоянной по модулю и направлению силы на результирующем перемещении роена алгебраической сумме работ этой силы на составляющих перемещениях. [15]
Страницы: 1 2 3 4
shpory
Теоретическая механика
(кинематика, динамика)
ОСНОВНЫЕ ПОЛОЖЕНИЯ, ЗАКОНЫ И ФОРМУЛЫ
КИНЕМАТИКА
Абсолютно твердое тело — это тело, взаимное расположение частиц которого при движении не меняется.
Материальной точкой называется тело, размерами которого в данной задаче можно пренебречь.
Система отсчета — это совокупность тела отсчета, системы координат и способа измерения времени.
Тело отсчета — это тело, условно принятое за неподвижное.
Траектория — это линия, вдоль которой движется тело.
Поступательным называется движение, при котором все точки тела движутся по одинаковым траекториям.
Пройденный путь l — это скалярная величина, численно равная длине траектории, пройденной телом за данный промежуток времени.
Перемещение — вектор, соединяющий начало и конец движения.
Скорость — векторная величина, характеризующая направление и быстроту перемещения материальной точки:
Ускорение — векторная величина, характеризующая направление и быстроту изменения скорости:
Равномерное прямолинейное движение — это движение с постоянной по модулю и направлению скоростью:
Равноускоренное прямолинейное движение — движение с постоянным по модулю и направлению ускорением:
Графическое изображение равномерного движения
Рис. 7 Рис. 8
Графическое изображение равноускоренного движения
Рис. 9 Рис. 10
Рис. 11
Рис. 12
По графику скорости можно определить путь, рассчитав площадь фигуры, образовавшейся между графиком скорости и осью времени.
Равномерное движение по окружности
Частота
Линейная скорость
Угловая скорость
Центростремительное ускорение
Рис. 13
Закон сложения скоростей:
скорость U движении тела относительно неподвижной системы отсчета равна векторной сумме скорости U1тела относительно неподвижной системы отсчета и скорости U2 самой подвижной системы относительно неподвижной.
Принцип независимости движений: если тело одновременно участвует в двух движениях, то результирующее перемещение равно векторной сумме перемещений:
Свободное падение — это движение в безвоздушном пространстве под действием силы тяжести с ускорением свободного падения , направленным к земле.
Равноускоренное движение
Свободное падение
Движение тела, брошенного вертикально вверх
Движение тела, брошенного горизонтально
Рис. 14
1) по горизонтали:
2) по вертикали:
В любой точке траектории:
Движение тела, брошенного под углом к горизонту
Это криволинейное движение, траектория которого — парабола, имеющая восходящую» и нисходящую ветви:
Рис. 15
Исходя из принципа независимости движений, сложное движение по параболе можно разложить на два простых:
1) по горизонтали:
2) по вертикали:
3) в момент падения:
4) учитывая, что обе ветви параболы одинаковы:
Пути, проходимые телом, движущимся с ускорением, в равные, последовательные промежутки времени, пропорциональны ряду нечетных чисел:
s1: s2: s3:… ; sn = 1 : 3 : 5 :…: (2n — 1)
Путь, проходимый телом в первую секунду падения:
ДИНАМИКА
Сила — это векторная величина, характеризующая действие одного тела на другое и сообщающая ускорение или деформацию последнему.
Масса тела — это мера его инертности и гравитации.
Инертность (бездействие) характеризует способность тел сохранять свое предыдущее состояние.
Первый закон Ньютона
Второй закон Ньютона
Второй закон Ньютона
в проекциях на оси ОХ, ОУ, OZ:
Fx = max; Fy — may; Fz = maz
Основное уравнение динамики
Третий закон Ньютона
Наклонная плоскость
Рис. 16
В вектором виде:
в скалярном виде в проекциях на оси:
Движение тела в лифте
Рис. 17
Движение по выпуклому и вогнутому мостам
Рис. 18
Закон всемирного тяготения
Вес тела на высоте
Вес тела при опускании в шахту
Закон Гука
Напряжение материала
Относительная деформация
Виды деформации:
продольного растяжения;
продольного сжатия;
всестороннего сжатия;
поперечного изгиба
продольного изгиба;
сдвига;
кручения.
Рис. 19
Импульс тела
Импульс силы
Сила трения
Закон сохранения импульса
Второй закон Ньютона
Рис. 20
В векторной форме (рис. 20):
в скалярной форме с учетом знаков проекций на выбранную ось ОХ:
m1V1 — m2V2 = (m1 +m2)v
Первая космическая скорость
Вторая космическая скорость
Движение спутника будет:
если v < v1 — тело упадет на Землю;
если — становится искусственным спутником Земли и движется в случае равенства v = v1 no окружности, а в случае v > v1 — по эллипсу;
если — тело преодолевает земное тяготение и уходит в космическое пространство по параболе или гиперболе (V >VII)
Механическая работа
Мощность
Работа положительна, если < а между векторами силы F и перемещения s равен нулю => cos = 1 => А — Fs > О
Работа отрицательна, если < =180° => cos = -1 => А= — Fs < 0:
работа силы трения всегда отрицательна
Рис. 21
Работа численно равна площади под графиком зависимости между силой и перемещением
Работа равна нулю, если < = 90° => cos = 0 => Amg = 0 => Работа силы тяжести при горизонтальном перемещении тела равна О
Консервативными называются силы, работа которых не зависит от вида траектории, а определяется только начальным и конечным положениями тела.
Работа консервативных сил по замкнутому контуру равна нулю.
Потенциальная энергия
Закон сохранения механической энергии
E = Ek + En = const
Кинетическая энергия
КПД
ПРИЛОЖЕНИЕ
Десятичные приставки к единицам СИ
Наименование | Обозначение | Отношение к главной единице | Наименование | Обозначение | Отношение к главной единице |
фемто | Ф | 10-15 | пета | П | 1015 |
пико | п | 10-12 | тера | Т | 1012 |
нано | н | 10-9 | гига | Г | 109 |
микро | мк | 10-6 | мега | М | 106 |
МИЛЛИ | м | 10-3 | кило | к | 103 |
санти | с | 10-2 | гекто | г | 102 |
деци | д | 10-1 | дека | да | 101 |
Единицы физических величин
Наименование | Обозначение | Единица измерения | Размерность |
Длина | L, l, s | метр | м |
Ширина | b | метр | м |
Высота | H, h | метр | м |
Толщина | H, h | метр | м |
Радиус | R, r | метр | м |
Диаметр | D, d | метр | м |
Время | t | секунда | с |
Температура | Т | Кельвин | К |
Температура | градус Цельсия | °С | |
Площадь | S | квадратный метр | м2 |
Объем | V | кубический метр | м3 |
Период | Т | секунда | с |
Заряд | g, Q | Кулон | Кл = А • с |
Сила тока | I | Ампер | А |
Потенциал | Вольт | В | |
Напряжение | U | Вольт | В |
эдс | Вольт | В | |
Работа (эл.) | А | Джоуль | Дж = А • В • с |
Энергия (эл.) | W | Джоуль | Дж = А • В • с |
Мощность (эл.) | Р | Ватт | Вт = А • В |
Частота | V | Герц | с-1 = Гц |
Угловая скорость | Герц | с-1 = Гц | |
Циклическая частота | Герц | с-1 = Гц | |
Магнитный поток | Ф | Всбер | Вб = В • с |
Коэффициент трения | , К | — | — |
Оптическая сила | D | диоптрия | днтр = м-1 |
Магнитная проницаемость | — | — | |
Диэлектрическая проницаемость | — | — | |
Жесткость | k | Ньютон на метр | |
Скорость | v, u | метр в секунду | |
Ускорение | а | метр в секунду в квадрате | |
Плотность | с | килограмм на кубический метр | |
Сила | F | Ньютон | |
Момент силы | М | Ньютон-метр | |
Импульс тела | mv | килограмм-метр на секунду | |
Импульс силы | Ft | Ньютон-секунда | |
Работа | А | Джоуль | |
Количество теплоты | Q | Джоуль | |
Энергия | W,E,U,П | Джоуль | |
Мощность | N | Ватт | |
Напряжение механическое | Паскаль | ||
Удельное сопротивление | Р | Ом-метр | ОМ • м |
Давление | Р | Паскаль | |
Удельная теплоемкость | Р | Джоуль на килограмм Кельвин | |
Сопротивление | R | Ом | В/А |
Проводимость | G | 1 /Ом = Сименс | А/В |
Электроемкость | С | Фарад | |
Индуктивность | L | Генри | |
Магнитная индукция | В | Тесла | |
Напряженность электрического поля | Е | Вольт на метр | В/ м |
Напряженность магнитного поля | Н | Ампер на метр | А/ м |
Плотность тока | j | Ампер на квадратный метр | А/ м2 |
Поверхностная плотность заряда | Кулон на квадратный метр | Кл/ м2 |
Международная система единиц (СИ)
Основные единицы системы СИ | |||
№ п/п | Величина | Наименование | Обозначение |
1 | Длина | метр | м |
2 | Масса | килограмм | кг |
3 | Время | секунда | с |
4 | Температура | Кельвин | К |
5 | Количество вещества | моль | моль |
6 | Сила электрического тока | ампер | А |
7 | Сила света | кандела | кд |
|
| ||
Дополнительные единицы системы СИ | |||
1 | Плоский угол | Радиан | рад |
2 | Телесный угол | Стерадиан | ср |
1.3. Перемещение. Длина пути
Линия, описываемая точкой при движении в пространстве, называется траекторией точки.В зависимости от формы траектории движение бываетпрямолинейным и криволинейным.Для того чтобы найти уравнение траектории точки, надо в уравнениях (1.1) и (1.2) исключить время.
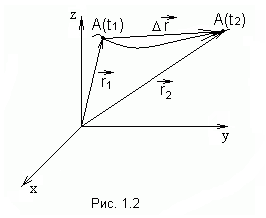
П усть
материальная точка переместилась вдоль
некоторой траектории из положенияАв положениеВ (рис. 1.2).
усть
материальная точка переместилась вдоль
некоторой траектории из положенияАв положениеВ (рис. 1.2). и
и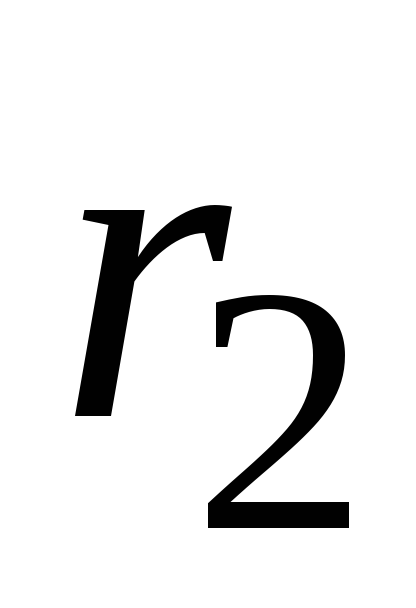 – радиусы-вектора точекАиВ.Вектор
– радиусы-вектора точекАиВ.Вектор 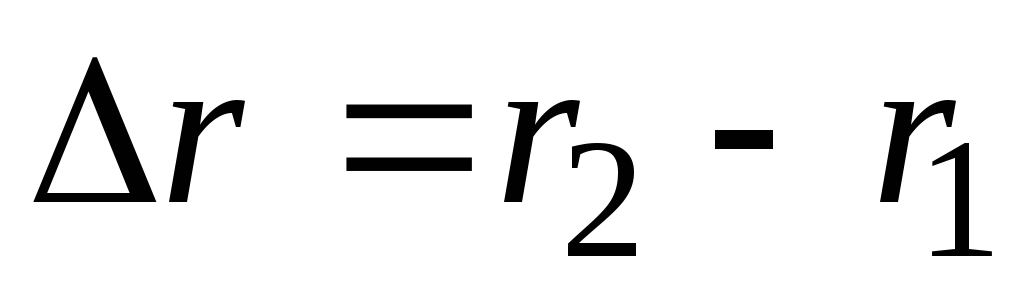 ,проведенный из начального положения
точки в конечное положение, называется вектором перемещения или
перемещением.Перемещение
,проведенный из начального положения
точки в конечное положение, называется вектором перемещения или
перемещением.Перемещение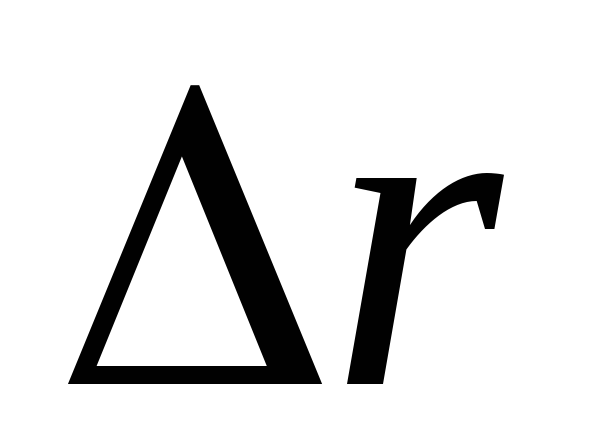 является приращением радиус-вектора
является приращением радиус-вектора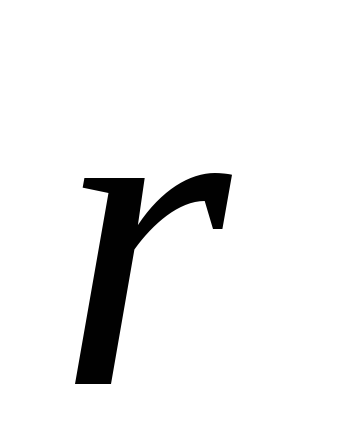 точки за рассматриваемый промежуток
времени.
точки за рассматриваемый промежуток
времени.
Длина
отрезка траектории АВ, пройденного
материальной точкой, называетсядлиной
пути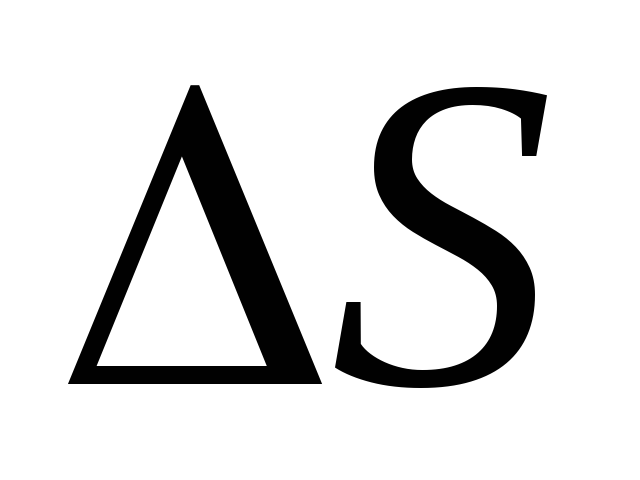 .
Надо помнить, что перемещение
.
Надо помнить, что перемещение – вектор, а длина пути
– вектор, а длина пути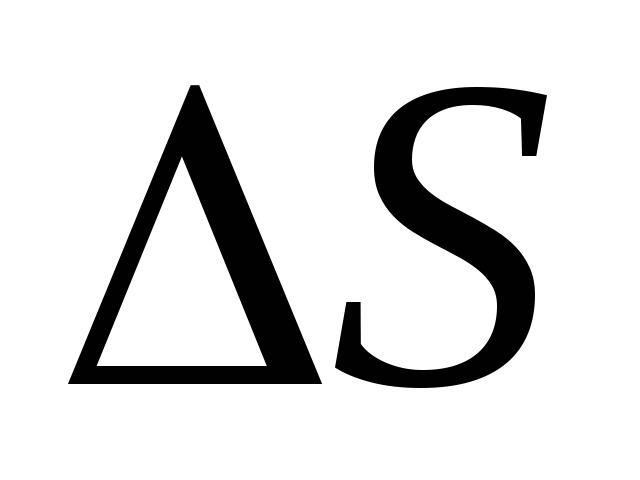 – скаляр.
– скаляр.
При прямолинейном движении модуль перемещения равен пройденному пути:
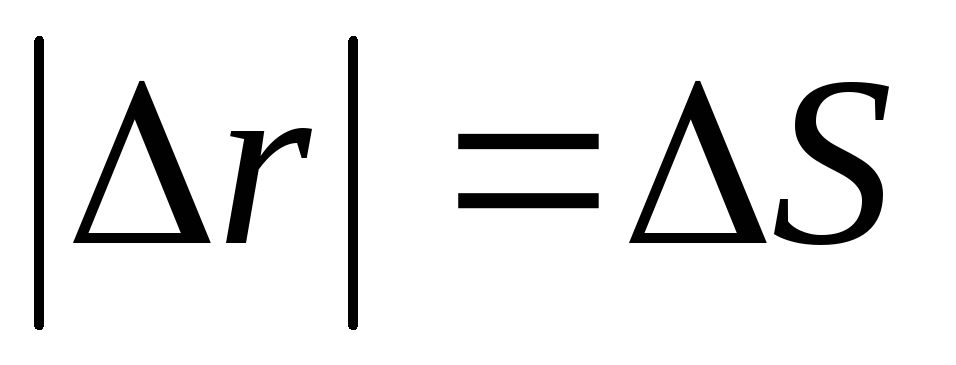 . (1.3)
. (1.3)
При криволинейном движении
 . (1.4)
. (1.4)
Но
если перемещение происходит в течение
бесконечно малого промежутка времени,
т.е. когда 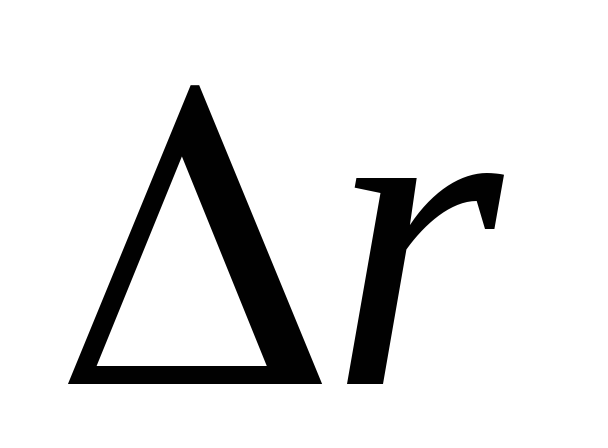 стремится к нулю, то в этом случае модуль
бесконечно малого перемещения можно
принять равным бесконечно малой длине
пути для любого произвольного движения:
стремится к нулю, то в этом случае модуль
бесконечно малого перемещения можно
принять равным бесконечно малой длине
пути для любого произвольного движения:
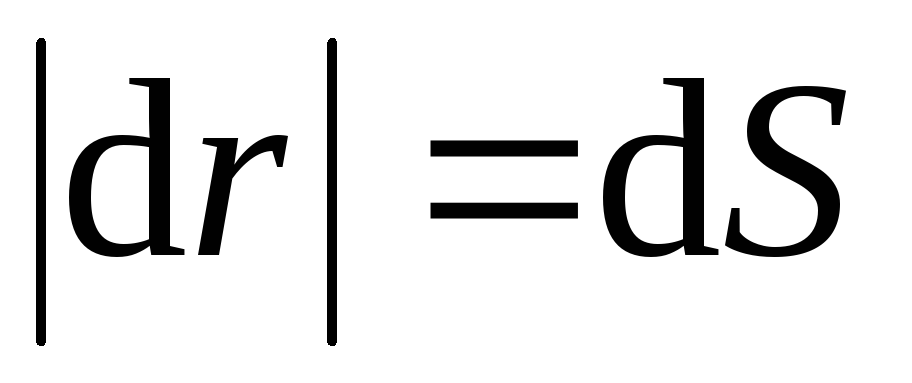 . (1.5)
. (1.5)
Если материальная точка участвует в нескольких перемещениях (рис. 1.3), то результирующее перемещение равно векторной сумме перемещений, совершаемых материальной точкой в каждом из движений в отдельности:
 ; (1.6)
; (1.6)
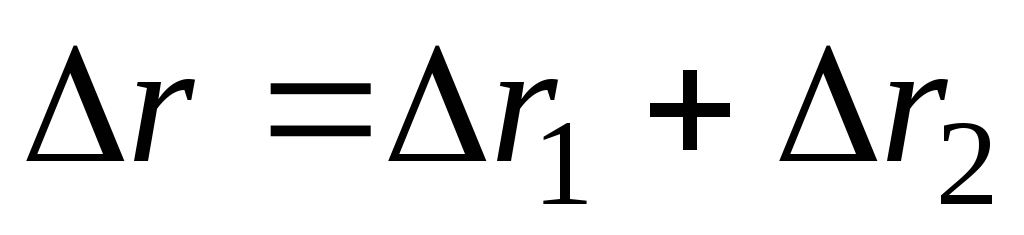 . (1.7)
. (1.7)

Рис. 1.3
1.4. Скорость
Для характеристики быстроты и направления движения вводится векторная величина – скорость.
Пусть
материальная точка в момент времени t находилась в положенииА, её
положение определяется радиус-вектором  (t).
(t).
При
движении в течение малого промежутка
времени  точка пройдет по траектории путь
точка пройдет по траектории путь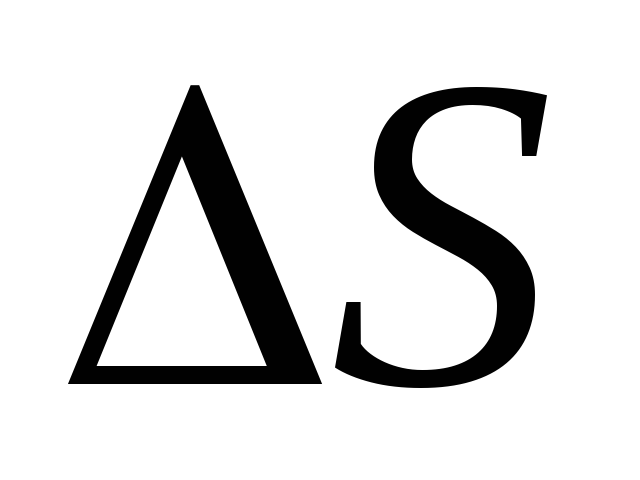 и получит элементарное перемещение
и получит элементарное перемещение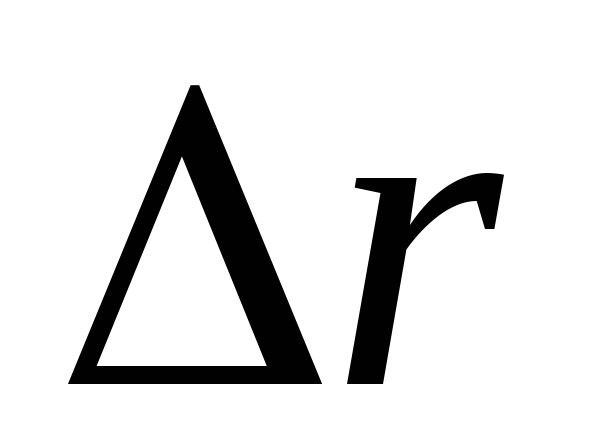 (рис. 1.4).
(рис. 1.4).
1. Средней скоростью перемещения  называется отношение приращения
называется отношение приращения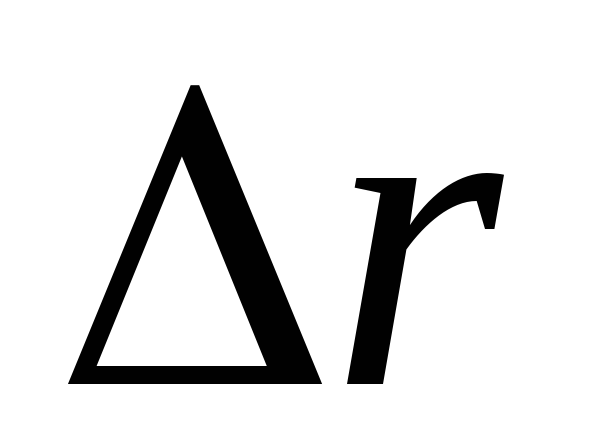 радиус-вектора точки к промежутку
времени
радиус-вектора точки к промежутку
времени :
:
 .
.  (1.8)
(1.8)
Направление
вектора средней скорости совпадает с
направлением  .
.
Вектор средней скорости – отношение перемещения к промежутку времени:
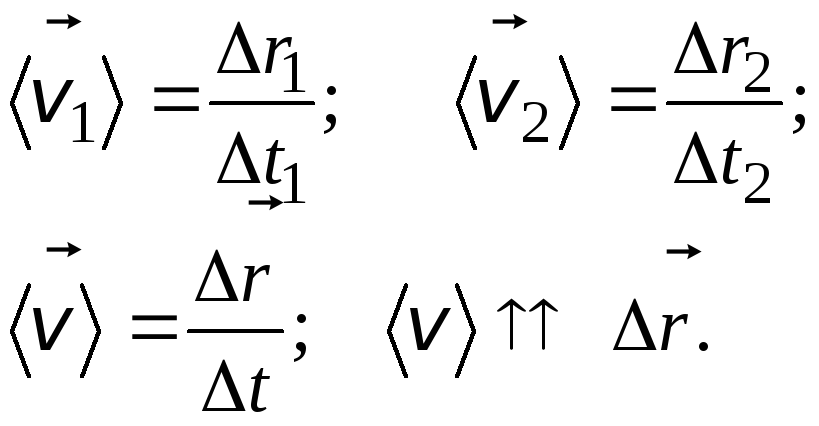
 (1.9)
(1.9)
Вектор средней скорости характеризует изменение положения радиус-вектора (рис. 1.5).
Материальная точка движется по криволинейной траектории.
За
время  точка проходит путь
точка проходит путь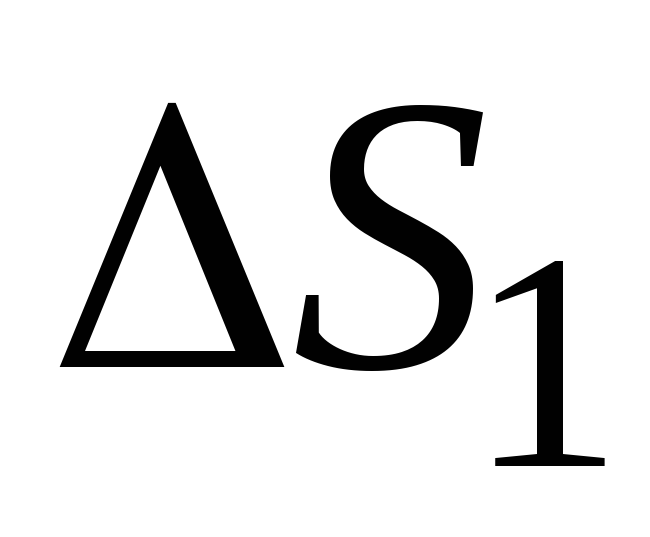 и получает приращение
и получает приращение ,
за время
,
за время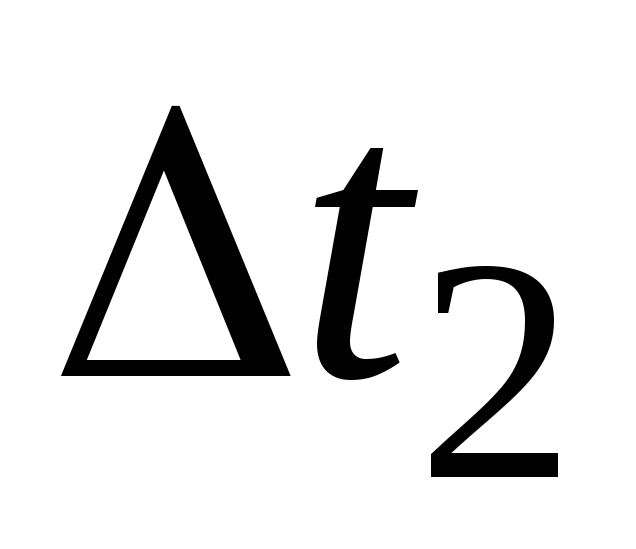 – приращение
– приращение .
.
Рис. 1.4 |
Рис. 1.5 |
2. Мгновенная скорость – это скорость
точки в данный момент времени в данной
точке траектории. Для определения
мгновенной скорости необходимо найти
перемещение точки за бесконечно малый
промежуток времени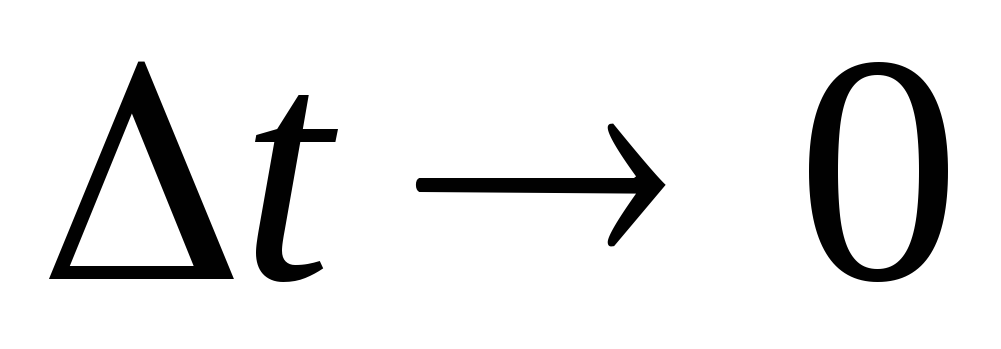 .
При
.
При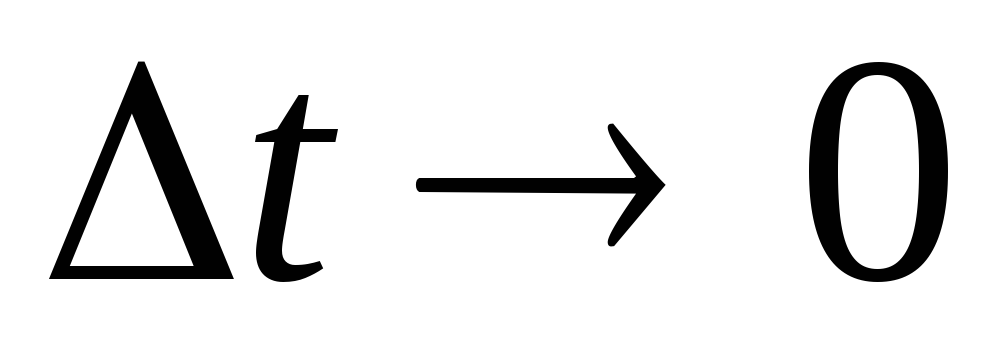 средняя скорость стремится к предельному
значению, которое называется мгновенной
скоростью
средняя скорость стремится к предельному
значению, которое называется мгновенной
скоростью :
:
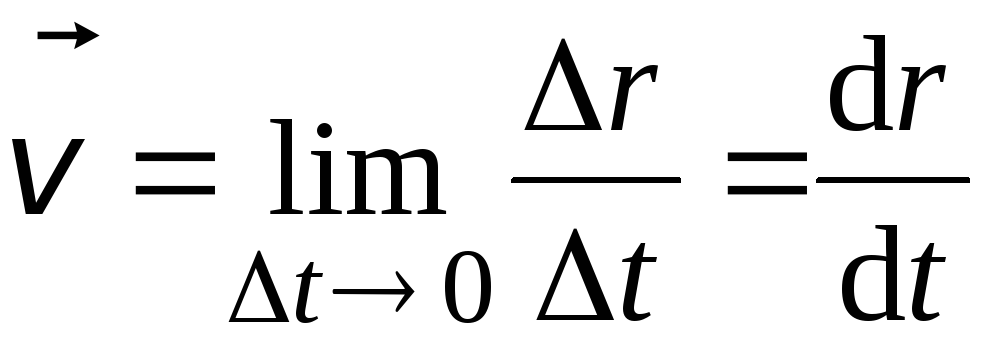 .
.  (1.10)
(1.10)
Таким
образом, мгновенная скорость  есть векторная величина, равная первой
производной радиуса – вектора движущейся
точки по времени.Вектор скорости
есть векторная величина, равная первой
производной радиуса – вектора движущейся
точки по времени.Вектор скорости  направлен по касательной к траектории
в сторону движения.
направлен по касательной к траектории
в сторону движения.
Мгновенная скорость – это вектор, поэтому
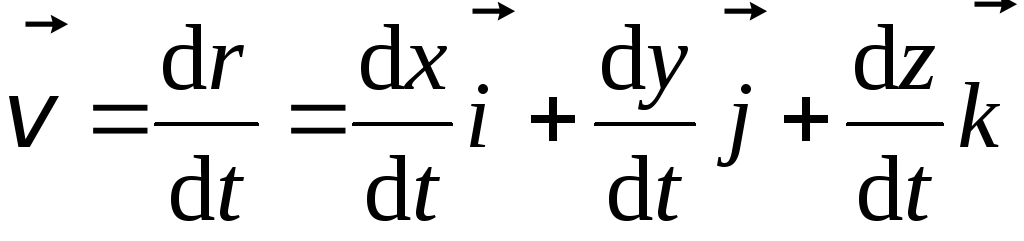 ,
,  (1.11)
(1.11)
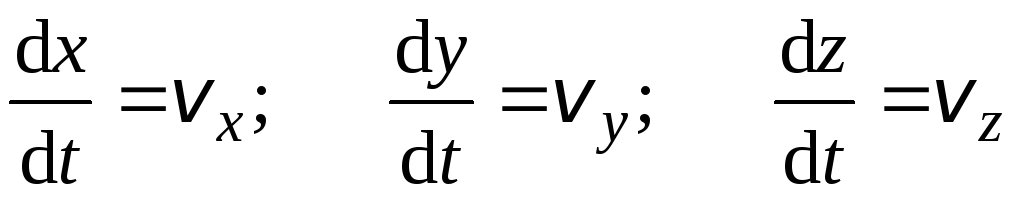 –проекции вектора
скорости на оси координат;
–проекции вектора
скорости на оси координат;
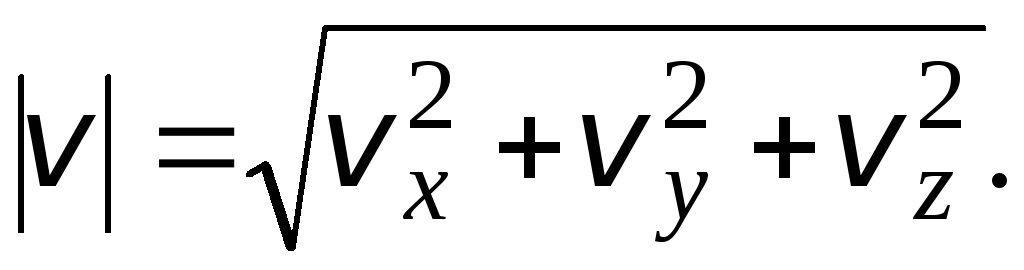 (1.12)
(1.12)
Так
как модуль бесконечно малого перемещения  можно принять равным бесконечно малой
длине пути (1.5), то модуль мгновенной
скорости
можно принять равным бесконечно малой
длине пути (1.5), то модуль мгновенной
скорости
 . (1.13)
. (1.13)
Таким образом, модуль мгновенной скорости равен первой производной пути по времени.
3. Средняя скорость пути (средняя путевая скорость). Средняя путевая скорость – это физическая величина, равная отношению пути к промежутку времени, за который этот путь пройден:
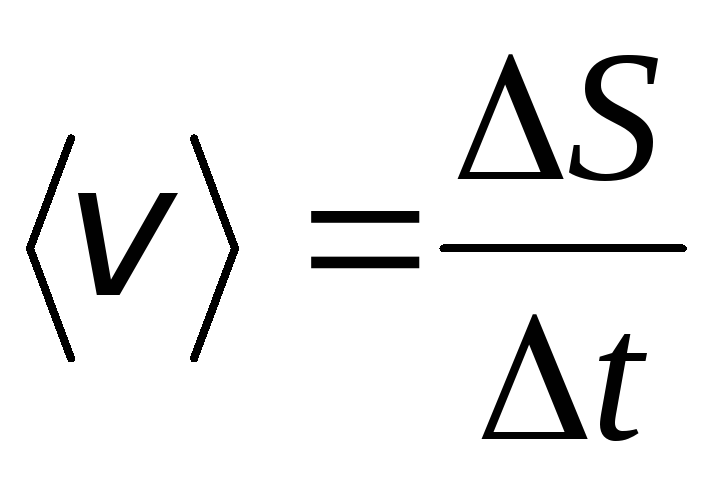 .
(1.14)
.
(1.14)
Средняя путевая скорость – величина скалярная, определяющая какое расстояние проходит точка в единицу времени по траектории.
1. Кинематика

 Введение
Введение
Физика в системе естественных наук. Общая структура и задачи дисциплины «Физика». Экспериментальная и теоретическая физика. Физические величины, их измерение и оценка погрешностей. Системы единиц физических величин. Краткая история физических идей, концепций и открытий. Физика и научно-технический прогресс.
Механическое движение. Пространство и время в механикеи ньютона. Кинематическое уравнение движения. Радиус-вектор. Траектория. Путь. Перемещение
Механическим движением называется изменение взаимного расположения тел или их частей.
Раздел физики, занимающийся изучением закономерностей механического движения и взаимодействия тел, называется механикой. При этом под механическим действием на тело понимают такое воздействие со стороны других тел, которое приводит к изменению состояния механического движения рассматриваемого тела или к его деформации, т.е. к изменению взаимного расположения его частей.
Классическая механика рассматривает движение макроскопических тел, скорости которых много меньше скорости света в вакууме с= 310 м/с. Основы классической механики были разработаны И.Ньютоном, поэтому ее обычно называют ньютоновской механикой.
Решая ту или иную конкретную задачу механики, всегда выделяют из множества тел только те, которые играют в данной задаче существенную роль. Эта совокупность тел называется механической системой.
Мы будем изучать два основных раздела классической механики: кинематику и динамику.
Кинематика описывает механическое движение тел безотносительно к причинам, вызвавшим движение. Динамика занимается исследованием влияния взаимодействия тел на их механическое движение.
В механике для описания реальных тел пользуются в зависимости от условий конкретной задачи различными упрощенными моделями: материальная точка, абсолютно твердое тело, абсолютно упругое тело, абсолютно неупругое тело и т.д. Выбор той или иной модели нужно производить так, чтобы учесть все существенные особенности поведения реального тела в данной задаче и отбросить все второстепенные, неоправданно усложняющие решение.
Материальной точкой называется тело, формой и размерами которого в данной задаче можно пренебречь.
Одно и то же тело в одних задачах можно считать материальной точкой, а в других – нельзя. Например, рассматривая движение Земли по орбите вокруг Солнца, ее можно считать материальной точкой, т.к. размеры Земли много меньше радиуса орбиты. В то же время при рассмотрении движения тел по Земле ее уже нельзя считать материальной точкой. Любое протяженное тело или систему тел, образующих механическую систему, можно представить как систему материальных точек. Для этого все тела системы разбивают на такие части, размерами каждой из которых можно пренебречь в сравнении с размерами самих тел.
Абсолютно твердым называется тело, деформацией которого можно пренебречь. При любых взаимодействиях расстояния между любыми двумя точками абсолютно твердого тела остаются неизменными.
Все тела существуют в пространстве и во времени. Любое тело имеет объем, т.е. пространственную протяженность. Пространство и время являются основными категориями движения материи. Пространство определяет порядок сосуществования отдельных объектов. Время выражает порядок смены состояний, составляющих любое движение. Оно служит мерой длительности процесса. Пространство и время служат основой конструирования теоретических моделей, интерпретирующих экспериментальные данные, и имеют решающее значение при построении физической картины мира.
В механике Ньютона существует понятие абсолютного пространства и абсолютного времени, которые не зависят друг от друга и от существующих в них материальных объектов и протекающих процессов. Длина масштабов и времени считаются абсолютными. Любой масштаб (расстояние) считается одинаковым во всех системах отсчета, т.е. не зависит от движения. То же касается и времени.
Положение тела в пространстве определяется только относительно каких-либо других тел. Для однозначного определения положения исследуемого тела в произвольный момент времени необходимо выбрать систему отсчета.
А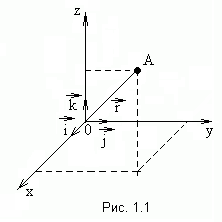 бсолютно
твердое тело и жестко связанную с ним
систему координат, снабженную часами,
используемую для определения положения
материальной точки в пространстве в
любой момент времени, называют системой
отсчета.
бсолютно
твердое тело и жестко связанную с ним
систему координат, снабженную часами,
используемую для определения положения
материальной точки в пространстве в
любой момент времени, называют системой
отсчета.
При этом под часами подразумевается любое устройство, измеряющее промежутки времени между событиями. Начало отсчета времени выбирается произвольно. Абсолютно твердое тело, с которым связывают систему координат, называют телом отсчета.
В
качестве системы координат в классической
механике наиболее часто используется
прямоугольная декартова система
координат, имеющая ортонормированный
базис, заданный ортами 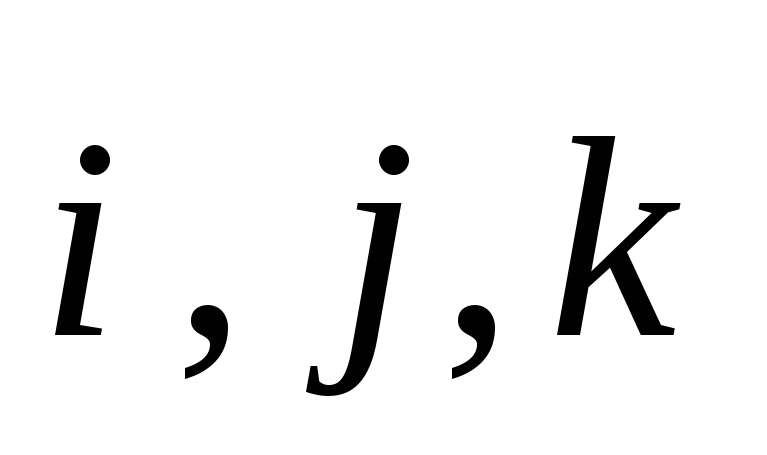 (рис.1.1). Положение точкиA относительно
этой системы координат задают
радиус-вектором
(рис.1.1). Положение точкиA относительно
этой системы координат задают
радиус-вектором 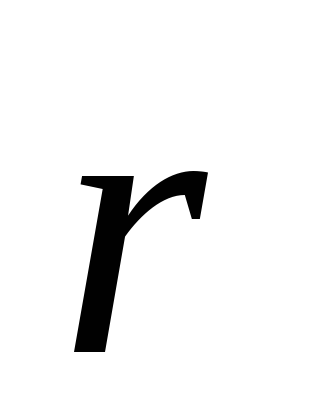 (это вектор, проведенный из начала
координат в данную точку),
(это вектор, проведенный из начала
координат в данную точку),
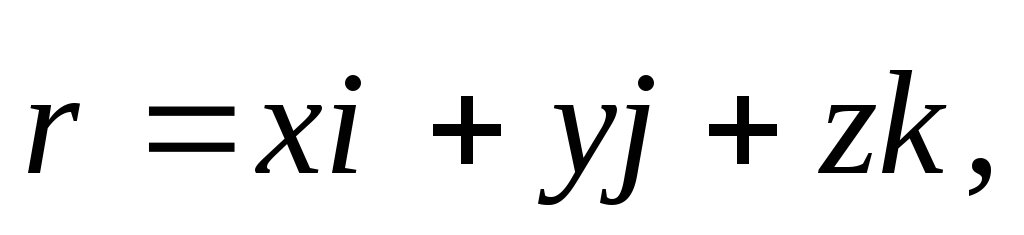 (1.1)
(1.1)
либо тремя координатами x, y, z.
При
движении точки A ее координаты и радиус-вектор изменяются
с течением времени, поэтому для задания
закона движения этой точки необходимо
указать три непрерывные и однозначные
функции времени 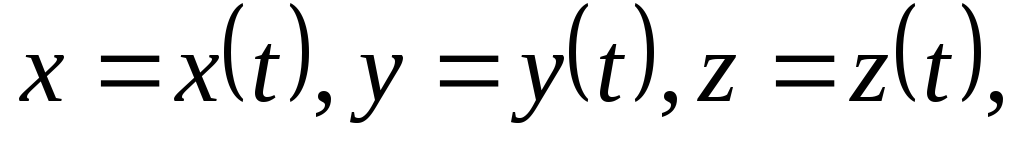
либо векторную функцию
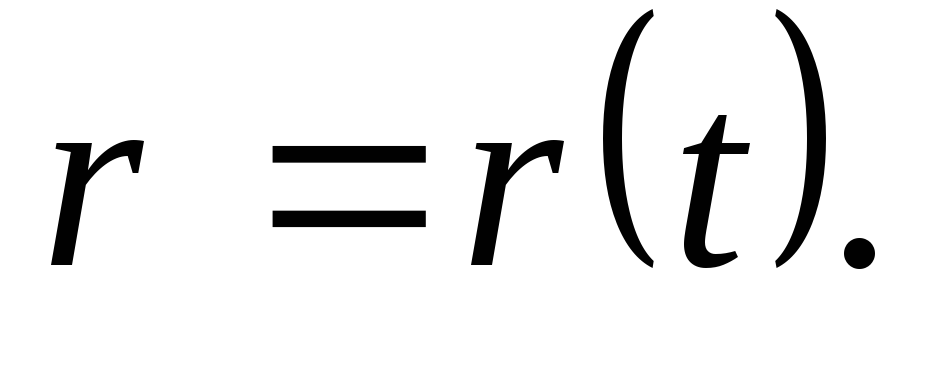 (1.2)
(1.2)
 Выражения вида
(1.2) называются кинематическими уравнениями
движения.
Выражения вида
(1.2) называются кинематическими уравнениями
движения.
Траекторией называется линия, которую описывает в пространстве движущаяся точка. В зависимости от формы траектории различают прямолинейное и криволинейное движение. Движение называют плоским, если все точки траектории лежат в одной плоскости. В этом случае уравнение траектории удобно задавать в виде y= y(x).
Механическое движение тела относительно: его характер, а, следовательно, и форма траектории, зависят от выбора системы отсчета. Например, тело, свободно падающее с полки в вагоне равномерно движущегося поезда, в системе отсчета, связанной с вагоном, движется вертикально вниз, а в системе отсчета, связанной с Землей, совершает плоское движение по параболе.
 Длиной
пути, пройденного точкой за некоторый
промежуток времени, называется сумма
длин всех участков траектории, пройденных
за этот промежуток. Длина пути
Длиной
пути, пройденного точкой за некоторый
промежуток времени, называется сумма
длин всех участков траектории, пройденных
за этот промежуток. Длина пути  –
это скалярная неотрицательная величина.
–
это скалярная неотрицательная величина.
Пусть
в момент времени 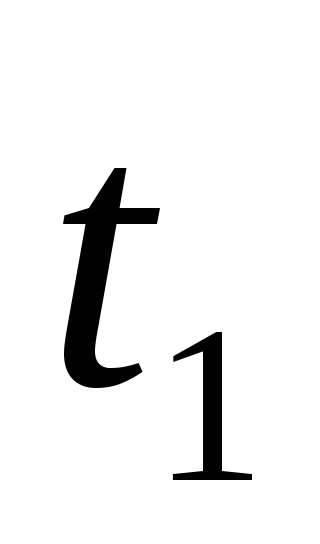 положение точки характеризовалось
радиус-вектором
положение точки характеризовалось
радиус-вектором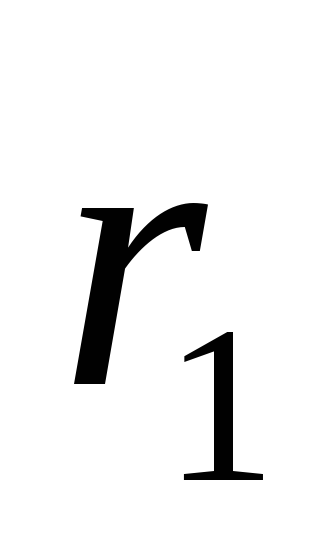 ,
а в момент времени
,
а в момент времени радиус-вектором
радиус-вектором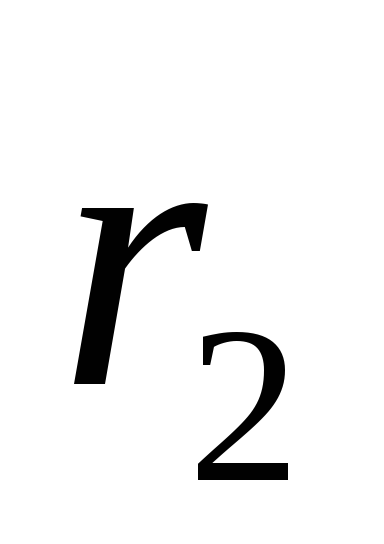 (рис.1.2). Перемещением точки за промежуток
времени
(рис.1.2). Перемещением точки за промежуток
времени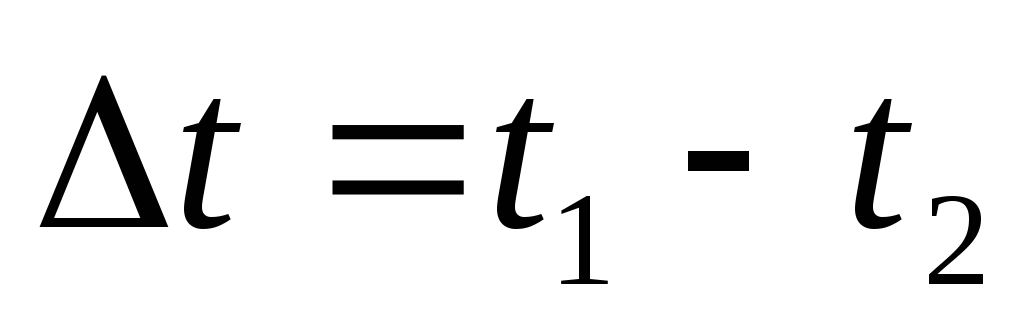 называется вектор
называется вектор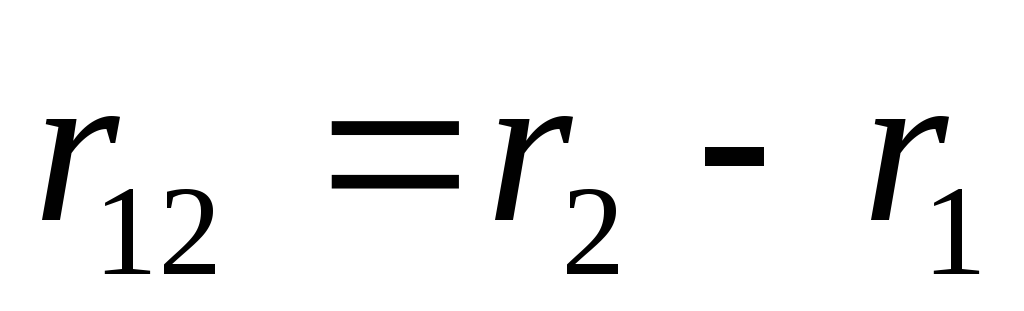 , проведенный из начального положения
точки ( в момент времени
, проведенный из начального положения
точки ( в момент времени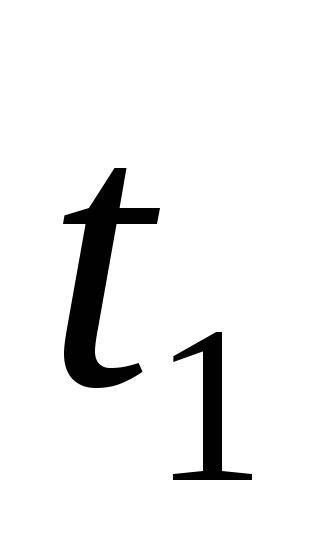 )
в ее конечное положение ( в момент времени
)
в ее конечное положение ( в момент времени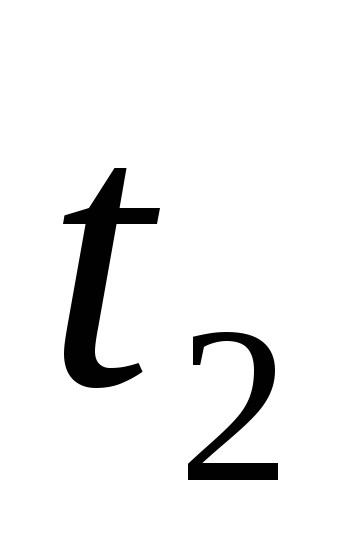 ).
).
Если
точка совершает последовательно два
перемещения  и
и ,
то результирующее перемещение равно
векторной сумме (рис.1.3):
,
то результирующее перемещение равно
векторной сумме (рис.1.3):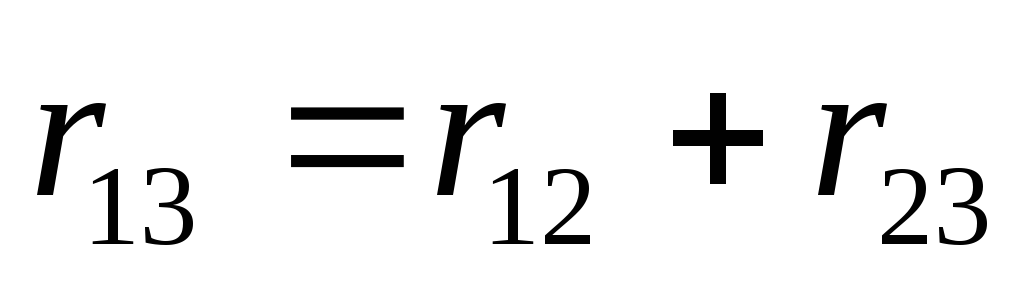 .
.
1.2. ОСНОВНЫЕ КИНЕМАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ КРИВОЛИНЕЙНОГО ДВИЖЕНИЯ: СКОРОСТЬ И УСКОРЕНИЕ. ФИЗИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ И ИНТЕГРАЛА. ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ ДВИЖЕНИЯ. РОЛЬ НАЧАЛЬНЫХ УСЛОВИЙ. СИСТЕМЫ КООРДИНАТ И ИХ ПРЕОБРАЗОВАНИЯ. НОРМАЛЬНОЕ И ТАНГЕНЦИАЛЬНОЕ УСКОРЕНИЕ
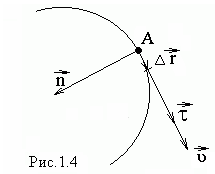 В
физике под скоростью понимают векторную
величину, характеризующую быстроту
перемещения материальной точки по
траектории и направление движения в
каждый момент времени. Разобьем траекторию
на бесконечно малые участки длины
В
физике под скоростью понимают векторную
величину, характеризующую быстроту
перемещения материальной точки по
траектории и направление движения в
каждый момент времени. Разобьем траекторию
на бесконечно малые участки длины  (рис.1.4), каждому из этих участков
сопоставим бесконечно малое перемещение
(рис.1.4), каждому из этих участков
сопоставим бесконечно малое перемещение .
Разделив это перемещение на соответствующий
промежуток времени
.
Разделив это перемещение на соответствующий
промежуток времени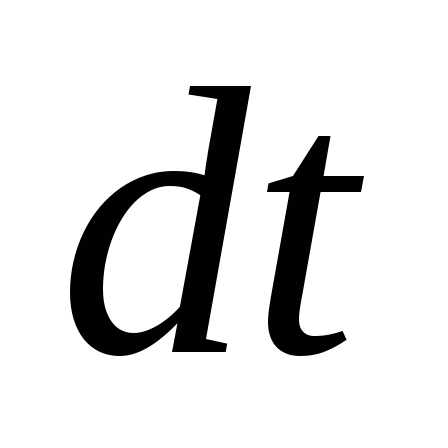 ,
получим мгновенную скорость в данной
точке траектории:
,
получим мгновенную скорость в данной
точке траектории:
 .
(1.3)
.
(1.3)
Таким
образом, скорость есть первая производная
радиус-вектора точки по времени.
Перемещение 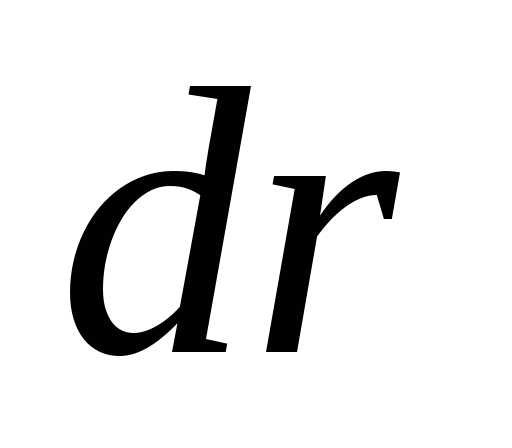 совпадает с бесконечно малым элементом
траектории, следовательно вектор
совпадает с бесконечно малым элементом
траектории, следовательно вектор направлен
по касательной к траектории (рис.1.4).
направлен
по касательной к траектории (рис.1.4).
Разложив вектор скорости по базису системы координат, получаем:
 ,
где
,
где 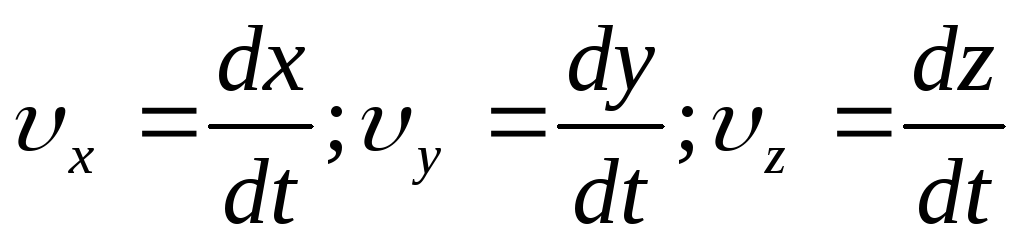 — проекции вектора
— проекции вектора на координатные оси. Модуль вектора
скорости равен
на координатные оси. Модуль вектора
скорости равен .
.
Можно показать, что модуль скорости равен производной пути по времени:
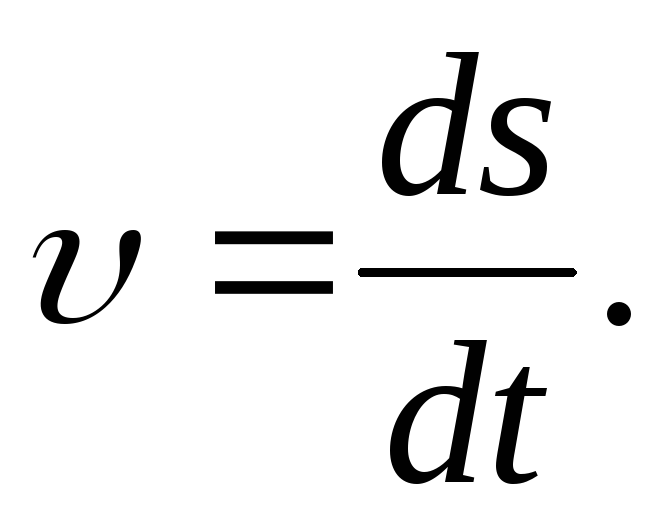
Движение называется равномерным, если вектор скорости остается постоянным по величине и направлению. В противном случае говорят о переменном движении.
В
соответствии с формулой (1.3), элементарное
перемещение материальной точки 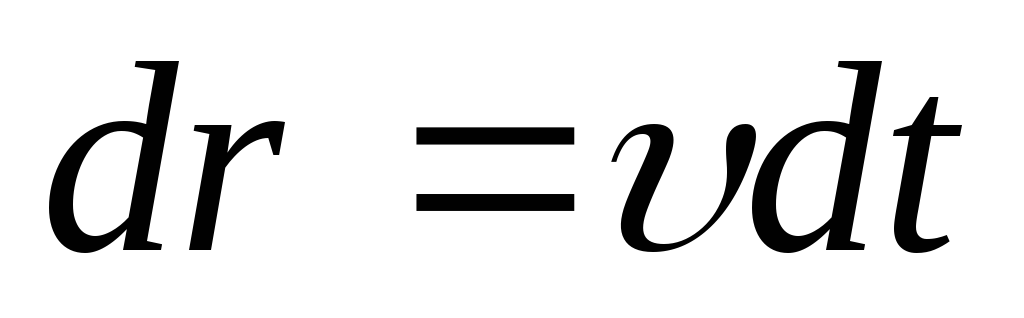 .
Тогда перемещение из положения 1 в
положение 2 (рис.1.2) равно интегралу
.
Тогда перемещение из положения 1 в
положение 2 (рис.1.2) равно интегралу
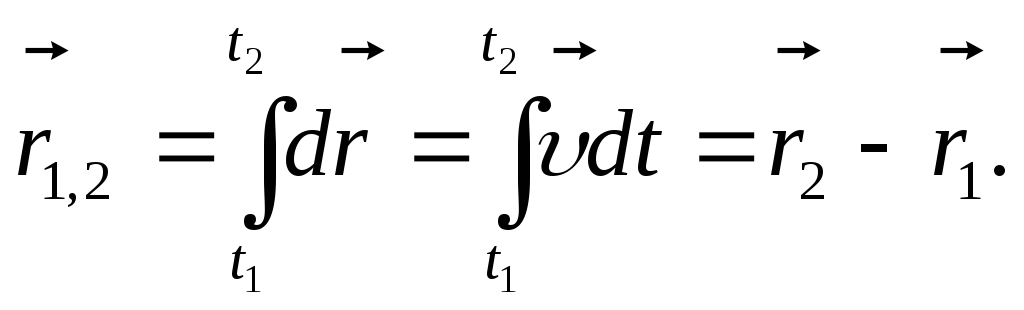
Пройденный
путь определяется выражением 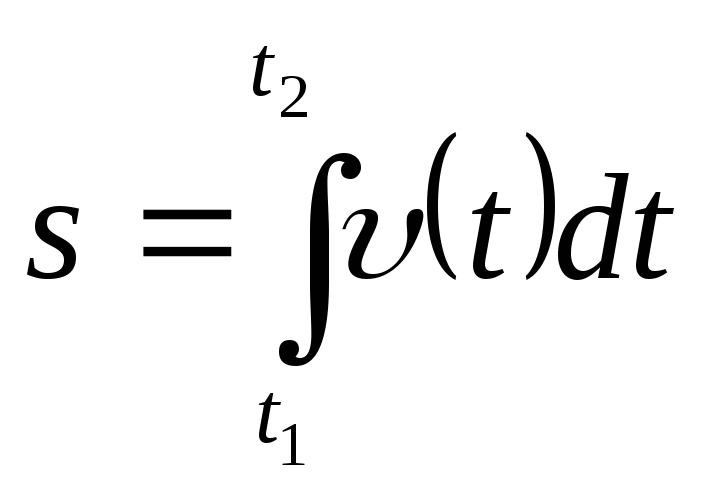 .
.
Среднее
значение модуля скорости за промежуток
времени от  до
до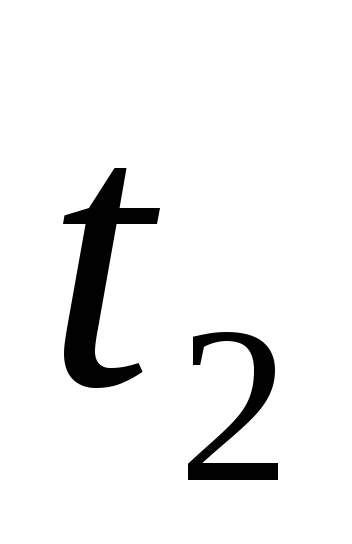 равно
равно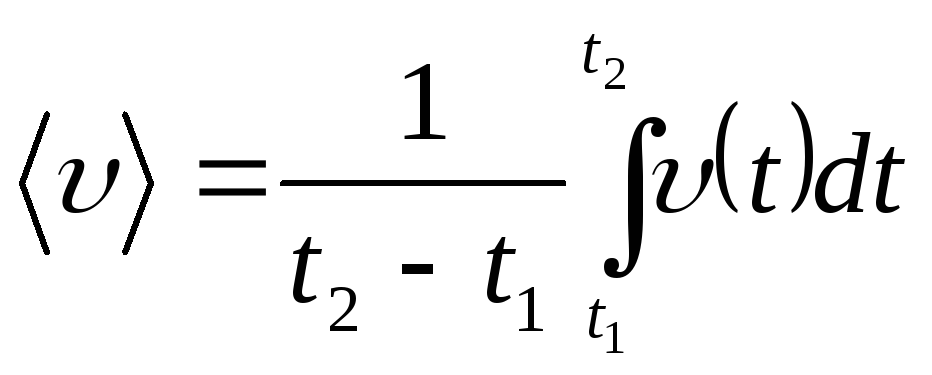 .
Средний вектор скорости:
.
Средний вектор скорости: .
.
Вектор скорости можно представить в виде
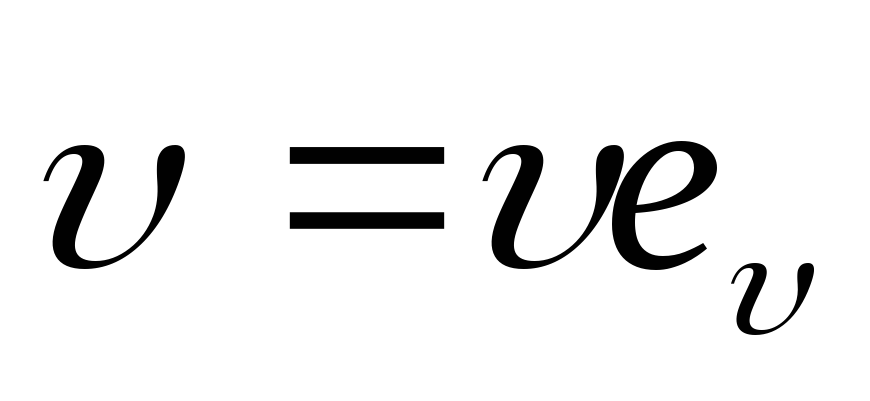 ,
(1.4)
,
(1.4)
где  – модуль скорости,
– модуль скорости, –
орт вектора
–
орт вектора .
Введем орт касательной к траектории
.
Введем орт касательной к траектории ,
условившись направлять его в ту же
сторону, что и
,
условившись направлять его в ту же
сторону, что и .
Тогда, очевидно, орты
.
Тогда, очевидно, орты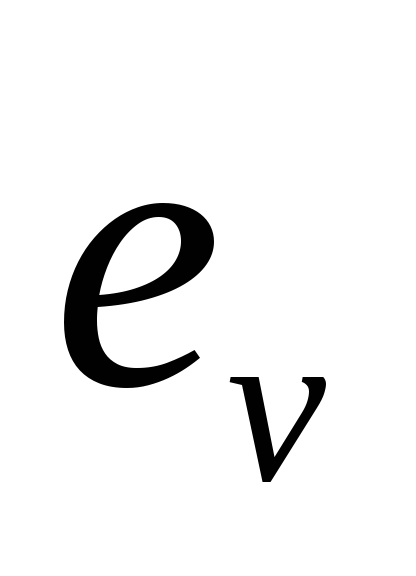 и
и совпадут, и можно записать
совпадут, и можно записать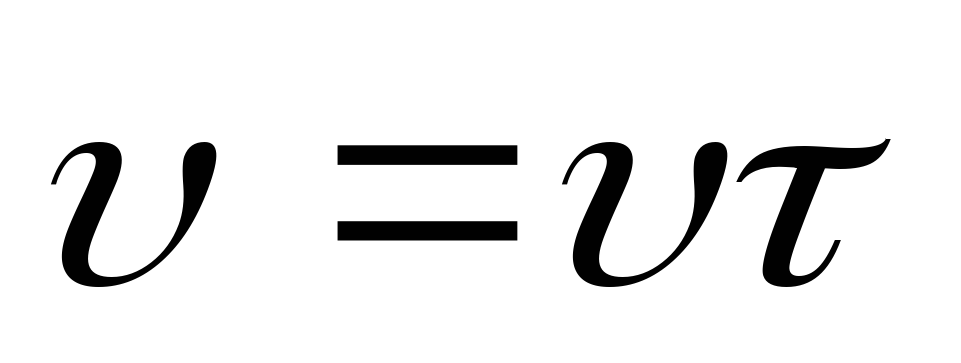
 Подставив
в выражение (1.3) радиус-вектор в виде
Подставив
в выражение (1.3) радиус-вектор в виде 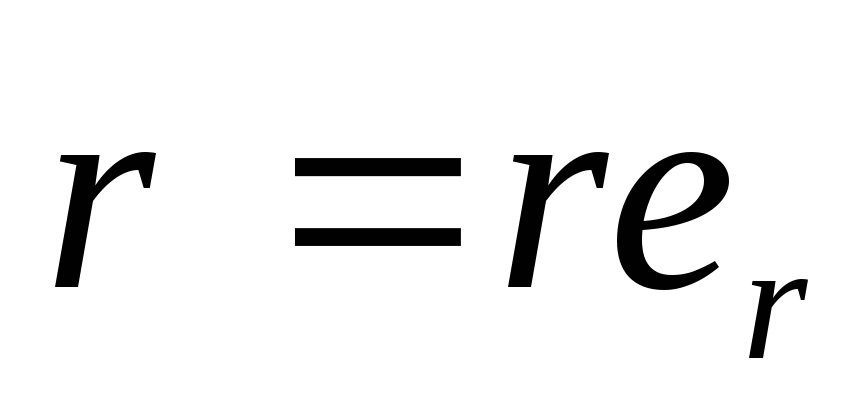 ,
получаем
,
получаем
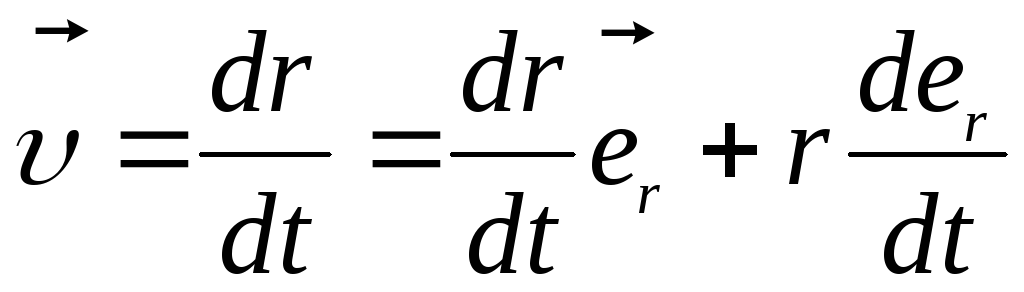 .
.
Для
простоты рассуждений будем считать
траекторию плоской кривой, лежащей в
плоскости 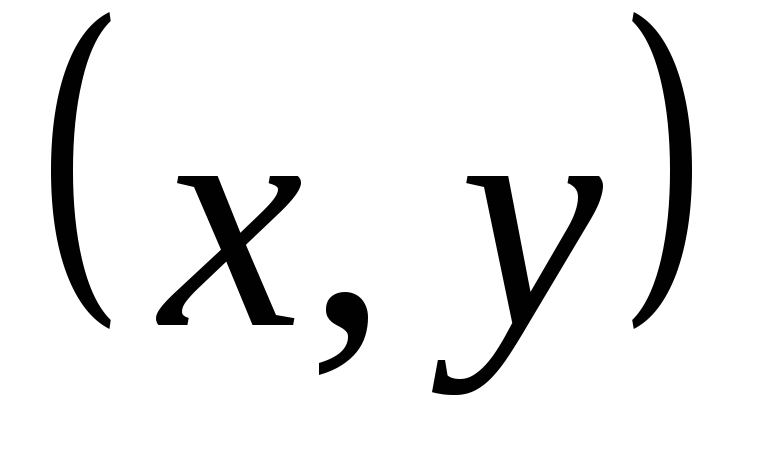 (рис.1.5). В записанной формуле первая
составляющая вектора скорости
(рис.1.5). В записанной формуле первая
составляющая вектора скорости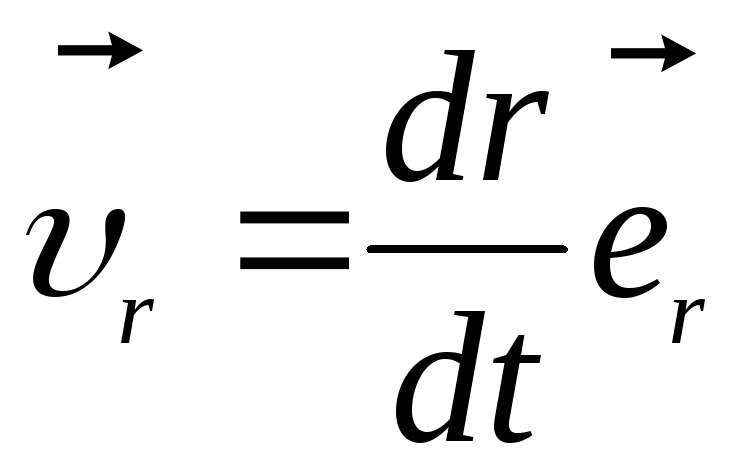 направлена вдоль радиус-вектора
направлена вдоль радиус-вектора и характеризует быстроту изменения
модуля
и характеризует быстроту изменения
модуля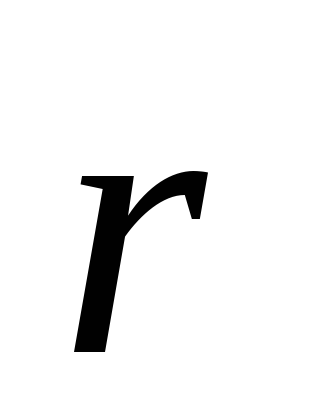 .
Вторая составляющая равна
.
Вторая составляющая равна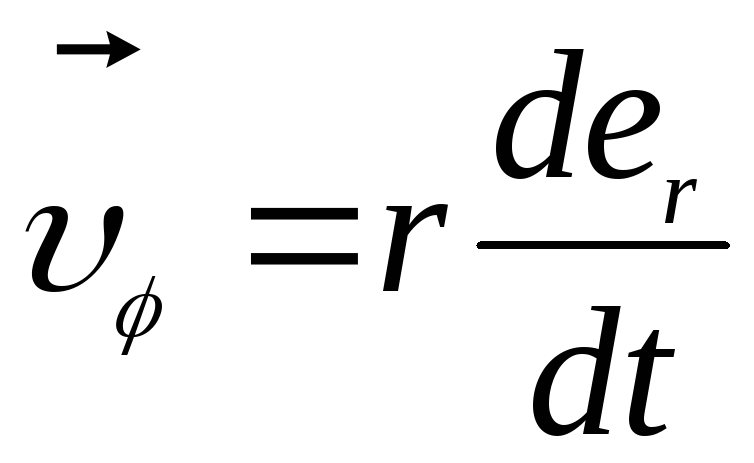 и характеризует быстроту изменения
радиус-вектора по направлению.
и характеризует быстроту изменения
радиус-вектора по направлению.
Из
математики известно: 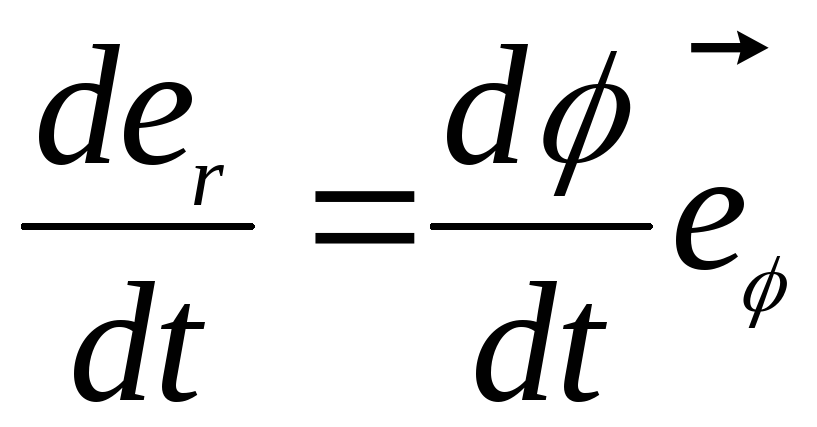 ,
где
,
где – угол между радиус-вектором и осью
– угол между радиус-вектором и осью ,
,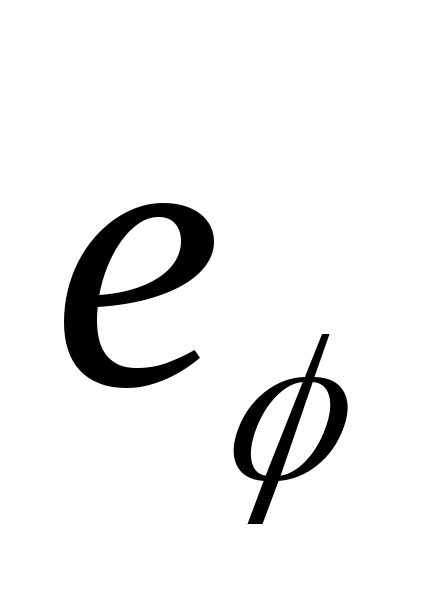 – перпендикулярный к радиус-вектору
орт, направленный в сторону возрастания
угла
– перпендикулярный к радиус-вектору
орт, направленный в сторону возрастания
угла .
Подставив
.
Подставив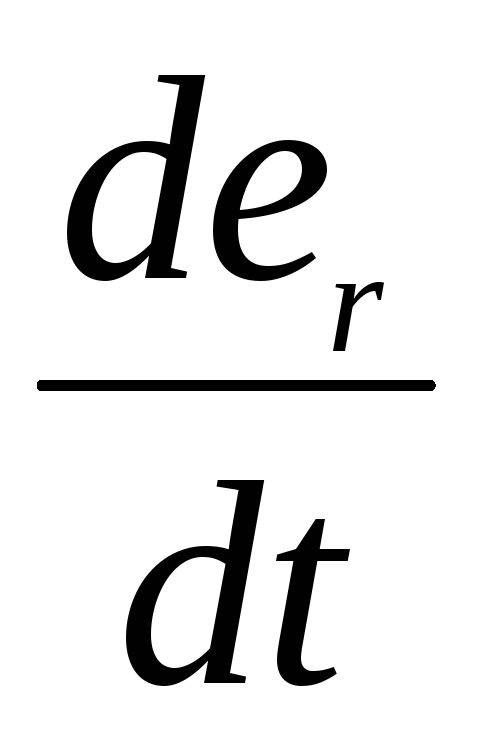 в формулу для
в формулу для ,
получаем
,
получаем
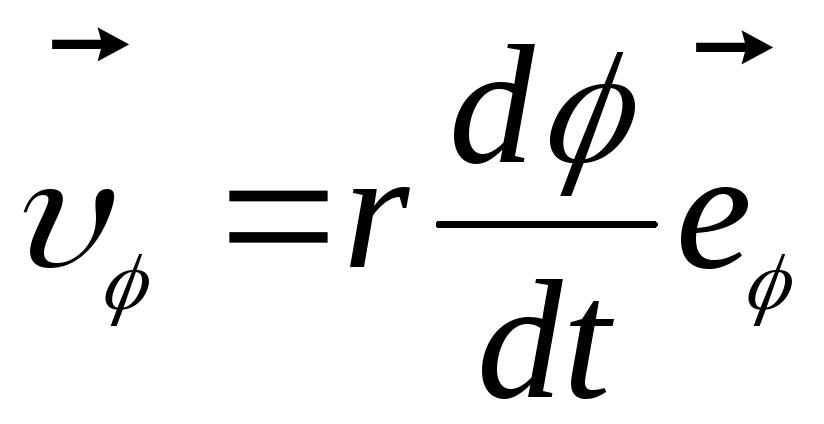 .
.
Таким
образом, составляющая 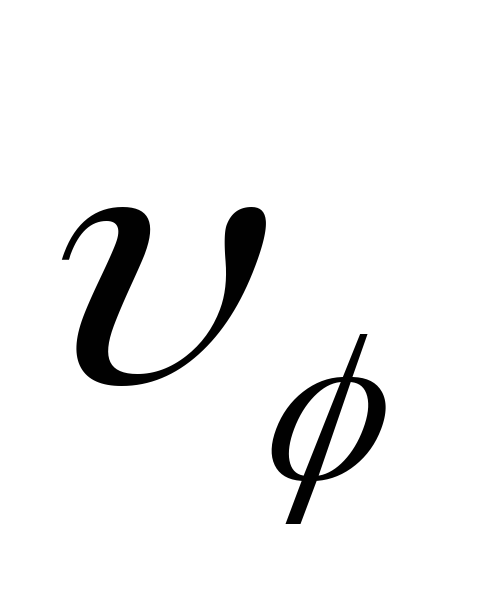 и
соответствующий орт
и
соответствующий орт связаны с изменением угла
связаны с изменением угла .
.
 Очевидно,
что векторы
Очевидно,
что векторы  и
и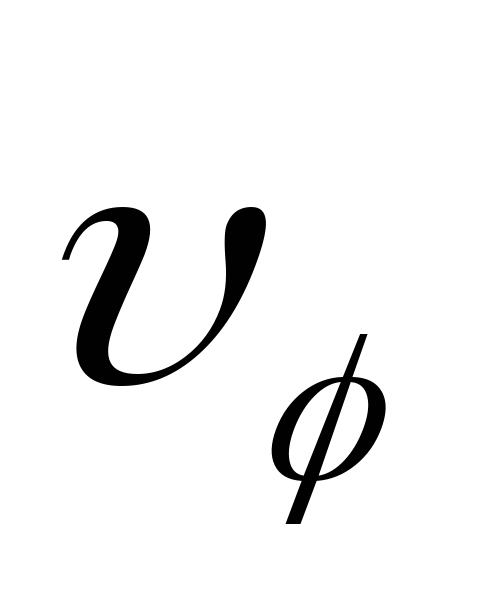 взаимно перпендикулярны, следовательно
взаимно перпендикулярны, следовательно

Быстрота
изменения вектора скорости  называется ускорением материальной
точки и определяется производной вектора
называется ускорением материальной
точки и определяется производной вектора по времени:
по времени:
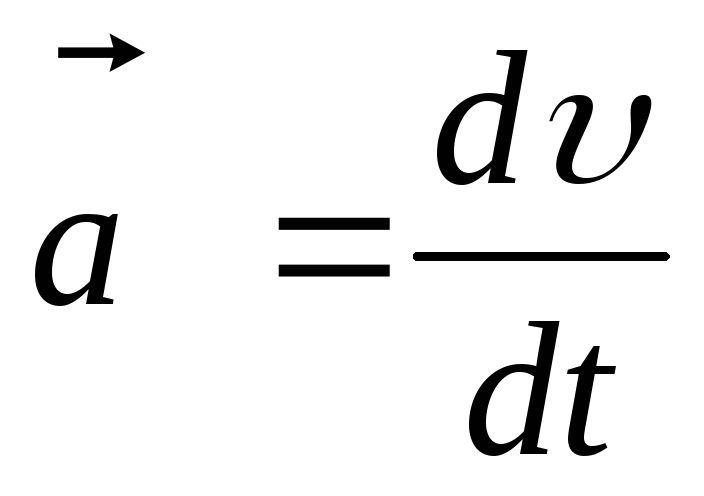 .
(1.5)
.
(1.5)
Cпроектируем
это выражение на координатные оси: 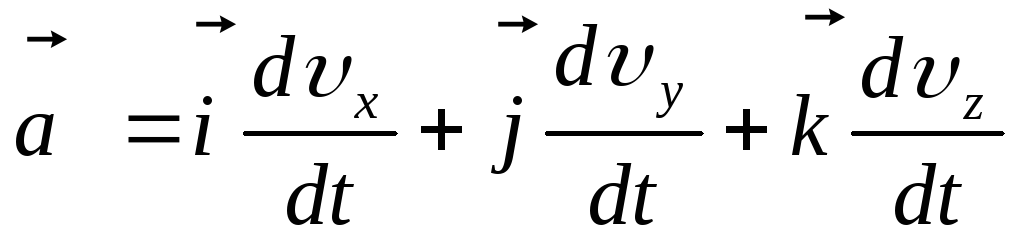 .
.
Обратная
задача кинематики состоит в том, чтобы,
зная зависимость от времени ускорения 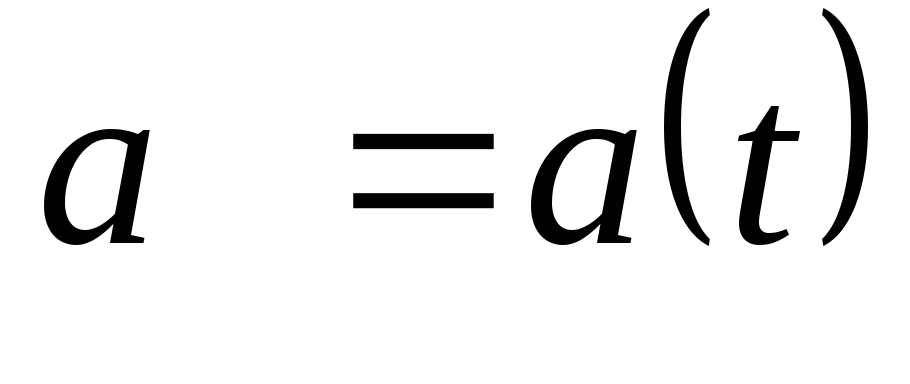 материальной точки, найти зависимость
скорости
материальной точки, найти зависимость
скорости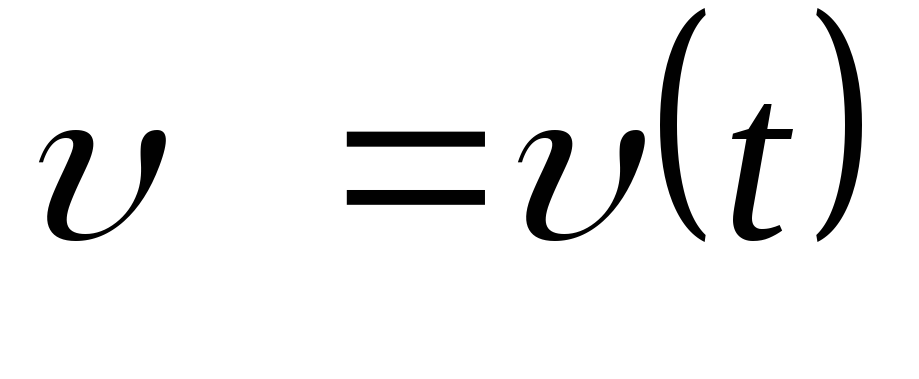 и
радиус-вектора от времени
и
радиус-вектора от времени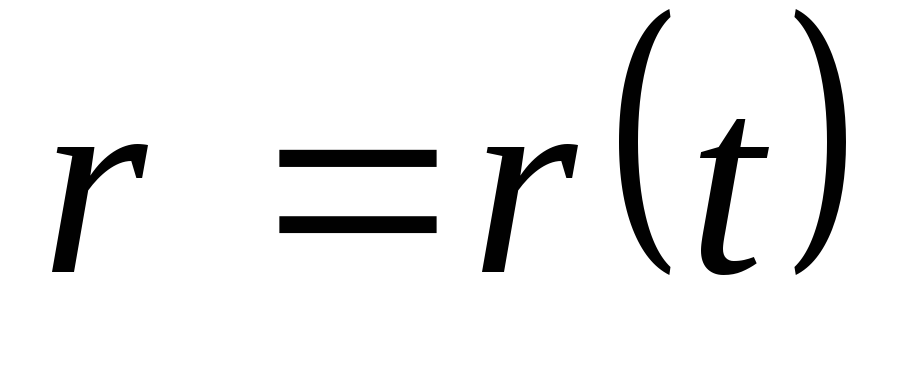 .
Для получения однозначного решения
этой задачи одной зависимости
.
Для получения однозначного решения
этой задачи одной зависимости оказывается недостаточно. Необходимо
знать еще начальные условия, т.е. скорость
оказывается недостаточно. Необходимо
знать еще начальные условия, т.е. скорость и
радиус-вектор
и
радиус-вектор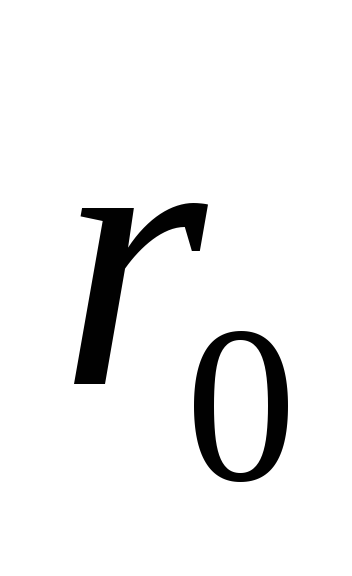 точки
в момент времени, принятый за начальный.
точки
в момент времени, принятый за начальный.
Рассмотрим
равноускоренное движение,  .
Изменение скорости точки за времяt,
очевидно, равно интегралу
.
Изменение скорости точки за времяt,
очевидно, равно интегралу 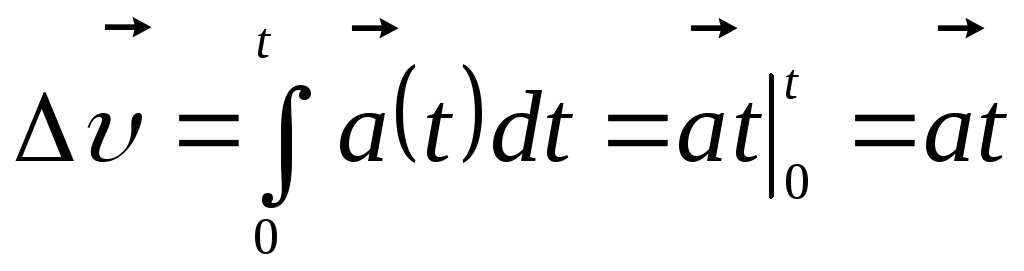 .
Чтобы найти
.
Чтобы найти ,
надо знать скорость
,
надо знать скорость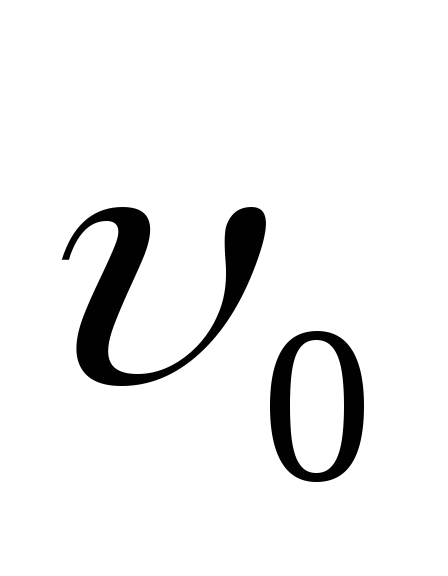 в
начальный момент времени. Тогда
в
начальный момент времени. Тогда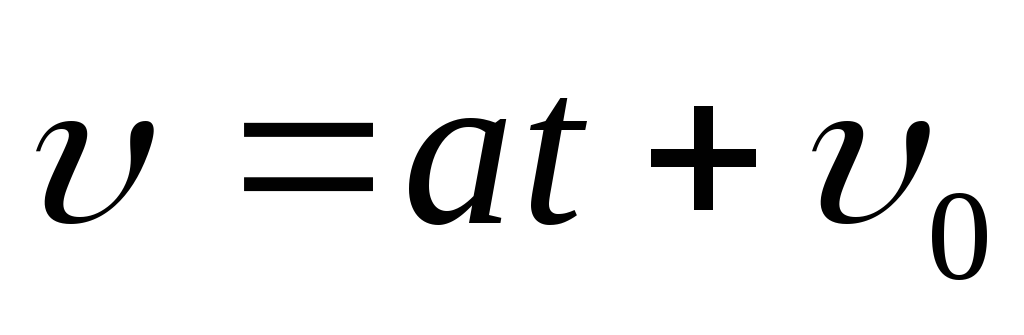 .
.
Изменение
радиус-вектора точки за время t равно
интегралу 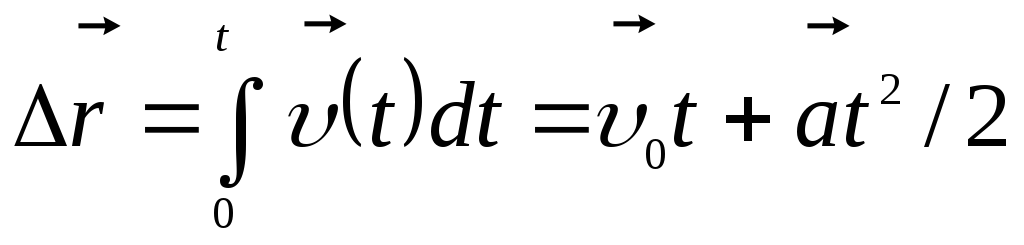 .
Чтобы найти
.
Чтобы найти ,
надо знать радиус-вектор в начальный
момент времени
,
надо знать радиус-вектор в начальный
момент времени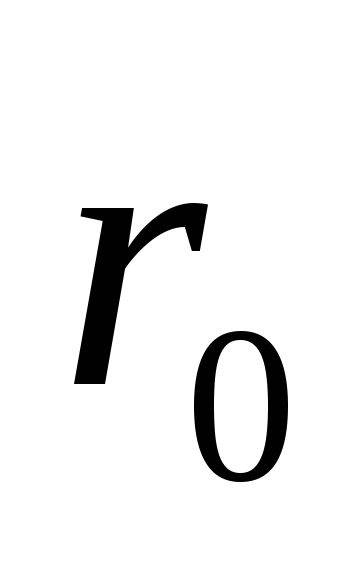 .
Тогда
.
Тогда .
.
Р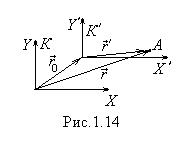 ассмотрим
две произвольные системы отсчетаК и К’,
движущиеся определенным образом друг
относительно друга. В К-системе
материальная точка А имеет скорость
ассмотрим
две произвольные системы отсчетаК и К’,
движущиеся определенным образом друг
относительно друга. В К-системе
материальная точка А имеет скорость  и ускорение
и ускорение .
Положение материальной точки в этой
системе отсчета задано радиус-вектором
.
Положение материальной точки в этой
системе отсчета задано радиус-вектором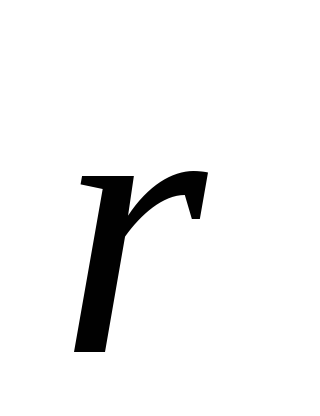 .
ВК’-системе
скорость точки
.
ВК’-системе
скорость точки 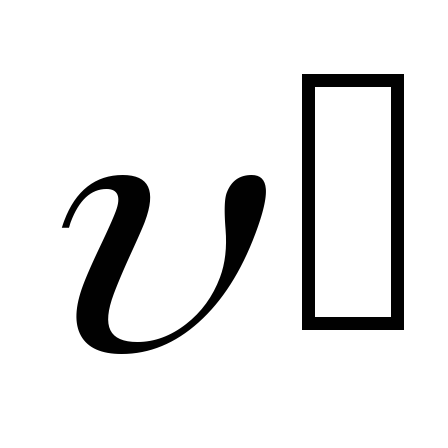 ,
ускорение
,
ускорение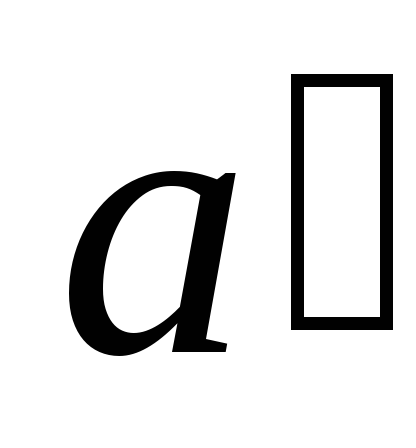 ,
радиус-вектор
,
радиус-вектор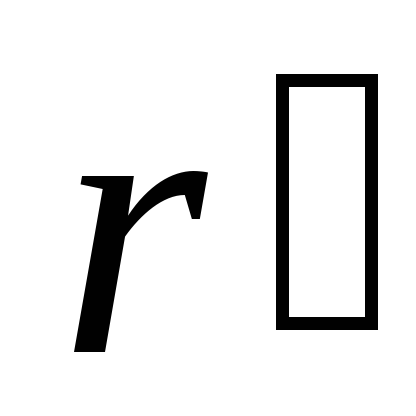 .К’-система
движется относительно К—
системы со скоростью
.К’-система
движется относительно К—
системы со скоростью 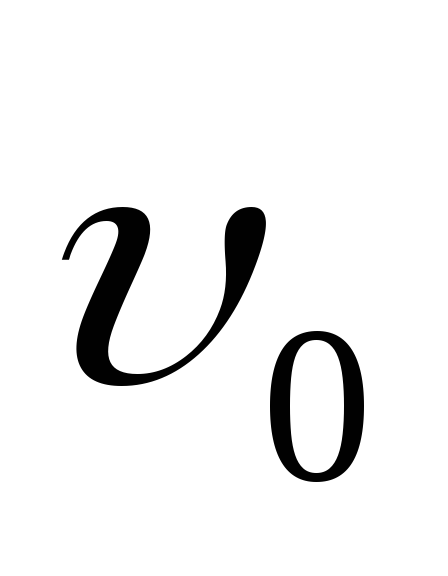 и ускорением
и ускорением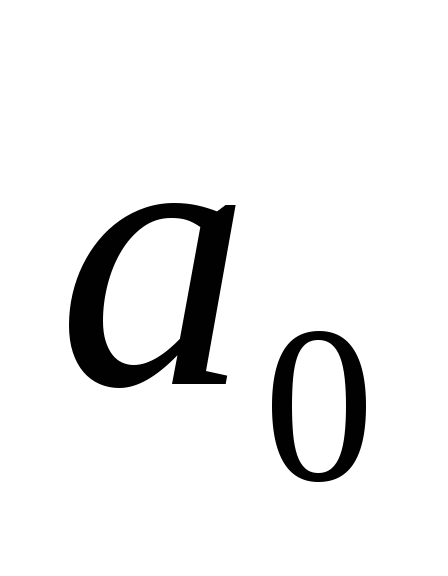 ,
в начальный момент времени начало
отсчетаК’-системы
в К-системе
задано радиус-вектором
,
в начальный момент времени начало
отсчетаК’-системы
в К-системе
задано радиус-вектором  (рис.1.14). Тогда, как следует из рис.1.14,
(рис.1.14). Тогда, как следует из рис.1.14, .
За промежуток времениdt точка А совершит в К –системе перемещение
.
За промежуток времениdt точка А совершит в К –системе перемещение  . Это перемещение складывается из
перемещения
. Это перемещение складывается из
перемещения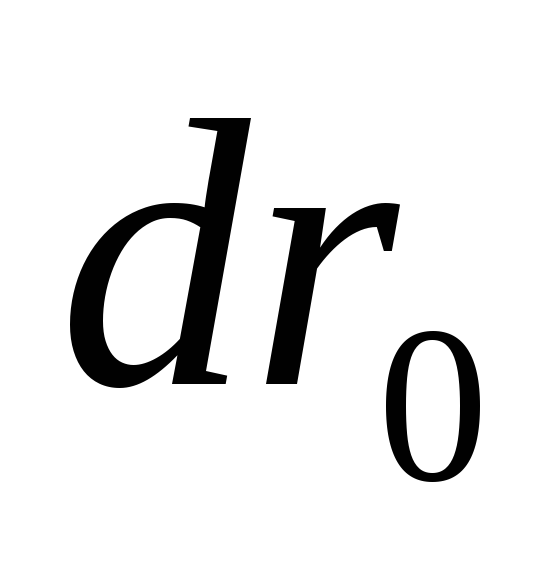 вместе сК’-системой
и перемещения
вместе сК’-системой
и перемещения 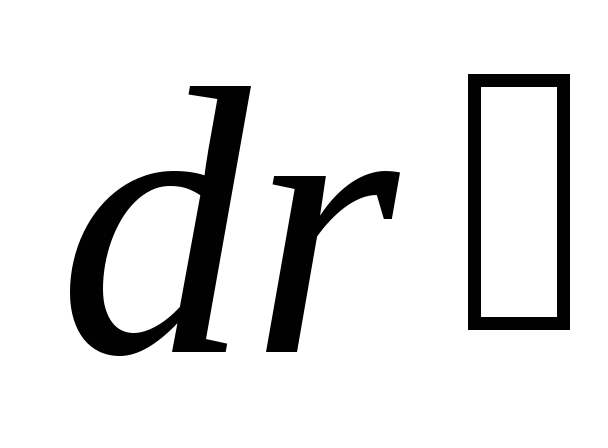 относительноК’-системы,
относительноК’-системы, 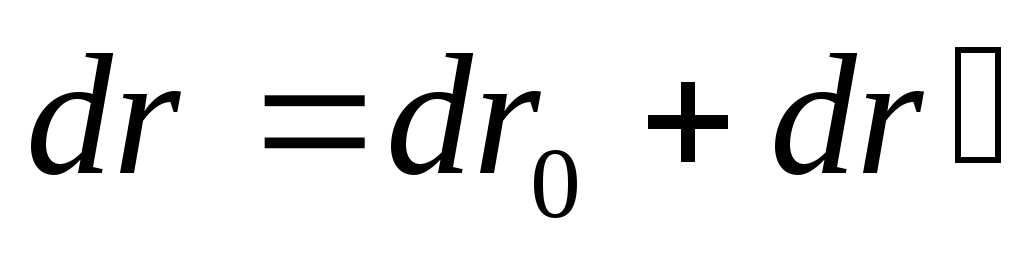 .
Разделив это выражение наdt,
получим формулу преобразования скорости:
.
Разделив это выражение наdt,
получим формулу преобразования скорости:
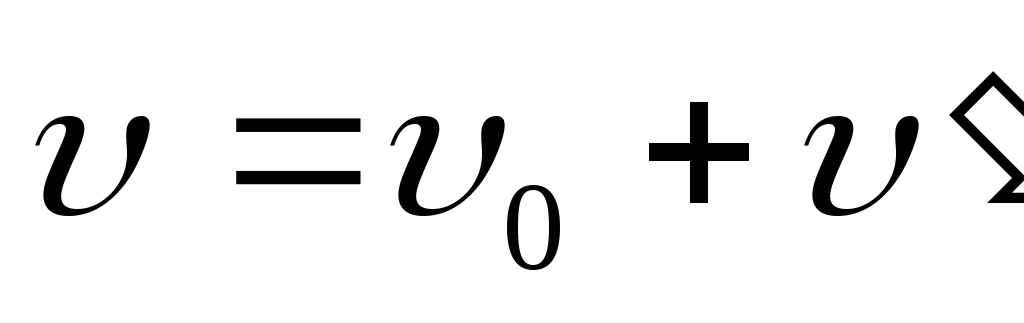 .
.
Продифференцировав
по времени, находим формулу преобразования
ускорения: 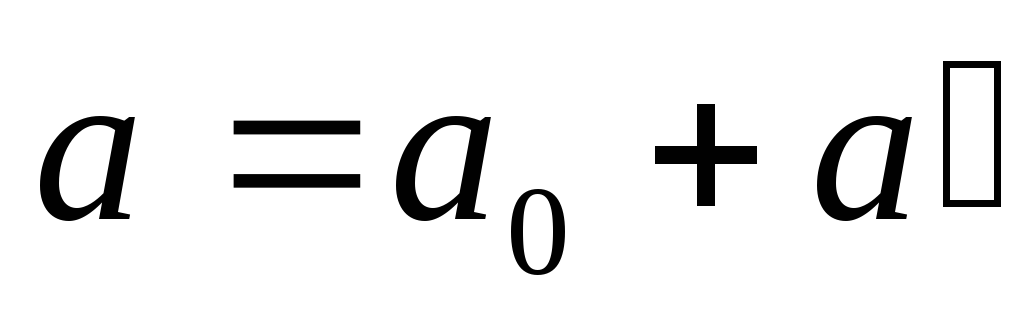 .
ЕслиК’-система
движется относительно К-системы
без ускорения,
.
ЕслиК’-система
движется относительно К-системы
без ускорения,  =0,
тогда
=0,
тогда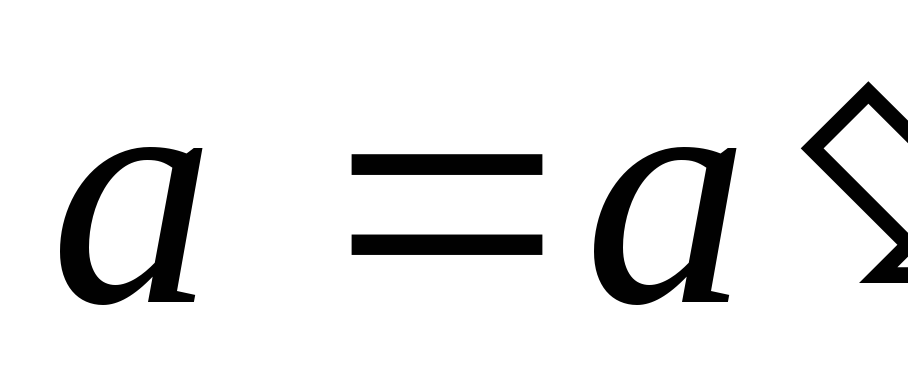 .
Этот факт будет прокомментирован позднее
(см.раздел Динамика).
.
Этот факт будет прокомментирован позднее
(см.раздел Динамика).
Подставив
в формулу (1.5) выражение (1.4), получаем: 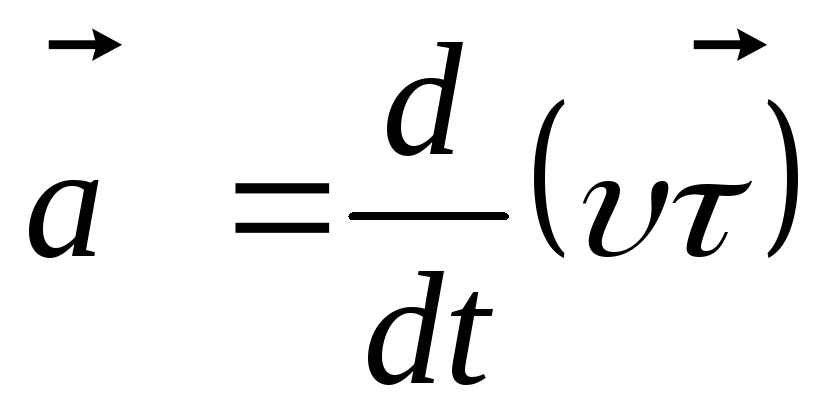 .
Продифференцировав, имеем:
.
Продифференцировав, имеем: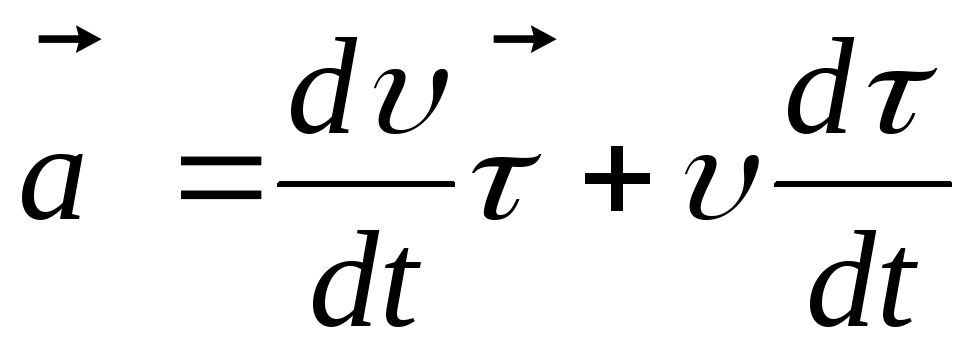 .
.
Следовательно, вектор  можно представить в виде суммы двух
взаимно перпендикулярных составляющих
(рис.1.6). Первая направлена по касательной
к траектории и называется тангенциальным
или касательным ускорением
можно представить в виде суммы двух
взаимно перпендикулярных составляющих
(рис.1.6). Первая направлена по касательной
к траектории и называется тангенциальным
или касательным ускорением
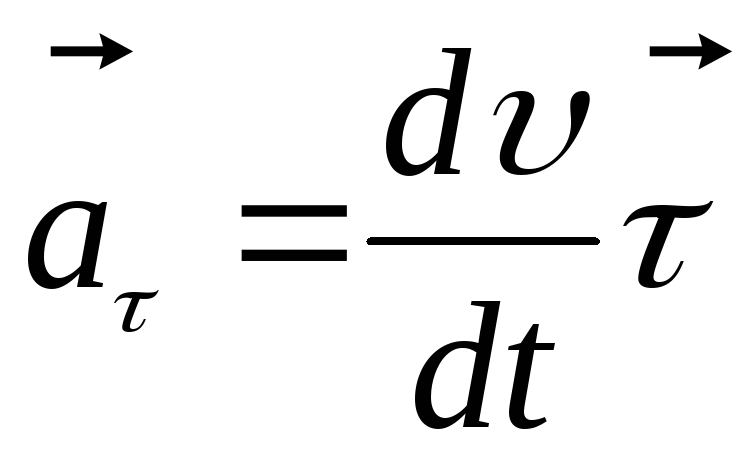 .
(1.6)
.
(1.6)
Вторая
составляющая направлена по 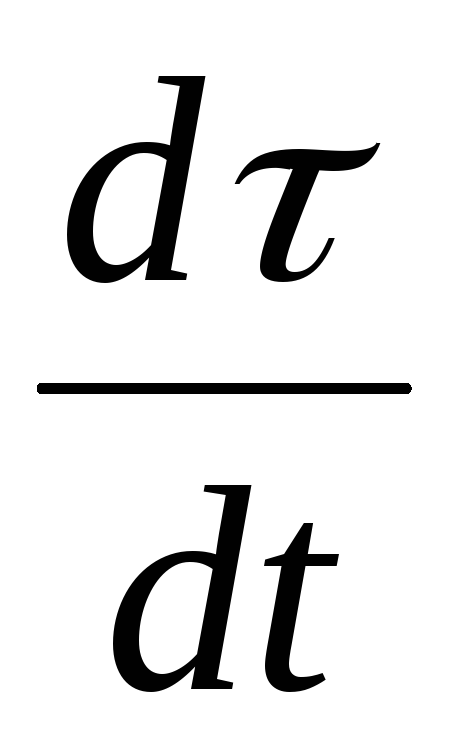 ,
т.е. перпендикулярно касательной, по
нормали к траектории, и называется
нормальным ускорением
,
т.е. перпендикулярно касательной, по
нормали к траектории, и называется
нормальным ускорением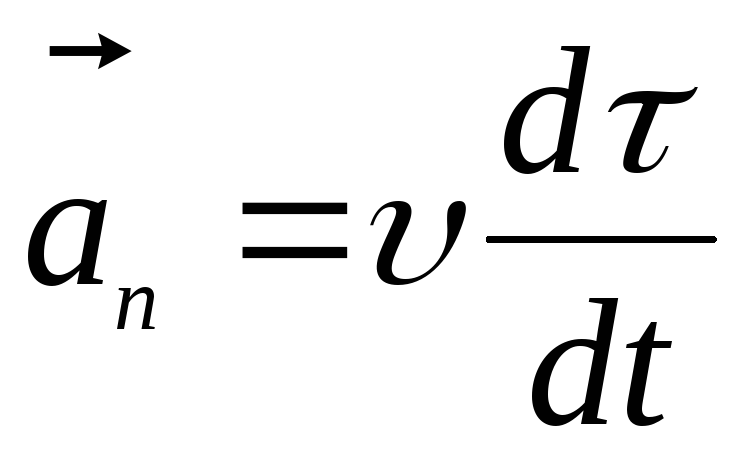 .
.
Исследуем
свойства обеих составляющих, ограничившись
случаем плоского движения. Модуль
тангенциального ускорения, как следует
из (1.6), равен 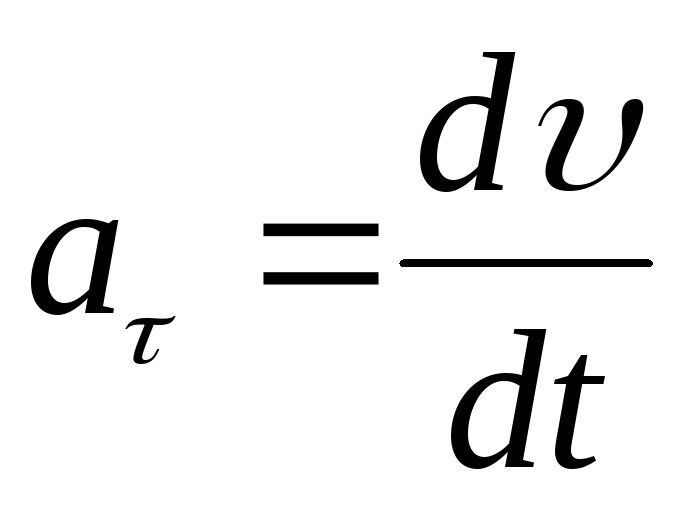 .
Если
.
Если (скорость растет по величине), вектор
(скорость растет по величине), вектор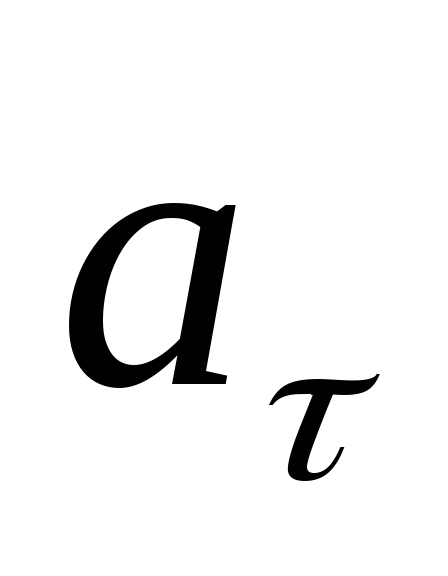 направлен в ту же сторону, что и
направлен в ту же сторону, что и (т.е. в ту же сторону, что и
(т.е. в ту же сторону, что и ).
Если
).
Если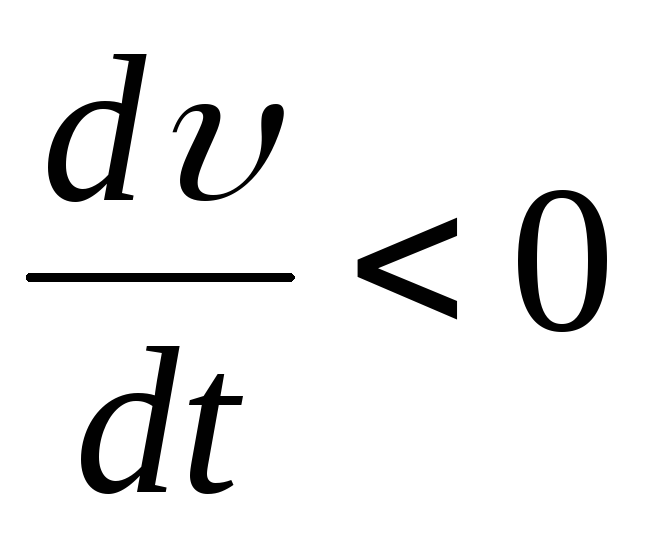 (скорость со временем уменьшается),
векторы
(скорость со временем уменьшается),
векторы и
и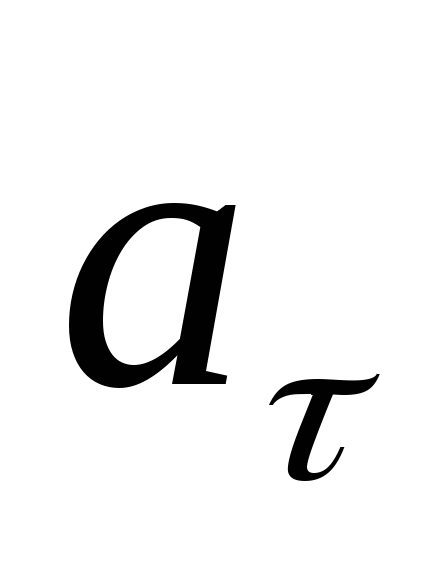 направлены противоположно. При равномерном
движении
направлены противоположно. При равномерном
движении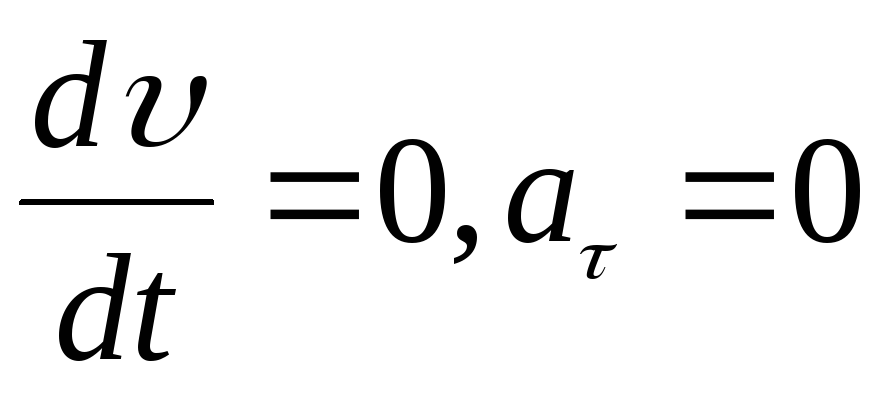 .
.
 Нормальное
ускорение определяется величиной
Нормальное
ускорение определяется величиной  ,
т.е. быстротой изменения во времени
направления касательной к траектории.
Эта быстрота будет тем больше, чем
сильнее искривлена траектория и чем
быстрее перемещается частица по
траектории.
,
т.е. быстротой изменения во времени
направления касательной к траектории.
Эта быстрота будет тем больше, чем
сильнее искривлена траектория и чем
быстрее перемещается частица по
траектории.
Степень искривления плоской кривой характеризуется кривизной С, которая определяется выражением
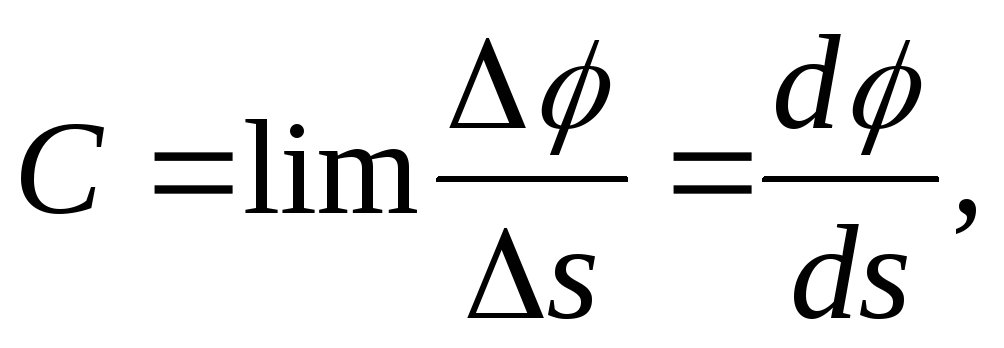
где 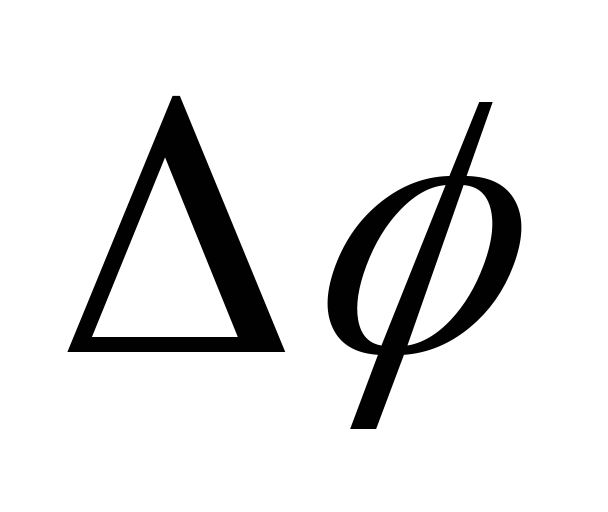 – угол между касательными к кривой в
точках, отстоящих друг от друга на
расстояние
– угол между касательными к кривой в
точках, отстоящих друг от друга на
расстояние (рис.1.7). Таким образом, кривизна определяет
скорость поворота касательной при
перемещении вдоль кривой. Величина,
обратная кривизнеС, называется радиусом кривизны
(рис.1.7). Таким образом, кривизна определяет
скорость поворота касательной при
перемещении вдоль кривой. Величина,
обратная кривизнеС, называется радиусом кривизны 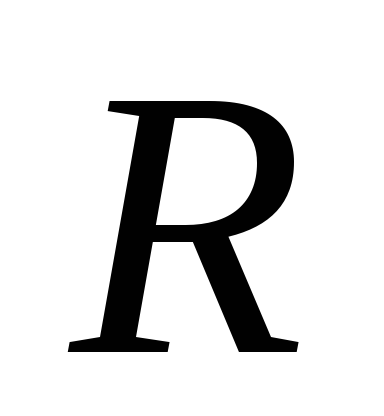 в
данной точке:
в
данной точке: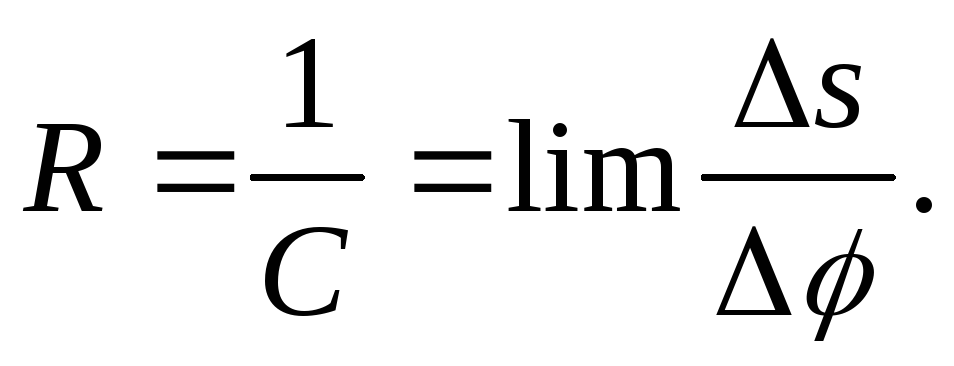
Радиус кривизны представляет собой радиус окружности, которая сливается в данном месте с кривой на бесконечно малом ее участке. Центр такой окружности называется центром кривизны для данной точки кривой.
Радиус
и центр кривизны в точке 1 (рис.1.7) определим
следующим образом. Возьмем вблизи точки
1 точку 1.
Построим в этих точках касательные  и
и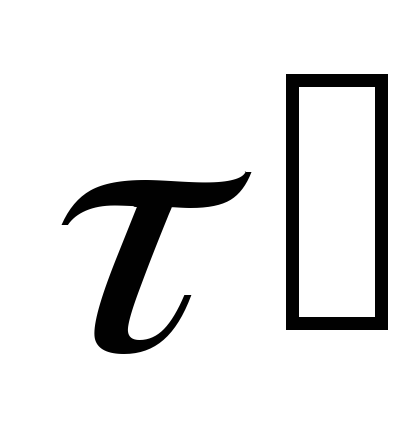 , перпендикуляры к которым пересекутся
в некоторой точкеО.
При этом для кривой, не являющейся
окружностью, расстояния
, перпендикуляры к которым пересекутся
в некоторой точкеО.
При этом для кривой, не являющейся
окружностью, расстояния 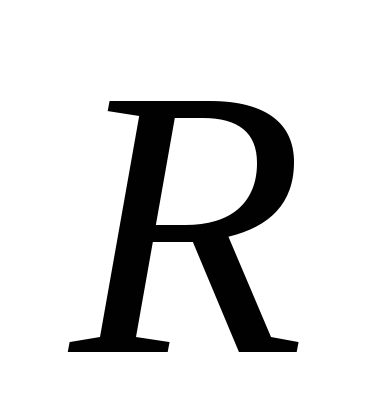
и
и 
несколько отличаются друг от друга.
Если точку 1
приближать к точке 1, пересечение
перпендикуляров O
будет перемещаться вдоль прямой
несколько отличаются друг от друга.
Если точку 1
приближать к точке 1, пересечение
перпендикуляров O
будет перемещаться вдоль прямой 
и в пределе окажется в некоторой точке О.
Эта точка и будет центром кривизны для
точки 1. Расстояния R
и R
будут стремиться к общему пределу
и в пределе окажется в некоторой точке О.
Эта точка и будет центром кривизны для
точки 1. Расстояния R
и R
будут стремиться к общему пределу  ,
равному радиусу кривизны.
,
равному радиусу кривизны.
Как
известно из математики, 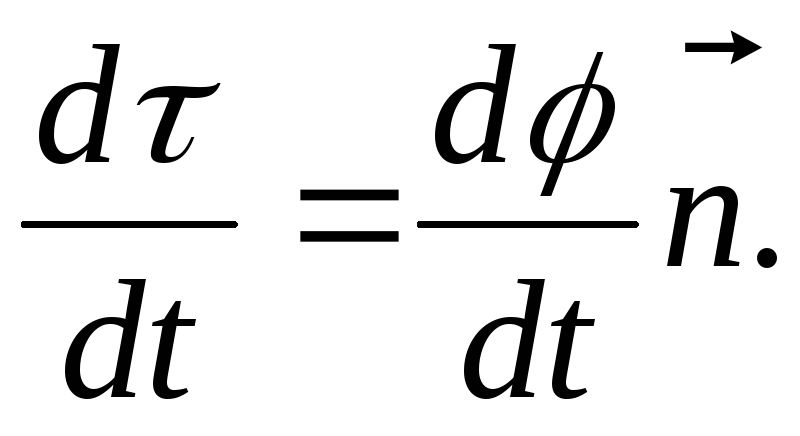 (1.7)
(1.7)
Здесь 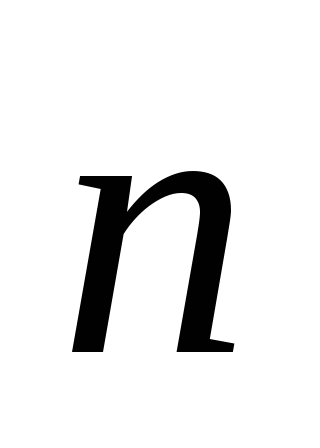 – орт нормали к траектории, направленный
в сторону поворота вектора
– орт нормали к траектории, направленный
в сторону поворота вектора при движении частицы по траектории.
Величину
при движении частицы по траектории.
Величину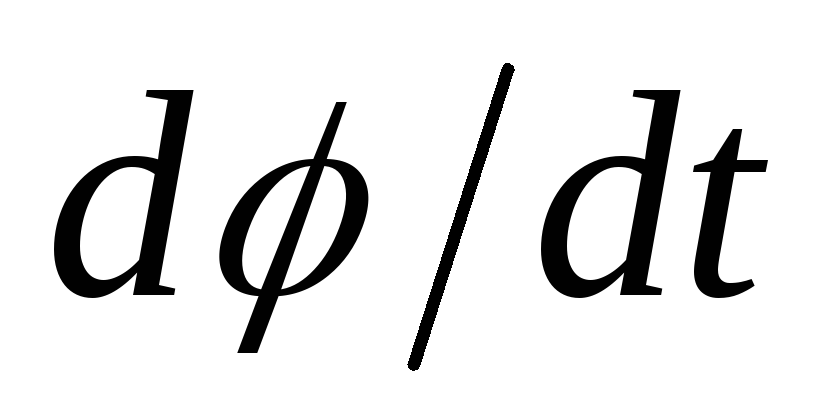 можно связать с радиусом кривизны
траектории и скоростью частицы
можно связать с радиусом кривизны
траектории и скоростью частицы .
Из рис. 1.7 следует, что
.
Из рис. 1.7 следует, что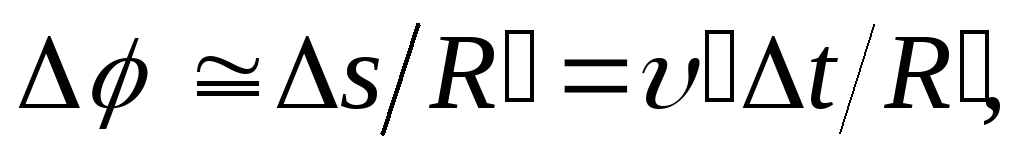 где
где — угол поворота вектора
— угол поворота вектора за время
за время (совпадающий с углом между перпендикулярами
(совпадающий с углом между перпендикулярами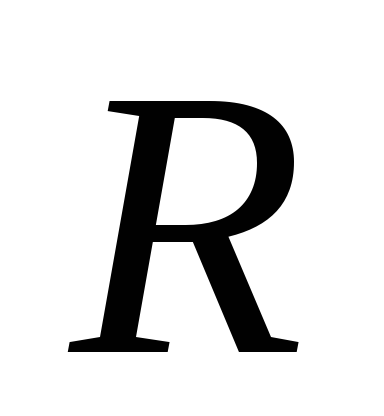
и
и 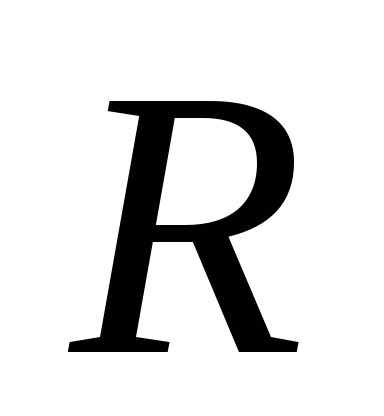 ),
), 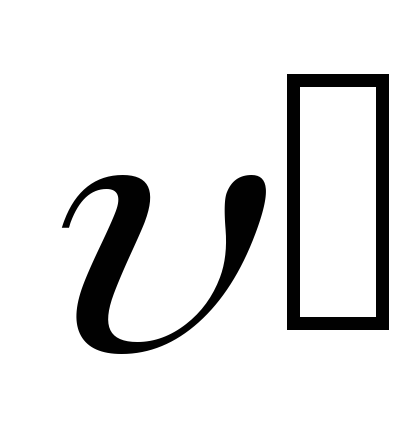 — средняя скорость на пути
— средняя скорость на пути .
Отсюда
.
Отсюда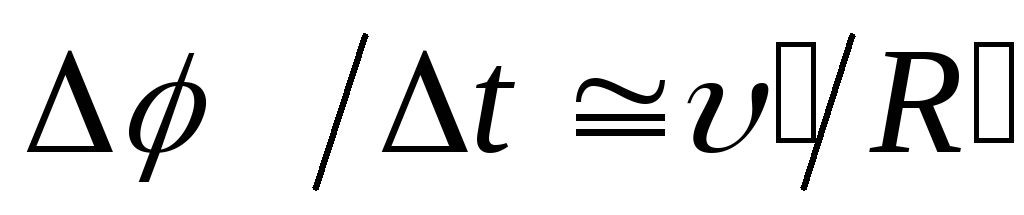 .
В пределе при
.
В пределе при
0 приближенное равенство станет строгим,
средняя скорость
0 приближенное равенство станет строгим,
средняя скорость  превратится в мгновенную скорость
превратится в мгновенную скорость в точке 1,
в точке 1,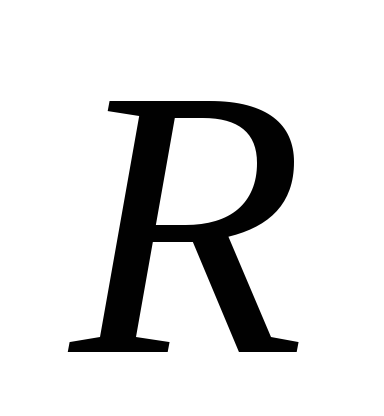 -
в радиус кривизны
-
в радиус кривизны 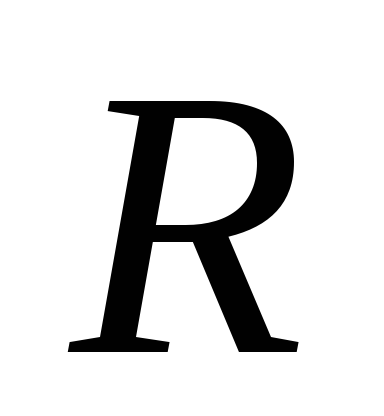 .
В результате получится равенство
.
В результате получится равенство
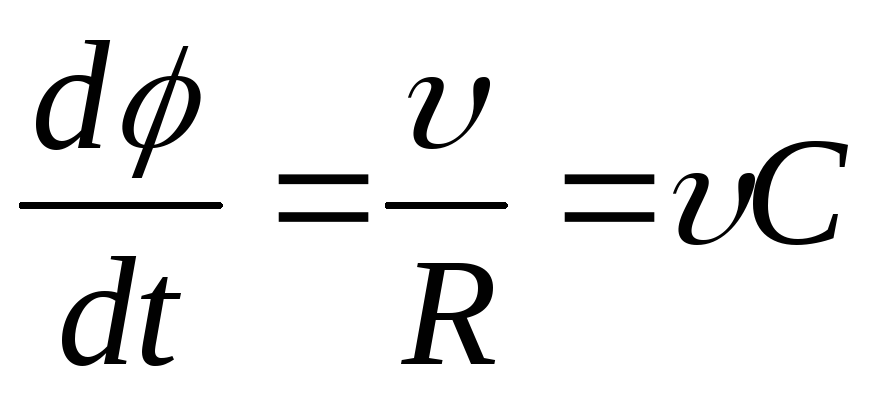 (1.8)
(1.8)
— быстрота поворота вектора скорости пропорциональна кривизне траектории и скорости перемещения частицы по траектории.
Подставив
(1.7) в формулу (1.8), получим 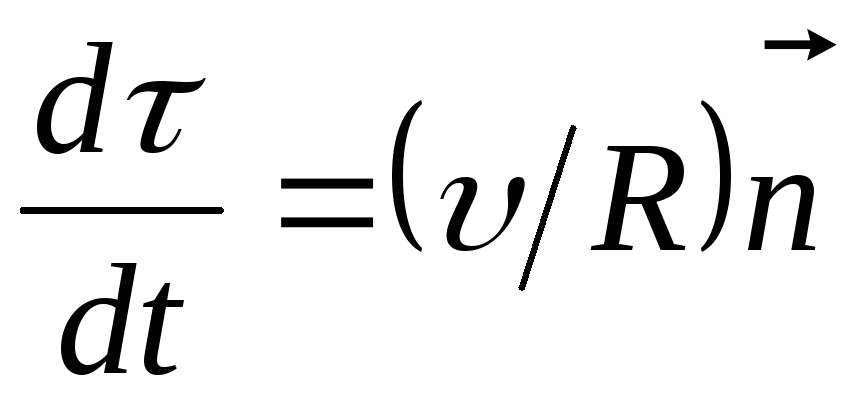 ,
тогда нормальное ускорение равно
,
тогда нормальное ускорение равно 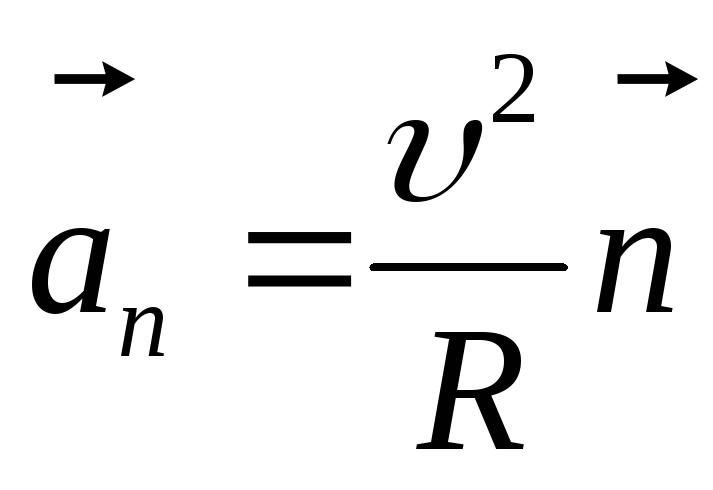 .
.
 Вектор
ускорения при движении материальной
точки по плоской кривой равен
Вектор
ускорения при движении материальной
точки по плоской кривой равен 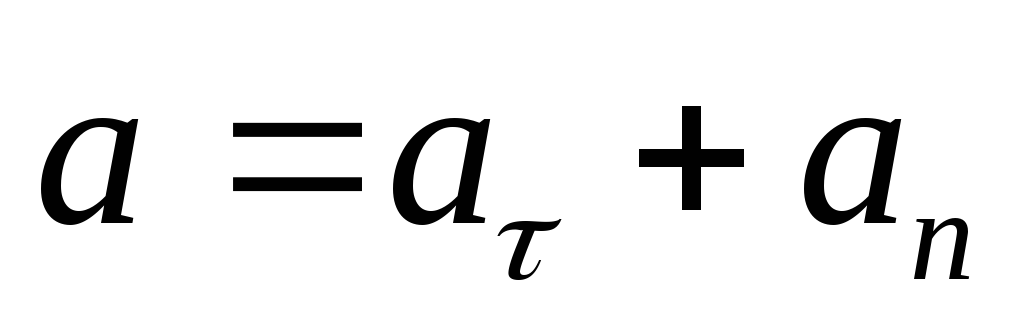 ,
а его модуль
,
а его модуль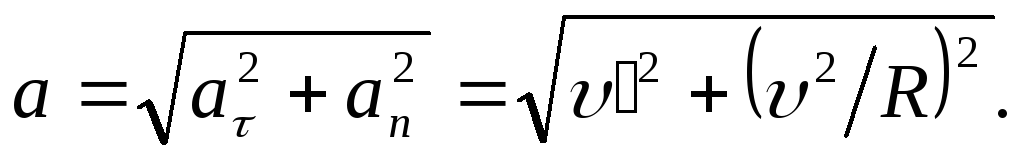
При
прямолинейном движении нормальное
ускорение отсутствует. Интересным
является тот факт, что 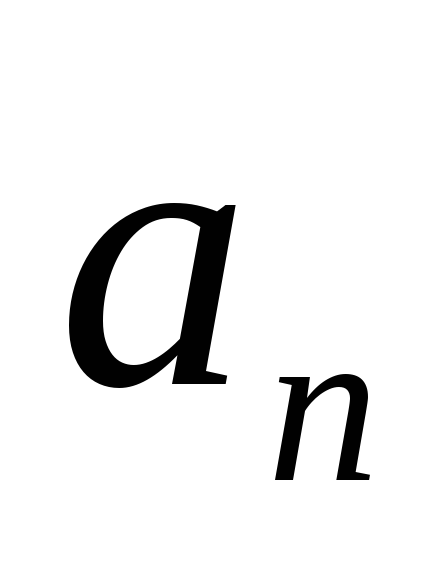 обращается в ноль в точке перегиба
криволинейной траектории (точка ТП на
рис.1.8). По обе стороны от этой точки
векторы
обращается в ноль в точке перегиба
криволинейной траектории (точка ТП на
рис.1.8). По обе стороны от этой точки
векторы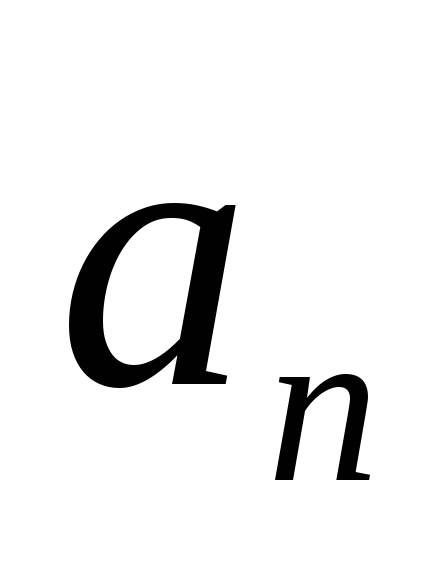 направлены в разные стороны. Вектор
направлены в разные стороны. Вектор не может изменяться скачком, изменение
направления на противоположное происходит
плавно с обращением
не может изменяться скачком, изменение
направления на противоположное происходит
плавно с обращением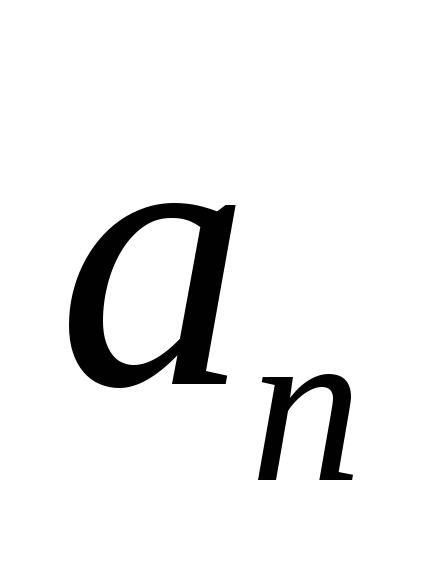 в ноль в точке перегиба.
в ноль в точке перегиба.
Если
материальная точка движется с постоянными
по величине скоростью и ускорением, то 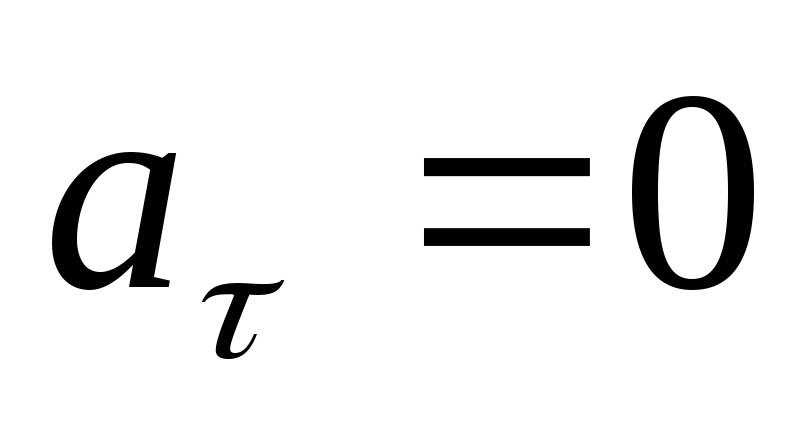 ,
так что
,
так что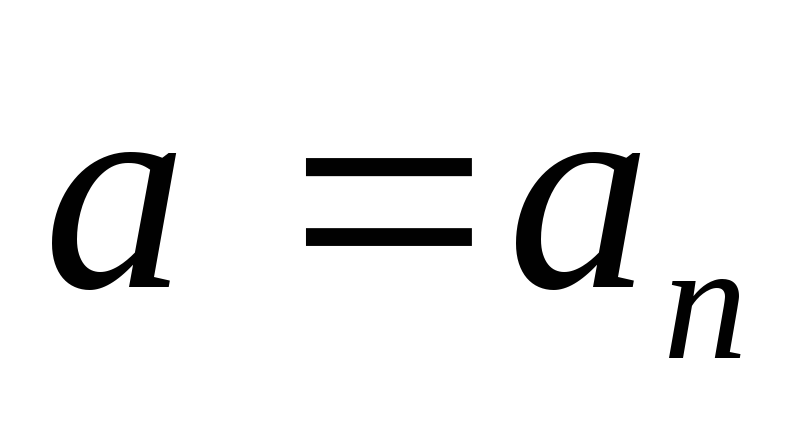 и
и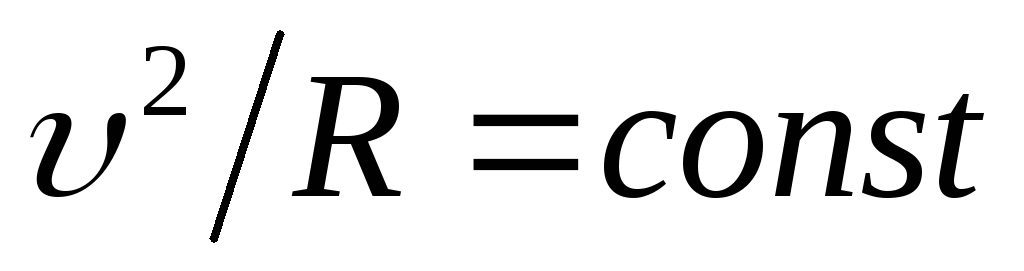 ,
поэтому
,
поэтому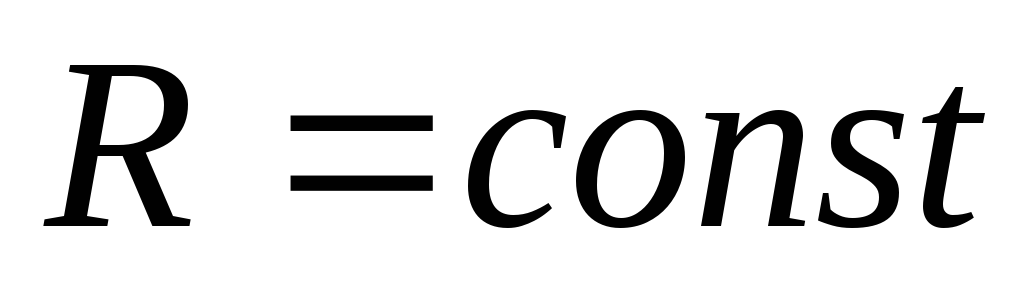 – частица движется по линии постоянной
кривизны, т.е. по окружности.
– частица движется по линии постоянной
кривизны, т.е. по окружности.
Траектория точки. Длина пути. Вектор перемещения (перемещение).

Принцип независимости движения
Число независимых координат, полностью определяющих положение
точки в пространстве, называется число степеней свободы.
r t — радиус вектор.
Траектория – кривая, которую описывает радиус вектор материальной точки при её движении.
Взависимости от формы траектории движение разделяется на
-прямолинейное, — криволинейное.
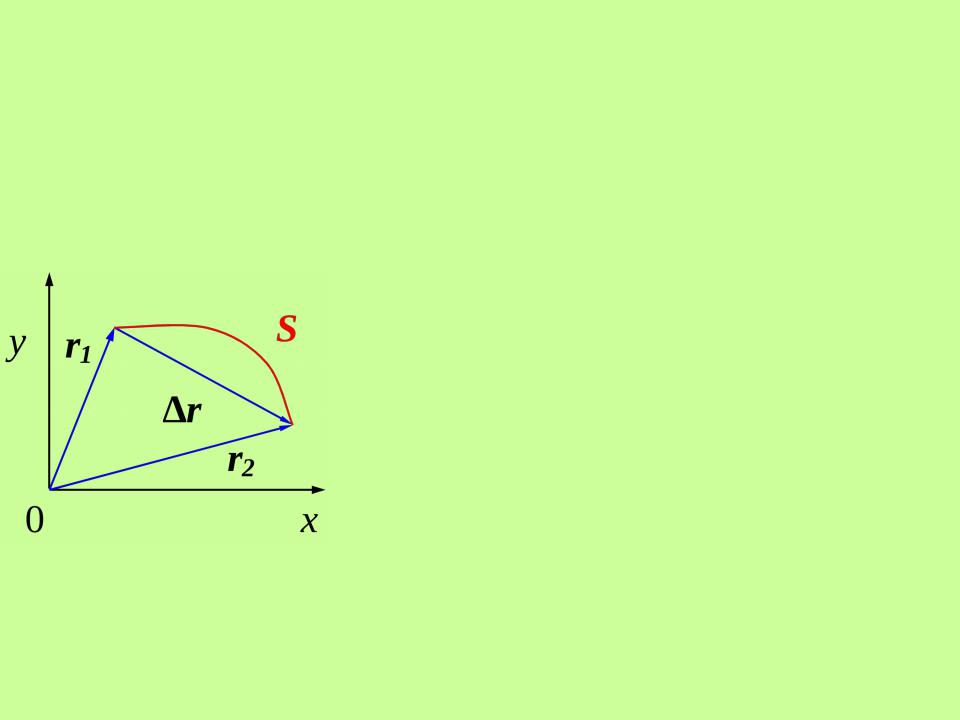
Расстояние, отсчитанное вдоль
траектории, (длина участка траектории) называется длиной пути S.
S t — скалярная функция.
Направленный отрезок прямой (вектор), соединяющий начальную и конечную точки
траектории называется
вектором перемещения
(перемещением).
r r2 r1; |
| r |
| S. |
|
|

При прямолинейном движении r S
Если движение происходит в течение бесконечно малого времени t → 0, то
по модулю путь равен перемещению
dS dr .
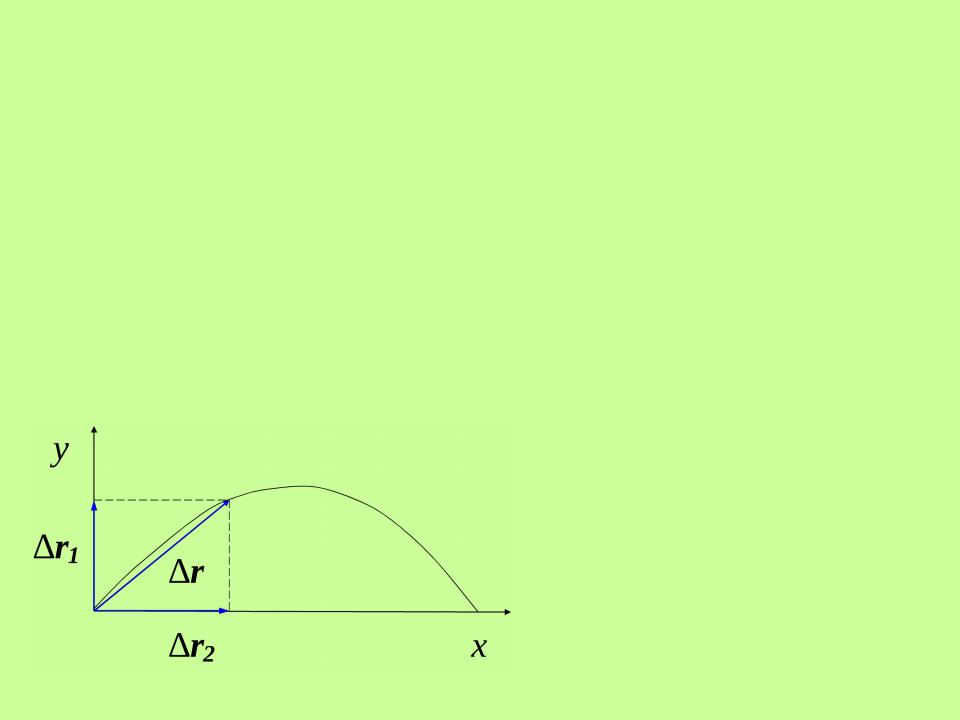
Если материальная точка участвует в нескольких перемещениях,
то результирующее перемещение равно векторной сумме перемещений, совершаемых материальной точкой в каждом из движений в отдельности:
r ri .
r r1 r2
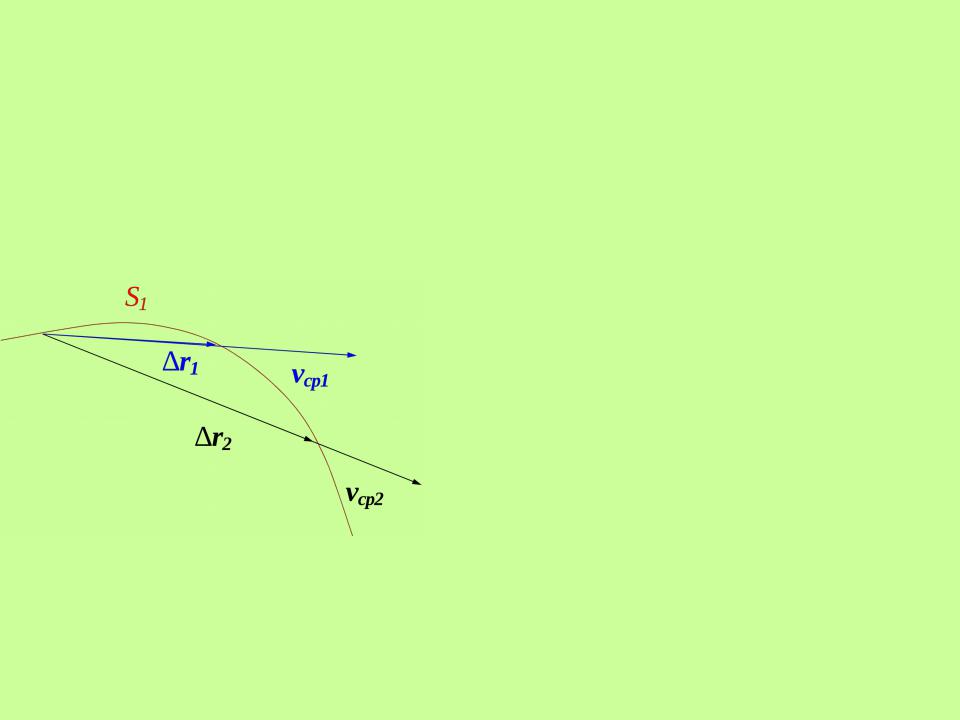
Скорость движения материальной точки. Понятие о кривизне
Для характеристики движения материальной точки вводится понятие скорости – векторная величина.
Материальная точка движется по криволинейной траектории.
За время t1 точка проходит путь S1 и
получает приращение r1 ,
За время t2 – r2 .
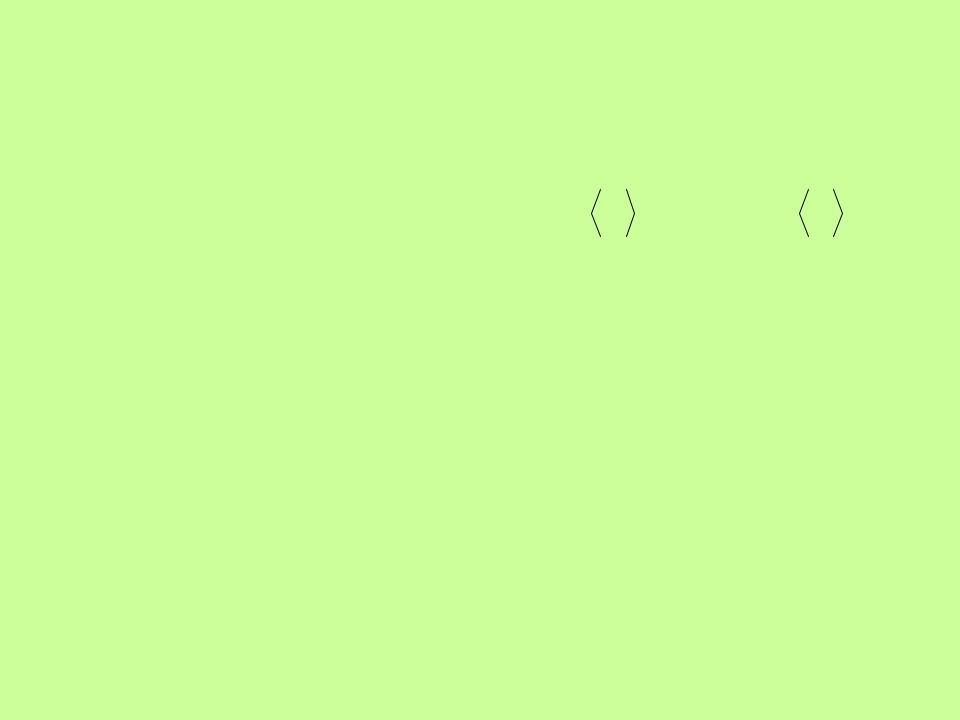
Вектор средней скорости – отношение перемещения к промежутку времени
|
| r |
|
| r |
|
| r | ; |
|
|
vср1 | 1 ; | vср2 | 2 ; | vср v | t | v | r. | ||||
|
| t1 |
|
| t2 |
|
|
|
|
| |
Вектор средней скорости характеризует изменение положения радиус-вектора.
Если t 0 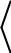 v
v 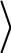 стремится к предельному значению.
стремится к предельному значению.

Мгновенная скорость материальной точки
–векторная величина, равная первой производной радиус-вектора
движущейся точки по времени.
|
|
|
|
| lim | r |
| dr | ||||
|
|
| v | t | dt | |||||||
|
|
|
|
|
|
|
|
| t 0 |
| ||
t 0 |
|
| dr |
|
| dS , следовательно, | ||||||
|
| |||||||||||
модуль мгновенной скорости равен | ||||||||||||
первой производной пути по времени: | ||||||||||||
|
|
|
|
|
|
| dS |
|
| |||
|
|
|
|
|
|
|
| |||||
|
|
|
| v |
|
| v dt . |
| ||||
|
|
|
|
|
|
|
|
|
| |||

В математике производной функции y f x
в точке x0 называется предел отношения изменения функции y в этой точке к вызвавшему его изменению аргумента x
при произвольном стремлении | x к нулю | |||||||
dy y x |
| y |
| x |
| lim | y . | |
dx |
|
|
| x 0 | x | |||
|
|
|
|
|
| |||

Физический смысл производной:
это среднее значение изменения функции на таком интервале, на котором среднее значение функции не меняется.
Мгновенная скорость
|
|
|
| dr | dx | dy |
| dz |
| |
|
| v | dt | dt i | dt | j dt k. |
| |||
dx | vx ; | dy vy ; | dz | vz | – проекции | |||||
dt |
|
|
| dt |
|
| dt | вектора скорости | ||
|
|
|
|
|
|
|
|
| на оси координат. | |
|
|
| vx2 | v2y vz2 . |
| |||||
| v |
|
|
|
|
| ||||
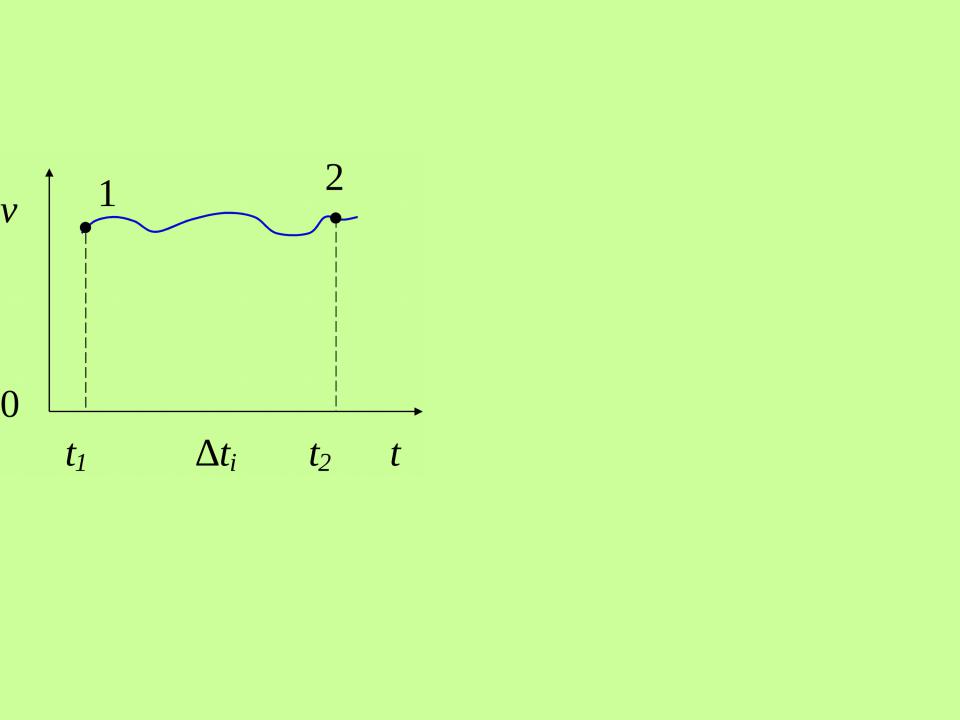
Вычисление пройденного пути. Понятие об интеграле
ti 0.
vi – мгновенная скорость.
Si vi ti . | (1) |
n | n |
S Si vi ti . (2) | |
i 1 | i 1 |
n | t2 |
S lim v t dt v t dt. (3) | |
t 0 i 1 | t1 |




 еремещение при равнопеременном движении
еремещение при равнопеременном движении
 авномерное движение тела по окружности – периодическое движение с постоянной по модулю скоростью.Путь по дуге. Перемещение по хорде. Скорость направлена по касательной. Ускорение к центру окружностиЦентростремительное ускорение a = υ2 /R. Скорость равна отношению пройденного пути ко времени. υ = S/t = 2 πR /Tгде 2 πR – путь, пройденный за один поворот, Т — период – время одного полного поворота. Частота – число поворотов в единицу времени ν = 1/Т .
авномерное движение тела по окружности – периодическое движение с постоянной по модулю скоростью.Путь по дуге. Перемещение по хорде. Скорость направлена по касательной. Ускорение к центру окружностиЦентростремительное ускорение a = υ2 /R. Скорость равна отношению пройденного пути ко времени. υ = S/t = 2 πR /Tгде 2 πR – путь, пройденный за один поворот, Т — период – время одного полного поворота. Частота – число поворотов в единицу времени ν = 1/Т . вижение по параболе (баллистическое движение)
вижение по параболе (баллистическое движение) олеблющееся тело вовлекает в колебательный процесс частицы окружающей среды. В среде возникает механическая волна – возмущение, распространяющееся в упругой среде. При этом происходит передача энергии без переноса вещества. Существую продольные и поперечные волны. Их вид определяется направлением колебания частиц среды.
олеблющееся тело вовлекает в колебательный процесс частицы окружающей среды. В среде возникает механическая волна – возмущение, распространяющееся в упругой среде. При этом происходит передача энергии без переноса вещества. Существую продольные и поперечные волны. Их вид определяется направлением колебания частиц среды. еремещениеS = Vt – при равномерном движении,
еремещениеS = Vt – при равномерном движении,