Резонатор — Википедия

Материал из Википедии — свободной энциклопедии

Резона́тор — колебательная система, в которой происходит накопление энергии колебаний за счёт резонанса с вынуждающей силой. Обычно резонаторы обладают дискретным набором резонансных частот.

В технике обычно встречаются резонаторы с колебанием электромагнитных или механических величин. Конструкция резонатора сильно зависит от его резонансных частот.

Механические резонаторы можно разделить на две условные группы:

• Резонатор накопительного действия.
• Резонатор мгновенного действия.

Резонатор накопительного действия[править | править код]

Отличительной чертой такого резонатора является накопление энергии внешнего воздействия за счет уменьшения частоты собственных колебаний. С математической точки зрения любой резонатор, частота колебаний которого строго больше частоты колебаний возмущающей силы, является накопительным. Классическим примером являются качели. Усиление выходной мощности происходит за счет сложения мощностей нескольких колебаний возмущающей силы.

Резонатор мгновенного действия[править | править код]

Под «мгновенным действием» подразумевается совершение одного периода колебания резонатора за время, не большее периода колебания возмущающей силы. Примером такого резонатора может служить резонатор Гельмгольца. Усиление в таких резонаторах может происходить за счет:

• смещения по времени мощности резонансной частоты на входе, то есть, плавно меняясь на входе резонатора, мощность может увеличиться на выходе за счет уменьшения длительности сигнала;
• поглощения энергии других (не резонансных) частот. Этот эффект используется певцами при практике резонансного пения;
• поглощения теплового движения окружающего пространства.

Резонаторы мгновенного действия могут иметь коэффициент усиления до 45 дБ (10 000 раз).

В генераторах СВЧ^[1]-излучений (клистрон, магнетрон) резонаторы представляют собой металлическую конструкцию, используемую для генерации волн определённой длины.

• Калинин В. А., Лобов Г. Д., Штыков В. В. Радиофизика для инженеров / Под ред. С.И.Баскакова. — М.: Изд-во МЭИ, 1994. — 130 с. — 500 экз.

Кварцевый резонатор — Википедия

Кварцевый резонатор в кристаллодержателе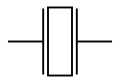 по ГОСТ 2.736-68^[1]

Ква́рцевый резона́тор (жарг. «кварц») — электронный прибор, в котором пьезоэлектрический эффект и явление механического резонанса используются для построения высокодобротного резонансного элемента электронной схемы.

Следует отличать кварцевый резонатор от устройств, использующих другие пьезоэлектрические материалы — например, специальную керамику (см. керамический резонатор^[en]).

На пластинку, тонкий цилиндр, кольцо или брусок, вырезанные из кристалла кварца с определённой ориентацией относительно кристаллографических осей монокристалла нанесены 2 или более электродов — проводящие металлические полоски, выполненные напылением в вакууме или вжиганием плёнки металла на заданные поверхности кристалла.

Резонатор механически крепится в узлах рабочей моды колебаний, чтобы снизить потери колебательной энергии через крепление кристалла. Для иных мод колебаний узлы собственных колебаний расположены в иных местах кристалла и поэтому иные моды колебаний подавлены. Для рабочей моды колебаний кристалл имеет некоторую собственную резонансную частоту механических колебаний, причем на этой частоте добротность механического резонатора очень высока.

При подаче напряжения на электроды благодаря обратному пьезоэлектрическому эффекту происходит изгиб, сжатие или сдвиг в зависимости от того, каким образом вырезан кристалл относительно кристаллографических осей, конфигурации возбуждающих электродов и расположения точек крепления.

Собственные колебания кристалла в результате пьезоэлектрического эффекта наводят на электродах дополнительную ЭДС и поэтому кварцевый резонатор электрически ведёт себя подобно резонансной цепи, — колебательному контуру, составленному из конденсаторов, индуктивности и резистора, причем добротность этой эквивалентной электрической цепи очень велика и близка к добротности собственных механических колебаний кристалла.

Если частота подаваемого напряжения равна или близка к частоте собственных механических колебаний пластинки, затраты энергии на поддержание колебаний пластинки оказываются намного ниже, нежели при большом отличии частоты. Это тоже соответствует поведению электрического колебательного контура.

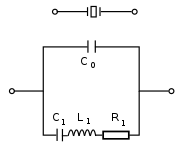Условное обозначение кварцевого резонатора (сверху) и его эквивалентная схема (снизу)

По поведению в электрических цепях кварцевый резонатор можно в первом приближении представить в виде эквивалентной электрической схемы, изображённой на рисунке где:

C0{\displaystyle C_{0}} — собственная ёмкость кристалла, образуемая электродами на кристалле — обкладками конденсатора, где диэлектриком является сам кристалл и параллельно соединённой с этой ёмкостью паразитной ёмкостью кристаллодержателя и электрических выводов;

C1{\displaystyle C_{1}}, L1{\displaystyle L_{1}} — эквивалентные ёмкость и индуктивность механической колебательной системы резонатора;

R1{\displaystyle R_{1}} — эквивалентное сопротивление потерь механической колебательной системы.

Математически электрический импеданс в виде преобразования Лапласа можно по правилам параллельного и последовательного соединения двухполюсников записать:

Z(s)=(1s⋅C1+s⋅L1+R1)‖(1s⋅C0),{\displaystyle Z(s)=\left({{\frac {1}{s\cdot C_{1}}}+s\cdot L_{1}+R_{1}}\right)\left\|\left({\frac {1}{s\cdot C_{0}}}\right)\right.,}

где s=jω{\displaystyle s=j\omega } — комплексная частота преобразования Лапласа, двумя вертикальными чертами обозначено параллельное соединение конденсатора C0{\displaystyle C_{0}} и цепи, состоящей из последовательно соединённых C1{\displaystyle C_{1}}, L1{\displaystyle L_{1}}, R1{\displaystyle R_{1}},

или:

Z(s)=s2+sR1L1+ωs2s⋅C0⋅(s2+sR1L1+ωp2).{\displaystyle Z(s)={\frac {s^{2}+s{\frac {R_{1}}{L_{1}}}+{\omega _{\mathrm {s} }}^{2}}{s\cdot C_{0}\cdot (s^{2}+s{\frac {R_{1}}{L_{1}}}+{\omega _{\mathrm {p} }}^{2})}}.}

В такой эквивалентной схеме наблюдается два вида резонанса — последовательный, который наступает при равенстве реактивных сопротивлений XC1{\displaystyle X_{C_{1}}} и XL1{\displaystyle X_{L_{1}}}, при этом резонансе полное электрическое сопротивление (модуль импеданса) мало и практически равно R1{\displaystyle R_{1}} и параллельный резонанс, при котором равны полные сопротивления XL1{\displaystyle X_{L_{1}}} и полное сопротивление цепи, состоящей их последовательно соединённых пары конденсаторов XC1,C2{\displaystyle X_{C_{1},C_{2}}}, при этом полное сопротивление цепи велико, так как ток при резонансе протекает во внутреннем контуре, состоящем из всех двухполюсников эквивалентной схемы.

Резонансная частота последовательного резонанса ωs{\displaystyle \omega _{\mathrm {s} }}:

ωs=1L1⋅C1.{\displaystyle \omega _{\mathrm {s} }={\frac {1}{\sqrt {L_{1}\cdot C_{1}}}}.}

Резонансная частота параллельного резонанса ωp{\displaystyle \omega _{\mathrm {p} }}:

ωp=C1+C0L1⋅C1⋅C0=ωs1+C1C0.{\displaystyle \omega _{\mathrm {p} }={\sqrt {\frac {C_{1}+C_{0}}{L_{1}\cdot C_{1}\cdot C_{0}}}}=\omega _{s}{\sqrt {1+{\frac {C_{1}}{C_{0}}}}}.}

Измерением импеданса кварцевого резонатора на четырёх различных частотах после решения системы 4 уравнений можно определить параметры всех двухполюсников, входящих в эквивалентную схему. Практически, типичная ёмкость конденсатора C1{\displaystyle C_{1}} составляет десятые и даже сотые доли пФ, индуктивность L1{\displaystyle L_{1}} единицы-десятки Гн, сопротивление R1{\displaystyle R_{1}} — десятки-сотни Ом, паразитная ёмкость C0{\displaystyle C_{0}} — десятки пФ.

Так как волновое сопротивление Rw=L1C1{\displaystyle R_{w}={\sqrt {\frac {L_{1}}{C_{1}}}}} при последовательном и параллельном резонансах очень велико относительно последовательного сопротивления R1{\displaystyle R_{1}}, это обеспечивает очень высокую добротность резонансной цепи, достигающей нескольких миллионов.

Так как практически C0≫C1{\displaystyle C_{0}\gg C_{1}} формулу для частоты параллельного резонанса можно упростить:

ωp=C1+C0L1⋅C1⋅C0=ωs1+C1C0≈ωs(1+C12C0).{\displaystyle \omega _{\mathrm {p} }={\sqrt {\frac {C_{1}+C_{0}}{L_{1}\cdot C_{1}\cdot C_{0}}}}=\omega _{s}{\sqrt {1+{\frac {C_{1}}{C_{0}}}}}\approx \omega _{s}\left(1+{\frac {C_{1}}{2C_{0}}}\right).}

Опять же, так как C0≫C1{\displaystyle C_{0}\gg C_{1}} из формул следует, что частоты последовательного и параллельного резонансов очень близки, например, для типичных C1=0,1{\displaystyle C_{1}=0,1} пФ и C0=10{\displaystyle C_{0}=10} пФ для кварцевого резонатора в несколько МГц частоты резонансов различаются на 0,5 %.

Резонансную частоту последовательного резонанса ωs{\displaystyle \omega _{\mathrm {s} }} невозможно изменить подключением к кварцевому резонатору внешней цепи, так как индуктивность и ёмкость C1{\displaystyle C_{1}}, L1{\displaystyle L_{1}} эквивалентной схемы определяются собственным механическим резонансом кристалла.

Резонансную частоту параллельного резонанса можно снижать в небольших пределах, практически на доли процента, так как C0≫C1{\displaystyle C_{0}\gg C_{1}} и ёмкость C0{\displaystyle C_{0}} входит в формулу для частоты подключением к кварцевому резонатору внешнего конденсатора. Также возможно в малых пределах увеличить резонансную частоту подключением внешней катушки индуктивности, этот способ применяется редко.

Изготовители кварцевых резонаторов при их изготовлении механически юстируют резонансную частоту при некотором подключённом внешнем конденсаторе. Ёмкость конденсатора, обеспечивающего заявленную изготовителем частоту параллельного резонанса обычно указывают в спецификации на конкретный резонатор, без подключения этого внешнего конденсатора резонансная частота будет немного выше.

Кварцевый резонатор в герметичном стеклянном корпусе пальчикового бесцокольного исполнения Резонатор на 4 МГц в миниатюрном металлическом герметизированном корпусе HC-49/US Металлические корпуса разнообразных размеров

Пьезоэлектрический эффект был впервые открыт братьями Жаком и Пьером Кюри в 1880 году. Поль Ланжевен впервые практически использовал этот эффект в ультразвуковом излучателе и приемнике ультразвука в гидролокатора перед первой мировой войной.

Первый электромеханический резонатор, на основе сегнетовой соли, был изготовлен в 1917 году и запатентован в 1918 году Александром М. Николсоном (Alexander M. Nicholson) из компании Bell Telephone Laboratories, хотя его приоритет оспаривался Уолтером Гайтоном Кэди (Walter Guyton Cady), который изготовил кварцевый резонатор в 1921 году.

Некоторые улучшения в конструкцию кварцевых резонаторов предложены позже Льюисом Эссеном и Джорджем Вашингтоном Пирсом (George Washington Pierce).

Первые стабильные по частоте кварцевые резонаторы были разработаны в 1920—1930-х годах. Начиная с 1926 года, кварцевые резонаторы на радиостанциях стали использоваться в качестве элементов, задающих несущую частоту. В это же время резко возросло количество компаний, начавших выпускать кварцевые резонаторы, например, только до 1939 года в США было выпущено более чем 100 тыс. штук.

Одним из самых популярных видов резонаторов являются резонаторы, применяемые в часовых схемах и таймерах. Резонансная частота часовых резонаторов составляет 32 768 Гц; будучи поделённой на 15-разрядном двоичном счётчике, она даёт интервал времени в 1 секунду.

Применяются в генераторах с фиксированной частотой, где необходима высокая стабильность частоты. В частности, в опорных генераторах синтезаторов частот и в трансиверных радиостанциях для формирования DSB-сигнала на промежуточной частоте и детектирования SSB или телеграфного сигнала.

Также применяются в кварцевых полосовых фильтрах промежуточной частоты супергетеродинных приёмников. Такие фильтры могут выполняться по лестничной или дифференциальной схеме и отличаются очень высокой добротностью и стабильностью по сравнению с LC-фильтрами.

По типу корпуса кварцевые резонаторы могут быть выводные для объёмного монтажа (стандартные и цилиндрические) и для поверхностного монтажа (SMD).

Качество схемы, в которую входят кварцевые резонаторы, определяют такие параметры, как допуск по частоте (отклонение частоты), стабильность частоты, нагрузочная ёмкость, старение.

Преимущества[править | править код]

• Достижение намного бо́льших значений добротности (10⁴—10⁶) эквивалентного колебательного контура, нежели любым другим способом.
• Малые размеры устройства (вплоть до долей миллиметра).
• Высокая температурная стабильность.
• Большая долговечность.
• Лучшая технологичность.
• Построение качественных каскадных фильтров без необходимости их ручной настройки.

Недостатки[править | править код]

• Чрезвычайно узкий диапазон подстройки частоты внешними элементами. На практике для многодиапазонных систем эта проблема решается построением синтезаторов частот различной степени сложности.

• Смагин А. Г., Ярославский М. И. Пьезоэлектричество кварца и кварцевые резонаторы. — М.: «Энергия», 1970. — 488 с. — 6000 экз.

• Альтшуллер Г. Б. Кварцевая стабилизация частоты. — М.: «Связь», 1974. — 272 с. — 5600 экз.

• Андросова В. Г., Банков В. Н., Дикиджи А. Н. и др. Справочник по кварцевым резонаторам / Под ред. П. Г. Позднякова. — Связь, 1978. — 288 с. — 15 000 экз.

• Глюкман Л. И. Пьезоэлектрические кварцевые резонаторы. — 3-е изд., перераб. и доп. — М.: Радио и связь, 1981. — 232 с. — 10 000 экз.

• Зеленка И. Пьезоэлектрические резонаторы на объёмных и поверхностных акустических волнах: Материалы, технология, конструкция, применение: Пер. с чешск. — М.: Мир, 1990. — 584 с. — 4050 экз. — ISBN 5-03-001086-6.

• Ладик А. И., Сташкевич А. И. Изделия электронной техники. Пьезоэлектрические и электромеханические приборы: Справочник. — М.: Радио и связь, 1993. — 104 с. — 3000 экз. — ISBN 5-256-01145-6, ISBN 5-256-00588-X.

Оптический резонатор — Википедия

Оптический резонатор — совокупность нескольких отражающих элементов, образующих открытый резонатор (в отличие от закрытых объёмных резонаторов, применяемых в диапазоне СВЧ), формирующих стоячую световую волну. Оптические резонаторы являются одним из основных элементов лазеров, обеспечивая положительную обратную связь для обеспечения многократного прохождения лазерного излучения через активную среду, что приводит к усилению светового потока.

В оптическом диапазоне резонатор с размерами порядка длины волны не может быть применен в силу технологических трудностей и из-за резкого падения добротности; резонатор типа замкнутой металлической полости больших по сравнению с длиной волны размеров не может быть применен в силу высокой плотности его собственных колебаний, приводящих к потере резонансных свойств. Необходимы резонаторы с разреженным спектром собственных колебаний. Такими свойствами обладают открытые резонаторы, что и обуславливает их применение в оптическом диапазоне.

Свет многократно отражается, образуя стоячие волны с определенными резонансными частотами. Продольные моды отличаются, как правило, только частотой, в то время как поперечные моды имеют существенно различное распределение интенсивности в сечении луча. Наиболее часто используются оптические резонаторы, образованные двумя отражающими элементами, такими как зеркала или уголковые отражатели, и простейшим оптическим резонатором является интерферометр Фабри-Перо, состоящий из двух плоских параллельных зеркал. Однако для лазеров случай двух плоских зеркал используется не очень часто, ввиду сложности юстировки. Используются резонаторы со сферическими зеркалами. Такие резонаторы отличаются радиусом кривизны (следовательно и фокусным расстоянием) отражающих элементов и расстоянием между ними. Геометрические параметры резонатора выбираются исходя из требований устойчивости, а также других факторов, таких как, например, формирование наименьшей перетяжки оптического пучка.

Оптические резонаторы обычно конструируются таким образом, чтобы иметь наиболее высокую добротность (порядка 103−109{\displaystyle 10^{3}-10^{9}}): свет должен отражаться максимальное количество раз, не затухая, поэтому ширина резонансных пиков очень мала по сравнению с частотой излучения лазера.

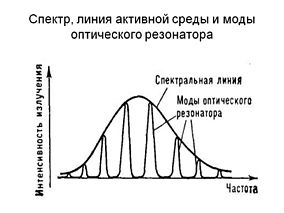Моды оптического резонатора Поперечные моды оптического резонатора со сферическими зеркалами Поперечные моды оптического резонатора с плоскими зеркалами

Свет в резонаторе многократно отражается от зеркал. Отраженные лучи интерферируют, что приводит к тому, что только определенные распределения полей на определенных частотах будут сохраняться в резонаторе, излучение на других частотах или с другим распределением будет подавлено за счет интерференции или быстро покинет резонатор. Распределения, которые повторяются при одном полном проходе резонатора являются наиболее стабильными и называются собственными модами или модами резонатора. Моды оптического резонатора подразделяют на две группы: продольные, отличающиеся частотой, и поперечные, которые отличаются как частотой, так и распределением поля в сечении пучка. Обычно основная поперечная мода представляет собой гауссовский пучок.

Исследования А. Фокса и Т. Ли в 1960-1961 гг. предоставили наглядную картину формирования собственных мод открытого резонатора методом рассмотрения изменений в распределении амплитуды и фазы первоначально плоской волны при её многократных последовательных проходах через резонатор. Анализ Фокса и Ли, выполненный ими для открытых резонаторов типа интерферометра Фабри-Перо в нескольких геометрических конфигурациях (прямоугольные плоские зеркала, круглые плоские зеркала), а также для конфокальных сферических и параболических зеркал, привел к следующим выводам:

1. Открытые резонаторы характеризуются дискретным набором колебательных мод.
2. Однородные плоские волны не являются нормальными модами открытых резонаторов
3. Электромагнитные волны, соответствующие собственным модам резонатора, почти полностью поперечны. Поэтому моды обозначаются символом ТЕМ.
4. Моды более высокого порядка имеют более высокие дифракционные потери, чем основная мода.
5. Для основной моды амплитуда поля сильно уменьшается к краям зеркала. Поэтому её дифракционные потери много меньше предсказываемых на основе представления об однородных плоских волнах и в реальных ситуациях пренебрежимо малы.

Частота моды пустого оптического резонатора с идеальными бесконечно большими зеркалами удовлетворяет соотношению:

Ωqnm=cL(πq+(1+n+m)arccos⁡g1g2){\displaystyle \Omega _{qnm}={\frac {c}{L}}(\pi q+(1+n+m)\arccos {\sqrt {g_{1}g_{2}}})}

Где Ωqnm{\displaystyle \Omega _{qnm}} — Угловая частота моды с индексами q,n,m. q — индекс продольной моды, n,m — индексы поперечной моды. c — скорость света. L — расстояние между зеркалами для плоского резонатора и половина периметра для кольцевого резонатора. g1,g2{\displaystyle g_{1},g_{2}} — g-параметры резонатора (см. #Устойчивость резонатора).^[1]

Оптические резонаторы могут содержать большое количество отражающих и других элементов, но наиболее часто применяются двухзеркальные резонаторы, зеркала которых плоские или сферические. В зависимости от радиусов зеркал и их взаимного расположения выделяют следующие типы двухзеркальных резонаторов (R1{\displaystyle R_{1}} и R2{\displaystyle R_{2}} — радиусы кривизны зеркал):

• Плоскопараллельный (R1=R2=∞{\displaystyle R_{1}=R_{2}=\infty }) — так называемый резонатор Фабри-Перо. Широко используемой в лазерной технике разновидностью резонатора с плоскопараллельными зеркалами является резонатор с брегговскими отражателями, представляющими собой многослойные диэлектрические или полупроводниковые структуры.

• Конфокальный (R1=R2=L{\displaystyle R_{1}=R_{2}=L}). Конфокальный резонатор образован двумя одинаковыми сферическими зеркалами, фокусы F1{\displaystyle F_{1}}и F2{\displaystyle F_{2}} которых совпадают. Поле в таком резонаторе концентрируется около оси, что снижает дифракционные потери. Данный тип резонатора мало чувствителен к разъюстировке, однако объем активной области используется неэффективно.
• Полуконфокальный (R1=2L,R2=∞{\displaystyle R_{1}=2L,R_{2}=\infty }). Полуконфокальный резонатор образован одним плоским и одним сферическим зеркалом, радиус кривизны которого равен удвоенной длине резонатора. По своим свойствам он аналогичен конфокальному резонатору с удвоенной длиной.
• Концентрический (R1=R2=L/2{\displaystyle R_{1}=R_{2}=L/2}). Концентрический резонатор образован двумя сферическими зеркалами, оси и центры кривизны которых совпадают. В таких резонаторах дифракционные потери для неаксиальных мод быстро возрастают, что используется для селекции мод.
• Полуконцентрический (R1=L,R2=∞{\displaystyle R_{1}=L,R_{2}=\infty }). Образован одним сферическим зеркалом и одним плоским, по своим свойствам близок к концентрическому резонатору.

Диаграмма устойчивости двухзеркальных резонаторов

Резонатор называется неустойчивым, когда произвольный луч, последовательно отражаясь от каждого из зеркал, удаляется на неограниченно большое расстояние от оси резонатора. Наоборот, резонатор, в котором луч остается в пределах ограниченной области, называется устойчивым. В резонаторе, образованном парой зеркал только для определенного диапазона значений длин резонатора и радиусов кривизны зеркал возможно выполнение условий обеспечивающих устойчивую локализацию света в резонаторе, в противном случае сечение пучка с каждым проходом будет увеличиваться, становясь больше размеров зеркал, и, в конечном итоге, будет потеряно.

Соотношение радиусов кривизны зеркал R1,R2{\displaystyle R_{1},R_{2}} и оптической длины резонатора L{\displaystyle L} для обеспечения устойчивости должно удовлетворять следующему соотношению:

0⩽(1−LR1)(1−LR2)⩽1.{\displaystyle 0\leqslant \left(1-{\frac {L}{R_{1}}}\right)\left(1-{\frac {L}{R_{2}}}\right)\leqslant 1.}

Введя обозначения

g1=1−LR1,g2=1−LR2{\displaystyle g_{1}=1-{\frac {L}{R_{1}}},\qquad g_{2}=1-{\frac {L}{R_{2}}}},

удобно графически показать области устойчивости в координатах g1,g2{\displaystyle g_{1},g_{2}}. Тёмные области на рисунке отвечают значениям, при которых резонатор устойчив.

Неустойчивые резонаторы можно подразделить на два класса: 1) резонаторы положительной ветви, которые удовлетворяют условию g1g2>1{\displaystyle g_{1}g_{2}>1}, и 2) резонаторы отрицательной ветви, которые соответствуют условию g1g2<0.{\displaystyle g_{1}g_{2}<0.} Отметим, что для устойчивого резонатора, соответствующего на плоскости g1,g2{\displaystyle g_{1},g_{2}} точке, которая расположена не очень близко к границе неустойчивости, размер пятна имеет тот же порядок, что и у конфокального резонатора, то есть, при длине резонатора порядка метра и для длин волн видимого диапазона размер пятна будет порядка или менее 1мм. При таком небольшом сечении моды выходная мощность (энергия) лазерного излучения, которую можно получить в одной поперечной моде, неизбежно оказывается ограниченной. В неустойчивых же резонаторах поле не стремится сосредоточиться вблизи оси, и в режиме одной поперечной моды можно получить большой модовый объем. Однако при этом возникает другая проблема, связанная с тем, что лучи стремятся покинуть резонатор. Поэтому соответствующие моды имеют значительно большие геометрические потери, чем моды устойчивого резонатора. Тем не менее, данное обстоятельство может быть обращено на пользу, если лучи, которые теряются на выходе резонатора, включить в полезное выходное излучение лазера.

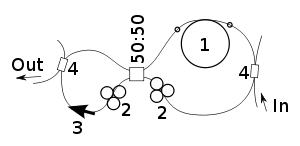
Кольцево́й резона́тор — оптический резонатор, в котором свет распространяется по замкнутой траектории в одном направлении. Объёмные кольцевые резонаторы состоят из трёх или более зеркал, ориентированных так, что свет последовательно отражается от каждого из них, совершая полный оборот. Кольцевые резонаторы находят широкое применение в лазерных гироскопах и лазерах.

Селекция мод — это совокупность методов, обеспечивающих режим, в котором резонатор поддерживает только одну или несколько избранных мод колебаний. В основе всех этих методов лежит создание неодинаковых для различных мод потерь в оптическом резонаторе или усиления в активной среде. Существует несколько способов, позволяющих проводить селекцию как продольных мод, поле которых испытывает осцилляции (перемены знака) вдоль оси резонатора, так и поперечных мод, поле которых осциллирует также и в поперечном направлении.

Селекцию поперечных мод используют обычно для создания генерации лишь на нулевой поперечной моде, имеющей минимальный диаметр и отличающейся гладким профилем интенсивности и минимальной расходимостью. Селекция осуществляется, как правило, помещением внутрь резонатора диафрагмы, затеняющей своими краями все поперечные моды, кроме нулевой. Наряду с этим для селекции поперечных мод иногда используют неустойчивые резонаторы, в которых размеры всех мод искусственно увеличиваются до такой степени, что роль диафрагм начинают играть зеркала резонатора или активный элемент. Возможны и другие способы — например, путём размещения в резонаторе фотонных кристаллов. Селекцию продольных мод используют главным образом для получения монохроматического излучения. Селекция за счёт неодинаковых потерь осуществляется помещением внутрь резонатора дополнительных полупрозрачных зеркал или дисперсионных элементов (призм, решёток, интерферометров).

Дополнительные зеркала вместе с основными образуют один или несколько дополнительных резонаторов, связанных с исходным. В генерацию выходят лишь те продольные моды исходного двухзеркального резонатора, которые наименее связаны с низкодобротным дополнительным резонатором. Дисперсионные элементы типа призм и решёток отклоняют под разными углами лучи с разными длинами волн. В итоге только для узкого спектра частот мод образуется высокодобротный резонатор. Внутрирезонаторные интерферометры осуществляют селекцию продольных мод за счёт того, что они обладают хорошей прозрачностью лишь для узких участков спектра мод. Селекция за счёт неодинаковости усиления осуществляется в основном в кольцевых твердотельных лазерах, в результате чего в них возникает однонаправленная генерация (бегущая волна). В этих условиях начинает сильно проявляться однородность уширения линии усиления активной среды и спектр генерации сужается до одной-двух мод.

Колебательные системы обычно характеризуются добротностью Q. Добротность резонатора можно определить несколькими способами, которые эквивалентны при больших значениях добротности.^[2]

1. ↑ Радина Т. В., Станкевич А. Ф. Резонансные и параметрические явления в задачах генерации и распространения лазерного излучения. — Санкт-Петербург: Издательство Санкт-Петербургского Государственного Университета, 2009. — С. 39-43. — 231 с. — ISBN 978-5-288-04965-1.
2. ↑ Архивированная копия (неопр.) (недоступная ссылка). Дата обращения 1 июля 2015. Архивировано 24 сентября 2015 года.

3. Формирование и селекция поперечных мод в лазерных резонаторах : монография / А. В. Дегтярёв, В. А. Маслов, В. А. Свич, А. Н. Топков.  Х. : ХНУ имени В. Н. Каразина, 2017. – 212 с. ISBN 978-966-285-374-2

Кольцевой резонатор — Википедия

Кольцево́й резона́тор — оптический резонатор, в котором свет распространяется по замкнутой траектории в одном направлении. Объемные кольцевые резонаторы состоят из трёх или более зеркал, ориентированных так, что свет последовательно отражается от каждого из них совершая полный оборот. Простейший кольцевой резонатор представляет собой два параллельных прямолинейных волновода и находящийся между ними резонатор в виде кольцевого волновода. Кольцевые резонаторы находят широкое применение в лазерных гироскопах и лазерах. В волоконных лазерах применяют специальные конструкции волоконных кольцевых резонаторов, обычно имеющих вид замкнутого в кольцо оптического волокна с WDM-ответвителями для ввода излучения накачки и вывода генерируемого излучения.

• Кольцевые резонаторы в лазерах
• 

  Схема объемного кольцевого резонатора с тремя зеркалами. Пунктиром показ путь света в резонаторе.

• 

  Обычный кольцевой резонатор, встроенный в волоконный лазер. In: излучение накачки. Out: выходное излучение. 1: активное волокно. 2: поляризатор. 3: оптический изолятор. 4 WDM-ответвитель.

• 

  Волоконный лазер с кольцевым резонатором в виде восьмерки.

  In: излучение накачки. Out: выходное излучение. 1: активное волокно. 2: поляризатор. 3: оптический изолятор. 4 WDM-ответвитель. 50:50 делитель 50/50.

Исследования Фокса и Ли (1960-1961)

В основе работы оптического кольцевого резонатора такие же свойства, как и у шепчущей галереи, за исключением того, что он использует свет и подчиняется свойствам конструктивной интерференции и полного внутреннего отражения. Когда свет резонансной частоты проходит через контур от входного волновода, его интенсивность накапливается в течение нескольких циклов из-за конструктивной интерференции и выводится на выходной волновод. Так как в резонаторе распространяются лишь определенные резонансные длины волн, кольцо оптического резонатора действует как фильтр. Кроме того, два или более кольцевых резонатора могут быть соединены друг с другом, чтобы сформировать оптический фильтр.

Полное внутреннее отражение[править | править код]

Полное внутреннее отражение в блоке из органического стекла

Свет, распространяющийся в оптическом кольцевом резонаторе, остается внутри волновода из-за явления лучевой оптики, называющегося полное внутреннее отражение.

Полное внутреннее отражение — это оптическое явление, которое возникает, когда луч света попадает на границу среды под углом, превосходящим некоторый критический угол, и показатель преломления среды, в которой распространяется луч больше, чем показатель преломления среды по другую сторону границы.

Интерференция[править | править код]

Интерференция — это процесс, при котором несколько волн накладываются друг на друга, образуя результирующую волну большей или меньшей амплитуды. Интерференция относится к взаимодействию волн, которые коррелируют или когерентны друг с другом.

Свет в резонаторе многократно отражается от зеркал. Отраженные лучи интерферируют, что приводит к тому, что только определенные распределения полей на определенных частотах будут сохраняться в резонаторе, излучение на других частотах или с другим распределением будет подавлено за счет интерференции или быстро покинет резонатор. Распределения, которые повторяются при одном полном проходе резонатора являются наиболее стабильными и называются собственными модами или модами резонатора.

Если предположить, что в системе нет потерь на поглощение, излучательных потерь, и условие резонанса выполнено, то интенсивность света, выходящего из кольцевого резонатора, будет равна интенсивности света, подаваемого в систему.

Оптическая связь (линейных волноводов с кольцевым)[править | править код]

Оптическая связь между кольцевым резонатором и волноводом

Когда луч проходит через волновод, часть излучения будет связана с оптическим кольцевым резонатором. Причиной этого является явление переходящего поля, которая выходит за пределы волноводного режима в экспоненциально убывающем радиальном профиле. Другими словами, если кольцо и волновод сведены близко друг к другу, некоторый свет от волновода может перейти в кольцо.

На оптическую связь влияют расстояние между волноводом и оптическим резонатором, длина связи и показатели преломления волновода и резонатора. Чаще всего, чтобы улучшить оптическую связь, уменьшают расстояние между волноводом и кольцевым резонатором.

Разница оптических путей[править | править код]

Резонансная частота[править | править код]

Добротность[править | править код]

Добротность — параметр колебательной системы, определяющий ширину резонанса и характеризующий, во сколько раз запасы энергии в системе больше, чем потери энергии за один цикл колебаний.

Добротность резонатора представляет собой число колебаний поля до того, как циркулирующая энергия истощается до 1/e{\displaystyle 1/e} от первоначальной энергии. Чтобы определить добротность, микрорезонатор возбуждается до определенного уровня и рассматривается уровень разложения мощности. Важно отметить, что добротность может быть нагруженной и ненагруженной. Ненагруженная добротность имеет место, когда резонатор не связан с волноводами. При соединении с волноводом в резонатор вводятся дополнительные потери.

Радиус кривизны, оптическая длина резонатора[править | править код]

Собственные моды. Частота[править | править код]

Селекция мод[править | править код]

Устойчивость резонатора[править | править код]

Лазеры, лазерные гироскопы, датчик угловой скорости

• Звелто О. Принципы лазеров = Principles of Lasers. — 3-е изд. — М.: Мир, 1990. — 558 с. — ISBN 5-03-001053-Х.
• Agrawal G. P. Lightwave technology: components and devices. — Wiley-IEEE, 2004. — 427 p. — ISBN 9780471215738.
• Agrawal G. P. Applications of nonlinear fiber optics. — 2nd ed. — Academic Press, 2008. — Vol. 10. — 508 p. — (Optics and Photonis Series). — ISBN 9780123743022.

ЖИГ-резонатор — Википедия

Материал из Википедии — свободной энциклопедии

ЖИГ-резонатор, резонатор на железо-иттриевом гранате — резонатор СВЧ-диапазона на основе ферромагнитного резонанса в железо-иттриевом гранате (сокр. ЖИГ).

Смеситель на гармониках, перестраиваемый YIG-фильтром, со снятой крышкой и магнитной системой. 4-каскадный YIG фильтр хорошо виден в левой верхней части снимка.

ЖИГ-резонаторы имеют исключительно высокую добротность (2…3⋅10³), при этом способны перестраиваться по частоте в широком диапазоне (в некоторых конструкциях — больше декады, в большинстве практических конструкций — порядка октавы).

На основе ЖИГ-резонаторов строятся перестраиваемые генераторы и фильтры СВЧ-диапазона. ЖИГ-генераторы используются в качестве гетеродинов анализаторов спектра и генераторов стандартных сигналов, благодаря сочетанию способности к перестройке в широком диапазоне и малых фазовых шумов. Фильтры, построенные на основе ЖИГ-резонаторов, находят применение в качестве преселекторов высококачественных приемников СВЧ-диапазона, в составе широкополосных умножителей частоты.

Работа ЖИГ-резонаторов основана на явлении ферромагнитного резонанса (резонанса прецессионного движения спиновых моментов электронов) в монокристалах феррита — железо-иттриевого граната. От прочих ферритов, в которых также проявляются аналогичные резонансные явления, ЖИГ отличается малыми потерями различного происхождения, что и объясняет высокую добротность. Частота резонанса с высокой степенью линейности пропорциональна внешнему магнитному полю, что и позволяет осуществлять перестройку резонатора, и не зависит от размера образца, что позволяет сделать резонатор весьма малым.

Упрощённая схема цепи связи ЖИГ-резонатора с микрополосковой схемой Открытый ЖИГ фильтр

Из-за сильной зависимости резонанса от формы^[1], резонирующий элемент обычно оформляется в виде сферы (редко — диска) диаметром около 0,5 мм, с хорошо обработанной поверхностью. Для использования в качестве фильтра связь с резонатором осуществляется, как правило, двумя взаимно перпендикулярными индуктивными полупетлями, одна из которых соединяется с входом фильтра, другая — с выходом. Резонатор помещается между полупетлями, на держателе из материала с хорошей теплопроводностью. На нерезонансных частотах ЖИГ ведёт себя как диэлектрик и связь между линиями отсутствует в силу их перпендикулярности. На частотах, близких к резонансу возникают компоненты поля, обеспечивающие сильную связь входной и выходной цепей. В случае использования резонатора в составе генератора можно обойтись одной петлёй связи, что упрощает конструкцию.

На аналогичном принципе действует фильтр с резонатором в окне между перпендикулярными волноводами.

Резонатор с цепями связи помещается в магнитную систему, обеспечивающую подмагничивание. Как правило, система состоит из двух соленоидов (один для создания основного поля, другой, с меньшим числом витков, для обеспечения модуляции поля) и постоянного магнита (для уменьшения потребления тока основным соленоидом).

• Сазонов Дмитрий Михайлович. &6.10. Перестраиваемые ферритовые фильтры // Антенны и устройства СВЧ. — «Высшая школа», 1988. — С. 178—180. — 434 с. — 30 000 экз.
• Хелзайн Джозеф. Пассивные и активные цепи СВЧ = Passive and Active microwave circuits. — «Радио и связь», 1981. — С. 110—122. — 200 с. — 4500 экз.

Резонатор — Википедия

Материал из Википедии — свободной энциклопедии

Резона́тор — колебательная система, в которой происходит накопление энергии колебаний за счёт резонанса с вынуждающей силой. Обычно резонаторы обладают дискретным набором резонансных частот.

В технике обычно встречаются резонаторы с колебанием электромагнитных или механических величин. Конструкция резонатора сильно зависит от его резонансных частот.

Механические резонаторы

Механические резонаторы можно разделить на две условные группы:

• Резонатор накопительного действия.
• Резонатор мгновенного действия.

Резонатор накопительного действия

Отличительной чертой такого резонатора является накопление энергии внешнего воздействия за счет уменьшения частоты собственных колебаний. С математической точки зрения любой резонатор, частота колебаний которого строго больше частоты колебаний возмущающей силы, является накопительным. Классическим примером являются качели. Усиление выходной мощности происходит за счет сложения мощностей нескольких колебаний возмущающей силы.

Резонатор мгновенного действия

Под «мгновенным действием» подразумевается совершение одного периода колебания резонатора за время, не большее периода колебания возмущающей силы. Примером такого резонатора может служить резонатор Гельмгольца. Усиление в таких резонаторах может происходить за счет:

• смещения по времени мощности резонансной частоты на входе, то есть, плавно меняясь на входе резонатора, мощность может увеличиться на выходе за счет уменьшения длительности сигнала;
• поглощения энергии других (не резонансных) частот. Этот эффект используется певцами при практике резонансного пения;
• поглощения теплового движения окружающего пространства.

Резонаторы мгновенного действия могут иметь коэффициент усиления до 45 дБ (10 000 раз).

Электромагнитные резонаторы

В генераторах СВЧ^[1]-излучений (клистрон, магнетрон) резонаторы представляют собой металлическую конструкцию, используемую для генерации волн определённой длины.

См. также

Примечания

Литература

• Калинин В. А., Лобов Г. Д., Штыков В. В. Радиофизика для инженеров / Под ред. С.И.Баскакова. — М.: Изд-во МЭИ, 1994. — 130 с. — 500 экз.

Ссылки

Резонанс Гельмгольца — Википедия

Материал из Википедии — свободной энциклопедии

Резонанс Гельмгольца — явление резонанса воздуха в полости, примером которого является гудение пустой бутылки от потока воздуха направленного перпендикулярно её горлышку. Резонатор Гельмгольца — медный сосуд сферической формы с открытой горловиной, изобретённый Гельмгольцем около 1850 года для анализа акустических сигналов, на основе наблюдаемых в нём явлений Гельмгольцем и Рэлеем разработана количественная теория резонанса данного типа^[1].

Когда воздух нагнетается в полость, давление в полости возрастает. Когда внешняя сила, нагнетающая воздух в полость, исчезает, повышенное давление заставляет воздух вытекать обратно. Через некоторое время давление внутри и снаружи сравняется, но воздух всё равно продолжит выходить вовне, поскольку струя воздуха в горлышке обладает массой и ненулевой скоростью, а значит, и кинетической энергией. Через некоторое время воздух перестанет выходить из полости, и при этом давление внутри полости будет меньше давления снаружи. Воздух снова устремится в полость. Этот цикл будет повторяться множество раз, с затухающей амплитудой. Частота цикла (собственная, или резонансная частота) зависит от формы полости. Если внешняя сила будет возникать и исчезать с частотой, равной собственной частоте полости, возникнет резонанс — колебания воздуха не будут затухать.

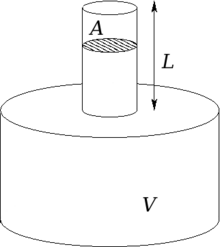Модель резонатора Гельмгольца

Может быть показано^[2] что собственная угловая частота колебаний равна

ωH=γA2mP0V0,{\displaystyle \omega _{\text{H}}={\sqrt {\gamma {\frac {A^{2}}{m}}{\frac {P_{0}}{V_{0}}}}},}

где γ{\displaystyle \gamma } — показатель адиабаты, значение которого обычно равно 1,4 для воздуха и двуатомных газов; A{\displaystyle A} — площадь сечения горлышка; m{\displaystyle m} — масса воздуха в горлышке; P0{\displaystyle P_{0}} — статическое давление в полости; V0{\displaystyle V_{0}} — статический объём полости.

Для цилиндрических горлышек

A=VnL,{\displaystyle A={\frac {V_{n}}{L}},}

где: L{\displaystyle L} — длина горлышка, Vn{\displaystyle V_{n}} — объём воздуха в горлышке, поэтому

ωH=γAmVnLP0V0.{\displaystyle \omega _{\text{H}}={\sqrt {\gamma {\frac {A}{m}}{\frac {V_{n}}{L}}{\frac {P_{0}}{V_{0}}}}}.}

По определению плотности:

Vnm=1ρ,{\displaystyle {\frac {V_{n}}{m}}={\frac {1}{\rho }},}

поэтому

ωH=γP0ρAV0L,{\displaystyle \omega _{\text{H}}={\sqrt {\gamma {\frac {P_{0}}{\rho }}{\frac {A}{V_{0}L}}}},}

и

fH=ωh3π,{\displaystyle f_{\text{H}}={\frac {\omega _{H}}{2\pi }},}

где fH{\displaystyle f_{H}} — резонансная частота.

Скорость звука в газах равна

v=γP0ρ,{\displaystyle v={\sqrt {\gamma {\frac {P_{0}}{\rho }}}},}

поэтому можно выразить резонансную частоту через неё:

fH=v2πAV0L.{\displaystyle f_{\text{H}}={\frac {v}{2\pi }}{\sqrt {\frac {A}{V_{0}L}}}.}

Длина горлышка появляется в знаменателе потому, что инерция воздуха в горлышке пропорциональна массе воздуха в горлышке, а значит, и длине. Объём появляется в знаменателе потому, что коэффициент сжимаемости воздуха в полости обратно пропорционален объёму. Площадь сечения горлышка влияет двояко — чем больше площадь, тем больше масса воздуха в горлышке, и тем меньше скорость, с которой воздух устремляется внутрь и вовне.

Эта формула имеет границы применимости, зависящие от формы горлышка и толщины стенок резонатора. Исходя из примерно такой же физической модели можно получить более точную формулу^[3]. Кроме этого, если скорость потока рядом с резонатором высока (более 0,3 числа Маха), необходимо вводить дополнительные поправки.

Резонанс Гельмгольца применяется в двигателях внутреннего сгорания и в акустических системах. Системы впрыска топлива, называемые системами Гельмгольца, использовались в двигателях Chrysler V10, которыми комплектовались автомобили Dodge Viper и пикапы Ram, а также в мотоциклах Buell. В струнных инструментах с полой декой, таких, как гитара или скрипка, один из пиков кривой резонанса — это резонанс Гельмгольца (остальные — это резонансные частоты деревянных частей инструмента). Окарина — резонатор с изменяемым сечением горлышка. Западноафриканский барабан джембе имеет относительно узкое горлышко, что придаёт ему глубокий басовый тон.

Теория резонанса Гельмгольца используется при проектировании выхлопных труб автомобилей и мотоциклов, с целью сделать звук двигателя более тихим или более красивым.

• Hermann von Helmholtz. On the sensations of tone as a physiological basis for the theory of music / Alexander John Ellis. — Longmans, Green, 1885. — 576 с.
• Колебания и волны. Лекции. В. А. Алешкевич, Л. Г. Деденко, В. А. Караваев (Физический факультет МГУ) Издательство Физического факультета МГУ, 2001 г.