Определение резонансной частоты подвески

Резонансные частоты определяются по АЧХ ускорения или перемещения, снятым при постоянном значении параметра возбуждения. При этом поддерживаемый постоянным параметр возбуждения устанавливается таким, чтобы ускорение и перемещение не превышали предельно допустимых значений, а для электромеханических вибростендов перемещение должно быть минимальным.

Резонансная частота подвески соответствует первому по частоте пику ускорения не менее чем в 1,5 раза превышающему ускорение на частоте 400 Гц для электродинамических вибростендов; на частоте, равной приблизительно fн, для электромеханических вибростендов и на частоте, равной приблизительно (fн * fв)1/2 — для других видов вибростендов.

Для измерения параметров АЧХ предназначены программы Снятие АЧХ лин. и Снятие АЧХ лог. (программы реализованы в SCADA ZETVIEW). На рисунке 1 показан внешний вид программы с уже снятой АЧХ поверяемого вибростенда.

Рисунок 1

Для снятия АЧХ вибростенда необходимо задать частотный диапазон, выходной уровень с генератора, который будет подаваться на вибростенд и тип сигнала: линейно-частотно модулированный с линейной (ЛинЧМ) или логарифмической (ЛогЧМ) разверткой по частоте. Программа позволяет снимать АЧХ по 8 контролируемым точкам одновременно. Отображение АЧХ может быть как в линейном, так и в логарифмическом масштабе.

В нашем случае использовался сигнал с линейной разверткой по частоте (ЛинЧМ-сигнал) от 20 Гц до 2,5 кГц. Благодаря удобным свойствам графического компонента Grid, используемого в программе снятия АЧХ, результаты измерения АЧХ можно записать в файл результатов, который имеет расширение DTU. Открыть файл с результатами можно с помощью программы

Просмотр результатов (см. рисунок 2).

Рисунок 2

Существует также и другой метод оценки резонансных частот не только виброустановок, но и различных конструкций, оснасток для крепления изделий на вибростенд и т.п. Данный метод основан на применении модального анализа для определения динамических характеристик конструкций на основе результатов измерений и анализа вынужденных механических колебаний. Для этого необходимо запустить программу Модальный анализ входящую в состав ZETLAB.

Для проведения модального анализа необходимо использовать ударный молоток (см. рисунок 3). Ударный молоток представляет собой конструкцию, очень похожую на обычный молоток, но только на конце ударной части прикреплен вибродатчик. Рукоять заканчивается кабелем и разъёмом для подключения к входным каналам анализаторов спектра.

Рисунок 3

Для получения ударного воздействия можно также воспользоваться программой Генератор ударных импульсов, которая позволяет воспроизводить на виброустановке импульсы синусоидальной, треугольной и прямоугольной формы с заданной длительностью и амплитудой.

На рисунке 4 показано главное окно программы Модальный анализ после воспроизведения удара при помощи программы Генератор ударных импульсов. Форма импульса показана на верхнем графике. На нижнем графике показана форма сигнала, полученного с контрольного вибродатчика, установленного на вибростоле. Синхронизация и остановка графиков по времени происходит автоматически, а порог срабатывания синхронизации настраивается по желанию пользователя.

Рисунок 4

При нажатии на кнопку Спектр

в программе Модальный анализ открывается дополнительное окно (рисунок 5), показывающее формы узкополосного спектра ударного импульса (верхний график) и сигнала с контрольного вибродатчика (нижний график). В правой части окна Спектр показаны рассчитанные значения добротностей — декрементов затухания. Чем больше декремент затухания, тем дольше остаточное явление в контролируемой точке от ударного воздействия. Данная величина будет полезна для конструкторских отделов, которые при разработке (доработке или модернизации) могут вносить изменения в конструкции для уменьшения низкочастотных или высокочастотных резонансов, их смещения за границу рабочего частотного диапазона.

Рисунок 5

Проведя визуальное и численное сравнение, можно убедиться, что «картинки» на рисунке 1 и нижний график на рисунке 5 совпадают, т.е. совпадают значения резонансных частот, полученных двумя способами: при использовании программы снятия АЧХ и программы Модальный анализ.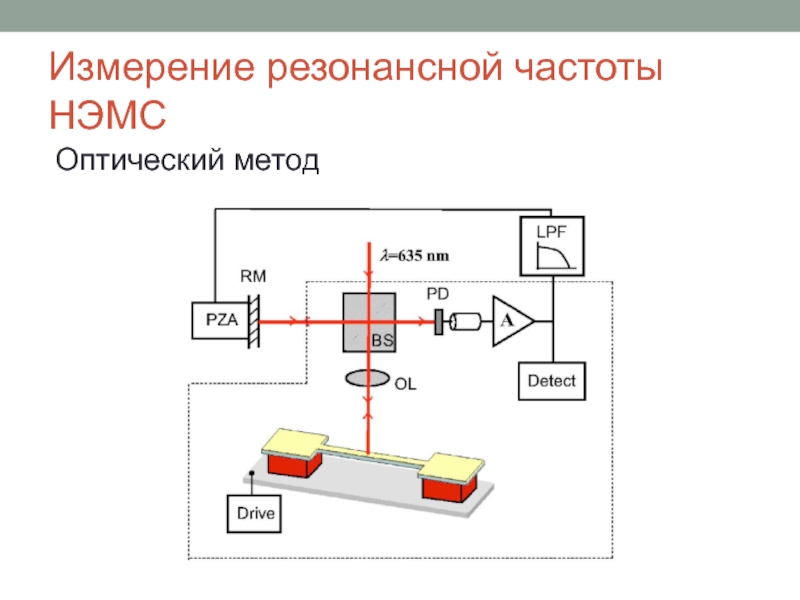 Это позволяет говорить о применимости двух методов и достоверности результатов при исследовании частотных характеристик вибростендов.

Как видно из рисунков 2 и 5 графики для различных методов оценки резонансных частот совпадают. Метод с использованием ударного молотка позволяет быстро измерять резонансные характеристики не только вибростендов, но и любых других конструкций. Всего один удар молотком — и картина готова — налицо рабочий частотный диапазон и резонансные частоты исследуемой конструкции.

См. также:

2.4.3 Методика расчета резонансных характеристик. Кривые подвода-отвода

В пункте 2.4.2 был приведен приближенный метод решения уравнения движения зонда в произвольном потенциале. Как было показано резонансные характеристики системы зонд-образец имеет следующий вид:

(1)

(2)

Однако уравнения (1,2) связывают амплитуду, фазу и частоту вынуждающей силы в неявной форме. Для того, чтобы облегчить расчет резонансных характеристик рассмотрим следующую методику.

Выразим в (1) обратную зависимость частоты вынуждающей силы от амплитуды колебаний. Проделывая не сложные выкладки, получим:

(3)

Выражение (3) описывает две ветви АЧХ системы, при этом знак «+» соответствует ветви , а знак «-» – ветви . Здесь введено новое обозначение . Но теперь, несмотря на наличие двух ветвей вместо одной, зависимость частоты от амплитуды колебаний имеет явную форму. Далее, используя выражение (2), получим полные резонансные характеристики системы:

      

(4)

      

(5)

где амплитуда колебаний выступает как параметр, который пробегает значения в интервале .

Обе ветви сшиваются в точке с максимальной амплитудой колебаний (резонанс) . Данному значению амплитуды колебаний соответствует частота вынуждающей силы . Таким образом, резонансная частота системы при расстоянии зонд-образец равном .

Теперь можно записать, как изменяется резонансная частота системы при изменении расстояния зонд образец. Вспоминая значение вспомогательной функции (см. (9)

пункта 2.4.2), получим для относительного сдвига резонансной частоты:

(6)

Таким образом, зависимость изменения резонансной частоты колебаний кантилевера при отводе его от образца содержит информацию о виде потенциала взаимодействия.

Если же амплитуда колебаний мала, т.е. , то выражение (6) можно переписать в виде:

(7)

где введено обозначение сила взаимодействия между зондом и образцом. Вспоминая теорию малых колебаний кантилевера в поле силы , сдвиг резонансной частоты в том случае в точности совпадает с выражением (7).

Для нахождения зависимости изменения амплитуды колебаний при отводе зонда от образца будем считать, что кантилевер возбуждается на частоте равной его собственной резонансной частоте при отсутствии взаимодействия зонд-образец, т.е. и, соответственно, . Исходя из вида АЧХ системы, легко получить, что в этом случае для амплитуды колебаний должно выполняться:

(8)

Выражение (8) можно записать в виде , которое задает вид зависимости амплитуды колебаний от расстояния зонд-образец. При этом в некоторых случаях (в зависимости от вида потенциала взаимодействия и расстояния зонд-образец) решение (8) неоднозначно, что соответствует случаю одновременного существования нескольких режимов колебаний с различной амплитудой и, соответственно, фазой, т.к. из (2) фаза колебаний является однозначной функцией от амплитуды.

Рассмотрим, что произойдет в случае малости колебаний. Как уже было показано в случае со сдвигом резонансной частоты колебаний, в этом случае выполняется:

(9)

Подставляя (9) в выражение (8), получим

(10)

Если вертикальный градиент силы взаимодействия зонд-образец мал (сила слабо меняется на амплитуде колебаний), то относительное изменение амплитуды можно выразить в виде:

(11)

Сравнив полученное выражение с изменением амплитуды, вычисленным в теории малых колебаний, легко убедиться, что обе теории дают полностью идентичные ответы.

Теперь рассмотрим сдвиг фазы колебаний, которые происходит при отводе зонда от поверхности образца. Как и в случае с амплитудой будет считать, что . С учетом (2) получим

(12)

Используя условие малости колебаний (9) выражение (12) преобразуется к виду:

(13)

который опять в точности соответствует выведенному в теории малых колебаний.

---

Выводы.

• Предложен метод расчета резонасных характеристик системы зонд-образец при произвольной амплитуде вынуждающей силы. Он позволяет в явной форме вычислить частоту и фазу колебаний, соответствующие определенной амплитуде колебаний. При этом отпадает необходимость решать неявную нелинейную систему уравнений (1, 2).
• Из вида резонансных характеристик системы выведены зависимости амплитуды, резонасной частоты и фазы колебаний при подводе-отводе зонда от образца.
• Показано, что в пределе малых амплитуд , теория возмущений дает результаты полностью идентичные полученным в теории малых колебаний кантилевера.

РЕЗОНАНС • Большая российская энциклопедия

• В книжной версии

  Том 28. Москва, 2015, стр. 336-337

• Скопировать библиографическую ссылку:

  ---

Авторы: В. В. Клиньшов, В. И. Некоркин

РЕЗОНА́НС (франц. resonance, от лат. resono – от­кли­кать­ся), из­би­ра­тель­ный от­клик ко­ле­бат. сис­те­мы на внеш­нее пе­рио­дич. воз­дей­ст­вие оп­ре­де­лён­ной час­то­ты. Яв­ле­ние Р. про­ис­хо­дит при при­бли­же­нии час­то­ты внеш­не­го воз­дей­ст­вия ω к час­то­те собств. ко­ле­ба­ний сис­те­мы ω₀ и за­клю­ча­ет­ся в рез­ком воз­рас­та­нии ам­пли­ту­ды её вы­ну­ж­ден­ных ко­ле­ба­ний. В этом слу­чае час­то­та воз­дей­ст­вия на­зы­ва­ет­ся ре­зо­нанс­ной (ω_р). Её ве­ли­чи­на оп­ре­де­ля­ет­ся свой­ст­ва­ми ко­ле­бат. сис­те­мы. Впер­вые Р. опи­сан Г. Га­ли­ле­ем для ме­ха­нич. сис­тем. От Р. при внеш­нем воз­дей­ст­вии сле­ду­ет от­ли­чать па­ра­мет­ри­че­ский ре­зо­нанс, воз­ни­каю­щий при пе­рио­дич. из­ме­не­нии па­ра­мет­ров ко­ле­бат. сис­те­мы.

Суть эф­фек­та Р. мож­но по­нять на при­ме­ре рас­ка­чи­ва­ния ка­че­лей пу­тём их пе­рио­дич. под­тал­ки­ва­ния. Для эф­фек­тив­но­го рас­ка­чи­ва­ния ка­че­лей час­то­та внеш­не­го под­тал­ки­ва­ния долж­на сов­па­дать с час­то­той их собств. ко­ле­ба­ний. В этом слу­чае ка­ж­дый тол­чок про­ис­хо­дит в од­ной и той же фа­зе дви­же­ния ка­че­лей, спо­соб­ст­вуя уве­ли­че­нию раз­ма­ха ко­ле­ба­ний. При не­пра­виль­но вы­бран­ной час­то­те под­тал­ки­ва­ния толч­ки про­ис­хо­дят в раз­ных фа­зах дви­же­ния, то ус­ко­ряя, то за­мед­ляя ка­че­ли, и су­ще­ст­вен­ной рас­кач­ки ко­ле­ба­ний не про­ис­хо­дит.

Рис. 1. Резонансная кривая линейной системы.

Осн. свой­ст­ва Р. мож­но на­блю­дать при воз­дей­ст­вии внеш­не­го гар­мо­нич.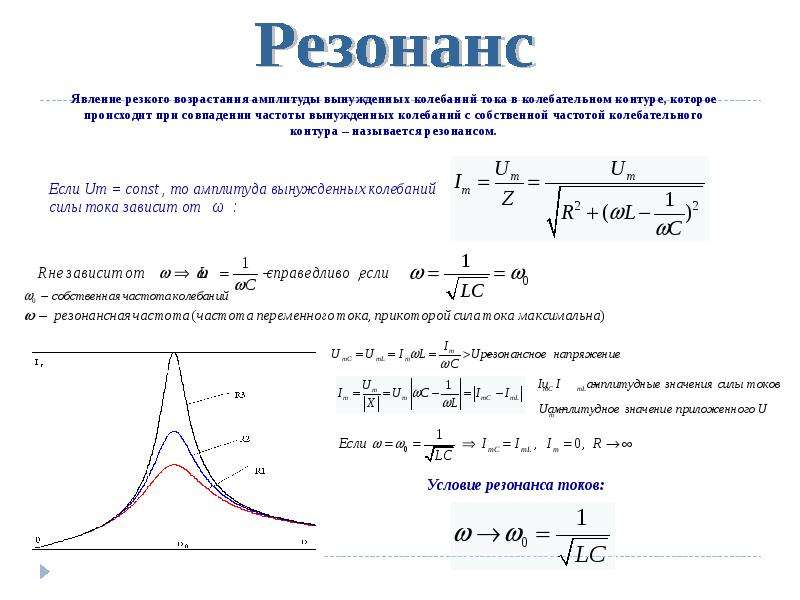 сиг­на­ла на ли­ней­ную сис­те­му с од­ной сте­пе­нью сво­бо­ды, та­кую как ко­ле­бат. кон­тур или ма­те­ма­тич. ма­ят­ник. За­ви­си­мость ам­пли­ту­ды A вы­ну­ж­ден­ных ко­ле­ба­ний та­кой сис­те­мы от час­то­ты внеш­не­го сиг­на­ла ω (ре­зо­нанс­ная кри­вая) име­ет чёт­ко вы­ра­жен­ный мак­си­мум на ре­зо­нанс­ной час­то­те ω_р (рис. 1). Для опи­са­ния ре­зо­нанс­ных свойств ли­ней­ной ко­ле­бат. сис­те­мы час­то ис­поль­зу­ют по­ня­тие доб­рот­но­сти, ха­рак­те­ри­зую­щее сте­пень за­ту­ха­ния ко­ле­ба­ний в сис­те­ме. Ве­ли­чи­на доб­рот­но­сти оп­ре­де­ля­ет фор­му ре­зо­нанс­ной кри­вой: чем боль­ше доб­рот­ность, тем мень­ше ши­ри­на пи­ка ре­зо­нанс­ной кри­вой, т. е. тем бо­лее из­би­ра­тель­ной яв­ля­ет­ся ко­ле­бат. сис­те­ма. С рос­том доб­рот­но­сти уве­ли­чи­ва­ет­ся вы­со­та пи­ка и умень­ша­ет­ся раз­ни­ца ме­ж­ду ре­зо­нанс­ной и собств. час­то­та­ми.

Рис. 2. Резонансная кривая нелинейной системы.

В не­ли­ней­ных сис­те­мах Р.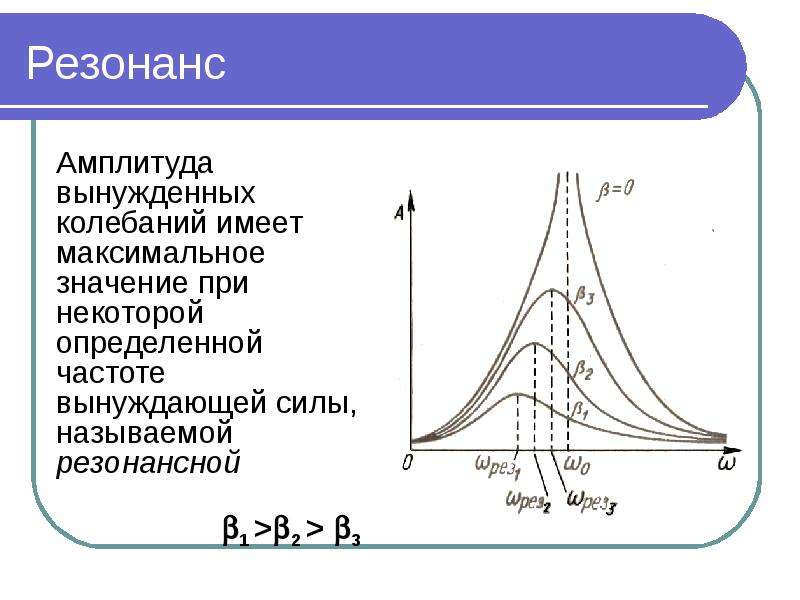 име­ет су­ще­ст­вен­ные осо­бен­но­сти по срав­не­нию с ли­ней­ны­ми. Во-пер­вых, ре­зо­нанс­ная час­то­та не­ли­ней­ной сис­те­мы за­ви­сит от ам­пли­ту­ды внеш­не­го воз­дей­ст­вия. Во-вто­рых, при дос­та­точ­но силь­ных воз­дей­ст­ви­ях ис­че­за­ет од­но­знач­ное со­от­вет­ст­вие ам­пли­ту­ды вы­ну­ж­ден­ных ко­ле­ба­ний па­ра­мет­рам внеш­не­го сиг­на­ла. При од­ной и той же час­то­те внеш­ней си­лы воз­мож­ны ре­жи­мы ко­ле­ба­ний с разл. ам­пли­ту­да­ми (рис. 2). Штри­хо­вой кри­вой на ри­сун­ке по­ка­за­на ветвь, со­от­вет­ст­вую­щая не­ус­той­чи­во­му ре­жи­му ко­ле­ба­ний. Пе­ре­клю­че­ние ме­ж­ду разл. ре­жи­ма­ми при пе­ре­строй­ке час­то­ты про­ис­хо­дит в ви­де скач­ков ам­пли­ту­ды и име­ет гис­те­ре­зис­ный ха­рак­тер.

Для ли­ней­ных сис­тем с не­сколь­ки­ми сте­пе­ня­ми сво­бо­ды и для рас­пре­де­лён­ных сис­тем, в ко­то­рых собств. ко­ле­ба­ния мо­гут про­ис­хо­дить на раз­ных час­то­тах, Р. на­блю­да­ет­ся при при­бли­же­нии час­то­ты внеш­не­го сиг­на­ла к од­ной из этих час­тот. В этом слу­чае ре­зо­нанс­ная кри­вая ха­рак­те­ри­зу­ет­ся на­ли­чи­ем не­сколь­ких мак­си­му­мов, и внеш­нее воз­дей­ст­вие рас­пре­де­ля­ет­ся по отд. ко­ор­ди­на­там сис­те­мы.

Р. иг­ра­ет важ­ную роль в при­ро­де, нау­ке и тех­ни­ке. В не­ко­то­рых слу­ча­ях он яв­ля­ет­ся не­же­ла­тель­ным, т. к. при­во­дит к не­га­тив­ным по­след­ст­ви­ям. Напр., при сов­па­де­нии час­то­ты на­бе­гаю­щих на ко­рабль волн с собств. час­то­той ки­ле­вой кач­ки воз­ни­ка­ет рез­кое уве­ли­че­ние ам­п­ли­ту­ды ко­ле­ба­ний ко­раб­ля, при ко­то­рых его нос «за­ры­ва­ет­ся» в вол­ну. Р. мо­жет вы­зы­вать силь­ные ко­ле­ба­ния и по­сле­дую­щие раз­ру­ше­ния при ра­бо­те виб­ри­рую­щих стан­ков, ма­шин, дви­га­те­лей внутр. сго­ра­ния. Из­вест­ны слу­чаи раз­ру­ше­ния мос­тов под дей­ст­ви­ем рит­мич. толч­ков от про­хо­дя­щих по ним войск. С др. сто­ро­ны, на яв­ле­нии Р. ос­но­ва­на ра­бо­та мн. при­бо­ров и уст­ройств. Напр., на­строй­ка час­то­ты ко­ле­бат. кон­ту­ра ра­дио­при­ём­ни­ка на час­то­ту элек­тро­маг­нит­но­го сиг­на­ла по­зво­ля­ет осу­ще­ст­в­лять его при­ём.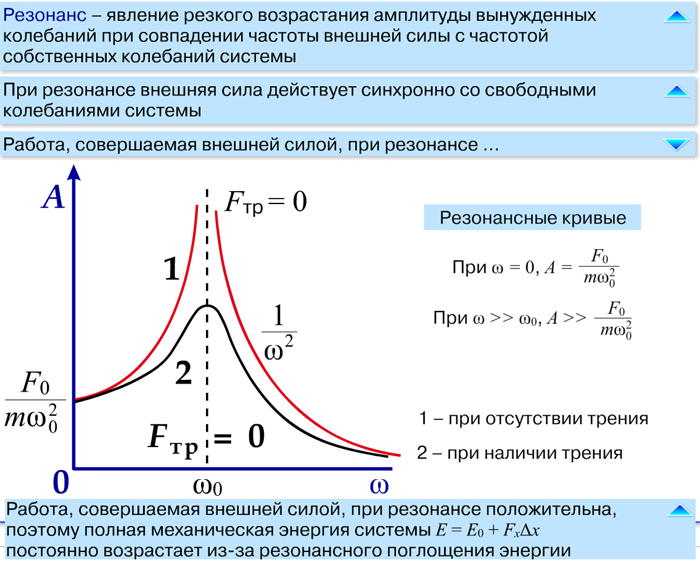 Яв­ле­ние Р. ле­жит в ос­но­ве прин­ци­па дей­ст­вия СВЧ элек­трон­ных при­бо­ров, напр. клис­тро­нов, ис­поль­зую­щих вы­со­ко­доб­рот­ные объ­ём­ные ре­зо­на­то­ры для уси­ле­ния СВЧ-сиг­на­лов.

РЕЗОНАНСНЫЕ КОЛЕБАНИЯ С ПРЕДЕЛЬНОЙ АМПЛИТУДОЙ В ВИБРАЦИОНОМ ЭЛЕКТРОМАГНИТНОМ АКТИВАТОРЕ

Актуальность исследования обусловлена тем, что вибрационные электромагнитные активаторы являются перспективными для применения в различных технологиях, связанных с добычей и транспортировкой георесурсов, в том числе при приготовлении буровых растворов и разжижении вязких нефтепродуктов. Вибрационный электромагнитный активатор представляет собой электрическую машину возвратно-поступательного движения с якорем-активатором, образующим в жидкой обрабатываемой среде турбулентные затопленные струи. В первом попупериоде якорь-активатор притягивается к стенке за счет импульса тока в катушках, при этом в упругой пружине накапливается потенциальная энергия. Этот режим является режимом вынужденных колебаний в механической системе вибрационного электромагнитного активатора. Во втором полупериоде ток в катушках отсутствует, а якорь-активатор отталкивается от стенок за счет энергии пружины – это режим свободных колебаний в механической системе. С точки зрения улучшения энергоэффективности следует настраивать вибрационный электромагнитный активатор на резонансную частоту. Резонансная частота не является постоянной и зависит от свойств обрабатываемой жидкости. Форма вынуждающей колебания силы должна быть такой, чтобы обеспечивать колебания в механической системе на резонансной частоте с предельной амплитудой, что обеспечит повышение энергоэффективности и производительности вибрационного электромагнитного активатора. Цель: провести аналитические исследования, позволяющие обеспечивать резонансные колебания с предельной амплитудой в вибрационном электромагнитном активаторе. Методы исследования основаны на использовании обыкновенных дифференциальных уравнений, преобразования Лапласа, амплитудно-частотных характеристик, систем нелинейных алгебраических уравнений, спектрального анализа, сопоставления аналитических и экспериментальных характеристик.  Результаты. На основе линеаризованной математической модели механической системы вибрационного электромагнитного активатора рассмотрен режим свободных колебаний якоря-активатора с предельной амплитудой. Режим вынужденных колебаний предлагается рассматривать как естественное дополнение к режиму свободных колебаний с вынуждающей силой, действующей половину периода и имеющей специальную форму. Показано, что режимы свободных и вынужденных колебаний существенно зависят от параметров механической системы, которые определяются свойствами обрабатываемой жидкой среды. Проведен спектральный анализ вынуждающей силы, обеспечивающей резонансные колебания с предельной амплитудой в механической системе вибрационного электромагнитного активатора. Предложено техническое решение, обеспечивающее управление вибрационным электромагнитным активатором с автоматической настройкой на резонансную частоту и предельную амплитуду колебаний якоря-активатора. Такой режим обеспечивает максимизацию энергоэффективности и производительности процессов перемешивания жидких обрабатываемых сред. На основе сопоставления аналитических и экспериментальных частотных характеристик подтверждена гипотеза о допустимости линеаризации математической модели механической системы вибрационного электромагнитного активатора при аналитическом исследовании вынуждающей силы оптимальной формы.

Ключевые слова:

Буровой раствор, высоковязкий нефтепродукт, вибрационный электромагнитный активатор, резонанс, вынуждающая колебания сила, свободные колебания, вынужденные колебания, спектральный анализ, настройка на резонансную частоту, оценка погрешности

Резонанс — друг и враг

Резонанс — это явление резкого возрастания амплитуды вынужденных колебаний системы, которое наступает при приближении частоты внешнего воздействия к определенным значениям (резонансных частот), обусловленным свойствами системы. Таким образом, причиной резонанса является совпадение внешней (возбуждающей) частоты с внутренней (собственной) частотой колебательной системы.

Резонанс встречается в механике, электронике, оптике, акустике, астрофизике.

Явление резонанса лежит в основе проектирования музыкальных инструментов: рояля, скрипки, флейты …

Используется явление резонанса и в электронике. Колебательный контур, состоящий из емкости и индуктивности, используется в элементах настройки и электрических фильтрах. Однако резонанс может быть и вредным, если он вызывает искажение сигнала или паразитные шумы.

Наблюдается резонанс и в космосе, когда два небесных тела, которые имеют периоды обращения, относящихся друг с другом как небольшие целые числа, делают регулярное гравитационное воздействие друг на друга, которое может стабилизировать их орбиты (орбитальный резонанс в небесной механике).

Однако наиболее часто резонанс бывает в классической и строительной механике, а также гидро- и аэромеханике. И, к ​​сожалению, во многих случаях именно тогда, когда он совершенно нежелателен.

… Известно, что военным подразделениям при прохождении мостов приписывается «сбивать ногу» и идти не строевым, а свободным шагом. Горький опыт некоторых катастроф научил военнослужащих в подобных ситуациях отходить от многовековых традиций.

Так, 12 апреля 1831 разрушился Бротонский подвесной мост через реку Ирвелл в Англии, когда по нему шел военный отряд. Частота шагов воинов, шагавших в ногу, совпала с частотой собственных колебаний моста, через которые амплитуда резко возросла, цепи оборвались, и мост рухнул в реку. Именно этот случай, в результате которого два десятка человек были травмированы, способствовал принятию в британской армии правила «идти не в ногу» при прохождении войсками мостов. По той же причине в 1850 году неподалеку от французского города Анже был разрушен подвесной цепной мост над рекой Мин длиной более ста метров, что привело к многочисленным жертвам. Также существует версия, что 1905 году в результате прохождения кавалерийского эскадрона через резонанс разрушился и Египетский мост через реку Фонтанку в Петербурге. Однако эта версия, скорее всего, безосновательна, поскольку не существует методов дрессировки значительного количества лошадей для их движения «в ногу».

Причиной разрушения мостов из-за резонанса могут стать не только пешеходы, но и железнодорожные поезда. Для исключения резонанса моста поезд может двигаться или медленно, или на максимальной скорости (вспомните, как замедляют ход поезда метрополитена во время их движения через мост Метро в Киеве). Это обычно делается для исключения совпадения частоты ударов колес по стыкам рельсов с собственной частотой колебаний моста (по этой же причине участок рельсов на мосту часто выполняют сплошной, т.е. без стыков).

Катастрофические последствия для мостов могут послужить также и от воздействия ветра. Так, 7 ноября 1940 через игнорирование действия ветровой нагрузки на мост при его проектировании и вследствие возникновения резонанса разрушился Такомский подвесной мост общей длиной 1800 м и длиной центрального пролета 850 м (США).

С резонансом можно столкнуться не только на суше, но и на море и в воздухе. Так, при некоторых частотах вращения гребного вала в резонанс входили даже корабли. А на заре развития авиации некоторые авиационные двигатели вызывали столь сильные резонансные колебания элементов самолета, что он полностью разрушался в воздухе.

Причиной резонанса элементов летательных аппаратов и их разрушение может стать и флаттер — сочетание самовозбуждающиеся незатухающих изгибающих и крутильных автоколебаний элементов конструкции (главным образом крыла самолета или несущего винта вертолета). Одним из путей борьбы с этим явлением является использование так называемых протифлатерных грузов.

Интересно, что крепления двигателей на пилонах крыльев самолетов — это не прихоть конструкторов и дизайнеров, а насущная необходимость, поскольку двигатели демпфирующие колебания крыла в полете воздушного судна, будучи при этом своеобразным протифлатерним грузом.

Также известны случаи, когда во время выступлений знаменитого русского певца Федора Ивановича Шаляпина часто лопались плафоны в люстрах. И происходило это опять же через резонанс, когда частота собственных колебаний стекла совпадала с частотой акустических волн, воспроизводимых певцом.

Еще более интересным фактом является то, что во время Великой Отечественной войны все тот же резонанс едва не поставил под угрозу существование единой ниточки, проходившей по льду Ладожского озера и связывала блокадный Ленинград с «большой землей».

… Во время наведения участка Дороги жизни по Ладожскому озеру защитники Ленинграда неожиданно столкнулись с необычным явлением, когда после нормального прохождения по льду тяжелого грузовика, легкая машина, которая шла по тому же пути, нередко проваливалась под лед.

Перед учеными была поставлена ​​задача срочно разобраться с ситуацией, сложившейся и предоставить рекомендации по преодоления автомобилями ледяного покрова. В южной части Ладожского озера, под артиллерийским и минометным огнем врага гидрограф и гидротехники проводили эксперименты по определению предельных нагрузок на лед. Все выводы ученых поступали в Ледовую службу Морской обсерватории. Было изучено деформационную устойчивость льда под статической нагрузкой и данные про упругие деформации льда при распространении по льду взрывной волны. При проведении автоколонн по Ладоге наблюдались и неизвестные ранее колебания ледяного покрова: водяной волна, образовавшаяся под льдом проседала, двигалась с постоянной для определенной толщины льда и глубины водоема скоростью. Она могла опережать приложенную нагрузку или отставать от нее, но опасным было совпадения этих скоростей — тогда вода прекращала поддержку ледяного покрова, и поддержка обеспечивалась только упругими свойствами льда. При этом наступал резонанс, что приводило к разрушению льда. Это проявление резонанса было названо изгибно-гравитационной волной.

По результатам исследований для автомобилей, которые двигались по льду, были установлены определенные скорости и дистанции. Ежедневно по ледяному покрову в обе стороны перевозилось около 6 тыс. Тонн грузов, а общее количество доставленных в Ленинград по Дороге жизни грузов за весь период ее существования составила более 1 млн 615 тыс. Тонн. Также за это же время с осажденного города было эвакуировано около 1 млн 376 тыс. Его жителей.

С учетом приобретенного опыта позже был разработан резонансный метод разрушения льда, энергоемкость которого в несколько раз меньше энергоемкости традиционного разрушения ледяного покрова с помощью ледоколов и ледокольного навесного оборудования.

Как видим, резонанс может быть достаточно коварным, но укротить его и вернуть на пользу человеку вполне по силам!

Резонанс шагового двигателя — статья

Шаговым двигателям свойственен нежелательный эффект, называемый резонансом. Эффект проявляется в виде внезапного падения момента на некоторых скоростях. Это может привести к пропуску шагов и потере синхронности. Эффект проявляется в том случае, если частота шагов совпадает с собственной резонансной частотой ротора двигателя.

Когда двигатель совершает шаг, ротор не сразу устанавливается в новую позицию, а совершает затухающие колебания. Дело в том, что систему ротор – магнитное поле – статор можно рассматривать как пружинный маятник, частота колебаний которого зависит от момента инерции ротора (плюс нагрузки) и величины магнитного поля. Ввиду сложной конфигурации магнитного поля, резонансная частота ротора зависит от амплитуды колебаний. При уменьшении амплитуды частота растет, приближаясь к малоамплитудной частоте, которая более просто вычисляется количественно. Эта частота зависит от угла шага и от отношения момента удержания к моменту инерции ротора. Больший момент удержания и меньший момент инерции приводят к увеличению резонансной частоты.

Резонансная частота вычисляется по формуле:

F₀ = (N*T_H/(J_R+J_L))^0.5/4*pi,

где F₀ – резонансная частота,
N – число полных шагов на оборот,
T_H – момент удержания для используемого способа управления и тока фаз,
J_R – момент инерции ротора,
J_L – момент инерции нагрузки.

Необходимо заметить, что резонансную частоту определяет момент инерции собственно ротора двигателя плюс момент инерции нагрузки, подключенной к валу двигателя. Поэтому резонансная частота ротора ненагруженного двигателя, которая иногда приводится среди параметров, имеет маленькую практическую ценность, так как любая нагрузка, подсоединенная к двигателю, изменит эту частоту.

На практике эффект резонанса приводит к трудностям при работе на частоте, близкой к резонансной. Момент на частоте резонанса равен нулю и без принятия специальных мер шаговый двигатель не может при разгоне пройти резонансную частоту. В любом случае, явление резонанса способно существенно ухудшить точностные характеристики привода.

В системах с низким демпфированием существует опасность потери шагов или повышения шума, когда двигатель работает вблизи резонансной частоты. В некоторых случаях проблемы могут возникать и на гармониках частоты основного резонанса.

Когда используется не микрошаговый режим, основной причиной появления колебаний является прерывистое вращение ротора. При осуществлении шага ротору толчком сообщается некоторая энергия. Этот толчок возбуждает колебания. Энергия, которая сообщается ротору в полушаговом режиме, составляет около 30% от энергии полного шага. Поэтому в полушаговом режиме амплитуда колебаний существенно меньше. В микрошаговом режиме с шагом 1/32 основного при каждом микрошаге сообщается всего около 0.1% от энергии полного шага. Поэтому в микрошаговом режиме явление резонанса практически незаметно.

Для борьбы с резонансом можно использовать различные методы. Например, применение эластичных материалов при выполнении механических муфт связи с нагрузкой. Эластичный материал способствует поглощению энергии в резонансной системе, что приводит к затуханию паразитных колебаний. Другим способом является применение вязкого трения. Выпускаются специальные демпферы, где внутри полого цилиндра, заполненного вяДля борьбы с резонансом можно использовать различные методы. Например, применение эластичных материалов при выполнении механических муфт связи с нагрузкой. Эластичный материал способствует поглощению энергии в резонансной системе, что приводит к затуханию паразитных колебаний. Другим способом является применение вязкого трения. Выпускаются специальные демпферы, где внутри полого цилиндра, заполненного вязкой кремнийорганической смазкой, может вращаться металлический диск. При вращении этой системы с ускорением диск испытывает вязкое трение, что эффективно демпфирует систему.

Существуют электрические методы борьбы с резонансом. Колеблющийся ротор приводит к возникновению в обмотках статора ЭДС. Если закоротить обмотки, которые на данном шаге не используются, это приведет к демпфированию резонанса.

И, наконец, существуют методы борьбы с резонансом на уровне алгоритма работы драйвера. Например, можно использовать тот факт, что при работе с двумя включенными фазами резонансная частота примерно на 20% выше, чем с одной включенной фазой. Если резонансная частота точно известна, то ее можно проходить, меняя режим работы.

Если это возможно, при старте и остановке нужно использовать частоты выше резонансной. Увеличение момента инерции системы ротор-нагрузка уменьшает резонансную частоту.

Самой эффективной мерой для борьбы с резонансом является применение микрошагового режима.

последствия игнорирования резонансных колебаний оснастки

23 Октября 2019

Питер Авитабиле (Peter Avitabile), журнал «Sound and vibration»
Под ред. специалиста отдела проектов ИО Валентина Дубенского
[email protected]
Перевод: Артем Вахитов

Периодически в оснастке вибростендов возникают резонансные колебания, частота которых лежит в диапазоне, необходимом для проведения вибрационных испытаний. Такие резонансные частоты могут вызвать значительные проблемы во время проведения вибрационных тестов, особенно в диапазонах, которые могут включать данные резонансные частоты. Для контроля уровня входных вибраций на тестовом образце инженеры-испытатели используют акселерометры с обратной связью. Однако акселерометр может только контролировать уровень вибраций, но не способен изменить резонансное поведение оснастки. В статье описаны некоторые проблемы, а также рассмотрены основные причины возникновения подобного явления.

Очень часто вибрационные испытания проводятся для подтверждения допустимости применения определенных устройств и изделий в некоторых средах. Вибростенды используются в качестве генераторов усилий или ускорений с целью воспроизводства известных рабочих условий или источников входных сигналов широкого спектра для имитации реальной эксплуатации.

Сопряжение между вибростендом и тестируемым изделием — это оснастка вибростенда. В статье мы будем рассматривать оснастку как элемент, который включает арматуру вибростенда, расширительный стол (или стол скольжения), а также крепежное приспособление (например, для размещения тестируемого изделия). Поэтому, когда мы говорим «оснастка», то имеем в виду все, что находится между приводом вибростенда и тестируемым образцом (то, что мы не видим арматуру, не означает, будто она не является составляющей всей системы). На рис. 1 схематически показана конструкция оснастки.

Рис. 1. Обычные компоненты оснастки

Наша основная цель — сделать оснастку очень жесткой и при этом безынерционной. Это подразумевает, что оснастка не будет испытывать резонансных колебаний, лежащих в рабочем диапазоне частот, и поверхность, на которую установлено тестируемое изделие, двигается как жесткое тело и имеет однородное смещение на границе с тестируемым образцом. Для крупных вибростендов этого добиться очень сложно, если не невозможно. В таких системах все равно будут появляться некоторые резонансные колебания из-за массы и жесткости оснастки, расширительного стола (или стола скольжения) и крепежных устройств для установки тестируемого изделия. Очень часто инженеры игнорируют эту проблему и предполагают, что контроллер, устанавливаемый на вибростенд, может компенсировать данные эффекты.

К сожалению, контроллер лишь удерживает уровень ускорения в том месте, где установлен управляющий акселерометр, и не может снизить резонансные колебания в оснастке. Наличие систем управления с обратной связью никак не влияет на резонансные колебания. Все, что делают данные системы, — регулируют (уменьшают или увеличивают) входные усилия, подаваемые на катушку привода вибростенда, для удержания необходимого уровня ускорений. Обычно на вибростенд устанавливается несколько акселерометров в разных точках на оснастке, а подаваемые ими сигналы усредняются в один контрольный. И опять же, это позволяет только удерживать среднее значение контрольного параметра — ускорения. Резонансные частоты и динамические характеристики не меняются. Усреднение сигналов с нескольких точек — прекрасный метод для получения «лучше выглядящего» спектра, но это не влияет на проблему резонансных колебаний, связанных с оснасткой.

Управляющий акселерометр должен устанавливаться на поверхности, которая двигается как жесткое тело без резонансных колебаний в требуемом диапазоне частот. Это то, что контроллер ожидает увидеть в качестве обратной связи. Если поверхность упругая, обратная связь от управляющего акселерометра в большой степени зависит от места, где он установлен.

Использование нескольких управляющих акселерометров, данные от которых усредняются, подразумевает, что будет контролироваться лишь некое среднее значение ускорения. Правильное применение нескольких акселерометров на упругой поверхности возможно только, если каждый акселерометр будет давать независимый ответ для отдельного вибростенда, которым он управляет. Конечно, это очень сложно практически воплотить, поскольку в таком случае понадобится несколько вибростендов и контроллеров типа MIMO (Multi-Input Multi-Output — многоканальные контроллеры входа/выхода).

Подобная ситуация может смутить многих инженеров-испытателей, так как они убеждены, что управляющие акселерометры — это все, на чем им нужно акцентировать свое внимание при проведении вибрационных испытаний. Но это ошибочное мнение.

Для того чтобы понять суть возникающих проблем, необходимо рассмотреть некоторые основные концепции теории вибраций, а также привести примеры и проиллюстрировать их. Динамическое взаимодействие между тестируемым изделием и оснасткой при переходе от собранных данных к лабораторным испытаниям уже неоднократно изучалось специалистами отрасли. Результаты исследований изложены в литературе, список которой представлен в конце этой статьи.

При опубликовании нашей концепции многие говорили: «это только научная теория», «это на самом деле не происходит», «убедитесь, что то, что должно быть описано, происходит на самом деле».

Что ж, давайте рассмотрим явление, а затем сделаем рациональные инженерные предположения и предложим решения, как лучше всего справиться с ситуацией.

Действительность заключается в том, что в некоторых случаях невозможно получить оснастку без резонансных колебаний. Однако инженерам-испытателям очень важно понимать и отслеживать динамику всей системы, чтобы проводить осмысленные вибрационные испытания. Например, если резонанс возник, то понимание типов и формы колебаний поможет или модифицировать конструкцию, поднимая частоту резонансных колебаний выше диапазона частот теста, или устанавливать тестируемое изделие так, чтобы минимизировать влияние этих нежелательных резонансных колебаний.

Теперь, иллюстрируя примерами, можно обсудить причины, почему это происходит (в следующем разделе читателя ждет информация не для слабонервных — возможно, вам не понравится изложенное).

Рис. 2. Система с одной степенью свободы (SDoF)

Основные теоретические выкладки

Демонстрируемые здесь формулы можно найти в любом учебнике по вибрациям (большинство формул взято из литературы [2]). Первое основное выражение приведем для систем с одной степенью свободы (SDoF) (рис. 2). Формула движения для таких систем выглядит следующимобразом:

Выражение, которое описывает систему SDoF с появлением синусоидального возбуждения, задается как:

Данное выражение записывается как соотношение динамического смещения к статическому смещению. Здесь ω — возбуждаемая синусоидальная частота, ωn — собственная частота, а ς — это критическое затухание, выраженное в процентах. Величина данного соотношения сначала увеличивается, а затем уменьшается после того, как мы проходим собственную частоту системы (рис. 3).

Рис. 3. Усиление системы с одной степенью свободы с помощью добавления синусоидального возбуждения

Теперь рассмотрим систему с двумя и более массами, соединенными между собой безынерционными пружинами, с несколькими степенями свободы (MDoF). Это следующий уровень аппроксимации. Для описания движения такой системы существует несколько выражений, так как в движении участвует большее количество масс, поэтому будем использовать матричную запись. Сначала рассмотрим системы с двумя степенями свободы, а затем обобщим на несколько систем DoF.

Рис. 4. Системы с несколькими (двумя) степенями свободы

Для системы с двумя массами (рис. 4) выражение, описывающее движение, выглядит следующим образом:

или в матричной форме:

или:

Используя такую форму представления, можно описать движение для систем с любым количеством масс. Теперь в данной форме выражение показывает связь между различными системами DoF. Мы используем математический метод, который называется «собственное решение», для того чтобы разбить эти более сложные связанные выражения в набор выражений для более простых систем SDoF. Затем получаем простые формулы:

Каждое выражение отделено от каждого другого выражения, и каждое из них описывает отдельно системы SDoF в соответствии с каждой собственной частотой системы. Таким образом мы взяли сложную систему и разбили ее на гораздо более простые. Схематически это показано на рис. 5.

Рис. 5. Развязанная система с несколькими степенями свободы (MDoF)

Это подтверждает, что системы SDoF можно использовать для описания каждого вида вибраций систем MDoF. Посмотрим на частотные характеристики для системы, показанной на рис. 6, представляющей не что иное как сумму систем SDoF.

Рис. 6. Совмещение каждой системы SDoF

Если мы предположим, что взаимодействие между оснасткой и тестируемым образцом похоже на динамическое взаимодействие между каждым видом вибрации каждой системы, то для описания динамического взаимодействия между оснасткой и тестируемым изделием можно использовать несколько простых выражений. Давайте вспомним формулу для двух систем DoF, описывающих частотные характеристики резонансного поглотителя. Это очень знакомая формула, которую можно найти во всех учебниках по вибрациям:

Рис. 7. Характеристики поглощения колебаний

Данное выражение, взятое из [3], устанавливает связь между собственной частотой и коэффициентом жесткости для каждой отдельной системы DoF. Количество динамических взаимодействий сильно зависит от относительного соотношения данных характеристик. Для заданного соотношения масс с двумя отдельными системами DoF, имеющими одинаковую собственную частоту, типичный график конечных динамических характеристик показан на рис. 7. Количество затуханий между этими двумя пиками связанной системы зависит от соотношения масс.

Теперь данное выражение можно применить для разработки поглотителя резонансных колебаний, изучения сейсмических масс и т. д. Кроме того, это выражение помогает описать динамическое взаимодействие между двумя любыми системами, если описать их как системы SDoF (вспомним, что любую сложную систему с несколькими степенями свободы всегда можно представить как набор простых систем с одной степенью свободы).

Простая модель для конструкции крепления

Для того чтобы продемонстрировать некоторые эффекты динамического взаимовлияния, упомянутые выше, давайте представим крепление и тестируемый образец с помощью простой модели и проиллюстрируем некоторые важные моменты.

Рассмотрим использование двух разных креплений для вибрационных испытаний. Для описания тестируемого образца возьмем простую систему из двух моделей, каждая из которых имеет две степени свободы DoF. А для описания первой резонансной частоты для каждого крепления — простую модель с двумя степенями свободы. Схематически эта система показана на рис. 8.

Рис. 8. Не связанные между собой крепление и тестируемый образец

В данном примере изделие нужно протестировать на максимальной частоте. Оба крепления имеют резонансные частоты за диапазоном рабочих тестовых частот, но крепление 1 имеет первую резонансную частоту, очень близкую к верхнему пределу диапазона рабочих частот.

Теперь рассмотрим связанные между собой элементы системы. На рис. 9 показана результирующая частота для обоих креплений.

Рис. 9. a) Несвязанные между собой крепление и тестируемые образцы; b) связанные между собой крепление и тестируемый образец

Первое, что необходимо отметить, — резонансные частоты тестируемого образца лишь немного отличаются друг от друга для двух различных креплений. Однако разница амплитуд колебаний значительная. Другими словами, интенсивность колебаний очень разная (не углубляясь в теорию, напомним, что амплитуды напрямую зависят от типа колебаний системы на каждой определенной частоте). Поэтому пока частоты меняются не сильно, формы колебаний (или, косвенно, интенсивность колебаний) очень отличаются. Это означает, что тестируемый образец будет подвергаться иным уровням ускорения, чем требуется из-за использования упругих креплений.

Данный пример ясно показывает, что крепления должны быть как можно более жесткими, а их резонансная частота должна находиться далеко за пределами частот, при которых производится тестирование, иначе может произойти динамическое взаимовлияние между тестируемым образцом и креплением.

Пример расширительного стола

Последний пример показал, что даже если резонансная частота крепления находится далеко за пределами тестовой частоты, все равно наблюдается некоторое динамическое взаимодействие между тестируемым изделием и креплением. Но что, если крепление имеет резонансные частоты, лежащие в рабочем диапазоне частот тестирования?

Изучим теоретическую модель расширительного стола с конструкцией из жестких ребер и простым креплением. Расширительная платформа теоретически смоделирована так, что имеет резонансные частоты в рабочем диапазоне частот теста. Если расширительная платформа бесконечно жесткая и не имеет резонансных частот, тогда неважно, где на расширительной платформе будет установлен тестируемый образец (но не там, где размещен акселерометр). Поэтому для такого случая были изучены две модели: одна — с тестируемым образцом, расположенным симметрично на расширительной платформе, а другая — с асимметрично расположенным на платформе образцом. Если расширительная платформа не имеет резонансных частот, тогда не имеет значения, где расположен тестируемый образец (или где расположен управляющий акселерометр).

Рис. 10. Форма колебаний для пустого расширительного стола

Для сравнения на рис. 10 показаны первые девять типов колебаний пустого расширительного стола. Заметьте, ни один тип колебаний относительно оси симметрии не будет возбуждаться однонаправленным входным воздействием.

Рис. 11. Формы колебаний для тестируемого образца, симметрично размещенного на расширительной платформе

На рис. 11 показаны первые девять типов колебаний расширительного стола с тестируемым образцом, расположенным на платформе симметрично. И снова, ни один тип колебаний относительно оси симметрии не будет возбуждаться однонаправленным входным воздействием. Заметьте, все формы колебаний в этом случае, когда крепление располагается симметрично относительно расширительного стола, также симметричны.

Рис. 12. Формы колебаний для тестируемых образцов, несимметрично размещенных на расширительной платформе

На рис. 12 показаны первые девять видов колебаний расширительного стола с тестируемым образцом, находящимся на платформе несимметрично.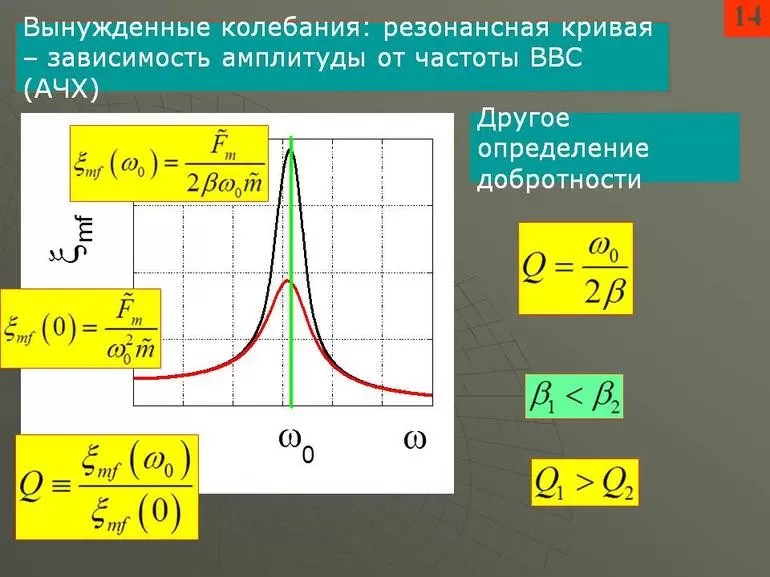 В этом случае, когда крепление расположено несимметрично относительно расширительного стола, все колебания также несимметричны. Важно отметить, что формы колебаний тестируемого образца значительно различаются для случаев симметричного и несимметричного расположения образца на расширительной платформе (рис. 11 и 12).

Рис. 13. Симметрично/несимметрично расположенные тестируемые образцы на резонирующей расширительной платформе

Если бы мы выполнили простые колебания и сравнили бы ответные колебания на одной из частот, то отметили бы большую разницу, как на рис. 13. Теперь, если посмотреть на ответные колебания на одной частоте, можно увидеть разницу, особенно вокруг верха испытуемого образца. При асимметричном расположении амплитуда колебаний заднего угла очень сильно отличается от амплитуд колебаний других частей. Очевидно, что и между двумя рассматриваемыми системами будет наблюдаться значительная разница.

Теперь нужно определить, где должен находиться управляющий акселерометр. В нашем случае с этим будут сложности, поскольку расширительная платформа не является жесткой на всех частотах. При этом в зависимости от выбранного места может наблюдаться серьезная перегрузка или недогрузка тестируемого образца. Что если управляющий акселерометр расположить на самом образце? Но при асимметричном расположении наблюдается большая разница колебаний верха рамы. Поэтому обычно в таком месте управляющий акселерометр лучше не устанавливать.

Но если корпус образца — это еще один промежуточный элемент на расширительной платформе, предназначенной для размещения тестируемых образов, будет ли динамический отклик корпуса/оснастки влиять на проводимый тест? Да, конечно!

Мы уже показали, как динамика движения крепления влияет на результаты проводимого теста. Управляющий акселерометр может только регулировать входной сигнал, меняя положение арматуры, и удерживать необходимый уровень. Управляющий акселерометр не может изменить динамику, основанную на взаимодействии расширительного стола и тестируемого образца.

Конечно, очень важно понять, что рассматриваемая оснастка — это не только крепление для размещения тестируемого образца, но и расширительная платформа (или стол скольжения), арматура вибростенда и промежуточное крепление для размещения тестируемого образца. При проведении вибрационных испытаний необходимо учитывать динамические характеристики всех этих элементов. Если любой из них будет иметь резонансные колебания с частотой, лежащей в диапазоне частот теста, могут возникнуть проблемы. Например, резонансная ситуация. Для изучения форм колебаний и определения данных потенциально проблемных частот полезно использовать модель конечных элементов или экспериментальный тест для определения формы колебаний.

Арматура в качестве крепления

До этого момента обсуждались только те части системы вибростенда, которые подвергаются воздействию. Однако даже пустая арматура вибростенда может иметь резонансные колебания ниже 2000 Гц. Это особенно верно для больших систем вибростендов с диаметром арматуры свыше 20 дюймов. В некоторых случаях арматура сама по себе может иметь более чем одно резонансное колебание с частотой ниже 2000 Гц.

Такие резонансные колебания часто проявляются как трудности управления вибростендом. Поэтому инженеры, проводящие тест, немедленно начинают винить во всех проблемах систему управления, утверждая, что она «работает некорректно». Если в систему вибростенда включена расширительная платформа, то источником всех проблем видят ее. Очень редко, когда в качестве причины рассматривают механическую часть вибростенда. Но часто дело именно в ней, поскольку если арматура имеет резонансные колебания, они очень сильно влияют на тестируемый образец, расположенный на монтажной платформе вибростенда.

Рис. 14. Узел крепление/арматура

На рис. 14 проиллюстрированы возникающие проблемы с арматурой/креплением. Относительно жесткое, хорошо сконструированное крепление устанавливается на упругую арматуру, которая имеет резонансные колебания с частотами, лежащими в рабочем диапазоне частот испытания. Даже если крепление не имеет резонансных колебаний (с резонансными частотами, которые не лежат в рабочем диапазоне частот), система все равно должна рассматриваться как одно целое — ведь когда жесткое крепление устанавливается на упругую арматуру, оно все равно будет испытывать деформацию, так как связано со всей системой. Это значит, что на крепление влияет арматура, и разработать крепление, не учитывая значительную динамику присоединенной арматуры, очень сложно.

Как уже обсуждалось, место размещения управляющего акселерометра вызывает проблему (например, как в случае на рис. 14). Место установки акселерометра — это деформированная гибкая поверхность, имеющая значительное влияние на проводимый тест.

Другое заблуждение состоит в том, что применение несколько управляющих акселерометров решае проблему. Но использование нескольких акселерометров для управления позволяет лишь откорректировать некое «среднее» значение ускорения согласно полученной обратной связи.

Решение задачи прежде всего связано с реконструкцией арматуры для снижения резонансных колебаний, вызывающих проблемы. Но в действительности никто не хочет вносить такие изменения в конструкции арматуры больших вибростендов из-за высокой стоимости и сложности. Кроме того, никто в лаборатории или на производстве не хочет стать «разоблачителем», обнаружившим, во-первых, что резонансные колебания существуют, а во-вторых, что они влияют на результаты теста.

Что же тогда делать?

Как было установлено, проблему решает разработка оснастки без резонансных колебаний для всех вибрационных испытаний. Следует помнить, что к оснастке относится арматура, расширительная платформа (или стол скольжения), промежуточные крепления и т. д.

Расчеты показали, что разработка бесконечно жесткой безынерционной оснастки без резонансных колебаний невозможна. И инженерам нужно определить эффективную стратегию, а также аккуратно и полно все задокументировать.

Арматура (или расширительная платформа) обычно имеют одно или два резонансных колебания, частоты которых необходимо определить, чтобы найти «обходной путь». На ранних стадиях разработки такой оснастки может использоваться модель конечных элементов для получения общего представления о слабых местах конструкции. Для уже существующих систем можно провести экспериментальное исследование колебаний, результаты которого помогут определить резонансные частоты и форму колебаний всего узла оснастки. Визуализация формы колебаний часто помогают наглядно выявить проблемные области. Все это позволит откорректировать возникающие проблемные частоты.

Основная задача — четко выявить проблемы, чтобы для их решения можно было применить именно инженерные решения и методы. Конечно, необходимо стремиться к получению конструкций без резонансных колебаний, а не прибегать к временным мерам, обходя проблемы.

Заключение

В статье обсуждались вопросы, связанные с выполнением динамических испытаний на вибростендах. Рассматривались резонансные и динамические воздействия и их влияние на проведение вибрационных испытаний. Данные воздействия могут иметь очень важное значение для общих характеристик теста.

Оснастка вибростендов — очень ответственная часть системы вибрационных испытаний, а потому необходимо учитывать все эти элементы (они не должны иметь резонансных колебаний в рабочем диапазоне частот испытания).

При появлении резонансных колебаний нельзя эффект от их влияния убрать только получением обратной связи от одного или нескольких акселерометров. Резонансные колебания необходимо полностью отслеживать и понять причину их возникновения. Затем необходимо получить инженерную оценку всей ситуации, чтобы проводить вибрационные тесты с лучшими возможными условиями.

Резонансные колебания имеют очень сильное влияние на проводимые вибрационные тесты. Они не исчезают при использовании системы виброконтроля и никуда не деваются, если кто-то не нашел времени для их изучения.

Частота резонанса

— обзор

Влияние уровней насыщения кислородом на сигналы ядерного магнитного резонанса

Частота ЯМР ядер с ненулевым спином пропорциональна ядерному гиромагнитному отношению и силе локального поля, испытываемого ядром. Таким образом, изменения в распределении поля внутри и вокруг эритроцитов влияют на несколько параметров ЯМР, включая резонансную частоту и времена релаксации ЯМР. Эти два параметра будут обсуждаться отдельно в следующих нескольких абзацах.Обсуждение будет сосредоточено на ядрах водорода, наиболее часто изучаемых ядерных частицах в биомедицинских ЯМР и МРТ. Наибольшая часть сигналов ЯМР водорода от живых организмов исходит от несвязанной воды, которая присутствует в высокой молярной концентрации во многих тканях, включая кровь. Высокая концентрация, большое гиромагнитное отношение и высокое содержание изотопов значительно увеличивают чувствительность ЯМР-обнаружения водорода, что позволяет получать МР-изображения живых организмов с высоким разрешением.

Локальное микроскопическое поле, которое испытывает ядро ​​в однородной среде с заданной восприимчивостью χ , погруженное во внешнее приложенное поле B ₀ isBL − B0 = Ds − 23χ − χ0B0, где D — размагничивающий фактор зависит от геометрии образца, а 2/3 — геометрический фактор сферы, нарисованной вокруг ядра. Эту конструкцию обычно называют «сферой Лоренца», условной сферической вакуумной полостью, окружающей ядро, что объясняет тот факт, что в атомном масштабе среда не может быть представлена ​​как континуум.Интересно отметить, что для сферического образца D _s = 2/3 и резонансная частота не зависит от изменений χ . Для эритроцитов геометрия далека от сферической, и следует ожидать сдвига резонансной частоты для молекул воды в суспензии эритроцитов при изменении восприимчивости клеток. Действительно, разница в 0,33 ppm в резонансной частоте ядер водорода в оксигенированной и деоксигенированной крови человека была измерена Thulburn и его коллегами в экспериментах, проведенных in vitro в сильных магнитных полях.Чтобы рассчитать влияние чувствительности на сигналы ЯМР в такой сложной среде, как кровь, необходимо уточнить теоретические основы.

В однородном материале фактический размер сферы Лоренца явно не появляется в расчетах. Однако кровь очень неоднородна, гемоглобин разделен на дискретные единицы (эритроциты), встроенные в плазму. Количественный расчет сдвига линии ЯМР протонов в крови требует немного более сложной конструкции, чтобы учесть различные масштабы характерной длины вкладов в локальное поле, обусловленных удаленными эритроцитами и гемоглобином.Сначала рисуется сфера Лоренца вокруг ядра достаточного размера, чтобы содержать большое количество эритроцитов, так что вклады в локальное поле от удаленных источников вокруг сферы плавно меняются. Поле, которое испытывает ядро ​​в центре сферы, равно BL = B0 + Ds − 23χbloodB0 + Bi, где B _i обозначает вклады в локальное поле от источников внутри сферы, а χ _кровь восприимчивость крови (сфера велика в клеточном масштабе, а внешняя среда выглядит как континуум). χ _кровь зависит от относительного объема, занимаемого RBC V _rbc (т. Е. Гематокрита): χblood = Vrbc × χrbc + Vrbc − 1χpl Для оценки B _i , секунда нарисована сфера Лоренца, меньше клетки, но большая в молекулярном масштабе. Если эта сфера полностью находится внутри внутриклеточного пространства: Bi = Drbc − 23χrbc − χplB0

Для сложной формы RBC геометрический фактор D _rbc должен быть оценен численно с помощью процедур, аналогичных тем, которые используются для расчета распределение поля, показанное на рисунке 3, и зависит от ориентации ячейки по отношению к внешнему магнитному полю.В высоких полях, используемых Тулберном и его сотрудниками, эритроциты полностью ориентированы в конфигурации с минимальной энергией, и D _rbc = 0,75.

Используя эту конструкцию, можно рассчитать частичные изменения локального поля, испытываемые ядрами, для компартментов плазмы и эритроцитов: ΔBpl / B0 = Ds − 23VrbcΔχrbcΔBrbc / B0 = Ds − 23VrbcΔχrbc + Drbc − 23Δχrbc

молекул воды быстро диффундируют. вне ячейки и динамически усреднять все распределение поля в типичной шкале времени ЯМР.В этом режиме быстрого обмена сигнал ЯМР состоит из узкого резонанса, центральная частота которого отражает среднее поле, испытываемое ядром. Таким образом, резонансный сдвиг для ядер водорода молекулы воды в крови пропорционален среднему значению изменений локального поля во внутри- и внеклеточной среде, взвешенных по относительным размерам водных компартментов (0,3 и 0,7 для эритроцитов и эритроцитов). плазма соответственно).

Для изменения внутриклеточной магнитной восприимчивости Δ χ _rbc = 2.5 × 10 ⁻⁶ , что соответствует разнице между оксигенированными и деоксигенированными эритроцитами, и для цилиндрической пробы крови с гематокритом 40% эти расчеты предсказывают сдвиг водородного резонанса на 0,3 ppm, что хорошо согласуется со сдвигом, измеренным с помощью Thulburn и его сотрудники в аналогичных условиях. Приведенная выше теоретическая оценка показывает, что этот сдвиг можно почти полностью объяснить изменениями магнитной восприимчивости крови, а не прямым взаимодействием молекул воды с парамагнитными центрами.

Сдвиг резонансной частоты — не единственное и не самое сильное влияние магнитных свойств крови, зависящих от оксигенации, на параметры ЯМР. Быстрая диффузия молекул воды в градиентах поля внутри и снаружи клеток, а также вблизи небольших капилляров способствует необратимой потере фазовой когерентности ядерной спиновой системы. Характерное время этого процесса называется временем спин-спиновой релаксации, или T ₂ . Для более крупных кровеносных сосудов несоответствие восприимчивости крови и окружающей ткани приводит к градиентам магнитного поля в большем масштабе, чем измеренный при диффузии молекул воды.Частично обратимая дефазировка спинов, вызванная этими более протяженными в пространстве градиентами, регулируется постоянной времени, называемой T2 *.

Оба механизма релаксации более эффективны в присутствии более сильных градиентов, а T ₂ и T2 * короче в деоксигенированной крови. Важно отметить, что изменения в оксигенации крови влияют не только на время ЯМР-релаксации ядерных спинов в крови, но и в окружающей ткани. Сосудистая сеть сильно структурирована, мельчайшие капилляры имеют диаметр всего несколько микрон и разделены несколькими десятками микрон.Следовательно, изменение оксигенации крови влияет на время релаксации большого количества спинов как во внутри-, так и во внесосудистом отделах, а времена релаксации ЯМР более чувствительны, чем относительно небольшой сдвиг резонансной частоты, к изменениям уровней оксигенации крови. МР-изображения могут быть сенсибилизированы к T ₂ и T2 * с помощью соответствующих последовательностей радиочастотных импульсов, что позволяет использовать эритроциты в качестве эндогенного источника контраста. Применение этих методов для отображения паттернов мозговой активности обсуждается в следующем разделе.

Частота механического резонанса и как ее анализировать

В какой-то момент своей карьеры системные инженеры, вероятно, столкнутся с ситуацией, когда резонансная реакция системы вызывает проблемы с движением и / или слышимое раздражение. Этот резонанс или вибрация нежелательны и могут привести к значительному снижению производительности. Например, фрезерный станок с ЧПУ (который обычно имеет высокую резонансную частоту из-за высокой жесткости) [1] будет дрожать вокруг желаемой траектории фрезерования при возбуждении резонансной частоты.Другой пример — фармацевтический инструмент для работы с жидкостью, в котором возникают неожиданные вибрации, вызывающие перемешивание транспортируемого жидкого раствора. В этой статье будет рассмотрено, почему присутствуют резонансы и какие инструменты можно использовать для их анализа.

Почему механические системы демонстрируют резонансную частоту?

Первым шагом в ответе на этот вопрос является создание модели механической системы. Для определения положения массы с учетом трения и податливости требуется, чтобы модель была системой одного или нескольких дифференциальных уравнений 2-го порядка (или выше).Чтобы найти решение, а также упростить анализ поведения, нерешенные уравнения временной области преобразуются в s-область с помощью преобразования Лапласа . Это облегчает создание передаточной функции системного уровня, которую также называют «характеристическим уравнением».

Знаменатель передаточной функции содержит переменные состояния порядка n. Значения s (действительные и / или мнимые), где знаменатель равен нулю, называются корнями знаменателя, которые называются «полюсами».Числитель может быть константой или содержать переменные состояния порядка n, аналогичные знаменателю. Значения s (действительные и / или мнимые), где числитель равен нулю, называются корнями числителя, которые называются «нулями». Если числитель постоянный, то нулей нет. Эта информация может быть использована для формулирования решения модели во временной области. Однако используемый здесь частотный анализ будет ограничен s-областью для простоты вычислений.

Полюса и нули очень полезны для определения поведения и стабильности.Например, критерии устойчивости диктуют, что порядок знаменателя (количества полюсов) не должен быть меньше порядка числителя (количества нулей). Кроме того, действительная часть доминирующих полюсов должна быть отрицательной (левая часть s-плоскости), чтобы система считалась стабильной. Полюса будут использоваться здесь для объяснения существования резонансной частоты.

Инерциальные системы имеют резонансную частоту, которая существует из-за внутренних свойств. Однако система должна быть более сложной, чем инерция чисто твердого тела, иначе ее характеристическое уравнение будет иметь только полюсы в нуле.Другие члены в характеристическом уравнении, которые могут быть такими же простыми, как член податливости (пружина), будут вводить ненулевые частотные составляющие (корни с мнимыми частями) в характеристическое уравнение. Чисто инерциальные системы будут иметь полюса на нуле и, следовательно, не будут показывать резонансную частоту.

«Твердое тело» — это на самом деле просто академическая конструкция, которой не существует в реальном мире, поэтому даже простые инерционные системы могут демонстрировать механическую резонансную частоту, когда к ним добавляются пружинные элементы (податливость) и / или демпфирующие компоненты (вязкое трение). модель.Некоторые системы достаточно демпфированы, чтобы подавить резонансную частоту. В этом случае резонансная частота все еще существует (мнимая часть корней), но она едва заметна, так как действительные части корней доминируют в отклике.

Демонстрационная установка

Система, используемая в этой демонстрации (рис. 1), представляет собой массу в верхней части металлической линейки, которая действует как пружина. Нижняя часть пружины прикреплена к ступени линейного двигателя. Для простоты будет анализироваться только движение в направлении линейного двигателя.Движение м ₂ будет рассматриваться как линейное, что является допустимым приближением для малых углов. Это упрощение все еще актуально в контексте описания источника резонансной частоты. Кроме того, измеряется только положение двигателя, м ₁ .

Модель содержит коэффициент демпфирования системы, b _s , который передает силу, пропорциональную скорости и противоположную направлению движения. Это свойство обычно называется «вязким трением» и представляет собой любые свойства трения, пропорциональные скорости.Сила, прикладываемая к системе магнитным полем двигателя, регулируется путем изменения тока в обмотках двигателя.

Рисунок 1 — Демонстрационная система

Реакция положения м ₁ на силу, действующую на эту систему, выражается следующим образом:

(Уравнение 1) — получено из реакции на скорость скручивания в ссылке 1

Обратите внимание, что член слева от правой части уравнения — это «несвязанный» отклик.Если пружина имеет бесконечную жесткость, крайний правый член равен единице, а две массы жестко прикреплены и действуют как одна масса. В этом случае есть только полюса на нуле и, следовательно, нет резонансной частоты.

Термин справа вводит корни с мнимыми компонентами, тем самым создавая потенциал для частотной характеристики. Для случая, когда b _s равно нулю, корни этого члена становятся:

(ур. 2)

Введение умеренного демпфирующего срока ( 0.1K _s s <0,6K _s / w _n ) [2], вводит реальную составляющую в корни и перемещает их так, чтобы резонансная частота была немного меньше незатухающей собственной частоты. . Более сильный демпфирующий член ( b _s <0,6K _s / w _n ) [2] еще больше уменьшит резонансную частоту, но отклик на частоте будет ослаблен и окажет небольшое влияние. В этом случае преобладают настоящие части корней.

Из-за нуля в числителе эта модель также будет показывать «антирезонансную» частоту. Это можно наблюдать как уменьшение отклика при заданном антирезонансе. Системы со связанными массами, подобные анализируемой здесь, будут содержать антирезонансную частоту чуть ниже резонансной частоты.

За пределами резонансной частоты отклик больше, чем у системы, в которой массы жестко связаны. В последнем случае вибрация создает больше всего проблем [1].

Экспериментальное определение резонансной частоты

Использование в качестве определения резонансной частоты «частота, на которой система будет демонстрировать локализованный максимальный отклик» означает, что эксперимент может быть проведен в системе, где отклик как функция частоты измеряется.

Один инструмент, называемый частотной разверткой, вводит в систему сигнал переменной частоты. Частотный ввод начинается с предварительно определенного значения и непрерывно изменяется до тех пор, пока не будет достигнуто определенное максимальное значение.Большинство механических систем имеют резонансные частоты в сотни герц или ниже. Если резонансная частота значительна, она обычно производит слышимый звук, который может воспринимать слушатель.

Аналогичный, но более точный инструмент, график Боде, анализирует усиление и фазу отклика и генерирует график в частотной области. Чтобы упростить вычисления на цифровом процессоре, дискретизируется набор дискретных частот, а результаты обрабатываются с помощью БПФ (быстрое преобразование Фурье).

Это видео на YouTube демонстрирует использование различных инструментов в Pro-Motion® для определения резонансной частоты системы на Рисунке 1:

Метод № 1: Расчет на основе трассировки фактического положения реакции на возмущение.

В систему введено нарушение. Функция Pro-Motion SCOPE используется для отслеживания реакции положения м ₁ . Резонансная частота — это величина, обратная периоду времени между одним пиком и другим.Из видео видно, что период довольно близок к 100 мс. Это соответствует резонансной частоте 10 Гц.

Метод № 2: развертка по частоте используется для перехода от низкой к высокой частоте.

На систему действует синусоидальная сила (через магнитное поле двигателя). Колебания системы наблюдаются визуально (или на слух). Отмечается частота локального максимума отклика. Из метода №1 уже известна приблизительная резонансная частота.Однако, если система быстро установится в ответ на введенный «импульс» метода № 1, то данных может не хватить для определения резонансной частоты. Непрерывное возмущение, вводимое методом № 2, предоставит больше данных в этом отношении, поскольку система никогда не успокаивается.

Как видно на видео, амплитуда колебаний фактического положения начинает увеличиваться около отметки 5,2 секунды (11 Гц). Частота продолжает увеличиваться до 14 Гц, и отклик гаснет после прохождения резонансной частоты.Затем развертка меняет направление и перемещается с 14 Гц на 10,5 Гц и остается там. Как и ожидалось, амплитуда отклика увеличивается по мере приближения к резонансной частоте.

Метод № 3: создается диаграмма Боде системы, охватывающая тот же диапазон частот.

И снова на систему действует синусоидальная сила. На этот раз реакция положения по отношению к приложенной силе используется для расчета усиления и фазы отклика.В этом случае пользователю не нужно полагаться на визуальные или звуковые подсказки. Пользователь может анализировать данные усиления, чтобы найти локальный максимум и частоту, связанную с этим максимумом. Для более детального анализа числовые данные могут быть перенесены в электронную таблицу и проанализированы.

Рис. 2: Данные об усилении Боде в виде электронной таблицы.

Рисунок 2 демонстрирует более точное определение резонансной частоты (10,6 Гц). Антирезонансная частота также может наблюдаться на Рисунке 2 около 10.1 Гц.

В конце дня…

Поскольку никакая инерциальная система не содержит истинных масс «твердого тела», все механические системы имеют ненулевую резонансную частоту. Возбуждение резонансной частоты ухудшит работу системы как с точки зрения кратковременной точности, так и с точки зрения долгосрочного технического обслуживания.

Продемонстрированы три метода экспериментального определения резонансной частоты. Метод №1 обеспечил результат в пределах 10%, но этот метод был ограничен системами, которые имеют недостаточно затухающий отклик на импульс.Метод № 2, который полагается на визуальные и звуковые подсказки, дал эквивалентную точность и работает как в системах с избыточным, так и с недостаточным демпфированием. Метод № 3 предоставил наиболее подробную информацию о частотной характеристике системы. Значительно улучшена точность оценки резонансной частоты. Кроме того, этот метод также позволил идентифицировать антирезонансную частоту.

Артикул:

1 Дж. Эллис, Средства от механического резонанса в промышленных сервосистемах
2 Дж.Д’Аццо и К. Хупис, Анализ и проектирование линейных систем управления: традиционные и современные, McGraw-Hill, Inc., 1995, стр. 292-293.

Продукты PMD, поддерживающие серводвигатели

PMD производит ИС, которые обеспечивают расширенное управление движением щеточных и бесщеточных двигателей постоянного тока более двадцати пяти лет. С тех пор мы также встраивали эти ИС в модули plug and play и платы управления движением. Несмотря на разную упаковку, все эти продукты контролируются C-Motion, простым в использовании языком управления движением PMD и идеально подходят для использования в медицинских, лабораторных, полупроводниковых, роботизированных и промышленных приложениях управления движением.

Программное обеспечение для анализа движения Pro-Motion

Pro-Motion — это простая в использовании программа для упражнений и анализа движения PMD на базе Windows. Он предлагает готовые возможности, которыми сможет поделиться вся ваша команда разработчиков. Пошаговый мастер настройки осей позволяет разработчикам быстро и легко настраивать контур положения, контур тока и параметры управляющего двигателя с ориентацией на поле. Опытные пользователи могут получить доступ к полному пакету анализа движения с генерацией графиков Боде и автонастройкой.

Подробнее >>

ИС серии MC58113

ИС серии MC58113 являются частью популярного семейства ИС Magellan Motion Control от PMD и обеспечивают расширенное управление положением для шаговых двигателей, BLDC и щеточных двигателей постоянного тока.Стандартные функции включают автонастройку, профилирование s-образной кривой, FOC (полевое управление), управление сигналом переключения высокого / низкого уровня, прямой энкодер, ввод импульсов и направления и многое другое. ИС семейства MC58113, используемые для автоматизации лабораторий, управления насосами, систем наведения или универсальной автоматизации, являются идеальным решением для вашей следующей конструкции машины.

Подробнее >>

Цифровые приводы ION

Цифровые приводы ION объединяют одноосную микросхему Magellan и сверхэффективный цифровой усилитель в компактном прочном корпусе.В дополнение к расширенному управлению серводвигателем, ION обеспечивают перемещение от точки к точке с S-образной кривой, управление питанием i2T, загружаемый код пользователя и ряд функций безопасности, включая обнаружение перегрузки по току, перенапряжения и перегрева. ION — это простые в использовании устройства plug and play, которые мгновенно запускают ваше приложение.

Подробнее >>

Платы управления движением Prodigy

Платы Prodigy® / CME Machine-Controller обеспечивают высокопроизводительное управление движением для медицинских, научных, автоматических, промышленных и роботизированных приложений.Доступные в конфигурациях с 1, 2, 3 и 4 осями, эти платы поддерживают щеточные двигатели постоянного тока, бесщеточные двигатели постоянного тока и шаговые двигатели и позволяют загружать и запускать написанный пользователем код на языке C непосредственно на плате. Машинный контроллер Prodigy / CME имеет встроенные усилители Atlas , которые устраняют необходимость во внешних усилителях. Для построения полностью функционирующей системы требуется только один высоковольтный источник питания, двигатели и кабели. Опции хост-интерфейса включают Ethernet UDP и TCP, CANbus, RS-232 и RS-485.

Подробнее >>

Вас также может заинтересовать:

Собственная частота: хорошее, плохое и катастрофическое

Крошащиеся мосты, разбитое стекло, кричащие дети, тяжелые басы — тот, кто считает, что у этих вещей нет ничего общего, ошибается. Все они создаются посредством вибраций, и, в частности, сильные колебания создаются собственными частотами. Читайте дальше, пока мы объясним науку, лежащую в основе этого принципа, и что такое резонансные катастрофы, а также рассмотрим игру резонанса крена, когда дело доходит до громкоговорителей.

Все вибрирует, а как?

Вибрация наушников всегда является реакцией на импульс энергии. Рука может запустить маятник в движение, ветер может раскачать небоскреб, а катушка с помощью магнита может сдвинуть мембрану громкоговорителя. Насколько сильно что-то вибрирует, зависит от приложенной мощности вибрации, а также от материала, включая конструкцию колебательной системы. С другой стороны, большое значение имеет частота, с которой действуют импульсы энергии.Ведь если частота подаваемой энергии совпадает с собственной частотой тела, тело вибрирует с особенно высокой амплитудой.

Как выглядит явление резонансной частоты на практике, можно понять с помощью маятника: если пружинный маятник является периодическим, то есть через регулярные промежутки времени, на который подается энергия, соответствующая собственной частоте маятника, отклонение маятника составляет его величайший. Если импульсы энергии имеют более низкую или более высокую частоту, чем собственная частота, отклонение маятника будет меньше.

На качелях вы можете попробовать на себе, как работает резонансная частота. Когда вы ударяете качелями в наивысшую точку, подача энергии точно соответствует собственной частоте системы. Вот почему качели имеют такой большой импульс качания. Если вы ударите до или после того, как замах достигнет своей наивысшей точки, сила передается менее эффективно или даже никуда не денется.

От хороших к плохим колебаниям

Корпус акустической гитары, качелей, стекла или моста может вибрировать с соответствующей резонансной частотой.Но это не везде желательно и даже может нанести большой ущерб. Это связано с тем, что системы могут так сильно вибрировать, что конструкция не может выдержать нагрузку.

Это явление можно наблюдать, когда человек направляет голос на бокал с вином с небольшого расстояния. Если высота голоса в точности соответствует собственной частоте стекла, оно через относительно короткое время разбивается — происходит так называемая резонансная катастрофа. Если голосовые связки заставляют молекулы воздуха колебаться с большей или меньшей частотой, стекло остается неповрежденным.Собственную частоту стекла можно услышать, когда вы ударите его каким-либо предметом.

Одна из самых известных резонансных катастроф произошла в США в 1940 году, когда ветер вызвал такую ​​сильную вибрацию моста Tacoma Narrows Bridge, которая разрушила его.

Чтобы избежать резонансных катастроф, кодекс дорожного движения запрещает группам людей, например военным частям, шагать по мостам.

С другой стороны, для музыкальных инструментов резонанс — это преднамеренный эффект для увеличения громкости звука.В акустической гитаре корпус действует как механический усилитель звуковых волн, которые запускаются струнами. Корпус гитары устроен таким образом, что резонансная частота возникает даже на разных тонах.

Громкоговорители Teufel

Резонансные эффекты в громкоговорителях нежелательны — за одним исключением

Резонансная частота в громкоговорителях не приветствуется. Громкоговорители сконструированы таким образом, что различные компоненты не вибрируют на своей резонансной частоте.Это означало бы, что звуки в том же частотном диапазоне, что и отдельные компоненты, будут воспроизводиться намного громче, чем другие. Именно здесь вступает в игру кроссоверная сеть: в многоканальных системах она направляет сигналы на динамики в соответствии с их частотой.

Резонансные эффекты также не должны возникать в корпусе громкоговорителя. Это может произойти, когда мембрана на ее задней стороне излучает звук внутрь громкоговорителя. Этот звук может вызвать вибрацию корпуса и, таким образом, негативно повлиять на звуковой образ.Чтобы предотвратить это, корпус громкоговорителя снабжен демпфером, который поглощает звуковые волны, излучаемые внутрь.

Исключением из этого правила являются фазоинверторные колонки. Эти шкафы имеют трубчатое отверстие, через которое излучаемый внутрь звук на определенных низких частотах может выходить в комнату. Это работает по принципу резонатора Гельмгольца, который мы объяснили в нашем тексте о сабвуферах.

Нам нужны басы: бас Teufel для более глубоких вибраций

Der Subwoofer der Kombo 42 BT Power Edition verleiht den Regallautsprechern ordentlich Wumms

• ▶ Моно-сабвуфер US 2106/1 SW: Этот сабвуфер для новичков предлагает мощные басы, не нарушая шума потока, несмотря на свой компактный размер.Это достигается с помощью двух ламп фазоинвертора.
• ▶ Ultima 40/20 «2.0> 5.1 Extension Set Surround»: динамики HiFi Ultima 40/20 — настоящая дьявольская классика для дома. С помощью этого набора вы можете расширить свою стереосистему до объемного звука 5.1. Сабвуфер T 10 обеспечивает хороший резонанс в диапазоне низких частот.

Еще товары от Teufel

Вывод: Полезна резонансная частота

• На резонансной частоте собственная частота колебательной системы совпадает с частотой подводимой энергии.
• В случае резонанса отклонение колебаний становится больше.
• В акустике более высокая амплитуда звуковых волн означает более высокое звуковое давление и, следовательно, большую громкость.
• Резонансные частоты обычно нежелательны для громкоговорителей.
• Громкоговорители с фазоинвертором являются исключением. Они усиливают низкие частоты по принципу резонатора Гельмгольца.

Наконец, классический «Багз Банни» на эту тему:

Resonance | HowStuffWorks

Резонанс. Объект, который может вибрировать, имеет тенденцию делать это с определенной скоростью, называемой естественной или резонансной частотой объекта.(Эта частота зависит от размера, формы и состава объекта.) Такой объект будет сильно вибрировать, когда он подвергается вибрациям или регулярным импульсам с частотой, равной или очень близкой к его собственной частоте. Это явление называется резонансом. Из-за резонанса сравнительно слабая вибрация одного объекта может вызвать сильную вибрацию другого. По аналогии, термин резонанс также используется для описания явления, при котором колеблющийся электрический ток усиливается электрическим сигналом определенной частоты.

Пример резонанса — двигатель, который вызывает вибрацию в предмете мебели в другой части того же дома. Эти колебания возникают из-за того, что мебель имеет собственную частоту, равную частоте колебаний, создаваемых двигателем. Говорят, что мебель находится в резонансе с двигателем. Резонанс также может наблюдаться в автомобиле, когда определенная часть пепельницы, например, вибрирует, когда автомобиль движется с определенной скоростью. Зольник находится в резонансе с вибрациями двигателя на этой скорости.

Механический резонанс может вызывать вибрации, достаточно сильные, чтобы разрушить объект, в котором они возникают. Например, солдаты, марширующие по мосту, могут создавать сильные вибрации на собственной частоте моста и раскачивать его. По этой причине солдаты ломают ступеньки, чтобы перейти мост. В 1940 году порывы ветра в районе Пьюджет-Саунд-Нарроуз, Такома, Вашингтон, вызвали колебания подвесного моста с собственной частотой, и мост рухнул.

В музыке резонанс используется для увеличения интенсивности (громкости) звука.Например, сравнительно слабые колебания, производимые на конце органной трубы, вызывают резонансную вибрацию столба воздуха в трубе, что значительно увеличивает громкость звука. Этот принцип также применим к человеческому голосу, в котором колебания голосовых связок усиливаются резонансными колебаниями в ротовой и носовой полости.

Электрический резонанс используется для настройки радиоприемников и телевизоров. Настройка заключается в создании контура с резонансной частотой, равной заданной частоте желаемой станции.

Исследование резонансных характеристик горных пород при гармоническом возбуждении

Для изучения резонансных характеристик горных пород при гармоническом возбуждении были представлены две модели колебаний для оценки собственной частоты горных пород, возникающих во время бурения. Первая — это разработанная модель с одной степенью свободы, которая учитывает свойства и размеры породы. Вторая — модель с несколькими степенями свободы, основанная на принципе наименьшего действия. Затем модальные характеристики, а также влияние частоты возбуждения, механических свойств и размеров породы на ее резонансную частоту анализируются с помощью МКЭ.Наконец, ультразвуковые испытания искусственных песчаников и материалов буровых инструментов проводятся в помещении, и для получения их резонансных частот применяется метод преобразования БПФ. На основании проведенного анализа можно сделать вывод, что собственная частота породы увеличивается с изменением режима колебаний. Для одного и того же вида породы резонансная частота обратно пропорциональна массе, в то время как для разных видов горных пород механические параметры, такие как плотность, модуль упругости и коэффициент Пуассона, вместе определяют резонансную частоту породы.Кроме того, форма камня также является одним из основных факторов, влияющих на его резонансную частоту. Наконец, результаты теоретических исследований подтверждаются ультразвуковыми исследованиями.

1. Введение

Хорошо известно, что резонанс — очень распространенное физическое явление в природе, и его можно наблюдать почти во всех областях инженерных технологий. Многие инженерные сооружения, машины и оборудование спроектированы таким образом, чтобы избежать возникновения резонансного эффекта.Однако резонанс имеет и положительную сторону, и он имеет большое значение в некоторых областях, например, в производстве музыкальных инструментов, медицинских испытаниях и т. Д. В настоящее время в нефтяной инженерии была предложена новая технология бурения, которая также использует преимущество повреждения, характерного для резонанса, а именно — бурение с усилением резонанса (RED). Основная идея этой технологии заключается в том, что долото, вращаясь, прикладывает динамическую ударную силу с регулируемой высокой частотой к породе, так что порода резонирует для достижения фрагментации породы [1].Технология RED может решить общие проблемы, такие как низкая скорость проходки и серьезный износ бурового долота при бурении глубоких и твердых пластов [2–4].

Ключ технологии RED — реализовать каменный резонанс. В настоящее время исследования резонанса горных пород в основном включают следующие аспекты. Основные характеристические параметры породы проверяются на основе принципов акустического и электромагнитного резонанса. В частности, модуль упругости [5–7], сжимаемость, плотность [8], модуль сдвига и коэффициент демпфирования [9] породы могут быть получены с помощью резонансного ультразвукового спектра и характеристик пор, насыщенности [10] и характеристик осадка. [11] горные породы могут быть извлечены с помощью технологии ядерного магнитного резонанса.Кроме того, резонансные характеристики различных структур горных пород идентифицируются и анализируются на основе принципа измерения сейсмического резонанса, чтобы обеспечить лучшее руководство для обеспечения экологической безопасности [12–14]. Кроме того, существует также большое количество исследований по преобразованию тротуаров и других каменных конструкций с использованием разрушительных свойств резонанса [15].

Однако, поскольку ключом к реализации технологии RED является определение величины или диапазона резонансной частоты горной породы, чтобы на горную породу можно было воздействовать соответствующим гармоническим вибрационным воздействием для достижения резонансной фрагментации.Более того, порода, встречающаяся при бурении, относительно мала по сравнению с каменными структурами, которые находятся в естественной среде. Поэтому, хотя многие эксперты и ученые провели множество соответствующих исследований резонанса горных пород [16–18], существующие результаты исследований все еще не полностью применимы к области бурения. Поэтому очень необходимо провести исследование резонансных характеристик породы, встречающейся в поле бурения.

В этой статье, нацеленной на небольшие камни, разработана модель собственной частоты с одной степенью резкости, учитывающая свойства и размеры породы.Затем, на основе принципа наименьшего воздействия, предлагается модель собственной частоты с несколькими степенями свободы. Таким образом, определяются основные влияющие факторы, влияющие на резонансные характеристики породы. Оставшаяся часть теста организована следующим образом. В разделе 3 проводится численное моделирование для анализа влияния ключевых факторов на резонансную частоту породы. Затем проводится ультразвуковое испытание искусственных песчаников и материалов бурового инструмента в Разделе 4 для проверки теоретических результатов исследования и объяснения осуществимости технологии RED.

2. Модели естественной частоты породы

В этом разделе предлагаются две модели вибрации, учитывающие свойства и размеры породы, для оценки ее собственной частоты.

2.1. Модель собственной частоты с одной степенью свободы

Система вибрации породы под буровым долотом во время бурения может быть представлена ​​физической моделью, показанной на рисунке 1. Масса м , которая представляет собой частицу, является абстракцией инерции и безмассовая пружина с жесткостью k — это абстракция упругости в системе вибрации горной породы.

Согласно теории колебаний [19], собственная частота вышеупомянутой системы может быть выражена следующим образом:

Предполагая, что порода является упругой однородной средой, ее жесткость может быть получена из формулы жесткости упругого материала. , а именно,

Подставив уравнение (2) в уравнение (1), собственная частота породы может быть дополнительно переписана как или

Уравнение (4) представляет собой модель собственной частоты породы с одной степенью свободы.

2.2. Модель собственной частоты с несколькими степенями свободы

Из-за ограничения демпфирования, энергии и других факторов ударная сила бурового долота может проходить через породу только на ограниченное расстояние во время бурения. В результате сначала разрушается поверхность породы, контактирующая с буровым долотом. Следовательно, поверхностная порода может рассматриваться как однородная упругая пластина по сравнению с формацией. Принимая во внимание фактическое положение породы на дне скважины, пластина подвергается простому опорному ограничению, как показано на Рисунке 2.

Основываясь на принципе наименьшего действия, уравнение вибрации приведенной выше модели может быть представлено как

Возьмите преобразование Фурье из приведенного выше уравнения, умножьте обе части уравнения на e ^iωt и интегрировать. Тогда уравнение (5) принимает вид

. Выбрав границу пластины в качестве координатной оси, граничное условие может быть выражено как

Решение, удовлетворяющее указанным выше граничным условиям, может быть записано как

Таким образом, собственная частота пластины может быть выражена как

. быть определено asor

Уравнение (10) представляет собой модель собственной частоты горной породы с несколькими степенями свободы.

Две вышеуказанные модели вибрации могут быть использованы для первоначальной оценки собственной частоты породы. Более того, независимо от того, является ли это расчетной моделью собственной частоты с одной или несколькими степенями свободы, мы можем обнаружить, что собственная частота породы связана как с ее механическими свойствами, такими как жесткость, модуль упругости, коэффициент Пуассона и плотность, так и размеры, такие как длина стороны, площадь и объем.

3. Численное моделирование

В этом разделе проводится модальный анализ и анализ гармонического отклика для дальнейшего изучения резонансных характеристик породы.Модальный анализ породы предназначен для определения ее собственной частоты, в то время как анализ гармонического отклика используется для расчета частоты отклика породы при определенной частоте возбуждения.

При моделировании камни имеют форму блока и цилиндра, а литология пород — песчаник и гранит. Модели интеллектуально соединены тетраэдрами, как показано на рисунке 3. Применяемая амплитуда гармоники составляет 1000 Н, а частоты воздействия составляют 10 кГц и 20 кГц, соответственно.Удельные свойства горных пород приведены в таблице 1.

мм Размеры Блок Литология Плотность кг / м 3 Модуль упругости Па Коэффициент Пуассона Цилиндр Гранит 2790 2,6 × 10 10 0,26 100 × 100 × 100 200 × 200 × 200 47 300 × 300 200 × 200 × 200 47 300 × 300 904 × 200 Φ100 × 200 Песчаник 2560 4 × 10 10 0.34

3.1. Модальный анализ

На рисунке 4 показаны собственные частоты первых 30 порядков гранита и песчаника размером 200 мм × 200 мм × 200 мм. Из рисунка видно, что собственная частота породы увеличивается с изменением режима колебаний, и порода имеет разные резонансные частоты в разных диапазонах частот. Здесь собственная частота песчаника во всех порядках выше, чем у гранита.Согласно теоретической модели, если порода имеет ту же форму, ее собственная частота пропорциональна модулю упругости и обратно пропорциональна коэффициенту Пуассона и плотности. Результаты, полученные в результате моделирования, согласуются с теоретическими результатами.

3.2. Влияние частоты возбуждения

Гармоническая ударная сила с амплитудой 1000 Н и частотой возбуждения 10 кГц и 20 кГц действует на гранит и песчаник размером 200 мм × 200 мм × 200 мм соответственно.Результаты отклика горных пород показаны на рисунке 5. Когда частота возбуждения находится в диапазоне 0 ~ 10 кГц, резонансная частота гранита составляет 6900 Гц, а песчаника — 8700 Гц. Однако, когда частота возбуждения находится в диапазоне 0 ~ 20 кГц, резонансные частоты гранита и песчаника составляют 10,6 кГц и 16,2 кГц соответственно. Видно, что резонансные частоты породы различны в разных диапазонах частот возбуждения. По мере увеличения частоты возбуждения увеличивается и резонансная частота породы.Это можно рассматривать как еще одно проявление того, что порода имеет разные собственные частоты для системы с несколькими степенями свободы.

3.3. Влияние механических параметров породы

Кривые резонансных частот песчаника под действием гармонической силы 1000 Н и 20 кГц с размерами 100 мм × 100 мм × 100 мм, 200 мм × 200 мм × 200 мм и 300 мм × 300 мм × 300 мм представлены на рисунке 6 (а). Видно, что чем больше порода, тем меньше резонансная частота при одинаковых механических параметрах.Можно также утверждать, что чем меньше масса камня, тем выше частота, необходимая для его резонанса. На рисунке 6 (b) показаны резонансные частоты гранита и песчаника одинакового объема и формы (200 мм × 200 мм × 200 мм) под действием гармонической силы 1000 Н и 20 кГц. Сравнивая результаты, представленные на рисунке 6 (б), мы отмечаем, что резонансная частота гранита ниже, чем у песчаника. В случае одинаковой формы и размера основным фактором, определяющим резонансную частоту породы, являются ее механические свойства.Сравнивая плотность, модуль упругости и коэффициент Пуассона этих двух видов горных пород, можно обнаружить, что результаты численного моделирования согласуются с теоретическими законами.

3.4. Влияние формы камня

На рис. 7 показаны кривые контраста резонансных частот гранита и песчаника различной формы. На рисунке 7 (а) показаны кривые гармонического отклика цилиндрического гранита размером Φ100 мм × 200 мм () и кубического гранита размером 100 мм × 100 мм × 100 мм ().Из результатов моделирования можно узнать, что резонансная частота цилиндрического гранита составляет 14,4 кГц, а кубического гранита — 10,6 кГц. Очевидно, что резонансная частота большего цилиндрического гранита выше, чем у меньшего кубического гранита. Аналогичный анализ проводится на песчанике, форма которого представляет собой цилиндр размером Φ200 × 200 () и блок размером 200 мм × 200 мм × 200 мм () соответственно. Мы также можем получить, что резонансная частота цилиндрического песчаника равна 14.8 кГц, а у кубического песчаника — 16,2 кГц. Из представленных результатов видно, что резонансная частота небольшого цилиндрического песчаника ниже, чем у большого кубического песчаника.

Основываясь на модели с одной глубиной резкости, мы можем знать, что порода с небольшим объемом должна иметь большую резонансную частоту. Однако вывод, который мы получаем из результатов моделирования, прямо противоположен, что указывает на то, что форма породы действительно влияет на ее резонансную частоту.Причина такого результата может быть связана с тем, что жесткость породы будет меняться вместе с ее формой, что в дальнейшем повлияет на ее резонансную частоту.

4. Ультразвуковой тест

Для дальнейшего подтверждения резонансных характеристик породы проводится ультразвуковой тест на резонансной частоте породы в помещении.

4.1. Устройство и ядра

Устройство, используемое в тесте, представляет собой ультразвуковую испытательную систему, которая в основном включает в себя генератор / приемник ультразвуковых импульсов, осциллограф и низкочастотные зонды.Генератор / приемник импульсов имеет частотный диапазон от 50 кГц до 20 МГц, а частоты зонда составляют 50 кГц и 250 кГц соответственно.

В качестве испытательного керна используется искусственный песчаник, а механические параметры горных пород были заданы численным моделированием. Песчаник перерабатывается в две формы, которые представляют собой цилиндры с размерами Φ8 см × 20 см, Φ8 см × 15 см, Φ8 см × 14 см, Φ8 см × 10 см, Φ8 см × 5 см и Φ8 см × 3. см и блоки размером 10 см × 10 см × 10 см, 5 см × 5 см × 5 см и 4 см × 4 см × 4 см, как показано на рисунке 8.

4.2. Процесс и принцип

При испытании генератор / приемник импульсов, осциллограф и датчики подключаются, как показано на рисунке 9. Торцевая поверхность керна из песчаника должна быть плоской, а низкочастотные датчики зажимаются с обоих концов. сердцевины со сливочным маслом в качестве клея.

Принцип испытания заключается в том, что предварительно установленный ультразвуковой сигнал, генерируемый устройством генератора / приемника импульсов, подается на керн песчаника через низкочастотный зонд.Здесь ультразвуковые частоты, установленные в тесте, составляют 50 кГц и 250 кГц. Затем другой низкочастотный зонд улавливает акустический сигнал, распространяющийся от активной зоны. В это время осциллограф отображает не только передаваемый сигнал, но и акустический сигнал, полученный от керна песчаника. По полученному сигналу могут быть получены амплитудно-временные данные породы. Однако, чтобы получить резонансную частоту сердечника, необходимо выполнить преобразование БПФ на кривой время-амплитуда и преобразовать ее в кривую амплитуды-частоты, как показано на рисунке 10.Затем можно получить резонансную частоту и максимальную амплитуду испытательного сердечника при определенной частоте возбуждения, а именно частоту и амплитуду на пике амплитудно-частотной кривой.

4.3. Результаты экспериментов и анализ

Резонансная частота и максимальная амплитуда породы на частотах возбуждения 50 кГц и 250 кГц могут быть получены путем обработки данных амплитуды времени. Результаты экспериментов приведены в таблице 2, а четыре характерные амплитудно-частотные кривые показаны на рисунке 11.

4953 No. Форма Размер Резонансная частота (50 кГц) кГц Амплитуда Резонансная частота (250 кГц 4684) 1 Цилиндр Φ8 см × 20 см 62 0,1691 92 0,1763 2 Φ8 см × 15 см 631438 92 0,2845 3 Φ8 см × 14 см 67 0,1874 93 0,317 4 см 93 0,4409 5 Φ8 см × 5 см 68 0,4277 204 0,1986 6 68469 см 204 0,1611 7 Блок 10 см × 10 см × 10 см 63 0,5264 1864 0,5264 1864 0,16 см × 5 см × 5 см 67 0.6015 197 0,1657 9 4 см × 4 см × 4 см 68 0,4888 206 0,18

4.3.1. Влияние частоты возбуждения

Кривые изменения резонансной частоты керна песчаника при частотах возбуждения 50 кГц и 250 кГц показаны на рисунке 12 (а), а увеличенная кривая резонансной частоты при частоте возбуждения 50 кГц приведена на рис. Рисунок 12 (б). Здесь керны 1–6 представляют собой песчаники цилиндрической формы, а керны 7–9 — песчаники кубической формы. Из рисунка видно, что резонансные частоты одного и того же керна песчаника не совпадают при разных частотах возбуждения, которые увеличиваются с увеличением частоты возбуждения.Результаты экспериментов еще раз подтверждают вывод теоретических исследований.

4.3.2. Влияние объема керна

На рис. 13 показано изменение резонансных частот кернов песчаника различного объема при частотах возбуждения 50 кГц и 250 кГц. Следует отметить, что девять ядер расположены по объему и не различают своей формы. Из обеих кривых видно, что по мере увеличения объема сердечника резонансная частота сердечника в основном уменьшается.Кроме того, на кривой есть особенность, вызванная разной формой скал. Это может быть подтверждено кривыми резонансной частоты на рисунке 12 (б), где объем цилиндрического песчаника уменьшается с 1 до 6, а объем кубического песчаника уменьшается с 7 до 9. Тогда мы можем сделать вывод, что резонансные частоты цилиндрические и кубические песчаники увеличиваются с уменьшением их объемов при двух частотах возбуждения.

Поскольку искусственный керн из песчаника однороден, его свойства, такие как плотность, можно считать одинаковыми.Таким образом, когда мы делаем качественный анализ, переменная объема активной зоны может быть эквивалентна переменной массы активной зоны. Таким образом, можно сделать вывод, что чем больше масса породы, тем ниже ее резонансная частота, что согласуется с анализом теоретической модели собственной частоты породы.

4.3.3. Влияние формы керна

Резонансные частоты цилиндрических и кубических кернов песчаника с аналогичными объемами сравниваются, как показано на рисунке 14. Как видно из гистограммы, при частоте возбуждения 50 кГц (рисунок 14 (a)) или 250 кГц (Рисунок 14 (b)), резонансные частоты крупных кернов песчаника выше, чем резонансные частоты небольших кернов песчаника.Это противоречит предыдущему выводу о том, что резонансная частота породы с теми же механическими параметрами обратно пропорциональна ее объему, что дополнительно подтверждает вывод о том, что форма породы будет влиять на ее резонансную частоту.

4.3.4. Сравнение частоты резонанса между горной породой и буровым инструментом

Чтобы убедиться в применимости технологии RED, важно выяснить, может ли частота возбуждения, которая вызывает резонанс горной породы, повредить буровой инструмент.Поэтому была проведена серия испытаний на резонансной частоте легированной стали, используемой в буровых инструментах, и карбида вольфрама, используемого в режущих зубах бурового долота, и результаты сравнения представлены на рисунке 15.

Рисунок 15 показывает кривые резонансной частоты горной породы, карбида вольфрама и легированной стали, полученные при частоте возбуждения 50 кГц соответственно. Из результатов видно, что резонансные частоты карбида вольфрама и горной породы сильно различаются, а резонансные частоты горной породы и легированной стали относительно близки.Однако это также связано с размером исследуемых материалов. Фактически, чтобы предотвратить воздействие высокочастотной вибрации на систему бурильной колонны, необходимо установить устройство изоляции вибрации между модулем RED и бурильной колонной, чтобы гарантировать, что бурильная колонна не будет затронута. Таким образом, даже при резонансе. Таким образом, даже если резонансные частоты легированной стали в бурильной колонне и горной породе аналогичны, буровые инструменты не будут повреждены во время резонанса горных пород.

5. Выводы

В данной работе резонансные характеристики породы, возникающие во время бурения при гармоническом возбуждении, исследованы теоретически и экспериментально.Были представлены две модели колебаний породы, которые можно использовать для оценки ее собственной частоты. Во-первых, разрабатывается модель с одной степенью свободы, учитывающая свойства и размеры породы. Затем предлагается модель с несколькими степенями свободы, основанная на принципе наименьшего действия. В результате можно сделать вывод, что резонансные характеристики породы связаны как с ее механическими свойствами, так и с размерами.

Численное моделирование было проведено для анализа резонансных характеристик породы.Из модального анализа можно узнать, что собственная частота породы увеличивается с изменением режима вибрации, и порода имеет разные резонансные частоты в разных диапазонах частот. Кроме того, анализ гармонического отклика показывает, что резонансная частота породы увеличивается с увеличением частоты возбуждения. Для одного и того же вида породы, чем меньше масса, тем больше резонансная частота, в то время как для разных видов горных пород механические параметры, такие как плотность, модуль упругости и коэффициент Пуассона, определяют резонансную частоту.Кроме того, форма камня также является одним из основных факторов, влияющих на резонансную частоту.

Наконец, были проведены внутренние испытания искусственных песчаников и материалов буровых инструментов с помощью ультразвуковой испытательной системы. Результаты, полученные в результате испытаний, дополнительно подтверждают правильность теоретического анализа и объясняют осуществимость технологии RED.

Номенклатура

4, б :

k :	Жесткость породы, Н / м
м :	Масса породы, кг
л породы
E :	Модуль упругости, МПа
A :	Площадь поперечного сечения горной породы, м 2
ω149149 4 естественный 4 n частота породы, рад / с
f n :	Собственная частота породы, Гц
ρ :	Плотность плиты, кг / м 3
u :	Вертикальное смещение точки на нейтральной плоскости, м
u tt :	Ускорение пластины, м / с 2
D :	Жесткость пластины при изгибе, Н · м 2
h :	Толщина листа, м
μ :	Коэффициент Пуассона
Длина плиты, м.

Доступность данных

Экспериментальные данные, использованные для подтверждения результатов этого исследования, включены в статью. Нет ограничений на использование данных.

Конфликт интересов

Авторы заявляют об отсутствии конфликта интересов.

Благодарности

Выражаем признательность за поддержку Национальному фонду естественных наук Китая (№ 51704074) и Молодежному научному фонду провинции Хэйлунцзян (№ QC2018049).Работа также поддерживается Фондом развития талантов (№ SCXHB201703, ts26180119 и td26180141) и Молодежным научным фондом (№ 2019QNL-07) Северо-восточного нефтяного университета.

Звуковые помехи и резонанс: стоячие волны в воздушных столбах

Цели обучения

К концу этого раздела вы сможете:

• Определите пучность, узел, основную частоту, обертоны и гармоники.
• Определите случаи звуковых помех в повседневных ситуациях.
• Опишите, как звуковые помехи, возникающие внутри открытых и закрытых трубок, изменяют характеристики звука и как это применимо к звукам, издаваемым музыкальными инструментами.
• Рассчитайте длину трубки, используя измерения звуковой волны.

Рис. 1. В некоторых типах наушников для подавления посторонних шумов используются явления конструктивных и деструктивных помех. (Источник: JVC America, Flickr)

Интерференция — отличительная черта волн, каждая из которых демонстрирует конструктивную и деструктивную интерференцию, точно аналогичную той, которая наблюдается для водных волн.Фактически, один из способов доказать, что что-то «является волной», — это наблюдать за интерференционными эффектами. Итак, поскольку звук является волной, мы ожидаем, что он будет иметь интерференцию; мы уже упоминали несколько таких эффектов, например, удары двух одинаковых нот, сыгранных одновременно.

На рис. 2 показано разумное использование звуковых помех для подавления шума. Предполагается более крупномасштабное применение активного снижения шума за счет деструктивных помех для целых пассажирских салонов коммерческих самолетов. Чтобы получить деструктивную интерференцию, выполняется быстрый электронный анализ, и вводится второй звук, максимумы и минимумы которого полностью противоположны входящему шуму.Звуковые волны в жидкостях — это волны давления, соответствующие принципу Паскаля; давление из двух разных источников складывается и вычитается, как простые числа; то есть положительное и отрицательное избыточное давление добавляют к гораздо меньшему давлению, производя звук меньшей интенсивности. Хотя полностью разрушительные помехи возможны только в самых простых условиях, с помощью этого метода можно снизить уровень шума на 30 дБ и более.

Рис. 2. Наушники, предназначенные для подавления шума с разрушительными помехами, создают звуковую волну, прямо противоположную входящему звуку.Эти наушники могут быть более эффективными, чем простое пассивное затухание, используемое в большинстве средств защиты слуха. Такие наушники использовались во время рекордного кругосветного беспосадочного полета самолета «Вояджер», чтобы защитить слух пилотов от шума двигателя.

Где еще можно наблюдать звуковые помехи? Все звуковые резонансы, например, в музыкальных инструментах, возникают из-за конструктивных и деструктивных помех. Только резонансные частоты конструктивно интерферируют, образуя стоячие волны, тогда как другие интерферируют деструктивно и отсутствуют.Резонанс и стоячие волны играют жизненно важную роль — от гудка, издаваемого надуванием бутылки, до характерного аромата звуковой коробки скрипки и узнаваемости голоса великого певца.

Помехи

Интерференция — это такой фундаментальный аспект волн, что наблюдение интерференции является доказательством того, что что-то является волной. Волновая природа света была установлена ​​экспериментами, показывающими интерференцию. Точно так же, когда электроны, рассеянные кристаллами, демонстрировали интерференцию, их волновая природа была подтверждена точно такой, как предсказывается симметрией с некоторыми волновыми характеристиками света.

Предположим, мы держим камертон около конца трубки, которая закрыта на другом конце, как показано на рисунках 3, 4, 5 и 6. Если камертон имеет только правильную частоту, столб воздуха в трубке громко резонирует, но на большинстве частот очень мало вибрирует. Это наблюдение просто означает, что столб воздуха имеет только определенные собственные частоты. На рисунках показано, как формируется резонанс на самой низкой из этих собственных частот. Возмущение распространяется по трубке со скоростью звука и отскакивает от закрытого конца.Если трубка правильной длины, отраженный звук возвращается на камертон ровно через полцикла и конструктивно мешает продолжающемуся звуку, производимому камертоном. Входящие и отраженные звуки образуют в трубке стоячую волну, как показано на рисунке.

Рис. 3. Резонанс воздуха в трубке, закрытой с одного конца, вызванный камертоном. Возмущение движется по трубе.	Рис. 4. Резонанс воздуха в трубке, закрытой с одного конца, вызванный камертоном.Возмущение отражается от закрытого конца трубки.
Рис. 5. Резонанс воздуха в трубке, закрытой с одного конца, вызванный камертоном. Если длина трубки L подходящая, помеха возвращается к камертону через полцикла и конструктивно мешает продолжающемуся звуку камертона. Эта интерференция образует стоячую волну, и столб воздуха резонирует.	Рис. 6. Резонанс воздуха в трубке, закрытой с одного конца, вызванный камертоном.График вытеснения воздуха по длине трубы показывает отсутствие на закрытом конце, где движение ограничено, и максимум на открытом конце. Эта стоячая волна имеет в трубке одну четверть своей длины волны, так что λ = 4 L .

Стоячая волна, сформированная в трубе, имеет максимальное смещение воздуха (пучность ) на открытом конце, где движение не ограничено, и отсутствие смещения (узел ) на закрытом конце, где движение воздуха остановился.Расстояние от узла до пучности составляет одну четвертую длины волны, и это равно длине трубки; таким образом, λ = 4 L . Такой же резонанс может быть вызван вибрацией, возникающей на закрытом конце трубы или около него, как показано на рисунке 7. Лучше всего рассматривать это как естественную вибрацию столба воздуха, независимо от того, как она вызвана.

Рис. 7. Такая же стоячая волна создается в трубке за счет вибрации, вносимой около ее закрытого конца.

Рисунок 8.{\ prime} = \ frac {4L} {3} \\ [/ latex]. Продолжая этот процесс, вы обнаружите целую серию коротковолновых и высокочастотных звуков, резонирующих в трубке. Мы используем определенные термины для обозначения резонансов в любой системе. Самая низкая резонансная частота называется основной , а все более высокие резонансные частоты называются обертонами . Все резонансные частоты являются целыми кратными основной гармоники, и вместе они называются гармониками . Основная гармоника — это первая гармоника, первый обертон — это вторая гармоника и так далее.На рисунке 9 показаны основная гармоника и первые три обертона (первые четыре гармоники) в трубке, закрытой с одного конца.

Рис. 9. Основной и три нижних обертона закрытой с одного конца трубки. У всех есть максимальные вытеснения воздуха на открытом конце и нет — на закрытом конце.

Основная и обертоны могут присутствовать одновременно в различных комбинациях. Например, средний C на трубе имеет звук, отчетливо отличающийся от среднего C на кларнете, причем оба инструмента являются модифицированными версиями закрытой с одного конца трубы.Основная частота одна и та же (и обычно самая интенсивная), но обертоны и их сочетание интенсивности различны и могут быть затемнены музыкантом. Этот микс — это то, что придает различным музыкальным инструментам (и человеческим голосам) их отличительные характеристики, независимо от того, есть ли у них воздушные колонны, струны, звуковые коробки или барабанные пластинки. Фактически, большая часть нашей речи определяется формированием полости, образованной горлом и ртом, и расположением языка для регулировки основных и сочетания обертонов.Например, простые резонансные полости могут резонировать со звуком гласных. (См. Рис. 10.) У мальчиков в период полового созревания растет гортань и изменяется форма резонансной полости, что приводит к разнице в преобладающих частотах речи мужчин и женщин.

Рис. 10. Горло и рот образуют закрытый с одного конца столб воздуха, который резонирует в ответ на вибрации голосового аппарата. Спектр обертонов и их интенсивность меняются в зависимости от формы рта и положения языка для формирования разных звуков.Голосовой аппарат можно заменить механическим вибратором, при этом возможна понятная речь. Вариации основных форм делают разные голоса узнаваемыми.

Теперь давайте поищем закономерность в резонансных частотах для простой трубки, закрытой с одного конца. Основное значение имеет λ = 4 L , а частота связана с длиной волны и скоростью звука, как указано как v _w = fλ.

Решение относительно f в этом уравнении дает

[латекс] f = \ frac {v _ {\ text {w}}} {\ lambda} = \ frac {v _ {\ text {w}}} {4L} \\ [/ latex],

, где v _w — скорость звука в воздухе.{\ prime} = 3 \ frac {v _ {\ text {w}}} {4L} = 3f \\ [/ latex].

Поскольку f ′ = 3 f , мы называем первый обертон третьей гармоникой. Продолжая этот процесс, мы видим закономерность, которую можно обобщить в одном выражении. Резонансные частоты трубки, закрытой с одного конца, равны

.

[латекс] f_n = n \ frac {v _ {\ text {w}}} {4L}, n ​​= 1,3,5 \\ [/ latex],

, где f ₁ — основной тон, f ₃ — первый обертон и т. Д.Интересно, что резонансные частоты зависят от скорости звука и, следовательно, от температуры. Эта зависимость представляет собой заметную проблему для органов в старых неотапливаемых соборах, а также является причиной того, что музыканты обычно доводят свои духовые инструменты до комнатной температуры перед тем, как играть на них.

Пример 1. Найдите длину трубки с фундаментальной частотой 128 Гц

1. Какой длины должна быть закрытая с одного конца трубка в день, когда температура воздуха 22,0ºC, если ее основная частота должна быть 128 Гц (C ниже средней C)?
2. Какова частота его четвертого обертона?

Стратегия

Длина L может быть найдена из соотношения в [latex] f_n = n \ frac {v _ {\ text {w}}} {4L} \\ [/ latex], но сначала нам нужно найти скорость звука v _w .

Решение для части 1

Определить известных:

• основная частота 128 Гц
• температура воздуха 22,0ºС

Используйте [latex] f_n = n \ frac {v _ {\ text {w}}} {4L} \\ [/ latex], чтобы найти основную частоту ( n = 1):

[латекс] f_1 = \ frac {v _ {\ text {w}}} {4L} \\ [/ latex]

Решите это уравнение для длины: [латекс] L = \ frac {v _ {\ text {w}}} {4f_1} \\ [/ latex].

Найдите скорость звука, используя [latex] v _ {\ text {w}} = \ left (331 \ text {m / s} \ right) \ sqrt {\ frac {T} {273 \ text {K}}} \\[/латекс].

[латекс] v _ {\ text {w}} = \ left (331 \ text {m / s} \ right) \ sqrt {\ frac {295 \ text {K}} {273 \ text {K}}} = 344 \ text {m / s} \\ [/ latex]

Введите значения скорости звука и частоты в выражение для L .

[латекс] L = \ frac {v _ {\ text {w}}} {4f_1} = \ frac {344 \ text {m / s}} {4 (128 \ text {Hz})} = 0,672 \ text { м} \\ [/ латекс]

Обсуждение части 1

Многие духовые инструменты представляют собой модифицированные трубки с отверстиями для пальцев, клапанами и другими устройствами для изменения длины резонирующего столба воздуха и, следовательно, частоты проигрываемой ноты.Для рожков, воспроизводящих очень низкие частоты, таких как тубы, нужны лампы такой длины, чтобы они были скручены в петли.

Решение для части 2

Определить известных:

• первый обертон имеет n = 3
• второй обертон имеет n = 5
• третий обертон имеет n = 7
• четвертый обертон имеет n = 9

Введите значение четвертого обертона в [латекс] f_n = n \ frac {v _ {\ text {w}}} {4L} \\ [/ latex]:

[латекс] f_9 = 9 \ frac {v _ {\ text {w}}} {4L} = 9f_1 = 1.15 \ text {кГц} \\ [/ latex]

Обсуждение части 2

Возникает ли этот обертон в простой трубке или музыкальном инструменте, зависит от того, как он стимулируется к вибрации, и от деталей его формы. Например, тромбон не производит своей основной частоты, а только издает обертоны.

Другой тип трубок — открытые с обоих концов. Примеры — органные трубы, флейты и гобои. Резонансы трубок, открытых с обоих концов, можно анализировать так же, как резонансы трубок, закрытых с одного конца.Столбы воздуха в трубках, открытых с обоих концов, имеют максимальное смещение воздуха на обоих концах, как показано на рисунке 11. Стоячие волны образуются, как показано.

Рис. 11. Показаны резонансные частоты трубки, открытой с обоих концов, включая основной тон и первые три обертона. Во всех случаях максимальные перемещения воздуха происходят на обоих концах трубы, что дает ей собственные частоты, отличные от собственных частот трубы, закрытой с одного конца.

Основываясь на том факте, что труба, открытая с обоих концов, имеет максимальное смещение воздуха с обоих концов, и используя рисунок 11 в качестве ориентира, мы можем видеть, что резонансные частоты трубы, открытой с обоих концов, составляют:

[латекс] f_n = n \ frac {v _ {\ text {w}}} {2L}, n ​​= 1,2,3, \ dots, \\ [/ latex]

, где f ₁ — основной обертон, f ₂ — первый обертон, f ₃ — второй обертон и т. Д.Обратите внимание, что трубка, открытая с обоих концов, имеет основную частоту в два раза больше, чем она была бы, если бы закрылась с одного конца. Он также имеет другой спектр обертонов, чем трубка, закрытая с одного конца. Итак, если у вас есть две лампы с одинаковой основной частотой, но одна открыта с обоих концов, а другая закрыта с одного конца, они будут звучать по-разному при игре, потому что у них разные обертоны. Средняя до, например, будет звучать богаче при игре на открытой трубе, потому что она имеет как четные, так и нечетные значения основной гармоники.В закрытой трубке есть только нечетные кратные.

Реальные приложения: резонанс в повседневных системах

Резонанс возникает во многих различных системах, включая струны, воздушные столбы и атомы. Резонанс — это управляемые или вынужденные колебания системы на ее собственной частоте. В резонансе энергия быстро передается колебательной системе, и амплитуда ее колебаний растет до тех пор, пока система больше не может быть описана законом Гука. Примером этого является намеренно искаженный звук в определенных типах рок-музыки.

Рис. 12. Струнные инструменты, такие как скрипки и гитары, используют резонанс в своих звуковых коробках, чтобы усилить и обогатить звук, создаваемый их вибрирующими струнами. Бридж и опоры передают колебания струны звуковым коробам и воздуху внутри. (кредиты: гитара, Фелисиано Гимарес, Fotopedia; скрипка, Стив Снодграсс, Flickr)

Рис. 13. Резонанс использовался в музыкальных инструментах с доисторических времен. Эта маримба использует тыквы в качестве резонансных камер для усиления звука.(кредит: APC Events, Flickr)

Духовые инструменты используют резонанс в воздушных столбах для усиления тонов, издаваемых губами или вибрирующими язычками. Другие инструменты также используют воздушный резонанс для усиления звука. На рисунке 12 показаны скрипка и гитара, у обеих есть звуковые коробки, но разной формы, что приводит к разным структурам обертонов. Вибрирующая струна создает звук, который резонирует в звуковой коробке, значительно усиливая звук и создавая обертоны, придающие инструменту его характерный аромат.Чем сложнее форма звуковой коробки, тем выше ее способность резонировать в широком диапазоне частот. Маримба, подобная той, что изображена на Рисунке 13, использует горшки или тыквы под деревянными планками, чтобы усилить их тон. Резонанс горшка можно отрегулировать, добавив воды.

Мы подчеркивали звуковые приложения в наших обсуждениях резонансных и стоячих волн, но эти идеи применимы к любой системе, которая имеет волновые характеристики. Например, вибрирующие струны на самом деле резонируют и имеют основы и обертоны, аналогичные таковым для воздушных колонн.Более тонкие резонансы в атомах из-за волнового характера их электронов. Их орбитали можно рассматривать как стоячие волны, которые имеют фундаментальное (основное состояние) и обертоны (возбужденные состояния). Удивительно, что волновые характеристики применимы к такому широкому кругу физических систем.

Проверьте свое понимание

Часть 1

Опишите, чем наушники с шумоподавлением отличаются от стандартных наушников, используемых для блокировки посторонних звуков.

Решение

Обычные наушники блокируют звуковые волны только физическим барьером.Наушники с шумоподавлением используют разрушительные помехи для уменьшения громкости внешних звуков.

Часть 2

Как можно использовать узел и пучность стоячей волны для определения длины трубы с закрытым концом?

Решение

Когда трубка резонирует на своей собственной частоте, узел волны находится на закрытом конце трубки, а пучность — на открытом. Длина трубки равна одной четвертой длины волны этой волны.Таким образом, если мы знаем длину волны волны, мы можем определить длину трубки.

Исследования PhET: звук

Это моделирование позволяет видеть звуковые волны. Отрегулируйте частоту или громкость, и вы сможете увидеть и услышать, как меняется волна. Перемещайте слушателя и слушайте то, что она слышит.

Щелкните, чтобы загрузить симуляцию. Запускать на Java.

Сводка раздела

• Звуковые помехи и резонанс имеют те же свойства, что и все волны.
• В воздушных столбах резонанс с самой низкой частотой называется основной, а все более высокие резонансные частоты — обертонами. Все вместе они называются гармониками.
• Резонансные частоты трубки, закрытой с одного конца: [латекс] {f} _ {n} = n \ frac {{v} _ {w}} {4L} \ text {,} n = 1, 3, 5 \ dots \\ [/ latex], f ₁ — основная, а L — длина трубки.
• Резонансные частоты трубки, открытой с обоих концов: [латекс] {f} _ {n} = n \ frac {{v} _ {w}} {2L} \ text {,} n = 1, 2, 3 \ точки \\ [/ латекс]

Концептуальные вопросы

1. Как гитара без усиления производит звуки намного более интенсивные, чем звуки натянутой струны, натянутой простой палкой?
2. Вам даны два духовых инструмента одинаковой длины.Один открыт с обоих концов, а другой закрыт с одного конца. Что может производить самую низкую частоту?
3. В чем разница между обертоном и гармоникой? Все ли гармоники обертоны? Все ли обертоны гармоничны?

Задачи и упражнения

1. «Эффектный» изготовленный на заказ автомобиль имеет два латунных рожка, которые должны выдавать одинаковую частоту, но на самом деле излучают 263,8 и 264,5 Гц. Какая частота ударов производится?

2. Какие частоты ударов будут присутствовать: (a) Если музыкальные ноты A и C играются вместе (частоты 220 и 264 Гц)? (б) Если D и F играть вместе (частоты 297 и 352 Гц)? (c) Если все четверо играют вместе?

3.Какие частоты ударов возникают, если молоток фортепиано ударяет по трем струнам, излучающим частоты 127,8, 128,1 и 128,3 Гц?

4. Настройщик фортепиано слышит ритм каждые 2,00 секунды при прослушивании камертона с частотой 264,0 Гц и одиночной струны фортепиано. Какие две возможные частоты струны?

5. а) Какова основная частота трубы длиной 0,672 м, открытой с обоих концов, в день, когда скорость звука составляет 344 м / с? б) Какова частота его второй гармоники?

6.Если духовой инструмент, такой как туба, имеет основную частоту 32,0 Гц, каковы его первые три обертона? Он закрыт с одного конца. (Обертоны настоящей тубы сложнее, чем в этом примере, потому что это коническая трубка.)

7. Каковы первые три обертона фагота с основной частотой 90,0 Гц? Он открыт с обоих концов. (Обертоны настоящего фагота сложнее, чем в этом примере, потому что его двойная трость заставляет его действовать больше, как трубка, закрытая с одного конца.)

8. Какой длины должна быть флейта, чтобы иметь основную частоту 262 Гц (эта частота соответствует средней C на равномерно темперированной хроматической шкале) в день, когда температура воздуха составляет 20,0 ° C? Он открыт с обоих концов.

9. Какой длины должен быть гобой, чтобы воспроизводить основную частоту 110 Гц в день, когда скорость звука составляет 343 м / с? Он открыт с обоих концов.

10. Какова длина трубки с основной частотой 176 Гц и первым обертоном 352 Гц, если скорость звука составляет 343 м / с?

11.(a) Найдите длину трубы для органа, закрытой с одного конца, которая дает основную частоту 256 Гц при температуре воздуха 18,0 ° C. (б) Какова его основная частота при 25,0 ° C?

12. На какую долю изменятся частоты, создаваемые духовым инструментом, когда температура воздуха повысится с 10,0 ° C до 30,0 ° C? То есть найти соотношение частот при этих температурах.

13. Слуховой проход резонирует, как трубка, закрытая с одного конца. (См. Рисунок 5 в разделе Слух.) Если длина ушных каналов колеблется от 1 до 1.От 80 до 2,60 см в среднем у населения, каков диапазон основных резонансных частот? Возьмем температуру воздуха 37,0 ° C, что соответствует температуре тела. Как этот результат соотносится с графиком зависимости интенсивности от частоты человеческого уха (рис. 14)?

Рис. 14. Заштрихованная область представляет частоты и уровни интенсивности, встречающиеся в нормальной разговорной речи. Линия с нулевым звуком представляет собой нормальный порог слуха, тогда как значения на 40 и 60 представляют собой пороги для людей с 40- и 60-фоновой потерей слуха, соответственно.

14. Вычислите первый обертон в слуховом проходе, который резонирует как трубка длиной 2,40 см, закрытая с одного конца, приняв температуру воздуха 37,0 ° C. Неужели ухо особенно чувствительно к такой частоте? (Резонансы слухового прохода усложняются его неоднородной формой, на что мы не будем обращать внимания.)

15. Грубое приближение к воспроизведению голоса состоит в том, чтобы рассматривать дыхательные пути и рот как резонирующую трубку, закрытую с одного конца. (См. Рисунок 10.) (a) Какова основная частота, если трубка равна 0.Длина 240 м, если принять температуру воздуха 37,0 ° С? б) Какой стала бы эта частота, если бы человек заменил воздух гелием? Предположим такую ​​же температурную зависимость для гелия, что и для воздуха.

16. (a) Студентов физической лаборатории просят определить длину столба воздуха в закрытой с одного конца трубке, имеющей основную частоту 256 Гц. Они держат трубку вертикально и наполняют ее водой до верха, затем опускают воду, пока вибрирует камертон с частотой 256 Гц, и прислушиваются к первому резонансу.Какова температура воздуха, если резонанс происходит на длине 0,336 м? б) Как долго они будут наблюдать второй резонанс (первый обертон)?

17. Какие частоты будет воспроизводить трубка длиной 1,80 м в слышимом диапазоне при 20,0 ° C, если: (a) Трубка закрыта с одного конца? б) он открыт с обоих концов?

Глоссарий

пучность: точка максимального смещения

узел: точка нулевого смещения

основной: самый низкочастотный резонанс

обертонов: все резонансные частоты выше основной

гармоник: термин, используемый для коллективного обозначения основной гармоники и ее обертонов

Избранные решения проблем и упражнения

1.0,7 Гц

3. 0,3 Гц, 0,2 Гц, 0,5 Гц

5. (а) 256 Гц; (б) 512 Гц

7. 180 Гц, 270 Гц, 360 Гц

9. 1,56 м

11. (а) 0,334 м; (б) 259 Гц

13. от 3,39 до 4,90 кГц

15. (а) 367 Гц; (б) 1,07 кГц

17. (а) f _n = n (47,6 Гц), n = 1, 3, 5,…, 419; (b) f _n = n (95,3 Гц), n = 1, 2, 3,…, 210

резонансных частот | Насосы и системы

Насосы и системы, июль 2013

Механический резонанс может быть проблемой для вертикальных насосов.Внешне похожие конструкции насосов могут работать по-разному в зависимости от геометрических особенностей и пропорций их роторов. В вертикальных насосах длинные сегменты вала направляются втулками амортизатора, обычно сделанными из бронзы, а иногда и из неметаллического материала.

Если длина и диаметр вала или любых его участков между втулками уменьшаются до определенного соотношения, может возникнуть состояние резонанса. Ротор будет «петь», как гитарная струна — и, к сожалению, это не самая лучшая песня.

Рисунок 1. Собственная частота (резонанс) может разрушить ротор вертикального турбинного насоса

Определение резонанса
Для расчета, прогнозирования и предотвращения условий резонанса разработчики насосов используют сложные компьютерные программы. Программное обеспечение учитывает следующие факторы (среди прочего):

• Длина сегментов вала

• Характер перекачиваемой жидкости (ее характеристики демпфирования и жесткости)

Однако урок можно извлечь из анализа упрощенной формулы, которая все еще используется в качестве оценки.Варианты формулы могут предполагать сегмент вала с концами различной конфигурации (см. Таблицу 1).
Рассмотрим формулу балки с равномерно распределенной массой. Луч с равномерно распределенной массой имеет бесконечные собственные частоты. Собственные частоты расположены в порядке возрастания. Самая низкая собственная частота называется основной частотой или основной собственной частотой.
Собственная частота ωn определяется по:

ωn2 = βn4 x EI / (м / л) [Уравнение 1]

Где:
E = модуль упругости Юнга
I = момент инерции поперечного сечения
L = длина балки (пролет)
м = общая распределенная масса (= Вт / г)
β1, β2 и β3 для различных граничных условий приведены в таблице 1.

Таблица 1. Значения β для граничных условий

Примеры
Используя уравнение 1, рассмотрим случай собственной частоты (с обоими концами сегментов вала, считающимися просто поддерживаемыми) для трех диаметров вала (1,44 дюйма, 1,8 дюйма и 2,4 дюйма) для тех же 6 футов (72 дюйма). -дюйм) сегмент вала. Если этот вал работает при 1800 об / мин (30 герц), проблемный диаметр вала может быть между 1,8 дюйма и 2,4 дюйма, вызывая резонанс вала ротора (см. Таблицу 2).

Таблица 2. Собственные частоты для трех диаметров вала
Примечание: данные рассчитаны с использованием уравнения 1. Таблица 3. Расчетные частоты для стержня, человека и бактерий

Используя уравнение 1, можно оценить собственные частоты других конструкций, независимо от того, насколько они велики или малы. В таблице 3 собственная частота 6-футового стального стержня рассчитана на уровне 183 Гц.

Собственная частота человека (предполагаемая средняя плотность костей) составляет 73 Гц, а частота бактериального червя — 16 мегагерц.
Некоторые интересные примеры структурного резонанса, встречающегося в жизни, можно найти по адресу:

Цифры в этом столбце являются приблизительными, но суть ясна. При правильной собственной частоте воздействие на насосы — и другие вещи — может быть плохим (или хорошим).

Таблица 3.