§56. Резонанс напряжений и резонанс токов
Явление резонанса.
Электрическая цепь, содержащая индуктивность и емкость, может служить колебательным контуром, где возникает процесс колебаний электрической энергии, переходящей из индуктивности в емкость и обратно. В идеальном колебательном контуре эти колебания будут незатухающими.
При подсоединении колебательного контура к источнику переменного тока угловая частота источника ω может оказаться равной угловой частоте ω0, с которой происходят колебания электрической энергии в контуре. В этом случае имеет место явление резонанса, т. е. совпадения частоты свободных колебаний ω0, возникающих в какой-либо физической системе, с частотой вынужденных колебаний ω, сообщаемых этой системе внешними силами.
Резонанс в электрической цепи можно получить тремя способами: изменяя угловую частоту ω источника переменного тока, индуктивность L или емкость С. Различают резонанс при последовательном соединении L и С — резонанс напряжений и при параллельном их соединении — резонанс токов. Угловая частота ω0, при которой наступает резонанс, называется резонансной, или собственной частотой колебаний резонансного контура.
Угловая частота ω0, при которой наступает резонанс, называется резонансной, или собственной частотой колебаний резонансного контура.
Резонанс напряжений.
При резонансе напряжений (рис. 196, а) индуктивное сопротивление XL равно емкостному Хси полное сопротивление Z становится равным активному сопротивлению R:
Z = √( R2 + [ω0L — 1/(ω0C)]2 ) = R
В этом случае напряжения на индуктивности UL и емкости Uc равны и находятся в противофазе (рис. 196,б), поэтому при сложении они компенсируют друг друга. Если активное сопротивление цепи R невелико, ток в цепи резко возрастает, так как реактивное сопротивление цепи X = XL—Xс становится равным нулю. При этом ток I совпадает по фазе с напряжением U и I=U/R. Резкое возрастание тока в цепи при резонансе напряжений вызывает такое же возрастание напряжений UL и Uc, причем их значения могут во много раз превышать напряжение U источника, питающего цепь.
Угловая частота ω0, при которой имеют место условия резонанса, определяется из равенства ωoL = 1/(ω0С).
Рис. 196. Схема (а) и векторная диаграмма (б) электрической цепи, содержащей R, L и С, при резонансе напряжений
Отсюда имеем:
ωo = 1/√(LC) (74)
Если плавно изменять угловую частоту ω источника, то полное сопротивление Z сначала начинает уменьшаться, достигает наименьшего значения при резонансе напряжений (при ωo), а затем увеличивается (рис. 197, а). В соответствии с этим ток I в цепи сначала возрастает, достигает наибольшего значения при резонансе, а затем уменьшается.
Рис. 197. Зависимость тока I и полного сопротивления Z от ω для последовательной (а) и параллельной (б) цепей переменного тока
Резонанс токов.
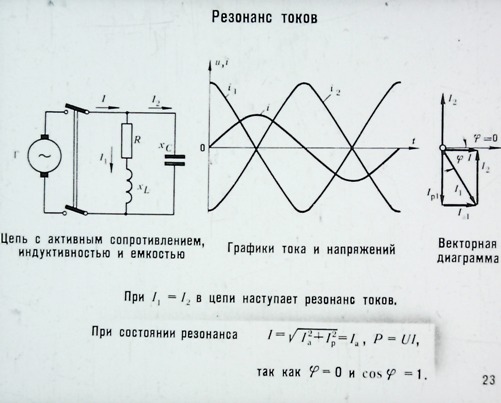
Резонанс токов может возникнуть при параллельном соединении индуктивности и емкости (рис. 198, а). В идеальном случае, когда в параллельных ветвях отсутствует активное сопротивление (R1=R2 = 0), условием резонанса токов является равенство реактивных сопротивлений ветвей, содержащих индуктивность и емкость, т. е. ωoL = 1/(ωoC).
е. ωoL = 1/(ωoC).
Рис. 198. Электрическая схема (а) и векторные диаграммы (б и в) при резонансе токов
Так как в рассматриваемом случае активная проводимость G = 0, ток в неразветвленной части цепи при резонансе I=U √(G2+(BL-BC)2)= 0. Значения токов в ветвях I1 и I2 будут равны (рис. 198,б), но токи будут сдвинуты по фазе на 180° (ток IL в индуктивности отстает по фазе от напряжения U на 90°, а ток в емкости I с опережает напряжение U на 90°).
Следовательно, такой резонансный контур представляет собой для тока I бесконечно большое сопротивление и электрическая энергия в контур от источника не поступает. В то же время внутри контура протекают токи IL и Iс, т. е. имеет место процесс непрерывного обмена энергией внутри контура. Эта энергия переходит из индуктивности в емкость и обратно.
Как следует из формулы (74), изменяя значения емкости С или индуктивности L, можно изменять частоту колебаний ω0 электрической энергии и тока в контуре, т. е. осуществлять настройку контура на требуемую частоту.
е. осуществлять настройку контура на требуемую частоту.
Если бы в ветвях, в которых включены индуктивность и емкость, не было активного сопротивления, этот процесс колебания энергии продолжался бы бесконечно долго, т. е. в контуре возникли бы незатухающие колебания энергии и токов IL и Iс.
Однако реальные катушки индуктивности и конденсаторы всегда поглощают электрическую энергию (из-за наличия в катушках активного сопротивления проводов и возникновения в конденсаторах токов смещения, нагревающих диэлектрик), поэтому в реальный контур при резонансе токов поступает от источника некоторая электрическая энергия и по неразветвленной части цепи протекает некоторый ток I.
Условием резонанса в реальном резонансном контуре, содержащем активные сопротивления R1 и R2, будет равенство реактивных проводимостей BL = BC ветвей, в которые включены индуктивность и емкость.
Из рис. 198, в следует, что ток I в неразветвленной части цепи совпадает по фазе с напряжением U, так как реактивные токи 1L и Iс равны, но противоположны по фазе, вследствие чего их векторная сумма равна нулю.
Если в рассматриваемой параллельной цепи изменять частоту ωо источника переменного тока, то полное сопротивление цепи начинает увеличиваться, достигает наибольшего значения при резонансе, а затем уменьшается (см. рис. 197,б). В соответствии с этим ток I начинает уменьшаться, достигает наименьшего значения Imin = Ia при резонансе, а затем увеличивается.
В реальных колебательных контурах, содержащих активное сопротивление, каждое колебание тока сопровождается потерями энергии. В результате сообщенная контуру энергия довольно быстро расходуется и колебания тока постепенно затухают. Для получения незатухающих колебаний необходимо все время пополнять потери энергии в активном сопротивлении, т. е. такой контур должен быть подключен к источнику переменного тока соответствующей частоты ω0.
Явления резонанса напряжения и тока и колебательный контур получили весьма широкое применение в радиотехнике и высокочастотных установках. При помощи колебательных контуров мы получаем токи высокой частоты в различных радиоустройствах и высокочастотных генераторах.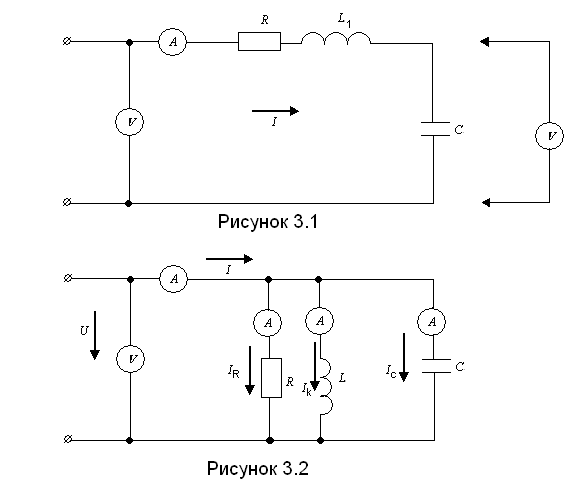
Колебательный контур — важнейший элемент любого радиоприемника. Он обеспечивает его избирательность, т. е. способность выделять из радиосигналов с различной длиной волны (т. е. с различной частотой), посланных различными радиостанциями, сигналы определенной радиостанции.
причины возникновения, способы использования и возможный вред, цепь переменного тока
Резонанс напряжений происходит в электрической цепи, включающей в себя несколько элементов: источник электроэнергии, катушку индуктивности и конденсатор. Перечисленные элементы соединяются последовательно. При этом источник напряжения имеет такую частоту, которая совпадает с внутренним контуром. Это часто применяется в полосовых фильтрах.
- Последовательное соединение
- Цепь переменного тока
- Понятие резонанса
- Польза и вред
Последовательное соединение
Катушка индуктивности и последовательно включенный в цепь конденсатор вместе особенным образом воздействуют на генератор, от которого запитана цепь. Также они влияют на фазовые соотношения напряжения и тока:
Также они влияют на фазовые соотношения напряжения и тока:
- Первый элемент сдвигает фазу, при этом напряжение начинает обгонять ток примерно на четверть периода.
- Второй элемент действует иначе. Он заставляет ток обгонять напряжение также на одну четвертую часть периода фазы.
Индуктивное сопротивление действует на смещение фаз, из-за чего его можно считать противоположным работе емкостного сопротивления. В результате итоговый сдвиг фаз между напряжением и током в цепи зависит от суммарного действия индуктивного и емкостного сопротивлений, а также соотношения между ними. От этого тоже зависит характер цепи.
Если одноимённая величина превосходит противоположную, то систему можно считать емкостной, ведь ток превосходит по фазе. При иной ситуации характер цепи считается индуктивным, ведь напряжение доминирует.
Общее реактивное сопротивление определить просто.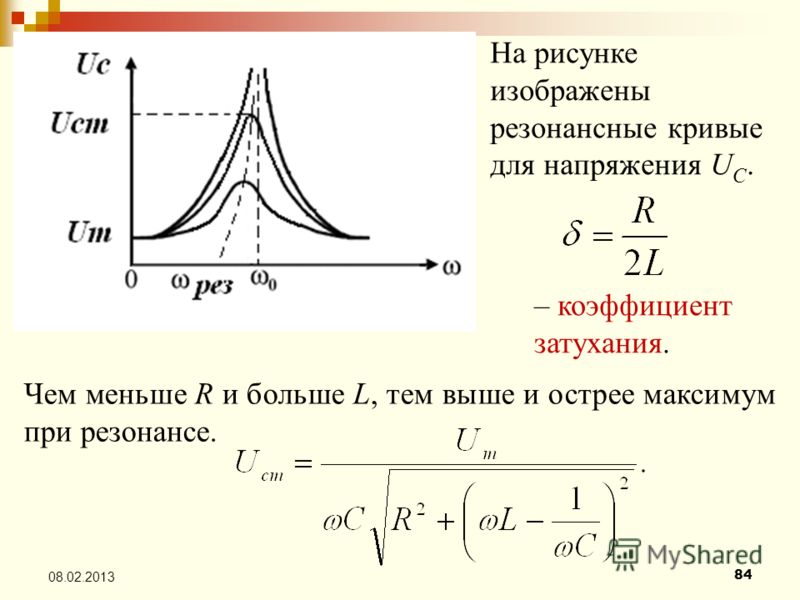
- Индуктивное от катушки.
- Емкостное от конденсатора.
Из-за того, что они оказывают противоположное воздействие, одному из них присваивается отрицательный знак (обычно ёмкостному сопротивлению конденсатора). Тогда общее реактивное сопротивление можно найти так: из показателя катушки вычесть конденсатор. Если общее напряжение разделить на найденный параметр, то по закону Ома получится сила тока. Эту формулу можно легко изменить, переведя на напряжение. Оно будет равно произведению силы тока и разности двух сопротивлений (индуктивное берется с катушки, а емкостное — с конденсатора).
Если раскрыть скобку, то первое значение отразит действительный показатель части общего напряжения, которая старается преодолеть сопротивление. Второе — слагающая всего напряжения, которая пытается преодолеть емкостный параметр. Так, общее напряжение можно рассматривать как сумму этих слагаемых.
Обычно значением активного сопротивления можно пренебречь.
Если оно слишком велико, учитывать его все же нужно.
Для определения этого значения нужно вычислить квадратный корень из суммы двух частей:
- Общее активное сопротивление, возведенное в квадрат.
- Квадрат разности индуктивного и емкостного сопротивлений, то есть общее реактивное.
Очевиден переход к закону Ома. Если разделить силу тока на найденное значение, то можно получить напряжение.
Цепь переменного тока
Если соединить катушку с конденсатором последовательно, происходит меньшее смещение по фазе, чем если бы эти элементы были включены отдельно. Это связано с тем, что эти элементы действуют на цепь совершенно иначе, сдвигая баланс в разные стороны. Они компенсируют фазовый сдвиг, усредняют его значение.
Возможен и равный баланс. Полная компенсация соотношения между напряжением и током произойдет, если сопротивление катушки и конденсатора будут равны друг другу. В этом случае цепь будет вести себя так, будто бы в нее не включены эти элементы. Действие системы сведется к чистому активному сопротивлению, образованному соединительными проводами и катушкой. Сила действующего тока достигнет максимального значения, его можно будет вычислить по стандартному закону Ома.
В этом случае цепь будет вести себя так, будто бы в нее не включены эти элементы. Действие системы сведется к чистому активному сопротивлению, образованному соединительными проводами и катушкой. Сила действующего тока достигнет максимального значения, его можно будет вычислить по стандартному закону Ома.
Понятие резонанса
При описанной ситуации действующие напряжения на катушке и конденсаторе сравняются, а также достигнут максимального значения. Если активное сопротивление в этой цепи минимальное, то локальные показатели будут в несколько раз превышать общее напряжение. Такое явление принято называть резонансом напряжений.
Важно понимать, что местные сопротивления напрямую зависят от показателей тока. Если частоту тока уменьшить, то индуктивное значение снизится, а емкостное — возрастет. Помимо активного сопротивления, в сети также возникнет реактивное, из-за чего резонанс сойдет на нет.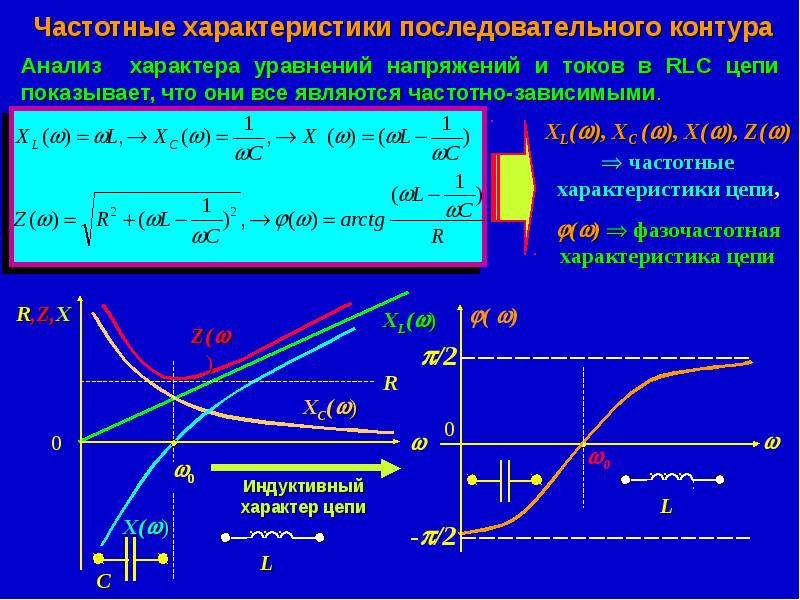 Это случится и в том случае, если изменить значения индуктивности или емкости.
Это случится и в том случае, если изменить значения индуктивности или емкости.
Если в цепи возникает резонанс, то энергия источника расходуется исключительно на нагрев проводов, то есть преодоление активного сопротивления, так как катушка перекидывает ток на конденсатор и обратно без усилий генератора. Ведь в цепи с одним из элементов ток колеблется, периодически переходя от истока в магнитное поле. Это касается катушки. В случае с конденсатором наблюдается аналогичная ситуация, только участвует электрическое поле. Если эти два элемента объединены, а также наблюдается резонанс, то энергия циклично движется от катушки к конденсатору и обратно. При этом она тратится в большей степени только из-за сопротивления проводника.
При нарушении резонанса количество энергии, требуемой первому и второму элементу, не совпадает. Возникнет избыток, который будет покрываться усилиями генератора. Этот процесс можно сравнить с механизмом часов с маятником. Если бы силы трения не было, он мог колебаться без использования дополнительного груза или пружины в механизме. Но эти элементы, когда необходимо, передают часть своей энергии маятнику, из-за чего тот преодолевает силу трения и движется непрерывно. При резонансе в электроцепи количество энергии, которую необходимо сообщить для поддержания колебаний, минимально.
Но эти элементы, когда необходимо, передают часть своей энергии маятнику, из-за чего тот преодолевает силу трения и движется непрерывно. При резонансе в электроцепи количество энергии, которую необходимо сообщить для поддержания колебаний, минимально.
Цепь считается колебательным контуром, если соблюдено несколько условий. Во-первых, ток должен быть переменным. Во-вторых, в систему должны входить генератор, конденсатор и катушка индуктивности. В-третьих, элементы должны быть соединены последовательно. В-четвертых, показатели внутренних сопротивлений должны быть равны.
Но резонанс невозможен, если частота генератора, емкость и индуктивность цепи не будут соответствовать значениям, зависящим от других параметров цепи. Все они вычисляются по специальным несложным формулам.
Польза и вред
Резонанс часто используют с пользой. Один из ярких бытовых примеров — починка радиоприемника. Электрика устройства настраивается таким образом, чтобы возник резонанс.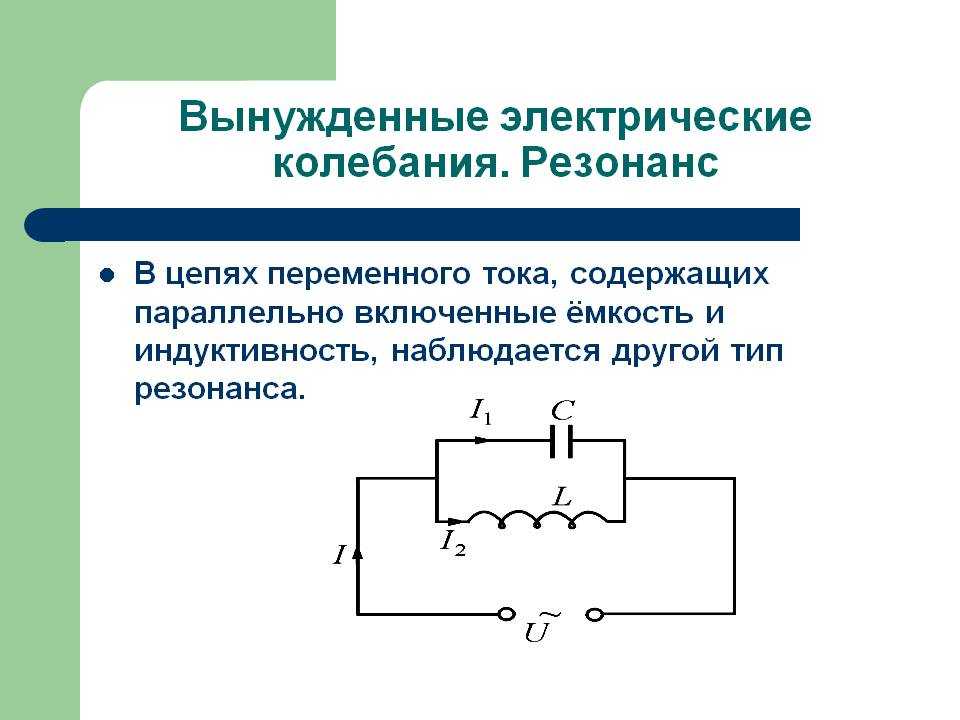 Благодаря этому напряжение на катушке повышается и превосходит значение в цепи, созданной антенной. Это необходимо для нормальной работы приемника.
Благодаря этому напряжение на катушке повышается и превосходит значение в цепи, созданной антенной. Это необходимо для нормальной работы приемника.
Но иногда действие резонанса сказывается на технике исключительно пагубно. Рост напряжения на некоторых участках может привести к их порче. Из-за того, что локальные значения не соответствуют генератору, отдельные детали или измерительные приборы могут выйти из строя.
Свойства цепи при резонансе напряжений ток
Область применения
Это явление в цепи колебательного контура имеет тенденцию к затуханию. Чтобы стало возможным использовать это явление в различных приборах и устройствах, необходимо постоянно поддерживать характеристики электричества в заданных пределах. Сделать этот процесс постоянным очень просто: достаточно подпитывать систему переменным напряжением с постоянными значениями частоты.
Радиовышка
Важно! Эффект резонанса широко применяется в различных радиопередающих и принимающих сигнал устройствах. Наиболее часто, это явление используется в различных фильтрах
Наиболее часто, это явление используется в различных фильтрах
Например, если на пути входящего электрического сигнала необходимо избавиться от составляющей определённой частоты, то параллельно проводнику устанавливают конденсатор, резистор и дроссель. Если фильтр необходим для того, чтобы «пропустить» сигнал определенной частоты, то также изготавливается фильтр из ёмкости, сопротивления и индуктивности, но подключается такая система последовательно
Наиболее часто, это явление используется в различных фильтрах. Например, если на пути входящего электрического сигнала необходимо избавиться от составляющей определённой частоты, то параллельно проводнику устанавливают конденсатор, резистор и дроссель. Если фильтр необходим для того, чтобы «пропустить» сигнал определенной частоты, то также изготавливается фильтр из ёмкости, сопротивления и индуктивности, но подключается такая система последовательно.
Электрический фильтр
Использовать эффект резонанса можно и для повышения напряжения. Например, в ситуации, когда электрический двигатель не способен работать на расчетных показателях мощности по причине низкого напряжения, достаточно установить по мощному конденсатору на каждую фазу, чтобы полностью разрешить проблему.
Например, в ситуации, когда электрический двигатель не способен работать на расчетных показателях мощности по причине низкого напряжения, достаточно установить по мощному конденсатору на каждую фазу, чтобы полностью разрешить проблему.
Резонанс в электрической цепи может возникать при наличии определенных условий, поэтому от него можно избавиться либо вызвать намеренно. Если такое явление является нежелательным, то, во многих случаях, достаточно изменить рабочую частоту или увеличить сопротивление, чтобы полностью устранить это паразитическое явление. Простейшая система этого типа состоит из конденсатора, резистора и дросселя, поэтому, при необходимости, можно легко собрать устройство, в котором это электрический эффект будет выполнять какую-либо полезную функцию.
Вам это будет интересно Особенности источников тока
В чем заключается явление резонанса напряжений
Как известно, в сети переменного тока домашней сети разность потенциалов изменяется с частотой 50 Гц. То есть, каждую секунду производится 50 полных колебаний. Такое явление несложно замерить даже бытовым частотомером, который определить точное значение этого параметра именно по эффекту электромагнитного поля, образованного вокруг проводника с током. Катушка с металлическим сердечником, которая устанавливается в измерительный прибор, будет колебаться с частотой электромагнитного поля домашней электросети.
То есть, каждую секунду производится 50 полных колебаний. Такое явление несложно замерить даже бытовым частотомером, который определить точное значение этого параметра именно по эффекту электромагнитного поля, образованного вокруг проводника с током. Катушка с металлическим сердечником, которая устанавливается в измерительный прибор, будет колебаться с частотой электромагнитного поля домашней электросети.
Вам это будет интересно Особенности свободной энергии
Частотомер
Таким образом, вырабатывается переменное напряжение, которое затем может быть увеличено, а его частота подсчитана микропроцессорным либо аналоговым устройством, после чего информация может быть выведена на экран.
Разобравшись, в чем заключается явление резонанса электрического напряжения, необходимо стараться всячески избегать этого явления, когда одновременные колебательные движения полей являются нежелательными. Если же в каком-либо устройстве такой эффект применяется с целью получения определенных физических явлений, то схема должна быть изготовлена с высокой добротностью, чтобы на поддержание процесса тратилось как можно меньше энергии (таким образом повышается КПД устройства).
Волновая проводимость
При ток в ветви с индуктивностью гораздо больше общего тока, поэтому такое явление называется резонансом токов и широко используется в силовых сетях промышленных предприятий для компенсации реактивной мощности.
Резонансную частоту тока найдем из условия равенства реактивных проводимостей ветвей.
После ряда преобразований получим:
Из формулы следует, что:
1) резонансная частота зависит от параметров не только реактивных сопротивлений, но и активных;
2) резонанс возможен, если и больше или меньше r, в противном случае частота будет мнимой величиной и резонанс невозможен;
3) если , то частота будет иметь неопределенное значение, что означает возможность существования резонанса на любой частоте при совпадении фаз напряжения питания и общего тока;
4) при резонансная частота напряжения равна резонансной частоте тока.
Энергетические процессы в цепи при резонансе токов аналогичны процессам, происходящим при резонансе напряжений.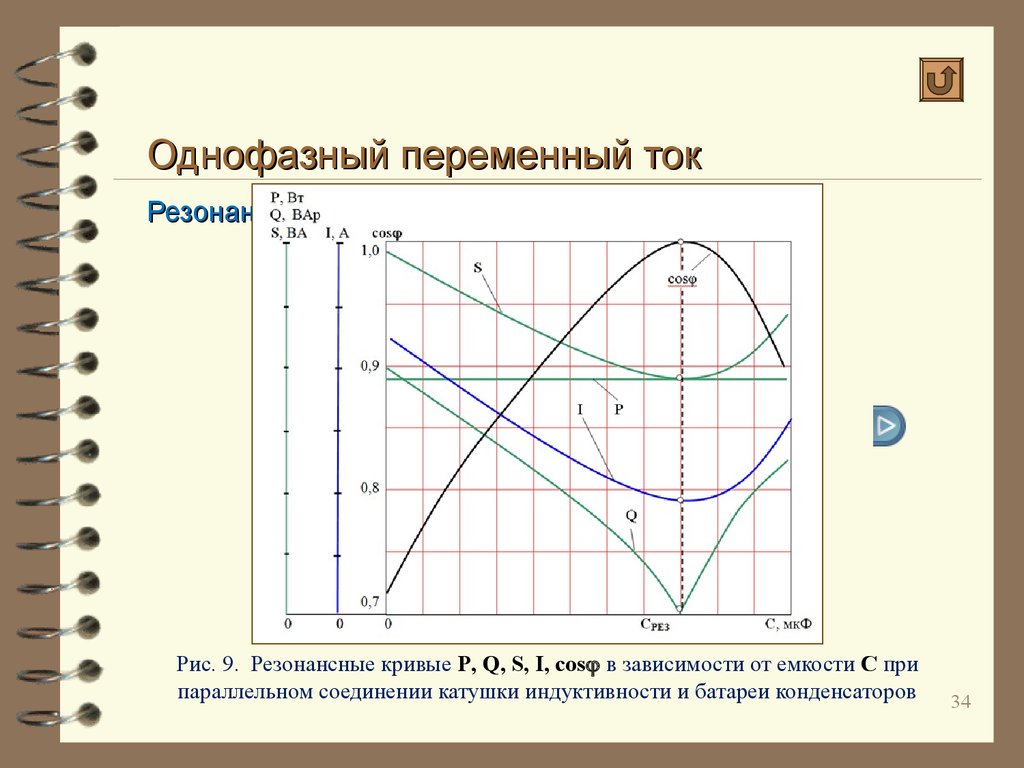
Реактивная энергия циркулирует внутри цепи: в одну часть периода энергия магнитного поля индуктивности переходит в энергию электрического поля емкости, в следующую часть периода происходит обратный процесс.
При резонансе токов реактивная мощность равна нулю.
Большинство промышленных потребителей переменного тока носит активно-индуктивный характер и, следовательно, потребляет реактивную мощность. К таким потребителям относятся асинхронные двигатели, установки электрической сварки и т.д.
Для уменьшения реактивной мощности и повышения коэффициента мощности параллельно потребителю включают батарею конденсаторов, что приводит к уменьшению тока в проводах, соединяющих потребителя с источником энергии.
Дополнительно по теме
- История формирования ТОЭ
- Основные понятия электрических цепей
- Электрические цепи постоянного тока
- Пример расчета цепей постоянного тока
- Электрические цепи переменного тока
- Расчет цепей переменного тока
- Символический метод расчета цепей
- Резонансные явления
- Переходные процессы
- Трехфазные цепи
- Симметричные составляющие трехфазной системы
- Нелинейные цепи
- Несинусоидальные токи и напряжения
- Магнитные цепи
Электрический резонанс
Для полноценного изучения (применения) явления надо учитывать полное сопротивление цепи (Z). Вместе с потерями его можно выразить следующей формулой при последовательном подключении функциональных элементов:
Вместе с потерями его можно выразить следующей формулой при последовательном подключении функциональных элементов:
Z = √ R2 + (2π * f * L — 1/2π * f * C)2.
По закону Ома:
I = U/Z = U/ √ R2 + (2π * f * L — 1/2π * f * C)2.
Если соблюдается равенство реактивных составляющих, сопротивление уменьшается с одновременным увеличением силы тока. При соблюдении такого условия несложно вычислить резонансную частоту (Fрез):
- 2π * f * L = 1/2π * f * C;
- Fрез = 1/2π * √ L*C.
Резонанс напряжений, достигающих максимальной амплитуды
Получить наибольшую амплитуду в последовательном контуре можно с помощью изменения следующих параметров:
- индуктивности;
- емкости;
- частоты.
Значения отдельных компонентов устанавливают с применением рассмотренных выше формул. Так, величину емкости можно вычислить следующим образом:
C = 1/ f2 * L.
Если реактивные компоненты значительно больше активного сопротивления, на клеммах конденсатора или катушки можно получить повышение напряжения, по сравнению с источником.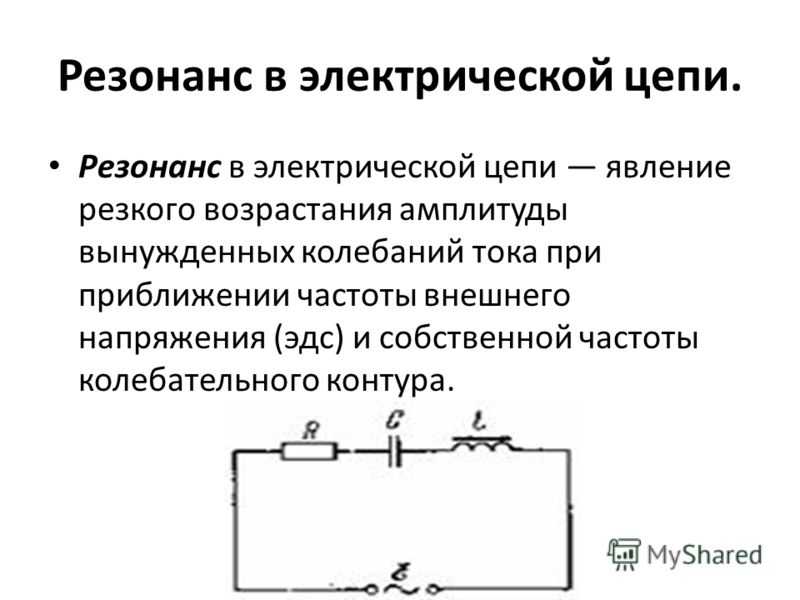
Резонанс токов через реактивные элементы
В параллельном контуре оперируют с понятиями реактивных проводимостей (BL и Bc). Как и в предыдущем примере, для создания резонансного режима необходимо обеспечить равенство этих параметров. Дополнительным условием является совпадение частот (источника и контура). Ток при резонансе будет проходить только через активное сопротивление R.
Общие сведения
Электрическим сопротивлением проводника является свойство проводить электрический ток. Для построения и расчета колебательного контура необходимо знать способы нахождения активного и реактивного сопротивлений. Сопротивление для цепей, питающихся от переменного тока (ЦПТ), бывает следующих видов: активное, реактивное и полное.
Активным сопротивлением является обыкновенный резистор. Реактивное состоит из следующих типов нагрузки: индуктивное и емкостное. Индуктивное (Xl) — сопротивление катушки индуктивности в цепи переменного тока, а емкостное (Xc) определяется наличием емкости в цепи (конденсатора).
Активное сопротивление
Активным сопротивлением в ЦПТ называется наличие любой нереактивной нагрузки. Его можно рассчитать следующими способами: при помощи измерения величины сопротивления и расчетным методом. Для измерения R применяется прибор, который называется омметром. Омметр входит в состав комбинированных приборов измерения электрических величин, которые называются мультиметрами. Он подключается параллельно нагрузке, причем для проведения измерений следует выключить электрическую цепь, поскольку наличие тока приведет прибор к выходу из строя.
Существует еще один способ, который является расчетным, однако он требует знаний в области физики. При вычислении величины R следует произвести измерения силы тока и напряжения, а точнее, их амплитудных значений (Uм и Iм соответственно). Это возможно сделать при помощи соответствующих приборов.
Для измерения величины напряжения применяется вольтметр, а силу тока можно измерить при помощи амперметра. Кроме того, эти приборы измеряют только действующие значения напряжения (Uд) и силы тока (Iд). Для расчета амплитудных значений следует воспользоваться следующими формулами:
Для расчета амплитудных значений следует воспользоваться следующими формулами:
- Uм = Uд * sqrt (2).
- Iм = Iд * sqrt (2).
Для расчета R, которое можно найти, используя закон Ома для участка цепи (Iм = Uм / R): R = Uм / Iм. Воспользовавшись соотношениями зависимостей амплитудных значений от действующих, возможно рассчитать R: R = Uд * sqrt (2) / Iд * sqrt (2) = Uд / Iд. На практике применяют способ измерения сопротивления омметром.
Другие виды нагрузок
При наличии в ЦПТ катушки индуктивности возникает Xl, которую необходимо только рассчитывать.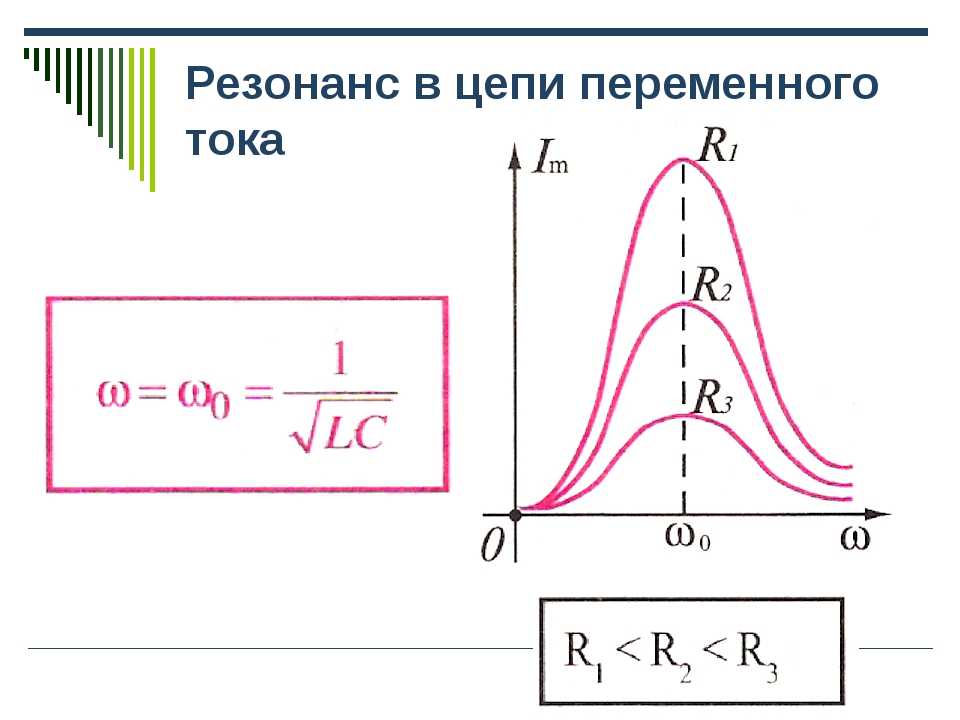 Индуктивное сопротивление рассчитывается по формуле, для которой необходимы циклическая частота (w) и индуктивность катушки (L): Xl = w * L.
Индуктивное сопротивление рассчитывается по формуле, для которой необходимы циклическая частота (w) и индуктивность катушки (L): Xl = w * L.
Циклическая частота рассчитывается по следующей формуле, для которой необходимо только знать частоту переменного тока (f) и число ПИ (3,1416): w = 2 * 3,1416 * f. Индуктивность катушки рассчитывается, исходя из значений диаметра катушки (D в мм), числа витков (n) и длины намотки (l): L = (sqr (D/10) * sqr (n)) / (4,5 * D + 10 * l). Если подставить в формулу расчета индуктивного сопротивления все соотношения, то получается: Xl = 2 * 3,1416 * f * (sqr (D/10) * sqr (n)) / (4,5 * D + 10 * l).
Если в ЦПТ присутствует конденсатор с емкостью C, то добавляется еще и емкостное сопротивление — Xl, которое рассчитывается по следующей формуле: Xc = 1 / (w * C) = 1 / (2 * 3,1416 * f * C). Полное сопротивление в ЦПТ обозначается литерой Z и рассчитывается по формуле: Z = sqrt . Если подставить в формулу полного сопротивления соотношения, по которым находятся R, Xl и Xc, то получается следующая формула: Z = sqrt [sqr (Uд / Iд) +sqr ((1 / (2 * 3,1416 * f * C)) — (2 * 3,1416 * f * (sqr (D/10) * sqr (n)) / (4,5 * D + 10 * l))]. Для упрощения вычисления можно рассчитать отдельно значения R, Xc и Xl.
Для упрощения вычисления можно рассчитать отдельно значения R, Xc и Xl.
Колебания и частота
Процедура, связанная с изменением положения системы рядом с точкой равновесного состояния и повторяющаяся с течением времени, называется колебаниями. Качающийся маятник повторяет свои движения относительно нормали к горизонтальной плоскости. При этом, если не прикладывать к его движению дополнительной энергии, его раскачивания затухнут.
Явление таких изменений можно классифицировать по следующим параметрам:
- по математической модели, используемой в колебаниях;
- по структуре периодичности;
- по природе физических свойств;
- по виду взаимодействия с окружающими условиями.
Внимание! Все колебания, независимо от своих физических свойств, имеют общие законы, которые можно описать волновыми явлениями. Эти закономерности исследует теория волновых колебаний. Механические колебания связаны с трансформацией одной формы энергии в другую, волновые – с пространственным передвижением и распространением энергии
Механические колебания связаны с трансформацией одной формы энергии в другую, волновые – с пространственным передвижением и распространением энергии.
Общими параметрами для всех колебаний являются:
- частота;
- период;
- амплитуда.
Частотой считают количество колебаний, совершаемых телом за единицу времени. Единица измерения – герц (Гц), графическое обозначение – f, ʋ. Частота может быть круговой – при периодичном движении точки по окружности, ещё её называют циклической:
ω = 2π*T, (рад/с).
Период (T) являет собой время целого (полного) колебания, во время которого можно зафиксировать повторение любой из характеристик состояния системы. Это значит, что она совершила полное колебание. Обозначение периода – Т, единица измерения – секунда (с).
Две величины T и f являются обратными, что следует из формул:
- T = 1/f;
- f = 1/T.
Наибольшее отклонение точки тела или любой величины системы от равновесного положения называется амплитудой колебаний и обозначается буквой A. Единицей измерения являются те величины, изменения которых рассматриваются. При механических отклонениях амплитуду измеряют в метрах (м), амплитуду переменного напряжения – в вольтах (В) и так далее.
Период и частота механических колебаний
Резонанс напряжений
Давайте возьмем другие параметры катушки и конденсатора и посмотрим, что у нас происходит на самих радиоэлементах. Нам ведь надо досконально все выяснить ;-). Беру катушку индуктивности с индуктивностью в 22 микрогенри:
и конденсатор в 1000 пФ
Из них собираю последовательный колебательный контур. Итак, чтобы поймать резонанс, я не буду в схему добавлять резистор. Поступлю более хитрее.
Так как мой генератор частоты китайский и маломощный, то при резонансе у нас в цепи остается только активное сопротивление потерь R. В сумме получается все равно маленькое значение сопротивления, поэтому ток при резонансе достигает максимальных значений. В результате этого, на внутреннем сопротивлении генератора частоты падает приличное напряжение и выдаваемая амплитуда частоты генератора падает. Я буду ловить минимальное значение этой амплитуды. Следовательно это и будет резонанс колебательного контура. Перегружать генератор — это не есть хорошо, но что не сделаешь ради науки!
Ну что же, приступим ;-).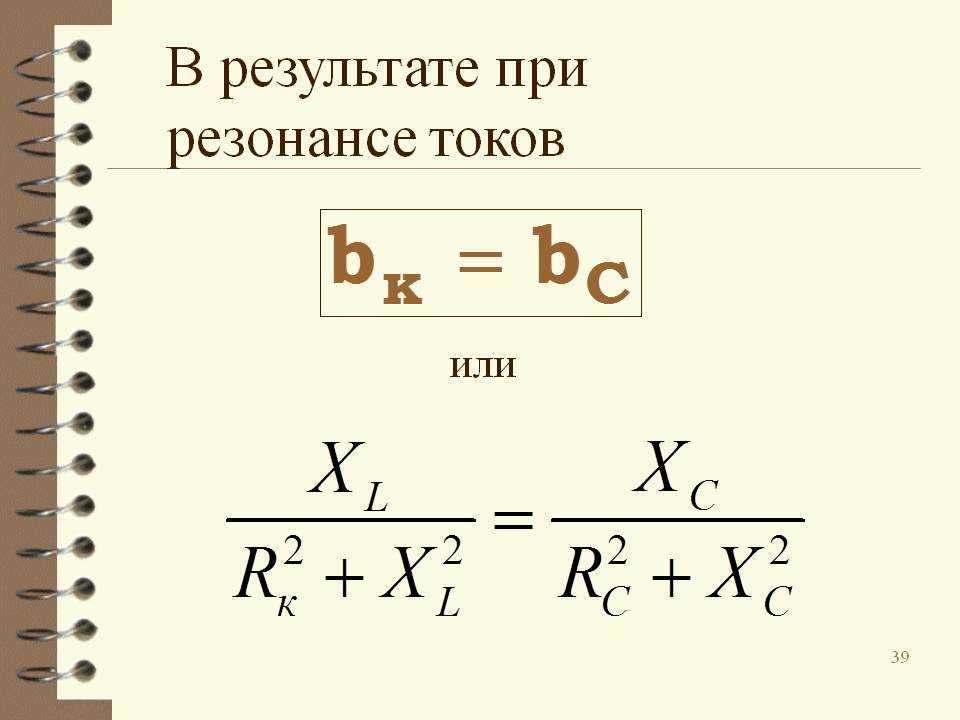 Давайте сначала посчитаем резонансную частоту по формуле Томсона. Для этого я открываю онлайн калькулятор на просторах интернета и быстренько высчитываю эту частоту. У меня получилось 1,073 Мегагерц.
Давайте сначала посчитаем резонансную частоту по формуле Томсона. Для этого я открываю онлайн калькулятор на просторах интернета и быстренько высчитываю эту частоту. У меня получилось 1,073 Мегагерц.
Ловлю резонанс на генераторе частоты по его минимальным значениям амплитуды. Получилось как-то вот так:
Размах амплитуды 4 Вольта
Хотя на генераторе частоты размах более 17 Вольт! Вот так вот сильно просело напряжение. И как видите, резонансная частота получилась чуток другая, чем расчетная: 1,109 Мегагерц.
Теперь небольшой прикол 😉
Вот этот сигнал мы подаем на наш последовательный колебательный контур:
Как видите, мой генератор не в силах выдать большую силу тока в колебательный контур на резонансной частоте, поэтому сигнал получился даже чуть искаженным на пиках.
Ну а теперь самое интересное. Давайте замеряем падение напряжения на конденсаторе и катушке на резонансной частоте. То есть это будет выглядеть вот так:
Смотрим напряжение на конденсаторе:
Размах амплитуды 20 Вольт (5х4)! Откуда? Ведь подавали мы на колебательный контур синус с частотой в 2 Вольта!
Ладно, может с осциллографом что-то произошло?. Давайте замеряем напряжение на катушке:
Давайте замеряем напряжение на катушке:
Народ! Халява!!! Подали 2 Вольта с генератора, а получили 20 Вольт и на катушке и на конденсаторе! Выигрыш энергии в 10 раз! Успевай только снимать энергию с конденсатора или с катушки!
Ну ладно раз такое дело… беру лампочку от мопеда на 12 Вольт и цепляю ее к конденсатору или катушке. Лампочке ведь вроде как по-барабану на какой частоте работать и какой ток кушать. Выставляю амплитуду, чтобы на катушке или конденсаторе было где то Вольт 20 так как среднеквадратичное напряжение будет где-то Вольт 14, и цепляю поочередно к ним лампочку:
Как видите — полный ноль. Лампочка гореть не собирается, так что побрейтесь фанаты халявной энергии). Вы ведь не забыли, что мощность определяется произведением силы тока на напряжение? Напряжения вроде как-бы хватает, а вот силы тока — увы! Поэтому, последовательный колебательный контур носит также название узкополосного (резонансного) усилителя напряжения, а не мощности!
Объяснение резонанса напряжения
При резонансе напряжение на катушке и на конденсаторе оказались намного больше, чем то, которое мы подавали на колебательный контур. В данном случае у нас получилось в 10 раз больше. Почему же напряжение на катушке при резонансе равняется напряжению на конденсаторе. Это легко объясняется. Так как в последовательном колебательном контуре катушка и кондер идут друг за другом, следовательно, в цепи протекает одна и та же сила тока.
В данном случае у нас получилось в 10 раз больше. Почему же напряжение на катушке при резонансе равняется напряжению на конденсаторе. Это легко объясняется. Так как в последовательном колебательном контуре катушка и кондер идут друг за другом, следовательно, в цепи протекает одна и та же сила тока.
При резонансе реактивное сопротивление катушки равняется реактивному сопротивлению конденсатора. Получаем по правилу шунта, что на катушке у нас падает напряжение UL = IXL , а на конденсаторе UC = IXC . А так как при резонансе у нас XL = XC , то получаем что UL = UC , ток ведь в цепи один и тот же ;-). Поэтому резонанс в последовательном колебательном контуре называют также резонансом напряжений, так как напряжение на катушке на резонансной частоте равняется напряжению на конденсаторе.
Электроника и электротехника. Шпаргалка. 18. РЕЗОНАНС ТОКОВ (Юлия Валерьевна Щербакова)
№27 Явление резонанса в электрических цепях.
Резонансом называют режим, когда в цепи, содержащей индуктивности и емкости, ток совпадает по фазе с напряжением. Входные реактивные сопротивление и проводимость равны нулю: x = ImZ = 0 и B = ImY = 0. Цепь носит чисто активный характер: Z = R; сдвиг фаз отсутствует (φ=0).
В цепи, содержащей последовательно соединенные участки с индуктивным и емкостным характерами сопротивлений, резонанс называется резонансом напряжений. Рассмотрим простейшую цепь, которую часто называют последовательным контуром. Для нее резонанс наступает при x = xL – xC = 0 или xL = xC, откуда:
Напряжения на индуктивности и емкости в этом режиме равны по величине и, находясь в противофазе, компенсируют друг друга. Все приложенное к цепи напряжение приходится на ее активное сопротивление (рис. 27.1, а).
Рис. 27.1 — Векторные диаграммы при резонансе напряжений(а) и токов(б)
Напряжения на индуктивности и емкости могут значительно превышать напряжения на входе цепи. Их отношение, называемое добротностью контура Q, определяется величинами индуктивного (или емкостного) и активного сопротивлений:
Добротность показывает, во сколько раз напряжения на индуктивности и емкости при резонансе превышают напряжение, приложенное к цепи.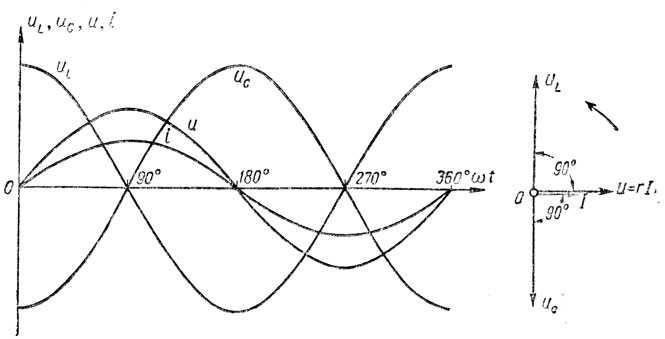 В радиотехнических цепях она может достигать нескольких сотен единиц.
В радиотехнических цепях она может достигать нескольких сотен единиц.
Аналогичные рассуждения можно провести и для цепи, состоящей из параллельно соединенных R, L и C. Векторная диаграмма ее резонансного режима приведена на рис. 27.1, б. Рассмотрим теперь более сложную цепь с двумя параллельными ветвями, содержащими активные и реактивные сопротивления (рис. 27.3, а).
Рис. 27.3 — Разветвленная цепь (а) и ее эквивалентная схема (б)
Для нее условием резонанса является равенство нулю ее реактивной проводимости: ImY = 0. Это равенство означает, что мы должны мнимую часть комплексного выражения Y приравнять к нулю.
Определяем комплексную проводимость цепи. Она равна сумме комплексных проводимостей ветвей:
Приравнивая к нулю выражение, стоящее в круглых скобках, получаем:
Левая и правая части последнего выражения представляют собой не что иное, как реактивные проводимости первой и второй ветвей B1 и B2. Заменяя схему на рис. 27.3, а эквивалентной (рис. 27.3, б), параметры которой вычисляем по формулам, и используя условие резонанса (B = B1 – B2 = 0), снова приходим к конечному выражению.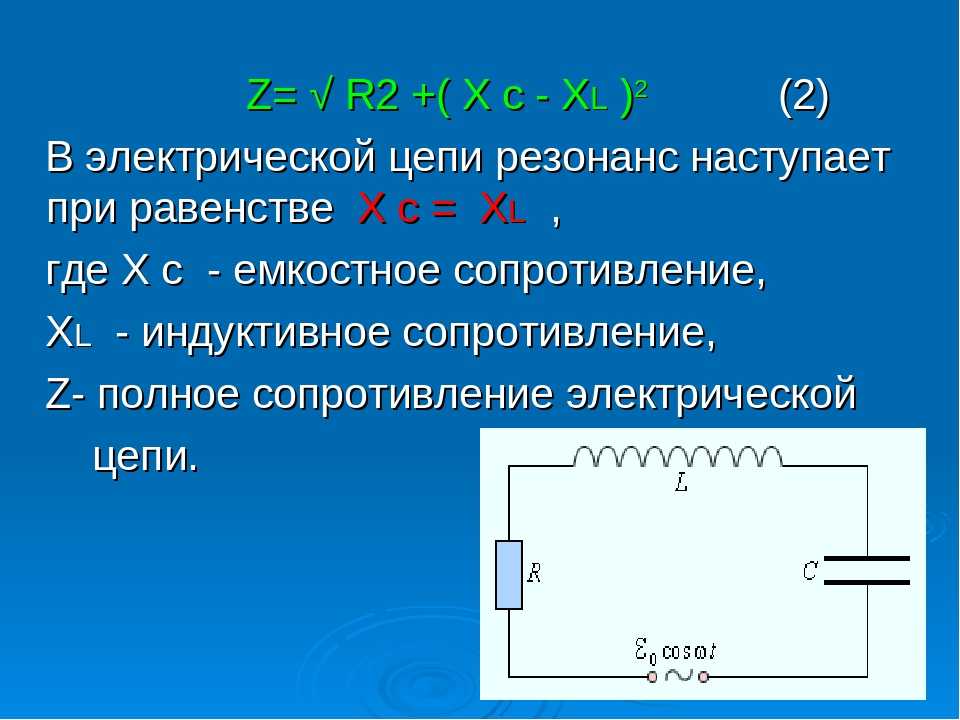
Схеме на рис. 27.3, б соответствует векторная диаграмма, приведенная на рис. 27.4
Рис. 27.4 — Векторная диаграмма резонансного режима разветвленной цепи
Резонанс в разветвленной цепи называется резонансом токов. Реактивные составляющие токов параллельных ветвей противоположны по фазе, равны по величине и компенсируют друг друга, а сумма активных составляющих токов ветвей дает общий ток.
Мнение эксперта
It-Technology, Cпециалист по электроэнергетике и электронике
Задавайте вопросы «Специалисту по модернизации систем энергогенерации»
Понятие о резонанс токов. Условия его возникновения и способы осуществления Электрический резонанс одно из самых распространенных в мире физических явлений, без которого не было бы TV, диагностических мед. Спрашивайте, я на связи!
Польза и вред резонансов
Механический резонанс
Полезный результат понятен из примера с колоколом. Человек со средними физическими способностями способен создать перезвон, который слышен на очень большом расстоянии.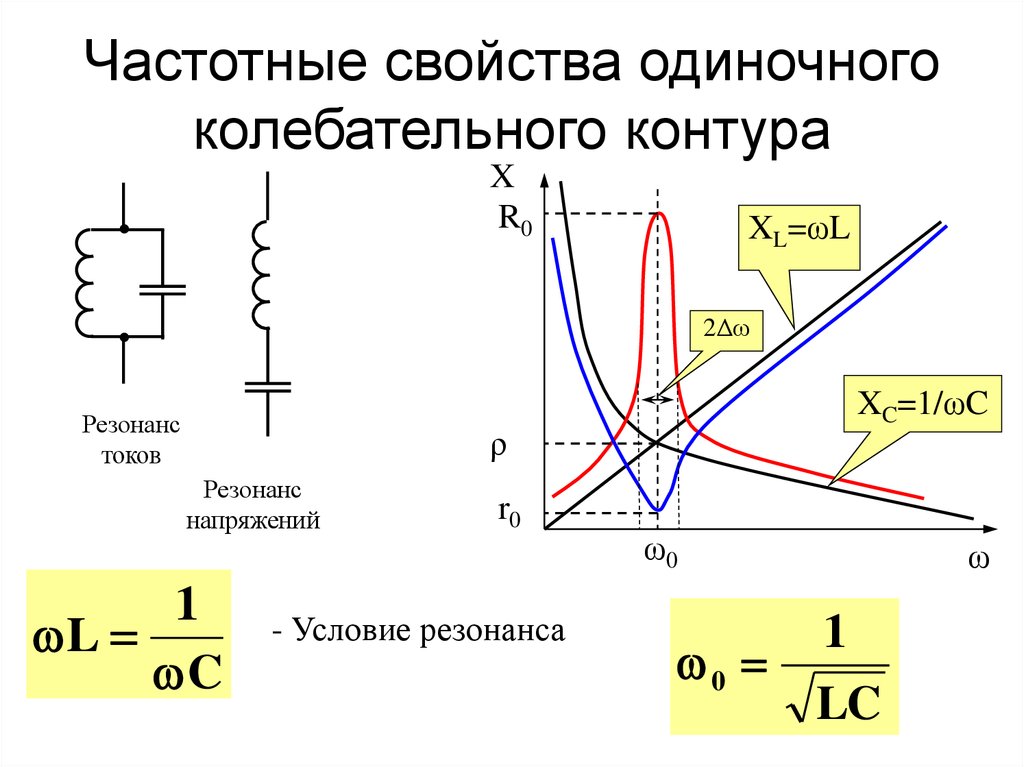 Для аналогичной силы звука с применением электронной аппаратуры необходимо применить мощнейший усилитель и огромный динамик.
Для аналогичной силы звука с применением электронной аппаратуры необходимо применить мощнейший усилитель и огромный динамик.
Для воспроизведения аудио сигнала с помощью подобной аппаратуры придется затратить много электроэнергии
Резкий нерегулируемый рост амплитуды на определенном уровне превышает прочностные характеристики конструкции. Именно такое воздействие ветровых нагрузок разрушило такомский мост в США. Чтобы исключить опасные ситуации, вместо сложного инженерного расчета офицеры командуют солдатам шагать не в ногу при переходе водных преград по таким конструкциям.
Описание явления
Если в некой электрической цепи (см. рис. 1) имеются ёмкостные и индуктивные элементы, которые обладают собственными резонансными частотами, то при совпадении этих частот амплитуда колебаний резко возрастёт. То есть происходит резкий всплеск напряжений на этих элементах. Это может вызвать разрушение элементов электрической цепи.
Рис. 1. Резонанс в электрической цепи
Давайте рассмотрим на этом примере, какие явления будут происходить при подключении генератора переменного тока к контактам схемы.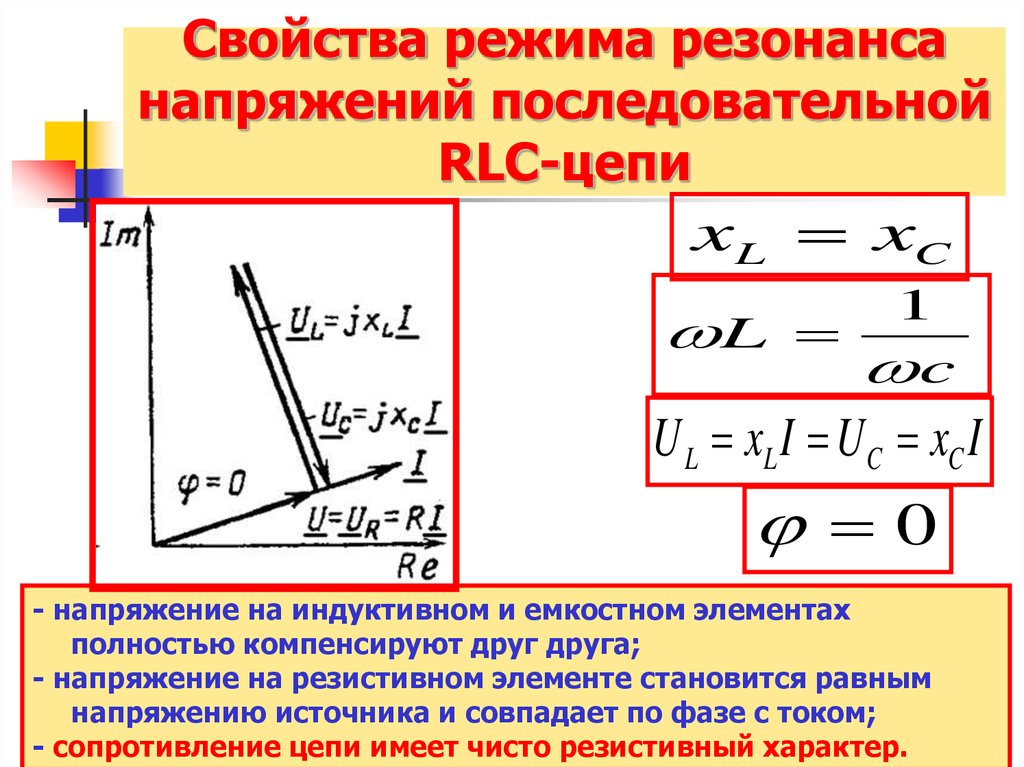 Заметим, что катушки и конденсаторы обладают свойствами, которые можно сравнить с аналогом реактивного резистора. В частности, дроссель в электрической цепи создаёт индуктивное сопротивление. Конденсатор является причиной ёмкостного сопротивления.
Заметим, что катушки и конденсаторы обладают свойствами, которые можно сравнить с аналогом реактивного резистора. В частности, дроссель в электрической цепи создаёт индуктивное сопротивление. Конденсатор является причиной ёмкостного сопротивления.
Индуктивный элемент вызывает сдвиг фаз, характеризующийся отставанием тока от напряжения на ¼ периода. Под действием конденсатора ток, наоборот, на ¼ периода опережает напряжение.
Другими словами, действие индуктивности противоположно действию на сдвиг фаз ёмкостного сопротивления. То есть катушки индуктивности и ёмкостные элементы по-разному воздействуют на генератор и по-своему корректируют фазовые соотношения между электрическим током и напряжением.
Формула
На рисунке 2 изображены графики зависимости полного сопротивления цепи и связанной с ним силы тока, от реактивного сопротивления индуктивного элемента
Обратите внимание на то, как падает полное сопротивление при уменьшении реактивной сопротивляемости RL (график б) и как при этом возрастает ток (график в)
Резонанс в электрической цепи
Резонанс напряжений
Если в цепи (см. рис. 1) подобрать так емкость С конденсатора и индуктивность катушки, чтобы \(~wL = \frac 1{wC}, \) то разность фаз между колебаниями силы тока и напряжения φ = 0, т.е. изменения тока и напряжения происходят синфазно. Из этого равенства \(~w_{rez} = \frac 1{\sqrt {LC}}.\) Эту частоту называют резонансной. При этом условии Z = R, т.е. полное сопротивление цепи становится наименьшим, амплитуда силы тока при данном напряжении принимает наибольшее значение (рис. 3).
рис. 1) подобрать так емкость С конденсатора и индуктивность катушки, чтобы \(~wL = \frac 1{wC}, \) то разность фаз между колебаниями силы тока и напряжения φ = 0, т.е. изменения тока и напряжения происходят синфазно. Из этого равенства \(~w_{rez} = \frac 1{\sqrt {LC}}.\) Эту частоту называют резонансной. При этом условии Z = R, т.е. полное сопротивление цепи становится наименьшим, амплитуда силы тока при данном напряжении принимает наибольшее значение (рис. 3).
В этом случае амплитуда напряжения на активном сопротивлении равна амплитуде внешнего напряжения, приложенного к участку цепи \(~(U_{0R} = U_0),\) а напряжения на катушке индуктивности и конденсаторе одинаковы по модулю и противоположны по фазе:
 \)
\)При этом \(~(U_{OL})_{rez} = (U_{OC})_{rez},\) и они могут значительно превышать \(~U_0.\) Это явление называется резонансом напряжений. Резонанс используется в радио- и электротехнике для усиления колебаний напряжения какой-либо определенной частоты. Его надо учитывать при расчете изоляции электрических линий, содержащих катушки индуктивности и конденсатора, иначе может наблюдаться их пробой.
Резонанс токов
Рассмотрим участок цепи переменного тока, содержащий параллельно включенные конденсатор емкостью С и катушку индуктивностью L (рис. 4).
Пусть активное сопротивление мало, им можно пренебречь. Если приложенное напряжение изменяется по закону \(~U=U_0 \sin wt,\), то в ветви 1С2 проходит ток
В ветви 1L2 проходит ток
 \)
\)Таким образом, разность фаз токов в ветвях 1С2 и 1L2 равна π, т.е. колебания токов в ветвях противоположны по фазе. Амплитуда тока во внешней (неразветвленной) цепи \(~I_{0C} = \left| I_{01} — I_{02} \right| = U_0 (wC — \frac 1 {wL}).\) Если \(~w = w_{rez} = \frac 1{\sqrt {LC}},\) то \(~I_{01} = I_{02}\) и \(~I_0 = 0.\) Амплитуда силы тока \(~I_0\) оказалась равной нулю потому, что активным сопротивлением участка пренебрегали. Если учесть сопротивление R, то разность фаз не будет равна π и \(~I_0 \not = 0,\) но \(~I_0\) примет наименьшее возможное значение, а амплитуды сил токов \(~I_{01} \) и \(~I_{02}\) могут значительно превышать амплитуду силы тока \(~I_0.\)
Явление резкого уменьшения амплитуды силы тока во внешней цепи, питающей параллельно включенные конденсатор и катушку индуктивности, при приближении частоты w приложенного напряжения к резонансной частоте wrez называется резонансом токов (параллельным резонансом).
Это явление используется в резонансных усилителях, позволяющих выделять одно определенное колебание из сигнала сложной формы, а также в индукционных печах, где параллельно нагревательной катушке включается конденсатор, емкость которого подбирается так, чтобы при частоте генератора получился резонанс токов, в результате сила тока через катушку будет гораздо больше, чем сила тока в подводящих проводах.
Цепи переменного тока
Определение 3
Цепи переменного тока – это такие электрические цепи, в которых под воздействием периодического источника тока происходят установившиеся вынужденные колебания.
Рассмотрим устройство колебательного контура, в который включен источник тока с напряжением, изменяющимся по периодическому закону:
e(t)=εcos ωt,
где ε – амплитуда, ω – круговая частота.
Фактически, это будет RLC-цепь.
Рисунок 2.3.1. Вынужденные колебания в контуре.
Будем считать, что для изображенной на этом рисунке электрической цепи выполняется условие квазистационарности.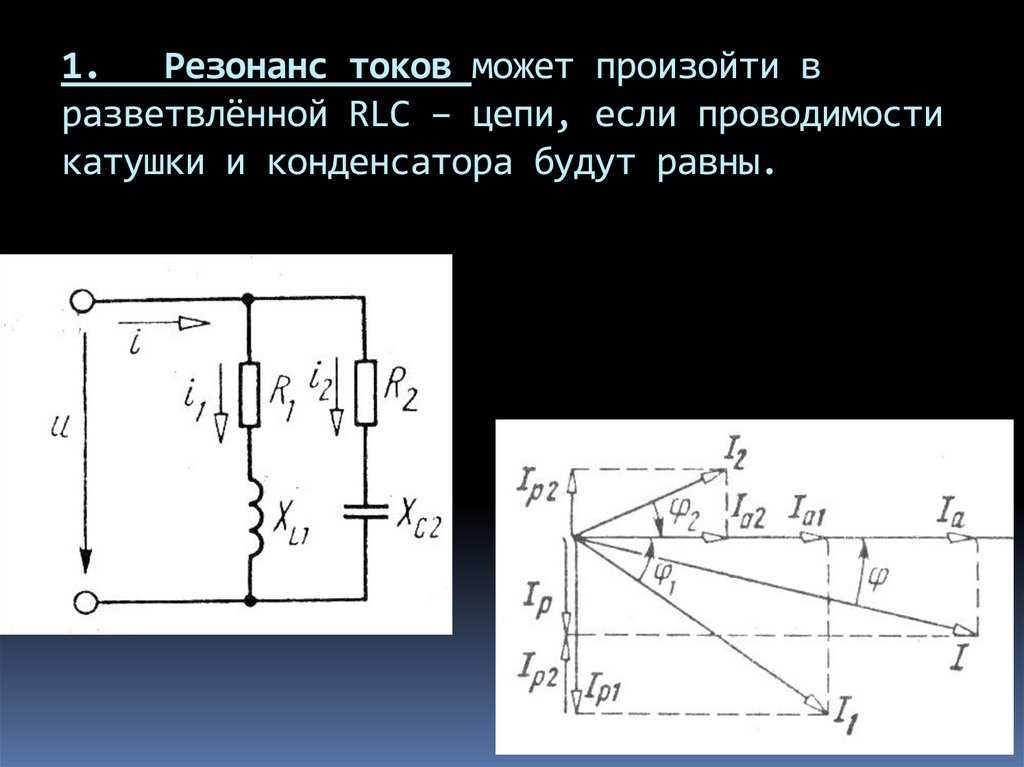 Это позволит нам записать закон Ома для мгновенных значений токов и напряжений:
Это позволит нам записать закон Ома для мгновенных значений токов и напряжений:
RJ+qC+LdJdt=εcoc ωt.
Величину LdJdt принято называть напряжением на катушке индуктивности. Фактически, это ЭДС самоиндукции катушки, которую мы для простоты вычислений перенесли с противоположным знаком в левую часть уравнения из правой.
Уравнение вынужденных колебаний можно записать в виде:
uR+uC+uL=e(t)=εcos ωt.
где uR (t), uC (t) и uL (t) – мгновенные значения напряжений на резисторе, конденсаторе и катушке соответственно. Амплитуды этих напряжений будем обозначать буквами UR, UC и UL. Напряжения при установившихся вынужденных колебаниях изменяются с частотой внешнего источника переменного тока ω.
Резонанс в распределённых колебательных системах, нелинейные процессы
Разделение автоматических выключателей по время токовым характеристикам
Общим понятием для всех явлений данной категории можно назвать действенную связь с окружающей средой. В механических системах влияние на амплитуду фазовых характеристик процесса оказывает определенное положение в пространстве. В колебательном контуре радиоприемника, кроме собственного затухания, приходится учитывать реальный электромагнитный фон. При определенных условиях с высоким значением добротности допустимо образование стоячих волн.
В колебательном контуре радиоприемника, кроме собственного затухания, приходится учитывать реальный электромагнитный фон. При определенных условиях с высоким значением добротности допустимо образование стоячих волн.
Если пружина создана с различным распределением плотности витков, типовые формулы не действуют. Стандартные расчеты подразумевают равномерные упругость и деформации каждой части. Для уточнения нелинейности применяют корректирующие коэффициенты, сложные многоэтапные схемы вычислений.
Аналогичные особенности учитывают при использовании диодов или других радиотехнических компонентов с переменными амплитудно-частотными характеристиками. Если катушку индуктивности намотать на сердечнике из ферромагнитного материала, также придется учитывать нелинейность выходных параметров. Ее не получится описать элементарным уравнением закона Ома.
В нелинейных контурах при определенном спектральном распределении внешних воздействий присутствуют гармонические колебания. Кроме совпадения частот, значение имеет их амплитуда. (1/2)
(1/2)
- Как устранить явление?
Увеличив активное сопротивление в цепи или изменив частоту.
Теперь вы знаете, что такое резонанс токов и напряжений, каковы условия его возникновения и варианты применения на практике. Для закрепления материала рекомендуем просмотреть полезное видео по теме:
Материалы по теме:
- Причины потерь электроэнергии на больших расстояниях
- Измерение частоты переменного тока
- Как рассчитать сопротивление провода
Резонанс токов | это.
 .. Что такое Резонанс токов?
.. Что такое Резонанс токов?Резонанс токов — резонанс, происходящий в параллельном колебательном контуре при его подключении к источнику напряжения, частота которого совпадает с собственной частотой контура.
Содержание
|
Описание явления
Пусть имеется колебательный контур с частотой собственных колебаний a, и пусть он подключен к генератору переменного тока такой же частоты f.
В момент подключения конденсатор заряжается от источника. После чего он начинает разряжаться на катушку, причем разряжается с такой же скоростью, с какой убывает напряжение на генераторе. Через некоторое время энергия конденсатора полностью переходит в энергию магнитного поля катушки. Напряжение на клеммах генератора в этот момент равно нулю.
Далее магнитное поле катушки начинает убывать, так как не может существовать стационарно — на выводах катушки появляется ЭДС индукции, которое начинает перезаряжать конденсатор. В цепи колебательного контура течет ток, только уже противоположно току заряда, так как витки пересекаются полем в обратном направлении. Обкладки конденсатора перезаряжаются зарядами, противоположными первоначальным. Одновременно растет напряжение на генераторе, причем с той же скоростью, с какой катушка заряжает конденсатор. Но ток от генератора не может течь через колебательный контур — как только на клеммах генератора появляется напряжение, точно такое же напряжение появляется на выводах конденсатора вследствие перезаряда его катушкой. Напряжения конденсатора и генератора друг друга компенсируют.
В цепи колебательного контура течет ток, только уже противоположно току заряда, так как витки пересекаются полем в обратном направлении. Обкладки конденсатора перезаряжаются зарядами, противоположными первоначальным. Одновременно растет напряжение на генераторе, причем с той же скоростью, с какой катушка заряжает конденсатор. Но ток от генератора не может течь через колебательный контур — как только на клеммах генератора появляется напряжение, точно такое же напряжение появляется на выводах конденсатора вследствие перезаряда его катушкой. Напряжения конденсатора и генератора друг друга компенсируют.
Далее энергия магнитного поля катушки полностью переходит в энергию электрического поля конденсатора. Напряжение генератора в этот момент достигает максимума. Далее конденсатор разряжается на катушку, цикл повторяется в обратном направлении. В результате, в колебательном контуре циркулируют весьма большие токи, но за его пределы не выходят — выходить им мешает точно такое же, только противоположно направленное напряжение на генераторе.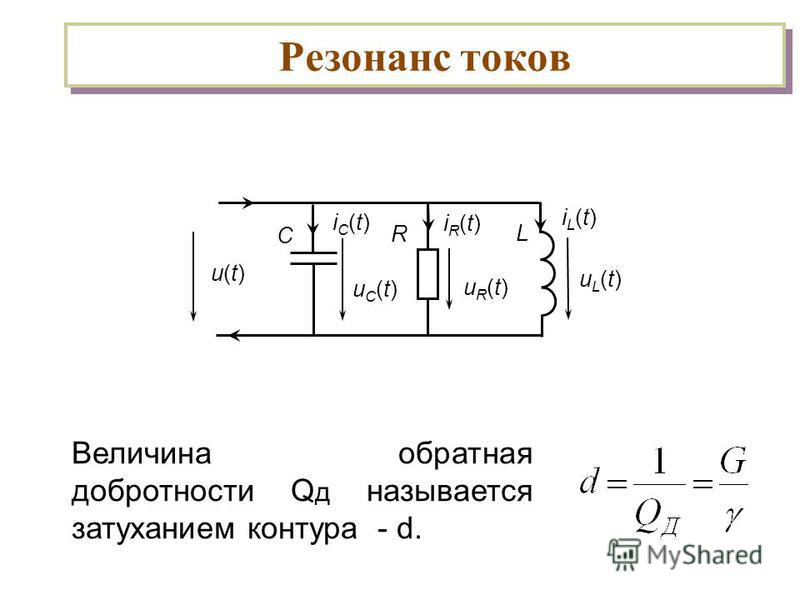 Большой ток от генератора течет через контур только короткое время после включения, когда заряжается конденсатор. Далее генератор работает почти вхолостую — как только на его клеммах появляется напряжение, точно такое же противоположно направленное напряжение появляется на конденсаторе и не пропускает ток от внешнего источника через контур.
Большой ток от генератора течет через контур только короткое время после включения, когда заряжается конденсатор. Далее генератор работает почти вхолостую — как только на его клеммах появляется напряжение, точно такое же противоположно направленное напряжение появляется на конденсаторе и не пропускает ток от внешнего источника через контур.
Вышесказанное справедливо для контура с очень хорошей добротностью (низкими потерями энергии за цикл).
Ситуация изменится, если отбирать от контура во время его работы некоторую мощность. Тогда за цикл часть энергии контура будет теряться и конденсатор будет перезаряжаться контурной катушкой до меньшего напряжения, чем напряжение внешнего генератора. В этом случае генератор будет дозаряжать конденсатор, компенсируя таким образом потери за цикл. Через контур потечет переменный ток, который, однако, может быть меньше того, что циркулирует в самом контуре.
Замечания
- Колебательный контур, работающий в режиме резонанса токов, не является усилителем мощности.

Большие токи, циркулирующие в контуре, возникают за счет мощного импульса тока от генератора в момент включения, когда заряжается конденсатор. При значительном отборе мощности от контура эти токи «расходуются», и генератору вновь приходится отдавать значительный ток подзарядки.
- Если генератор слабый, большой ток подзарядки может сжечь его. Выйти из положения можно, постепенно повышая напряжение на клеммах генератора, «раскачивая» контур.
- Колебательный контур с низкой добротностью слишком хорошо «накачивается» энергией (образует короткое замыкание по катушке), что может привести к выходу из строя задающего генератора. Для повышения добротности колебательного контура нужно по возможности увеличить L и уменьшить C.
Если увеличить L с помощью увеличения витков катушки или увеличения длины провода не представляется возможным, используют ферромагнитные сердечники или ферромагнитные вставки в катушку; катушка обклеивается пластинками из ферромагнитного материала и т п.
Применение
- Высокодобротный колебательный контур оказывает току определенной частоты f значительное сопротивление. Вследствие чего явление резонанса токов используется в полосовых фильтрах как электрическая «пробка», задерживающая определенную частоту.
- Так как току с частотой f оказывается значительное сопротивление, то и падение напряжения на контуре при частоте f будет максимальным. Это свойство контура получило название избирательность, оно используется в радиоприемниках для выделения сигнала конкретной радиостанции.
- Колебательный контур, работающий в режиме резонанса токов, является одним из основных узлов электронных генераторов.
См. также
Резонанс напряжений
Колебательный контур
Литература
- Власов В. Ф. Курс радиотехники. М.: Госэнергоиздат, 1962. С. 928.
- Изюмов Н. М., Линде Д. П. Основы радиотехники. М.: Госэнергоиздат, 1959. С. 512.
Ссылки
Резонанс токов
Circuits. A/C Circuits. Parallel Resonance
A/C Circuits. Parallel Resonance
Резонансные явления в электрических сетях
Идеальное активное сопротивление от частоты не зависит, индуктивное сопротивление линейно зависит от частоты, емкостное сопротивление зависит от частоты по гиперболическому закону:
Резонанс напряжений
Резонансом в электрических цепях называется режим участка электрической цепи, содержащей индуктивный и емкостной элементы, при котором разность фаз между напряжением и током равна нулю . Режим резонанса может быть получен при изменении частоты питающего напряжения или изменением параметров элементов L и С.
При последовательном соединении возникает резонанс напряжения.
Последовательное соединение R, L, C.
Знаменатель данного выражения есть модуль комплексного сопротивления, который зависит от частоты. При достижении некоторой частоты реактивная составляющая сопротивления исчезает, модуль сопротивления становится минимальным, ток в данной схеме возрастает до максимального значения, причем вектор тока совпадает с вектором напряжения по фазе:
Максимальная амплитуда силы тока достигается при условии минимума полного сопротивления, т. е. при
е. при
где
— резонансная частота напряжения, определяемая из условия
При последовательном соединении в цепь конденсатора и соленоида силы токов в каждом из участков цепи, как известно, равны. Поэтому, умножив левую и правую части последнего соотношения на силу тока Im, получим
В этом выражении слева — амплитуда напряжения на концах соленоида, а справа — амплитуда напряжения на обкладках конденсатора.
Мы видим, что . Отсюда получаем
Знак минус указывает на то, что колебания напряжения на участках с индуктивностью и емкостью происходят в противофазе.
Режим электрической цепи при последовательном соединении индуктивности и емкости, характеризующийся равенством напряжений на индуктивности и емкости, называют резонансом напряжений.
Волновое или характеристическое сопротивление последовательного контура
Отношение напряжения на индуктивности или емкости к напряжению на входе в режиме резонанса называется добротностью контура:
Добротность контура представляет собой коэффициент усиления по напряжению и в катушках индуктивности может достигать сотен единиц:
При напряжение на индуктивности (или емкости) может быть гораздо больше напряжения на входе, что широко используется в радиотехнике. В промышленных сетях резонанс напряжений является аварийным режимом, так как увеличение напряжения на конденсаторе может привести к его пробою, а рост тока — к нагреву проводов и изоляции.
В промышленных сетях резонанс напряжений является аварийным режимом, так как увеличение напряжения на конденсаторе может привести к его пробою, а рост тока — к нагреву проводов и изоляции.
Резонанс токов
При параллельном соединении конденсатора и соленоида (смотри рисунок), так же как и при последовательном, сила тока в цепи зависит от значений емкости и индуктивности. При изменении емкости и индуктивности при определенном их соотношении сила тока в неразветвленном участке цепи оказывается минимальной (практически близкой к нулю).
В этом случае:
Параллельное соединение реактивных элементов
тогда
При определенной частоте, называемой резонансной, реактивные составляющие проводимости могут сравняться по модулю и суммарная проводимость будет минимальной. Общее сопротивление при этом становится максимальным, общий ток минимальным, вектор тока совпадает с вектором напряжения. Такое явление называется резонансом токов.
Волновая проводимость
При ток в ветви с индуктивностью гораздо больше общего тока, поэтому такое явление называется резонансом токов и широко используется в силовых сетях промышленных предприятий для компенсации реактивной мощности.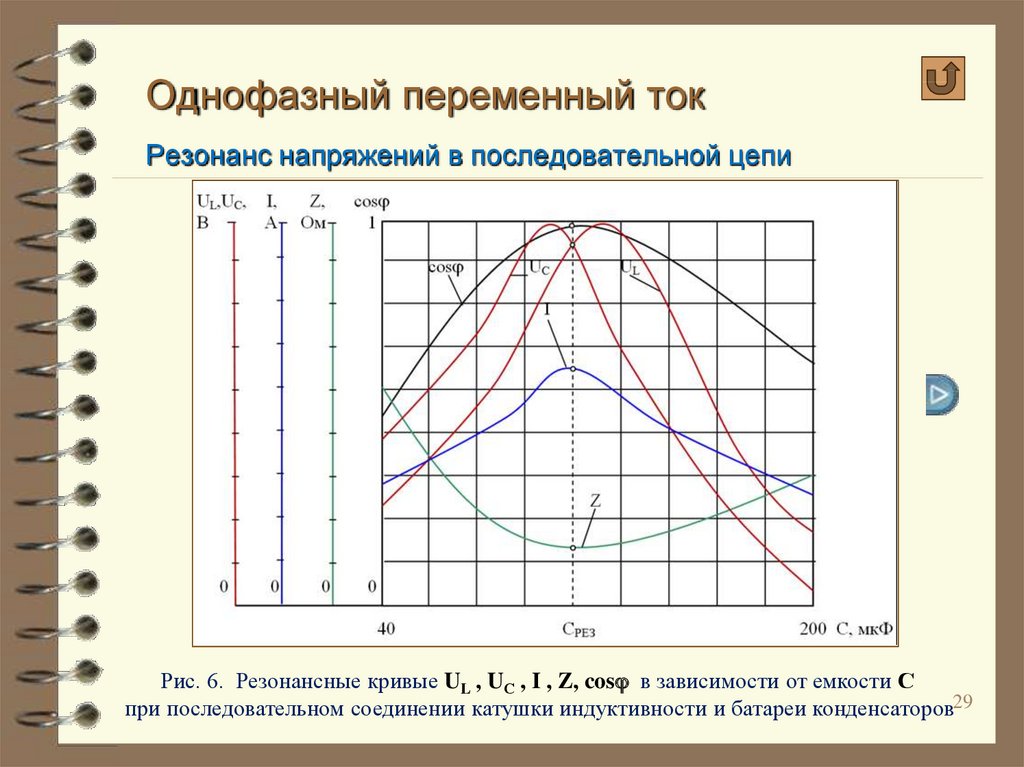
Резонансную частоту тока найдем из условия равенства реактивных проводимостей ветвей.
После ряда преобразований получим:
Из формулы следует, что:
1) резонансная частота зависит от параметров не только реактивных сопротивлений, но и активных;
2) резонанс возможен, если и больше или меньше ρ, в противном случае частота будет мнимой величиной и резонанс невозможен;
3) если , то частота будет иметь неопределенное значение, что означает возможность существования резонанса на любой частоте при совпадении фаз напряжения питания и общего тока;
4) при резонансная частота напряжения равна резонансной частоте тока.
Энергетические процессы в цепи при резонансе токов аналогичны процессам, происходящим при резонансе напряжений.
Реактивная энергия циркулирует внутри цепи: в одну часть периода энергия магнитного поля индуктивности переходит в энергию электрического поля емкости, в следующую часть периода происходит обратный процесс.
При резонансе токов реактивная мощность равна нулю.
Большинство промышленных потребителей переменного тока носит активно-индуктивный характер и, следовательно, потребляет реактивную мощность. К таким потребителям относятся асинхронные двигатели, установки электрической сварки и т.д.
Для уменьшения реактивной мощности и повышения коэффициента мощности параллельно потребителю включают батарею конденсаторов, что приводит к уменьшению тока в проводах, соединяющих потребителя с источником энергии.
Понятие резонанса напряжений в электрических цепях переменного тока
Содержание
- Причины резонанса
- Элементы резонансной цепи
- Задача из ЕГЭ по физике про резонанс в цепи переменного тока
- Что такое резонанс?
- Какие последствия резонанса напряжений
- Добротность RLC-цепи
- Емкость и индуктивность в цепи переменного тока
- Использование резонанса напряжений для передачи радиосигнала
- Что такое резонанс в электрической цепи
- Область применения
- Что такое резонансное напряжение
Причины резонанса
Классический пример с приказом командира идти марширующим солдатам «не в ногу» перед мостом наглядно демонстрирует суть этого явления
Если не использовать такую предосторожность, колебания могут увеличиться до критичного значения, вплоть до разрушения конструкции. Для получения максимальной амплитуды раскачивают в определенном ритме качели
Для получения максимальной амплитуды раскачивают в определенном ритме качели
Приведенные примеры демонстрируют существенное увеличение результата при совпадении частот внешнего воздействия и непосредственно самой системы.
Электрический резонанс по своим принципам не отличается от механических аналогов. Он образуется при совпадении частот внешнего сигнала и контура. Функции накопителей энергии выполняют реактивные индукционные и емкостные элементы. Потери (постепенное уменьшение амплитуды) обеспечивает электрическое сопротивление цепи, что аналогично коэффициенту трения.
Элементы резонансной цепи
Явление резонанса может возникнуть в так называемой RLC-цепи, содержащей следующие компоненты:
- R — резисторы. Эти устройства, относящиеся к так называемым активным элементам электрической цепи, преобразуют электрическую энергию в тепловую. Другими словами, они удаляют энергию из контура и преобразуют ее в тепло.
- L — индуктивность. Индуктивность в электрических цепях — аналог массы или инерции в механических системах.
 Этот компонент не очень заметен в электрической цепи, пока не попробуешь сделать в ней какие-либо изменения. В механике, например, таким изменением является изменение скорости. В электрической цепи — изменение тока. Если оно по какой-либо причине происходит, индуктивность противодействует такому изменению режима цепи.
Этот компонент не очень заметен в электрической цепи, пока не попробуешь сделать в ней какие-либо изменения. В механике, например, таким изменением является изменение скорости. В электрической цепи — изменение тока. Если оно по какой-либо причине происходит, индуктивность противодействует такому изменению режима цепи. - С – обозначение для конденсаторов, которые представляют собой устройства, хранящие электрическую энергию подобно тому, как пружины сохраняют механическую энергию. Индуктивность концентрирует и сохраняет магнитную энергию, в то время как конденсатор концентрирует заряд и тем самым хранит электрическую энергию.
Задача из ЕГЭ по физике про резонанс в цепи переменного тока
| При подключении трех неизвестных элементов A, B и C электрической цепи к выходу генератора переменного тока с изменяемой частотой гармонических колебаний при неизменной амплитуде колебаний напряжения, обнаружены следующие зависимости действующих значений силы тока от частоты: Установите соответствие между буквой графика и соответствующим элементом из списка, который был подключен: 1) активное сопротивление
|
- Правильный ответ для графика A — 1 (активное сопротивление), поскольку из представленных в списке элементов лишь активное сопротивление не имеет зависимости от частоты в цепи переменного тока.

- Правильный ответ для графика B — 2 (катушка), поскольку индуктивное сопротивление катушки возрастает пропорционально частоте переменного тока. Тогда действующее значение силы переменного тока уменьшается обратно пропорционально частоте.
- Правильный ответ для графика B — 4 (RLC-контур), так как на кривой зависимости действующего значения силы переменного тока от частоты имеется ярко выраженный резонансный максимум, что является характерным признаком RLC-контура.
Что такое резонанс?
мощность
Данный вариант является характерным преимущественно для схем с переменными показателями токовых величин и обладает не только положительными свойствами, но и некоторыми совершенно нежелательными качествами, которые в обязательном порядке учитываются еще в процессе проектирования.
Положительное резонансное действие — явление из области радиотехники, автоматики и проволочной телефонии. Резонанс напряжений относится к категории нежелательных явлений, обусловленных перенапряжениями. При этом добротным электрическим контуром принято считать величину:
При этом добротным электрическим контуром принято считать величину:
Достижение токового резонанса осуществляется подбором необходимого индуктивного или емкостного значения, а также показателей частотности питающих сетей.
Токовый резонанс получается подбором параметров электроцепи в условиях заданной частоты источника питания, а также посредством выбора обратных показателей.
Какие последствия резонанса напряжений
Если в электрической системе с ёмкостью, индуктивностью и сопротивлением не учитывать воздействие этого явления, то работа устройств может быть нестабильной. Если этот эффект носит паразитический характер, то от него следует обязательно избавляться. Увеличение напряжения вследствие возникновения резонансного явления в цепи переменного напряжения может привести к выходу элементов из строя.
Важно! При возникновении этого явления могут быть разрушены конденсаторы из-за превышения реактивной мощности. При перегреве вследствие резонанса напряжений электротехника может не только выйти из строя, но и загореться
При перегреве вследствие резонанса напряжений электротехника может не только выйти из строя, но и загореться.
Возгорание электрической подстанции
На крупных производственных объектах такое явление может привести к аварии с человеческими жертвами. Если высоковольтные линии электропередач находятся слишком близко, то эффект электрического резонанса может возникать и в системах этого типа.
Шунтирующие генераторы ЛЭП
Чтобы защитить ЛЭП от негативного воздействия этого явления применяются шунтирующие генераторы, которые устанавливаются через каждые 300 – 400 км.
Добротность RLC-цепи
Резонансные цепи используют для того, чтобы выделить сигнал на нужной частоте, отфильтровав остальные сигналы на других частотах. Если отложить по вертикали действующее значение силы тока вынужденных колебаний в RLC-контуре, а по горизонтали — частоту генерируемой источником переменной ЭДС, то получится резонансная кривая данного RLC-контура, подобная той, что изображена на рисунке:
Если резонансная кривая имеет острый пик на резонансной частоте, говорят, что схема обладает высокой «селективностью».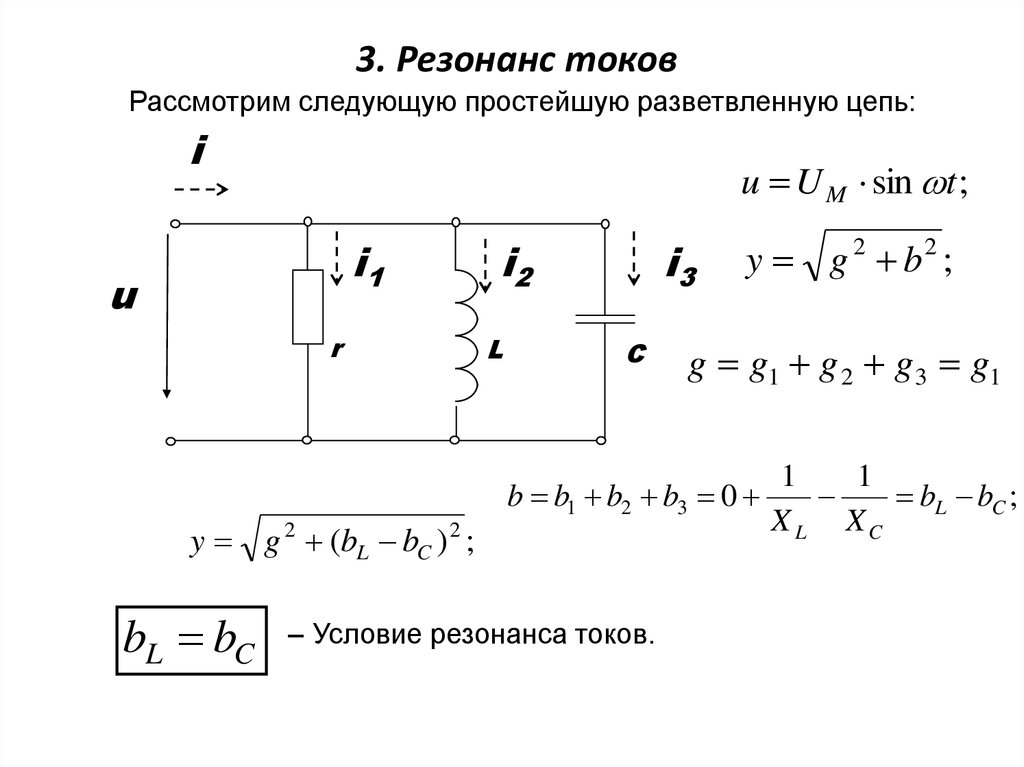 Параметр, характеризующий данное свойство, в физике называют добротностью . Добротность RLC-контура определяется как отношение его резонансной частоты к ширине резонансной полосы на полувысоте максимума :
Параметр, характеризующий данное свойство, в физике называют добротностью . Добротность RLC-контура определяется как отношение его резонансной частоты к ширине резонансной полосы на полувысоте максимума :
Добротность RLC-цепи зависит от величины активного сопротивления. Чем меньше активное сопротивление , тем больше добротность при данных значениях индуктивности и электроемкости . Для RLC-контура добротность определяется по формуле:
Емкость и индуктивность в цепи переменного тока
Если в цепях постоянного тока емкость в общем смысле представляет собой разорванный участок цепи, а индуктивность — проводник, то в переменном конденсаторы и катушки представляют собой реактивный аналог резистора.
Реактивное сопротивление катушки индуктивности определяется по формуле:
Векторная диаграмма:
Реактивное сопротивление конденсатора:
Здесь w — угловая частота, f — частота в цепи синусоидального тока, L — индуктивность, C — емкость.
Векторная диаграмма:
Стоит отметить, что при расчете соединенных последовательно реактивных элементов используют формулу:
Обратите внимание, что емкостная составляющая принимается со знаком минус.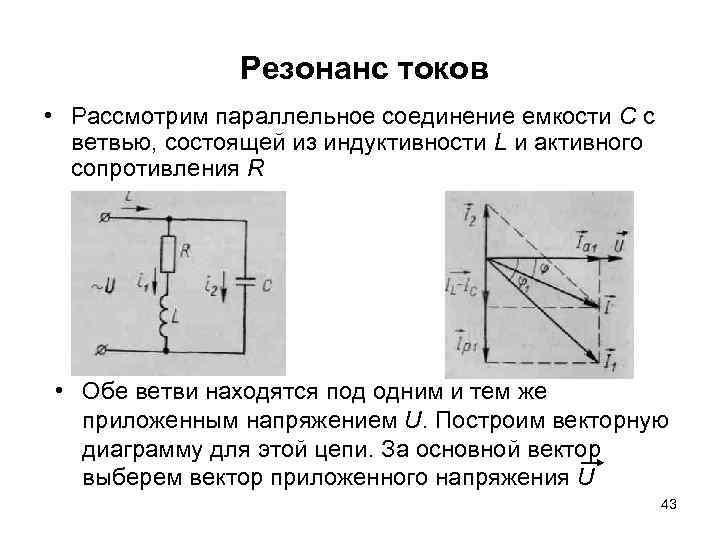 Если в цепи присутствует еще и активная составляющая (резистор), то складывают по формуле теоремы Пифагора (исходя из векторной диаграммы):. От чего зависит реактивное сопротивление? Реактивные характеристики зависят от величины емкости или индуктивности, а также от частоты переменного тока
Если в цепи присутствует еще и активная составляющая (резистор), то складывают по формуле теоремы Пифагора (исходя из векторной диаграммы):. От чего зависит реактивное сопротивление? Реактивные характеристики зависят от величины емкости или индуктивности, а также от частоты переменного тока
От чего зависит реактивное сопротивление? Реактивные характеристики зависят от величины емкости или индуктивности, а также от частоты переменного тока.
Если посмотреть на формулу реактивной составляющей, то можно заметить, что при определенных значениях емкостной или индуктивной составляющей их разность будет равна нулю, тогда в цепи останется только активное сопротивление. Но это не все особенности такой ситуации.
Использование резонанса напряжений для передачи радиосигнала
Применение последовательного колебательного контура удобно изучать на конкретном примере. При конструировании передающих устройств, например, уменьшение импеданса на определенной частоте позволяет сделать настройку на определенный сигнал. Такую задачу решают с помощью колебательного контура.
Такую задачу решают с помощью колебательного контура.
Распределение спектра на экране измерительного прибора после обработки фильтром
Точно спроектированный фильтр будет «убирать» паразитные составляющие без дополнительных средств контроля и автоматизации. Такое решение, кроме простоты и минимальной стоимости, обеспечивает экономное потребление энергии генератором сигнала.
Как показано на практических примерах, резонанс может выполнять полезные и вредные функции. Точный расчет поможет создать качественную электрическую цепь с заданными техническими параметрами.
Что такое резонанс в электрической цепи
В повседневной жизни слово «Резонанс» ассоциируется, прежде всего, с реакцией общественности на какое-либо значимое событие. В действительности, это явление окружает людей повсюду.
Резонанс в электрической цепи.
Например, работа акустических систем домашнего кинотеатра не производила бы такого эффекта, в том числе по громкости, если бы в корпусах колонок не использовался бы эффект акустического резонанса. Корпуса практически всех музыкальных инструментов изготавливаются таким образом, чтобы максимально увеличить громкость звучания колеблющегося тела. Человеческий голосовой аппарат, также представляет собой резонаторную систему, которая оказывает значительное влияние на тембр и громкость звука.
Корпуса практически всех музыкальных инструментов изготавливаются таким образом, чтобы максимально увеличить громкость звучания колеблющегося тела. Человеческий голосовой аппарат, также представляет собой резонаторную систему, которая оказывает значительное влияние на тембр и громкость звука.
Акустический резонанс.
Аналогичным образом осуществляется «отклик» и в различных электрических системах. Отличие заключается только в том, что в резонанс входят не звуковые колебания, а электромагнитные поля.
Важно! Следует отметить, что явление резонанса возможно только в цепи переменного тока
Область применения
Это явление в цепи колебательного контура имеет тенденцию к затуханию. Чтобы стало возможным использовать это явление в различных приборах и устройствах, необходимо постоянно поддерживать характеристики электричества в заданных пределах. Сделать этот процесс постоянным очень просто: достаточно подпитывать систему переменным напряжением с постоянными значениями частоты.
Радиовышка
Важно! Эффект резонанса широко применяется в различных радиопередающих и принимающих сигнал устройствах. Наиболее часто, это явление используется в различных фильтрах
Например, если на пути входящего электрического сигнала необходимо избавиться от составляющей определённой частоты, то параллельно проводнику устанавливают конденсатор, резистор и дроссель. Если фильтр необходим для того, чтобы «пропустить» сигнал определенной частоты, то также изготавливается фильтр из ёмкости, сопротивления и индуктивности, но подключается такая система последовательно
Наиболее часто, это явление используется в различных фильтрах. Например, если на пути входящего электрического сигнала необходимо избавиться от составляющей определённой частоты, то параллельно проводнику устанавливают конденсатор, резистор и дроссель. Если фильтр необходим для того, чтобы «пропустить» сигнал определенной частоты, то также изготавливается фильтр из ёмкости, сопротивления и индуктивности, но подключается такая система последовательно.
Электрический фильтр
Использовать эффект резонанса можно и для повышения напряжения. Например, в ситуации, когда электрический двигатель не способен работать на расчетных показателях мощности по причине низкого напряжения, достаточно установить по мощному конденсатору на каждую фазу, чтобы полностью разрешить проблему.
Резонанс в электрической цепи может возникать при наличии определенных условий, поэтому от него можно избавиться либо вызвать намеренно. Если такое явление является нежелательным, то, во многих случаях, достаточно изменить рабочую частоту или увеличить сопротивление, чтобы полностью устранить это паразитическое явление. Простейшая система этого типа состоит из конденсатора, резистора и дросселя, поэтому, при необходимости, можно легко собрать устройство, в котором это электрический эффект будет выполнять какую-либо полезную функцию.
youtube.com/embed/DogVEYLUhZQ?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»>Что такое резонансное напряжение
Если в сеть с переменным электротоком последовательно подключены дроссель и конденсаторный элемент, они способны по-своему воздействовать на генератор, который питает всю схему. Также они влияют на фазовые отношения тока и напряженности. Индуктивная катушка привносит в цепь сдвиг фаз, который заставляет электроток отставать от напряжения на четверть периода. Конденсирующий элемент, наоборот, работает так, что U отстает от тока на четверть по фазе.
Процесс резонирования, основанный на использовании трансформатора
Это означает, что сопротивляемость индуктивного типа, которое работает на сдвижение фазы напряжения и тока в сети, функционирует противоположно силе емкостного сопротивления.
Основная формула резонанса электрической цепи
К сведению! Данный процесс приводит к тому, что общий сдвиг по фазе между силой тока и напряженностью в сети всегда зависит от отношения величины индуктивной и емкостной сопротивляемостей.
Резонирование токов
Если емкостное R в сети больше индуктивного, то все соединение является емкостным. Это значит, что напряжение характеризуется разностью фаз по току. Иногда бывает и обратная ситуация, индуктивное сопротивление сети получается большим, чем емкостное. В этом случае вся сеть становится индуктивной.
Tags: автомат, бра, вред, выбор, генератор, двигатель, диаграмма, дом, е, емкость, знак, как, конденсатор, контур, кт, лс, магнит, мощность, напряжение, принцип, провод, проект, р, работа, расчет, резистор, резонанс, резонансный, ряд, сеть, система, соединение, сопротивление, средство, схема, тен, тип, ток, трансформатор, ук, фильтр, щит, эффект
Урок Видео: Резонанс в цепях переменного тока
Стенограмма видео
В этом видео мы будем учиться
о явлении резонанса в цепях переменного тока. Резонанс возникает потому, что оба
емкостное и индуктивное сопротивления зависят от частоты переменного
напряжение и ток.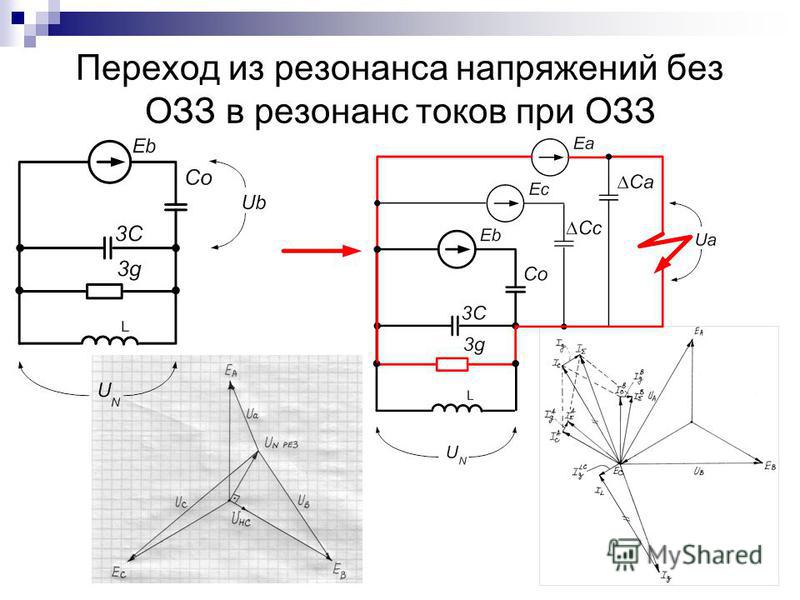 Начнем с рассмотрения реактивного сопротивления,
который обобщает противодействующее току качество сопротивления резисторов на
включают катушки индуктивности и конденсаторы, а также.
Начнем с рассмотрения реактивного сопротивления,
который обобщает противодействующее току качество сопротивления резисторов на
включают катушки индуктивности и конденсаторы, а также.
Резистор обладает особым свойством что его противостояние току фиксировано. То есть сопротивление резистора, обычно обозначается символом 𝑅, на него не влияет сила, направление или частота напряжения в цепи. То же самое не относится к индукторам и конденсаторы в цепях переменного тока. Хотя емкость 𝐶 и индуктивность 𝐿 не зависит от напряжения, сопротивления катушки индуктивности и конденсатора ток зависит от частоты напряжения в цепи.
Для конденсатора более заряженный
тем больше оно противостоит току. Чем быстрее электродвижущая сила
меняет направление, то есть чем выше его частота, тем меньше конденсатор
заряжается перед повторной разрядкой. Таким образом, на более высоких частотах
конденсатор имеет меньшее реактивное сопротивление. Индуктор, с другой стороны,
создает магнитное поле. И чем сильнее магнитное поле
получает, тем меньше индуктор противодействует току. Однако это магнитное поле занимает
время наращивать. Таким образом, чем выше частота
электродвижущая сила, тем слабее будет магнитное поле перед изменением
направления. В результате индуктивный
реактивное сопротивление будет больше на более высоких частотах.
Таким образом, на более высоких частотах
конденсатор имеет меньшее реактивное сопротивление. Индуктор, с другой стороны,
создает магнитное поле. И чем сильнее магнитное поле
получает, тем меньше индуктор противодействует току. Однако это магнитное поле занимает
время наращивать. Таким образом, чем выше частота
электродвижущая сила, тем слабее будет магнитное поле перед изменением
направления. В результате индуктивный
реактивное сопротивление будет больше на более высоких частотах.
Как формулы, емкостная
реактивное сопротивление — это единица, деленная на угловую частоту напряжения и тока, умноженная на
емкость. Индуктивное сопротивление – это
угловая частота напряжения и тока, умноженная на индуктивность. Обратите внимание, что обе эти формулы
дать правильную качественную зависимость между реактивным сопротивлением и частотой. Емкостное сопротивление равно
обратно пропорциональна частоте, а индуктивное сопротивление прямо
пропорциональна частоте.
Емкостное сопротивление равно
обратно пропорциональна частоте, а индуктивное сопротивление прямо
пропорциональна частоте.
Таким образом, на более высоких частотах индуктивное сопротивление больше, а емкостное сопротивление меньше. 𝜔, угловая частота, определяется как два 𝜋 радиана, умноженные на обычную частоту, или циклов в секунду. Мы используем 𝜔, потому что это помогает нам просто выпишите эти формулы, не прибегая к двойным множителям. 𝜋.
Последнее, что нам нужно вспомнить, это
что для цепи как с индуктивными, так и с емкостными компонентами общее
реактивное сопротивление — это не просто сумма индуктивного и емкостного сопротивлений. Это связано с тем, что катушки индуктивности и
конденсаторы также вносят фазовый сдвиг между током и ЭДС. Конденсаторы вызывают ток
оставить ЭДС, в то время как катушки индуктивности заставляют ток отставать от ЭДС. Чистый эффект этих различных
фазовых сдвигов заключается в том, что правильной комбинацией для полного реактивного сопротивления является разница
между двумя реактивными сопротивлениями, индуктивное сопротивление минус емкостное сопротивление.
Чистый эффект этих различных
фазовых сдвигов заключается в том, что правильной комбинацией для полного реактивного сопротивления является разница
между двумя реактивными сопротивлениями, индуктивное сопротивление минус емкостное сопротивление.
Возможен резонанс в цепи переменного тока именно потому, что полное реактивное сопротивление представляет собой разницу вместо суммы. Итак, давайте посмотрим, как разница между индуктивным и емкостным сопротивлениями может привести к резонансу. Рассмотрим простую схему питается от источника переменного напряжения с катушкой индуктивности и конденсатором, включенными в серии. Хотя мы ограничим нашу дискуссию к последовательным цепям те же принципы применимы и к параллельным цепям.
В любом случае общее реактивное сопротивление в
схема представляет собой индуктивное сопротивление минус емкостное сопротивление. Помните, что индуктивность и
емкостные реактивные сопротивления зависят от частоты противоположным образом. Итак, если мы изменим частоту от,
скажем, от очень низкого значения до очень высокого значения, емкостное сопротивление изменится от
от очень больших до очень маленьких. Но индуктивное сопротивление будет
измениться от очень маленького до очень большого. Это говорит о том, что может быть
некоторая частота в середине нашего диапазона, для которой индуктивное сопротивление и
емкостные реактивные сопротивления равны.
Помните, что индуктивность и
емкостные реактивные сопротивления зависят от частоты противоположным образом. Итак, если мы изменим частоту от,
скажем, от очень низкого значения до очень высокого значения, емкостное сопротивление изменится от
от очень больших до очень маленьких. Но индуктивное сопротивление будет
измениться от очень маленького до очень большого. Это говорит о том, что может быть
некоторая частота в середине нашего диапазона, для которой индуктивное сопротивление и
емкостные реактивные сопротивления равны.
Если индуктивная и емкостная
реактивные сопротивления равны, то их разность, общее реактивное сопротивление, равна нулю. Итак, катушка индуктивности и конденсатор
комбинация не обеспечивает сопротивления току на этой частоте. Чтобы найти специальную частоту,
мы начнем с приравнивания частотно-зависимых формул для индуктивной и
емкостное реактивное сопротивление. Чтобы найти 𝜔, мы умножим
с обеих сторон на 𝜔 над 𝐿. С левой стороны 𝐿 от
наша формула отменяет 𝐿 в знаменателе. А справа 𝜔
из нашей формулы отменяет 𝜔 в числителе. Это оставляет нам 𝜔 в квадрате
равно единице, деленной на 𝐿𝐶.
Чтобы найти 𝜔, мы умножим
с обеих сторон на 𝜔 над 𝐿. С левой стороны 𝐿 от
наша формула отменяет 𝐿 в знаменателе. А справа 𝜔
из нашей формулы отменяет 𝜔 в числителе. Это оставляет нам 𝜔 в квадрате
равно единице, деленной на 𝐿𝐶.
Если мы сейчас возьмем квадратный корень из обеих частей этого равенства, мы получаем, что угловая частота относительно полное реактивное сопротивление равно нулю, равно единице, деленной на квадратный корень из индуктивность дросселя, умноженная на емкость конденсатора. Мы часто пишем 𝜔 с нижним индексом нуля, когда речь идет именно об этой частоте.
Явление индуктивного и
емкостные реактивные сопротивления, точно компенсирующие на определенной частоте, известны как
резонанс. И 𝜔 ничего, частота на
которой возникает резонанс, называется резонансной частотой. Поскольку при резонансе общее
реактивное сопротивление равно нулю, катушка индуктивности и конденсатор в нашей схеме ведут себя как проводники
провода. Но это означает, что на резонансе
идеальная схема, которую мы нарисовали, фактически представляет собой короткое замыкание. Если бы это была реальная цепь,
короткое замыкание может привести к серьезному повреждению различных компонентов и блока питания переменного тока.
источник напряжения. Однако, если бы это был настоящий
цепи, будет некоторое сопротивление, присущее компонентам и
провода.
Но это означает, что на резонансе
идеальная схема, которую мы нарисовали, фактически представляет собой короткое замыкание. Если бы это была реальная цепь,
короткое замыкание может привести к серьезному повреждению различных компонентов и блока питания переменного тока.
источник напряжения. Однако, если бы это был настоящий
цепи, будет некоторое сопротивление, присущее компонентам и
провода.
Итак, давайте смоделируем это из реальной жизни.
ситуация с идеальной цепью, состоящей из катушки индуктивности, конденсатора, а также
резистор. Здесь у нас есть цепь с
резистор, катушка индуктивности и конденсатор, соединенные последовательно, питаемые переменным напряжением
источник. Так как эта схема имеет оба
резистивных и реактивных элементов, полное противодействие току определяется
комбинация сопротивления и реактивного сопротивления, известная как импеданс. Величина импеданса равна
квадратный корень из суммы квадратов сопротивления и полного реактивного сопротивления. Мы должны использовать этот специальный
комбинация, потому что реактивные компоненты изменяют фазу между ЭДС и током,
но резистивные компоненты — нет.
Величина импеданса равна
квадратный корень из суммы квадратов сопротивления и полного реактивного сопротивления. Мы должны использовать этот специальный
комбинация, потому что реактивные компоненты изменяют фазу между ЭДС и током,
но резистивные компоненты — нет.
Ладно, посмотрим, что будет с импеданс, когда мы управляем цепью на резонансной частоте. Напомним, что при резонансе индуктивное и емкостное сопротивления равны. Таким образом, полное реактивное сопротивление равно нулю. Таким образом, импеданс в резонансе равен квадратный корень из 𝑅 в квадрате плюс ноль, который является квадратным корнем из 𝑅 в квадрате, что просто 𝑅. Таким образом, при резонансе импеданс цепь тождественно сопротивлению.
Это говорит нам о нескольких важных
вещи. Во-первых, поскольку суммарная реактивная
вклад в импеданс равен нулю в резонансе, фазовый сдвиг не вносится
между током и ЭДС. Во-вторых, для общего
цепь переменного тока, закон Ома говорит нам, что напряжение равно току
раз импеданс. При резонансе это становится напряжением
равно текущему времени сопротивления, что является просто законом Ома для чисто резистивного
цепи переменного тока.
Во-вторых, для общего
цепь переменного тока, закон Ома говорит нам, что напряжение равно току
раз импеданс. При резонансе это становится напряжением
равно текущему времени сопротивления, что является просто законом Ома для чисто резистивного
цепи переменного тока.
Кроме того, оглядываясь на нашу формула для величины импеданса, квадрат полного реактивного сопротивления всегда положителен, если это ноль. Так что на резонансе, когда тотал реактивное сопротивление равно нулю, импеданс минимален. Возвращаясь к закону Ома, если пиковое напряжение не изменяется, тогда как импеданс уменьшается, пиковый ток становится меньше. больше. Таким образом, минимальное сопротивление подразумевает максимальный пиковый ток.
Теперь, когда мы увидели, что происходит
когда мы запускаем схему на резонансной частоте, давайте посмотрим, что произойдет, когда мы
управлять цепью на частотах, отличных от резонансной частоты. Чтобы увидеть, как ток ведет себя при
частот, отличных от резонансной, используем график с угловой частотой
по горизонтальной оси и относительная амплитуда течения по вертикальной
ось. Относительная амплитуда для
ток на определенной угловой частоте находится путем деления пикового тока на
этой частоты пиковым током на резонансной частоте.
Чтобы увидеть, как ток ведет себя при
частот, отличных от резонансной, используем график с угловой частотой
по горизонтальной оси и относительная амплитуда течения по вертикальной
ось. Относительная амплитуда для
ток на определенной угловой частоте находится путем деления пикового тока на
этой частоты пиковым током на резонансной частоте.
Итак, по определению относительный амплитуда тока на резонансной частоте равна единице. Если на другой частоте ток имел пиковое значение, составляющее половину значения тока на резонансном частота, то относительная амплитуда тока на этой частоте будет одна половина. Использование относительного вместо абсолютного амплитуда позволяет этому обсуждению быть очень общим, поэтому оно применимо к широкому спектру резонансных явлений.
Возвращаясь, в частности, к нашим
электронных цепей на частотах, все более больших по сравнению с резонансными
частота, индуктивное сопротивление все больше и больше.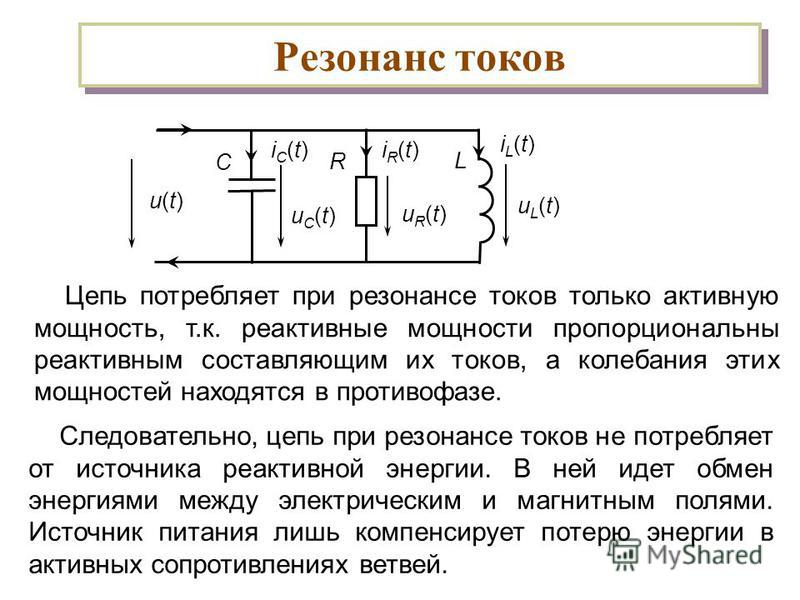 Таким образом, относительная амплитуда
ток все меньше и меньше. Аналогично, на частотах
все меньше по отношению к резонансной частоте, емкостное сопротивление
больше и больше. И так, опять же, родственник
амплитуда тока все меньше и меньше.
Таким образом, относительная амплитуда
ток все меньше и меньше. Аналогично, на частотах
все меньше по отношению к резонансной частоте, емкостное сопротивление
больше и больше. И так, опять же, родственник
амплитуда тока все меньше и меньше.
Этот график, который мы нарисовали на самом деле имеет форму, типичную для самых разных резонансных систем. Одна из самых ярких особенностей этого графика является резким пиком на резонансной частоте. Мы говорим, что пик острый потому что он намного уже, чем в высоту. Физически это означает, что ток в нашей цепи будет намного больше при возбуждении на резонансной частоте чем при возбуждении на частотах, не более меньших или больших, чем резонансная частота.
Для многих приложений от
измерительного оборудования для радиосвязи, полезно количественно определить резкость
резонансного пика. Это связано с тем, что чем острее
резидентный пик, тем более избирательно наша система реагирует на конкретный
частота. Соответственно, чем острее пик,
чем больше наши системы реагируют на изменения для меньших сдвигов в сторону от резонансного
частота.
Это связано с тем, что чем острее
резидентный пик, тем более избирательно наша система реагирует на конкретный
частота. Соответственно, чем острее пик,
чем больше наши системы реагируют на изменения для меньших сдвигов в сторону от резонансного
частота.
Число, которое мы используем для количественной оценки
острота пика называется 𝑄- или добротностью резонанса. Для последовательных цепей типа
мы рассматривали, 𝑄-фактор равен угловой частоте
резонанс, умноженный на индуктивность катушки индуктивности, деленную на сопротивление
резистор. Есть ряд других способов, которыми мы
может определить 𝑄-фактор. Хотя, как бы мы это ни определяли,
большие 𝑄-факторы соответствуют графикам с более резким пиком вокруг
резонансная частота. А меньшие 𝑄-факторы соответствуют
к графикам, которые более широко разбросаны вокруг резонансной частоты.
На самом деле оказывается, что ширина пика примерно на половине максимального значения примерно равна резонансной частота деленная на добротность. Это обеспечивает довольно хороший способ определить 𝑄, так как просто взглянув на график, мы можем определить ширину пик, а также его частота, которая является резонансной частотой. Кроме того, если мы знаем любые три величин, фигурирующих в нашей полной формуле, мы можем использовать эту формулу, чтобы найти четвертый.
Хорошо, теперь, когда мы узнали о резонансной частоте и 𝑄-факторе, давайте проработаем некоторые Примеры.
Цепь состоит из резистора,
конденсатор и катушка индуктивности, все они включены последовательно. Источник переменного напряжения – это
подключен к цепи, и генерируется переменный ток. Как изменяется резонансная частота
схема изменится, если увеличить индуктивность катушки индуктивности? (а) Резонансная частота
уменьшается. (б) Резонансная частота
увеличивается. в) Резонансная частота не
сдача.
(б) Резонансная частота
увеличивается. в) Резонансная частота не
сдача.
Вопрос касается нас резонансная частота цепи переменного тока. В частности, для последовательной цепи с резистором, конденсатором и катушкой, вопрос в том, что произойдет если индуктивность катушки индуктивности увеличить. Вот схема нашего схема. У нас переменное напряжение источник, резистор сопротивлением 𝑅, катушка индуктивности 𝐿 и конденсатор емкости 𝐶. Мы будем использовать символ 𝜔 для угловая частота источника напряжения.
Напомним, что резонанс будет возникать в
эта схема, когда разница между индуктивным и емкостным сопротивлениями, что
то есть полное реактивное сопротивление равно нулю. Другими словами, резонанс – это когда
индуктивное и емкостное сопротивления равны. У нас также есть формулы, которые
свяжите угловую частоту с реактивным сопротивлением, поскольку индуктивное реактивное сопротивление — это угловая частота
время индуктивности и емкостного сопротивления равно единице, деленной на угловую частоту, умноженную на
емкость. Если мы приравняем эти выражения, как
будет верным на резонансной частоте, получим, что 𝜔 ноль 𝐿 равно единице
деленное на 𝜔 нуль 𝐶, где 𝜔 нуль — резонансная угловая частота.
Если мы приравняем эти выражения, как
будет верным на резонансной частоте, получим, что 𝜔 ноль 𝐿 равно единице
деленное на 𝜔 нуль 𝐶, где 𝜔 нуль — резонансная угловая частота.
Если мы решим это равенство для 𝜔
ничего, находим, что резонансная угловая частота равна единице, деленной на
квадратный корень из индуктивности дросселя, умноженный на емкость
конденсатор. Эта формула связывает резонансные
частоты к индуктивности, так что давайте использовать его, чтобы ответить на наш вопрос. По мере увеличения индуктивности
квадратный корень из индуктивности, умноженной на емкость, увеличивается. Итак, знаменатель нашей дроби
становится больше, что означает, что значение общей фракции становится
меньше. Но значение этой дроби равно
только резонансная частота. Так как индуктивность
индуктивности увеличивается, резонансная частота уменьшается. Интересно, что мы можем видеть из нашего
формуле, что резонансная частота также уменьшится, если мы увеличим
емкость конденсатора. Но если мы изменим сопротивление
резистор, резонансная частота не изменится.
Интересно, что мы можем видеть из нашего
формуле, что резонансная частота также уменьшится, если мы увеличим
емкость конденсатора. Но если мы изменим сопротивление
резистор, резонансная частота не изменится.
Давайте теперь посмотрим на другой пример, который имеет дело с резонансом более количественным способом.
Какова резонансная частота цепь, показанная на схеме?
Схема состоит из
источник переменного напряжения, соединенный последовательно с резистором сопротивлением 35 Ом,
Дроссель на 7,5 генри и конденсатор на 350 мкФ. И нас просят найти
резонансная частота этого контура. Напомним, что индуктивное сопротивление
в цепи – это угловая частота источника напряжения, умноженная на
индуктивность. А емкостное сопротивление одно
деленная на угловую частоту источника напряжения, умноженную на емкость. При резонансе эти два сопротивления
равны.
При резонансе эти два сопротивления
равны.
Если мы называем резонансным угловым частота 𝜔 ноль, то имеем, что 𝜔 ноль 𝐿 равно единице над 𝜔 ноль 𝐶, которое мы можем решить за 𝜔 ноль. Когда мы решим это уравнение для 𝜔 ничего, находим, что резонансная угловая частота равна единице, деленной на квадратный корень из индуктивности дросселя, умноженный на емкость конденсатор. Теперь это формула для углового частота, но мы ищем только обычную частоту. Поэтому нам нужно использовать отношение эта угловая частота в два раза больше обычной частоты.
Итак, давайте подключим наш
определение угловой частоты в наше уравнение для резонансного углового
частота. У нас в два раза 𝜋 раз больше
резонансная частота равна единице, деленной на квадратный корень из индуктивности
раз больше емкости. Чтобы получить это выражение в
нужная нам окончательная форма, мы просто делим обе части на два 𝜋. С левой стороны два 𝜋
разделить на два 𝜋 равно единице, и у нас просто останется 𝑓 ноль. С правой стороны два 𝜋
просто становится частью знаменателя нашей дроби. Это оставляет нас с финалом
нужная нам формула. Резонансная частота равна единице
деленное на два 𝜋, умноженное на квадратный корень из индуктивности, в генри, умноженное на
емкость, в фарадах.
С левой стороны два 𝜋
разделить на два 𝜋 равно единице, и у нас просто останется 𝑓 ноль. С правой стороны два 𝜋
просто становится частью знаменателя нашей дроби. Это оставляет нас с финалом
нужная нам формула. Резонансная частота равна единице
деленное на два 𝜋, умноженное на квадратный корень из индуктивности, в генри, умноженное на
емкость, в фарадах.
Теперь нам просто нужно подключить ценности. У нас есть индуктивность в Генри. Это 7,5 генри. Однако наша емкость дается в микрофарадах вместо фарад. Чтобы перевести в фарады, вспомним, что в одной фараде миллион микрофарад. Другими словами, одна микрофарад эквивалентен 10 в минус шестой фарад. Так как у нас 350 микрофарад, то наш емкость эквивалентна 350 умножить на 10 с минус шестой фарад.
Затыкаем нашу индуктивность и
емкость в нашу формулу резонансной частоты, это дает нам единицу, деленную на
два 𝜋, умноженные на квадратный корень из 350, умноженный на 10, в минус шестой фарад, умноженный на 7,5
Генри. Оказывается, квадратный корень
Один фарад, умноженный на один генри, равен одной секунде. Таким образом, мы можем переписать знаменатель
с единицами секунд.
Оказывается, квадратный корень
Один фарад, умноженный на один генри, равен одной секунде. Таким образом, мы можем переписать знаменатель
с единицами секунд.
Теперь единица, деленная на секунды, равна единица герц, которая используется для частоты. Итак, теперь у нас есть выражение для резонансная частота. Это число, умноженное на единицу герц, что является правильной единицей измерения частоты. Итак, теперь все, что нам нужно сделать, это оцените это число с помощью калькулятора. Когда мы делаем эту оценку, мы находим что все числовое выражение приблизительно равно 3,1. Таким образом, резонансная частота этого цепь 3,1 герц. Стоит отметить, что 35-Ом резистор не играл никакой роли в нашем расчете резонансной частоты.
Хорошо, теперь, когда мы увидели кое-что
примеры, давайте рассмотрим некоторые ключевые моменты, которые мы узнали на этом уроке. В этом видео мы рассмотрели
цепь, состоящая из источника переменного напряжения, питающего резистор, катушку индуктивности,
и конденсатор, все соединены последовательно. Потому что индуктивная и емкостная
реактивное сопротивление зависит от частоты источника переменного напряжения, мы видели
чтобы можно было найти частоту, при которой полное реактивное сопротивление, индуктивное минус
емкостное сопротивление равно нулю.
В этом видео мы рассмотрели
цепь, состоящая из источника переменного напряжения, питающего резистор, катушку индуктивности,
и конденсатор, все соединены последовательно. Потому что индуктивная и емкостная
реактивное сопротивление зависит от частоты источника переменного напряжения, мы видели
чтобы можно было найти частоту, при которой полное реактивное сопротивление, индуктивное минус
емкостное сопротивление равно нулю.
Приравнивая частотно-зависимую
формулы для индуктивных и емкостных сопротивлений, мы смогли найти, что
резонансная угловая частота равна единице, деленной на квадратный корень из
индуктивность дросселя, умноженная на емкость конденсатора. Когда частота напряжения
равна резонансной частоте, суммарному эффекту катушек индуктивности и
конденсаторы должны не оказывать сопротивления току в цепи. Это означает, что единственная оппозиция
к току от резистора, и поэтому полное сопротивление идентично
сопротивление. Это также минимально возможный
значение импеданса из-за отсутствия резонанса, реактивный вклад в
импеданс больше нуля. Соответственно тогда по закону Ома
если импеданс минимален, то амплитуда тока максимальна.
Это также минимально возможный
значение импеданса из-за отсутствия резонанса, реактивный вклад в
импеданс больше нуля. Соответственно тогда по закону Ома
если импеданс минимален, то амплитуда тока максимальна.
Наконец, мы рассмотрели, как
относительная амплитуда тока зависит от угловой частоты. Мы видели, что граф с относительным
амплитуда по вертикальной оси и угловая частота по горизонтальной оси показывают
резкий пик на резонансной частоте. Это соответствует тому же
величина управляющего напряжения, приводящая к гораздо большему току на резонансном
частота, чем на более низких и более высоких частотах. Для количественной оценки остроты
резонансный пик, мы определяем 𝑄- или добротность как резонансную угловую частоту
произведение индуктивности катушки индуктивности на сопротивление резистора. Большие значения 𝑄 соответствуют
резонансы с более острыми пиками, а меньшие значения 𝑄 соответствуют резонансам
с более широкими вершинами.
Наконец, мы заявили, но не доказали что мы можем определить значение 𝑄 из графика, подобного этому, путем измерения ширина пика, а также местоположение пика, которое является резонансной частотой. Таким образом, зная любые три из значения в нашей формуле для добротности, мы можем определить значение четвертая величина.
Цепи переменного тока серии RLC | Физика
Цели обучения
К концу этого раздела вы сможете:
- Вычислите импеданс, фазовый угол, резонансную частоту, мощность, коэффициент мощности, напряжение и/или ток в последовательной цепи RLC.
- Нарисуйте принципиальную схему последовательной цепи RLC.
- Объясните значение резонансной частоты.
Полное сопротивление
В цепи переменного тока катушки индуктивности, конденсаторы и резисторы препятствуют току. Как они ведут себя, когда все три встречаются вместе? Интересно, что их индивидуальные сопротивления в омах не просто складываются.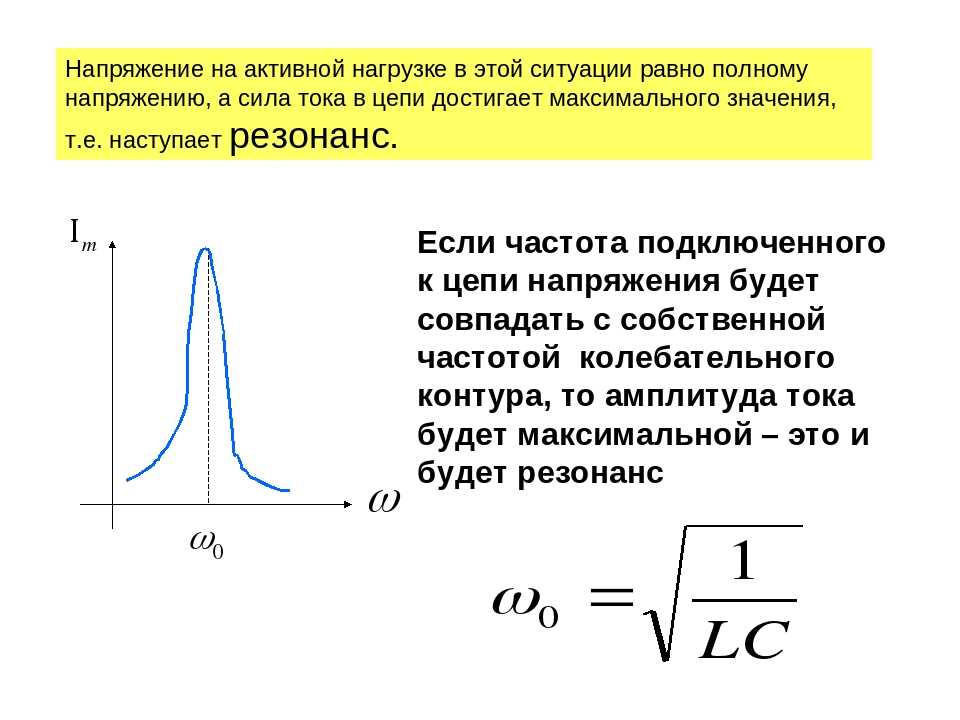 Поскольку катушки индуктивности и конденсаторы ведут себя противоположным образом, они частично или полностью компенсируют эффект друг друга. На рис. 1 показана цифра 9.0101 Цепь серии RLC с источником переменного напряжения, поведение которой является предметом настоящего раздела. Суть анализа цепи RLC состоит в частотной зависимости X L и X C и их влиянии на фазу зависимости напряжения от тока (установлено в предыдущий раздел). Это приводит к частотной зависимости схемы с важными «резонансными» свойствами, которые лежат в основе многих приложений, таких как радиотюнеры.
Поскольку катушки индуктивности и конденсаторы ведут себя противоположным образом, они частично или полностью компенсируют эффект друг друга. На рис. 1 показана цифра 9.0101 Цепь серии RLC с источником переменного напряжения, поведение которой является предметом настоящего раздела. Суть анализа цепи RLC состоит в частотной зависимости X L и X C и их влиянии на фазу зависимости напряжения от тока (установлено в предыдущий раздел). Это приводит к частотной зависимости схемы с важными «резонансными» свойствами, которые лежат в основе многих приложений, таких как радиотюнеры.
Рис. 1. Цепь серии RLC с источником переменного напряжения.
Комбинированный эффект сопротивления R , индуктивная реактивность x L , и емкостная реактивность x C определяется до . . Ток, напряжение и импеданс в цепи RLC связаны версией закона Ома для переменного тока:
[латекс]{I}_{0}=\frac{{V}_{0}}{Z}\ text{ или }{I}_{\text{rms}}=\frac{{V}_{\text{rms}}}{Z}\\[/latex].
Здесь I 0 — пиковое значение тока, В 0 — пиковое напряжение источника, а Z — полное сопротивление цепи. Единицами импеданса являются омы, и его влияние на цепь, как и следовало ожидать: чем больше импеданс, тем меньше ток. Чтобы получить выражение для Z через R , X L и X C , мы теперь рассмотрим, как различные компоненты связаны с напряжением на источнике. Напряжение. Эти напряжения обозначены цифрой 9.0101 V R , V L и V C , и V C на рис. так что мы можем сказать, что токи в R , L и C равны и находятся в фазе. Но из предыдущего раздела мы знаем, что напряжение на катушке В L опережает ток на одну четвертую периода, напряжение на конденсаторе В C соответствует току на одну четвертую периода, а напряжение на резисторе В R точно совпадает по фазе с током. Figure 2 shows these relationships in one graph, as well as showing the total voltage around the circuit V = V R + V L + V C , где все четыре напряжения являются мгновенными значениями. Согласно петлевому правилу Кирхгофа, общее напряжение в цепи равно В также является напряжением источника. Из рисунка 2 видно, что, хотя V R находится в фазе с током, V L опережает на 90°, а V 0 следует за 07 0. Таким образом, V L и V C сдвинуты по фазе на 180º (гребень к впадине) и имеют тенденцию сокращаться, хотя и не полностью, если они не имеют одинаковую величину. Поскольку пиковые напряжения не выровнены (не по фазе), пиковое напряжение 9{2}}}\\[/latex],
Figure 2 shows these relationships in one graph, as well as showing the total voltage around the circuit V = V R + V L + V C , где все четыре напряжения являются мгновенными значениями. Согласно петлевому правилу Кирхгофа, общее напряжение в цепи равно В также является напряжением источника. Из рисунка 2 видно, что, хотя V R находится в фазе с током, V L опережает на 90°, а V 0 следует за 07 0. Таким образом, V L и V C сдвинуты по фазе на 180º (гребень к впадине) и имеют тенденцию сокращаться, хотя и не полностью, если они не имеют одинаковую величину. Поскольку пиковые напряжения не выровнены (не по фазе), пиковое напряжение 9{2}}}\\[/latex],
where V 0 R , V 0 L , and V 0 C are the peak voltages across R , L и C соответственно. Теперь, используя закон Ома и определения из Реактивного, Индуктивного и Емкостного, подставляем В 0 = I 0 Z в приведенное выше, а также В 0 9{2}}\\[/latex],
Теперь, используя закон Ома и определения из Реактивного, Индуктивного и Емкостного, подставляем В 0 = I 0 Z в приведенное выше, а также В 0 9{2}}\\[/latex],
, который представляет собой импеданс цепи переменного тока серии RLC . Для цепей без резистора принять R = 0; для тех, у кого нет индуктора, принять X L = 0; а для тех, у кого нет конденсатора, возьмите X C = 0,
Рисунок 2. На этом графике показано отношение напряжения в цепи RLC к току. Напряжения на элементах схемы складываются, чтобы равняться напряжению источника, которое, как видно, не совпадает по фазе с током.
Пример 1. Расчет импеданса и тока
Схема серии RLC имеет резистор 40,0 Ом, катушку индуктивности 3,00 мГн и конденсатор 5,00 мкФ. (a) Найдите полное сопротивление цепи при 60,0 Гц и 10,0 кГц, отметив, что эти частоты и значения для L и C такие же, как в примере 1 и примере 2 из Реактивного, индуктивного и емкостного сопротивления.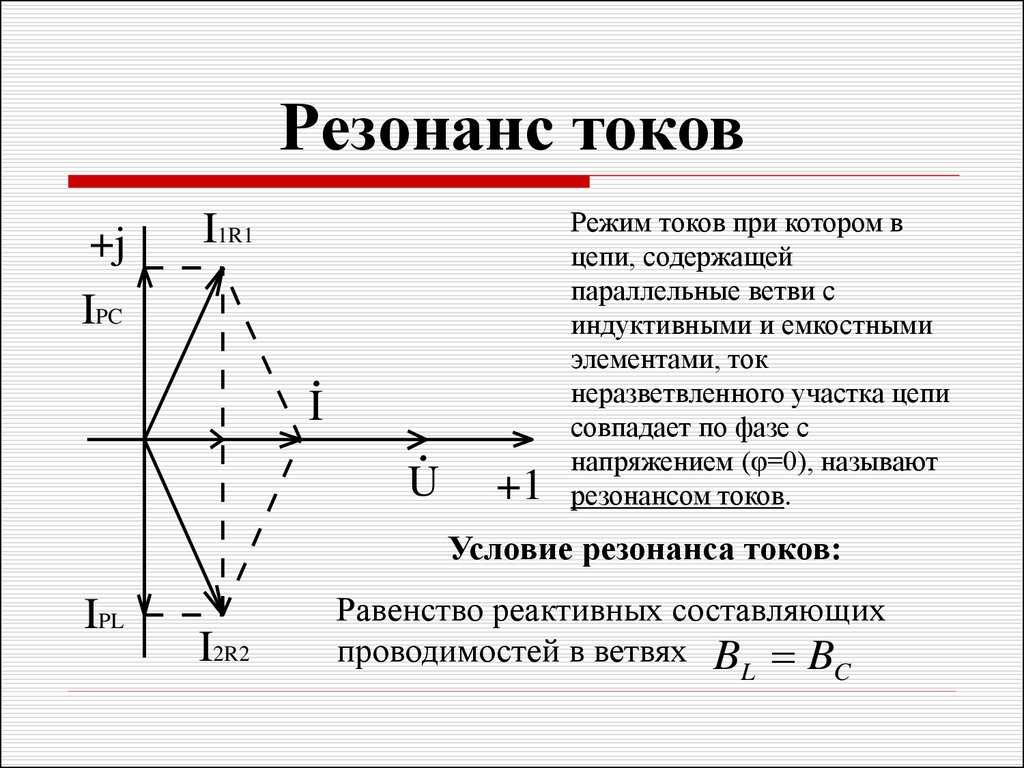 {2 }}\\[/латекс] дает 9{2}}\\ & =& 190\text{ }\Omega\text{ на частоте }10,0\text{ кГц}\end{array}\\[/latex]
{2 }}\\[/латекс] дает 9{2}}\\ & =& 190\text{ }\Omega\text{ на частоте }10,0\text{ кГц}\end{array}\\[/latex]
In В обоих случаях результат почти совпадает с наибольшим значением, а импеданс определенно не является суммой отдельных значений. Видно, что на высокой частоте доминирует X L , а на низкой частоте X C .
Раствор для (б)Текущий I среднеквадратичное значение можно найти, используя версию закона Ома для переменного тока в уравнении rms}}=\frac{{V}_{\text{rms}}}{Z}=\frac{120\text{V}}{531\text{}\Omega}=0,226\text{A}\ \[/латекс] при 60,0 Гц
Наконец, при 10,0 кГц мы находим
[латекс]{I}_{\text{rms}}=\frac{{V}_{\text{rms}}} {Z}=\frac{120\text{ V}}{190\text{ }\Omega}=0,633\text{ A}\\[/latex] на частоте 10,0 кГц
Обсуждение для (a) Ток при частоте 60,0 Гц такой же (с точностью до трех цифр), что и для одного конденсатора в примере 2 из Reactance, Inductive, and Capacitive. Конденсатор доминирует на низких частотах. Ток на частоте 10,0 кГц лишь немного отличается от тока, найденного только для индуктора в примере 1 из Reactance, Inductive, and Capacitive. Индуктор доминирует на высоких частотах.
Конденсатор доминирует на низких частотах. Ток на частоте 10,0 кГц лишь немного отличается от тока, найденного только для индуктора в примере 1 из Reactance, Inductive, and Capacitive. Индуктор доминирует на высоких частотах.
Резонанс в цепях переменного тока серии
RLC 9{2}}}\\[/latex]Реактивные сопротивления зависят от частоты: X L большие на высоких частотах и X C большие на низких частотах, как мы видели в трех предыдущих примерах. На некоторой промежуточной частоте f 0 реактивные сопротивления будут равны и взаимно компенсируются, что дает0107 среднеквадратичное значение результатов. Мы можем получить выражение для f 0 , взяв:
Подстановка определений X L и X C ,
[latex]2\pi f_{0}{0}L=\frac }C}\\[/латекс].
Решение этого выражения для f 0 дает
[латекс]{f}_{0}=\frac{1}{2\pi \sqrt{LC}}\\[/latex],
, где f 0 — резонансная частота цепи серии RLC .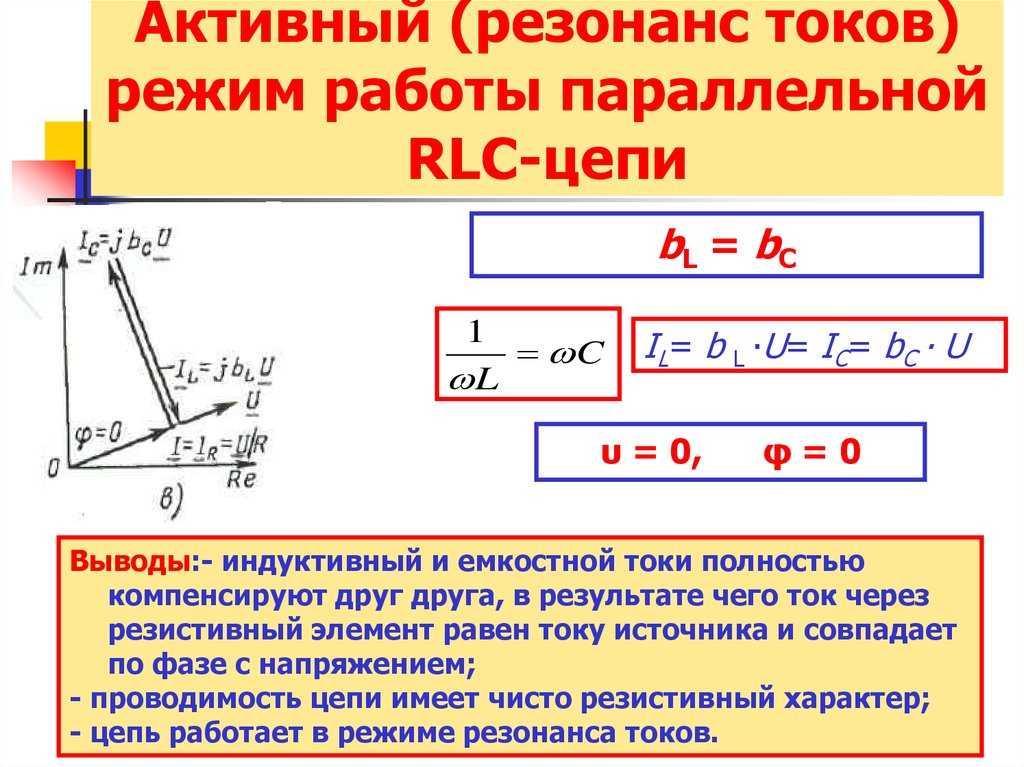 Это также собственная частота , при которой схема будет колебаться, если не будет управляться источником напряжения. При f 0 эффекты катушки индуктивности и конденсатора компенсируются, так что Z = R , а I среднеквадратичное значение является максимальным.
Это также собственная частота , при которой схема будет колебаться, если не будет управляться источником напряжения. При f 0 эффекты катушки индуктивности и конденсатора компенсируются, так что Z = R , а I среднеквадратичное значение является максимальным.
Резонанс в цепях переменного тока аналогичен механическому резонансу, где резонанс определяется как вынужденные колебания (в данном случае вызванные источником напряжения) на собственной частоте системы. Приемник в радио — это Цепь RLC , лучше всего генерирующая f 0 . Переменный конденсатор часто используется для настройки f 0 для получения желаемой частоты и отклонения других. На рисунке 3 представлен график зависимости тока от частоты, иллюстрирующий резонансный пик в I среднеквадратичное значение при f 0 . Две кривые относятся к двум разным цепям, которые отличаются только величиной сопротивления в них. Пик ниже и шире для схемы с более высоким сопротивлением. Таким образом, цепь с более высоким сопротивлением не резонирует так сильно и не будет такой избирательной, например, в радиоприемнике.
Пик ниже и шире для схемы с более высоким сопротивлением. Таким образом, цепь с более высоким сопротивлением не резонирует так сильно и не будет такой избирательной, например, в радиоприемнике.
Рис. 3. График зависимости тока от частоты для двух цепей серии RLC, отличающихся только величиной сопротивления. Оба имеют резонанс при f 0 , но при более высоком сопротивлении он ниже и шире. Источник управляющего переменного напряжения имеет фиксированную амплитуду В 0 .
Пример 2. Расчет резонансной частоты и тока
Для той же цепи серии RLC , имеющей резистор 40,0 Ом, катушку индуктивности 3,00 мГн и конденсатор 5,00 мкФ: (a) Найдите резонансную частоту. (б) Вычислить I rms при резонансе, если V rms равно 120 V.
Стратегия
Резонансная частота находится с помощью выражения 1}{2\pi\sqrt{LC}}\\[/латекс]. Ток на этой частоте такой же, как если бы в цепи был только резистор.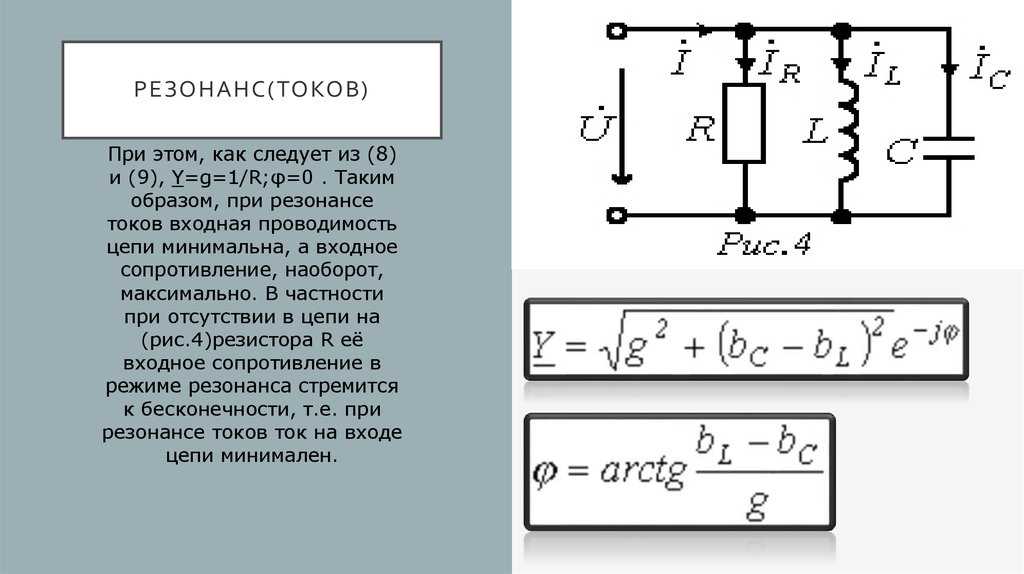
Решение для (a)
Ввод заданных значений для L и C в выражение для f 9{-6}\text{ F}\right)}}=1.30\text{ кГц}\end{array}\\[/latex]
Обсуждение для (a)Мы видим, что резонансная частота равна между 60,0 Гц и 10,0 кГц, двумя частотами, выбранными в предыдущих примерах. Этого и следовало ожидать, поскольку на низкой частоте преобладал конденсатор, а на высокой частоте — катушка индуктивности. Их эффекты одинаковы на этой промежуточной частоте.
Решение для (b)Ток определяется законом Ома. В резонансе два реактивных сопротивления равны и компенсируются, так что импеданс равен одному сопротивлению. Таким образом,
[латекс] {I} _ {\ text {rms}} = \ frac {{V} _ {\ text {rms}}} {Z} = \ frac {120 \ text {V}} {40,0 \ text { }\Omega}=3.00\text{ A}\\[/latex].
Обсуждение для (b) При резонансе ток больше, чем на более высоких и более низких частотах, рассмотренных для той же цепи в предыдущем примере.
Мощность в цепях переменного тока серии
RLCЕсли ток в цепи RLC зависит от частоты, то подводимая к ней мощность также зависит от частоты. Но средняя мощность — это не просто ток, умноженный на напряжение, как в чисто резистивных цепях. Как видно на рисунке 2, напряжение и ток не совпадают по фазе в Цепь RLC . Между напряжением источника V и током I имеется фазовый угол ϕ , который можно найти из
[латекс]\cos\varphi =\frac{R}{Z}\\[ /latex]
Например, на резонансной частоте или в чисто резистивной цепи Z = R , так что [latex]\text{cos}\varphi =1\\[/latex]. Это означает, что ϕ = 0º и что напряжение и ток совпадают по фазе, как и ожидается для резисторов. На других частотах средняя мощность меньше, чем на резонансе. Это происходит как из-за того, что напряжение и ток не совпадают по фазе, так и из-за того, что I среднеквадратичное значение ниже.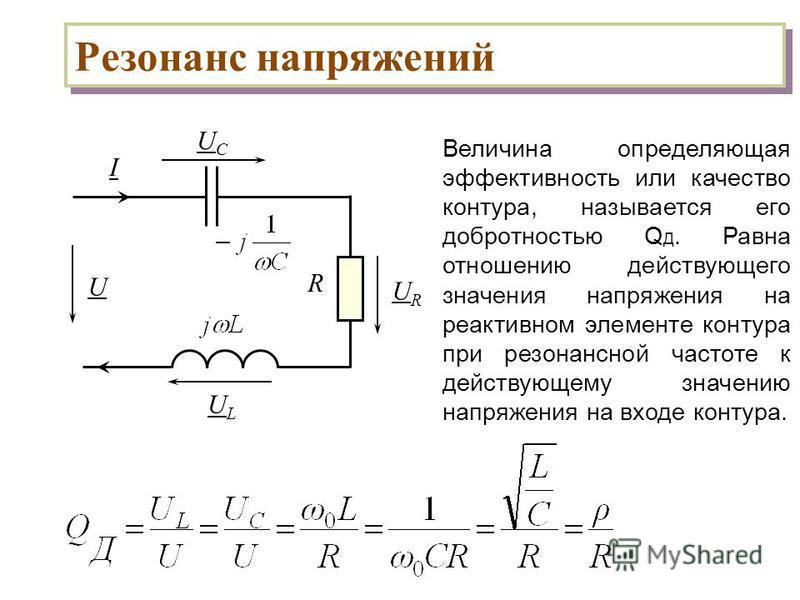 Тот факт, что напряжение и ток источника не совпадают по фазе, влияет на мощность, подаваемую в цепь. Можно показать, что средняя мощность равна
Тот факт, что напряжение и ток источника не совпадают по фазе, влияет на мощность, подаваемую в цепь. Можно показать, что средняя мощность равна
[латекс] {P} _ {\ text {ave}} = {I} _ {\ text {rms}} {V} _ {\ text {rms }}\cos\varphi\\[/latex],
Таким образом, cos ϕ называется коэффициентом мощности , который может принимать значения от 0 до 1. Коэффициенты мощности, близкие к 1, желательны при проектировании эффективного двигателя, например . На резонансной частоте cos ϕ = 1.
Пример 3. Расчет коэффициента мощности и мощности
Для той же цепи RLC , имеющей резистор 40,0 Ом, катушку индуктивности 3,00 мГн, конденсатор 5,00 мкФ и источник напряжения с V rms для 120 В: (a) Рассчитайте коэффициент мощности и фазовый угол для f = 60,0 Гц. (b) Какова средняя мощность при 50,0 Гц? в) Найдите среднюю мощность на резонансной частоте контура.
Стратегия и решение для (а)Коэффициент мощности при 60,0 Гц определяется из
[латекс]\cos\varphi =\frac{R}{Z}\\[/латекс]. {-1} 0,0753=\текст{85,7º}\текст{ при }60,0\текст{Гц}\\[/латекс].
{-1} 0,0753=\текст{85,7º}\текст{ при }60,0\текст{Гц}\\[/латекс].
Фазовый угол близок к 90º, что согласуется с тем фактом, что конденсатор доминирует в цепи на этой низкой частоте (чистая RC-цепь имеет напряжение и ток, сдвинутые по фазе на 90º) .
Стратегия и решение для (B)Средняя мощность при 60,0 Гц составляет
P AVE = I RMS V RMS 110110110110 1101101101101101101101101101101101101101101101101101101101101101110 .
I Среднеквадратичное значение оказалось равным 0,226 А в Пример 1: Расчет импеданса и тока . Ввод известных значений дает
P ср = (0,226 А)(120 В)(0,0753) = 2,04 Вт при 60,0 Гц.
Стратегия и решение для (c) На резонансной частоте мы знаем, что cos ϕ = 1, и I среднеквадратичное значение равно 6,00 А в . . Таким образом, P ср = (3,00 А)(120 В)(1) = 360 Вт при резонансе (1,30 кГц)
. Таким образом, P ср = (3,00 А)(120 В)(1) = 360 Вт при резонансе (1,30 кГц)
Мощность, подаваемая в цепь переменного тока RLC серии , рассеивается только за счет сопротивления. Катушка индуктивности и конденсатор имеют входную и выходную энергию, но не рассеивают ее из цепи. Скорее они передают энергию туда и обратно друг другу, при этом резистор рассеивает именно то, что источник напряжения помещает в цепь. Это предполагает отсутствие значительного электромагнитного излучения от катушки индуктивности и конденсатора, такого как радиоволны. Такое излучение может происходить и может быть даже желательным, как мы увидим в следующей главе об электромагнитном излучении, но его также можно подавить, как в случае с этой главой. Схема аналогична колесу автомобиля, движущегося по неровной дороге, как показано на рис. 4. Равномерно расположенные неровности на дороге аналогичны источнику напряжения, приводящему в движение колесо вверх и вниз.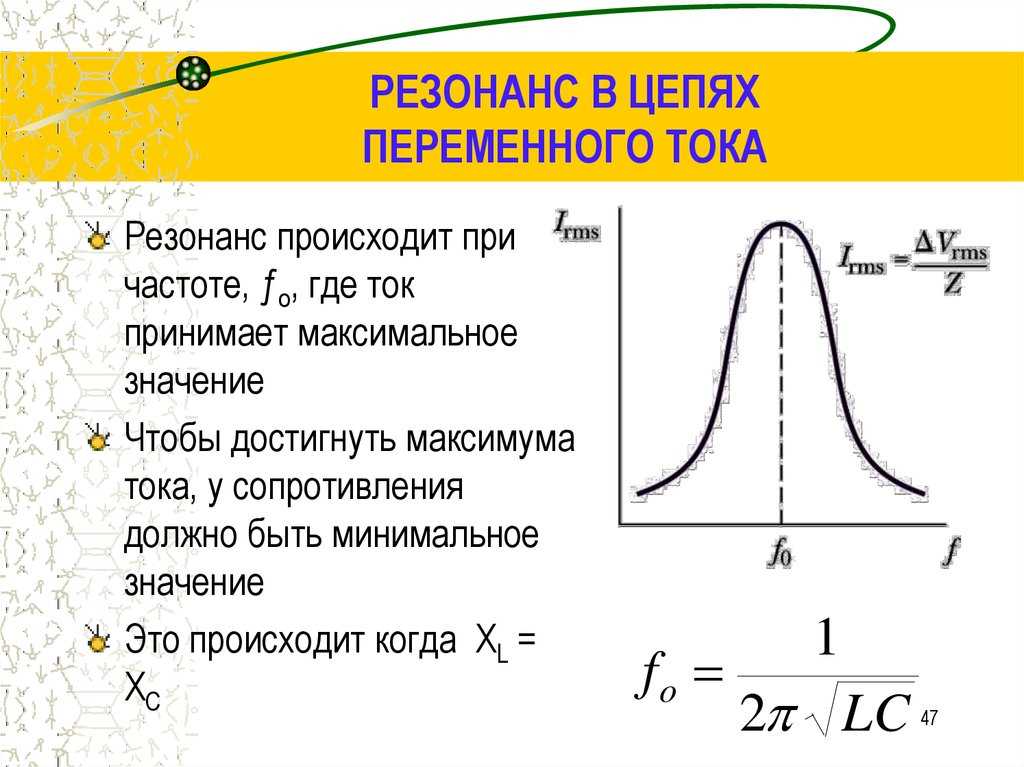 Амортизатор аналогичен сопротивлению, демпфирующему и ограничивающему амплитуду колебаний. Энергия внутри системы переходит туда и обратно между кинетической (аналогично максимальному току и энергии, хранящейся в индукторе) и потенциальной энергией, запасенной в автомобильной пружине (аналогично отсутствию тока и энергии, запасенной в электрическом поле конденсатора). Амплитуда движения колес максимальна, если удары о неровности дороги происходят на резонансной частоте.
Амортизатор аналогичен сопротивлению, демпфирующему и ограничивающему амплитуду колебаний. Энергия внутри системы переходит туда и обратно между кинетической (аналогично максимальному току и энергии, хранящейся в индукторе) и потенциальной энергией, запасенной в автомобильной пружине (аналогично отсутствию тока и энергии, запасенной в электрическом поле конденсатора). Амплитуда движения колес максимальна, если удары о неровности дороги происходят на резонансной частоте.
Рис. 4. Принудительное, но демпфированное движение колеса на рессоре автомобиля аналогично цепи переменного тока RLC серии . Амортизатор гасит движение и рассеивает энергию, аналогично сопротивлению в цепи RLC . Масса и пружина определяют резонансную частоту.
Чистый контур LC с незначительным сопротивлением колеблется на частоте f 0 , той же резонансной частоте, что и контур RLC . Он может служить эталоном частоты или тактовой схемой, например, в цифровых наручных часах. При очень малом сопротивлении для поддержания колебаний требуется лишь очень небольшая затрата энергии. Схема аналогична автомобилю без амортизаторов. Как только он начинает колебаться, он некоторое время продолжает работать на своей собственной частоте. На рис. 5 показана аналогия между LC цепь и масса на пружине.
При очень малом сопротивлении для поддержания колебаний требуется лишь очень небольшая затрата энергии. Схема аналогична автомобилю без амортизаторов. Как только он начинает колебаться, он некоторое время продолжает работать на своей собственной частоте. На рис. 5 показана аналогия между LC цепь и масса на пружине.
Рис. 5. LC-контур аналогичен массе, колеблющейся на пружине без трения и движущей силы. Энергия движется вперед и назад между катушкой индуктивности и конденсатором точно так же, как она движется от кинетической к потенциальной в системе масса-пружина.
PhET Explorations: комплект для построения цепей (AC+DC), виртуальная лабораторияСоздавайте схемы с конденсаторами, катушками индуктивности, резисторами и источниками переменного или постоянного напряжения и проверяйте их с помощью лабораторных приборов, таких как вольтметры и амперметры.
Нажмите, чтобы загрузить симуляцию. Запуск с использованием Java.
Резюме раздела
- Аналогией сопротивления переменного тока является импеданс Z , комбинированный эффект резисторов, катушек индуктивности и конденсаторов, определяемый версией закона Ома для переменного тока:
[латекс] {I}_{0}=\frac{{V}_{0}}{Z}\text{ или }{I}_{\text{rms}}=\frac{{V}_ {\text{rms}}}{Z}\\[/латекс],
, где I o — пиковое значение тока, а В o — пиковое напряжение источника.
 9{2}}\\[/латекс].
9{2}}\\[/латекс]. - Резонансная частота f 0 , при которой X L = X C , равна
[латекс]{f}_{0}=\frac{1}{2\pi \sqrt{LC}}\\[/latex]
- В цепи переменного тока имеется фазовый угол ϕ между напряжением источника В и током I , который можно найти из
[латекс]\текст{cos}\varphi =\frac{R}{Z}\\[/латекс],
- ϕ = 0º для чисто резистивной цепи или RLC Цепь в резонансе.
- Средняя мощность, подаваемая в цепь RLC , зависит от фазового угла и определяется выражением
[латекс] {P} _ {\ text {ave}} = {I} _ {\ text {rms}} {V} _ {\ text {rms}} \ cos \ varphi \\ [/latex],
cos ϕ называется коэффициентом мощности, который принимает значения от 0 до 1.
Концептуальные вопросы
1. Зависит ли резонансная частота цепи переменного тока от пикового напряжения источника переменного тока? Объясните, почему да или почему нет.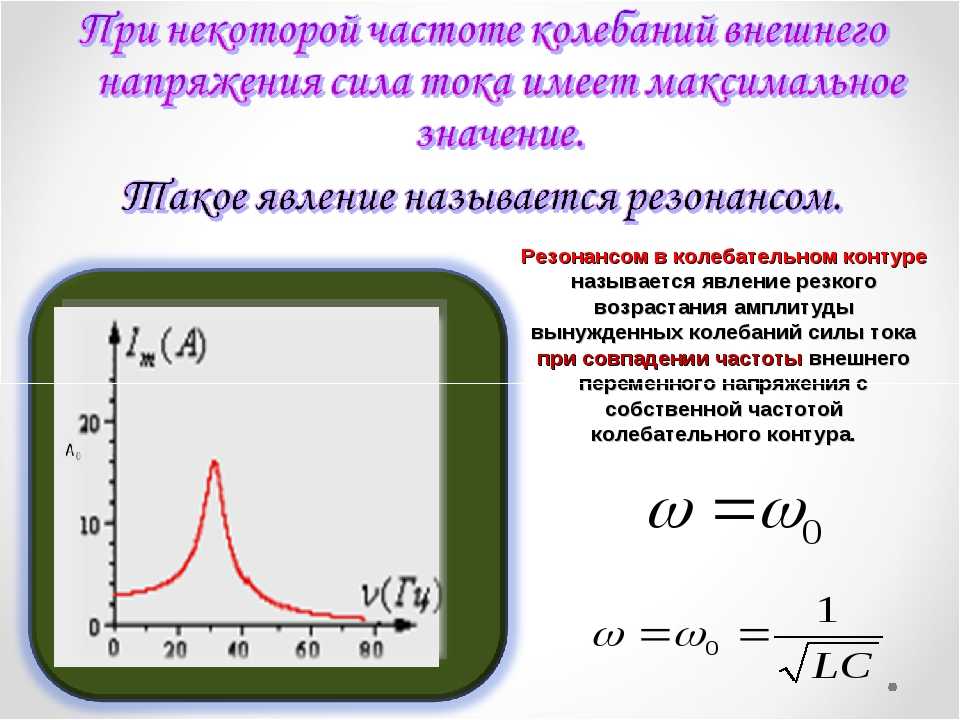
2. Предположим, у вас есть двигатель с коэффициентом мощности значительно меньше 1. Объясните, почему было бы лучше улучшить коэффициент мощности в качестве метода улучшения выходной мощности двигателя, а не увеличивать входное напряжение.
Задачи и упражнения
1. Схема RL состоит из резистора 40,0 Ом и катушки индуктивности 3,00 мГн. (а) Найдите его импеданс Z на частотах 60,0 Гц и 10,0 кГц. (b) Сравните эти значения Z со значениями, найденными в Пример 1: расчет импеданса и тока , в котором также был конденсатор.
2. Цепь RC состоит из резистора 40,0 Ом и конденсатора 5,00 мкФ. (а) Найдите его импеданс на частотах 60,0 Гц и 10,0 кГц. (b) Сравните эти значения Z со значениями, найденными в Пример 1: Расчет импеданса и тока , в котором также была катушка индуктивности.
3. Цепь LC состоит из катушки индуктивности 3,00 мГн и конденсатора 5,00 мкФ. (а) Найдите его импеданс на частотах 60,0 Гц и 10,0 кГц.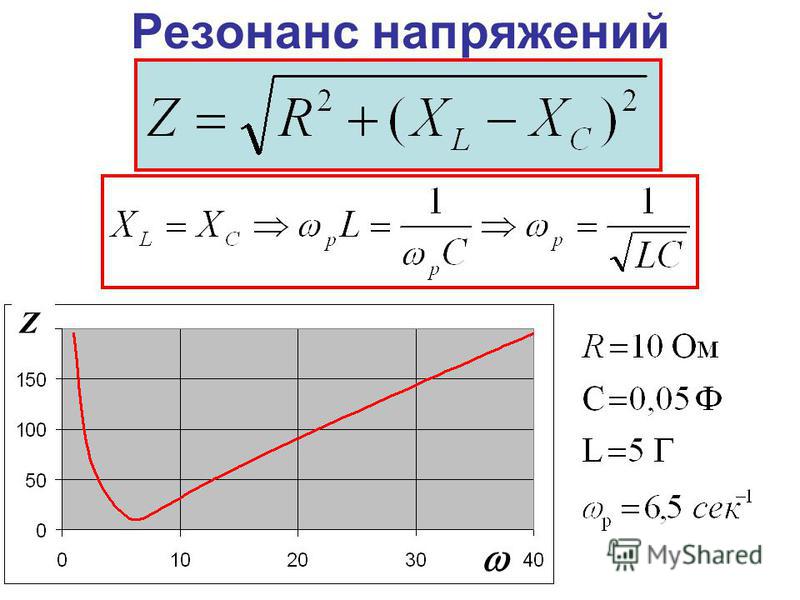 (б) Сравните эти значения Z с найденными в Пример 1: Расчет импеданса и тока , в котором также был резистор.
(б) Сравните эти значения Z с найденными в Пример 1: Расчет импеданса и тока , в котором также был резистор.
4. Какова резонансная частота катушки индуктивности 0,500 мГн, подключенной к конденсатору емкостью 40,0 мкФ?
5. Для приема AM-радиосигнала вам понадобится схема RLC , которую можно заставить резонировать на любой частоте от 500 до 1650 кГц. Это достигается с помощью фиксированной катушки индуктивности 1,00 мкГн, соединенной с переменным конденсатором. Какой диапазон емкости нужен?
6. Предположим, у вас есть запас катушек индуктивности в диапазоне от 1,00 нГн до 10,0 Гн и конденсаторов в диапазоне от 1,00 пФ до 0,100 Ф. Каков диапазон резонансных частот, который может быть получен при комбинации одной катушки индуктивности и одного конденсатора ?
7. Какая емкость необходима для получения резонансной частоты 1,00 ГГц при использовании катушки индуктивности 8,00 нГн?
8. Какая индуктивность необходима для получения резонансной частоты 60,0 Гц при использовании конденсатора 2,00 мкФ?
9. Самая низкая частота в диапазоне FM-радио составляет 88,0 МГц. а) Какая индуктивность необходима для получения этой резонансной частоты, если он подключен к конденсатору емкостью 2,50 пФ? (b) Конденсатор переменный, что позволяет регулировать резонансную частоту до 108 МГц. Какая должна быть емкость на этой частоте?
Самая низкая частота в диапазоне FM-радио составляет 88,0 МГц. а) Какая индуктивность необходима для получения этой резонансной частоты, если он подключен к конденсатору емкостью 2,50 пФ? (b) Конденсатор переменный, что позволяет регулировать резонансную частоту до 108 МГц. Какая должна быть емкость на этой частоте?
10. Цепь RLC серии имеет резистор 2,50 Ом, катушку индуктивности 100 мкГн и конденсатор 80,0 мкФ. (a) Найдите полное сопротивление цепи при частоте 120 Гц. (b) Найдите полное сопротивление цепи на частоте 5,00 кГц. (c) Если источник напряжения имеет В СКЗ = 5,60 В, чему равно I СКЗ на каждой частоте? г) Какова резонансная частота цепи? (e) Чему равно I среднеквадратичное значение при резонансе?
11. Цепь серии RLC имеет резистор 1,00 кОм, катушку индуктивности 150 мкГн и конденсатор 25,0 нФ. а) Найдите полное сопротивление цепи на частоте 500 Гц. (b) Найдите полное сопротивление цепи на частоте 7,50 кГц. (c) Если источник напряжения имеет В среднеквадратичное значение = 408 В, чему равно I среднеквадратичное значение на каждой частоте? г) Какова резонансная частота цепи? (e) Чему равно I среднеквадратичное значение при резонансе?
(c) Если источник напряжения имеет В среднеквадратичное значение = 408 В, чему равно I среднеквадратичное значение на каждой частоте? г) Какова резонансная частота цепи? (e) Чему равно I среднеквадратичное значение при резонансе?
12. Цепь RLC серии имеет резистор 2,50 Ом, катушку индуктивности 100 мкГн и конденсатор 80,0 мкФ. (а) Найдите коэффициент мощности при 90 101 f 90 102 = 120 Гц. (b) Каков фазовый угол на частоте 120 Гц? в) Какова средняя мощность на частоте 120 Гц? г) Найдите среднюю мощность на резонансной частоте контура.
13. Цепь серии RLC имеет резистор 1,00 кОм, катушку индуктивности 150 мкГн и конденсатор 25,0 нФ. (а) Найдите коэффициент мощности при 90 101 f 90 102 = 7,50 Гц. б) Каков фазовый угол на этой частоте? в) Какова средняя мощность на этой частоте? г) Найдите среднюю мощность на резонансной частоте контура.
14. Цепь серии RLC имеет резистор 200 Ом и катушку индуктивности 25,0 мГн. При 8000 Гц фазовый угол составляет 45,0º. а) Чему равно сопротивление? б) Найдите емкость цепи. (в) Если 9{2}}\\[/латекс]
При 8000 Гц фазовый угол составляет 45,0º. а) Чему равно сопротивление? б) Найдите емкость цепи. (в) Если 9{2}}\\[/латекс]
- резонансная частота:
- частота, при которой импеданс в цепи минимален, а также частота, при которой цепь колебалась бы, если бы она не приводилась в действие источником напряжения; рассчитано по формуле [латекс]{f}_{0}=\frac{1}{2\pi \sqrt{\text{LC}}}\\[/latex]
- фазовый угол:
- обозначается как ϕ , величина, на которую напряжение и ток не совпадают по фазе друг с другом в цепи .
- коэффициент мощности:
- величина, на которую мощность, подаваемая в цепь, меньше теоретического максимума цепи из-за того, что напряжение и ток не совпадают по фазе; рассчитывается по cos ϕ
Избранные решения задач и упражнений
1. (a) 40,02 Ом при 60,0 Гц, 193 Ом при 10,0 кГц (b) При 60 Гц, с конденсатором Z = 531 Ом, что более чем в 13 раз выше, чем без конденсатора. конденсатор. Конденсатор имеет большое значение на низких частотах. На 10 кГц, с конденсатором Z=190 Ом, примерно как без конденсатора. Конденсатор оказывает меньшее влияние на высоких частотах.
конденсатор. Конденсатор имеет большое значение на низких частотах. На 10 кГц, с конденсатором Z=190 Ом, примерно как без конденсатора. Конденсатор оказывает меньшее влияние на высоких частотах.
3. (a) 529 Ом при 60,0 Гц, 185 Ом при 10,0 кГц (b) Эти значения близки к значениям, полученным в Пример 1: Расчет импеданса и тока , поскольку на низкой частоте преобладает конденсатор, а на высокой частоте преобладает индуктор. Таким образом, в обоих случаях резистор вносит небольшой вклад в общий импеданс.
5. от 9,30 нФ до 101 нФ
7. 3,17 пФ
9. (а) 1,31 мкГн (б) 1,66 пФ
11. (а) 12,8 кОм (б) 1,31 кОм (в) 31,9 мА при 500 Гц, 312 мА при 7,50 кГц (г) 82,2 кГц (д) 0,408 A
13. (a) 0,159 (b) 80,9º (c) 26,4 Вт (d) 166 Вт
15. 16,0 Вт
напряжение — Можно ли увеличить ток с помощью резонанса переменного тока?
спросил
Изменено 5 лет, 4 месяца назад
Просмотрено 2к раз
\$\начало группы\$
При резонансе, особенно если мы резонируем на собственной частоте, интенсивность генерируемых волн будет складываться, что приведет к волне все возрастающей интенсивности.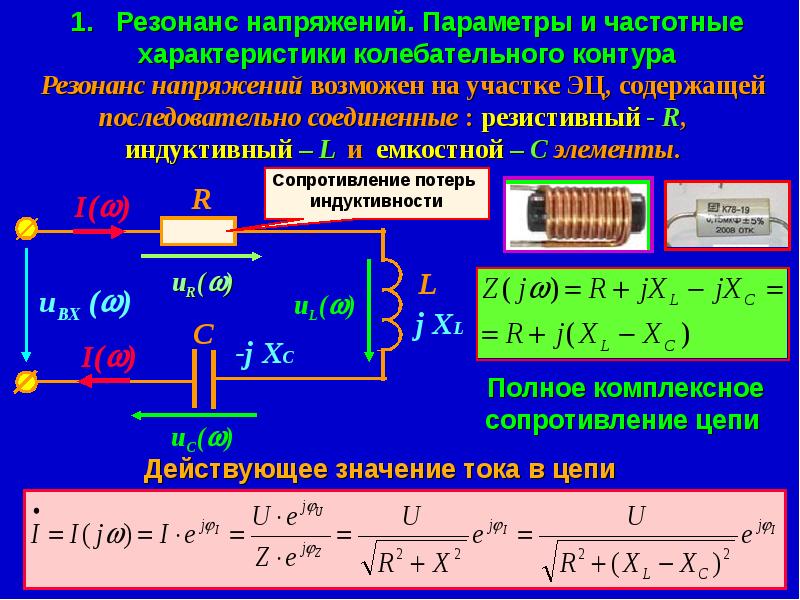
Это явление вызывает обрушение мостов, когда ветер достигает резонансной частоты материала моста, и сила ветра начинает добавляться к уже резонирующим волнам, а материал моста разрушается и разрушается.
Интересно, сможем ли мы сделать то же самое для электрического тока.
Учитывая источник переменного напряжения (не очень высокого напряжения) с постоянными верхней и нижней границами для источника переменного напряжения, могу ли я подать его в «резонансный контур», такой как ток, измеренный амперметром с течением времени, будет выглядеть как :
И использовать это как искусственный способ увеличения тока в нагрузке? (зная, что это, вероятно, будет рецепт, чтобы сжечь все из-за превышения тока)
- напряжение
- ток
- переменный ток
- резонанс
- резонанс-преобразователь
\$\конечная группа\$
8
\$\начало группы\$
Если пассивный резонансный контур имеет высокую добротность, то энергия может накапливаться в контуре в течение многих циклов. Точно так же он естественным образом затухнет в течение многих циклов.
Точно так же он естественным образом затухнет в течение многих циклов.
Однако интенсивность не «постоянно увеличивается». По мере увеличения интенсивности увеличиваются и потери, и в какой-то момент потери равны входной мощности, поэтому у вас есть равновесие.
Представьте себе камертон. Если продолжать его возбуждать, вибрации будут нарастать (как и потери), и в какой-то момент форма металла может измениться, если возбуждение будет достаточно мощным, но это маловероятно. Большинство реальных схем имеют гораздо более низкую добротность, чем механическая добротность камертона.
В реальном LC-резонансном контуре потери обычно связаны с сопротивлением катушки индуктивности, потерями в сердечнике (если используется сердечник) и электромагнитным излучением, особенно на более высоких частотах. Вносят свой вклад и диэлектрические потери конденсатора. Сверхпроводящие схемы могут иметь огромные добротности (исчисляемые тысячами), резонансные схемы, сделанные из деталей от вашего любимого дистрибьютора, вызывают гораздо большее разочарование.
\$\конечная группа\$
2
\$\начало группы\$
Да, резонанс работает и с напряжением, и с током. Найдите что-нибудь под названием схема бака . Это катушка индуктивности и конденсатор параллельно. С идеальными компонентами схема хранит энергию в виде синусоидального напряжения и тока вместе. Он постоянно выплескивает энергию между крышкой и катушкой индуктивности. Это происходит на резонансной частоте, то есть на частоте, при которой величина импеданса двух частей одинакова.
Опять же, для идеальных компонентов этой энергии некуда деваться после помещения в резервуар. Если вы продолжаете добавлять больше энергии, то общая энергия в баке увеличивается, а также должны увеличиваться амплитуды напряжения и тока. Полная энергия пропорциональна квадрату напряжения или тока.
Величины импедансов конденсатора и катушки индуктивности:
Z cap = 1 / ωC
Z ind = ωL
Приравнивая их, находим, что
ω = 1 / sqrt(LC)
f = 1/2Π sqrt(LC)
Если L в генри, а C в фарадах, то f в герцах.
До сих пор это были идеальные компоненты, которые, к сожалению, трудно достать. Реальные компоненты имеют реальные потери. В основном это связано с сопротивлением провода в катушке индуктивности и потерями в керамике конденсатора.
Одним из способов количественной оценки потерь в контуре резервуара является использование коэффициента добротности , что означает добротность . Более высокие значения означают меньшие потери. Идеальный резервуар имеет бесконечную добротность. Обратная величина добротности связана с долей энергии, теряемой за каждый цикл. Реальные контуры бака могут иметь добротность в диапазоне нескольких сотен. Вы можете довольно легко построить что-то самостоятельно с коэффициентом добротности в диапазоне 10 с.
\$\конечная группа\$
\$\начало группы\$
Вы можете сделать ток в катушке очень большим по сравнению с входным током, если катушка является частью настроенной схемы с малыми потерями: —
Здесь у нас есть катушка 1 мкГн, резонирующая на частоте около 300 кГц.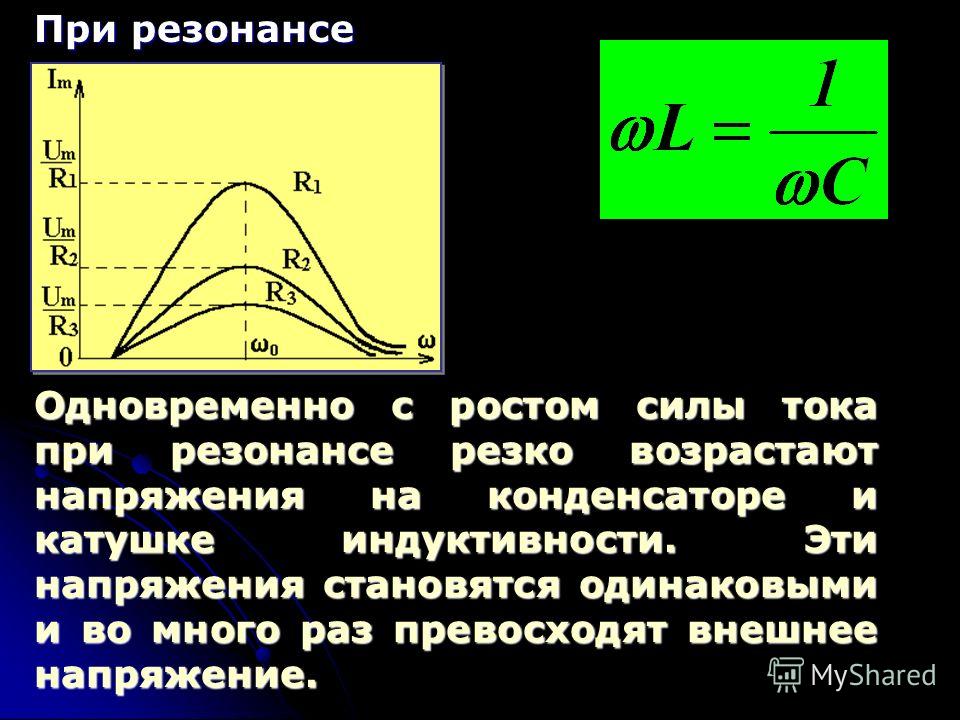 Источник напряжения 1 В RMS питается через конденсатор 10 нФ (C1), а пиковое напряжение на дросселе составляет 36,5 дБВ (66,8 В RMS) при резонансе. Напряжение на катушке 1 мкГн подразумевает ток 35,4 ампер. Этот ток также должен протекать пропорционально через C1 и C2, но, поскольку C2 в 27,2 раза больше, чем C1, ток, подаваемый источником напряжения, составляет всего около 1,25 ампер.
Источник напряжения 1 В RMS питается через конденсатор 10 нФ (C1), а пиковое напряжение на дросселе составляет 36,5 дБВ (66,8 В RMS) при резонансе. Напряжение на катушке 1 мкГн подразумевает ток 35,4 ампер. Этот ток также должен протекать пропорционально через C1 и C2, но, поскольку C2 в 27,2 раза больше, чем C1, ток, подаваемый источником напряжения, составляет всего около 1,25 ампер.
В конце дня источник переменного напряжения все еще подает питание для нагрева резистора, который неизбежно включается последовательно с катушкой. Кроме того, если вы попытаетесь извлечь энергию из магнитного поля катушки, эта мощность также должна будет подаваться от источника переменного напряжения, и вы обнаружите, что резонансный пик начнет падать из-за падения добротности настроенной цепи.
\$\конечная группа\$
4
\$\начало группы\$
Я нашел кое-что: http://www.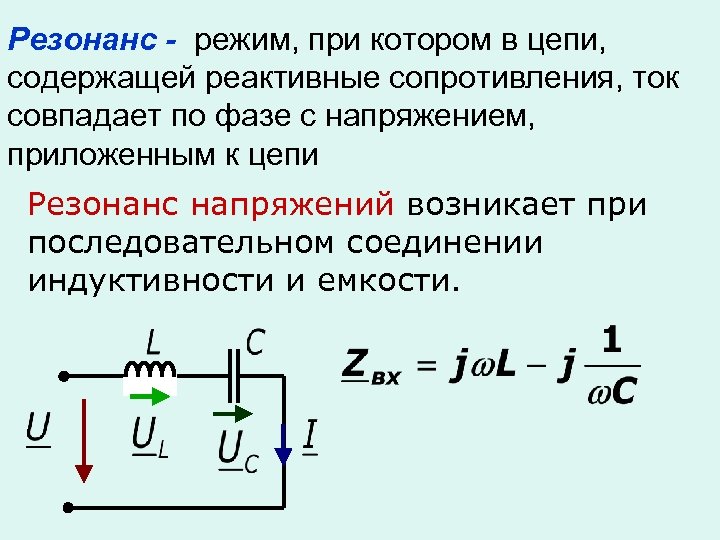 richieburnett.co.uk/resonant.html
richieburnett.co.uk/resonant.html
Автор говорит, что это возможно, но для предотвращения всплеска напряжения в миллисекундах и достижения стабильного усиления по напряжению потребуются некоторые инженерные решения. .
Я не ученый, но сказать, что добиться свободного усиления по напряжению за счет резонанса невозможно, он ограничивает. Мы должны принять это как идею и попытаться доказать ее правильность, а не ошибочность (легко сказать, что все невозможно и неправильно). Это было бы огромным открытием, поэтому слова «это невозможно» следует заменить словами «мы не знаем, как это можно сделать», а ученые должны продолжать эксперименты.
\$\конечная группа\$
1
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
Полоса пропускания резонансных контуров | GBC Electronics Technician
Важным свойством резонансного контура является его полоса пропускания. Полоса пропускания определяется как размер частотного диапазона, который проходит или отвергается настроенной схемой. Чтобы лучше понять пропускную способность, давайте подумаем о радио. Когда вы включаете радиоприемник и пытаетесь выбрать радиостанцию, вы используете характеристики полосы пропускания схемы настройки в радиоприемнике для выбора конкретной станции. Другое название схемы настройки — резонансный контур . Резонансный контур имеет определенную частоту и полосу пропускания, и мы используем это в радиоприемнике.
Полоса пропускания определяется как размер частотного диапазона, который проходит или отвергается настроенной схемой. Чтобы лучше понять пропускную способность, давайте подумаем о радио. Когда вы включаете радиоприемник и пытаетесь выбрать радиостанцию, вы используете характеристики полосы пропускания схемы настройки в радиоприемнике для выбора конкретной станции. Другое название схемы настройки — резонансный контур . Резонансный контур имеет определенную частоту и полосу пропускания, и мы используем это в радиоприемнике.
Резонанс может быть получен либо в последовательных, либо в параллельных цепях, содержащих три электрические характеристики, а именно; сопротивление, индуктивность и емкость. Приведенный ниже резонансный контур состоит из резистора, катушки индуктивности и конденсатора, последовательно соединенных с измерителем тока и источником напряжения. Источник напряжения, обозначенный символом переменного тока, также имеет переменную частоту. Чаще всего мы используем одно конкретное напряжение переменного тока: 120 вольт 60 Гц, но в этом случае нас очень интересует переменная частота, поэтому она должна быть не 60 Гц.
Ток в цепи можно измерить с помощью измерителя или, мы можем рассчитать ток, используя форму закона Ома, которая равна – ток (I) равен приложенному напряжению (E) разделить на полное сопротивление или полную оппозицию в цепи (Z) , то есть Ток = Напряжение/Сопротивление, I = E/Z . Последовательно-резонансный контур обеспечивает низкое сопротивление протеканию тока на определенной частоте. Цепь называется резонансной, когда частота приложенного напряжения регулируется для получения максимального тока, в то время как величина напряжения поддерживается постоянной. Частота этого напряжения и тока называется резонансная частота и определяется как частота, при которой данная система или объект будет реагировать с максимальной амплитудой.
Полное сопротивление В последовательной сети RLC полное сопротивление определяется уравнением: индуктор ( индуктивное сопротивление или X L ), и оппозиция конденсатора ( емкостное реактивное сопротивление или X C ). Как показано на графике ниже, импеданс цепи переменного тока зависит от частоты. Индуктивное сопротивление прямо пропорционально частоте, если увеличить частоту, подаваемую на цепь, то X L увеличится. С другой стороны, емкостное сопротивление обратно пропорционально частоте, поэтому при увеличении частоты значение Х С убыль. Связь между частотой и реактивным сопротивлением выражается уравнениями:
Как показано на графике ниже, импеданс цепи переменного тока зависит от частоты. Индуктивное сопротивление прямо пропорционально частоте, если увеличить частоту, подаваемую на цепь, то X L увеличится. С другой стороны, емкостное сопротивление обратно пропорционально частоте, поэтому при увеличении частоты значение Х С убыль. Связь между частотой и реактивным сопротивлением выражается уравнениями:
На более низких частотах большая часть оппозиции равна X C или емкостная реактивность, а на более высоких частотах оппозиция в основном 9125 X L или индуктивное реактивное сопротивление. При резонансной частоте (f r ) индуктивное и емкостное сопротивления нейтрализуют друг друга, оставляя только сопротивление для противодействия протеканию тока. Когда схема имеет равные значения индуктивного сопротивления и емкостного сопротивления, она имеет тенденцию отклонять сигналы, частоты которых удалены от резонансной частоты. Другими словами, он будет подавлять сигналы выше или ниже частоты, создающей резонанс. Следовательно, в резонансных схемах одни сигналы выбираются для прохождения, а другие отбрасываются или блокируются, и этот сигнал называется полосой частот.
Другими словами, он будет подавлять сигналы выше или ниже частоты, создающей резонанс. Следовательно, в резонансных схемах одни сигналы выбираются для прохождения, а другие отбрасываются или блокируются, и этот сигнал называется полосой частот.
Приведенная ниже кривая зависимости тока от частоты показывает, что ток достигает максимума или 100 % при резонансной частоте (f r ) . Полоса пропускания (BW) резонансного контура определяется как общее количество циклов ниже и выше резонансной частоты, для которых ток равен или превышает 70,7% его резонансного значения . Две частоты на кривой, составляющие 0,707 от максимального тока, называются полосовыми или частотами половинной мощности. Эти частоты обозначены на кривой как f1 и f2 и часто называются критическими частотами или частотами среза резонансного контура.
Резонансная частота может быть определена из критических частот по следующему уравнению:
или
Bandwidth может быть выражена по математию, как:
.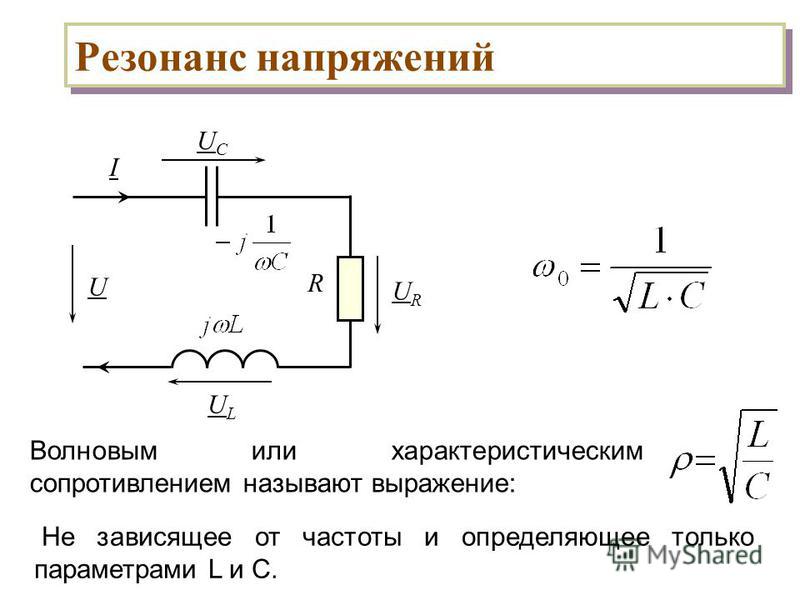 пропускная способность: , где добротность является мерой качества резонансного контура, представленного буквой Q . Коэффициент добротности рассчитывается по формуле:
пропускная способность: , где добротность является мерой качества резонансного контура, представленного буквой Q . Коэффициент добротности рассчитывается по формуле:
Вспомните пример с радио. Когда мы настраиваемся на радиостанцию, мы настраиваем резонансную частоту цепи, чтобы она соответствовала частоте несущий сигнал от радиостанции. В то же время мы согласовываем полосу пропускания с музыкой и звуком, передаваемым по несущему сигналу радиостанции.
Мы надеемся, что это было полезно для вас как техника или студента, приступающего к работе. Если у вас есть какие-либо вопросы о программах Electronics или Electromechanical Technician, вы можете связаться с одним из наших консультантов по программе по бесплатному телефону 1-888-553-5333 или по электронной почте [email protected].
Комментарии
Электроника Система связи
Опубликовано Тимоти (не проверено) в Вт, 11. 05.2021 — 09:04
05.2021 — 09:04
Какова полоса пропускания резонансного контура с частотой 28 МГц и добротностью 80?
В ответ на Electronics Communication system Тимоти (не проверено)
Тимоти, наша служба поддержки…
Тимоти, наша группа поддержки готова помочь всем студентам, изучающим технику электроники, по бесплатному номеру 1-866-279.-1457 или по электронной почте [email protected].
Центр поддержки открыт с понедельника по пятницу с 9:00 до 22:00 вечера, а по субботам и воскресеньям с 9:00 до 17:00 (EST).
Формула действительна для…
Опубликовано Anonymous (не проверено) вт, 26.04.2022 — 02:18
Формула действительна как для последовательно настроенных, так и для параллельных цепей, верно?
В ответ на Формула действительна для… от Аноним (не проверено)
В этом блоге рассказывается о пропускной способности…
В этом блоге рассказывается о ширине резонансной цепи, и, как уже упоминалось, «Резонанс может быть получен либо в последовательных, либо в параллельных цепях, содержащих три электрические характеристики, а именно; сопротивление, индуктивность и емкость», он фокусируется на последовательных цепях.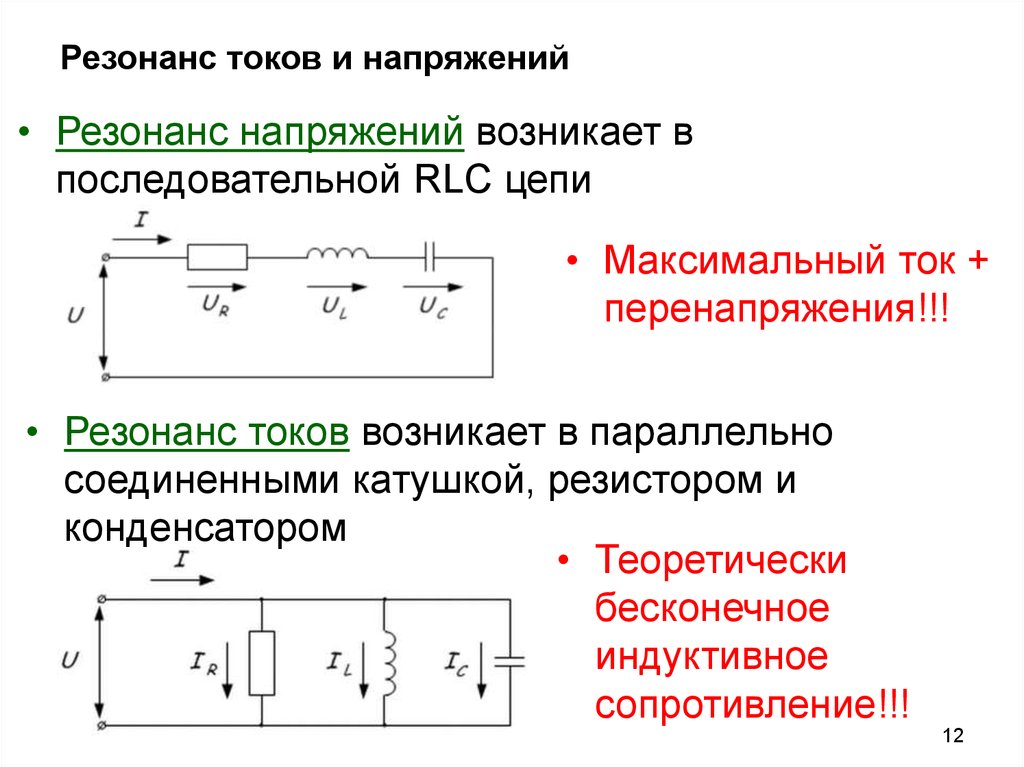 Формулы для расчета полосы пропускания ( BW ) и резонансной частоты ( fr ) одинаковы как для последовательных, так и для параллельных цепей. Когда Q больше примерно 2 или 3 для параллельного резонансного контура или меньше 1/2 или 1/3 для последовательного контура, можно сделать определенные упрощающие предположения. Тогда полоса пропускания может быть выражена через резонансную частоту и добротность по следующей формуле: BW = fr / Q . Однако формулы для расчета импеданса ( Z ) и добротности ( Q ) параллельной цепи переменного тока отличаются от формул, используемых для расчета этих значений в последовательной цепи. Параллельно Z = L/RC и Q = R/XL
Формулы для расчета полосы пропускания ( BW ) и резонансной частоты ( fr ) одинаковы как для последовательных, так и для параллельных цепей. Когда Q больше примерно 2 или 3 для параллельного резонансного контура или меньше 1/2 или 1/3 для последовательного контура, можно сделать определенные упрощающие предположения. Тогда полоса пропускания может быть выражена через резонансную частоту и добротность по следующей формуле: BW = fr / Q . Однако формулы для расчета импеданса ( Z ) и добротности ( Q ) параллельной цепи переменного тока отличаются от формул, используемых для расчета этих значений в последовательной цепи. Параллельно Z = L/RC и Q = R/XL
Поставщики беспроводных радиочастот и ресурсы
Веб-сайт RF Wireless World является домом для поставщиков и ресурсов RF и Wireless.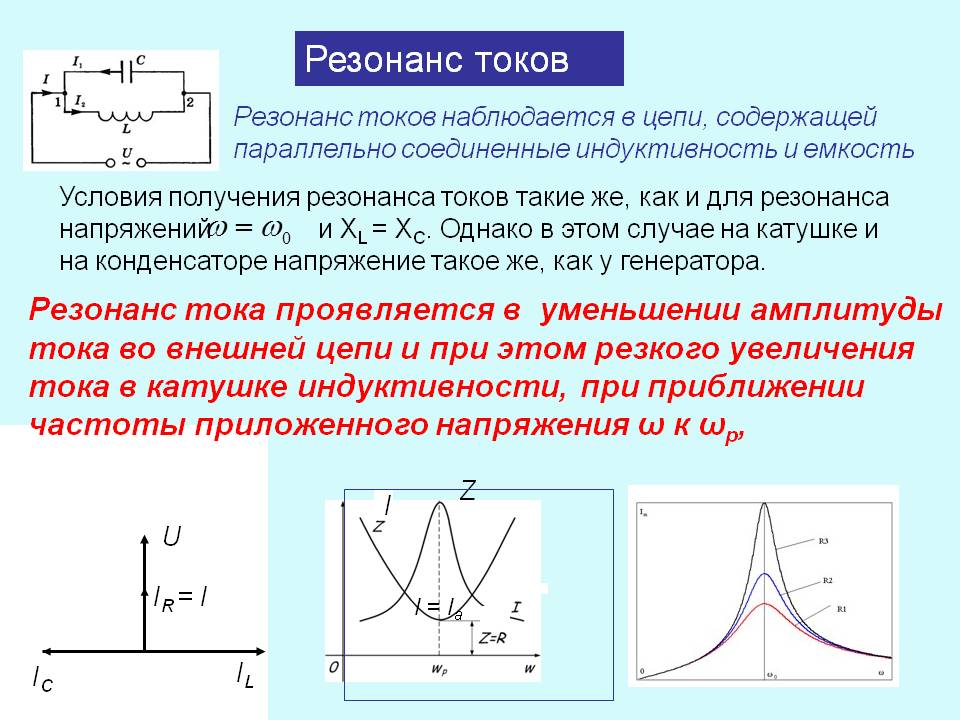 На сайте представлены статьи, учебные пособия, поставщики, терминология, исходный код (VHDL, Verilog, MATLAB, Labview), тесты и измерения,
калькуляторы, новости, книги, загрузки и многое другое.
На сайте представлены статьи, учебные пособия, поставщики, терминология, исходный код (VHDL, Verilog, MATLAB, Labview), тесты и измерения,
калькуляторы, новости, книги, загрузки и многое другое.
Сайт RF Wireless World охватывает ресурсы по различным темам, таким как RF, беспроводная связь, vsat, спутник, радар, оптоволокно, микроволновая печь, wimax, wlan, zigbee, LTE, 5G NR, GSM, GPRS, GPS, WCDMA, UMTS, TDSCDMA, Bluetooth, Lightwave RF, z-wave, Интернет вещей (IoT), M2M, Ethernet и т. д. Эти ресурсы основаны на стандартах IEEE и 3GPP. Он также имеет академический раздел, который охватывает колледжи и университеты по инженерным дисциплинам и дисциплинам MBA.
Статьи о системах на основе IoT
Система обнаружения падений для пожилых людей на основе IoT : В статье рассматривается архитектура системы обнаружения падений, используемой для пожилых людей.
В нем упоминаются преимущества или преимущества системы обнаружения падения IoT.
Подробнее➤
См. также другие статьи о системах на основе IoT:
также другие статьи о системах на основе IoT:
• Система очистки туалетов AirCraft.
• Система измерения удара при столкновении
• Система отслеживания скоропортящихся продуктов и овощей
• Система помощи водителю
• Система умной розничной торговли
• Система мониторинга качества воды
• Система интеллектуальной сети
• Умная система освещения на основе Zigbee
• Умная система парковки на базе Zigbee
• Умная система парковки на базе LoRaWAN.
Изделия для беспроводных радиочастот
Этот раздел статей охватывает статьи о физическом уровне (PHY), уровне MAC, стеке протоколов и сетевой архитектуре на основе WLAN, WiMAX, zigbee, GSM, GPRS, TD-SCDMA, LTE, 5G NR, VSAT, Gigabit Ethernet на основе IEEE/3GPP и т. д. , стандарты. Он также охватывает статьи, связанные с испытаниями и измерениями, посвященные испытаниям на соответствие, используемым для испытаний устройств на соответствие RF/PHY. СМ. УКАЗАТЕЛЬ СТАТЕЙ >>.
Физический уровень 5G NR : Обработка физического уровня для канала 5G NR PDSCH и канала 5G NR PUSCH была рассмотрена поэтапно. Это описание физического уровня 5G соответствует спецификациям физического уровня 3GPP.
Подробнее➤
Это описание физического уровня 5G соответствует спецификациям физического уровня 3GPP.
Подробнее➤
Основные сведения о повторителях и типы повторителей : В нем объясняются функции различных типов повторителей, используемых в беспроводных технологиях. Подробнее➤
Основы и типы замираний : В этой статье рассматриваются мелкомасштабные замирания, крупномасштабные замирания, медленные замирания, быстрые замирания и т. д., используемые в беспроводной связи. Подробнее➤
Архитектура сотового телефона 5G : В этой статье рассматривается блок-схема сотового телефона 5G с внутренними модулями 5G. Архитектура сотового телефона. Подробнее➤
Основы помех и типы помех: В этой статье рассматриваются помехи по соседнему каналу, помехи в одном канале, Электромагнитные помехи, ICI, ISI, световые помехи, звуковые помехи и т. д. Подробнее➤
5G NR Раздел
В этом разделе рассматриваются функции 5G NR (новое радио), нумерология, диапазоны, архитектура, развертывание, стек протоколов (PHY, MAC, RLC, PDCP, RRC) и т. д.
5G NR Краткий справочный указатель >>
д.
5G NR Краткий справочный указатель >>
• Мини-слот 5G NR
• Часть полосы пропускания 5G NR
• БАЗОВЫЙ НАБОР 5G NR
• Форматы 5G NR DCI
• 5G NR UCI
• Форматы слотов 5G NR
• IE 5G NR RRC
• 5G NR SSB, SS, PBCH
• 5G NR PRACH
• 5G NR PDCCH
• 5G NR PUCCH
• Опорные сигналы 5G NR
• 5G NR m-Sequence
• Золотая последовательность 5G NR
• 5G NR Zadoff Chu Sequence
• Физический уровень 5G NR
• MAC-уровень 5G NR
• Уровень 5G NR RLC
• Уровень PDCP 5G NR
Учебные пособия по беспроводным технологиям
В этом разделе рассматриваются учебные пособия по радиочастотам и беспроводным сетям. Он охватывает учебные пособия по таким темам, как сотовая связь, WLAN (11ac, 11ad), wimax, bluetooth, zigbee, zwave, LTE, DSP, GSM, GPRS, GPS, UMTS, CDMA, UWB, RFID, радар, VSAT, спутник, беспроводная сеть, волновод, антенна, фемтосота, тестирование и измерения, IoT и т. д. См. ИНДЕКС УЧЕБНЫХ ПОСОБИЙ >>
Учебное пособие по 5G — В этом учебном пособии по 5G также рассматриваются следующие подтемы, посвященные технологии 5G:
Учебник по основам 5G
Диапазоны частот
учебник по миллиметровым волнам
Рамка волны 5G мм
Зондирование канала миллиметровых волн 5G
4G против 5G
Испытательное оборудование 5G
Архитектура сети 5G
Сетевые интерфейсы 5G NR
звучание канала
Типы каналов
5G FDD против TDD
Нарезка сети 5G NR
Что такое 5G NR
Режимы развертывания 5G NR
Что такое 5G ТФ
В этом учебном пособии GSM рассматриваются основы GSM, сетевая архитектура, сетевые элементы, системные спецификации, приложения,
Типы пакетов GSM, структура кадров GSM или иерархия кадров, логические каналы, физические каналы,
Физический уровень GSM или обработка речи, вход в сеть мобильного телефона GSM или настройка вызова или процедура включения питания,
Вызов MO, вызов MT, модуляция VAMOS, AMR, MSK, GMSK, физический уровень, стек протоколов, основы мобильного телефона,
Планирование RF, нисходящая линия связи PS и восходящая линия связи PS.
➤Читать далее.
LTE Tutorial , описывающий архитектуру системы LTE, включая основы LTE EUTRAN и LTE Evolved Packet Core (EPC). Он предоставляет ссылку на обзор системы LTE, радиоинтерфейс LTE, терминологию LTE, категории LTE UE, структуру кадра LTE, физический уровень LTE, Стек протоколов LTE, каналы LTE (логические, транспортные, физические), пропускная способность LTE, агрегация несущих LTE, Voice Over LTE, расширенный LTE, Поставщики LTE и LTE vs LTE advanced.➤Подробнее.
RF Technology Материал
На этой странице мира беспроводных радиочастот описывается пошаговое проектирование преобразователя частоты на примере повышающего преобразователя частоты 70 МГц в диапазон C.
для микрополосковой платы с использованием дискретных радиочастотных компонентов, а именно. Смесители, гетеродин, MMIC, синтезатор, опорный генератор OCXO,
амортизирующие прокладки. ➤Читать дальше.
➤ Проектирование и разработка радиочастотного приемопередатчика
➤Дизайн радиочастотного фильтра
➤Система VSAT
➤Типы и основы микрополосковых
➤Основы волновода
Секция испытаний и измерений
В этом разделе рассматриваются ресурсы по контролю и измерению, контрольно-измерительное оборудование для тестирования тестируемых устройств на основе
Стандарты WLAN, WiMAX, Zigbee, Bluetooth, GSM, UMTS, LTE.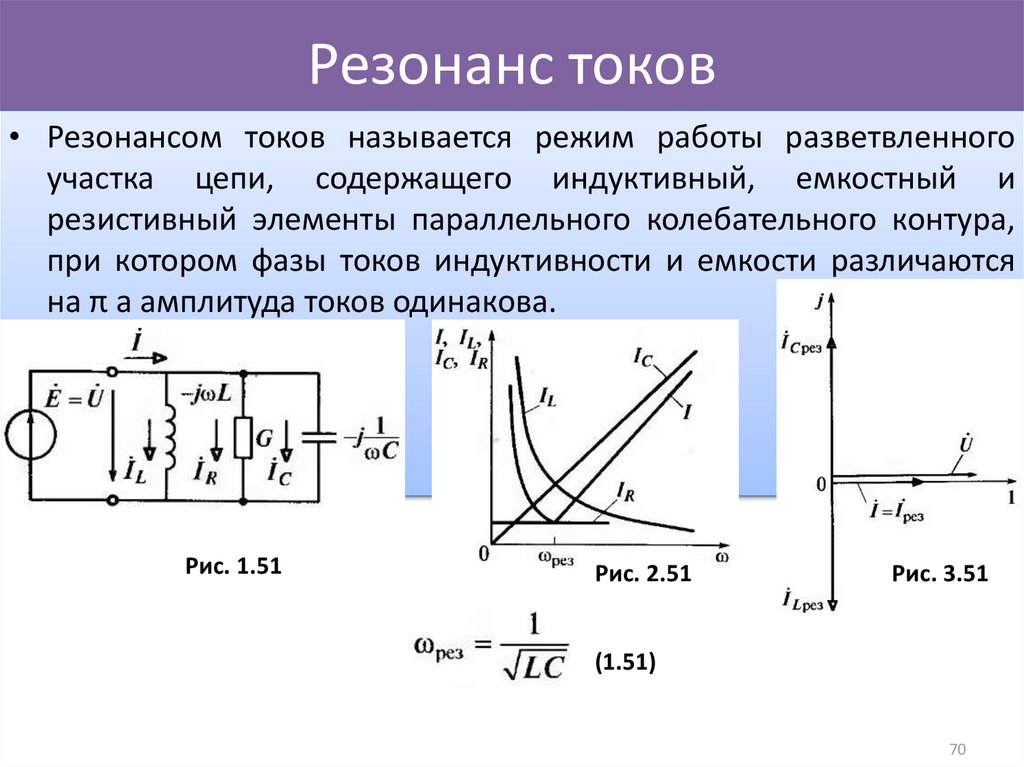 ИНДЕКС испытаний и измерений >>
ИНДЕКС испытаний и измерений >>
➤Система PXI для контрольно-измерительных приборов.
➤ Генерация и анализ сигналов
➤ Измерения физического уровня
➤ Тестирование устройства WiMAX на соответствие
➤ Тест на соответствие Zigbee
➤ Тест на соответствие LTE UE
➤ Тест на соответствие TD-SCDMA
Волоконно-оптические технологии
Волоконно-оптический компонент основы, включая детектор, оптический соединитель, изолятор, циркулятор, переключатели, усилитель,
фильтр, эквалайзер, мультиплексор, разъемы, демультиплексор и т. д. Эти компоненты используются в оптоволоконной связи.
ИНДЕКС оптических компонентов >>
➤Руководство по оптоволоконной связи
➤APS в SDH
➤Основы SONET
➤ Структура кадра SDH
➤ SONET против SDH
Поставщики беспроводных радиочастотных устройств, производители
Сайт RF Wireless World охватывает производителей и поставщиков различных радиочастотных компонентов, систем и подсистем для ярких приложений,
см. ИНДЕКС поставщиков >>.
Поставщики ВЧ-компонентов, включая ВЧ-изолятор, ВЧ-циркулятор, ВЧ-смеситель, ВЧ-усилитель, ВЧ-адаптер, ВЧ-разъем, ВЧ-модулятор, ВЧ-трансивер, PLL, VCO, синтезатор, антенну, осциллятор, делитель мощности, сумматор мощности, фильтр, аттенюатор, диплексер, дуплексер, чип-резистор, чип-конденсатор, чип-индуктор, ответвитель, ЭМС, программное обеспечение RF Design, диэлектрический материал, диод и т. д.
Поставщики радиочастотных компонентов >>
➤Базовая станция LTE
➤ РЧ-циркулятор
➤РЧ-изолятор
➤Кристаллический осциллятор
MATLAB, Labview, Embedded Исходные коды
Раздел исходного кода RF Wireless World охватывает коды, связанные с языками программирования MATLAB, VHDL, VERILOG и LABVIEW.
Эти коды полезны для новичков в этих языках.
СМ. ИНДЕКС ИСТОЧНИКОВ >>
➤ 3–8 код VHDL декодера
➤Скремблер-дескремблер Код MATLAB
➤32-битный код ALU Verilog
➤ T, D, JK, SR триггеры лабораторные коды
*Общая медицинская информация*
Сделайте эти пять простых вещей, чтобы помочь остановить коронавирус (COVID-19).
СДЕЛАЙТЕ ПЯТЬ
1. РУКИ: Мойте их часто
2. ЛОКТ: кашляйте в него
3. ЛИЦО: не прикасайтесь к нему
4. НОГИ: держитесь на расстоянии более 3 футов (1 м) друг от друга
5. ЧУВСТВУЙТЕ: заболели? Оставайтесь дома
Используйте технологию отслеживания контактов >> , следуйте рекомендациям по социальному дистанцированию >> и установить систему наблюдения за данными >> спасти сотни жизней. Использование концепции телемедицины стало очень популярным в таких стран, как США и Китай, чтобы остановить распространение COVID-19так как это заразное заболевание.
Радиочастотные калькуляторы и преобразователи
Раздел «Калькуляторы и преобразователи» охватывает ВЧ-калькуляторы, беспроводные калькуляторы, а также преобразователи единиц измерения.
Они охватывают беспроводные технологии, такие как GSM, UMTS, LTE, 5G NR и т. д.
СМ. КАЛЬКУЛЯТОРЫ Указатель >>.
➤ Калькулятор пропускной способности 5G NR
➤ 5G NR ARFCN и преобразование частоты
➤ Калькулятор скорости передачи данных LoRa
➤ LTE EARFCN для преобразования частоты
➤ Калькулятор антенны Yagi
➤ Калькулятор времени выборки 5G NR
IoT-Интернет вещей Беспроводные технологии
В разделе, посвященном IoT, рассматриваются беспроводные технологии Интернета вещей, такие как WLAN, WiMAX, Zigbee, Z-wave, UMTS, LTE, GSM, GPRS, THREAD, EnOcean, LoRa, SIGFOX, WHDI, Ethernet,
6LoWPAN, RF4CE, Bluetooth, Bluetooth с низким энергопотреблением (BLE), NFC, RFID, INSTEON, X10, KNX, ANT+, Wavenis, Dash7, HomePlug и другие.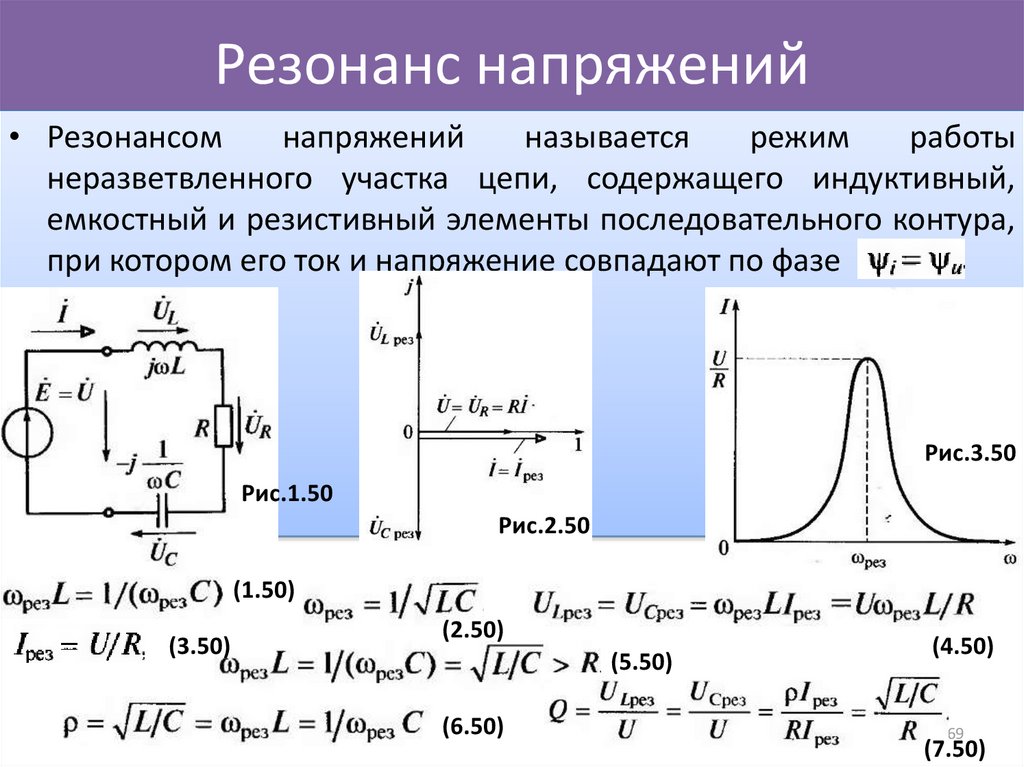 Он также охватывает датчики IoT, компоненты IoT и компании IoT.
Он также охватывает датчики IoT, компоненты IoT и компании IoT.
См. главную страницу IoT>> и следующие ссылки.
➤РЕЗЬБА
➤EnOcean
➤ Учебник LoRa
➤ Учебник по SIGFOX
➤ WHDI
➤6LoWPAN
➤Зигби RF4CE
➤NFC
➤Лонворкс
➤CEBus
➤УПБ
СВЯЗАННЫЕ ПОСТЫ
Учебные пособия по беспроводной связи
GSM ТД-СКДМА ваймакс LTE UMTS GPRS CDMA SCADA беспроводная локальная сеть 802.11ac 802.11ad GPS Зигби z-волна Bluetooth СШП Интернет вещей Т&М спутник Антенна РАДАР RFID
Различные типы датчиков
Датчик приближения Датчик присутствия против датчика движения Датчик LVDT и RVDT Датчик положения, смещения и уровня датчик силы и датчик деформации Датчик температуры датчик давления Датчик влажности датчик МЭМС Сенсорный датчик Тактильный датчик Беспроводной датчик Датчик движения Датчик LoRaWAN Световой датчик Ультразвуковой датчик Датчик массового расхода воздуха Инфразвуковой датчик Датчик скорости Датчик дыма Инфракрасный датчик Датчик ЭДС Датчик уровня Активный датчик движения против пассивного датчика движения
Поделиться этой страницей
Перевести эту страницу
СТАТЬИ
Раздел T&M
ТЕРМИНОЛОГИИ
Учебники
Работа и карьера
ПОСТАВЩИКИ
Интернет вещей
Онлайн калькуляторы
исходные коды
ПРИЛОЖЕНИЕ. ЗАМЕТКИ
Всемирный веб-сайт T&M
ЗАМЕТКИ
Всемирный веб-сайт T&M
Activity: Resonance in RLC Circuits
Эта версия (07 февраля 2022 г., 15:13) была одобрена Дугом Мерсером. Доступна ранее утвержденная версия (05 сентября 2019 г., 10:51).
Содержание
Деятельность: Резонанс в цепях RLC — ADALM2000
Цель:
Фон:
Материалы:
Настройка оборудования:
Процедура:
Вопросы:
Цель:
Целью этой лабораторной работы является изучение явления резонанса в цепях RLC. Определите резонансную частоту и ширину полосы данной сети, используя амплитудную характеристику синусоидального источника.
Фон:
Резонансный контур, также называемый настроенным контуром, состоит из катушки индуктивности и конденсатора вместе с источником напряжения или тока. Это одна из самых важных схем, используемых в электронике.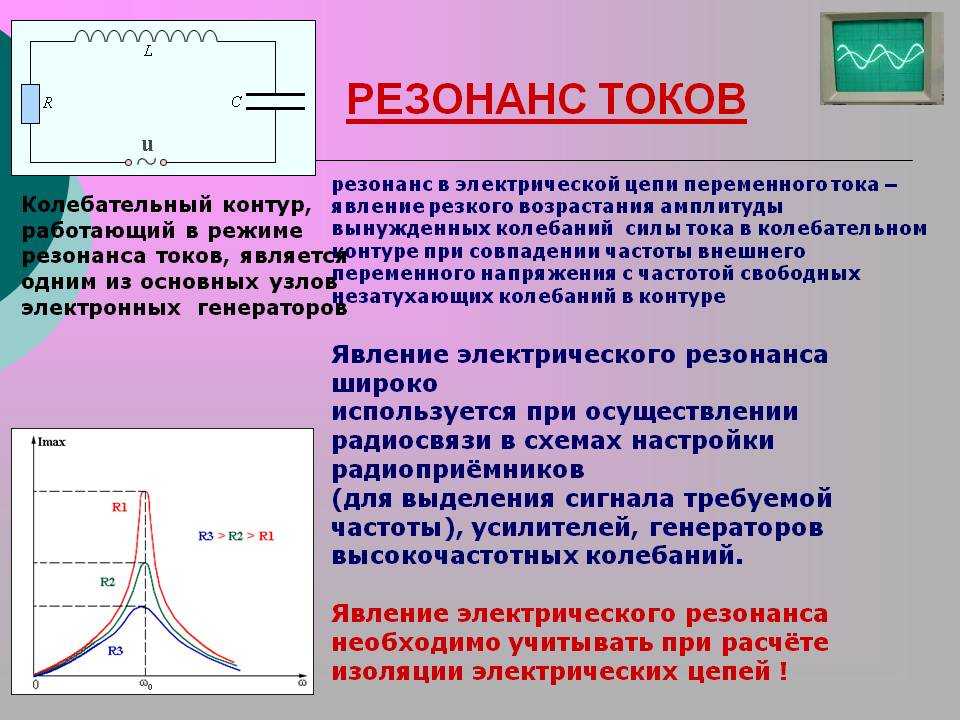 Например, резонансный контур в одной из многих форм позволяет нам настроиться на желаемую радио- или телевизионную станцию из огромного количества сигналов, окружающих нас в любое время.
Например, резонансный контур в одной из многих форм позволяет нам настроиться на желаемую радио- или телевизионную станцию из огромного количества сигналов, окружающих нас в любое время.
Сеть находится в резонансе, когда напряжение и ток на входных клеммах сети совпадают по фазе, а входное сопротивление сети чисто резистивное.
Рисунок 1: Параллельная цепь RLC
Рассмотрим параллельную RLC-цепь на рис. 1. Установившаяся проводимость, обеспечиваемая схемой, равна:
Резонанс возникает, когда напряжение и ток на входных клеммах совпадают по фазе. Это соответствует чисто действительному допущению, так что необходимое условие определяется выражением:
Резонансное состояние может быть достигнуто путем регулировки L, C или ω. При постоянных L и C резонансная частота ω o определяется:
рад/с (1)
ИЛИ ЖЕ
Герц (2)
Частотная характеристика: это график величины выходного напряжения резонансного контура в зависимости от частоты. Отклик, конечно, начинается с нуля, достигает максимального значения вблизи собственной резонансной частоты, а затем снова падает до нуля, когда ω становится бесконечным. Частотная характеристика показана на рисунке 2.
Отклик, конечно, начинается с нуля, достигает максимального значения вблизи собственной резонансной частоты, а затем снова падает до нуля, когда ω становится бесконечным. Частотная характеристика показана на рисунке 2.
Рисунок 2: Частотная характеристика параллельной цепи RLC
Также указаны две дополнительные частоты ω 1 и ω 2 , которые называются частотами половинной мощности. Эти частоты определяют те точки на кривой, в которых отклик по напряжению составляет 1/sqrt(2) или 0,707 от максимального значения. Они используются для измерения ширины полосы кривой отклика. Это называется полосой частот резонансного контура по половинной мощности и определяется как:
(3)
Рисунок 3: Цепь последовательного резонанса
Материалы:
Модуль активного обучения ADALM2000
Макет без пайки и набор перемычек
1 Резистор 100 Ом
1 Резистор 1 кОм
1 Конденсатор 1 мкФ
1 Индуктор 20 мГн (2 индуктора по 10 мГн последовательно)
Настройка оборудования:
Установите схему, показанную на рис. 4, на макетной плате без пайки.
4, на макетной плате без пайки.
Рисунок 4: Параллельная резонансная цепь
Рисунок 5: Соединения макетной платы параллельного резонансного контура
Процедура:
Используя инструмент Анализатор цепей, вы можете построить частотную характеристику резонансного контура. Начните с вычисления резонансной частоты, используя уравнение (1). В соответствии с этим установите параметры логарифмической развертки. В этом случае резонансная частота составляет 1,1 кГц, поэтому развертка может начинаться со 100 Гц до 10 кГц . Установите минимальную фазу на -90, максимальную фазу на 90. Ось амплитуды может быть установлена от -15 дБ до 0 дБ. На рисунке 6 представлена передаточная функция цепи RLC, полученная при запуске анализатора цепей.
Рисунок 6: Частотная характеристика параллельной цепи RLC
Отклик схемы во временной области можно проанализировать с помощью инструментов генератора сигналов и осциллографа. На канале генератора сигналов 1 выберите синусоидальный сигнал с амплитудой 2 вольта от пика к пику. Установите частоту, равную резонансной частоте. На канале 1 осциллографа вы увидите входной сигнал и выходной сигнал на канале 2.
Обратите внимание на рис. 7, как выходной сигнал почти совпадает по фазе с входным.
На канале генератора сигналов 1 выберите синусоидальный сигнал с амплитудой 2 вольта от пика к пику. Установите частоту, равную резонансной частоте. На канале 1 осциллографа вы увидите входной сигнал и выходной сигнал на канале 2.
Обратите внимание на рис. 7, как выходной сигнал почти совпадает по фазе с входным.
Рисунок 7: Входные и выходные сигналы RLC-цепи для частоты, равной 1,1 кГц
Выберите еще два значения частоты, например значения в конце интервала развертки, и посмотрите, как на них реагирует схема.
Рисунок 8: Входные и выходные сигналы цепи RLC для частоты, равной 100 Гц
Рисунок 9: Входные и выходные сигналы RLC-цепи для частоты, равной 10 кГц
Вопросов:
1. Найдите резонансную частоту ω o , используя уравнение (1), и сравните ее с экспериментальным значением.
2. Получите ширину полосы из частот половинной мощности, используя уравнение (3).


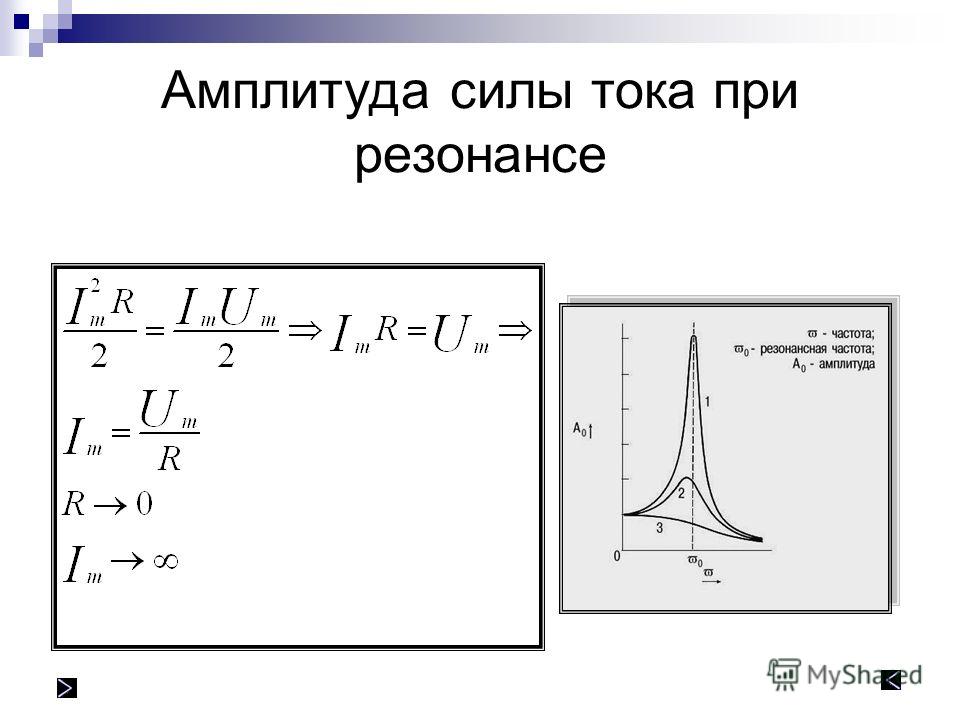 Если оно слишком велико, учитывать его все же нужно.
Если оно слишком велико, учитывать его все же нужно.
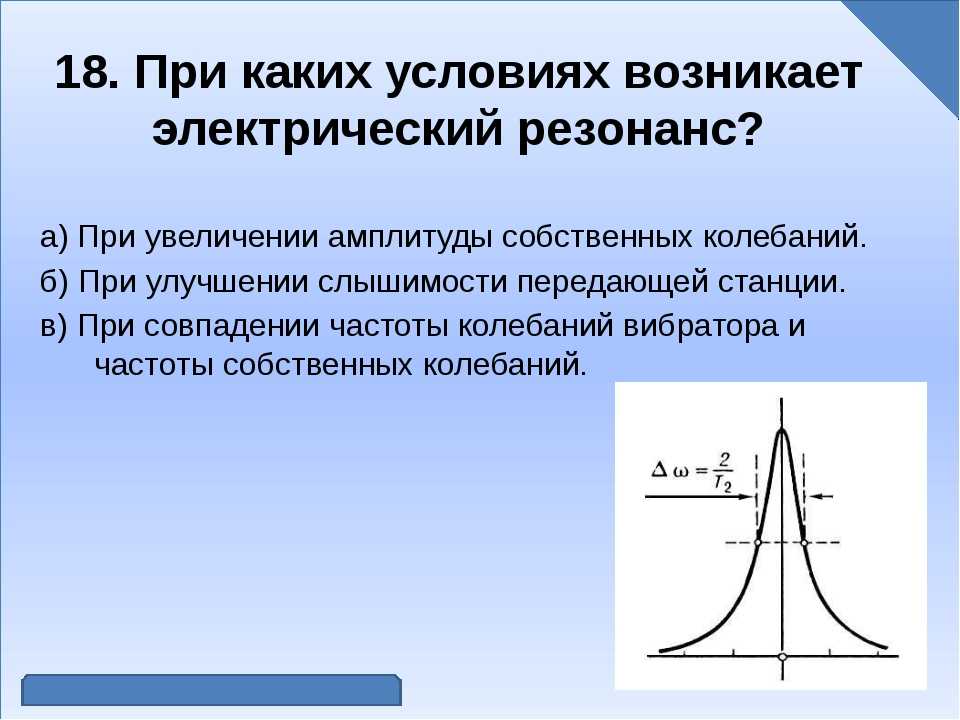 Этот компонент не очень заметен в электрической цепи, пока не попробуешь сделать в ней какие-либо изменения. В механике, например, таким изменением является изменение скорости. В электрической цепи — изменение тока. Если оно по какой-либо причине происходит, индуктивность противодействует такому изменению режима цепи.
Этот компонент не очень заметен в электрической цепи, пока не попробуешь сделать в ней какие-либо изменения. В механике, например, таким изменением является изменение скорости. В электрической цепи — изменение тока. Если оно по какой-либо причине происходит, индуктивность противодействует такому изменению режима цепи.
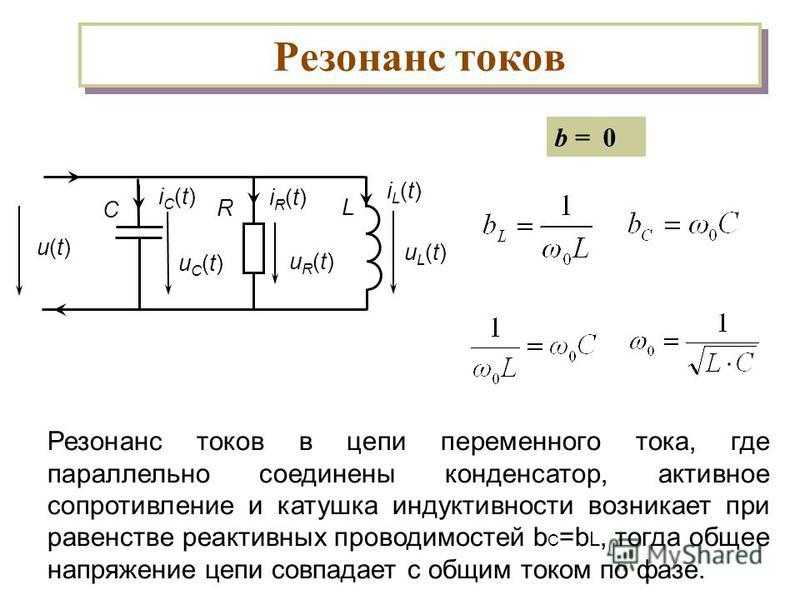 9{2}}\\[/латекс].
9{2}}\\[/латекс].