Резонанс токов в параллельном колебательном контуре
Рассмотрим случай параллельного соединения колебательного контура с источником тока (рис. 1) и посмотрим, каково будет сопротивление контура для токов различных частот в этом случае. Если частота тока невелика (ниже резонансной), то почти весь ток пойдет по наиболее легкому для него пути — через индуктивную ветвь; сопротивление контура при низких частотах будет небольшим по величине и индуктивным по своему характеру.
Для токов высоких частот (выше резонансной) более легким путем будет путь через емкостную ветвь, и, следовательно, сопротивление контура будет также небольшим по величине, но емкостным по характеру.
При резонансной частоте, когда емкостное сопротивление равно индуктивному, путь для тока будет одинаково трудным через обе ветви. Мы знаем, что при параллельном соединении двух равных сопротивлений общее сопротивление равняется половине любого из них. Поэтому, казалось бы, что сопротивление контура при резонансе должно равняться половине одного из реактивных сопротивлений.
Однако, не следует забывать, что мы имеет дело, с сопротивлениями, хотя и одинаковыми по величине, но имеющими принципиально различный характер. Это различие проявляется в том, что токи в индуктивной и емкостной ветвях контура сдвинуты по фазе друг относительно друга на 180°. Отсюда непосредственно следует, что в неразветвленной части цепи всегда протекает не суммарный, а разностный ток (рис. 1).
Рисунок 1. Токи при параллельном резонансе. В неразвлетвленной части цепи протекает не скммарный, а разностный ток.
Поэтому при резонансе, когда токи в емкостной и индуктивной ветвях равны между собой, ток в неразветвленной части цепи будет равен нулю, какое бы напряжение мы ни прилагали к контуру. При резонансе между точками АВ цепь будет казаться разорванной, т. е. сопротивление ее между этими точками будет бесконечно велико, а отнюдь не будет равным половине одного из реактивных сопротивлений. Практически бесконечно большого сопротивления контура при резонансе не бывает, так как из-за наличия активного сопротивления в контуре (сопротивление провода катушки) сдвиг фаз токов никогда не может быть равным точно 180°.
Однако активное сопротивление катушки обычно бывает много меньше ее индуктивного сопротивления, и поэтому сопротивление колебательного контура при резонансе может достигать очень больших величин.
Сопротивление колебательного контура при параллельном резонансе равно:
где L выражено в гн, С—в ф, RL—в ом.
Полное сопротивление колебательного контура при резонансе является чисто активным в силу того обстоятельства, что индуктивное и емкостное сопротивления взаимно компенсируются.
Кривые изменения полного сопротивления колебательного контура между точками АВ при изменении частоты тока приведены на рис. 2,б.
Рисунок 2. Резонанс токов. а) — схема и обозначения; б) — график полного сопротивления.
При параллельном резонансе токи ,в ветвях контура достигают наибольшей величины; поэтому параллельный резонанс называется резонансом токов.
Явление резонанса имеет огромнейшее значение в радиотехнике.
На земном шаре имеется большое количество передающих радиостанций. Передачи всех этих радиостанций распространяются в эфипе и все одновременно принимаются приемной антенной. Нетрудно представить себе, каким получилось бы нагромождение друг на друга передач, если бы мы не могли выделить из этого хаоса только одну нужную нам. Вот тут-то на помощь приходит явление резонанса. Передающие радиостанции излучают в пространство электромагнитную энергию на различных частотах, мы же, настраивая контуры нашего приемника в резонанс с той или иной частотой, тем самым выбираем нужную нам передачу.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
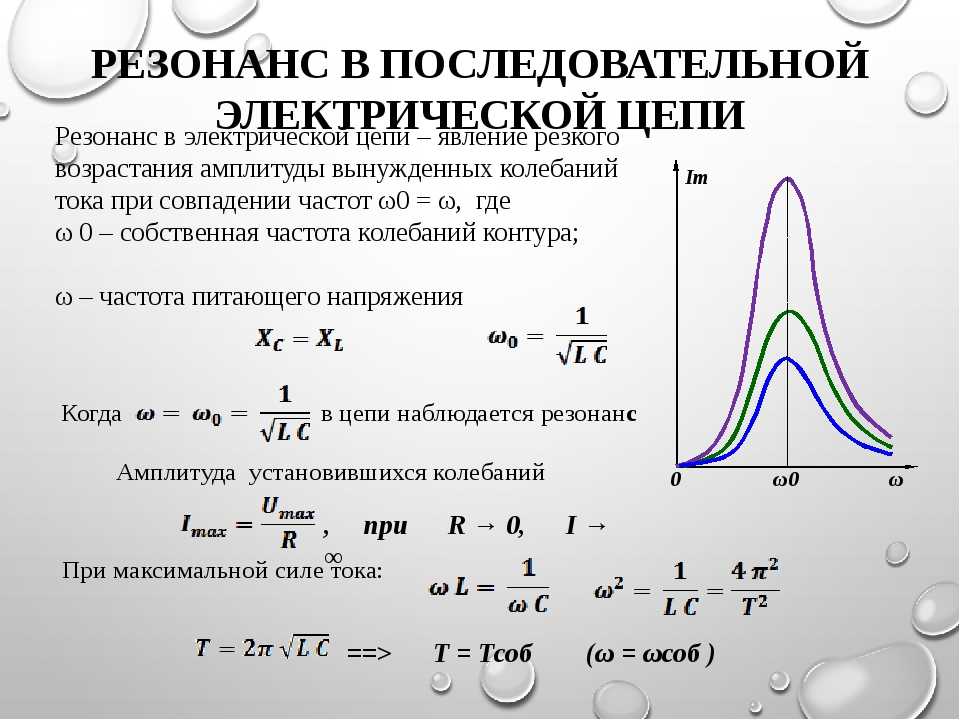
Резонанс напряжений и резонанс токов в цепи переменного тока. — Студопедия
Поделись
Напряжений. Если в цепи переменного тока, содержащей последовательно включенные конденсатор, катушку индуктивности и резистор ωL=1/(ωC), то угол сдвига фаз между током и напряжением обращается в нуль (j=0).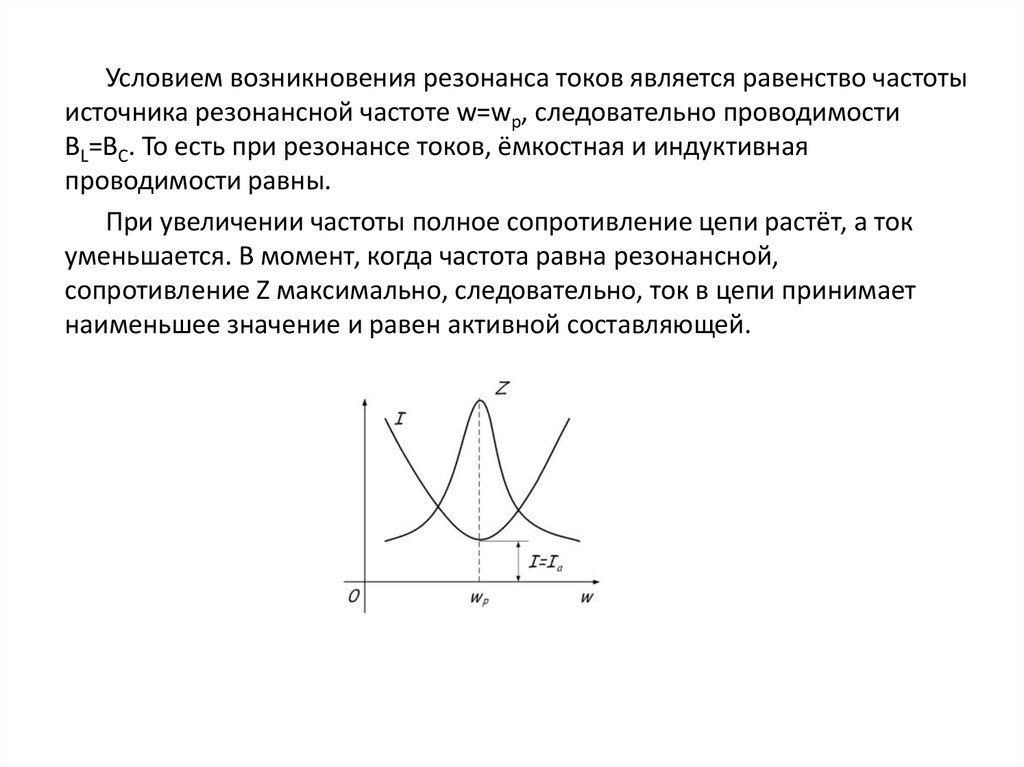
Этому условию удовлетворяет частота . В данном случае полное сопротивление цепи Z становится min, равным активному сопротивлению R цепи, и ток в цепи определяется этим сопротивлением, принимая max (возможные при данном Um) значения. При этом падение напряжения на активном сопротивлении равно внешнему напряжению, приложенному к цепи (UR=U), а падения напряжений на конденсаторе (UC) и катушке индуктивности (UL) одинаковы по амплитуде и противоположны по фазе. Это явление называетсярезонансом напряжений (последовательным резонансом),
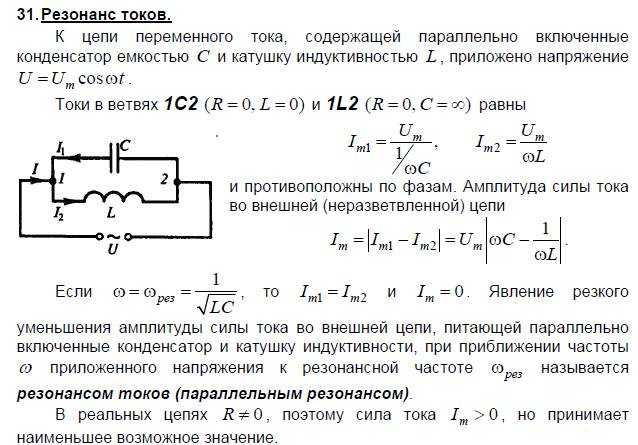
Токов.Рассмотрим цепь переменного тока, содержащую параллельно включенные конденсатор емкостью С и катушку индуктивностью L.
Допустим, что активное сопротивление обеих ветвей настолько мало, что им можно пренебречь. Если приложенное напряжение изменяется по закону U= Um
Амплитуда силы тока Im оказалась равна нулю потому, что активным сопротивлением контура пренебрегли. Если учесть сопротивление R, то разность фаз j1—j2будет равна p, поэтому при резонансе токов амплитуда силы тока Im будет отлична от нуля, но примет наименьшее возможное значение. Таким образом, при резонансе токов во внешней цепи токи
Резонансный контур RLC серии— цепи переменного тока
Цепи переменного тока
Было показано, что индуктивное сопротивление прямо пропорционально частоте,
а емкостное сопротивление обратно пропорционально частоте.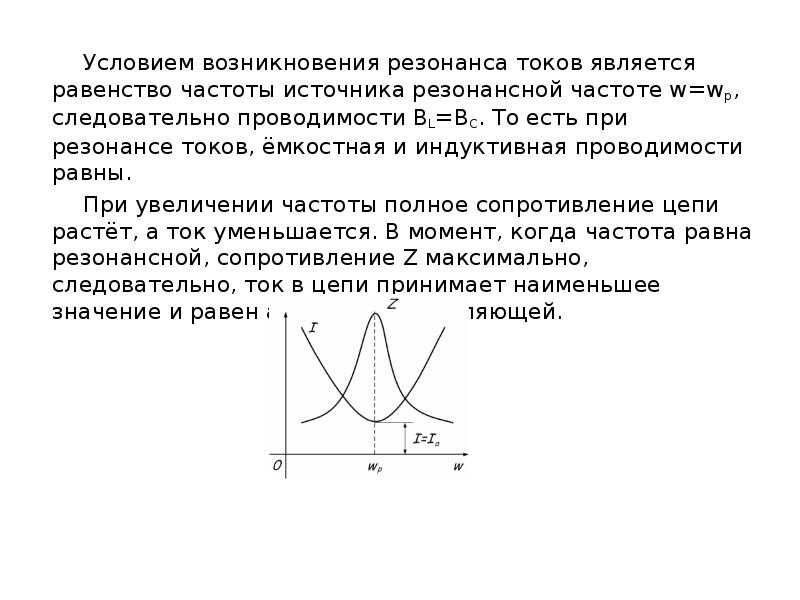
Серии R, L и C цепи.
R, L и C соединены последовательно, как показано на рисунке выше. Уравнение Кирхгофа для контура напряжения:
С текущего I — общий множитель,
Чтобы вектор напряжения в приведенном выше уравнении был равен 0 °,
сумма реактивных капель должна равняться нулю.
и
Поэтому
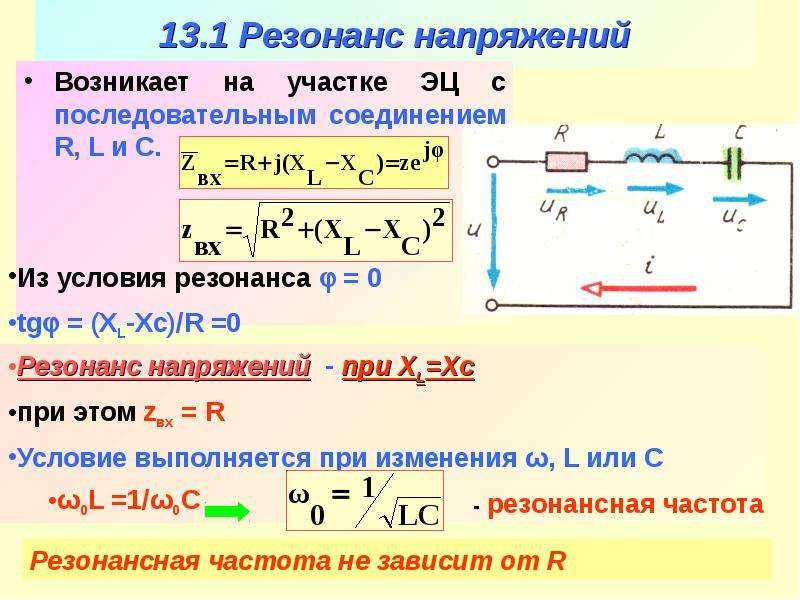
Вышеупомянутое уравнение утверждает, что когда индуктивное и емкостное реактивное сопротивление цепь последовательного RLC равна, цепь оказывается чисто резистивной. Когда цепь последовательного RLC кажется чисто резистивной, говорят, что цепь быть в 9Резонанс серии 0018
Частоту, при которой возникает последовательный резонанс, можно определить из предыдущее уравнение как функция реактивных компонентов L и C. Последовательно-резонансная частота f r получается в следующим образом.
Приведенное выше уравнение можно использовать для определения резонансной частоты, если элементы последовательной цепи известны. Это продемонстрировано в Примере 1.
Пример 1 : Элементы схемы на рисунке выше: L
Решение:
1. Используя приведенное выше уравнение,
2. Сумма реактивных напряжений равна нулю при резонансе. Следовательно,
3. Теперь можно рассчитать напряжение на каждом компоненте с помощью общий ток ступени 2.
Из шага 3 примера 1 видно, что падение напряжения на индуктивность и емкость больше приложенного напряжения
На резонансной частоте импеданс последовательного RLC-контура чисто резистивный и по минимуму. Следовательно, ток максимален в резонансе. Когда частота снижается ниже резонанса, емкостное сопротивление увеличивается. и индуктивное сопротивление уменьшается. Чистое реактивное сопротивление на частотах ниже резонансная частота емкостная, и она увеличивается по величине по мере дальнейшего снижения частоты ниже резонансной частоты.
Полное сопротивление цепи ниже резонанса представляет собой векторную сумму сопротивления
и чистое емкостное сопротивление.
Если частота увеличивается выше резонансной частоты, индуктивная реактивное сопротивление увеличивается, а емкостное сопротивление уменьшается. Чистое реактивное сопротивление выше резонансной частоты является индуктивным и увеличивается по величине по мере того, как частота увеличивается. Сопротивление увеличивается, а ток уменьшается по мере частота возрастает выше резонанса. Текущие отставания приложенное напряжение на увеличивающийся угол по мере того, как частота выше резонансной частоты.
Резонанс в цепях RLC, для ADALM1000 [Analog Devices Wiki]
Эта версия (03 ноября 2021 г., 20:15) была одобрена Дугом Мерсером. Доступна ранее одобренная версия (11 сентября 2019 г., 20:06).
Содержание
Деятельность: Резонанс в цепях RLC, для ADALM1000
Цель:
Примечания:
Фон:
Материалы:
Процедура:
Вопросы:
Приложение, графики частотной характеристики с ALICE-SA
Цель:
Целью этой лабораторной работы является изучение явления резонанса в цепях RLC.
Определите резонансную частоту и ширину полосы данной сети, используя амплитудную характеристику синусоидального источника.
Примечания:
Как и во всех лабораториях ALM, мы используем следующую терминологию при описании подключений к разъему M1000 и настройке оборудования. Заштрихованные зеленым прямоугольники обозначают подключения к разъему аналогового ввода-вывода M1000. Выводы канала аналогового ввода/вывода обозначаются как CA и CB. При настройке на форсирование напряжения/измерение тока — V добавляется как в CA- V или при настройке на форсирование тока/измерения напряжения добавляется -I как в CA-I. Когда канал сконфигурирован в режиме высокого импеданса только для измерения напряжения, -H добавляется как CA-H.
Следы осциллографа аналогичным образом обозначаются по каналу и напряжению/току. Например, CA- V , CB- V для сигналов напряжения и CA-I, CB-I для сигналов тока.
Фон:
Резонансный контур, также называемый настроенным контуром, состоит из катушки индуктивности и конденсатора вместе с источником напряжения или тока. Это одна из самых важных схем, используемых в электронике. Например, резонансный контур в одной из многих форм позволяет нам настроиться на желаемую радио- или телевизионную станцию из огромного количества сигналов, окружающих нас в любое время.
Сеть находится в резонансе, когда напряжение и ток на входных клеммах сети совпадают по фазе, а входное сопротивление сети чисто резистивное.
Рисунок 1: Параллельная резонансная цепь
Рассмотрим параллельную RLC-цепь на рис. 1. Установившаяся проводимость, обеспечиваемая схемой, равна:
Резонанс возникает, когда напряжение и ток на входных клеммах совпадают по фазе. Это соответствует чисто действительному допущению, так что необходимое условие определяется выражением:
Резонансное состояние может быть достигнуто путем регулировки L, C или ω.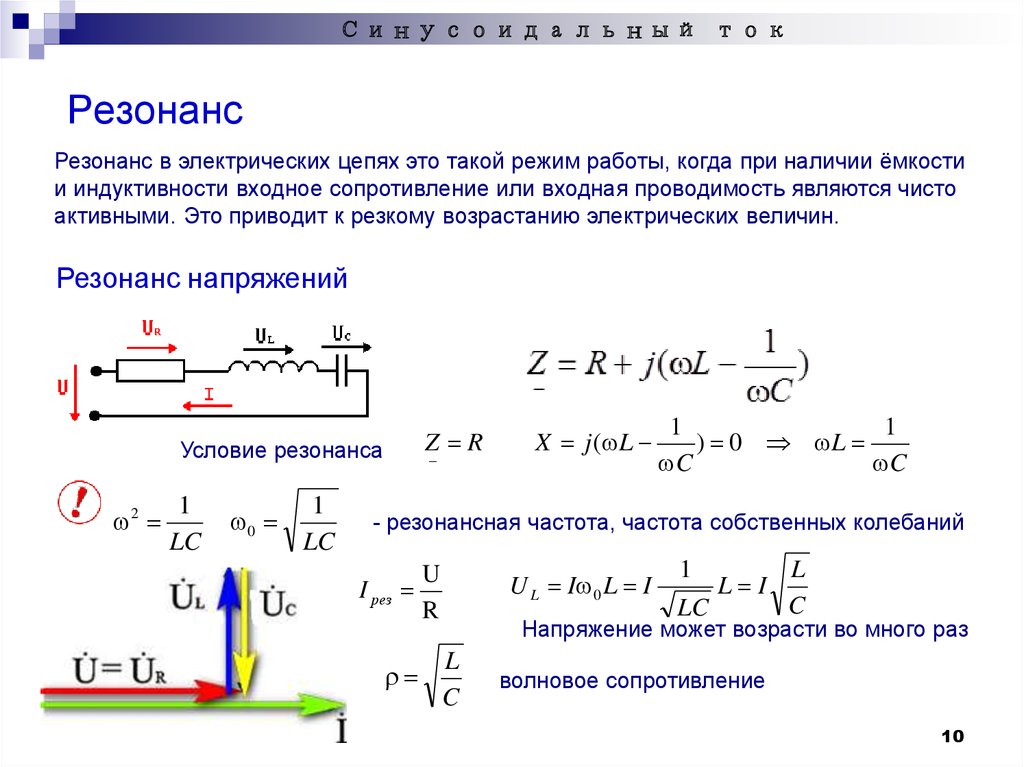
Сохраняя L и C постоянными, резонансная частота ω o определяется выражением:
рад/с (1)
ИЛИ
Герц (2)
Частотная характеристика: это график величины выходного напряжения резонансного контура в зависимости от частоты. Отклик, конечно, начинается с нуля, достигает максимального значения вблизи собственной резонансной частоты, а затем снова падает до нуля, когда ω становится бесконечным. Частотная характеристика показана на рисунке 2.
Рисунок 2: Частотная характеристика параллельного резонансного контура
Также указаны две дополнительные частоты ω 1 и ω 2 , которые называются частотами половинной мощности. Эти частоты определяют те точки на кривой, в которых отклик по напряжению составляет 1/sqrt(2) или 0,707 от максимального значения. Они используются для измерения ширины полосы кривой отклика. Это называется полосой частот резонансного контура по половинной мощности и определяется как:
(3)
Рисунок 3: Цепь последовательного резонанса
Материалы:
Аппаратный модуль ADALM1000
Резисторы 100 Ом, 1 кОм
Конденсаторы 1 мкФ, 0,01 мкФ
Катушки индуктивности 20 мГн
Процедура:
1.
Настройте цепь RLC, как показано на рис. 4, на макетной плате со значениями компонентов R S = 100 Ом, R 1 = 1 кОм, C 1 = 1 мкФ и L 1 = 20 мГн.
Рисунок 4: Параллельная резонансная цепь с последовательным сопротивлением, подключенным к источнику.
Рисунок 5: Соединения макетной платы
2. Установите минимальное значение канала A AWG на 0,5 и максимальное значение на 4,5 В, чтобы подать синусоиду 4 Впик-пик с центром на 2,5 В в качестве входного напряжения для схемы. В раскрывающемся меню AWG A Mode выберите режим SVMI. В раскрывающемся меню AWG A Shape выберите Sine. В раскрывающемся меню AWG B Mode выберите режим Hi-Z.
3. В раскрывающемся меню ALICE Curves выберите CA- V и CB- V для отображения. В раскрывающемся меню Trigger выберите CA- V и Auto Level. Установите Hold Off на 2 (мсек).
Отрегулируйте временную базу, пока на сетке дисплея не будет примерно два периода синусоиды. В раскрывающемся меню Meas CA выберите P-P в CA- V и сделайте то же самое для CB. Также в меню Meas CA выберите A-B Phase.
4. Измените частоту синусоиды в меню AWG A от 500 Гц до 2,5 кГц с шагом 100 Гц. Для каждой частоты запишите напряжение Р-Р для каналов А и В и фазы А-В. Обратите внимание, при какой частоте напряжение, наблюдаемое на выходе схемы на канале В, максимально. Это будет близко к резонансной частоте контура. Обратите внимание, что на этой частоте фаза должна быть около нуля градусов. Отрегулируйте частоту с шагом 10 Гц в том месте, где вы видите максимум напряжения CB PP, до тех пор, пока фаза A-B не станет точно нулевой.
5. Повторите эксперимент, используя последовательную резонансную схему на рис. 3, и используйте L 1 = 20 мГн, C 1 = 0,01 мкФ и R 1 = 1 кОм. Напряжение Vo на резисторе пропорционально току последовательной цепи RLC.
Вопросы:
1. Найдите резонансную частоту ω o с помощью уравнения (1) и сравните ее с экспериментальным значением в обоих случаях.
2. Постройте характеристику цепи по напряжению и получите полосу пропускания по частотам половинной мощности, используя уравнение (3).
Приложение, графики частотной характеристики с ALICE-SA
Программное обеспечение ALICE для настольных ПК может значительно упростить построение графиков частотной и фазовой характеристик. Используя параллельную резонансную схему RLC на рисунке 4, мы можем свипировать входную частоту от 10 Гц до 5000 Гц и построить амплитуду сигнала обоих каналов A и B и относительный фазовый угол между каналами B и A.
Со схемой, подключенной к ALM1000, как показано на рисунке 4, запустите настольное программное обеспечение ALICE. Откройте окно построения графика Боде.
В меню Curves выберите CA-dBV, CB-dBV и Phase BA.
В раскрывающемся меню «Параметры» нажмите «Cut-DC», чтобы выбрать его.
Установите минимальное значение канала A AWG на 1,086 и максимальное значение на 3,914. Это будет амплитуда 1 В (среднеквадратичное значение) (0 дБВ) с центром в середине диапазона аналогового входного сигнала 2,5 В. Установите для режима AWG A значение SVMI, а для формы — значение Sine. Установите канал AWG B в режим Hi-Z. Убедитесь, что установлен флажок Sync AWG.
Используйте кнопку «Начать частоту», чтобы установить развертку по частоте, чтобы она начиналась с 10 Гц, и используйте кнопку «Остановить частоту», чтобы остановить развертку на 5000 Гц. В раскрывающемся меню Sweep Gen выберите CHA в качестве канала для сканирования. Также используйте кнопку Sweep Steps, чтобы ввести количество шагов частоты, используйте 400 в качестве числа.
Теперь вы сможете нажать зеленую кнопку Run и запустить развертку по частоте. После завершения развертки вы должны увидеть что-то вроде снимка экрана на рисунке A1. Вы можете использовать кнопки LVL и dB /div для оптимизации графиков, чтобы они лучше всего соответствовали сетке экрана.
