12. Полосовой фильтр второго порядка.

Передаточная функция фильтра нижних частот первого порядка.

(12.1)

Если применить преобразование (11.1), то передаточная функция полосового фильтра будет иметь второй порядок:

(12.2)

Основными характеристиками такого фильтра является коэффициент передачи на резонансной частоте А_r и добротность Q.

Из свойств рассмотренного преобразования A_r = А₀ (это подтверждается формулой (12.2) при  = 1 т.е. Р = j). При этом A_r имеет действительное значение и фазовый сдвиг на резонансной частоте полосового фильтра равен нулю.

Определим добротность полосового фильтра как отношение резонансной частоты f_r к ширине полосы В.

Тогда передаточная функция полосового фильтра:

(12.

3)

Основные параметры полосового фильтра второго порядка непосредственно из его передаточной функции.

Пусть P = j, тогда

Амплитудно-частотная характеристика:

; (12.4)

Фазово-частотная характеристика:

. (12.5)

12.1 Реализация полосового фильтра второго порядка

Рис. 12.1. Полосовой фильтр на основе фильтра нижних частот и фильтра верхних частот первого порядка

Включим последовательно фильтры нижних и верхних частот первого порядка, как показано на рис 12.1. Получим полосовой фильтр с передаточной функцией.

Передаточная функция фильтра:

;

Учитывая, что резонансная частота передаточная функция в нормированном виде:

.

Приравняв к выражению (12.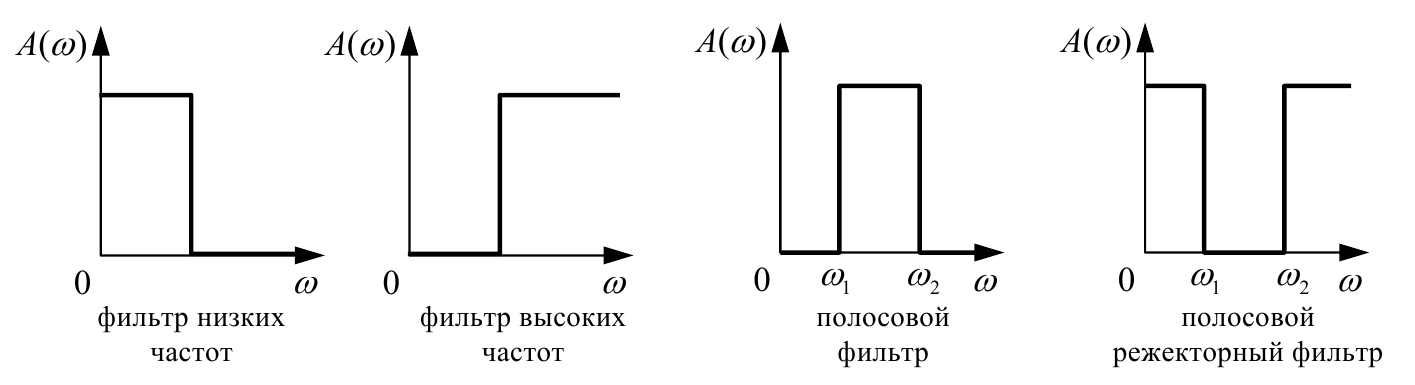 3) получим формулу для вычисления добротности фильтра:

При  = 1 — при последовательном соединении фильтров второго порядка.

12.2 Полосовой фильтр со сложной отрицательной обратной связью.

Сложную отрицательную обратную связь можно использовать для построения полосовых фильтров.

Рис12.2. Полосовой фильтр со сложной отрицательной обратной связью.

Схема фильтра приведена на рис.12.2. Ее передаточная функция имеет вид:

Принимая из сравнения с (12.3.)

Откуда:

Резонансная частота

Коэффициент передачи на резонансной частоте

Добротность

Ширина полосы

Коэффициент передачи, добротность и резонансная частота полосового фильтра могут выбираться произвольно.

Полоса пропускания В не зависит от R

1 и R₃, A_r – не зависит от R₃. Поэтому можно изменять резонансную частоту f_r, варьируя величиной R₃, что не приведет к изменению коэффициента передачи A_r и ширины полосы пропускания фильтра В.

Схема будет более работоспособно, если исключить R₃, но тогда Q будет зависеть от A_r.

При этом, если K_ooc>> 1, то дифференциальный коэффициент усиления операционного усилителя (ОУ) должен быть больше 2Q². Выполнение этого требования должно удовлетворяться и на резонансной частоте.

Числовой пример

Необходим полосовой фильтр с:

f_r = 10Гц

Q = 100

Частоты среза примерно 9,95Гц и 10,05Гц

А_r = -10

Пусть С = 1Мкф

–дифференциальный коэффициент усиления ОУ на резонансной частоте.

13. Преобразование фильтров нижних частот в заграждающие полосовые фильтры.

Запрещающие фильтры (ЗФ) производят подавление определенных частот. Коэффициент передачи на резонансной частоте равен нулю, а для нижних и верхних частот имеет постоянные значения.

Избирательность ЗФ оценивается добротностью подавления сигнала Q = f_r / B ; где В – полоса частот, на краях которой коэффициент передачи падает на 3дБ.

Амплитудно-частотную характеристику ЗФ можно получить из частотной характеристики ФНЧ с помощью следующего частотного преобразования. Заменим переменную Р на .

где:

— нормированная полоса частот.

В результате преобразования амплитудная характеристика ФНЧ из области 0   1 переходит в область пропускаемых частот     _g1 запрещающего фильтра. Кроме того, она зеркально отображает в логарифмическом масштабе относительно резонансной частоты ( = 1), для которой значение передаточной функции равно нулю.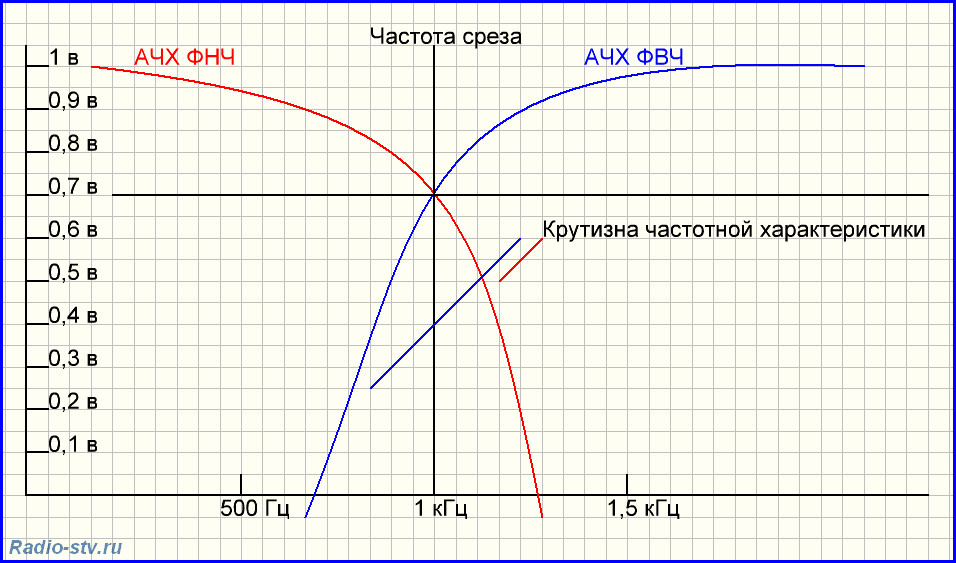

При преобразовании порядок фильтра удваивается. Так, при преобразовании фильтра нижних частот первого порядка получаем ЗФ второго порядка с передаточной функцией:

(13.1)

Откуда, получается выражение, для амплитудной и фазово-частотных характеристик фильтра:

С помощью пассивных RC – цепей можно получить минимальную добротность Q = 1 / 2.

Для обеспечения большей добротности следует применять специальные активные RC– схемы.

Регулируемый активный режекторный фильтр

 

Устройство относится к приборостроению, а именно к частотно-избирательным средствам, и предназначено для использования в устройствах фильтрации сигналов от помех на фиксированных частотах, в частности сетевой частоты 50 или 60 Гц, а также в акустических системах для устранения акустической «завязки». Технический результат заключается в повышении оперативности подстройки добротности активного режекторного фильтра (неинвертирующего симметричного второго порядка) путем регулировки одного элемента; в исключении влияния изменения величины добротности на коэффициент передачи фильтра; в уменьшении общего количества используемых в схеме элементов, что удешевляет устройство; в обеспечении работы фильтра от источников напряжения с различным выходным сопротивлением. Для достижения технического результата в регулируемом активном режекторном фильтре неинвертирующий вход дифференциального операционного усилителя подсоединен к клемме, предназначенной для подключения источника напряжения, и является входом всего устройства, а резистивный делитель напряжения выполнен в виде потенциометра, у которого вывод движка является выходом резистивного делителя напряжения и соединен с инвертирующим входом дифференциального операционного усилителя, а первый и второй выводы сопротивления потенциометра являются соответственно первым и вторым выводами резистивного делителя напряжения, при чем первый вывод резистивного делителя напряжения соединен с выходом дифференциального операционного усилителя, а второй вывод резистивного делителя напряжения соединен с выходом исходного режекторного фильтра, то есть с выходом всего устройства. 1 с.п. ф-лы, 3 илл.

Заявляемое устройство относится к приборостроению, а именно к частотно-избирательным средствам, и предназначено для использования в устройствах фильтрации сигналов от помех на фиксированных частотах, в частности сетевой частоты 50 или 60 Гц, а также в акустических системах для устранения акустической «завязки».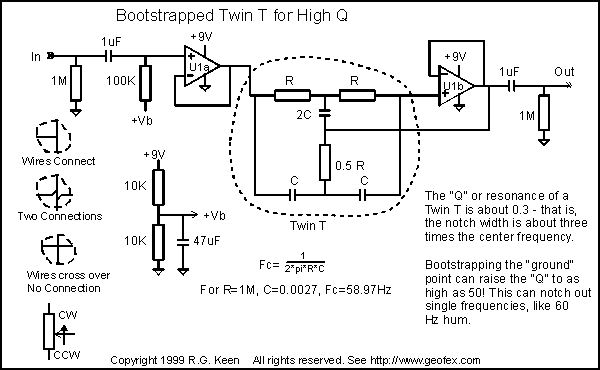

Известно, что режекторные фильтры широко применяются в системах связи, в различных измерительных приборах для соответствующей обработки сигналов.

Для режекторных фильтров требуется, чтобы на частоте режекции коэффициент передачи фильтра равнялся нулю. Для точной регулировки желательно иметь возможность подстройки величины коэффициента добротности независимо от величины коэффициента передачи.

Коэффициент передачи или передаточная функция фильтра являются основными характеристиками, отражающими способность фильтра к частотной селекции.

Для исходного режекторного фильтра, который является неинвертирующим симметричным режекторным фильтром второго порядка, (далее — исходный неинвертирующий РФ) передаточная функция имеет вид:

где р=j* — оператор Лапласа, — текущая частота (независимая переменная, ₀ — круговая частота режекции, Q _исх — коэффициент добротности исходного РФ, N _РФ(р) — числитель передаточной функции, D _РФ(р) — знаменатель передаточной функции.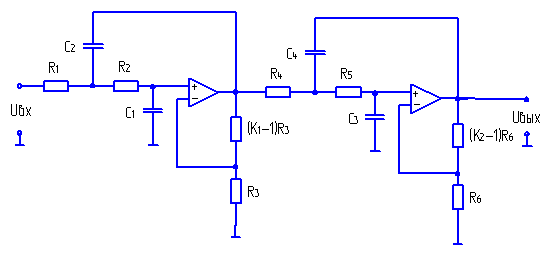

При этом не учитывается, с помощью каких конкретно RC или LC звеньев обеспечивается селективность фильтра.

Величина добротности Q _исх=₀/(₂—₁) (₂ и ₁ — частоты, на которых коэффициент передачи режекторного фильтра снижается на 3 дБ) характеризует селективные свойства режекторного фильтра, во многих случаях бывает недостаточна и требуется увеличение добротности режекторного фильтра.

Каскадное включение двух режекторных фильтров с одинаковой добротностью не позволяет увеличить добротность, поскольку дает результирующий режекторный фильтр с более низкой добротностью, чем исходный.

Из уровня техники известен режекторный фильтр с включением на вход исходного неинвертирующего РФ дополнительного корректирующего фильтра, являющегося амплитудным корректором и имеющим частоту подъема коэффициента усиления, совпадающего с частотой режекции (₀) (Справочник по расчету и проектированию ARC схем, М. Издательство «РиС», 1984, стр.42 и стр.327 и Кисель В.А. Аналоговые и цифровые корректоры. Справочник. М. «РиС», 1986, стр.19).

При каскадном (последовательном) включении дополнительного корректирующего фильтра (амплитудного корректора) с передаточной функцией (2) и исходного неинвертирующего РФ с передаточной функцией (1) происходит компенсация низко добротных полюсов знаменателя передаточной функции исходного неинвертирующего РФ (1) нулями числителя передаточной функции корректирующего фильтра. При этом полиномом знаменателя передаточной функции результирующего режекторного фильтра (3) становится полином знаменателя передаточной функции корректирующего фильтра, имеющего большую добротность, что и обеспечивает повышение добротности результирующего режекторного фильтра (Qнов).

Недостатком такого решения является необходимость использования дополнительных реактивных элементов в частотно- избирательных цепях корректирующего фильтра, что усложняет и удорожает режекторный фильтр. Кроме того, усложняется настройка величины добротности из-за необходимости регулировки большого числа элементов. В этом случае практически невозможно оперативно регулировать добротность режекторного фильтра.

Известны также режекторные фильтры, повышение величины добротности у которых достигается за счет введения в исходный РФ частотнонезависимой положительной обратной связи (ПОС) (Мошиц Г., Хорн П. Проектирование активных фильтров, М. «Мир», 1984, стр.175 и Активные избирательные устройства радиоаппаратуры, под ред В.В.Масленникова, М. «РиС», 1987, стр.28) в селективную цепь на основе Т- или 2Т-мостов.

Режекторный фильтр с 2Т-мостом и частотнонезависимым резистивным делителем (Соклоф С. Аналоговые интегральные схемы, М. «Мир», 1988, стр.373) позволяет регулировать добротность, но компоненты 2Т-моста требуют тщательного подбора и поддержания точных значений номиналов резисторов и конденсаторов 2Т-моста, что усложняет и удорожает производство режекторного фильтра. Также, повышение добротности за счет введения фиксированной ПОС в частотноселективную цепь Т-моста не

позволяет регулировать добротность режекторного фильтра в процессе эксплуатации и повышает уровень шумов фильтра.

Наиболее близким аналогом по совокупности существенных признаков к предлагаемому режекторному фильтру является режекторный фильтр по патенту США №4 242 642 (МПК H 03 F 1/34, 1980).

Этот режекторный фильтр (фиг.1) содержит дифференциальный операционный усилитель (ОУ) 1, инвертирующий вход которого соединен с выходом резистивного делителя напряжения 2, а выход — с входом исходного неинвертирующего РФ 3. При этом инвертирующий вход дифференциального ОУ 1 через резистор 4 с сопротивлением R₁ соединен с клеммой Uвх, предназначенной для подключения источника напряжения (на схеме не показан), а неинвертирующий вход дифференциального ОУ 1 и один вывод исходного неинвертирующего РФ 3 соединены с общим проводом (заземлением) 7. Резистивный делитель напряжения 2 образуется резистором 5 с сопротивлением R₂ и резистором 6 с сопротивлением R₃, при чем их первые выводы соединены и являются выходом резистивного делителя напряжения 2, соединенного с инвертирующим входом дифференциального ОУ 1, второй вывод резистора 5 является первым выводом резистивного делителя напряжения 2 и соединен с выходом дифференциального ОУ 1, а второй вывод резистора 6 является вторым выводом резистивного делителя напряжения 2 и соединен с выходом исходного неинвертирующего РФ 3, то есть с выходом всего устройства.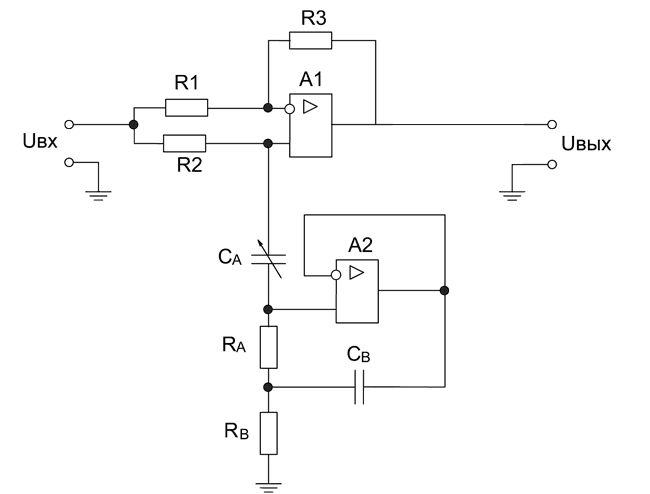

Передаточная функция этого режекторного фильтра имеет вид:

где коэффициент передачи режекторного фильтра на постоянном токе или бесконечно большой частоте определяется отношением:

а добротность —

Достоинствами этого режекторного фильтра являются:

— исключение дополнительных реактивных элементов, усложняющих настройку фильтра,

— использование только отрицательной обратной связи для подстройки величины добротности в виде резистивного делителя,

— компенсирование влияния изменения величины добротности на общий коэффициент передачи фильтра.

Недостатками прототипа являются:

— трудности оперативной регулировки величины добротности;

— влияние регулировки величины добротности на величину коэффициента передачи на постоянном токе и бесконечно большой частоте;

— невозможность работы режекторного фильтра от источников напряжения с большим внутренним сопротивлением.

Из формул (5) и (6) следует что регулирование величины добротности Qнов, можно обеспечить путем изменения величины сопротивления R3 резистора 5 при фиксированном значении сопротивления R ₂ резистора 6.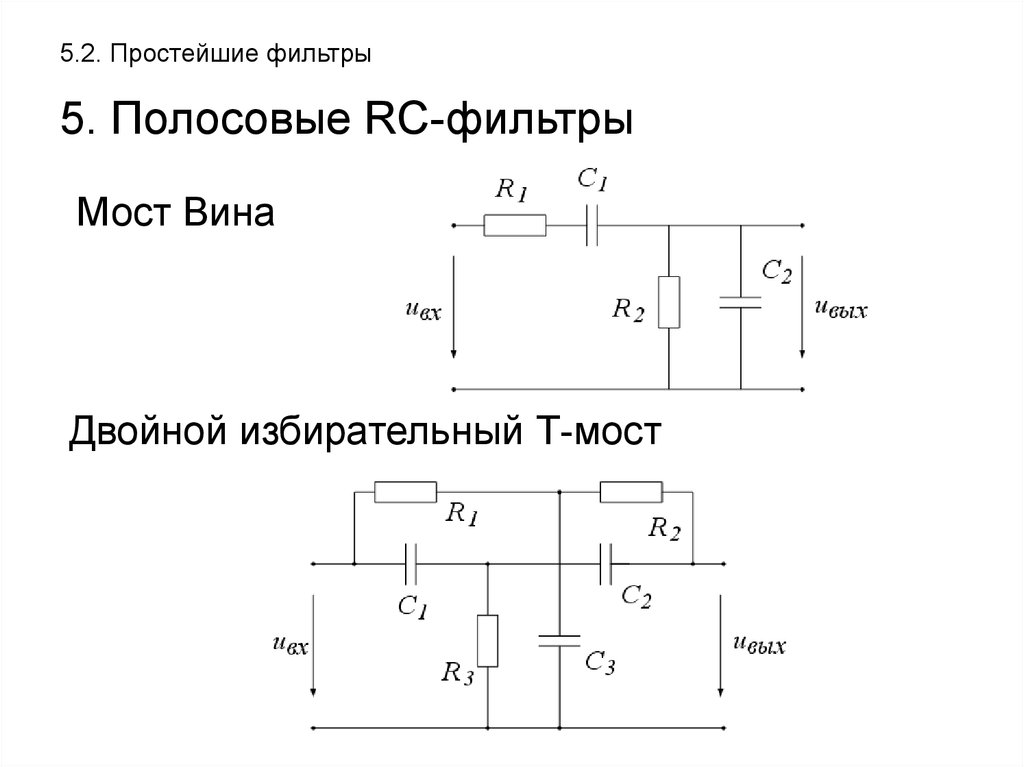 Однако варьирование величины R ₃ вызывает изменение величины коэффициента передачи всего фильтра на постоянном токе (или бесконечно большой частоте) k ₀, что нежелательно и является недостатком схемы фильтра. Изменение коэффициента передачи k₀ может быть скомпенсировано изменением величины сопротивлении R ₁ резистора 4, но данная операция требует наличия точно подобранных элементов (резисторов), а также итерационных процедур их настройки, что не позволяет оперативно регулировать величину добротности.

Технический результат, на достижение которого направлено предлагаемое техническое решение, заключается в повышении оперативности подстройки добротности активного режекторного фильтра (неинвертирующего симметричного второго порядка) путем регулировки одного элемента; в исключении влияния изменения величины добротности

на коэффициент передачи фильтра; в уменьшении общего количества используемых в схеме элементов, что удешевляет устройство; в обеспечении работы фильтра от источников напряжения с различным выходным сопротивлением.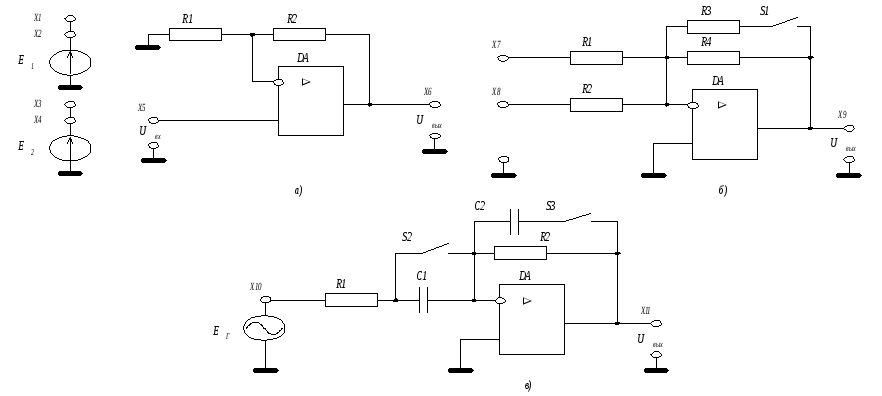

Для достижения этого технического результата предлагаемый регулируемый активный режекторный фильтр содержит дифференциальный ОУ, инвертирующий вход которого соединен с выходом резистивного делителя напряжения, а выход соединен с входом исходного неинвертирующего РФ, один вывод которого подсоединен к общему проводу (заземлению), первый вывод резистивного делителя напряжения соединен с выходом дифференциального ОУ, а второй вывод резистивного делителя напряжения соединен с выходом исходного неинвертирующего РФ, но при этом неинвертирующий вход дифференциального ОУ подсоединен к клемме, предназначенной для подключения источника напряжения, и является входом всего устройства, а резистивный делитель напряжения выполнен в виде потенциометра, у которого вывод движка является выходом резистивного делителя напряжения, а первый и второй выводы сопротивления потенциометра являются соответственно первым и вторым выводами резистивного делителя напряжения.

Предлагаемый регулируемый активный режекторный фильтр поясняется чертежами, представленными на фиг. 1-3, где на фиг.1 приведена схема режекторного фильтра, являющегося прототипом предлагаемого устройства, на фиг.2 — схема предлагаемого регулируемого активного режекторного фильтра, на фиг.3 — амплитудно частотные характеристики (АЧХ) регулируемого активного режекторного фильтра в различных точках схемы.

Регулируемый активный режекторный фильтр (фиг.2) содержит дифференциальный ОУ 1, инвертирующий вход которого соединен с выходом резистивного делителя напряжения 2. Неинвертирующий вход дифференциального ОУ 1 подсоединен к клемме Uвх, предназначенной для

подключения источника напряжения, и является входом всего устройства. Выход дифференциального ОУ 1 соединен с входом исходного неинвертирующего РФ 3, один вывод которого подсоединен к общему проводу (заземлению) 4. Резистивный делитель напряжения 2 включает потенциометр 5, у которого вывод движка является выходом резистивного делителя напряжения 2, а первый и второй выводы сопротивления потенциометра 5 являются соответственно первым и вторым выводами резистивного делителя напряжения 2, при этом первый вывод резистивного делителя напряжения 2 соединен с выходом дифференциального ОУ 1, а второй вывод резистивного делителя напряжения 2 соединен с выходом исходного неинвертирующего РФ 3, то есть с выходом всего устройства (Uвых).

Передаточная функция регулируемого активного режекторного фильтра получается следующим образом:

где

R₂ — значение сопротивления плеча потенциометра 5, подключенного одним выводом (выводом движка) к инвертирующему входу дифференциального ОУ 1, а вторым выводом (первым выводом потенциометра 5) к выходу дифференциального ОУ 1,

R₃ — значение сопротивления плеча потенциометра 5, подключенного одним выводом (выводом движка) к инвертирующему входу дифференциального ОУ 1, а вторым выводом (вторым выводом потенциометра 5) к выходу исходного неинвертирующего РФ 3,

R₂ +R₃=Rпот — значение сопротивления всего потенциометра.

Обозначим =R₃/(R₂+R ₃), и (1-)=R₂/(R₂+R ₃), тогда имеем:

После подстановки введенных обозначений, в том числе из формул (1) и (6), получаем передаточную функцию регулируемого активного режекторного фильтра:

где

и k₀=+1

Из рассмотрения формул (9) и (10) можно сделать следующие выводы:

— добротность фильтра Qрф_нов зависит только от коэффициента , то есть от величин сопротивлений плечей потенциометра 5 R₂ и R₃, которые настраиваются регулировкой только положения движка потенциометра 5;

— коэффициент передачи на постоянном токе или бесконечно большой частоте постоянен и равен единице и не зависит от , а значит и от величины сопротивления резистивного делителя напряжения 2, включенного в отрицательную обратную связь.

Важным достоинством регулируемого активного режекторного фильтра является высокое входное сопротивление, что позволяет работать фильтру с источниками напряжения с различным выходным сопротивлением без использования дополнительного развязывающего усилителя.

На фиг.3 показаны кривые АЧХ, которые иллюстрируют повышение добротности регулируемого активного режекторного фильтра в сравнении с добротностью исходного неинвертирующего РФ, обеспечиваемое в результате применения предложенного технического решения. На фиг.3 кривая 1 — АЧХ исходного неинвертирующего РФ, кривая 2 — АЧХ регулируемого активного режекторного фильтра, кривая 3 — АЧХ на выходе дифференциального ОУ.

Регулируемый активный режекторный фильтр работает следующим образом.

При нахождении движка потенциометра 5 в крайнем левом положении (фиг.2), когда R₂=0, а R₃=Rпот, имеем передачу дифференциального ОУ 1 равную единице от входа до выхода, (т.е. дифференциальный ОУ 1 работает в режиме повторителя напряжения за счет соединения выхода регулируемого активного режекторного фильтра с неинвертирующим входом дифференциального ОУ 1, и весь фильтр с учетом работы повторителя напряжения будет иметь добротность Орф_нов=Qисх. ).

При перемещении движка к положению на середине потенциометра 5, т.е. R ₂=R₃, тогда на частоте режекции ₀, где передача исходного неинвертирующего РФ 3 равна нулю, коэффициент передачи сигнала с неинвертирующего входа на выход дифференциального ОУ 1 будет равен двум, т.е. на входе исходного неинвертирующего РФ 3 будет действовать удвоенное входное напряжение. Увеличение частотнозависимого напряжения на входе исходного неинвертирующего РФ 3 компенсирует снижение усиления исходного неинвертирующего РФ 3 за счет малого значения исходной величины его добротности Qисх, что приводит к увеличению добротности регулируемого активного режекторного фильтра Орф_нов.

При расстройке частоты источника напряжения от частоты режекции ₀ регулируемого активного режекторного фильтра в сторону снижения, на выходе всего фильтра будет появляться напряжение с фазовым сдвигом в

сторону отставания, или в сторону опережения в случае отклонения частоты в сторону повышения (фиг. 3). При большом отклонении частоты источника напряжения от значения ₀ в сторону понижения или повышения сдвиг фазы выходного напряжения относительно входного напряжения становится равной нулю. Можно считать, что выходное напряжение будет синфазно входному: на первом выводе потенциометра 5 будет появляться напряжение в той же фазе, что и на втором выводе, причем равное по амплитуде, следовательно, ток через потенциометр 5 протекать не будет. В результате на всех трех выводах потенциометра 5 появится входное напряжение, вследствие виртуального нуля напряжения между входами дифференциального ОУ 1. Из этого следует, что коэффициент передачи будет равен единице, а перемещение движка потенциометра 5 на частотах, достаточно удаленных от частоты режекции не влияет на величину передачи регулируемого активного режекторного фильтра.

Регулируемый активный режекторный фильтр, содержащий дифференциальный операционный усилитель, инвертирующий вход которого соединен с выходом резистивного делителя напряжения, а выход соединен с входом исходного неинвертирующего режекторного фильтра, один вывод которого подсоединен к общему проводу (заземлению), при этом первый вывод резистивного делителя напряжения соединен с выходом дифференциального операционного усилителя, а второй вывод резистивного делителя напряжения соединен с выходом исходного неинвертирующего режекторного фильтра, отличающийся тем, что неинвертирующий вход дифференциального операционного усилителя подсоединен к клемме, предназначенной для подключения источника напряжения, а резистивный делитель напряжения выполнен в виде потенциометра, у которого вывод движка является выходом резистивного делителя, а первый и второй выводы сопротивления потенциометра являются соответственно первым и вторым выводами резистивного делителя напряжения.

2)} $$

Где:

$\omega_n$ — центральная частота метки (в радианах/выборке)

$\alpha$ — положительная действительная константа $<1$, которая устанавливает ширину полосы метки.

Чем ближе значение $\alpha$ к 1, тем уже полоса пропускания метки.

Соотношение между полосой режекции -3 дБ и $\alpha$:

$$\alpha = \sec(\omega_c/2)- \tan(\omega_c/2) \tag{1} \label{1 }$$

Где:

$\omega_c$ — полоса режекции -3 дБ (в радианах/отсчет), которая представляет собой диапазон частот от верхней границы среза -3 дБ до нижней границы среза -3 дБ.

Детали и вывод

Поворот фильтра на постоянный ток, чтобы сделать его фильтром нижних частот, упрощает уравнение; отсюда мы можем установить взаимосвязь между $\alpha$ и полосой пропускания, поскольку односторонняя полоса пропускания фильтра нижних частот первого порядка будет составлять половину полосы пропускания двустороннего режекторного фильтра второго порядка, когда частота режекции достаточно далеко от постоянного тока. или Найквиста, и достаточно узкая полоса пропускания, чтобы не было взаимодействия между положительными и отрицательными частотами.

Это продемонстрировано на сравнительных графиках ниже, показывающих амплитудно-частотную характеристику обнуляющего фильтра постоянного тока 1-го порядка и режекторного фильтра 2-го порядка с одинаковым значением для $\alpha$. Низкое значение $\alpha=0,6$ использовалось для преувеличения пропускной способности, чтобы сделать ее видимой для сравнения на графиках. Обычно $\alpha$ будет намного ближе к 1 для более жесткого обнуления постоянного тока и пропускной способности режекции.

Полюса и нули на плоскости z для каждого из этих фильтров показаны ниже (что преувеличенно низкое $\alpha$, как сделано выше), что при понимании обеспечивает интуитивное понимание частотной характеристики для этих фильтров как в амплитуда и фаза: 9{j\omega}$ для $\omega \in [0, 2\pi)$, что соответствует нормализованной частоте в радианах в выборках/цикл от постоянного тока к частоте выборки. Таким образом, единичная окружность является осью частот. Как мы видим ниже, для произвольной точки на оси частот, помеченной $z$, угол к $z$ является частотой, и для этой конкретной частоты величина обнуляющего фильтра постоянного тока первого порядка будет отношением длины вектор числителя $v_1 = z-z_1$ разделить на длину вектора знаменателя $v_2 = z-p_1$. При типичной работе с $\alpha$, очень близким к 1 (но меньше 1, чтобы быть внутри единичного круга и, следовательно, стабильным), мы можем видеть, что для большинства точек на единичном круге два вектора будут примерно равны по длине. и, таким образом, обеспечить постоянную величину. Только когда мы приблизимся к $z=1$ (то есть DC с $\omega =0$), мы получим существенную разницу в длине двух векторов, при этом числитель будет приближаться к нулю, что приведет к жесткому нулевой. Примечательно, что с помощью режекторного фильтра 2-го порядка мы можем видеть, что когда $\alpha$ близко к 1, а $\omega_n$ достаточно далеко от $0$ или $\pi$, то при приближении $z$ к одной метке эффект другой метки будет минимальным по отклику.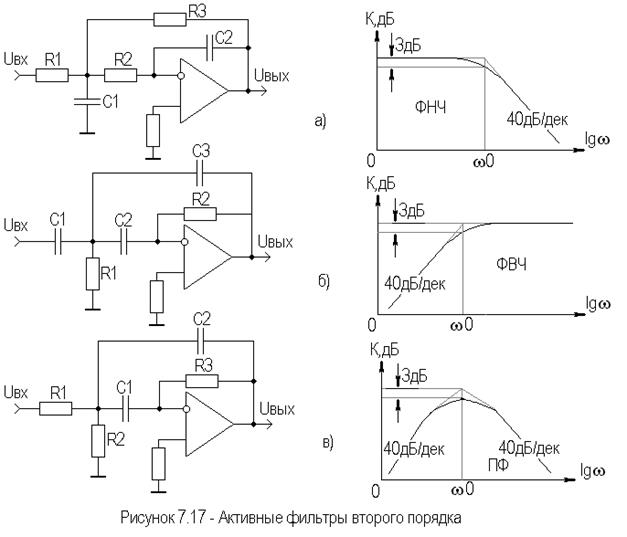 В частности, на приведенном ниже графике, если бы у нас было большее значение $\alpha$, когда $z$ приближается к выемке в $+\omega_n$ с $z = z_1$, была бы значительная разница в длинах между $v_3$ и $v_4$ создает нулевое значение, но длины $v_5$ и $v_6$ будут приблизительно равными, что сведет к минимуму любое влияние на отклик амплитуды. Оставшийся вывод предполагает, что это так, что упрощает результат. 92}$$

Представляет собой каскад двух обнуляющих фильтров постоянного тока первого порядка с передаточной функцией, заданной как:

$$G(z) = \bigg(\frac{1+\alpha}{2}\bigg) \frac{z-1}{z-\alpha}$$

Режекторный фильтр второго порядка будет иметь ту же частотную характеристику на одной стороне спектра относительно центральной частоты, что и эквивалентный фильтр нижних частот первого порядка. Таким образом, мы можем использовать характеристику фильтра обнуления постоянного тока первого порядка $G(z)$, чтобы определить взаимосвязь между $\alpha$ и его частотой среза -3 дБ $\omega_c/2$, которая тогда будет составлять половину полосы пропускания для второго заказать режекторный фильтр $\omega_c$. {j\omega}$: 92+1}\bigg) \tag{3} \label{3}$$

Перестановка \ref{3} для решения $\alpha$ на основе $\omega_c$ дает:

$$\alpha = \sec(\omega_c/2)- \tan(\omega_c/2) \tag{4}\label{4}$$

Пропускная способность указана в нормализованной частоте в радианах ($2\pi f/f_s$, где $f_s $ — частота дискретизации, $\pi$ соответствует $f_s/2$).

Так, например, если частота дискретизации составляет 1 кГц, и мы хотим получить двухстороннюю полосу пропускания 5 Гц с полосой пропускания 3 дБ около 50 Гц, значение для $\alpha$ будет определяться следующим образом:

$$\omega_c/2 = \frac{2\pi f_c}{f_s} = \frac{2\pi 2,5}{1000} \приблизительно 0,0157$$

$$\alpha \приблизительно \frac{1} {cos(0,0157)}- \tan(0,0157) = 0,9844$$

Приведенные выше расчеты показаны на графике ниже:

На увеличенном графике показано точное решение для полосы пропускания -3 дБ:

Дополнительные сведения о реализации фильтра обнуления DC см. по этой ссылке.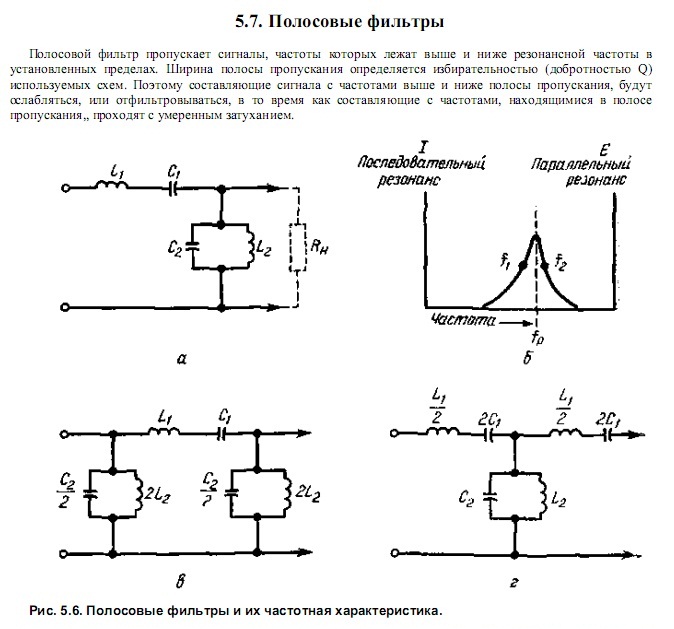

Схема и режекторный фильтр с использованием двух фильтров Баттерворта параллельно (MATLAB)

Задавать вопрос

спросил 2 года, 7 месяцев назад

Изменено 2 года, 2 месяца назад

Просмотрено 183 раза

$\begingroup$

Я делаю проект по фильтрации шума 1 кГц, вставленного в 30-секундный аудиофайл .wav. Чтобы отфильтровать шум частотой 1 кГц, мне необходимо спроектировать с использованием двух фильтров Баттерворта, подключенных параллельно, один из которых является фильтром нижних частот, а другой — фильтром Баттерворта высоких частот.

Я попытался вырезать шум 1 кГц, установив полосу пропускания на (+/-10 Гц) шума 1 кГц. Следовательно, диапазон шумового сигнала, подлежащего ослаблению, будет составлять от 990 Гц до 1010 Гц.

Я планирую сначала получить передаточную функцию в s-домене, а затем преобразовать ее в z-домен.

Разработанная передаточная функция будет введена в MATLAB, и будет получен отфильтрованный аудиофайл.

Могу ли я узнать этапы разработки этого фильтра? Подчеркнута экономичность и простота реализации фильтра.

Спасибо.

• Matlab
• конструкция фильтра
• фильтр нижних частот
• полоса пропускания
• Баттерворт

$\endgroup$

1

$\begingroup$

Особое внимание уделяется экономичности и простоте реализации фильтра.

Если это ваша цель, то вам действительно не следует использовать два фильтра Баттерворта. Вместо этого используйте режекторный фильтр. Если есть «требование» использовать другие фильтры, объясните, почему это необходимо.