Михайлова Наталья — Физика 11

Основы электродинамики

Глава 1. Магнитное поле

Урок 1. Взаимодействие токов. Магнитное поле

Урок 2. Магнитное поле и его характеристики

Урок 3. Закон Ампера и его применение

Урок 4. Решение задач. Сила Ампера

Урок 5. Лабораторная работа по теме «Оценка модуля вектора магнитной индукции подковообразного магнита»

Урок 6. Сила Лоренца

Урок 7. Применение силы Лоренца

Урок 8. Решение задач. Сила Лоренца

Урок 9. Магнитное поле вещества. Магнитное поле Земли

Урок 10. Контрольная работа. Электрический заряд и электромагнитное поле

Глава 2. Электромагнитная индукция

Урок 11. Индукция электрического поля. Правило Ленца

Урок 12. Закон электромагнитной индукции

Урок 13. Лабораторная работа по теме «Изучение явления электромагнитной индукции»

Урок 14. Решение задач. Законы электромагнитной индукции

Урок 15. Вихревое электрическое поле. ЭДС-индукции в движущихся проводниках

Урок 16. Самоиндукция

Урок 17. Решение задач

Урок 18. Решение экспериментальных задач

Урок 19. Решение задач

Урок 20. Решение качественных задач

Урок 21. Контрольная работа

Колебания и волны

Глава 3. Механические колебания

Урок 22. Динамика свободных колебаний

Урок 23. Решение задач по теме «Механические колебания»

Урок 24. Вынужденные колебания. Резонанс

Урок 25. Колебательная система под действием внешних сил

Урок 26. Лабораторная работа по теме «Измерение ускорения свободного падения с помощью маятника»

Урок 27. Решение задач по теме «Механические колебания»

Урок 28. Решение экспериментальных задач

Глава 4. Электромагнитные колебания

Урок 29. Колебательный контур

Урок 30. Переменный электрический ток

Урок 31. Сопротивление в цепи переменного тока

Урок 32. Лабораторная работа по теме «Измерение силы тока в цепи с конденсатором»

Урок 33. Лабораторная работа по теме «Измерение индуктивного сопротивления катушки»

Урок 34. Автоколебания

Урок 35. Лабораторная работа по теме «Исследование электрических схем с индуктивными, емкостными и активными элементами»

Урок 36. Решение задач

Урок 37. Решение экспериментальных задач

Глава 5. Производство, передача и использование электрической энергии

Урок 38. Генераторы тока

Урок 39. Трансформатор. Передача электроэнергии

Урок 40. Лабораторная работа по теме «Определение числа витков в обмотках трансформатора»

Урок 41. Производство, передача и использование электрической энергии

Урок 42. Решение задач по теме «Электромагнитные колебания. Переменный ток»

Урок 43. Электрификация России

Глава 6. Механические волны

Урок 44. Распространение волн в упругой среде

Урок 45. Стоячие волны

Урок 46. Периодические волны

Урок 47. Звуковые волны. Высота, тембр, громкость звука

Урок 48. Решение экспериментальных задач

Урок 49. Волны. Решение задач

Урок 50. Контрольная работа по теме «Механические и звуковые волны»

Глава 7.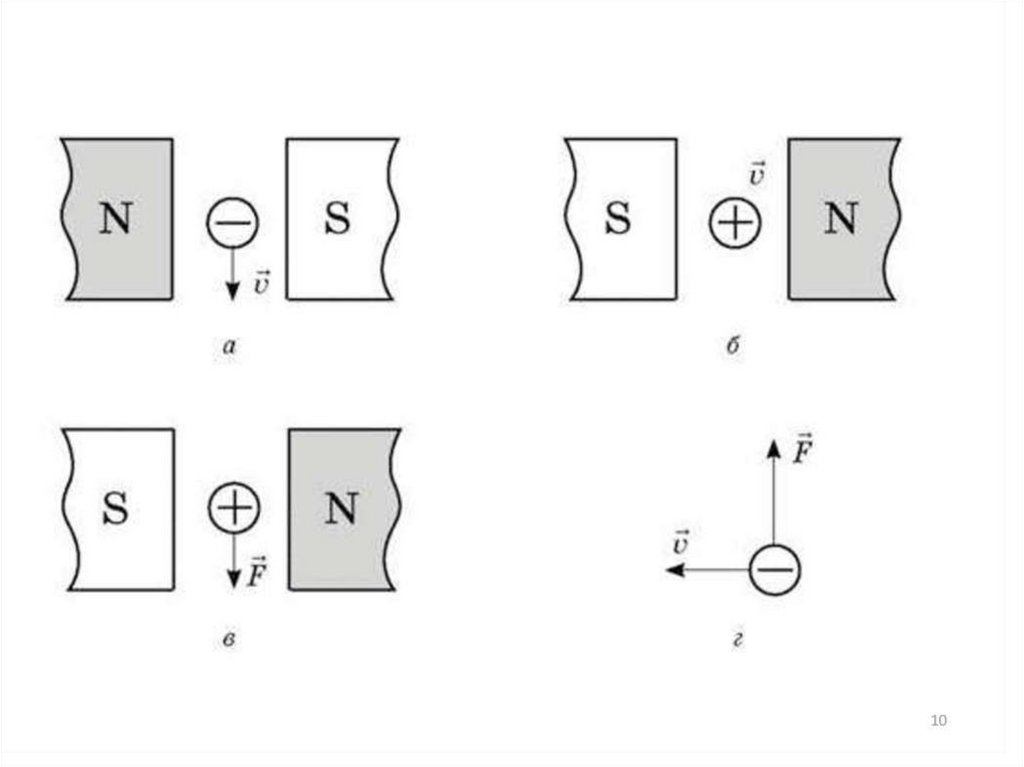 Электромагнитные волны

Урок 51. Электромагнитное поле

Урок 52. Электромагнитные волны

Урок 53. Открытие электромагнитных волня

Урок 54. Создатели беспроводной связи. Радио

Урок 55. Принцип радиосвязи

Урок 56. Лабораторная работа по теме «Сборка простейшего радиоприемника»

Урок 57. Блицтурнир по теме «Механические и электромагнитные волны»

Урок 58. Влияние искусственных и естественных электромагнитных колебаний на живые организмы

Урок 59. Обобщающий познавательно-развлекательный урок

Оптика

Глава 8. Световые волны

Урок 60. Развитие взглядов на природу света

Урок 61. Опытное определение скорости света

Урок 62. Преломление света

Урок 63. Принцип Гюйгенса. Закон отражения света

Урок 64. Решение задач на тему «Преломление света на плоской границе»

Урок 65. Решение задач

Урок 66. Полное внутреннее отражение

Урок 67. Решение задач

Урок 68. Лабораторная работа по теме «Измерение показателя преломления стекла»

Урок 69.

Линзы. Построение в линзах. Формула линзы

Урок 70. Решение задач по теме «Собирающая линза»

Урок 71. Решение задач по теме «Рассеивающая линза»

Урок 72. Лабораторная работа по теме «Определение фокусного расстояния линзы»

Урок 73. Глаз. Лупа

Урок 74. Лабораторная работа по теме «Изучение моделей оптических приборов»

Урок 75. Решение задач по теме: «Оптика»

Урок 76. Лабораторная работа по теме «Определение разрешающей способности глаза»

Урок 77. Контрольная работа по теме: «Оптика»

Урок 78. Дисперсия света

Урок 79. Интерференция и ее применение

Урок 80. Дифракция

Урок 81. Лабораторная работа по теме «Наблюдение интерференции и дифракции света»

Урок 82. Дифракционная решетка

Урок 83. Лабораторная работа по теме: «Измерение длины световой волны»

Урок 84. Поперечность световых волн. Поляризация света

Урок 85. Урок-игра. Конкурс умников и умниц по теме: «Оптика»

Глава 9. Элементы теории относительности

Урок 86. Постулаты специальной теории относительности

Урок 87. Релятивистский закон сложения скоростей

Урок 88. Относительность времени

Урок 89. Замедление времени

Урок 90. Взаимосвязь массы и энергии

Урок 91. Контрольная работа по теме: «Релятивистская механика»

Глава 10. Излучение и спектры

Урок 92. Виды излучений. Источники света

Урок 93. Лабораторная работа по теме: «Использование зависимости мощности теплового излучения тела от его температуры»

Урок 94. Спектры и спектральный анализ

Урок 95. Лабораторная работа по теме «Наблюдение сплошного и линейчатого спектров»

Урок 96. Инфракрасное и ультрафиолетовое излучение

Урок 97. Рентгеновские лучи

Урок 98. Шкала электромагнитных волн

Урок 99. Игра «Что? Где? Когда»

Квантовая физика

Глава 11. Световые кванты

Ads by optAd360

Урок 100. Квантовая физика

Урок 101. Фотоэффект

Урок 102. Решение задач

Урок 103. Лабораторная работа по теме: «Измерение работы выхода электрона при фотоэлектрическом эффекте»

Урок 104. Фотоны

Урок 105. Решение задач

Урок 106. Самостоятельная работа

Урок 107. Фотоэлементы и их применение

Урок 108. Контрольная работа по теме «Волновые и квантовые свойства света»

Урок 109. Давление света

Урок 110. Химическое действие света

Глава 12. Атомная физика

Урок 111. Строение атома. Опыты Резерфорда

Урок 112. Квантовые постулаты Бора. Трудности теории Бора

Урок 113. Лазеры

Урок 114. Урок-игра «Своя игра»

Глава 13. Физика атомного ядра

Урок 115. Радиоактивность. Радиоактивные превращения атомных ядер

Урок 116. Экспериментальные методы исследования частиц

Урок 117. Лабораторная работа по теме: «Изучение треком заряженных частиц»

Урок 118. Строение атомного ядра

Урок 119. Правило смещения

Урок 120. Ядерные силы, ядерные реакции. Энергия связи. Дефект масс

Урок 121. Закон радиоактивного распада

Урок 122. Нейтрон

Урок 123. Деление ядер урана

Урок 124. Решение задач

Урок 125. Решение задач

Урок 126. Контрольная работа по теме «Ядерная физика»

Урок 127. Цепная ядерная реакция

Урок 128. Термоядерные реакции

Урок 129. Ядерный реактор

Урок 130. Атомная энергетика

Урок 131. Биологическое действие радиоактивного излучения

Глава 14. Элементарные частицы

Урок 132. Зарождение физики элементарных частиц

Урок 133. Элементарные частицы, их классификация

Урок 134. Урок-игра «Поле чудес» по теме: «Атомная физика и физика атомного ядра»

 

Решение сложных задач по физике

1. Введение. Правила и приемы решения физических задач. Как работать над тестовыми заданиями. Общие требования при решении физических задач. Этапы решения физической задачи. Работа с текстом задачи. Анализ физического явления. Различные приемы и способы решения физических задач: алгоритмы, аналогии, геометрические приемы.

2. Кинематика. Решение тестовых задач с использованием формул, устанавливающих взаимосвязь между основными кинематическими параметрами (Уравнение прямолинейного равноускоренного движения. Движение по окружности.)

3. Динамика. Решение тестовых заданий на применение основных динамических законов (законов Ньютона). Решение задач на движение тела под действием нескольких сил. Задачи на применение закона всемирного тяготения, закона Гука. Решение задач по интересам: занимательных, экспериментальных и т.д.

4. Законы сохранения в механике. Решение задач на применение закона сохранения импульса и реактивного движения. Решение задач на применение закона сохранения и превращения механической энергии. Решение задач несколькими способами.

5. Механические и электромагнитные колебания и волны. Решение задач на применение законов колебательного движения. Решение задач на применение формул, описывающих свободные колебания в колебательном контуре. Электромеханическая аналогия при решении задач на описание колебательных процессов. Решение задач на описание различных свойств электромагнитных волн.

6. Основы молекулярно-кинетической теории. Решение задач на применение уравнения Клапейрона-Менделеева, газовых законов для изопроцессов. Решение графических задач. Решение задач на определение относительной влажности.

7. Основы термодинамики. Решение комбинированных задач на применение первого закона термодинамики. Решение задач на определение КПД тепловых двигателей.

8. Электростатика. Решение задач на применение закона сохранения электрического заряда и закона Кулона. Решение тестовых задач на определение напряженности и потенциала электростатического поля. Решение задач на применение формул заряженного конденсатора, энергии электрического поля конденсатора.

9. Законы постоянного электрического тока. Решение задач на расчет сопротивления сложных электрических цепей. Решение задач на закон Ома для участка цепи, законов последовательного и параллельного соединения проводников. Решение задач на описание законов постоянного тока с использованием закона Джоуля – Ленца. Решение задач на описание постоянного электрического тока в электролитах.

10. Магнитное поле. Решение задач на описание магнитного поля. Магнитная индукция, магнитный поток, сила Ампера и сила Лоренца. Решение комбинированных задач.

11. Оптика. Решение задач на применение законов геометрической оптики, формулы тонкой линзы, волновой оптики.

12. Квантовая и ядерная физика. Решение задач на применение формулы Планка, законов фотоэффекта, уравнения Эйнштейна. Решение задач на применение закона сохранения массового числа и электрического заряда.

электромагнетизм — Алгоритм решения электромагнитных задач с использованием только сил

спросил 2 года, 6 месяцев назад

Изменено 2 года, 6 месяцев назад

Просмотрено 167 раз

$\begingroup$

Есть ли принципиальная проблема при решении электромагнитных задач с помощью следующего алгоритма? (практичность в сторону)

i) Установить положение, скорость, массу и заряд для набора частиц.

ii) Вычислите электрическое поле в положении каждой частицы, созданной всеми другими частицами по закону Кулона.

iii) Рассчитайте магнитное поле в положении каждой частицы, создаваемой всеми другими частицами, с помощью закона Био-Савара.

iv) Переместить все частицы на дифференциальную величину, используя второй закон Ньютона с силой Лоренца:

для каждой частицы i вычислить: $m \vec a = q(\vec E + \vec v \times \vec B)$

v) Перейти к шагу ii.

• электромагнетизм
• вычислительная физика
• моделирование
• закон кулона

$\endgroup$

0

$\begingroup$

Да. По крайней мере, два, которые я вижу навскидку:

1. Закон Кулона выполняется только в Электростатике , то есть он не верен для движущихся зарядов, даже движущихся с одинаковой скоростью по отношению друг к другу. 2$, как вы можете видеть в главе 26 Фейнмановских лекций (см. рис. 26-4).

2. Закон Био-Савара также справедлив только для Магнитостатика , где вы имеете дело с постоянными токами . Один движущийся точечный заряд, конечно же, не постоянный ток!

Кроме того, поскольку эти поля непостоянны, вы также должны помнить, что изменения в электромагнитном поле распространяются со скоростью света $c$. Другими словами, заряды будут ощущать не мгновенную силу, как вы описываете, а 0047 запаздывал запаздывал на время $t — r/c$, где $r$ — расстояние между зарядами.

Теперь вы могли бы сделать немного лучше, фактически используя точные электрические и магнитные поля движущихся зарядов (они получены в главе Фейнмановских лекций, на которые я ссылался выше), принимая во внимание запаздывание, и , а затем использовать формула:

$$\mathbf{F} = q (\mathbf{E + v \times B}),$$

но я также вижу четвертую проблему: ускоренные заряды излучают энергию в виде электромагнитных волн. Это излучение вызывает силу отдачи заряженной частицы, называемую силой Абрахама-Лоренца (или радиационной реакцией). Вам также необходимо принять это во внимание для полного описания. Однако и это справедливо только при скоростях, малых по сравнению со скоростью света $c$. Думаю, ее релятивистской версией является сила Абрахама-Лоренца-Дирака.

Но это звучит как очень сложная задача без предварительных предположений (принятие нерелятивистского предела и т.д.).

$\endgroup$

$\begingroup$

Кажется, я на самой первой странице лекций Fenyman Vol 2 упоминает об этом, когда пытается объяснить, почему мы используем поля, а не только силы.

https://www.feynmanlectures.caltech.edu/

Немного скудно, но: https://www.feynmanlectures.caltech.edu/II_01.html

Оказывается, формы простейших законов электродинамики не такие, как можно было бы ожидать. Непросто дать формулу для силы, с которой один заряд действует на другой. Это правда, что когда заряды стоят на месте, закон силы Кулона прост, но когда заряды движутся, отношения усложняются, среди прочего, задержками во времени и эффектами ускорения. В результате мы не хотим представлять электродинамику только через законы силы между зарядами; нам удобнее рассмотреть другую точку зрения — точку зрения, при которой законы электродинамики кажутся наиболее легко управляемыми.

Итак, я полагаю, что ответ на ваш вопрос заключается в том, что ваш метод не учитывает конечную скорость, с которой возмущения в магнитном и электрическом полях распространяются между зарядами.

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

Навье-Стокса с членом силы Лоренца — вариационная формулировка

Привет, Нейт!

Да, стандартная пара Тейлор-Худ работает намного лучше, хотя мне приходится довольно высоко увеличивать относительный допуск (1e-02), чтобы модель сходилась во всех случаях. Не уверен, насколько это нормально.

Я также начал адаптировать демо-версию Stokes, сначала преобразовав ее в Navier-Stokes, прежде чем пытаться реализовать эффекты MHD, однако у меня возникли некоторые проблемы.

У меня есть вариационная форма как

 a = form([[inner(grad(u), grad(v)) * dx, inner(dot(grad(u), u), v) * dx, inner( p, div(v)) * dx],
          [внутренний (div (u), q) * dx, нет]])
 

Тем не менее, я думаю, что у меня неправильная форма, так как я получаю ошибки.

Вот используемый код и сообщение об ошибке:

 импортировать numpy как np
импорт УФЛ
из dolfinx импортировать cpp как _cpp
от dolfinx импорт фем
из импорта dolfinx.fem (Constant, Function, FunctionSpace, dirichletbc,
                         Extract_function_spaces, форма,
                         locate_dofs_geometrical, locate_dofs_topological)
из dolfinx.io импортировать XDMFFile
из импорта dolfinx.mesh (CellType, GhostMode, create_rectangle,
                          locate_entities_boundary)
импорт из ufl div, dx, grad, inner, dot, nabla_grad
из mpi4py импортировать MPI
из petsc4py импортировать PETSc
# Создаем сетку
msh = create_rectangle(MPI. COMM_WORLD,
                       [np.массив ([0, 0]), np.массив ([1, 1])],
                       [100, 100],
                       CellType.triangle, GhostMode.none)
защита noslip_boundary(x):
    вернуть np.logical_or (np.logical_or (np.isclose (x [0], 0.0),
                                       np.isclose(x[0], 1.0)),
                         np.isclose (х [1], 0,0))
защитная крышка (x):
    вернуть np.isclose(x[1], 1.0)
определение lid_velocity_expression(x):
    вернуть np.stack((np.ones(x.shape[1]), np.zeros(x.shape[1])))
P2 = ufl.VectorElement("Лагранж", msh.ufl_cell(), 2)
P1 = ufl.FiniteElement("Лагранж", msh.ufl_cell(), 1)
V, Q = FunctionSpace(msh, P2), FunctionSpace(msh, P1)
# граничные условия:
noslip = np.zeros(msh.geometry.dim, dtype=PETSc.ScalarType)
фасеты = locate_entities_boundary (msh, 1, noslip_boundary)
bc0 = dirichletbc(noslip, locate_dofs_topological(V, 1, фасеты), V)
lid_velocity = Функция (V)
lid_velocity.interpolate(lid_velocity_expression)
фасеты = locate_entities_boundary (msh, 1, крышка)
bc1 = dirichletbc(lid_velocity, locate_dofs_topological(V, 1, фасеты))
bcs = [bc0, bc1]
# Определить вариационную задачу
(u, p) = ufl. TrialFunction(V), ufl.TrialFunction(Q)
(v, q) = ufl.TestFunction(V), ufl.TestFunction(Q)
f = Константа (msh, (PETSc.ScalarType(0), PETSc.ScalarType(0)))
a = form([[inner(grad(u), grad(v)) * dx, inner(dot(grad(u), u), v) * dx, inner(p, div(v)) * dx] ,
          [внутренний (div (u), q) * dx, нет]])
L = form([inner(f, v) * dx, inner(Constant(msh, PETSc.ScalarType(0)), q) * dx])
# блочно-диагональный предобуславливатель:
a_p11 = форма (внутренняя (p, q) * dx)
а_р = [[а[0][0], нет],
       [Нет, a_p11]]
# ### Итеративный решатель монолитных блоков
A = fem.petsc.assemble_matrix_block(a, bcs=bcs)
А.собрать()
P = fem.petsc.assemble_matrix_block (a_p, bcs = bcs)
P.собрать()
b = fem.petsc.assemble_vector_block(L, a, bcs=bcs)
# Установить около нуля для давления
null_vec = A.createVecLeft()
смещение = V.dofmap.index_map.size_local * V.dofmap.index_map_bs
null_vec.array[смещение:] = 1,0
null_vec.normalize ()
nsp = PETSc.NullSpace().create(vectors=[null_vec])
утверждать nsp.test(A)
A.setNullSpace(nsp)
# Создавать наборы индексов для каждого поля (глобальные индексы глубины резкости для каждого поля)
V_map = V. dofmap.index_map
Q_map = Q.dofmap.index_map
offset_u = V_map.local_range[0] * V.dofmap.index_map_bs + Q_map.local_range[0]
offset_p = offset_u + V_map.size_local * V.dofmap.index_map_bs
is_u = PETSc.IS().createStride(V_map.size_local * V.dofmap.index_map_bs, offset_u, 1, comm=PETSc.COMM_SELF)
is_p = PETSc.IS().createStride(Q_map.size_local, offset_p, 1, comm=PETSc.COMM_SELF)
# Создать решатель Крылова
ksp = PETSc.KSP().create(msh.comm)
ksp.setOperators(A, P)
ksp.setTolerances(rtol=1e-9)
ksp.setType("минрес")
ksp.getPC().setType("разделение полей")
ksp.getPC().setFieldSplitType(PETSc.PC.CompositeType.ADDITIVE)
ksp.getPC().setFieldSplitIS(
    ("у", is_u),
    ("р", is_p))
# Настройте вспомогательные KSP скорости и давления
ksp_u, ksp_p = ksp.getPC().getFieldSplitSubKSP()
ksp_u.setType("только предварительно")
ksp_u.getPC().setType("игра")
ksp_p.setType("только предварительно")
ksp_p.getPC().setType("Якоби")
# Мониторинг сходимости KSP
opts = PETSc.Options()
опции["ksp_monitor"] = Нет
опции["ksp_view"] = Нет
ksp. setFromOptions()
# Вычислить решение
х = A.createVecRight()
ksp.solve(b, x)
 

и ошибка:

 Трассировка (последний последний вызов):
 Файл "/home/fenics/shared/test.py", строка 59, в  a = form([[inner(grad(u), grad(v)) * dx, inner(dot(grad(u), u), v) * dx, inner(p, div(v)) * dx] ,
 Файл "/usr/local/dolfinx-real/lib/python3.10/dist-packages/dolfinx/fem/forms.py", строка 166, в форме
 вернуть _create_form (форма)
 Файл "/usr/local/dolfinx-real/lib/python3.10/dist-packages/dolfinx/fem/forms.py", строка 163, в _create_form
 список возврата (карта (лямбда sub_form: _create_form (sub_form), форма))
 Файл "/usr/local/dolfinx-real/lib/python3.10/dist-packages/dolfinx/fem/forms.py", строка 163, в  список возврата (карта (лямбда sub_form: _create_form (sub_form), форма))
 Файл "/usr/local/dolfinx-real/lib/python3.10/dist-packages/dolfinx/fem/forms.py", строка 163, в _create_form
 список возврата (карта (лямбда sub_form: _create_form (sub_form), форма))
 Файл "/usr/local/dolfinx-real/lib/python3. 10/dist-packages/dolfinx/fem/forms.py", строка 163, в  список возврата (карта (лямбда sub_form: _create_form (sub_form), форма))
 Файл "/usr/local/dolfinx-real/lib/python3.10/dist-packages/dolfinx/fem/forms.py", строка 161, в _create_form
 вернуть _form (форма)
 Файл "/usr/local/dolfinx-real/lib/python3.10/dist-packages/dolfinx/fem/forms.py", строка 135, в _form
 ufcx_form, модуль, код = jit.ffcx_jit (mesh.comm, форма,
 Файл "/usr/local/dolfinx-real/lib/python3.10/dist-packages/dolfinx/jit.py", строка 56, в mpi_jit
 вернуть local_jit(*args, **kwargs)
 Файл "/usr/local/dolfinx-real/lib/python3.10/dist-packages/dolfinx/jit.py", строка 204, в ffcx_jit
 r = ffcx.codegeneration.jit.compile_forms([ufl_object], параметры=p_ffcx, **p_jit)
 Файл "/usr/local/lib/python3.10/dist-packages/ffcx/codegeneration/jit.py", строка 168, в compile_forms
 impl = _compile_objects(decl,forms,form_names,module_name,p,cache_dir,
 Файл "/usr/local/lib/python3.10/dist-packages/ffcx/codegeneration/jit. py", строка 232, в _compile_objects
 _, code_body = ffcx.compiler.compile_ufl_objects(ufl_objects, префикс=имя_модуля, параметры=параметры)
 Файл "/usr/local/lib/python3.10/dist-packages/ffcx/compiler.py", строка 97, в compile_ufl_objects
 анализ = analysis_ufl_objects(ufl_objects, параметры)
 Файл "/usr/local/lib/python3.10/dist-packages/ffcx/analysis.py", строка 85, в analysis_ufl_objects
 form_data = tuple (_analyze_form (форма, параметры) для формы в формах)
 Файл "/usr/local/lib/python3.10/dist-packages/ffcx/analysis.py", строка 85, в  form_data = tuple (_analyze_form (форма, параметры) для формы в формах)
 Файл "/usr/local/lib/python3.10/dist-packages/ffcx/analysis.py", строка 168, в _analyze_form
 form_data = ufl.algorithms.compute_form_data(
 Файл "/usr/local/lib/python3.10/dist-packages/ufl/algorithms/compute_form_data.py", строка 407, в calculate_form_data
 check_form_arity(preprocessed_form, self.original_form.arguments(), complex_mode) # Сейчас проверяем, насколько это быстро
 Файл "/usr/local/lib/python3. 10/dist-packages/ufl/algorithms/check_arities.py", строка 177, в check_form_arity
 check_integrand_arity(itg.integrand(), аргументы, комплексный_режим)
 Файл "/usr/local/lib/python3.10/dist-packages/ufl/algorithms/check_arities.py", строка 159., в check_integrand_arity
 arg_tuples = map_expr_dag (правила, выражение, сжатие = ложь)
 Файл "/usr/local/lib/python3.10/dist-packages/ufl/corealg/map_dag.py", строка 36, в map_expr_dag
 результат, = map_expr_dags(функция, [выражение], сжатие=сжатие,
 Файл "/usr/local/lib/python3.10/dist-packages/ufl/corealg/map_dag.py", строка 99, в map_expr_dags
 r = handlers[v._ufl_typecode_](v, *[vcache[u] для u в v.ufl_operands])
 Файл "/usr/local/lib/python3.10/dist-packages/ufl/algorithms/check_arities.py", строка 63, в продукте
 поднять ArityMismatch("Умножение выражений с перекрывающимся номером аргумента формы {0}, аргумент равен {1}.".format(x[0].number(), _afmt(x)))
 Файл "/usr/local/lib/python3.10/dist-packages/ufl/algorithms/check_arities.