Простая физика — EASY-PHYSIC

Самые простые задачи на определение силы, индукции поля, длины проводника или угла, под которым этот проводник расположен. Направление силы определяем по правилу ЛЕВОЙ руки: если расположить руку так, чтобы магнитные линии втыкались в ладонь, а четыре пальца направить по току, то отведенный большой палец укажет направление действия силы.

Задача 1.

Прямолинейный проводник длиной м находится в однородном магнитном поле с индукцией Тл. Сила тока в проводнике А. Проводник перпендикулярен магнитной индукции (рис.). Найти модуль и направление силы, действующей на проводник.

К задаче 1

Со стороны поля на проводник с током действует сила Ампера:

У нас проводник перпендикулярен линиям индукции, поэтому

Определяем направление. Левую руку расположим так, чтобы линии индукции втыкались в ладонь, то есть ладошкой вниз. Четыре вытянутых пальца направим вдоль тока – то есть влево. Тогда большой палец укажет направление действия силы – за плоскость рисунка, от нас.

Ответ: Н, от нас за плоскость рисунка.

Задача 2.

Прямолинейный проводник длиной м находится в однородном магнитном поле (рис.). На проводник со стороны поля действует сила Н. Сила тока в проводнике А. Найти модуль и направление индукции магнитного поля, если она перпендикулярна проводнику.

К задаче 2

Со стороны поля на проводник с током действует сила Ампера:

У нас проводник перпендикулярен линиям индукции, поэтому

Для определения направления левую руку расположим пальцами вниз – они указывают направление тока, большим пальцем вправо – он указывает направление действия силы. Тогда ладонь окажется развернутой к нам – в раскрытую ладонь должны втыкаться линии магнитной индукции, следовательно, они направлены от нас за плоскость чертежа.

Ответ: Тл, от нас за плоскость чертежа.

Задача 3.

На прямой проводник длиной м, расположенный под углом к силовым линиям поля с индукцией Тл, действует сила Н.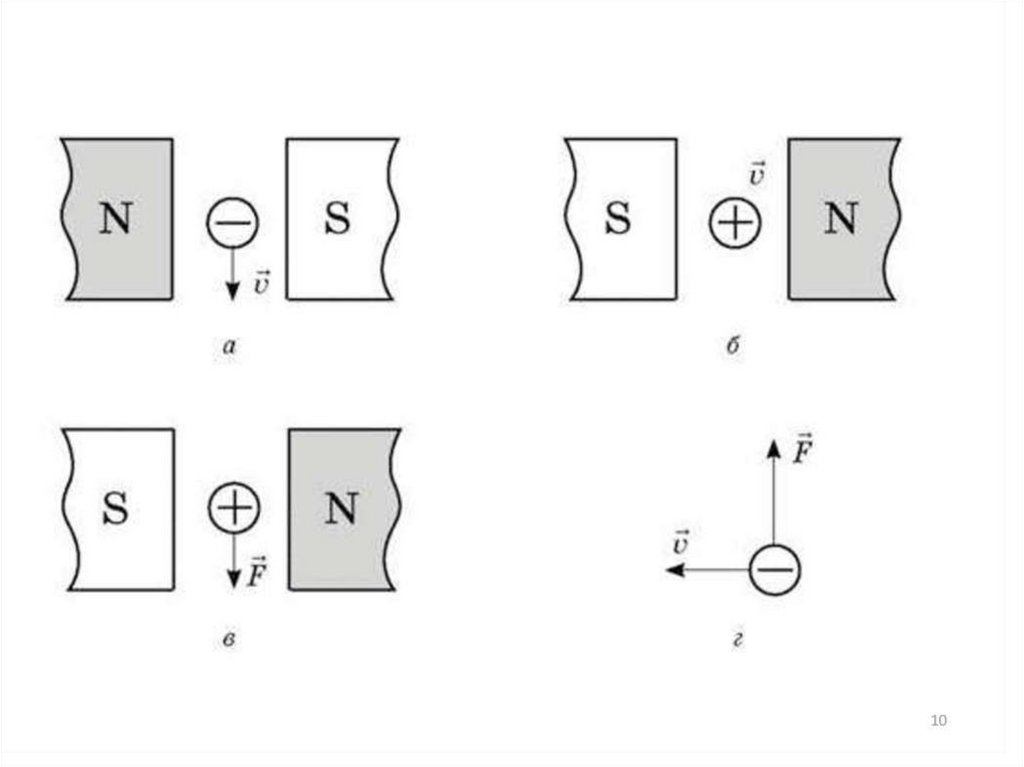 Найти силу тока в проводнике.

Со стороны поля на проводник с током действует сила Ампера:

Ответ: 30 А.

Задача 4.

Прямой провод длиной см находится в однородном магнитном поле с индукцией Тл. Сила тока в проводнике А. Найти угол  между направлением магнитной индукции и направлением тока, если на провод действует сила Н.

Со стороны поля на проводник с током действует сила Ампера:

Синус, равный , имеет угол в .
Ответ: .

 

Задача 5.

Проводник находится в равновесии в горизонтальном магнитном поле с индукцией мТл. Сила тока в проводнике А. Угол между направлением тока и вектором магнитной индукции  . Определить длину проводника, если его масса  кг.

Так как поле горизонтально, а проводник в нем «висит», то очевидно, что сила Ампера уравновесила силу тяжести:

Откуда

Ответ: 25,8 см.

Задача 6.

Проводник длиной м расположен перпендикулярно силовым линиям горизонтального магнитного поля с индукцией мТл. Какой должна быть сила тока в проводнике, чтобы он находился в равновесии в магнитном поле? Масса проводника кг.

Аналогично предыдущей задаче,

Откуда

Ответ: 10 А.

Физика, 9 кл. (Буховерцев Б.Б.)

Физика, 9 кл. (Буховерцев Б.Б.)

Буховцев Б.Б., Климонтович Ю.Л., Мякишев Г.Я. Физика. 9 класс. Учебник. — 6-е изд. — М.: Просвещение, 1982. — 272 с. В учебнике на современном уровне изложены фундаментальные вопросы школьной программы, представлены основные технические применения законов физики, рассмотрены методы решения задач. Книга адресована учащимся средних школ, слушателям и преподавателям подготовительных отделений вузов, а также читателям, занимающимся самообразованием и готовящимся к поступлению в вуз. Оглавление ТЕПЛОВЫЕ ЯВЛЕНИЯ. МОЛЕКУЛЯРНАЯ ФИЗИКА Глава I. ОСНОВЫ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ 1. ОСНОВНЫЕ ПОЛОЖЕНИЯ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ. РАЗМЕРЫ МОЛЕКУЛ 2. МАССА МОЛЕКУЛ. ПОСТОЯННАЯ АВОГАДРО 3. БРОУНОВСКОЕ ДВИЖЕНИЕ. 4. СИЛЫ ВЗАИМОДЕЙСТВИЯ МОЛЕКУЛ 5. СТРОЕНИЕ ГАЗООБРАЗНЫХ, ЖИДКИХ И ТВЕРДЫХ ТЕЛ 6. ИДЕАЛЬНЫЙ ГАЗ В МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ 7. ОСНОВНОЕ УРАВНЕНИЕ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ I Глава II. ТЕМПЕРАТУРА. ЭНЕРГИЯ ТЕПЛОВОГО ДВИЖЕНИЯ МОЛЕКУЛ 8. ТЕПЛОВОЕ РАВНОВЕСИЕ. ТЕМПЕРАТУРА 9. ИЗМЕРЕНИЕ ТЕМПЕРАТУРЫ 10. АБСОЛЮТНАЯ ТЕМПЕРАТУРА. ТЕМПЕРАТУРА — МЕРА СРЕДНЕЙ КИНЕТИЧЕСКОЙ ЭНЕРГИИ МОЛЕКУЛ 11. ИЗМЕРЕНИЕ СКОРОСТЕЙ МОЛЕКУЛ ГАЗА ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ II Глава III. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА. ГАЗОВЫЕ ЗАКОНЫ 12. 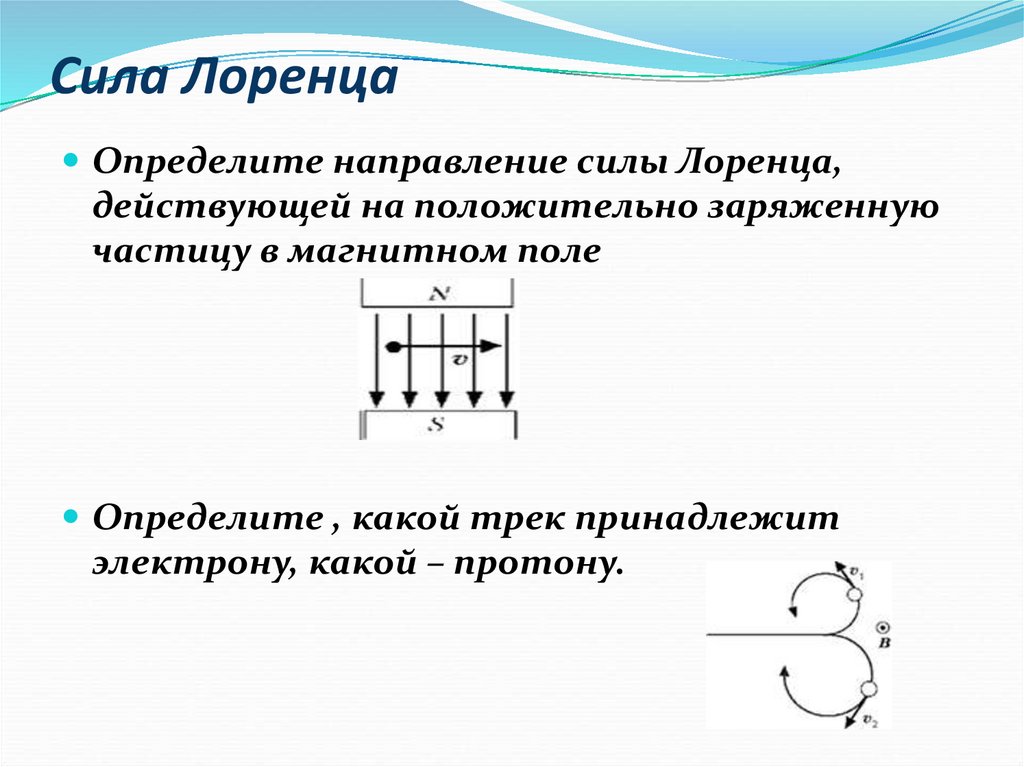УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА 13. ПРИМЕНЕНИЕ УРАВНЕНИЯ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА К РАЗЛИЧНЫМ ПРОЦЕССАМ 14. ПРИМЕНЕНИЕ ГАЗОВ В ТЕХНИКЕ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ III Глава IV. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ 16. РАБОТА В ТЕРМОДИНАМИКЕ 17. КОЛИЧЕСТВО ТЕПЛОТЫ 18. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ 19. ПРИМЕНЕНИЕ ПЕРВОГО ЗАКОНА ТЕРМОДИНАМИКИ К РАЗЛИЧНЫМ ПРОЦЕССАМ 20. НЕОБРАТИМОСТЬ ПРОЦЕССОВ В ПРИРОДЕ 21. ПРИНЦИПЫ ДЕЙСТВИЯ ТЕПЛОВЫХ ДВИГАТЕЛЕЙ 22. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ (КПД) ТЕПЛОВОГО ДВИГАТЕЛЯ. ТЕПЛОВЫЕ ДВИГАТЕЛИ И ОХРАНА ПРИРОДЫ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ IV Глава V. ВЗАИМНЫЕ ПРЕВРАЩЕНИЯ ЖИДКОСТЕЙ И ГАЗОВ 23. НАСЫЩЕННЫЙ ПАР 24. ЗАВИСИМОСТЬ ДАВЛЕНИЯ НАСЫЩЕННОГО ПАРА ОТ ТЕМПЕРАТУРЫ. КИПЕНИЕ. КРИТИЧЕСКАЯ ТЕМПЕРАТУРА 25. ВЛАЖНОСТЬ ВОЗДУХА ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ V Глава VI. ПОВЕРХНОСТНОЕ НАТЯЖЕНИЕ ЖИДКОСТЕЙ 27. СИЛА ПОВЕРХНОСТНОГО НАТЯЖЕНИЯ 28. КАПИЛЛЯРНЫЕ ЯВЛЕНИЯ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ VI Глава VII. 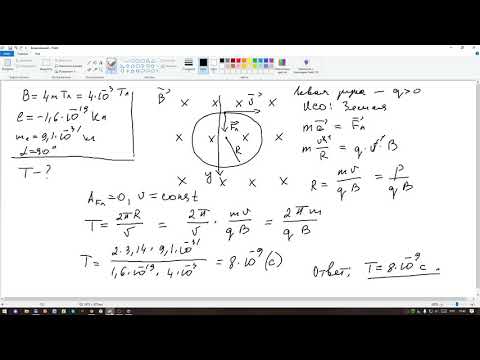ТВЕРДЫЕ ТЕЛА 29. КРИСТАЛЛИЧЕСКИЕ ТЕЛА 30. АМОРФНЫЕ ТЕЛА 31. ДЕФОРМАЦИЯ. ВИДЫ ДЕФОРМАЦИИ ТВЕРДЫХ ТЕЛ 32. МЕХАНИЧЕСКИЕ СВОЙСТВА ТВЕРДЫХ ТЕЛ. ДИАГРАММА РАСТЯЖЕНИЯ 33. ПЛАСТИЧНОСТЬ И ХРУПКОСТЬ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ VII ОСНОВЫ ЭЛЕКТРОДИНАМИКИ 34. ЧТО ТАКОЕ ЭЛЕКТРОДИНАМИКА? Глава VIII. ЭЛЕКТРОСТАТИКА 35. ЭЛЕКТРИЧЕСКИЙ ЗАРЯД И ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ 36. ЗАРЯЖЕННЫЕ ТЕЛА. ЭЛЕКТРИЗАЦИЯ ТЕЛ 37. ЗАКОН СОХРАНЕНИЯ ЭЛЕКТРИЧЕСКОГО ЗАРЯДА 38. ОСНОВНОЙ ЗАКОН ЭЛЕКТРОСТАТИКИ — ЗАКОН КУЛОНА 39. ЕДИНИЦА ЭЛЕКТРИЧЕСКОГО ЗАРЯДА ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ 40. БЛИЗКОДЕЙСТВИЕ И ДЕЙСТВИЕ НА РАССТОЯНИИ 41. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ 42. НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ. ПРИНЦИП СУПЕРПОЗИЦИИ ПОЛЕЙ 43. СИЛОВЫЕ ЛИНИИ ЭЛЕКТРИЧЕСКОГО ПОЛЯ 44. ПРОВОДНИКИ В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ 45. НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ РАВНОМЕРНО ЗАРЯЖЕННОГО ПРОВОДЯЩЕГО ШАРА И БЕСКОНЕЧНОЙ ПЛОСКОСТИ 46. ДИЭЛЕКТРИКИ В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ. ДВА ВИДА ДИЭЛЕКТРИКОВ 47. 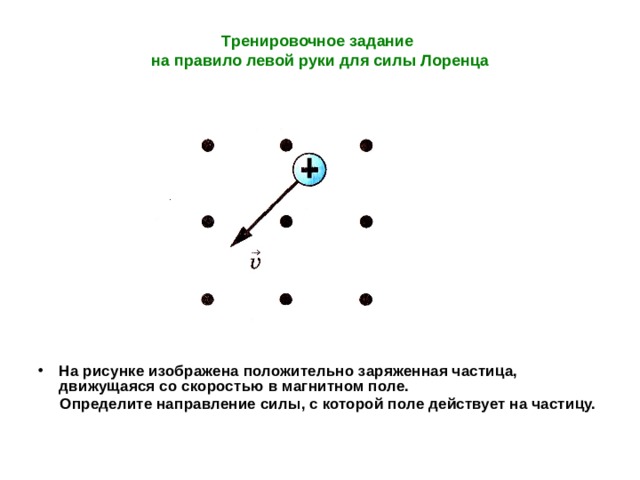ПОЛЯРИЗАЦИЯ ДИЭЛЕКТРИКОВ. ДИЭЛЕКТРИЧЕСКАЯ ПРОНИЦАЕМОСТЬ 48. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ЗАРЯЖЕННОГО ТЕЛА В ОДНОРОДНОМ ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ 49. ПОТЕНЦИАЛ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ И РАЗНОСТЬ ПОТЕНЦИАЛОВ 50. ПОТЕНЦИАЛ ЭЛЕКТРИЧЕСКОГО ПОЛЯ ТОЧЕЧНОГО ЗАРЯДА 51. СВЯЗЬ МЕЖДУ НАПРЯЖЕННОСТЬЮ ЭЛЕКТРИЧЕСКОГО ПОЛЯ И РАЗНОСТЬЮ ПОТЕНЦИАЛОВ. ЭКВИПОТЕНЦИАЛЬНЫЕ ПОВЕРХНОСТИ 52. ИЗМЕРЕНИЕ РАЗНОСТИ ПОТЕНЦИАЛОВ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ 53. ЭЛЕКТРОЕМКОСТЬ. ЕДИНИЦЫ ЭЛЕКТРОЕМКОСТИ 54. КОНДЕНСАТОРЫ. ЭЛЕКТРОЕМКОСТЬ ПЛОСКОГО КОНДЕНСАТОРА 55. ЭНЕРГИЯ ЗАРЯЖЕННОГО КОНДЕНСАТОРА. ПРИМЕНЕНИЯ КОНДЕНСАТОРОВ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ X Глава IX. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК 56. ЭЛЕКТРИЧЕСКИЙ ТОК. СИЛА ТОКА 57. УСЛОВИЯ, НЕОБХОДИМЫЕ ДЛЯ СУЩЕСТВОВАНИЯ ЭЛЕКТРИЧЕСКОГО ТОКА 58. ЗАКОН ОМА ДЛЯ УЧАСТКА ЦЕПИ. СОПРОТИВЛЕНИЕ 59. ЗАВИСИМОСТЬ СОПРОТИВЛЕНИЯ ПРОВОДНИКА ОТ ТЕМПЕРАТУРЫ 60. СВЕРХПРОВОДИМОСТЬ 61. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ. ПОСЛЕДОВАТЕЛЬНОЕ И ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЯ ПРОВОДНИКОВ 62. ИЗМЕРЕНИЕ СИЛЫ ТОКА И НАПРЯЖЕНИЯ 63. РАБОТА И МОЩНОСТЬ ПОСТОЯННОГО ТОКА ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ 64. ЭЛЕКТРОДВИЖУЩАЯ СИЛА 65. ЗАКОН ОМА ДЛЯ ЗАМКНУТОЙ ЦЕПИ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ IX Глава X. ЭЛЕКТРИЧЕСКИЙ ТОК В РАЗЛИЧНЫХ СРЕДАХ 66. ЭЛЕКТРИЧЕСКАЯ ПРОВОДИМОСТЬ РАЗЛИЧНЫХ ВЕЩЕСТВ 67. ЭЛЕКТРОННАЯ ПРОВОДИМОСТЬ МЕТАЛЛОВ 68. ЭЛЕКТРИЧЕСКИЙ ТОК В ЖИДКОСТЯХ 69. ЗАКОН ЭЛЕКТРОЛИЗА 70. ЭЛЕКТРИЧЕСКИЙ ТОК В ГАЗАХ 71. НЕСАМОСТОЯТЕЛЬНЫЙ И САМОСТОЯТЕЛЬНЫЙ РАЗРЯДЫ 72. РАЗЛИЧНЫЕ ТИПЫ САМОСТОЯТЕЛЬНОГО РАЗРЯДА И ИХ ТЕХНИЧЕСКИЕ ПРИМЕНЕНИЯ 73. ПЛАЗМА 74. ЭЛЕКТРИЧЕСКИЙ ТОК В ВАКУУМЕ 75. ДВУХЭЛЕКТРОДНАЯ ЭЛЕКТРОННАЯ ЛАМПА-ДИОД 76. ЭЛЕКТРОННЫЕ ПУЧКИ. ЭЛЕКТРОННОЛУЧЕВАЯ ТРУБКА 77. ЭЛЕКТРИЧЕСКИЙ ТОК В ПОЛУПРОВОДНИКАХ 78. ЭЛЕКТРИЧЕСКАЯ ПРОВОДИМОСТЬ ПОЛУПРОВОДНИКОВ ПРИ НАЛИЧИИ ПРИМЕСЕЙ 79. ЭЛЕКТРИЧЕСКИЙ ТОК ЧЕРЕЗ КОНТАКТ ПОЛУПРОВОДНИКОВ p- И n- ТИПОВ 80. ПОЛУПРОВОДНИКОВЫЙ ДИОД 81. ТРАНЗИСТОР 82. ТЕРМИСТОРЫ И ФОТОРЕЗИСТОРЫ ПРИМЕР РЕШЕНИЯ ЗАДАЧИ КРАТКИЕ ИТОГИ ГЛАВЫ X Глава XI. МАГНИТНОЕ ПОЛЕ 83. ВЗАИМОДЕЙСТВИЕ ТОКОВ. МАГНИТНОЕ ПОЛЕ 84. ВЕКТОР МАГНИТНОЙ ИНДУКЦИИ 85. ЛИНИИ МАГНИТНОЙ ИНДУКЦИИ 86. ЭЛЕКТРОИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ 87. МОДУЛЬ ВЕКТОРА МАГНИТНОЙ ИНДУКЦИИ. МАГНИТНЫЙ ПОТОК 88. ЗАКОН АМПЕРА 89. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ДВИЖУЩИЙСЯ ЗАРЯД. СИЛА ЛОРЕНЦА 90. МАГНИТНЫЕ СВОЙСТВА ВЕЩЕСТВА ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ XI Глава XII. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ 91. ОТКРЫТИЕ ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ 92. НАПРАВЛЕНИЕ ИНДУКЦИОННОГО ТОКА. ПРАВИЛО ЛЕНЦА 93. ЗАКОН ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ 94. ВИХРЕВОЕ ЭЛЕКТРИЧЕСКОЕ ПОЛЕ 95. ЭДС ИНДУКЦИИ В ДВИЖУЩИХСЯ ПРОВОДНИКАХ 96. САМОИНДУКЦИЯ. ИНДУКТИВНОСТЬ 97. ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ ТОКА 98. ОСНОВНЫЕ ЗАКОНЫ ЭЛЕКТРОДИНАМИКИ И ИХ ТЕХНИЧЕСКОЕ ПРИМЕНЕНИЕ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ XII ЗАКЛЮЧЕНИЕ ЛАБОРАТОРНЫЕ РАБОТЫ ОТВЕТЫ К УПРАЖНЕНИЯМ

Применение и примеры магнетизма

Страница 6

Этот текст предназначен для обсуждения в классе. Это еще не все, что нужно знать о равномерном круговом движении. Это подготовка к уроку. Более подробные примечания и примеры приведены в конспектах занятий, презентациях и демонстрациях. См. ссылки ниже.

Нажмите, чтобы получить ответы на вопросы, связанные с этим чтением

На этой странице приведены примеры действия закона Ампера и магнитной силы, связанной с силой Лоренца. Примеры 7, 8, 9 и 10 идут вместе, потому что они основаны друг на друге. Чтобы получить максимальную отдачу от этих примеров, постарайтесь решить каждый из них, прежде чем выбирать решение для видео. При решении задач вернитесь к предыдущим страницам, чтобы увидеть, сможете ли вы определить используемую концепцию и как ее использовать. Если вы не сделаете этого усилия, вы также не поймете материал.

Пример 7 Вопрос Ответить Решение для видео Это видео можно найти на YouTube по адресу https://youtu.be/b8DKRixGSw0

Пример 8 Вопрос Ответить Решение для видео Это видео можно найти на YouTube по адресу https://youtu. be/cietVmyLva8

Пример 9 Вопрос Решение для видео Это видео можно найти на YouTube по адресу https://youtu.be/tWpJxqIwM7c

Пример 10 Вопрос Ответить Решение для видео Это видео можно найти на YouTube по адресу https://youtu. be/GlZGcob9bTo

Предыдущий пример очень важен. Если дает возможность посмотреть на силу между двумя токоведущими проводами. Обратите внимание, что уравнение вычисляет не силу напрямую, а силу на единицу длины. Его единицы: N / m . Чтобы определить, притягиваются или отталкиваются провода с током, используйте закон Ампера (правило замкнутой правой руки). Если b-поля между токами указывают в одном направлении, то провода отталкиваются. Если b-поля между проводами направлены в противоположные стороны, то провода притягиваются. См. пример ниже.

Пример 11 Вопрос Решение для видео Это видео можно найти на YouTube по адресу https://youtu.be/aDq3uha6DSE

Пример 12 Вопрос Решение для видео Это видео можно найти на YouTube по адресу https://youtu.be/gM4WEdLjijg

электромагнетизм — закон силы Лоренца в ньютоновской теории относительности

Я действительно не знаю точную историческую цепь событий, поэтому могу даже привести результат, появившийся после появления СТО. На самом деле, я нашел два разных способа объяснить это, которые я дал здесь. Первый ИМХО классический, но то, что закон Кулона только для статических случаев, может быть неверным в классической физике. Хотя я в этом сомневаюсь; Максвелл знал связь электромагнитных полей с электромагнитными волнами. Второе объяснение имеет смысл с точки зрения чистой классической точки зрения до Максвелла. Они противоречат друг другу, хотя оба объясняют это. Так что я даю оба здесь. Комментарии оцениваются по тому, какой из них более правильный.

Я имею в виду электрическое поле как E и магнитное поле как B здесь, со стандартными обозначениями.

Ответ #1

В классической механике эту проблему можно решить, изменив определения электрического и магнитного полей. Это одно и то же. Движение со скоростью превращает поле E в поле B или наоборот. Кроме того, закон Кулона применим только к электростатическим ситуациям. Когда частица движется, поле Е другое.

В конце концов, в инерциальных системах отсчета должна быть одинакова только сила. Если Е стало В при изменении скорости, формулы будут такими, что сила останется прежней. Наблюдатель, путешествующий вместе с движущимися частицами, увидит E, а не B, тогда как наблюдатель в «покое» (в основном движущийся относительно частиц) увидит поле B и меньшее поле E. Но оба наблюдателя почувствуют одинаковую силу и увидят, что частицы притягиваются/отталкиваются на одинаковую величину.

Одним из способов взглянуть на это является тот факт, что электромагнитные поля передаются/опосредованы электромагнитным излучением. Таким образом, движение со скоростью изменяет поведение волн в вашем кадре.

На самом деле, у меня была эта путаница несколько лет назад (для двух параллельных частиц). Я предполагал электростатическую силу в обоих случаях и получил некоторые странные результаты. Зная, что происхождение СТО возникло где-то в электромагнетизме, я предположил неизвестное сокращение длины и решил его. Удивительно, но в моих уравнениях появился фактор Лоренца (поскольку $\mu_0\epsilon_0=1/c^2$ за исключением того, что сокращение длины происходило в перпендикулярном направлении.