Активная мощность. Единица измерения — ватт (w, Вт).

Среднее за период T значение мгновенной мощности называется активной мощностью: В цепях однофазного синусоидального токагдеU и I — среднеквадратичные значения напряжения и тока, φ — угол сдвига фаз между ними.

Реактивная мощность. Единица измерения — вольт-ампер реактивный (var, вар)

Реактивная мощность — величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи синусоидального переменного тока, равна произведению среднеквадратичных значений напряжения U и тока I, умноженному на синус угла сдвига фаз φ между ними: 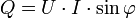(если ток отстаёт от напряжения, сдвиг фаз считается положительным, если опережает — отрицательным). Реактивная мощность связана с полной мощностью

S и активной мощностью Р соотношением: .

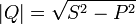17. Как определяется коэффициент мощности электрической цепи?

Коэффициент мощности — безразмерная физическая величина, характеризующая потребителя переменного электрического тока с точки зрения наличия в нагрузке реактивной составляющей. Коэффициент мощности показывает, насколько сдвигается по фазе переменный ток, протекающий через нагрузку, относительно приложенного к ней напряжения.

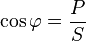
26

Активная, реактивная, полная мощность и коэффициент мощности

Мощностные характеристики нагрузки можно точно задать одним единственным параметром (активная мощность в Вт) только для случая постоянного тока, так как в цепи постоянного тока существует единственный тип сопротивления – активное сопротивление.

Мощностные характеристики нагрузки для случая переменного тока невозможно точно задать одним единственным параметром, так как в цепи переменного тока существует два разных типа сопротивления – активное и реактивное. Поэтому только два параметра: активная мощность (это полезная мощность, отбираемая нагрузкой, в том числе и ИБП, из электросети и преобразуемая в энергию любого иного вида (механическую, тепловую, электрическую, электромагнитную и др.) и реактивная мощность ( это мощность или поток энергии, циркулирующий через реактивное сопротивление электрической цепи (емкостное или индуктивное).

Рассеяния энергии на реактивных элементах не происходит, так как полученная ими энергия от источника и энергия и возвращенная обратно в сеть в течение периода эквивалентны. Считается, что в большинстве случаев реактивная энергия (мощность), циркулирующая в электрической цепи, является паразитной и приводит к нежелательному разогреву проводников, а также к перегреву и ухудшению режимов работы прочих устройств сети, как генерирующих электричество, так и его потребителей.) точно характеризуют нагрузку.

Принцип действия активного и реактивного сопротивлений совершенно различный. Активное сопротивление – необратимо преобразует электрическую энергию в другие виды энергии (тепловую, световую и т.д.) – примеры: лампа накаливания, электронагреватель (параграф 39, Физика 11 класс В.А. Касьянов М.: Дрофа, 2007). Реактивное сопротивление – попеременно накапливает энергию затем выдаёт её обратно в сеть – примеры: конденсатор, катушка индуктивности (параграф 40,41, Физика 11 класс В.А. Касьянов М.: Дрофа, 2007).

Дальше в любом учебнике по электротехнике Вы можете прочитать, что активная мощность (рассеиваемая на активном сопротивлении) измеряется в ваттах, а реактивная мощность (циркулирующая через реактивное сопротивление) измеряется в варах; так же для характеристики мощности нагрузки используют ещё два параметра: полную мощность и коэффициент мощности.

Все эти 4 параметра:

1. Активная мощность: обозначение P, единица измерения: Ватт
2. Реактивная мощность: обозначение Q, единица измерения: ВАр (Вольт Ампер реактивный)
3. Полная мощность:обозначение S, единица измерения: ВА (Вольт Ампер)
4. Коэффициент мощности: обозначение k или cosФ, единица измерения: безразмерная величина

Эти параметры связаны соотношениями:  S*S=P*P+Q*Q,   cosФ=k=P/S
Также cosФ называется коэффициентом мощности (Power Factor – PF)

Поэтому в электротехнике для характеристики мощности задаются любые два из этих параметров так как остальные могут быть найдены из этих двух.

То же самое и с источниками питания. Их мощность (нагрузочная способность) характеризуется одним параметром для источников питания постоянного тока – активная мощность (Вт), и двумя параметрами для ист. питания переменного тока. Обычно этими двумя параметрами являются полная мощность (ВА) и активная (Вт). См. например параметры ДГУ и ИБП.

Большинство офисной и бытовой техники, активные (реактивное сопротивление отсутствует или мало), поэтому их мощность указывается в Ваттах. В этом случае при расчёте нагрузки используется значение мощности ИБП в Ваттах. Если нагрузкой являются компьютеры с блоками питания (БП) без коррекции входного коэффициента мощности (APFC), лазерный принтер, холодильник, кондиционер, электромотор (например погружной насос или мотор в составе станка), люминисцентные балластные лампы и др. – при расчёте используются все вых. данные ибп: кВА, кВт, перегрузочные характеристики и др.

Нагрузочная способность ИБП и ДГУ нормирована на стандартную промышленную нагрузку (коэффициент мощности 0.8 с индуктивным характером). Например, ИБП 100 кВА / 80 кВт. Это означает, что устройство может питать активную нагрузку максимальной мощности 80 кВт, или смешанную (активно-реактивную) нагрузку максимальной мощности 100 кВА с индуктивным коэффициентом мощности 0.8. В стабилизаторах напряжения дело обстоит иначе.

Для стабилизатора напряжения коэффициент мощности нагрузки безразличен. Например, стабилизатор напряжения 100 кВА. Это означает, что устройство может питать активную нагрузку максимальной мощности 100 кВт, или любую другую (чисто активную, чисто реактивную, смешанную) мощностью 100 кВА или 100 кВАр с любым коэффициентом мощности емкостного или индуктивного характера. Обратите внимание, что это справедливо для линейной нагрузки (без высших гармоник тока). При больших гармонических искажениях тока нагрузки (высокий КНИ) выходная мощность стабилизатора снижается.

В чем физический смысл активной, реактивной и полной мощностей? Назовите единицы измерения?

⇐ ПредыдущаяСтр 4 из 4

Активная мощность потребляется в активных сопротивлениях, и, в конечном итоге, за счет нее выполняется механическая работа или происходит нагревание резисторов. Реактивная мощность-эта та мощность, которая попросту «болтается в проводах». Она не потребляется активно цепью, но системы передачи оказываются ею загруженными.

Пусть приемник электро­энергии присоединен к источнику синусоидального напряжения u(t) = 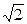Usin(ωt) и потребляет синусоидальный ток i(t) = 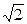I sin (ωt -φ), сдви­нутый по фазе относительно напряжения на угол φ. U и I – действующие значения. Значение мгновенной мощности на зажимах приемника определяется выражением

p(t) = u(t) ∙i(t) = 2UI sin(ωt) sin (ωt -φ) = UI cos φ — UI cos (2ωt -φ)

(5.1)

и является суммой двух величин, одна из которых постоянна во времени, а другая пульсирует с двойной частотой.

Среднее значение p(t) за период Т называется активной мощностью и полностью определяется первым слагаемым уравнения (5.1):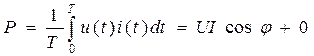

Активная мощность ха­рактеризует энергию, расходуемую необратимо источником в единицу времени на производство полезной работы потребителем. Активная энергия, потребляемая электроприёмниками, преобразуется в другие виды энергии: механическую, тепловую, энергию сжатого воздуха и

газа и т. п.

Среднее значение от второго слагаемого мгновенной мощности (1.1) (пульсирует с двойной частотой) за время Т равно нулю, т. е. на ее создание не требуется каких-либо материальных затрат и поэтому она не может совершать полезной ра­боты. Однако ее присутствие указывает, что между источником и приемником происходит обратимый процесс обмена энергией. Это возможно, если имеются элементы, способные накапливать и отдавать электромагнитную энергию – емкость и индуктивность. Эта составляющая характеризует реактивную мощность.

Полную мощность на зажимах приемника в комп­лексной форме можно представить следующим образом:

.

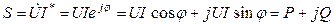(5.2)

Единица измерения полной мощности S = UI – ВА.

Реактивная мощность – величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями (обменом) энергии между источником и приемником. Для синусоидального тока она равна произведению действующих значений тока I и напряжения U на синус угла сдвига фаз между ними:

Q = UI sinφ. Единица измерения – В∙Ар.

Реактивная мощность не связана с полезной работой ЭП и расходуется только на создание переменных электромагнитных полей в электродвигателях, трансформаторах, аппаратах, линиях и т. д.

Для реактивной мощности приняты такие понятия, как генерация, потребление, передача, потери, баланс. Считается, что если ток отстает по фазе от напряжения (индуктивный характер нагрузки), то реактивная мощ­ность потребляется и имеет положительный знак, а если ток опережает напряжение (емкостный характер нагрузки), то реактивная мощность ге­нерируется и имеет отрицательное значение.

Основными потребителями реактивной мощности на промышленных предприятиях являются асинхронные двигатели (60–65 % общего потреб­ления), трансформаторы (20–25 %), вентильные преобразователи, реакторы, воздушные электрические сети и прочие приемники (10 %).

Передача реактивной мощности загружает электрические сети и установленное в ней оборудование, уменьшая их пропускную способность. Реактивная мощность генерируется синхронными генераторами электростанций, синхронными компенса­торами, синхронными двигателями (регулирование током возбуждения), батареями конденсаторов (БК) и линиями электропередачи.

Реактивная мощность, вырабатываемая емкостью сетей, имеет следующий порядок величин: воздушная линия 20 кВ генерирует 1 кВ∙Ар на 1 км трехфазной линии; подземный кабель 20 кВ – 20 кВ∙Ар/км; воздушная линия 220 кВ – 150 кВ∙Ар/км; подземный кабель 220 кВ – 3 МВ∙Ар/км.

Коэффициент мощности и коэффициент реактивной мощности.Векторное представление величин, характеризующих состояние сети, приводит к представлению реактивной мощности Q вектором, перпендикулярным вектору активной мощности Р (рис. 5.2 ). Их векторная сумма дает полную мощность S.

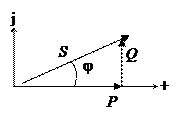
Рис. 5.1. Треугольник мощностей

Согласно рис. 5.1 и (5.2) следует, что S² = Р² + Q²; tgφ = Q/P; cosφ = P/S.

Основным нормативным показателем, характе­ризующим реактивную мощность, ранее был коэффициент мощности cosφ. На вводах, питающих промышленное предприятие, средневзвешенное значение этого коэффициента должно было находиться в пределах 0,92–0,95. Однако выбор соотношения P/S в качестве нормативного не дает четкого представления о динамике изменения реального значения реактивной мощности. Например, при изменении коэффициента мощности от 0,95 до 0,94 реактивная мощность изменяется на 10 %, а при изменении этого же коэффициента от 0,99 до 0,98 приращение реактивной мощности составляет уже 42 %. При расчетах удобнее оперировать соотношением tgφ = Q/P, которое называют коэффициентом реактивной мощности.

Предприятиям, у которых присоединенная мощность более 150 кВт (за исключением «бытовых» потребителей), определены предельные значения коэффициента реактивной мощности, потребляемой в часы больших суточных нагрузок электрической сети – с 7 до 23 часов (Приказ Министерства промышленности и энергетики РФ от 22.02.2007 г. № 49 «О порядке расчета значений соотношения потребления активной и реактивной мощности для отдельных энергопринимающих устройств потребителей электрической энергии, применяемых для определения обязательств сторон в договорах об оказании услуг по передаче электрической энергии»).

Контрольные вопросы лаб. работы № 2

Законы Кирхгофа.

Для формулировки законов Кирхгофа, в электрической цепи выделяются узлы — точки соединения трёх и более проводников и контуры — замкнутые пути из проводников. При этом каждый проводник может входить в несколько контуров.

В этом случае законы формулируются следующим образом.

Первый закон гласит, что суммарный ток, втекающий в любой узел цепи, равен нулю. Иными словами, сколько тока втекает в узел, столько из него и вытекает. Данный закон следует из закона сохранения заряда. Если цепь содержит p узлов, то она описывается p − 1 уравнениями токов.

Второй закон гласит, что суммарное напряжение по любому замкнутому контуру цепи, равно сумме ЭДС, которые в нём находятся. Если в контуре нет ЭДС, то суммарное напряжение равно нулю. Иными словами, при обходе цепи по контуру, потенциал, изменяясь, возвращается к исходному значению. Если цепь содержит m ветвей, то она описывается m − (p − 1) уравнениями напряжений.

Законы Кирхгофа –правила, которые показывают, как соотносятся токи и напряжения в электрических цепях. Эти правила были сформулированы Густавом Кирхгофом в 1845 году. В литературе часто называют законами Кирхгофа, но это не верно, так как они не являются законами природы, а были выведены из третьего уравнения Максвелла при неизменном магнитном поле. Но все же, первое более привычное для них название, поэтому и мы будет их называть, как это принято в литературе – законы Кирхгофа.

Первый закон Кирхгофа – сумма токов сходящихся в узле равна нулю.

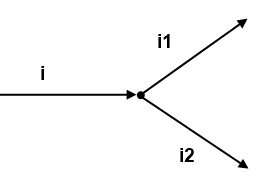
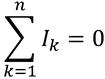
Давайте разбираться. Узел это точка, соединяющая ветви. Ветвью называется участок цепи между узлами. На рисунке видно, что ток i входит в узел, а из узла выходят токи i₁ и i₂. Составляем выражение по первому закона Кирхгофа, учитывая, что токи, входящие в узел имеют знак плюс, а токи, исходящие из узла имеют знак минус i-i₁-i₂=0. Ток i как бы растекается на два тока поменьше и равен сумме токов i₁ и i₂ i=i₁+i₂. Но если бы, например, ток i₂ входил в узел, тогда бы ток I определялся как i=i₁-i₂. Важно учитывать знаки при составлении уравнения.

Первый закон Кирхгофа это следствие закона сохранения электричества: заряд, приходящий к узлу за некоторый промежуток времени, равен заряду, уходящему за этот же интервал времени от узла, т.е. электрический заряд в узле не накапливается и не исчезает.

Второй закон Кирхгофа – алгебраическая сумма ЭДС, действующая в замкнутом контуре, равна алгебраической сумме падений напряжения в этом контуре.

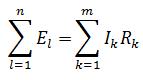
Напряжение выражено как произведение тока на сопротивление (по закону Ома).

 

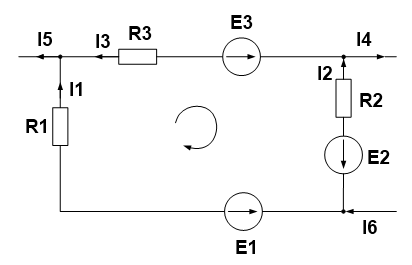
В этом законе тоже существуют свои правила по применению. Для начала нужно задать стрелкой направление обхода контура. Затем просуммировать ЭДС и напряжения соответственно, беря со знаком плюс, если величина совпадает с направлением обхода и минус, если не совпадает. Составим уравнение по второму закону Кирхгофа, для нашей схемы. Смотрим на нашу стрелку, E₂ и Е₃ совпадают с ней по направлению, значит знак плюс, а Е₁ направлено в противоположную сторону, значит знак минус. Теперь смотрим на напряжения, ток I₁ совпадает по направлению со стрелкой, а токи I₂ и I₃ направлены противоположно. Следовательно:

-E₁+E₂+E₃=I₁R₁-I₂R₂-I₃R₃

На основании законов Кирхгофа составлены методы анализа цепей переменного синусоидального тока. Метод контурных токов – метод основанный на применении второго закона Кирхгофа и метод узловых потенциалов основанный на применении первого закона Кирхгофа.

Рекомендуемые страницы:

Обсуждение:Коэффициент мощности — Википедия

В нынешней редакции говорится только об узком значении термина «коэффициент мощности» — для случая, когда нагрузка имеет только активно-реактивный характер. Нужно расширить/переработать текст, поскольку коэффициент мощности в общем случае определяется иначе и характеризует нагрузку не только (не обязательно) с точки зрения наличия реактивной составляющей! 37.192.247.194 04:29, 3 сентября 2015 (UTC)

С каких это пор нелинейные искажения и несинусоидальность имеют отношение к коэффициенту мощности? —8O8AH 14:25, 6 февраля 2010 (UTC)

«В качестве единицы измерения полной мощности принято использовать вольт-ампер (В∙А), а не ватт (Вт), так как реактивная мощность, входящая в состав полной мощности, не производит никакой работы.»

Эта фраза не очень хорошая по следующим причинам:

1. Про то, что работу производит активная мощность, уже было сказано, повторять не нужно.

2. В состав полной мощности может не входить реактивная мощность (т.е. индуктивная или ёмкостная составляющие). Полная мощность может возрастать, например, из-за импульсного характера чисто активной нагрузки. Хотя это в значительной степени вопрос терминологии, но лучше более строго относиться к терминам.

3. Самое главное. Единица измерения физической величины определяется исключительно её размерностью, с которой она участвует в формулах. Если это мощность, то не важно, полезная ли это мощность или расходуемая впустую, активная или кажущаяся — она имеет размерность мощности, т.е. измеряется в ваттах. Далее, Вт = Дж/с = ВА = В^2/Ом и т.д. — это всё эквивалентные единицы измерения. Не нужно смешивать понятия физической величины и её единицы измерения. Разные физические величины (например, полная и активная мощности) могут иметь одинаковые единицы измерения. Использование вольт-ампера вместо эквивалентного этой единицы ватта сделано исключительно по соображениям удобства — чтобы не нужно было каждый раз указывать, о какой мощности идёт речь. Если бы это было не так, то отношение активной и полной мощностей не являлось бы безразмерным косинусом фи.

Поэтому, прошу прощения, но эту фразу я исправил, хотя постарался это сделать более демократично.

78.40.81.9 18:17, 9 февраля 2010 (UTC)

Нелинейные искажения связаны с коэффициентом мощности. Собственно коэффициент мощности характеризует нелинейные искажения потребляемого нагрузкой тока — чем коэффициент мощности меньше, тем меньше форма тока повторяет исходную синусоиду, форму которой имеет напряжение. Так вот, если нелинейная нагрузка в сети будет достаточно большой, то вслед за током появятся искажения и в форме напряжения — напряжение будет нелинейно «просаживаться».

78.40.81.9 18:16, 9 февраля 2010 (UTC)

Вынужден также не согласиться с концовкой фразы «Коэффициент мощности характеризует приёмник электроэнергии переменного тока, а именно — степень реактивной составляющей сопротивления нагрузки.»

Реактивная составляющая даёт только один из видов нелинейных искажений (фазовый сдвиг). Однако коэффициент мощности реагирует на любую нелинейность нагрузки (нелинейность ВАХ), когда ток меняется непропорционально приложенному напряжению. Например, нетрудно посчитать, что коэффициент мощности нагрузки, которая представляет собой последовательно соединённые диод и обычный резистор, составляет около 0,71. Здесь нет никакой реактивной нагрузки, просто нелинейная ВАХ диода приводит к уменьшению коэффициента мощности. Фразу исправил.

78.40.81.9 18:16, 9 февраля 2010 (UTC)

Добавьте про синхронные компенсаторы.

Компенсация реактивной мощности в бытовом секторе электрических сетей общего пользования[править код]

В последние годы нестабильность напряжения крупных электроэнергетических систем мира, связанная с ростом потребляемой мощности потребителей разных секторов экономики, привела к ряду дорогостоящих отключений подачи электроэнергии. Особенно выделяется среди них потребители электрической энергии, которые используют её в основном для бытовых нужд. Это административные здания и сооружения, учреждения и организации, в том числе бюджетные и общественные, а также население и назовем их бытовыми потребителями. Основной причиной является рост электрической мощности у данных потребителей, вызванный с освоением ими электробытовых приборов которыми насыщен рынок республики. Применение новых технологий, которые экономичны и технологически эффективны, которые улучшают жизнь людей, создают приятный колорит в быту, иногда отрицательно сказывается на качество электрической энергии и данный рост электрической мощности, также негативно сказывается на нормальное функционирование распределительных сетей, проектированные в 70-80г.г. и не рассчитанные на текущую мощность бытовых потребителей, которая продолжает стабильно расти. 213.230.99.77 14:51, 13 января 2016 (UTC) Существует старое понятие, можно так сказать закон, в среде «Бывалых» специалистов электроэнергетической системы, что «Бытовой (население) потребитель не потребляет реактивный ток». Но, это было 70-80 годы, когда у бытового потребителя всего было около 3 или 4 единиц электроприборов. На сегодняшний день у этого же потребителя количество электроприборов существенно увеличился и за счет количества увеличился и общая мощность электроприборов, пусть если они даже маломощные, но они потребляют реактивный ток, чем ранее. Ток, который негативно влияет на качество электрической энергии в общих сетях и на пропускной способности системы сетей (0,4кВ, 6-10кВ). Это микроволновые печи, кондиционеры, холодильники, телевизоры которые в режиме ожидания тоже работают, кипятильники, забытые зарядные устройства на розетках, компьютеры и т.д.. Практически все аварии и отключения подачи электроэнергии были обусловлены нарушением энергетического баланса, как по активной, так и реактивной мощности, в большей мере ответственной за стабильность напряжения на разделе сетей общего пользования и распределительных сетей потребителей электроэнергии. Именно повышенная плотность перетоко по реактивной мощности в распределительных сетях вызывает наиболее негативное в плане последствий понижение напряжения во время тяжелых условий нагрузки, что зачастую приводит к коллапсу напряжения — аномально низкому или нулевому сетевому напряжению. В этой связи исключительно важным становится проведение мероприятий по компенсации реактивной мощности у самих потребителей электроэнергии, а также у бытовых потребителей, подключенных к низковольтным сетям предприятий территориальных электрических сетей, что позволит сохранить общий баланс мощности в системе и обеспечить устойчивость сетевого напряжения. В результате реактивная мощность емкости нивелирует реактивную мощность намагничивания и сеть разгружается от перетоков реактивной мощности, что повышает ее пропускную способность и стабилизирует сетевое напряжение. Также данный метод регулирования способствует к снижению технологического расхода электрической энергии при её транспортировке. На сегодняшний день особое внимание уделяется выше приведенным вопросам и совокупно на проблемы по сокращению расходов топливно-энергетических ресурсов, путем внедрение современных энергосберегающих технологий и снижение технологического расхода электрической энергии. По статистике самые разветвлённые сети энергоснабжающих организаций являются сети напряжением 0,4кВ, 6-10кВ, доля которых от общего объема составляют более 80% и от них потребляют электрическую энергию самое большое количество потребителей. Индивидуальный их мощность очень мала, но в целом они и являются самым энергоемким потребителем. Особенно в часы пиковой нагрузки (утро и вечер) энергосистемы.