Колебательный контур — Википедия

Колебательный контур — электрическая цепь, содержащая катушку индуктивности, конденсатор и источник электрической энергии. При последовательном соединении элементов цепи колебательный контур называется последовательным, при параллельном — параллельным^[1].

Колебательный контур — простейшая система, в которой могут происходить свободные электромагнитные колебания.

Резонансная частота контура определяется так называемой формулой Томсона:

f0=12πLC.{\displaystyle f_{0}={1 \over 2\pi {\sqrt {LC}}}.}

Пусть конденсатор ёмкостью C заряжен до напряжения U0{\displaystyle U_{0}}. Энергия, запасённая в конденсаторе, составляет

EC=CU022.{\displaystyle E_{C}={\frac {CU_{0}^{2}}{2}}.}

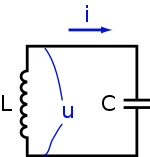Параллельный колебательный контур Осциллограмма LC-контура во время замыкания заряженного конденсатора на катушку индуктивности.
С — 240 нФ (заряженный)
L — 360 нГн
F₀ ≈ 542 кГц

При соединении конденсатора с катушкой индуктивности в цепи потечёт ток I{\displaystyle I}, что вызовет в катушке электродвижущую силу (ЭДС) самоиндукции, направленную на уменьшение тока в цепи. Ток, вызванный этой ЭДС (при отсутствии потерь в индуктивности), в начальный момент будет равен току разряда конденсатора, то есть результирующий ток будет равен нулю. Магнитная энергия катушки в этот (начальный) момент равна нулю.

Затем результирующий ток в цепи будет возрастать, а энергия из конденсатора будет переходить в катушку до полного разряда конденсатора. В этот момент электрическая энергия конденсатора EC=0{\displaystyle E_{C}=0}. Магнитная же энергия, сосредоточенная в катушке, напротив, максимальна и равна

EL=LI022,{\displaystyle E_{L}={\frac {LI_{0}^{2}}{2}},}

где L{\displaystyle L} — индуктивность катушки, I0{\displaystyle I_{0}} — максимальное значение тока.

После этого начнётся перезарядка конденсатора, то есть зарядка конденсатора напряжением другой полярности. Перезарядка будет проходить до тех пор, пока магнитная энергия катушки не перейдёт в электрическую энергию конденсатора. Конденсатор в этом случае снова будет заряжен до напряжения −U0{\displaystyle -U_{0}}.

В результате в цепи возникают колебания, длительность которых будет обратно пропорциональна потерям энергии в контуре.

Описанные выше процессы в параллельном колебательном контуре называются резонанс токов, что означает, что через индуктивность и ёмкость протекают токи больше тока, проходящего через весь контур, причём эти токи больше в определённое число раз, которое называется добротностью. Эти большие токи не покидают пределов контура, так как они противофазны и сами себя компенсируют. Стоит также заметить, что сопротивление параллельного колебательного контура на резонансной частоте стремится к бесконечности (в отличие от последовательного колебательного контура, сопротивление которого на резонансной частоте стремится к нулю), а это делает его незаменимым фильтром.

Стоит заметить, что помимо простого колебательного контура, есть ещё колебательные контуры первого, второго и третьего рода, что учитывают потери и имеют другие особенности.

Напряжение на идеальной катушке индуктивности при изменении протекающего тока:

uL=LdiLdt.{\displaystyle u_{L}=L{\frac {di_{L}}{dt}}.}

Ток, протекающий через идеальный конденсатор, при изменении напряжения на нём:

iC=CduCdt.{\displaystyle i_{C}=C{\frac {du_{C}}{dt}}.}

Из правил Кирхгофа, для цепи, составленной из параллельно соединённых конденсатора и катушки, следует:

uL+uC=0,{\displaystyle u_{L}+u_{C}=0,} — для напряжений,

и

iC=iL{\displaystyle i_{C}=i_{L}} — для токов.

Совместно решая систему дифференциальных уравнений (дифференцируя одно из уравнений и подставляя результат в другое), получаем:

d2q(t)dt2+1LCq(t)=0.{\displaystyle {\frac {d^{2}q(t)}{dt^{2}}}+{\frac {1}{LC}}q(t)=0.}

Это дифференциальное уравнение гармонического осциллятора с циклической частотой собственных колебаний ω=1LC{\displaystyle \omega ={\frac {1}{\sqrt {LC}}}} (она называется собственной частотой гармонического осциллятора).

Решением этого уравнения 2-го порядка является выражение, зависящее от двух начальных условий:

i(t)=Iasin⁡(ωt+φ),{\displaystyle i(t)=I_{a}\sin({\omega }t+\varphi ),}

где Ia{\displaystyle I_{a}} — некая постоянная, определяемая начальными условиями, называемая амплитудой колебаний, φ{\displaystyle \varphi } — также некоторая постоянная, зависящая от начальных условий, называемая начальной фазой.

Например, при начальных условиях φ=0{\displaystyle \varphi =0} и амплитуде начального тока Ia{\displaystyle I_{a}} решение сведётся к:

i(t)=Iasin⁡(ωt).{\displaystyle i(t)=I_{a}\sin({\omega }t).}

Решение может быть записано также в виде

i(t)=Ia1sin⁡(ωt)+Ia2cos⁡(ωt),{\displaystyle i(t)=I_{a1}\sin({\omega }t)+I_{a2}\cos({\omega }t),}

где Ia1{\displaystyle I_{a1}} и Ia2{\displaystyle I_{a2}} — некоторые константы, которые связаны с амплитудой Ia{\displaystyle I_{a}} и фазой φ{\displaystyle \varphi } следующими тригонометрическими соотношениями:

Ia1=Iacos⁡(φ),{\displaystyle I_{a1}=I_{a}\cos {(\varphi )},}

Ia2=Iasin⁡(φ).{\displaystyle I_{a2}=I_{a}\sin {(\varphi )}.}

Колебательный контур может быть рассмотрен как двухполюсник, представляющий собой параллельное включение конденсатора и катушки индуктивности. Комплексное сопротивление такого двухполюсника можно записать как

z^(iω)=iωL1−ω2LC,{\displaystyle {\hat {z}}(i\omega )\;={\frac {i\omega L}{1-\omega ^{2}LC}},}

где i — мнимая единица.

Для такого двухполюсника может быть определена т. н. характеристическая частота (или резонансная частота), когда импеданс колебательного контура стремится к бесконечности (знаменатель дроби стремится к нулю).

Эта частота равна

ωh=1LC{\displaystyle \omega _{h}={\frac {1}{\sqrt {LC}}}}

и совпадает по значению с собственной частотой колебательного контура.

Из этого уравнения следует, что на одной и той же частоте может работать множество контуров с разными величинами L и C, но с одинаковым произведением LC. Однако выбор соотношения между L и C зачастую не бывает полностью произвольным, так как обуславливается требуемым значением добротности контура.

Для последовательного контура добротность растёт с увеличением L:

Q=1RLC,{\displaystyle Q={\frac {1}{R}}{\sqrt {\frac {L}{C}}},}

где R — активное сопротивление контура. Для параллельного контура:

Q=ReCL,{\displaystyle Q=R_{e}{\sqrt {\frac {C}{L}}},}

где Re=LCRL+C{\displaystyle R_{e}={\frac {L}{CR_{L+C}}}}, (RL+C{\displaystyle R_{L+C}} — сумма активных сопротивлений в цепи катушки и цепи конденсатора^[2]).

Понятие добротности связано с тем, что в реальном контуре существуют потери энергии (на излучение^[3] и нагрев проводников). Обычно считают, что все потери сосредоточены в некотором эквивалентном сопротивлении Re{\displaystyle R_{e}}, которое в последовательном контуре включено последовательно с L и C, а в параллельном — параллельно им. Малые потери (то есть высокая добротность) означают, что Re{\displaystyle R_{e}} в последовательном контуре мало, а в параллельном — велико. В низкочастотном последовательном контуре Re{\displaystyle R_{e}} легко обретает физический смысл — это активное сопротивление провода катушки и проводников цепи.

Резонансные контуры широко используются как полосовые и режекторные фильтры — в усилителях, радиоприёмниках, а также в различных устройствах автоматики. Например, на самолётах Ил-62М, Ил-76 и Ту-154М установлены блоки регулирования частоты БРЧ-62БМ, в главном элементе которых — блоке измерения частоты БИЧ-1 — имеются два колебательных контура, настроенных на частоты 760 и 840 Гц. На них поступает напряжение с номинальной частотой 800 Гц от подвозбудителя генератора (сам генератор при этом выдаёт 400 Гц). При отклонении частоты от номинальной реактивное сопротивление одного из контуров становится больше, чем другого, и БРЧ выдаёт на привод постоянных оборотов генератора управляющий сигнал для коррекции оборотов генератора. Если частота поднялась выше номинальной — сопротивление второго контура станет меньше, чем первого, и БРЧ выдаст сигнал на уменьшение оборотов генератора, если частота упала — то наоборот. Так поддерживается постоянство частоты напряжения генератора при изменении оборотов двигателя^[4].

• Попов В. П. Основы теории цепей: Учеб. для вузов / В. П. Попов. — 4-е изд., испр. — М.: Высш. шк., 2003. — 575 с.
• Скрипников Ю. Ф. Колебательный контур — М.: Энергия, 1970—128 с.: ил. — (МРБ; Вып. 739)
• Изюмов Н. М., Линде Д. П. Основы радиотехники. — М.:Радио и связь, 1983

Параллельный колебательный контур | Практическая электроника

В прошлой статье мы с вами рассмотрели последовательный колебательный контур, так как все участвующие в нем радиоэлементы соединялись последовательно. В этой же статье мы  рассмотрим параллельный колебательный контур, в котором катушка и конденсатор  соединяются параллельно.

Параллельный колебательный контур на схеме

На схеме идеальный колебательный контур выглядит вот так:

В реальности у нас катушка обладает приличным сопротивлением потерь, так как намотана из провода, да и конденсатор тоже имеет некоторое сопротивление потерь. Потери в емкости очень малы и ими обычно пренебрегают. Поэтому оставим только одно сопротивление потерь катушки R. Тогда схема

реального колебательного контура примет вот такой вид:

где

R – это сопротивление потерь контура, Ом

L – собственно сама индуктивность, Генри

С – собственно сама емкость, Фарад

Работа параллельного колебательного контура

Давайте подцепим к генератору частоты реальный параллельный колебательный контур

Что будет, если мы подадим на контур ток с частотой в ноль Герц, то есть постоянный ток? Он спокойно побежит через катушку и будет ограничиваться лишь сопротивлением потерь R самой катушки. Через конденсатор ток не побежит, потому что конденсатор не пропускает постоянный ток. Об это я писал еще в статье конденсатор в цепи постоянного и переменного тока.

Давайте тогда будем добавлять частоту. Итак, с увеличением частоты у нас конденсатор и катушка начнут оказывать реактивное сопротивление электрическому току.

Реактивное сопротивление катушки выражается по формуле

а конденсатора по формуле

Более подробно про это можно прочитать в этой статье.

Если плавно увеличивать частоту, то можно понять из формул, что в самом начале при плавном увеличении частоты конденсатор будет оказывать бОльшее сопротивление, чем катушка индуктивности. На какой-то частоте реактивные сопротивления катушки X_L и конденсатора X_C уравняются. Если далее увеличивать частоту, то уже катушка уже будет оказывать большее сопротивление, чем конденсатор.

Резонанс параллельного колебательного контура

Очень интересное свойство параллельного колебательного контура заключается в том, что при Х_L = Х_С  

у нас колебательный контур войдет в резонанс. При резонансе колебательный контур начнет оказывать большее сопротивление переменному электрическому току. Еще часто это сопротивление называют резонансным сопротивлением контура и оно выражается формулой:

где

R_рез  – это сопротивление контура на резонансной частоте

L – собственно сама индуктивность катушки

C – собственно сама емкость конденсатора

R – сопротивление потерь катушки

Формула резонанса

Для параллельного колебательного контура также работает формула Томсона для резонансной частоты как и для последовательного колебательного контура:

где

F – это резонансная частота контура, Герцы

L – индуктивность катушки, Генри

С – емкость конденсатора, Фарады

Как найти резонанс на практике

Ладно, ближе к делу. Берем паяльник в руки и спаиваем катушку и конденсатор параллельно. Катушка на 22 мкГн, а конденсатор на 1000пФ.

Итак, реальная схема этого контура будет вот такая:

Для того, чтобы все показать наглядно и понятно, давайте добавим к контуру последовательно резистор на 1 КОм и соберем вот такую схему:

На генераторе мы будет менять частоту, а с клемм X1 и X2 мы будем снимать напряжение и смотреть его на осциллографе.

Нетрудно догадаться, что у нас сопротивление параллельного колебательного контура будет зависеть от частоты генератора, так как в этом колебательном контуре мы видим два радиоэлемента, чьи реактивные сопротивления напрямую зависит от частоты, поэтому заменим колебательный контур эквивалентным сопротивлением контура R_кон.

Упрощенная схема будет выглядеть вот так:

Интересно, на что похожа эта схема? Не на делитель ли напряжения? Именно! Итак, вспоминаем правило делителя напряжения: на меньшем сопротивлении падает меньшее напряжение, на бОльшем сопротивлении падает бОльшее напряжение. Какой вывод можно сделать применительно к нашему колебательному контуру? Да все просто: на резонансной частоте сопротивление R_кон будет максимальным, вследствие чего у нас на этом сопротивлении “упадет” бОльшее напряжение.

Начинаем наш опыт. Поднимаем частоту на генераторе, начиная с самых маленьких частот.

200 Герц.

Как вы видите, на колебательном контуре “падает” малое напряжение, значит, по правилу делителя напряжения, можно сказать, что сейчас у контура малое сопротивление R

кон

Добавляем частоту. 11,4 Килогерца

Как вы видите, напряжение на контуре поднялось. Это значит, что  сопротивление  колебательного контура увеличилось.

Добавляем еще частоту. 50 Килогерц

Заметьте, напряжение на контуре повысилось еще больше. Значит его сопротивление еще больше увеличилось.

723 Килогерца

Обратите внимание на цену деления одного квадратика по вертикали, по сравнению с прошлым опытом. Там было 20мВ на один квадратик, а сейчас уже 500 мВ на один квадратик. Напряжение выросло, так как сопротивление колебательного контура стало еще больше.

И вот я поймал такую частоту, на которой получилось максимальное напряжение на колебательном контуре. Обратите внимание на цену деления по вертикали. Она равняется двум Вольтам.

Дальнейшее увеличение частоты приводит к тому, что напряжение начинает падать:

Снова добавляем частоту и видим, что напряжение стало еще меньше:

Разбираем частоту резонанса

 Давайте более подробно рассмотрим эту осциллограмму, когда у нас было максимальное напряжение с контура.

Что здесь у нас произошло?

Так как на этой частоте был всплеск напряжения, следовательно, на этой частоте параллельный колебательный контур имел самое  высокое сопротивление R_кон. На этой частоте Х_L = Х_С. Потом с ростом частоты сопротивление контура снова упало. Это и есть то самое резонансное сопротивление контура, которое выражается формулой:

Резонанс токов

Итак, давайте допустим, мы вогнали наш колебательный контур в резонанс:

Чему будет равняться резонансный ток  I_рез ? Считаем по закону Ома:

I_рез = U_ген /R_рез  , где  R_рез = L/CR.

Но самый прикол в том, что у нас при резонансе в контуре появляется свой собственный контурный ток I_кон , который не выходит за пределы контура и остается только в самом контуре! Так как с математикой у меня туго, поэтому я не буду приводить различные математические выкладки с производными и комплексными числами и объяснять откуда берется контурный ток при резонансе. Именно поэтому резонанс параллельного колебательного контура называется резонансом токов.

Добротность

Кстати, этот контурный ток будет намного больше, чем ток, который проходит через контур. И знаете во сколько раз? Правильно, в Q раз.  Q – это и есть добротность! В параллельном колебательном контуре она показывает во сколько раз сила  тока в контуре  I_кон  больше сила тока в общей цепи I_рез

Или формулой:

Если сюда еще прилепить сопротивление потерь, то формула примет вот такой вид:

где

Q – добротность

R – сопротивление потерь на катушке, Ом

С – емкость, Ф

L – индуктивность, Гн

Заключение

Ну и в заключении хочу добавить, что параллельный колебательный контур применяется в радиоприемном оборудовании, где надо выделить частоту какой-либо станции. Также с помощью колебательного контура можно построить различные резонансные фильтры, которые бы выделяли нужную нам частоту, а другие частоты пропускали бы через себя, что в принципе мы и делали в нашем опыте.

Постоянная времени RC

Электрическая цепь RC

Рассмотрим ток в электрической цепи, состоящей из конденсатора ёмкостью C и резистора сопротивлением R, соединённых параллельно.
Значение тока заряда или разряда конденсатора определится выражением I = C(dU/dt), а значение тока в резисторе, согласно закону Ома, составит U/R, где U — напряжение заряда конденсатора.

Из рисунка видно, что электрический ток I в элементах C и R цепи будет иметь одинаковое значение и противоположное направление, согласно закону Кирхгофа. Следовательно, его можно выразить следующим образом:

Решаем дифференциальное уравнение C(dU/dt)= -U/R

Интегрируем:

Из таблицы интегралов здесь используем преобразование

Получаем общий интеграл уравнения: ln|U| = — t/RC + Const.
Выразим из него напряжение U потенцированием: U = e^-t/RC * e^Const.
Решение примет вид:

U = e^-t/RC * Const.

Здесь Const — константа, величина, определяемая начальными условиями.

Следовательно, напряжение U заряда или разряда конденсатора будет меняться во времени по экспоненциальному закону e^-t/RC.

Экспонента — функция exp(x) = e^x
e – Математическая константа, приблизительно равная 2.718281828…

---

Постоянная времени τ

Если конденсатор емкостью C последовательно с резистором сопротивлением R подключить к источнику постоянного напряжения U, в цепи пойдёт ток, который за любое время t зарядит конденсатор до значения U_C и определится выражением:

Тогда напряжение U_C на выводах конденсатора будет увеличиваться от нуля до значения U по экспоненте:

U_C = U(1 — e^-t/RC)

При t = RC, напряжение на конденсаторе составит U_C = U(1 — e^-1) = U(1 — 1/e) .
Время, численно равное произведению RC, называется постоянной времени цепи RC и обозначается греческой буквой τ.

Постоянная времени τ = RC

За время τ конденсатор зарядится до (1 — 1/e)*100% ≈ 63,2% значения U.
За время 3τ напряжение составит (1 — 1/e³)*100% ≈ 95% значения U.
За время 5τ напряжение возрастёт до (1 — 1/e⁵)*100% ≈ 99% значения U.

---

Если к конденсатору емкостью C, заряженному до напряжения U, параллельно подключить резистор сопротивлением R, тогда в цепи пойдёт ток разряда конденсатора.

Напряжение на конденсаторе при разряде будет составлять U_C = Ue^-t/τ = U/e^t/τ.

За время τ напряжение на конденсаторе уменьшится до значения U/e, что составит 1/e*100% ≈ 36.8% значения U.
За время 3τ конденсатор разрядится до (1/e³)*100% ≈ 5% от значения U.
За время 5τ до (1/e⁵)*100% ≈ 1% значения U.

Параметр τ широко применяется при расчётах RC-фильтров различных электронных цепей и узлов.

---

Замечания и предложения принимаются и приветствуются!

Расчёт частоты резонанса колебательного контура

Колебательный контур — электрическая цепь, в которой могут возникать колебания с частотой, определяемой параметрами цепи.

Простейший колебательный контур состоит из конденсатора и катушки индуктивности, соединенных параллельно или последовательно.

— Конденсатор C – реактивный элемент. Обладает способностью накапливать и отдавать электрическую энергию.
— Катушка индуктивности L – реактивный элемент. Обладает способностью накапливать и отдавать магнитную энергию.

Свободные электрические колебания в параллельном контуре.

Основные свойства индуктивности:

— Ток, протекающий в катушке индуктивности, создаёт магнитное поле с энергией .
— Изменение тока в катушке вызывает изменение магнитного потока в её витках, создавая в них ЭДС, препятствующую изменению тока и магнитного потока.

Период свободных колебаний контура LC можно описать следующим образом:

Если конденсатор ёмкостью C заряжен до напряжения U, потенциальная энергия его заряда составит.
Если параллельно заряженному конденсатору подключить катушку индуктивности L, в цепи пойдёт ток его разряда, создавая магнитное поле в катушке.

Магнитный поток, увеличиваясь от нуля, создаст ЭДС в направлении противоположном току в катушке, что будет препятствовать нарастанию тока в цепи, поэтому конденсатор разрядится не мгновенно, а через время t₁, которое определяется индуктивностью катушки и ёмкостью конденсатора из расчёта t₁ = .
По истечении времени t₁, когда конденсатор разрядится до нуля, ток в катушке и магнитная энергия будут максимальны.
Накопленная катушкой магнитная энергия в этот момент составит.
В идеальном рассмотрении, при полном отсутствии потерь в контуре, E_C будет равна E_L. Таким образом, электрическая энергия конденсатора перейдёт в магнитную энергию катушки.

Изменение (уменьшение) магнитного потока накопленной энергии катушки создаст в ней ЭДС, которая продолжит ток в том же направлении и начнётся процесс заряда конденсатора индукционным током. Уменьшаясь от максимума до нуля в течении времени t₂ = t₁, он перезарядит конденсатор от нуля до максимального отрицательного значения (-U).
Так магнитная энергия катушки перейдёт в электрическую энергию конденсатора.

Описанные интервалы t₁ и t₂ составят половину периода полного колебания в контуре.
Во второй половине процессы аналогичны, только конденсатор будет разряжаться от отрицательного значения, а ток и магнитный поток сменят направление. Магнитная энергия вновь будет накапливаться в катушке в течении времени t₃, сменив полярность полюсов.

В течении заключительного этапа колебания (t₄), накопленная магнитная энергия катушки зарядит конденсатор до первоначального значения U (в случае отсутствия потерь) и процесс колебания повторится.

В реальности, при наличии потерь энергии на активном сопротивлении проводников, фазовых и магнитных потерь, колебания будут затухающими по амплитуде.
Время t₁ + t₂ + t₃ + t₄ составит период колебаний .
Частота свободных колебаний контура ƒ = 1 / T

Частота свободных колебаний является частотой резонанса контура, на которой реактивное сопротивление индуктивности X_L=2πfL равно реактивному сопротивлению ёмкости X_C=1/(2πfC).

---

Расчёт частоты резонанса LC-контура:

Предлагается простой онлайн-калькулятор для расчёта резонансной частоты колебательного контура.

Необходимо вписать значения и кликнуть мышкой в таблице.
При переключении множителей автоматически происходит пересчёт результата.

Частота резонанса колебательного контура LC. ƒ = 1/(2π√(LC))

Расчёт ёмкости:

Ёмкость для колебательного контура LC C = 1/(4𲃲L)

Расчёт индуктивности:

Индуктивность для колебательного контура LC L = 1/(4𲃲C)

---

Похожие страницы с расчётами:

Рассчитать импеданс.
Рассчитать реактивное сопротивление.
Рассчитать реактивную мощность и компенсацию.

Цепь генератора RC

В данной статье мы рассмотрим RC генератор и принцип его работы, подробно рассмотрим его схемы, в том числе на операционном усилителе.

Описание и принцип работы

В руководствах по усилителю мы видели, что одноступенчатый транзисторный усилитель может генерировать 180 ^o фазового сдвига между его выходным и входным сигналами при подключении в конфигурации типа класса А.

Чтобы генератор мог бесконечно выдерживать колебания, должна быть обеспечена достаточная обратная связь правильной фазы, то есть «положительная обратная связь», а транзисторный усилитель используется в качестве инвертирующего каскада для достижения этой цели.

В цепи RC-генератора вход смещен на 180 ^o через ступень усилителя и на 180 ^o снова через вторую инвертирующую ступень, что дает нам «180 ^o  + 180 ^o  = 360 ^o » фазового сдвига, который фактически равен 0 ^o, тем самым давая нам требуемый положительный отзыв. Другими словами, фазовый сдвиг контура обратной связи должен быть равен «0».

В генераторе сопротивления-емкости или просто в генераторе RC мы используем тот факт, что фазовый сдвиг происходит между входом в сеть RC и выходом из той же сети, например, с использованием элементов RC в ветви обратной связи.

Фазовая цепь RC

Схема слева показывает одну сеть резистор-конденсатор, выходное напряжение которой «опережает» входное напряжение на угол менее 90 ^o . Идеальная однополюсная RC-цепь будет производить фазовый сдвиг точно на 90 ^o , а поскольку для колебаний требуется 180 ^o фазового сдвига, в конструкции RC-генератора необходимо использовать как минимум два однополюсных.

Однако в действительности трудно получить ровно 90 ^o фазового сдвига, поэтому используется больше стадий. Величина фактического фазового сдвига в цепи зависит от значений резистора и конденсатора, а выбранная частота колебаний с фазовым углом (  Φ  ) задается как:

Где: X _C — емкостное сопротивление конденсатора, R — сопротивление резистора, а ƒ — частота.

В нашем простом примере выше значения R и C были выбраны таким образом, чтобы на требуемой частоте выходное напряжение опережало входное напряжение под углом около 60 ^o . Затем фазовый угол между каждым последующим участком RC увеличивается еще на 60 ^o,, давая разность фаз между входом и выходом 180 ^o (3 x 60 ^o ), как показано на следующей векторной диаграмме.

Векторная диаграмма

Затем, соединяя вместе три такие RC-сети последовательно, мы можем произвести полный фазовый сдвиг в цепи 180 ^o на выбранной частоте, и это образует основы «генератора фазового сдвига», иначе называемого RC-генератором .

Мы знаем, что в схеме усилителя, использующей биполярный транзистор или операционный усилитель, он будет производить сдвиг фазы на 180 ^o между своим входом и выходом. Если трехступенчатая RC-сеть с фазовым сдвигом подключена между этим входом и выходом усилителя, общий фазовый сдвиг, необходимый для регенеративной обратной связи, составит 3 x 60 ^o + 180 ^o = 360 ^o, как показано ниже.

Три каскада RC каскадно соединены, чтобы получить необходимый наклон для стабильной частоты колебаний. Сдвиг фазы контура обратной связи составляет -180 ^o, когда фазовый сдвиг каждой ступени составляет -60 ^o . Это происходит, когда ω = 2πƒ = 1.732 / RC ( tan 60 ^o  = 1.732 ). Затем для достижения требуемого фазового сдвига в цепи генератора RC необходимо использовать несколько RC-фазосдвигающих сетей, таких как схема ниже.

Основная схема генератора RC

Базовый RC генератор, также известный как генератор фазового сдвига, генерирует выходной синусоидальный сигнал, используя регенеративную обратную связь, полученную из комбинации резистор-конденсатор. Эта регенеративная обратная связь от RC- сети обусловлена ​​способностью конденсатора накапливать электрический заряд (аналогично схеме LC-бака).

Эта сеть обратной связи резистор-конденсатор может быть подключена, как показано выше, для создания начального фазового сдвига (сеть с фазовым переходом) или взаимозаменяться для создания запаздывающего фазового сдвига (сеть с фазовым запаздыванием), результат остается тем же, что и синусоидальные колебания, которые возникают только при частота, на которой общий фазовый сдвиг составляет 360 ^o .

Изменяя один или несколько резисторов или конденсаторов в сети с фазовым сдвигом, можно изменять частоту, и, как правило, это делается путем поддержания одинаковых резисторов и использования 3-х значного переменного конденсатора.

Если все резисторы R и конденсаторы C в сети фазового сдвига равны по величине, то частота колебаний, создаваемых RC-генератором, определяется как:

Где:
ƒ _r — выходная частота в герцах
R — сопротивление в омах
C — емкость в Фарадах
N — количество стадий RC, (N = 3)

Поскольку комбинация резистор-конденсатор в цепи RC-генератора также действует как аттенюатор, создавая полное затухание -1 / 29th (Vo / Vi = β) на всех трех ступенях, усиление напряжения усилителя должно быть достаточно высоким, чтобы преодолеть эти потери RC. Следовательно, в нашей трехступенчатой ​​RC-сети, приведенной выше, усиление усилителя тоже должно быть равно или больше 29.

Влияние нагрузки усилителя на сеть обратной связи влияет на частоту колебаний и может привести к тому, что частота генератора будет на 25% выше расчетной. Затем сеть обратной связи должна управляться от выходного источника с высоким импедансом и подаваться на нагрузку с низким импедансом, такую ​​как транзисторный усилитель с общим эмиттером, но лучше использовать операционный усилитель, поскольку он полностью удовлетворяет этим условиям.

Операционный усилитель RC генератора

При использовании в качестве RC-генераторов RC-генераторы с операционным усилителем встречаются чаще, чем их аналоги на биполярных транзисторах. Цепь генератора состоит из операционного усилителя с отрицательным усилением и трехсекционной RC- сети, которая генерирует сдвиг фазы на 180 ^o . Сеть с фазовым сдвигом подключается от выхода операционного усилителя обратно к его «инвертирующему» входу, как показано ниже.

Поскольку обратная связь подключена к инвертирующему входу, операционный усилитель, следовательно, подключен в своей конфигурации «инвертирующего усилителя», которая создает требуемый сдвиг фазы на 180 ^o, тогда как сеть RC производит другой сдвиг фазы на 180 ^o на требуемой частоте (180 ^o + 180 ^о ).

Хотя возможно обеспечить каскадное соединение только двух однополюсных RC-каскадов, чтобы обеспечить требуемый сдвиг фазы на 180 ^o (90 ^o + 90 ^o ), стабильность генератора на низких частотах обычно плохая.

Одной из наиболее важных особенностей RC-генератора является его стабильность частоты, которая заключается в его способности обеспечивать выходной синусоидальный сигнал постоянной частоты при различных условиях нагрузки. При каскадном соединении трех или даже четырех каскадов RC (4 x 45 ^o ) стабильность генератора может быть значительно улучшена.

Обычно используются RC-генераторы с четырьмя каскадами, потому что общедоступные операционные усилители поставляются в четырехслойных интегральных схемах, поэтому проектирование четырехступенчатого генератора с фазовым сдвигом 45 ^o относительно друг друга относительно легкое.

RC-генераторы стабильны и обеспечивают хорошо сформированный синусоидальный выход с частотой, пропорциональной 1 / RC, и, следовательно, более широкий диапазон частот возможен при использовании переменного конденсатора. Однако RC-генераторы ограничены частотными приложениями из-за ограничений полосы пропускания для получения желаемого сдвига фазы на высоких частотах.

Цепь генератора ОУ

В следующем уроке об Осцилляторах мы рассмотрим другой тип RC-генератора,называемый мостовыми осцилляторами Wien, который использует резисторы и конденсаторы в качестве контура для создания низкочастотного синусоидального сигнала.

RC цепи — RC circuit

Резистор-конденсатор цепи ( RC — цепи ), или RC — фильтр или сеть RC , является электрическая цепь состоит из резисторов и конденсаторов с приводом от напряжения или источника тока . Первый заказ RC — цепь состоит из одного резистора и конденсатора одного и является простым типом RC цепи.

RC схемы могут быть использованы для фильтрации сигнала, блокируя определенные частоты и передачи других. Два наиболее распространенных фильтров RC являются высокочастотные фильтры и фильтры нижних частот ; полосовые фильтры и ленточно-стоп фильтры обычно требуют фильтров УКР , хотя грубые из них могут быть сделаны с помощью фильтров RC.

Вступление

Существует три основные, линейная пассивная сосредоточенные аналоговые цепи компоненты: резистор (R), конденсатор (С), а катушка индуктивность (L). Они могут быть объединены в цепи RC, в цепи RL , в цепи LC , и цепи RLC , с указанием аббревиатур , которые используются компоненты. Эти схемы, среди них, проявляют большое количество важных типов поведения , которые имеют основополагающее значение для большей части аналоговой электроники . В частности, они могут выступать в качестве пассивных фильтров . В статье рассматривается схема RC, в обоих рядов и параллельных форм, как это показано на схемах ниже.

Естественный ответ

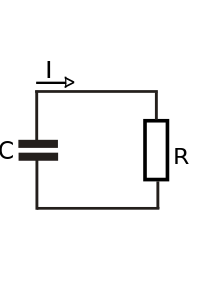
Простейший RC — цепь конденсатор и резистор параллельно. Когда контур состоит только из заряженного конденсатора и резистора, конденсатор будет выполнять свою накопленную энергию через резистор. Напряжение на конденсаторе, который зависит от времени, могут быть найдены с помощью тока закон Кирхгофа , где ток разряда конденсатора должен быть равен тока через резистор. Это приводит к линейному дифференциальному уравнению

СdВdT+Врзнак равно0,{\ Displaystyle С {\ гидроразрыва {дУ} {дт}} + {\ гидроразрыва {V}, {К}} = 0 \ ,,}

где С представляет собой емкость конденсатора.

Решая это уравнение для V дает формулу для экспоненциального распада :

В(T)знак равноВ0е-TрС,{\ Displaystyle V (т) = V_ {0} е ^ {- {\ гидроразрыва {т} {RC}}} \ ,,}

где V ₀ является напряжение на конденсаторе в момент времени Т = 0 .

Время , необходимое для напряжения снизится до V ₀ / е называется время RC постоянным и задается

τзнак равнорС,{\ Displaystyle \ тау = RC \ ,.}

Там, где τ измеряется в секундах, R в Ом и С в Фарадах.

Комплексное сопротивление

Комплексное сопротивление , Z _С (в Ом ) конденсатора с емкостью С (в фарадах ) является

ZСзнак равно1sС{\ Displaystyle Z_ {C} = {\ гидроразрыва {1} {СБН}}}

Комплексная частота ы является, вообще говоря , комплексное число ,

sзнак равноσ+Jω,{\ Displaystyle s = \ сигм + J \ Omega \ ,,}

где

Синусоидальная устойчивое состояние

Синусоидальное устойчивое состояние представляет собой частный случай , в котором входное напряжение состоит из чистой синусоиды (без экспоненциального затухания). В результате, и импеданс становится σзнак равно0{\ Displaystyle \ сигма = 0}

ZСзнак равно-JωС,{\ Displaystyle Z_ {C} = — {\ гидроразрыва {J} {\ Omega C}} \ ,.}

схема серии

Рассматривая схему в качестве делителя напряжения , то напряжение на конденсаторе является:

ВС(s)знак равно1Сsр+1СsВяN(s)знак равно11+рСsВяN(s){\ Displaystyle V_ {C}, (з) = {\ гидроразрыва {\ гидроразрыва {1} {Cs}} {К + {\ гидроразрыва {1} {Cs}}}} V _ {\ mathrm {в}} (з) = {\ гидроразрыва {1} {1 + РЦ}} V _ {\ mathrm {в}} (ы)}

и напряжение на резисторе:

Вр(s)знак равнорр+1СsВяN(s)знак равнорСs1+рСsВяN(s),{\ Displaystyle V_ {К} (з) = {\ гидроразрыва {R} {R + {\ гидроразрыва {1} {Cs}}}} V _ {\ mathrm {в}} (з) = {\ гидроразрыва {РЦ} { 1 + РЦ}} V _ {\ mathrm {в}} (ы) \ ,.}

Передаточные функции

Функция передачи от входного напряжения до напряжения на конденсаторе

ЧАСС(s)знак равноВС(s)ВяN(s)знак равно11+рСs,{\ Displaystyle Н_ {C}, (з) = {\ гидроразрыва {V_ {C}, (с)} {V _ {\ mathrm {в}} (ы)}} = {\ гидроразрыва {1} {1 + РЦ}} \ ,.}

Аналогичным образом, функция передачи от входа к напряжению через резистор

ЧАСр(s)знак равноВр(s)ВяN(s)знак равнорСs1+рСs,{\ Displaystyle Н_ {К} (з) = {\ гидроразрыва {V_ {К} (ы)} {V _ {\ тт {в}} (ы)}} = {\ гидроразрыва {РЦ} {1 + РЦ}} \ ,.}

Поляки и нули

Обе функции передачи имеет один полюс , расположенный в

sзнак равно-1рС,{\ Displaystyle з = — {\ гидроразрыва {1} {RC}} \ ,.}

Кроме того, функция передачи для резистора имеет нуль , расположенный в происхождении .

Коэффициент усиления и фазы

Величина прибыли через два компонента

гСзнак равно|ЧАСС(Jω)|знак равно|ВС(Jω)ВяN(Jω)|знак равно11+(ωрС)2{\ Displaystyle G_ {C} = {\ большой |} Н- {C} (J \ омега) {\ большой |} = \ влево | {\ гидроразрыва {V_ {C} (J \ Omega)} {V _ {\ mathrm {в}} (J \ Omega)}} \ право | = {\ гидроразрыва {1} {\ SQRT {1+ \ влево (\ омега RC \ справа) ^ {2}}}}}

а также

грзнак равно|ЧАСр(Jω)|знак равно|Вр(Jω)ВяN(Jω)|знак равноωрС1+(ωрС)2,{\ Displaystyle G_ {R} = {\ большой |} Н- {R} (J \ омега) {\ большой |} = \ влево | {\ гидроразрыва {V_ {R} (J \ Omega)} {V _ {\ mathrm {в}} (J \ Omega)}} \ право | = {\ гидроразрыва {\ омеги RC} {\ SQRT {1+ \ влево (\ омега RC \ справа) ^ {2}}}} \ ,,}

и фазовые углы являются

φСзнак равно∠ЧАСС(Jω)знак равнозагар-1⁡(-ωрС){\ Displaystyle \ Phi _ {C} = \ угол Н- {C} (J \ омега) = \ загаром ^ {- 1} \ влево (- \ омега RC \ справа)}

а также

φрзнак равно∠ЧАСр(Jω)знак равнозагар-1⁡(1ωрС),{\ Displaystyle \ Phi _ {R} = \ угол Н- {R} (J \ омега) = \ загаром ^ {- 1} \ влево ({\ гидроразрыва {1} {\ омеги RC}} \ справа) \ ,. }

Эти выражения вместе могут быть замещены в обычное выражение для фазора , представляющего выход:

ВСзнак равногСВяNеJφСВрзнак равногрВяNеJφр,{\ Displaystyle {\ начинаются {выровнены} V_ {C}, & = G_ {C} V _ {\ mathrm {в}} е ^ {J \ Phi _ {C}} \\ V_ {R} & = G_ {R} V _ {\ mathrm {в}} е ^ {J \ Phi _ {R}} \,. \ {конец выровнен}}}

Текущий

Ток в цепи везде одинакова, так как цепь последовательно:

я(s)знак равноВяN(s)р+1Сsзнак равноСs1+рСsВяN(s),{\ Displaystyle I (S) = {\ гидроразрыва {V _ {\ mathrm {в}} (ы)} {R + {\ гидроразрыва {1} {Cs}}}} = {\ гидроразрыва {Cs} {1 + РЦ} } V _ {\ mathrm {в}} (ы) \ ,.}

Импульсивный ответ

Импульсная характеристика для каждого напряжения является обратным преобразованием Лапласа соответствующей передаточной функции. Она представляет собой реакцию цепи с входным напряжением , состоящим из импульса или дельта функции Дирака .

Импульсная характеристика для напряжения конденсатора является

часС(T)знак равно1рСе-TрСU(T)знак равно1τе-TτU(T),{\ Displaystyle H_ {C}, (т) = {\ гидроразрыва {1} {RC}} е ^ {- {\ гидроразрыва {T} {RC}}} и (г) = {\ гидроразрыва {1} {\ тау }} е ^ {- {\ гидроразрыва {т} {\ тау}}} и (т) \ ,,}

где у ( т ) является функцией Хевисайда и τ = RC является постоянной времени .

Аналогичным образом, импульсный отклик на напряжение резистора

часр(T)знак равноδ(T)-1рСе-TрСU(T)знак равноδ(T)-1τе-TτU(T),{\ Displaystyle H_ {К} (т) = \ дельта (т) — {\ гидроразрыва {1} {RC}} е ^ {- {\ гидроразрыва {T} {RC}}} и (г) = \ дельта ( т) — {\ гидроразрыва {1} {\ тау}} е ^ {- {\ гидроразрыва {т} {\ тау}}} и (т) \ ,,}

где δ ( т ) является дельта — функция Дирака

соображения частотной области

Это частотная область выражение. Анализ них покажет , какие частоты цепи (или фильтры) проходят и отвергают. Этот анализ основывается на учете того , что происходит с этими выгодами , как частота становится очень большой и очень маленькими.

Как ш → ∞ :

гС→0а такжегр→1,{\ Displaystyle G_ {C}, \ до 0 \ четырехъядерных {\ Mbox {и}} \ четырехъядерных G_ {R}, \ 1 \ ,.}

Как ш → 0 :

гС→1а такжегр→0,{\ Displaystyle G_ {C}, \ 1 \ четырехъядерных {\ Mbox {и}} \ четырехъядерных G_ {R}, \ до 0 \} ,.

Это показывает , что, если выходной сигнал принимается через конденсатор, высокие частоты ослабляются (короткое замыкание на землю) и пропускают низкие частоты. Таким образом, схема ведет себя как фильтр нижних частот . Если, тем не менее, выходной сигнал принимаются через резистор, высокие частоты передаются и низкие частоты ослабляются (с конденсатором блоков сигнал в качестве его частоты приближается к 0). В этой конфигурации, схема ведет себя как фильтр высоких частот .

Диапазон частот , который проходит фильтр называется ее пропускная способность . Точка , в которой фильтр ослабляет сигнал на половину своей мощности нефильтрованной называют его частоты среза . Это требует, чтобы коэффициент усиления схемы быть сведено к

гСзнак равногрзнак равно12{\ Displaystyle G_ {C} = G_ {R} = {\ гидроразрыва {1} {\ SQRT {2}}}},

Решение вышеуказанных выходов уравнения

ωсзнак равно1рСили жеесзнак равно12πрС{\ Displaystyle \ омега _ {\ mathrm {C}} = {\ гидроразрыва {1} {RC}} \ четырехъядерных {\ Mbox {или}} \ четырехъядерных F _ {\ mathrm {C}} = {\ гидроразрыва {1} {2 \ пи RC}}}

что частота, на которой фильтр будет затухать до половины своей первоначальной мощности.

Очевидно, что фазы также зависит от частоты, хотя этот эффект менее интересен, как правило, чем изменения коэффициента усиления.

Как ш → 0 :

φС→0а такжеφр→90∘знак равноπ2 радиан,{\ Displaystyle \ Phi _ {C}, \ до 0 \ четырехугольника {\ Mbox {и}} \ четырехъядерных \ Phi _ {R}, \ 90 ^ {\ CIRC} = {\ гидроразрыва {\ Pi} {2}} { \ Mbox {радианы}} \ ,.}

Как ш → ∞ :

φС→-90∘знак равно-π2 радиана такжеφр→0,{\ Displaystyle \ Phi _ {C} \ -90 ^ {\ циркуляр} = — {\ гидроразрыва {\ пи} {2}} {\ Mbox {радианы}} \ четырехъядерных {\ Mbox {и}} \ четырехъядерных \ фита _ {R} \ 0, \ ,.}

Таким образом , в DC (0  Гц ), напряжение на конденсаторе находится в фазе с напряжением сигнала , а напряжение резистора приводит его на 90 °. При увеличении частоты, напряжение на конденсаторе приходит иметь 90 ° задержки относительно сигнала и напряжение резистора приходит , чтобы быть в фазе с сигналом.

соображения во временной области

Этот раздел опирается на знание е , с естественной логарифмической константой .

Самый простой способ вывести поведение во временной области является использование преобразования Лапласа выражений для V _C и V _R , приведенной выше. Это фактически превращает jω → сек . Если предположить, что входной сигнал шага (т.е. V _в = 0 до т = 0 , а затем V _в = V впоследствии):

ВяN(s)знак равноВ⋅1sВС(s)знак равноВ⋅11+sрС⋅1sВр(s)знак равноВ⋅sрС1+sрС⋅1s,{\ Displaystyle {\ начинаются {выровнен} V _ {\ mathrm {в}} (ы) & = V \ CDOT {\ гидроразрыва {1} {s}} \\ V_ {C} (ы) & = V \ CDOT { \ гидроразрыва {1} {1 + Src}} \ CDOT {\ гидроразрыва {1} {s}} \\ V_ {К} (ы) & = V \ CDOT {\ гидроразрыва {Src} {1 + Src}} \ CDOT {\ гидроразрыва {1} {s}} \,. \ {конец выровнен}}}

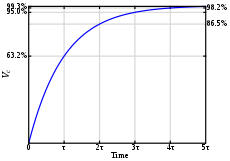Конденсатор напряжение шага отклик. 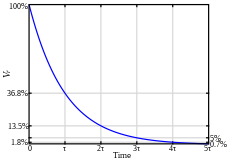Резистор напряжение шага отклик.

Дробей разложение и обратное преобразование Лапласа выхода:

ВС(T)знак равноВ(1-е-TрС)Вр(T)знак равноВе-TрС,{\ Displaystyle {\ {начинаются выровнены} V_ {C}, (т) & = V \ слева (1-е ^ {- {\ гидроразрыва {T} {RC}}} \ справа) \\ V_ {К} (т ) & = Ve ^ {- {\ гидроразрыва {T} {RC}}}. \, \ {конец выровнен}}}

Эти уравнения для расчета напряжения на конденсатор и резистор соответственно , в то время как конденсатор зарядки ; для выпуска, уравнения наоборот. Эти уравнения можно переписать в терминах заряда и тока с использованием соотношения C = Q / V и V = IR (см закон Ома ).

Таким образом, напряжение на конденсаторе стремится к V с течением времени, в то время как напряжение на резисторе стремится к 0, как показано на фигурах. Это согласуется с интуитивной точкой , что конденсатор будет зарядками от напряжения питания , как проходит время, и в конечном счете будет полностью заряжено.

Эти уравнения показывают , что RC — цепь , имеет постоянное время , обычно обозначается τ = RC является временем, необходимым напряжение на компоненту либо подъем (через конденсатор) или осенью (через резистор) с точностью до 1 / е из своих конечное значение. То есть, τ есть время, которое требуется V _C , чтобы достичь V (1 — 1 / е ) и V _R достичь V ( 1 / е ) .

Скорость изменения является дробным 1 — 1 / е за т . Таким образом, при переходе от т = Nτ к т = ( N + 1) т , напряжение будет переместились около 63,2% пути от его уровня , при т = Nτ к своему конечному значению. Таким образом, конденсатор будет заряжаться до 63,2% после т , и по существу , полностью заряжена (99,3%) после того, как около 5 т . Когда источник напряжения заменяется коротким замыканием, с конденсатором полностью заряженном, напряжение на конденсаторе падает экспоненциально с т из V в направлении 0. Конденсатор будет разряжаться до около 36,8% после того, как т , и по существу полностью разряженной (0,7 %) после того, как около 5 т . Обратите внимание , что в настоящее время, я , в цепи ведет себя как напряжение на резисторе делает, с помощью закона Ома .

Эти результаты могут быть также получены путем решения дифференциальных уравнений , описывающих схему:

ВяN-ВСрзнак равноСdВСdTВрзнак равноВяN-ВС,{\ Displaystyle {\ {начинаются выровнены} {\ гидроразрыва {V _ {\ mathrm {в}} -V_ {C}} {R}} & = C {\ гидроразрыва {dV_ {C}} {дт}} \\ V_ {R}, & = V _ {\ mathrm {в}} -V_ {C} \,. \ {конец выровнен}}}

Первое уравнение решается с помощью интегрирующего множителя и второй легко следует; решения точно так же , как и те , полученных с помощью преобразования Лапласа.

интегратор

Рассмотрим вывод через конденсатор при высокой частоте, т.е.

ω»1рС,{\ Displaystyle \ Omega \ гг {\ гидроразрыва {1} {RC}} \ ,.}

Это означает , что конденсатор имеет недостаточно времени для зарядки и поэтому его напряжение очень мало. Таким образом , входное напряжение приблизительно равно напряжению на резисторе. Чтобы убедиться в этом, рассмотрим выражение для приведенной выше: я{\ Displaystyle I}

язнак равноВяNр+1JωС,{\ Displaystyle I = {\ гидроразрыва {V _ {\ mathrm {в}}} {{R + \ гидроразрыва {1} {J \ омега C}}}} \ ,,}

но обратите внимание, что частотное условие означает, что описано

ωС»1р,{\ Displaystyle \ омега-С \ {гг \ гидроразрыва {1} {R}} \ ,,}

так

я≈ВяNр{\ Displaystyle I \ около {\ гидроразрыва {V _ {\ mathrm {в}}} {R}}}

который только закон Ома .

Сейчас,

ВСзнак равно1С∫0TяdT,{\ Displaystyle V_ {C} = {\ гидроразрыва {1} {C}} \ int _ {0} ^ {т} I \, дт \ ,,}

так

ВС≈1рС∫0TВяNdT,{\ Displaystyle V_ {C} \ около {\ гидроразрыва {1} {RC}} \ int _ {0} ^ {т} V _ {\ mathrm {в}} \, дт \ ,,}

которая представляет собой интегратор через конденсатор .

дифференциатор

Рассмотрим вывод через резистор на низкой частоте , т.е.,

ω«1рС,{\ Displaystyle \ Omega \ ЛЛ {\ гидроразрыва {1} {RC}} \ ,.}

Это означает , что конденсатор успевает зарядить до тех пор , пока напряжение не его почти равно напряжению источника. Учитывая выражение для I раз, когда

р«1ωС,{\ Displaystyle R \ {LL \ гидроразрыва {1} {\ Omega C}} \ ,,}

так

я≈ВяN1JωСВяN≈яJωСзнак равноВС,{\ Displaystyle {\ начинаются {выровнены} I & \ около {\ гидроразрыва {V _ {\ mathrm {в}}} {\ гидроразрыва {1} {J \ омега С}}} \\ V _ {\ mathrm {в}} & \ около {\ гидроразрыва {Я} {J \ омега C}} = V_ {C}, \,. \ {конец выровнен}}}

Сейчас,

Врзнак равноярзнак равноСdВСdTрВр≈рСdВяNdT,{\ Displaystyle {\ {начинаются выровнены} V_ {R}, & = ИК = С {\ {гидроразрыва dV_ {C}} {дт}} R \\ V_ {R} & \ около RC {\ гидроразрыва {{dV_ в} } {дт}} \ ,, \ {конец выровнен}}}

которая представляет собой дифференцирующий через резистор .

Более точная интеграция и дифференциация могут быть достигнута путем размещения резисторов и конденсаторов по мере необходимости на вход и обратной петле операционных усилителей (см операционного усилителя интегратора и операционный усилитель дифференциатор ).

параллельная цепь

Параллельная RC — цепь , как правило , меньший интерес , чем последовательной цепи. Это в значительной степени потому , что выходное напряжение V _вне равно входному напряжению V _в — в результате, эта схема не действует в качестве фильтра на входной сигнал , если не подается с помощью источника тока .

С комплексными сопротивлениями:

ярзнак равноВяNряСзнак равноJωСВяN,{\ Displaystyle {\ начинаются {выровнены} I_ {R}, & = {\ гидроразрыва {V _ {\ mathrm {в}}} {R}} \\ I_ {C}, & = J \ Omega CV _ {\ mathrm {в} } \,. \ {конец выровнен}}}

Это показывает, что ток конденсатора составляет 90 ° по фазе с резистором (и источник) током. В качестве альтернативы могут быть использованы управляющие дифференциальные уравнения:

ярзнак равноВяNряСзнак равноСdВяNdT,{\ Displaystyle {\ начинаются {выровнены} I_ {R}, & = {\ гидроразрыва {V _ {\ mathrm {в}}} {R}} \\ I_ {C} & = С {\ гидроразрыва {дУ _ {\ mathrm { в}}} {дт}} \,. \ {конец выровнен}}}

При подаче от источника тока, передаточная функция параллельной цепи RC является:

ВоUTяяNзнак равнор1+sрС,{\ Displaystyle {\ гидроразрыва {V _ {\ mathrm {из}}} {I _ {\ mathrm {в}}}} = {\ гидроразрыва {R}, {1 + Src}} \ ,.}

Смотрите также

Рекомендации

Делайте бизнес — остальным займутся сервисы Контура

Заполните, пожалуйста, все поля.

Ваше имя: *

Электронная почта: *

Телефон:

Название организации:

ИНН:

Регион: *

01 – Республика Адыгея02 – Республика Башкортостан03 – Республика Бурятия04 – Республика Алтай05 – Республика Дагестан06 – Республика Ингушетия07 – Республика Кабардино-Балкария08 – Республика Калмыкия09 – Республика Карачаево-Черкесия10 – Республика Карелия11 – Республика Коми12 – Республика Марий Эл13 – Республика Мордовия14 – Республика Саха (Якутия)15 – Республика Северная Осетия — Алания16 – Республика Татарстан17 – Республика Тыва18 – Республика Удмуртия19 – Республика Хакасия20 – Республика Чечня21 – Республика Чувашия22 – Алтайский край23 – Краснодарский край24 – Красноярский край25 – Приморский край26 – Ставропольский край27 – Хабаровский край28 – Амурская область29 – Архангельская область30 – Астраханская область31 – Белгородская область32 – Брянская область33 – Владимирская область34 – Волгоградская область35 – Вологодская область36 – Воронежская область37 – Ивановская область38 – Иркутская область39 – Калининградская область40 – Калужская область41 – Камчатский край42 – Кемеровская область43 – Кировская область44 – Костромская область45 – Курганская область46 – Курская область47 – Ленинградская область48 – Липецкая область49 – Магаданская область50 – Московская область51 – Мурманская область52 – Нижегородская область53 – Новгородская область54 – Новосибирская область55 – Омская область56 – Оренбургская область57 – Орловская область58 – Пензенская область59 – Пермский край60 – Псковская область61 – Ростовская область62 – Рязанская область63 – Самарская область64 – Саратовская область65 – Сахалинская область66 – Свердловская область67 – Смоленская область68 – Тамбовская область69 – Тверская область70 – Томская область71 – Тульская область72 – Тюменская область73 – Ульяновская область74 – Челябинская область75 – Забайкальский край76 – Ярославская область77 – Москва78 – Санкт-Петербург79 – Еврейская АО83 – Ненецкий АО86 – Ханты-Мансийский АО87 – Чукотский АО89 – Ямало-Ненецкий АО91 – Республика Крым92 – Севастополь99 – Байконур

Вопрос: *