Фильтр высоких частот (ФВЧ) | Основы электроакустики
Фильтр высоких частот
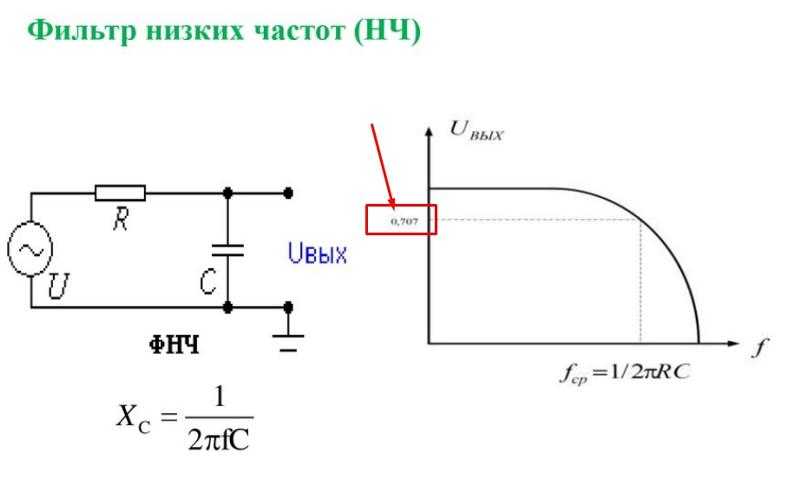
ФВЧ – это схема, которая передает без изменений сигналы высоких частот, а на низких обеспечивает затухание сигналов и опережение их по фазе относительно входных сигналов. Схема простого RC-фильтра верхних частот приведена на рис.3.5.
Рис.3.5. Простой ФВЧ
Частотная характеристика фильтра определяется выражением:
Отсюда находим АЧХ и ФЧХ:Обе кривые представлены на рис.3.6.
Рис.3.6. АЧХ и ФЧХ ФВЧ
Выражение для частоты среза совпадает с соответствующим выражением для ФНЧ:
fСР = 1/2πRC. Фазовый сдвиг на этой частоте составляет +45º. Как и для ФНЧ, наиболее просто составить АЧХ в двойном логарифмическом масштабе с помощью асимптот:
- Ā = 1 = 0дБ на высоких частотах f>>fCР.
- На низких частотах f<<fСР, согласно формуле (3.

- При f =fСР, как и для ФНЧ, Ā = 1/корень2 = –3 дБ.
Постоянная времени, как и для фильтра нижних частот, равна τ = RC. Реакция цепи на импульс напряжения описывается формулой: UВЫХ(t) = UВХ0 e–t/RC. Для определения начального значения UВЫХ0 = UВЫХ (t=0) используем дополнительное соображение: в момент, когда входное напряжение изменяется скачкообразно, заряд конденсатора остается неизменным. Он действует как источник напряжения Выходное напряжение повторяет скачок ΔU входного напряжения (рис. 3,7, а) от нуля до U1, а затем убывает по экспоненте, согласно равенству (3.13), снова до нуля. Если входное напряжение скачком изменяется от U1 до нуля, то UВЫХ скачком уменьшается от нуля до -U1 (рис. 3.7, б). При этом важно заметить, что выходное напряжение имеет отрицательные значения, хотя входное напряжение всегда положительно. Это обстоятельство часто используется в схемотехнике.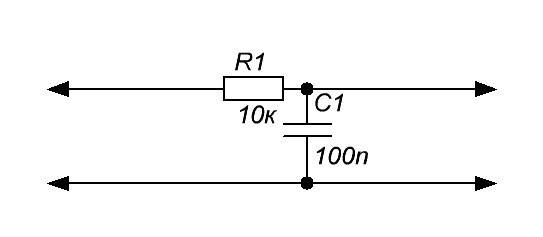
Фильтр верхних частот как дифференцирующее звено. Если приложено входное напряжение с частотой f<<fСР, то |UВЫХ|<<|UВХ|. Тогда UВЫХ = RC(dUВХ / dt). Таким образом, низкочастотные входные напряжения дифференцируются. Вид переходных характеристик ФВЧ показан на рис 3.8.
Рис.3.7. Реакция ФВЧ на скачок напряжения
Рис.3.8. Импульсный режим работы ФВЧ при различных соотношениях частоты и постоянной времени: верхняя кривая:
fВХ ≥ 10fСР; средняя кривая: fВХ = fСР; нижняя кривая: fВХ ≤ 1/10 fСР
Фильтр верхних частот как элемент RC-связи. Если на входе фильтра верхних частот приложено напряжение прямоугольной формы с периодом Т<<τ, то конденсатор в течение половины периода почти полностью перезаряжается и выходное напряжение будет равно входному с точностью до постоянной величины.
Рис. 3.9. Прохождение последовательности однополярных
импульсов через ФВЧ
В связи с тем, что через конденсатор не может протекать постоянный ток, среднее значение выходного напряжения равно нулю. Следовательно, постоянная составляющая входного напряжения не передается. На этом основано применение фильтра верхних частот в качестве элемента RС-связи.
Следовательно, постоянная составляющая входного напряжения не передается. На этом основано применение фильтра верхних частот в качестве элемента RС-связи.
Пассивный полосовой фильтр — принцип работы, характеристики, схемы, формулы — Кови
Пассивные полосовые фильтры можно изготовить, соединив вместе фильтр низких частот и фильтр высоких частот.
Полосно-пропускающие фильтры могут использоваться для изоляции или фильтрации определенных частот, которые находятся в определенной полосе или диапазоне частот. Частота среза или точка ƒc в простом пассивном RC-фильтре может точно контролироваться с помощью одного резистора, включенного последовательно с неполяризованным конденсатором, и в зависимости от того, как они подключены, мы видели, что получается либо низкочастотный, либо высокочастотный фильтр.
Одно из простых применений этих типов пассивных фильтров — использование в усилителях звука или схемах, например, в фильтрах кроссовера громкоговорителя или регуляторах тембра предварительного усилителя.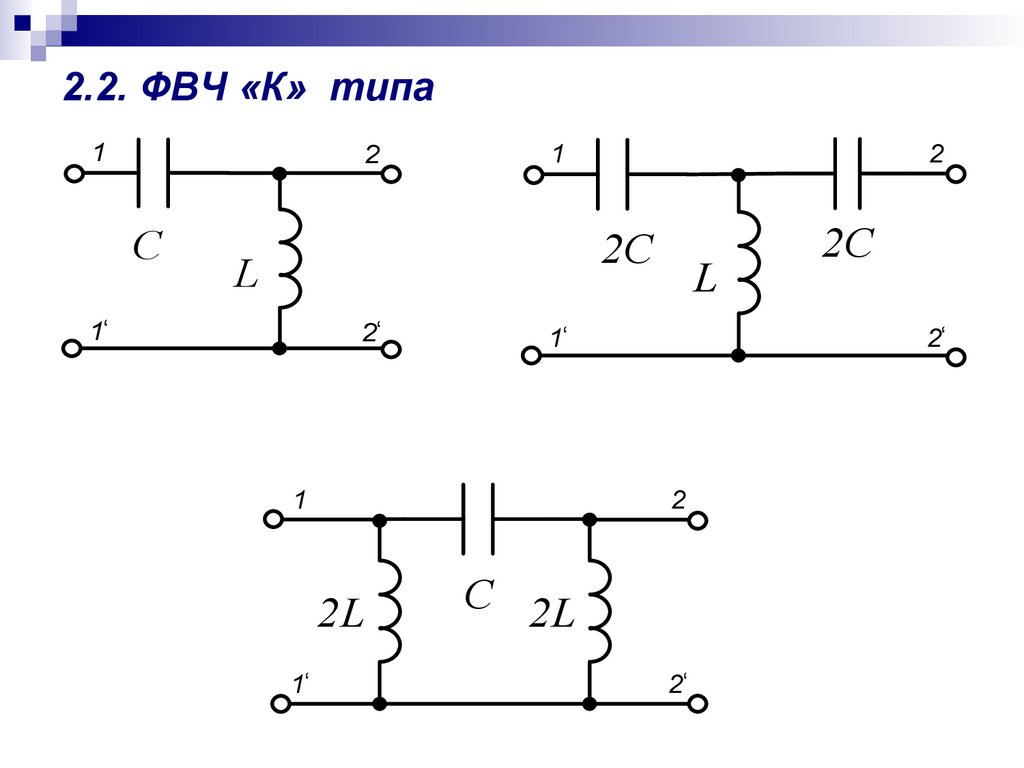 Иногда необходимо пропускать только определенный диапазон частот, которые не начинаются с 0 Гц (постоянный ток) или заканчиваются в верхней высокочастотной точке, но находятся в определенном диапазоне или полосе частот, узкой или широкой.
Иногда необходимо пропускать только определенный диапазон частот, которые не начинаются с 0 Гц (постоянный ток) или заканчиваются в верхней высокочастотной точке, но находятся в определенном диапазоне или полосе частот, узкой или широкой.
Соединяя или «каскадируя» вместе одну цепь фильтра низких частот с цепью фильтра высоких частот, мы можем получить другой тип пассивного RC-фильтра, который пропускает выбранный диапазон или «полосу» частот, которые могут быть как узкими, так и широкими, при этом ослабляя все те, которые находятся за пределами этого диапазона. Этот новый тип пассивного фильтра создает частотно-избирательный фильтр, известный как Band Pass Filter или сокращенно BPF.
Содержание
Схема полосового фильтра
В отличие от фильтра низких частот, пропускающего только сигналы низкого диапазона частот, или фильтра высоких частот, пропускающего сигналы более высокого диапазона частот, полосовые фильтры пропускают сигналы в пределах определенной «полосы» или «разброса» частот, не искажая входной сигнал и не внося дополнительного шума. Эта полоса частот может быть любой ширины и обычно называется полосой пропускания фильтра.
Эта полоса частот может быть любой ширины и обычно называется полосой пропускания фильтра.
Полоса пропускания обычно определяется как диапазон частот, существующий между двумя заданными точками отсечения частот ( ƒc ), которые на 3 дБ ниже максимального центра или резонансного пика, при одновременном ослаблении или затухании остальных за пределами этих двух точек.
Тогда для широко разнесенных частот мы можем просто определить термин «полоса пропускания», BW, как разницу между точками нижней частоты среза ( ƒcLOWER ) и верхней частоты среза ( ƒcHIGHER ). Другими словами, BW = ƒH — ƒL. Очевидно, что для правильной работы полосового фильтра частота среза фильтра низких частот должна быть выше частоты среза фильтра высоких частот.
«Идеальный» полосовой фильтр пропускания может также использоваться для изоляции или фильтрации определенных частот, лежащих в определенной полосе частот, например, для подавления шума. Полосно-пропускающие фильтры известны как фильтры второго порядка (двухполюсные), потому что в их схеме есть «два» реактивных компонента — конденсаторы. Один конденсатор в цепи низких частот и другой конденсатор в цепи высоких частот.
Один конденсатор в цепи низких частот и другой конденсатор в цепи высоких частот.
Частотная характеристика полосового пропускающего фильтра 2-го порядка
Приведенный выше график Боде или кривая частотной характеристики показывает характеристики полосового фильтра. Здесь сигнал ослабляется на низких частотах, а выходное напряжение увеличивается с наклоном +20 дБ/декада (6 дБ/октава), пока частота не достигнет точки «нижней отсечки» ƒL. На этой частоте выходное напряжение снова составляет 1/√2 = 70,7% от значения входного сигнала или -3 дБ (20*log(VOUT/VIN)) от входного.
Выходной сигнал продолжает усиливаться до достижения точки «верхней отсечки» ƒH, где выходной сигнал уменьшается со скоростью -20 дБ/декада (6 дБ/октава), ослабляя любые высокочастотные сигналы. Точка максимального выходного усиления обычно является средним геометрическим двух значений -3 дБ между нижней и верхней точками отсечки и называется «центральной частотой» или «резонансным пиком» ƒr. Это среднее геометрическое значение рассчитывается как ƒr 2 = ƒ(UPPER) x ƒ(LOWER).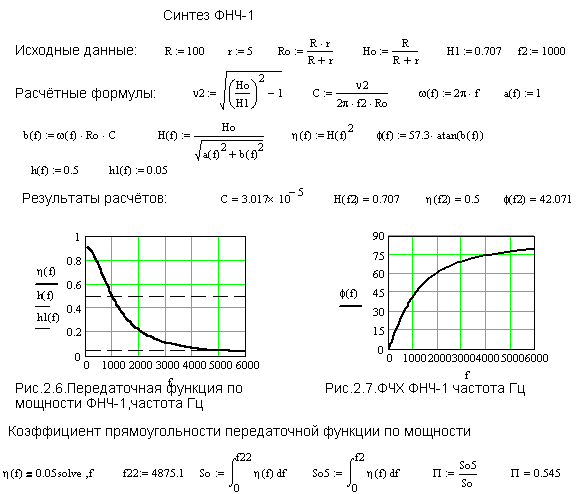
Полосовой фильтр считается фильтром второго порядка (двухполюсным), поскольку в его структуре есть «два» реактивных компонента, то фазовый угол будет в два раза больше, чем у ранее рассмотренных фильтров первого порядка, т.е. 180o. Фазовый угол выходного сигнала опережает входной на +90o до центральной или резонансной частоты, ƒr точки, где он становится «нулем» градусов (0o) или «синфазным», а затем изменяется в сторону отставания от входного на -90o по мере увеличения выходной частоты.
Верхняя и нижняя точки частоты среза для полосового фильтра могут быть найдены по той же формуле, что и для фильтров низких и высоких частот, например.
Тогда очевидно, что шириной полосы пропускания фильтра можно управлять с помощью расположения двух точек частоты среза двух фильтров.
Пример полосового фильтра No1
Необходимо построить полосовой фильтр второго порядка с использованием RC-компонентов, который будет пропускать только диапазон частот выше 1 кГц (1 000 Гц) и ниже 30 кГц (30 000 Гц).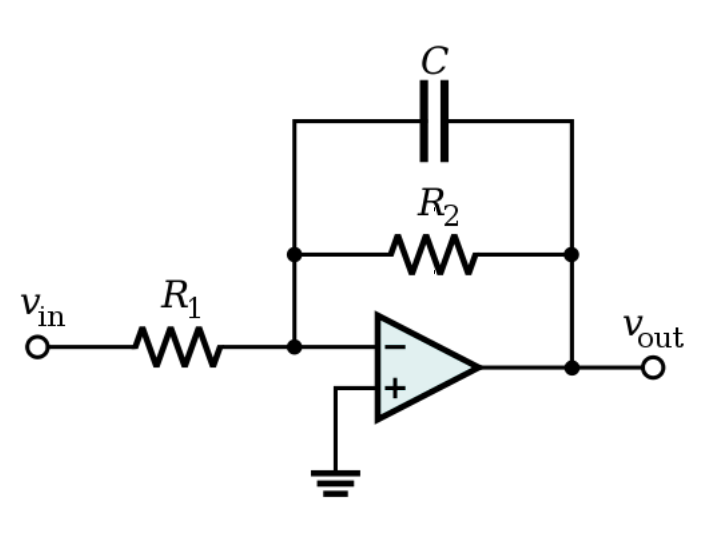 Предполагая, что оба резистора имеют значения 10kΩ, рассчитайте значения двух необходимых конденсаторов.
Предполагая, что оба резистора имеют значения 10kΩ, рассчитайте значения двух необходимых конденсаторов.
Этап фильтра высоких частот
Значение конденсатора C1, необходимое для получения частоты среза ƒL 1 кГц при значении резистора 10 кОм, рассчитывается следующим образом:
Тогда значения R1 и C1, необходимые для каскада высоких частот, чтобы обеспечить частоту среза 1,0 кГц, следующие: R1 = 10kΩ и, с точностью до предпочтительного значения, C1 = 15nF.
Этап фильтра низких частот
Значение конденсатора C2, необходимое для получения частоты среза ƒH 30 кГц при значении резистора 10 кОм, рассчитывается следующим образом:
Тогда значения R2 и C2, необходимые для низкочастотного каскада, чтобы обеспечить частоту среза 30 кГц, составляют R = 10 кОм и C = 530 пФ. Однако ближайшим предпочтительным значением рассчитанного значения конденсатора 530пФ является 560пФ, поэтому вместо него используется это значение.
Учитывая, что значения сопротивлений R1 и R2 равны 10kΩ, а значения конденсаторов C1 и C2, найденные для фильтров высоких и низких частот, равны 15nF и 560pF соответственно, схема нашего простого пассивного полосового фильтра имеет вид.
Законченная схема полосового фильтра
Резонансная частота полосового фильтра
Мы также можем рассчитать «резонансную» или «центральную частоту» (ƒr) полосового фильтра, когда выходное усиление достигает максимального или пикового значения. Это пиковое значение не является средним арифметическим верхней и нижней точек отсечки -3 дБ, как можно было бы ожидать, а представляет собой «геометрическое» или среднее значение. Это среднее геометрическое значение рассчитывается, например, как ƒr 2 = ƒc(UPPER) x ƒc(LOWER):
Уравнение центральной частоты
Где, ƒr — резонансная или центральная частота
ƒL — нижняя точка частоты среза по уровню -3 дБ
ƒH — верхняя точка среза частоты -3 дБ
и в нашем простом примере выше, рассчитанные частоты среза составили ƒL = 1 060 Гц и ƒH = 28 420 Гц, используя значения фильтра.
Подставив эти значения в вышеприведенное уравнение, можно получить центральную резонансную частоту:
Краткое описание полосового фильтра
Простой пассивный полосовой фильтр может быть изготовлен путем каскадного соединения одного фильтра низких частот с фильтром высоких частот.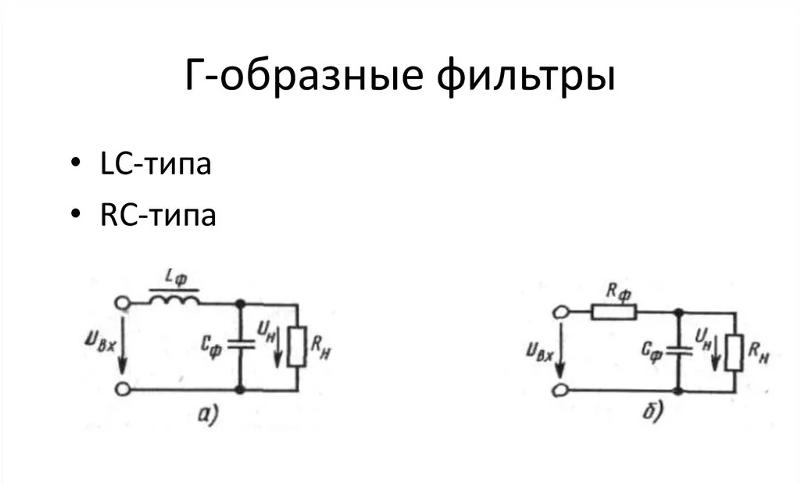 Диапазон частот в герцах между нижней и верхней точками среза по уровню -3 дБ комбинации RC называется «полосой пропускания» фильтра.
Диапазон частот в герцах между нижней и верхней точками среза по уровню -3 дБ комбинации RC называется «полосой пропускания» фильтра.
Ширина или частотный диапазон полосы пропускания фильтра может быть очень маленькой и селективной или очень широкой и неселективной в зависимости от используемых значений R и C.
Точка центральной или резонансной частоты является средним геометрическим нижнего и верхнего срезов. На этой центральной частоте выходной сигнал максимален, а фазовый сдвиг выходного сигнала такой же, как и входного.
Амплитуда выходного сигнала полосового фильтра или любого другого пассивного RC-фильтра всегда будет меньше амплитуды входного сигнала. Другими словами, пассивный фильтр также является аттенюатором, дающим коэффициент усиления по напряжению менее 1 (Единство). Чтобы обеспечить выходной сигнал с коэффициентом усиления по напряжению больше единицы, в конструкции схемы требуется некоторая форма усиления.
Пассивный полосовой фильтр классифицируется как фильтр второго порядка, поскольку в его конструкции есть два реактивных компонента — конденсаторы.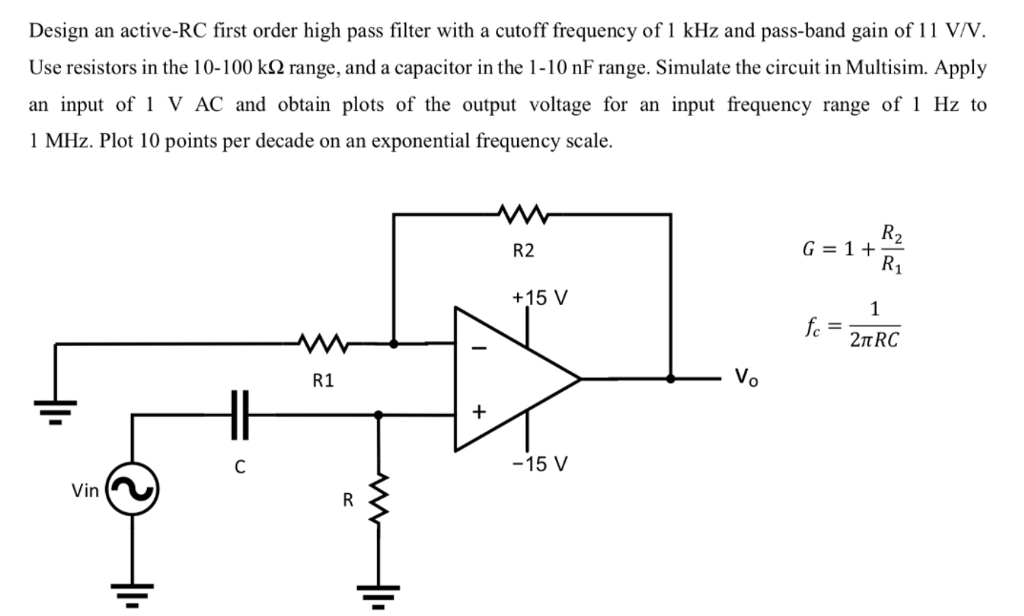 Он состоит из двух отдельных фильтрующих RC-цепей, которые сами являются фильтрами первого порядка.
Он состоит из двух отдельных фильтрующих RC-цепей, которые сами являются фильтрами первого порядка.
При каскадном соединении нескольких фильтров результирующая схема будет называться фильтром «n-го порядка», где «n» означает количество отдельных реактивных компонентов и, следовательно, полюсов в цепи фильтра. Например, фильтры могут быть 2-го порядка, 4-го порядка, 10-го порядка и т.д.
Чем выше порядок фильтра, тем круче будет наклон при n раз -20 дБ/декада. Однако один конденсатор, полученный путем объединения двух или более отдельных конденсаторов, все равно остается одним конденсатором.
Наш пример выше показывает кривую выходной частотной характеристики для «идеального» полосового фильтра с постоянным коэффициентом усиления в полосе пропускания и нулевым коэффициентом усиления в полосе останова. На практике частотная характеристика этой схемы полосового фильтра не будет такой же, поскольку входное реактивное сопротивление цепи высоких частот будет влиять на частотную характеристику цепи низких частот (компоненты подключены последовательно или параллельно) и наоборот.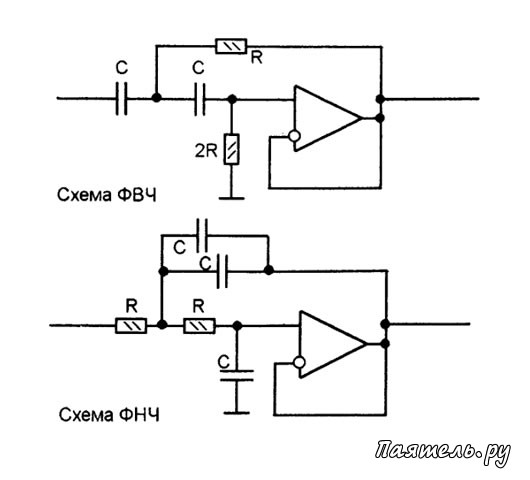 Один из способов преодоления этой проблемы — обеспечить электрическую развязку между двумя цепями фильтра, как показано ниже.
Один из способов преодоления этой проблемы — обеспечить электрическую развязку между двумя цепями фильтра, как показано ниже.
Буферизация отдельных ступеней фильтра
Одним из способов объединения усиления и фильтрации в одной схеме является использование операционного усилителя (Op-amp), примеры которого приведены в разделе «Операционный усилитель». В следующем уроке мы рассмотрим схемы фильтров, в которых операционный усилитель используется не только для усиления, но и для обеспечения изоляции между каскадами. Такие схемы фильтров обычно называются активными фильтрами.
Видеообзор: Пассивный полосовой фильтрИзготовление фильтров нижних и верхних частот с помощью RC-схем Манекены
Изучите книгу Купить на Amazon
Используя простые RC-схемы, вы можете создавать RC-фильтры первого порядка нижних частот (ФНЧ) и верхних частот (ФВЧ).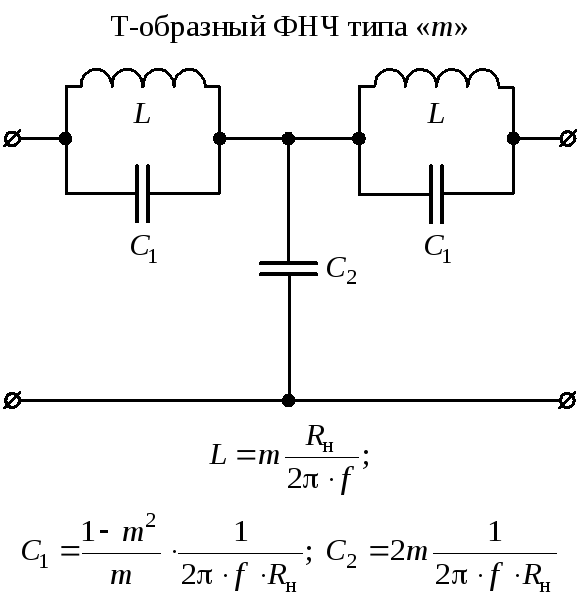
RC-фильтр нижних частот (ФНЧ) первого порядка
Вот цепь RC-цепи — цепь с резистором и конденсатором, соединенными последовательно. Получить ФНЧ можно, сформировав передаточную функцию как отношение напряжения конденсатора В С (с) к напряжению источника В С (2) .
Вы начинаете с уравнения делителя напряжения:
Передаточная функция T(s) равно V C (s)/V S (s) . С некоторой алгеброй (включая умножение числителя и знаменателя на
У вас есть полюсная или угловая (граничная) частота при с = –1/(RC) , и у вас есть коэффициент усиления по постоянному току, равный 1 при с = 0.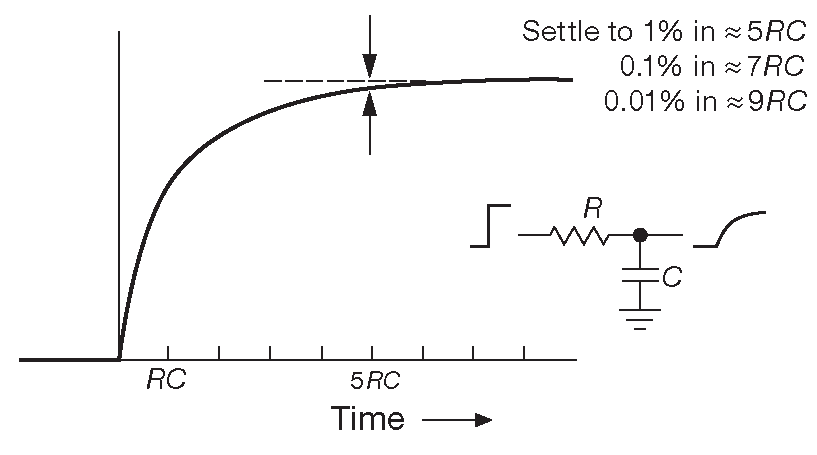 Частотная характеристика начинается при с = 0 с плоское усиление 0 дБ. Когда он достигает 1/(RC) частотная характеристика имеет наклон –20 дБ/декаду.
Частотная характеристика начинается при с = 0 с плоское усиление 0 дБ. Когда он достигает 1/(RC) частотная характеристика имеет наклон –20 дБ/декаду.
Для цепей только с пассивными устройствами коэффициент усиления никогда не превышает 1.
RC-фильтр верхних частот первого порядка (HPF)
Чтобы сформировать фильтр верхних частот, вы можете использовать те же резистор и конденсатор, соединенные последовательно, как показано ранее, но на этот раз вы измеряете напряжение резистора
С помощью некоторых алгебраических операций (включая умножение числителя и знаменателя на s/R ) можно найти передаточную функцию фильтр верхних частот:
У вас есть ноль на с = 0 и полюс на с = –1/(RC ). Вы начинаете частотную характеристику с нуля с положительным наклоном 20 дБ/декаду, а затем характеристика выравнивается, начиная с 9.
Об этой статье
Эта статья взята из книги:
- Анализ цепей для чайников,
Об авторе книги:
Джон М. Сантьяго-младший, доктор наук, служил в ВВС США (USAF). ) в течение 26 лет. В течение этого времени он занимал различные руководящие должности в области управления техническими программами, разработки приобретений и поддержки исследований в области эксплуатации. Находясь в Европе, он руководил более чем 40 международными научными и инженерными конференциями/семинарами.
Эту статью можно найти в категории:
- Схема ,
Пассивный фильтр высоких частот
Ранее мы обсуждали пассивный фильтр нижних частот, теперь пришло время взглянуть на пассивный фильтр высоких частот.
То же, что и раньше, если вы посмотрите на имя, оно покажет «Пассивный», «Высокий», «Проходной» и «Фильтр». Итак, как следует из названия, это фильтр, который блокирует низкие частоты , но пропускает высокие частоты выше заданного значения, которое будет рассчитано по формуле.
Это «пассивный» , что означает отсутствие внешнего питания, отсутствие усиления входного сигнала; мы сделаем схему, используя «пассивные» компоненты, которые не требуют внешнего источника питания. Пассивные компоненты такие же, как фильтр нижних частот, но порядок подключения будет точно обратным. Пассивными компонентами являются резистор (R) и конденсатор
(C). Опять же, это конфигурация RC-фильтра.
Давайте посмотрим, что произойдет, если мы построим схему и проверим отклик или «график Боде»…
Вот схема на этом изображении:
Это RC-фильтр. Как правило, входной сигнал подается на эту комбинацию серии из неполяризованного конденсатора и резистора .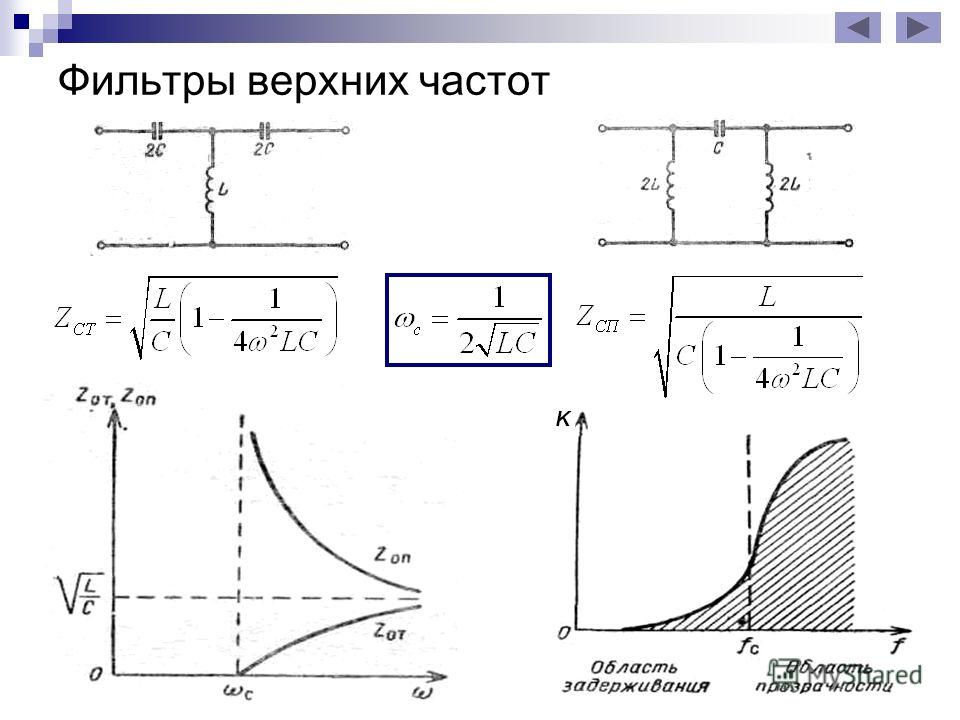 Это фильтр первого порядка, так как в схеме есть только один реактивный компонент — конденсатор. Отфильтрованный выход будет доступен через резистор. Комбинация этого дуэта прямо противоположна фильтру нижних частот. Если мы сравним схему с фильтром нижних частот, то увидим, что резистор и конденсатор поменялись местами.
Это фильтр первого порядка, так как в схеме есть только один реактивный компонент — конденсатор. Отфильтрованный выход будет доступен через резистор. Комбинация этого дуэта прямо противоположна фильтру нижних частот. Если мы сравним схему с фильтром нижних частот, то увидим, что резистор и конденсатор поменялись местами.
Как работает фильтр верхних частот?
На низких частотах реактивное сопротивление конденсатора будет очень большим, поэтому он будет действовать как разомкнутая цепь и блокировать входной сигнал ниже частоты среза (fc). Но когда достигается частота среза, реактивное сопротивление конденсатора начинает уменьшаться, позволяя сигналу проходить напрямую. Мы увидим это подробно на кривой частотной характеристики.
Вот кривая, как это выглядит на выходе конденсатора: —
Частотная характеристика и частота среза
Это кривая частотной характеристики этой схемы фильтра верхних частот первого порядка .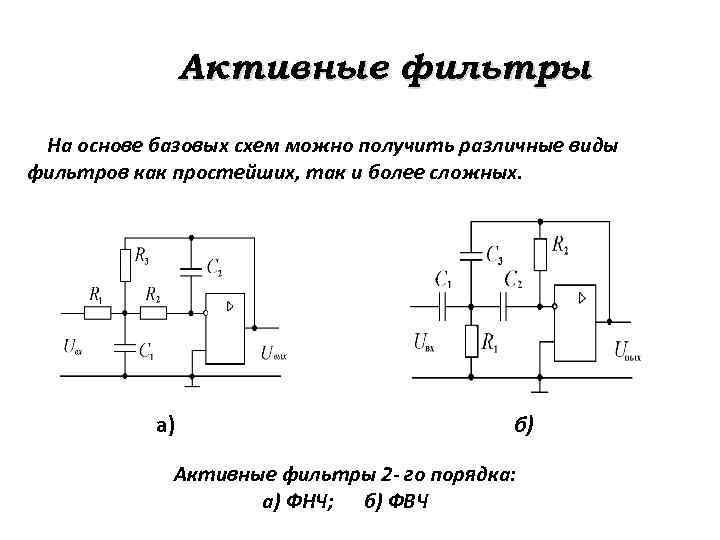
f c Частота среза фильтра. В точке
Формула расчета усиления такая же, как мы использовали в нашем предыдущем уроке для пассивного фильтра нижних частот.
Усиление (дБ) = 20 log (Vout / Vin)
После сигнала отсечки ответы схемы постепенно увеличиваются до
Эта кривая частотной характеристики представляет собой график Боде фильтра верхних частот. Выбрав правильный конденсатор и соответствующий резистор, мы могли бы остановить низкие частоты, ограничить сигнал, проходящий через схему фильтра, не влияя на сигнал, поскольку нет активного отклика.
Выбрав правильный конденсатор и соответствующий резистор, мы могли бы остановить низкие частоты, ограничить сигнал, проходящий через схему фильтра, не влияя на сигнал, поскольку нет активного отклика.
На изображении выше есть слово Пропускная способность . Это означает, после какой частоты будет проходить сигнал. Итак, если это фильтр высоких частот 600 кГц, то полоса пропускания будет от 600 кГц до 9 кГц.0137 Бесконечность
На частоте среза мы получим усиление -3дБ. В этот момент, если мы сравним амплитуду выходного сигнала с входным сигналом, мы увидим, что амплитуда выходного сигнала будет составлять 70,7% от входного сигнала. Также при усилении -3 дБ емкостное сопротивление и сопротивление будут одинаковыми. R=Хс.
Какова формула частоты среза?
Формула частоты среза точно такая же, как у фильтра низких частот.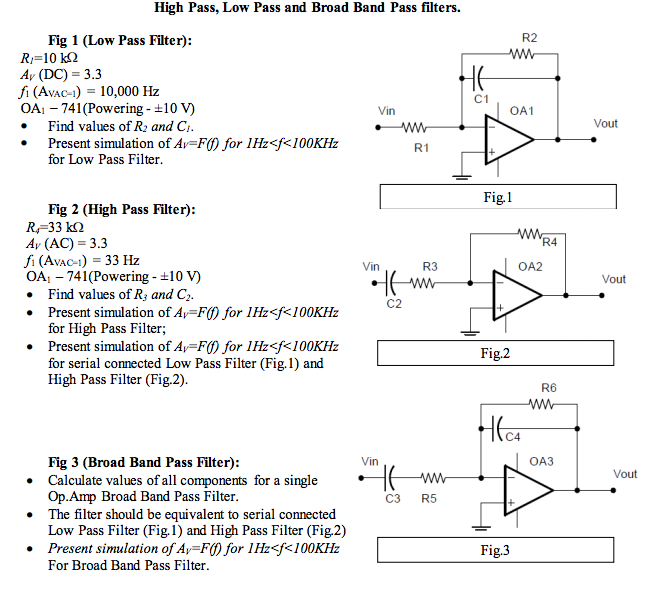
f c = 1/2πRC
Итак, R — сопротивление, а C — емкость. Если мы поставим значение, мы будем знать частоту среза.
Расчет выходного напряжения
Давайте посмотрим на первое изображение, схему, в которой 1 резистор и один конденсатор используются для формирования фильтра верхних частот или RC-цепи.
Когда сигнал постоянного тока подается на цепь, сопротивление цепи создает падение при протекании тока. Но в случае сигнала переменного тока не сопротивление, а импеданс отвечает за падение напряжения, которое тоже измеряется в Омах.
В RC цепи два резистивных элемента . Один — сопротивление, а другой — емкостное реактивное сопротивление конденсатора. Итак, нам нужно сначала измерить емкостное реактивное сопротивление конденсатора, так как это потребуется для расчета импеданса схемы.
Первая резистивная оппозиция является емкостной реактивностью , формула:-
Xc = 1 / 2πfC
Выход формулы будет в Омах, поскольку Ом является единицей емкостного реактивного сопротивления, потому что это сопротивление означает сопротивление.
Второй оппозицией является сам резистор . Значение резистора также является сопротивлением.
Таким образом, объединив эти две оппозиции, мы получим общее сопротивление, которое является импедансом в цепи RC (вход переменного тока).
Полное сопротивление обозначается как Z
Формула:-
конденсатор 9.0137 Бесконечность на низкой частоте поэтому блокирует сигнал. Выходное усиление равно 0 в это время , и из-за блокировки выходное напряжение остается равным 0 , пока не будет достигнута частота среза.
Но на высокой частоте произойдет обратное реактивное сопротивление конденсатора слишком низкое, что приведет к короткому замыканию , реактивное сопротивление конденсатора равно 0 на высокой частоте поэтому сигнал передается. Выходное усиление в это время равно 1, то есть ситуация с единичным усилением, и из-за единичного усиления выходное напряжение такое же, как и входное напряжение после достижения частоты среза.
Пример с расчетом
Поскольку мы уже знаем, что на самом деле происходит внутри схемы и как узнать значение. Выберем практические значения.
Возьмем наиболее распространенные значения резистора и конденсатора, 330k и 100pF. Мы выбрали значение, так как оно широко доступно и его легче рассчитать.
Посмотрим, какая будет частота среза и какое будет выходное напряжение.
Частота отсечки будет:-
При решении этого уравнения частота среза составляет 4825 Гц или 4,825 кГц .
Посмотрим, правда это или нет…
Это схема примера.
В соответствии с частотной характеристикой, описанной ранее, на частоте среза дБ будет
-3 дБ, независимо от частоты. Мы будем искать -3dB в выходном сигнале и посмотрим, является ли это 4825 Гц (4,825 кГц) или нет.
Вот частотная характеристика: —
Установите курсор на -3 дБ и посмотрите результат.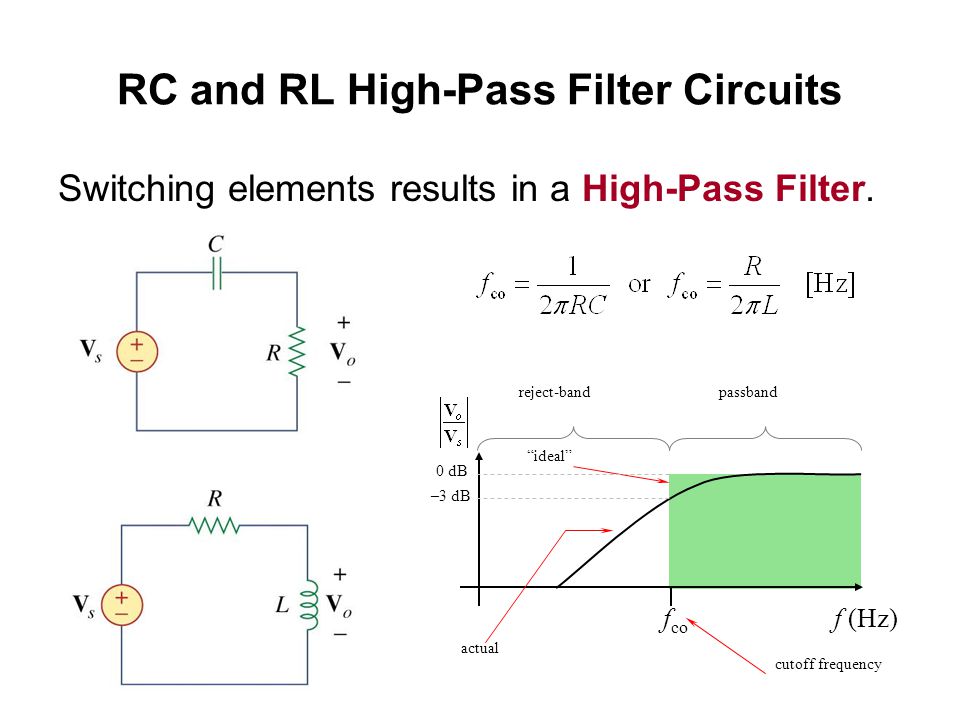
Поскольку мы можем видеть частотную характеристику (также называемую графиком Боде ), мы устанавливаем курсор на -3,03 дБ и получаем 4,814 кГц Полоса частот .
Фазовый сдвиг
Фазовый угол, обозначаемый как φ (Phi), будет на выходе равен +45 от входного сигнала при -3 дБ или частоте среза.
Как видно из АЧХ фильтра, он может пропускать все сигналы выше частоты среза до бесконечности. Это просто теоретическая практика. В практическом и реальном мире полоса пропускания ограничена ограничениями практических компонентов.
Формула фазового сдвига отличается от формулы фильтра нижних частот, так как в фильтре нижних частот фаза стала отрицательной, а в фильтре верхних частот сдвиг фазы положительный, поэтому формула подразумевает следующее: —
Фазовый сдвиг φ = arctan (1 / 2πfRC)
Давайте посмотрим на кривую фазового сдвига схемы: —
Это фазовый сдвиг схемы, используемый в качестве практического примера.
Узнаем значение фазового сдвига на частоте среза:-
Устанавливаем курсор на +45 и получаем в результате частоту среза 4.82КГц .
Постоянная времени
Как мы уже узнали ранее о фазовом сдвиге и частотной характеристике, конденсатор заряжается и разряжается в зависимости от частот входного сигнала. Этот эффект зарядки и разрядки является постоянной времени и обозначается как τ (Тау). Это также связано с частотой среза.
Как?
τ = RC = 1/2π f c
Иногда нам нужно знать частоту среза, когда у нас есть значение постоянной времени, в таком случае, изменяя формулу, мы можем легко получить это: —
фк = 1/2πRC Где RC = τ fc = 1 / 2πτ
Влияние постоянной времени в фильтре верхних частот:
Фильтр верхних частот является дифференциатором. Если мы подадим прямоугольную волну и предоставим ее в идеальной временной области, форма выходной волны фильтра создаст пики или короткие импульсы. Если постоянная времени короткая, фильтр будет генерировать дифференцированную прямоугольную волну. Мы можем различать сигнал, используя это свойство фильтра верхних частот.
Если постоянная времени короткая, фильтр будет генерировать дифференцированную прямоугольную волну. Мы можем различать сигнал, используя это свойство фильтра верхних частот.
Фильтр нижних частот второго порядка: формулы, расчеты и частотные кривые
Когда две каскадные RC-цепи нижних частот первого порядка соединены вместе, это называется фильтром второго порядка, поскольку имеется две цепи RC-ступеней.
Вот схема: —
Это фильтр верхних частот второго порядка. КОНДЕНСАТОР и РЕЗИСТОР — это первый порядок, а КОНДЕНСАТОР1 и РЕЗИСТОР1 — второй порядок. Каскадируя вместе, они образуют фильтр верхних частот второго порядка.
Фильтр второго порядка играет роль наклона 2 x +20 дБ/декада или +40 дБ (12 дБ/октава).
Вот кривая отклика: —
Наклон +20дБ/декада и красный на конечном выходе, который имеет наклон +40дБ/декада.
Это рассчитает частоту среза контура верхних частот второго порядка.