Последовательная RC- цепочка на переменном токе. OrCAD PSpice. Анализ электрических цепей
Последовательная RC- цепочка на переменном токе. OrCAD PSpice. Анализ электрических цепейВикиЧтение
OrCAD PSpice. Анализ электрических цепей
Кеоун Дж.
Содержание
Последовательная RC-цепочка на переменном токе
Заменив в схеме на рис. 2.1 катушку индуктивности конденсатором С, получим следующую схему (рис. 2.3).
Значения компонентов в этой схеме: R=5 Ом; С=100 мкФ и f=318 Гц.
Рис. 2.3. Схема с последовательной RC-цепочкой
Входной файл будет следующим:
AC Circuit with Resistance and Capacitance in Series
V 1 0 AC 1V
R 1 2 5
С 2 0 100uF
.AC LIN 1 318Hz 318Hz
.PRINT AC I(R) IP(R) V(2) VP(2)
.END
В команде .PRINT через V(2) и VP(2) обозначены модуль и фазовый угол напряжения на конденсаторе соответственно.
Рис. 2.4. Векторная диаграмма для последовательной RC-цепи
Данный текст является ознакомительным фрагментом.
Пример: последовательная обработка файлов с использованием метода отображения
Пример: последовательная обработка файлов с использованием метода отображения Программа atou (программа 2.4) иллюстрирует последовательную обработку файлов на примере преобразования ASCII-файлов к кодировке Unicode, приводящего к удвоению размера файла. Этот случай является
7.2.6.2. Цепочка allowed
7.
2.6.2. Цепочка allowed
TCP пакет, следуя с интерфейса $INET_IFACE, попадает в цепочку tcp_packets, если пакет следует на разрешенный порт, то после этого проводится дополнительная проверка в цепочке allowed.Первое правило проверяет, является ли пакет SYN пакетом, т.е. запросом на соединение.
7.2.6.3. Цепочка для TCP
7.2.6.3. Цепочка для TCP Итак, мы подошли к TCP соединениям. Здесь мы указываем, какие порты могут быть доступны из Internet. Несмотря на то, что даже если пакет прошел проверку здесь, мы все равно все пакеты передаем в цепочку allowed для дополнительной проверки.Я открыл TCP порт с номером
7.2.6.4. Цепочка для UDP
7.2.6.4. Цепочка для UDP
Пакеты UDP из цепочки INPUT следуют в цепочку udp_packets Как и в случае с TCP пакетами, здесь они проверяются на допустимость по номеру порта назначения.
1. Анализ цепей на постоянном токе
1. Анализ цепей на постоянном токе Цепи постоянного тока важны не только сами по себе, но и потому, что многие приемы, применяемые при их анализе, используются и при анализе цепей переменного тока. В действительности анализ большинства электронных цепей и приборов может
Вариация параметров на постоянном токе
Вариация параметров на постоянном токе Поскольку в задачах на применение контурных токов мы столкнулись с проблемой вариации параметров на постоянном токе (dc sweep), рассмотрим пример, в котором такая вариация используется нормальным образом, в некотором диапазоне
2. Анализ цепей на переменном токе (для установившихся синусоидальных режимов)
2.
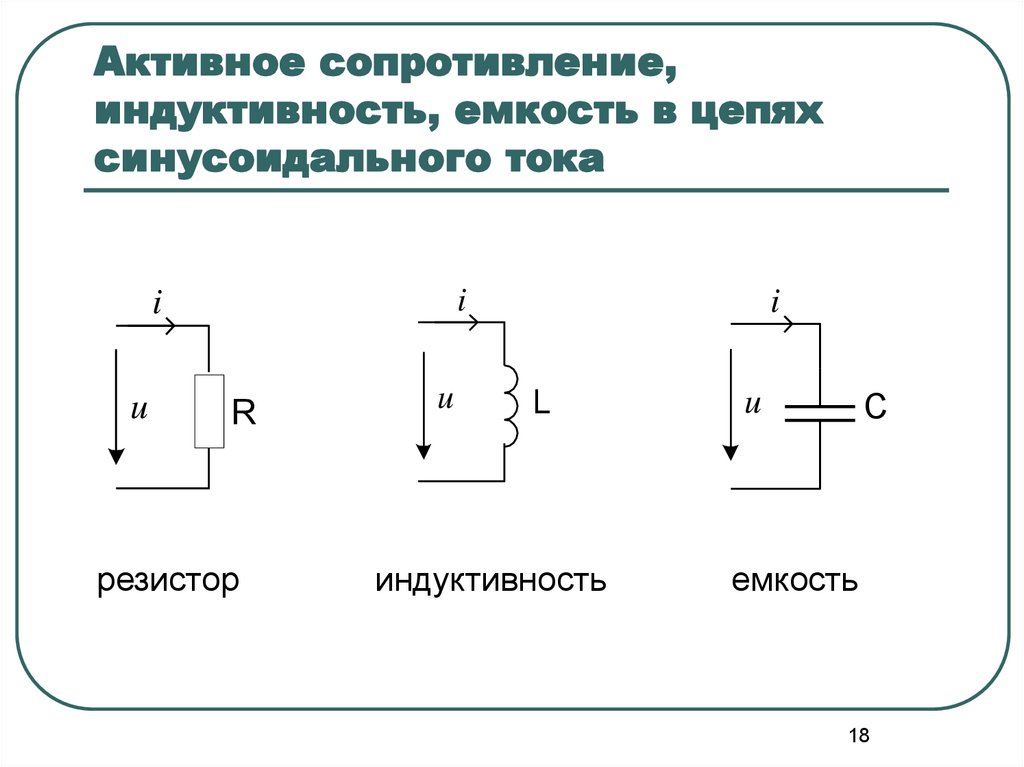Анализ цепей на переменном токе (для установившихся синусоидальных режимов)
Spice показывает напряжения узлов на постоянном токе без всяких специальных команд, поскольку определение напряжений постоянного тока является необходимым для получения рабочих точек в
Последовательная RC- цепочка на переменном токе
Последовательная RC-цепочка на переменном токе Заменив в схеме на рис. 2.1 катушку индуктивности конденсатором С, получим следующую схему (рис. 2.3).Значения компонентов в этой схеме: R=5 Ом; С=100 мкФ и f=318 Гц. Рис. 2.3. Схема с последовательной RC-цепочкойВходной файл будет
Параллельные ветви на переменном токе
Параллельные ветви на переменном токе
Рассмотрим теперь процессы в параллельной RL-цепи при питании ее от источника переменного тока (рис. 2.5).
Рис. 2.5. Схема с параллельной RL-цепьюПараметры компонентов: I=100?0° мА; R=8,33333 Ом; L=6,36 мГн.
Для этой цепи необходимо найти напряжение
Анализ на переменном токе
Анализ на переменном токе Чтобы показать, как ведет себя эта схема в качестве усилителя ОЭ, добавим несколько компонентов (рис. 10.9). Максимальное значение переменного напряжения равно 10 мВ, внутреннее сопротивление источника Rs=50 Ом, кроме того добавлены конденсаторы Сb и
Последовательные цепи на постоянном токе
Последовательные цепи на постоянном токе Простая схема постоянного тока, состоящая из источника напряжения и трёх резисторов, могла бы быть описана в уже знакомом нам листинге:Series Circuit with Source and Three ResistorsV1 1 0 2 4VR1 1 2 50R2 2 3 100R3 3 0 80В PSpice это был бы листинг входного или схемного
Проведение анализа с вариацией на переменном токе
Проведение анализа с вариацией на переменном токе
Начните моделирование, выбрав PSpice, New Simulation Profile.
Введите имя ac1s. Выберите тип анализа AC Sweep/Noise при линейной вариации частоты от 60 до 60 Гц (рис. 14.18). Затем нажмите OK. Вспомним, что в главе 2 значения переменного тока
Получение синусоидальных временных диаграмм при анализе на переменном токе
Последовательная RC- цепь
Последовательная RC-цепь
Во втором примере главы 2 рассматривалась схема, содержащая источник переменного тока, включенный последовательно с резистором и конденсатором. Анализ выполнялся при частоте f=318 Гц. Используйте Capture, чтобы создать новый проект ac2.
Анализ на переменном токе
Анализ на переменном токе Дополним рисунок предыдущего примера, который был назван bjtcase (откройте его опять в случае необходимости). Добавим компоненты, как показано на рис. 10.9, преобразовав его в усилитель ОЭ, выходное напряжение которого снимается с коллектора. Если
Цепочка вызовов
Цепочка вызовов Обсуждая механизм обработки исключений, полезно иметь ясную картину последовательности вызовов, приведших в итоге к исключению. Это понятие уже появлялось при рассмотрении механизма языка Ada. Рис. 12.1. Цепочка вызововПусть r0 будет корневой процедурой
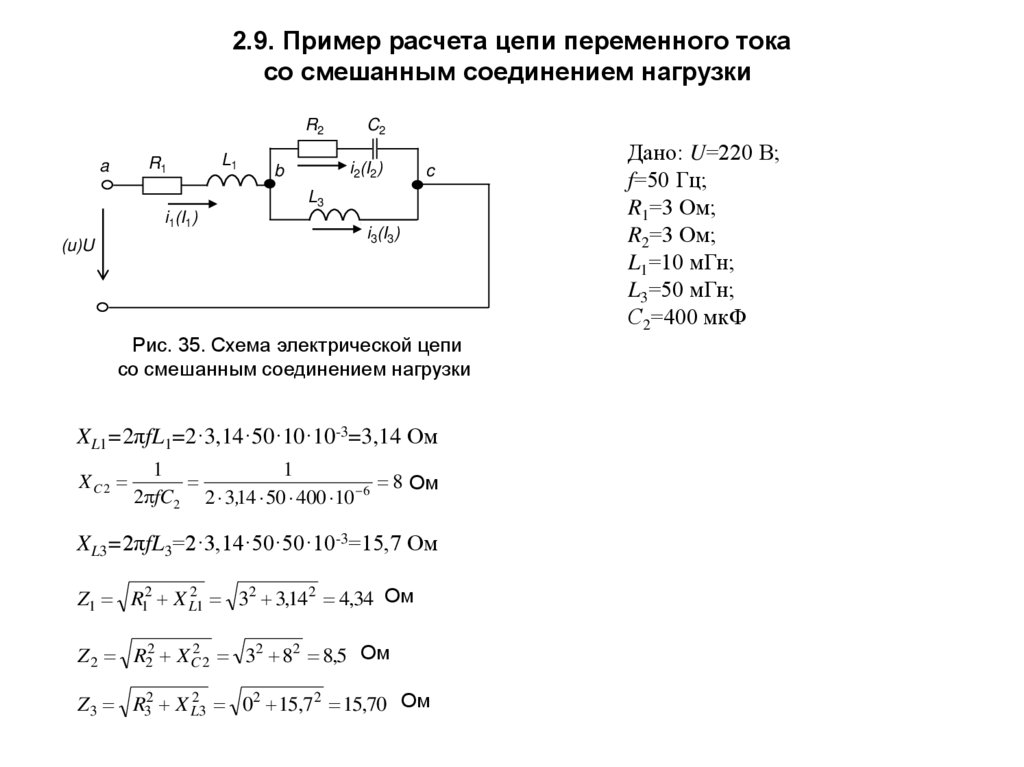
2.6 Примеры расчета в цепях переменного тока
2.6.1 Последовательная r-c цепь
Рассмотрим R—C цепь на примере задачи.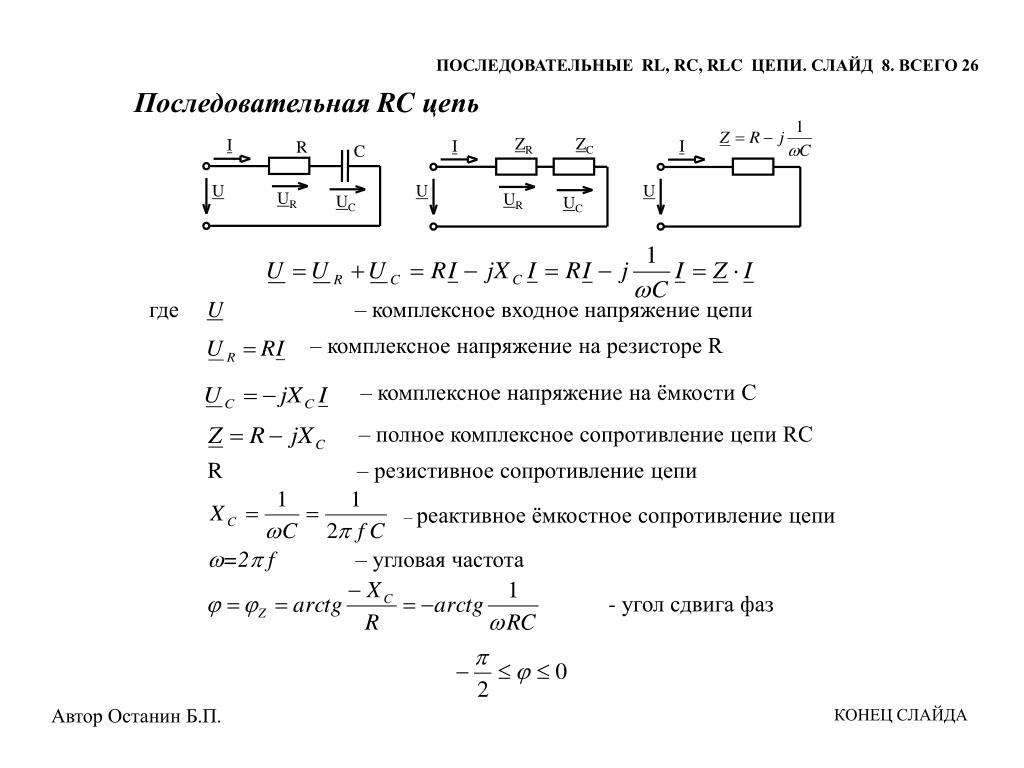
Дана цепь из последовательно соединенных R и C элементов (рис. 2.11) , Напряжение на входе
Найти ток , падения напряжений на каждом из элементов, мощности , построить векторную диаграмму токов и напряжений.
Рис. 2.11 – Цепь последовательно соединенных R и C элементов
Решение:
Записываем комплексы сопротивлений: , .
Сопротивление всей цепи равно сумме комплексных сопротивлений .
Модуль полного сопротивления .
По закону Ома:
.
Модуль тока: ,
Модуль тока можно определить так же следующим способом:
Комплексное падение напряжения на резистивном элементе R по закону Ома:
.
Комплексное падение напряжения на емкостном элементе С по закону Ома:
.
Измерительные приборы (вольтметр, амперметр, ваттметр) показывает модуль комплекса измеряемой величины.
Модуль (то, что покажет вольтметр):
;
.
Проверка:
По второму закону Кирхгофа:
,
или из прямоугольного треугольника (рис. 2.10):
.
Рассчитываем мощности:
Активная: ;
Реактивная: ;
Полная: ;
.
Коэффициент мощности: .
Угол φ определяем по тангенсу угла или из векторной диаграммы. Угол положительный.
Ток I опережает напряжение на входе на угол .
Строим векторную диаграмму по точкам (координатам) в соответствии с выбранным масштабом.
Рис.
2.12 – Векторная
диаграмма
2.6.2 Последовательная r-l цепь
Рассмотрим R—L цепь на примере задачи.
Дана цепь из последовательно соединенных R и L элементов (рис. 2.13) б, Напряжение на входе
Найти ток I, падения напряжений на каждом из элементов, мощности , построить векторную диаграмму токов и напряжений.
Рис. 2.13 – Цепь последовательно соединенных R и L элементов
Решение:
1) Записываем комплексы сопротивлений: , ;
2) Общее сопротивление цепи равно сумме комплексов сопротивлений ;
3) Модуль ;
4) Рассчитаем комплексный ток в цепи по закону Ома:
;
5) Модуль тока: .
Модуль тока можно определить и стандартным способом:
6) Комплексное падение напряжения на резистивном элементе R по закону Ома:
;
7) Комплексное падение напряжения индуктивном элементе L по закону Ома:
.
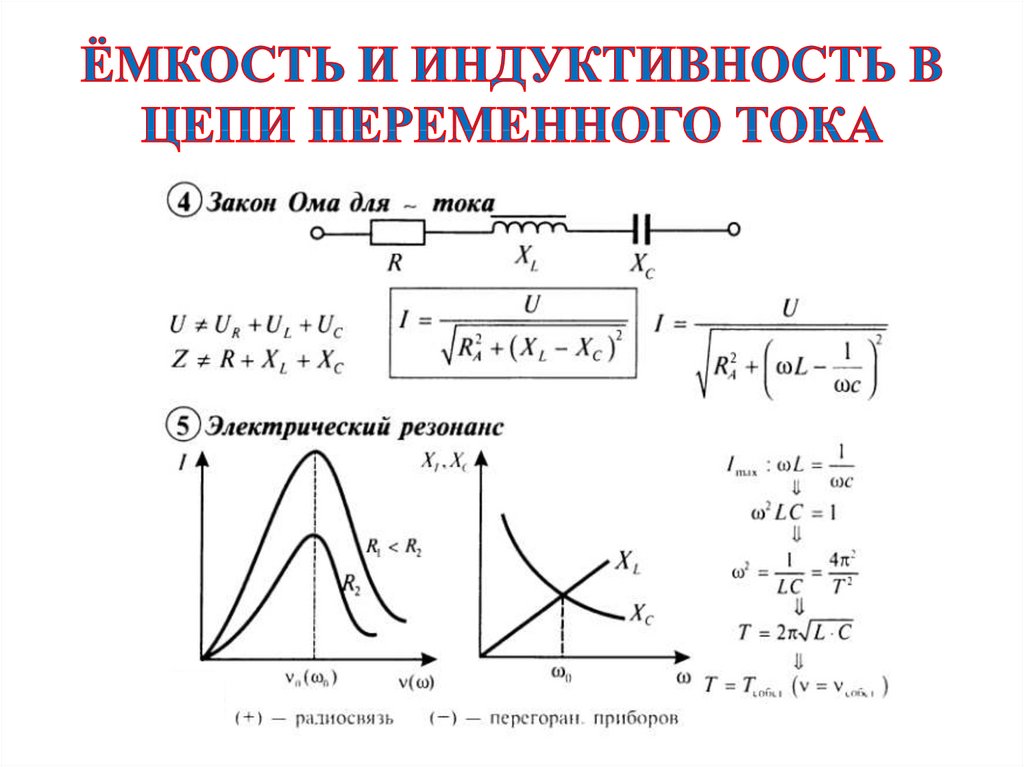
Измерительные приборы (вольтметр, амперметр, ваттметр) показывает модуль комплекса измеряемой величины;
8) Рассчитаем модули падений напряжений:
;
;
9) Проверка:
По второму закону Кирхгофа:
,
или из прямоугольного треугольника (рис. 2.10):
;
10) Рассчитываем мощности:
Активная: ;
Реактивная: ;
Полная : ;
;
11) Коэффициент мощности: ;
12) Знак угла φ определяем по тангенсу угла или из векторной диаграммы. Угол положительный.
Ток в цепи отстает от входного напряжения на угол 360.
Строим векторную диаграмму по точкам
(координатам) в соответствии с выбранным
масштабом.
Рис. 2.14 – Векторная диаграмма
2.7 Частотные свойства цепей переменного тока
Частотной характеристикой называется зависимость параметров цепи от частоты (например ). Активное сопротивление устройств от частоты не зависит. Зависимость индуктивного и емкостного сопротивлений от частоты определяется формулами:
и . Графики зависимости реактивных сопротивлений от частоты представлены на рис. 2.15.
Рис. 2.15 – Графики зависимости реактивных сопротивлений
от частоты
Рассмотрим цепь из последовательно соединенных R, L, C элементов (рис. 2.15). На участке цепи с последовательно соединенными R, L, C элементами найдется такая частота (резонансная) при которой сопротивления и окажутся равными.
При этом, и полное сопротивление Z окажется чисто активным и равным R.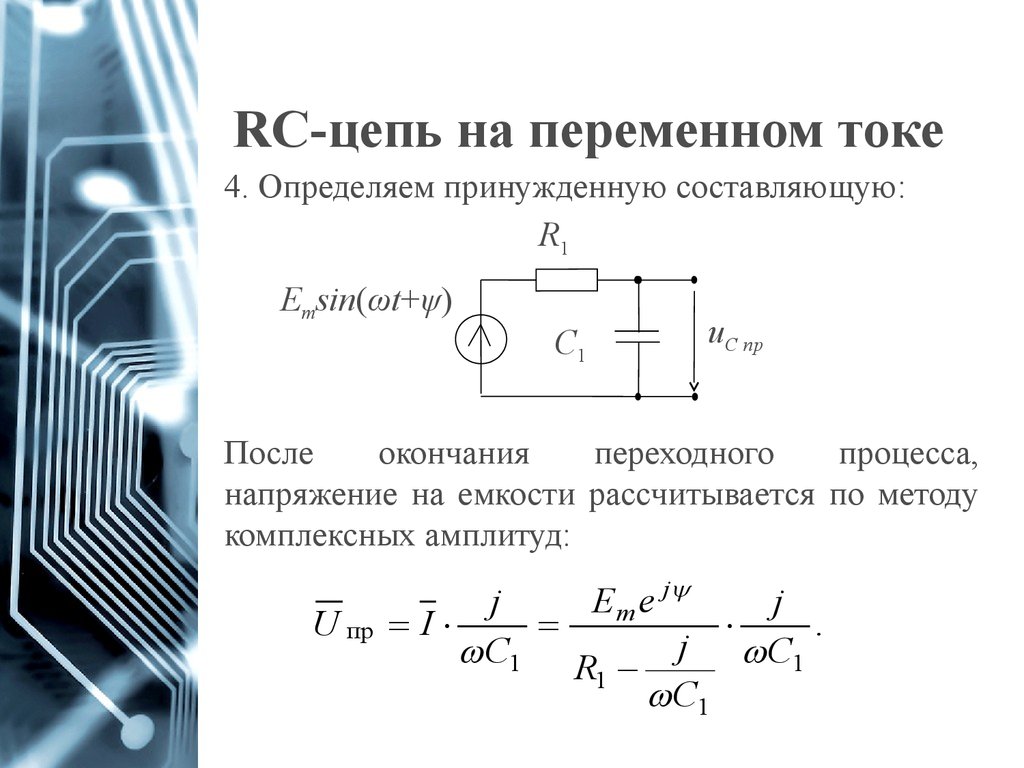
Такой режим называется режимом резонанса
напряжений. Резонансная частота:
.
Пример: Дана цепь из последовательно соединенных R, L, C элементов . Определить токи , напряжения, мощности и и изучить их зависимости от частоты.
Рис. 2.16
1) Согласно второго закона Кирхгофа:
ЭДС источника отсутствует, Е = 0, контур К обходим по часовой стрелке
Так как цепь последовательная, то ток один и тот же, поэтому:
.
Рассчитаем ток в цепи: .
Если
,
то то есть сопротивление цепи становиться
чисто омическим, при этом ток в цепи
максимальный
,
а падения напряжений на емкости и
индуктивности будут по величине
одинаковыми: , но фазы напряжений
,
,
сдвинуты на 180 градусов, то есть направления
векторов
,
,
противоположны.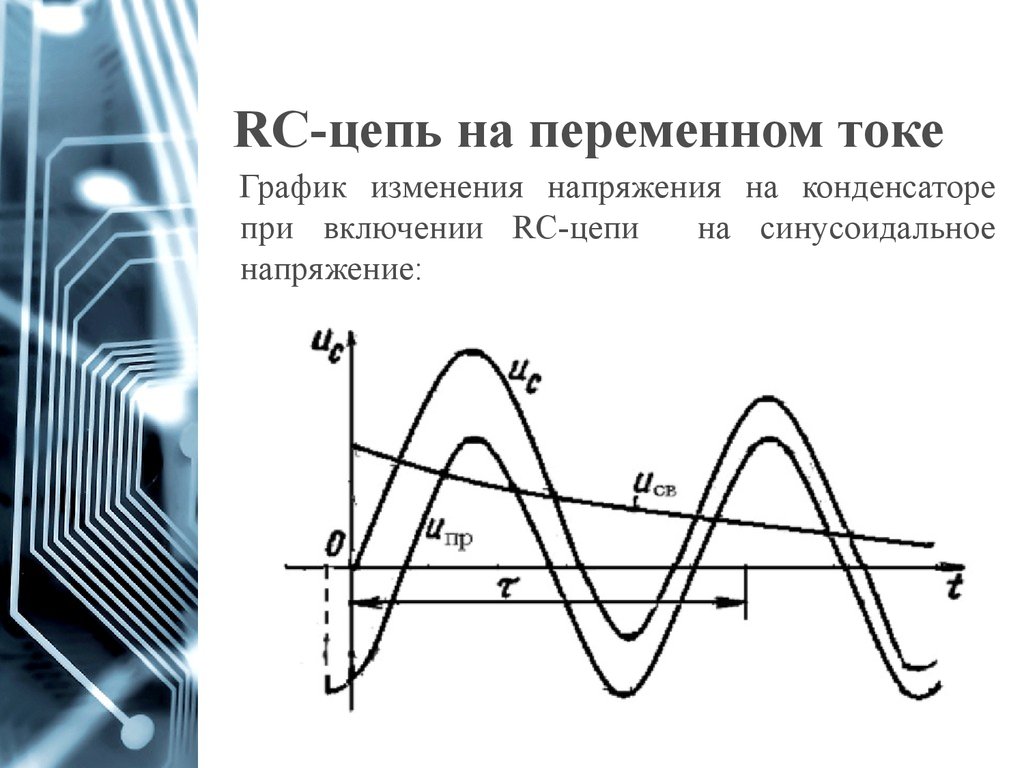
Или говорят, что
напряжения на индуктивности и на емкости
находятся в противофазе.
Сдвиг фаз между током и входным напряжением:
,
так как при резонансе .
Вывод:
1) При резонансе напряжений величина напряжения на конденсаторе равна величине напряжения на индуктивности.
2) Напряжения на всех элементах схемы максимальны:
.
3) При резонансе напряжений сдвиг фаз между входным напряжением и током в цепи равен нулю.
4) Резонансная частота рассчитывается из условия равенства величин реактивных сопротивлений: или .
5) Суммарное напряжение на реактивных элементах при резонансе равно нулю. Между точками б и г напряжение равно нулю. Вольтметр, включенный между точками б и г покажет 0 (ноль) вольт.
6) Падение напряжения на сопротивлении равно входному напряжению
.
7) Полная мощность в цепи будет чисто активной. , так как .
Активная мощность в цепи будет максимальной: .
8) Реактивные мощности на каждом из реактивных элементов так же максимальны и равны соответственно:
;
.
Суммарная реактивная мощность при резонансе равна нулю, .
Рис. 2.17 – Векторная диаграмма токов и напряжений при резонансе при последовательномсоединении R, L, C элементов
Вероятные вопросы при тестировании по теме 2.7:
1.Резонансная частота в цепи при последовательном соединении R,L,C элементов равна :
(а)
(б)
(в)
(г)
(Ответ (в)
1. При резонансе в цепи при последовательном соединении R,L,C элементов максимальный ток равен:
(а)
(б)
(в)
(г)
(Ответ (б)
3.
При
резонансе коэффициент мощности cos
φ
равен:
(а)- 0;
(б)- 0,5;
(в)- 0,865;
(г)- 1.0
(Ответ (г)
4.При резонансе напряжение на конденсаторе UC сдвинуто относительно напряжения на индуктивности UL на угол:
(а)- 0 ˚;
(б)- минус180˚;
(в)- плюс90˚;
(г)- плюс 45˚
(Ответ( б)
4.При резонансе потребляемая мощность :
(а)- чисто активная;
(б)- чисто реактивная ;
(в)- ;
(г )-
(Ответ( а)
3
3.1 Трехфазные цепи. Основные понятия. Элементы трехфазных цепей
Определения
Трехфазной цепью называют электрическую цепь образованной из источника трехфазной ЭДС и трехфазного приемника.
Трехфазный
генератор, принцип действия и устройство.
Трехфазный генератор состоит из трех однофазных генераторов расположенных в одном корпусе. Оси обмоток каждого из генераторов геометрически смещены относительно друг друга на или на 1/3 оборота.
На рис. 3.1 (а) схематично показано устройство трех фазного генератора.
Рис. 3.1 –Трехфазный генератор
а – схематичное изображение устройства генератора, b – схема соединения обмоток генератора по схеме звезда без нейтрального провода, c – схема замещения (идеального) трехфазного генератора
На статоре расположены 3 пары обмоток AX, BY, CZ. Ротор (электромагнит
или постоянный магнит) при равномерном
вращении возбуждает в каждой из обмоток
(фазах) переменную (синусоидальную) ЭДС
(согласно закону электромагнитной
индукции). Так как оси обмоток геометрически
смещены на
,
(1/3 оборота), то время наступления
максимума ЭДС в каждой обмотке будет
сдвинуто на 1/3 периода вращения ротора.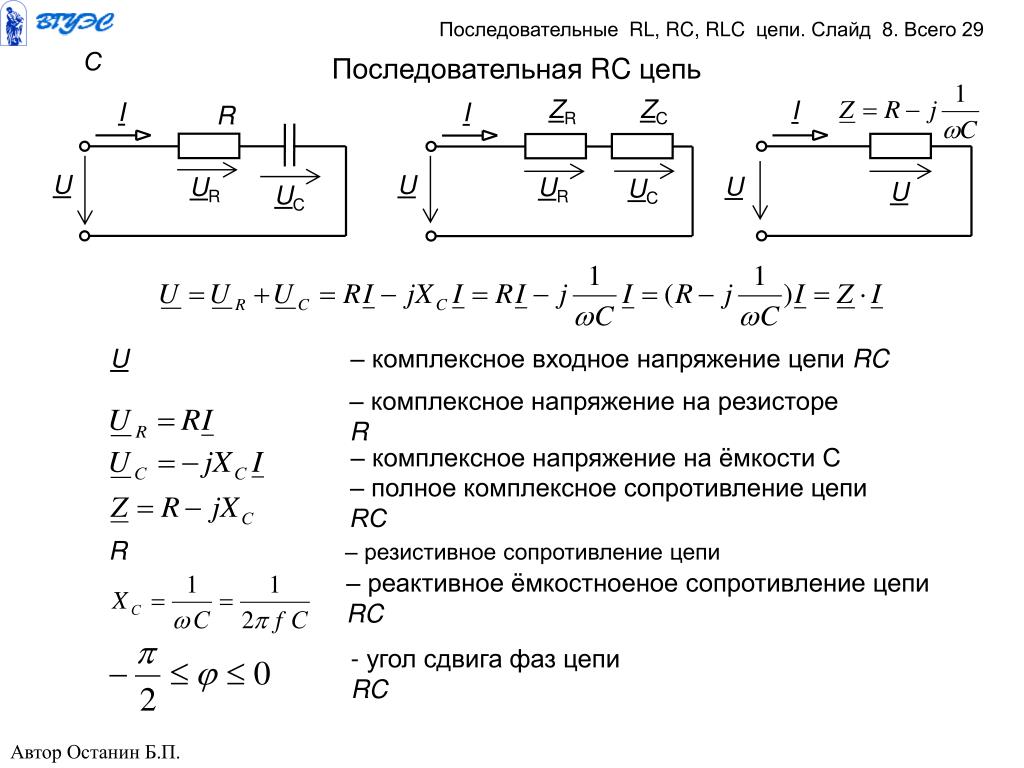
Говорят, что фазы ЭДС в каждой из обмоток
сдвинуты на 1200.
Закон изменения и соответствующие графики мгновенных значений фазных ЭДС на клеммах генераторов можно представить в виде уравнений и графиков на рис. 3.2:
Рис. 3.2 – Эпюры мгновенных значений фазных напряжений трех фазного генератора
Большими буквами А, В, С и X, Y, Z обозначают начала и концы обмоток генератора. Концы и начала сопротивлений нагрузки обозначают малыми буквами a, b, с и x, y, z соответственно.
Обмотки генератора могут соединяться по схеме звезда (с выводом и без вывода нейтрального провода) или по схеме треугольник. Внутренне сопротивление генератора мало и в дальнейшем будем считать его равным нулю ().
а б
Рис.
3.3 – Схемы замещения и условные
обозначение схем соединения трех фазных
обмоток генератора по схеме звезда (а)
и по схеме треугольник (б)
На электрических схемах они обозначаются следующим образом:
Рис. 3.4 – Условные обозначения схем соединений обмоток генератора: звезда, звезда с нейтральным проводом, треугольник
Комплексные ЭДС генератора представляются в виде:
Напряжение на клеммах генератора , , (при ) равно соответственно ЭДС генератора , , .
Для симметричного генератора выполняется соотношение:
.
Соединение генератора и приемника по схеме звезда – звезда
Соединение генератора и приемника по схеме звезда –звезда приведены на рис. 3.5.
Рис. 3.5 – Соединение приемника и генератора звездой
Определения и обозначения
– фазные напряжения генератора;
При соединении звездой фазные напряжения генератора обозначают: ;
– фазное напряжение нагрузки;
– линейные напряжения генератора;
– линейные напряжения нагрузки;
– фазный ток нагрузки фазы А;
– линейный ток в проводе Аа;
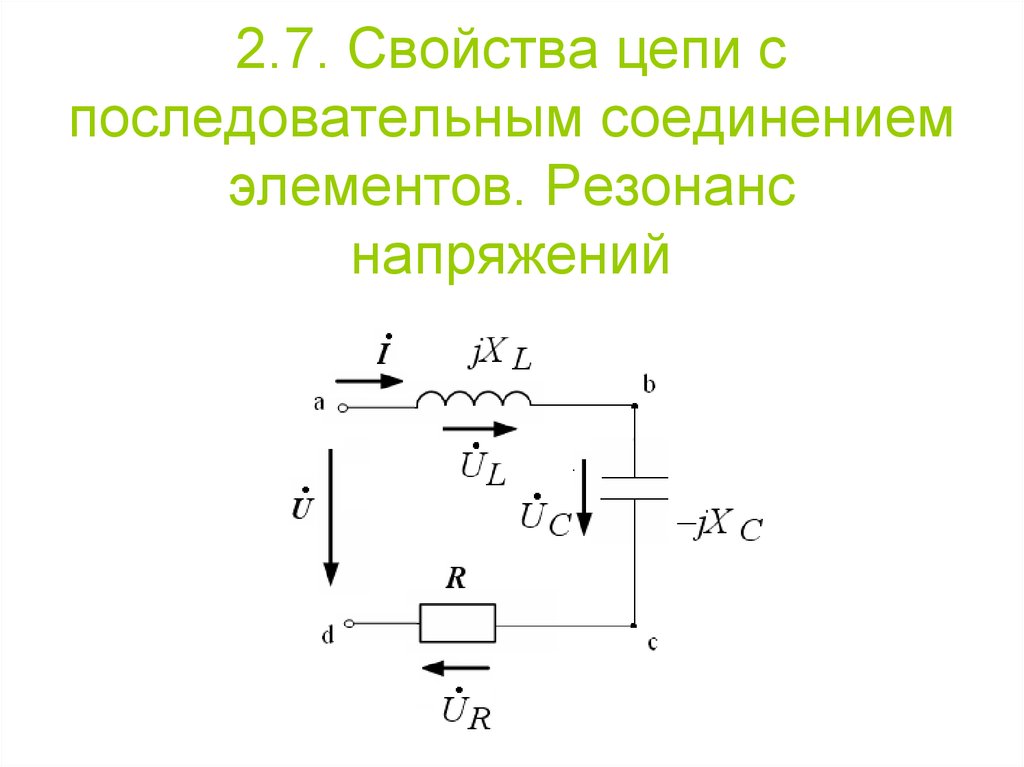
Обычно вместо
,
, пишут
,
()
или
.
Если все фазные напряжения равны, то генератор называется симметричным.
Приемник соединен по схеме звезда аналогичным образом. Точка соединения концов нагрузок фаз приемника обозначают буквой n.
Если нейтрального провода нет, то при неравномерной нагрузке () между точками и появляется напряжение . называют напряжением смещения нейтрали.
Для симметричного приемника:
;
. (3.5д)
Для несимметричного приемника с нейтральным проводом в нейтральном проводе появляется ток:
.
Для симметричного генератора линейные и фазные напряжения связаны соотношением:
.
Соединение генератора и приемника по схеме звезда –треугольник
Соединение генератора звездой и приемника
треугольником представлено на рис.
3.6.
Рис. 3.6 – Соединение генератора звездой и приемника треугольником
По первому закона Кирхгофа для приемника:
.
Линейные напряжения генератора равны напряжениям на фазных нагрузках приемника:
; ; . (3.7в)
Вектор линейного напряжения генератора равен разности векторов фазных напряжений генераторов:
; ; .
dc — Анализ переходных процессов переменного тока в цепях RL или RC
спросил
Изменено 1 год, 6 месяцев назад
Просмотрено 195 раз
\$\начало группы\$
При подаче переменного тока катушка индуктивности в исходном состоянии (незаряженная) не ведет себя как разомкнутая цепь, даже если величина мгновенного переменного напряжения постоянно меняется.
Почему его поведение отличается от состояния переключения во входной цепи постоянного тока, хотя переменное напряжение можно рассматривать как постоянно переключаемый вход?
- переменный ток
- постоянный ток
- пассивные сети
- переходные процессы
- переходные процессы переключения
\$\конечная группа\$
2
\$\начало группы\$
При подаче переменного тока катушка индуктивности в исходном состоянии (незаряженная) не действует как разомкнутая цепь
Вы говорите о конденсаторе. Индуктор — это короткое замыкание.
, хотя величина мгновенного переменного напряжения постоянно меняется.
Почему его поведение отличается от состояния переключения во входной цепи постоянного тока, хотя переменное напряжение можно рассматривать как постоянно переключаемый вход?
Анализ . не выполняется с формой сигнала во временной области, которая чередуется через раз , вместо этого используется сложный сигнал, который является ровным по всей частота , но изменяется в схеме в соответствии с ее топологией (если только у вас нет чистых резисторов или подобных). Таким образом, нет никакого переменного сигнала.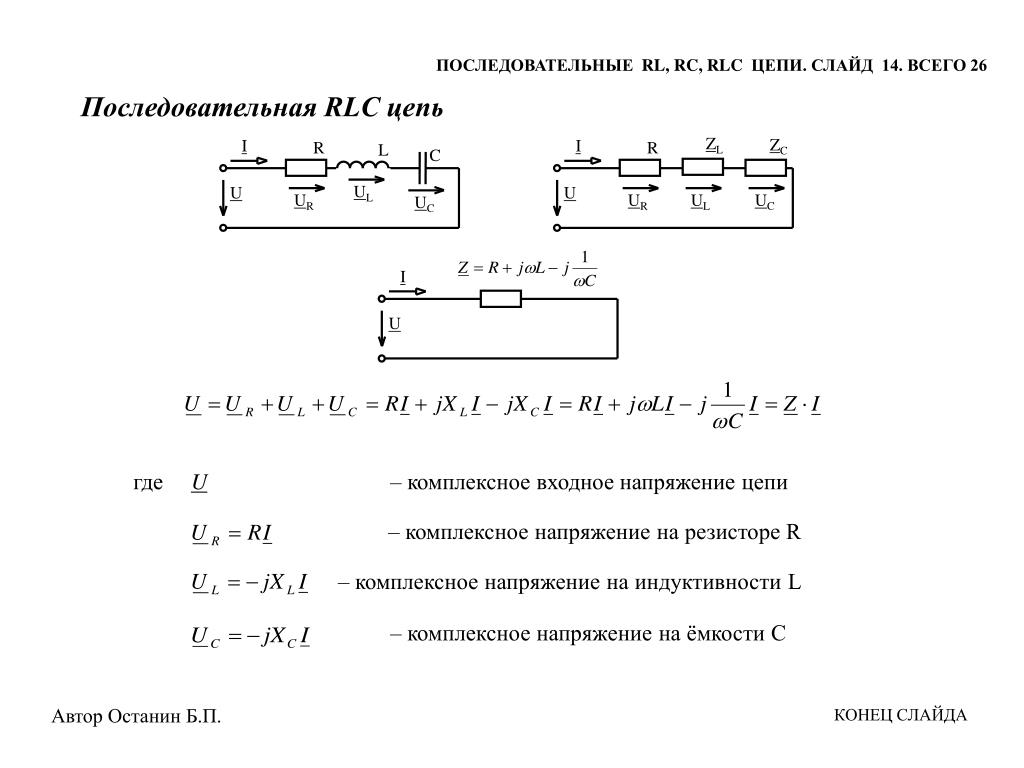
AC
Следовательно, начальные условия катушки индуктивности не имеют значения в анализе .AC , в то время как в анализе .DC или .TRAN они имеют значение, потому что эти IC влияют на начальную рабочую точку отклика во временной области.
\$\конечная группа\$
3
\$\начало группы\$
При подаче переменного тока катушка индуктивности в начальном состоянии (незаряженная) не ведет себя как разомкнутая цепь, даже если величина мгновенного переменного напряжения постоянно меняется.
Кто сказал, что это не так?
Вот простая схема LR:
А вот и ответ (стимул напряжения синего цвета, ток катушки индуктивности зеленым):
Вы можете видеть, что хотя напряжение подскочило до 1 В, ток дросселя не изменился в первые миллисекунды после этого. То есть индуктор не реагирует в течение короткого промежутка времени на изменение приложенного к нему напряжения. Это именно то, что мы имеем в виду, когда говорим, что он «ведет себя как разомкнутая цепь» в коротких промежутках времени или сразу после изменения стимула.
\$\конечная группа\$
\$\начало группы\$
Шкалы времени для переменного тока различны, например, для двигателя переменного тока, питаемого от сети, и импульса 10 кГц с временем нарастания 1 мкс. Частотный состав источника напряжения зависит от этой скорости dV/dt, которая влияет на ток и импеданс индуктора, поскольку ток индуктора не будет изменяться мгновенно с напряжением, а скорее накапливает или интегрирует это изменение медленно в соответствии с постоянной времени L/R.
.
Последовательная катушка индуктивности повышает импеданс с частотным составом ступенчатого импульса, но низкочастотное напряжение сети имеет больше времени для протекания.
Таким образом, на катушке индуктивности может мгновенно появиться быстрый импульс, но ток нагрузки R начнет изменяться только с линейной скоростью dI/dt = V/L для этого ступенчатого напряжения. Но опять же, временные рамки могут отличаться.
$$V_L=L ~dI/dt$$
\$\конечная группа\$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Как рассчитать изменение частоты цепи RC/IC?
Изменение частоты цепи RC/IC определяется как частота сигналов, которые могут проходить по цепи. Она также известна как характеристическая частота. Резистивно-емкостная цепь состоит из резистора и конденсатора, соединенных последовательно. Он подавляет частоты ниже f, позволяя свободно протекать сигналам с частотами выше f. Однако сигналы с частотами, близкими к f, тем не менее частично передаются. В зависимости от конструкции RC-фильтр может использоваться для фильтрации низких или высоких частот. Интегральная схема (ИС) — это полупроводник, содержащий сотни миллионов небольших конденсаторов, резисторов и транзисторов.
Формула
Формула изменения частоты дается обратной величиной удвоенного произведения пи, сопротивления и емкости цепи. Обозначается символом f. Его стандартной единицей измерения является герц или секунда (Гц или с -1 ), а его размерная формула определяется как [M 0 L 0 T -1 ].
f = 1/(2πRC)
Где,
- f – изменение частоты,
- π — константа со значением 3,14,
- R — сопротивление,
- Кл — емкость цепи.
Проблемы с образцами
Задача 1: Рассчитайте вариацию частоты для схемы с сопротивлением 2 Ом и емкостью 3 F.
Раствор:
Мы имеем
R = 2
55555555555550 гг.C = 3
Используя формулу, которую мы имеем,
f = 1/(2πRC)
= 1 / (2 × 3,14 × 2 × 3)
= 0,0265 Гц
Задача 2: Рассчитайте вариацию частоты для схемы с сопротивлением 4 Ом и емкостью 5 F.
Раствор:
Мы имеем
R = 4
555555992 90: вариант для цепи с сопротивлением 2,5 Ом и емкостью 6 Ф.Мы имеем
R = 4
5.C = 5
Используя формулу, которую мы имеем,
f = 1/(2πRC)
= 1 / (2 × 3,14 × 4 × 5)
= 0,007958 Гц
Решение:
Мы имеем,
R = 2,5
C = 6
Используем формулу, которую мы имеем,
F = 1 / (2πrc)
= 1 / (2 × 3,14 ×. 2,5 × 6)
= 0,01061 Гц
Задача 4: Рассчитайте сопротивление схемы с изменением частоты 0,2 Гц и емкостью 1 F.
Решение:
мы. f = 0,2
С = 1
Используя полученную формулу,
f = 1/(2πRC)
=> R = 1/(2πfC)
= 1 / (2 × 3,14 × 0,2 × 1)
= 0,7958 Ом
7 Задача 5. Вычислить сопротивление цепи с изменением частоты 0,06 Гц и емкостью 3,5 Ф.Решение:
Имеем,
f = 0,06
C = 0,5 Используя формулу 90 имеем
f = 1/(2πRC)
=> R = 1/(2πfC)
= 1 / (2 × 3,14 × 0,06 × 3,5)
= 0,758 Ом
Задача 6. Рассчитать емкость цепи с изменением частоты 0,03 Гц и сопротивлением 2 Ом.
