RC цепь | Практическая электроника

R – это резистор, С – конденсатор, а вместе они образуют RC-цепь, то есть это цепь, которая состоит из конденсатора и резистора. Все просто  😉

Немного теории

Как вы помните, конденсатор представляет из себя две обкладки на некотором расстоянии друг от друга.

Вы, наверное, помните, что его емкость зависит от площади обкладок, от расстояния между ними, а также от вещества, которое находится между обкладками.  Или формулой для плоского конденсатора:

где

Ладно, ближе к делу. Пусть у нас имеется конденсатор. Что с ним можно сделать? Правильно, зарядить 😉  Для этого берем источник постоянного напряжения и подаем заряд на конденсатор, тем самым заряжая его:

В результате, у нас конденсатор зарядится. На одной обкладке будет положительный заряд, а на другой обкладке – отрицательный:

Даже если убрать батарею, у нас заряд на конденсаторе все равно сохранится в течение какого-то времени.

Сохранность заряда зависит от сопротивления материала между пластинами. Чем оно меньше, тем быстрее со временем будет разряжаться конденсатор, создавая ток утечки. Поэтому самыми плохими, в плане сохранности заряда, являются электролитические конденсаторы, или в народе – электролиты:

Но что произойдет, если к конденсатору мы подсоединим резистор?

Конденсатор разрядится, так как цепь станет замкнутой.

Постоянная времени RC-цепи

Кто хоть чуть-чуть шарит в электронике, прекрасно понимает эти процессы. Это все банальщина. Но дело в том, что мы не можем наблюдать процесс разрядки конденсатора, просто посмотрев на цепь. Для этого нам понадобится цифровой осциллограф с функцией записи сигнала. Благо на моем рабочем столе уже есть место этому прибору:

Итак, план действий будет такой: мы будем заряжать конденсатор с помощью блока питания, а потом разряжать  его на резисторе и смотреть осциллограмму, как разряжается конденсатор. Соберем классическую схему, которая есть в любом учебнике по электронике:

в этот момент мы заряжаем конденсатор

потом переключаем тумблер S в другое положение и разряжаем конденсатор, наблюдая процесс разряда конденсатора на осциллографе

Думаю, с этим все понятно. Ну что же, приступим к сборке.

Берем макетную плату и собираем схемку. Конденсатор я взял емкостью в 100мкФ, а резистор 1 КилоОм.

Вместо тумблера S я буду вручную перекидывать желтый проводок.

Ну все, цепляемся щупом осциллографа к резистору

и смотрим осциллограмму, как разряжается конденсатор.

Те, кто впервые читает про RC-цепи, думаю, немного удивлены. По логике, разряд должен проходить прямолинейно, но здесь мы видим загибулину.  Разряд происходит по так называемой экспоненте. Так как я не люблю алгебру и матанализ, то не буду приводить различные математические выкладки. Кстати, а что  такое экспонента? Ну экспонента – это график функции “е в степени икс”. Короче, все учились в школе, вам лучше знать 😉

Так как при замыкании тумблера у нас получилась RC-цепь, то у нее есть такой параметр, как постоянная времени RC-цепи. Постоянная времени RC-цепи обозначается буквой t , в другой литературе обозначают большой буквой T. Чтобы было проще для понимания, давайте также будем обозначать постоянную времени RC цепи большой буквой Т.

Итак, думаю стоит запомнить, что постоянная времени RC-цепи равняется произведению номиналов сопротивления и емкости и выражается в секундах, или формулой:

T=RC

где T – постоянная времени , Секунды

R – сопротивление, Ом

С – емкость, Фарады

Давайте посчитаем, чему равняется постоянная времени нашей цепи. Так как у меня конденсатор емкостью в 100 мкФ, а резистор 1 кОм, то постоянная времени равняется T=100 x 10

-6 x 1 х 10³ =100 x 10^-3 = 100 миллисекунд.

Для тех, кто любит считать глазами, можно построить уровень в 37% от амплитуды сигнала и затем уже аппроксимировать на ось времени. Это и будет постоянная времени RC-цепи. Как вы видите, наши алгебраические расчеты почти полностью сошлись с геометрическими, так как цена деления стороны одного квадратика по времени равняется 50 миллисекундам.

В идеальном случае конденсатор сразу же заряжается, если на него подать напряжение. Но в реальном все-таки есть некоторое сопротивление ножек, но все равно можно считать, что заряд происходит почти мгновенно. Но что будет, если заряжать конденсатор через резистор? Разбираем прошлую схему и стряпаем новую:

исходное положение

как только мы замыкаем ключ S, у нас конденсатор начинает заряжаться от нуля и до значения 10 Вольт, то есть до значения, которое мы выставили на блоке питания

Наблюдаем осциллограмму, снятую с конденсатора

Ничего общего не увидели с прошлой осциллограммой, где мы разряжали конденсатор на резистор? Да, все верно. Заряд тоже идет по экспоненте ;-). Так как радиодетали у нас одинаковые, то и постоянная времени тоже одинаковая. Графическим способом она высчитывается как 63% от амплитуды сигнала

Как вы видите, мы получили те же самые 100 миллисекунд.

По формуле постоянной времени RC-цепи, нетрудно догадаться, что изменение номиналов сопротивления и конденсатора повлечет за собой изменение и постоянной времени. Поэтому, чем меньше емкость и сопротивление, тем короче по времени постоянная времени. Следовательно, заряд или разряд будет происходить быстрее.

Для примера, давайте поменяем значение емкости конденсатора в меньшую сторону. Итак, у нас был конденсатора номиналом в 100 мкФ, а мы поставим 10 мкФ, резистор оставляем такого же номинала в 1 кОм. Посмотрим еще раз на графики заряда и разряда.

Вот так заряжается наш конденсатор номиналом в 10 мкФ

А вот так он разряжается

Как вы видите, постоянная времени цепи в разы сократилась. Судя по моим расчетам она стала равняться T=10 x 10

-6 x 1000 = 10 x 10^-3 = 10 миллисекунд. Давайте проверим графо-аналитическим способом, так ли это?

Строим на графике заряда или разряда прямую на соответствующем уровне и аппроксимируем ее на ось времени. На графике разряда будет проще 😉

Одна сторона квадратика по оси времени у нас 10 миллисекунд (чуть ниже рабочего поля написано M:10 ms), поэтому нетрудно посчитать, что постоянная времени у нас 10 миллисекунд ;-). Все элементарно и просто.

То же самое можно сказать и про сопротивление.  Емкость я оставляю  такой же, то есть 10 мкФ, резистор меняю с 1 кОм на 10 кОм. Смотрим, что получилось:

По расчетам постоянная времени должна быть T=10 x 10^-6 x 10 x 10³ = 10 x 10^-2 = 0,1 секунда или 100 миллисекунд. Смотрим графо-аналитическим способом:

100 миллисекунд 😉

Вывод: чем больше номинал конденсатора и резистора, тем больше постоянная времени, и наоборот, чем меньше номиналы этих радиоэлементов, тем меньше постоянная времени.

Все просто 😉

Ладно, думаю, с этим все понятно. Но куда можно применить этот принцип зарядки и разрядки конденсатора?  Оказывается, применение нашлось…

 

Интегрирующая цепь

Собственно сама схема:

А что будет, если мы на нее будем подавать прямоугольный сигнал с разной частотой?  В дело идет китайский генератор функций:

Выставляем на нем частоту 1 Герц и размахом в 5 Вольт

Желтая осциллограмма – это сигнал с генератора функций, который подается на вход интегрирующей цепи на клеммы Х1, Х2, а с выхода мы снимаем красную осциллограмму, то есть с клемм Х3, Х4:

Как вы могли заметить, конденсатор почти полностью успевает зарядиться и  разрядиться.

Но что будет, если мы добавим частоту? Выставляю на генераторе частоту в 10 Герц. Смотрим что у нас получилось:

Конденсатор не успевает заряжаться и разряжаться как уже приходит новый  прямоугольный импульс. Как мы видим, амплитуда выходного сигнала очень сильно просела, можно сказать, он скукожился ближе к нулю.

А сигнал в 100 Герц вообще не оставил ничего от сигнала, кроме малозаметных волн

Сигнал в 1 Килогерц на выходе вообще не дал ничего…

Еще бы! Попробуй-ка с такой частотой перезаряжать конденсатор 🙂

Все то же самое касается и других сигналов: синусоиды и треугольного. везде выходной сигнал почти равен нулю на частоте 1 Килогерц и выше.

“И это все, на что способна интегрирующая цепь?” – спросите вы. Конечно нет! Это было только начало.

Давайте разберемся… Почему у нас с возрастанием частоты сигнал стал прижиматься к нулю и потом вообще пропал?

Итак, во-первых, эта цепь у нас получается как делитель напряжения, и во-вторых, конденсатор – это частотно-зависимый радиоэлемент. Его сопротивление зависит от частоты. Про это можно прочитать в статье конденсатор в цепи постоянного и переменного тока. Следовательно, если бы мы подавали постоянный ток на вход (у постоянного тока частота 0 Герц), то и на выходе бы тоже получили тот же самый постоянный ток такого же значения, которое загоняли на вход. В это случае конденсатору ведь по барабану. Все что он сможет сделать в этой ситуации – тупо зарядиться по экспоненте и все. На этом его участь  в цепи постоянного тока заканчивается и он стает диэлектриком для постоянного тока.

Но как только в цепь подается переменный сигнал, конденсатор вступает в игру. Тут его сопротивление уже зависит от частоты. И чем она больше, тем меньшим сопротивлением обладает конденсатор. Формула сопротивления конденсатора от частоты:

где

_ХС  – это сопротивление конденсатора, Ом

П – постоянная и равняется приблизительно 3,14

F – частота, Герц

С – емкость конденсатора, Фарад

Итак, что в результате получается? А получается то, что чем больше частота, тем меньше сопротивление конденсатора. На нулевой частоте у нас сопротивление конденсатора в идеале стает равно бесконечности (поставьте в формулу 0 Герц частоту). А так как у нас получился делитель напряжения

следовательно, на меньшем сопротивлении падает меньшее напряжение. С ростом частоты сопротивление конденсатора очень сильно уменьшается и поэтому падение напряжения на нем стает почти 0 Вольт, что мы и наблюдали на осциллограмме.

Но на этом ништяки не заканчиваются.

Давайте вспомним, что из себя представляет сигнал с постоянной составляющей. Это есть ничто иное, как сумма переменного сигнала и постоянного напряжения. Взглянув на рисунок ниже, вам все станет ясно.

То есть в нашем случае можно сказать, этот сигнал (ниже на картинке) имеет в своем составе постоянную составляющую, другими словами, постоянное напряжение

Для того, чтобы выделить постоянную составляющую из этого сигнала, нам достаточно прогнать его через нашу интегрирующую цепь. Давайте  рассмотрим все это на примере. С помощью нашего генератора функций мы поднимем нашу синусоиду “над полом”, то есть сделаем вот так:

Итак, все как обычно, желтый входной сигнал цепи, красный  – выходной. Простая двухполярная синусоида дает нам на выходе RC интегрирующей цепи 0 Вольт:

Чтобы  понять, где нулевой уровень сигналов, я их пометил квадратиком:

Теперь давайте я добавлю постоянную составляющую в синусоиду, а точнее – постоянное напряжение, благо это сделать мне позволяет генератор функций:

Как вы видите, как только я поднял синус “над полом”, на выходе цепи я получил постоянное напряжение величиной в 5 Вольт. Именно на 5 Вольт я поднимал сигнал в генераторе функций ;-). Цепочка  выделила постоянную составляющую из синусоидального приподнятого сигнала без проблем. Чудеса!

Но мы так и не разобрались, почему цепь называется интегрирующей? Кто хорошо учился в школе, в классе эдак 8-9, то наверняка помнит геометрический смысл интеграла – это есть ничто иное, как площадь под кривой.

Давайте рассмотрим тазик с кубиками льда в двухмерной плоскости:

Что будет, если весь лед растает и превратится в воду? Все верно, вода ровным слоем покроет тазик одной плоскостью:

Но какой будет этот уровень воды? Вот именно – средний. Это среднее значение этих башен из кубиков льда. Так вот, интегрирующая цепочка делает то же самое! Тупо усредняет значение сигналов до одного постоянного уровня! Можно сказать, усредняет площадь до одного постоянного уровня.

Но самый смак получается тогда, когда мы подаем на вход прямоугольный сигнал. Давайте так и сделаем. Подадим положительный меандр на RC интегрирующую цепь.

Как вы видите, постоянная составляющая меандра равна половине его амплитуды. Думаю, вы уже и сами догадались, если бы представили тазик с кубиками льда). Или просто подсчитайте площадь каждого импульса и размажьте его равномерным слоем по осциллограмме, как гов…  как сливочное масло по хлебу 😉

Ну а теперь самое веселое. Сейчас я буду менять скважность  нашего прямоугольного сигнала, так как скважность – это ничто иное, как отношение периода на длительность импульса, следовательно, мы будем менять длительность импульсов.

Уменьшаю длительность импульсов

Увеличиваю длительность импульсов

Если никто ничего до сих пор не заметил, просто взгляните на уровень красной осциллограммы и все станет понятно.  Вывод: управляя скважностью, мы можем менять уровень постоянной составляющей. Именно этот принцип и заложен в ШИМ (Широтно-Импульсной Модуляции). О ней как-нибудь поговорим в отдельной статье.

 

Дифференцирующая цепь

Еще одно ругательное слово, которое пришло с математики – дифференцирующий. Башка начинает сразу же болеть от одного только их произношения. Но, куда деваться? Электроника и математика неразлучные друзья.

А вот и сама дифференциальная цепочка

В схеме мы только переставили резистор и конденсатор местами

Ну а теперь проведем также все опыты, как мы делали с интегрирующей цепью. Для начала подаем на вход дифференциальной цепи низкочастотный двухполярный меандр с частотой в 1,5 Герца и с размахом в 5 Вольт.  Желтый сигнал – это сигнал с генератора частоты, красный –  с выхода дифференциальной цепочки:

Как вы видите, конденсатор успевает почти полностью разрядится, поэтому у нас получилась вот такая красивая осциллограмма.

Давайте увеличим частоту до 10 Герц

Как видите, конденсатор не успевает разрядиться, как уже приходит новый импульс.

Сигнал в 100 Герц сделал кривую разряда еще менее заметной.

Ну и добавим частоту до 1 Килогерца

Какой на входе, такой и на выходе 😉 С такой частотой конденсатор вообще не успевает разряжаться, поэтому вершинки выходных импульсов гладкие и ровные.

Но и на этом тоже ништяки не заканчиваются.

Давайте я подниму входной сигнал над “уровнем моря”, то есть выведу его в положительную часть полностью. Смотрим, что получается на выходе (красный сигнал)

Ничего себе, красный сигнал по форме и по положению остался таким же, посмотрите – в нем нет постоянной составляющей, как в желтом сигнале, который мы подавали из нашего генератора функций.

Могу даже желтый сигнал вывести в отрицательную область, но на выходе мы все равно получим переменную составляющую сигнала без всяких хлопот:

Да и вообще пусть сигнал будет с небольшой  отрицательной постоянной составляющей, все равно на выходе мы получим переменную составляющую:

Все то же самое касается и любых других сигналов:

В результате опытов мы видим, что основная функция дифференциальной цепи – это выделение переменной составляющей из сигнала, который содержит в себе как переменную, так и постоянную составляющую. Иными словами – выделение переменного тока из сигнала, который состоит из суммы переменного тока и постоянного тока.

Почему так происходит? Давайте разберемся. Рассмотрим нашу дифференциальную цепь:

Если внимательно рассмотреть эту схему, то мы можем увидеть тот же самый делитель напряжения, как и в интегрирующей цепи. Конденсатор – частотно-зависимый радиоэлемент. Итак, если подать сигнал с частотой  в 0 Герц (постоянный ток), то у нас конденсатор тупо зарядится и потом вообще перестанет пропускать через себя ток. Цепь будет в обрыве. Но если мы будем подавать переменный ток, то и через конденсатор он тоже начнет проходить. Чем больше частота – тем меньше сопротивление конденсатора. Следовательно, весь переменный сигнал будет падать на резисторе, с которого мы как раз и снимаем сигнал.

Но если мы будем подавать смешанный сигнал, то есть переменный ток + постоянный ток, то на выходе мы получим просто переменный ток. В этом мы с вами уже убеждались на опыте. Почему так произошло? Да потому что конденсатор не пропускает через себя постоянный ток!

Заключение

Интегрирующую цепь также называют фильтром низких частот (ФНЧ), а дифференцирующую – фильтром высоких частот (ФВЧ). Более подробно про фильтры читаем здесь. Чтобы точнее их сделать, нужно провести расчет на нужную вам частоту. RC цепи используются везде, где надо выделить постоянную составляющую (ШИМ), переменную составляющую (межкаскадное соединение усилителей), выделить фронт сигнала, сделать задержку и тд… По мере глубины погружения в электронику вы будете часто встречаться с ними.

Конденсатор и RC цепочка | Электроника для всех

Если соединить резистор и конденсатор, то получится пожалуй одна из самых полезных и универсальных цепей.
 

О многочисленных способах применения которой я сегодня и решил рассказать. Но вначале про каждый элемент в отдельности:
 

Резистор — его задача ограничивать ток. Это статичный элемент, чье сопротивление не меняется, про тепловые погрешности сейчас не говорим — они не слишком велики. Ток через резистор определяется законом ома — I=U/R, где U напряжение на выводах резистора, R — его сопротивление.
 

Конденсатор штука поинтересней. У него есть интересное свойство — когда он разряжен то ведет себя почти как короткое замыкание — ток через него течет без ограничений, устремляясь в бесконечность. А напряжение на нем стремится к нулю. Когда же он заряжен, то становится как обрыв и ток через него течь перестает, а напряжение на нем становится равным заряжающему источнику. Получается интересная зависимость — есть ток, нет напряжения, есть напряжение — нет тока.
 

Чтобы визуализировать себе этот процесс, представь ган… эмм.. воздушный шарик который наполняется водой. Поток воды — это ток. Давление воды на упругие стенки — эквивалент напряжения. Теперь смотри, когда шарик пуст — вода втекает свободно, большой ток, а давления еще почти нет — напряжение мало. Потом, когда шарик наполнится и начнет сопротивляться давлению, за счет упругости стенок, то скорость потока замедлится, а потом и вовсе остановится — силы сравнялись, конденсатор зарядился. Есть напряжение натянутых стенок, но нет тока!
 

Теперь, если снять или уменьшить внешнее давление, убрать источник питания, то вода под действием упругости хлынет обратно. Также и ток из конденсатора потечет обратно если цепь будет замкнута, а напряжение источника ниже чем напряжение в конденсаторе.
 

Емкость конденсатора. Что это?
Теоретически, в любой идеальный конденсатор можно закачать заряд бесконечного размера. Просто наш шарик сильней растянется и стенки создадут большее давление, бесконечно большое давление.
А что же тогда насчет Фарад, что пишут на боку конденсатора в качестве показателя емкости? А это всего лишь зависимость напряжения от заряда (q = CU). У конденсатора малой емкости рост напряжения от заряда будет выше.
 

Представь два стакана с бесконечно высокими стенками. Один узкий, как пробирка, другой широкий, как тазик. Уровень воды в них — это напряжение. Площадь дна — емкость. И в тот и в другой можно набузолить один и тот же литр воды — равный заряд. Но в пробирке уровень подскочит на несколько метров, А в тазике будет плескаться у самого дна. Также и в конденсаторах с малой и большой емкостью.
Залить то можно сколько угодно, но напряжение будет разным.
 

Плюс в реале у конденсаторов есть пробивное напряжение, после которого он перестает быть конденсатором, а превращается в годный проводник 🙂
 

А как быстро заряжается конденсатор?
В идеальных условиях, когда у нас бесконечно мощный источник напряжения с нулевым внутренним сопротивлением, идеальные сверхпроводящие провода и абсолютно безупречный конденсатор — этот процесс будет происходить мгновенно, с временем равным 0, равно как и разряд.
 

Но в реальности всегда существуют сопротивления, явные — вроде банального резистора или неявные, такие как сопротивление проводов или внутреннее сопротивление источника напряжения.
В этом случае скорость заряда конденсатора будет зависить от сопротивлений в цепи и емкости кондера, а сам заряд будет идти по экспоненциальному закону.
 

 

А у этого закона есть пара характерных величин:

• Т — постоянная времени, это время при котором величина достигнет 63% от своего максимума. 63% тут взялись не случайно, тут прямая завязка на такую формулу VALUE_T=max—1/e*max.
• 3T — а при троекратной постоянной значение достигнет 95% своего максимума.

 

Постоянная времени для RC цепи Т=R*C.
 

Чем меньше сопротивление и меньше емкость, тем быстрей конденсатор заряжается. Если сопротивление равно нулю, то и время заряда равно нулю.
 

Рассчитаем за сколько зарядится на 95% конденсатор емкостью 1uF через резистор в 1кОм:
T= C*R = 10^-6 * 10³ = 0.001c
3T = 0.003c через такое время напряжение на конденсаторе достигнет 95% от напряжения источника.
 

Разряд пойдет по тому же закону, только вверх ногами. Т.е. через Твремени в на конденсаторе остаенется всего лишь 100% — 63% = 37% от первоначального напряжения, а через 3T и того меньше — жалкие 5%.
 

Ну с подачей и снятием напряжения все ясно. А если напряжение подали, а потом еще ступенчато подняли, а разряжали также ступеньками? Ситуация тут практически не изменится — поднялось напряжение, конденсатор дозарядился до него по тому же закону, с той же постоянной времени — через время 3Т его напряжение будет на 95% от нового максимума.
Чуть понизилось — подразрядился и через время 3Т напряжение на нем будет на 5% выше нового минимума.
Да что я тебе говорю, лучше показать. Сварганил тут в мультисиме хитровыдрюченный генератор ступечнатого сигнала и подал на интегрирующую RC цепочку:

 

Видишь как колбасится 🙂 Обрати внимание, что и заряд и разряд, вне зависимости от высоты ступеньки, всегда одной длительности!!!
 

А до какой величины конденсатор можно зарядить?
В теории до бесконечности, этакий шарик с бесконечно тянущимися стенками. В реале же шарик рано или поздно лопнет, а конденсатор пробьет и закоротит. Вот поэтому у всех конденсаторов есть важный параметр — предельное напряжение. На электролитах его часто пишут сбоку, а на керамических его надо смотреть в справочниках. Но там оно обычно от 50 вольт. В общем, выбирая кондер надо следить, чтобы его предельное напряжение было не ниже того которое в цепи. Добавлю что при расчете конденсатора на переменное напряжение следует выбирать предельное напряжение в 1.4 раза выше. Т.к. на переменном напряжении указывают действующее значение, а мгновенное значение в своем максимуме превышает его в 1.4 раза.
 

Что следует из вышеперечисленного? А то что если на конденсатор подать постоянное напряжение, то он просто зарядится и все. На этом веселье закончится.
 

А если подать переменное? То очевидно, что он будет то заряжаться, то разряжаться, а в цепи будет туда и обратно гулять ток. Движуха! Ток есть!
 

Выходит, несмотря на физический обрыв цепи между обкладками, через конденсатор легко протекает переменный ток, а вот постоянному слабо.
 

Что нам это дает? А то что конденсатор может служить своего рода сепаратором, для разделения переменного тока и постоянного на соответствующие составляющие.
 

Любой изменяющийся во времени сигнал можно представить как сумму двух составляющих — переменной и постоянной.

Например, у классической синусоиды есть только переменная часть, а постоянная равна нулю. У постоянного же тока наоборот. А если у нас сдвинутая синусоида? Или постоянная с помехами?
 

Переменная и постоянная составляющие сигнала легко разделяются!
Чуть выше я тебе показал как конденсатор дозаряжается и подразряжается при изменениях напряжения. Так что переменная составляющая сквозь кондер пройдет на ура, т.к. только она заставляет конденсатор активно менять свой заряд. Постоянная же как была так и останется и застрянет на конденсаторе.
 

Но чтобы конденсатор эффективно разделял переменную составляющую от постоянной частота переменной составляющей должна быть не ниже чем 1/T
 

Возможны два вида включения RC цепочки:
Интегрирующая и дифференцирующая. Они же фильтр низких частот и фильтр высоких частот.
 

Фильтр низких частот без изменений пропускает постоянную составляющую (т.к. ее частота равна нулю, ниже некуда) и подавляет все что выше чем 1/T. Постоянная составляющая проходит напрямую, а переменная составляющая через конденсатор гасится на землю.
Такой фильтр еще называют интегрирующей цепочкой потому, что сигнал на выходе как бы интегрируется. Помнишь что такое интеграл? Площадь под кривой! Вот тут она и получается на выходе.
 

Как здесь вычисляется постоянная составляющая? А с виду и не скажешь, но надо помнить, что любой периодически сигнал раскладывается в ряд Фурье, превращаясь в сумму из постоянной составляющей и пачки синусоид разной частоты и амплитуды.
 

Фильтр высоких частот работает наоборот. Он не пускает постоянную составляющую (т.к. ее частота слишком низка — 0) — ведь конденсатор для нее равносилен обрыву, а вот переменная пролазит через кондер без проблем.

А дифференцирующей цепью ее называют потому, что на выходе у нас получается дифференциал входной функции, который есть не что иное как скорость изменения этой функции.

• На участке 1 происходит заряд конденсатора, а значит через него идет ток и на резисторе будет падение напряжения.
• На участке 2 происходит резкое увеличение скорости заряда, а значит и ток резко возрастет, а за ним и падение напряжения на резисторе.
• На участке 3 конденсатор просто удерживает уже имеющийся потенциал. Ток через него не идет, а значит на резисторе напряжение тоже равно нулю.
• Ну и на 4м участке конденсатор начал разряжаться, т.к. входной сигнал стал ниже чем его напряжение. Ток пошел в обратную сторону и на резисторе уже отрицательное падение напряжения.

А если подать на вход прямоугольнй импульс, с очень крутыми фронтами и сделать емкость конденсатора помельче, то увидим вот такие иголки:

Вверху идет осциллограма того что на входе, внизу то что на выходе дифференциальной цепи.
Как видишь, тут мощные всплески на фронтах. Оно и понятно, в этом месте функция меняется резко, а значит производная (скорость изменения) этой функции велика, на пологих участках сигнал константа и его производная, скорость изменения, равна нулю — на графике ноль.
 

А если загнать в дифференциатор пилу, то на выходе получим…

прямоугольник. Ну, а чо? Правильно — производная от линейной функции есть константа, наклон этой функции определяет знак константы.
 

Короче, если у тебя сейчас идет курс матана, то можешь забить на богомерзкий Mathcad, отвратный Maple, выбросить из головы матричную ересь Матлаба и, достав из загашников горсть аналоговой рассыпухи, спаять себе истинно ТРУЪ аналоговый компьютер 🙂 Препод будет в шоке 🙂
 

Правда на одних только резисторах кондерах интеграторы и диффернциаторы обычно не делают, тут юзают операционные усилители. Можешь пока погуглить на предмет этих штуковин, любопытная вещь 🙂
 

А вот тут я подал обычный приямоугольный сигнал на два фильтра высоких и низких частот. А выходы с них на осциллограф:

И вот что получилось на осциллографе:

Вот, чуть покрупней один участок:

>

Как видишь, на одном срезало постоянную составляющую, на другом переменную.
 

Ладно, что то мы отвлеклись от темы.
 

Как еще можно применить RC цепь?
Да способов много. Часто ее используют не только в качестве фильтров, но и как формирователи импульсов. Например, на сбросе контроллера AVR, если надо чтобы МК стартанул не сразу после включения питания, а с некоторой выдержкой:

При старте кондер разряжен, ток через него вваливат на полную, а напряжение на нем мизерное — на входе RESET сигнал сброса. Но вскоре конденсатор зарядится и через время Т его напряжение будет уже на уровне логической единицы и на RESET перестанет подаваться сигнал сброса — МК стартанет.
А для AT89C51 надо с точностью наоборот RESET организовать — вначале подать единицу, а потом ноль. Тут ситуация обратная — пока кондер не заряжен, то ток через него течет большой, Uc — падение напряжения на нем мизерное Uc=0. А значит на RESET подается напряжение немногим меньше напряжения питания Uпит-Uc=Uпит.
Но когда кондер зарядится и напряжение на нем достигнет напряжения питания (Uпит=Uс), то на выводе RESET уже будет Uпит-Uc=0
 

Аналоговые измерения
Но фиг сними с цепочками сброса, куда прикольней использовать возможность RC цепи для замера аналоговых величин микроконтроллерами в которых нет АЦП.
Тут используется тот факт, что напряжение на конденсаторе растет строго по одному и тому же закону — экспоненте. В зависимости от кондера, резистора и питающего напряжения. А значит его можно использовать как опорное напряжение с заранее известными параметрами.
 

Работает просто, мы подаем напряжение с конденсатора на аналоговый компаратор, а на второй вход компаратора заводим измеряемое напряжение. И когда хотим замерить напряжение, то просто вначале дергаем вывод вниз, чтобы разрядить конденсатор. Потом возвращем его в режим Hi-Z, cбрасываем и запускаем таймер. А дальше кондер начинает заряжаться через резистор и как только компаратор доложит, что напряжение с RC догнало измеряемое, то останавливаем таймер.

Зная по какому закону от времени идет возрастание опорного напряжения RC цепи, а также зная сколько натикал таймер, мы можем довольно точно узнать чему было равно измеряемое напряжение на момент сработки компаратора. Причем, тут не обязательно считать экспоненты. На начальном этапе зарядки кондера можно предположить, что зависимость там линейная. Или, если хочется большей точности, аппроксимировать экспоненту кусочно линейными функциями, а по русски — отрисовать ее примерную форму несколькими прямыми или сварганить таблицу зависимости величины от времени, короче, способов вагон просто.
 

Если надо заиметь аналоговую крутилку, а АЦП нету, то можно даже компаратор не юзать. Дрыгать ножкой на которой висит конденсатор и давать ему заряжаться через перменный резистор.
 

По изменению Т, которая, напомню T=R*C и зная что у нас С = const, можно вычислить значение R. Причем, опять же необязательно подключать тут математический аппарат, в большинстве случаев достаточно сделать замер в каких-нибудь условных попугаях, вроде тиков таймера. А можно пойти другим путем, не менять резистор, а менять емкость, например, подсоединяя к ней емкость своего тела… что получится? Правильно — сенсорные кнопки!
 

Если что то непонятно, то не парься скоро напишу статью про то как прикрутить к микроконтроллеру аналоговую фиговину не используя АЦП. Там подробно все разжую.
 

Теперь, думаю, ты понял за что я так люблю RC цепочки и почему на моей отладочной плате PinBoard их несколько и с разными параметрами 🙂
 

RC-цепи, 5 самых распространенных и как просто их рассчитать

RC-цепь, такое частое явление радиоэлектроники. Понимание характера влияния на форму АЧХ и их предназначения во многом определяет правильность чтения электронной схемы. В статье собранны 5 основных RC-фильтров, приведены их АЧХ и упрощенные формулы расчета.

В ранние годы развития радиоэлектроники основным видом воздействие на АЧХ сигнала были LC — фильтры, т.е. фильтры состоящие из катушки индуктивности и конденсатора. Со временем им на смену пришла RC-цепь, которая была плотно взята в оборот радиоэлектроникой ввиду меньшей стоимости и габаритов.

Конечно, RC-цепь не могут полностью вытеснить LC собратьев. Например в фильтрах для АС предпочтительнее использование LC-фильтров. Но практически во всей остальной маломощной электронике главенствуют рассматриваемые RC-цепи. Например двойная RC-цепь в фильтре RIAA-корректора.

Упрощенные формулы

Далее вы увидите, что в формулах присутствует коэффициент 160000 (сто шестьдесят тысяч). Это немного округленное значение, возникающее из за того, что емкость для расчета берется в микрофарадах (10^-6 Фарада), а так же из за перехода от круговой частоты к цикличной возникает множитель 2π, как результат имеем

1 / (2⋅π⋅10^-6) = 159154 ≈ 160000

1. Фильтр Низких Частот (ФНЧ) — он же интегратор:

ФНЧ — фильтр, пропускающий без изменения частоты ниже частоты среза (f₀) и подавляющий частоты выше f₀. На частоте среза имеет значение амплитуды в -3dB. Это фильтр первого порядка и крутизна среза составляет 6дБ/октаву. Чаще всего такие фильтры используются для отсечения высокочастотных помех и шумов.

Октавой называется такой интервал частот, у которого конечное значение частоты больше начального в два раза.

2. Фильтр Высоких Частот (ФВЧ) — он же дифференциатор

ФВЧ — фильтр, ослабляющий частоты ниже частоты среза(f0) и пропускающий без изменения частоты выше f₀. Так же как и у приведенного выше ФНЧ, сигнал на частоте среза обладает амплитудой в -3дБ, а крутизна среза 6 дБ на октаву.

И ФНЧ и ФВЧ работают как делитель напряжения, в котором одно плечо представлено постоянным резистором, а второе конденсатором, имеющим частотную зависимость.

Такие фильтры часто применяются на выходах звуковых усилителей для отсечения инфранизких, которые могут повредить АС.

3. Избирательный фильтр

Такой фильтр выделяет определенную частоту или полосу частот за счет подавления других частот. По сути этот фильтр представляет из себя последовательное включение ФНЧ и ФВЧ. Соответственно при равенстве между собой емкостей и сопротивлений выделена будет определенная частота, а в обе стороны будет ослабление с крутизной 6 дБ/окт .

Но никто не мешает расширить полосу пропускания, если рассчитать каждую RC-цепь R1С1 и R2C2 для разных f₀.

4. Т- образные фильтры

Т- образные фильтры это те же Г-образными фильтры ФНЧ и ФВЧ к которым добавляется еще один элемент. Но особенностью Т-образных фильтров является то, что по сравнению с Г-образными оказывают меньшее шунтирующее действие на цепи стоящие за фильтром.

5. Двойной Т-образный фильтр — пробка

Фильтр имеет бесконечное затухание (порядка 60дБ) которое возникает благодаря сложению двух сигналов имеющих на частоте среза разность фаз 1800. Применение такого фильтра весьма эффективно для устранения сигнала помехи, например сетевой наводки 50 или 60Гц

«Волшебные» свойства RC цепочки / Схемотехника / Сообщество EasyElectronics.ru

«Волшебные» свойства обычного ФНЧ — RC фильтра. В данном топике я расскажу, как можно использовать свойства данного типа пассивного фильтра не по прямому назначению. Иногда может быть полезнее, проще и «дешевле» использовать аналоговую схемотехнику, чем сложные программные реализации или другое более дорогостоящее оборудование.

Предисловие.

Рассмотрим простейший аналоговый фильтр – RC цепочку или ФНЧ (фильтр низких частот). Про него написано много и по делу. Но мы попробуем использовать его свойства не по прямому назначению. Данный фильтр является пассивным ФНЧ 1-го порядка. Его характеристики для качественной фильтрации сигнала далеки от оптимальных. Но для рассматриваемого случая их хватит.

Не много формул

Вспомним основные характеристики RC цепи. Схема данного ФНЧ выглядит следующим образом.

Комплексный коэффициент передачи данного фильтра вычисляется по закону Ома и имеет следующий вид:

Значение силы тока в цепи равно:

Подставляя значение тока в первую формулу получим:

R- сопротивление резистора в цепочки, Zc – реактивное сопротивление конденсатора в цепи.

Где. Формула для передаточного коэффициента примет окончательный вид:

Так как коэффициент является мнимой функцией, то у нас возникает разность фаз между входным и выходным напряжением. Угол этого сдвига вычисляется по формуле:

Так как угол со знаком «минус», это означает что выходное напряжение отстает от входного на угол ⱷ.
Этим свойством фильтра мы и воспользуемся.

АЧХ и ФЧХ фильтра.

Вспомним две основные характеристики любого фильтра: АЧХ и ФЧХ. Вот АЧХ и ФЧХ RC цепочки:

Вспомним тригонометрию и табличные значения тангенса:

Как видим тангенс 90&deg в таблице не указан, стоит прочерк. Это означает, что его нельзя вычислить.

Так что и в нашем пассивном фильтре отставание выходного напряжения от входного не может быть больше 90&deg, да и 90&deg получить не получится. 89,9&deg реально, а вот больше уже практически невозможно. Теперь основной вопрос. Зачем нам получать этот сдвиг в 89,9&deg?

Зачем городить все это?

Обрисуем задачу. Необходимо вычислять момент, создаваемый асинхронным высоковольтным двигателем. Не важно зачем он нам нужен, для того что бы знать механическую работу совершенную двигателем, или так для статистики. Необходимо и все тут. Практическое применение этого может возникнуть в разных областях промышленности. Давайте решим её. Тут правда придется вспомнить теорию электрических машин. Приступим.

Асинхронный электродвигатель.

Номинальный момент рассчитывается по формуле:

Где Pн – номинальная мощность на валу двигателя, nн — номинальная частота вращения ротора.

А как известно Pн есть не что иное, как Раст – Рпот. Мощность потерь складывается из потерь в обмотках, потерь в железе и механических потерь. Механические потери равны константе и зависит от типа двигателя. А вот потери в обмотках и железе динамические. Обмотки и железо греются, следовательно, возрастают и потери. Для больших мощностей этот параметр будет носить характер в 0.5 % или менее.

Теперь о расчете активной (полезной) мощности.

В трехфазной сети она вычисляется следующим образом:

Где ⱷ — угол между током и напряжением. Для симметричной нагрузки это справедливо, а исправный электродвигатель является симметричной нагрузкой.

Так вот для вычисления момента на валу, необходимо измерять две основные электрические величины: U и I. Фазное напряжение и ток. С током все понятно, ставим трансформатор тока и вперед. А вот с напряжением сложнее.

Не забудем, что разговор мы ведем о высоковольтном электродвигателе. Так что 6 кВ не подашь на схему измерения.

Решений как всегда может быть несколько.

1. Поставить трансформатор напряжения фазный.
2. Использовать свойства RC цепи при измерении линейного напряжения.

В высоковольтных ячейках, с которых осуществляется пуск двигателя, в своем составе уже имеют трансформаторы напряжения и тока, как для устройств защиты, так и для средств измерения.

Типовые схемы включения трансформаторов напряжения представлено ниже:

При чем вариант В применяется реже. В основном вариант А или Б. Как видно с трансформаторов мы снимаем линейное напряжение высоковольтной сети. А для расчета Активной мощности необходимо фазное. Ну и что, возразите ВЫ? Поделили на корень из 3 и вуаля!

Делением мы вычислим среднеквадратичное значение напряжения, но для вычисления активной мощности этого мало. Если мы умножим среднеквадратичные U*I, то получим ПОЛНУЮ мощность. А это не совсем то, совсем не то.

Применение свойств RC цепи.

Добрались до самой сути статьи.
Если обрабатывать сигналы тока и напряжения МК, что в современных реалиях считается обязательным. То мы придем к следующим формулам. Для среднеквадратичного напряжения:

Где К – коэффициент трансформации, N – количество замеров за период напряжения, u – мгновенные значения напряжения. Для тока все будет тоже самое. Для вычисления полной мощности остается умножить U*I*3 для трехфазной симметричной нагрузки. А как же быть с активной мощностью? Активная мощность может быть вычислена следующим образом:

Осталось только взять замеры тока и напряжения в одни и те же отрезки времени на протяжении периода, просуммировать их произведение.

Рассмотрим типовую схему включения трансформатора напряжения в ВВ ячеки. Это вариант А.

Трансформатор тока включен в фазу B. Посмотрим диаграмму напряжений в трехфазной сети.

Фазное напряжение Ub и линейное напряжение Uac располагаются под углом в 90&deg. При чем напряжение Uac отстает от фазного напряжения Ub. Ничего не напоминает.

Правда, амплитуда линейного напряжения больше фазного в корень из 3 раз. Но на МК уменьшить коэффициент на эту величину не составляет труда.

Значит у нас два критерия для нашего фильтра. Сдвиг фазы выходного напряжения относительно входного должно составлять ≈90&deg. Коэффициент передачи на данной частоте, должно быть такой, чтобы обеспечить выходное напряжение после фильтра в пределах 1-1.5 вольта.

Приступим к вычислениям.

Расчет фильтра.

С трансформатора напряжения приходит 100 вольт напряжения (стандарт). Это действующее напряжение, следовательно, чтобы нам определить амплитудное значение умножим на корень из 2.

ИТОГО: Umax=U*1.41=141В.

Это синусоида, и она имеет как положительную полуволну, так и отрицательную. Значит, нам для МК необходимо эту синусоиду поднять в положительное напряжение.

Напряжение питание МК возьмем 3 в. Значит, средняя точка для синусоиды будет 1.5 вольта. Итого размах полуволны напряжения нам остается 1.5вольта. Отсюда коэффициент передачи RC цепи будет:

Теперь вычислим значение τ=RC, исходя из коэффициента К. Частота сигнала известна 50 Гц.

После математических преобразований получаем: τ=RC = 0,318

Отсюда

Угол нас устраивает. Вычислим погрешность измерений, при ошибки фазы в 0,57&deg, следовательно ошибка равна: (0,57&deg/90&deg)*100%=0,63%, это за четверть периода, следовательно за 360&deg и того меньше. Вряд ли трансформаторы тока и напряжения будут классом точности выше чем 0,5%. Так что, искажениями, вносимыми нашем фильтром можно пренебречь.

Осталось рассчитать сами значения R и C. Отталкиваться лучше от конденсатора. Возьмем С=4,7 мкФ, отсюда R= τ/С=0,318/4,7*10-6=318*10-3/4,7*10-6=67,66*103 Ом или 67,66 кОм.

Теперь подтвердим наши расчеты симулятором Proteus и посмотрим, отличается ли его математика от нашей.

Проект протеуса прикладываю к статье. Можете убедиться, что расчеты верны.

Вот таким нехитрым способом можно заставить работать RC цепочку не по назначению.

ВИДЕО демонстрирующее возможности RC фильтра.

Применение в практике данного способа использования RC цепи я опишу в следующей раз.

UPD:

Пользователь Santik в комментариях затронул вопрос о реальных сетях, с присутствующими искажениями основной частоты 50 Гц гармониками. Было высказано предложение просимулировать в протеусе данную ситуацию. Схема протеуса конечно, не реальная картина на производстве, но показывает, что если сигнал основной частоты искажен гармониками небольшой амплитуды, то RC фильтр хорошо выделяет основную частоту и нормализует синус.
Видео, демонстрирующее работу фильтра с сигналом, искаженным гармониками.

Интегрирующая цепь RC. Расчёт постоянной времени RC-цепочки

Рассмотрим RC-цепь, изображенную на рис. 3.20,а. Пусть на входе этой цепи действует напряжение u1(t).

Рис. 3.20. Дифференцирующие RC-(а) и RL-(б) цепи.

Тогда для этой цепи справедливо соотношение

и с учетом преобразований будем иметь

(3.114)

Если для данного сигнала выбрать постоянную времени цепи τ=RC настолько большим, что вкладом второго члена правой части (3.114) можно пренебречь, то переменная составляющая напряжения uR≈u1. Это значит, что при больших постоянных времени напряжение на сопротивлении R повторяет входное напряжение. Такую цепь применяют тогда, когда необходимо передать изменения сигнала без передачи постоянной составляющей.

При очень малых значениях τ в (3.114) можно пренебречь первым слагаемым. Тогда

(3.115)

т. е. при малых постоянных времени τ RC-цепь (рис. 3.20,а) осуществляет дифференцирование входного сигнала, поэтому такую цепь называют дифференцирующей RC-цепью.

Аналогичными свойствами обладает и RL-цепь (рис. 3.20,б).

Рис. 3.21. Частотные (а) и переходная (б) характеристики дифференцирующих цепей.

Сигналы при прохождении через RС- и RL-цепи называют быстрыми, если

или медленными, если

Отсюда следует, что рассмотренная RC-цепь дифференцирует медленные и пропускает без искажения быстрые сигналы.

Для гармонической э. д. с. аналогичный результат легко получить, вычисляя коэффициент передачи цепи (рис. 3.20,а) как коэффициент передачи делителя напряжения со стационарными сопротивлениямиR и XC=1/ωC:

(3.116)

При малых τ, а именно когда τ

При этом фаза выходного напряжения (аргумент K) равна π/2. Сдвиг гармонического сигнала по фазе на π/2 эквивалентен его дифференцированию. При τ>>1/ω коэффициент передачи K≈1.

В общем случае модуль коэффициента передачи (3.116), или частотная характеристика цепи (рис. 3.20,а):

(3.118)

а аргумент K, или фазовая характеристика этой цепи:

Эти зависимости показаны на рис. 3.21,а.

Такими же характеристиками обладает RL-цепь на рис. 3.20,б с постоянной времени τ=L/R.

Если в качестве выходного сигнала взять единичный скачок напряжения , то интегрированием уравнения (3.114) можно получить переходную характеристику дифференцирующей цепи, или временную зависимость выходного сигнала при единичном скачке напряжения на входе:

График переходной характеристики показан на рис. 3.21,б.

Рис. 3.22. Интегрииующие RC-(а) и LC-(б) цепи.

Рассмотрим RC-цепь, изображенную на рис. 3.22,а. Она описывается уравнением

(3.121)

При малых τ=RC (для «медленных» сигналов) uC≈u1. Для «быстрых» сигналов напряжение u1 интегрируется:

Поэтому RC-цепь, выходное напряжение которого снимается с емкости C называют интегрирующей цепью.

Коэффициент передачи интегрирующей цепи определяется выражением

(3.123)

При ω

Частотная и фазовая характеристики описываются соответственно выражениями

(3.124)

Рис. 3.23. Частотные (а) и переходная (б) характеристики интегрирующих цепей.

и изображены на рис. 3.23,а. Переходная характеристика (рис. 3.23,б) получается интегрированием (3.121) при :

При равных постоянных времени такими же свойствами обладает RL-цепь, изображенная на рис. 3.22,б.

Электрическая цепь, в к-рой выходное напряжение U вых (t)(или ток) пропорционально интегралу по времени от входного напряжения U вх (t) (или тока):


Рис. 1. Интегратор на операционном усилителе. С под действием приложенного тока или накопление магн. потока в катушке с индуктивностью L под действием приложенного напряжения Преимущественно используются И. ц. с конденсатором. R, равен току заряда

конденсатора С, а напряжение в точке их соединения равно нулю. В результате Произведение RС=t, характеризующее скорость заряда конденсатора, наз. постоянной времени И. ц. RC-И. ц. (рис. 2, а). В этой схеме ток заряда конденсатора определяется разностью входного и выходного напряжений поэтому интегрирование входного напряжения выполняется приближённо и тем точнее, чем меньше выходное напряжение по сравнению с входным. Последнее условие выполняется, если постоянная времени t много больше интервала времени, по к-рому происходит интегрирование. Для правильного интегрирования импульсного входного сигнала необходимо, чтобы t была много больше длительности импульса Т(рис. 3). Аналогичными свойствами обладает RL-И. ц., показанная на рис. 2, б, для к-рой постоянная времени равна L/R.

Рис. 3. 1 — входной прямоугольный импульс; 2 — выходное напряжение интегрирующей цепи при tдT.

И. ц. применяются для преобразования импульсов, модулированных по длительности, в импульсы, модулированные по амплитуде, для удлинения импульсов, получения пилообразного напряжения, выделения низкочастотных составляющих сигнала и т. п. И. ц. на операц. усилителях применяются в устройствах автоматики и аналоговых ЭВМ для реализации операции интегрирования.

53.Переходные процессы. Законы коммутации и их применение.

Перехо́дные проце́ссы — процессы, возникающие в электрических цепях при различных воздействиях, приводящих их из стационарного состояния в новое стационарное состояние, то есть, — при действии различного рода коммутационной аппаратуры, например, ключей, переключателей для включения или отключения источника или приёмника энергии, при обрывах в цепи, при коротких замыканиях отдельных участков цепи и т. д.

Физическая причина возникновения переходных процессов в цепях — наличие в них катушек индуктивности и конденсаторов, то есть индуктивных и ёмкостных элементов в соответствующих схемах замещения. Объясняется это тем, что энергия магнитного и электрического полей этих элементов не может изменяться скачком при коммутации (процесс замыкания или размыкания выключателей) в цепи.

Переходный процесс в цепи описывается математически дифференциальным уравнением

• неоднородным (однородным), если схема замещения цепи содержит (не содержит) источники ЭДС и тока,
• линейным (нелинейным) для линейной (нелинейной) цепи.

Длительность переходного процесса длятся от долей наносекунд до годов. Зависят от конкретной цепи. Например, постоянная времени саморазряда конденсатора с полимерным диэлектриком может достигать тысячелетия. Длительность протекания переходного процесса определяется постоянной времени цепи.

Законы коммутации относятся к энергоемким (реактивным) элементам, т. е. к емкости и индуктивности. Они гласят: напряжение на емкости и ток в индуктивности при конечных по величине воздействиях являются непрерывными функциями времени, т. е. не могут изменяться скачком.

Математически эта формулировка может быть записана следующим образом

Для емкости;

Для индуктивности.

Законы коммутации являются следствием определений элементов емкости и индуктивности.

Физически закон коммутации для индуктивности объясняется противодействием ЭДС самоиндукции изменению тока, а закон коммутации для емкости – противодействием напряженности электрического поля конденсатора изменению внешнего напряжения.

54.Вихревые токи, их проявления и использование.

Вихревые токи или токи Фуко́ (в честь Ж. Б. Л. Фуко) — вихревые индукционные токи, возникающие в проводниках при изменении пронизывающего их магнитного поля.

Впервые вихревые токи были обнаружены французским учёным Д. Ф. Араго (1786-1853) в 1824 г. в медном диске, расположенном на оси под вращаю

Импульс. RC и RL цепи

Всем доброго времени суток. Сегодняшний мой пост начинает серию статей про импульсные устройства. Такие устройства предназначены для формирования и преобразования электрических сигналов, имеющих характер импульсов и перепадов напряжений. К импульсным устройствам относятся все цифровые микросхемы и некоторые аналоговые, например, микросхемы генераторов и компараторов. Ранее я рассматривал один из основных элементов импульсных устройств – транзистор, работающий в ключевом режиме.

Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.

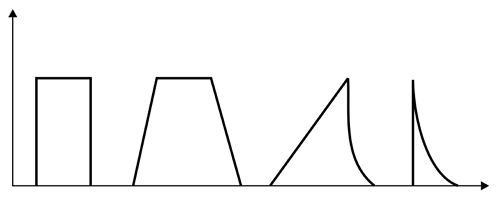
Формы импульса (слева направо): прямоугольная, трапецеидальная, пилообразная, экспоненциальная.

В радиоэлектронике используются импульсы самых разнообразных форм, но наиболее распространённые это: прямоугольные, трапецеидальные, пилообразные и экспоненциальные формы импульсов. Форма любого импульса характеризуется следующими основными параметрами:

• амплитуда (максимальное значение) импульса, U_m;
• начальное значение импульса, U₀;
• длительность импульса, t_и;
• длительность переднего фронта (или просто фронта) импульса, t_ф;
• длительность заднего фронта (или среза) импульса, t_с;
• длительность вершины импульса, t_в;
• снижение вершины импульса, Δu;
• крутизна фронта импульса (скорость изменения напряжения при формировании переднего или заднего фронта).

В случае использовании периодичности повторяющихся импульсов имеют большое значение такие параметры, как скважность импульсов (ξ или S), коэффициент заполнения импульсов (η или D), частота повторения импульсов (f) и период повторения импульсов (T). Данные параметры имеют следующие соотношения между собой

[math]S = \frac{T}{t_{i}}, D = \frac{1}{S}=\frac{t_{i}}{T}, f=\frac{1}{T}=\frac{1}{St_{i}}[/math]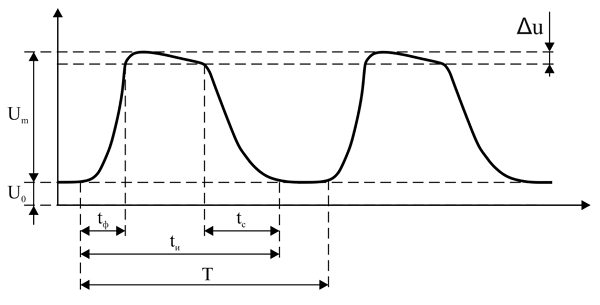

Форма реального импульса

Временные параметры импульса (t_и, t_ф, t_с, t_в) имеют точное значение только в случае идеального импульса, а в реальности лишь в некоторой степени имеют приближённое значение. Поэтому временные параметры отсчитываются от некоторых приближённых величин, которые в достаточной для практики точности имеют значения 0,05 и 0,95. Поясню на примере формы реального импульса, изображённого выше: при определении длительности фронта (t_ф) импульса, за начало фронта принимают значение 0,05*U_m, а за окончание фронта – 0,95*U_m. В случае длительности среза, соответственно, начало – 0,95*U_m, а окончание – 0,05*U_m.

Переходный процесс

Рассмотрение импульсных устройств и схем не возможно без представлении о переходном процессе. Он возникает в цепях при различных коммутациях, то есть при включении или выключении элементов схемы, источников напряжения, при коротких замыканиях отдельных цепей и т.д. Переходный процесс объясняется тем, что энергия электромагнитных полей, связанных с цепью, в разные промежутки времени неодинакова, а резкое изменение энергии невозможно из-за ограниченной мощности источников питания.

Исходя из вышесказанного, можно сделать вывод, что напряжение на ёмкости и ток в индуктивность не могут изменяться скачкообразно, так как данные параметры определяют энергию электрического поля конденсатора и магнитного поля катушки индуктивности.

Таким образом, можно сделать вывод, что при рассмотрении импульсных схем наибольшее внимание необходимо обратить на цепи, представляющие собой комбинации резисторов и конденсаторов или резисторов и катушек индуктивностей (RC- и RL-цепей). Такие цепи применяются непосредственно для формирования импульсов, а также являются важнейшими элементами релаксационных генераторов, триггеров и других устройств. Поэтому ниже рассмотрим основные свойства элементарных RC- и RL-цепей, а также изменение формы импульсов при прохождении через эти цепи.

Влияние RC- и RL-цепей на импульсы различной формы

Несмотря на то, что формы электрических импульсов довольно разнообразны, их можно представить в виде суммы элементарных (типовых) напряжений трёх форм: скачкообразного, линейно изменяющегося и экспоненциального. Поэтому рассмотрим воздействие различных форм напряжений на RC- и RL-цепи.

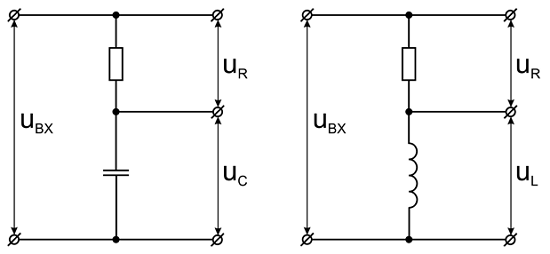
Изображение RC- и RL-цепей.


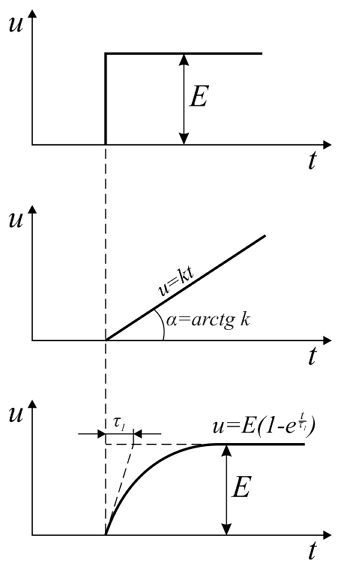
Элементарные формы напряжения (сверху вниз): ступенчатое, линейно-изменяющееся, экспоненциальное.

Ступенчатое изменение напряжения. При подключении RC-цепи к источнику постоянного напряжения u_вх = Е = const, напряжения на конденсаторе и резисторе будет изменяться по экспоненциальному закону:

[math]u_{R}=Ee^{- \frac{t}{\tau}}[/math]
[math]u_{C}=E(1 — e^{- \frac{t}{\tau}})[/math]

где е – математическая постоянная, е = 2,72;
t – время, с;
τ – постоянная времени, с. τ = RC.

С определением напряжения всё понятно, но в практике чаще возникает вопрос о времени установления напряжения. Например, необходимо вычислить время за которое на конденсаторе установится напряжение равное u_С = 0,95 Е. Простым преобразованием формулы напряжения получим

[math]t=- \tau \ln(1 — \frac{u_{C}}{E})[/math]
[math]t=- \tau \ln(1 — \frac{0,95E}{E})=- \tau \ln(0,05) \approx 3 \tau[/math]

Аналогично при подключении RL-цепи к источнику постоянного напряжения u_вх = Е = const

[math]u_{R}=E(1 — e^{- \frac{t}{\tau}})[/math]
[math]u_{L}=Ee^{- \frac{t}{\tau}}[/math]

где τ – постоянная времени, с. τ = L/R.

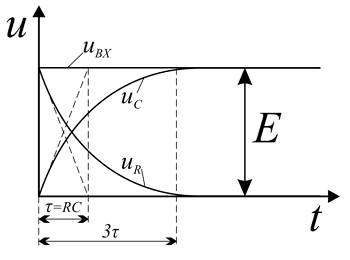
Линейно изменяющееся напряжение. При подключении RC-цепи к источнику линейно изменяющегося напряжения u_ВХ = kt, напряжения на резисторе и конденсаторе будут изменяться согласно следующей формуле

[math]u_{R}=k \tau (1 — e^{- \frac{t}{\tau}})[/math]
[math]u_{C}=kt — k \tau (1 — e^{- \frac{t}{\tau}})[/math]

Для RL-цепи подключённой к источнику с линейно изменяющимся напряжением u_ВХ = kt, напряжения на элементах соответственно будут такими

[math]u_{R}=kt — k \tau (1 — e^{- \frac{t}{\tau}})[/math]
[math]u_{L}=k \tau (1 — e^{- \frac{t}{\tau}})[/math]


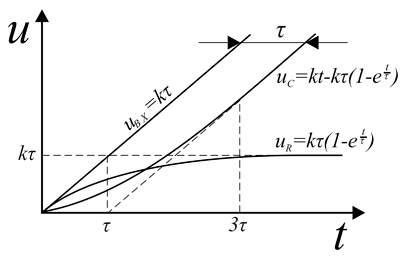
Временные диаграммы напряжений при линейно изменяющемся напряжении в RC- и RL-цепях.

Экспоненциально изменяющееся напряжение. При подключении RC-цепи к источнику экспоненциально изменяющегося напряжения [math]u=E(1-e^{- \frac{t}{\tau}})[/math], напряжения на резисторе и конденсаторе будут изменяться согласно следующей формуле

[math]u_{R}= \frac{Eq}{q-1}(e^{- \frac{t}{\tau}}-e^{- \frac{t}{\tau}})[/math]

где q = τ/τ₁.

Соответственно напряжение на конденсаторе будет равно разности напряжений источника и напряжения на резисторе

[math]u_{C}=E(1-e^{- \frac{t}{\tau}}) \frac{Eq}{q-1}(e^{- \frac{t}{\tau}}-e^{- \frac{t}{\tau_{1}}})[/math]

Временные диаграммы для u_R представлены ниже при различных значениях q. При больших значениях q, то есть постоянной времени цепи τ, формы напряжений u_R близки к формам, соответствующим ступенчатому изменению входного напряжения. При уменьшении τ, кроме сокращения длительности спада напряжения u_R, уменьшается и максимальное значение u_R.

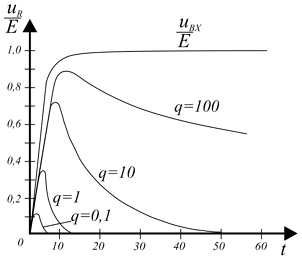
Временные диаграммы напряжений на резисторе RC-цепи при различных значениях
q = τ/τ₁.

Формулы и временные диаграммы для напряжений на выходе RL-цепи оказываются такими же, как и для RC-цепи.

Дифференцирующие цепи

Довольно часто в электронике вообще, а в импульсной в частности требуется преобразовать один вид импульсов в другой (например, прямоугольный преобразовать в треугольный). Для этой цели используют различные схемы, в основе которых простейшие RC- и RL-цепи. Такие цепи называются дифференцирующими и интернирующими цепями. Для начала рассмотрим дифференцирующие цепи, которые показаны на изображении ниже.

Своё название дифференцирующие цепи получили от того, что напряжение на выходе такой цепи пропорционально производной входного напряжения, а нахождение производной в математике называется дифференцирование. В случае RC-цепи напряжение снимается с резистора, а в случае RL-цепи – с индуктивности.

Простейшие .

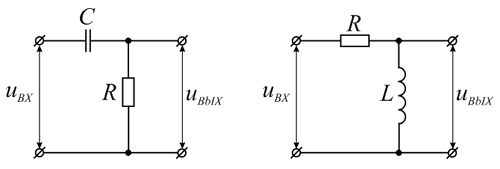
В настоящее время большинство дифференцирующих цепей основаны на RC-цепях, поэтому будем рассматривать их, но все основные выкладки соответствуют также и RL-цепям.

Рассмотрим, как дифференцирующая цепь будет реагировать на прямоугольный импульс. Прямоугольный импульс представляет собой как бы два скачка напряжения. Реакцию RC-цепи на скачкообразное изменение напряжения рассматривалась выше, а в случае прямоугольного импульса выходное напряжение с дифференцирующей цепи будет в виде двух коротких импульсов различной полярности, длительность которых соответствует 3τ = 3RC и 3τ = 3L/R, в случае RL-цепи.

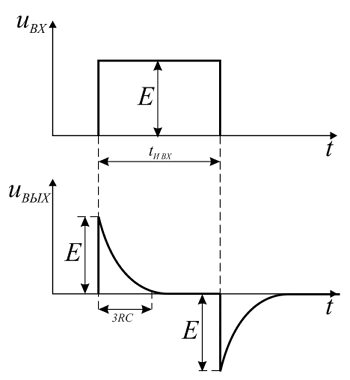
Реакция дифференцирующей цепи на прямоугольный импульс.

Из величины и формы выходного напряжения можно сделать вывод, что дифференциальные цепи вполне могут применяться для уменьшения длительности импульсов, что довольно часто применяется на практике и ранее такие цепи иногда называли укорачивающими.

Интегрирующие цепи

Интегрирующие цепи, так же как и дифференцирующие строят на основе RC- и RL-цепей, отличие заключается в том, откуда снимают выходное напряжение.

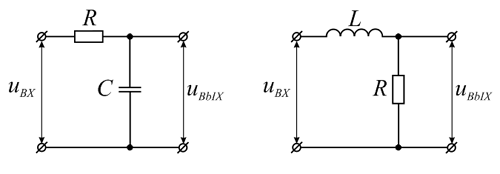
Простейшие RC и RL интегрирующие цепи.

Своё название интегрирующие цепи получили от того, что выходное напряжение, снимаемое с их выхода пропорционально интегралу от входного напряжения. Рассмотрим реакцию интегрирующей цепи на прямоугольный импульс напряжения. Напомню, что прямоугольный импульс, по сути, является напряжением, которое изменяется ступенчато два раза. В результате первого скачка напряжения конденсатор начинает заряжаться до тех пор, пока напряжение на входе не изменится, после этого начнётся разряд конденсатора по экспоненциальному закону.

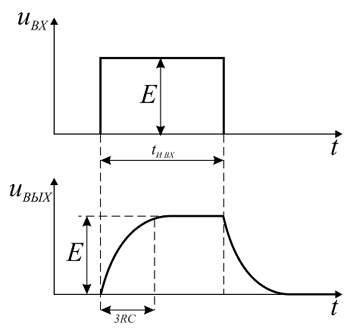
Реакция интегрирующей цепи на прямоугольный импульс.

Не трудно заметить, что длительность импульса на выходе интегрирующей цепи несколько больше, чем длительность импульса на входе. Эту особенность нередко используют для увеличения длительности импульса, и такие цепи ранее называли расширяющими.

Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.

3. Расчеты напряжения и тока в RC и L/R цепях | 15. RC и L/R цепи | Часть1

3. Расчеты напряжения и тока в RC и L/R цепях

Расчеты напряжения и тока в RC и L/R цепях

Существует простой способ расчета любой величины реактивной цепи постоянного тока в любой момент времени. Первый шаг этого способа заключается в определении начальных и конечных значений тех величин, против изменения которых выступает конденсатор или катушка индуктивности (которые они пытаются держать на постоянном уровне, независимо от реактивной составляющей). Для конденсаторов такой величиной будет напряжение, а для катушек индуктивности — ток. Начальное значение — это такое значение, которое было до момента замыкания (размыкания) контактов выключателя, и которое реактивный компонент пытается удерживать на постоянном уровне после замыкания (размыкания) контактов. Конечное значение — это значение, которое устанавливается по истечении неопределенно длительного периода времени. Оно может быть определено путем анализа емкостной цепи, когда конденсатор выступает в качестве обрыва цепи, и индуктивной цепи, когда катушка индуктивности выступает в роли короткозамкнутой перемычки, потому что именно так ведут себя эти элементы при достижении «полной зарядки» через неопределенно длительный промежуток времени.

Следующим шагом является вычисление постоянной времени цепи. Постоянная времени представляет собой промежуток времени, в течение которого величина напряжения или тока в переходном процессе изменится примерно на 63% от начального до конечного значения. В последовательной RC-цепи, постоянная времени равна общему сопротивлению (в Омах) умноженному на общую емкость (в Фарадах). В последовательной L/R-цепи она равно общей индуктивности (в Генри) деленной на общее сопротивление  (в Омах). В обоих случаях постоянная времени выражается в секундах и обозначается греческой буквой «тау» (τ):

 

 

Увеличение и уменьшение значений тока и напряжения в переходных процессах, как уже отмечалось ранее, носит асимптотический характер. А это значит, что они начинают быстро изменяться в начальный момент времени, и практически не изменяются в последующем. На графике данные изменения отображаются в виде экспоненциальных кривых.

Как уже было сказано выше, постоянная времени представляет собой промежуток времени, в течение которого величина напряжения или тока в переходном процессе изменится примерно на 63% от начального до конечного значения. Каждая последующая постоянная времени приближает эти величины к конечному значению еще примерно на 63%. Математическая формула для определения точного процента довольно проста:

 

 

Буква e здесь — иррациональная константа, равная приблизительно 2,7182818. За время τ, процент изменения от начального до конечного значения составит:

 

 

За время 2τ, процент изменения от начального до конечного значения составит:

 

 

За время 10τ, процент изменения  составит:

 

 

Для расчета напряжений и токов в реактивных цепях эту формулу можно сделать более универсальной:

 

 

Давайте проанализируем повышение напряжения в RC-цепи, показанной в первой статье этого раздела:

 

 

Обратите внимание, мы выбрали для анализа напряжение, так как именно эту величину конденсатор пытается поддерживать на постоянном уровне. Зная сопротивление резистора (10 кОм) и емкость конденсатора (100 мкФ) мы можем рассчитать постоянную времени данной цепи:

 

 

Так как в момент замыкания контактов выключателя напряжение на конденсаторе равно 0 вольт, то именно это значение мы и будем использовать в качестве начального. Конечным значением конечно же будет напряжение источника питания (15 Вольт). С учетом всех этих цифр наше уравнение примет следующий вид:

 

 

Таким образом, через 7,25 секунд (к примеру) после подачи напряжения в схему через замкнутые контакты выключателя, напряжение на конденсаторе увеличится на:

 

 

Из этих расчетов можно сделать следующий вывод: если начальное напряжение конденсатора составляло 0 вольт, то через 7,25 секунд после замыкания контактов выключателя оно будет равно 14,989 вольт.

При помощи этой же формулы можно рассчитать и ток через конденсатор. Поскольку разряженный конденсатор первоначально действует как короткозамкнутая перемычка, ток через него будет максимальным. Рассчитать этот ток можно поделив напряжение источника питания (15 вольт) на единственное сопротивление (10 кОм):

 

 

Известно также, что конечный ток будет равен нулю, так как конденсатор в конечном итоге ведет себя как разомкнутая цепь. Теперь мы можем подставить эти значения в нашу универсальную формулу для расчета величины тока через 7,25 секунд после замыкания контактов выключателя:

 

 

Обратите внимание, что полученное значение является отрицательным, а не положительным! Это говорит об уменьшении тока с течением времени. Так как начальное значение тока составляет 1,5 мА, то его уменьшение на 1,4989 мА за 7,25 секунд даст в конечном итоге  0,001065 мА (1,065 мкА).

Это же значение можно получить при помощи закона Ома, отняв напряжение конденсатора (14,989 вольт) от напряжения источника питания (15 вольт) и поделив полученное значение на сопротивление (10кОм):

 

 

Рассмотренная выше универсальная формула хорошо подходит и для анализа L/R цепи. Давайте применим ее к цепи, рассмотренной во второй статье данного раздела:

 

 

При индуктивности 1 Генри и последовательном сопротивлении 1 Ом постоянная времени будет равна 1 секунде:

 

 

Поскольку катушка индуктивности в данной цепи выступает против изменения тока, именно эту величину мы и выберем для анализа. Начальным значением здесь выступит величина тока через катушку индуктивности в момент замыкания контактов выключателя. Она будет равна нулю. В качестве конечного значения мы возьмем величину тока, которая установится в катушке индуктивности по прошествии неопределенно длительного промежутка времени (максимальная величина). Рассчитать ее можно поделив напряжение источника питания на последовательное сопротивление: 15 В/1 Ом = 15 А.

Если мы хотим определить величину тока через 3,5 секунды после замыкания контактов выключателя, то формула примет следующий вид:

 

 

Учитывая тот факт, что начальный ток через катушку индуктивности равнялся нулю, через 3,5 секунды с момента замыкания контактов выключателя его величина составит 14,547 ампер.

Расчет напряжений в индуктивной цепи осуществляется при помощи закона Ома и начинается с резисторов, а заканчивается катушкой индуктивности. При наличии в нашем примере только одного резистора  (имеющего значение 1 Ом), произвести эти расчеты довольно легко:

 

 

Отняв полученное значение от напряжения источника питания (15 В), мы получим напряжение, которое будет на катушке индуктивности через 3,5 секунды после замыкания контактов выключателя: