3.1. Разряд конденсатора через активное сопротивление
Разряд предварительно заряженного конденсатора через активное сопротивление (через резистор) является простейшим переходным процессом.
Пусть конденсатор ёмкостью С заряжен до напряжения U. В момент t=0 замыкается ключ К и конденсатор начинает разряжаться через активное сопротивление R. Так как здесь внешнего воздействия нет, то в цепи будет только свободный процесс.
Выбрав направление обхода, запишем для этой цепи второе уравнение Кирхгофа:
uR−uC=0,
или
iR−uC=0. (1)
А так как для конденсатора ток i здесь является разрядным, то , и тогда, (2)
или ,

Общее решение этого однородного уравнения имеет вид (проинтегрировать самостоятельно; однако, решение уравнения такого типа надо знать):
,
где А – коэффициент, определяемый начальным условием, т.е. − напряжением на конденсаторев первый момент после замыкания ключа К. Так как, по условию, до замыкания напряжение , а напряжение на конденсаторе скачком измениться не может (это привело бы к тому, что, тогда как в уравнении (2)иС – конечно), то
(это второе правило коммутации).
. (3)
Отсюда видно, что τ – это время, за которое напряжение на конденсаторе убывает в е раз:
2,7.
Реально время
переходного процесса оценивается
примерно в 3τ, когда напряжение уменьшается
в е3 = 20 раз, или
когда до установившегося значения
осталось лишь 1/20 = 5 % от исходного
напряжения U.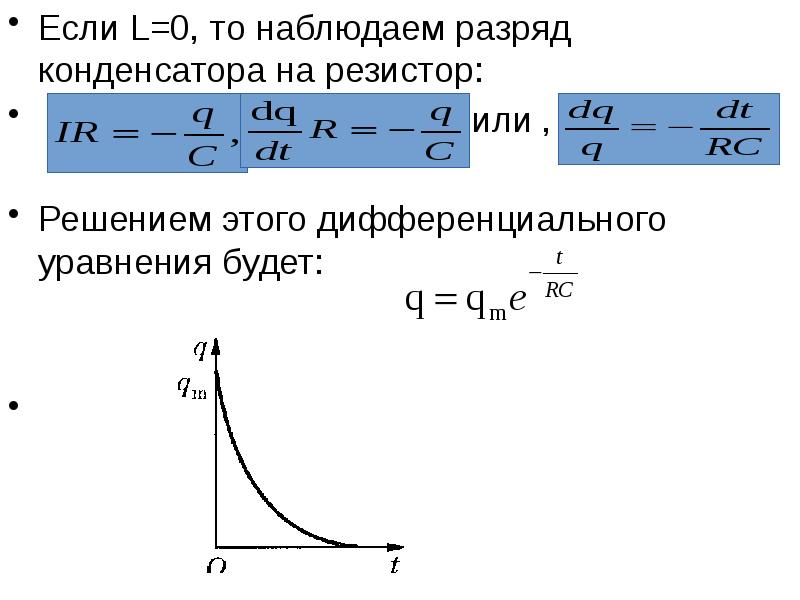
Пример. Пусть С=1 мкФ, R=1 кОм. Тогда время переходного процесса Δ
Теперь легко получить закон убывания тока в цепи:
.
Видно, что он точно такой же, как и закон убывания напряжения.
3.2. Включение постоянного напряжения
в последовательную цепь RC
Рассмотрим теперь процесс заряда конденсатора через активное сопротивление R от генератора с постоянным напряжением U.
Пусть в момент t=0 замыкается ключ К. Тогда второе уравнение Кирхгофа для выбранного направления обхода контура будет таким:
,
или, так как i
, (4)
где
−постоянная
времени RC-цепочки.
Общее решение этого неоднородного уравнения равно сумме его частного решения и общего решения соответствующего однородного. Частное решение легко угадывается: иС частн.=U (оно проверяется простой подстановкой). Тогда
.
Коэффициент А определяется из начального условия:
.
Ток заряда
.
3.3. Включение постоянного напряжения
в последовательную цепь RL
Процессы при коммутациях в цепи RL описываются такими же дифференциальными уравнениями, как и (2) или (4), поэтому подробнее остановимся лишь на некоторых специфических особенностях.
Второе уравнение Кирхгофа:
, или: .
Или: , (5)
где
−постоянная
времени цепи RL.
Общее решение неоднородного уравнения (5): i = iоднор.+iчастн.=.
Начальное условие:i(+0) = i(−0)=0 (ток через индуктивность скачком измениться не может, так как это противоречило бы уравнению (5)). Отсюда А=−U/R, и тогда
. (6)
Замечание 1. При R=0 (подключение напряжения U к идеальной индуктивности) уравнение (5) принимает вид: , откуда, т.е. ток в катушке линейно и бесконечно растёт (наклонный пунктир на рисунке). Это следует и из (6) при разложении экспоненты в ряд Тейлора по малому параметру (
Замечание 2. Если скачки тока через индуктивности и скачки напряжения на ёмкости запрещены, то скачки напряжения на катушке и тока на конденсаторе не противоречат уравнениям Кирхгофа.
Разряд конденсатора
Пусть конденсатор,
заряженный предварительно до напряжения
U0,
замыкается на резистор R,
т.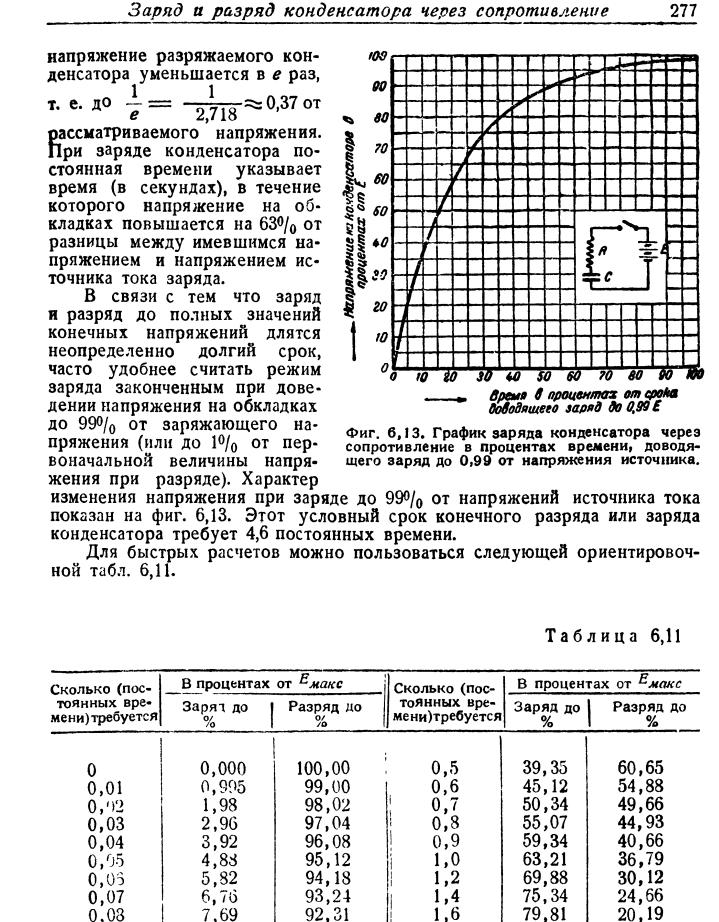 е. ключ К находится в положение 2.
Очевидно, что в любой момент времени
е. ключ К находится в положение 2.
Очевидно, что в любой момент времени
UC =UR = U | (10) |
Ток через резистор (ток проводимости) равен по модулю току через конденсатор (ток смещения) и противоположен ему по знаку (направлению): IC = —IR. Т.к. IC = dq / dt , а IR = U / R , то получаем дифференциальное уравнение
, или | (11) |
Его решением
является: (при t = 0 U = U0).
Ток через резистор:
(12) |
где I0 – начальный ток разряда. Выражение (12) совпадает с выражением (7). Итак, при разрядке конденсатора напряжение на нем и ток разряда экспоненциально уменьшаются. Введем обозначение:
= R C | (13) |
Величина , имеющая размерность времени, называется временем релаксации RC цепи (или постоянной времени цепи). Это время, за которое ток зарядки или разрядки уменьшается в e раз (приблизительно в 2,7 раза).
Описание экспериментальной установки
Цель работы –
экспериментальная проверка формулы
(13) и определение с ее помощью неизвестных
емкостей и сопротивлений. Установка
содержит источник ЭДС, два резистора –
известный и неизвестный, два конденсатора
– известный и неизвестный. С помощью
переключателей резисторы и конденсаторы
могут соединяться в цепь для заряда или
разряда конденсатора. Ток в цепи
измеряется микроамперметром, собственное
сопротивление которого пренебрежимо
мало. Имеется также кнопка «калибр» для
ускоренного разряда подключенного
конденсатора.
Установка
содержит источник ЭДС, два резистора –
известный и неизвестный, два конденсатора
– известный и неизвестный. С помощью
переключателей резисторы и конденсаторы
могут соединяться в цепь для заряда или
разряда конденсатора. Ток в цепи
измеряется микроамперметром, собственное
сопротивление которого пренебрежимо
мало. Имеется также кнопка «калибр» для
ускоренного разряда подключенного
конденсатора.
Выполнение работы
1. Подключить в схему конденсатор и резистор известных номиналов. Включить цепь на заряд и записать значения тока через каждые 20 30 секунд (порядка 12 значений). Затем цепь переключить на разряд и провести аналогичные измерения тока разряда. По полученным данным построить графики зависимостей натуральных логарифмов токов от времени. По графикам определить времена релаксации и сравнить их с рассчитанными по формуле (13).
2. Включить в цепь
известный конденсатор и неизвестный
резистор. Аналогично предыдущему пункту
получить зависимость тока заряда или
разряда от времени.
Контрольные вопросы
Принцип заряда и разряда конденсатора.
Графические зависимости U = U(t), I = I(t).
Понятие времени релаксации.
Доказать, что имеет размерность времени.
Графики зависимости E = E(t), где E = UC + UR.
Определение емкости конденсатора в данной работе.
Работа №9 изучение дифференцирующих и интегрирующих цепей
В электронике
зачастую возникает необходимость в
устройствах, выходной сигнал которых
пропорционален производной от входного
сигнала или интегралу от него.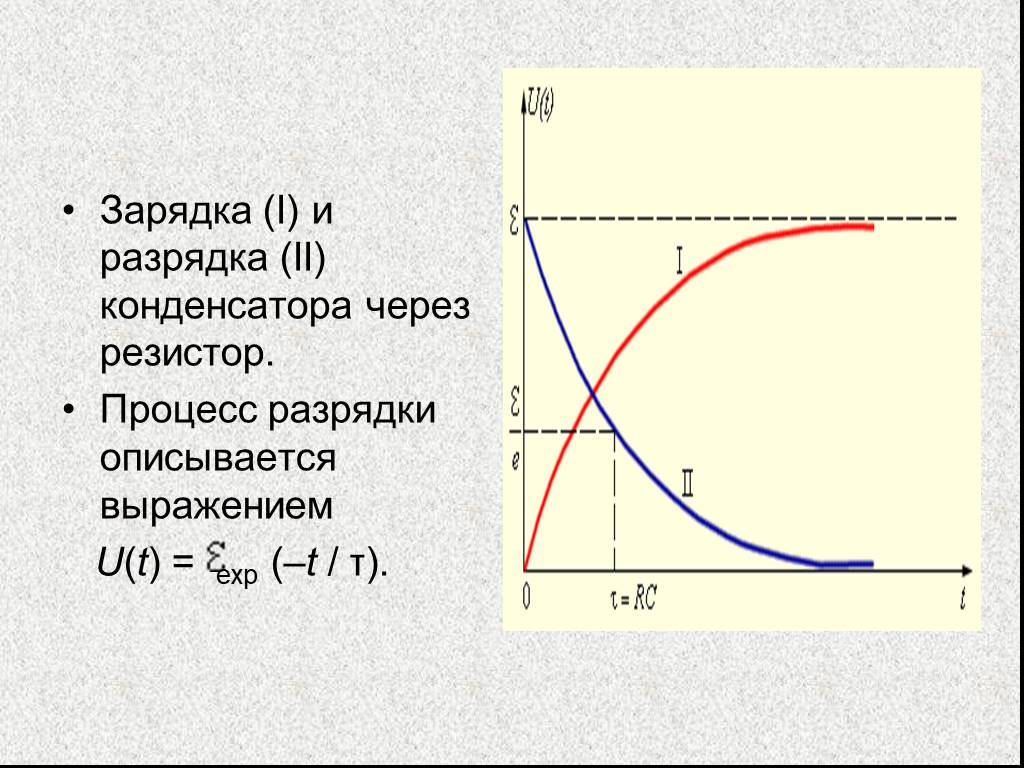 Простейшие
устройства, осуществляющие эти операции
– дифференцирующие и интегрирующие
цепи.
Простейшие
устройства, осуществляющие эти операции
– дифференцирующие и интегрирующие
цепи.
5.18: Разрядка конденсатора через резистор
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 6026
- Джереми Татум
- Университет Виктории
\(\text{РИСУНОК V.24}\)
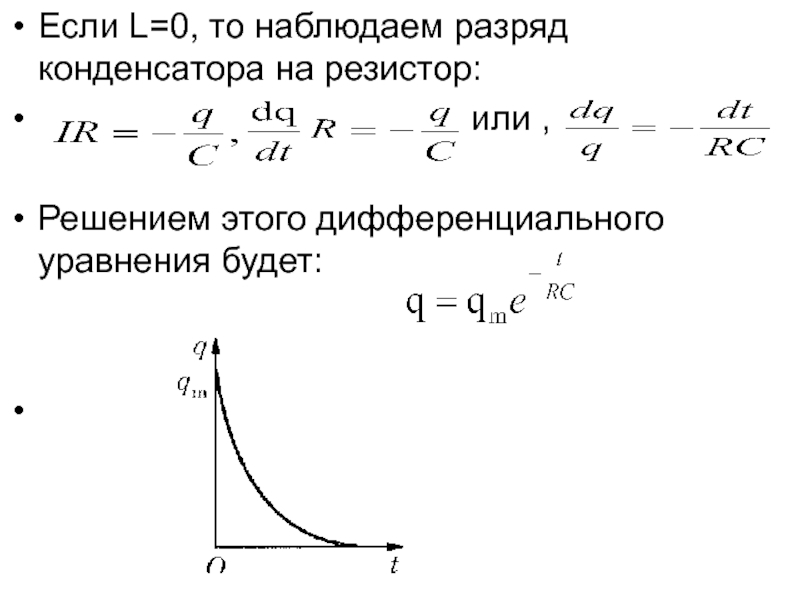
В этом и следующем разделах вы должны быть уверены в правильности знаков . Например, если заряд, удерживаемый в конденсаторе в какой-то момент времени, равен \(Q\), то символ \(\dot Q,\text{ или}dQ/dt\) означает скорость увеличения \(Q\) относительно времени. Если конденсатор разряжается, \(\dot Q\) отрицателен. Выражаясь иначе, символ, используемый для обозначения скорости, с которой конденсатор теряет заряд равен \(-\точка Q\).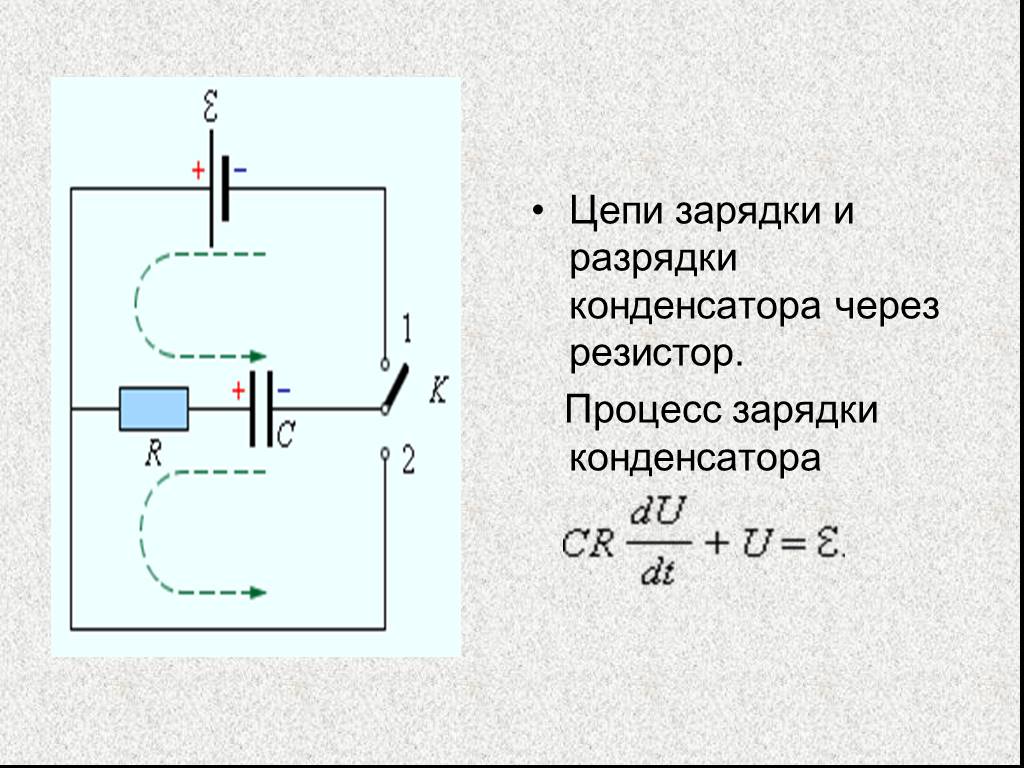 t dt, \метка{5.18.2}\] 9{-t/(RC)}.\label{5.18.3}\]
t dt, \метка{5.18.2}\] 9{-t/(RC)}.\label{5.18.3}\]
Здесь \(RC\) — постоянная времени . (Убедитесь, что оно имеет размерность времени.) Это время, когда заряд должен уменьшиться до \(1/e = 36,8\)% от начального заряда. Период полураспада заряда равен \(RC \ln 2 = 0,6931RC\).
Эта страница под названием 5.18: Разрядка конденсатора через резистор распространяется под лицензией CC BY-NC 4.0 и была создана, изменена и/или курирована Джереми Татумом посредством исходного контента, который был отредактирован в соответствии со стилем и стандартами LibreTexts. Платформа; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Джереми Татум
- Лицензия
- CC BY-NC
- Версия лицензии
- 4,0
- Показать оглавление
- нет
- Теги
- source@http://orca.
 phys.uvic.ca/~tatum/elmag.html
phys.uvic.ca/~tatum/elmag.html
- source@http://orca.
Как разрядить конденсатор? Использование продувочного резистора, отвертки, лампы
Конденсатор является важным компонентом, используемым в электрических и электронных устройствах. Наряду с резистором и индуктором конденсатор является одним из трех основных пассивных компонентов. Будучи широко используемым компонентом, конденсаторы подвержены неисправностям и повреждениям, и мы должны их заменить. Поскольку конденсаторы накапливают электрический заряд, вы должны правильно разрядить их, прежде чем работать с ними, чтобы вас не разрядило. В этом уроке мы узнаем, как разрядить конденсатор, используя несколько методов.
Краткое описание
Что такое конденсатор?
В своей простейшей форме конденсатор состоит из двух проводников, состоящих из проводящих пластин, фольги, проволоки или твердых тел и разделенных диэлектриком, который может быть воздухом, бумагой, вакуумом или любым изоляционным материалом.
При наличии разности потенциалов между двумя пластинами конденсатора с помощью источника питания он накапливает электрический заряд. Если мы удалим или отключим источник питания, конденсатор сможет подавать свой накопленный заряд в цепь.
Важным моментом в отношении конденсаторов является то, что если полностью заряженный конденсатор не разряжается в цепи, он может удерживать заряд даже после отключения основного источника питания. Таким образом, вы должны быть крайне осторожны при работе с конденсаторами в целом.
Что делает конденсатор?
Когда мы подключаем источник питания постоянного тока к выводам конденсатора, конденсатор постепенно накапливает заряд между своими пластинами, пока напряжение не сравняется с напряжением питания. Даже если мы отключим источник питания, конденсатор продолжает накапливать заряд, и таким образом конденсатор действует как маленькая батарея.
Мы можем использовать эту энергию в конденсаторе в цепи, а также можем контролировать скорость заряда и разряда с помощью последовательного резистора.
Помимо накопления электрического заряда, конденсаторы также могут блокировать постоянный ток при прохождении переменного тока, шума, звука и других сигналов, не являющихся постоянными. Мы можем использовать это свойство конденсатора, чтобы сгладить выходной сигнал источников питания, удалить скачки напряжения из сигналов, которые могут вызвать ненужное срабатывание цепей, защитить компоненты от постоянного тока, а также обеспечить чистую передачу аудиосигналов.
Зачем нужно разряжать конденсаторы?
Как упоминалось ранее, конденсаторы накапливают электрический заряд, и они могут удерживать заряд, даже если мы отключим основной источник питания. Если вы случайно коснулись выводов конденсатора после отключения питания, думая, что питание отсутствует; нет проблем, тогда вы можете получить удар током, когда конденсатор разрядится через ваше тело.
В зависимости от количества заряда вы можете получить небольшое покалывание или ожог пальцев, а в худшем случае это может привести к летальному исходу.
Так что, если вы планируете работать с конденсаторами, лучше разрядить их как следует даже после отключения питания. Конденсаторы в больших источниках питания переменного/постоянного тока очень большие и могут удерживать заряд в течение нескольких дней или месяцев, если их не разряжать. Если вы собираете детали от таких старых устройств, не думайте, что опасности не будет.
Как разрядить конденсатор?
Теперь, когда мы увидели, что разрядка конденсатора чрезвычайно важна для работы с ним в цепях и печатных платах. Но вопрос в том; Как разрядить конденсатор? Если вы хотите проверить конденсатор, посмотрите это руководство о том, как проверить конденсатор с помощью мультиметра.
Существует несколько способов правильной разрядки конденсатора. Мы рассмотрим детали для каждой техники один за другим. Как бы мы ни разряжали конденсатор, ни в коем случае нельзя касаться выводов конденсатора голыми руками. Будьте предельно осторожны.
Использование металлического предмета (отвертки)
Этот метод не самый безопасный, но он может легко разрядить конденсаторы. Для этого метода вам понадобится металлический предмет, например отвертка. Чтобы быть в безопасности, мы можем выбрать изолированную отвертку, только ее кончик будет металлической частью.
Для этого метода вам понадобится металлический предмет, например отвертка. Чтобы быть в безопасности, мы можем выбрать изолированную отвертку, только ее кончик будет металлической частью.
Прежде всего, отключите устройство от основного источника питания. Если конденсатор находится на печатной плате, выпаивайте его и не прикасайтесь к выводам конденсатора. Когда конденсатор извлечен из печатной платы, держите его одной рукой за основание.
Теперь возьмите отвертку в другую руку. Соедините кончик отвертки с обоими выводами конденсатора. Конденсатор разряжается с небольшими или средними искрами в зависимости от степени его заряда. Сделайте это пару раз, чтобы убедиться, что конденсатор полностью разряжен.
Если вам не нравятся искры или вы беспокоитесь о своей безопасности при разрядке с помощью отвертки, вы можете пропустить эту процедуру и попробовать любой другой метод, упомянутый ниже.
Использование продувочного резистора
Это профессиональный и безопасный способ разрядить конденсатор. На самом деле правильно спроектированный блок питания использует этот метод для разрядки выходных конденсаторов после отключения блока питания.
На самом деле правильно спроектированный блок питания использует этот метод для разрядки выходных конденсаторов после отключения блока питания.
В этом методе резистор, известный как продувочный резистор, подключается к выводам конденсатора. Когда питание схемы отключено, конденсатор разряжается через этот стравливающий резистор. Если в вашей схеме уже есть стабилизирующий резистор, то конденсатор автоматически разряжается через него после отключения питания, а скорость разряда зависит как от емкости конденсатора, так и от номинала резистора.
Но если в вашей схеме нет стабилизирующего резистора или вы не уверены, используется ли стабилизирующий резистор или нет, вы можете попробовать подключить его самостоятельно. Возьмите продувочный резистор и подключите его выводы к паре зажимов типа «крокодил». Теперь подключите эти зажимы-крокодилы к выводам конденсатора. Подождите расчетное время, и конденсатор полностью разрядится.
Но какой номинал резистора выбрать? Вот интересный калькулятор от Digi-Key, который вычисляет номинал резистора и его номинальную мощность после ввода емкости, напряжения и времени разряда.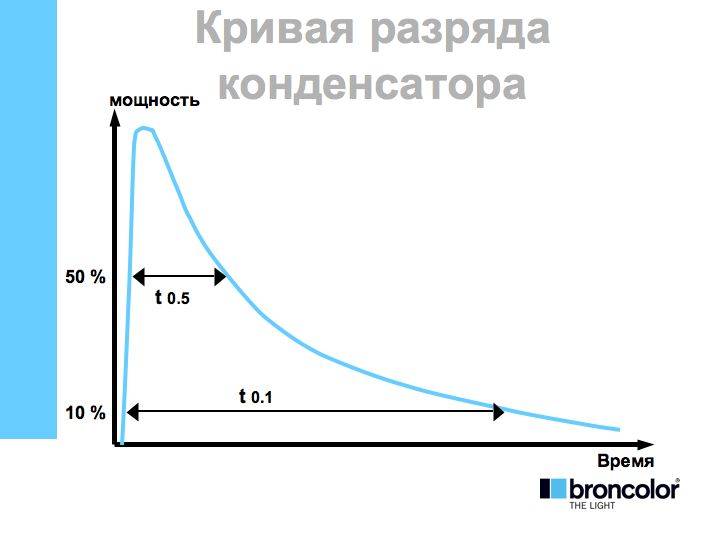
Например, если у нас есть конденсатор 470 мкФ, рассчитанный на 50 В, и мы хотим разрядить этот конденсатор до 0,1 В. Если мы используем резистор 1 кОм на выводах конденсатора, он разрядится за 3 с. Но важно помнить о номинальной мощности резистора. Чтобы безопасно разрядить конденсатор, резистор должен быть рассчитан на рассеиваемую мощность не менее 2,5 Вт. Итак, в этом случае выберите резистор 5 Вт 1 кОм, чтобы быть в безопасности. Эти мощные резисторы обычно дороги.
Использование резистивной нагрузки
Другой простой способ разрядить конденсатор — использовать резистивную нагрузку, например вольфрамовую лампу. Если у вас завалялась старая вольфрамовая лампа с приличной номинальной мощностью, вы можете использовать ее в качестве «разрядного резистора» для разряда конденсатора.
Вольфрамовые лампы представляют собой резистивные провода, заключенные в стеклянную колбу, заполненную вакуумом/инертным газом. Выбирайте вольфрамовые лампы мощностью не менее 10 Вт, чтобы они могли правильно разрядить конденсатор без повреждения.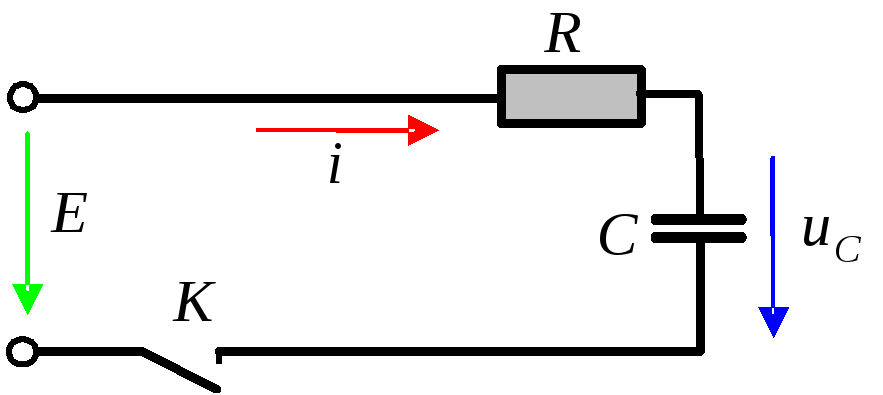


 phys.uvic.ca/~tatum/elmag.html
phys.uvic.ca/~tatum/elmag.html