Разностные фильтры
Разностные фильтры часто используются для нахождения границ в изображениях. При этом используют дифференциальный оператор, вычисляющий приближенное значение градиент1 яркости изображения. Результатом применения такого оператора в каждой точке изображения является либо вектор градиента яркости в этой точке, либо его норма.
Результат показывает, насколько «резко» или «плавно» меняется яркость изображения в каждой точке, а значит, вероятность нахождения точки на грани, а также ориентацию границы. На практике, вычисление величины изменения яркости (вероятности принадлежности к границе) надежнее и проще в интерпретации, чем расчет направления.
Если на изображении будет
присутствовать однотонная область или
область с плавными переходами цветов,
то в результирующем изображении подобные
участки будут закрашены черным цветом.
Там, где имеются перепады (резкие
переходы, края), крутизна изменения
яркости высока и в конечном изображении
в таких местах появятся яркие светлые
линии.
Математически, градиент функции двух переменных для каждой точки изображения (которой и является функция яркости) — двумерный вектор, компонентами которого являются производные яркости изображения по горизонтали и вертикали. В каждой точке изображения градиентный вектор ориентирован в направлении наибольшего увеличения яркости, а его длина соответствует величине изменения яркости.
Одним из способов нахождения границ на изображении является реализация фильтра или оператора Собеля (Sobel), который позволяет найти неточное приближение градиента яркости изображения.
Строго говоря, оператор использует ядра 3×3, с которыми сворачивают исходное изображение для вычисления приближенных значений производных по горизонтали и по вертикали. Формально оператор Собеля определяется следующим образом:
Пусть A исходное изображение, а Gx и Gy — два изображения, где каждая точка
содержит приближенные производные по x и по y. Они
вычисляются следующим образом:
Они
вычисляются следующим образом:
где * обозначает двухмерную операцию свертки (операцию линейной фильтрации, рассмотренную ранее).
Координата x здесь возрастает «направо», а y — «вниз». В каждой точке изображения приближенное значение величины градиента можно вычислить, используя полученные приближенные значения производных:
Используя эту информацию, мы также можем вычислить направление градиента:
где, к примеру, угол Θ равен нулю для вертикальной границы, у которой тёмная сторона слева.
Операции свертки Gx и Gy можно использовать отдельно для нахождения вертикальных и горизонтальных границ. На Рис. 4 .37 приведен пример применения свертки
 4 .38.
4 .38.а) | б) | в) |
Рис. 4.37. Пример нахождения вертикальных и горизонтальных границ
В отличии от сглаживающих и контрастоповышающих фильтров, не меняющих среднюю интенсивность изображения (сумма элементов ядра равна единице), в результате применения разностных операторов получается, как правило, изображение со средним значением пикселя близким к нулю (сумма элементов ядра равна нулю). При этом пиксели со значениями близкими к нулю можно отображать белым цветом. Пиксели значения яркости, которых получились большего некоего порога, можно отображать черным цветом.
Заметим, что выделение всех
пикселей, значения которых по модулю
больше некоторого порога, является
некоторой нелинейной локальной операцией,
которую можно рассматривать как
простейший пример нелинейной фильтрации.
Рис. 4.38. Пример использования оператора Собеля
Кроме фильтра Собеля можно использовать оператор Прюита (Prewitt) или оператор Щарра (Scharr), подобные алгоритму оператора Собеля, за исключением использования других матриц.
У алгоритмов нахождения границ существует несколько недостатков. Главный из них — неопределенность в выборе величины порога. Для разных частей изображения приемлемый результат обычно получается при существенно разных пороговых значениях. Кроме того, разностные фильтры очень чувствительны к шумам изображения.
НОУ ИНТУИТ | Лекция | Фильтрация изображений
Аннотация: Введение. Линейные фильтры: определение, сглаживающие фильтры, контрастоповышающие фильтры, разностные фильтры. Нелинейные фильтры: примеры нелинейных фильтров, морфологические операторы
8.1. Введение
Представим себе, что, глядя на какую-нибудь сцену одним глазом, мы подносим к нему стеклянную пластину. Если эта пластина не была идеально прозрачной, то наблюдаемое изображение изменится. В зависимости от стекла, из которого сделана пластина, изменение может быть самым разнообразным. К примеру, если это стекло было цветным, то изображение приобретет соответствующий оттенок, а от мутного стекла — станет размытым.
Если эта пластина не была идеально прозрачной, то наблюдаемое изображение изменится. В зависимости от стекла, из которого сделана пластина, изменение может быть самым разнообразным. К примеру, если это стекло было цветным, то изображение приобретет соответствующий оттенок, а от мутного стекла — станет размытым.
Фильтрация изображений аналогична такому разглядыванию мира через стеклянную пластину, хотя и позволяет добиться гораздо большего разнообразия эффектов, чем эксперименты с разными пластинами. Под фильтрацией изображений понимают операцию, имеющую своим результатом изображение того же размера, полученное из исходного по некоторым правилам. Обычно интенсивность (цвет) каждого пикселя результирующего изображения обусловлена интенсивностями (цветами) пикселей, расположенных в некоторой его окрестности в исходном изображении.
Правила, задающие фильтрацию (их называют фильтрами ), могут быть самыми разнообразными.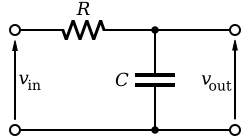 В этой лекции мы рассмотрим простейшие фильтры. Заметим, что, согласно предложенному определению, операция, заключающаяся в последовательном применении двух или более фильтраций, тоже является фильтрацией. Таким образом, можно говорить о составных фильтрах, соответствующих комбинациям простых. Изучив
основные типы фильтров в данной лекции, мы будем иметь дело с применением фильтров, составленных из них, для решения разнообразных задач в последующих лекциях. Фильтрация изображений является одной из самых фундаментальных операций компьютерного зрения, распознавания образов и обработки изображений. Фактически, с той или иной фильтрации исходных изображений начинается работа подавляющего большинства методов. Рассматриваемые в этой лекции фильтры имеют, таким образом, чрезвычайную важность с точки зрения их применения в различных приложениях.
В этой лекции мы рассмотрим простейшие фильтры. Заметим, что, согласно предложенному определению, операция, заключающаяся в последовательном применении двух или более фильтраций, тоже является фильтрацией. Таким образом, можно говорить о составных фильтрах, соответствующих комбинациям простых. Изучив
основные типы фильтров в данной лекции, мы будем иметь дело с применением фильтров, составленных из них, для решения разнообразных задач в последующих лекциях. Фильтрация изображений является одной из самых фундаментальных операций компьютерного зрения, распознавания образов и обработки изображений. Фактически, с той или иной фильтрации исходных изображений начинается работа подавляющего большинства методов. Рассматриваемые в этой лекции фильтры имеют, таким образом, чрезвычайную важность с точки зрения их применения в различных приложениях.
8.2. Линейные фильтры
Определение
Линейные фильтры представляют собой семейство фильтров, имеющих очень простое математическое описание.
| ( 8.1) |
Результатом служит изображение B. В определении (8.1) мы опустили пределы суммирования. Обычно ядро фильтра отлично от нуля только в некоторой окрестности N точки (0, 0). За пределами этой окрестности F(i, j) или в точности равно нулю, или очень близко к нему, так что можно им пренебречь. Суммирование в (8.1)
производится по , и значение каждого пикселя B(x, y) определяется пикселями изображения A, которые лежат в окне N, центрированном в точке (x, y) (мы будем обозначать это множество N(x, y) ). Ядро фильтра, заданное на прямоугольной окрестности N, может рассматриваться как матрица m на n, где длины сторон являются нечетными числами. При задании ядра матрицей M
Суммирование в (8.1)
производится по , и значение каждого пикселя B(x, y) определяется пикселями изображения A, которые лежат в окне N, центрированном в точке (x, y) (мы будем обозначать это множество N(x, y) ). Ядро фильтра, заданное на прямоугольной окрестности N, может рассматриваться как матрица m на n, где длины сторон являются нечетными числами. При задании ядра матрицей M
| ( 8.2) |
Также нуждается в дополнительном прояснении ситуация, когда пиксель (x, y) находится в окрестности краев изображения. В этом случае A(x + i, y + j) в определении (8.1) может соответствовать пикселю A, лежащему за пределами изображения A. Данную проблему можно разрешить несколькими способами.
- Не проводить фильтрацию для таких пикселей, обрезав изображение B по краям или закрасив их, к примеру, черным цветом.
- Не включать соответствующий пиксель в суммирование, распределив его вес F(i, j) равномерно среди других пикселей окрестности N(x, y).
- Доопределить значения пикселей за границами изображения при помощи экстраполяции. Например, считать постоянным значение интенсивности вблизи границы (для пикселя (-2, 5) имеем A(-2, 5) = A(0, 5) ) или считать постоянным градиент интенсивности вблизи границы ( A(-2, 5) = A(0, 5) + 2(A(0, 5) — A(1, 5)) ).
- Доопределить значения пикселей за границами изображения, при помощи зеркального отражения ( A(-2, 5) = A(2, 5) ).
Выбор конкретного способа нужно производить с учетом конкретного фильтра и особенностей конкретного приложения.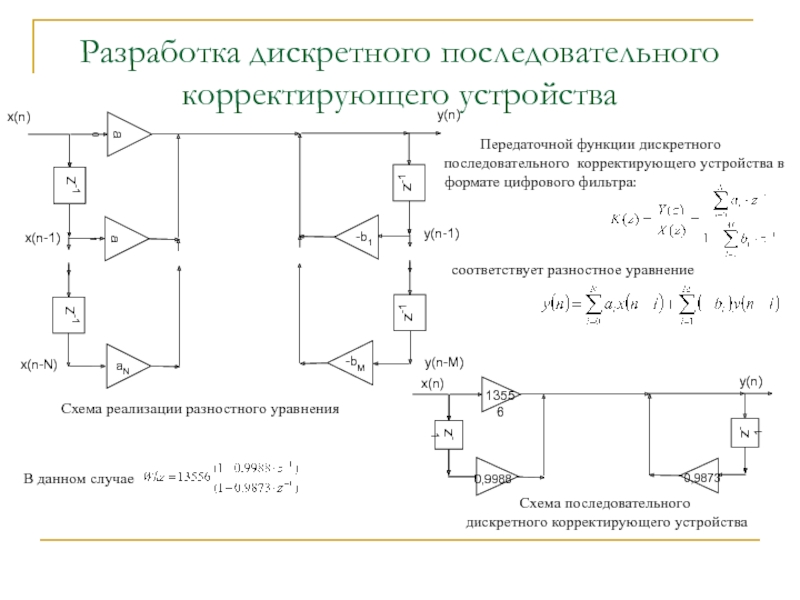
Разобрав общее определение линейных фильтров, перейдем к примерам.
Понимание и проектирование дифференциальных фильтров для систем связи
Скачать PDF
В системах связи всегда можно использовать дифференциальные цепи. обеспечивают лучшую производительность по сравнению с односторонними цепями. Они могут предоставить более высокая линейность, устойчивость к сигналам синфазных помех и более. Однако вокруг дифференциальных цепей часто скрывается много загадок. Некоторые инженеры ВЧ считают, что их сложно проектировать, тестировать и отлаживать. Этот кажется, особенно верно для дифференциального фильтра. Пришло время поднять завесу от конструкции дифференциального фильтра.
Для этого мы начнем с цепочки приема системы связи IF
ступенчатый фильтр. Мы рассмотрим некоторые основные понятия спецификаций ключей фильтров,
несколько типов часто используемых характеристик фильтра, фильтр Чебышева типа 1
применение, и как начать с проектирования несимметричного фильтра, а затем передать
что к конструкции дифференциального фильтра. Мы также рассмотрим дифференциальный фильтр
пример конструкции, а также несколько пунктов о том, как оптимизировать дифференциал
Схема печатной платы.
Мы также рассмотрим дифференциальный фильтр
пример конструкции, а также несколько пунктов о том, как оптимизировать дифференциал
Схема печатной платы.
в цепях радиочастотных сигналов
Пользователь может получить более высокую амплитуду сигнала с дифференциальной схемой, чем с односторонней схемой. При одинаковом напряжении питания дифференциальный сигнал может обеспечить удвоенную амплитуду по сравнению с односторонний сигнал. Он также обеспечивает лучшую линейность и характеристики SNR
&amp ;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;lt;img src=’https://www. .analog.com/-/media/analog/en/landing-pages/technical-articles/understanding-and-designing-Differential-Filters-for-Communications-Systems/figure1.png?w=435 ‘ alt=’Рисунок 1 ‘& amp; amp; amp; amp; amp; amp; amp; amp; amp; amp; amp; amp; amp; amp; amp; amp; amp; amp; amp; amp; amp; ;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;gt;
Рисунок 1. Дифференциальная выходная амплитуда
Дифференциальная выходная амплитуда
Дифференциальные цепи практически невосприимчивы к внешним электромагнитным помехам и перекрестным помехам от близлежащие сигналы. Это связано с тем, что принимаемое напряжение удваивается и, теоретически шум влияет на сильно связанные трассы в равной степени, отменяя друг друга.
Дифференциальные сигналы также вызывают меньше электромагнитных помех. Это потому, что изменения уровней сигнала (dV/dt или dI/dt) создают противоположные магнитные поля, снова нейтрализуя друг друга.
Дифференциальные сигналы могут подавлять гармоники четного порядка. Это показано в следующий пример с непрерывной волной (CW), проходящей через один этап усиления. При использовании одного несимметричного усилителя выход может быть выражается, как показано на рис. 2, уравнение 1 и уравнение 2.
&amp ;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;lt;img src=’https://www.
 analog. .com/-/media/analog/en/landing-pages/technical-articles/understanding-and-designing-Differential-Filters-for-Communications-Systems/figure2.png?w=435 ‘ alt=’Рисунок 2’& ;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp ;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;gt;
analog. .com/-/media/analog/en/landing-pages/technical-articles/understanding-and-designing-Differential-Filters-for-Communications-Systems/figure2.png?w=435 ‘ alt=’Рисунок 2’& ;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp ;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;gt;Рисунок 2. Несимметричный усилитель
При использовании одного дифференциального усилителя вход и выход отображаются на Рисунок 3 и уравнения 3, уравнения 4, уравнения 5 и уравнения 6.
&amp ;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;lt;img src=’https://www.analog.com/- /media/analog/en/landing-pages/technical-articles/understanding-and-designing-Differential-Filters-for-Communications-Systems/figure3.png?w=435 ‘ alt=’Рисунок 3’&amp ;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp ;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;gt;
Рис. 3. Дифференциальный усилитель
3. Дифференциальный усилитель
В идеале на выходе не должно быть гармоник четного порядка, что делает дифференциальная схема лучший выбор для системы связи.
Фильтры
Спецификация фильтра
Частота среза, частота излома или частота излома является границей в частотная характеристика системы, при которой энергия течет через систему начинает уменьшаться (ослабляться или отражаться), а не проходить.
&amp ;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;lt;img src=’https://www.analog.com/-/media/analog/en/landing-pages. /технические-статьи/понимание-и-проектирование-дифференциальных-фильтров-для-коммуникационных-систем/figure4.png?w=435 ‘ alt=’Рисунок 4’& ;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp ;amp;gt;
Рисунок 4. Точка частоты среза 3 дБ
Точка частоты среза 3 дБ
Внутриполосная пульсация — это колебания вносимых потерь в пределах полосы пропускания
&amp ;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;lt;img src=’https://www.analog.com/-/media/analog/en/landing-pages. /технические-статьи/понимание-и-проектирование-дифференциальных-фильтров-для-коммуникационных-систем/figure5.png?w=435 ‘ alt=’Рисунок 5’& ;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp ;amp;gt;
Рис. 5. Внутриполосная пульсация.
Фазовая линейность – это прямо пропорциональная зависимость фазового сдвига от частоты в течение интересующий диапазон частот.
&amp ;amp;amp;amp;amp;amp;amp;amp;amp;amp;lt;img src=’https://www.
 analog.com/-/media/analog/en/landing-pages/technical-articles/understanding -и разработать дифференциальные фильтерные фильтерные из-за коммуникаций-systems/figure 6.png? W = 435 ‘alt =’ Рисунок 6 ‘& amp; amp; amp; amp; amp; amp; amp; amp; amp; amp; amp; amp; amp; amp; amp; amp; ;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;gt;
analog.com/-/media/analog/en/landing-pages/technical-articles/understanding -и разработать дифференциальные фильтерные фильтерные из-за коммуникаций-systems/figure 6.png? W = 435 ‘alt =’ Рисунок 6 ‘& amp; amp; amp; amp; amp; amp; amp; amp; amp; amp; amp; amp; amp; amp; amp; amp; ;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;gt;Рисунок 6. Фазовая линейность
Групповая задержка – это мера временной задержки огибающих амплитуды различные синусоидальные компоненты сигнала через тестируемое устройство, и является функцией частоты для каждого компонента.
&amp ;amp;amp;amp;amp;amp;amp;amp;amp;amp;lt;img src=’https://www.analog.com/-/media/analog/en/landing-pages/technical-articles/understanding -и дифференциально-фильтерные фильтерные фильтерные фильтерные системы/рисунок/рисунок 7.
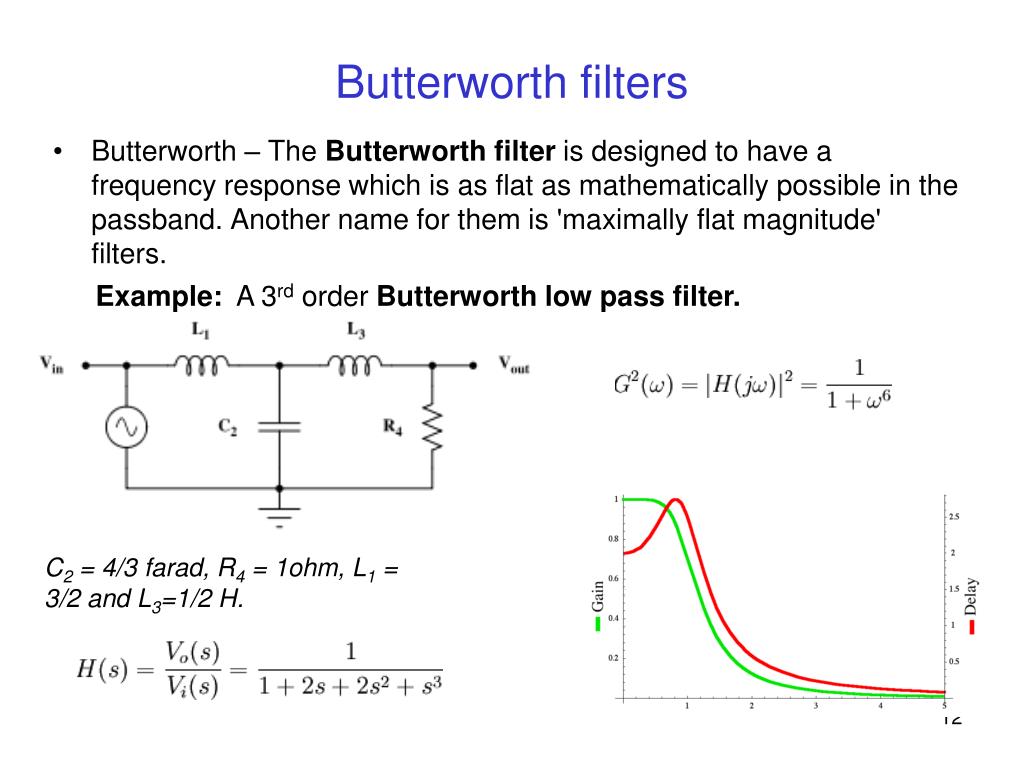 png? w = 435 ‘alt =’ Рисунок 7 ‘& amp; amp; amp; amp; amp; amp; amp; amp; amp; ;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;gt;
png? w = 435 ‘alt =’ Рисунок 7 ‘& amp; amp; amp; amp; amp; amp; amp; amp; amp; ;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;gt;Рисунок 7. Групповая задержка
Сравнение фильтров
| Ответ S21 | Плюсы | Минусы |
| Баттерворт | ||
| См. рис. 8 | Очень хорошая плоскостность в полосе прохода | Медленно скатывается в стопорной полосе |
| Эллиптический | ||
| См. рис. 9 | Очень быстро скатывается в зоне остановки | Выравнивает пульсации как в полосе пропускания, так и в полосе задерживания; это влияет на эффективность подавления полосы остановки |
| Бессель | ||
См. рис. 10 рис. 10 | Максимальная фиксированная групповая/фазовая задержка | Очень медленный спад в полосе останова |
| Чебышев Тип I | ||
| См. рис. 11 | Быстрое скатывание в полосе останова; отсутствие уравновешенной пульсации в полосе задерживания | Выровнял пульсации в полосе пропускания |
| Чебышев Тип II | ||
| См. рис. 12 | Отсутствие пульсаций в полосе пропускания | Спад не очень быстрый; выровнял пульсации в полосе заграждения |
&amp ;amp;amp;amp;amp;lt;img src=’https://www.analog.com/-/media/analog/en/landing-pages/technical-articles/understanding-and-designing-differential-filters -для-коммуникационных-систем/figure8.
 png?w=435 ‘ alt=’Рисунок 8’&amp ;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;gt;
png?w=435 ‘ alt=’Рисунок 8’&amp ;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;gt;Рисунок 8. Отклик фильтра Баттерворта S21.
&amp ;amp;amp;amp;amp;lt;img src=’https://www.analog.com/-/media/analog/en/landing-pages/technical-articles/understanding-and-designing-differential-filters -for-communications-systems/figure9.png?w=435 ‘ alt=’Рисунок 9’&amp ;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;gt;
Рисунок 9. Эллиптический фильтр S21 ответ
&amp ;amp;amp;amp;amp;lt;img src=’https://www.analog.com/-/media/analog/en/landing-pages/technical-articles/understanding-and-designing-differential-filters -для-коммуникационных-систем/figure10.
 png?w=435 ‘ alt=’Рисунок 10’&amp ;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;gt;
png?w=435 ‘ alt=’Рисунок 10’&amp ;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;gt;Рисунок 10. Отклик фильтра Беселя S21.
&amp ;amp;amp;amp;amp;lt;img src=’https://www.analog.com/-/media/analog/en/landing-pages/technical-articles/understanding-and-designing-differential-filters -для-коммуникационных-систем/figure11.png?w=435 ‘ alt=’Рисунок 11’&amp ;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;gt;
Рис. 11. Отклик фильтра Чебышева I типа S21.
&amp ;amp;amp;amp;amp;lt;img src=’https://www.analog.com/-/media/analog/en/landing-pages/technical-articles/understanding-and-designing-differential-filters -для-коммуникационных-систем/figure12.
 png?w=435 ‘ alt=’Рисунок 12’&amp ;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;gt;
png?w=435 ‘ alt=’Рисунок 12’&amp ;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;gt;Рисунок 12. Отклик S21 фильтра Чебышева II типа
Фильтр ПЧ в цепочке приема связи в основном является фильтром нижних частот. фильтр или полосовой фильтр. Он используется для отклонения сигналов наложения вдоль со шпорами, генерируемыми активными компонентами. Шпоры включают гармоники и продукты IMD, среди прочего. С помощью фильтра цепочка приема может обеспечивают сигналы с высоким отношением сигнал-шум для анализа АЦП.
В качестве топологии был выбран фильтр Чебышева типа I, поскольку он хорошая внутриполосная неравномерность, быстрый спад и отсутствие равноволнового отклика в полоса стоп.
Разработка фильтра нижних частот
Поскольку фильтр ПЧ приемника используется для подавления паразитных сигналов и наложенных сигналов,
спад полосы остановки должен быть максимально быстрым. Однако более быстрый откат
означает компоненты более высокого порядка, и есть несколько причин, по которым
фильтрация не рекомендуется:
Однако более быстрый откат
означает компоненты более высокого порядка, и есть несколько причин, по которым
фильтрация не рекомендуется:
- Сложность настройки на этапе проектирования и отладки.
- Сложность массового производства: конденсаторы и катушки индуктивности различаются между собой, и фильтры на каждой печатной плате не могут иметь одинаковую характеристику.
- Большой размер печатной платы
Как правило, используйте фильтр седьмого порядка или ниже. В то же время, если больше внутриполосная неравномерность не является проблемой для компонентов того же порядка, тогда более быстрый спад в стоп-полосе является выплатой.
Затем определите требуемый отклик, указав требуемое затухание. в выбранной частотной точке.
Чтобы определить максимальное количество пульсаций в полосе пропускания, держите
спецификации до максимального предела системных требований. Это может
помочь получить более быстрый спад в стоп-полосе.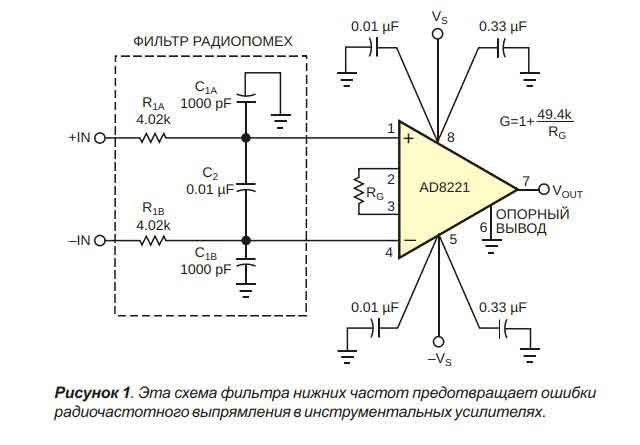
Используйте программное обеспечение фильтра, такое как MathCad, ® MATLAB, ® или ADS для проектирования однотактный фильтр нижних частот.
В качестве альтернативы спроектируйте фильтр вручную. Полезным руководством является RF Circuit Design. Крис Боуик.
Чтобы определить порядки фильтра, нормализуйте интересующую частоту на разделив его на частоту среза фильтра.
Например, если внутриполосная неравномерность должна быть 0,1 дБ, отсечка 3 дБ
частота 100 МГц. На частоте 250 МГц подавление должно составлять 28 дБ, поэтому
отношение частот 2,5. Этому требованию может удовлетворить фильтр нижних частот третьего порядка.
Если импеданс источника фильтра равен 200 Ом, импеданс нагрузки
фильтр также 200 Ом, RS/RL равен 1 — используйте конденсатор в качестве первого компонента.
Затем пользователь получает нормализованное значение C1 = 1,433, L2 = 1,59.4, С3 = 1,433.
Если fc составляет 100 МГц, используйте уравнение 7 и уравнение 8, чтобы получить окончательные результаты.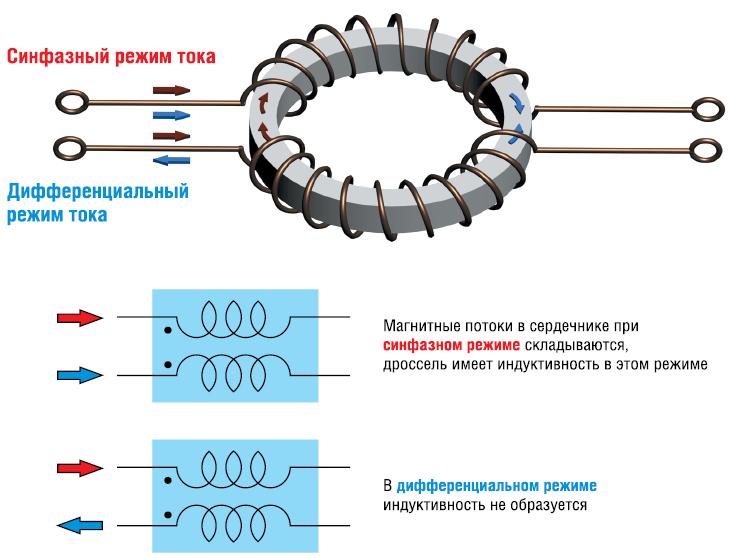
Где:
C SCALED — окончательное значение конденсатора.
L В МАСШТАБЕ — окончательное значение индуктора.
C n — значение элемента прототипа нижних частот.
L n — значение элемента прототипа нижних частот.
R L — конечное значение нагрузочного резистора.
ф c — конечная частота среза.
C1 В МАСШТАБЕ = 1,433/(2π × 100 × 106 × 200) = 11,4 пФ
L2 В МАСШТАБЕ = (1,594 × 200)/ (2π × 100 × 106) = 507,4 нГн
C3 В МАСШТАБЕ = 11,4 пФ
Схема показана на рисунке 13.
<img src=’https:/ /www.analog.com/-/media/analog/en/landing-pages/technical-articles/understanding-and-designing-differential-filters-for-communication-systems/figure13.
 png?w=435 ‘ alt=’ Рисунок 13
png?w=435 ‘ alt=’ Рисунок 13Рисунок 13. Пример несимметричного фильтра
Преобразуйте несимметричный фильтр в дифференциальный фильтр (см. рис. 14).
<img src=’https://www .analog.com/-/media/analog/en/landing-pages/technical-articles/understanding-and-designing-Differential-Filters-for-Communications-Systems/figure14.png?w=435 ‘ alt=’ ‘>
Рисунок 14. Преобразование несимметричного фильтра в дифференциальный фильтр
Используя реальное значение для каждого компонента, фильтр обновляется как показано на рисунке 15.
<img src=’https://www.analog .com/-/media/analog/en/landing-pages/technical-articles/understanding-and-designing-Differential-Filters-for-Communications-Systems/figure15.
 png?w=435 ‘ alt=’Рисунок 15’& ;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;gt;
png?w=435 ‘ alt=’Рисунок 15’& ;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;gt;Рисунок 15. Конечный дифференциальный фильтр
Обратите внимание, что если выходное сопротивление микшера или усилителя ПЧ и входное сопротивление АЦП емкостное, лучше рассмотреть возможность использования конденсатор в качестве первого компонента и конденсатор в качестве последнего компонента. Кроме того, важно настроить первый конденсатор и конденсатор последней ступени. значение с большей скоростью (не менее 0,5 пФ), чем емкость выходного импеданс смесителя или усилителя ПЧ и входной импеданс АЦП. В противном случае очень сложно настроить отклик фильтра.
Разработка полосового фильтра
В системах связи, когда частота ПЧ достаточно высока, некоторые низкие
частотные выбросы должны быть отфильтрованы, например, половинные выбросы ПЧ. Сделать это,
сконструировать полосовой фильтр. Для полосового фильтра не обязательно
симметричный для подавления низких и высоких частот. Простой способ
чтобы спроектировать полосовой сглаживающий фильтр, нужно сначала спроектировать фильтр нижних частот,
затем добавьте одну шунтирующую катушку индуктивности параллельно с шунтирующим конденсатором на
конечная ступень фильтра для ограничения низкочастотных составляющих (шунтирующая катушка индуктивности
является высокочастотным резонансным полюсом). Если одноступенчатый высокочастотный индуктор не
Достаточно добавить еще один шунтирующий индуктор параллельно шунту первой ступени.
конденсатор, чтобы получить больше подавления для низкочастотных шпор. После добавления
шунтируйте катушку индуктивности, снова настройте все компоненты, чтобы добиться правильного внеполосного сигнала.
спецификации отклонения, а затем окончательно определите значение компонентов фильтра.
Простой способ
чтобы спроектировать полосовой сглаживающий фильтр, нужно сначала спроектировать фильтр нижних частот,
затем добавьте одну шунтирующую катушку индуктивности параллельно с шунтирующим конденсатором на
конечная ступень фильтра для ограничения низкочастотных составляющих (шунтирующая катушка индуктивности
является высокочастотным резонансным полюсом). Если одноступенчатый высокочастотный индуктор не
Достаточно добавить еще один шунтирующий индуктор параллельно шунту первой ступени.
конденсатор, чтобы получить больше подавления для низкочастотных шпор. После добавления
шунтируйте катушку индуктивности, снова настройте все компоненты, чтобы добиться правильного внеполосного сигнала.
спецификации отклонения, а затем окончательно определите значение компонентов фильтра.
Обратите внимание, что, как правило, для полосового фильтра последовательные конденсаторы не
рекомендуется, поскольку они увеличивают сложность настройки и отладки.
Значение емкости обычно довольно мало и сильно зависит от
паразитная емкость.
Пример применения
Вот пример конструкции фильтра между ADL5201 и AD6641. ADL5201 — это высокопроизводительный усилитель ПЧ с цифровым управлением усилением. (DGA), который предназначен для реального приложения приемника ПЧ базовой станции или путь наблюдения с цифровым предварительным искажением (DPD). Имеет регулировку усиления 30 дБ. диапазон, очень высокая линейность, OIP3 которой достигает 50 дБм, и коэффициент усиления по напряжению около 20 дБ. AD6641 представляет собой наблюдательный DPD с полосой пропускания 250 МГц. приемник, который объединяет 12-разрядный АЦП 500 MSPS, 16 000 × 12 FIFO и многорежимный сервер, который позволяет пользователям извлекать данные через Серийный порт. Этот пример фильтра представляет собой приложение DPD.
Ниже приведены некоторые характеристики полосового фильтра, взятые из реальный дизайн системы связи:
- Центральная частота: 368,4 МГц
- Полоса пропускания: 240 МГц
- Входное и выходное сопротивление: 150 Ом
- Внутриполосная пульсация: 0,2 дБ
- Вносимые потери: 1 дБ
- Подавление внеполосных сигналов: 30 дБ на частоте 614,4 МГц
Для создания примера проекта:
1. Начните с несимметричного фильтра нижних частот (см. рис. 16).
Начните с несимметричного фильтра нижних частот (см. рис. 16).
<img src=’https://www.analog.com/-/media /аналог/ru/целевые страницы/технические статьи/понимание и проектирование дифференциальных фильтров для систем связи/figure16.png?w=435 ‘ alt=’Рисунок 16’&amp ;amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;gt;
Рисунок 16. Несимметричный фильтр нижних частот
2. Замените несимметричный фильтр дифференциальным фильтром. Держите источник и импеданс нагрузки такой же, зашунтируйте все конденсаторы и отключите все последовательные катушки индуктивности пополам и поместите их в другой дифференциальный тракт (см. рис. 17).
<img src=’https://www.analog.com/-/media/analog /en/landing-pages/technical-articles/understanding-and-designing-Differential-Filters-for-Communications-Systems/figure17.
 png?w=435 ‘ alt=’Рисунок 17’&amp ;amp;amp;amp;amp;amp;amp;amp;amp;gt;
png?w=435 ‘ alt=’Рисунок 17’&amp ;amp;amp;amp;amp;amp;amp;amp;amp;gt;Рис. 17. Дифференциальный фильтр нижних частот с идеальными компонентами.
3. Оптимизируйте идеальную ценность компонентов с реальной ценностью (см. рис. 18).
<img src=’https://www.analog.com/-/media/analog/en /landing-pages/technical-articles/understanding-and-designing-Differential-filters-for-Communications-Systems/figure18.png?w=435 ‘ alt=’Рисунок 18’& ;amp;amp;amp;amp;amp;amp;gt;
Рисунок 18. Дифференциальный фильтр нижних частот с реальным значением
4. Для моделирования на уровне подсистемы добавьте параметр ADL5201 DGA S.
файл на входе, используйте источник напряжения управления напряжением для моделирования
АЦП AD6641 на выходе фильтра. Чтобы заменить фильтр нижних частот
в полосовой фильтр добавить две шунтирующие катушки индуктивности: L7 параллельно
С9и L8 параллельно с C11. C12 представляет собой вход AD6641.
емкость. R3 и R4 — два нагрузочных резистора, включенных на входе
AD6641 будет нагрузкой фильтра. Вход AD6641 имеет высокое сопротивление.
После настройки см. рис. 19.
C12 представляет собой вход AD6641.
емкость. R3 и R4 — два нагрузочных резистора, включенных на входе
AD6641 будет нагрузкой фильтра. Вход AD6641 имеет высокое сопротивление.
После настройки см. рис. 19.
<img src=’https://www.analog.com/-/media/analog/en/landing -страницы/технические-статьи/понимание-и-проектирование-дифференциальных-фильтров-для-коммуникационных-систем/рисунок19.png?w=435 ‘ alt=’Рисунок 19’>
Рисунок 19. Дифференциальный полосовой фильтр.
5. Результаты моделирования с идеальными компонентами показаны на рисунке 20.
<img src=’https://www.analog.com/-/media/analog/en/landing-pages/technical -статьи/понимание-и-проектирование-дифференциальных-фильтров-для-коммуникационных-систем/figure20.png?w=435 ‘ alt=’Рисунок 20’&gt ;
Рис. 20. Отклик передачи фильтра с идеальными катушками индуктивности.
20. Отклик передачи фильтра с идеальными катушками индуктивности.
6. Замените все идеальные индукторы файлами параметров индуктора S из предполагаемое устройство (например, Murata LQW18A). Вносимые потери немного выше, чем при использовании идеальных катушек индуктивности. Результат моделирования слегка изменится, как показано на рис. 21.
<img src=’https://www.analog.com/-/media/analog/en/landing-pages/technical-articles /понимание-и-проектирование-дифференциальных-фильтров-для-коммуникационных-систем/figure21.png?w=435 ‘ alt=’Рисунок 21’>
Рис. 21. Отклик передачи фильтра с катушками индуктивности Murata LQW18A.
Рассмотрение компоновки дифференциального фильтра
Дифференциальные трассы в паре должны быть одинаковой длины. Это правило возникло
из-за того, что дифференциальный приемник определяет, где отрицательный
и положительные сигналы пересекаются друг с другом в одно и то же время — пересечение
точка. Таким образом, сигналы поступают на приемник в одно и то же время.
правильная эксплуатация.
Таким образом, сигналы поступают на приемник в одно и то же время.
правильная эксплуатация.
Трассы в дифференциальной паре должны быть проложены близко друг к другу. Связь между соседними линиями внутри пары мала, если расстояние между ними более чем в 2 раза превышает толщину диэлектрика. Также это правило на том факте, что, поскольку дифференциальные сигналы равны и наоборот, и если внешние шумы одинаково интерферируют с этими сигналами, то шум обнуляется. Точно так же любой нежелательный шум, вызванный дифференциальными сигналами в соседние проводники отменяется, если дорожки проложены рядом.
Расстояние между трассами в дифференциальной паре должно быть постоянным Вся длина. Если дифференциальные трассы проложены близко друг к другу, они влияют на общий импеданс. Если это разделение не соблюдается от драйвера к приемнику, на пути есть несоответствия импеданса, приводит к отражениям.
Используйте большое расстояние между парами, чтобы свести к минимуму перекрестные помехи между парами.
При использовании медного наполнителя на том же слое увеличьте зазор от дифференциальные следы до медной заливки. Минимальный зазор в 3 раза больше трассы рекомендуется ширина от дорожки до медной заливки.
Уменьшить внутрипарный перекос в дифференциальной паре путем введения небольших извилистых поправки близко к источнику перекоса (см. рис. 22).
<img src=’https://www.analog.com/-/media/analog/en/landing-pages/technical-articles/understanding -и-разработка-дифференциальных-фильтров-для-коммуникационных-систем/figure22.png?w=435 ‘ alt=’Рисунок 22’>
Рисунок 22. Использование коррекции меандра
Избегайте узких (90°) изгибов при прокладке дифференциальных пар (см. Рисунок 23).
<img src=’https://www.analog.com/-/media/analog/en/landing-pages/technical-articles/understanding-and -designing-differential-filters-for-communications-systems/figure23.
 png?w=435 ‘ alt=’Рисунок 23’>
png?w=435 ‘ alt=’Рисунок 23’>Рисунок 23. Избегайте изгибов под углом 90°
Используйте симметричную маршрутизацию при маршрутизации дифференциальных пар (см. рис. 24). Если требуются контрольные точки, избегайте введения заглушек трассировки и размещайте тестовые точки симметрично (см. рис. 25).
<img src=’https://www.analog.com/-/media/analog/en/landing-pages/technical-articles/understanding-and-designing -дифференциальные-фильтры-для-коммуникационных-систем/figure24.png?w=435 ‘ alt=’Рисунок 24’>
Рисунок 24. Рекомендации по симметричной маршрутизации
<img src=’https://www.analog.com/-/media/analog/en/landing-pages/technical-articles/understanding-and-designing -дифференциальные-фильтры-для-коммуникационных-систем/figure25.png?w=435 ‘ alt=’Рисунок 25’>
Рисунок 25. Как избежать заглушек трассировки
С точки зрения ослабления рабочих нагрузок настройки значения компонента фильтра на
печатная плата (PCB), важно сохранить паразитную емкость
и индуктивность как можно меньше. Паразитная индуктивность не может
быть значительным по сравнению с расчетным значением катушки индуктивности в фильтре
дизайн. Паразитная емкость более критична для дифференциального фильтра ПЧ.
Емкость конденсаторов в фильтрах ПЧ составляет всего несколько пикофарад. Если паразит.
емкость достигает десятых долей пикофарад, это влияет на фильтр
ответ значительно. Для предотвращения паразитной емкости рекомендуется
чтобы избежать каких-либо слоев земли или питания в области дифференциальной маршрутизации
и под дросселями блока питания.
Паразитная индуктивность не может
быть значительным по сравнению с расчетным значением катушки индуктивности в фильтре
дизайн. Паразитная емкость более критична для дифференциального фильтра ПЧ.
Емкость конденсаторов в фильтрах ПЧ составляет всего несколько пикофарад. Если паразит.
емкость достигает десятых долей пикофарад, это влияет на фильтр
ответ значительно. Для предотвращения паразитной емкости рекомендуется
чтобы избежать каких-либо слоев земли или питания в области дифференциальной маршрутизации
и под дросселями блока питания.
Одним из примеров компоновки печатной платы дифференциального фильтра является ссылка на приемник ADI. макетная плата (см. рис. 26). Это показывает фильтр пятого порядка между ADL5201 и AD6649. AD6649 — это 14-разрядный конвейерный АЦП с частотой 250 МГц. с очень хорошими характеристиками SNR.
<img src=’https://www.analog.com/-/media/analog/en/landing-pages/technical-articles/understanding-and-designing-дифференциал -filters-for-communication-systems/figure26.
 png?w=435 ‘ alt=’Рисунок 26’>
png?w=435 ‘ alt=’Рисунок 26’>Рисунок 26. Пример компоновки печатной платы дифференциальной схемы
Лучшее понимание конструкции дифференциального фильтра
Дифференциальные схемы дают разработчикам значительные преимущества. Возможно, самой большой проблемой при их использовании является простое преодоление мысль о том, что их сложно спроектировать, протестировать и исправить. Как только вы возьмете хороший посмотрите, как работать с дифференциальными фильтрами, вы можете столкнуться с ценный новый инструмент для проектирования RF.
Дифференциальные фильтры: фильтр верхних частот, фильтр нижних частот, полосовой
спросил
Изменено 3 года, 7 месяцев назад
Просмотрено 3к раз
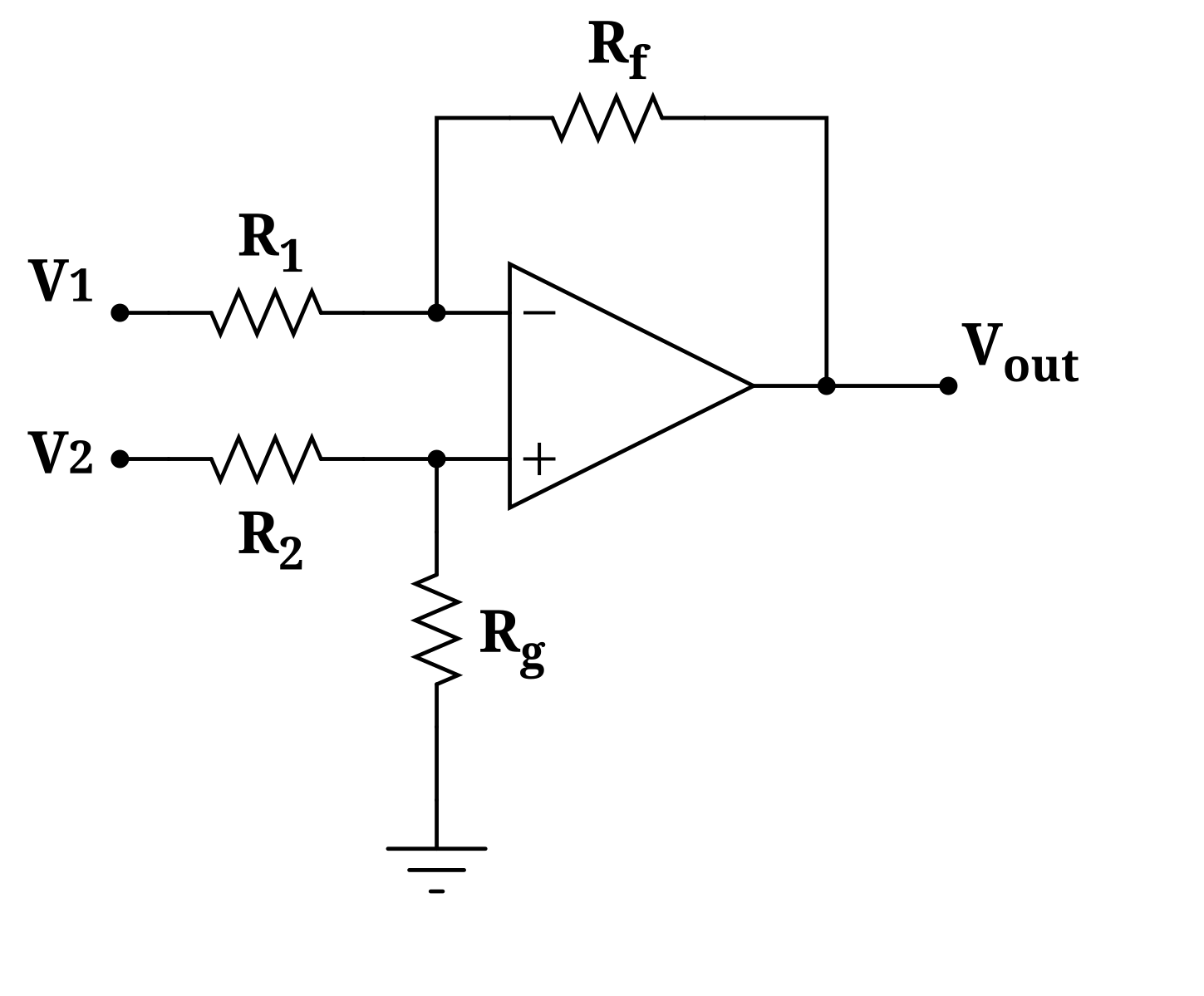
\$\начало группы\$ Я хочу использовать полосовой фильтр в конструкции схемы ЭМГ, используя дифференциальные сигналы, которые вы получаете от операционного усилителя (дифференциальный/инструментальный).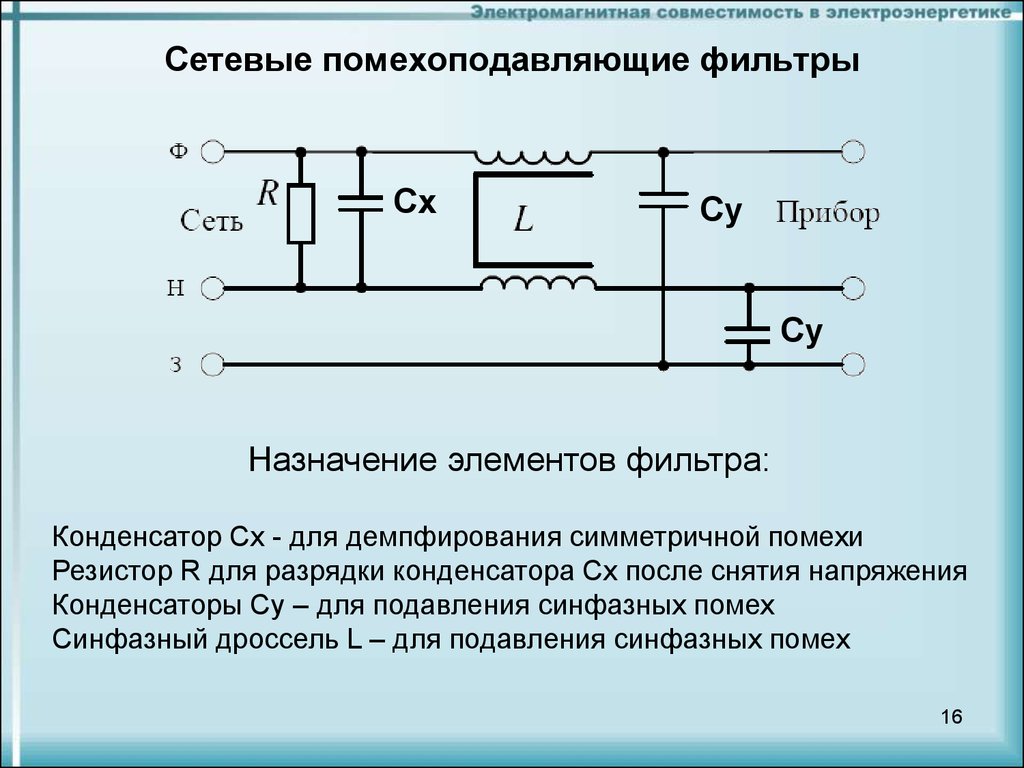 Я искал, как правильно выполнять фильтрацию, и пока не нашел объяснения фильтра верхних частот или полосы пропускания, как в статье ниже. Я понимаю, что есть некоторые нюансы в дифференциальных и однополюсных фильтрах, о которых говорится в статье TI здесь, например, когда «дифференциальный конденсатор» в 10 раз превышает значение «синфазных конденсаторов».
Я искал, как правильно выполнять фильтрацию, и пока не нашел объяснения фильтра верхних частот или полосы пропускания, как в статье ниже. Я понимаю, что есть некоторые нюансы в дифференциальных и однополюсных фильтрах, о которых говорится в статье TI здесь, например, когда «дифференциальный конденсатор» в 10 раз превышает значение «синфазных конденсаторов».
Статья TI с рекомендациями по проектированию фильтров
Пожалуйста, обратите особое внимание на рисунок 4 :
Это очень полезно и показывает, что я буду использовать для фильтра нижних частот на двух линиях, уравнение 3 вычисляет частоту среза. Я не видел эквивалентной статьи для фильтра верхних частот, поэтому я решил спросить здесь, так ли это просто, как я думаю, или есть другие вещи, о которых нужно подумать.
Мой главный вопрос
- , будет ли фильтр верхних частот аналогичен схеме на рис. 4, за исключением того, что резисторы и конденсаторы переключаются, поскольку они предназначены для однополюсного режима; и
- , будь то полоса пропускания, в этом случае вы просто последовательно используете HPF и LPF.

Я попытаюсь сделать схему позже сегодня, когда у меня будет время, если это неясно, и я смогу найти хороший инструмент для использования.
- дифференциальный
- низкочастотный
- полосовой
- фильтр верхних частот
- фильтр
Am, предполагая, что инструментальный усилитель с дифференциальным выходом обеспечивает низкий выходной импеданс на как инвертирующем, так и неинвертирующем выходах … что-то, что нужно проверить в его листе данных. Низкий выходной импеданс упрощает конструкцию фильтра.
В любом случае рассмотрите возможность добавления входного фильтра нижних частот к инструментальному усилителю, хотя бы для того, чтобы убрать радиочастотные компоненты.
Возможно, вы сможете объединить фильтры нижних и верхних частот вместе, как показано ниже. Два синфазных конденсатора (C3cm, C4cm) представляют собой паразитную емкость и не являются реальными компонентами. Интересующие частотные компоненты сигнала EMG , вероятно, находятся ниже мегагерцового диапазона… показанный фильтр имеет угловые частоты верхних и нижних частот, которые могут не подходить для вашего приложения (рассмотрите его только как пример схемы):
Интересующие частотные компоненты сигнала EMG , вероятно, находятся ниже мегагерцового диапазона… показанный фильтр имеет угловые частоты верхних и нижних частот, которые могут не подходить для вашего приложения (рассмотрите его только как пример схемы):
Обратите внимание, что в этом случае усиление в средней полосе @ 796 Гц это около -3дБ. С R1=R2=R3 и C1=C2=C3 вы получаете усиление около -14 дБ и узкую полосу пропускания. Если вам нужна более узкая полоса пропускания, рассмотрите возможность использования компонентов LC-фильтра (не рекомендуется).
Усиление средней полосы максимально, когда частота среза нижних частот >> частота среза верхних частот. Высокое усиление в средней полосе и узкая полоса пропускания являются взаимоисключающими с этой компоновкой RC. Полосовые фильтры LC могут быть спроектированы с узкой полосой пропускания и с высоким коэффициентом усиления в средней полосе. Катушки индуктивности LC-фильтров в диапазоне частот сигналов ЭМГ достаточно велики и подвержены попаданию мешающих помех.
, например, если «дифференциальный конденсатор» в 10 раз превышает значение «синфазных конденсаторов».
Существует вероятность неправильного толкования: статья не говорит вам использовать в 10 раз большее значение для той же частоты среза , а разработать фильтр для , помогая синфазному фильтру.
Поскольку все, что подключено к дифференциальному фильтру, не должно быть нагрузкой для частотно-селективного делителя напряжения, что, по сути, является таковой, имеет смысл использовать для дифференциального фильтра значение C, намного большее, чем для синфазного фильтра.
Кстати, в этот момент становится очень сложно вообще оправдать конденсаторы СМ — если «мысленно» разделить C_diff посередине, то вы увидите точку, которая хотя бы теоретически должна быть идентична потенциалу земли, и вы увидите гораздо большие «раздельные конденсаторы», подключенные параллельно одному C_CM, что делает их практически бесполезными.
(Правда в том, что они все еще служат цели, но только потому, что дифференциальные усилители не идеальны и из-за электромагнитных помех.)
Мой главный вопрос заключается в том, будет ли фильтр верхних частот похож на схему на рис. 4, за исключением того, что резисторы и конденсаторы переключаются
Да, очень.
Для полосы пропускания, я полагаю, вы просто использовали бы HPF и LPF последовательно, если это так.
Нет. Вы бы разработали полосовой фильтр RLC. Опять же, вы не можете «просто» объединить фильтры, потому что второй фильтр не должен загружать первый фильтр, поэтому либо он должен быть сделан из гораздо «более слабых» компонентов, либо вам нужно фактически спроектировать полосу пропускания как единое целое.
Я бы порекомендовал последнее.
\$\конечная группа\$ 1 \$\начало группы\$ Это простые однополюсные ФНЧ для антиалиасинга, а для полосового и ВЧ аналогов вы вряд ли найдете.
Возможно, правильный подход заключается в том, чтобы как можно меньше касаться сигнала перед сэмплированием. Хороший мягкий однополюсный фильтр нижних частот, если у вас есть место для этого между интересующим вас сигналом и частотой Найквиста, — отличный способ.
Для высоких и полосовых частот в частотном диапазоне EMG вам, вероятно, понадобятся фильтры более высокого порядка.
Одним из подходов может быть фильтрация в соответствии с диаграммой, а затем выполнение всей дальнейшей обработки в цифровой области. Это вряд ли сработает для вас. Вы, вероятно, захотите фильтр верхних частот, чтобы вы могли усилить больше, не насыщая ваши усилители.
Стандартный подход заключается в использовании многоступенчатого усиления. Первый каскад представляет собой инструментальный усилитель, вероятно, с низкочастотным фильтром на входе и небольшим коэффициентом усиления, чтобы избежать насыщения. Затем вы пропускаете звук через высокие частоты на выходе этого усилителя, а затем усиливаете его с помощью одиночного операционного усилителя. Вывод этого фильтра должен соответствовать фильтру, который вы указали в своем вопросе. Обратите внимание, что после инструментального усилителя ваши сигналы несимметричны.
Вывод этого фильтра должен соответствовать фильтру, который вы указали в своем вопросе. Обратите внимание, что после инструментального усилителя ваши сигналы несимметричны.
Другой альтернативой может быть выборка с очень высоким разрешением без фильтрации верхних частот. Я не рекомендую это, если у вас нет большого опыта.
\$\конечная группа\$Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google Зарегистрироваться через Facebook Зарегистрируйтесь, используя адрес электронной почты и парольОпубликовать как гость
Электронная почтаТребуется, но не отображается
Опубликовать как гость
Электронная почтаТребуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания и подтверждаете, что прочитали и поняли нашу политику конфиденциальности и кодекс поведения.