Полярный момент инерции — Википедия
Материал из Википедии — свободной энциклопедии
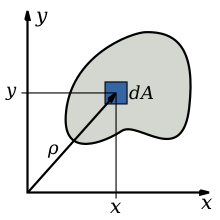 Схема к вычислению полярного момента инерции
Схема к вычислению полярного момента инерцииПоля́рный моме́нт ине́рции — интегральная сумма произведений площадей элементарных площадок dA на квадрат расстояния их от полюса — ρ2 (в полярной системе координат), взятая по всей площади сечения. То есть:
- Jp0=∫Aρ2dA{\displaystyle J_{p0}=\int _{A}\rho ^{2}\,dA}
Эта величина используется для прогнозирования способности объекта оказывать сопротивление кручению. Она имеет размерность единиц длины в четвёртой степени (м4, см4) и может быть лишь положительной.
Для площади сечения, имеющей форму круга радиусом r полярный момент инерции равен:
- Jp0=∫02π∫0rρ2ρdρdϕ=πr42{\displaystyle J_{p0}=\int _{0}^{2\pi }\int _{0}^{r}\rho ^{2}\rho \,d\rho \,d\phi ={\frac {\pi r^{4}}{2}}}
Если совместить начало декартовой прямоугольной системы координат 0 с полюсом полярной системы (см. рис.), то
- Jp0=Jx+Jy{\displaystyle J_{p0}=J_{x}+J_{y}}
потому что ρ2=x2+y2{\displaystyle \rho ^{2}=x^{2}+y^{2}}.
Полярный момент инерции используется в формулах, которые описывают зависимость между касательными напряжениями и крутящим моментом, который их вызывает. Касательное напряжение:
- τ=TrJp0{\displaystyle \tau ={\frac {Tr}{J_{p0}}}}
где
- T{\displaystyle T} — крутящий момент,
- r{\displaystyle r} — расстояние от оси кручения
- Jp0{\displaystyle {J_{p0}}} — полярный момент инерции.
Полярный момент инерции для некоторых случаев[править | править код]
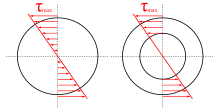 Распределение касательных напряжений при кручении
Распределение касательных напряжений при крученииДля круглого сплошного сечения:
- Jp0=πD432{\displaystyle J_{p0}={\frac {\pi D^{4}}{32}}}
где D{\displaystyle D} — диаметр круга.
Для кольцевого сечения (полый вал):
- Jp0=πD432(1−d4D4){\displaystyle J_{p0}={\frac {\pi D^{4}}{32}}\left(1-{\frac {d^{4}}{D^{4}}}\right)}
где
- D{\displaystyle D} — внешний диаметр кольца,
- d{\displaystyle d} — внутренний диаметр кольца.
- Феодосьев В.И. Сопротивление материалов. Изд. 10-е, перераб. и доп. — М.: МГТУ им. Н. Э. Баумана, 1999 год. Рецензенты академик РАН Образцов И. Ф. и д. т. н профессор Чирков И. П.
Момент инерции тела относительно оси
П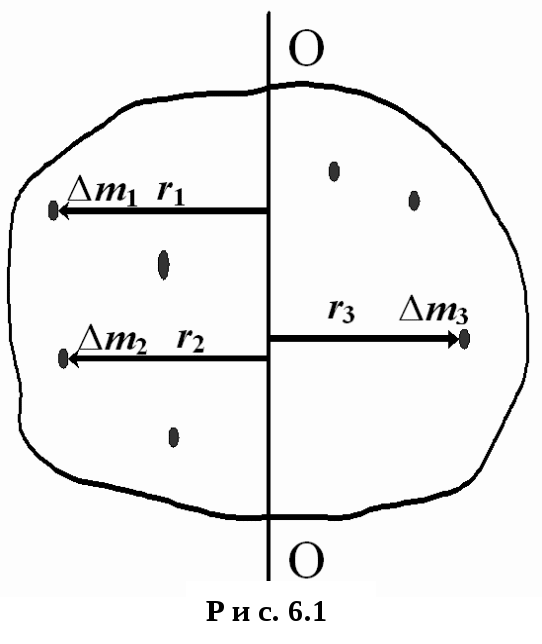 усть
имеется твердое тело. Выберем некоторую
прямую ОО (рис.6.1), которую будем называть
осью (прямая OO может быть и вне тела).
Разобьем тело на элементарные участки
(материальные точки) массами
усть
имеется твердое тело. Выберем некоторую
прямую ОО (рис.6.1), которую будем называть
осью (прямая OO может быть и вне тела).
Разобьем тело на элементарные участки
(материальные точки) массами 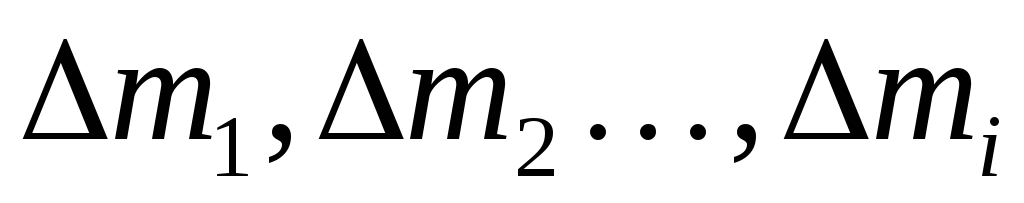 ,
находящиеся от оси на расстоянии
,
находящиеся от оси на расстоянии  соответственно.
соответственно.
Моментом инерции материальной точки относительно оси (OO) называется произведение массы материальной точки на квадрат ее расстояния до этой оси:
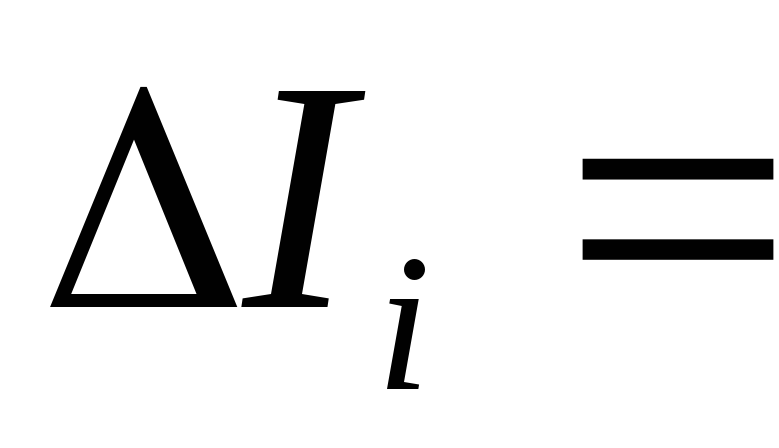
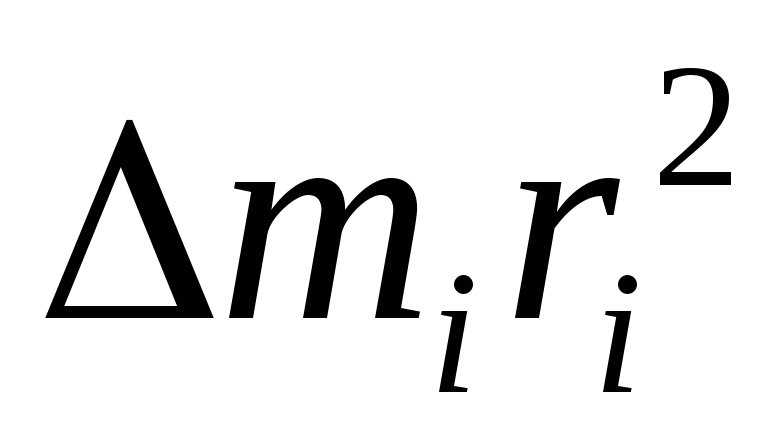 . (6.1)
. (6.1)
Моментом инерции (МИ) тела относительно оси (OO) называется сумма произведений масс элементарных участков тела на квадрат их расстояния до оси:
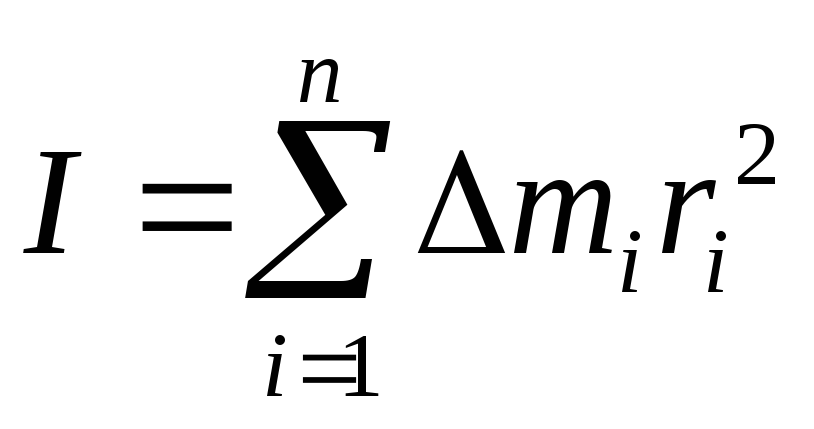 . (6.2)
. (6.2)
Как видно момент инерции тела есть величина аддитивная – момент инерции всего тела относительно некоторой оси равен сумме моментов инерции отдельных его частей относительно той же оси.
В данном случае
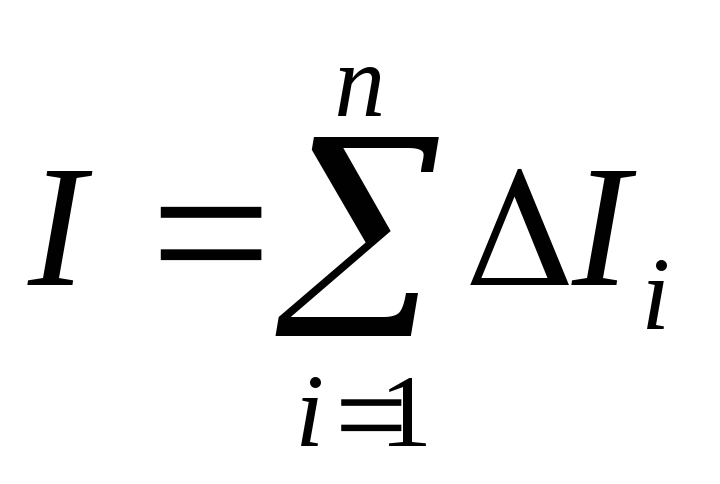 .
.
Измеряется момент инерции в кгм2. Так как
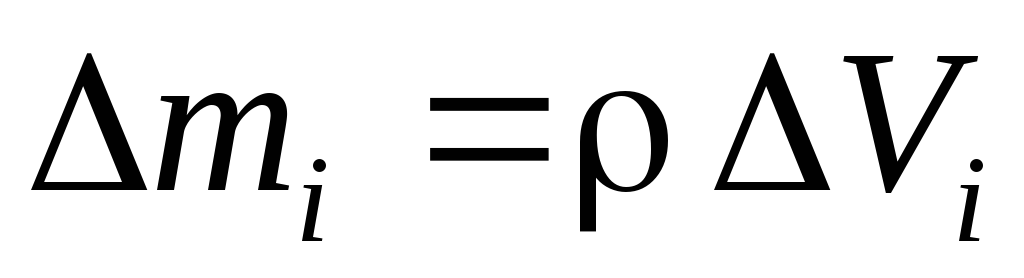 , (6.3)
, (6.3)
где
–
плотность вещества, 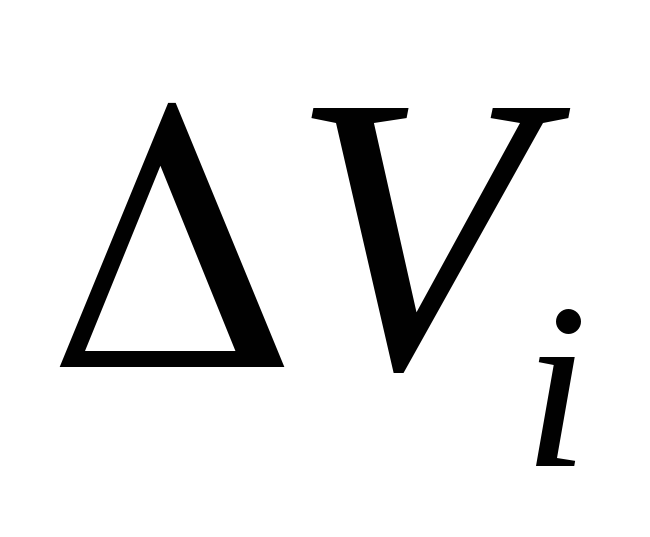 – объемi — го участка, то
– объемi — го участка, то
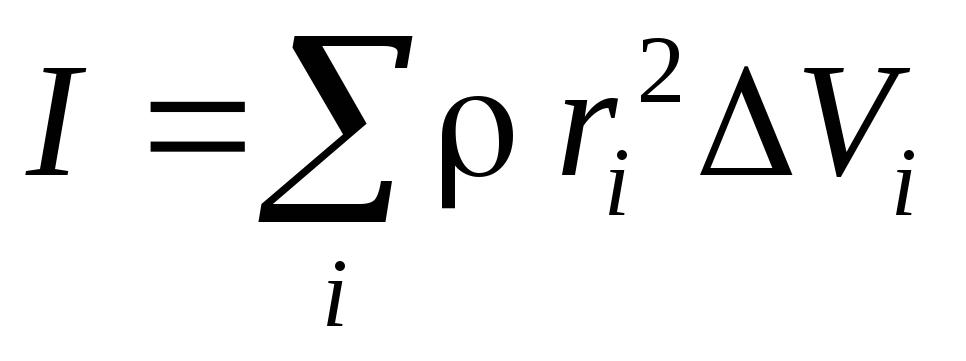 ,
,
или, переходя к бесконечно малым элементам,
 . (6.4)
. (6.4)
Формулу (6.4) удобно использовать для вычисления МИ однородных тел правильной формы относительно оси симметрии, проходящей через центр масс тела. Например, для МИ цилиндра относительно оси, проходящей через центр масс параллельно образующей, эта формула дает
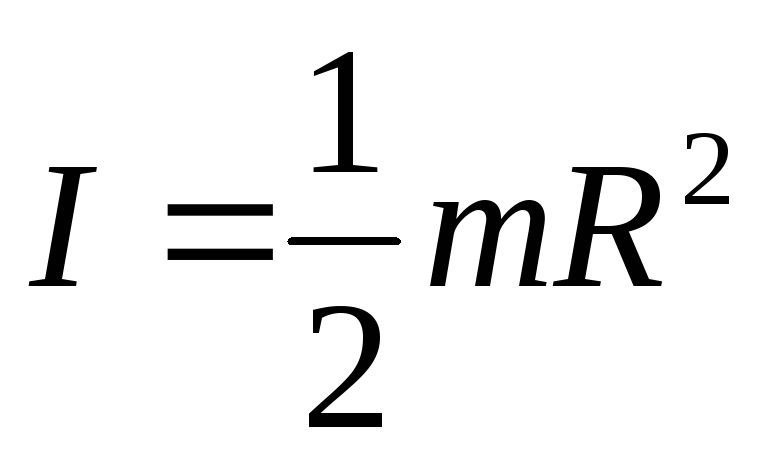 ,
,
где т — масса; R — радиус цилиндра.
Большую помощь при вычислении МИ тел относительно некоторых осей оказывает теорема Штейнера: МИ тела
 . (6.5)
. (6.5)
Момент силы относительно оси
Пусть
на тело действует сила F.
Примем для простоты, что сила F лежит в плоскости, перпендикулярной
некоторой прямой ОО (рис.6.2,а),
которую назовем осью (например, это ось
вращения тела). На рис. 6.2,а А — точка приложения силы F, 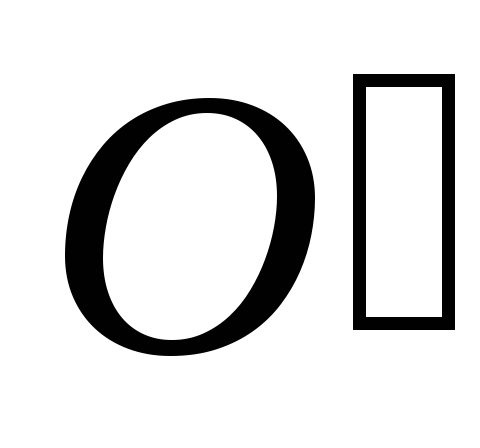
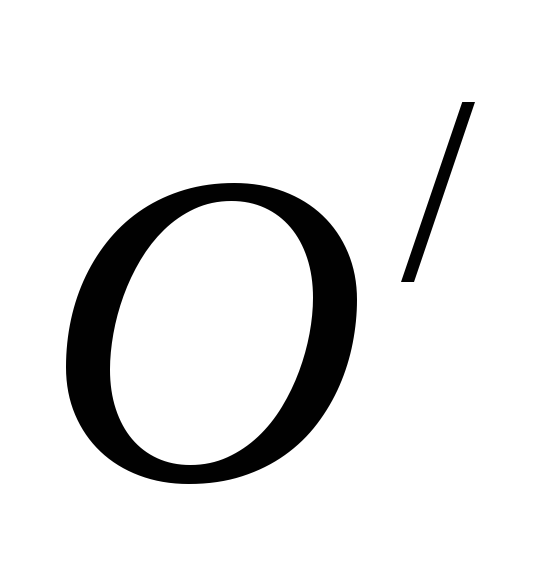 к
этой прямой).
к
этой прямой).Моментом силы относительно оси называется векторная величина, определяемая равенством
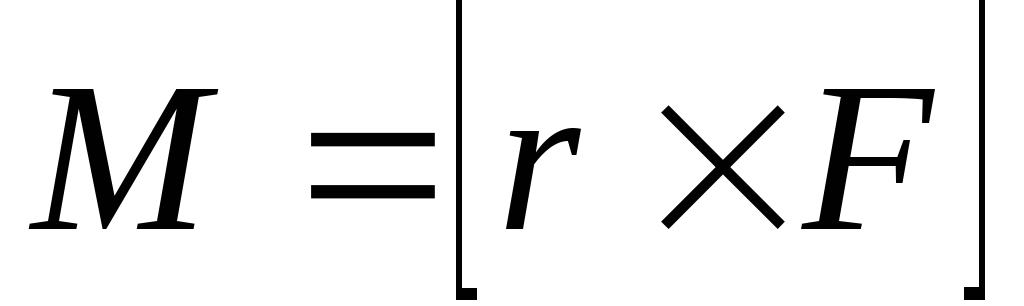 . (6.6)
. (6.6)

Модуль
этого вектора 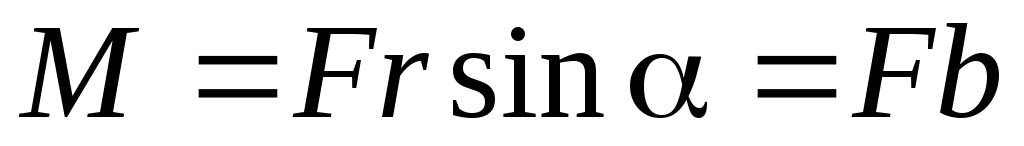 .
Иногда, поэтому говорят, что момент силы
относительно оси – это произведение
силы на ее плечо.
.
Иногда, поэтому говорят, что момент силы
относительно оси – это произведение
силы на ее плечо.
Если
сила F направлена произвольно, то ее можно
разложить на две составляющие; 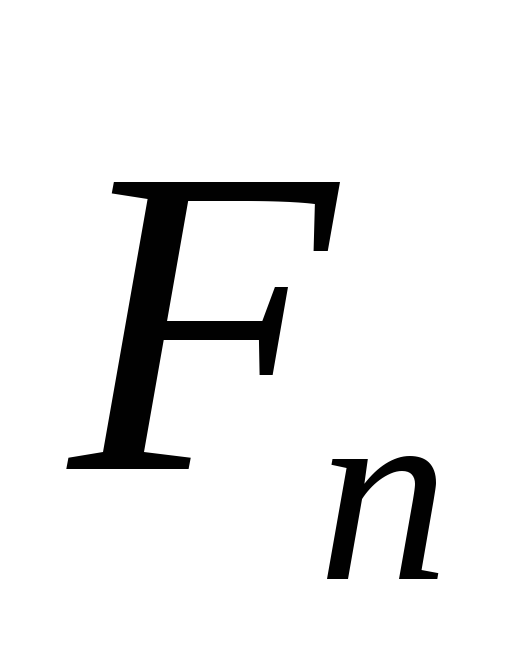 и
и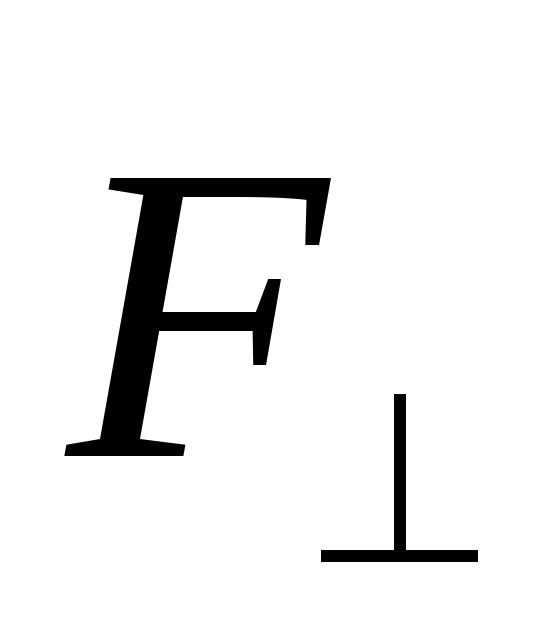 (рис.6.2,б),
т.е.
(рис.6.2,б),
т.е. 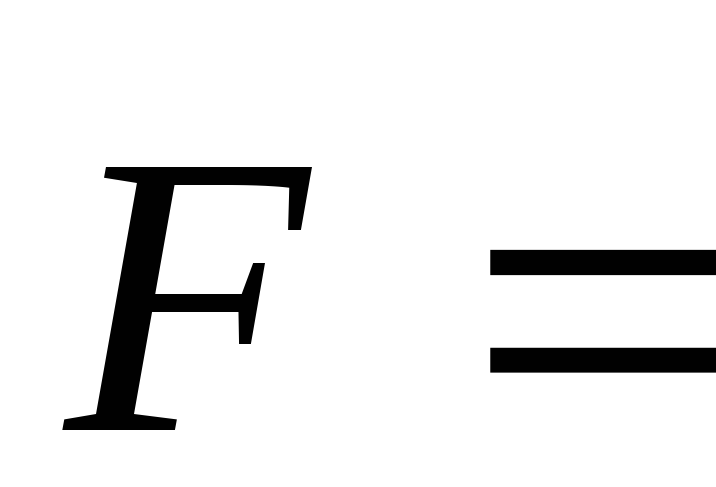
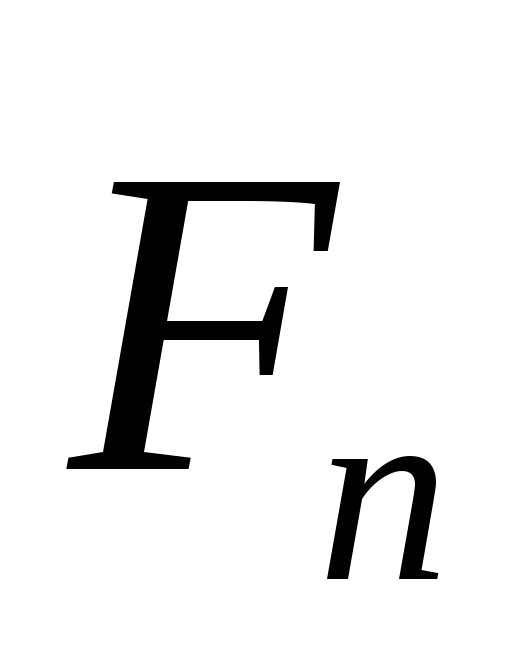
 ,
где
,
где —
составляющая, направленная параллельно
оси ОО, а
—
составляющая, направленная параллельно
оси ОО, а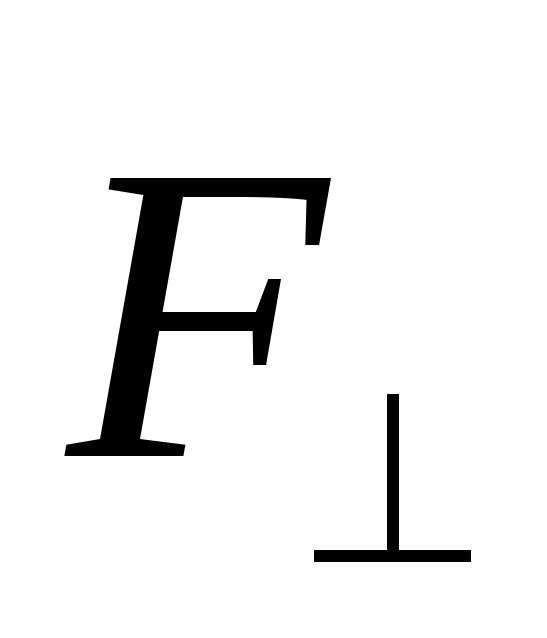 лежит в плоскости, перпендикулярной
оси. В этом случае под моментом силыF относительно оси OO понимают вектор
лежит в плоскости, перпендикулярной
оси. В этом случае под моментом силыF относительно оси OO понимают вектор  . (6.7)
. (6.7)
В соответствии с выражениями (6.6) и (6.7) вектор М
Момент импульса тела относительно оси вращения
П усть
тело вращается вокруг некоторой оси ОО
с угловой скоростью
усть
тело вращается вокруг некоторой оси ОО
с угловой скоростью .
Разобьем это тело мысленно на элементарные
участки с массами
.
Разобьем это тело мысленно на элементарные
участки с массами 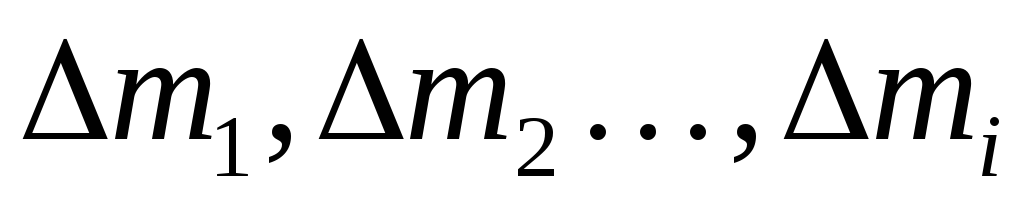 ,
которые находятся от оси соответственно
на расстояниях
,
которые находятся от оси соответственно
на расстояниях  и вращаются по окружностям, имея линейные
скорости
и вращаются по окружностям, имея линейные
скорости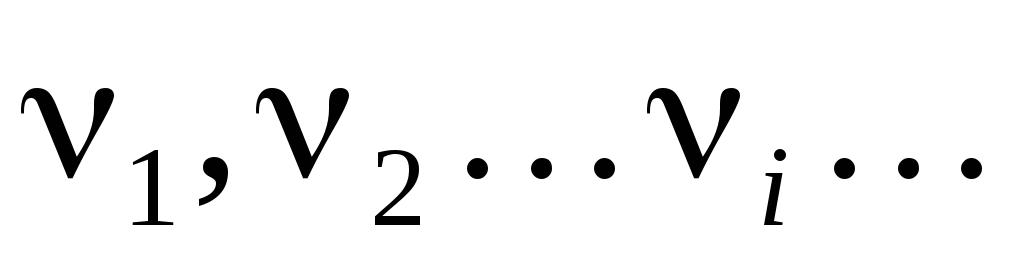
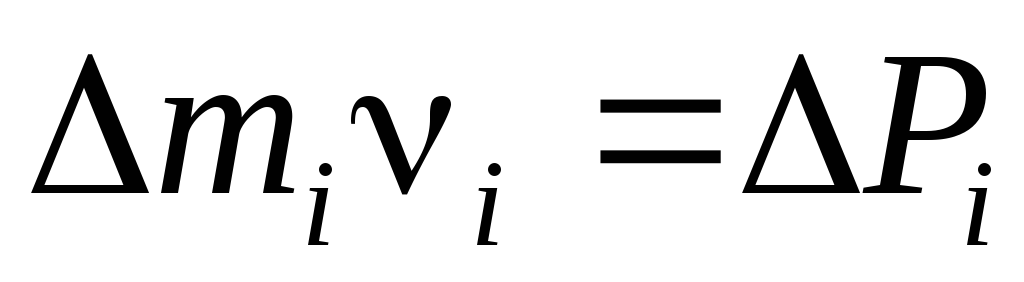 — есть импульсi-участка.
Моментом импульса i-участка
(материальной точки) относительно оси
вращения называется вектор (точнее
псевдовектор)
— есть импульсi-участка.
Моментом импульса i-участка
(материальной точки) относительно оси
вращения называется вектор (точнее
псевдовектор)  , (6.8)
, (6.8)
где ri– радиус-вектор, определяющий положение i — участка относительно оси.
Моментом импульса всего тела относительно оси вращения называют вектор
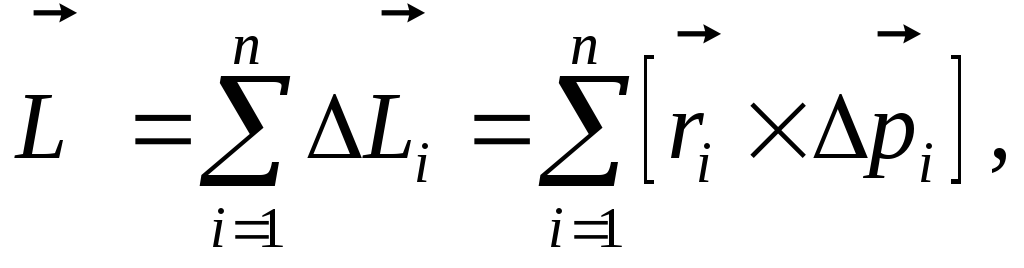
модуль
которого  .
.
В
соответствии с выражениями (6.8) и (6.9)
векторы  и
и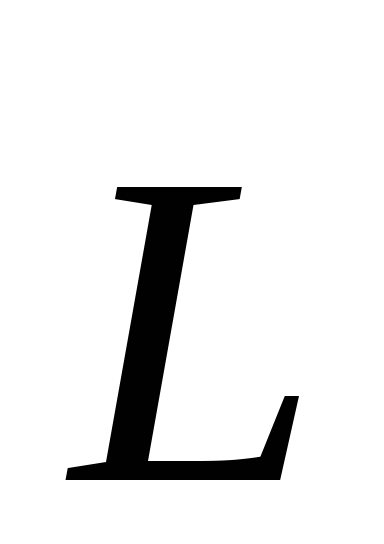 направлены
по оси вращения (рис.6.3). Легко показать,
что момент импульса тела L относительно оси вращения и момент
инерции I этого тела относительно той же оси
связаны соотношением
направлены
по оси вращения (рис.6.3). Легко показать,
что момент импульса тела L относительно оси вращения и момент
инерции I этого тела относительно той же оси
связаны соотношением
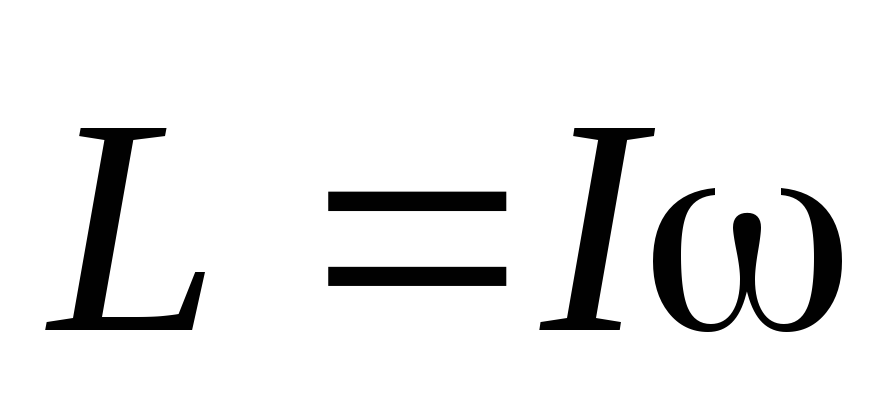
1.2. Осевые моменты инерции Jx ; Jy
Осевой момент инерции равен сумме произведений элементарных площадок на квадрат расстояния до соответствующей оси.
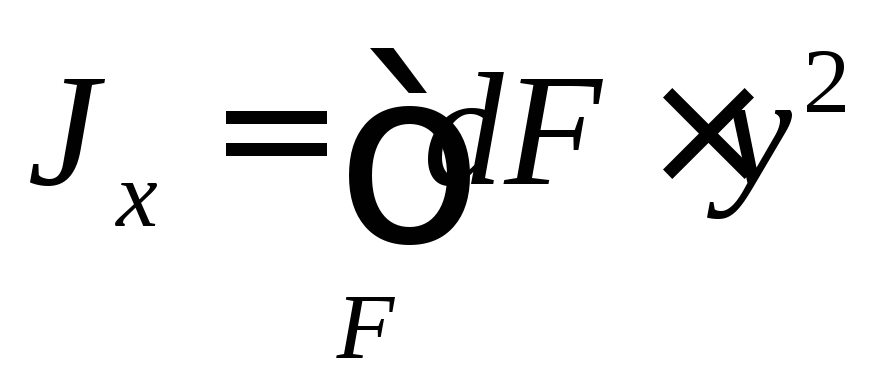 (7)
(7)
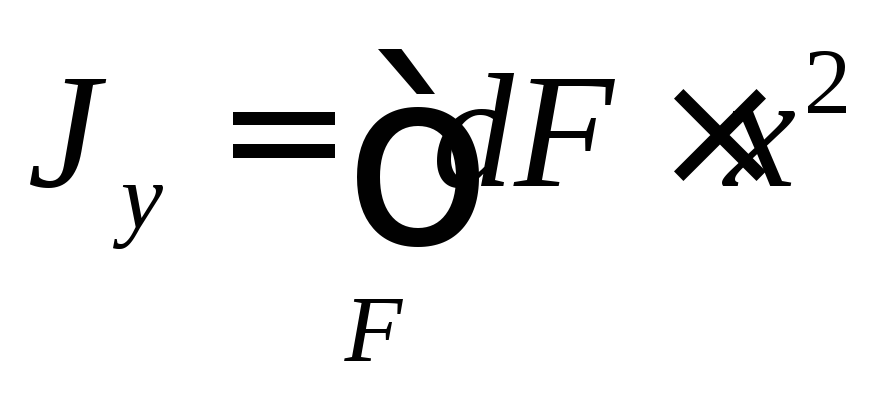 (8)
(8)
Единица измерения [см4], [мм4].
Знак всегда «+».
Не бывает равным 0.
Свойство:Принимает минимальное значение, когда точка пересечения координатных осей совпадает с центром тяжести сечения.
Чем дальше площадь удалена от центральной оси, тем осевой момент инерции сечения больше. Жесткость конструкции повышается.
Осевой момент инерции сечения применяют при расчетах на прочность, жесткость и устойчивость.
1.3. Полярный момент инерции сечения Jρ
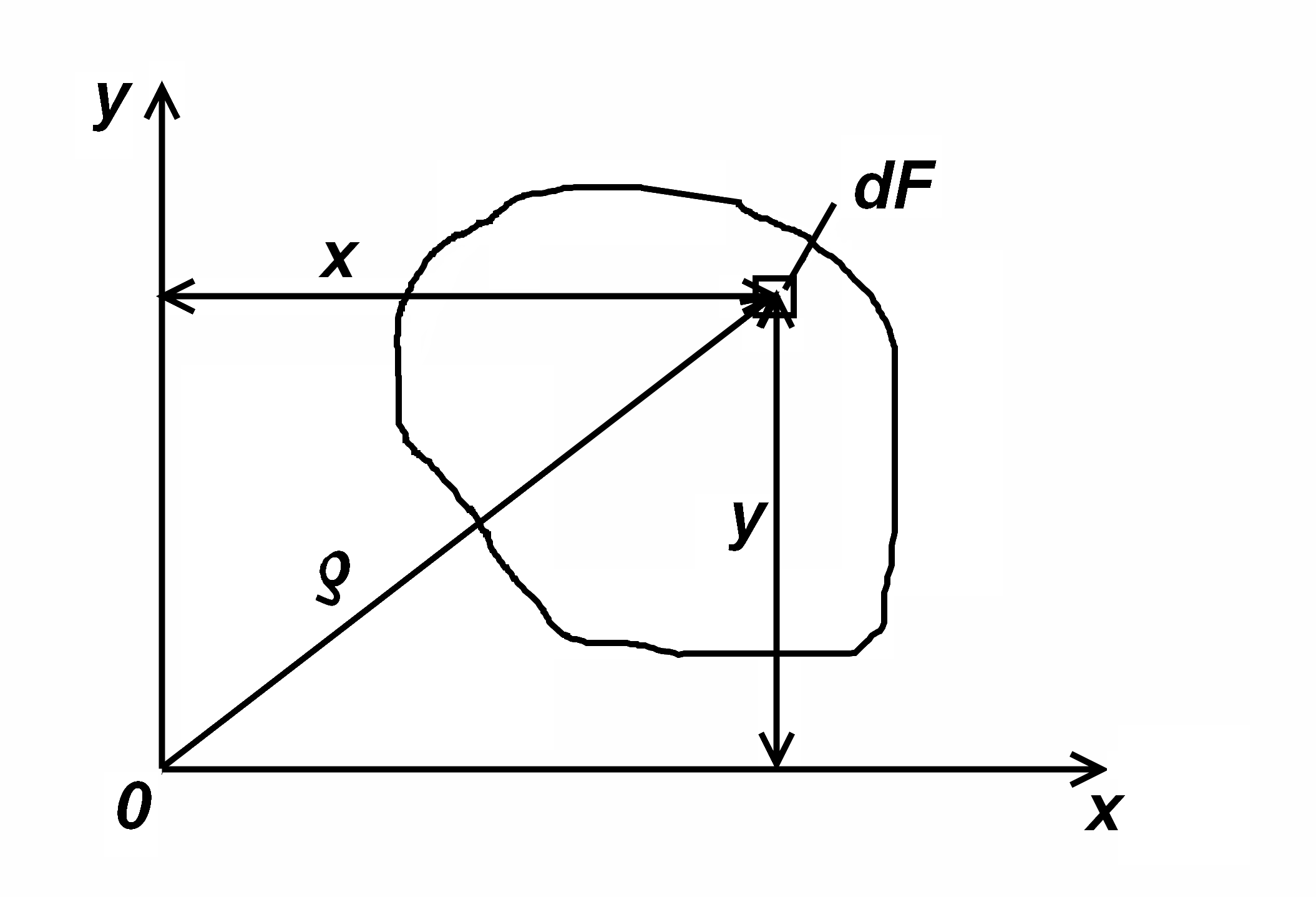
Рис. 3
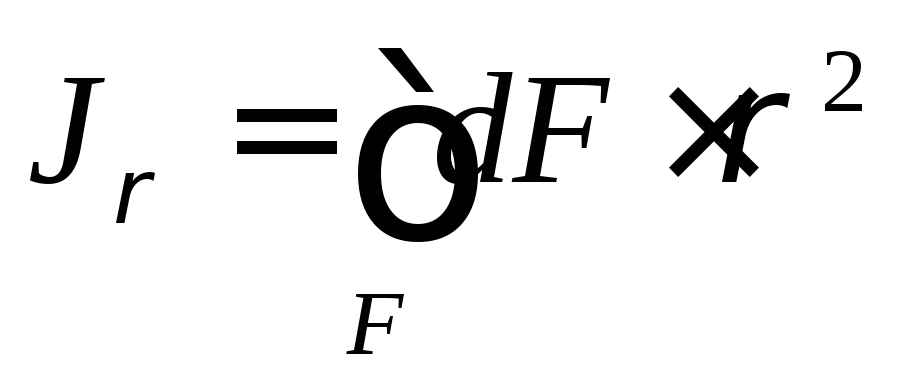 (9)
(9)
Взаимосвязь полярного и осевого моментов инерции:
 (10)
(10)
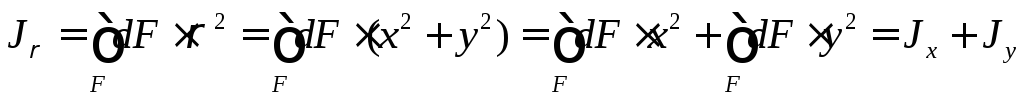
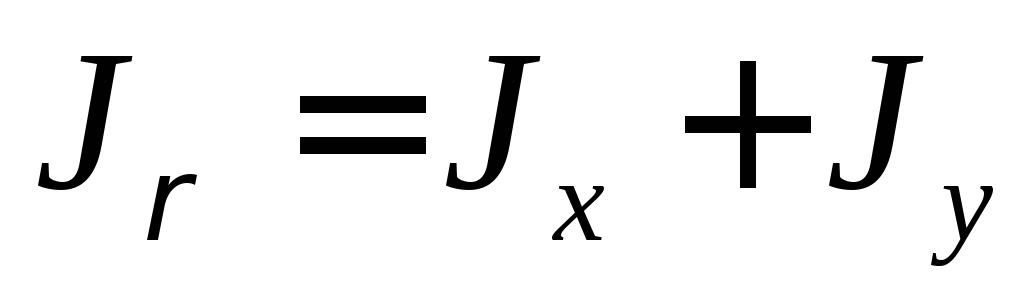 (11)
(11)
Полярный момент инерции сечения равен сумме осевых моментов.
Свойство:
при повороте осей в любую сторону, один из осевых моментов инерции возрастает, а другой убывает (и наоборот). Сумма осевых моментов инерции остается величиной постоянной.
1.4. Центробежный момент инерции сечения Jxy
Центробежный момент инерции сечения равен сумме произведений элементарных площадок на расстояния до обеих осей
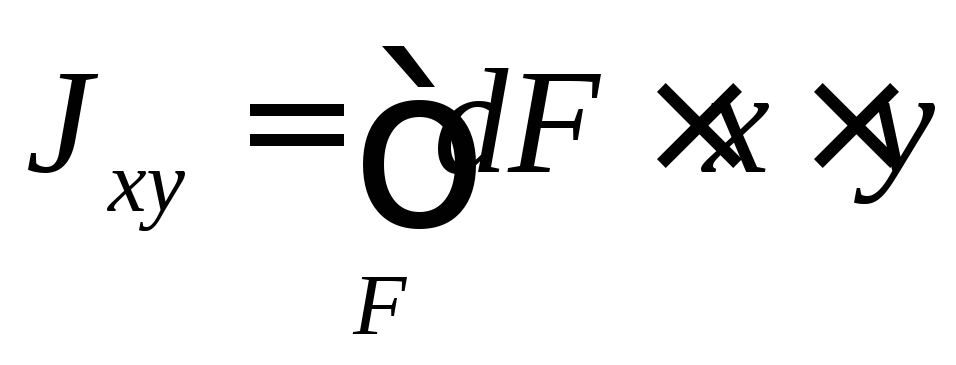 (12)
(12)
Единица измерения [см4], [мм4].
Знак «+» или «-».
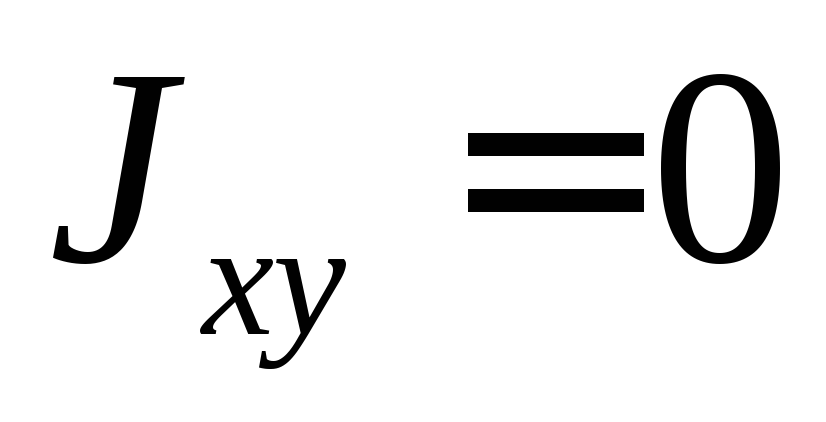 ,
если координатные оси являются осями
симметрии (пример – двутавр, прямоугольник,
круг), или одна из координатных осей
совпадает с осью симметрии (пример –
швеллер).
,
если координатные оси являются осями
симметрии (пример – двутавр, прямоугольник,
круг), или одна из координатных осей
совпадает с осью симметрии (пример –
швеллер).
Таким образом для симметричных фигур центробежный момент инерции равен 0.
Координатные оси uиv, проходящие через центр тяжести сечения, относительно которых центробежный момент равен нулю, называютсяглавными центральными осями инерции сечения. Главными они называются потому, что центробежный момент относительно них равен нулю, а центральными – потому, что проходят через центр тяжести сечения.
У
сечений, не обладающих симметрией
относительно осей xилиy, например у
уголка,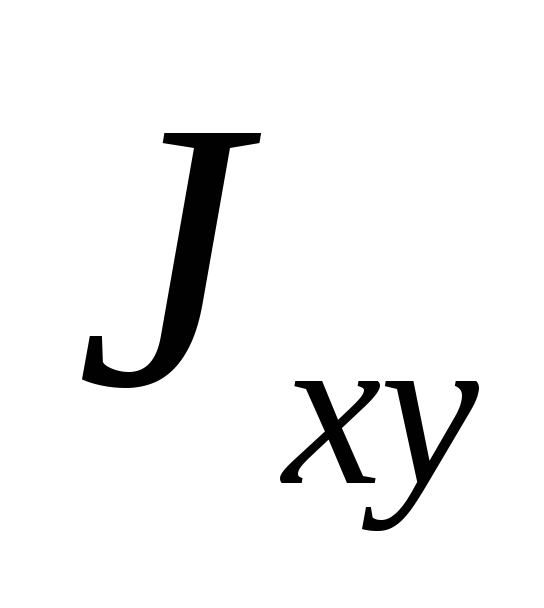 не будет равен нулю. Для этих сечений
определяют положение осейuиvс помощью
вычисления угла поворота осейxиy
не будет равен нулю. Для этих сечений
определяют положение осейuиvс помощью
вычисления угла поворота осейxиy
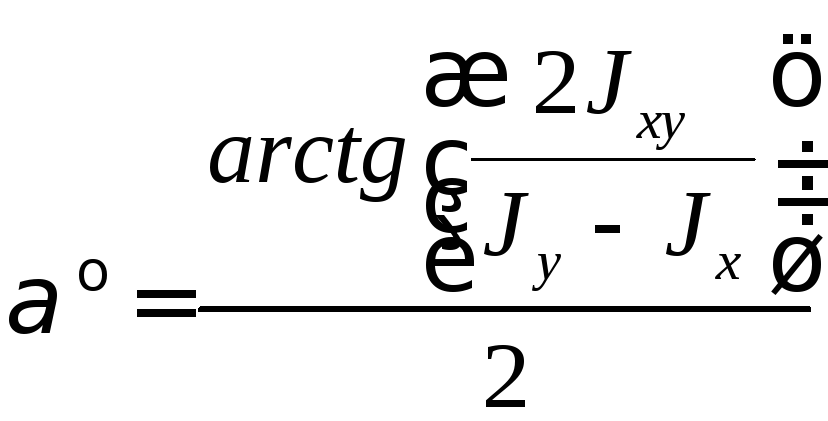 (13)
(13)
Центробежный
момент относительно осей uиv—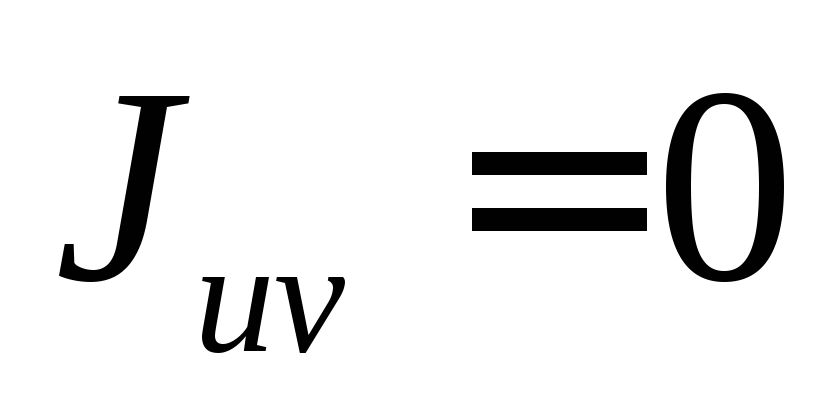
Формула для определения осевых моментов инерции относительно главных центральных осей uиv:
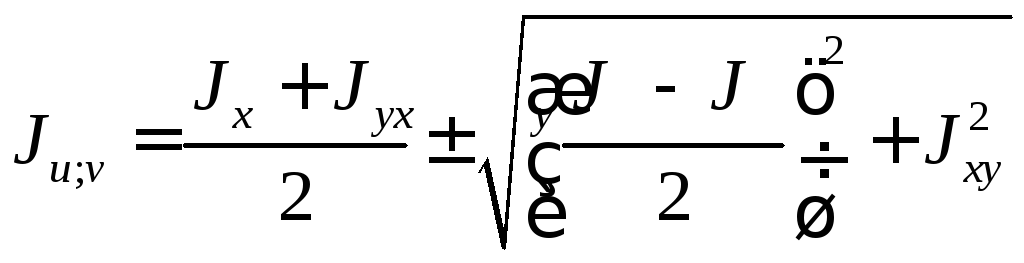 (14)
(14)
где 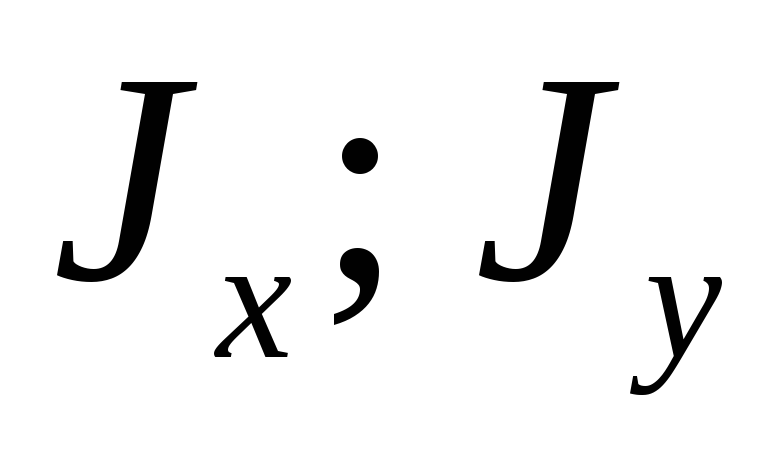 — осевые моменты инерции относительно
центральных осей,
— осевые моменты инерции относительно
центральных осей,
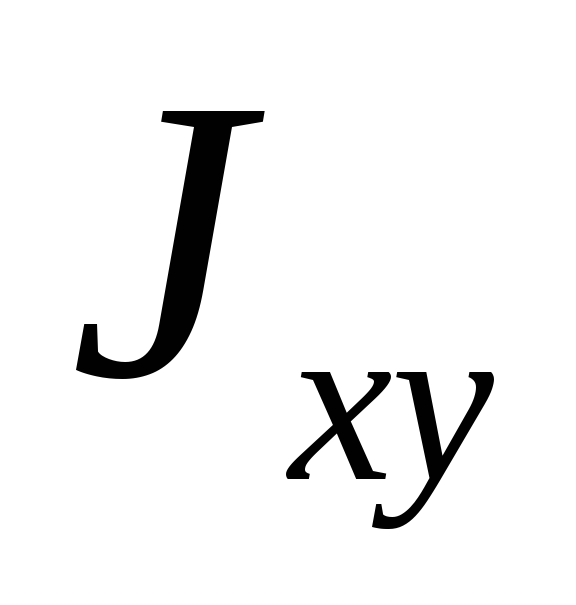 — центробежный момент инерции относительно
центральных осей.
— центробежный момент инерции относительно
центральных осей.
1.5. Момент инерции относительно оси, параллельной центральной (теорема Штейнера)
Теорема Штейнера:
Момент инерции относительно оси, параллельной центральной, равен центральному осевому моменту инерции плюс произведение площади всей фигуры на квадрат расстояния между осями.
 (15)
(15)
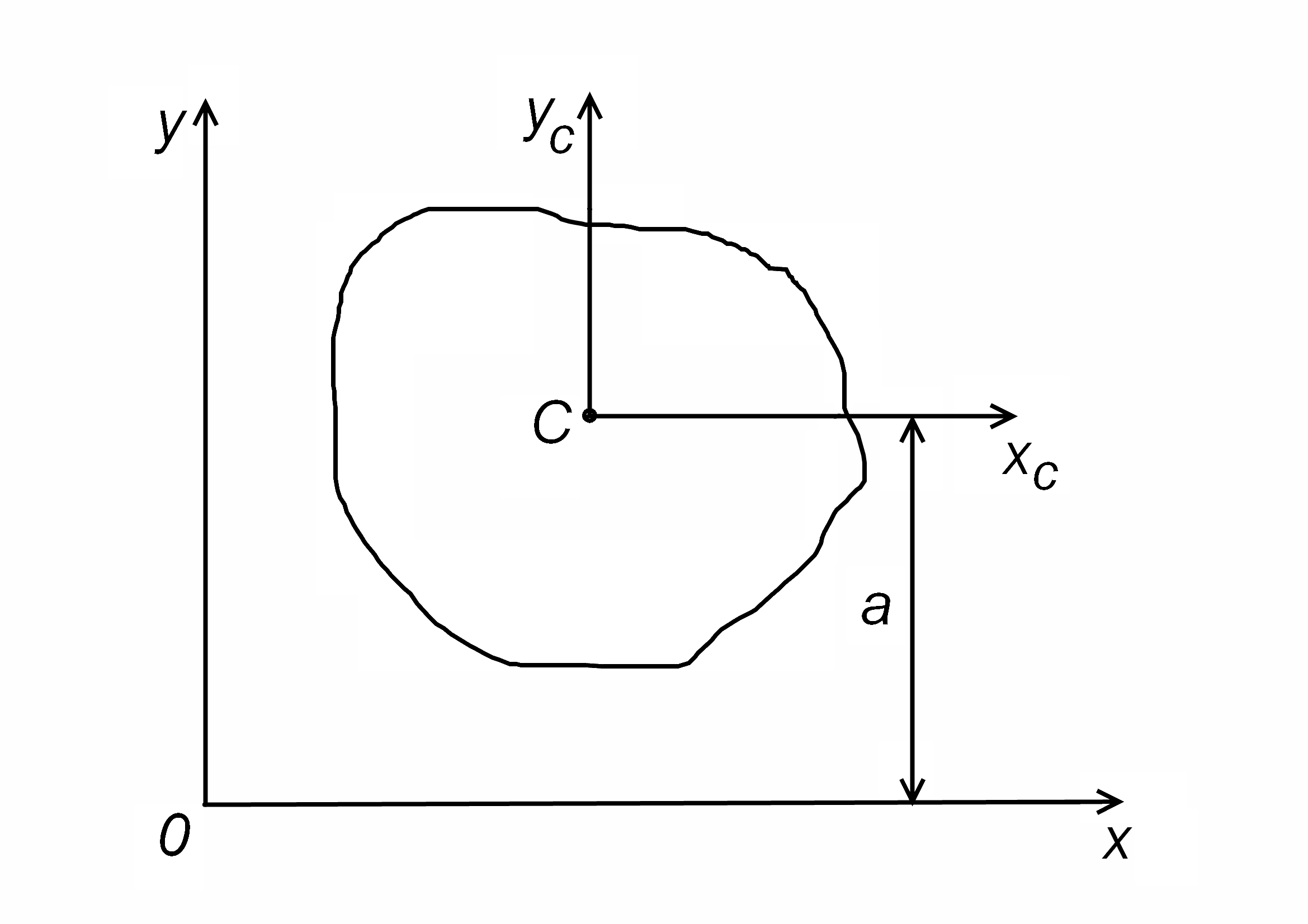
Рис. 4
Доказательство теоремы Штейнера.
Согласно рис. 5 расстояние удо элементарной площадкиdF

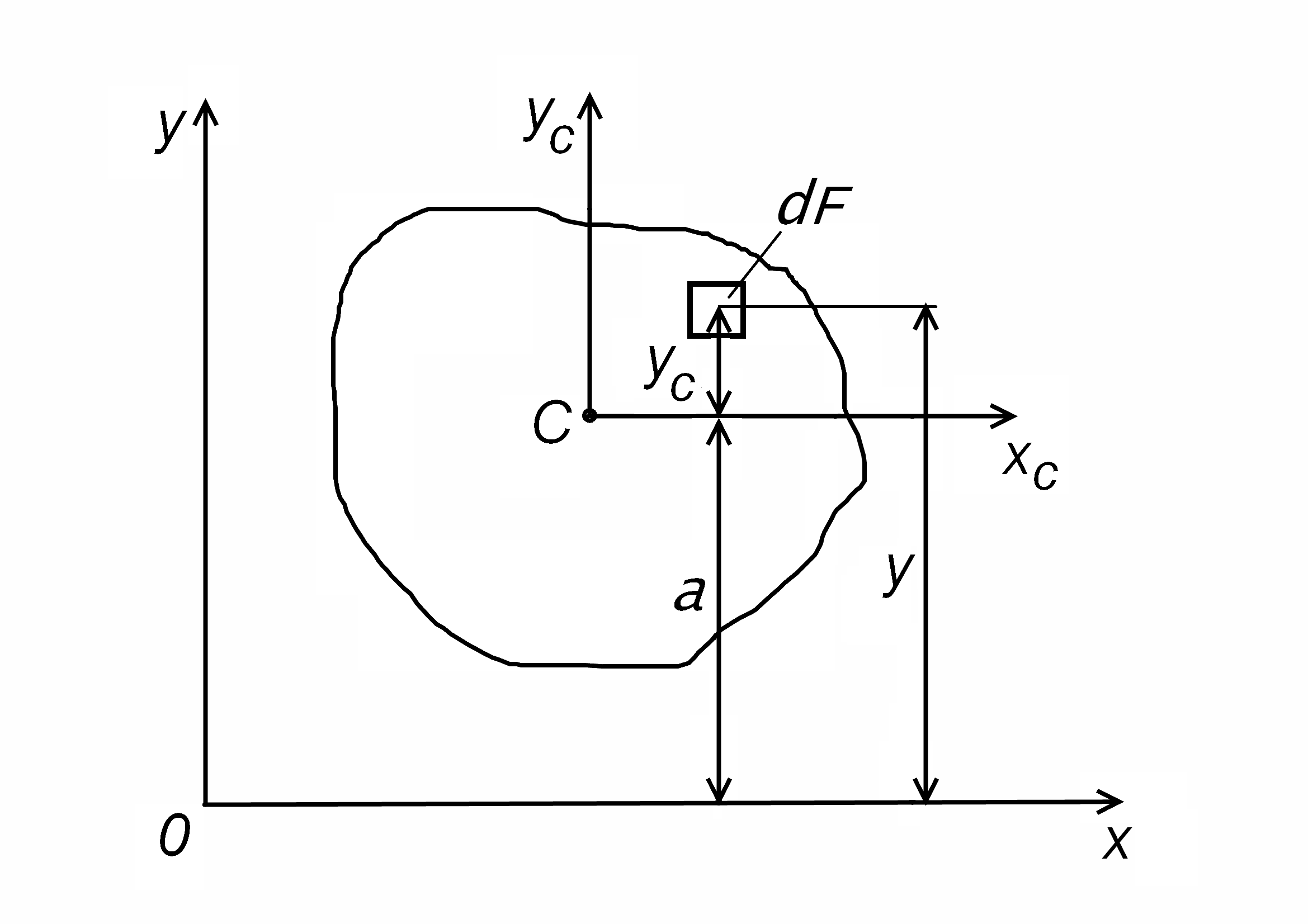
Рис. 5
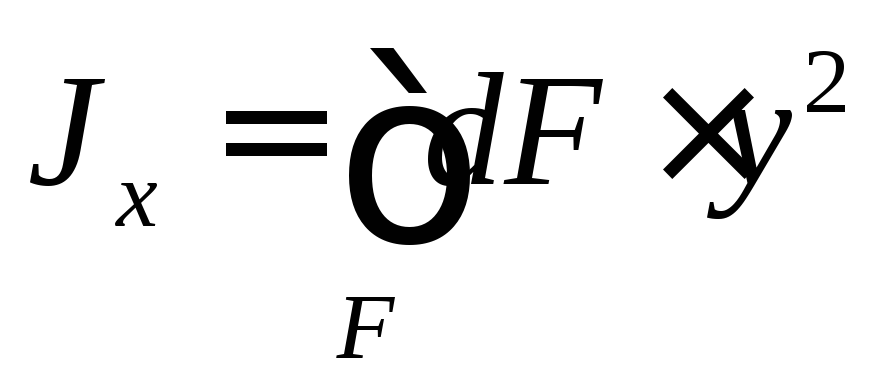
Подставляя значение ув формулу, получим:
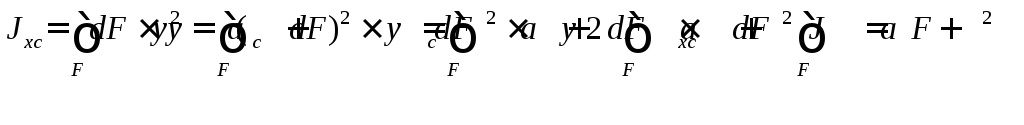
Слагаемое 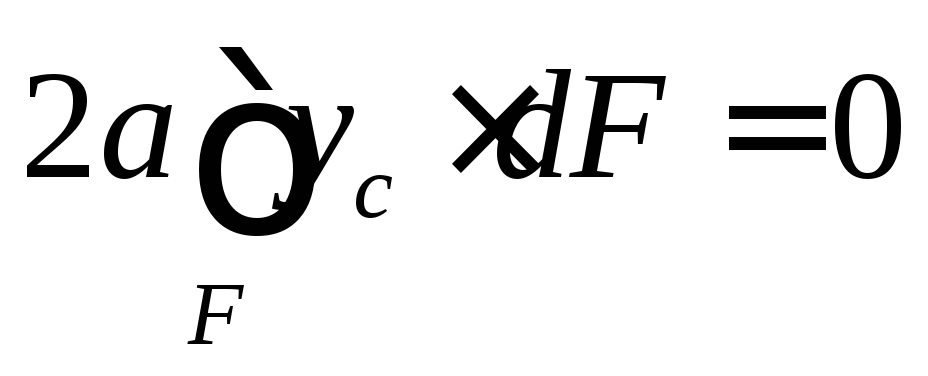 ,
так как точка С является центром тяжести
сечения (см. свойство статических
моментов площади сечения относительно
центральных осей).
,
так как точка С является центром тяжести
сечения (см. свойство статических
моментов площади сечения относительно
центральных осей).
Для прямоугольника высотой h и шириной b :
Осевой момент инерции:
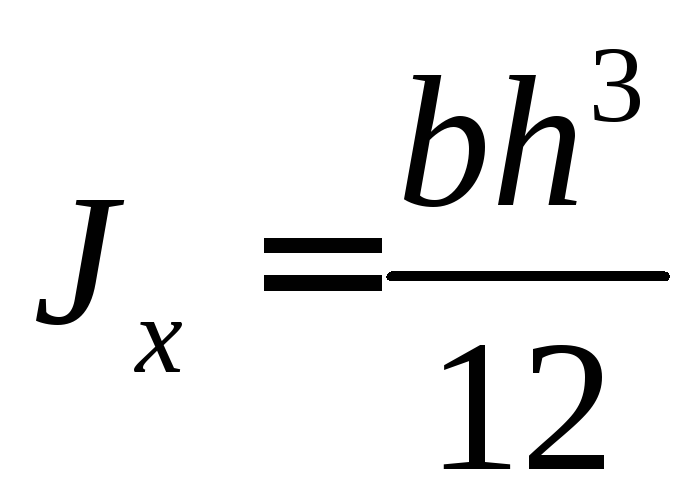
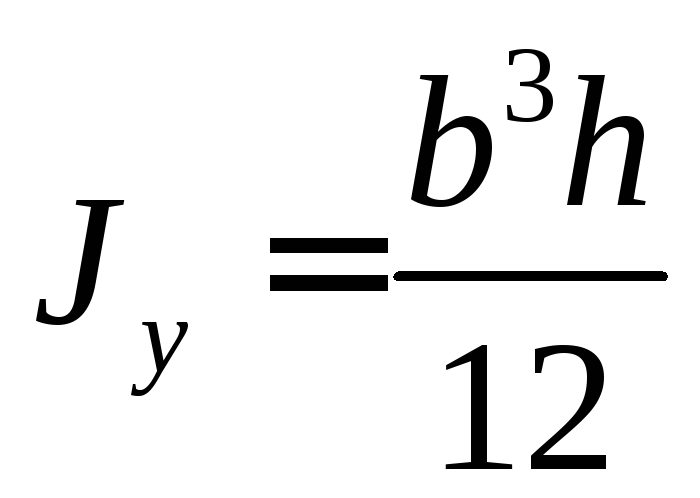
Момент сопротивления изгибу:
момент сопротивления изгибу равен отношению момента инерции к расстоянию наиболее удаленного волокна от нейтральной линии:
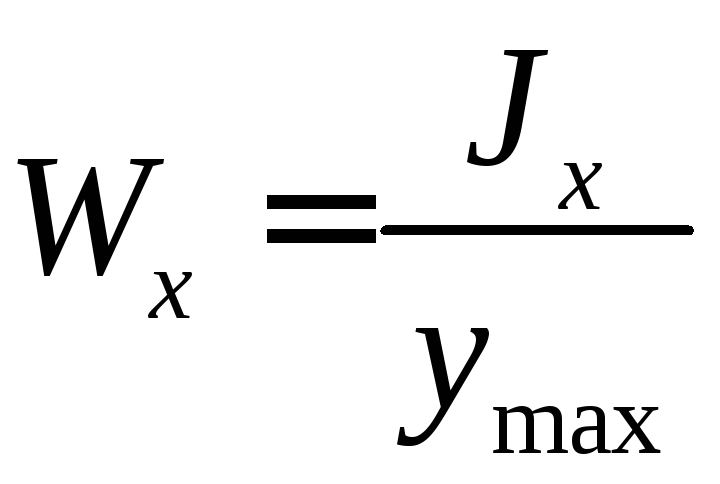
т.к. 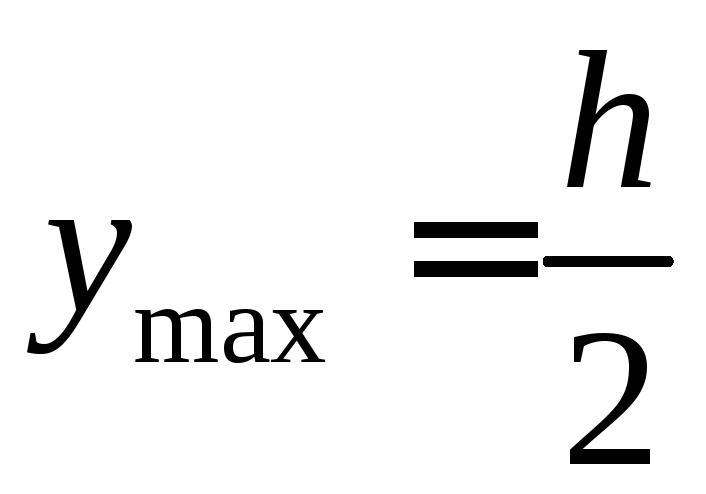 ,
то
,
то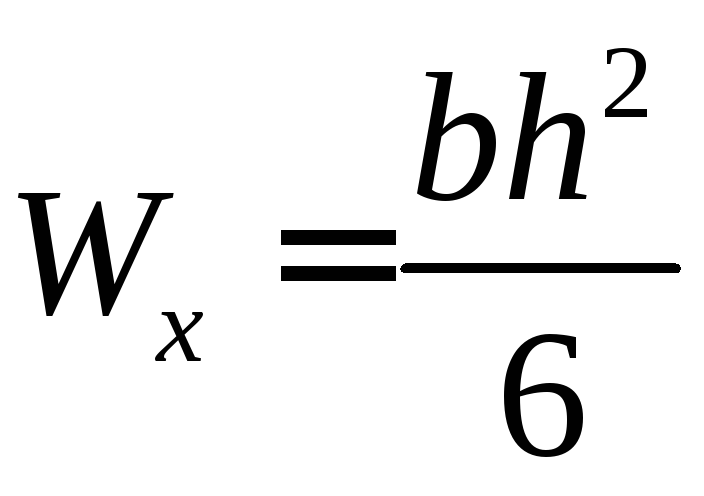
Для круга:
Полярный
момент инерции: 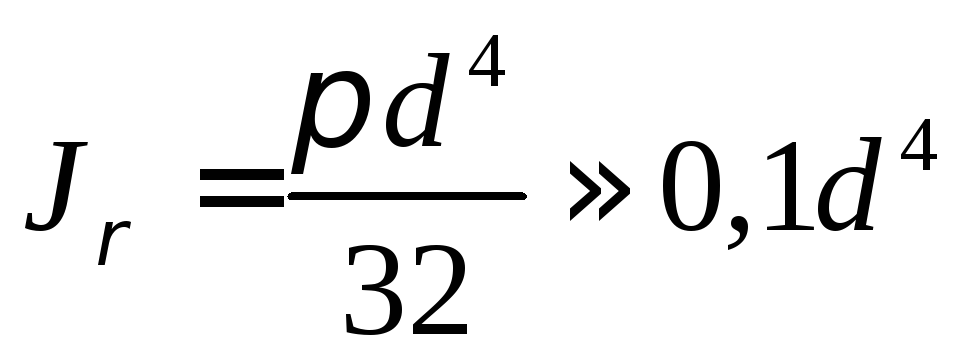
Осевой
момент инерции: 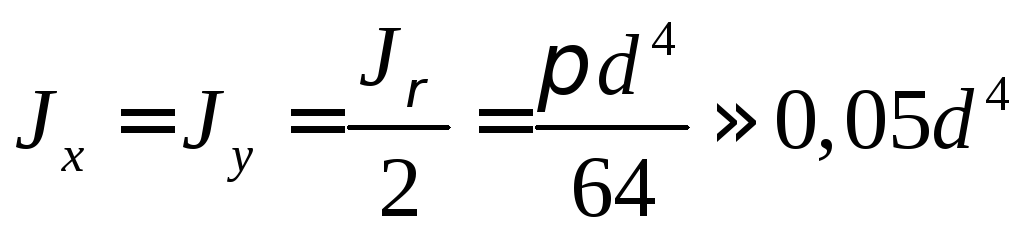
Момент
сопротивления кручению: 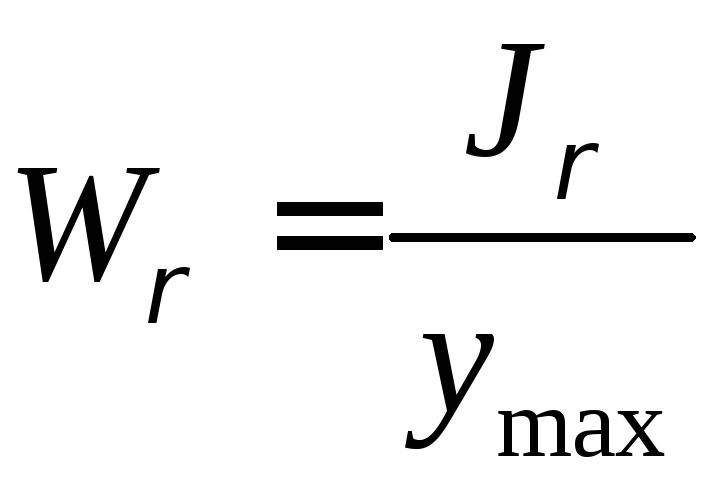
Т.к. 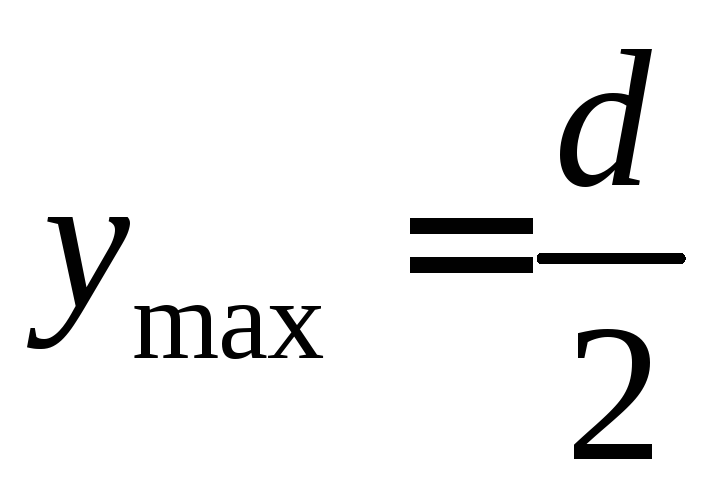 ,
то
,
то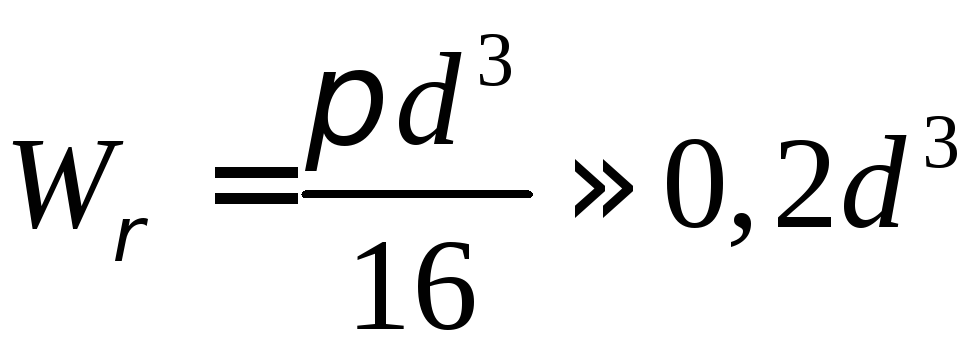
Момент
сопротивления изгибу: 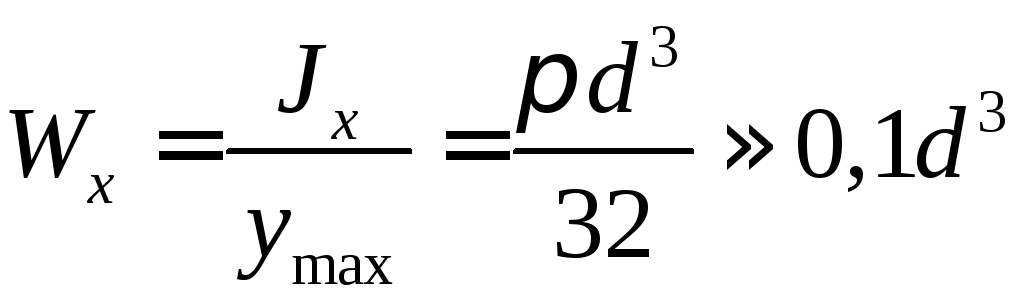
Пример 2. Определить момент инерции прямоугольного сечения относительно центральной оси Сx.

Рис. 6
Решение. Разобьём площадь прямоугольника на элементарные прямоугольники с размерами b(ширина) иdy(высота). Тогда площадь такого прямоугольника (на рис. 6 заштрихована) равна dF=bdy. Вычислим значение осевого момента инерции Jx
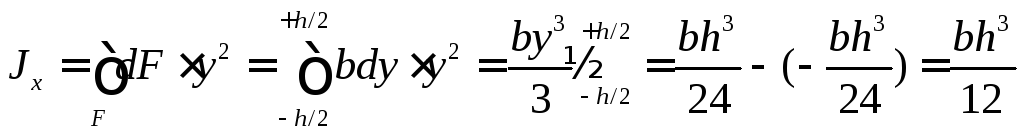
По аналогии запишем
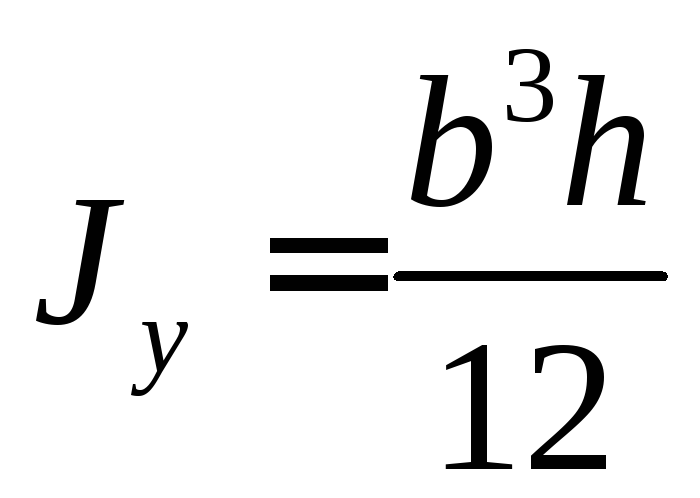 — осевой момент инерции сечения
относительно центральной
— осевой момент инерции сечения
относительно центральной
оси у
Центробежный момент инерции
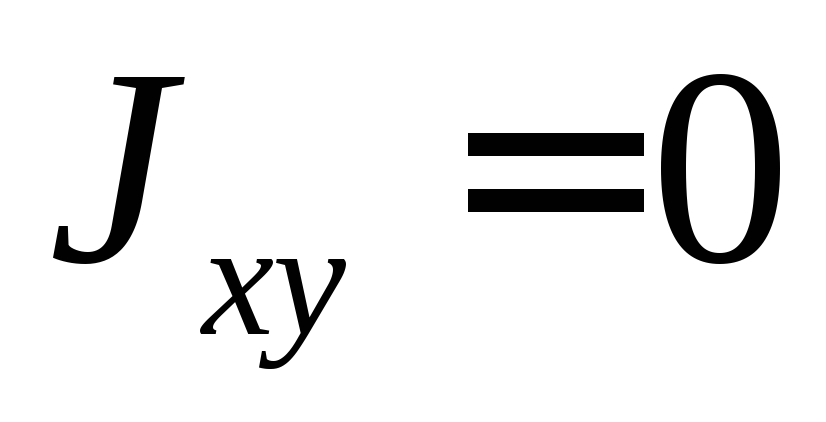 ,
так как оси Сxи Сyявляются
осями симметрии.
,
так как оси Сxи Сyявляются
осями симметрии.
Пример 3. Определить полярный момент инерции круглого сечения.
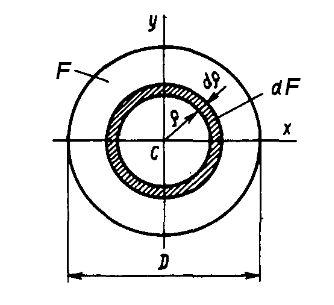
Рис. 7
Решение.
Разобьём круг на бесконечно тонкие
кольца толщиной 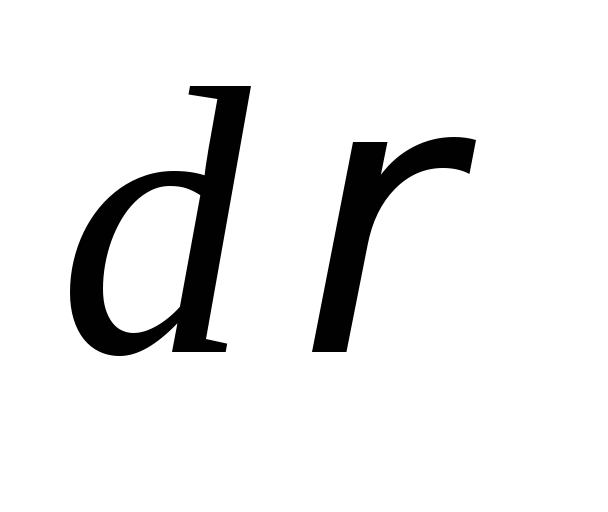 радиусом
радиусом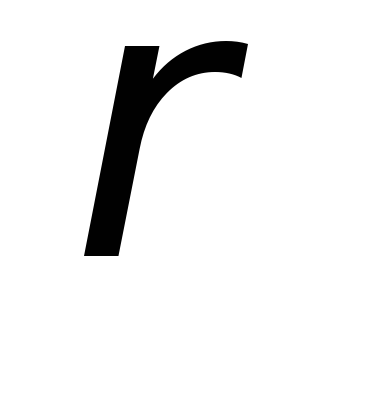 ,
площадь такого кольца
,
площадь такого кольца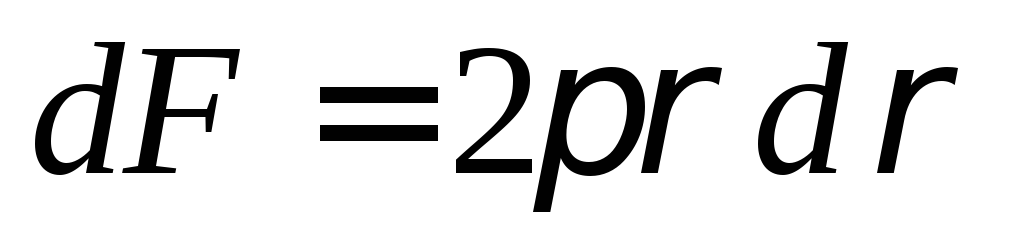 .
Подставляя значение
.
Подставляя значение в выражение для полярного момента
инерции интегрируя, получим
в выражение для полярного момента
инерции интегрируя, получим
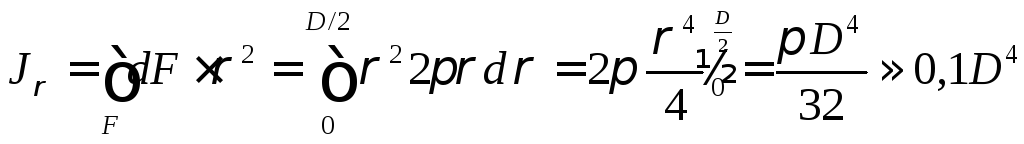
Учитывая
равенство осевых моментов круглого
сечения 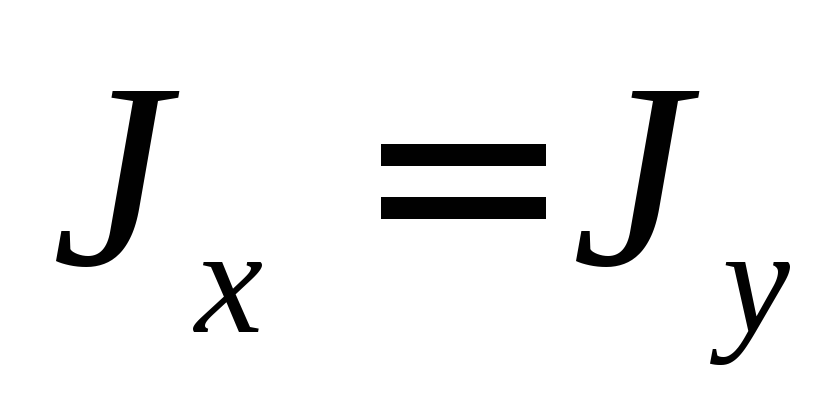 и
и
, получаем
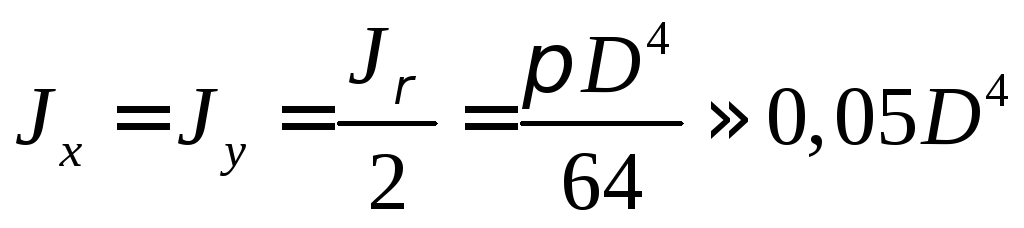
Осевые моменты инерции для кольца равны

с – отношение диаметра выреза к наружному диаметру вала.
Лекция №2 «Главные оси иглавные моментыинерции
Рассмотрим, как изменяются моменты
инерции при повороте координатных осей.
Положим, даны моменты инерции некоторого
сечения относительно осей 0х, 0у(не обязательно центральных)- 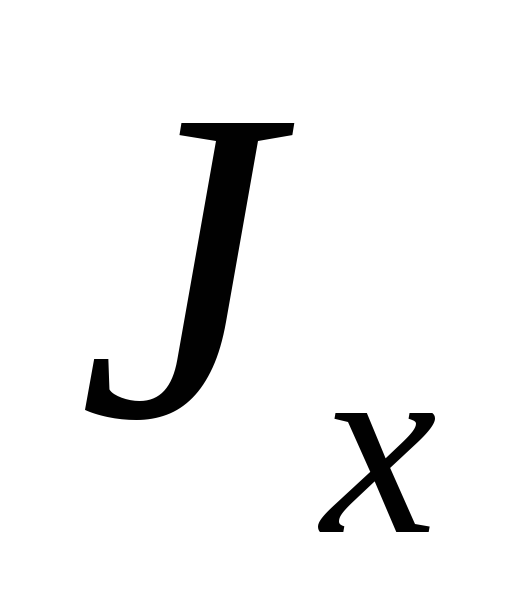 ,
, —
осевые моменты инерции сечения. Требуется
определить
—
осевые моменты инерции сечения. Требуется
определить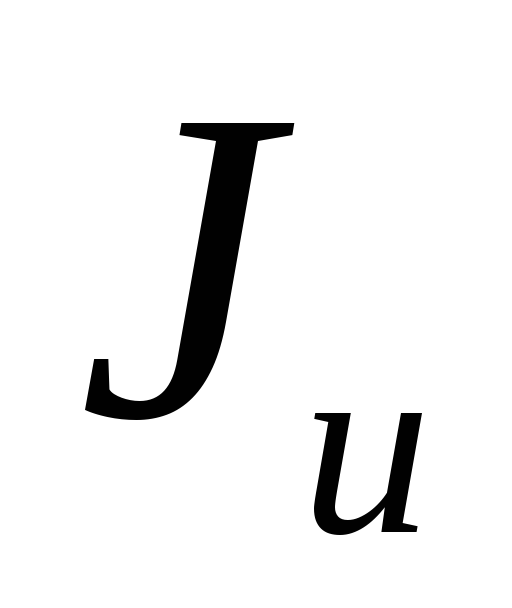 ,
,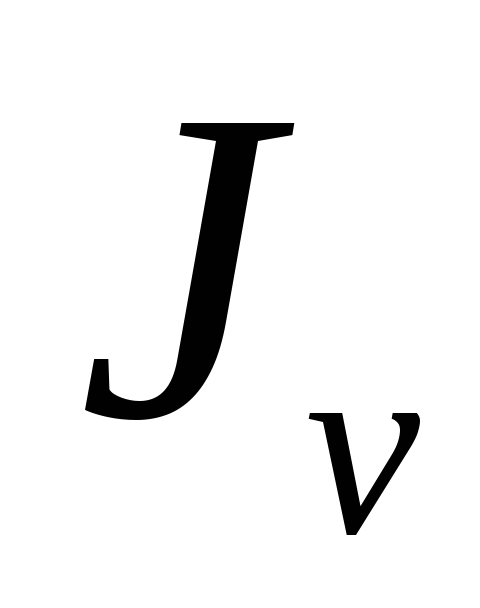 —
осевые моменты относительно осейu,v, повёрнутых
относительно первой системы на угол
—
осевые моменты относительно осейu,v, повёрнутых
относительно первой системы на угол (рис. 8)
(рис. 8)
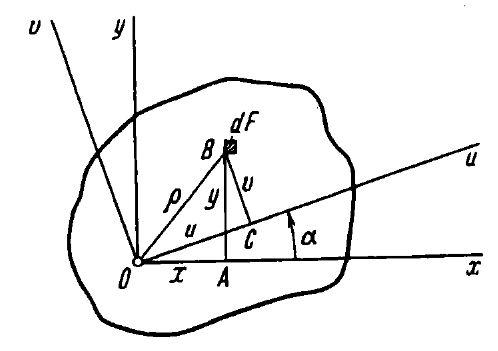
Рис. 8
Так как проекция ломаной линии ОАВС равна проекции замыкающей, находим:
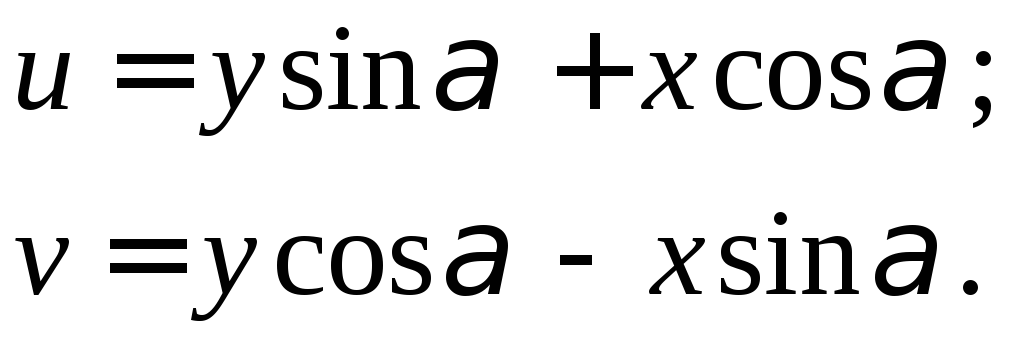 (15)
(15)
Исключим uиvв выражениях моментов инерции:
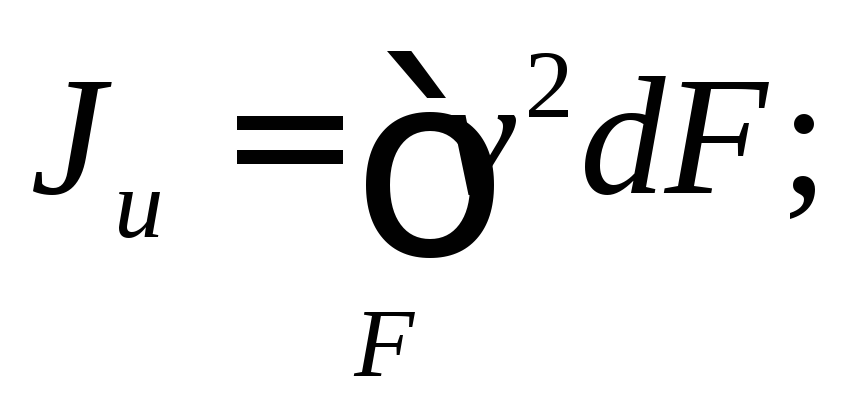
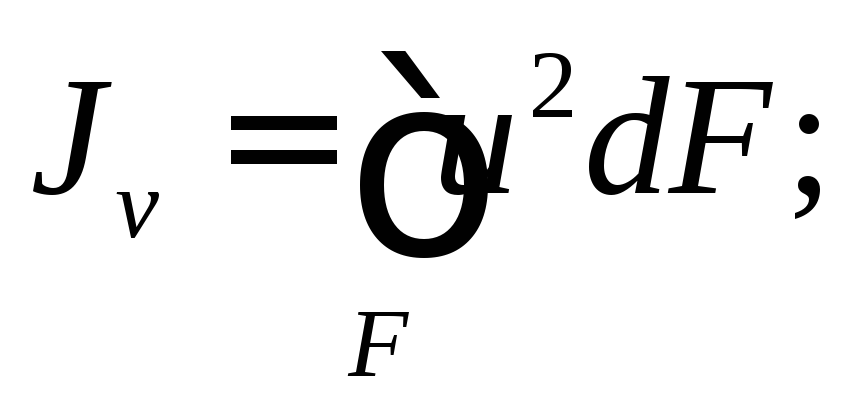
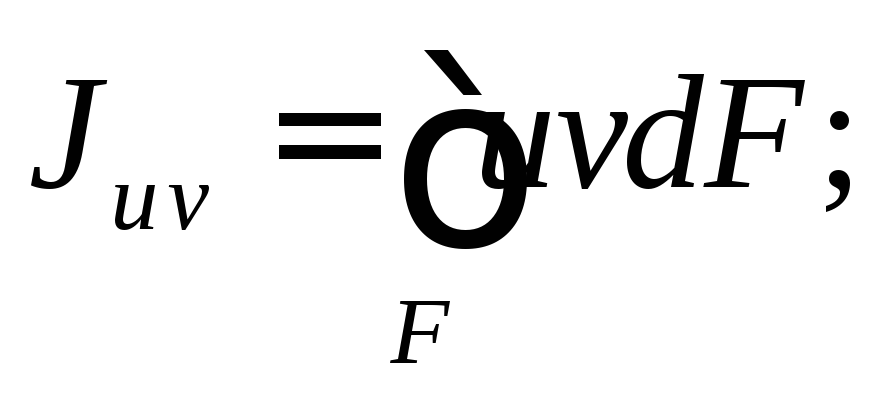
Тогда
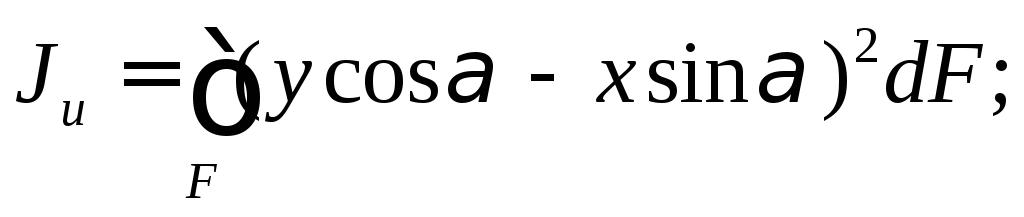
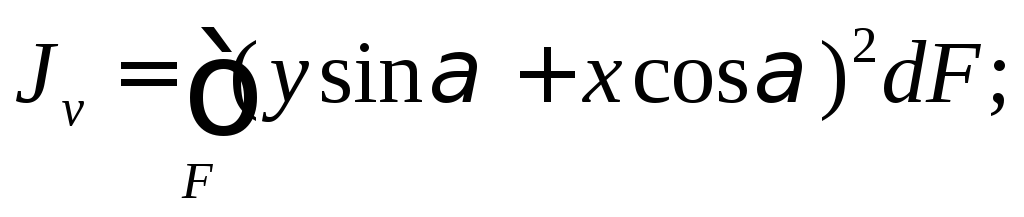
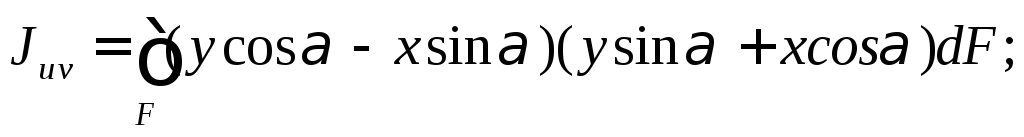
Откуда
 (16)
(16)
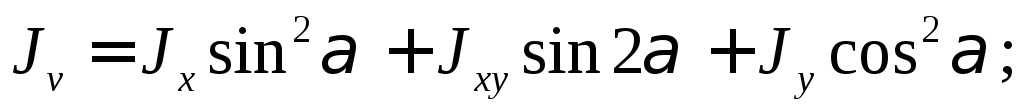 (17)
(17)
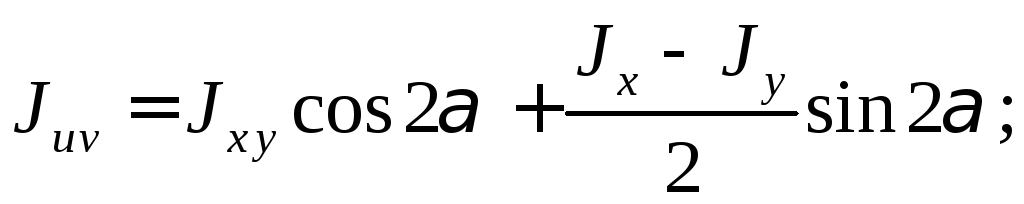 (18)
(18)
Рассмотрим два первых уравнения. Складывая их почленно, получим
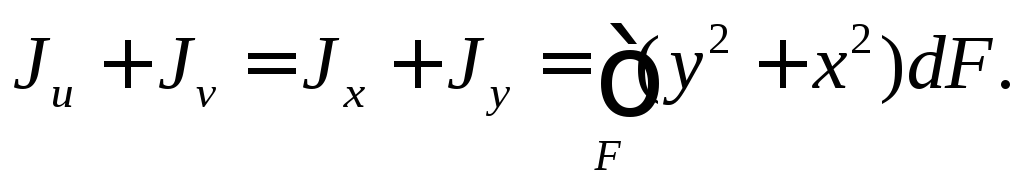
Таким
образом, сумма осевых моментов инерции
относительно двух взаимно перпендикулярных
осей не зависит от угла  и при повороте осей остается постоянной.
Заметим при этом, что
и при повороте осей остается постоянной.
Заметим при этом, что
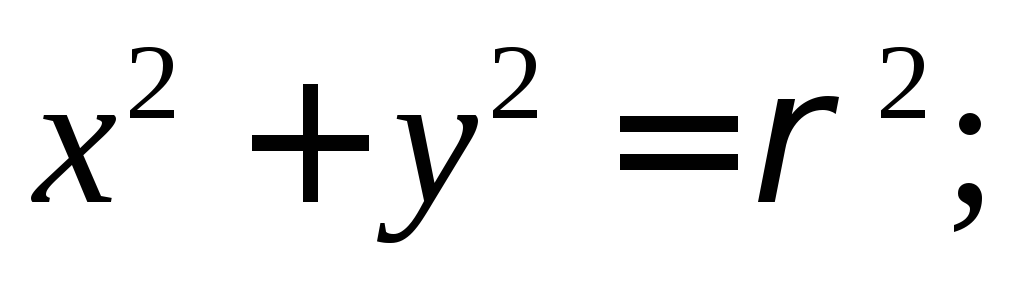
Где 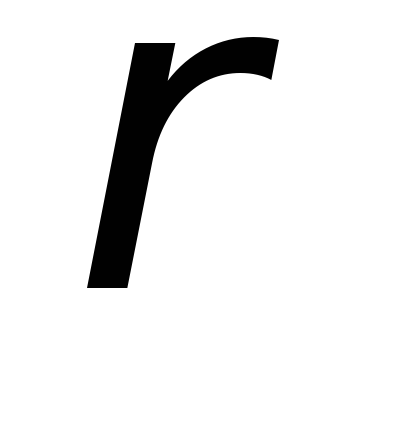 — расстояние от начала координат до
элементарной площадки (см. рис.5). Таким
образом
— расстояние от начала координат до
элементарной площадки (см. рис.5). Таким
образом
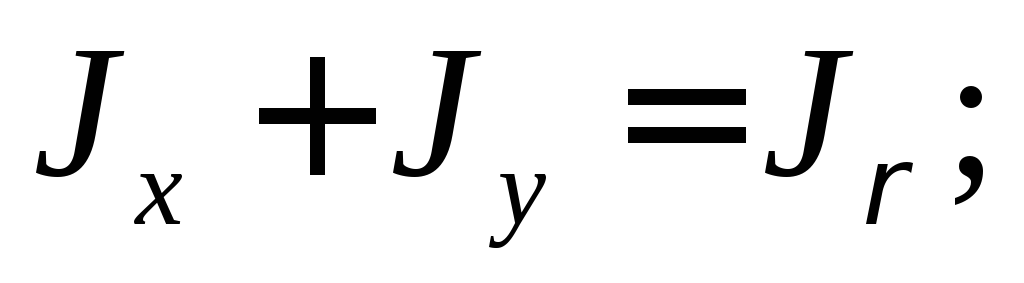
Где 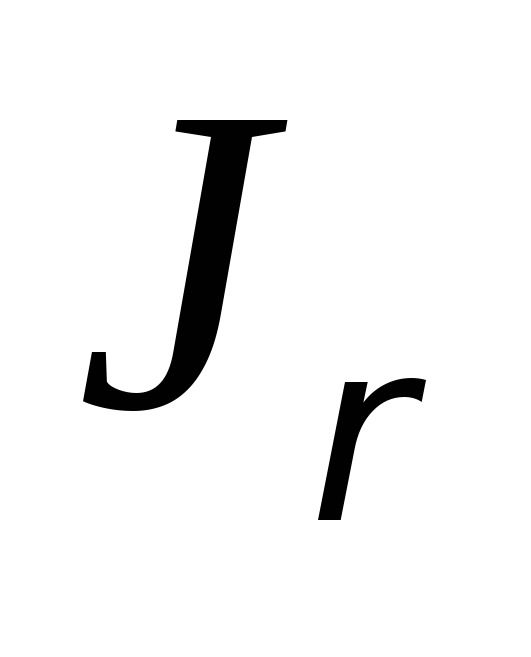 —
уже знакомый нам полярный момент инерции:
—
уже знакомый нам полярный момент инерции:
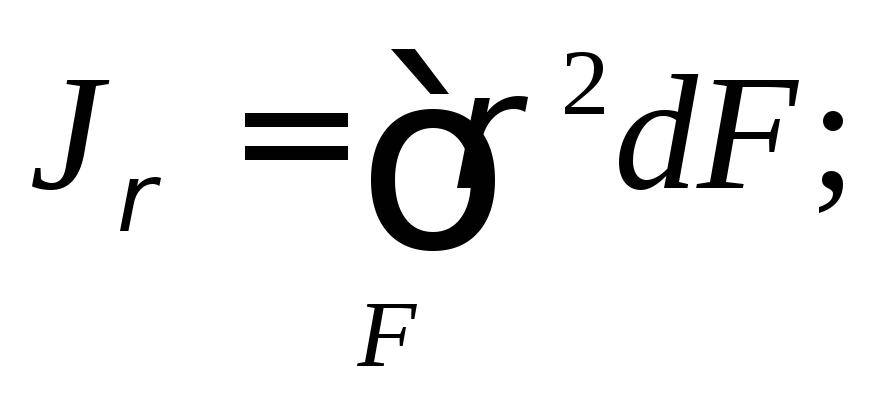
Определим осевой момент инерции круга относительно диаметра.
Так
как в силу симметрии  но, как известно,
но, как известно,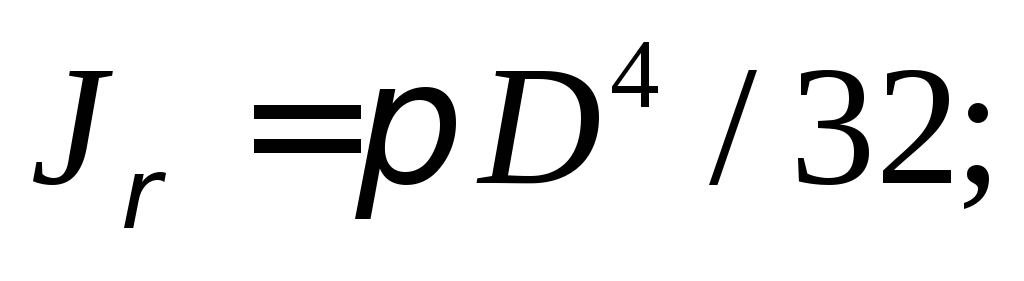
Следовательно, для круга
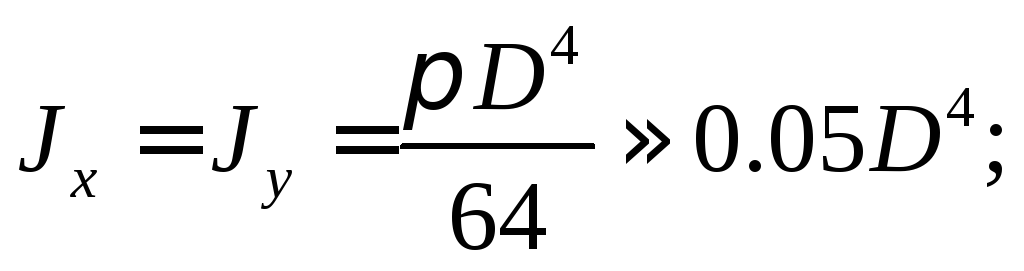
С
изменением угла поворота осей  значения моментов
значения моментов 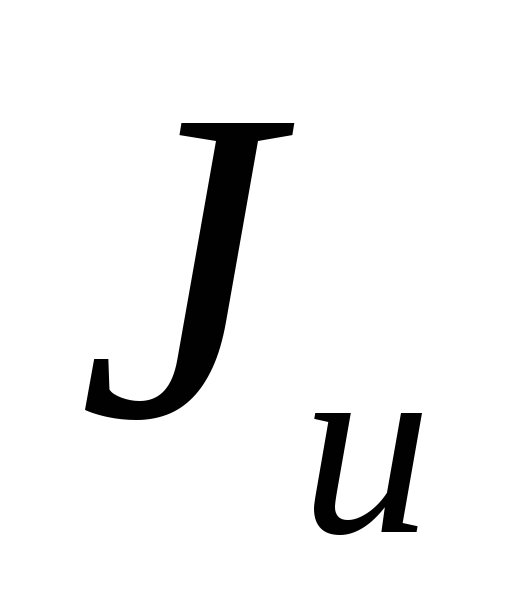 и
и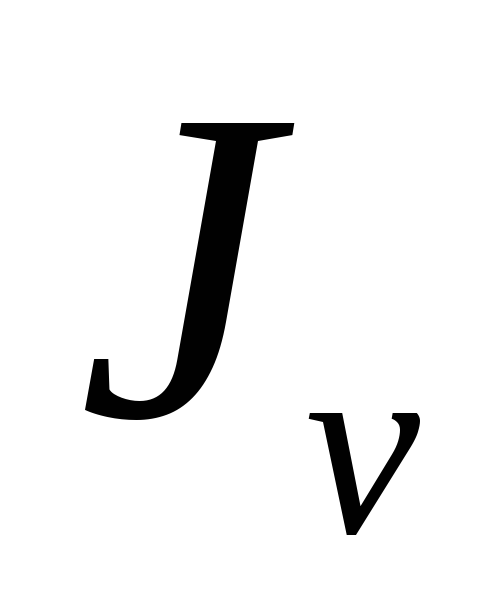 меняются, но сумма остается неизменной.
Следовательно существует такое значение
меняются, но сумма остается неизменной.
Следовательно существует такое значение ,
при котором один из моментов инерции
достигает своего максимального значения,
в то время как другой момент принимает
минимальное значение. Дифференцируя
выражение
,
при котором один из моментов инерции
достигает своего максимального значения,
в то время как другой момент принимает
минимальное значение. Дифференцируя
выражение по углу
по углу и приравнивая производную к нулю, находим
и приравнивая производную к нулю, находим
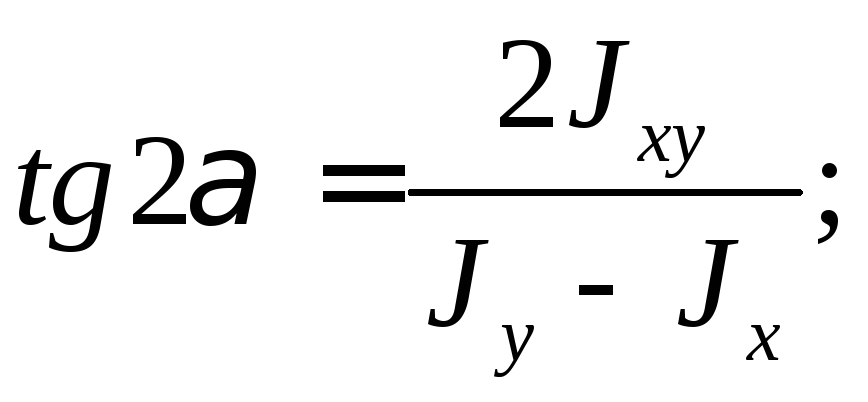 (19)
(19)
При
этом значении угла  один из осевых моментов будет наибольшим,
а другой — наименьшим. Одновременно
центробежный момент инерции
один из осевых моментов будет наибольшим,
а другой — наименьшим. Одновременно
центробежный момент инерции  обращается в нуль, что можно легко
проверить, приравнивая к нулю формулу
для центробежного момента инерции
обращается в нуль, что можно легко
проверить, приравнивая к нулю формулу
для центробежного момента инерции  .
.
Оси,
относительно которых центробежный
момент инерции равен нулю, а осевые
моменты принимают экстремальные
значения, называются главнымиосями.Если они к тому же являются центральными
(точка начала координат совпадает с
центром тяжести сечения), то тогда они
называютсяглавными центральными
осями (u; v).Осевые моменты инерции относительно
главных осей называютсяглавными
моментами инерции —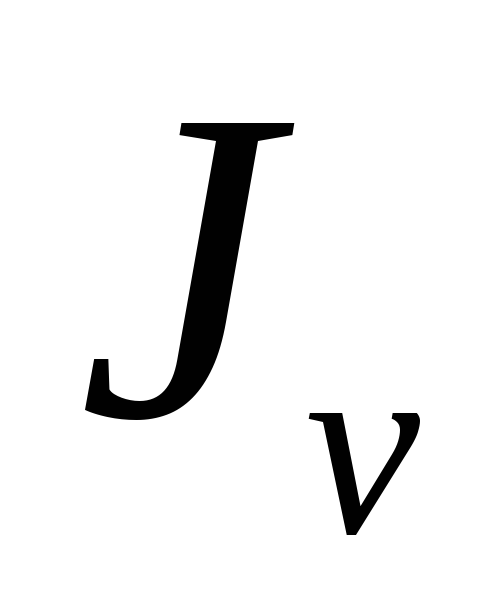 и
и 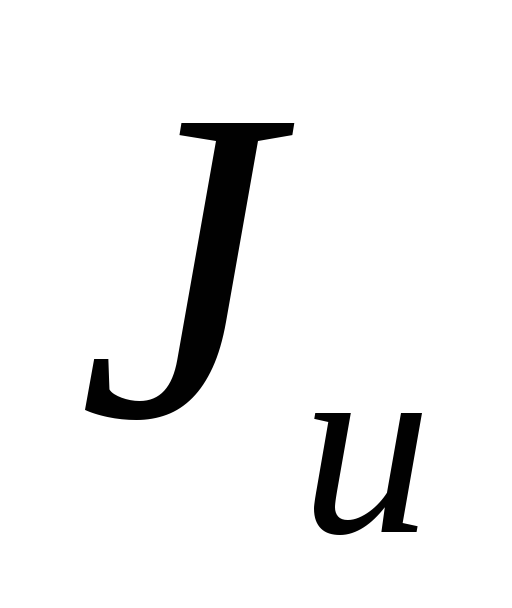
И их значение определяется по следующей формуле:
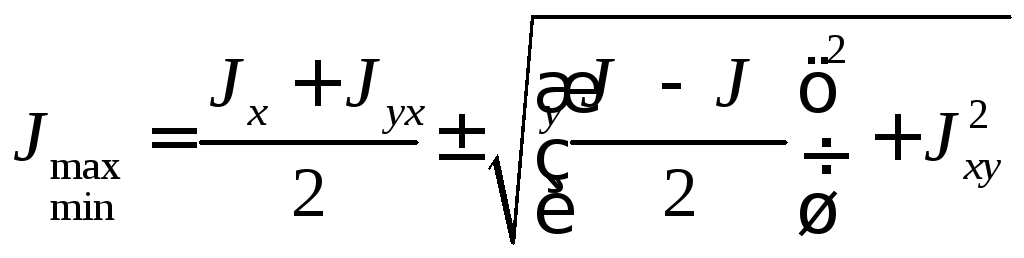 (20)
(20)
Знак плюс соответствует максимальному моменту инерции, знак минус — минимальному.
Существует ещё одна геометрическая характеристика – радиус инерциисечения.Эта величина часто используется в теоретических выводах и практических расчётах.
Радиусом
инерции сечения относительно некоторой
оси, например 0x,называется величина 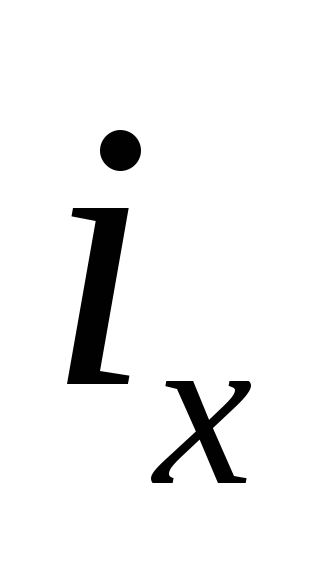 ,определяемая из равенства
,определяемая из равенства
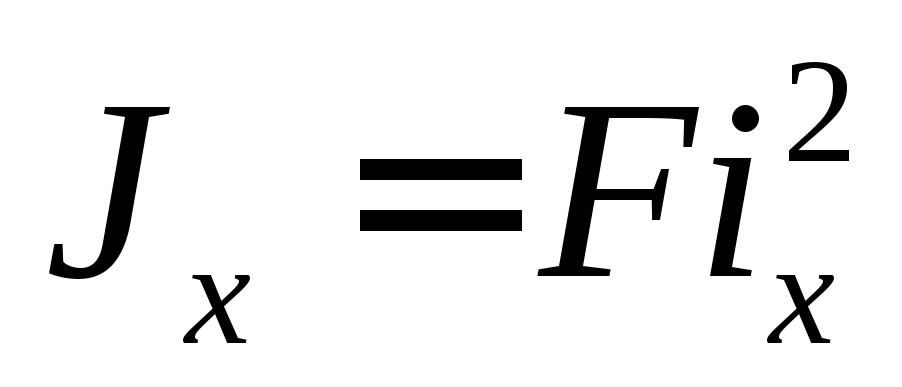 (21)
(21)
F– площадь поперечного сечения,
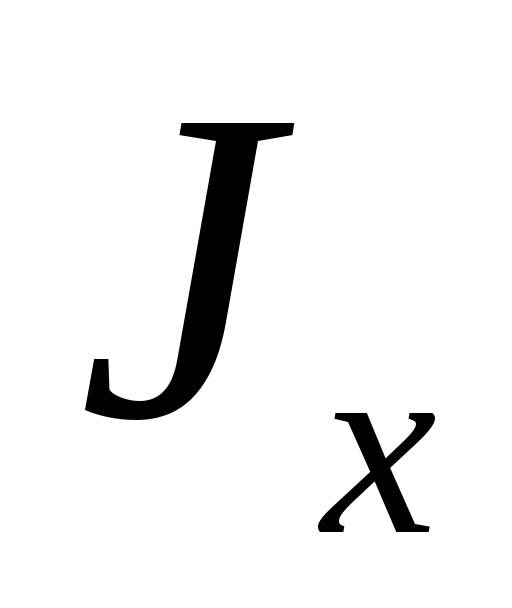 — осевой момент инерции сечения,
— осевой момент инерции сечения,
Из определения следует, что радиус инерции равен расстоянию от оси 0хдо той точки, в которой следует сосредоточить (условно) площадь сеченияF, чтобы момент инерции одной этой точки был равен моменту инерции всего сечения. Зная момент инерции сечения и его площадь, можно найти радиус инерции относительно оси 0х :
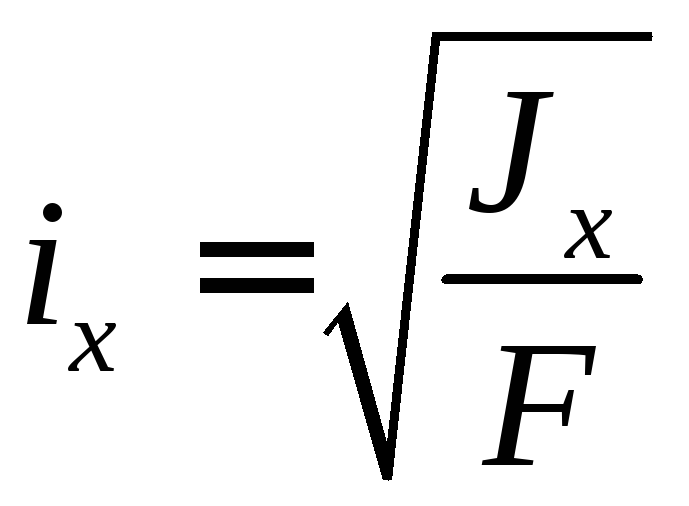 (22)
(22)
Радиусы инерции, соответствующие главным осям, называютсяглавными радиусами инерциии определяются по формулам
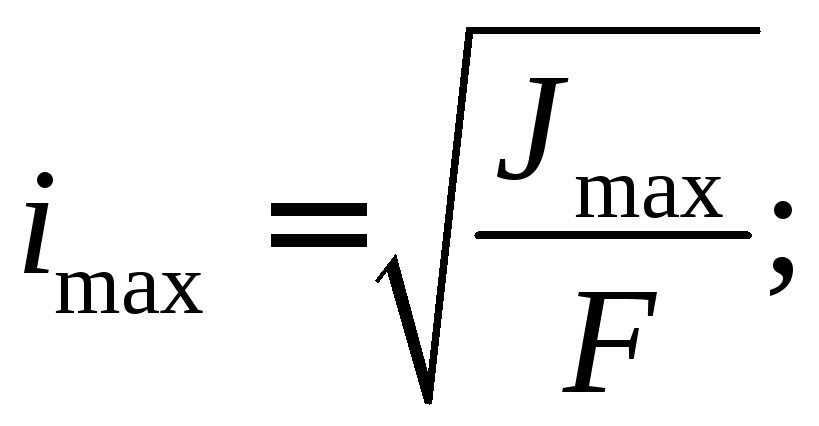
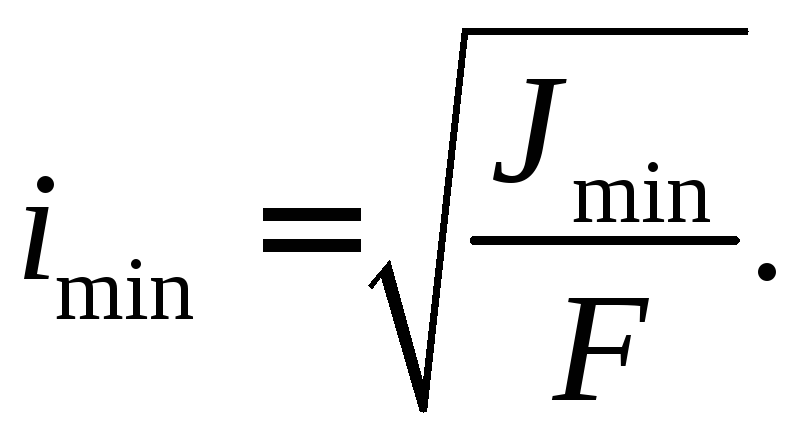 (23)
(23)
Лекция 3. Кручение стержней круглого поперечного сечения.
Геометрические характеристики плоских сечений — Лекции и примеры решения задач технической механики
При расчете элементов конструкций на прочность, жесткость и устойчивость приходится кроме общеизвестной характеристики – площади поперечного сечения A, оперировать такими геометрическими характеристиками сечений, как статический момент площади, момент инерции, момент сопротивления, радиус инерции.
Статический момент площади
Интегралы вида:
называются статическими моментами площади сечения A относительно осей X и Y соответственно.
В тех случаях, когда сечение может быть разделено на простейшие фигуры площади Ai и координаты центров тяжести xi и yi которых известны, статические моменты площади сложной фигуры определяются через суммирование
Статические моменты площади имеют размерность [м3] и могут принимать любые числовые значения. Для осей XC, YC, проходящих через центр тяжести сечения C (центральные оси), статические моменты равны нулю:
Координаты центров тяжести сечения определяются относительно так называемых вспомогательных осей по формулам:
Если сечение имеет ось симметрии, то центр тяжести находится на этой оси и его положение определяется одной координатой.
При наличии двух и более осей симметрии центр тяжести совпадает с точкой пересечения этих осей.
Моменты инерции
Моментами инерции площади сечения называют интегралы вида:
где:
Ix, Iy — осевые моменты инерции площади сечения относительно осей OX, OY соответственно;
Ixy — центробежный момент инерции;
Iρ — полярный момент инерции.
Размерность момента инерции [м4], Ix, Iy, I ρ всегда положительны, Ixy может принимать любые значения, при этом, если хотя бы одна из осей является осью симметрии, Ixy=0.
Зависимости между моментами инерции относительно параллельных осей выражаются формулами:
где a, b – расстояния между осями X, XC и Y, YC.
Оси, относительно которых Ixy=0, называют главными, а осевые моменты инерции относительно них – главными моментами инерции.
Главные оси, проходящие через центр тяжести сечения, называют главными центральными осями, а соответствующие им моменты инерции – главными центральными моментами инерции.
Главные оси характерны тем, что их моменты инерции принимают экстремальные значения (Imax, Imin).
Момент инерции сложного сечения относительно какой-либо оси находится суммированием моментов инерции составляющих его частей относительно той же оси:
Радиусы инерции
Величины
называют радиусами инерции сечения относительно осей OX и OY соответственно.
Эллипс, построенный в главных осях, с полуосями, равными главным радиусам инерции
называют эллипсом инерции.
Лекции по сопромату >
Примеры решения задач >
Полярный момент инерции — это… Что такое Полярный момент инерции?
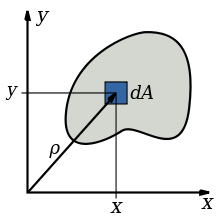 Схема к вычислению полярного момента инерции
Схема к вычислению полярного момента инерцииПоля́рный моме́нт ине́рции — интегральная сумма произведений площадей элементарных площадок dA на квадрат расстояния их от полюса — ρ2 (в полярной системе координат), взятая по всей площади сечения. То есть:
Эта величина используется для прогнозирования способности объекта оказывать сопротивление кручению. Она имеет размерность единиц длины в четвёртой степени (м4, cм4) и может быть лишь положительной.
Для площади сечения, имеющей форму круга радиусом r полярный момент инерции равен:
Если совместить начало декартовой прямоугольной системы координат 0 с полюсом полярной системы (см. рис.), то
потому что .
Применение
Полярный момент инерции используется в формулах, которые описывают зависимость между касательными напряжениями и крутящим моментом, который их вызывает. Касательное напряжение:
где
- — крутящий момент,
- — расстояние от оси кручения
- — полярный момент инерции.
Полярный момент инерции для некоторых случаев
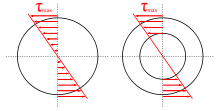 Распределение касательных напряжений при кручении
Распределение касательных напряжений при крученииДля круглого сплошного сечения:
где D — диаметр круга.
Для кольцевого сечения (полый вал):
где
- D — внешний диаметр кольца,
- d — внутренний диаметр кольца.
См. также
Литература
- Феодосьев В.И. Сопротивление материалов. Изд. 10-е, перераб. и доп. — М.: МГТУ им. Н. Э. Баумана, 1999 год. Рецензенты академик РАН Образцов И. Ф. и д. т. н профессор Чирков И. П.
Осевой момент инерции, теория и примеры
Определение и общие понятия осевого момента инерции
ОПРЕДЕЛЕНИЕ Осевым (или экваториальным) моментом инерции сечения относительно оси называется величина, которую определяют как:
Выражение (1) обозначает, для вычисления осевого момента инерции берется по всей площади S сумма произведений бесконечно малых площадок () умноженных на квадраты расстояний от них до оси вращения:
Сумма осевых моментов инерции сечения относительно взаимно перпендикулярных осей (например, относительно осей X и Y в декартовой системе координат) дают полярный момент инерции () относительно точки пересечения этих осей:
ОПРЕДЕЛЕНИЕ
Полярным моментом инерции называют момент инерции сечением по отношению к некоторой точке.
Осевые моменты инерции всегда больше нуля, так как в их определениях (1) под знаком интеграла стоят величина площади элементарной площадки (), всегда положительная и квадрат расстояния от этой площадки до оси.
Если мы имеем дело с сечением сложной формы, то часто при расчетах используют то, что осевой момент инерции сложного сечения по отношению к оси равен сумме осевых моментов инерции частей этого сечения относительно той же оси. Однако следует помнить, что нельзя суммировать моменты инерции, которые найдены относительно разных осей и точек.
Осевой момент инерции относительно оси проходящей через центр тяжести сечения имеет наименьшее значение из всех моментов относительно параллельных с ней осей. Момент инерции относительно любой оси () при условии ее параллельности с осью, проходящей через центр тяжести равен:
где – момент инерции сечения относительно оси проходящей через центр тяжести сечения; – площадь сечения; – расстояние между осями.
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
Радиус инерции сечения — Википедия
Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 29 апреля 2013; проверки требуют 6 правок. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 29 апреля 2013; проверки требуют 6 правок.Радиус инерции сечения — геометрическая характеристика сечения, связывающая геометрический момент инерции фигуры J{\displaystyle J} с её площадью F{\displaystyle F} следующими формулами:
- Jy=iy2F{\displaystyle J_{y}=i_{y}^{2}F}
- Jz=iz2F{\displaystyle J_{z}=i_{z}^{2}F}
Отсюда, формула радиуса инерции:
- iy=JyF{\displaystyle i_{y}={\sqrt[{}]{\frac {J_{y}}{F}}}}
- iz=JzF{\displaystyle i_{z}={\sqrt[{}]{\frac {J_{z}}{F}}}}
Таким образом, радиус инерции отражает отношение жесткости стержня на изгиб (EJ{\displaystyle EJ}) и на сжатие (EF{\displaystyle EF}).
В сопротивлении стержней продольному изгибу (потере устойчивости прямолинейной формы при сжатии) основную роль играет гибкость стержня, а значит и величина наименьшего радиуса инерции сечения. Таким образом, большую экономичность будут иметь те сечения, у которых наименьший радиус инерции равен наибольшему, то есть сечения у которых все центральные моменты инерции равны, а эллипс инерции обратился бы в круг.
Единица измерения СИ — м. В строительной литературе чаще записывается в миллиметрах или сантиметрах, ввиду небольшой величины на практике.
Если моменты инерции Jy{\displaystyle J_{y}} и Jz{\displaystyle J_{z}} являются главными моментами инерции, то iy{\displaystyle i_{y}} и iz{\displaystyle i_{z}} — также являются главными радиусами инерции.
В некоторой литературе радиус инерции обозначается просто r{\displaystyle r}.
- Беляев Н. М. Сопротивление материалов. — 15-е изд., перераб. — М.: Наука, 1976. — 607 с. — 200 000 экз.

