Трение качения — природа явления и его суть. Устойчивость от опрокидывания.



Трение качения

Трением качения называется трение движения, при котором скорости соприкасающихся тел в точках касания одинаковы по значению и направлению.

Если движение двух соприкасающихся тел происходит при одновременном качении и скольжении, то в этом случае возникает трение качения с проскальзыванием.

Рассмотрим качение без скольжения цилиндра весом G и радиусом r по горизонтальной опорной плоскости (см. рисунок 1).
В результате действия силы G произойдет деформация цилиндра и опорной плоскости в месте их соприкосновения.
Если сила P не действует, то сила G будет уравновешиваться реакцией R опорной плоскости и цилиндр будет находиться в покое (реакция R будет вертикальна).
Если к цилиндру приложить небольшую силу Р, то он по-прежнему будет находиться в покое. При этом произойдет перераспределение давлений на опорную поверхность и полная реакция R пройдет через некоторую точку А и через точку О (согласно теореме о равновесии трех непараллельных сил).

При каком-то критическом значении силы Р цилиндр придет в движение и будет равномерно перекатываться по опорной плоскости, а точка А займет при этом крайнее правое положение.
Отсюда видно, что трение качения в состоянии покоя может изменяться от нуля до какого-то максимального значения, причем максимальным оно будет в момент начала движения.

Обозначим k максимальное значение плеча силы G относительно точки А. Тогда в случае равномерного перекатывания цилиндра (т. е. равновесия):

ΣM_А = 0      или      – Pr + Gh = 0,

причем плечо силы Р вследствие незначительности деформации тел считаем равным радиусу цилиндра r (сила Р – горизонтальная). Из последнего равенства определим силу, необходимую для равномерного качения цилиндра:

Р = kG/r

Максимальное значение плеча k называется коэффициентом трения качения; он имеет размерность длины и выражается в сантиметрах или миллиметрах.

Из полученной формулы видно, что усилие, необходимое для перекатывания цилиндрического катка, прямо пропорционально его весу G и обратно пропорционально радиусу r катка. Из этого следует, что каток, имеющий бóльший диаметр, легче перекатывать.

Коэффициент трения качения определяется опытным путем, его значения для различных условий приводятся в справочниках. Ниже приведены ориентировочные значения коэффициента трения качения k для катка по плоскости (см):

• Мягкая сталь по мягкой стали……………………….0,005
• Закаленная сталь по закаленной стали…………..0,001
• Чугун по чугуну…………………………………………0,005
• Дерево по стали………………………………..0,03…0,04
• Дерево по дереву……………………………..0,05…0,08
• Резиновая шина по шоссе………………………….0,24

Коэффициент трения качения практически не зависит от скорости движения тела.

В ряде случаев при изучении трения качения активные и реактивные силы, действующие на каток, удобно представлять в ином виде (см. рисунок 2а, б).

Разложим полную реакцию R опорной поверхности на составляющие N и F_тр, тогда:

R = N + F_тр,

где F_тр – сила трения качения; N — реакция, нормальная к недеформированной опорной плоскости.

Составим три уравнения равновесия катка:

ΣX = 0;    P – F_тр = 0;
ΣY = 0;    N – G = 0;
ΣM_А = 0;     — Pr + Gk = 0.

Из этих уравнений имеем:

P = F_тр;    N = G;    Pr = Gk.

Введем обозначения Pr = M,    Gk = M_тр,    где М – момент трения качения, М_тр – момент трения.

Возможны следующие частные случаи качения цилиндрического катка:

• М ≥ М_тр, но Р < F_тр – имеет место только качение;
• М < М_тр, но Р > F_тр – имеет место только скольжение;
• М > М_тр, но Р > F_тр – качение с проскальзыванием;
• М < М_тр , но Р < F_тр – каток находится в состоянии покоя.

Трение качения в большинстве случаев меньше трения скольжения, поэтому вместо подшипников скольжения широко применяют шариковые, роликовые или другие подшипники качения, которые, несмотря на более высокую стоимость, дают значительный выигрыш в экономии энергии из-за уменьшения потерь на трение.

***



Устойчивость против опрокидывания

Рассмотрим твердое тело весом G, опирающееся на плоскость и способное опрокидываться вокруг какого-нибудь ребра под действием горизонтальной силы Р (см. рисунок 3).

Допустим, что силы Р и G лежат в одной плоскости, пересекающейся с ребром в точке А.
В момент начала опрокидывания на тело будут действовать также нормальная реакция N_А и сила трения F_тр, приложенные в точке А, причем в случае равновесия системы всех четырех сил можно записать два уравнения равновесия:

ΣY = 0;    N_А – G = 0;    ΣX = 0;    F_тр – P = 0,  откуда   P = F_тр.

Таким образом, в момент начала опрокидывания через ребро А на рассматриваемое тело действует пара сил (Р,F

тр), стремящихся опрокинуть тело, и пара сил (G,N_А), противодействующих опрокидыванию.

Очевидно, что опрокидывание не произойдет, если М(G,N_А) > М(Р,F_тр),    или    Gb > Pa.

Произведение Gb равно моменту силы G относительно точки А и называется моментом устойчивости.
Момент силы Р относительно той же точки, равный произведению Pa, называется опрокидывающим моментом.

Условие устойчивости против опрокидывания можно записать в виде неравенства:

М_уст > М_опр

Это выражение можно сформулировать следующим образом: для устойчивости твердого тела против опрокидывания необходимо и достаточно, чтобы момент устойчивости был больше опрокидывающего момента.

Если на тело действуют несколько сил, стремящихся его опрокинуть, то опрокидывающий момент равен сумме моментов этих сил относительно точки, вокруг которой может произойти опрокидывание. То же относится и к моменту устойчивости – если опрокидыванию тела препятствуют несколько сил, то момент устойчивости будет равен сумме моментов этих сил относительно точки (полюса) опрокидывания.

Отношение момента устойчивости к опрокидывающему моменту называется коэффициентом устойчивости:

М_уст/М_опр = k_уст.

Очевидно, что в сооружениях коэффициент устойчивости k_уст должен быть больше единицы.

Расчет на устойчивость особенно важен для высоких сооружений, таких, как дымовые трубы, высотные здания, мачты, краны и т. д. Подобные инженерные конструкции, как правило, подвержены горизонтальным опрокидывающим силам, вызываемым ветрами (ветровые нагрузки), что необходимо учитывать при расчетах подобных сооружений на устойчивость против опрокидывания.

Следует отметить, что в случае, когда Р > F_тр (опрокидывающая сила больше силы трения), а опрокидывающий момент меньше момента устойчивости М_опр < М_уст

, тело будет скользить по опорной плоскости, если, конечно, конструкция опоры тела допускает такое движение.

***

Центр тяжести



Главная страница

• Страничка абитуриента

Дистанционное образование

• Группа ТО-81
• Группа М-81
• Группа ТО-71
  

Специальности

• Ветеринария
• Механизация сельского хозяйства
• Коммерция
• Техническое обслуживание и ремонт автотранспорта

Учебные дисциплины

• Инженерная графика
• МДК.01.01. «Устройство автомобилей»
•    Карта раздела
•       Общее устройство автомобиля
•       Автомобильный двигатель
•       Трансмиссия автомобиля
•       Рулевое управление
•       Тормозная система
•       Подвеска
•       Колеса
•       Кузов
•       Электрооборудование автомобиля
•       Основы теории автомобиля
•       Основы технической диагностики
• Основы гидравлики и теплотехники
• Метрология и стандартизация
• Сельскохозяйственные машины
• Основы агрономии
• Перевозка опасных грузов
• Материаловедение
• Менеджмент
• Техническая механика
• Советы дипломнику

Олимпиады и тесты

• «Инженерная графика»
• «Техническая механика»
• «Двигатель и его системы»
• «Шасси автомобиля»
• «Электрооборудование автомобиля»

Способ определения коэффициентов трения качения и сопротивления качению

Изобретение относится к технике и способам определения параметров трения, а именно к способам определения коэффициентов трения качения. Технический результат состоит в применении устройств видеосъёмки для отображения и фиксации контактной линии, являющейся пересечением исследуемого колеса транспортного средства с дорожным покрытием, в аналоговой или цифровой форме для определения коэффициентов трения качения и сопротивления качению. Поставленная цель решается за счет того, что в способе, включающем операцию размещения испытуемого пневматического колеса на горизонтальном твердом покрытии, а также операцию фиксации деформации пневматической части колеса, эта операция выполняется с помощью записи видеокамерой картины деформации зоны контакта пневматической части колеса и твердого покрытия, возникающей при придании колесу движений взад-вперед, после чего заснятый на носитель процесс с помощью компьютера разбивают на кадры с дискретностью 0,04 с или меньше, интересующие кадры вызывают на экран дисплея, увеличивают изображение до нужных размеров и с помощью координатной сетки на экране определяют величину и направление горизонтального смещения центра контактной площадки пневматической части колеса с твердым покрытием в плоскости, параллельной его движению, относительно точки пересечения перпендикуляра, проведенного через ось подвеса колеса к твердой поверхности, т.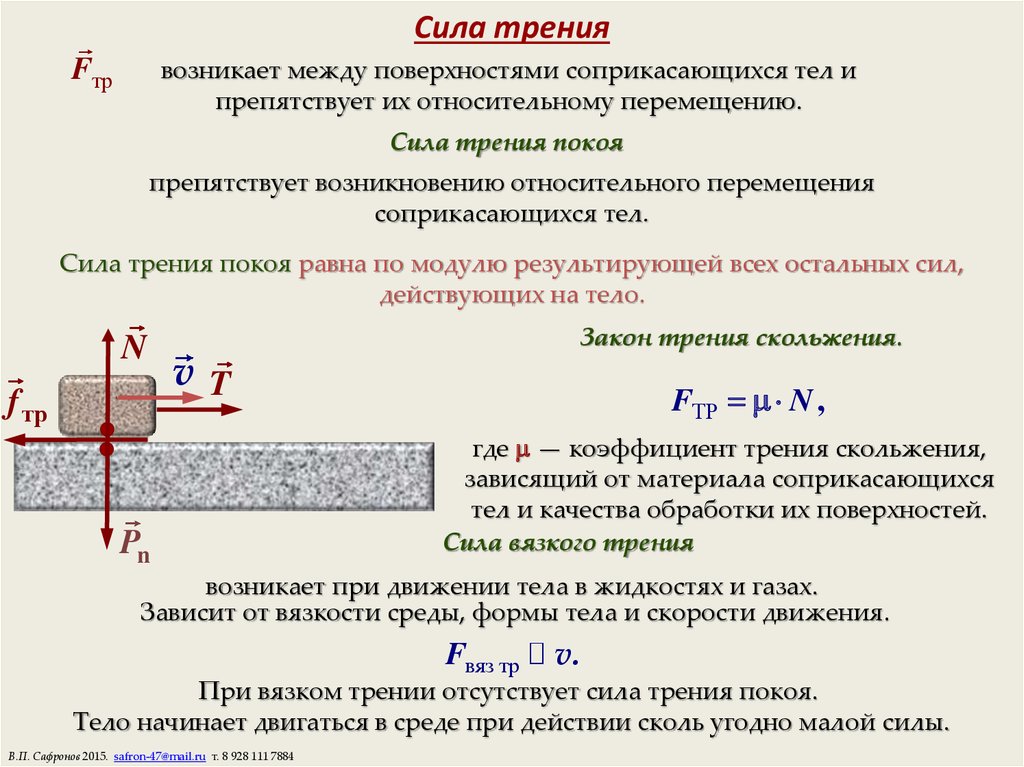 е. величину предварительного смещения Δх, при этом с учетом масштаба изображения, найденного путем сопоставления размера известного элемента транспортного средства в натуре х_H и размера этого же элемента на экране дисплея компьютера х, равного отношению х_H/х, определяют величину предварительного смещения в натуре по формуле , которая является коэффициентом трения качения, после этого определяют коэффициент сопротивления качению К_C по формуле , где R — радиус колеса, и эти операции повторяют для всех кадров съемки, обеспечивая определение коэффициентов Δ_H и К_C на всех стадиях движения и сопротивления колеса. 2 ил.

 

Изобретение относится к технике и способам определения параметров трения, а именно к способам определения коэффициентов трения качения, причем не только в отдельных телах качения — шарах, катках, цилиндрах, но и, в первую очередь, в колесах в собранных функционирующих автомобилях, тракторах и других колесных транспортных средствах. Оно может быть использовано для бесконтактного дистанционного определения коэффициентов трения качения не только у малоподвижных тел качения, но и в скоростных транспортных средствах в процессе их движений. Другим достоинством предлагаемого изобретения является упрощение состава технических средств и методики получения и обработки результатов измерений. Известен способ определения коэффициентов трения и скольжения (А.С. СССР №405056 «Способ определения коэффициентов трения». МПК G01N 19/02. Автор Д.М.Толстой. Бюл. №4, 1973), согласно которому образец, выполненный в виде тела вращения, например шара, жестко закрепляют в физическом маятнике, помещают на наклонную плоскость с переменным углом наклона и измеряют угол наклона маятника и угол наклона плоскости и определяют указанные выше коэффициенты в функции этих углов, маятниковости и радиуса тела вращения. Недостатком способа является то, что коэффициенты трения качения и скольжения определяются для малых углов наклона наклонной плоскости маятника с шаром от исходного положения, т. е. в статике. После начала скольжения коэффициенты практически не могут быть определены из-за того, что в этом режиме качение отсутствует, а коэффициент трения скольжения динамический отличается от коэффициента скольжения трогания.

Указанный недостаток устранен в изобретении А.С. СССР №1434334 «Способ определения коэффициента трения». МПК G01N 19/02. Автор А.П.Рамзаев. Бюл. №40, 1988. Эффект достигнут за счет того, что испытуемое тело вращения закрепляют, как и в маятнике по предыдущему изобретению, помещают на наклонную плоскость для придания ему движения. При скатывании тела измеряют с помощью двух акселерометров линейные ускорения двух точек физического маятника, связанного с испытуемым телом качения. Результаты измерения линейных ускорений учитывают в виде углового ускорения в формуле при расчете динамического коэффициента трения качения. Недостатком изобретения является сложность реализации способа — нужны наклонная плоскость с изменяемым углом наклона, два акселерометра, физический маятник с устройством их крепления на нем, а кроме того, знание момента инерции тел, входящего в формулу коэффициента трения, устройство для измерения угла наклона маятника по отношению к вертикали.

Известно устройство для определения коэффициента сцепления пневматических колес (А.С. СССР №976778 «Устройство для определения коэффициента сцепления пневматических колес с дорожным покрытием». МПК G01N 19/02. Авторы Печерский М.А. и др. Бюл. №4, 1981). В этом изобретении отражено не только устройство, но и способ измерения коэффициента трения сцепления в пневматическом колесе. Способ состоит в том, что входящее в состав устройства измерительное колесо приводится во вращение благодаря его связи посредством трансмиссии и верхнего плеча двуплечего рычага с неведущими колесами транспортного средства. Возникающая при этом сила трения в контакте измерительного колеса с поверхностью дорожного покрытия регистрируется с помощью динамометрического элемента, расположенного на измерительной тяге. Благодаря двуплечему рычагу, установленному на оси колеса под углом φ к горизонту, где φ=π/2-arctgµ_k (µ_k — коэффициент сопротивления качению, определенный заранее), нагружатель воздействует на ось измерительного колеса в вертикальном направлении, через коэффициент сцепления в горизонтальном направлении возникает сила, равная сопротивлению качения его по поверхности дорожного покрытия. В результате динамометрический элемент регистрирует лишь силу трения скольжения между измерительным колесом и поверхностью дорожного покрытия. По величине этой силы и нормальной нагрузке с учетом силы от нагружателя определяют коэффициент сцепления между измерительным колесом и дорожным покрытием.

Недостатком описанного способа является использование сложной конструкции — специального измерительного колеса с двуплечим рычагом, имеющим возможность поворачиваться вокруг оси подвеса. Верхний конец рычага связан через трансмиссию с неведущими колесами транспортного средства, с другим концом рычага связана измерительная тяга с динамометром. Все это делает устройство дорогим и сложным в эксплуатации. Не сказано, как регистрировать показания динамометра. Визуально — сложно, а если электрическим путем, это требует применения измерительных средств. К тому же коэффициент µ_k в процессе эксплуатации меняется, а т.к. угол φ=const, то это приводит к увеличению погрешности. Не сказано, как изменять нагрузку на пружину. Много неясного в применении способа и технических устройств, снижающих его точность и удобство пользования. В книге. Крагельский И.В. и др. Основы расчетов на трение и износ. — М.: Машиностроение. 1977. — 528 с. на с.259-263 приведены данные по определению коэффициентов сопротивления качению. Так, на рис.7, для бронзы (прямые 2) при N=3 кгс имеем F_тркач=10 гс, т.е. .

На стр.263, рис.10, коэффициенты сопротивления качению цилиндров по резине, отмеченные линиями 1, 2, 3, лежат в пределах µ_k=(0,005…0,025) безразм. ед. Эти данные свидетельствуют о том, что угол µ_k мал (tgµ_k=T/N, Т — сила трения качения; N — нормальная нагрузка). Самый большой коэффициент по рис.10 µ_k — 0,025 соответствует углу µ_k=0,025 рад =1,44 угл. град =85 угл. мин. По результатам экспериментов, проведенных автором для легкового автомобиля, величина µ_k сопоставима со значением 1,44 угл. град. Данные результаты свидетельствуют о том, что угол µ_k мал и что при увеличении нагрузки по фиг. 2, с.259 (Крагельский И.В. и др. Основы расчетов на трение и износ. — М.: Машиностроение. 1977. — 528 с.) он будет увеличиваться, что снизит точность измерений. К тому же при смене знака скорости автомобиля у угла µ_k должен смениться знак, чего не предусмотрено. Другой недостаток способа и устройства по [А.С. СССР №976778 «Устройство для определения коэффициента сцепления пневматических колес с дорожным покрытием». МПК G01N 19/02. Авторы Печерский М.А. и др. Бюл. №4, 1981.] — это то, что измерения производятся в измерительном колесе, а коэффициент сцепления нужно определять в колесах автомобиля. Это еще один источник погрешности. Кстати, в этом изобретении коэффициент сцепления в режиме качения (скольжения) совпадает с коэффициентом сопротивления качению.

Данное изобретение принято за прототип. 3адача, решаемая предлагаемым изобретением, — упрощение способа и технических средств, повышение точности и расширение функциональных возможностей.

Предлагаемое изобретение гораздо проще по способу определения коэффициента трения качения и коэффициента сопротивления качению. Соответственно, для его технической реализации требуется несопоставимо меньший набор технических средств, не требуется усложнять конструкцию транспортного средства, ибо не требуются дополнительные измерения по отношению к параметрам исследуемого пневматического колеса. При этом измерения могут быть произведены в любых колесах транспортного средства, интересующих исследователей, при любом знаке и величине скорости.

Технический результат изобретения состоит в применении устройств видеосъемки для отображения и фиксации контактной линии, являющейся пересечением исследуемого колеса транспортного средства с дорожным покрытием, в аналоговой или цифровой форме. Этот результат с аналогового носителя видеокамеры при ее подключении переносят в компьютер с помощью редактора «Windows Movie Maker». С помощью, например, компьютерного редактора видеоизображений «Virtual Dub-MPEG2» производят разбиение всего временного процесса съемки на кадры. Затем изображение каждого кадра увеличивают и в нем в нужных элементах производят необходимые измерения. После этого для последовательных моментов времени с шагом дискретности следования кадров получают последовательность значений коэффициента трения качения.

Поставленная задача решается за счет того, что в способе определения коэффициентов трения качения и сопротивления качению, включающем операцию размещения испытуемого пневматического колеса на горизонтальном твердом дорожном покрытии, а также операцию фиксации деформации пневматической части колеса, эта операция выполняется с помощью записи видеокамерой картины деформации зоны контакта пневматической части колеса и твердого дорожного покрытия, возникающей при придании колесу движений взад-вперед, после чего заснятый на носитель процесс с помощью компьютера разбивают на кадры с дискретностью 0,04 с или меньше, интересующие кадры вызывают на экран дисплея, увеличивают изображение до нужных размеров и с помощью координатной сетки на экране определяют величину и направление горизонтального смещения центра контактной площадки пневматической части колеса с твердым покрытием в плоскости, параллельной его движению, относительно точки пересечения перпендикуляра, проведенного через ось подвеса колеса к твердой поверхности, т. е. величину предварительного смещения Δх, при этом с учетом масштаба изображения, найденного путем сопоставления размера известного элемента транспортного средства в натуре х_H и размера этого же элемента на экране дисплея компьютера х, равного отношению х_H/х, определяют величину предварительного смещения в натуре по формуле

,

которая является коэффициентом трения качения, после этого определяют коэффициент сопротивления качению К_C по формуле

,

где R — радиус колеса,

и эти операции повторяют для всех кадров съемки, обеспечивая определение коэффициентов Δ_H и К_C на всех стадиях движения колеса.

На фиг.1 представлена расчетная схема для определения коэффициентов трения качения и сопротивления качению по упругой деформации пневматической части колеса в горизонтальном направлении в плоскости, параллельной плоскости его движения. На фиг.2 изображен снимок фрагмента машины с испытуемым колесом при испытаниях.

Суть способа раскрывается описанием следующих операций.

1. Испытуемое транспортное средство размещают на горизонтальной площадке с твердым покрытием. Около испытуемого колеса на кузове помещают отсчетную шкалу.

2. Сбоку от него на штативе размещают видеокамеру объективом против испытуемого колеса и устанавливают в кадре размер изображения. Водитель совершает с транспортным средством движения вперед-назад, при которых испытуемое колесо не выходит за пределы кадра видеокамеры.

3. На твердом покрытии на пневматической части колеса наносят одна против другой пометки, обозначающие нижнюю среднюю точку пневматической части колеса.

4. После этого включают видеозаписывающее устройство на запись съемки транспортного средства. Транспортному средству задают движения вперед-назад на расстояния, при которых линия пересечения пневматической части испытуемого колеса и твердого покрытия не выходит за пределы кадра изображения видеокамеры.

5. Останавливают автомобиль и выключают процесс записи. Носитель записи, например лазерный диск, помещают в компьютер, в котором в соответствии с редактором «Virtual Dub-MPEG2» производят разбиение заснятого процесса на кадры. При обычной съемке каждый кадр снимается через время с дискретностью 0,04 с, при скоростной — с меньшим временем дискретности. Дискретность 0.04 с определена в киносъемках для обеспечения при движении кадров восприятия глазами непрерывного движения изображения. Это используется и в видеотехнике. Так меньшую величину дискретности можно применять при съемке движения автомобиля со скоросью больше 1.5 м/с, при которой сделан снимок фиг.2. На нем уже заметна некоторая размытость изображения, не исказившая результата. Отметим, что, например,в видеокамере «Panasonic» предусмотрена дискретность съемки 0.01 с.

6. В соответствии с программой просмотра «Windows» на экране компьютера устанавливают нужный кадр с нужным его увеличением и производят измерения в колесе согласно схеме фиг.1 либо с помощью пикселей по редактору «Virtual Dub-MPEG2», либо с помощью мерной линейки. В этом случае на экране помещают координатную сетку соответствующих размеров, нанесенную на прозрачную пленку.

7. На экране компьютера проводят перпендикуляр OO’ к поверхности (фиг.1). Измеряют части O’B и O’А хорды AB, контактной площадки колеса, сместившейся в направлении движения транспортного средства на величину:

В’B=О’O₁=A’A.

Определяют разность частей O’А и O’В хорды АВ и величину предварительного смещения

O’A-O’B=2Δx;

8. Определяют масштаб изображения путем измерения размера x элемента на экране и сопоставления с известным размером x^H в натуре. Это, например, диаметр обода колеса. Определяют натуральную величину Δ_н предварительного смещения на основе пропорции:

x→x_H

Δx→Δ_H

Из этой пропорции рассчитывают величину предварительного смещения:

9. Повторяют операции 6-7 для других кадров съемки. При необходимости строят график для Δ_H для части или полной дистанции.

10. Из теории известно (Крагельский И.В. и др. Основы расчетов на трение и износ. — М: Машиностроение. 1977. — 528, с.251-252; Плотников П.К. Модель сил трения шара с предварительным смещением качения по шероховатой поверхности // ДАН РФ, 2010, том. 432, №4, с.481-485), что смещение пятна контакта Δ_н, т.е. величина предварительного смещения, есть в то же время коэффициент трения качения, т.е. Δ_H=k. Поэтому, зная нормальную нагрузку N на испытуемое колесо, определяют по формуле

момент сил трения качения в колесе. Зная радиус колеса R (фиг.1), определяют силу трения качения:

Согласно книге (Крагельский И.В. и др. Основы расчетов на трение и износ. — М: Машиностроение. 1977. — 528 с.) величина есть коэффициент сопротивления качению. Согласно А.С. СССР №976778 «Устройство для определения коэффициента сцепления пневматических колес с дорожным покрытием». МПК G01N 19/02. Авторы Печерский М.А. и др. Бюл. №4, 1981 и фиг.1 . По этой формуле рассчитывают коэффициент сопротивления качению К_C.

11. В случае, если требуется определять коэффициенты трения качения Δ_H=k и сопротивления качению К_с на большой дистанции, видеокамеру нужно закрепить на корпусе автомобиля с помощью кронштейна, направив объектив на место контакта колеса с покрытием, и повторять операции по п.4-9. При этом можно применять скоростную видеосъемку. Следует заметить, что описанный способ поддается автоматизации операций измерений, что можно произвести с помощью компьютера.

Технико-экономический эффект изобретения состоит в существенном упрощении методики и техники определения коэффициентов трения качения и сопротивления качению, в повышении точности. Т.к. способ является бесконтактным и дистанционным, опирающимся на возможности видеотехники и компьютерные технологии, это дает возможность определять параметры трения в автомобилях, тракторах и другом колесном транспорте без вмешательства в их конструкции при их движении с произвольными скоростями. Зная вес транспортного средства, приходящийся на колесо, по формулам (Крагельский И. В. и др. Основы расчетов на трение и износ. — М.: Машиностроение. 1977, с.251)

;

Δ_H=K;

определяют момент и силу трения качения, т.е. в итоге находят и . Налицо признаки упрощения процедуры, повышения точности измерений в движении, сокращения времени и экономических затрат.

Способ определения коэффициентов трения качения и сопротивления качению, включающий операции размещения испытуемого пневматического колеса на горизонтальном твердом покрытии, а также фиксации деформации пневматической части колеса, отличающийся тем, что колесу придают движения взад-вперед и с помощью видеокамеры фиксируют на носитель картину деформаций зоны контакта пневматической части колеса и твердого покрытия, после чего заснятый на носитель процесс с помощью компьютера разбивают на кадры, следующие с временной дискретностью 0,04 с или меньше, интересующие кадры вызывают на экран дисплея, увеличивают изображение до нужных размеров и с помощью координатной сетки на экране определяют величину и направление смещения центра контактной площадки пневматической части колеса с твердым покрытием в плоскости, параллельной его движению, относительно точки пересечения перпендикуляра, проведенного через ось подвеса колеса к твердой поверхности, т. е. величину предварительного смещения Δх, при этом с учетом масштаба изображения, найденного путем сопоставления размера известного элемента транспортного средства в натуре х_H и размера этого элемента на экране дисплея компьютера х, определяют величину предварительного смещения в натуре Δ_H по формуле Δ_H=Δх·х_H/х, которая является коэффициентом трения качения, после этого определяют коэффициент сопротивления качению Кс по формуле:

где R — радиус колеса, и эти операции повторяют для всех кадров съемки, обеспечивая определение коэффициентов Δ_H и К_C на всех стадиях движения колеса.

Что из следующего является измерением коэффициента трения? ..

Главная

Класс 11

Физика

Физический мир

A

[M2 L2 T]

B

[M0 L0 T0 T0 ]

C

[ML2 T -2]

D

[M2 L2 T — 2]

Уровень сложности: Easy

Просмотр: 5725 Студенты

(1)

9002 Коэплекто трение безразмерно и безразмерно.

57

Поделиться

Свяжись с более чем 50 000 опытных наставников за 60 секунд, круглосуточно и без выходных

Задай вопрос наставнику

Практические вопросы из похожих книг

Уравнение волны задается формулой y=​asinω(vx​−kω) где ω — угловая скорость, а v — линейная скорость. Размерность k будет

1. [T2]
2. [T−1]
3. [T]
4. [LT]

Посмотреть решение

Найдите формулу размерности следующих величин:

1. Плотность
   
2. Скорость
   
3. Ускорение
   
4. Momentum
   (E) Сила
   (F) Рабочая или энергия
   (G) Power
   (H) Давление
9

. от взрыва под водой, колеблется с периодом T, пропорциональным padbEc, где p — статическое давление, d — плотность воды, E — полная энергия взрыва. Найдите значения a, b и c.

Посмотреть решение

. Пусть x и a обозначают расстояние. Правильно ли размерно ∫a2−x2

dx=a1 sin−1xa?

Просмотр решения

Практика Подробнее Вопросы из физического мира

Пусть A

= 2i

+3J

+4K

и B

= 3i

+4J

+5K

. Найдите угол между ними.

Посмотреть решение

Твердый шар свободно вращается вокруг своей оси симметрии в свободном пространстве. Радиус сферы увеличился, а масса осталась прежней. Какая из следующих физических величин останется постоянной для сферы?

1. Кинетическая энергия вращения
2. Момент инерции
3. Угловая скорость
4. Угловой момент

Посмотреть решение

Частица движется по заданной прямой с постоянной скоростью ν. В некоторый момент времени он находится в точке P на своем прямолинейном пути. О — неподвижная точка. Показать, что OP

×ν

не зависит от положения P.

Посмотреть решение

Три частицы P, Q и R, движущиеся вдоль векторов A 9соответственно. Они ударяют по точке и начинают двигаться в разные стороны. Теперь частица P движется нормально к плоскости, содержащей вектора A

и B

. Точно так же частица Q движется по нормали к плоскости, содержащей вектора A

и C

. Угол между направлениями движения P и Q равен cos−1(x

​1​). Тогда значение х равно _______.

Просмотреть решение

Просмотреть еще

Практические вопросы по похожим понятиям, заданные студентами Filo

3. График ускорение-время (a-t) для частицы, движущейся по прямой, показан на рисунке. При t=0 скорость частицы составляет 5 м/с.

Посмотреть решение

A,B,C,D и E — компланарные векторы, имеющие одинаковую величину в каждой из 10 единиц и угол между последовательными векторами 72∘. Если A перевернуть, то величина равнодействующей будет

1. 10 единиц
2. 20 единиц
3. 30 единиц
4. 40 единиц

Посмотреть решение

18. Мальчик при поливе огорода держит выход шланга h=0,8 м над землей. Из шланга непрерывно вытекает вода с постоянной скоростью u=6 м/с под углом θ=30∘ над горизонтом. Площадь поперечного сечения выпускного отверстия A=1,5 см2, плотность воды ρ= 1000 кг/м3, ускорение свободного падения g=10 м/с2. Найдите массу воды в водном потоке?

Посмотреть решение

∴ (t) 20 Дж γ

​=3 [NCERT Pg. 157]

1. 5 Дж
2. 2,5 Дж
3. 40 J

Посмотреть решение

Посмотреть больше

Текст вопроса	Что из следующего является размерностью коэффициента трения?
Тема	Физический мир
Тема
Класс	Класс
. 0205	57

Задачи двух тел

В разделе законов Ньютона была введена тема задач двух тел. Пара стратегий решения проблем была обсуждена и применена для решения трех примеров задач. Такие задачи двух тел обычно включают решение для ускорения объектов и силы, действующей между объектами. Одна из стратегий решения задач двух тел включает использование системного анализа для определения ускорения в сочетании с анализом отдельных объектов для определения силы, передаваемой между объектами. Вторая стратегия заключалась в использовании анализа двух отдельных объектов для разработки системы двух уравнений для решения двух неизвестных величин. При необходимости найдите время, чтобы просмотреть страницу, посвященную решению задач двух тел. Эта страница будет основываться на уроках, полученных ранее в разделе «Законы Ньютона».

В этом уроке мы будем анализировать задачи двух тел, в которых объекты движутся в разных направлениях. В этих задачах два объекта соединены нитью, которая передает силу одного объекта другому объекту. Струна наматывается на шкив, который изменяет направление действия силы без изменения ее величины. В качестве иллюстрации того, как работает шкив, рассмотрите диаграмму справа. Объект A связан с объектом B цепочкой. Веревка наматывается на шкив в конце стола. Объект А подвешен в воздухе, а объект Б лежит на столе. В этой ситуации объект А упадет вниз под действием силы тяжести, потянув вниз один конец веревки, к которой он подключен. Согласно закону действия-противодействия Ньютона, этот нижний конец нити будет тянуть вверх объект А. Противоположный конец нити соединен с объектом В. Этот конец нити тянет вправо объект В. Таким образом, струна соединение двух объектов означает притяжение обоих объектов с одинаковой силой, но в разных направлениях. Струна тянет вверх объект А и вправо объект В. Блок изменил направление приложения силы.

Задачи, связанные с двумя объектами, соединяющими струны и шкивы, характеризуются объектами, которые движутся (или даже ускоряются) в разных направлениях.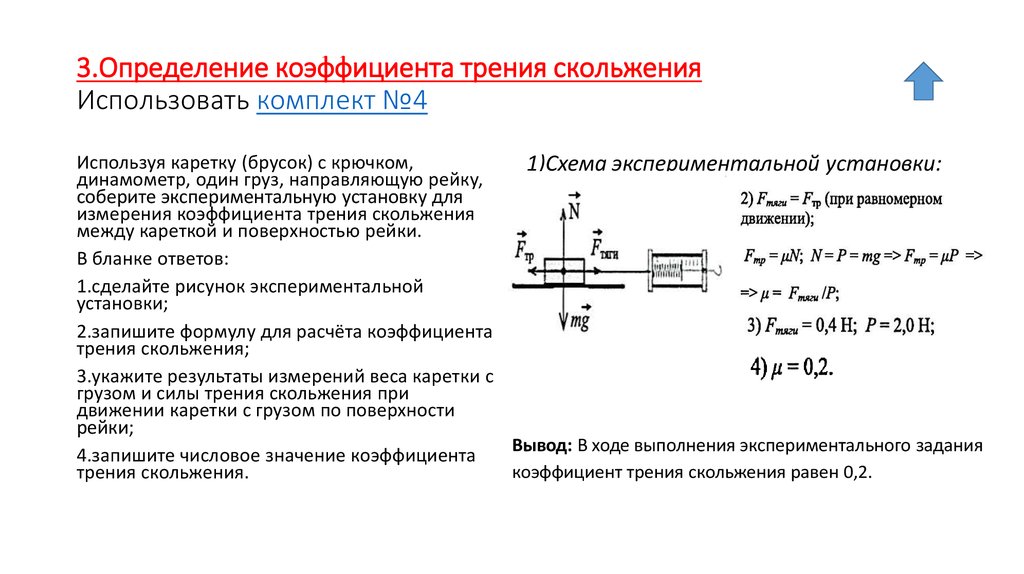 Они движутся или ускоряются с одинаковой скоростью, но в разных направлениях. Таким образом, при подходе к таким проблемам становится важным выбрать другую систему отсчета и систему координат для каждого объекта. Следует уделить внимание выбору такой системы координат, чтобы оба объекта ускорялись вдоль оси в положительном направлении. С правильно определенными осями для каждого отдельного объекта можно построить диаграмму свободного тела. Затем к каждой диаграмме можно применить законы Ньютона, чтобы составить систему из двух уравнений для решения двух неизвестных. Этот процесс решения проблем будет продемонстрирован для трех различных примеров задач.

 

Пример задачи 1

Груз массой 200,0 грамм (m ₁ ) и груз массой 50,0 грамм (m ₂ ) соединены нитью. Нить натянута на шкив. Определить ускорение масс и натяжение нити.

Как это часто бывает, в этом примере задачи запрашивается информация о двух неизвестных — ускорении объектов и силе, действующей между объектами. В такой ситуации, как эта, с двумя объектами, подвешенными на шкиве, более массивный объект будет ускоряться вниз, а наименее массивный объект будет ускоряться вверх. Величина ускорения будет одинаковой для каждого объекта. Система координат выбрана для m ₁ имеет положительную ось ординат, направленную вниз; система координат, выбранная для m ₂ , имеет положительную ось y, направленную вверх. При таком выборе осей направление ускорения будет положительным для каждого объекта. Диаграммы свободного тела для каждой отдельной массы показаны ниже. На каждый объект действует направленная вниз сила тяжести, которая рассчитывается как m ₁ •g и m ₂ •g соответственно. Каждый объект также испытывает восходящую силу натяжения, которая притягивает два объекта друг к другу.

Уравнение второго закона Ньютона (F _net = m•a) можно применить к обеим диаграммам, чтобы написать два уравнения для двух неизвестных. Сеть F будет выражаться как сила, направленная в направлении ускорения, за вычетом силы, противодействующей ему. Таким образом, для массы 200,0 грамм F _нетто записывается как 1,960 N — F _{десяток} . Для массы 50,0 грамм F _нетто записывается как F _{десятки} — 0,490 Н. Уравнения 1 и 2 являются результатом применения уравнения второго закона Ньютона к массам 200,0 грамм и 50,0 грамм. (Обратите внимание, что перед использованием в уравнениях значения массы преобразуются в стандартные килограммы. Также обратите внимание, что единицы измерения были опущены, чтобы уравнения читались более четко.)

1,960 — F _{десятков} = 0,2000•a

F _{десятков} — 0,490 = 0,0500•a

С этого момента несколько шагов алгебры приводят к ответам на задачу. Уравнение 2 можно изменить, чтобы получить выражение для F _{десятков} , записанное через ускорение.

F _{десятков} = 0,0500•a + 0,490

Теперь это выражение для F _{десятков} можно подставить в уравнение 1, чтобы преобразовать его в уравнение с одним неизвестным. Это уравнение и последующие шаги алгебры, ведущие к значению ускорения, показаны ниже.

1,96 — (0,0500•а + 0,490) = 0,2000•а
1,96 — 0,0500•а — 0,490 = 0,2000•а
1,47 = 0,2500•а
a = 1,47/0,2500 = 5,88 м/с ²

Теперь, когда ускорение найдено из уравнения 1, его значение можно подставить в уравнение 3, чтобы определить натяжение.

F _{десятки} = 0,0500•(5,88) + 0,490
F _{десятки} = 0,784 N

Рассматриваемую здесь систему шкивов иногда называют машиной Атвуда. Подход к решению проблем — это стандартный подход, который будет использоваться на этой странице для решения двух неизвестных. Это будет повторено в примере задачи 2, чтобы решить то, что обычно называют модифицированной машинной задачей Этвуда.




 

Пример задачи 2

Рассмотрим ситуацию с двумя телами справа. Подвесной груз массой 20,0 грамм (m ₂ ) прикреплен к планеру с воздушной гусеницей массой 250,0 грамм (m ₁ ). Определить ускорение системы и натяжение нити.

Как и в примере задачи 1, эту систему необходимо сначала концептуально проанализировать, чтобы определить направление ускорения двух объектов. Это позволит назначить оси координат для каждого объекта. Так как нечего толкать м ₁ влево, мы думаем, что он ускорится вправо из-за натяжения нити. Подвешенная масса (m ₂ ) явно будет ускоряться вниз под действием силы тяжести. Таким образом, выбрана система координат для m ₂ с положительной осью ординат, направленной вниз; система координат, выбранная для m ₁ , имеет положительную ось x, направленную вправо. При таком выборе осей направление ускорения будет положительным для каждого объекта.

Диаграмма свободного тела для каждой отдельной массы показана ниже. На каждый объект действует направленная вниз сила тяжести (F _грав ) – вычисляемая как m ₁ •g и m ₂ •g соответственно. Планер (m ₁ ) испытывает восходящую поддерживающую силу (воздух давит на него), чтобы уравновесить силу тяжести. На планер также действует горизонтальная сила — сила натяжения (F _{десятков} ) вправо. Подвешенная масса (m ₂ ) испытывает направленную вверх силу растяжения (F _{десятков} ), что оказывает некоторое сопротивление нисходящему притяжению гравитации.

Уравнение второго закона Ньютона (F _net = m•a) можно применить к обеим диаграммам свободного тела, чтобы написать два уравнения для двух неизвестных. Сеть F будет выражена как сила в направлении ускорения за вычетом всех сил, противодействующих ему. Для планера весом 250,0 грамм (0,250 кг) F _нетто — это просто неуравновешенная сила натяжения (F _{десятки} ). Для подвесной массы 20,0 г (0,020 кг) F _нетто записывается как 0,196 N — F _{десятки} . Уравнения 4 и 5 являются результатом применения уравнения второго закона Ньютона к 250,0-граммовому планеру и 20,0-граммовому подвесу. (Обратите внимание, что перед использованием в уравнениях значения массы преобразуются в стандартные килограммы. Также обратите внимание, что единицы измерения были опущены, чтобы уравнения читались более четко.)

F _{десятки} = 0,2500•a

0,196 — F _{десятков} = 0,0200•a

С этого момента несколько шагов алгебры приводят к ответам на задачу. Уравнение 4 выражает F _{десятков} значение с точки зрения ускорения. Это выражение для F _{десятков} можно подставить в уравнение 5, чтобы преобразовать его в уравнение с одним неизвестным. Это уравнение и последующие шаги алгебры, ведущие к значению ускорения, показаны ниже.

0,196 — 0,2500•а = 0,0200•а
0,196 = 0,2700•а
а = 0,196/0,2700 = 0,72593 м/с ²
a = ~0,726 м/с ²

Теперь, когда ускорение найдено из уравнения 5, его значение можно подставить в уравнение 4, чтобы определить натяжение.

F _{десятки} = 0,2500•(0,72593) = 0,18148
F _{десятки} = ~0,181 N

Систему шкивов, проанализированную в примере задачи 2, иногда называют модифицированной машиной Этвуда. Анализ немного сложнее, чем анализ машины Этвуда из примера задачи 1. Последний пример задачи будет представлять собой случай модифицированной машины Этвуда с наклонной поверхностью, как показано ниже. Подход к решению проблемы будет таким же.

 

Пример задачи 3

Рассмотрим ситуацию с двумя телами справа. Ящик размером 2,50×10 ³ кг (m ₁ ) опирается на наклонную плоскость и соединен тросом с массой 4,00×10 ³ кг (m ₂ ). Эта вторая масса (m ₂ ) подвешена на шкиве. Угол наклона составляет 30,0°, поверхность не имеет трения. Определить ускорение системы и натяжение троса.

Как и в предыдущей задаче, первая задача включает анализ ситуации, чтобы определить, в каком направлении будут ускоряться объекты. Такой анализ позволит присвоить каждому объекту систему координатных осей. В этом случае висящая масса (m ₂ ) могла ускоряться вверх или вниз. Направление, в котором он ускоряется, зависит от сравнения его веса (силы тяжести) с противодействующей силой, действующей на другую массу (m ₁ ). Масса на наклонной плоскости сталкивается с тремя силами — силой тяжести, нормальной силой и силой натяжения. Сила тяжести направлена ​​вниз (как обычно) и рассчитывается как m ₁ •г. Нормальная сила направлена ​​перпендикулярно поверхности (как обычно). Сила натяжения направлена ​​вверх и вправо — параллельно наклонной плоскости и вдоль той же ориентации, что и струна, создающая эту силу. Как обсуждалось на предыдущей странице, объекты, расположенные на наклонных плоскостях, анализируются путем разделения силы тяжести на две составляющие. Одна компонента направлена ​​параллельно плоскости (и вниз под этим углом), а другая компонента направлена ​​перпендикулярно плоскости (и вверх под этим углом). Именно параллельная составляющая силы тяжести пытается притянуть m ₁ вниз по наклонной плоскости. Как упоминалось ранее, эту составляющую можно рассчитать, умножив вес объекта (m ₁ •g) на синус угла наклона (30°). Значение для F _{, параллельного} , равно

F _{, параллельного} = m ₁ •g•sine(θ) = (2500 кг)•(9,8 Н/кг)•sine(30°)
F _{параллельно} = 12250 N

Эта параллельная составляющая силы тяжести пытается тянуть m ₁ вниз по наклонной плоскости. С м ₁ крепится кабелем к m ₂ , с ним будет тянуться подвесная масса. Однако существует противоположное действие силы тяжести, тянущей m ₂ вниз; это противодействующее действие, если оно преобладает, будет тянуть объект m ₁ вверх по наклонной плоскости. Сила тяжести на м ₂ равна

F _грав-2 = м ₂ •g = (4000 кг)•(9,8 Н/кг) = 39200 Н

Эта сила тяжести на м ₂ является доминирующей силой. И так м ₁ будет ускоряться вверх по наклонной плоскости, а m ₂ будет ускоряться вниз. Оси координат назначаются соответствующим образом, чтобы каждый объект имел положительное ускорение.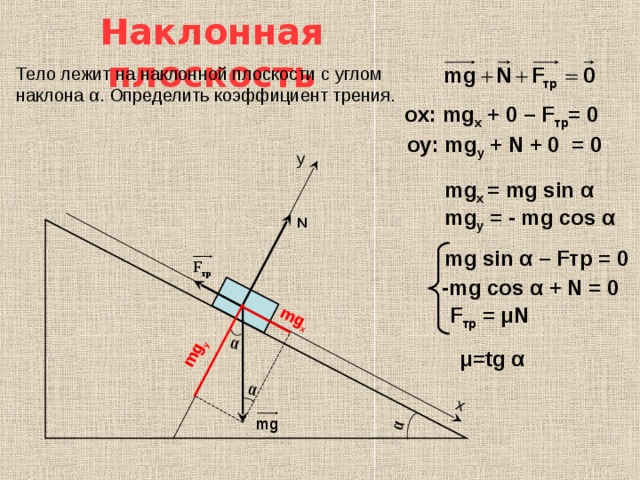

На рисунках ниже показаны эти координатные оси и силы, действующие на два объекта. Три силы на m ₁ уже обсуждались. На диаграмме показаны два компонента F _grav . Как упоминалось на предыдущей странице, перпендикулярная составляющая силы тяжести рассчитывается как

F _{перпендикулярно} = м ₁ •g•cosθ = (2500 кг)•(9,8 Н/кг)•cos(30°)
F _{перпендикулярно} = 21218 N

Нормальная сила (F _норма ), действующая на m ₁ , уравновешивает F _{перпендикулярно} так, что ускорение перпендикулярно наклонной плоскости отсутствует. Значение нормы F также равно 21218 Н. Подвешенная масса (m ₂ ) испытывает только две силы – направленную вниз силу тяжести и восходящую силу растяжения.

Теперь уравнение второго закона Ньютона (F _net = m•a) можно применить к обеим диаграммам свободного тела, чтобы написать два уравнения для двух неизвестных. Сеть F выражается как сила, направленная в направлении ускорения, за вычетом любых противодействующих сил. Для массы 2500 кг на склоне (м ₁ ) F _net представляет собой просто силу натяжения (F _{десятков} ) за вычетом параллельной составляющей силы тяжести. Для подвесной массы 4000 кг (м ₂ ), F _net – сила тяжести (39200 Н) минус сила натяжения (F _{десяток} ). Уравнения 6 и 7 являются результатом применения уравнения второго закона Ньютона к m ₁ и m ₂ . (Обратите внимание, что единицы были опущены, чтобы уравнения читались более четко.)

F _{десятки} — 12250 = 2500•a

39200 — F _{десятки} = 4000•a

С этой точки a несколько шагов алгебры приводят к ответам на проблему. Уравнение 6 можно изменить, чтобы создать выражение для F _{десятков} , выраженное через ускорение.

F _{десятков} = 2500•a + 12250

Это выражение для F _{десятков} можно подставить в уравнение 7, чтобы преобразовать его в уравнение с одним неизвестным. Это уравнение и последующие шаги алгебры, ведущие к значению ускорения, показаны ниже.

39200 — (2500•а + 12250) = 4000•а
39200 — 2500•а — 12250 = 4000•а
26950= 6500•а
а = 26950/6500 = 4,1462 м/с ²
a = ~4,15 м/с ²

Теперь, когда ускорение найдено из уравнения 7, его значение можно подставить в уравнение 8, чтобы определить силу натяжения (F _{десятков} ).

F _tens = 2500•a + 12250 = 2500•(4.1462) + 12250 = 22615 N
F _tens = ~2.26 x 10 ⁴ N

 

Two-body problems like these three примеры проблем могут быть довольно сложной задачей. Наличие системного подхода, применяемого к каждой проблеме, упрощает анализ. Хорошее концептуальное понимание, приверженность использованию диаграмм свободного тела и твердое понимание второго закона Ньютона являются важными составляющими успеха.

 

 

 

Мы хотели бы предложить .