Равные вектора

Равные вектора

Навигация по странице:

• Определение равных векторов
• Условие равенства векторов
• Примеры задач на равенство векторов
  • плоские задачи
  • пространственные задачи

Определение. Вектора a и b называются равными, если они имеют одинаковую длину, лежат на параллельных прямых или на одной прямой, и направлены в одном направлении. (рис. 1).

То есть, два вектора равны, если они коллинеарные, сонаправленые и имеют равные длины:

a = b, если a↑↑b и |a| = |b|.

Условие равенства векторов.Вектора равны, если их координаты равны.

рис. 1

Примеры плоских задач на равенство векторов

Пример 1. Определить какие из векторов равны a = {1; 2}, b = {1; 2}, c = {3; 2}.

Решение:

a = b — так как их координаты равны,

a ≠ c — так как их координаты не равны,
b ≠ c — так как их координаты не равны.

Пример 2. При каком значении параметра n вектора a = {1; 8;} и b = {1; 2n} равны.

Решение:

Проверим равенство компонентов векторов
a_x = b_x = 1
a_y = b_y => 8 = 2n => n = 8/2 = 4

Ответ: при n = 4 вектора a и b равны.

Примеры пространственных задач на равенство векторов

Пример 3. Определить какие из векторов равны a = {1; 2; 4}, b = {1; 2; 2}, c = {1; 2; 4}.

Решение:

a = c — так как их координаты равны,
a ≠ b — так как их координаты не равны,
b ≠ c — так как их координаты не равны.

Пример 4. При каком значении параметра n вектора a = {1; 2; 4} и b = {1; 2; 2n} равны.

Решение:

Проверим равенство компонентов векторов
a_x = b_x = 1
a_y = b_y = 2
a_z = b_z => 4 = 2n => n = 4/2 = 2

Ответ: при n = 2 вектора a и b равны.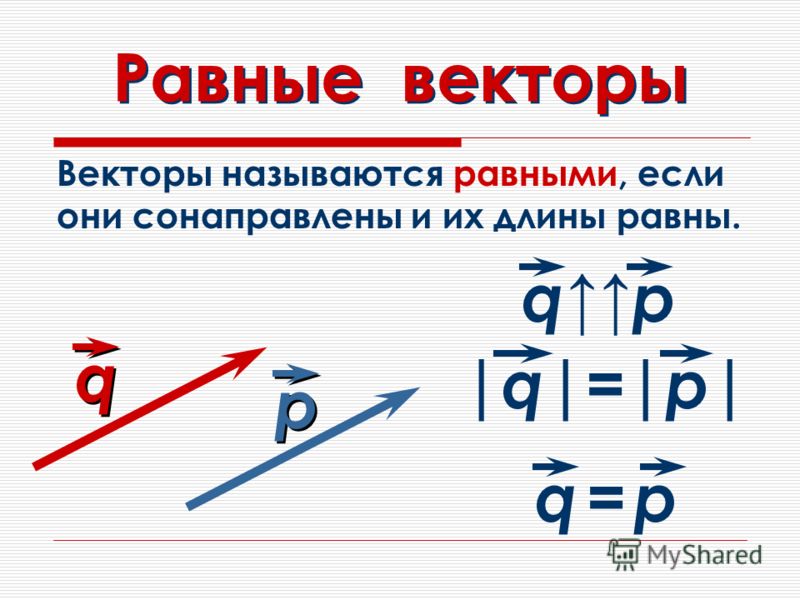

Вектора Вектор: определение и основные понятия Определение координат вектора заданного координатами его начальной и конечной точки Модуль вектора. Длина вектора Направляющие косинусы вектора Равенство векторов Ортогональность векторов Коллинеарность векторов Компланарность векторов Угол между векторами Проекция вектора Сложение и вычитание векторов Умножение вектора на число Скалярное произведение векторов Векторное произведение векторов Смешанное произведение векторов Линейно зависимые и линейно независимые вектора Разложение вектора по базису

Онлайн калькуляторы с векторами

Онлайн упражнения с векторами на плоскости

Онлайн упражнения с векторами в пространстве

Равенство двух векторов: условие, примеры задач

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

В данной публикации мы рассмотрим, какие векторы называются равными и как определить их равенство. Также разберем примеры задач по этой теме.

• Условие равенства векторов
• Примеры задач

Условие равенства векторов

Векторы a и b равны, если у них одинаковая длина, они лежат на одной или параллельных прямых, а также направлены одну и ту же сторону. То есть такие векторы коллинеарны, сонаправлены и равны по длине.

a = b, если a ↑↑ b и |a| = |b|.

Примечание: векторы равны, если равны их координаты.

Примеры задач

Задание 1
Какие из векторов являются равными: a = {6; 8}, b = {-2; 5} и c = {6; 8}.

Решение:
Из перечисленных векторов равны a и c, так как у них одинаковые координаты:
a_x = c_x = 6
a_y = c_y = 8.

Задание 2
Выясним, при каком значении n векторы a = {1; 18; 10} и b = {1; 3n; 10} равны.

Решение:
Сначала проверим равенство известных координат:
a_x = b_x = 1
a_z = b_z = 10

Чтобы равенство было верным, нужно чтобы a_y = b_y:
3n = 18, следовательно n = 6.

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

равных векторов

равных векторов

Навигация по странице:

• Равные векторы — определение
• Условия равенства векторов
• Примеры задач
  • плоские задачи
  • пространственных задач

Определение.

Векторы a и b являются равными векторами , если они лежат на одной или параллельных прямых, их направления совпадают и длины равны (рис. 1).

Два вектора равны, если они коллинеарны, сонаправлены и имеют одинаковую длину:

a = b, если a↑↑b и |a| = |б|.

Условия равенства векторов. Векторы равны , если их координаты равны.

Рис. 1

Примеры плоских задач

Пример 1. Определить, какие из векторов равны a = {1; 2}, б = {1; 2}, с = {3; 2}.

Решение:

a = b — так как их координаты равны,
a ≠ c — так как их координаты не равны,
b ≠ c — так как их координаты не равны.

Пример 2. При каком значении параметра n векторы a = {1; 8;} и b = {1; 2n} равны.

Решение:

Проверить равенство компонентов векторов
а _х = б _х = 1
_г = b _y => 8 = 2n => n = 8/2 = 4

Ответ: при n = 4 векторы a и b равны.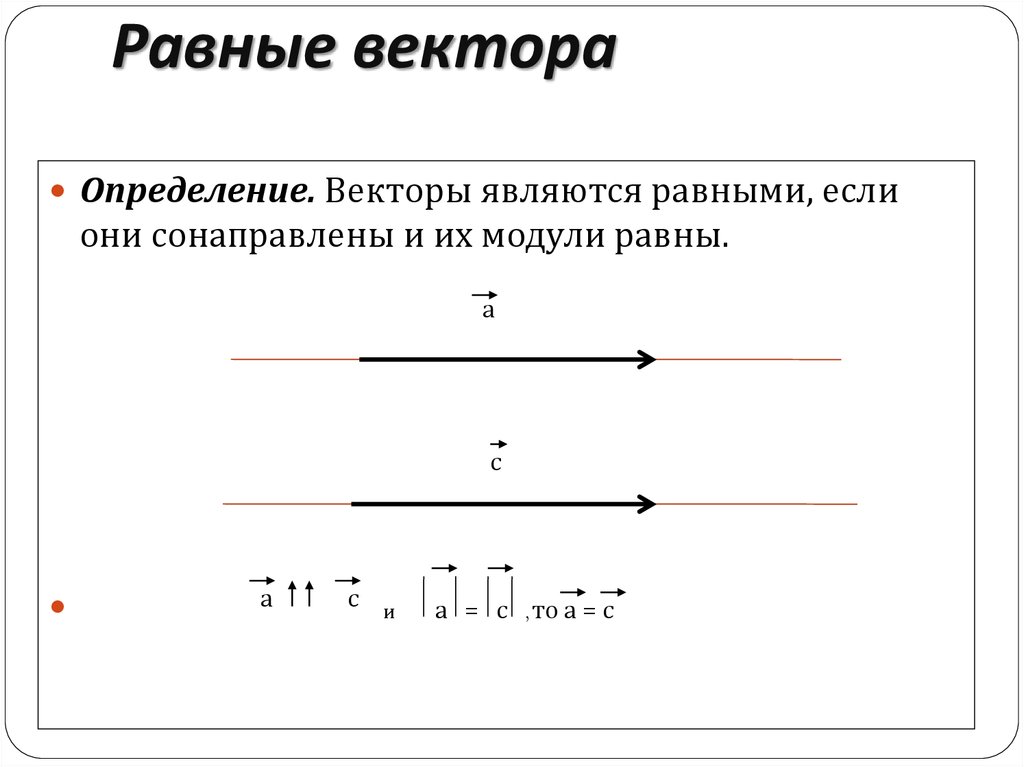

Примеры пространственных задач

Пример 3. Определить, какие из векторов равны a = {1; 2; 4}, б = {1; 2; 2}, с = {1; 2; 4}.

Решение:

a = c — так как их координаты равны,
a ≠ b — так как их координаты не равны,
b ≠ c — так как их координаты не равны.

Пример 4. При каком значении параметра n векторы a = {1; 2; 4} и б = {1; 2; 2n} равны.

Решение:

Проверить равенство компонентов векторов
а _х = б _х = 1
а _у = б _у = 2
a _z = b _z => 4 = 2n => n = 4/2 = 2

Ответ: при n = 2 векторы a и b равны.

Векторы Определение векторов. Основная информация Компонентная форма вектора с начальной и конечной точками Длина вектора Направленные косинусы вектора Равные векторы Ортогональные векторы Коллинеарные векторы Компланарные векторы Угол между двумя векторами Векторная проекция Сложение и вычитание векторов Скалярно-векторное умножение Скалярное произведение двух векторов Перекрестное произведение двух векторов (векторное произведение) Скалярное тройное произведение (смешанный продукт) Линейно зависимые и линейно независимые векторы Разложение вектора по базису

Онлайн калькуляторы с векторами

Задания и упражнения с вектором 2D

Задания и упражнения с векторным 3D

Узнайте определение, уравнения, угол, примеры здесь

Векторы — это геометрические объекты с величиной и направлением в двух или более измерениях.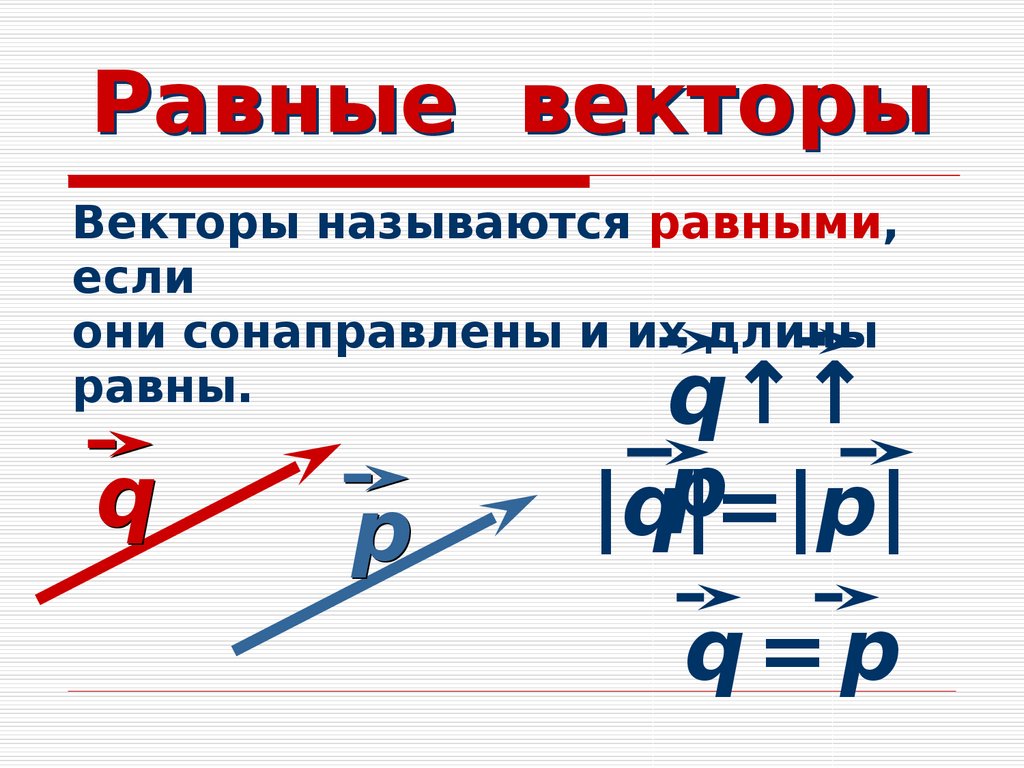 Вектор представлен линией со стрелкой, указывающей в направлении вектора, а ее длина представляет собой величину вектора.

Если вектор и другой вектор имеют одинаковую величину и направление, говорят, что они равны. Проще говоря, два или более вектора называются равными, если их длины одинаковы и все они указывают в одном направлении. Мы можем сравнить координаты двух векторов, чтобы увидеть, равны ли они в векторной алгебре.

Векторы равны, если координаты двух или более векторов одинаковы. В результате, если вектор A и вектор B имеют одинаковые координаты, они называются равными векторами.

Равные векторы

Равные векторы имеют одинаковую величину и направление. Равные векторы могут начинаться в разных точках. Направленные отрезки параллельны, когда векторы равны.

Если вектор A и вектор B имеют одинаковую величину и направлены в одном и том же направлении, говорят, что они равны. Два или более вектора называются равными, если они направлены в одном направлении, лежат на одной прямой и имеют одинаковую длину.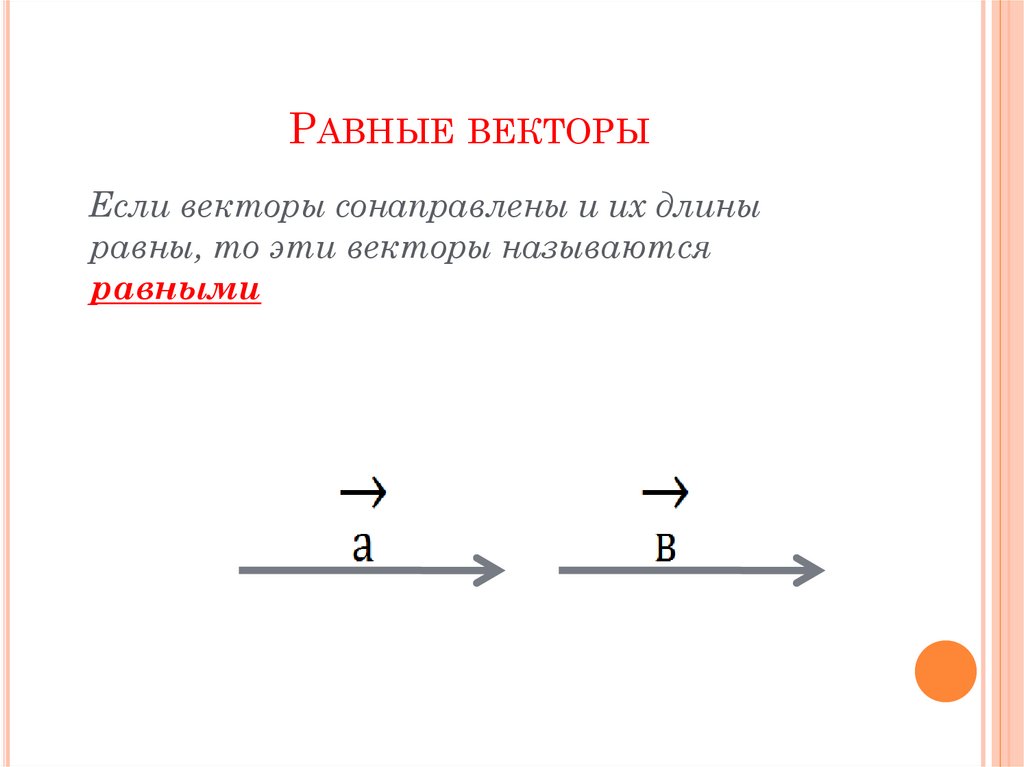 Это означает, что параллельные векторы также являются равными векторами. Мы также можем искать равный вектор, если он имеет те же компоненты x, y и z, что и другой вектор. Равные векторы не обязательно должны начинаться с одной и той же точки.

Диаграмма равенства вектора A и вектора B показана ниже. Два вектора равны, но не совпадают, то есть они не начинаются с одной и той же точки. В результате равные векторы не обязательно должны иметь одинаковые начальные точки. Это векторы одинаковой величины, параллельные и сонаправленные. Если два вектора имеют одинаковую величину, но антипараллельны (движутся в противоположных направлениях), они не равны.

Уравнения для равных векторов

Если у нас есть два вектора, мы можем использовать следующую формулу, чтобы узнать, равны ли они:

\( \vec{A} = x\hat{i} + y\hat{j} + z\hat{k} \)

\( \vec{B} = q\hat{i} + r \hat{j} + s\hat{k} \)

Тогда векторы A и B равны тогда и только тогда, когда x = q, y = r и z = s, а это означает, что они имеют одинаковые координаты.

Например:

Найдите значения x и y, если два вектора \( \vec{A} = 2\hat{i} + 5\hat{j} – 10\hat{k} \) и \( \vec{B} = x\hat{i} -y\hat{j} – 10\hat{k} \) равны.

Поскольку векторы \( \vec{B} \) и \( \vec{B} \) равны, они должны иметь одинаковые компоненты.

В результате

2 = x , 5 = — y, -10 = -10

x = 2, y = -5

В результате значения x и y равны x = 2 и y = -5 соответственно.

Угол равных векторов

Равные векторы также являются параллельными векторами, а угол между параллельными векторами, как мы знаем, равен нулю радиан. Теперь мы продемонстрируем это, используя формулу векторного скалярного произведения. Рассмотрим два равных вектора A и B с координатами (x, y).

\( \vec{A} = x\шляпа{i} + y\шляпа{j} \)

\( \vec{B} = x\hat{i} + y\hat{j} \)

Рассмотрим \( \theta \) угол между ними.

Возьмем скалярное произведение векторов \( \vec{A}\) и \( \vec{B} \) теперь:

\( A. {2}} \right )}} \right ]} \) 9{2} \right )} \right ] \)

\( \Стрелка вправо \theta = \arccos \left ( 1 \right ) \)

\( \Стрелка вправо \theta = \left ( 0 \right ) \)

В результате угол, образованный двумя равными векторами, равен нулю.

Скалярное произведение двух равных векторов

Скалярное произведение обозначается точкой в ​​центре:

a.b

Это означает, что скалярное произведение a и b

Скалярное произведение двух равных векторов можно вычислить как следует:

\( a.b = \left | a \ right |\times \left | b \right |\times \cos \left ( \theta \right ) \)

Где,

\( | a \right |\ ) = длина вектора a

\( | b \right |\) = длина вектора b

\( \theta \) = угол, образованный a и b

Итак, мы умножаем длину a на длину b, затем на косинус угла, образованного a и b.

Результат скалярного произведения двух равных векторов лежит в той же плоскости, что и исходные два равных вектора.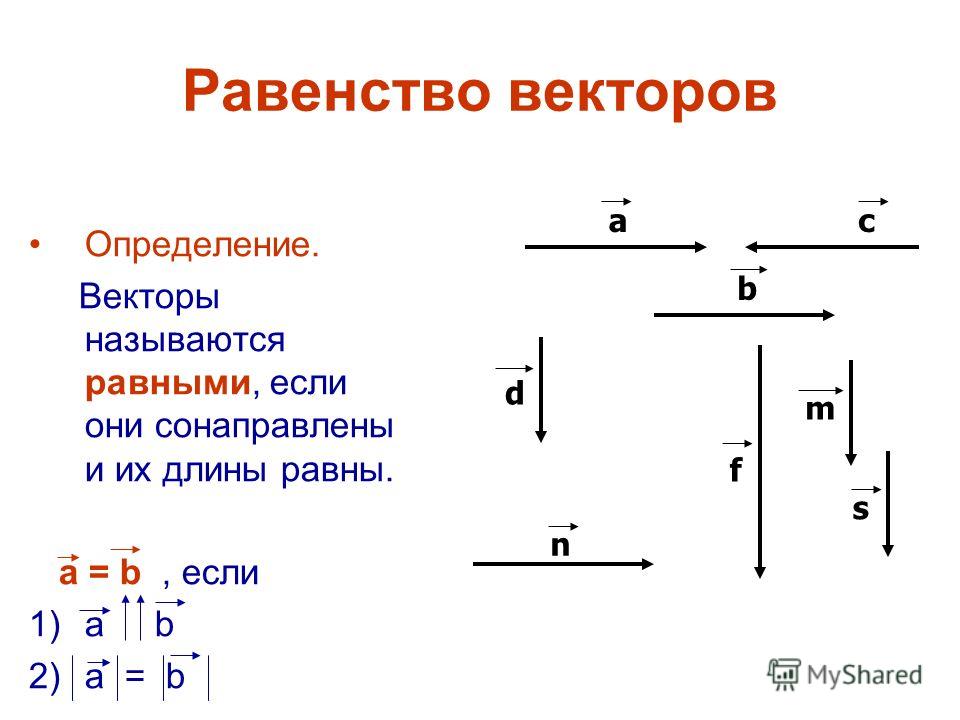 Скалярный продукт может быть либо положительным действительным числом, либо отрицательным действительным числом, либо нулем.

Например:

Найдите скалярное произведение \( a = \left ( 1,2,3 \right ) \) & \( b = \left ( 4,-5,6 \right ) \)

Решение:

Используя компонентное уравнение для скалярного произведения трехмерного вектора,

\( a.b = a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3 } \)

\( a.b = 1\влево ( 4 \вправо )+2\влево ( -5 \вправо )+3\влево ( 6 \вправо ) \)

= 4-10+18

= 12

В результате a.b положительный.

Перемножение двух равных векторов

Метод умножения двух векторов представляет собой перекрестное произведение двух равных векторов. Перекрестное произведение обозначается знаком умножения (x) между двумя векторами.

Вектор имеет не только направление, но и величину. Мы можем использовать перекрестное произведение и скалярное произведение для умножения двух или более векторов.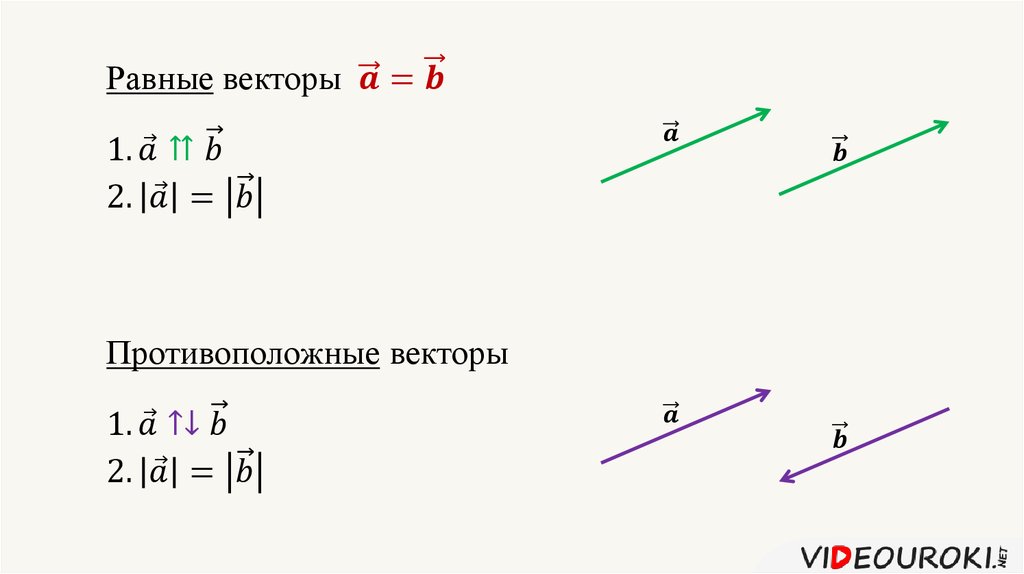 Когда два вектора перемножаются, а произведение векторов также является векторной величиной, результирующий вектор известен как перекрестное произведение двух векторов или векторное произведение. Результирующий вектор перпендикулярен плоскости, содержащей два заданных вектора.

Перекрестное произведение двух равных векторов показано как:

\( a\times b = \left | a \right | \left | b \right |\sin \theta \)

Решенный пример

Задача: 1 При каком значении параметра n вектора \( \bar{a} = \left \{ 1;8 \right \} \) и \( \bar{b} = \left \ { 1;2n \right \}\(\) равны?

Решение:

Проверить равенство компонент вектора.

\( a_{y} = b_{y}\Rightarrow 8 = 2n \Rightarrow n =\frac{8}{2}=4 \) 9{2} \right ) \right )} = \sqrt{\left ( 25+36 \right )} = \sqrt{61} =\left | Б \ справа | \)

Теперь векторы A и B имеют одинаковую величину, но действуют в противоположном направлении, поскольку A = -B, поэтому они не равны.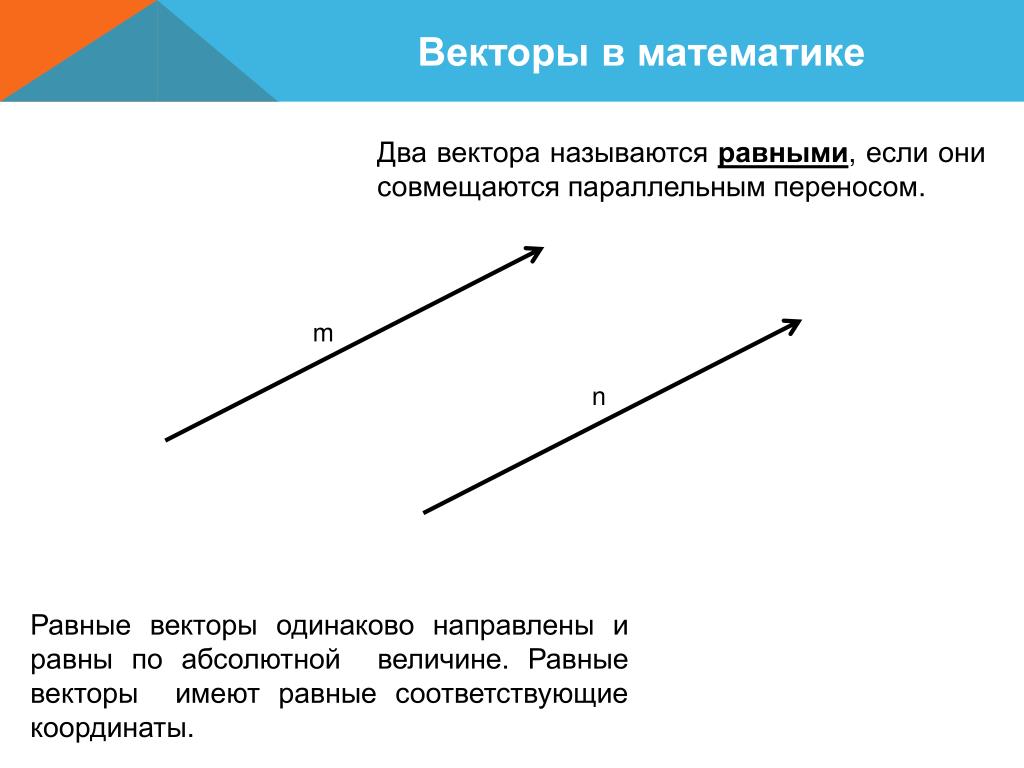

A и B не являются векторами одинаковой длины.

Часто задаваемые вопросы о равных векторах

В.1 Каков угол между двумя равными векторами?

Ответ 1 Угол, образованный двумя равными векторами, равен нулю.

Q.2 Что означает равенство двух векторов?

Ответ 2 Когда два вектора имеют одинаковую длину или величину и направлены в одном направлении, говорят, что они равны.

В.3 Все ли равные векторы параллельны?

Ответ 3 Равные векторы — это векторы с одинаковыми координатами. В результате, хотя равные векторы являются параллельными векторами, параллельные векторы могут не быть равными векторами.

В.4 Все ли равные векторы коллинеарны?

Ответ 4 Это векторы с одинаковой или параллельной опорой. Кроме того, их величины могут быть равными или неравными, а их направления могут быть противоположными или одинаковыми.