Элементарные шифры на понятном языке / Habr

Привет, Хабр!

Все мы довольно часто слышим такие слова и словосочетания, как «шифрование данных», «секретные шифры», «криптозащита», «шифрование», но далеко не все понимают, о чем конкретно идет речь. В этом посте разберемся, что из себя представляет шифрование и рассмотрим элементарные шифры с тем расчетом, чтобы даже далекие от IT люди поняли суть этого явления.

Прежде всего, разберемся в терминологии.

Шифрование – это такое преобразование исходного сообщения, которое не позволит всяким нехорошим людям прочитать данные, если они это сообщение перехватят. Делается это преобразование по специальным математическим и логическим алгоритмам, некоторые из которых мы рассмотрим ниже.

Исходное сообщение – это, собственно, то, что мы хотим зашифровать. Классический пример — текст.

Шифрованное сообщение – это сообщение, прошедшее процесс шифрования.

Шифр — это сам алгоритм, по которому мы преобразовываем сообщение.

Ключ — это компонент, на основе которого можно произвести шифрование или дешифрование.

Алфавит – это перечень всех возможных символов в исходном и зашифрованном сообщении. Включая цифры, знаки препинания, пробелы, отдельно строчные и заглавные буквы и т.д.

Теперь, когда мы говорим на более-менее одном языке, разберем простые шифры.

Самый-самый простой шифр. Его суть – переворот алфавита с ног на голову.

Например, есть у нас алфавит, который полностью соответствует обычной латинице.

a b c d e f g h i j k l m n o p q r s t u v w x y z

Для реализации шифра Атбаша просто инвертируем его. «А» станет «Z», «B» превратится в «Y» и наоборот. На выходе получим такую картину:

И теперь пишем нужное сообшение на исходном алфавите и алфавите шифра

Исходное сообщение: I love habr
Зашифрованное: r olev szyi

Тут добавляется еще один параметр — примитивный ключ в виде числа от 1 до 25 (для латиницы). На практике, ключ будет от 4 до 10.

Опять же, для наглядности, возьмем латиницу

a b c d e f g h i j k l m n o p q r s t u v w x y z

И теперь сместим вправо или влево каждую букву на ключевое число значений.

Например, ключ у нас будет 4 и смещение вправо.

Исходный алфавит: a b c d e f g h i j k l m n o p q r s t u v w x y z
Зашифрованный: w x y z a b c d e f g h i j k l m n o p q r s t u v

Пробуем написать сообщение:

hello world

Шифруем его и получаем следующий несвязный текст:

dahhk sknhz

• Шифр Вернама (XOR-шифр)

Простейший шифр на основе бинарной логики, который обладает абсолютной криптографической стойкостью. Без знания ключа, расшифровать его невозможно (доказано Клодом Шенноном).

Исходный алфавит — все та же латиница.

Сообщение разбиваем на отдельные символы и каждый символ представляем в бинарном виде.
Классики криптографии предлагают пятизначный код бодо для каждой буквы. Мы же попробуем изменить этот шифр для кодирования в 8 бит/символ на примере ASCII-таблицы. Каждую букву представим в виде бинарного кода.

Теперь вспомним курс электроники и элемент «Исключающее ИЛИ», также известный как XOR.

XOR принимает сигналы (0 или 1 каждый), проводит над ними логическую операцию и выдает один сигнал, исходя из входных значений.

Если все сигналы равны между собой (0-0 или 1-1 или 0-0-0 и т.д.), то на выходе получаем 0.
Если сигналы не равны (0-1 или 1-0 или 1-0-0 и т.д.), то на выходе получаем 1.

Теперь для шифровки сообщения, введем сам текст для шифровки и ключ такой же длины. Переведем каждую букву в ее бинарный код и выполним формулу сообщение XOR ключ

Например:

сообщение: LONDON
ключ: SYSTEM

Переведем их в бинарный код и выполним XOR:

01001100 01001111 01001110 01000100 01001111 01001110
01010011 01011001 01010011 01010100 01000101 01001101
_______________________________________________________
00011111 00010110 00011101 00010000 00001010 00000011

В данном конкретном примере на месте результирующих символов мы увидим только пустое место, ведь все символы попали в первые 32 служебных символа. Однако, если перевести полученный результат в числа, то получим следующую картину:

31 22 29 16 10 3. 

С виду — совершенно несвязный набор чисел, но мы-то знаем.

• Шифр кодового слова

Принцип шифрования примерно такой же, как у шифра цезаря. Только в этом случае мы сдвигаем алфавит не на определенное число позиций, а на кодовое слово.

Например, возьмем для разнообразия, кириллический алфавит.

абвгдеёжзийклмнопрстуфхцчшщъыьэюя

Придумаем кодовое слово. Например, «Лукоморье». Выдернем из него все повторяющиеся символы. На выходе получаем слово «Лукомрье».

Теперь вписываем данное слово в начале алфавита, а остальные символы оставляем без изменений.

абвгдеёжзийклмнопрстуфхцчшщъыьэюя
лукомрьеабвгдёжзийнпстфхцчшщъыэюя

И теперь запишем любое сообщение и зашифруем его.

"Златая цепь на дубе том"

Получим в итоге следующий нечитаемый бред:

"Адлпля хриы жл мсур пиё"

• Шифр Плейфера

Классический шифр Плейфера предполагает в основе матрицу 5х5, заполненную символами латинского алфавита (i и j пишутся в одну клетку), кодовое слово и дальнейшую манипуляцию над ними.

Пусть кодовое слово у нас будет «HELLO».

Сначала поступаем как с предыдущим шифром, т.е. уберем повторы и запишем слово в начале алфавита.

Теперь возьмем любое сообщение. Например, «I LOVE HABR AND GITHUB».

Разобьем его на биграммы, т.е. на пары символов, не учитывая пробелы.

IL OV EH AB RA ND GI TH UB.

Если бы сообщение было из нечетного количества символов, или в биграмме были бы два одинаковых символа (LL, например), то на место недостающего или повторившегося символа ставится символ X.

Шифрование выполняется по нескольким несложным правилам:

1) Если символы биграммы находятся в матрице на одной строке — смещаем их вправо на одну позицию. Если символ был крайним в ряду — он становится первым.

Например, EH становится LE.

2) Если символы биграммы находятся в одном столбце, то они смещаются на одну позицию вниз. Если символ находился в самом низу столбца, то он принимает значение самого верхнего.

Например, если бы у нас была биграмма LX, то она стала бы DL.

3) Если символы не находятся ни на одной строке, ни на одном столбце, то строим прямоугольник, где наши символы — края диагонали. И меняем углы местами.

Например, биграмма RA.

По этим правилам, шифруем все сообщение.

IL OV EH AB RA ND GI TH UB.
KO HY LE HG EU MF BP QO QG

Если убрать пробелы, то получим следующее зашифрованное сообщение:

KOHYLEHGEUMFBPQOQG

Поздравляю. После прочтения этой статьи вы хотя бы примерно понимаете, что такое шифрование и знаете как использовать некоторые примитивные шифры и можете приступать к изучению несколько более сложных образцов шифров, о которых мы поговорим позднее.

Спасибо за внимание.

Перевод информации в двоичный код – что это такое, его виды, расшифровка

Оглавление:

1. Что такое двоичный код?
2. Разрядность двоичного кода
3. Расшифровка двоичного кода
4. Виды двоичных кодов

Всем известна такая способность компьютеров, как вычисление больших групп данных практически за считанные секунды. Однако не каждый знает, что это умение электронных машин зависит от наличия тока и напряжения.

Что такое двоичный код?

Как же компьютеру удаётся быстро обрабатывать огромные объёмы информации? Помогает ему в этом двоичная система исчисления. Данные, поступающие в это умное устройство, выглядят как единицы и нули. Каждой единице и каждому нулю соответствует определённое состояние электропровода:

• 1 — высокое напряжение.
• 0 — низкое.

Или же для единиц — наличие напряжения, а для нулей — отсутствие.

Основой двоичной системы исчисления являются двоичные коды. Что такое двоичный код?

Процесс, когда данные преобразуются в нули и единицы, называют «двоичная конверсия», а окончательное их обозначение — «двоичный код».

Разрядность двоичного кода

Все двоичные числа являются совокупностью битов, то есть, единиц и нулей, а каждый бит является одним разрядом или одной позицией в двоичном числе. Часто в задачах по информатике встречается вопрос, какое количество информации несёт тот или иной двоичный код. Следует знать, что в каждой цифре двоичного кода содержится количество информации, которое равно одному биту.

Что такое разрядность двоичного кода? Если смотреть с точки зрения арифметики, то под разрядностью понимается место, которое занимает цифра при записи чисел. Тогда под разрядностью двоичного кода подразумевается количество мест знаков (разрядов) или количество битов, которые заранее отведены для того, чтобы записать число.

Расшифровка двоичного кода

Как же расшифровать двоичный код? Десятичное обозначение основано на десятичной системе исчисления, которую обычно используют в повседневной жизни и числовые значения здесь представлены в виде десяти цифр от нуля до девяти. Каждое из мест в числах в десять раз больше по ценности, чем место, находящееся справа. Для представления числа больше 9 в десятичной системе используется ноль, который ставится справа. А единица расположена слева на следующем, более ценном месте.

Подобным образом устроена и двоичная система, в которой используют только две цифры — ноль и единицу. Места слева ценнее в два раза, чем места справа. Так, для двоичного кода характерно, что одноместными числами могут быть только 0 и 1, а для любых чисел больше единицы требуется уже 2 места.

После 0 и 1 следуют такие двоичные числа:

• 10 (то есть, 1,0).
• 11 (1,1).
• 100 (1,0,0).

В двоичной системе 100 — это эквивалент цифры 4 десятичной системы. Таким образом, любое число можно выразить в виде двоичного кода, но оно будет занимать больше места. Также, закрепив за каждой буквой алфавита определённые двоичные числа, можно осуществить перевод в двоичный код любое слово.

Видео о переводе чисел в двоичный код

К примеру, для передачи сообщения по цифровому каналу связи, его кодируют, то есть, сопоставляют каждый символ исходного сообщения с некоторым кодом (кодовым словом). Для этого используются двоичные коды — последовательность единиц и нулей.

Например, чтобы закодировать слово «мама» выбирается следующий код:

• М — 00.
• А — 1.
• Ы — 01.
• Л — 0.
• У — 10.

Пробел — 11.

Закодированные буквы соединятся в одну битовую строчку и будут переданы по сети в таком виде:

МАМА МЫЛА ЛАМУ → 0010011100010111010010

После того как эта строка будет доставлена к пункту назначения, следует решить проблему восстановления исходного сообщения. Так, получив сообщение «001001», его раскодирование можно осуществить несколькими способами. К примеру, предположив, что оно состоит только из букв Л (код 0) и А (код 1), получится:

ЛЛАЛЛАААЛЛЛАЛАААЛАЛЛАЛ

Это значит, что вышеприведённый код не декодируется однозначно. Однозначно декодируемые коды — это такие коды, в которых любые кодовые сообщения расшифровываются только одним способом.

Равномерные коды

Данная проблема решается путём правильного разбития битовой цепочки на отдельно закодированные слова. Это можно сделать, к примеру, с использованием равномерного кода, длина слов в котором всегда одинакова. К примеру, данная фраза состоит из шести символов, а это значит, что можно применить трехбитный код.

Например, если закодировать вышеприведённую фразу с помощью такого кода:

• М — 000.
• А — 001.
• Ы — 010.
• Л — 011.
• Пробел — 101, то получится следующее:

МАМА МЫЛА ЛАМУ → 000001000001101000010011001101011001000100

Это сообщение имеет длину 42 бита. Несмотря на то что оно длиннее, чем первое, состоящее всего из 22 бит, его значительно легче разобрать на отдельные слова для раскодирования:

000 001 000 001 101 000 010 011 001 101 011 001 000 100

М  А  М  А  _  М  Ы  Л  А  _  Л  А  М  У 

Хотя такой равномерный код нельзя назвать экономичным, зато его можно однозначно декодировать.

Видео о переводе букв в двоичный код

Неравномерные коды

Неравномерный двоичный код — что это такое? Его иногда применяют для сокращения длины сообщений. В неравномерном коде кодовое слово, соответствующее определённому символу в алфавите, может отличаться по длине от других слов.

Например, если использовать для кодирования «Мама мыла ламу» такой код:

• М — 01.
• А — 00.
• Ы — 1011
• Л — 100.
• У — 1010.
• Пробел — 11, то получится:

МАМА МЫЛА ЛАМУ → 0100010011011011100001110000011010

Данное сообщение состоит из 34 бит. Эту битовую цепочку можно декодировать однозначно, поскольку в первой букве — М, имеющей код 01, код является уникальным, ведь другие кодовые слова не начинаются с 01. Таким же образом можно определить вторую букву — А. Свойство, когда кодовые слова не совпадают с началом других кодовых слов, называют условием Фано, а коды, декодируемые с помощью свойства Фано, называются префиксными.

Префиксные коды отличаются важным практическим значением — с их помощью декодируются символы получаемых сообщений по мере их поступления, не ожидая, когда всё сообщение придёт к получателю.

Виды двоичных кодов

Для представления целых чисел существуют следующие виды двоичных кодов:

• Знаковые.
• Беззнаковые.

Отрицательные числа могут быть представлены только в знаковом виде. Хранение целых чисел в компьютере осуществляется в формате с фиксированной запятой.

Беззнаковые коды

В целых беззнаковых двоичных кодах все двоичные разряды представлены в степени цифры 2:

Значение минимально возможного числа равняется нулю, а максимальное определяется по формуле:

С помощью этих двух чисел определяется диапазон чисел, представленных в виде двоичного кода.

• Если представлено восьмиразрядное беззнаковое целое число, то диапазон чисел записывается с помощью кода: 0…255.
• Если представлен шестнадцатиразрядный код — 0…65535.

В восьмиразрядных процессорах такие числа хранятся в двух ячейках памяти, которые расположены в соседних адресах. Работа с подобными числами осуществляется с помощью специальных команд.

Знаковые коды

В прямых целых знаковых кодах представление знака числа осуществляется с помощью старшего разряда в слове. Для прямого знакового кода для обозначения знака «+» используется ноль, а знака «-» — единица. При введении знакового разряда произойдёт смещение диапазона чисел в сторону отрицательных значений.

• Двоичное восьмиразрядное знаковое целое число записывается с помощью такого диапазона: -127…+127.
• Шестнадцатиразрядный код будет записан в диапазоне: -32767…+32767.

В восьмиразрядных процессорах такие числа хранятся также в двух ячейках памяти, адреса которых расположены рядом.

В качестве недостатка этого кода можно назвать необходимость раздельной обработки знакового и цифрового разрядов. Программы, работающие в таких алгоритмах, являются довольно сложными. Для того чтобы выделить и изменить знаковый разряд, придётся применить метод маскирования разрядов, что приводит к увеличению размера программы и уменьшению её быстродействия. Для предотвращения возникновения различий в алгоритме обработки цифрового и знакового разрядов используются обратные двоичные коды.

Отличие знаковых обратных двоичных кодов от прямых заключается в образовании отрицательных чисел с помощью инвертирования всех разрядов чисел. Однако при этом цифровой и знаковый разряды не имеют различий. Такие коды позволяют значительно упростить алгоритм работы.

Но, несмотря на это, работа с обратными кодами требует специального алгоритма для того, чтобы распознавать знаки, вычислять абсолютные значения чисел, восстанавливать знак результата числа. Также прямой обратный код числа требует для запоминания нуля использовать два кода в то время, когда известно, что ноль является положительным числом, и отрицательным он быть не может никогда.

А Вы знаете, что такое двоичный код и как его расшифровать? Помогли ли Вам в жизни эти знания? Расскажите об этом в комментариях.

Двоичный код — представление данных в виде комбинации двух знаков

Двоичный код — это представление информации в комбинации 2-х знаков 1 или 0, как говориться в программирование есть или нет, истина или лож, true или false. Обычному, человеку трудно понять, как информацию можно представить в виде нулей и единиц. Я постараюсь немного прояснить эту ситуацию.

На самом деле двоичный код — это просто! Например, любую букву алфавита можно представить в виде набора нулей и единиц. Например, буква H латинского алфавита будет иметь такой вид в двоичной системе – 01001000, буква E – 01000101, бука L имеет такое двоичное представление – 01001100, P – 01010000.

Теперь не сложно догадаться, что для того чтобы написать английское слово HELP на машинном языке нужно использовать вот такой двоичный код:

01001000 01000101 01001100 01010000

Именно такой код использует для своей работы наш домашний компьютер. Обычному человеку читать такой код очень сложно, а вот для вычислительных машин он самый понятный.

Двоичный код (машинный код) в наше время используется в программировании, ведь компьютер работает именно благодаря двоичному коду. Но не стоит думать, что процесс программирования сводится к набору единиц и нулей. Специально, чтобы упростить понимание между человеком и компьютером придумали языки программирования (си++, бейсик и т.п.). Программист пишет программу на понятом ему языке, а потом с помощью специальной программы-компилятора переводит свое творение в машинный код, который и запускает компьютер.

Переводим натуральное число десятичной системы счисления в двоичную

Берем нужное число, у меня это будет 5, делим число на 2:
5 : 2 = 2,5 есть остаток, значит, первое число двоичного кода будет 1(если нет — 0). Откидываем остаток и снова делим число на 2:
2 : 2 = 1 ответ без остатка, значит, второе число двоичного кода будет — 0.Снова делим результат на 2:
1 : 2 = 0.5 число получилось с остатком значит записываем 1.
Ну а так как результат равный 0 нельзя больше поделить, двоичный код готов и в итоге у нас получилось число двоичного кода 101. Я думаю, переводить из десятичного числа в двоичное мы научились, теперь научимся делать наоборот.

Переводим число из двоичной системы в десятичную

Тут тоже достаточно просто, давайте наше с вами двоичное число пронумеруем, начинать необходимо с нуля с конца числа.

101 это 1^2 0^1 1^0.

Что из этого вышло? Мы предали степени числам! теперь по формуле:

(x * 2^y) + (x * 2^y) + (x * 2^y)

где x — порядковое число двоичного кода
y — степень этого числа.
Формула будет растягиваться в зависимости от размера вашего числа.
Получаем:

(1 * 2^2) + (0 * 2^1) + (1 * 2^0) = 4 + 0 + 1 = 5.

История двоичной системы счисления

Впервые двоичную систему предложил Лейбиц, он полагал, что данная система поможет в сложных математических вычислениях, да и вообще принесет пользу науке. Но по некоторым данным, до того как Лейбиц предложил двоичную систему счисления в Китае на стене появилась надпись, которую можно было расшифровать используя двоичный код. На этой надписи были нарисованы длинные и короткие палочки и если предположить, что длинная это 1, а короткая 0, вполне возможно, что в Китае идея двоичного кода ходила за много лет до его изобретения. Хотя расшифровка кода найденного на стене выявила там простое натуральное число, но все же факт остается фактом.

что это и зачем придумали эту систему

 

Сегодня я по-особому рад своей встрече с вами, дорогие мои читатели, ведь я чувствую себя учителем, который на самом первом уроке начинает знакомить класс с буквами и цифрами. А поскольку мы живем в мире цифровых технологий, то я расскажу вам, что такое двоичный код, являющийся их основой.

Начнем с терминологии и выясним, что означит двоичный. Для пояснения вернемся к привычному нам исчислению, которое называется «десятичным». То есть, мы используем 10 знаков-цифр, которые дают возможность удобно оперировать различными числами и вести соответствующую запись.

Следуя этой логике, двоичная система предусматривает использование только двух знаков. В нашем случае, это всего лишь «0» (ноль) и «1» единица. И здесь я хочу вас предупредить, что гипотетически на их месте могли бы быть и другие условные обозначения, но именно такие значения, обозначающие отсутствие (0, пусто) и наличие сигнала (1 или «палочка»), помогут нам в дальнейшем уяснить структуру двоичного кода.

 

Зачем нужен двоичный код?

До появления ЭВМ использовались различные автоматические системы, принцип работы которых основан на получении сигнала. Срабатывает датчик, цепь замыкается и включается определенное устройство. Нет тока в сигнальной цепи – нет и срабатывания. Именно электронные устройства позволили добиться прогресса в обработке информации, представленной наличием или отсутствием напряжения в цепи.

Дальнейшее их усложнение привело к появлению первых процессоров, которые так же выполняли свою работу, обрабатывая уже сигнал, состоящий из импульсов, чередующихся определенным образом. Мы сейчас не будем вникать в программные подробности, но для нас важно следующее: электронные устройства оказались способными различать заданную последовательность поступающих сигналов. Конечно, можно и так описать условную комбинацию: «есть сигнал»; «нет сигнала»; «есть сигнал»; «есть сигнал». Даже можно упростить запись: «есть»; «нет»; «есть»; «есть».

Но намного проще обозначить наличие сигнала единицей «1», а его отсутствие – нулем «0». Тогда мы вместо всего этого сможем использовать простой и лаконичный двоичный код: 1011.

Безусловно, процессорная техника шагнула далеко вперед и сейчас чипы способны воспринимать не просто последовательность сигналов, а целые программы, записанные определенными командами, состоящими из отдельных символов.

Но для их записи используется все тот же двоичный код, состоящий из нулей и единиц, соответствующий наличию или отсутствию сигнала. Есть он, или его нет – без разницы. Для чипа любой из этих вариантов – это единичная частичка информации, которая получила название «бит» (bit — официальная единица измерения).

Условно, символ можно закодировать последовательностью из нескольких знаков. Двумя сигналами (или их отсутствием) можно описать всего четыре варианта: 00; 01;10; 11. Такой способ кодирования называется двухбитным. Но он может быть и:

• Четырехбитным (как в примере на абзац выше 1011) позволяет записать 2^4 = 16 комбинаций-символов;
• Восьмибитным (например: 0101 0011; 0111 0001). Одно время он представлял наибольший интерес для программирования, поскольку охватывал 2^8 = 256 значений. Это давало возможность описать все десятичные цифры, латинский алфавит и специальные знаки;
• Шестнадцатибитным (1100 1001 0110 1010) и выше. Но записи с такой длинной – это уже для современных более сложных задач. Современные процессоры используют 32-х и 64-х битную архитектуру;

Скажу честно, единой официальной версии нет, то так сложилось, что именно комбинация из восьми знаков стала стандартной мерой хранящейся информации, именуемой «байт». Таковая могла применяться даже к одной букве, записанной 8-и битным двоичным кодом. Итак, дорогие мои друзья, запомните пожалуйста (если кто не знал):

8 бит = 1 байт.

Так принято. Хотя символ, записанный 2-х или 32-х битным значением так же номинально можно назвать байтом. Кстати, благодаря двоичному коду мы можем оценивать объемы файлов, измеряемые в байтах и скорость передачи информации и интернета (бит в секунду).

 

Бинарная кодировка в действии

Для стандартизации записи информации для компьютеров было разработано несколько кодировочных систем, одна из которых ASCII, базирующаяся на 8-и битной записи, получила широкое распространение. Значения в ней распределены особым образом:

• первый 31 символ – управляющие (с        00000000 по 00011111). Служат для служебных команд, вывода на принтер или экран, звуковых сигналов, форматирования текста;
• следующие с 32 по 127       (00100000 – 01111111) латинский алфавит и вспомогательные символы и знаки препинания;
• остальные, до 255-го           (10000000 – 11111111) –     альтернативная, часть таблицы для специальных задач и отображения национальных алфавитов;

Расшифровка значений в ней показано в таблице.

Если вы считаете, что «0» и «1» расположены в хаотичном порядке, то глубоко ошибаетесь. На примере любого числа я вам покажу закономерность и научу читать цифры, записанные двоичным кодом. Но для этого примем некоторые условности:

• Байт из 8 знаков будем читать справа налево;
• Если в обычных числах у нас используются разряды единиц, десятков, сотен, то здесь (читая в обратном порядке) для каждого бита представлены различные степени «двойки»: 256-124-64-32-16-8- 4-2-1;
• Теперь смотрим на двоичный код числа, например 00011011. Там, где в соответствующей позиции есть сигнал «1» – берем значения этого разряда и суммируем их привычным способом. Соответственно: 0+0+0+32+16+0+2+1 = 51. В правильности данного метода вы можете убедиться, взглянув на таблицу кодов.

Теперь, мои любознательные друзья, вы не только знаете что такое двоичный код, но и умеете преобразовать зашифрованную им информацию.

 

Язык, понятный современной технике

Конечно, алгоритм считывания двоичного кода процессорными устройствами намного сложнее. Но зато его помощью можно записать все что угодно:

• Текстовую информацию с параметрами форматирования;
• Числа и любые операции с ними;
• Графические и видео изображения;
• Звуки, в том числе и выходящие и за предел нашей слышимости;

Помимо этого, благодаря простоте «изложения» возможны различные способы записи бинарной информации:

• Дырочки на перфоленте и перфокарте, соответствующие «1», были одновременно и одним из языков программирования;

• Чередование ровной поверхности и выжженных впадин используется в CD и DVD дисках;

• Состоянием отдельных элементов группы транзисторов в USB накопителях;
• Изменением магнитного поля на HDD дисках;

Дополняет преимущества двоичного кодирования практически неограниченные возможности по передаче информации на любые расстояния. Именно такой способ связи используется с космическими кораблями и искусственными спутниками.

Так что, сегодня двоичная система счисления является языком, понятным большинству используемых нами электронных устройств. И что самое интересное, никакой другой альтернативы для него пока не предвидится.

Думаю, что изложенной мною информации для начала вам будет вполне достаточно. А дальше, если возникнет такая потребность, каждый сможет углубиться в самостоятельное изучение этой темы.

Я же буду прощаться и после небольшого перерыва подготовлю для вас новую статью моего блога, на какую-нибудь интересную тему.

Лучше, если вы сами ее мне подскажите 😉

До скорых встреч.

 

 

Text To Hex / Hex To Text

Описание: Text в Hex / Hex в Text — преобразование текста в шестнадцатеричные коды его символов и обратно. Работает для текста в кодировках Windows-1251, UTF-16. Декодирует UTF-8 текст с кириллицей, который при закодировании в JSON переводится штатной php функцей json_encode() в \uXXXX кодировку.

В математике и вычислениях шестнадцатеричная (также базовая 16, или шестнадцатеричная) — это позиционная система счисления с основанием 16. Он использует шестнадцать различных символов, чаще всего символы 0-9 для представления значений от нуля до девяти, и A, B, C, D, E, F (или альтернативно a, b, c, d, e, f) для представления значений от десяти до пятнадцати.

Шестнадцатеричные цифры широко используются разработчиками компьютерных систем и программистами. Поскольку каждая шестнадцатеричная цифра представляет собой четыре двоичные цифры (биты), она позволяет более удобное для человека представление двоичных кодированных значений. Одна шестнадцатеричная цифра представляет собой кусочек (4 бита), который составляет половину октета или байта (8 бит). Например, один байт может иметь значения в диапазоне от 00000000 до 11111111 в двоичном виде, но это может быть более удобно представлено как 00 до FF в шестнадцатеричном виде.

В контексте, не относящемся к программированию, индекс обычно используется, чтобы дать rix, например, десятичное значение 10,995 было бы выражено в шестнадцатеричном виде как 2AF316. Несколько обозначений используются для поддержки шестнадцатеричного представления констант в языках программирования, обычно включающих префикс или суффикс. Префикс «0x» используется в языках C и связанных языках, где это значение может быть обозначено как 0x2AF3.

Ресурсы:

Бинарный код — это… Что такое Бинарный код?

Двоичная система счисления — это позиционная система счисления с основанием 2. В этой системе счисления натуральные числа записываются с помощью всего лишь двух символов (в роли которых обычно выступают цифры 0 и 1).

Двоичная система используется в цифровых устройствах, поскольку является наиболее простой и соответствует требованиям:

• Чем меньше значений существует в системе, тем проще изготовить отдельные элементы, оперирующие этими значениями. В частности, две цифры двоичной системы счисления могут быть легко представлены многими физическими явлениями: есть ток — нет тока, индукция магнитного поля больше пороговой величины или нет и т. д.
• Чем меньше количество состояний у элемента, тем выше помехоустойчивость и тем быстрее он может работать. Например, чтобы закодировать три состояния через величину индукции магнитного поля, потребуется ввести два пороговых значения, что не будет способствовать помехоустойчивости и надёжности хранения информации.
• Двоичная арифметика является довольно простой. Простыми являются таблицы сложения и умножения — основных действий над числами.
• Возможно применение аппарата алгебры логики для выполнения побитовых операций над числами.

В цифровой электронике одному двоичному разряду в двоичной системе счисления соответствует один двоичный логический элемент (инвертор с логикой на входе) с двумя состояниями (открыт, закрыт).

1 + 0 = 1
1 + 1 = 10
10 + 10 = 100

Таблица умножения двоичных чисел

0 • 0 = 0
0 • 1 = 0
1 • 0 = 0
1 • 1 = 1

Использование двоичной системы при измерении дюймами

При указании линейных размеров в дюймах по традиции используют двоичные дроби, а не десятичные, например: 5¾″, 7¹⁵/₁₆″, 3¹¹/₃₂″ и т. д.

Преобразование чисел

Для преобразования из двоичной системы в десятичную используют следующую таблицу степеней основания 2:

512

256

128

64

32

16

8

4

2

1

Начиная с цифры 1 все цифры умножаются на два. Точка, которая стоит после 1 называется двоичной точкой.

Преобразование двоичных чисел в десятичные

Допустим, вам дано двоичное число 110011. Какому числу оно эквивалентно? Чтобы ответить на этот вопрос, прежде всего запишите данное число следующим образом:

512	256	128	64	32	16	8	4	2	1
				1	1	0	0	1	1
				32	+16			+2	+1

Затем, начиная с двоичной точки, двигайтесь влево. Под каждой двоичной единицей напишите её эквивалент в строчке ниже. Сложите получившиеся десятичные числа. Таким образом, двоичное число 110011 равнозначно 51.
Либо .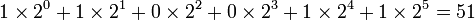

Преобразование методом Горнера

Для того, что бы преобразовывать числа из двоичной в десятичную систему данным методом, надо суммировать цифры слева-направо, умножая ранее полученный результат на основу системы (в данном случае 2). Например, двоичное число 1011011 переводится в десятичную систему так: 0*2+1=1 >> 1*2+0=2 >> 2*2+1=5 >> 5*2+1=11 >> 11*2+0=22 >> 22*2+1=45 >> 45*2+1=91 То есть в десятичной системе это число будет записано как 91. Или число 101111 переводится в десятичную систему так: 0*2+1=1 >> 1*2+0=2 >> 2*2+1=5 >> 5*2+1=11 >> 11*2+1=23 >> 23*2+1=47 То есть в десятичной системе это число будет записано как 47.

Преобразование десятичных чисел к ближайшей степени двойки, неменьшей этого числа

Ниже приведена функция, возвращающая число, неменьшее аргумента, и являющееся степенью двух.

unsigned int to_deg_2(unsigned int num){
  int i;
  if ( num == 1 ) return 2;
  for( num-=1,i=1; i < sizeof(unsigned int)*8; i*=2 ) num = num|(num>>i);
  return num+1;
}

Преобразование десятичных чисел в двоичные

Допустим, нам нужно перевести число 19 в двоичное. Вы можете воспользоваться следующей процедурой :

19 /2 = 9  с остатком 1
9  /2 = 4  c остатком 1
4  /2 = 2  с остатком 0
2  /2 = 1  с остатком 0
1  /2 = 0  с остатком 1

Итак, мы делим каждое частное на 2 и записываем в остаток 1 или 0. Продолжать деление надо пока в делимом не будет 1. Ставим числа из остатка друг за другом, начиная с конца. В результате получаем число 19 в двоичной записи (начиная с конца): 10011.

Другие системы счисления

В статье «Системы счисления (продолжение)»^[1] описываются преимущества и недостатки 4-ричной системы счисления по сравнению с двоичной в компьютерах, созданных Хитогуровым.

См. также

Ссылки

1. ↑ http://potan.livejournal.com/91399.html Системы счисления (продолжение)

Wikimedia Foundation. 2010.

Онлайн калькулятор: Двоично-десятичное кодирование

После калькулятора Перевод дробных чисел из одной системы счисления в другую я думал, что тема с системами счисления уже закрыта. Но, как оказалось, еще нет.
Как я писал по ссылке выше, основная проблема при переводе дробных чисел из одной системы счисления в другую это потеря точности, когда, например, десятичное число 0.8 нельзя перевести в двоичное без погрешности.

Поскольку десятичные числа активно используются человеком, а двоичные — компьютером, этой проблемой в применении к двоичной и десятичной системам однажды уже озаботились какие-то светлые умы и придумали двоично-десятичное кодирование (binary coded decimal, BCD). Суть идеи проста — берем и для каждой десятичной цифры заводим байт. И в этом байте тупо пишем значение десятичной цифры в двоичном коде. Тогда число, например, 0.8 будет 0.00001000. Потом, правда, подумали еще, и решили, что раз уж верхняя часть байта всегда пустует (так как максимум 9 — это 1001), то давайте для каждой десятичной цифры заводить полубайт. И назвали это упакованным двоично-десятичным кодированием (packed BCD).
В упакованном кодировании наше 0.8 будет 0.1000, а какое-нибудь 6.75 будет 0110.01110101.

Прекрасная идея, конечно. Точность не теряется, человек может двоичные числа переводить в десятичные и наоборот прямо на лету, округлять можно, откидывая лишнее. Но как-то не получила она широкого распространения, потому как жизнь машинам она, наоборот, усложняла — и памяти для хранения чисел надо больше, и операции над числами реализовать сложнее. Так и осталась забавным курьезом, и я бы ничего о ней не знал, если бы пользователи не подсказали, что есть такая.

Ну и небольшой калькулятор по этому поводу — вводим либо десятичное число, либо двоичное, подразумевая, что это упакованный двоично-десятичный код, и получаем результат. Понятно, что все преобразования можно проделать и в уме, и в этом ее преимущество; но зачем же лишний раз мозги напрягать, верно?

Двоично-десятичное кодирование

Десятичное число, либо двоично-десятичный код

Десятичное число

 

Двочно-десятичный код

 

save Сохранить share Поделиться extension Виджет