Расчет сопротивления цепи
Расчет сопротивления цепи необходим при решении различных задач по электротехнике. Суть заключается в приведении сложной разветвленной электрической цепи к цепи с единственным эквивалентным сопротивлением, которую называют простой электрической цепью.
Пример 1
Цепь в данном примере состоит из двух последовательно соединенных сопротивлений, следовательно, их общее сопротивление будет равно сумме их сопротивлений. Подробнее о видах соединений тут.
Допустим, что R1=10 Ом R2=20 Ом, тогда
Пример 2
Два сопротивления соединены параллельно, значит при сворачивании схемы, общее сопротивление будет равно (значения R1,R2 такие же как и в примере 1)
Можно заметить, что при параллельном соединении общее сопротивление меньше, чем при последовательном в несколько раз.
Пример 3
В данном примере ситуация аналогична примеру 2, за тем лишь исключением, что сопротивлений три. Тогда общее сопротивление будет равно (R1,R2 прежние, R3=105 Ом)
Пример 4
Чтобы рассчитать общее сопротивление смешанного соединения проводников, необходимо для начала найти общее сопротивление резисторов R1 и R2 соединенных параллельно, а затем общее сопротивление, как сумму R12 и R3 соединенных последовательно.
Пример 5
Данная электрическая цепь сложнее, чем предыдущие, но как можно увидеть, она также состоит из последовательно или параллельно соединенных сопротивлений, которые можно постепенно сворачивать, приводя цепь к единственному эквивалентному сопротивлению R.
R4=20 Ом, R5=40 Ом, R6=15 Ом
Путем сворачивания цепи с помощью преобразований последовательно и параллельно соединенных проводников, можно максимально упростить для дальнейшего расчета сколь угодно сложную схему. Исключением служат цепи содержащие сопротивления, соединенные по схеме звезда и треугольник.
Расчет входного сопротивления. Расчет комплексного входного сопротивления цепи
ОБЩИЕ ПОЛОЖЕНИЯ
Для расчета транзисторных усилителей используются два способа:
Согласно ЕСКД по выполнению электрических схем в процессе проектирования необходимо составлять перечень элементов принципиально электронных схем (по аналогии со спецификацией механических устройств).
Для составления перечня элементов проектируемого усилителя, элементы его принципиальной схемы необходимо пронумеровать с использованием буквенно-цифровой системы обозначений, принятой в ГОСТ.
С-конденсаторы;
D-микросхемы;
DA-аналоговые микросхемы;
DD-цифровые микросхемы.
L-индуктивности;
R-резисторы;
VD-полупроводниковые диоды;
VT-транзисторы.
Нумерация элементов принципиальной схемы осуществляется в направлении «сверху вниз » и «слева направо ».
Краткие теоретические сведения
Схемы транзисторных усилителей классифицируются по названию заземленного (общего) электрода транзистора-эмиттера, коллектора и базы. Существует три схемы включения биполярных транзисторов: схемы с общим эмиттером
Усилительные свойства транзистора характеризуются следующими статическими параметрами:
Статический коэффициент передачи тока эмиттера транзистора;
статический коэффициент передачи тока базы транзистора.
Параметры a и b связаны соотношениями:
a=b/(1+b) ; b=a/(1-a).
Схема с ОЭ является усилителем мощности входного сигнала. В данной схемевходной и выходной сигналы находятся в противофазе (сдвиг по фазе на угол ). Усилитель с ОЭ обладает сравнительно низким входным сопротивлением и достаточно высоким выходным сопротивлением (импедансом). Вместе с этим схема с ОЭ обеспечивает усиление, как по току
Для обеспечения заданного коэффициента усиления по переменному току в схеме с ОЭ резистор R э в эмиттерной цепи транзистора шунтируется конденсатором С э. Поэтому импеданс эмиттерной цепи соответствует параллельному соединению резистора R э и емкостного сопротивления конденсатора С э.
Комплексный коэффициент усиления в схеме с ОЭ определяется выражением:
,
где R k , R э – активное сопротивление в коллекторной и эмиттерной цепи транзистора соответственно; фазовый сдвиг в эмиттерной цепи транзистора; круговая частота входного сигнала.
Рисунок 1 – Электрическая схема усилителя с общим эмиттером
Методика расчета усилителя с общим эмиттером
Расчет усилителей осуществляется в направлении с
1. Выбор транзистора (по индивидуальному заданию)
Выбор транзистора осуществляется по типу проводимости и по
параметру b.(bºh 21э -статический коэффициент передачи тока базы для
различных транзисторов b лежит в диапазоне 10…150).
2. Расчет емкости разделительного конденсатора на выходе
Разделительный конденсатор С3 не пропускает постоянный потенциал коллектора в нагрузку. Совместно с сопротивлением нагрузки R н =R5, конденсатор С3 образует RС-цепь, которая подавляет низкие частоты и пропускает высокие частоты.
Величина конденсатора С3 определяются по формуле:
С 3 расч. ³1/(2pf сигн R н).
Рассчитанное значение емкости С3 будет соответствовать ослаблению входного сигнала в раз относительно сигнала на более высоких частотах. Для уменьшения ослабления входного сигнала и расширения за счет этого полосы пропускания усилителя расчетное значение емкости С 3расч увеличиваются на 1-2 порядка (в 10-100 раз).
3. Расчет тока коллектора
При заданном значении тока эмиттера I э ток коллектора I к определяется по формуле
4. Расчет сопротивления в коллекторной цепи транзистора
Для обеспечения усиления сигнала с минимальными искажениями потенциал коллектора относительно земли в статическом режиме U к0 (при отсутствии входного сигнала), выбирается из условия:
U к0 =0,5Е пит.
Сопротивление R к в цепи коллектора определяется по закону Ома
R к =R3= Uк 0 / I к =0,5Е пит /I к.
Определяется мощность Р 3 , рассеиваемая на сопротивлении R3 в коллекторной цепи транзистора
Р 3 = (I k) 2 *R3.
5. Расчет эквивалентного сопротивления нагрузки переменному току
При достаточно большой емкости разделительного конденсатора С3 эквивалентное сопротивление нагрузки на переменном токе R н.экв.оэ определяется параллельным соединением коллекторного резистора R к =R3 и сопротивления нагрузки R н =R5
R н.экв.оэ =.
6. Расчет сопротивления в цепи эмиттера
Сопротивление R э =R4 обеспечивает температурную стабилизацию режима транзистора по постоянному току. Для уменьшения влияния температуры на параметры усилителя в целом потенциал эмиттера U э относительно земли выбирается в диапазоне 1…2 В. Обычно U э =1В.
Сопротивление R э определяется по закону Ома:
R э = U э / I э.
Ток эмиттера I э выбирается в диапазоне (0,5…1,0)мА, либо задается
индивидуально.
Определяется мощность Р 4 , рассеиваемая на сопротивлении R э =R4 в эмиттерной цепи транзистора
Р 4 = (I э) 2 *R4.
7. Расчет входного сопротивления транзистора со стороны базы
Входное сопротивление транзистора со стороны базы h 11 определяется по формуле
h 11 =R э *(b+1).
8. Расчет резистивного делителя в цепи базы транзистора на постоянном токе.
Для температурной стабилизации режима транзистора по постоянному току (при отсутствии входного сигнала) необходимо следить за разностью потенциалов между эмиттером и базой при изменении температуры . Для обеспечения следящей обратной связи по температуре в цепь эмиттера вводится резистор R э =R4, а в цепь базы — резистивный делитель R1, R2, с помощью которого стабилизируется потенциал базы транзистора относительно земли. Если в режиме максимального сигнала ток делителя I д превышает ток базы I б, то потенциал базы U б будет определяться только напряжением питания Е пит и соотношением резисторов R1, R2. Поэтому обеспечения температурной стабилизации режима обеспечивается условие:
I д = Е п /(R1+R2)= I э.
По второму закону Кирхгофа определяется потенциал базы U б:
U б = j d +U э,
где j d — статический потенциал рn-перехода (для германиевых транзисторов j d =0,3…0,4 В; для кремневых транзисторов j d =0,6…0,8В).
По закону Ома определяются резисторы R1, R2:
R2=U б /I д = (j d +U э) /I э;
R1= (E пит -U б)/I д =(E пит -U б)/I э.
Определяются мощности Р 1 , Р 2 рассеиваемые на сопротивлениях делителя R1, R2:
Р 1 = (I д) 2 *R1;
Р 2 = (I д) 2 *R2.
9. Расчет резистивного делителя в цепи базы транзистора на
При усилении сигналов переменного тока шина питания Е пит заземлена через конденсатор фильтра С Ф (имеет нулевой потенциал). Поскольку при достаточно большой емкости С Ф емкостное сопротивление фильтра Х С.Ф достаточно мало (X С.Ф =1/wС Ф ®0), резисторы R1, R2 по переменному току соединены параллельно .
Эквивалентное сопротивление делителя R1, R2 переменному току R д.экв определяется выражением
R д.экв = R1* R2/(R1 + R2).
10. Расчет входного сопротивления усилителя с ОЭ
На низких частотах, несоизмеримых с быстродействием выбранного транзистора, входное сопротивление усилителя R вх является чисто активным и соответствует параллельному соединению сопротивлений h 11 и R д.экв,
R вх. = h 11 * R д.экв / (h 11+ R д.экв).
Примечание . На высоких частотах, соизмеримых с быстродействием выбранного транзистора, сказываются межэлектродные емкости между выводами эмиттер – база , база – коллектор и эмиттер – коллектор . Поэтому в области высоких частот входное сопротивление (импеданс) является комплексной величиной .
11. Расчет входного конденсатора в цепи базы транзистора
Разделительный конденсатор С1 предназначен для отделения постоянной составляющей входного сигнала. Совместно с эквивалентным входным сопротивлением ЭП R вх.экв конденсатор С1 образует RС-цепь, которая не пропускает постоянный потенциал базы U б в источник входного сигнала, подавляет низкие частоты и пропускает высокие частоты.
Величина емкости конденсатора С1 определяется по формуле
С 1 расч. ³1/(2pf сигн R
Расчет входного сопротивления транзистора. Расчет комплексного входного сопротивления цепи
В прошлой статье мы с вами говорили о самой простой схеме смещения транзистора. Эта схема (рисунок ниже) зависит от коэффициента бета , а он в свою очередь зависит от температуры, что не есть гуд. В результате на выходе схемы могут появиться искажения усиливаемого сигнала.
В случае транзистора можно рассчитать вакуумное напряжение и ток короткого замыкания, исключая расчет сопротивления эмиттера, оставив входной генератор активным и вычислив две величины, как показано на рисунке. Вычисление напряжения вакуума происходит немедленно. Поскольку излучатель не связан ни с чем, ток коллектора должен быть противоположен основанию, то есть.
Поскольку существует единственное решение. Так как базовый ток равен нулю, то длительное падение напряжения отсутствует, и поэтому напряжение эмиттера, а затем вакуум действительно. Если бы сопротивление эмиттера присутствовало, счет был бы длиннее. Для оценки тока короткого замыкания следует отметить, что и последовательно, и их голова есть напряжение, поэтому базовый ток стоит. Ток короткого замыкания определяется суммой и так.
Чтобы такого не произошло, в эту схему добавляют еще парочку резисторов и в результате получается схема с 4-мя резисторами:
Резистор между базой и эмиттером назовем R бэ , а резистор, соединенный с эмиттером, назовем R э . Теперь, конечно же, главный вопрос: «Зачем они нужны в схеме?»
И, наконец, разделив его на. Который по-прежнему является выражением. Обычно независимый генератор, оставшийся в схеме, упрощается, и результат не зависит от амплитуды сигнала. В этом случае сигнал, который активирует сеть, является нормальным входом схемы, и он также должен быть упрощен, так как в результате получается передаточная функция.
Прежде чем отказаться от раздела электротехнических методов, представлен формальный и абстрактный метод расчета метода импеданса, матрицы и детерминанта. Метод узлов или потенциала в узлах является очень общим и используется для анализа с калькулятор, позволяющий рассчитать размер сети.
Начнем, пожалуй, с R э .
Как вы помните, в предыдущей схеме его не было. Итак, давайте предположим, что по цепи +Uпит—->R к ——> коллектор—> эмиттер—>R э —-> земля бежит электрический ток, с силой в несколько миллиАмпер (если не учитывать крохотный ток базы, так как I э = I к + I б ) Грубо говоря, у нас получается вот такая цепь:
Основная идея метода узла заключается в том, чтобы написать операционные уравнения схемы, используя потенциалы различных узлов как неизвестные, а также известные термины используются токи входного тока. Генераторы с действующим напряжением должны иметь пилот-сигнал, задаваемый потенциалом на узле, или разность потенциалов между двумя узлами. Схема на рисунке 9 представляет собой обычную схему, подготовленную для анализа метода узлов. Входной сигнал был преобразован в генератор тока, а пилот-генератор теперь управляется напряжением, и его усиление является допустимым.
Следовательно, на каждом резисторе у нас будет падать какое-то напряжение. Его величина будет зависеть от силы тока в цепи, а также от номинала самого резистора.
Чуток упростим схемку:
Матричная система, описывающая схему, где — матрица допуска, может быть написана в поле зрения, если вы знаете метод направленной проводимости, иначе вам нужно сделать некоторую алгебру. Знаки токов принимаются положительно из каждого узла, также для генератора пилот-сигнала, размер пилот-сигнала которого должен быть записан последовательно с этим соглашением.
Также в матрице указаны термины, связанные с ведомым генератором. Поскольку выполняется поиск только импеданса на узле эмиттера, он работает только на матрице допусков, и искомый импеданс действителен. Где он является определителем матрицы допуска, и является алгебраическим дополнением к матрице допусков, удалив второй и второй столбцы, поскольку импеданс на узле 2 должен быть найден относительно ссылки. получает.
R кэ — это сопротивление перехода коллектор-эмиттер. Как вы знаете, оно в основном зависит от базового тока.
В результате, у нас получается простой делитель напряжения , где
И сброса допусков с соответствующими импедансами, которые у вас есть. Тот же результат впервые достигнут с работой со скукой! С формулой Блэкмана мы выходим из электротехнических методов и вступаем в систему ретроактивных электронных схем. Эти схемы, как правило, трудно анализировать, поскольку они требуют решения систем уравнений, поскольку экспериментальный генератор имеет величину пилот-сигнала, которая зависит от самого генератора. Метод Блэкмена позволяет вам отбросить эту зависимость, а учетные записи стали намного проще.
Где импеданс между двумя мертвыми терминалами, то есть с выбранным управляемым генератором, отменяется, устанавливается с нулевым коэффициентом усиления. Величины — это коэффициенты возврата, рассчитанные относительно выбранного управляемого генератора и терминалы, на которых он находится хочет найти импеданс короткого замыкания или разомкнутую цепь.
Мы видим, что на эмиттере уже НЕ БУДЕТ напряжения в ноль Вольт, как это было в прошлой схеме. Напряжение на эмиттере уже будет равняться падению напряжения на резисторе R э .
А чему равняется падение напряжения на R э ? Вспоминаем закон Ома и высчитываем:
В случае импеданса эмиттера имеется только один ведомый генератор, на котором будут выполняться различные операции. Помните, что отмена ведомого генератора означает, что его коэффициент усиления равен нулю, поэтому генератор тока превращается в разомкнутую цепь. Операция отмены — это «электротехническая» операция, выполняемая только на ведомом генераторе. Транзистор не отключается, что также меняет только усиление генератора, сопротивление и, возможно, все другие параметры зависят от коэффициента усиления, который они остаются неизменными: он работает на управляемом генераторе, а не на транзисторной модели.
Как мы видим из формулы, напряжение на эмиттере будет равняться произведению силы тока в цепи на номинал сопротивления резистора R э . С этим вроде как разобрались. Для чего вся эта канитель, мы разберем чуть ниже.
Какую же функцию выполняют резисторы R б и R бэ ?
Расчет отчетов о возврате
Сопротивление мертвого состояния оценивается, потому что больше нет генераторов и, конечно. Расчет коэффициента возврата выполняется с помощью следующих простых шагов. Расчет должен повторяться два раза, один с клеммами разомкнутой цепи и один в коротком замыкании. Часто один из двух отчетов о возврате является нулевым.
Две схемы для расчета коэффициентов возврата показаны на рисунке. Модельный генератор тока транзистора был удален и подключен к короткому замыканию, в противном случае генератор тока разомкнутой цепи сильно недоволен! Пилотный генератор все еще управляется током, который должен оцениваться в соответствии с тестовым током. Обратите внимание, что тестовый генератор является токовым и толкает ток в том же направлении, что и исходный генератор пилот-сигнала.
Именно эти два резистора представляют из себя опять же простой делитель напряжения . Они задают определенное напряжение на базу, которое будет меняться, если только поменяется +Uпит , что бывает крайне редко. В остальных случаях напряжение на базе будет стоять мертво.
Если клеммы, на которых должен быть закорочен импеданс, тестовый генератор не может запускать базовый ток. Из которого получается коэффициент краткосрочного возврата. В этом случае тестовый генератор может перемещать движущийся ток, и вы видите, что. При расчете коэффициента возврата отрицательный знак неизбежен!
Даже если это отношение возврата было нулевым, это означало бы, что схема не реагирует. Если бы оба они отличались от нуля и равны, это означало бы, что импеданс, который вы ищете, находится за пределами цикла обратной связи. Наконец, если одно из двух коэффициентов возвра
Импеданс. Расчёт
Импеданс (impedance) – комплексное, полное сопротивление переменному току электрической цепи с активным и реактивным сопротивлением.
Импеданс и общий сдвиг фаз для синусоидального тока можно рассчитать исходя из последовательного или параллельного соединения элементов цепи.
Последовательное соединение
При последовательном соединении, согласно Закону Ома для переменного тока,
во всех элементах цепи ток будет общим I = U/Z, а значения напряжений на каждом элементе определятся пропорционально его сопротивлению:
на выводах резистора UR = IR; на выводах конденсатора UC = IXC; на выводах катушки UL = IXL.
Векторы индуктивной и ёмкостной составляющих напряжения направлены в противоположные стороны.
С учётом отрицательного ёмкостного сдвига, общее напряжение на реактивных элементах UX = UL — UC .
Пропорционально напряжению, получим общее реактивное сопротивление X = XL — XC .
Векторы напряжений на активной и реактивной составляющей импеданса имеют угол сдвига фаз 90 градусов.
U , UR и UX представим в виде прямоугольного треугольника напряжений с углом сдвига фаз φ.
Тогда получим соотношение, согласно Теореме Пифагора, U ² = UR² + UX² .
Следовательно, с учётом пропорциональности элементов R, L, C значениям напряжений на их выводах,
определим импеданс, который будет равен квадратному корню из суммы квадратов активного и реактивного сопротивлений цепи.
XL = ωL = 2πfL — реактивное сопротивление индуктивности.
XC = 1/(ωC) = 1/(2πfC) — реактивное сопротивление ёмкости.
Угол сдвига фаз φ и его дополнение до 90° δ определятся тригонометрическими функциями из треугольника сопротивлений с катетами R, X и гипотенузой Z, как показано на рисунке:
Обычно, для облегчения расчётов, импеданс представляют в виде комплексного числа,
где действительной его частью является активное сопротивление, а мнимой — реактивное.
Для последовательного соединения импеданс можно записать в комплексном виде следующим образом:
Z = R + jX
Тогда в тригонометрической интерпретации модулем этого числа будет импеданс, а аргументом — угол φ.
В соответствии с формулой Эйлера, запишем показательную форму комплексного импеданса:
Z = |Z|ejargZ = Zejφ
Отсюда активная составляющая импеданса R = Zcosφ
Реактивная составляющая X = Zsinφ.
Параллельное соединение
Для вычисления импеданса при параллельном соединении активных и реактивных сопротивлений будем исходить из суммы обратных им величин — проводимостей y = 1/Z, G = 1/R, b = 1/X.
y = 1/Z = √(G2 + b2)
Сдвиг фаз в этом случае будет определён треугольником сопротивлений следующим образом:
Комплексную проводимость, как величину, обратную комплексному импедансу, запишем в алгебраической форме:
Y = G — jb
Либо в показательной форме:
Y = |Y|e -jφ = ye -jφ
Здесь:
Y — комплексная проводимость.
G — активная проводимость.
b — реактивная проводимость.
y — общая проводимость цепи, равная модулю комплексной проводимости.
e — константа, основание натурального логарифма.
j — мнимая единица.
φ — угол сдвига фаз.
Онлайн-калькулятор расчёта импеданса и угла сдвига фаз
Необходимо вписать значения и кликнуть мышкой в таблице.
При переключении множителей автоматически происходит пересчёт результата.
Последовательное соединение | Параллельное соединение |
Похожие страницы с расчётами:
Реактивное сопротивление. Расчёт.
Частота резонанса колебательного контура LC. Расчёт.
Реактивная мощность и компенсация. Расчёт.
Входное сопротивление транзистора формула. Расчет комплексного входного сопротивления цепи
ОБЩИЕ ПОЛОЖЕНИЯ
Для расчета транзисторных усилителей используются два способа: графоаналитический и аналитический . При графоаналитическом методе необходима информация о входных и выходных характеристиках транзистора (по справочнику). Аналитический метод расчета вытекает из теории полупроводниковых приборов и является приближенным. Однако на практике данный метод дает вполне удовлетворительные результаты.
Согласно ЕСКД по выполнению электрических схем в процессе проектирования необходимо составлять перечень элементов принципиально электронных схем (по аналогии со спецификацией механических устройств).
Для составления перечня элементов проектируемого усилителя, элементы его принципиальной схемы необходимо пронумеровать с использованием буквенно-цифровой системы обозначений, принятой в ГОСТ.
С-конденсаторы;
D-микросхемы;
DA-аналоговые микросхемы;
DD-цифровые микросхемы.
L-индуктивности;
R-резисторы;
VD-полупроводниковые диоды;
VT-транзисторы.
Нумерация элементов принципиальной схемы осуществляется в направлении «сверху вниз » и «слева направо ».
Краткие теоретические сведения
Схемы транзисторных усилителей классифицируются по названию заземленного (общего) электрода транзистора-эмиттера, коллектора и базы. Существует три схемы включения биполярных транзисторов: схемы с общим эмиттером , с общим коллектором , с общей базой .
Усилительные свойства транзистора характеризуются следующими статическими параметрами:
Статический коэффициент передачи тока эмиттера транзистора;
статический коэффициент передачи тока базы транзистора.
Параметры a и b связаны соотношениями:
a=b/(1+b) ; b=a/(1-a).
Схема с ОЭ является усилителем мощности входного сигнала. В данной схемевходной и выходной сигналы находятся в противофазе (сдвиг по фазе на угол ). Усилитель с ОЭ обладает сравнительно низким входным сопротивлением и достаточно высоким выходным сопротивлением (импедансом). Вместе с этим схема с ОЭ обеспечивает усиление, как по току , так и по напряжению .
Для обеспечения заданного коэффициента усиления по переменному току в схеме с ОЭ резистор R э в эмиттерной цепи транзистора шунтируется конденсатором С э. Поэтому импеданс эмиттерной цепи соответствует параллельному соединению резистора R э и емкостного сопротивления конденсатора С э.
Комплексный коэффициент усиления в схеме с ОЭ определяется выражением:
,
где R k , R э – активное сопротивление в коллекторной и эмиттерной цепи транзистора соответственно; фазовый сдвиг в эмиттерной цепи транзистора; круговая частота входного сигнала.
Рисунок 1 – Электрическая схема усилителя с общим эмиттером
Методика расчета усилителя с общим эмиттером
Расчет усилителей осуществляется в направлении с выхода к входу устройства (от нагрузки к источнику входного сигнала).
1. Выбор транзистора (по индивидуальному заданию)
Выбор транзистора осуществляется по типу проводимости и по
параметру b.(bºh 21э -статический коэффициент передачи тока базы для
различных транзисторов b лежит в диапазоне 10…150).
2. Расчет емкости разделительного конденсатора на выходе
Разделительный конденсатор С3 не пропускает постоянный потенциал коллектора в нагрузку. Совместно с сопротивлением нагрузки R н =R5, конденсатор С3 образует RС-цепь, которая подавляет низкие частоты и пропускает высокие частоты.
Величина конденсатора С3 определяются по формуле:
С 3 расч. ³1/(2pf сигн R н).
Рассчитанное значение емкости С3 будет соответствовать ослаблению входного сигнала в раз относительно сигнала на более высоких частотах. Для уменьшения ослабления входного сигнала и расширения за счет этого полосы пропускания усилителя расчетное значение емкости С 3расч увеличиваются на 1-2 порядка (в 10-100 раз).
3. Расчет тока коллектора
При заданном значении тока эмиттера I э ток коллектора I к определяется по формуле
4. Расчет сопротивления в коллекторной цепи транзистора
Для обеспечения усиления сигнала с минимальными искажениями потенциал коллектора относительно земли в статическом режиме U к0 (при отсутствии входного сигнала), выбирается из условия:
U к0 =0,5Е пит.
Сопротивление R к в цепи коллектора определяется по закону Ома
R к =R3= Uк 0 / I к =0,5Е пит /I к.
Определяется мощность Р 3 , рассеиваемая на сопротивлении R3 в коллекторной цепи транзистора
Р 3 = (I k) 2 *R3.
5. Расчет эквивалентного сопротивления нагрузки переменному току
При достаточно большой емкости разделительного конденсатора С3 эквивалентное сопротивление нагрузки на переменном токе R н.экв.оэ определяется параллельным соединением коллекторного резистора R к =R3 и сопротивления нагрузки R н =R5
R н.экв.оэ =.
6. Расчет сопротивления в цепи эмиттера
Сопротивление R э =R4 обеспечивает температурную стабилизацию режима транзистора по постоянному току. Для уменьшения влияния температуры на параметры усилителя в целом потенциал эмиттера U э относительно земли выбирается в диапазоне 1…2 В. Обычно U э =1В.
Сопротивление R э определяется по закону Ома:
R э = U э / I э.
Ток эмиттера I э выбирается в диапазоне (0,5…1,0)мА, либо задается
индивидуально.
Определяется мощность Р 4 , рассеиваемая на сопротивлении R э =R4 в эмиттерной цепи транзистора
Р 4 = (I э) 2 *R4.
7. Расчет входного сопротивления транзистора со стороны базы
Входное сопротивление транзистора со стороны базы h 11 определяется по формуле
h 11 =R э *(b+1).
8. Расчет резистивного делителя в цепи базы транзистора на постоянном токе.
Для температурной стабилизации режима транзистора по постоянному току (при отсутствии входного сигнала) необходимо следить за разностью потенциалов между эмиттером и базой при изменении температуры . Для обеспечения следящей обратной связи по температуре в цепь эмиттера вводится резистор R э =R4, а в цепь базы — резистивный делитель R1, R2, с помощью которого стабилизируется потенциал базы транзистора относительно земли. Если в режиме максимального сигнала ток делителя I д превышает ток базы I б, то потенциал базы U б будет определяться только напряжением питания Е пит и соотношением резисторов R1, R2. Поэтому обеспечения температурной стабилизации режима обеспечивается условие:
I д = Е п /(R1+R2)= I э.
По второму закону Кирхгофа определяется потенциал базы U б:
U б = j d +U э,
где j d — статический потенциал рn-перехода (для германиевых транзисторов j d =0,3…0,4 В; для кремневых транзисторов j d =0,6…0,8В).
По закону Ома определяются резисторы R1, R2:
R2=U б /I д = (j d +U э) /I э;
R1= (E пит -U б)/I д =(E пит -U б)/I э.
Определяются мощности Р 1 , Р 2 рассеиваемые на сопротивлениях делителя R1, R2:
Р 1 = (I д) 2 *R1;
Р 2 = (I д) 2 *R2.
9. Расчет резистивного делителя в цепи базы транзистора на
переменном токе.
При усилении сигналов переменного тока шина питания Е пит заземлена через конденсатор фильтра С Ф (имеет нулевой потенциал). Поскольку при достаточно большой емкости С Ф емкостное сопротивление фильтра Х С.Ф достаточно мало (X С.Ф =1/wС Ф ®0), резисторы R1, R2 по переменному току соединены параллельно .
Эквивалентное сопротивление делителя R1, R2 переменному току R д.экв определяется выражением
R д.экв = R1* R2/(R1 + R2).
10. Расчет входного сопротивления усилителя с ОЭ
На низких частотах, несоизмеримых с быстродействием выбранного транзистора, входное сопротивление усилителя R вх является чисто активным и соответствует параллельному соединению сопротивлений h 11 и R д.экв,
R вх. = h 11 * R д.экв / (h 11+ R д.экв).
Примечание . На высоких частотах, соизмеримых с быстродействием выбранного транзистора, сказываются межэлектродные емкости между выводами эмиттер – база , база – коллектор и эмиттер – коллектор . Поэтому в области высоких частот входное сопротивление (импеданс) является комплексной величиной .
11. Расчет входного конденсатора в цепи базы транзистора
Разделительный конденсатор С1 предназначен для отделения постоянной составляющей входного сигнала. Совместно с эквивалентным входным сопротивлением ЭП R вх.экв конденсатор С1 образует RС-цепь, которая не пропускает постоянный потенциал базы U б в источник входного сигнала, подавляет низкие частоты и пропускает высокие частоты.
Величина емкости конденсатора С1 определяется по формуле
С 1 расч. ³1/(2pf сигн R вх).
Рассчитанное значение емкости С1 будет соответствовать ослаблению входного сигнала в раз относительно сигнала на более высоких частотах. Поэтому для уменьшения ослабления входного сигнала расчетные значение емкости С1 увеличивается на 1-2 порядка (в 10-100 раз).
12. Расчет коэффициента усиления
12.1. Предварительный расчет емкости С э в цепи эмиттера по заданному значению статического коэффициента усиления К u
.
12.2. Расчет фазового сдвига в эмиттерной цепи
12.3. Проверочный расчет модуля коэффициента
Физическая формула расчета эквивалентного сопротивления в цепи
Расчёт электрических схем, содержащих несколько сопротивлений (резисторов), при нахождении силы тока в цепи, напряжения или мощности, производится с использованием метода свёртывания. Метод заключается в том, чтобы найти эквивалентное сопротивление выделенных участков цепи. Основная задача – замена резисторов, имеющих различное подключение относительно друг друга, на эквивалент (Rэкв.).

Эквивалентное сопротивление резисторов
Определение эквивалентного сопротивления
При рассмотрении схем любых электрических или электронных устройств можно увидеть, что такие компоненты, как резисторы, имеют разные типы соединений между собой. Чтобы определить эквивалентное соединение, необходимо рассматривать два элемента, включенных в определённом порядке. Несмотря на то, что на чертеже их может быть несколько десятков, и соединены они по-разному, есть только два типа включения их друг с другом: последовательное и параллельное. Остальные конфигурации – это лишь их вариации.
Последовательное соединение элементов
Подобное включение подразумевает комбинацию деталей в прямой последовательности. Выход одного сопротивления подключается к входу другого. При этом отсутствуют какие-либо ответвления на участке. Величина тока, который проходит через все соединённые последовательно компоненты, будет одна и та же.
Внимание! Снижение потенциала на каждом резистивном элементе в сумме даст полное напряжение, приложенное к последовательной цепи.
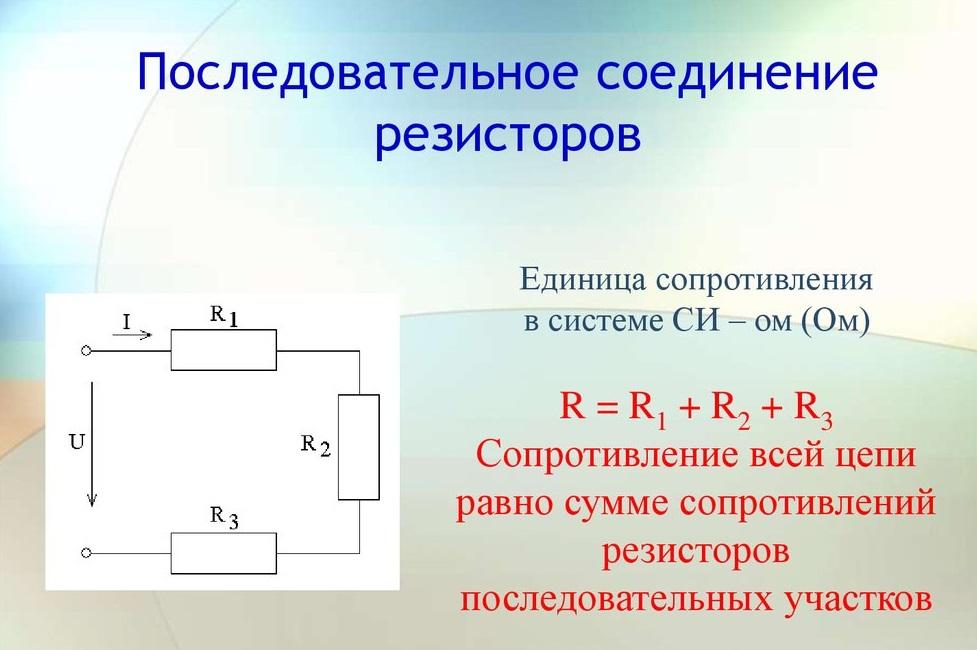
Последовательное включение резисторов
В случае постоянного тока формула закона Ома для отрезка цепи имеет вид:
I = U/R.
Сила тока зависит от приложенного напряжения и оказанного ему сопротивления. Если выразить R, его формула:
R = U/I.
Параметры последовательной цепи, включающей n соединённых друг с другом элементов, имеют свои особенности.
Проходящий по цепи ток везде одинаковый:
I = I1= I2= … = In.
Прикладываемое напряжение является суммой напряжений на каждом резисторе:
U = U1 + U2+ … + Un.
Следовательно, рассчитать можно общее:
Rэкв.= U1/I + U2/I + … +Un/I) = R1 + R2 + … +Rn.
Важно! Последовательная цепь, имеющая в своём составе N резисторов равного номинала, имеет эквивалентное сопротивление Rэкв. = N*R.
Параллельное соединение
Когда условные выходы деталей имеют общий контакт в одной точке (узле) схемы, а условные входы так же объединены во второй, говорят о параллельном соединении. Узел на чертеже обозначается графической точкой. Это место, где происходят разветвления цепей в схемах. Такой вариант подключения резисторов обеспечивает одинаковое падение напряжения U для всех параллельных элементов. Ток в этой позиции будет равен сумме токов, идущих по каждому компоненту.
Когда в параллельное подключение входит n резистивных элементов, то разность потенциалов, ток и общее сопротивление будут иметь следующие выражения:
- общий ток: I = I1 + I2 + … + In;
- общее напряжение: U = U1 = U2 = … = Un;
- Rобщ. = Rэкв. = U/I1 + U/I2 + …+ U/In) = 1/R1 + 1/R2 +…+ 1/Rn.
Величину, обратно пропорциональную сопротивлению 1/R, называют проводимостью.
Если n равных по номиналу сопротивлений включить параллельно, то Rэкв. = (R*R)/n*R = R/n. Формула подходит и для индуктивных сопротивлений проволочных катушек и ёмкостных сопротивлений конденсаторов.
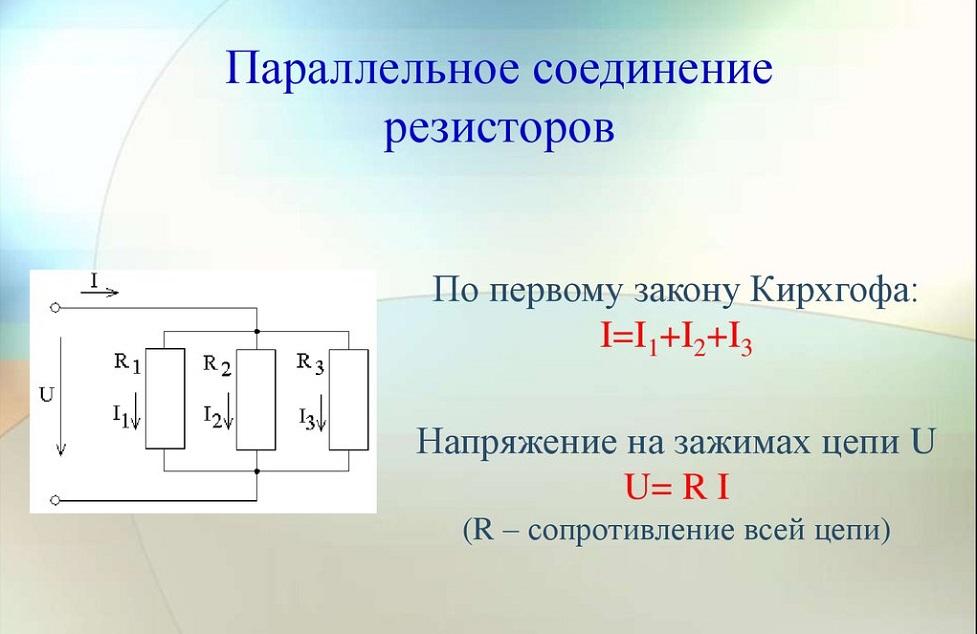
Параллельное включение резисторов
Расчёт при смешанном соединении устройств
Произвести расчет сопротивления цепи, когда она разветвлена и наполнена разными видами резистивных соединений, просто не получится. Затрудняет решение задачи множество участков, где детали подключены друг другу в разных комбинациях. В таких обстоятельствах желательно выполнять ряд преобразований, добиваясь упрощения схемы вводом отдельных эквивалентных элементов. Выявляют при этом подходящие контуры последовательных и параллельных присоединений.
Например, выискав некоторое количество последовательных подключений резисторов, заменяют их на один эквивалентный компонент. Определив элементы, соединённые последовательно, также рисуют вместо него эквивалент. Вновь начинают искать подобные простые соединения.
Метод называют «методом свёртывания». Схему упрощают до тех пор, пока в ней не останется одно Rэкв.
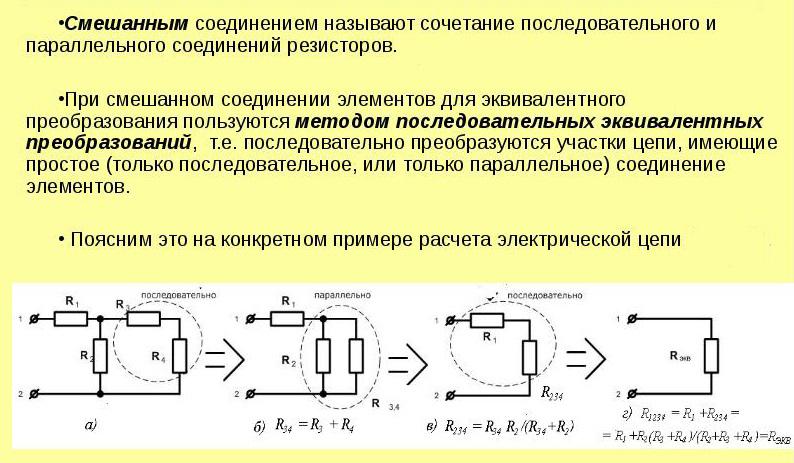
Способ расчёта при смешанном соединении
Важно! Метод эквивалентных преобразований применяется тогда, когда питание рассматриваемого участка цепи осуществляется от одного источника электрического тока, а также при определении Rэкв. в замкнутом контуре с одной ЭДС.
Такой относительный способ определения Rэкв используют и для изучения зависимости токов в некоторой цепи от значения R нагрузки. Это метод эквивалентного генератора, при котором сложный двухполюсник, являющийся активным, представляют эквивалентным генератором. При этом считают, что ЭДС его соответствует Uх.х. (холостого хода) на зажимах, R внутреннее соответствует R входному двухполюсника пассивного на тех же зажимах. Для такого определения источники тока разъединяют, а канал ЭДС закорачивают.
Физические формулы и примеры вычислений
Формулы для эквивалентных сопротивлений цепи, состоящей из пары резисторов R1 и R2, можно выделить в определённый ряд:
- параллельное присоединение определяют по формуле Rэкв. = (R1*R2)/R1+R2;
- последовательное включение вычисляют, определяя его сумму Rэкв. = R1+R2.
У смешанного соединения резистивных элементов нет конкретной формулы. Чтобы не запутаться при длительных преобразованиях, здесь допустимо воспользоваться специальной программой из интернета. Это сервис «онлайн-калькулятор». Он поможет разобраться со сложными схемами соединения, будь то треугольник, квадрат, пятиугольник или иная схематичная фигура, образованная резистивными элементами.
Понять, как работают все формулы и методы, можно на конкретной задаче. На представленном первом рисунке – смешанная электрическая схема. Она включает в себя 10 резисторов. Элементы представлены в следующих номиналах:
- R1 = 1 Ом;
- R2 = 2 Ом;
- R3 = 3 Ом;
- R4 = 6 Ом;
- R5 = 9 Ом;
- R6 = 18 Ом;
- R7 = 2Ом;
- R8 = 2Ом;
- R9 = 8 Ом;
- R10 = 4 Ом.
Напряжение, поданное на схему:
U = 24 В.
Требуется рассчитать токи на всех резистивных элементах.
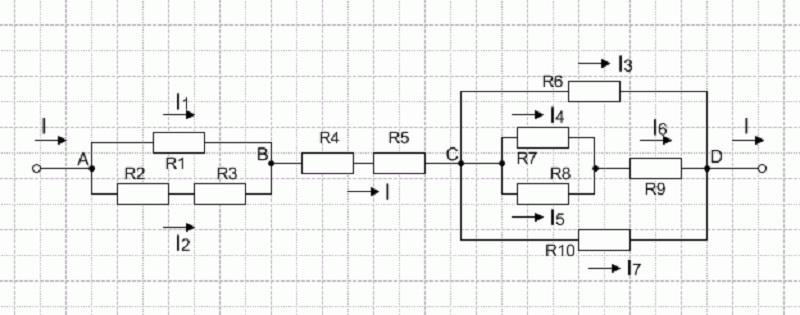
Исходная цепь
Для расчётов применяется закон Ома:
I = U/R, подставляя вместо R эквивалентное сопротивление.
Внимание! Для решения этой задачи сначала вычисляют общее (эквивалентное) R, после чего уже рассчитывают ток в цепи и напряжение на каждом резистивном компоненте.
Вычисляя Rэкв., разделяют заданную цепь на звенья, вмещающие в себя параллельные и последовательные включения. Делают расчёты для каждого такого звена, после – всей цепи целиком.
На рисунке выше изображено смешанное соединение сопротивлений. Его можно разбить на три участка:
- АВ – участок, имеющий две параллельных ветви;
- ВС – отрезок, вмещающий в себя последовательное сопряжение;
- CD – отрезок схемы с расположением трёх параллельных цепочек.
Сопротивления R2 и R3, образующие нижнюю ветку отрезка АВ, соединены последовательно, что учитывается при расчёте.
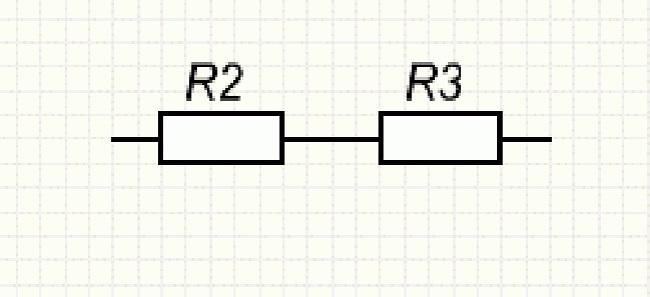
Последовательно соединённые резисторы R2 и R3
Если посмотреть на участок СD, то можно отметить смешанное включение резистивных элементов.
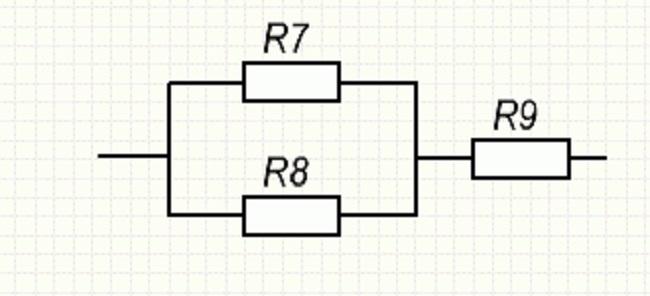
Смешанное включение на участке CD
Начало расчётов состоит в определении эквивалентных сопротивлений для этих смешанных фрагментов. Выполняют это в следующем порядке:
- Rэкв.2,3 = R2+R3=2 + 3 = 5 Ом;
- Rэкв.7,8 = (R7*R8)/R7 + R8 = (2*2)/2 + 2 = 1 Ом;
- Rэкв.7,8,9 = Rэкв.7,8 + R9 = 1 + 8 = 9 Ом.
Зная значения полученных эквивалентов, упрощают первоначальную схему. Она будет иметь вид, представленный на рисунке ниже.
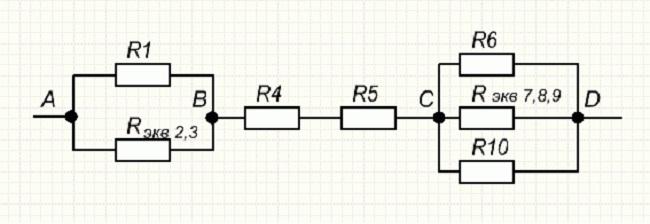
Результат первого свёртывания
Далее можно уже определить Rэкв. для участков AB, BC, CD, по формулам:
- Rэкв.AB = (R1*Rэкв 2,3)/R1 + Rэкв 2,3 = (1*5)/1 + 5 = 0,83 Ом;
- Rэкв.BC = R4 + R5 = 6 + 9 = 15 Ом;
- 1/Rэкв.CD = 1/R6 + 1/Rэкв.7,8,9 + 1/R10 = 1/18 + 1/9 + 1/4 = 0,05 + 0,11 + 0,25 = 0,41 Ом.
В результате выполненных вычислений получается эквивалентная схема, в которую входят три Rэкв. сопротивления. Она имеет вид, показанный на рисунке ниже.
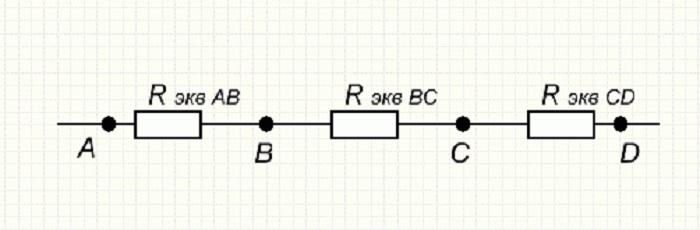
Результат последующего свёртывания
Теперь можно определить эквивалентное сопротивление всей первоначальной схемы, сложив эквивалентные значения всех трёх участков:
Rэкв. = Rэкв.AB + Rэкв.BC + Rэкв.CD = 0,83 + 15 + 0,41 = 56,83 Ом.
Далее, используя закон Ома, находят ток в последнем последовательном участке:
I = U/ Rэкв. = 24/56,83 = 0,42 А.
Зная силу тока, можно найти, какое падение напряжения на рассмотренных участках AB, BC, CD. Это выполняется следующим образом:
- UAB = I* Rэкв.AB= 0,42*0,83 = 0,35 В;
- UBC = I* Rэкв.BC= 0,42*15 = 6,3В;
- UCD = I* Rэкв.CD = 0,42*0,41 = 0,17 В.
Следующим шагом станет определение токов на параллельных отрезках AB и CD:
- I1 = UAB/R1 = 0,35/1 = 0,35 А;
- I2 = UAB/Rэкв.2,3 = 0,35/5 = 0,07 А;
- I3 = UCD/R6 = 0,17/18 = 0,009 А;
- I6 = UCD/Rэкв.7,8,9= 0,17/9 = 0,02 А;
- I7 = UCD/R10 = 0,17/4 = 0,04 А.
Далее, чтобы найти значения токов, проходящих через R7 и R8, нужно рассчитать напряжение на этих двух резисторах. Предварительно находят падение напряжения на R9.
U9 = R9*I6 = 8*0,02 = 0,16 В.
Теперь напряжение, падающее на Rэкв.7,8, будет разностью между U CD и U9.
U7,8 = UCD – U9= 0,17 – 0,16 = 1 В.
После этого можно уже узнать значение токов, движущихся по резисторам R7 и R8, используя формулы:
- I4 = U7,8/R7 = 1/2 = 0,5 A;
- I5 = U7,8/R8 = 1/2 = 0,5 A.
Стоит заметить! Ток, протекающий через R4 и R5, по своему значению равен току на отрезке, не имеющем разветвления.
Рассчитывая схемы и решая задачи по нахождению значений электрических параметров, необходимо использовать эквивалентные сопротивления. С помощью такой замены сложные построения превращаются в элементарные цепи, которые сводятся к параллельным и последовательным соединениям резистивных элементов.
Видео
1.4. Способы соединения сопротивлений и расчет эквивалентного сопротивления электрической цепи
Сопротивления в электрических цепях могут быть соединены последовательно, параллельно, по смешанной схеме и по схемам «звезда», «треугольник». Расчет сложной схемы упрощается, если сопротивления в этой схеме заменяются одним эквивалентным сопротивлением Rэкв, и вся схема представляется в виде схемы на рис. 1.3, где R=Rэкв, а расчет токов и напряжений производится с помощью законов Ома и Кирхгофа.
Электрическая цепь с последовательным соединением элементов
|
|
Последовательным называют такое соединение элементов цепи, при котором во всех включенных в цепь элементах возникает один и тот же ток I (рис. 1.4).
На основании второго закона Кирхгофа (1.5) общее напряжение U всей цепи равно сумме напряжений на отдельных участках:
U = U1 + U2 + U3 или IRэкв = IR1 + IR2 + IR3,
откуда следует
(1.5)
Rэкв = R1 + R2 + R3.
Таким образом, при последовательном соединении элементов цепи общее эквивалентное сопротивление цепи равно арифметической сумме сопротивлений отдельных участков. Следовательно, цепь с любым числом последовательно включенных сопротивлений можно заменить простой цепью с одним эквивалентным сопротивлением Rэкв (рис. 1.5). После этого расчет цепи сводится к определению тока I всей цепи по закону Ома
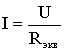 ,
,
и по вышеприведенным формулам рассчитывают падение напряжений U1, U2, U3 на соответствующих участках электрической цепи (рис. 1.4).
Недостаток последовательного включения элементов заключается в том, что при выходе из строя хотя бы одного элемента, прекращается работа всех остальных элементов цепи.
Электрическая цепь с параллельным соединением элементов
Параллельным называют такое соединение, при котором все включенные в цепь потребители электрической энергии, находятся под одним и тем же напряжением (рис. 1.6).

Рис. 1.6
В этом случае они присоединены к двум узлам цепи а и b, и на основании первого закона Кирхгофа (1.3) можно записать, что общий ток I всей цепи равен алгебраической сумме токов отдельных ветвей:
I
= I1 + I2 + I3,
т.е. 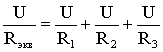 ,
,
откуда следует, что
(1.6)
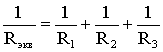 .
.
В том случае, когда параллельно включены два сопротивления R1 и R2, они заменяются одним эквивалентным сопротивлением
(1.7)
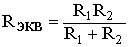 .
.
Из соотношения (1.6), следует, что эквивалентная проводимость цепи равна арифметической сумме проводимостей отдельных ветвей:
gэкв = g1 + g2 + g3.
По мере роста числа параллельно включенных потребителей проводимость цепи gэкв возрастает, и наоборот, общее сопротивление Rэкв уменьшается.
Напряжения в электрической цепи с параллельно соединенными сопротивлениями (рис. 1.6)
U = IRэкв = I1R1 = I2R2 = I3R3.
Отсюда следует, что
 ,
,
т.е. ток в цепи распределяется между параллельными ветвями обратно пропорционально их сопротивлениям.
По параллельно включенной схеме работают в номинальном режиме потребители любой мощности, рассчитанные на одно и то же напряжение. Причем включение или отключение одного или нескольких потребителей не отражается на работе остальных. Поэтому эта схема является основной схемой подключения потребителей к источнику электрической энергии.
Электрическая цепь со смешанным соединением элементов
Смешанным называется такое соединение, при котором в цепи имеются группы параллельно и последовательно включенных сопротивлений.
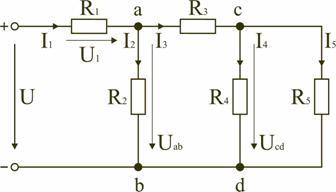
Рис. 1.7
Для цепи, представленной на рис. 1.7, расчет эквивалентного сопротивления начинается с конца схемы. Для упрощения расчетов примем, что все сопротивления в этой схеме являются одинаковыми: R1=R2=R3=R4=R5=R. Сопротивления R4 и R5 включены параллельно, тогда сопротивление участка цепи cd равно:
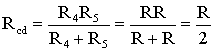 .
.
В этом случае исходную схему (рис. 1.7) можно представить в следующем виде (рис. 1.8):
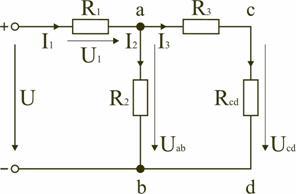
Рис. 1.8
На схеме (рис. 1.8) сопротивление R3 и Rcd соединены последовательно, и тогда сопротивление участка цепи ad равно:
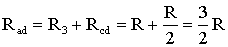 .
.
Тогда схему (рис. 1.8) можно представить в сокращенном варианте (рис. 1.9):
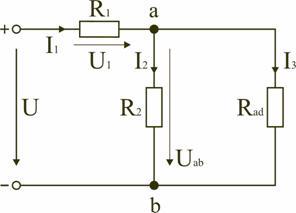
Рис. 1.9
На схеме (рис. 1.9) сопротивление R2 и Rad соединены параллельно, тогда сопротивление участка цепи аb равно
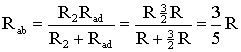 .
.
Схему (рис. 1.9) можно представить в упрощенном варианте (рис. 1.10), где сопротивления R1 и Rab включены последовательно.
Тогда эквивалентное сопротивление исходной схемы (рис. 1.7) будет равно:
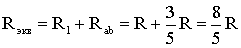 .
.
|
|
В результате преобразований исходная схема (рис. 1.7) представлена в виде схемы (рис. 1.11) с одним сопротивлением Rэкв. Расчет токов и напряжений для всех элементов схемы можно произвести по законам Ома и Кирхгофа.
Соединение элементов электрической цепи по схемам «звезда» и «треугольник»
В электротехнических и электронных устройствах элементы цепи соединяются по мостовой схеме (рис. 1.12). Сопротивления R12, R13, R24, R34 включены в плечи моста, в диагональ 1–4 включен источник питания с ЭДС Е, другая диагональ 3–4 называется измерительной диагональю моста.
|
|
В мостовой схеме сопротивления R13, R12, R23 и R24, R34, R23 соединены по схеме «треугольник». Эквивалентное сопротивление этой схемы можно определить только после замены одного из треугольников, например треугольника R24 R34 R23 звездой R2 R3 R4 (рис. 1.13). Такая замена будет эквивалентной, если она не вызовет изменения токов всех остальных элементов цепи. Для этого величины сопротивлений звезды должны рассчитываться по следующим соотношениям:
(1.8)
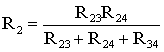 ;
;  ;
; 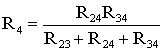 .
.
Для замены схемы «звезда» эквивалентным треугольником необходимо рассчитать сопротивления треугольника:
(1.9)
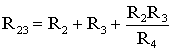 ;
;  ;
; 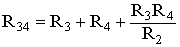 .
.
После проведенных преобразований (рис. 1.13) можно определить величину эквивалентного сопротивления мостовой схемы (рис. 1.12)
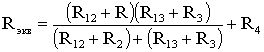 .
.


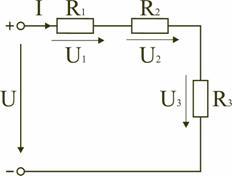 Рис.
1.4
Рис.
1.4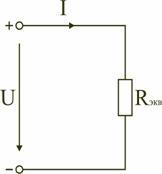 Рис.
1.5
Рис.
1.5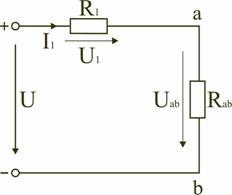 Рис.
1.10
Рис.
1.10 Рис.
1.11
Рис.
1.11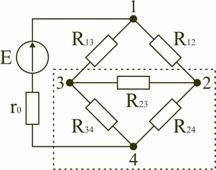 Рис.
1.12
Рис.
1.12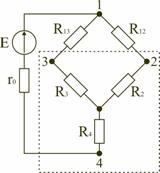 Рис.
1.13
Рис.
1.13