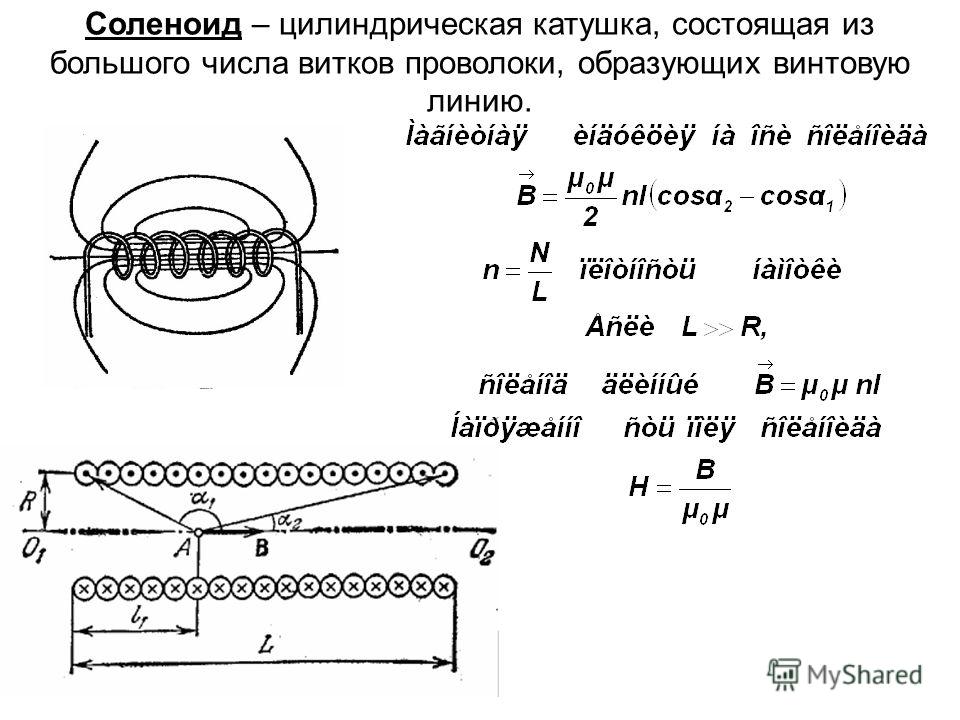
|
Random converter |
Калькулятор магнитной индукции соленоидаКалькулятор определяет модуль магнитной индукции длинного соленоида без ферромагнитного сердечника, если известно число витков, длина соленоида и текущий через катушку ток. Пример: Через содержащий 500 витков провода соленоид длиной 5 см протекает ток 10 ампер. Рассчитать магнитную индукцию в центре соленоида. Входные данные Число витков N Длина катушки Lмиллиметр (мм)сантиметр (см)метр (м)дюймфут Ток Iмикроампер (мкА)миллиампер (мА)ампер (А)килоампер (кА) Поделиться Поделиться ссылкой на этот калькулятор, включая входные параметры Twitter Facebook Google+ VK Закрыть Выходные данные Магнитное поле B Тл Определения и формулыСоленоид представляет собой намотанную виток к витку катушку, длина которой значительно больше ее диаметра. Модуль магнитной индукции B длинного соленоида в воздухе без сердечника рассчитывается по формуле где μ₀=4π × 10⁻⁷ Гн/м — магнитная постоянная, N число витков катушки соленоида, I протекающий через катушку ток и L — длина соленоида. Соленоиды и ферромагнитные жидкостиСоленоидные исполнительные механизмы — довольно шумные устройства, поэтому иногда в зазор между сердечником и каркасом катушки вводят ферромагнитную жидкость. Еще одно применение ферромагнитных жидкостей в соленоидах — в качестве эластичного сердечника. Это позволяет изготовить эластичные соленоиды, которые можно использовать в современных гибких электронных устройствах, например, в носимых компьютерах и устройствах биомедицинского контроля. Общие сведения Свойства Использование ферромагнитных жидкостей Как смазочные вещества В герметизирующих уплотнениях В искусстве В системах звуковоспроизведения В медицине В диагностике магнитных носителей В теплообменниках В заключение Общие сведенияСиний и зеленый лазерные лучи хорошо видны через коллоидную смесь благодаря эффекту Тиндаля В этой статье поговорим о занимательных и необычных ферромагнитных жидкостях. 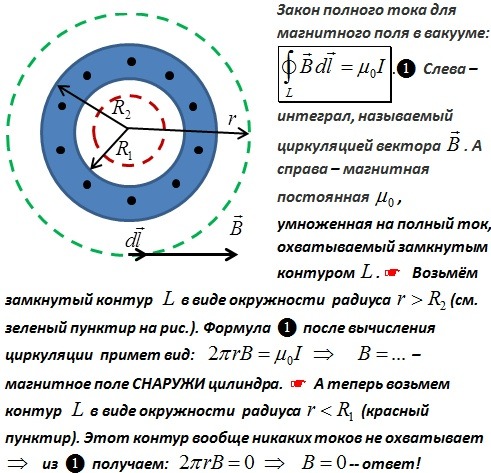 Пронаблюдать ван-дер-ваальсовы силы в действии можно, когда гекконы, ящерицы анолисы, сцинковые и некоторые насекомые перемещаются по вертикальным поверхностям стен, или даже по потолку Зеленая ящерица анолис Молекулы поверхностно-активного вещества присоединяются к наночастицам и окружают каждую частицу, создавая, таким образом, буфер вокруг частицы. Притяжение между наночастицами регулируется ван-дер-ваальсовыми силами, которые ослабевают при увеличении расстояния между этими частицами. Поэтому, когда расстояние между наночастицами увеличивается благодаря поверхностно-активному веществу, притяжение между этими частицами ослабевает. Магнетит В некоторых случаях поверхностно-активные вещества работают по-другому. Их молекулы присоединяются к наночастице так, что их наружная полярность одинакова по всей наружной поверхности (например, наружная оболочка приобретает положительный заряд). Таким образом, вокруг каждой наночастицы образуется оболочка с определенным зарядом. Магнетит, как естественный магнит Мы немного поговорили о жидкостях-носителях. Но из чего же состоят сами наночастицы? Иногда для этого используют частицы магнетита — минерала с магнитными свойствами. СвойстваФерромагнитные жидкости под действием магнитного поля — завораживающее зрелище. Разобранный гидродинамический подшипник накопителя на жестких магнитных дисках Свойства ферромагнитных жидкостей изменяются с температурой. При очень высоких температурах, известных как температура или точка Кюри, наночастицы теряют магнитные свойства и ферромагнитная жидкость превращается в обычную жидкость. Также, со временем поверхностно-активное вещество теряет отталкивающие свойства, и наночастицы слипаются, так что при этом свойства ферромагнитной жидкости пропадают. Использование ферромагнитных жидкостейФерромагнитные жидкости реагируют на магнит и следуют за ним, поэтому с помощью магнита их можно либо перемещать с места на место, либо удерживать в нужном месте. Как смазочные веществаФерромагнитные жидкости используют как смазки во вращающихся механизмах. Как и традиционные смазки, они помогают уменьшить трение между механическими деталями, но при этом их главное преимущество в том, что с помощью магнита или магнитного поля ферромагнитные жидкости легко удерживать в нужном положении. Ферромагнитная жидкость под действием сильного магнита В герметизирующих уплотненияхВ некоторых случаях герметизирующие уплотнения могут быть в виде жидкости — в этой ситуации очень удобно использовать именно ферромагнитные жидкости. Их используют, к примеру, чтобы герметизировать внутреннюю часть накопителя на жестком магнитном диске, в которой находятся электропривод шпинделя, сами жесткие диски и сервопривод блока головок. Магниты удерживают ферромагнитную жидкость в нужном месте, а она, в свою очередь, не пропускает пыль извне в гермозону жесткого диска, и помогает предотвратить повреждение дисков. В искусствеНекоторые скульпторы и художники используют ферромагнитную жидкость для создания современных произведений искусства. Кроме объемных и подвижных скульптур, которые демонстрируют во всей красе игру складок ферромагнитной жидкости под действием магнита, художники создают также плоские картины из этой жидкости. Ферромагнитные жидкости не смешиваются с водой и красками на водной основе, поэтому такие краски и пигменты (например, люминесцентные) добавляют в ферромагнитную жидкость, а потом двигают ее магнитом для создания красочных форм. На сайте YouTube много интересных примеров картин и скульптур из ферромагнитной жидкости. Ферромагнитная жидкость под действием сильного магнита В системах звуковоспроизведенияВ электродинамических громкоговорителях систем звуковоспроизведения ферромагнитную жидкость используют для охлаждения звуковой катушки. Ферромагнитные жидкости используют, также, для демпфирования диффузора с катушкой на резонансных частотах. Это сглаживает амплитудно-частотную характеристику динамика. Для этого ферромагнитные жидкости помещают в зазор между звуковой катушкой и магнитом. При выборе ферромагнитной жидкости руководствуются знаниями о том, в какой среде ее будут использовать. Так, например, выбирая жидкость-носитель или при выборе вязкости ферромагнитной жидкости, учитывают такие факторы как влажность окружающей среды, в которой эта жидкость будет использоваться, или будет ли устройство, в котором используется ферромагнитная жидкость, соприкасаться с водой. В медицинеВ медицине у ферромагнитных жидкостей несколько применений. На данный момент ученые проводят исследования по использованию ферромагнитных жидкостей как носителей лекарств и других необходимых больным препаратов. С помощью магнита эти лекарственные препараты перемещают в определенный участок организма. Обычно в этом случае наночастицы покрывают слоем препарата, после чего ферромагнитную жидкость вводят в организм (чаще всего путем инъекции) и удерживают на месте с помощью магнита, пока препарат не окажет нужное действие. Существует ряд других методов локализированного введения лечебных препаратов, но ученные надеются, что этот метод обеспечит наибольшую точность. Еще одно интересное применение ферромагнитных жидкостей в медицине — теплотерапия определенных участков тела. Чаще всего она используется для уничтожения раковых клеток. Для этого ферромагнитную жидкость вводят в организм, а после этого заставляют ферромагнитные частицы колебаться с высокой частотой, используя электромагниты. В диагностике магнитных носителейФерромагнитные жидкости используют для определения структуры магнитных доменов различных магнитных носителей, таких как накопители на магнитной ленте, жесткие диски и кредитные карты. Также с их помощью проверяют дефекты на поверхности материалов, не имеющих отношения к магнитным носителям, например сварочных швов, а также природных минералов и металлов. Это применяется, например, в производстве миниатюрных компонентов. Для этого поверхность материала покрывают ферромагнитной жидкостью, и она распределяется по этой поверхности в соответствии с магнитным полем материала. После того, как жидкость-носитель испарилась, на поверхности остаются ферромагнитные частицы, по которым и определяют структуру магнитного поля поверхности. Обычно для этого нужен микроскоп. Этот метод используют не только для проверки поверхности магнитных носителей и материалов, описанных выше, но и в судебно-медицинской экспертизе. В теплообменникахПерегрев — широко распространенная проблема в радиоэлектронике. Чтобы избежать поломки, электронные приборы необходимо охлаждать. Ферромагнитные жидкости иногда используют в этих целях, например в громкоговорителях и некоторых микроэлектронных приборах. В начале этой статьи, когда мы обсуждали свойства ферромагнитных жидкостей, мы уже упоминали, что при высоких температурах (температурах Кюри) ферромагнитные жидкости теряют магнитные свойства. Эту особенность ферромагнитных жидкостей используют в системах охлаждения. Во время охлаждения ферромагнитная жидкость, удерживаемая возле детали, которую охлаждают, теряет свои магнитные свойства после того, как в ней достигнута температуры Кюри. Магнит перестает ее удерживать и ее замещает холодная ферромагнитная жидкость, у которой еще есть магнитные свойства. Новая жидкость нагревается, а нагретая — охлаждается, и процесс периодически повторяется. В заключениеВ этой статье мы поговорили о том, что собой представляют ферромагнитные жидкости и о том, как их использовать. На них очень интересно смотреть, когда они под воздействием магнита, и мы очень советуем вам посмотреть примеры видео ферромагнитных жидкостей в интернете, например на сайте YouTube. Автор статьи: Kateryna Yuri Вас могут заинтересовать и другие калькуляторы из группы «Магнитостатика, магнетизм и электродинамика»:Калькулятор магнитодвижущей силы Калькулятор электромагнитного спектра Калькуляторы Магнитостатика, магнетизм и электродинамика |
Расчет катушки соленоида
Исполнительный орган в виде соленоидального плунжерного электромагнита состоит из обмотки, окруженной ферромагнитным сердечником и якоря в виде плунжера. Задача состоит в расчете магнитного поля в устройстве и тягового усилия, приложенного к якорю. Тип задачи: Нелинейная осесимметричная задача магнитостатики. Все размеры заданы в миллиметрах. Решение: Магнитная система соленоида полностью замкнута, поэтому внешнюю границу модели можно поместить относительно близко к сердечнику соленоида. Более протяженный слой воздуха включен в модель со стороны якоря, поскольку в этой зоне нельзя пренебречь выпучиванием поля.
Тип задачи: Нелинейная осесимметричная задача магнитостатики. Все размеры заданы в миллиметрах. Решение: Магнитная система соленоида полностью замкнута, поэтому внешнюю границу модели можно поместить относительно близко к сердечнику соленоида. Более протяженный слой воздуха включен в модель со стороны якоря, поскольку в этой зоне нельзя пренебречь выпучиванием поля.
Поиск данных по Вашему запросу:
Схемы, справочники, даташиты:
Прайс-листы, цены:
Обсуждения, статьи, мануалы:
Дождитесь окончания поиска во всех базах.
По завершению появится ссылка для доступа к найденным материалам.
Содержание:
- Как упрощённо рассчитать соленоид/электромагнитный клапан?
- Индуктивность: формула
- Magn2: Плунжерный электромагнит
- Электромагнит расчет силы.
Расчет обмоток электромагнитов - Расчёт соленоида
- Расчет обмоток электромагнитов
- Самоиндукция. Энергия магнитного поля
- Расчет обмоток электромагнитов Расчет обмотки электромагнита постоянного тока
- Вы точно человек?
- Расчет обмотки электромагнита постоянного тока
Как упрощённо рассчитать соленоид/электромагнитный клапан?
Всем доброго времени суток. Сегодняшняя статья является продолжением предыдущей. Здесь продолжим рассматривать расчёт индуктивностей индуктивных элементов без сердечников.
Здесь продолжим рассматривать расчёт индуктивностей индуктивных элементов без сердечников.
В прошлой статье я рассказал, как рассчитать индуктивность прямого провода и провода свёрнутого в кольцо виток , в данной статье будем рассчитывать индуктивность круговых катушек, то есть поперечный профиль, которых представляет собой окружности. Круговые катушки индуктивности являются, наверное, самыми распространёнными. В тоже время из-за разнообразия их форм существует некоторая трудность в расчёте индуктивности. Для некоторого упрощения расчёта катушки индуктивности делятся на несколько видов.
Рассмотрим основные конструктивные особенности круговых катушек индуктивности. Расчёт индуктивности катушки. Для расчёта индуктивности круговой катушки необходимо знать следующие размеры:. D 1 — внутренний диаметр, D 2 — внешний диаметр, D ср — средний диаметр, l — длина катушки аксиальный размер , t — толщина обмотки радиальный размер , где t можно вычислить.
Поэтому, в зависимости от соотношения между этими размерами различают следующие катушки индуктивности:.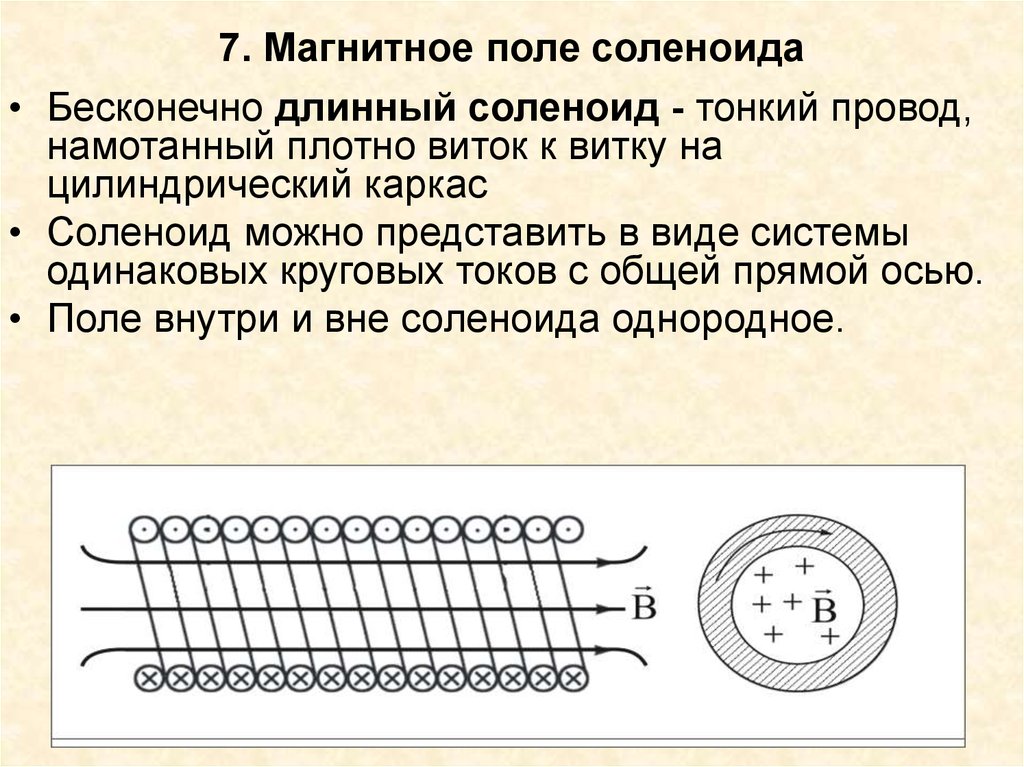 Кроме конструктивных параметров, на индуктивность влияет также параметры обмоточного провода диаметр, толщина изоляции, шаг намотки , хотя в большинстве случаев влияние их незначительно, но в некоторых случаях, например, при большом шаге намотки их следует учитывать. Поэтому общая индуктивность катушки можно представить следующим выражением.
Кроме конструктивных параметров, на индуктивность влияет также параметры обмоточного провода диаметр, толщина изоляции, шаг намотки , хотя в большинстве случаев влияние их незначительно, но в некоторых случаях, например, при большом шаге намотки их следует учитывать. Поэтому общая индуктивность катушки можно представить следующим выражением.
Особенности расчёта круговых катушек индуктивности состоят в следующем:. При определении расчётной индуктивности L P , средний диаметр принимается равным среднему диаметру реальной катушки;. Если у катушки в каком-либо направлении по длине намотки l или по толщине намотки t имеется только один ряд или слой , то в этом направлении размер l или t можно принять равным нулю, то есть расчёт ведётся как для соленоида или плоской катушки.
В некоторых случаях, при большом диаметре провода или шаге намотки у однослойных катушках размер l или t принимается равным диаметру голого провода d. Приступим к расчётным выражениям, в начале рассчитаем простейшие круговые катушки — соленоид и плоскую катушку. Определение индуктивности соленоида, d — диаметр соленоида, l — длина соленоида.
Определение индуктивности соленоида, d — диаметр соленоида, l — длина соленоида.
Стоит отметить, что формула расчёта соленоида подходит для большинства однослойных катушек с точностью в несколько процентов. Определение индуктивности плоской катушки, D 1 — внутренний диаметр, D 2 — внешний диаметр, D — средний диаметр, t — толщина намотки. Выражения для индуктивности тонкой катушки позволяют рассчитать индуктивность и большинства катушек с малой длиной и большой толщиной обмоток. Теперь перейдём от идеализированных катушек к реальным, которые в своем сечении представляют собой прямоугольник.
Таким образом, индуктивность прямоугольной катушки можно вычислить по следующей формуле. В принципе реальную катушку индуктивности, в зависимости от отношения длины намотки l к среднему диаметру D cp , можно разделить на несколько типов:. Данные поправки зависят от взаимного расположения витков в катушке. Для провода круглого сечения возможны следующие варианты заполнения катушки.
Расположение провода круглого сечения в катушке индуктивности. В общем случае поправка на собственную индуктивность витков рассчитывается по следующему выражению.
В общем случае поправка на собственную индуктивность витков рассчитывается по следующему выражению.
Для варианта а , провод намотан с небольшим коэффициентом заполнения. Для варианта б , провод намотан с большим коэффициентом заполнения. Для варианта г , провод намотан в один слой по длине катушки с шагом p.
В зависимости от способа вычисления расчётной индуктивности L P. Для варианта д , провод намотан в один слой по толщине намотки с шагом q , также возможно два случая. Для катушки, выполненной в один слой по толщине намотки плоская катушка :.
На сегодня всё. В следующей статье я закончу с индуктивными элементами без сердечников. Теория это хорошо, но без практического применения это просто слова. Здесь можно всё сделать своими руками. Скажите, пожалуйста, в каком справочнике можно найти формулу для индуктивности короткого соленоида?
Чем не устраивает данная статья? Если необходимо более точно рассчитать индуктивность различных индуктивностей, то книга автора П. Ваш e-mail не будет опубликован. Предыдущий пост: Расчёт индуктивности. Часть 1. Следующий пост: Расчёт индуктивности. Часть 3. Расчёт индуктивности. Виды катушек индуктивности Круговые катушки индуктивности являются, наверное, самыми распространёнными.
Ваш e-mail не будет опубликован. Предыдущий пост: Расчёт индуктивности. Часть 1. Следующий пост: Расчёт индуктивности. Часть 3. Расчёт индуктивности. Виды катушек индуктивности Круговые катушки индуктивности являются, наверное, самыми распространёнными.
Похожие записи: Классификация трансформаторов Дроссель переменного тока и его расчёт Дроссель фильтра и его расчёт Нагрев и охлаждение дросселя Потери мощности в дросселе. Часть 2. AndrewsaCaulp :. Мария :. SarmAt :. Добавить комментарий Отменить ответ Ваш e-mail не будет опубликован.
Разделы сайта Импульсная техника Начинающим Новости Силовая электроника Усилительная схемотехника Цифровая схемотехника. Последнии посты Классификация трансформаторов Дроссель переменного тока и его расчёт Дроссель фильтра и его расчёт Нагрев и охлаждение дросселя Потери мощности в дросселе. Свежие комментарии Алексей к записи Дифференциальные усилители Михаил к записи Дифференциальные усилители Сергей к записи Блокинг-генератор.
Расчёт блокинг-генератора Тимур к записи Блокинг-генератор. Расчёт блокинг-генератора Edward к записи Катушки индуктивности с малым воздушным зазором. Популярные Блокинг-генератор. Расчёт блокинг-генератора Стабилитрон. Параметрические стабилизаторы напряжения Компенсационные стабилизаторы напряжения. Что такое мультивибратор? Расчёт мультивибратора Схемы включения операционных усилителей Обратная связь. Часть 1 Диодные ограничители Триггер Шмитта на транзисторах.
Расчёт блокинг-генератора Edward к записи Катушки индуктивности с малым воздушным зазором. Популярные Блокинг-генератор. Расчёт блокинг-генератора Стабилитрон. Параметрические стабилизаторы напряжения Компенсационные стабилизаторы напряжения. Что такое мультивибратор? Расчёт мультивибратора Схемы включения операционных усилителей Обратная связь. Часть 1 Диодные ограничители Триггер Шмитта на транзисторах.
About This is the deafult sidebar, add some widgets to change it. Все права защищены. Запрещено использование материалов сайта без согласия его авторов и обратной ссылки. Дизайн: TechElectronics Themes.
Индуктивность: формула
Теория и практика. Кейсы, схемы, примеры и технические решения, обзоры интересных электротехнических новинок. Уроки, книги, видео. Профессиональное обучение и развитие. Сайт для электриков и домашних мастеров, а также для всех, кто интересуется электротехникой, электроникой и автоматикой. Как сделать электромагнит в домашних условиях. Электромагнит — искусственный магнит, у которого магнитное поле возникает и концентрируется в ферромагнитном сердечнике в результате прохождения электрического тока по охватывающей его обмотке, то есть при пропускании тока через катушку помещенный внутри нее сердечник приобретает свойства естественного магнита.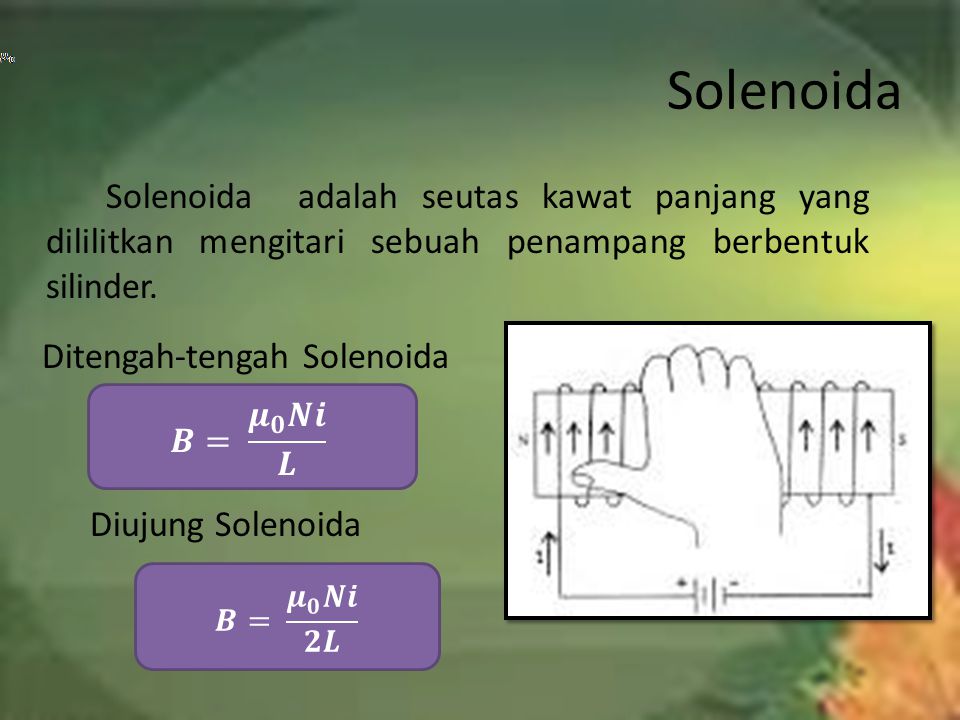
Решено: Расчёт соленоида Электроника Ответ. Ошибочка токи есть наведенные нигнитным полем катушки соленоида. 0.
Magn2: Плунжерный электромагнит
Катушка может быть каркасной и бескаркасной. Обмотка выполняется изолированным приводом, которой наматывается на каркас. Для расчета обмотки напряжения должны быть заданы напряжение U и МДС. Сечение обмоточного провода q находим, исходя из потребляемой МДС. Если при неизменном U и l ср требуется увеличить м. Ток в обмотке возрастает. При этом обмотка будет иметь меньшее число витков увеличенного сечения. По найденному сечению с помощью таблиц сортаментов находится ближайший стандартный диаметр провода. Мощность, выделяемая в обмотке в виде тепла.
Электромагнит расчет силы. Расчет обмоток электромагнитов
Данный комплекс [1, 4] позволяет осуществлять проверку магнитометров инклинометра непосредственно на буровых площадках нефтегазовых месторождений. Целью работы является подтверждение возможности создания однородного магнитного поля заданной величины в ограниченном геометрическими размерами установки объеме. Комплекс состоит из установки 1 для базирования на ней проверяемого инклинометра 5, блока связи 2 с компьютером 3, соединительных кабелей и источника питания установки 4. Для работы с комплексом подходит любой персональный компьютер. Кольцами Гельмгольца называется система из двух одинаковых тонких катушек, расположенных соосно на расстоянии, равном их радиусу.
Комплекс состоит из установки 1 для базирования на ней проверяемого инклинометра 5, блока связи 2 с компьютером 3, соединительных кабелей и источника питания установки 4. Для работы с комплексом подходит любой персональный компьютер. Кольцами Гельмгольца называется система из двух одинаковых тонких катушек, расположенных соосно на расстоянии, равном их радиусу.
Однослойная катушка индуктивности представляет собой провод, свернутый в спираль.
Расчёт соленоида
Расчёт частоты кварца имеем: 1. Как доказать, что магнитное поле в центре соленоида и внутри соленоида одинаковое Как доказать то, что магнитное поле в центре соленоида и внутри соленоида одинаковое и равно Определить площадь поперечного сечения соленоида, энергию магнитного поля соленоида при токе 0,5 А Соленоид длиной 40 см и индуктивностью микрогенри содержит витков провода. Расчёт площади для парковки авто тип авто, площадь, расчёт средней общей Расчёт площади для парковки авто тип авто, площадь, расчёт средней общей.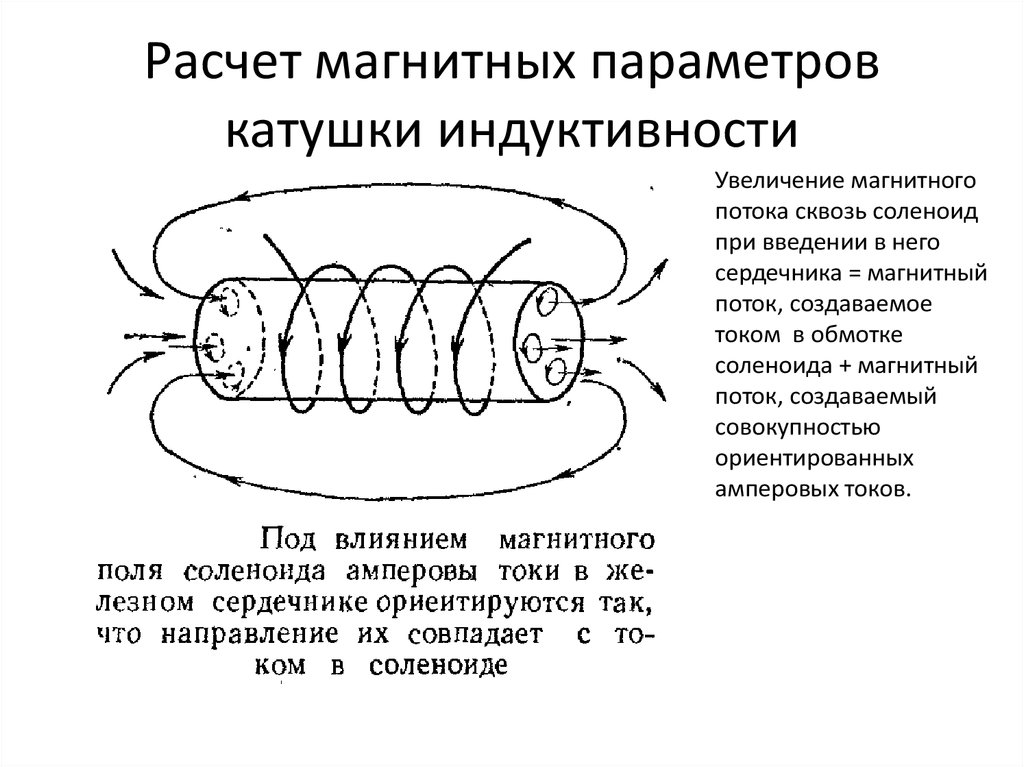 Индукция магнитного поля внутри соленоида при Блоги программистов и сисадминов.
Индукция магнитного поля внутри соленоида при Блоги программистов и сисадминов.
Расчет обмоток электромагнитов
Самоиндукция — это значимый частный случай электромагнитной индукции, когда магнитный поток, изменяясь и вызывая ЭДС индукции, создается током в самом контуре. В случае, когда ток рассматриваемого контура по каким-либо причинам изменен, то имеет место изменение и магнитного поля этого тока, а значит и собственного магнитного потока, проходящего через контур. В контуре создается ЭДС самоиндукции, создавая препятствие для изменений тока в контуре по правилу Ленца. Единица индуктивности в С И носит название генри Г н. Для наглядности произведем расчет индуктивности длинного соленоида, который имеет N витков, площадь сечения S и длину l. Соленоид — это цилиндрическая катушка индуктивности, у которой длина много больше диаметра. Магнитное поле соленоида задается формулой:. Результат, который мы получили, не берет в расчет краевых эффектов, а значит он является приближенно верным лишь для катушек достаточной длины.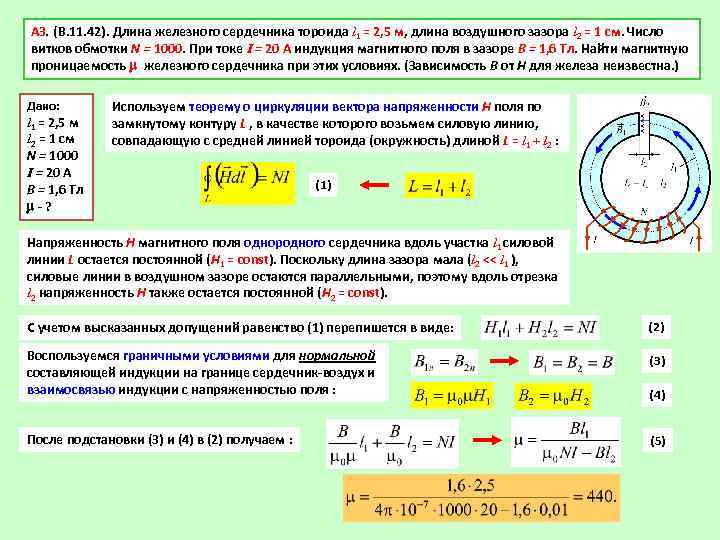
Поток магнитного поля соленоида пронизывает При расчете катушек используют такое понятие.
Самоиндукция. Энергия магнитного поля
Выбор провода. В первую очередь следует ориентировочно выбрать диаметр провода марки ПЭЛ или какой-либо другой марки. Так как расчет несложный, его можно выполнить для проводов различного сечения и выбрать тот, который дает наилучшие результаты по напряженности магнитного поля при минимальной мощности потребляемой электромагнитом. Определение длины провода в обмотке электромагнита.
Расчет обмоток электромагнитов Расчет обмотки электромагнита постоянного тока
Однажды, в очередной раз, перелистывая книгу, которую нашел у мусорного бачка, обратил внимание на простой, приблизительный расчет электромагнитов. Титульный лист книги показан на фото1. Вообще их расчет это сложный процесс, но для радиолюбителей, расчет, приведенный в этой книге, вполне подойдет. Электромагнит применяется во многих электротехнических приборах. Он представляет собой катушку из проволоки, намотанной на железный сердечник, форма которого может быть различной. Железный сердечник является одной частью магнитопровода, а другой частью, с помощью которой замыкается путь магнитных силовых линий, служит якорь.
Железный сердечник является одной частью магнитопровода, а другой частью, с помощью которой замыкается путь магнитных силовых линий, служит якорь.
Тема: Расчет катушки электромагнитного аппарата при постоянном и переменном токе. Цель работы: Рассчитать обмоточные данные и размеры катушки электромагнита.
Вы точно человек?
Для расчета обмотки напряжения электромагнита должны быть известны исходные величины: напряжение катушки и МДС F. Сечение обмоточного провода определяется исходя из величины необходимой МДС:. Мощность, выделяющаяся в обмотке в виде тепла, определяется зависимостью. Число витков обмотки при заданном сечении катушки определяется коэффициентом заполнения по меди :. Откуда можно выразить число витков обмотки. Следовательно, мощность, потребляемая обмоткой, обратно пропорциональна коэффициенту заполнения и площади окна.
Расчет обмотки электромагнита постоянного тока
X Вы должны быть Авторизованы Для возможности скачивания калькулятора Вы должны быть зарегистрированным пользователем.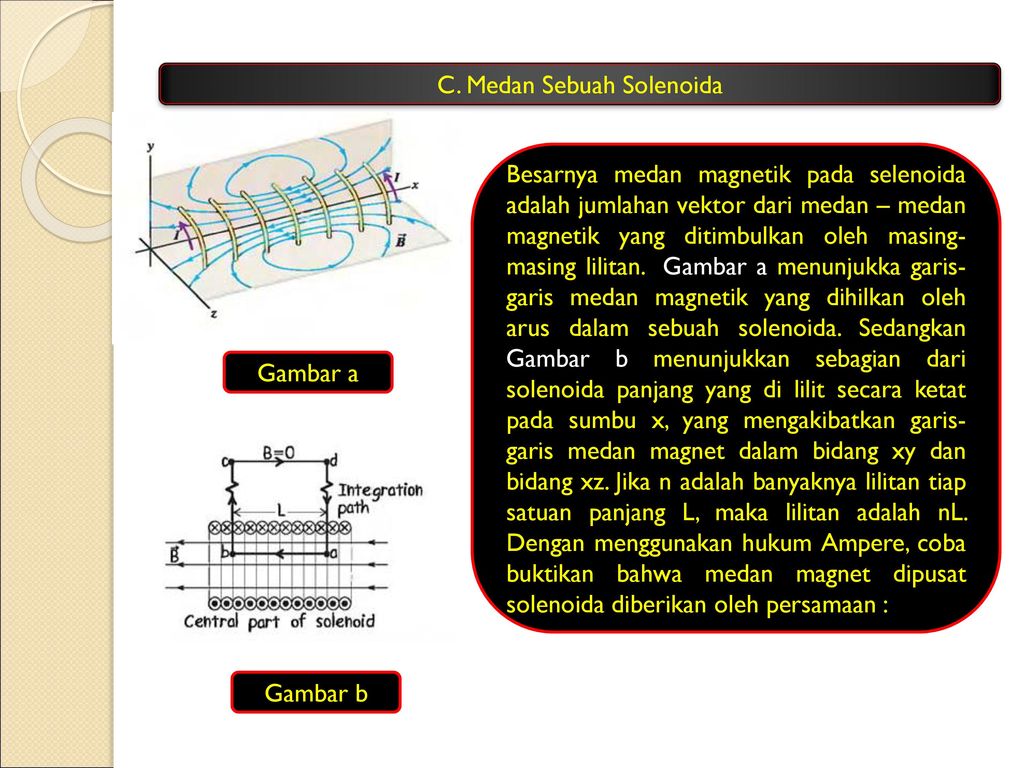 Рассчитайте силу электромагнита с помощью этого калькулятора. Введите значения тока, площади, количества витков и длины катушки, чтобы найти результат. Калькулятор электромагнитной силы.
Рассчитайте силу электромагнита с помощью этого калькулятора. Введите значения тока, площади, количества витков и длины катушки, чтобы найти результат. Калькулятор электромагнитной силы.
Расчет соленоида
Сила электромагнита — это сила, с которой электромагнит притягивает ферромагнитные материалы, зависит от магнитного потока Ф или, что то же самое, от индукции B и площади сечения электромагнита S. Рассчитайте силу электромагнита с помощью этого калькулятора. Введите значения тока, площади, количества витков и длины катушки, чтобы найти результат. Считал сам по формулам , всё сходится. Напряжение здесь учитывать ненужно ведь магнитное поле зависит то тока и количества витков а сила притяжения зависит от силы поля,сечения сердечника и зазора сердечника.
Поиск данных по Вашему запросу:
Схемы, справочники, даташиты:
Прайс-листы, цены:
Обсуждения, статьи, мануалы:
Дождитесь окончания поиска во всех базах.
По завершению появится ссылка для доступа к найденным материалам.
Содержание:
- Расчет соленоида и его потребляемой мощности
- Сила электромагнита
- Magn2: Плунжерный электромагнит
- Калькулятор для расчета электромагнитной силы
- Сила электромагнита
- Расчет обмоток электромагнитов
- Расчет соленоида и его потребляемой мощности
- Magn2: Плунжерный электромагнит
- Вы точно человек?
ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: 🔥 ЭЛЕКТРОМАГНИТ любой мощности своими руками. Проверим на практике.
Проверим на практике.
Расчет соленоида и его потребляемой мощности
Данный комплекс [1, 4] позволяет осуществлять проверку магнитометров инклинометра непосредственно на буровых площадках нефтегазовых месторождений. Целью работы является подтверждение возможности создания однородного магнитного поля заданной величины в ограниченном геометрическими размерами установки объеме.
Комплекс состоит из установки 1 для базирования на ней проверяемого инклинометра 5, блока связи 2 с компьютером 3, соединительных кабелей и источника питания установки 4.
Для работы с комплексом подходит любой персональный компьютер. Кольцами Гельмгольца называется система из двух одинаковых тонких катушек, расположенных соосно на расстоянии, равном их радиусу.
В пространстве между катушками получается поле высокой однородности [2]. Для системы двух колец Гельмгольца выражение магнитной индукции в геометрическом центре примет вид:.
Магнитное поле, создаваемое кольцами Гельмгольца, в каждой точке продольной оси Х вычисляется по формуле:. Магнитометры инклинометра помещены в цилиндрический корпус диаметром 30 мм на расстоянии 10 мм друг от друга и расположены ортогонально. Длина самого магнитометра 28 мм. Исходя из этого, необходимо создать кольца Гельмгольца и соленоид таких размеров, магнитное поле которых будет равномерным в объеме, вдвое превышающем объем, занимаемый чувствительными элементами.
Исходя из технических требований к изделию, кольца Гельмгольца и соленоид должны питаться от одного источника, максимальный ток которого не должен превышать 0,3 А.
Максимальный диаметр колец мм. Диаметр используемого намоточного провода равен 0,45 мм. Такая погрешность допустима для осуществления проверки работоспособности магнитометров инклинометра. Имея исходные данные, по формуле 2 можно вычислить число витков намоточного провода на каждом кольце:.
Действующее напряжение на концах намоточного провода колец определяется:. Расчетные значения индукции магнитного поля, созданного кольцами Гельмгольца вдоль оси Х, представлены на рис.
Расчетные значения индукции магнитного поля, созданного кольцами Гельмгольца вдоль оси Х, представлены на рис.
Из формулы 9 , имея известные данные магнитной индукции, силы тока и геометрических размеров соленоида, можно найти требуемое число витков намоточного провода:. Расчетные значения индукции магнитного поля, созданного соленоидом вдоль оси Z, представлены на рис.
Данные геометрических размеров, величины протекающих токов и количества витков использовались те же, что и при аналитическом расчете, а также, согласно техническому заданию, на разработку комплекса для проверки магнитометров инклинометра.
Так как кольца Гельмгольца и соленоид включаются поочередно, то сначала моделируется работа соленоида, а затем работа колец Гельмгольца. На рис. Представленная на рис. Результаты аналитического моделирования показывают расхождения с графиками зависимости величины магнитного поля от координаты точки по осям соленоида и колец Гельмгольца, полученными при моделировании в среде Comsol.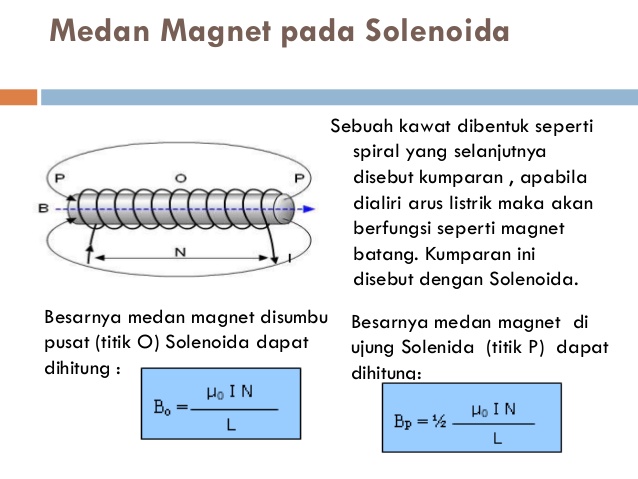 Вследствие чего неоднородность магнитного поля увеличивается.
Вследствие чего неоднородность магнитного поля увеличивается.
Статья в формате PDF. Гормаков А. АИС, Матвеев А. Огородников А. Часть 1: учебное пособие. Ульянов И. Сочи, октября Академия Естествознания готовит к изданию реестр новых научных направлений, разработанных российскими учеными.
Сила электромагнита
Дневники Файлы Справка Социальные группы Все разделы прочитаны. Расчет соленоида и его потребляемой мощности. Доброго времени суток всем! Оценка 0.
Расчёт магнитной индукции катушки. Допустим имеется катушка индуктивности, известны: её длинна l, её число витков w и сила тока.
Magn2: Плунжерный электромагнит
Соленоид можно представить в виде системы одинаковых круговых токов с общей прямой осью. Бесконечно длинный соленоид симметричен любой, перпендикулярной к его оси плоскости. Взятые попарно рис. Возьмём воображаемый прямоугольный контур 1—2—3—4—1 и разместим его в соленоиде, как показано на рисунке 2. Возьмём участок 3—4 — на большом расстоянии от соленоида, где поле стремится к нулю; и пренебрежём третьим интегралом, тогда.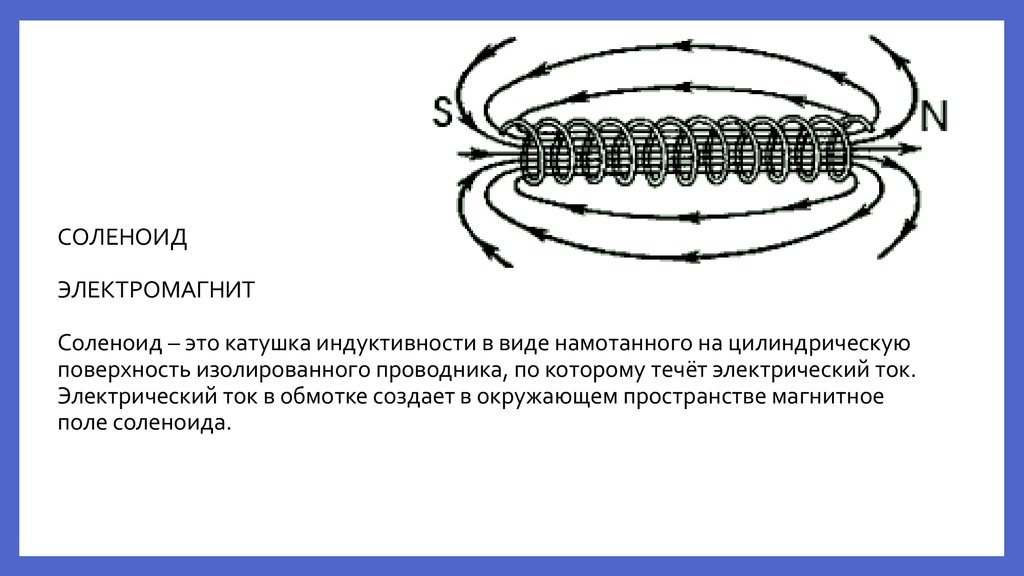 Если отрезок 1—2 внутри соленоида, контур охватывает ток:. Тогда магнитная индукция внутри соленоида :. Бесконечно длинный соленоид аналогичен плоскому конденсатору — и тут, и там поле однородно и сосредоточено внутри. Произведение nI — называется число ампер витков на метр.
Если отрезок 1—2 внутри соленоида, контур охватывает ток:. Тогда магнитная индукция внутри соленоида :. Бесконечно длинный соленоид аналогичен плоскому конденсатору — и тут, и там поле однородно и сосредоточено внутри. Произведение nI — называется число ампер витков на метр.
Калькулятор для расчета электромагнитной силы
Исполнительный орган в виде соленоидального плунжерного электромагнита состоит из обмотки, окруженной ферромагнитным сердечником и якоря в виде плунжера. Задача состоит в расчете магнитного поля в устройстве и тягового усилия, приложенного к якорю. Тип задачи: Нелинейная осесимметричная задача магнитостатики. Все размеры заданы в миллиметрах.
Конструктивно длинные соленоиды выполняются как в виде однослойной намотки см.
Сила электромагнита
Однажды, в очередной раз, перелистывая книгу, которую нашел у мусорного бачка, обратил внимание на простой, приблизительный расчет электромагнитов. Титульный лист книги показан на фото1. Вообще их расчет это сложный процесс, но для радиолюбителей, расчет, приведенный в этой книге, вполне подойдет. Электромагнит применяется во многих электротехнических приборах. Он представляет собой катушку из проволоки, намотанной на железный сердечник, форма которого может быть различной. Железный сердечник является одной частью магнитопровода, а другой частью, с помощью которой замыкается путь магнитных силовых линий, служит якорь.
Электромагнит применяется во многих электротехнических приборах. Он представляет собой катушку из проволоки, намотанной на железный сердечник, форма которого может быть различной. Железный сердечник является одной частью магнитопровода, а другой частью, с помощью которой замыкается путь магнитных силовых линий, служит якорь.
Расчет обмоток электромагнитов
А какая формула для расчёта магнитной индукции катушки со стальным стрдечником? Нужно просто знать магнитную проницаемость стали Я пока не нашел или не понял. Дело в том что у стали магнитная проницаемость меняется в зависимости от напряжённости H. И при том при намагничивании и размагничивании по разному. В справочниках могут приводиться конкретные кривые B H для определённых сталей. Здравствуйте Сергей! А как расчитать эелектро магнит с сердечником тоже вопрос, не знаю какой выбрать с сибой в 0,5 — 1 Тесла?
Усилия соленоида может нехватить для вытягивания-втягивания механизма. Или же соленоид достигнет некомпактных размеров, для.
Расчет соленоида и его потребляемой мощности
В процессе эксплуатации электрического оборудования львиная доля логических схем используют в своей работе в качестве исполнительного органа катушку с магнитным сердечником. Принцип работы данного устройства заключается в появлении магнитной силы внутри витков, которая притягивает соленоид и совершает механическую работу. За счет такого воздействия происходит перемещение контактов реле, открытие или закрытие клапанов, механическое включение кнопок и прочие манипуляции.
Magn2: Плунжерный электромагнит
ВИДЕО ПО ТЕМЕ: Лекция 162. Сила тяги электромагнита
Между прочим. Калькулятор англоязычный. На англоязычном зеркале нашего калькулятора есть ссылки на три наилучших, по нашему мнению, англоязычных калькулятора. В том числе и на этот вторая ссылка в References Калькулятор действительно детальный.
Схема магнитоэлектрического привода.
Вы точно человек?
Coil: программа для расчета параметров и магнитного поля цилиндрического соленоида: активное сопротивление, индуктивность, потребляемый ток, рассеиваемая мощность, магнитная индукция в центре и в заданной точке пространства. На рисунке показан цилиндрический соленоид без сердечника в разрезе. Окружающая среда немагнитная и токонепроводящая как правило, воздух. Расчетные данные: R — активное сопротивление обмотки соленоида условия нормальные , Ом L — индуктивность соленоида, Гн ZL — реактивное сопротивление соленоида, Ом N — число витков Id — действующее значение тока через соленоид, А P — рассеиваемая в соленоиде мощность, Вт B0d — магнитная индукция действующее значение в центре соленоида точка 0, 0 , Тл Bxd x, z — радиальная составляющая магнитной индукции действующее значение в точке с координатами x, z относительно точки 0, 0 , Тл Bzd x, z — аксиальная составляющая магнитной индукции действующее значение в точке с координатами x, z относительно точки 0, 0 , Тл. Программа Coil позволяет рассчитывать по заданным геометрическим размерам R1, R2, H , диаметру провода D и фактору упаковки Lambda: активное сопротивление R по меди , индуктивность L, число витков N, величину тока Id в обмотке при заданном напряжении Ed заданной частоты f, рассеиваемую при этом мощность P, реактивное сопротивление ZL, величину магнитной индукции Bxd, Bzd в заданной точке пространства x, z , величину магнитной индукции B0 в центре соленоида 0, 0. Расчеты производятся в системе СИ. Результаты выводятся на экран монитора, а также при необходимости на принтер в некоторых версиях программы.
Программа Coil позволяет рассчитывать по заданным геометрическим размерам R1, R2, H , диаметру провода D и фактору упаковки Lambda: активное сопротивление R по меди , индуктивность L, число витков N, величину тока Id в обмотке при заданном напряжении Ed заданной частоты f, рассеиваемую при этом мощность P, реактивное сопротивление ZL, величину магнитной индукции Bxd, Bzd в заданной точке пространства x, z , величину магнитной индукции B0 в центре соленоида 0, 0. Расчеты производятся в системе СИ. Результаты выводятся на экран монитора, а также при необходимости на принтер в некоторых версиях программы.
Электромагнит применяется во многих электротехнических приборах. Он представляет собой катушку из проволоки, намотанной на железный сердечник, форма которого может быть различной. Железный сердечник является одной частью магнитопровода, а другой частью, с помощью которой замыкается путь магнитных силовых линий, служит якорь.
4. Пример расчета п-образного электромагнита
Для выполнения расчета электромагнита заданы исходные данные:
геометрические размеры электромагнита;
характеристики катушек (протекающий ток и число витков),
индукция в рабочем воздушном зазоре.

4.1. Расчет электромагнита классическим методом
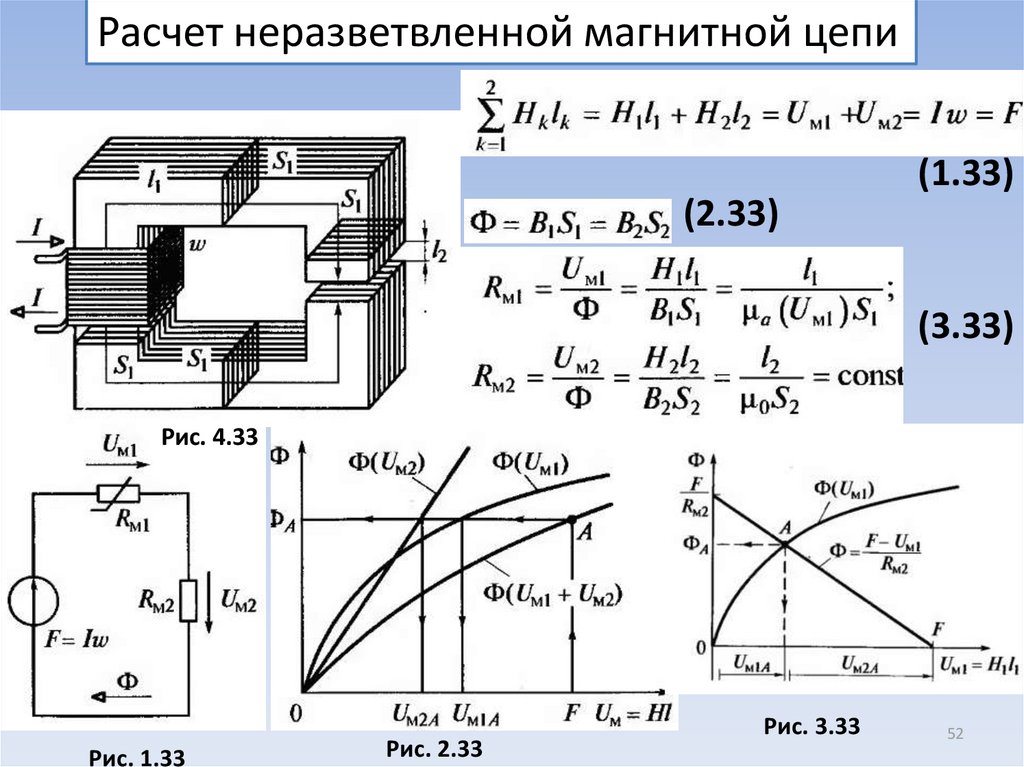
Рассмотрим магнитную систему П-образного электромагнита постоянного тока (рис. 4.1). Размеры приведены в миллиметрах.
Рис. 4.1. Сечение электромагнита
Индукция в воздушном зазоре составляет . Ярмо и сердечник электромагнита изготовлены из стали M-27. Катушки электромагнита соединены последовательно и протекающий по ним ток составляет , в каждой катушке по 80 витков ( ). и выполнении расчетов принять, что магнитный поток в воздушном зазоре равен потоку в сердечнике и ярме (потоками рассеяния пренебречь).
Толщина электромагнита составляет 20 мм.
Определим площади поперечного сечения частей магнитной системы:
,
,
.
Поток в воздушном зазоре:
,
.
Индукция в ярме и сердечнике:
,
.
Найдем средние напряженности для сердечника и ярма (используя кривую намагничивания для стали M-27).
,
.
Магнитодвижущая сила (МДС) в участках (длина магнитных силовых линий определяется в соответствии с рис. 4.1):
,
,
,
,
,
где N – количество рабочих воздушных зазоров.
Суммарная МДС:
.
МДС развиваемая катушками (по исходным данным):
.
Определяем силу притяжения сердечника с ярму:
,
где N – количество рабочих воздушных зазоров.
Коэффициент насыщения ( ):
4.2. Расчет электромагнита численным методом
Запускаем программу
FEMM
4. 0.1, выбираем в главном меню пункт новая
задача (New)
и в появившемся окне выбираем пункт
Magnetics
Problem
(Магнитостатическая задача) – рис. 4.2.
0.1, выбираем в главном меню пункт новая
задача (New)
и в появившемся окне выбираем пункт
Magnetics
Problem
(Магнитостатическая задача) – рис. 4.2.
Рис. 4.2
Сперва задаем основные параметры задачи: единицы измерения – миллиметры (Millimeters) и толщину устройства (Depth). Задание вышеуказанных параметров для рассматриваемой задачи приведено на рис. 4.3.
Рис. 4.3
Построение геометрии начинаем с расстановки точек в соответствии с их координатами (рис. 4.4).
Рис. 4.4
Затем строим линии и расставляем метки блоков (рис. 4.5).
Рис. 4.5
Задаем или создаем
собственные материалы в редакторе
материалов. Редактор вызывается через
главное меню Properties – Materials Library.
Для Рассматриваемого электромагнита
нужно задать следующие материалы (рис. 4.6):
4.6):
Рис. 4.6
Для материалов “Tok +” и “Tok – ” нужно задать плотность тока со знаком “+” и “–”, соответственно. Значение плотности тока рассчитывается в соответствии со следующей формулой:
,
где – поперечное сечение одной катушки. В рассматриваемой модели .
Плотность тока в катушке:
.
Задаем материалы на построенной модели – рис. 4.7.
Рис. 4.7
Создаем нулевые граничные условия (A=0) – рис. 4.8. Редактор граничных условий вызывается через главное меню Properties – Boundary. В появившемся окне выбираем Add Property.
Рис. 4.8
Вокруг построенного
электромагнита строим замкнутый контур
и в свойствах контура указываем граничное
условие “ A=0”
(рис. 4.9).
Рис. 4.9
Построение модели закончено и после сохранения в файл созданной геометрии можно приступить к расчету.
В результате расчета можно просмотреть распределение линий магнитной индукции (рис. 4.10) и цветовую картину магнитной индукции (рис. 4.11).
Рис. 4.10
Рис. 4.11
График изменения индукции в воздушном зазоре – рис. 4.12.
Рис. 4.12
Средняя индукция в различных частях электромагнита:
воздушный зазор ,
ярмо ,
сердечник .
МДС в различных частях электромагнита:
воздушный зазор ,
ярмо ,
сердечник .
Магнитный поток в ярме составляет .
Сила притяжения
сердечника к ярму .
Определение силы тяги показано на рис. 4.13.
4.13.
Рис. 4.13
Расчет переходных процессов в соленоиде размагничивающего устройства рельсовых плетей при включении его на импульсное воздействие
АННОТАЦИЯ
В статье рассматриваются переходный процесс при включении соленоида с сердечником на первую гармонику напряжения, используя метод последовательных приближений и применением метода наложения для основного действия и первой и третьей гармонических составляющих тока определены вебер амперные характеристики соленоида с сердечником.
ABSTRACT
The article discusses the transient process when a solenoid with a core is turned on to the first harmonic of the voltage, using the method of successive approximations and applying the superposition method for the main action and the first and third harmonic components of the current determined the Weber ampere characteristics of the solenoid with a core.
Ключевые слова: переходный процесс; соленоид; размагничивающее устройство; импульсное воздействие; метод последовательных приближений; метод наложения.
Keywords: transitional process; solenoid; demagnetizing device; impulse impact; method of successive approximations; overlay method.
Любое импульсное воздействие представляет собой периодические несинусоидальные напряжения, токи, потокосцепление. Поэтому необходимо раскладывать в ряд Фурье импульсы в виде прямоугольника, треугольника, полуволны синусоид, следующих периодически. Для качественного размагничивающего устройства необходимо учесть импульсы в виде прямоугольника и треугольника[4-7]. Формы показаны на рис.1.
Для расчетов используем реальные значения прямоугольного импульса параметрами: частота ; период ; длительность импульса ; напряжение .
а) б)
Рисунок 1. Периодические функции несинусоидального напряжения в устройстве размагничивания. а) прямоугольный импульс; б) треугольный импульс
Вначале рассмотрим разложение в ряд прямоугольного импульса, который запишется в виде:
.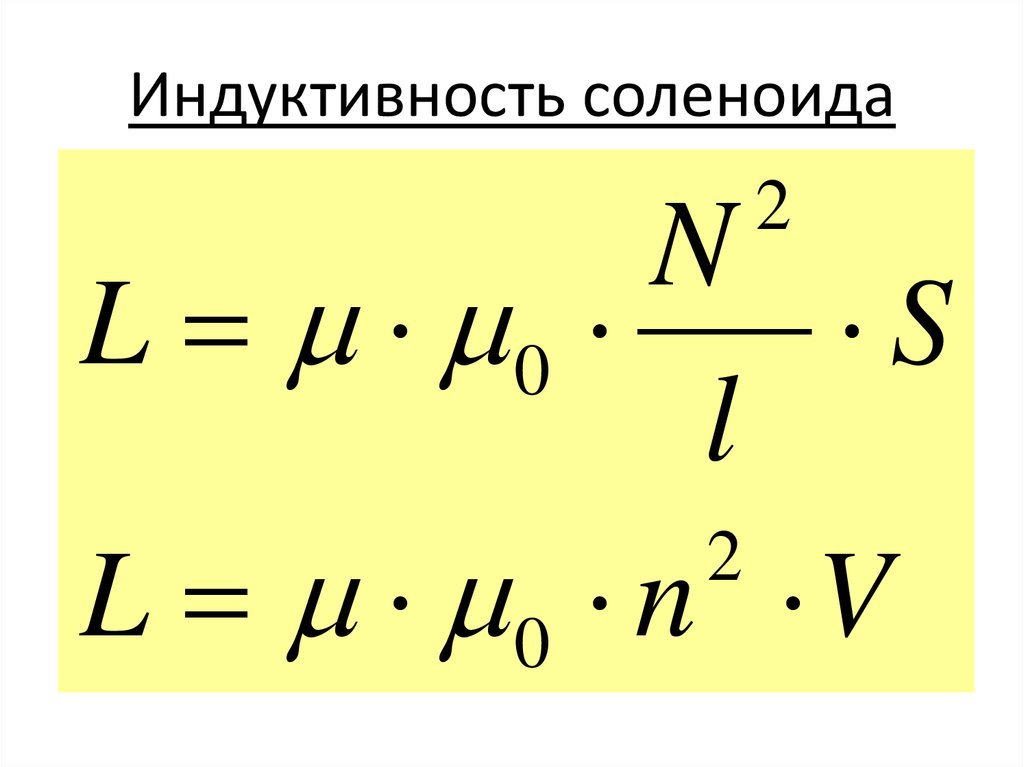 (1)
(1)
С учетом цифровых данных можно записать:
(2)
Переходный процесс в соленоиде с сердечником на подачу напряжения прямоугольного импульса включает в себя расчет на постоянную, первую, третью и пятую гармонические составляющие разложенного в ряд Фурье напряжения[1-3]. Кроме того, надо учесть, что переходный процесс на импульсное воздействие учитывает включение соленоида с сердечником до промежутка времени от и отключение цепи при . Рассмотрим процесс включения соленоида с сердечником на промежутке времени . Расчет включает постоянную составляющую, первую, третью и пятую гармонические составляющие напряжения. Затем применим метод наложения. Используем основную кривую намагничивания нелинейной индуктивности, аппроксимирую её выражением:
. (3)
Кривая намагничивания представлена на рисунке 2.
Рисунок 2. График функции ψ(t) включения соленоида с сердечником на постоянное напряжение
i, А
Рисунок 3.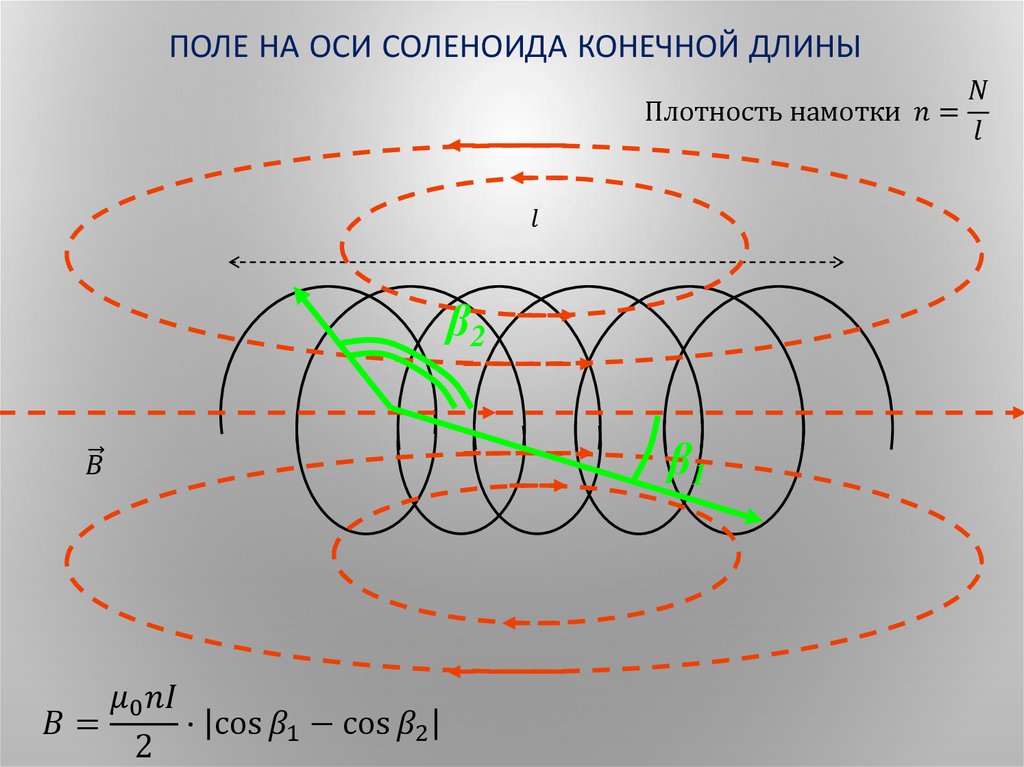 График функции i (t) включения соленоида с сердечником на постоянное напряжение
График функции i (t) включения соленоида с сердечником на постоянное напряжение
Для определения времени используем известное выражение:
. (4)
Расчет проведем по программе Excel, используя при этом данные: , =4,33Ом; .
При этом получены следующие результаты: ; L=0,154Гн.
Рассмотрим переходный процесс при включении соленоида с сердечником на первую гармонику напряжения, используя метод последовательных приближений:
. (5)
Используем дифференциальное уравнение:
. (6)
Примем , тогда уравнение (3.44) преобразуется в новое:
. (7)
Решением уравнения (3.45) будет:
. (8)
Потокосцепления , где , то есть мы получили цифровой ответ.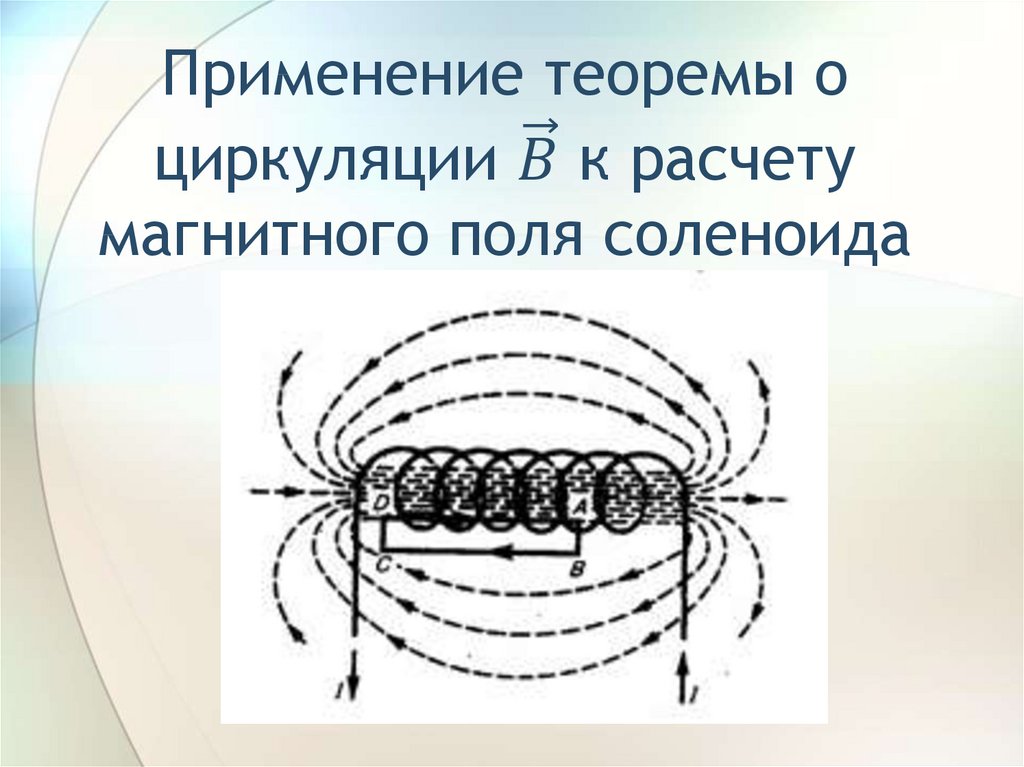
При уравнение (8) будет: ,
откуда . Решение уравнения запишется:
, .
Полученные результаты предслены в таблице 1 и рис. 4 и 5.
Таблица 1.
Для первой гармонической составляющей графика
|
, c |
i, A |
|
|
0 |
0 |
0 |
|
-0,67 |
0,066 |
-4,35868 |
|
0,77 |
0,077 |
5,059136 |
|
-1,16 |
0,112 |
-7,58595 |
|
-1,30 |
0,172 |
-8,48683 |
|
1,32 |
0,263 |
8,581039 |
, c
Рисунок 4. График для первой гармонической составляющей
График для первой гармонической составляющей
i, A
, c
Рисунок 5. График для первой гармонической составляющей
Для третьей гармонической составляющей напряжения имеем уравнение:
. (9)
Решением данного уравнения будет:
. (10)
Уравнение (10) преобразуем в следующий вид: , где . Общее решение уравнения для переходного процесса имеем вид: , где .
Результаты расчетов по 3-ей гармонической составляющей представлены в таблице 2. и на рис.6 и 7.
Таблица 2.
Для третьей гармонической составляющей графика
|
, c |
i, A |
|
|
0 |
0 |
0 |
|
0,066 |
46,70394 |
303,2724 |
|
0,077 |
-41,8647 |
-271,849 |
|
0,112 |
-5,67574 |
-36,8554 |
|
0,172 |
-32,3708 |
-210,2 |
, c
Рисунок 6.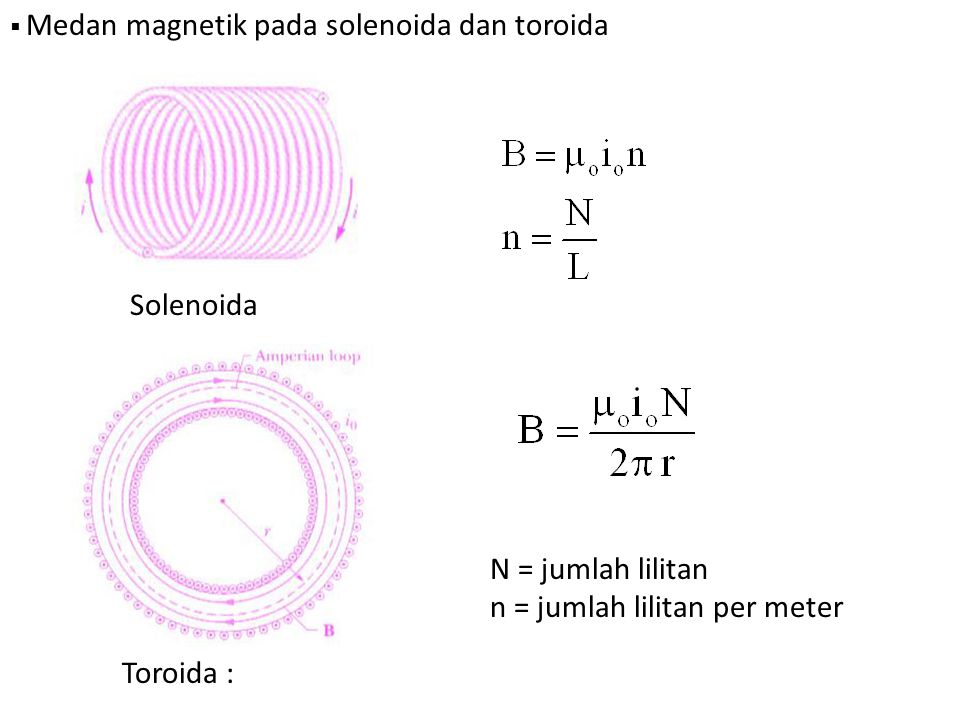 График для третьей гармонической составляющей
График для третьей гармонической составляющей
i, A
, c
Рисунок 7. График для третьей гармонической составляющей
Применим метод наложения для основного действия и первой и третьей гармонических составляющих:
(11)
в интервале , где , для постоянной составляющей;, для первой гармонической составляющей; , для третьей гармонической составляющей [9,10].
Таблица 3.
Для интервала , гармонической составляющей
|
i0, A |
i1, A |
i3, A |
||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0,066 |
1,008 |
-0,67 |
46,70394 |
0,78 |
-4,35868 |
303,2724 |
|
0,077 |
2,016 |
0,77 |
-41,8647 |
1,3 |
5,059136 |
-271,849 |
|
0,112 |
3,024 |
-1,16 |
-5,67574 |
3,64 |
-7,58595 |
-36,8554 |
|
0,172 |
3,276 |
-1,30 |
-32,3708 |
5,2 |
-8,48683 |
-210,2 |
|
0,263 |
3,299 |
1,32 |
44,44006 |
5,49 |
8,581039 |
288,5718 |
Таблица 4.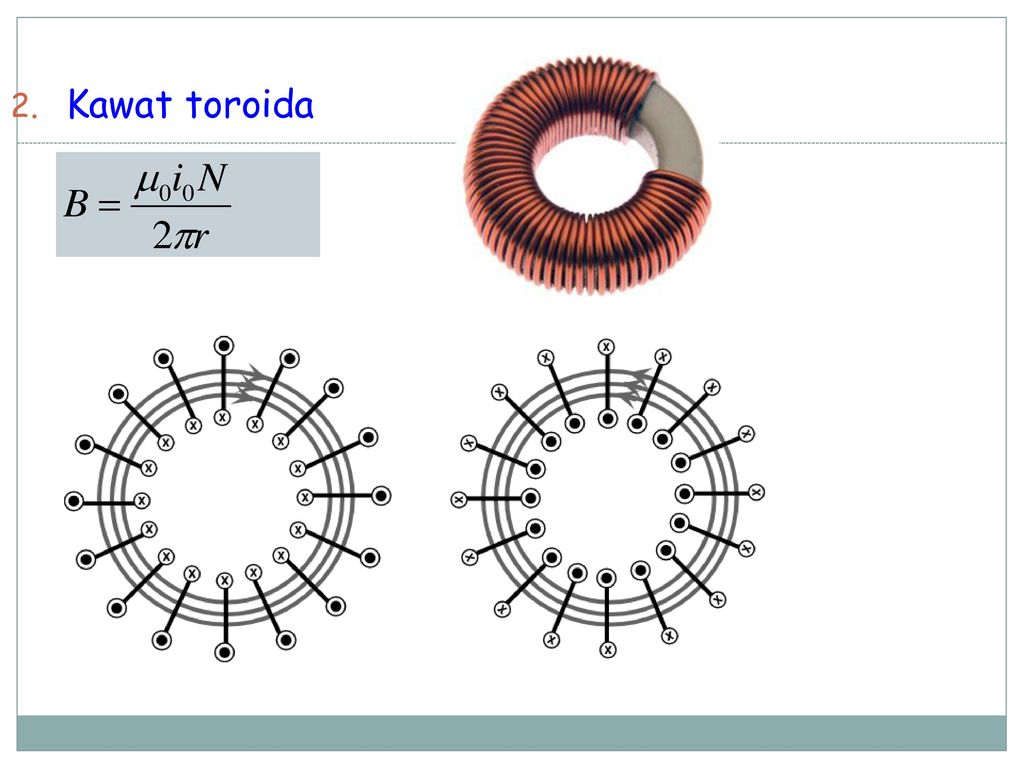
Для переходного процесса при включении соленоида с сердечником
|
i, A |
||
|
0 |
0 |
0 |
|
0,066 |
47,04194 |
299,6937 |
|
0,077 |
-39,0787 |
-265,49 |
|
0,112 |
-3,81174 |
-40,8014 |
|
0,172 |
-30,3948 |
-213,487 |
|
0,263 |
49,05906 |
302,6428 |
, c
Рисунок 8. Общий график переходного процесса при включении соленоида с сердечником
Общий график переходного процесса при включении соленоида с сердечником
Рисунок 9. Общий график переходного процесса при включении соленоида с сердечником
Рисунок 10. Вебер амперная характеристика соленоида с сердечником а-первоначальная кривая намагничивания; б-нисходящая ветвь убывания потока до остаточного значения .
Переходный процесс на участке будем рассматривать, как замыкание накоротко соленоида с сердечником, используя при этом нисходящую ветвь вебер-амперной характеристики (рис.10). Нисходящую ветвь намагничивания выразим в аналитическом виде:
. (12)
Обозначим: , . При замыкания накоротко соленоида сердечника, уравнение короткого замыкания будет иметь вид:
При замыкания накоротко соленоида сердечника, уравнение короткого замыкания будет иметь вид:
. (13)
Рисунок 11. Переходный процесс в соленоиде с сердечником
Решением данного уравнения является:
. (14)
|
t,c |
i,A |
|
0 |
0 |
|
0,066 |
299,6937 |
|
0,077 |
-265,49 |
|
0,112 |
-40,8014 |
|
0,172 |
-213,487 |
|
0,263 |
302,6428 |
|
0,3 |
2,727105 |
|
0,4 |
1,275773 |
|
0,466 |
299,6937 |
|
0,543 |
-265,49 |
|
0,655 |
-40,8014 |
|
0,827 |
-213,487 |
|
1,09 |
302,6428 |
|
1,39 |
2,727105 |
|
1,79 |
1,275773 |
|
2,256 |
299,6937 |
Для соленоида с сердечником нисходящая характеристика удовлетворяется,
если представить: ; , при этих значениях коэффициентов будем иметь: ; ; . Переходный процесс для потокосцепления записывается уравнением:
Переходный процесс для потокосцепления записывается уравнением:
. (15)
Общий график переходного процесса в соленоиде с сердечником, при включении на прямоугольный импульс показан на рис.11.
Общий переходный процесс в соленоиде с сердечником для тока показан на рис.12.
i, A t,c
Рисунок 12. Переходный процесс в соленоиде с сердечником
Заключение
На основании полученных результатов можно сделать заключение о том, что оптимальным для размагничивания будет применение импульсных воздействий, так как получается большое количество максимумов и минимумов токов, как в отрицательных, так и в положительных областях. Понижение тока равносильно уменьшению насыщения стали сердечника, и экономии электроэнергии а следовательно приводит к размагничиванию стали рельсовых плетей.
Список литературы:
- Колесников И.
 К., Курбанов Ж.Ф. Программное обеспечение системы управления единым пространственным полем // Современные состояние и перспективы применения информационных технологий в управлении, доклады республиканской научно-технической конференции,5-6сентябрь 2016г., Джизак.
К., Курбанов Ж.Ф. Программное обеспечение системы управления единым пространственным полем // Современные состояние и перспективы применения информационных технологий в управлении, доклады республиканской научно-технической конференции,5-6сентябрь 2016г., Джизак. - Халиков А.А., Колесников И.К., Курбанов Ж.Ф. Исследование и разработка единого пространственного электромагнитного поля и устройств на их основе. / Монография. Издательства «Фан ва технология», 2019. – С.238.
- Халиков А.А., Колесников И.К., Кадыров О.Х., Яронова Н.В. Влияния электромагнитного поля на свойства жидких и твердых тел // Наука образование техника №4, 2007г. Ош, Киргизия, – С.104-106.
- Халиков А.А., Курбанов Ж.Ф., Ортиков М.С. Устройства намагничивания и размагничивания рельсовых плетей и их сравнительный анализ. // UNIVERSUM Технические науки. Москва– 2019. №10 (67) – С.78-80. Электронный научный журнал [email protected] .
- Халиков А.А., Курбанов Ж.Ф., Ортиков М.
 С. Параметры магнетизма, намагничивания и размагничивания материалов и рельсовых плетей. // UNIVERSUM Технические науки. Москва– 2019. №10 (67). – С.81-83. Электронный научный журнал. [email protected] .
С. Параметры магнетизма, намагничивания и размагничивания материалов и рельсовых плетей. // UNIVERSUM Технические науки. Москва– 2019. №10 (67). – С.81-83. Электронный научный журнал. [email protected] . - Халиков А.А., Мирсагдиев О.А. Разработка информационно-измерительных систем на основе волоконно-оптических датчиков. //ПРОБЛЕМЫ ПОЛУЧЕНИЯ, ОБРОБОТКИ И ПЕРЕДАЧИ ИЗМЕРИТЕЛЬНОЙ ИНФОРМАЦИИ. II Международная научно-техническая конференция, посвященная 90-летию со дня рождения профессора Зарипова Мадияра Фахритдиновича. Уфа-2019. – С.207-212.
- Халиков А.А., Ибрагимова О.А. Исследование устройств систем управления единым пространственным электромагнитным полем. Монография. / Под ред.проф. ХаликоваА.А. Ташкент–Тамбов: Консальтинговая компания Юком, 2020. 102с. https: //ukonf.com/doc/mon.2020.05.01.pdf. E-mail: [email protected].
- Khalikov A.A. Analysis of methods for determining the characteristics of a single spatial electromagnetic field. // Индонезия.
 Icon Beat 2019. [email protected]. International Conference on Bioinergy and Environmtntally Sustainable Agriculture Technology. (Международная конференция)
Icon Beat 2019. [email protected]. International Conference on Bioinergy and Environmtntally Sustainable Agriculture Technology. (Международная конференция) - Kurbanov J.F. The spectral characteristics of the new functional materials based on a single device spatial field // «American Journal of Science and Tehnologies» International collaboration in Eurasia // American Journal of Science and Tehnologies, «Hrinceton University Press», 2015, №2(20). –P.11-16.
- Kurbanov J.F., Khalikov A.A., Ortikov M.S. Devices for magnetization and demagnization of rail lashes and their comparative analysis with existing. Сборник статьей XXVIII международной научно-практической конференции «Технические науки: проблемы и решения». Сайт https://internauka.org/ .
Магнитек — Пример простейшего расчёта электромагнита
Электромагнит применяется во многих электротехнических приборах. Он представляет собой катушку из проволоки, намотанной на железный сердечник, форма которого может быть различной.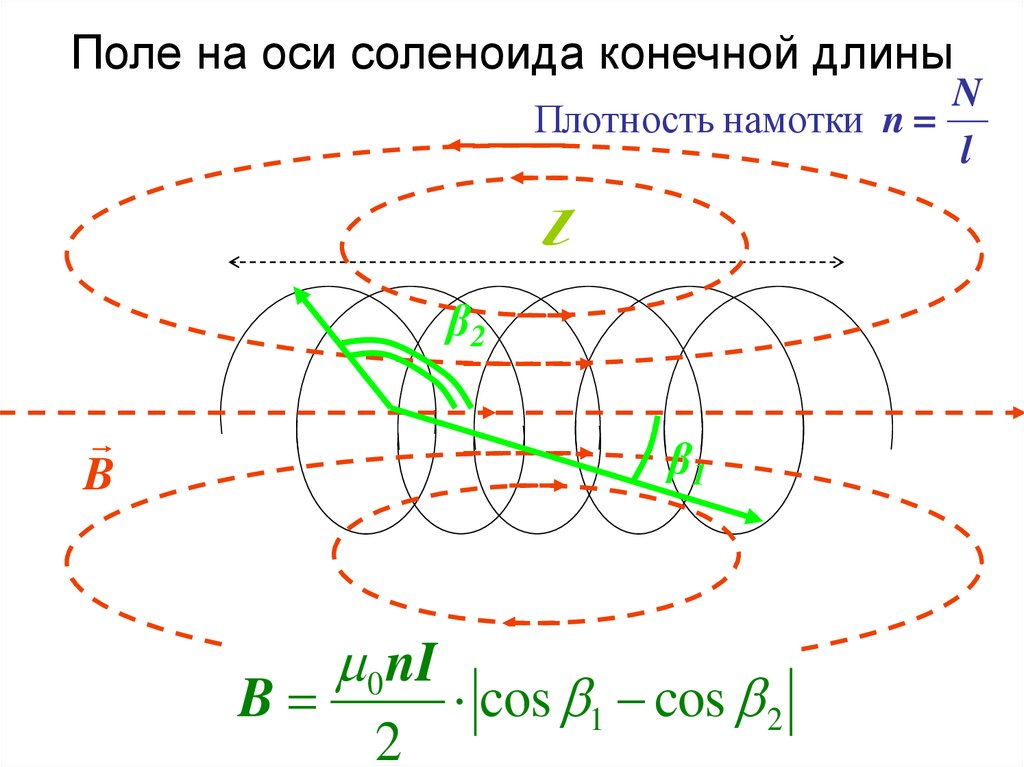 Железный сердечник является одной частью магнитопровода, а другой частью, с помощью которой замыкается путь магнитных силовых линий, служит якорь. Магнитная цепь характеризуется величиной магнитной индукции — В, которая зависит от напряженности поля и магнитной проницаемости материала. Именно поэтому сердечники электромагнитов делают из железа, обладающего высокой магнитной проницаемостью.
Железный сердечник является одной частью магнитопровода, а другой частью, с помощью которой замыкается путь магнитных силовых линий, служит якорь. Магнитная цепь характеризуется величиной магнитной индукции — В, которая зависит от напряженности поля и магнитной проницаемости материала. Именно поэтому сердечники электромагнитов делают из железа, обладающего высокой магнитной проницаемостью.
При конструировании электромагнитов весьма желательно получить большой силовой поток. Добиться этого можно, если уменьшить магнитное сопротивление. Для этого надо выбрать магнитопровод с наименьшей длиной пути силовых линий и с наибольшим поперечным сечением, а в качестве материала — железоматериал с большой магнитной проницаемостью.
Другой путь увеличения силового потока путем увеличения ампервитков не является приемлемым, так как в целях экономии проволоки и питания следует стремиться к уменьшению ампервитков.
Обычно расчеты электромагнитов делаются по специальным графикам. В целях упрощения в расчетах мы будем также пользоваться некоторыми выводами из графиков. Предположим, требуется определить ам-первитки и силовой поток замкнутого железного магнитопровода, изображенного на рисунке 4,а и сделанного из железа самого низкого качества.
В целях упрощения в расчетах мы будем также пользоваться некоторыми выводами из графиков. Предположим, требуется определить ам-первитки и силовой поток замкнутого железного магнитопровода, изображенного на рисунке 4,а и сделанного из железа самого низкого качества.
Рассматривая график намагничивания железа, нетрудно убедиться, что наиболее выгодной является магнитная индукция в пределах от 10 000 до 14 000 силовых линий на 1 см2, что соответствует от 2 до 7 ампервиткам на 1 см. Для намотки катушек с наименьшим числом витков и более экономичных в смысле питания для расчетов надо принимать именно эту величину (10 000 силовых линий на 1 см2 при 2 ампервитках на 1 см длины). В этом случае расчет может быть произведен следующим образом. Так, при длине магнитопровода Z=/1-)-/2, равной 20 см -f- 10 см = 30 см, потребуется 2×30=60 ампервитков.
Для двухполюсного магнита этот, результат следует удвоить. Следовательно, Р=24,8 кг ^ 25 кг. При определении подъемной силы необходимо помнить, что она зависит не только от длины магнитопровода, но, и от площади соприкосновения якоря и сердечника. Поэтому якорь должен точно прилегать к полюсным наконечникам, иначе даже малейшие воздушные прослойки вызовут сильное уменьшение подъемной силы.
При определении подъемной силы необходимо помнить, что она зависит не только от длины магнитопровода, но, и от площади соприкосновения якоря и сердечника. Поэтому якорь должен точно прилегать к полюсным наконечникам, иначе даже малейшие воздушные прослойки вызовут сильное уменьшение подъемной силы.
Далее производится расчет катушки электромагнита. В нашем примере подъемная сила в 25 кг обеспечивается 60 ампервитками. Рассмотрим, какими средствами можно получить произведение N-J—60 ампервиткам.
Очевидно, этого можно добиться либо путем использования большого тока при малом количестве витков катушки, например 2 а и 30 витков, либо путем увеличения числа витков катушки при уменьшении, тока, например 0,25 а и 240 витков. Таким обра-1 зом, чтобы электромагнит имел подъемную силу в 25 кг, на его сердечник можно намотать, и 30 витков и 240 витков, но при этом изменить величину питающего тока. Конечно, можно выбрать и другое соотношение.
Однако изменение величины тока в больших пределах не всегда возможно, так как оно обязательно потребует изменения диаметра применяемой проволоки.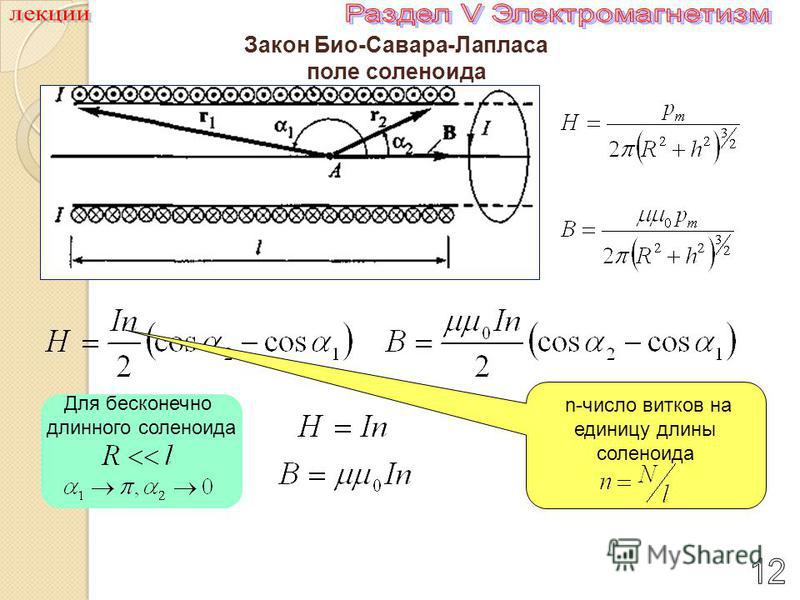 Так, при кратковременной работе (несколько минут) для проводов диаметром до 1. мм допустимую плотность тока, при которой не происходит сильного перегревания провода, можно принять равной 5 A/мм2. В нашем примере проволока должна быть следующего сечения: для тока в 2A — 0,4 мм2, а для тока в 0,25A — 0,05 мм2.
Так, при кратковременной работе (несколько минут) для проводов диаметром до 1. мм допустимую плотность тока, при которой не происходит сильного перегревания провода, можно принять равной 5 A/мм2. В нашем примере проволока должна быть следующего сечения: для тока в 2A — 0,4 мм2, а для тока в 0,25A — 0,05 мм2.
Каким же из этих проводов следует производить обмотку?
С одной стороны, выбор диаметра провода может определяться имеющимся у руководителя ассортиментом проволоки, с другой — возможностями источников питания как по току, так и по напряжению. Действительно, две катушки, одна из которых изготовлена из толстой проволоки в 0,7 мм и с небольшим числом витков — 30, а другая — из проволоки в 0,2 мм и числом витков 240, будут иметь резко различное сопротивление.
Зная диаметр проволоки и ее длину, можно легко определить сопротивление. Длина проволоки равна произведению общего числа витков на длину одного из них (среднюю): l=Nxlt где lt — длина одного витка, равная 3,14 x Д. В нашем примере Д = 2 см, и 1г x 6,3 см. Следовательно, для первой катушки длина провода будет 30 x 6,3 = 190 см, а для второй — 240 X 6,3 = 1 512 см. Сопротивления обмоток будут также различными.
В нашем примере Д = 2 см, и 1г x 6,3 см. Следовательно, для первой катушки длина провода будет 30 x 6,3 = 190 см, а для второй — 240 X 6,3 = 1 512 см. Сопротивления обмоток будут также различными.
Пользуясь законом Ома, нетрудно вычислить необходимое напряжение. Так, для создания в обмотках тока в 2A необходимое напряжение равно 0,2B, а для тока в 0,25A — 2,5B.
Таким образом, для питания первой катушки достаточно одного элемента или аккумулятора, причем для понижения напряжения приходится включать реостат; для питания второй катушки необходимо взять два элемента, соединяя их последовательно. Ясно, что во втором случае имеется меньше потерь электроэнергии и обмотка получается более выгодной.
Анализ полученных результатов позволяет сделать еще такой вывод: диаметр проволоки подбирается так, чтобы питание катушки можно было производить только от одного элемента (или аккумулятора) без каких-либо реостатов, где энергия тратится непроизвольно. Нетрудно заметить, что при диаметре проволоки приблизительно 0,4 мм и силе тока около 0,4 а нужное напряжение для питания катушки составит 1,3-г-1,4 в,-то-есть как раз напряжение одного элемента.
Таков элементарный расчет электромагнитов.
Магнитное поле в соленоиде
- Автор Saurav_C
- Последнее изменение 20-07-2022
- Автор Саурав_C
- Последнее изменение 20-07-2022
Когда ток проходит через проводник, создается магнитное поле. То же самое происходит с соленоидом, когда через него проходит электрический ток. Когда ток проходит через соленоид, он становится электромагнитом. Формула для магнитного поля в соленоиде равно \(B = {\mu _0}nI.\)
Кроме того, знаете ли вы, что соленоиды обычно используются в электронике и электромагнитах как способ создания однородного магнитного поля ? Знаете ли вы, как петля соленоида с током создает магнитное поле? В магнетике для расчета магнитного поля высокосимметричной конфигурации, несущей постоянный ток, мы используем закон Ампера. В этой статье мы обсудим магнитное поле внутри соленоида, формулу соленоида, магнитное поле, обусловленное током в соленоиде, и магнитное поле формулы соленоида.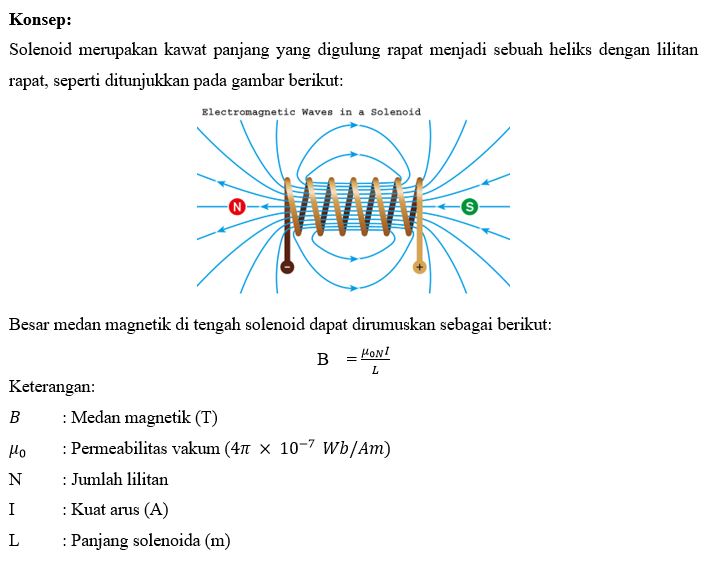
Соленоид представляет собой длинный провод, намотанный в виде спирали, и с помощью этой конфигурации мы можем создать достаточно однородное магнитное поле. Мы можем рассматривать каждый виток соленоида как круговую петлю, когда витки расположены близко друг к другу, а чистое магнитное поле представляет собой векторную сумму полей, возникающих от всех витков. Внутреннее поле становится более однородным и по мере увеличения длины соленоида.
Когда витки расположены близко друг к другу, а длина намного больше радиуса витков, то мы можем аппроксимировать это как идеальный соленоид . Внешнее поле равно нулю, а внутреннее поле в этом случае однородно в большом объеме. Закон Ампера используется для получения выражения для магнитного поля в идеальном соленоиде.
Круговой закон Ампера Рассмотрим границу, состоящую из множества мелких линейных элементов. Рассмотрим один такой элемент длины \((d\vec l).\) Возьмите тангенциальную составляющую магнитного поля, создаваемого этим элементом, и умножьте ее на длину этого элемента \((d\vec l).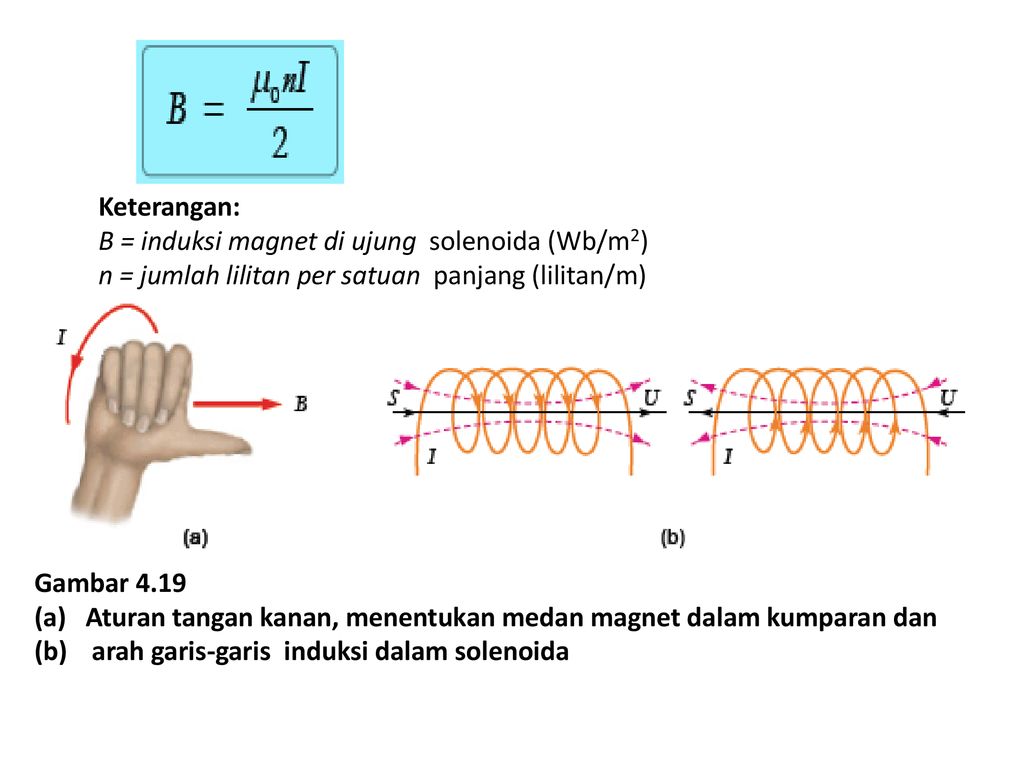 \) Все такие произведения складываются и считаются пределом по мере уменьшения длины элементов и увеличения их числа. Тогда сумма стремится к интегралу. Закон Ампера гласит, что линейный интеграл магнитного поля вокруг замкнутого контура пропорционален величине тока, протекающего по контуру. 9{ – 7}}\;\rm{T – м/А}\)
\) Все такие произведения складываются и считаются пределом по мере уменьшения длины элементов и увеличения их числа. Тогда сумма стремится к интегралу. Закон Ампера гласит, что линейный интеграл магнитного поля вокруг замкнутого контура пропорционален величине тока, протекающего по контуру. 9{ – 7}}\;\rm{T – м/А}\) Единица измерения: Магнитное поле является векторной величиной и имеет единицу измерения СИ тесла \(\left( \rm{T} \right). \)
Направление: Мы можем определить направление магнитного поля с помощью правила большого пальца правой руки.
Линии магнитного поля в соленоиде Чтобы понять природу силовых линий магнитного поля внутри соленоида, давайте возьмем два одинаковых тока, несущих круговые петли, расположенные коаксиально рядом друг с другом. Магнитное поле, создаваемое каждой катушкой, показано на рисунке ниже. В любой точке \(P\) на некотором расстоянии (более радиуса катушки) от оси мы можем наблюдать, что магнитное поле каждой катушки имеет противоположное направление.
Если расстояние между обеими катушками будет очень маленьким, они почти нейтрализуют друг друга, и результирующее магнитное поле будет очень слабым. Возьмем другую точку \(Q\) на оси или вблизи оси. В этот момент магнитное поле из-за обеих катушек имеет одинаковое направление, поэтому результирующее поле будет более сильным по своей природе.
Когда стержень круглой катушки расположен близко друг к другу, он образует соленоид. В любой внешней точке поле любой катушки будет противодействовать другим соседним катушкам. Это вызовет тенденцию к нулевому магнитному полю вне катушки. С другой стороны, в любой внутренней точке поле каждой катушки будет аддитивным по своей природе. Это вызывает стремление иметь более сильное и однородное магнитное поле внутри катушки. Тенденция иметь нулевые поля снаружи и однородное поле внутри становится все более и более эффективной, когда соленоид плотно намотан и имеет большое количество катушек.
Для идеального соленоида магнитное поле в любой внешней точке будет равно нулю, а внутри будет однородным.
Интеграл по замкнутому амперному прямоугольному пути будет равен
\(\oint {\vec B} \cdot d\vec l = Bh…..\left( 1 \right)\)
область, ограниченная путем интегрирования, равна присутствует в правой части уравнения закона Ампера.
 В этом случае
В этом случае \({I_{{\text{enc}}}} = \left( {{\text{число}}\,{\text{из}}\,{\text{поворотов}}\ , {\ text {внутри}} \, {\ text {}} \, {\ text {область}}} \ right) \ times \ left ( {\ text {current}} \, {\ text {через }}\,{\text{каждый}}\,{\text{поворот}}} \вправо)\)
\({I_{{\text{enc }}}} = \left({nh}\right)\left( I \right)\quad \ldots …\left( 2 \right)\)
Используя закон Ампера мы имеем,
\(\oint {\vec B} \cdot d\vec l = {\mu _0}{I_{{\text{enc}}}}\)
Или,
Используя уравнения \(\left( 1 \right)\) и \(\left( 2 \right),\) имеем
\(Bh = {\mu _0}{I_{{\text{enc}}}},\)
\( \ Стрелка вправо Bh = {\mu _0}I\left({nh} \right),\)
\( \Стрелка вправо B = {\mu _0}nI\quad \ldots \left(3\right)\)
Формула магнитного поля дает хороший результат, когда длина соленоида много больше радиуса петли. Это уравнение используется для получения величины магнитного поля внутри длинного соленоида.
Итак, можно сказать, что магнитное поле внутри длинного идеального соленоида зависит от трех основных факторов.
(i) Число витков на единицу длины в соленоиде \(\left( n \right)\)
(ii) Сила тока в катушке соленоида \(\left( I \right)\)
(iii) Проницаемость материала внутри соленоида \(\left( \mu \right)\)
Решенные примеры
Магнитного поля в соленоидеQ.1. Какова величина магнитного поля внутри длинного соленоида, если через него протекает ток \(5\;\rm{A}\)? Дано, что длина соленоида \(0,5\,\rm{м}\) и имеет \(500\) витков. 9{– 7}}}} = 0,3\;\rm{A}\)
Сводка Соленоид представляет собой длинный провод, намотанный в виде спирали, который может создавать достаточно однородное магнитное поле. Магнитное поле почти однородно внутри соленоида и близко к нулю вне соленоида. Мы используем закон Ампера, чтобы получить выражение для внутреннего магнитного поля в идеальном соленоиде, которое утверждает, что линейный интеграл магнитного поля вокруг замкнутого контура пропорционален величине тока, протекающего по контуру. 9{ – 7}}\;\rm{T – m/A}).\) Величина магнитного поля будет постоянной внутри длинного соленоида.
9{ – 7}}\;\rm{T – m/A}).\) Величина магнитного поля будет постоянной внутри длинного соленоида.
Q.1. Какова формула магнитного поля соленоида?
Ответ: Магнитное поле внутри идеального соленоида имеет величину \(B = {\mu _0}nI.\) Здесь число витков на единицу длины равно \(n,\), длина равна \(L,\ ), а ток равен \(I.\). Его можно вычислить из выражения, полученного из закона Ампера.
Q.2. Какова природа магнитного поля внутри идеального соленоида?
Ans: Внутри идеального соленоида магнитное поле однородно, а силовые линии представляют собой прямые параллельные линии.
Q.3. Чему равно магнитное поле вне соленоида?
Ответ : Линии магнитного поля существуют вне соленоида, но количество силовых линий на единицу площади вне соленоида намного меньше по сравнению с количеством линий на единицу площади внутри соленоида. Следовательно, магнитное поле считается практически нулевым, потому что магнитное поле вне соленоида очень слабое. Для идеального соленоида его значение будет равно нулю.
Следовательно, магнитное поле считается практически нулевым, потому что магнитное поле вне соленоида очень слабое. Для идеального соленоида его значение будет равно нулю.
Q.4. Каково использование соленоида?
Ответ : Когда ток проходит через соленоид, он становится электромагнитом. Электромагниты используются в магнитных дверных замках, клапанах давления воды в системах кондиционирования воздуха, аппаратах МРТ, жестких дисках, динамиках, микрофонах и т. д.
Q.5. Какие факторы влияют на соленоиды?
Ответ : Некоторые важные факторы, влияющие на соленоид, приведены ниже:
(i) Количество витков на единицу длины в соленоиде
(ii) Сила тока в катушке соленоида
(iii) Материал внутри соленоида
Пройдите бесплатные пробные тесты, связанные с магнитным полем
Магнитное поле в формуле соленоида
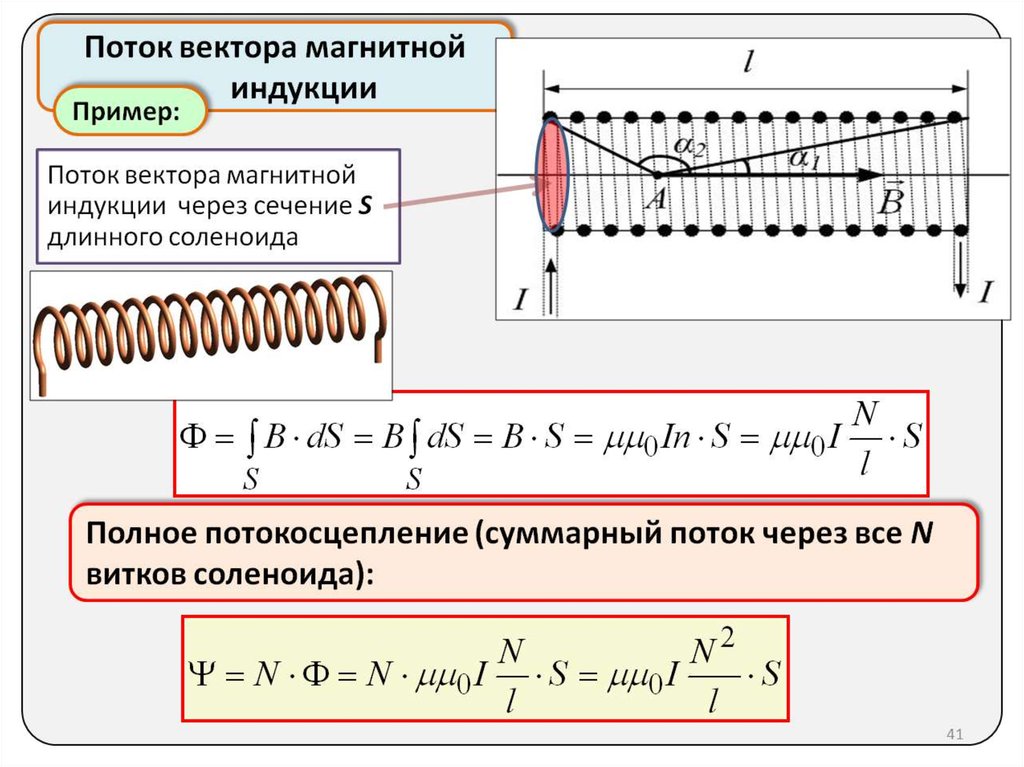
Термин соленоид в переводе с греческого означает «трубчатый». Это тип электромагнита, его цель — генерировать контролируемое магнитное поле с помощью катушки, которая намотана в виде плотно упакованной спирали. Катушка может быть устроена так, чтобы создавать однородное магнитное поле в объеме пространства при пропускании через нее электрического тока. Согласно изучению электромагнетизма, соленоид представляет собой катушку, длина которой больше ее диаметра; это означает, что он имеет форму палочки. Спиральная катушка соленоида не обязательно должна вращаться вокруг прямолинейной оси, например, электромагнит Уильяма Стерджена 1824 г. состоял из соленоида, изогнутого в виде подковы. Следовательно, формула магнитного поля уравнения соленоида имеет следующий вид:
Это тип электромагнита, его цель — генерировать контролируемое магнитное поле с помощью катушки, которая намотана в виде плотно упакованной спирали. Катушка может быть устроена так, чтобы создавать однородное магнитное поле в объеме пространства при пропускании через нее электрического тока. Согласно изучению электромагнетизма, соленоид представляет собой катушку, длина которой больше ее диаметра; это означает, что он имеет форму палочки. Спиральная катушка соленоида не обязательно должна вращаться вокруг прямолинейной оси, например, электромагнит Уильяма Стерджена 1824 г. состоял из соленоида, изогнутого в виде подковы. Следовательно, формула магнитного поля уравнения соленоида имеет следующий вид:
B=μ 0 nl
Here B represents the magnetic flux density,
μ 0 is the magnetic constant whose value is 4π x 10 — ⁷ Hm
or 12.57 x 10 − ⁷ Hm, N — число витков, I — ток, протекающий через соленоид, l — длина соленоида.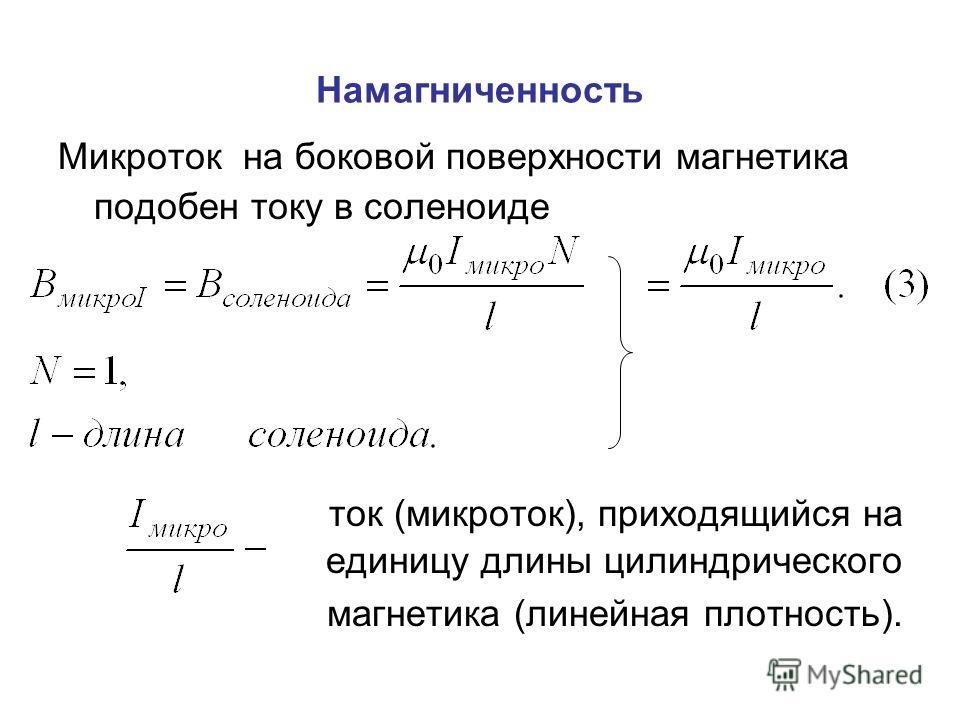
Магнитное поле внутри соленоида Формула
Магнитное поле внутри бесконечно длинного соленоида однородно, и его напряженность не зависит ни от расстояния до оси, ни от площади поперечного сечения соленоида.
Расчет плотности магнитного потока, окружающего соленоид, достаточно длинный, чтобы можно было игнорировать краевые эффекты. Мы сразу знаем, что из рисунка плотность потока векторных точек направлена в положительном направлении по оси z внутри соленоида, а вне соленоида — в отрицательном направлении по оси z. Мы можем подтвердить это, применив правило правой руки или правило большого пальца правой руки для поля, присутствующего вокруг провода. Если мы обхватим провод правой рукой, указывая большим пальцем в направлении тока, изгиб пальцев покажет, как ведет себя поле. Поскольку мы имеем дело с длинным соленоидом, из-за симметрии все компоненты магнитного поля, не направленные вверх, могут компенсироваться.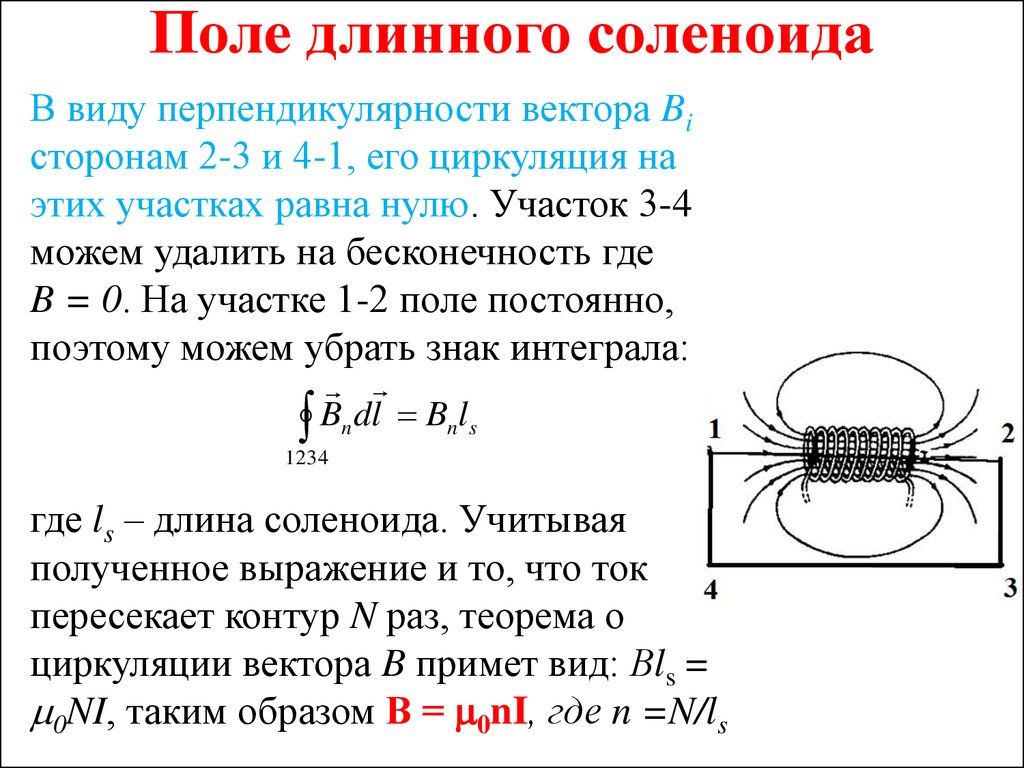
Теперь рассмотрим воображаемую петлю «с» на рисунке, она расположена внутри соленоида. По закону Ампера мы можем сказать, что линейный интеграл от B, который представляет собой вектор плотности магнитного потока вокруг этой петли, равен нулю. Это происходит потому, что в нем отсутствуют электрические токи. Выше мы показали, что внутри соленоида поле направлено вверх, поэтому горизонтальные части петли с ничего не дают в интеграл. Таким образом, интеграл верхней стороны фигуры, изображающей единицу, равен интегральной части стороны два, которая движется вниз. Поскольку изменение размеров цикла может производиться произвольно для получения одного и того же результата, подынтегральные выражения равны. Это означает, что магнитное поле внутри соленоида радиально однородно.
Соленоид представляет собой катушку из проволоки, по которой течет ток, а магнитное поле внутри нее определяется с помощью вклада каждого контура в соленоиде. Следовательно, полное магнитное поле зависит от числа витков катушки и длины соленоида.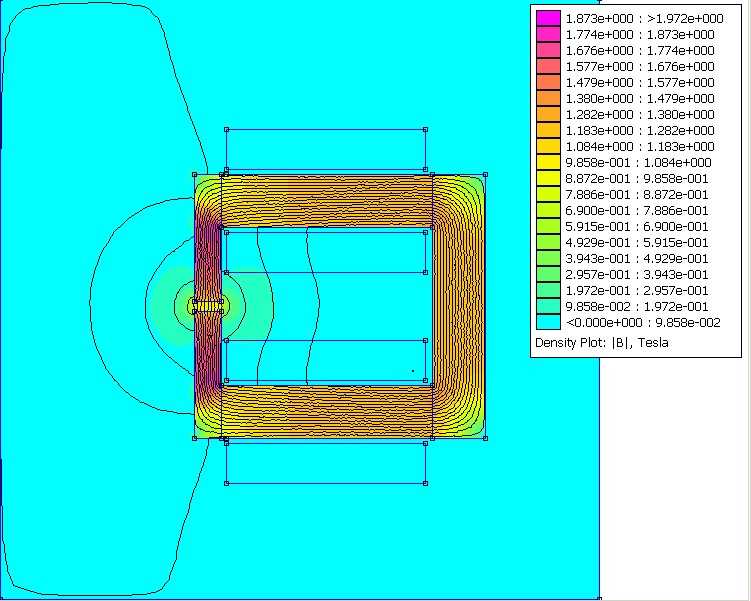
Магнитное поле внутри соленоида является максимальным, а магнитное поле внутри соленоида формулой: соленоид.
Магнитное поле вне соленоида Формула
Аналогичный аргумент можно применить к контуру, чтобы сделать вывод, что поле вне соленоида радиально однородно или постоянно. Можно также использовать интуитивный аргумент, чтобы показать, что плотность потока вне соленоида равна нулю. Силовые линии магнитного поля существуют только в виде петель, они не могут расходиться или сходиться в одной точке, как линии электрического поля. Линии магнитного поля в соленоиде следуют продольному пути, поэтому вне соленоида эти силовые линии магнитного поля должны двигаться в противоположном направлении. Это происходит из-за того, что линии образуют петлю. Однако объем, который присутствует снаружи соленоида, намного больше, чем объем, присутствующий внутри. Таким образом, плотность силовых линий магнитного поля вне соленоида сильно снижается. Таким образом, можно сказать, что поле вне соленоида постоянно. Чтобы общее количество силовых линий сохранялось, внешнее поле должно стремиться к нулю по мере того, как соленоид становится длиннее.
Чтобы общее количество силовых линий сохранялось, внешнее поле должно стремиться к нулю по мере того, как соленоид становится длиннее.
Уравнение магнитного поля соленоида вне его
B=μ0 nl
Поскольку поле снаружи соленоида сравнительно меньше, чем внутри, мы можем считать его равным нулю по мере увеличения длины соленоида, и, таким образом, B = 0.
Забавные факты о магнитном поле
Магнитное поле Земли в 1000 раз слабее, чем стержневой магнит
В нашей Солнечной системе есть планеты, обладающие магнитным полем. Этими планетами являются Земля, Сатурн, Юпитер, Нептун и Уран.
Земля имеет свое магнитное поле из-за наличия в ее центре большого железного ядра
Поезда на магнитной подвеске используют в своей работе принципы, связанные с магнитным полем.

Многие американские горки используют электромагнит, чтобы толкать свои автомобили на трассе
Феномен полярного сияния наблюдается вблизи полюсов, когда силовые линии магнитного поля Земли взаимодействуют с набегающими солнечными ветрами.
Заключение
Магнитное поле в формуле соленоида является очень важной темой в учебной программе по физике для 12 класса, а также на различных вступительных экзаменах на национальном уровне и уровне штата.
Здесь Веданту рассмотрел теоретические, а также формулы, связанные с магнитными полями в соленоиде. Чтобы сделать эту тему интересной для студентов, в конце статьи добавлены различные интересные факты, связанные с магнитными полями.
Веданту стремится предоставить своим ученикам самое лучшее всеми возможными способами. Таким образом, он предоставил вам все эти учебные материалы бесплатно. Прочитав «Магнитное поле в формуле соленоида» от Vedantu, вы сможете ответить на все вопросы, которые могут возникнуть по этой теме на любом заданном экзамене.
Прочитав «Магнитное поле в формуле соленоида» от Vedantu, вы сможете ответить на все вопросы, которые могут возникнуть по этой теме на любом заданном экзамене.
Вопрос Видео: Расчет тока в соленоиде
Стенограмма видео
Соленоид состоит из 35 витков проволока длиной 42 миллиметра. Магнитное поле в центре соленоид измеряется как 4,9 умножить на 10 в отрицательных четырех тесла. Рассчитать ток в провод. Дайте ответ в амперах до двух десятичные разряды. Используйте значение четыре 𝜋, умноженное на 10, чтобы отрицательные семь тесла-метров на ампер для 𝜇 ноль.
Этот вопрос касается нас
соленоид, который представляет собой проволоку, имеющую форму, подобную показанной здесь, состоящую из
из серии равноотстоящих петель или поворотов. В этом случае нам говорят, что
соленоид имеет 35 таких витков. И обозначим это число как
𝑁. Нам также говорят, что эти обороты
провода распределяются по нашей длине 42 миллиметра. И обозначим эту длину как
𝐿. Стоит уточнить, что это
длина 𝐿 — это расстояние между этими двумя концами соленоида, а не общее
длина проволоки, которая используется для его формирования.
Нам также говорят, что эти обороты
провода распределяются по нашей длине 42 миллиметра. И обозначим эту длину как
𝐿. Стоит уточнить, что это
длина 𝐿 — это расстояние между этими двумя концами соленоида, а не общее
длина проволоки, которая используется для его формирования.
Другая информация, которую мы в вопросе есть напряженность магнитного поля в центре соленоид. Нам говорят, что это измеряется быть равным 4,9 умножить на 10 минус четыре тесла. И мы назвали это магнитным поле как 𝐵. Теперь причина, по которой магнитное поле внутри соленоида заключается в том, что есть ток, который мы обозначим как 𝐼, в проводе. Значение этого тока равно нас просят поработать над этим вопросом.
Для этого вспомним
что существует уравнение, связывающее магнитное поле 𝐵 внутри соленоида с
ток 𝐼 в проводе, количество витков 𝑁 этого провода и длина 𝐿
соленоида. В частности, 𝐵 равно 𝜇
ноль, умноженный на 𝑁, умноженный на 𝐼, разделенный на 𝐿, где 𝜇 ноль — это
постоянная, известная как проницаемость свободного пространства.
В частности, 𝐵 равно 𝜇
ноль, умноженный на 𝑁, умноженный на 𝐼, разделенный на 𝐿, где 𝜇 ноль — это
постоянная, известная как проницаемость свободного пространства.
Так как мы пытаемся найти значение тока 𝐼, нам нужно изменить уравнение, чтобы сделать 𝐼 предмет. Для этого умножаем обе части уравнения на 𝐿 над 𝜇 ничем 𝑁. С правой стороны уравнения, мы можем видеть, что 𝐿s, 𝜇 нули и 𝑁 сокращаются из числитель и знаменатель. Тогда, если мы поменяем местами левый и правых частей уравнения, мы имеем, что ток 𝐼 равен 𝐵 раз 𝐿 разделить на 𝜇 ноль умножить на 𝑁.
Прежде чем мы подставим наши значения
в правой части уравнения, мы должны уделить минутку, чтобы подумать о
единицы величин. Нам дали значение для
постоянная 𝜇 ноль с единицами тесла-метры на ампер. Внутри этой единицы мы имеем длину
единицы метров. Но длина 𝐿 соленоида
дается в миллиметрах.
Но длина 𝐿 соленоида
дается в миллиметрах.
Чтобы сделать эти устройства совместимыми, мы нужно преобразовать значение 𝐿 из миллиметров в метры. Для этого вспомним, что префикс единицы в нижнем регистре м или милли- означает коэффициент, превышающий 1000. Это означает, что один миллиметр равен равна одной тысячной метра. И так, чтобы перевести из единиц миллиметры в единицы метров, мы умножаем на коэффициент один больше 1000, или эквивалентно делим на коэффициент 1000. Применив это к соленоиду длина 𝐿 42 миллиметра, получаем, что 𝐿 равно 42 разделить на 1000 метров. Это работает как длина 0,042 метров.
Теперь мы готовы принять наши ценности
для величин 𝐵, 𝐿 и 𝑁 вместе со значением постоянной 𝜇 равно нулю и
подставьте их в это уравнение, чтобы вычислить текущий 𝐼. Когда мы это делаем, мы получаем
это выражение здесь для текущего 𝐼. В числителе у нас 4,9
умножить на 10 до минус четырех тесла, что является нашим значением для 𝐵, силы
магнитное поле внутри соленоида, умноженное на 0,042 метра, что является
длина соленоида 𝐿. Тогда в знаменателе имеем
четыре 𝜋 умножить на 10 до отрицательных семи тесла-метров на ампер. Это наша ценность для константы
𝜇 ничего. И это умножается на 35, что
это количество витков провода 𝑁.
В числителе у нас 4,9
умножить на 10 до минус четырех тесла, что является нашим значением для 𝐵, силы
магнитное поле внутри соленоида, умноженное на 0,042 метра, что является
длина соленоида 𝐿. Тогда в знаменателе имеем
четыре 𝜋 умножить на 10 до отрицательных семи тесла-метров на ампер. Это наша ценность для константы
𝜇 ничего. И это умножается на 35, что
это количество витков провода 𝑁.
Мы можем заметить, что оба устройства Тесла и метры сокращаются из числителя и знаменателя дробная часть. Это оставляет нас с общими единицами для тока 𝐼 единицы, деленной на единицу, в амперах, что, как мы можем заметить, является то же, что и единицы ампер. Оценивая это выражение, получаем результат для 𝐼 0,4679 и так далее ампер.
Обратите внимание, что нас просят
дайте наш ответ в амперах с точностью до двух знаков после запятой. Наш результат для текущего 𝐼:
уже в правильных единицах ампер. Так что нам просто нужно округлить это значение
с точностью до двух знаков после запятой. С точностью до двух знаков после запятой результат
округляется до 0,47 ампер. Тогда наш ответ заключается в том, что для
соленоид в этом вопросе, ток в проводе равен 0,47 ампера.
Наш результат для текущего 𝐼:
уже в правильных единицах ампер. Так что нам просто нужно округлить это значение
с точностью до двух знаков после запятой. С точностью до двух знаков после запятой результат
округляется до 0,47 ампер. Тогда наш ответ заключается в том, что для
соленоид в этом вопросе, ток в проводе равен 0,47 ампера.
Общие | Нужна помощь с расчетом соленоида | Практик-механик
Оноффон
Пластик
- #1
Привет всем
Это мой первый пост, и так как я не нашел тему введения нового участника, я напишу здесь краткую биографию. Меня зовут Юрай, и я родом из города Сплит, расположенного в Хорватии. Я работаю в компании по изготовлению вывесок, и в свободное время я люблю возиться с 3D-принтерами (у меня есть дубликатор wanhao 4s), я люблю токарную обработку металла (токарный станок proxxon pd400), и мне нравится создавать электронные схемы, а также управлять различными радиоуправляемыми моделями.
Меня зовут Юрай, и я родом из города Сплит, расположенного в Хорватии. Я работаю в компании по изготовлению вывесок, и в свободное время я люблю возиться с 3D-принтерами (у меня есть дубликатор wanhao 4s), я люблю токарную обработку металла (токарный станок proxxon pd400), и мне нравится создавать электронные схемы, а также управлять различными радиоуправляемыми моделями.
В настоящее время я работаю над прототипом конкретного устройства, и для того, чтобы оно работало и подходило, мне нужно рассчитать и изготовить электромагнитный клапан на заказ.
Здесь я застрял. Я умею что-то делать, но у меня возникают проблемы со сложными расчетами электрических цепей.
Отступить не вариант, поэтому я очень надеюсь, что здесь есть кто-то, кто хорошо разбирается в этой теме и готов научить меня, как это сделать самому.
Итак, поехали.
Мне нужно рассчитать электромагнитный клапан, который принудительно закрывается с пружиной в выключенном положении. Пружина будет оказывать усилие около 4-5 Н на иглу клапана. Размеры соленоида должны быть около 30-40 мм в длину и 20-30 мм в диаметре. Точного диаметра воздушного сердечника я не знаю, но рабочий поршень должен быть где-то от 4 до 6 мм в диаметре.
Размеры соленоида должны быть около 30-40 мм в длину и 20-30 мм в диаметре. Точного диаметра воздушного сердечника я не знаю, но рабочий поршень должен быть где-то от 4 до 6 мм в диаметре.
Мне нужно произвести расчеты для версии 6В и 12В (DC).
Я нашел в Интернете всевозможные соленоидные калькуляторы, но я не знаю, как правильно ими пользоваться, и все они рассчитывают силу. Я знаю, какое усилие должен преодолевать соленоид, но я не знаю, какой калибр проволоки мне нужно использовать, и сколько витков будет достаточно. Кроме того, ход поршня может быть небольшим. Я думаю, что хода в 2 мм более чем достаточно
Кроме того, все эти калькуляторы просят меня ввести ток, который будет использоваться.
Извините, если я ошибаюсь, но я думал, что потребляемый ток определяется сечением провода, длиной и общим сопротивлением катушки? Итак, как я могу узнать потребляемый ток, если я не знаю, сколько витков конкретного провода я буду использовать? Или это значение означает, сколько тока я готов позволить соленоиду рисовать?
Конрад Хоффман
Титан
- #2
Это большая тема, и вам придется довольно долго учиться, но это выполнимо. Вы можете скачать бесплатную программу FEMM для имитации соленоида. Нарисуйте свои базовые проекты в САПР и импортируйте их в виде файла DXF — интерфейс рисования FEMM довольно примитивен. Вы, вероятно, сконструируете круглый соленоид, поэтому начертите его половину и выберите осесимметричную модель. Просто начните где-нибудь и дайте себе произвольное окно для намотки провода. Выясните по диаметру проволоки, сколько поместится в окне, и это ваше количество витков. Все дело в ампер-витках, поэтому вы выбираете некоторое количество ампер для запуска катушки. Затем программа сообщит вам сопротивление катушки и сколько вольт требуется, чтобы получить этот уровень тока. Вы можете интегрировать, чтобы найти силу, легко, занимает пару секунд. У них есть куча примеров, поэтому вы должны начать с них.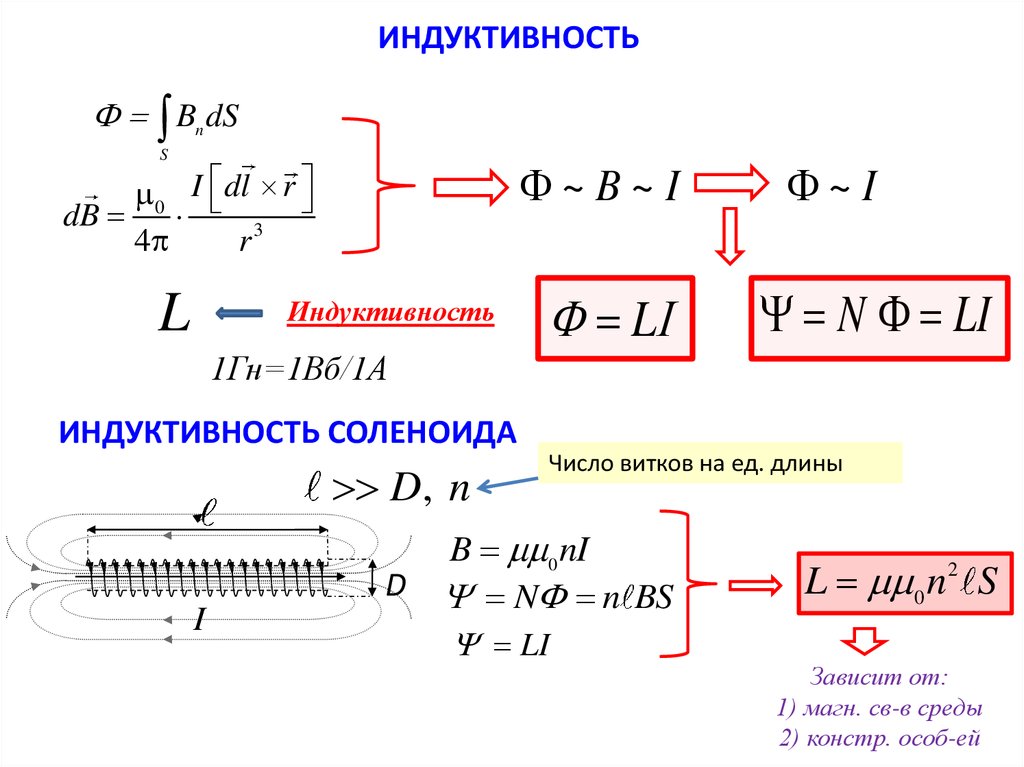 Соленоид похож на громкоговоритель (хотя и не совсем тот же механизм), поэтому, возможно, начнем с их примеров. У меня нет опыта работы с программами FEA, но у меня достаточно опыта работы с громкоговорителями и электроникой. Мне потребовалась пара дней фальстартов, чтобы добраться до рабочих моделей. Получить значительную силу на более длинном расстоянии крайне сложно при разумных уровнях мощности.
Соленоид похож на громкоговоритель (хотя и не совсем тот же механизм), поэтому, возможно, начнем с их примеров. У меня нет опыта работы с программами FEA, но у меня достаточно опыта работы с громкоговорителями и электроникой. Мне потребовалась пара дней фальстартов, чтобы добраться до рабочих моделей. Получить значительную силу на более длинном расстоянии крайне сложно при разумных уровнях мощности.
Вы можете захотеть сделать электронную таблицу для первоначального проекта, чтобы рассчитать окна и обмотки, просто чтобы убедиться, что программа FEMM сообщает что-то разумное. Если это согласуется с ручными электрическими расчетами, вы, вероятно, на правильном пути.
9100
Алмаз
- #3
Это простой двухпозиционный клапан или вы хотите изменить расход?
При простом открытии-закрытии величина хода важна, поскольку управляющим фактором является зазор, когда клапан не находится под напряжением. Ток, необходимый для удержания клапана открытым, намного меньше, чем ток для его открытия, потому что зазор будет закрыт, что приведет к большему магнитному потоку. Для соленоидов постоянного тока обычной практикой является подача тока через резистор с конденсатором, который заряжается, когда на клапан не подается питание. Катушка получает мгновенный импульс более высокого напряжения, чтобы сдвинуть ее, затем ток падает до уровня удержания.
Проектирование — это гораздо больше, чем расчет размера провода и количества витков.
Существует множество различных типов клапанов. Есть ли особая причина, по которой вы хотите сделать его вместо того, чтобы покупать?
Добро пожаловать на форум.
Билл
Конрад Хоффман
Титан
- #4
Да, всегда приятно, если работу можно выполнить с помощью простого включения/выключения катушки, но все, над чем я работаю, кажется, нуждается в довольно сильном ударе, чтобы преодолеть большие, чем хотелось бы, зазоры. , и на скорость, потому что вмешивается индуктивность катушки. Как я уже сказал, ожидайте крутой кривой обучения! Вам также необходимо узнать о различных магнитных материалах и о том, как вы собираетесь их добывать и изготавливать детали. Некоторые вещи, которые я хотел бы использовать, не доступны легко или в небольших количествах. Выполните поиск изображений в Google по конструкции соленоида, чтобы увидеть, как другие подошли к этой проблеме.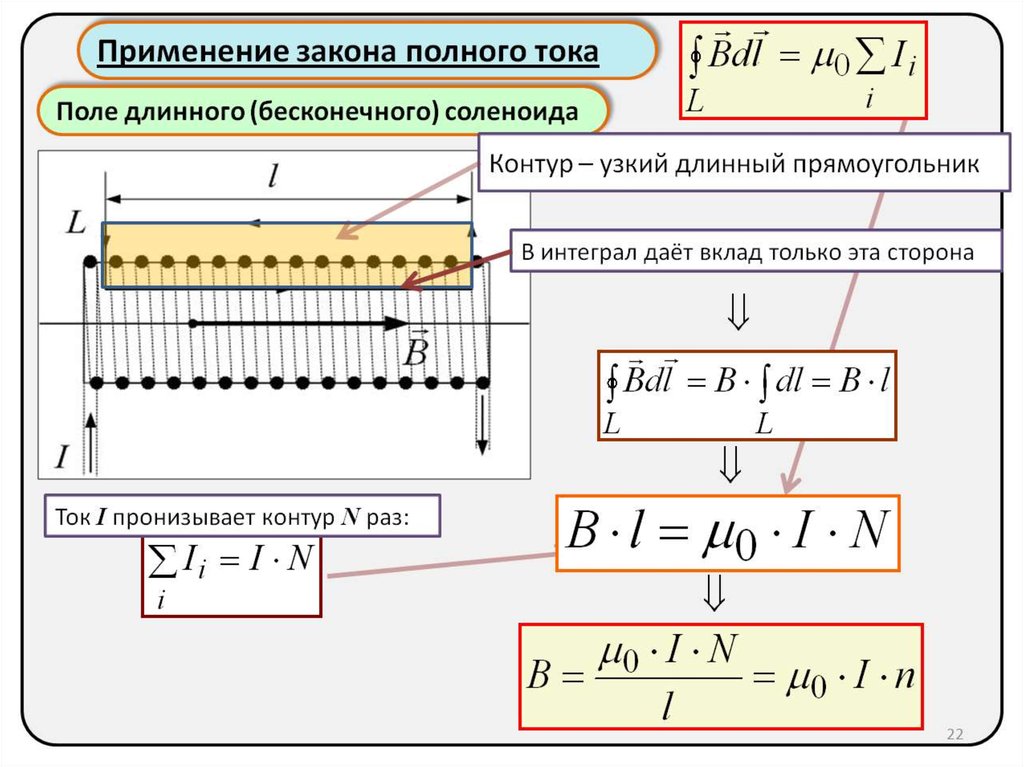
JST
Алмаз
- #5
Splt был очень хорош, когда я был там в 1960-х. Видел там оперу в римском дворце (дворец Диоклетиана?).
Так что, думаю, вам лучше купить эту деталь. Расчеты включают в себя гораздо больше, чем просто катушку, поскольку магнитная сила передается через стальную раму соленоида, что означает также расчет способности рамы выдерживать поле и ряд других связанных с этим вопросов.
Люди, которые делают клапаны, очень хороши в этом, и на них можно положиться, они сделают это правильно. И в целом дешевле купить, чем тратить время на расчеты, обучение расчетам, а затем изготовление устройства. Некоторые вещи не стоит делать без крайней необходимости.
Некоторые вещи не стоит делать без крайней необходимости.
АА+
Алюминий
- #6
Я думаю, что расчеты могут просто приблизить вас к удачному дизайну. Затем вы должны построить полный блок и варьировать размеры проводов и количество витков, чтобы создать успешную конструкцию, которая, как вы знаете, будет работать экспериментально.
С наилучшими пожеланиями — Аллен
Билл D
Алмаз
- #7
12 вольт, я бы посмотрел, что можно найти в легковом или грузовом автомобиле в готовом виде. Многие соленоиды используются в современной трансмиссии и средствах контроля дыма под капотом. Какое давление и расход он должен контролировать? Даже если клапан должен быть изготовлен по индивидуальному заказу, я думаю, вы могли бы использовать существующую катушку на 12 вольт. Как насчет регулирующих клапанов полива, я думаю, они могут быть на 24 вольта переменного тока.
Bill D.
внимательно посмотрите на змеевик ниже и подумайте, сможете ли вы спроектировать клапан вокруг этого змеевика проще, чем изготовить герметичный и хорошо сделанный змеевик по индивидуальному заказу. Конечно, вам может понадобиться другое напряжение или больше/меньше мощности в катушке. Но в основном они выглядят очень похоже, просто увеличены или уменьшены.
Результаты для ».
Я купил подержанный на ebay на 120 вольт, размер трубы 1/2 дюйма, с доставкой менее 12 долларов. Стоимость покупки бывшей в употреблении катушки, даже с присоединенным клапаном, вероятно, меньше, чем стоимость катушки с магнитной проволокой.
Открывается красный пластиковый колпачок, и катушка снимается. В этом случае отверстие в катушке, вероятно, около 1 см. Эта катушка, вероятно, примерно 3-5 см в высоту.
Последнее редактирование:
Адама
Алмаз
- #8
Вы легко можете купить небольшие круглые соленоидные катушки в металлической банке с резьбовым монтажным концом, которые делают именно то, что вам нужно. Перейдите к компонентам Farnel или RSc, и вы сможете загрузить таблицы данных для них, которые дадут вам значения силы и расстояния.
Перейдите к компонентам Farnel или RSc, и вы сможете загрузить таблицы данных для них, которые дадут вам значения силы и расстояния.
Не нужно изобретать или изобретать это колесо, все это есть по простой дешевой покупной цене 🙂
Всегда лучше приложить усилия к битам, которые нельзя купить в готовом виде!
Оноффон
Пластик
- #9
Во-первых, ВАУ.
Я не ожидал такого количества ответов и спасибо всем за попытку помочь!
@Conrad Hoffman
Я скачал программу FEMM и чуть не потерял сознание. Я нашел несколько руководств на YouTube, и вы были правы, если я решу его использовать, будет сложно научиться.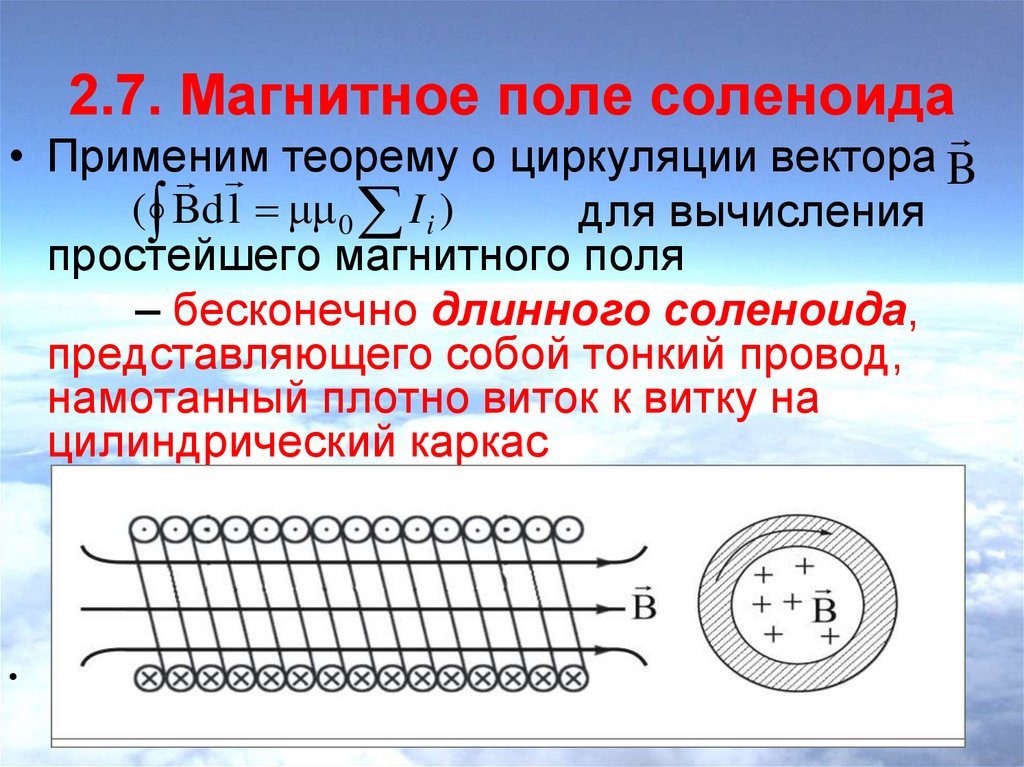 ..
..
Этот соленоид должен быть простой версии ON-OFF.
Многие из вас предлагали купить соленоид, а не делать его. Ну, это невозможно по нескольким причинам.
Во-первых, они чертовски дороги. Я нашел один на Farnell, который достаточно близок к спецификации, необходимой для моего проекта, но соленоид + доставка обойдутся мне в 60 долларов, а моя целевая цена для всего продукта составляет 40-50 долларов.
Дешёвые не подходят для моих нужд… Кроме того, соленоид должен быть сконструирован таким образом, чтобы он идеально помещался внутри устройства, чтобы изделие было компактным и имело привлекательный внешний вид.
@Bill D
Скорость потока не так важна, а давление газа на игольчатом клапане будет 6,14 фунтов на квадратный дюйм. Исходя из этого значения, я рассчитал, что сила, которую газ оказывает на круглую площадь 5 мм, будет равна 3,325 Н. Я предполагаю, что пружины с силой 4-5 Н будет достаточно, чтобы держать клапан закрытым, а соленоид должен быть немного сильнее, чтобы преодолеть силу пружины и площадь зазора. Пожалуйста, поправьте меня, если я ошибаюсь, чтобы я мог внести исправления и указать конструкцию соленоида таким образом.
Пожалуйста, поправьте меня, если я ошибаюсь, чтобы я мог внести исправления и указать конструкцию соленоида таким образом.
@Adama
Возможно, вы не знаете об этом, но вы на самом деле дали мне отличную отправную точку для процесса проектирования соленоидов, и я всегда благодарен!
Ранее упомянутый соленоид, который я нашел на Farnell, поставляется с таблицей данных, и в этой таблице данных есть полные данные, включая длину, внешний диаметр, диаметр воздушного сердечника, номинальную мощность, толщину провода AWG и количество витков для версии 6 В и даже для версии 12 В. Свойства металлических материалов неизвестны, но я буду экспериментировать с числами, пока не получу желаемый результат.
Теперь общий вопрос. Какой тип стали лучше всего подходит для конструкции соленоида и плунжера. Я должен отметить, что его нужно легко найти. Итак, что-то с приемлемыми свойствами, но не экзотическое…
P.S.
@JST
Да, это дворец Диоклетиана
Адама
Алмаз
- #10
Мягкая блестящая сталь хорошо работает и не обладает магнетизмом. Избегайте легированных сталей, они будут менее магнитными и более склонными к магнетизму.
Честно говоря, я бы адаптировал конструкцию для использования полочных катушек и просто сделал специальный поршень, это намного проще и быстрее. Намотка катушки несложная, но сделать ее хорошо и требует времени, которое лучше потратить на другие вещи. Я наматываю катушки только для действительно нестандартных вещей.
Оноффон
Пластик
- #11
Спасибо за стальной наконечник.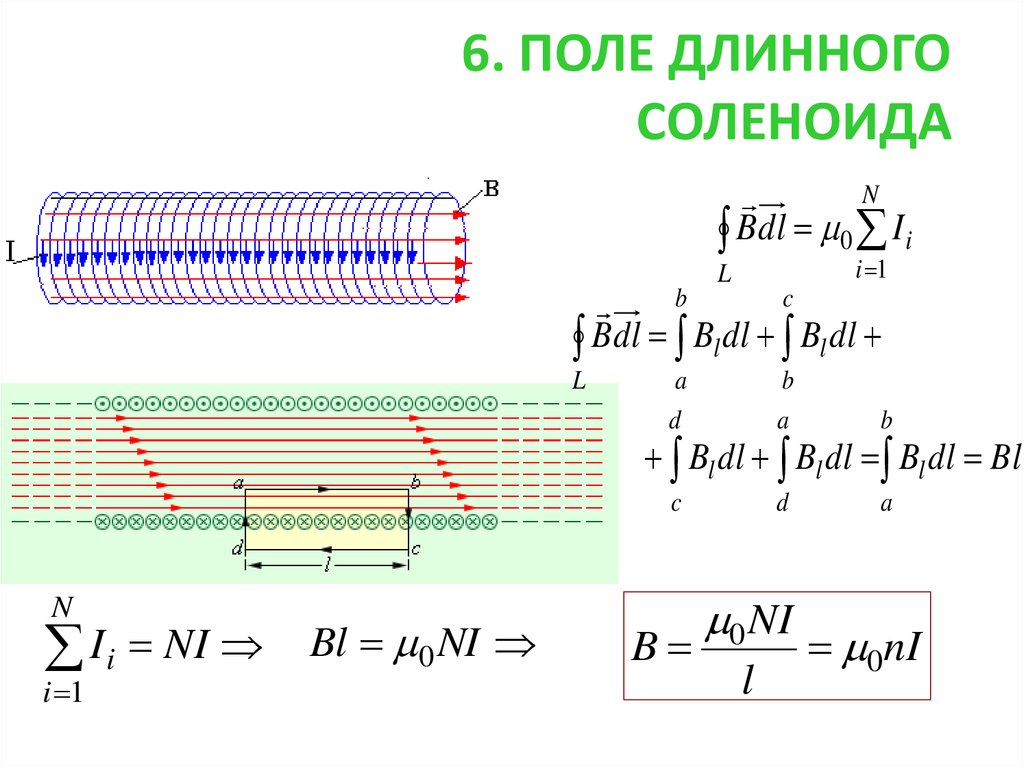
Я уважаю ваш совет, но это большие дополнительные расходы, которых я хотел бы избежать. У меня есть токарный станок и 3D-принтер, поэтому я сделаю приспособление для намотки катушки со счетчиком оборотов (или посчитаю общую длину провода). Я постараюсь сделать так и надеюсь, что все получится хорошо.
Конрад Хоффман
Титан
- #12
О каких количествах здесь идет речь? На дюжину витков несложно сделать простую намотку, не более чем сверлильный патрон с кривошипом и счетчиком оборотов, как вы описали. Или просто посчитайте в уме. Некоторые люди используют свой токарный станок, но он никогда не подходит для мелких вещей, которые я делаю, и я думаю, что это немного опасно.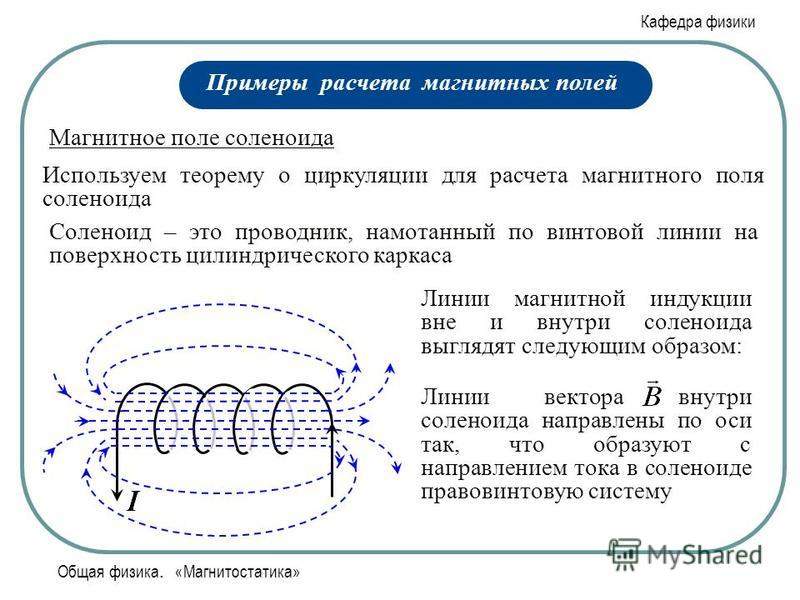 То же и с винтовыми пружинами. Будут ли части соленоида намокать? Возможно, вам понадобится нержавеющая сталь 430F, но, скорее всего, подойдет дешевая нелегированная сталь.
То же и с винтовыми пружинами. Будут ли части соленоида намокать? Возможно, вам понадобится нержавеющая сталь 430F, но, скорее всего, подойдет дешевая нелегированная сталь.
Не надо так бояться FEMM. Как только вы загрузите геометрию и назначите материалы, ее анализ займет всего несколько секунд. Я ненавижу изучать новые программы, но эта была не такой уж сложной, и она показала мне поля и силы, на которые у меня ушли бы часы вручную или с помощью эксперимента.
Вы можете скачать пример соленоидного типа под названием «rotors1b», чтобы увидеть, как это сделать. Он смоделирован как 1/2 устройства и вращается вокруг левой нулевой оси. Сила рассчитана на зеленую область (ядро) Выглядит так-
Оноффон
Пластик
- №13
Ну, я думаю, что это будет не менее дюжины катушек, но если повезет, их может быть намного больше.
С проводом 30 AWG и 572 витками подсчет голов — нет-нет
Соленоиды не предназначены для погружения в воду. Возможно, иногда будут происходить брызги пресной воды, но она будет закрытой, поэтому я думаю, что нержавеющая сталь не нужна.
Я понимаю, что рисование и расчет силы с помощью FEMM не так уж и сложны, но что меня напугало, так это свойства материала. Есть так много мелких настроек, которые нужно сделать для материала сердечника и свойств катушки, и я не понимаю, что означает половина этого материала. (Английский не мой родной язык).
Я попробую еще раз с предложенным примером и посмотрю, что получится…
Конрад Хоффман
Титан
- №14
Программа поставляется с библиотекой материалов, так что вам не нужно много делать, просто назначьте их там, где вы хотите. В общем, огромное количество витков с использованием тонкой тонкой проволоки даст вам огромное рассеивание мощности, поэтому вам нужно быть немного осторожным в выборе наилучшего решения.
Выбор соленоидного клапана
: не дайте себя обмануть скоростью потока
Электромагнитные клапаны широко используются в химической промышленности. Однако выбор лучшего клапана для данного применения может быть затруднен. Скорость потока, критический параметр для выбора, может быть рассчитана с использованием различных подходов. Однако многие из этих методов неточны или дают безразмерные результаты.
Ситуацию осложняет тот факт, что не существует единой общепринятой в отрасли методики расчета расхода газа для электромагнитных клапанов. Некоторые производители клапанов экспериментируют с несколькими формулами, чтобы определить, какая из них даст наиболее благоприятные значения для их клапанов. Эта практика может сбить с толку конечных пользователей, попусту тратя время и деньги и ставя под угрозу безопасность и эффективность, когда указан неправильный клапан.
Эта практика может сбить с толку конечных пользователей, попусту тратя время и деньги и ставя под угрозу безопасность и эффективность, когда указан неправильный клапан.
В этой статье обобщаются основные вопросы, связанные с выбором электромагнитных клапанов для применения в химической промышленности, а также обсуждаются их характеристики потока и методы, наиболее часто используемые для расчета расхода газа. Кроме того, в нем рекомендуется формула с двумя коэффициентами, разработанная ISA (Общество приборостроения, систем и автоматизации), и показано, как ее использовать для определения наилучшего электромагнитного клапана.
Электромагнитные клапаны 101
Важно отметить, что в химических процессах электромагнитные клапаны обычно не работают со средой напрямую. Во многих случаях клапан действует как предохранительное запорное устройство для более крупной системы. Производительность в этом качестве имеет решающее значение. Клапан может быть в системе, но не использоваться в течение длительного периода времени, даже до года. Когда его призывают отключить систему, он должен действовать немедленно и предсказуемо.
Когда его призывают отключить систему, он должен действовать немедленно и предсказуемо.
Электромагнитные клапаны используют электричество для открытия и закрытия отверстия в корпусе клапана, пропуская или предотвращая поток данной среды. В своей простейшей форме этот тип клапана открывается и закрывается плунжером, который поднимается и опускается при включении и выключении соленоида. Магнитное поле, создаваемое катушкой соленоида, превращает стопор плунжера в электромагнит, притягивающий и поднимающий стальной плунжер. Соответствующая пружина сжимается при открытии отверстия. При отключении питания магнитное поле прекращается, и пружина возвращается, прижимая поршень к отверстию и перекрывая поток.
Электромагнитные клапаны также можно использовать для управления или запуска других процессов. Например, они могут управлять движением других управляющих устройств, таких как большие технологические клапаны, которые управляют средой приложения, или подавать питание на такие компоненты, как адсорбционные осушители или вентиляционные системы, которым требуется давление воздуха.
При выборе электромагнитного клапана необходимо учитывать следующее:
- Тип клапана (двух-, трех- или четырехходовой)
- Напряжение
- Давление
- Средняя ручка
- Материалы (нержавеющая сталь, латунь, пластик или другой материал)
- Соединение для жидкости с размером порта
- Обесточенное положение (нормально открытый или закрытый и т. д.)
- Окружающие условия
- Требуются сертификаты (UL, CSA, FM, CENELEC)
- Тип катушки/соединения
- Ограничение потребления тока
- Рабочий цикл (непрерывный или прерывистый)
- Электрический шкаф типа
- Ожидаемая продолжительность жизни (минимальное ожидаемое количество циклов в год)
- Максимальный и минимальный перепады рабочего давления
- Диаметр отверстия
- Допустимая внутренняя утечка Рейтинги
- (NEMA 4, 7, 9 и т. д.)
Наконец, необходимо учитывать скорость потока.
Подъемы и спады газовых потоков
Давайте рассмотрим основы. Расход – это количество среды, проходящее в данной точке за данный период времени. Он измеряется с использованием термина C V , который представляет собой количество воды в галлонах в минуту, которое пройдет через клапан с перепадом давления на нем 1 фунт на квадратный дюйм (фунт на квадратный дюйм). Эта мера используется для определения пропускной способности клапана при более высоких перепадах давления, но также применяется к потокам жидкости и газа при достаточно малых перепадах давления, при которых изменения плотности незначительны.
Расход – это количество среды, проходящее в данной точке за данный период времени. Он измеряется с использованием термина C V , который представляет собой количество воды в галлонах в минуту, которое пройдет через клапан с перепадом давления на нем 1 фунт на квадратный дюйм (фунт на квадратный дюйм). Эта мера используется для определения пропускной способности клапана при более высоких перепадах давления, но также применяется к потокам жидкости и газа при достаточно малых перепадах давления, при которых изменения плотности незначительны.Другим, более точным термином для течения газа является «поток сжимаемой жидкости». Сжимаемость относится к способности газа изменять плотность при изменении температуры и давления. Расходы сжимаемых жидкостей рассчитать значительно сложнее, чем несжимаемых, просто из-за их свойств.
Плотность потока сжимаемой жидкости сильно колеблется при более высоких температурах и, особенно, давлениях. При более низких давлениях поведение воды, пара или инертных газов может быть очень похожим, но оно резко меняется для газов при экстраполяции на высокие перепады давления.

В случаях, когда поток становится сжимаемым внутри клапана, эффекты могут включать кавитацию, вспышку или эффекты числа Маха, что еще больше затрудняет согласованность расчетов.
Путь потока внутри клапана также может изменить значение C V (см. рис. 1). Более прямолинейный и прямой путь означает, что среда будет подвергаться меньшему гидравлическому воздействию при прохождении через клапан. Извилистый (или запутанный) путь будет иметь противоположный эффект. Фактически, два электромагнитных клапана, одинаковых во всем, кроме внутренней конструкции и пути потока, могут иметь совершенно разные C В рейтинга.
Рисунок 1. Траектория потока определяет скорость
На скорость потока в электромагнитных клапанах может влиять множество факторов, включая внутреннюю конструкцию. Если путь потока клапана несложный (вверху), среда будет проходить через него без напряжения. Извилистый путь потока (внизу), как и в этом пятиходовом клапане, приведет к более низкой скорости потока из-за большей нагрузки на среду, когда она проходит через клапан.

Монтаж и ориентация клапана, а также соответствующие гравитационные эффекты могут также влиять на скорость потока для некоторых типов электромагнитных клапанов при очень низком перепаде давления.
Со всеми этими потенциальными проблемами расчет расхода сжимаемой жидкости для электромагнитных клапанов может оказаться сложной задачей. Путаницу усугубляет тот факт, что существует несколько методов, с помощью которых можно производить расчеты.
Методы расчета
Давление на выходе: Этот метод используется Национальной ассоциацией противопожарной защиты для пневматических направляющих клапанов. Это уравнение аппроксимирует поток через идеальное сопло. В арматуростроении он часто используется для расчета C V для пневматических распределителей. Тем не менее, он может переоценить дросселированный поток, «точку, в которой снижение выходного давления клапана не может привести к увеличению потока, как это обычно наблюдается в шаровых, поворотных и электромагнитных клапанах».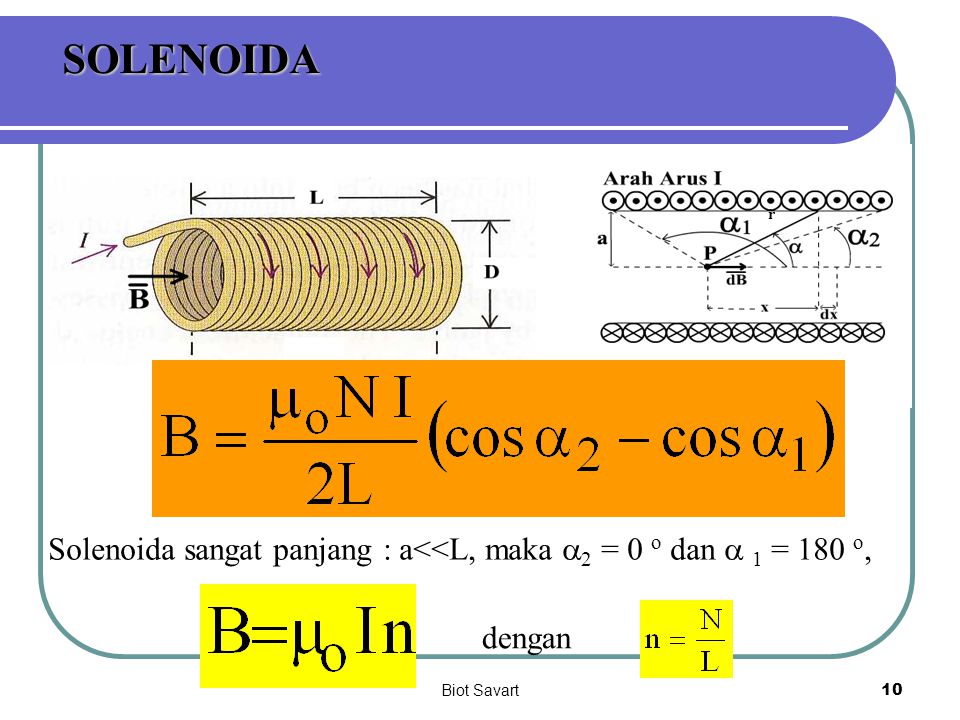
Сегодня можно использовать несколько методов для расчета расхода сжимаемой жидкости. значения расхода для электромагнитных клапанов:
Среднее давление: Уравнение средней плотности выводится непосредственно из уравнений для потока жидкости через клапаны и из-за его простоты широко используется в промышленности.Однако из-за различий между газом и жидкости (сжимаемой и несжимаемой), это уравнение может значительно переоценить расход для большинства типов клапанов, особенно при высоких перепадах давления.
Давление на входе: Это уравнение, как и другие, получено из уравнения, используемого для потока жидкости. Следовательно, на него нельзя полагаться при работе с ситуациями с забитым потоком. Опять же, он будет завышать расход для большинства типов клапанов, особенно при высоких перепадах давления, и не сможет предсказать засорение.
Так в чем проблема?
Так почему нет единого стандарта? Электромагнитные клапаны используются в самых разных отраслях, конечные пользователи которых озабочены совершенно разными вещами.
Все эти уравнения широко используются уважаемыми организациями и промышленными органами управления. Ни в одном из них нет ничего изначально плохого. Однако, имея дело с конкретными обстоятельствами потоков сжимаемой жидкости и электромагнитными клапанами, эти уравнения могут дать только безразмерное представление скорости потока.
Однако ясно, что вывод стандартных уравнений для течения несжимаемой жидкости не может быть надежно применен к течениям сжимаемой жидкости. Непредсказуемая природа газов и изменения их плотности означает, что эти уравнения могут давать неточные C V значения при больших перепадах давления. Использование этих уравнений там, где они лучше всего подходят, при низких перепадах давления, дает более точное, хотя и одномерное, представление о возможностях клапана, что не идеально для потенциального покупателя.
Есть и другие соображения. Для клиентов в химической промышленности измерение C V обычно является ориентиром при покупке электромагнитного клапана.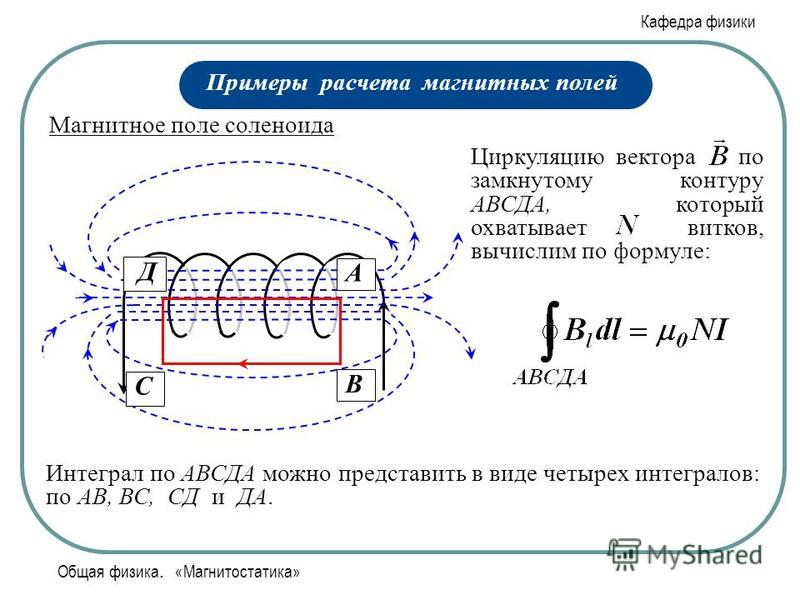 Часто клиенты, знакомые со своими приложениями, знают приблизительное C V 9Значение 0162, необходимое для нового клапана. Однако они могут полагаться на неточное число, рассчитанное с использованием любого из ранее обсуждавшихся методов. В этом случае производитель должен работать с потребителем в обратном направлении и спросить, как было определено это расчетное значение C V . В этом случае, как правило, требуется повторный анализ применения для определения надлежащего C V , чтобы производитель мог применить правильную модель клапана.
Часто клиенты, знакомые со своими приложениями, знают приблизительное C V 9Значение 0162, необходимое для нового клапана. Однако они могут полагаться на неточное число, рассчитанное с использованием любого из ранее обсуждавшихся методов. В этом случае производитель должен работать с потребителем в обратном направлении и спросить, как было определено это расчетное значение C V . В этом случае, как правило, требуется повторный анализ применения для определения надлежащего C V , чтобы производитель мог применить правильную модель клапана.
Тестирование для проверки скорости потока всегда является хорошей идеей, особенно в химических процессах. Когда для приведения в действие используется электромагнитный клапан, неправильный C V может привести к вибрации или другим аномалиям в системе. В других случаях клапан может неравномерно приводить в действие более крупный клапан, вызывая слишком быстрое, медленное или сильное опускание более крупного технологического или регулирующего клапана.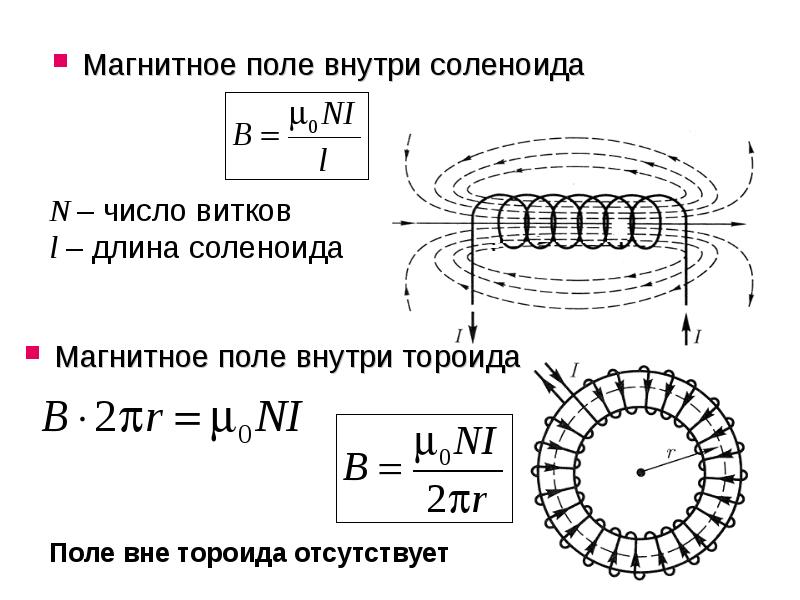
Наконец, рассмотрим вопросы, которые возникают у потенциального конечного пользователя, пытающегося выбрать новый электромагнитный клапан. Безразмерные представления этих уравнений о возможностях клапанов могут привести к неверной информации. Производители могут испытать клапан при заданном перепаде давления, чтобы определить расход в различных точках данных, а затем включить их в любое из вышеупомянутых эмпирических уравнений по своему выбору для определения коэффициента. Этот коэффициент может не описывать клапан многомерным образом. Возьмите тот же клапан и рассчитайте разные коэффициенты, используя разные методы, и вы можете получить другие, менее лестные C В значения. Многие расчеты усреднены. Можно даже повторно запускать тесты и расчеты, пока не будут подобраны наиболее благоприятные числа. На рис. 2 показано, как даже клапаны с одинаковыми номинальными значениями C V могут фактически иметь очень разные скорости потока. Клапаны были изготовлены разными производителями, что отмечено на графиках MFR X и MFR Y.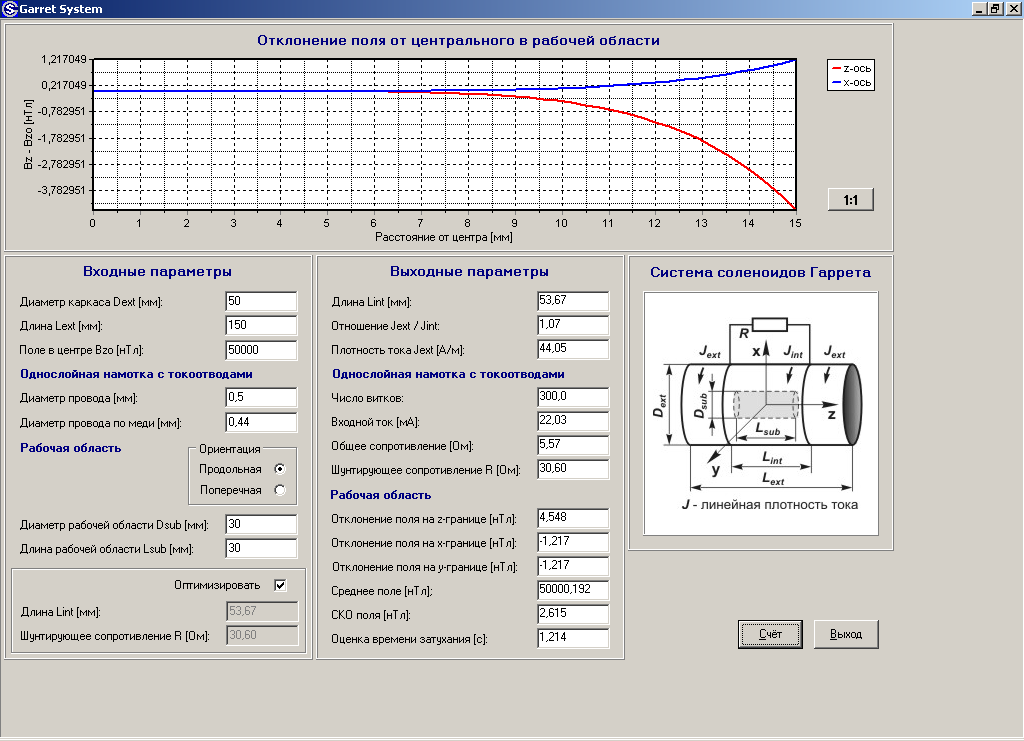
Рис. 2. Большие различия для соленоидов 0,75Cv
На графике выше представлены коэффициенты расхода и сжимаемого потока в зависимости от перепада давления для различных клапанов при 0,75 Резюме. Клапаны были изготовлены разными производителями (обозначены здесь как MFR X и Y).
Аргумент для двухкоэффициентного уравнения ISA
Уравнение выглядит следующим образом:
ISA разработала уравнение для определения расхода, которое включает второй коэффициент расхода, XT. Этот второй коэффициент разработан специально для корреляции C
V
где:
Q — расход в станд. куб. Т UP — температура на входе в °F
SG — удельный вес газа по отношению к воздуху при стандартных условиях
Y — коэффициент расширения, определяемый: неточностей других, производных методов. Типичные значения XT для электромагнитных клапанов могут находиться в диапазоне от 0,25 до 0,5, причем более низкое значение применяется к клапанам с более извилистыми путями потока. Хотя тип пути потока может обеспечить приблизительное значение XT, тестирование сжимаемого потока является лучшим методом для определения фактических значений.
Хотя тип пути потока может обеспечить приблизительное значение XT, тестирование сжимаемого потока является лучшим методом для определения фактических значений.
где:
X — безразмерный перепад давления
XT — второй коэффициент расхода
F K — коэффициент газовой постоянной, определяемый F K = k / k ВОЗДУХ
Это уравнение был разработан на основе широко используемых стандартов для расходомеров с большой диафрагмой. Позже он был принят ISA для расчетов расхода клапана управления технологическим процессом. Он может надежно прогнозировать точки, в которых клапан будет запираться. Его основное преимущество заключается в том, что он разработан специально для специальных условиях потоков сжимаемой жидкости, поэтому он может более точно показать, как электромагнитный клапан будет реагировать на более высокие перепады давления.0017
Вот пример одного клапана, в котором расход сжимаемой жидкости рассчитывается сначала с использованием метода среднего давления, а затем с использованием двухкоэффициентного уравнения ISA.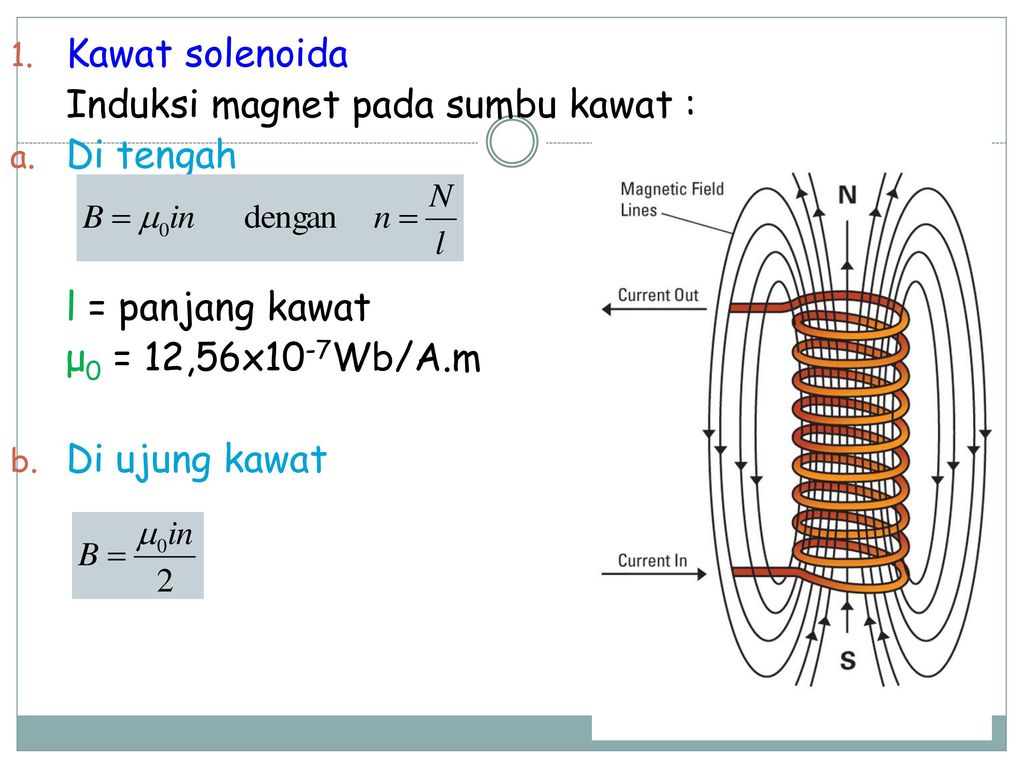
Пример расчета (данные C V Определить Q)
C V =0,75 (метод P avg ) 75F
Скорость потока (Q)=34 станд. куб. футов в минуту
C V =0,75 (метод ISA)
Безразмерный перепад давления (X) = 0,54
Расход (Q) = 19 станд. футов в минуту
для XT = 0,5 (-44 % от 34 станд.
Пример расчета (учитывая Q, определить C V )
Расход (Q)=34,4 станд. куб. фут/мин
Падение давления=40 фунтов на кв. 75 °F
Безразмерный перепад давления (X) = 0,54
Коэффициент расхода (C V ) = 0,64 для метода давления перед входом
Коэффициент расхода (C V ) = 0,75 для метода среднего давления
Коэффициент расхода (C V ) = 0,94 для метода давления на выходе 0,25
Программное обеспечение и стороннее тестирование: не панацея
Сегодня одно только программное обеспечение недостаточно простое или недорогое, чтобы служить ответом отрасли. В то же время, несмотря на то, что независимые агентства по тестированию, такие как UL или CSA, могут предоставлять безупречные результаты, стоимость тестирования одного продукта может составлять тысячи долларов.
В то же время, несмотря на то, что независимые агентства по тестированию, такие как UL или CSA, могут предоставлять безупречные результаты, стоимость тестирования одного продукта может составлять тысячи долларов.
Программы вычислительной гидродинамики (CFD), используемые для определения расхода, становятся все более точными с каждой новой версией. Они дают хорошие результаты для несжимаемого потока, и программы хорошо прогнозируют поведение потока; однако сложность их использования заключается в создании правильных моделей для точного сравнения прогнозов с тестовыми данными.
В идеальном мире клиенты и производители знали бы, что везде используются одни и те же меры расхода. До тех пор, пока это не станет реальностью, двухкоэффициентное уравнение ISA может заменить догадки уверенностью, предоставляя многомерное представление о расходе сжимаемого электромагнитного клапана в широком диапазоне перепадов давления.
Чарльз Болд последние пять лет работал старшим инженером-конструктором в подразделении управления жидкостями компании Parker. Его 15-летний опыт работы в отрасли включает термический анализ и анализ расхода компонентов газотурбинных реактивных двигателей, конструкций центробежных компрессоров и систем охлаждения для вакуумной перегонки. Ричард Кондон занимал различные должности в течение последних восьми лет и в настоящее время специализируется на приводах клапанов, мобильном оборудовании, топливных элементах и промышленном оборудовании для подразделения Parker Fluid Control.
Его 15-летний опыт работы в отрасли включает термический анализ и анализ расхода компонентов газотурбинных реактивных двигателей, конструкций центробежных компрессоров и систем охлаждения для вакуумной перегонки. Ричард Кондон занимал различные должности в течение последних восьми лет и в настоящее время специализируется на приводах клапанов, мобильном оборудовании, топливных элементах и промышленном оборудовании для подразделения Parker Fluid Control.
Что такое коэффициент расхода клапана и как его рассчитать?
Коэффициент расхода клапана — важный параметр, который помогает рассчитать, сколько жидкости может пройти через клапан. Коэффициент расхода клапана (Cv) может измерять скорость, с которой любой газ или жидкость может проходить через клапан.
В этой статье мы подробно расскажем о том, что такое коэффициент расхода клапана, а также о том, как его рассчитать. Мы дадим вам пошаговую разбивку того, как выполнить эти вычисления.
Наконец, мы дадим вам несколько примеров, над которыми вы можете поработать самостоятельно, чтобы проверить, правильно ли вы рассчитали коэффициент расхода клапана.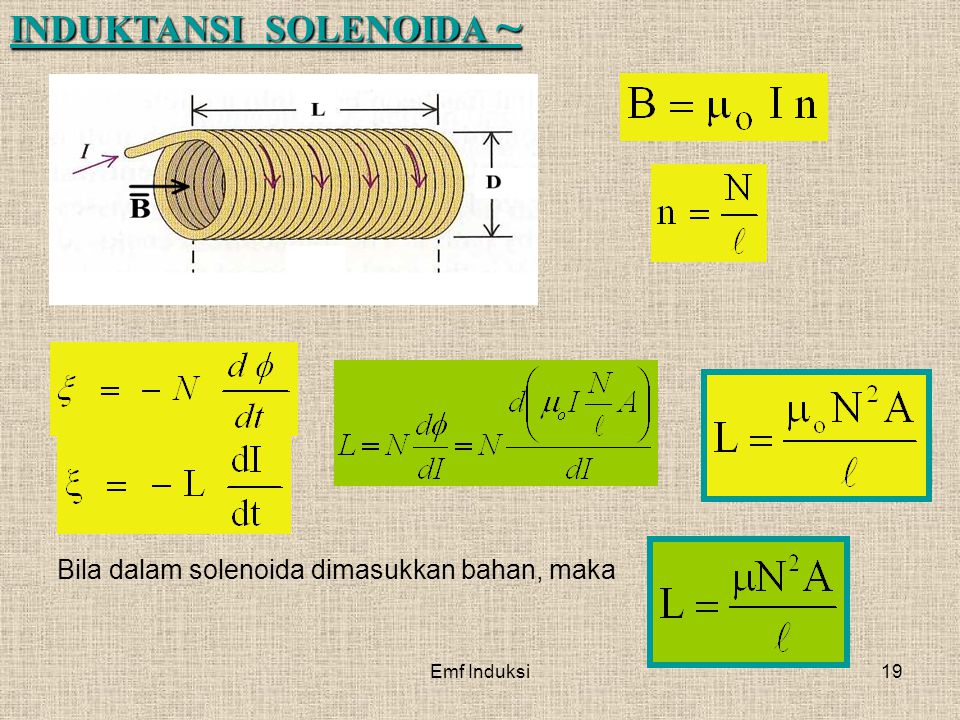
Что такое коэффициент расхода клапана?
Коэффициент расхода клапана — это показатель, который используют трубопроводчики, инженеры и производители, чтобы подобрать клапаны нужного размера для количества жидкости, которое будет проходить через них.
Проще говоря; Cv помогает рабочим выбрать клапан правильного размера, чтобы все жидкости могли проходить через него при желаемом давлении.
Коэффициент расхода клапана определяется как «количество галлонов США в минуту воды, которое проходит через данную площадь отверстия при перепаде давления в 1 фунт-сила на квадратный дюйм (PSI)».
Хотя вода является основным показателем, вы можете рассчитать коэффициент расхода клапана для газов или других жидкостей, используя тот же принцип.
Давайте приведем пример, который поможет вам понять этот принцип. Если конкретный клапан имеет коэффициент потока клапана 1,00, он пропускает 1 галлон воды в минуту (GPM) через клапан при перепаде давления 1 PSI.
Поскольку мы используем воду, ее удельный вес (G) равен 1.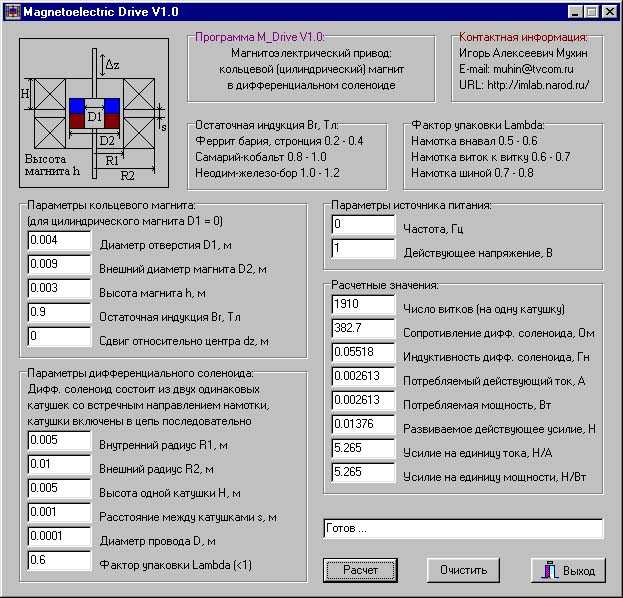 Мы рассмотрим удельный вес во время расчетов в этой статье.
Мы рассмотрим удельный вес во время расчетов в этой статье.
Давайте изменим некоторые переменные. У вас тот же перепад давления, равный 1 фунту на квадратный дюйм, и, поскольку мы используем воду, удельный вес такой же, как и раньше. Но теперь вы хотите, чтобы ваш клапан пропускал 2 галлона в минуту. В этом случае вам понадобится другой клапан с коэффициентом потока 2,0.
Как видите, коэффициент расхода клапана является важным расчетом для всех, кто работает с трубами. Прежде чем мы приступим к вычислениям, давайте определим все различные переменные, которые нам нужно будет использовать для вычислений.
Переменные коэффициента расхода клапана
При расчете коэффициента расхода клапана вам необходимо знать определенные аспекты жидкости, клапана и того, сколько жидкости вы хотите пропустить через клапан. Давайте рассмотрим различные переменные, прежде чем объяснять, как рассчитать коэффициент расхода клапана.
Удельный вес
Удельный вес (SG) — это отношение веса жидкости к весу воды при температуре 62ºF. Наиболее очевидным примером этого является сама вода. Вода имеет удельный вес 1,00, потому что это соотношение самой себя. Более плотная жидкость будет иметь более высокое отношение, в то время как менее плотная жидкость будет иметь более низкое отношение.
Наиболее очевидным примером этого является сама вода. Вода имеет удельный вес 1,00, потому что это соотношение самой себя. Более плотная жидкость будет иметь более высокое отношение, в то время как менее плотная жидкость будет иметь более низкое отношение.
В качестве примера рассмотрим удельный вес гидравлического масла. Гидравлическое масло весит 0,8 г/мл. Вода, как известно, весит 1 грамм на миллилитр.
Таким образом, гидравлическое масло имеет удельный вес 0,8, что намного ниже, чем у воды. Если вы можете найти вес любой жидкости в граммах на миллилитр, вы можете легко рассчитать удельный вес жидкости.
Скорость потока
Скорость потока (Q) — это переменная, которая показывает, сколько жидкости проходит через клапан в данный момент времени. Обычно мы представляем это число в GPM. Чтобы рассчитать скорость потока, вам нужно знать объем (V) и время (t), за которое этот объем проходит через клапан.
Чтобы найти Q, разделите V на t. Итак, если у нас есть объем воды в 1 галлон, и требуется 10 секунд, чтобы пройти через клапан, скорость потока составляет 6 галлонов в минуту. В качестве другого примера, если у нас есть 100 галлонов воды и требуется 15 минут, чтобы пройти через клапан, скорость потока будет 6,66 галлонов в минуту.
Итак, если у нас есть объем воды в 1 галлон, и требуется 10 секунд, чтобы пройти через клапан, скорость потока составляет 6 галлонов в минуту. В качестве другого примера, если у нас есть 100 галлонов воды и требуется 15 минут, чтобы пройти через клапан, скорость потока будет 6,66 галлонов в минуту.
Падение давления
Падение давления (P) является самой сложной переменной для расчета, поэтому рекомендуется использовать диаграммы для определения падения давления для конкретных типов труб.
Если вы не пользуетесь диаграммами, вам необходимо вычислить коэффициент трения трубы, длину трубы, гидравлический диаметр, плотность жидкости и скорость потока. В общем, лучше всего использовать диаграмму, чтобы помочь разобраться в этих расчетах.
Для стальных труб различного диаметра в Engineering Toolbox есть удобная таблица. Вы можете использовать эту таблицу для других труб, включая медные и ПВХ.
При использовании этих таблиц вам необходимо знать тип трубы, ее внутренний диаметр и скорость потока, которую вы должны рассчитать с помощью предыдущего уравнения.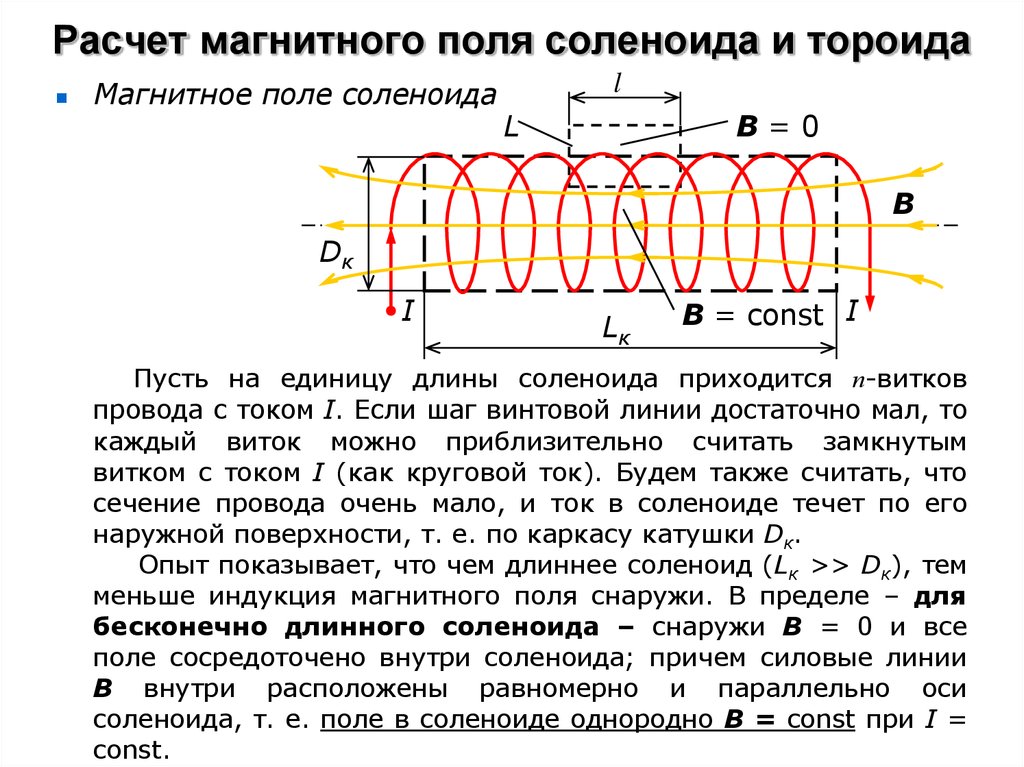
Как только вы определите диаметр и скорость потока, вы сможете определить соответствующее падение давления на графиках. Обычно мы представляем падение давления в фунтах на квадратный дюйм.
Как рассчитать коэффициент потока клапана
Уравнение для коэффициента потока клапана довольно сложное. Давайте пройдемся по уравнениям шаг за шагом.
Шаг 1. Определите переменные
Первым шагом в любом уравнении является вычисление чисел, которые вы будете подставлять в переменные. Помните, нам нужно найти соответствующие ответы на удельный вес (SQ), расход (Q) и падение давления (P) .
В нашем примере мы будем использовать воду, удельный вес которой равен 1,00. Скорость потока составит 10,0 галлонов в минуту. Мы также будем использовать трубу из ПВХ с внутренним диаметром два дюйма, и знание этого поможет нам определить падение давления. В случае двухдюймовой трубы из ПВХ P будет равно 0,11, согласно этой диаграмме.
Итак, для этого примера наши переменные выглядят следующим образом:
- Падение давления = P = 0,11
- Удельный вес = SG = 1,00
- Скорость потока = Q = 10,00
Шаг 2: Подставьте значения в уравнение
Уравнение для расчета коэффициента потока клапана: Cv = Q √ (SQ/P).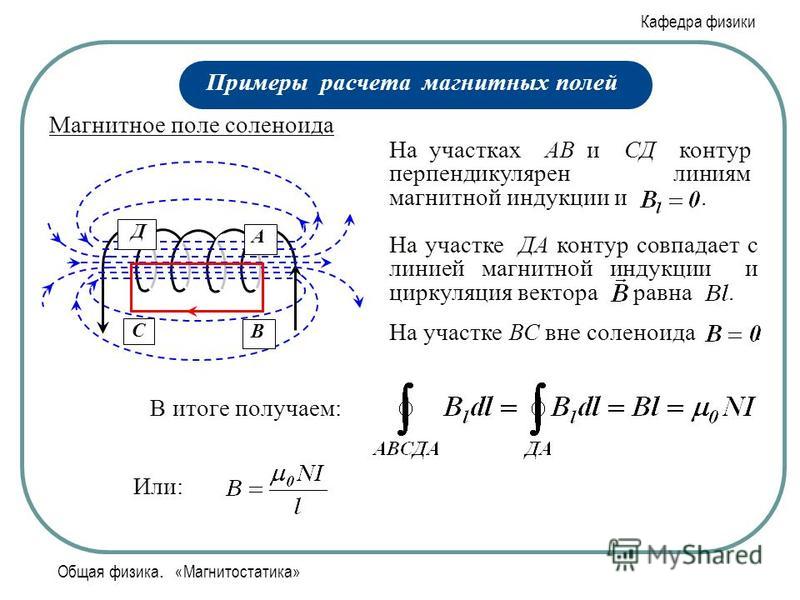 Теперь, когда мы установили значения для наших переменных, мы можем подставить их в уравнение. Как только мы это сделаем, наш пример должен выглядеть так: Cv = 10 √ (1/0,11).
Теперь, когда мы установили значения для наших переменных, мы можем подставить их в уравнение. Как только мы это сделаем, наш пример должен выглядеть так: Cv = 10 √ (1/0,11).
Шаг 3. Решение уравнения
Теперь, когда мы подставили переменные в уравнение, мы можем работать над его решением. Не забывайте всегда использовать свой надежный школьный PEMDAS при выполнении алгебры, чтобы вы всегда могли прийти к правильному ответу.
Поскольку в уравнении есть скобки, мы начнем с них. В скобках указано SG, деленное на P. Таким образом, для нашего примера 1, деленное на 0,11, дает нам ответ 9,0909 повторений. Далее нам нужно найти квадратный корень из этого числа. Квадратный корень из 9,0909 повторений равен 3,0151134457776.
Теперь, когда мы нашли и квадрат, последний расчет прост. Умножьте Q на число, которое мы только что нашли. Вычисление должно быть 10, умноженное на 3,0151134457776, что дает нам ответ 30,151134457776.
Таким образом, в нашем примере мы обнаружили, что коэффициент расхода клапана (Cv) округлен до 30,15, с которым могут работать эти 2-дюймовые электромагнитные клапаны из латуни или 2-дюймовые электромагнитные клапаны из нержавеющей стали.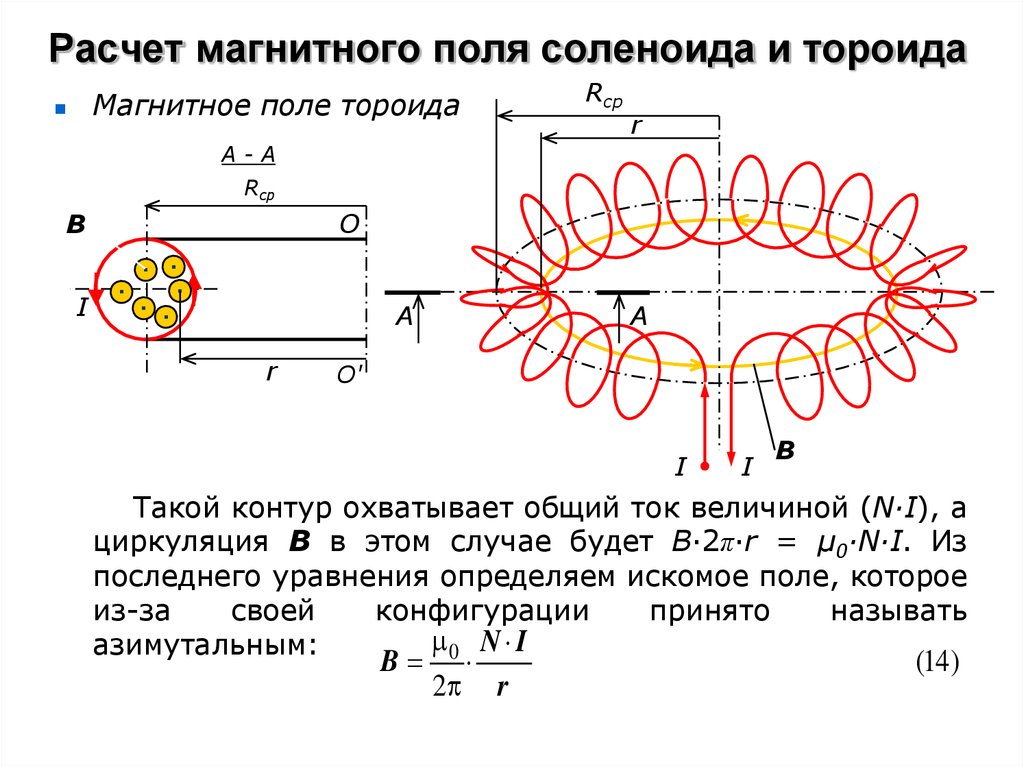


 Если через катушку соленоида протекает электрический ток, в ней образуется однородное магнитное поле. Соленоиды с ферромагнитными сердечниками часто используются в качестве исполнительных механизмов для преобразования электрической энергии в линейное перемещение сердечника. Самым привычным примером такого соленоида является реле стартера, которое выполняет две функции: подает напряжение на двигатель стартера и вводит шестерню двигателя стартера в зацепление с маховиком коленвала двигателя на время запуска.
Если через катушку соленоида протекает электрический ток, в ней образуется однородное магнитное поле. Соленоиды с ферромагнитными сердечниками часто используются в качестве исполнительных механизмов для преобразования электрической энергии в линейное перемещение сердечника. Самым привычным примером такого соленоида является реле стартера, которое выполняет две функции: подает напряжение на двигатель стартера и вводит шестерню двигателя стартера в зацепление с маховиком коленвала двигателя на время запуска. Она уменьшает или даже полностью устраняет шум при срабатывании соленоида, а также увеличивает силу притяжения, что позволяет уменьшить размеры соленоидных исполнительных устройств при сохранении их характеристик. Ферромагнитные жидкости также позволяют уменьшить утечку магнитного поля в магнитопроводе, а также улучшают охлаждение соленоида.
Она уменьшает или даже полностью устраняет шум при срабатывании соленоида, а также увеличивает силу притяжения, что позволяет уменьшить размеры соленоидных исполнительных устройств при сохранении их характеристик. Ферромагнитные жидкости также позволяют уменьшить утечку магнитного поля в магнитопроводе, а также улучшают охлаждение соленоида. Если их намагнитить, воздействуя на них магнитным полем, то эти жидкости формируют интересные складки на поверхности. Ферромагнитные жидкости — это коллоидные системы, состоящие из наночастиц размером около 10 нм, распределенных во взвешенном состоянии в воде или в другой жидкости-носителе. Большая часть этих жидкостей-носителей — органические растворители, то есть такие жидкости, в которых можно растворить другое вещество.
Если их намагнитить, воздействуя на них магнитным полем, то эти жидкости формируют интересные складки на поверхности. Ферромагнитные жидкости — это коллоидные системы, состоящие из наночастиц размером около 10 нм, распределенных во взвешенном состоянии в воде или в другой жидкости-носителе. Большая часть этих жидкостей-носителей — органические растворители, то есть такие жидкости, в которых можно растворить другое вещество.  Так как оболочки всех наночастиц заряжены одинаково, они отталкивают друг друга, потому что одинаковые заряды отталкиваются. Это и предотвращает слипание.
Так как оболочки всех наночастиц заряжены одинаково, они отталкивают друг друга, потому что одинаковые заряды отталкиваются. Это и предотвращает слипание. На поверхности образуются складки похожие на конусы, и при перемещении магнитного поля эти складки движутся за полем. Они располагаются по силовым линиям, и их высота зависит от силы магнитного поля. Сила магнитного поля, в свою очередь, зависит от того, как близко расположен магнит относительно жидкости. Ниже мы обсудим различные применения ферромагнитных жидкостей. Все эти применения основываются на этом свойстве ферромагнитной жидкости двигаться за магнитным полем.
На поверхности образуются складки похожие на конусы, и при перемещении магнитного поля эти складки движутся за полем. Они располагаются по силовым линиям, и их высота зависит от силы магнитного поля. Сила магнитного поля, в свою очередь, зависит от того, как близко расположен магнит относительно жидкости. Ниже мы обсудим различные применения ферромагнитных жидкостей. Все эти применения основываются на этом свойстве ферромагнитной жидкости двигаться за магнитным полем.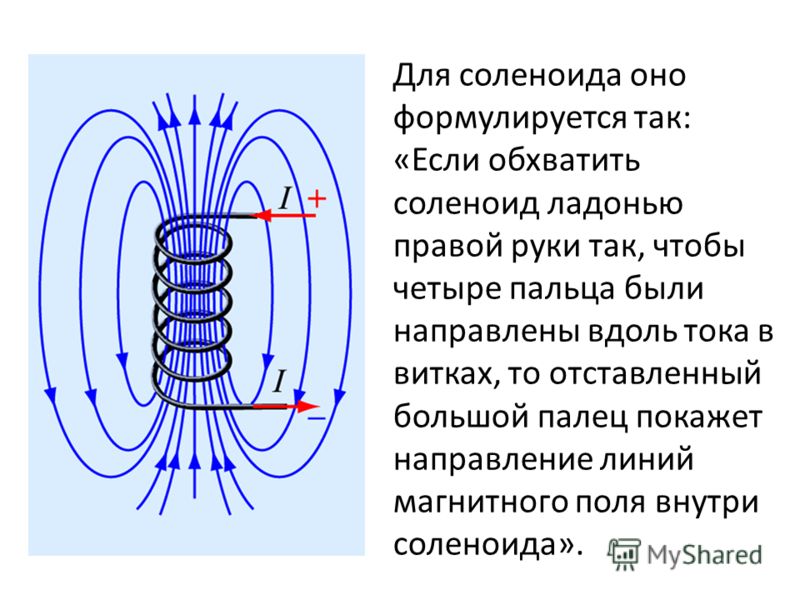 Благодаря этому они нашли широкое применение в науке, технике и медицине.
Благодаря этому они нашли широкое применение в науке, технике и медицине.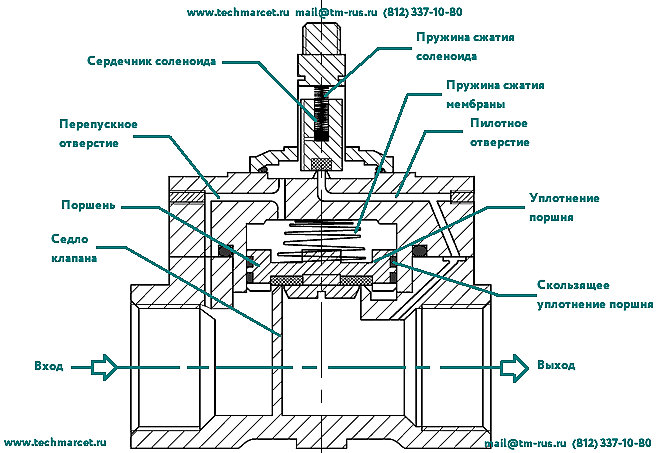 Некоторые производители ферромагнитных жидкостей продают для этих целей саму жидкость, а некоторые разрабатывают и выпускают полный комплект магнитожидкостных уплотнений, и не продают саму жидкость отдельно, чтобы предотвратить ее неправильное использование.
Некоторые производители ферромагнитных жидкостей продают для этих целей саму жидкость, а некоторые разрабатывают и выпускают полный комплект магнитожидкостных уплотнений, и не продают саму жидкость отдельно, чтобы предотвратить ее неправильное использование. Из-за низкой энергетической эффективности звуковоспроизводящих систем, во время их работы большая часть электрической энергии преобразуется в тепловую, и это тепло может привести к выводу из строя звуковой катушки, если ее не охладить. Ферромагнитные жидкости отводят это тепло от звуковой катушки, а в зазоре их удерживает магнит, так же как и в других системах, описанных выше.
Из-за низкой энергетической эффективности звуковоспроизводящих систем, во время их работы большая часть электрической энергии преобразуется в тепловую, и это тепло может привести к выводу из строя звуковой катушки, если ее не охладить. Ферромагнитные жидкости отводят это тепло от звуковой катушки, а в зазоре их удерживает магнит, так же как и в других системах, описанных выше.
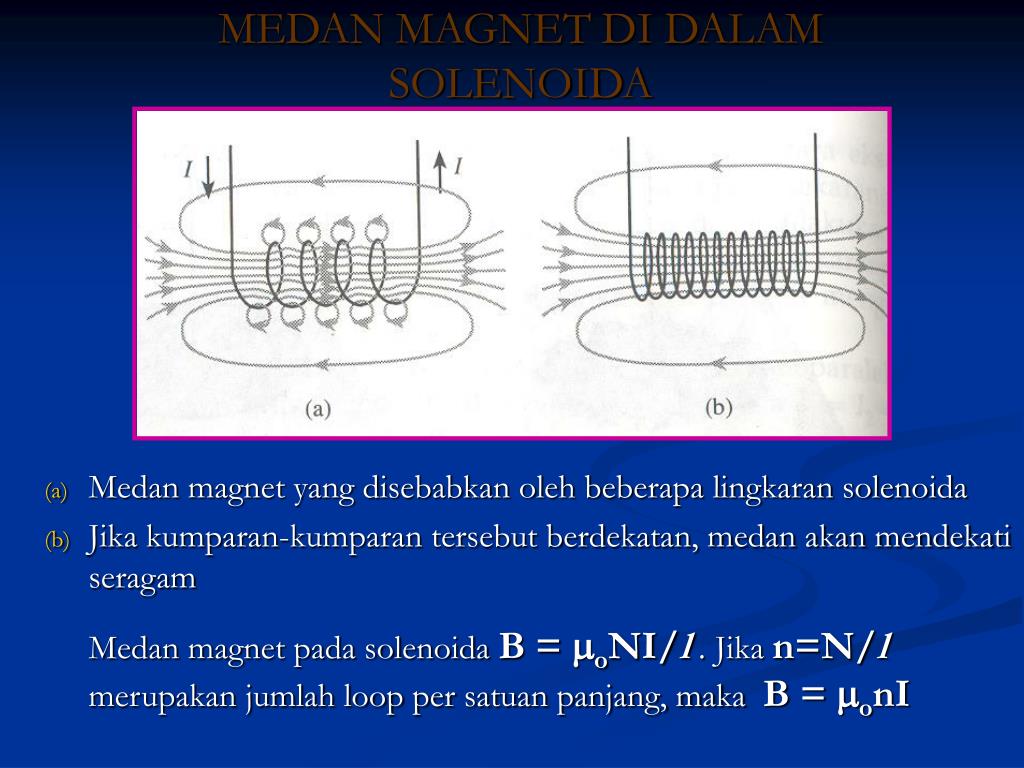 При этом выделяется большое количество тепла, и высокие температуры разрушают ткани на этом участке, убивая раковые клетки.
При этом выделяется большое количество тепла, и высокие температуры разрушают ткани на этом участке, убивая раковые клетки. Например, с помощью ферромагнитной жидкости можно определить удаленные в домашних условиях заводские номера на огнестрельном оружии.
Например, с помощью ферромагнитной жидкости можно определить удаленные в домашних условиях заводские номера на огнестрельном оружии. В этом случае магнит выступает в роли насоса, так как он помогает замещать менее намагниченную горячую жидкость более намагниченной холодной.
В этом случае магнит выступает в роли насоса, так как он помогает замещать менее намагниченную горячую жидкость более намагниченной холодной.
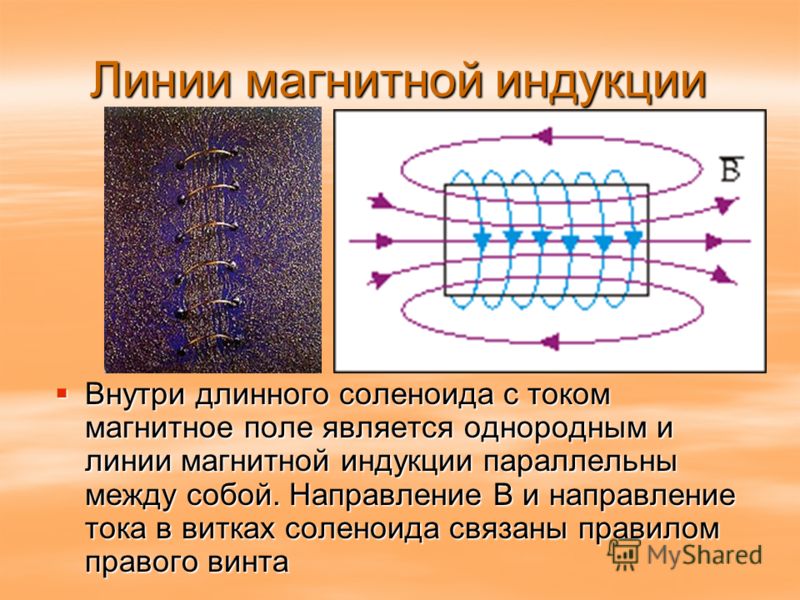
 К., Курбанов Ж.Ф. Программное обеспечение системы управления единым пространственным полем // Современные состояние и перспективы применения информационных технологий в управлении, доклады республиканской научно-технической конференции,5-6сентябрь 2016г., Джизак.
К., Курбанов Ж.Ф. Программное обеспечение системы управления единым пространственным полем // Современные состояние и перспективы применения информационных технологий в управлении, доклады республиканской научно-технической конференции,5-6сентябрь 2016г., Джизак.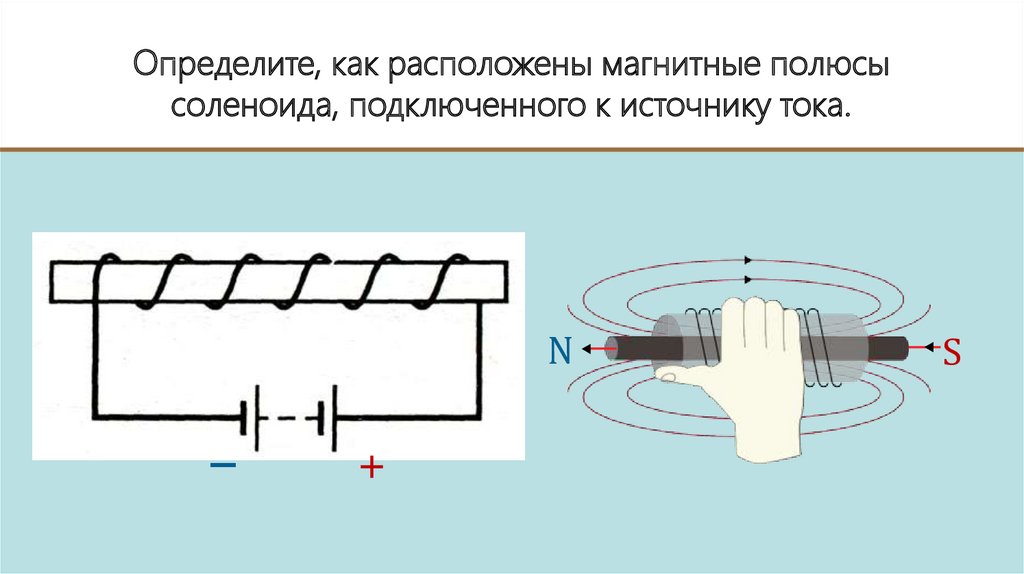 С. Параметры магнетизма, намагничивания и размагничивания материалов и рельсовых плетей. // UNIVERSUM Технические науки. Москва– 2019. №10 (67). – С.81-83. Электронный научный журнал.
С. Параметры магнетизма, намагничивания и размагничивания материалов и рельсовых плетей. // UNIVERSUM Технические науки. Москва– 2019. №10 (67). – С.81-83. Электронный научный журнал.  Icon Beat 2019.
Icon Beat 2019. 
 Расход – это количество среды, проходящее в данной точке за данный период времени. Он измеряется с использованием термина C V , который представляет собой количество воды в галлонах в минуту, которое пройдет через клапан с перепадом давления на нем 1 фунт на квадратный дюйм (фунт на квадратный дюйм). Эта мера используется для определения пропускной способности клапана при более высоких перепадах давления, но также применяется к потокам жидкости и газа при достаточно малых перепадах давления, при которых изменения плотности незначительны.
Расход – это количество среды, проходящее в данной точке за данный период времени. Он измеряется с использованием термина C V , который представляет собой количество воды в галлонах в минуту, которое пройдет через клапан с перепадом давления на нем 1 фунт на квадратный дюйм (фунт на квадратный дюйм). Эта мера используется для определения пропускной способности клапана при более высоких перепадах давления, но также применяется к потокам жидкости и газа при достаточно малых перепадах давления, при которых изменения плотности незначительны.