Калькулятор расчета делителя напряжения
Онлайн расчет. Применение на. Схема традиционного резисторного делителя напряжения. Расчет резистивного делителя напряжения. Онлайн расчет с примерами резистивного делителя напряжения.
Поиск данных по Вашему запросу:
Схемы, справочники, даташиты:
Прайс-листы, цены:
Обсуждения, статьи, мануалы:
Дождитесь окончания поиска во всех базах.
По завершению появится ссылка для доступа к найденным материалам.
Содержание:
- Онлайн калькулятор расчета делителя напряжения
- Расчет резистора для понижения напряжения калькулятор. Делитель напряжения на резисторах
- Формулы, позволяющие рассчитать сопротивление для понижения напряжения
- Нахождение делителя напряжения
- Делитель напряжения
- Расчет делителя напряжения
ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: Куда уходят вольты? «Фокус» с делителем напряжения
youtube.com/embed/Re5AkIHOCCw» frameborder=»0″ allowfullscreen=»»/>Онлайн калькулятор расчета делителя напряжения
Для того, чтобы получить из исходного напряжения лишь его часть используется делитель напряжения voltage divider. Это схема, строящаяся на основе пары резисторов. В примере, на вход подаются стандартные 9 В.
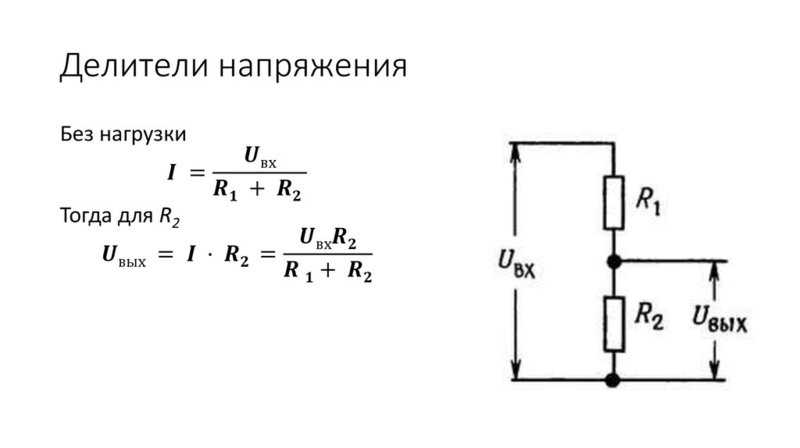
Но какое напряжение получится на выходе V out? Или эквивалентный вопрос: какое напряжение покажет вольтметр? Ток, протекающий через R1 и R2 одинаков пока к выходу V out ничего не подключено. А суммарное сопротивление пары резисторов при последовательном соединении:. Так с помощью пары резисторов мы изменили значение входного напряжения с 9 до 5 В. Это простой способ получить несколько различных напряжений в одной схеме, оставив при этом только один источник питания.
Другое применение делителя напряжения — это снятие показаний с датчиков. Существует множество компонентов, которые меняют своё сопротивление в зависимости от внешних условий.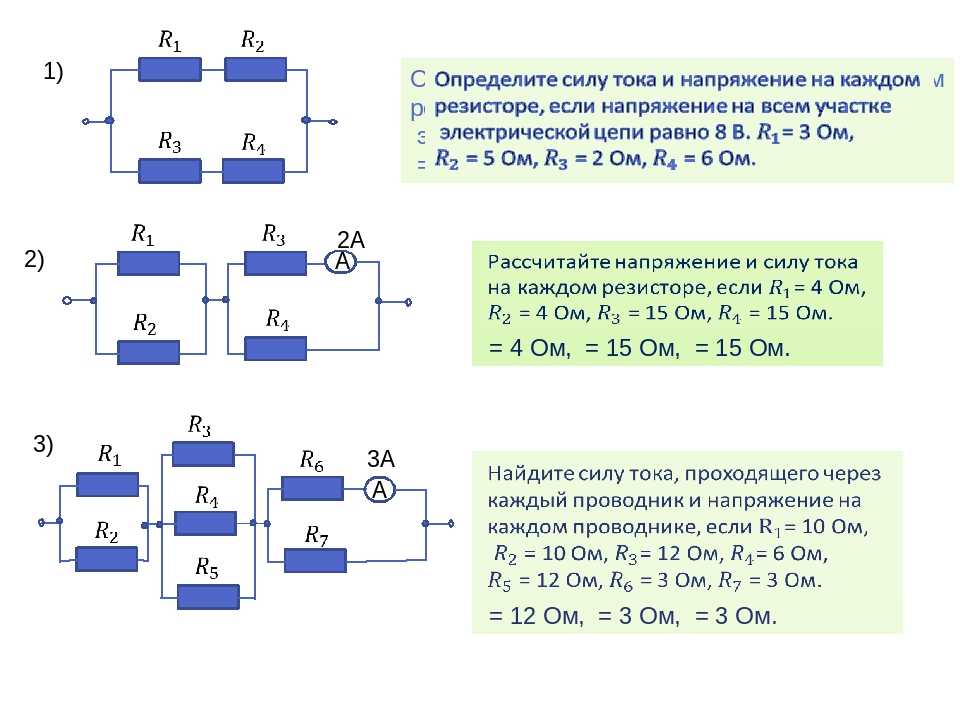 Так термисторы меняют сопротивление от нуля до определённого значения в зависимости от температуры, фоторезисторы меняют сопротивление в зависимости от интенсивности попадающего на них света и т. Если в приведённой выше схеме заменить R1 или R2 на один из таких компонентов, V out будет меняться в зависимости от внешних условий, влияющих на датчик.
Так термисторы меняют сопротивление от нуля до определённого значения в зависимости от температуры, фоторезисторы меняют сопротивление в зависимости от интенсивности попадающего на них света и т. Если в приведённой выше схеме заменить R1 или R2 на один из таких компонентов, V out будет меняться в зависимости от внешних условий, влияющих на датчик.
Подключив это выходное напряжение к аналоговому входу Ардуино, можно получать информацию о температуре, уровне освещённости и других параметрах среды. Значение выходного напряжения при определённых параметрах среды можно расчитать, сопоставив документацию на переменный компонент и общую формулу расчёта V out.
С делителем напряжения не всё так просто, когда к выходному подключения подключается какой-либо потребитель тока, который ещё называют нагрузкой load :. В этом случае V out уже не может быть расчитано лишь на основе значений V in , R1 и R2 : сама нагрузка провоцирует дополнительное падение напряжения voltage drop. Пусть нагрузкой является нечто, что потребляет ток в 10 мА при предоставленных 5 В.
Как видно, мы потеряли более полутора вольт напряжения из-за подключения нагрузки. И тем ощутимее будут потери, чем больше номинал R2 по отношению к сопротивлению L. Чтобы нивелировать этот эффект мы могли бы использовать в качестве R1 и R2 резисторы, например, в 10 раз меньших номиналов.
Однако, у снижения сопротивления делящих резисторов есть обратная сторона медали. Большое количество энергии от источника питания будет уходить в землю. В том числе при отсоединённой нагрузке. Это небольшая проблема, если устройство питается от сети, но — нерациональное расточительство в случае питания от батарейки. Кроме того, нужно помнить, что резисторы расчитаны на определённую предельную мощьность.
В нашем случае нагрузка на R1 равна:. А это в раз выше максимальной мощности самых распространённых резисторов! Попытка воспользоваться описанной схемой со сниженными номиналами и стандартными 0.
Чем меньшие номиналы выбраны для делящих резисторов, тем больше энергии расходуется впустую и тем выше нагрузка на сами резисторы. Чем номиналы больше, тем больше и дополнительное нежелательное падение напряжения, провоцируемое самой нагрузкой. Если потребление тока нагрузкой неравномерно во времени, V out также будет неравномерным. Делитель напряжения на резисторах — это схема, позволяющая получить из высокого напряжения пониженное напряжение.
Используя всего два резистора, мы можем создать любое выходное напряжение, составляющее меньшую часть от входного напряжения. Делитель напряжения является фундаментальной схемой в электронике и робототехнике. Для начала рассмотрим электрическую схему и формулу для расчета. Для того, чтобы разобраться в принципе работы резисторного делителя напряжения и понять, как рассчитать делитель напряжения на резисторах, следует ознакомиться с его принципиальной схемой см.
Для того, чтобы разобраться в принципе работы резисторного делителя напряжения и понять, как рассчитать делитель напряжения на резисторах, следует ознакомиться с его принципиальной схемой см.
Схема включает в себя входное напряжение и два резистора. Резистор, находящийся ближе к плюсу входного напряжения Vвх , обозначен R1 , резистор находящийся ближе к минусу обозначен R2. Падение напряжения Vвых — это пониженное выходное напряжение, полученное в результате резисторного делителя напряжения.
Для расчета выходного напряжения необходимо знать три величины из приведенной схемы — входное напряжение и сопротивление обоих резисторов. Эта формула показывает, что выходное напряжение резисторного делителя прямо пропорционально входному напряжению и обратно пропорционально отношению сопротивлений R1 и R2.
На этом принципе работают потенциометры переменные резисторы и многие резистивные датчики, например, датчик освещенности на фоторезисторе. Смотрите калькулятор делителя напряжения на резисторах онлайн.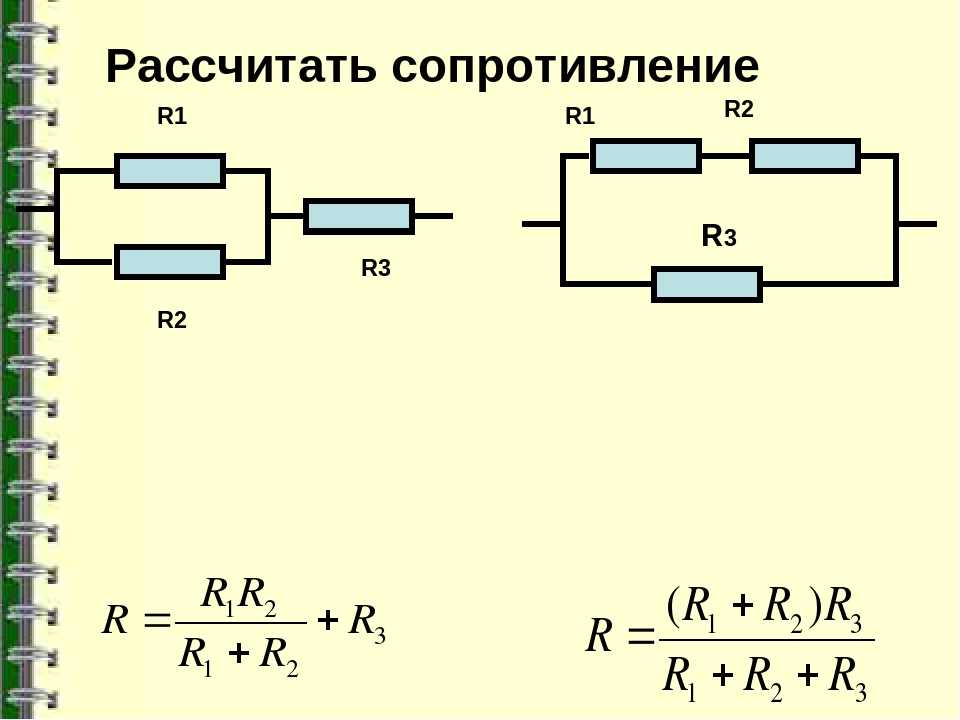 Делитель напряжения применяется, если нужно получить заданное напряжение при условии стабилизированного питания. Сейчас мы поговорим о постоянном токе и резисторных делителях. О делителях с использованием конденсаторов, диодов, стабилитронов, индуктивностей и других элементов будет отдельная статья.
Делитель напряжения применяется, если нужно получить заданное напряжение при условии стабилизированного питания. Сейчас мы поговорим о постоянном токе и резисторных делителях. О делителях с использованием конденсаторов, диодов, стабилитронов, индуктивностей и других элементов будет отдельная статья.
Подпишитесь на новости, чтобы ее не пропустить. В конце для примера расскажу, как сделать делитель напряжения для осциллографа, чтобы снимать осциллограммы высокого напряжения. Резисторные делители также могут применяться для уменьшения в заданное количество раз сигналов сложной формы. На делителях напряжения с регулируемым коэффициентом ослабления строятся, например, регуляторы громкости.
Для применения делителя напряжения нам надо уметь рассчитывать три величины: напряжение на выходе делителя, его эквивалентное выходное сопротивление, его входное сопротивление. С напряжением все понятно. Эквивалентное выходное сопротивление скажет нам, насколько изменится напряжение на выходе с изменением тока нагрузки делителя.
Если эквивалентное выходное сопротивление равно Ом, то изменение тока нагрузки на 10 мА приведет к изменению напряжения на выходе на 1 В. Входное сопротивление показывает, насколько делитель нагружает источник сигнала или источник питания. Дополнительно посчитаем коэффициент ослабления сигнала. Он может пригодиться при работе с сигналами сложной формы.
Из этой формулы, в частности, видно, что резисторные резистивные делители выдают стабильное выходное напряжение, если напряжение питания фиксировано.
Эта формула верна для ненагруженного делителя. Если мы хотим получить осциллограмму высокого напряжения, то сразу приходит в голову делитель напряжения. Изготавливаем делитель, подключаем его вход к источнику высоковольтного сигнала, а выход к входу осциллографа. Должны получить на входе осциллографа уменьшенную копию входного сигнала. Если наш сигнал имеет достаточно большую частоту или просто резкие фронты например, меандр , то ничего не получится. Осциллограмма не будет похожа на изначальный сигнал.
Причина в том, что осциллограф имеет некоторую входную емкость, которая образует с эквивалентным выходным сопротивлением делителя фильтр нижних частот. Все высшие гармоники сигнала подавляются. Кроме того этот фильтр формирует фазовый сдвиг. Это бывает существенным для многолучевых осциллографов, когда мы анализируем соотношения сигналов. Чтобы этого избежать, резистор R1 нужно зашунтировать конденсатором.
Как не спутать плюс и минус? Защита от переполярности. Схема защиты от неправильной полярности подключения переполюсовки зарядных уст Бесперебойник своими руками. Синус, синусоида Как сделать бесперебойник самому? Чисто синусоидальное напряжение на выходе, при Применение тиристоров динисторов, тринисторов, симисторов. Тиристоры в электронных схемах. Тонкости и особенности использования.
Виды тирис Соединение светодиодов. Последовательное, параллельное включение оптоэ Как правильно включить светодиод, соединять их и входные цепи приборов на их осн Параллельное, последовательное соединение резисторов. Расчет сопротивл Вычисление сопротивления и мощности при параллельном и последовательном соединен Как сделать делитель напряжения на резисторах? Часто в практике электронщика возникает необходимость снизить величину входного напряжения либо напряжение на отдельном участке цепи в строго определенной количество раз.
Расчет сопротивл Вычисление сопротивления и мощности при параллельном и последовательном соединен Как сделать делитель напряжения на резисторах? Часто в практике электронщика возникает необходимость снизить величину входного напряжения либо напряжение на отдельном участке цепи в строго определенной количество раз.
Например, величина входного напряжения 50 В , а выходное напряжение нужно получить в 10 раз меньше, т. Для этого используются делители напряжения.
Они бывают разных типов и выполняются на безе , катушек индуктивности рис. Однако мы рассмотрим только наиболее применяемые на практике делители напряжения. Наиболее простым делителем напряжения являются два последовательно соединенных резистора R1 и R2 , которые подключены к источнику напряжения U рис.
Расчет резистора для понижения напряжения калькулятор. Делитель напряжения на резисторах
Делитель напряжения — устройство, в котором входное и выходное напряжение связаны коэффициентом передачи. В качестве делителя напряжения обычно применяют регулируемые сопротивления потенциометры. Можно представить как два участка цепи, называемые плечами, сумма напряжений на которых равна входному напряжению. Плечо между нулевым потенциалом и средней точкой называют нижним, а другое — верхним.
Можно представить как два участка цепи, называемые плечами, сумма напряжений на которых равна входному напряжению. Плечо между нулевым потенциалом и средней точкой называют нижним, а другое — верхним.
Онлайн калькулятор подбора резисторов для делителя напряжения обратной связи в DC-DC преобразователях. Калькулятор делителя.
Формулы, позволяющие рассчитать сопротивление для понижения напряжения
Код для вставки без рекламы с прямой ссылкой на сайт. Код для вставки с рекламой без прямой ссылки на сайт. Скопируйте и вставьте этот код на свою страничку в то место, где хотите, чтобы отобразился калькулятор. Калькулятор справочный портал. Избранные сервисы. Кликните, чтобы добавить в избранные сервисы. Калькулятор расчета делителя напряжения поможет вам рассчитать выходное напряжение электрической цепи с резистивным или ёмкостным делителем напряжения, по значениям входного напряжения, сопротивлениям резисторов и емкостям конденсаторов.
Нахождение делителя напряжения
В статье теория и примеры расчета параметров делителя напряжения.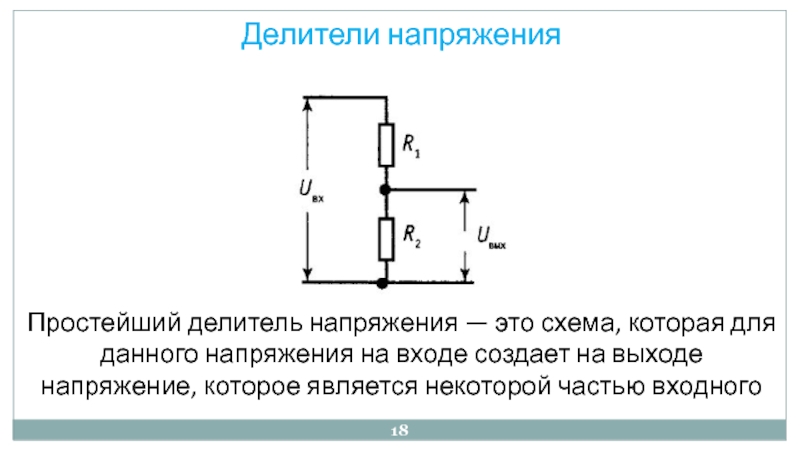 Так же резистивный делитель напряжения помогает измерить. В таком случае если: U1 — падение напряжения на участке R1, U — падение напряжения на всей цепи, R1 — сопротивление с которого снимают часть. Расчет делителя напряжения.
Так же резистивный делитель напряжения помогает измерить. В таком случае если: U1 — падение напряжения на участке R1, U — падение напряжения на всей цепи, R1 — сопротивление с которого снимают часть. Расчет делителя напряжения.
Резисторный делитель напряжения — одна из основополагающих конструкций в электронике, без которой не обходится ни одно устройство.
Делитель напряжения
Схема делителя напряжения является простой, но в тоже время фундаментальной электросхемой, которая очень часто используется в электронике. Принцип работы ее прост: на входе подается более высокое входное напряжение и затем оно преобразуется в более низкое выходное напряжение с помощью пары резисторов. Формула расчета выходного напряжения основана на законе Ома и приведена ниже. Существует несколько обобщений, которые следует учитывать при использовании делителей напряжения. Это упрощения, которые упрощают оценку схемы деления напряжения. Это верно независимо от значений резисторов.
Расчет делителя напряжения
Используя только два резистора и входное напряжение, мы можем создать выходное напряжение, составляющее определенную часть от входного. Делитель напряжения является одной из наиболее фундаментальных схем в электронике. В вопросе изучения работы делителя напряжения следует отметить два основных момента — это сама схема и формула расчета. Схема делителя напряжения включает в себя входной источник напряжения и два резистора. Ниже вы можете увидеть несколько схематических вариантов изображения делителя, но все они несут один и тот же функционал. Обозначим резистор, который находится ближе к плюсу входного напряжения Uin как R1, а резистор находящийся ближе к минусу как R2. Падение напряжения Uout на резисторе R2 — это пониженное напряжение, полученное в результате применения резисторного делителя напряжения.
Делитель напряжения является одной из наиболее фундаментальных схем в электронике. В вопросе изучения работы делителя напряжения следует отметить два основных момента — это сама схема и формула расчета. Схема делителя напряжения включает в себя входной источник напряжения и два резистора. Ниже вы можете увидеть несколько схематических вариантов изображения делителя, но все они несут один и тот же функционал. Обозначим резистор, который находится ближе к плюсу входного напряжения Uin как R1, а резистор находящийся ближе к минусу как R2. Падение напряжения Uout на резисторе R2 — это пониженное напряжение, полученное в результате применения резисторного делителя напряжения.
Онлайн калькулятор расчета делителя напряжения. Как гласит Википедия: Делитель напряжения — устройство, в котором входное и выходное.
Делитель напряжения можно представить как два последовательных участка цепи, называемые плечами, сумма напряжений на которых равна входному напряжению. Плечо между нулевым потенциалом и средней точкой называют нижним с него обычно снимается выходное напряжение делителя , а другое — верхним.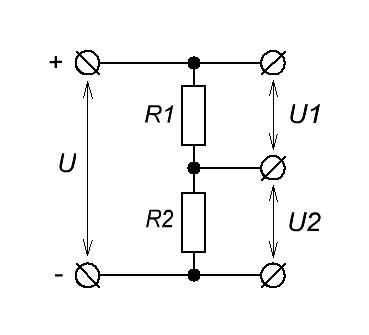 Различают линейные и нелинейные делители напряжения. В линейных выходное напряжение изменяется по линейному закону в зависимости от входного.
Различают линейные и нелинейные делители напряжения. В линейных выходное напряжение изменяется по линейному закону в зависимости от входного.
Благодарим пользователя zapimir за разработку и предоставление калькулятора для www. Блог new. Технические обзоры. Калькулятор делителя напряжения Делитель напряжения Подбор резисторов, для оптимального делителя напряжения обратной связи в DC-DC преобразователях. U out В. Поддержать проект Все материалы на сайте и советы бесплатны, однако мы будем благодарны за поддержку проекта и канала!
Делитель может использоваться в электрической цепи для того, чтобы взять из исходного напряжения лишь его долю, а также для снятия данных с датчиков.
Делитель напряжения используется в электрических цепях, если необходимо понизить напряжение и получить несколько его фиксированных значений. Состоит он из двух и более элементов резисторов, реактивных сопротивлений. Элементарный делитель можно представить как два участка цепи, называемые плечами. Участок между положительным напряжением и нулевой точкой — верхнее плечо , между нулевой и минусом — нижнее плечо. Делитель напряжения на резисторах может применятmся как для постоянного, так и для переменного напряжений.
Делитель напряжения на резисторах может применятmся как для постоянного, так и для переменного напряжений.
Обнаружен блокировщик рекламы. Сайт Паяльник существует только за счет рекламы, поэтому мы были бы Вам благодарны если Вы внесете сайт в список исключений. Как это сделать?
Онлайн калькулятор закона ома для участка цепи
Содержание
- Расчет делителя напряжения на резисторах
- Делитель напряжения
- Делитель тока
- Расчет резисторов
- Ограничения в применении
- Зависимость сопротивления от температуры
- Применимость
- Параметры резисторного элемента
- Применение
- Величина напряжения, обеспеченная резисторным элементом
- Резистивный делитель напряжения
- Удельное электрическое сопротивление
- Применение делителя для считывания показаний датчика
Расчет делителя напряжения на резисторах
Удельное сопротивление меди
В простейшей схеме применяют два резистора.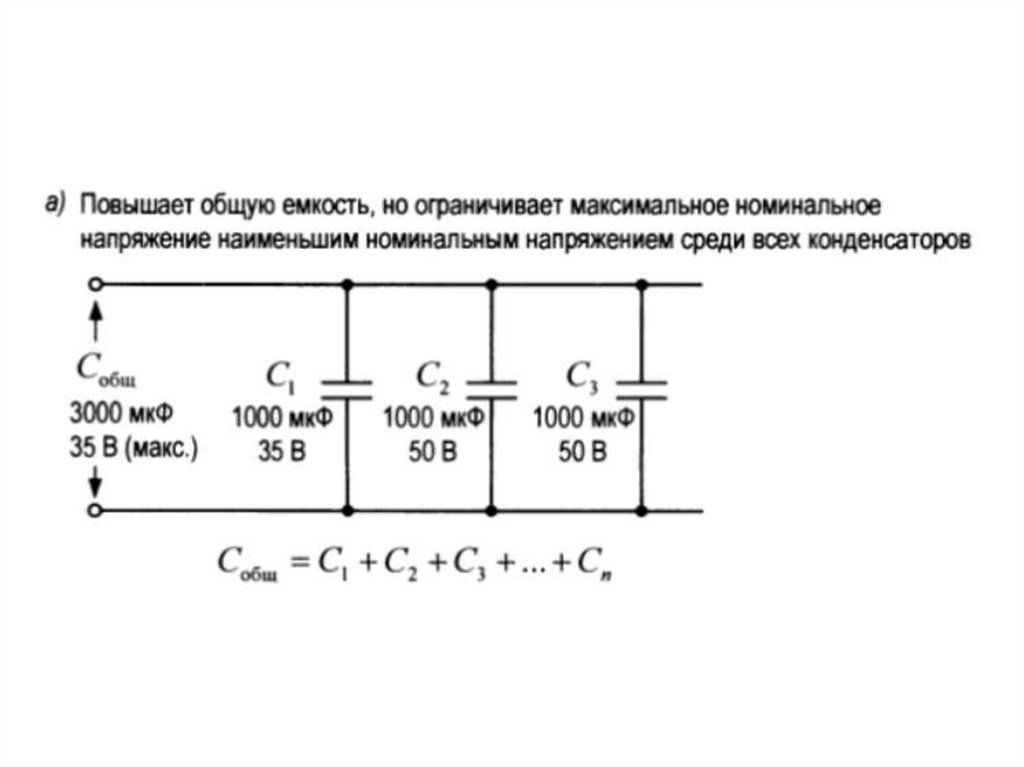 При необходимости количество компонентов увеличивают для обеспечения ступенчатой регулировки. Чтобы рассчитать делитель напряжения, калькулятор онлайн использовать не обязательно. Приведенная ниже подробная инструкция поможет получить точный результат собственными силами за несколько минут.
При необходимости количество компонентов увеличивают для обеспечения ступенчатой регулировки. Чтобы рассчитать делитель напряжения, калькулятор онлайн использовать не обязательно. Приведенная ниже подробная инструкция поможет получить точный результат собственными силами за несколько минут.
Формула делителя напряжения
Для примера взяты определенные значения:
- Входного постоянного напряжения (Uвх) – 20 Вольт;
- Сопротивления резисторов R1 и R2 – 20 и 50 кОм, соответственно.
Самостоятельный расчет резистивного делителя онлайн
Уменьшение входного напряжения в два раза получится при равных значениях сопротивлений резисторов. Для настоящего примера придется рассчитать пропорцию, пользуясь формулой закона Ома:
I=Uвх/ (R1+R2)
Подставив исходные значения, несложно узнать силу тока, протекающего по данной последовательной цепи:
20/ (20 000 + 50 000) = 0,000286 А
На отдельных элементах падения напряжения составят:
- UR1 = 0,000286 * 20 000 = 5,72 V;
- UR2 = 0,000286 * 50 000 = 14,3 V.

Для непосредственного расчета напряжения на рабочем плече можно пользоваться формулой:
UR2 = Uвх * R2/ (R1+R2)
Расчет делителя напряжения калькулятором онлайн
Соответствующие программы предлагают посетителям «Паяльник» и другие специализированные сайты бесплатно и без регистрации. В стандартной форме заполняют «окошки» с напряжением на входе и выходе. После подтверждения автоматически выполняется расчет с отображением значений электрических сопротивлений резисторов и рассеиваемых мощностей.
Как понятно из примера, основные формулы не отличаются повышенной сложностью. Однако автоматизированный расчет делителя напряжения на резисторах онлайн (online) позволяет выполнять многократные теоретические эксперименты с минимальными затратами времени. Такой инструмент пригодится для точного определения основных параметров делителя.
Таблица расчетов
| Входное напряжение Uвх, V | Эл. сопротивление, Ом | Рассеиваемая мощность, Вт | Напряжение на выходе Uвых, V | ||
| R1 | R2 | R1 | R2 | ||
| 12 | 1000 | 2000 | 0,016 | 0,032 | 8 |
| 12 | 50000 | 4545 | 0,00242 | 0,00022 | 1 |
| 12 | 50000 | 550000 | 0,00002 | 0,00022 | 11,5 |
| 12 | 100 | 200 | 0,16 | 0,32 | 8 |
Приведенные цифры демонстрируют, что для существенного уменьшения Uвых сопротивление R1 должно быть значительно больше R2.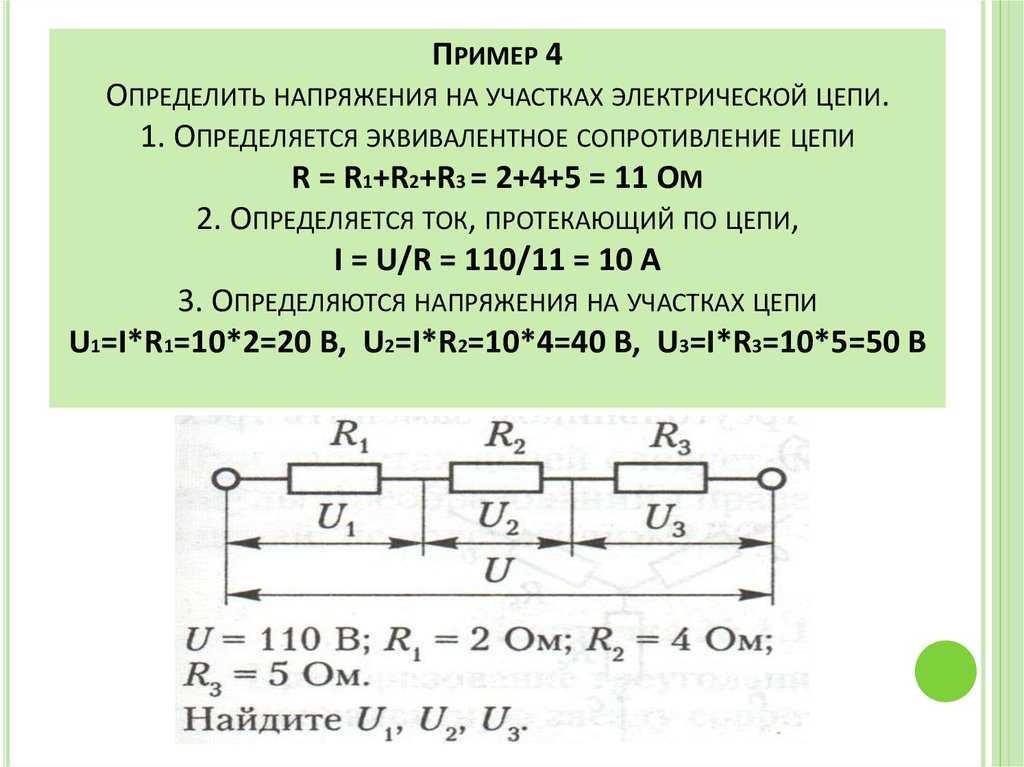 Обратные пропорции применяют для примерного равенства напряжений на входе и выходе.
Обратные пропорции применяют для примерного равенства напряжений на входе и выходе.
Совокупные потери в цепи определяют по рассеиваемой мощности. Чем меньше сопротивление, тем сильнее ток. Для самостоятельных расчетов пользуются формулой:
P=I2*R.
Делитель напряжения
Наиболее применяемые готовые блоки питания рассчитаны на выходные напряжения: 9, 12 или 24 вольта. В то же время большинство электронных схем и устройств использует напряжение питания в интервале от 3 до 5 В. В этом случае возникает потребность снизить величину Uпит до необходимого значения. Сделать это можно, используя делитель напряжения, который имеет много вариантов исполнения. Самый простой – делитель на резисторах.
Схема делителя, выполненного на резисторах
Подключение светодиода через резистор и его расчет
Подобные делители напряжения применяются исключительно в маломощных контурах. Это обусловлено их низким КПД. Часть мощности блока питания рассеивается на делителе, превращаясь в тепло.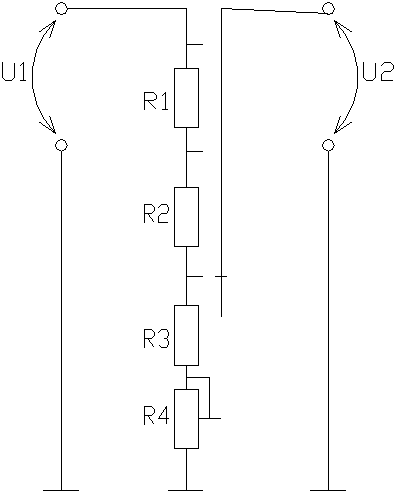 Эти потери тем больше, чем больше нужно уменьшить исходное напряжение. Подключение нагрузки параллельно одному плечу требует того, чтобы Rн было намного больше резистора, установленного в этом плече. Иначе делитель будет выдавать нестабильное питание.
Эти потери тем больше, чем больше нужно уменьшить исходное напряжение. Подключение нагрузки параллельно одному плечу требует того, чтобы Rн было намного больше резистора, установленного в этом плече. Иначе делитель будет выдавать нестабильное питание.
При такой схеме напряжение по плечам делителя распределяется согласно полученным соотношениям между R1 и R2. Величина сопротивлений при этом роли не играет. Но следует помнить, что при низких значениях R1 и R2 увеличивается и мощность на нагрузке, и величина потерь на нагревание элементов.
Внимание! Перед тем, как вычислять точные параметры, нужно помнить, как подобрать резисторы. При их равном значении напряжение на выходе делится пополам
Если равенство не соблюдается, снимать поделенное напряжение нужно с элемента, имеющего больший номинал.
Пример схемы делителей на резисторах с малыми и большими значениями
Делитель тока
Делитель тока – устройство позволяющее поделить ток в цепи на две составные части, с целью использования одной из них. Другими словами, делитель тока необходим в том случае, если устройство не рассчитано на большой ток, и нам необходима лишь некоторая часть этого тока.
Другими словами, делитель тока необходим в том случае, если устройство не рассчитано на большой ток, и нам необходима лишь некоторая часть этого тока.
Принцип действия делителя тока основан на первом законе Кирхгофа – сумма токов сходящихся в узле равна нулю. Если провести аналогию с водой, то его можно представить как русло реки, которое разветвляется на два более маленьких оттока.
Для нахождения токов I1 и I2 воспользуемся законом Ома, но для начала найдем эквивалентное сопротивление для параллельного соединения.
Делители тока применяются в измерительных устройствах, например при измерении больших токов. С помощью добавочного сопротивления – “шунта” расширяют предел измерения амперметра. Для этого, шунт подключается параллельно амперметру. В результате, через амперметр протекает ток, зная который, можно найти общий ток, протекающий в цепи. Обычно шунт имеет сопротивление меньше, чем амперметр, для того чтобы значительная часть тока ушла через него.
Выведем коэффициент деления (шунтирования) n. Будем считать, что параметры с индексом 1 принадлежат амперметру (прибору), а параметры с индексом 2 – шунту. Параметры без индексов общие.
Будем считать, что параметры с индексом 1 принадлежат амперметру (прибору), а параметры с индексом 2 – шунту. Параметры без индексов общие.
Рассмотрим пример.
Амперметром с пределом измерения 1 А и внутренним сопротивлением 12 Ом, необходимо измерить ток в 3 А. Каким должно быть сопротивление шунта?
Из формулы для коэффициента шунтирования, выразим Rш
Еще один пример
Каким станет новый предел измерения амперметра, после его шунтирования сопротивлением в 10 Ом, если старый предел был равен 0,5 А? Сопротивление измерительного механизма амперметра – 25 Ом.
Посчитаем коэффициент шунтирования
Тогда новый предел измерения амперметра
Спасибо за внимание!
Рекомендуем — делитель напряжения
- electroandi.ru
Расчет резисторов
Для подбора и установки элементов в схему необходимо предварительно рассчитать номинал и мощность компонентов.
Формула для расчета сопротивления и мощности
Сопротивление тока: формула
Используют Закон Ома для участка цепи, чтобы вычислить сопротивление резистора, формула имеет вид:
R = U/I,
где:
- U – напряжение на выводах элемента, В;
- I – сила тока на участке цепи, А.

Эта формула применима для токов постоянного направления. В случае расчётов для переменного тока берут в расчёт импеданс цепи Rz.
Важно! Строение схем не ограничивается установкой только одного резистора. Обычно их множество, соединены они между собой параллельно и последовательно
Для нахождения общего показателя применяют отдельные методы и формулы.
Последовательное соединение
При таком соединении «выход» одного элемента соединяется с «входом» другого, они идут последовательно друг за другом. Как рассчитать резистор в этом случае? Можно использовать электронный онлайн-калькулятор, можно применить формулу.
Общее значение будет составлять сумму сопротивлений компонентов, входящих в последовательное соединение:
R123 = R1+R2+R3.
На каждом из них произойдёт одинаковое падение напряжения: U1, U2, U3.
Параллельное соединение
При выполнении данного вида соединения одноимённые выводы соединяются попарно, формула имеет вид:
R = (R1 x R2)/ (R1 + R2).
Обычно полученное значение R бывает меньше меньшего из всех значений соединённых элементов.
Последовательное и параллельное соединения
Информация. На практике параллельное или последовательное присоединение применяют, когда нет детали необходимого номинала. Элементы для таких случаев подбирают одинаковой мощности и одного типа, чтобы не получить слабого звена.
Смешанное соединение
Рассчитывать общее сопротивление смешанных соединений возможно, применяя правило объединения. Сначала выбирают все параллельные и последовательные присоединения и составляют эквивалентные схемы замещения. Их начинают рассчитывать, используя формулы для каждого случая. Из полученной более простой схемы вновь выделяют параллельные и последовательные звенья и опять производят расчёты. Делают это до тех пор, пока не получат самое элементарное соединение или один эквивалентный элемент. Вычисленный результат будет являться искомым.
Метод расчёта при смешанном соединении
Мощность
Одного поиска значения сопротивления недостаточно для того, чтобы применить деталь.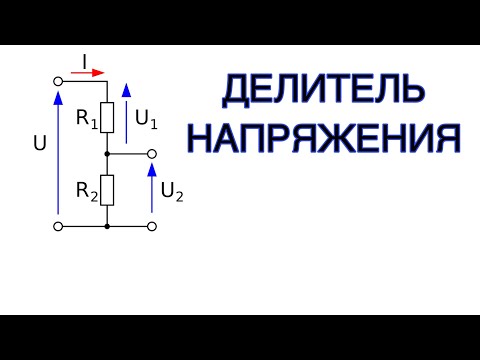 Необходимо узнать, на какую мощность должен быть рассчитан элемент. В противном случае он будет перегреваться и выйдет из строя. Мощные детали при поверхностном монтаже лучше устанавливать на радиатор.
Необходимо узнать, на какую мощность должен быть рассчитан элемент. В противном случае он будет перегреваться и выйдет из строя. Мощные детали при поверхностном монтаже лучше устанавливать на радиатор.
Расчет мощности резистора выполняется по формуле:
Р = I² * R = U²/R,
где:
- Р – мощность, Вт;
- I – ток, А;
- U – напряжение, В;
- R – сопротивление, Ом.
После определения мощности резисторов по формуле подбирают комплектующие, исходя из графического обозначения на схемах.
Основные обозначения мощности резисторов
Ограничения в применении
Из приведенных в таблице примеров расчетов хорошо видно, как значительно увеличиваются потери при уменьшении сопротивления цепи. Энергия расходуется впустую для нагрева окружающей среды. При большой мощности рассеивания приходится использовать принудительные системы охлаждения, пассивные радиаторы.
В приведенных расчетах не учитывалась нагрузка. Если добавить соответствующее реальным условиям сопротивление, образуются дополнительные потери в параллельной цепи.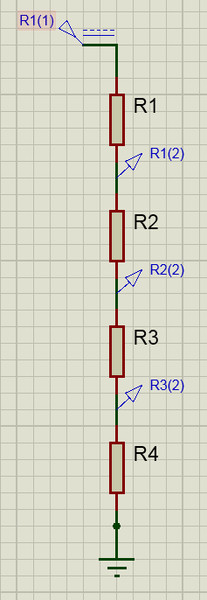
Влияние сопротивления нагрузки
На первой части рисунка изображен типовой делитель, обеспечивающий выходное напряжение 5 V. При потреблении тока 0,01 А сопротивление нагрузки составит 0,5 кОм. Пользуясь формулой расчета для параллельной цепи, несложно выяснить суммарное значение R = 1/(1/R2 + 1/Rнагрузки) = 0,25 кОм. Это добавление уменьшит плановое значение Uвых до 3,46 V.
Уменьшением R2 можно снизить вредное влияние на выходное напряжение (4,75 V). Однако такой способ, приведенный на второй части рисунка, сопровождается значительными потерями энергии. Ток будет проходить по участку с меньшим сопротивлением, не выполняя полезные функции. В данном примере необходимо выбрать R1, рассчитанный на мощность не менее 2 Вт, чтобы обеспечить надежную работу устройства.
Зависимость сопротивления от температуры
Использование резисторов, как термометров, обусловлено почти линейной зависимостью их сопротивления от температуры. Это касается тех резисторов, у которых в качестве резистивного материала используется проволока или металл.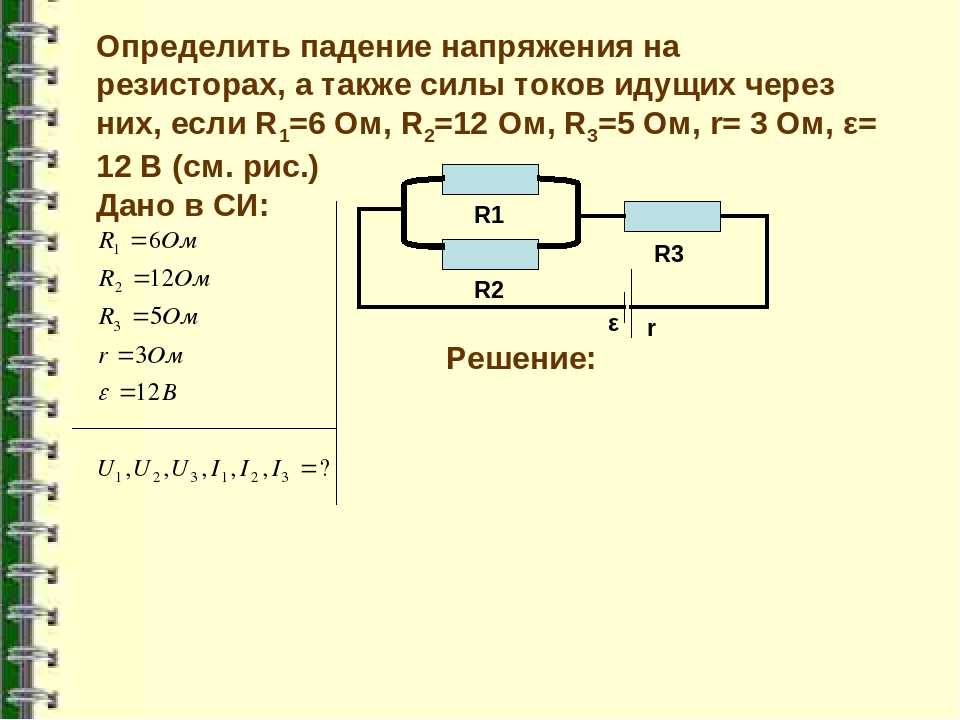 Формула зависимости:
Формула зависимости:
R = R0+α(t-t0),
- α – температурный коэффициент, К-1;
- R0 – сопротивление проводника при 00К;
- t0 – температура проводника при 00К.
Речь идёт о значении температуры в Кельвинах. При температурах, приближающихся к нулю по Кельвину (-273°С), у множества металлов при охлаждении R скачком падает до нулевой отметки. В этом случае можно говорить о сверхпроводимости.
Интересно. Металлы, имеющие хорошую проводимость при нормальной температуре, могут не быть сверхпроводниками при критической отметки этой физической величины. Сверхпроводники в нормальном состоянии имеют сопротивление большее, чем традиционные тоководы: медные, серебряные или золотые.
При нагревании проводников изменение сопротивления происходит в основном за счёт изменения его удельного значения и имеет линейную зависимость.
Применимость
Делитель напряжения подходит для получения необходимого заниженного напряжения в случаях, когда подключенная
нагрузка потребляет небольшой ток (доли или единицы миллиампер). Примером подходящего использования является
Примером подходящего использования является
считывание напряжения аналоговым входом микроконтроллера, управление базой/затвором транзистора.
Делитель не подходит для подачи напряжения на мощных потребителей вроде моторов или светодиодных лент.
Чем меньшие номиналы выбраны для делящих резисторов, тем больше энергии расходуется впустую и тем выше нагрузка
на сами резисторы. Чем номиналы больше, тем больше и дополнительное (нежелательное) падение напряжения, провоцируемое
самой нагрузкой.
Если потребление тока нагрузкой неравномерно во времени, Vout также будет неравномерным.
Параметры резисторного элемента
Внутреннее сопротивление – формула
При нанесении на схемы графического обозначения элемента сопротивления на нём указывается некоторые из его параметров.
Графическое обозначение резистора на схемах
К главным параметрам и элементарным характеристикам относятся:
- номинальное значение сопротивления;
- температурный коэффициент;
- максимальная рассеиваемая мощность;
- допустимое рабочее напряжение;
- коэффициент шума;
- относительное отклонение от номинала;
- устойчивость элемента к высокой температуре и влажности.

На чертежах и схемах резистор обозначается буквой R, с нанесением его порядкового номера.
Применение
Использование такой схемотехники на практике демонстрируют следующие примеры. Для расчетов электрических параметров без учета сопротивления нагрузки подойдут рассмотренные выше ручные и автоматизированные методики.
Потенциометры
Если резистор оснастить ползунком и соответствующим приводом, сопротивления можно будет менять плавно. Это решение позволяет точнее менять напряжения на выходе, по сравнению с дискретными схемами. Главный недостаток – усложнение конструкции, что, кроме удорожания, снижает надежность. Приходится обеспечивать герметичность рабочей зоны для исключения загрязнения и предотвращения коррозийных процессов.
Принципиальная схема потенциометра
Резистивные датчики
В этом варианте пользуются способностью некоторых материалов увеличивать/ уменьшать электрическое сопротивление под воздействием температуры, светового потока, других внешних воздействий. Созданный на основе этих принципов датчик устанавливают в плечо делителя. По уровню напряжения на выходе контролируют изменение соответствующих параметров.
Созданный на основе этих принципов датчик устанавливают в плечо делителя. По уровню напряжения на выходе контролируют изменение соответствующих параметров.
Цепи обратной связи в усилителях
Таким решением обеспечивают необходимый коэффициент усиления. На представленной ниже схеме этот параметр не будет никогда ниже единицы. Для повышения уровня преобразования увеличивают значение сопротивления R2 по отношению к R1.
Делитель напряжения в цепи обратной связи
Простейшие электрические фильтры
Для фильтрации заменяют конденсатором резисторы R1 или R2. В первом варианте устройство беспрепятственно пропускает высокочастотные составляющие. При снижении частоты до определенного уровня реактивное сопротивление увеличивается, препятствует прохождению тока. Аналогичным образом делают изменения в нижнем плече делителя с целью отсечения низких частот.
Усилитель напряжения
Переменным резистором изменяют уровень сигнала для получения необходимой громкости звучания. В таких устройствах применяют элементы с логарифмической характеристикой изменения сопротивления, что хорошо соответствует естественному механизму восприятия человеческими органами слуха.
В таких устройствах применяют элементы с логарифмической характеристикой изменения сопротивления, что хорошо соответствует естественному механизму восприятия человеческими органами слуха.
Параметрический стабилизатор напряжения
В таких схемах нижнее плечо делителя можно создать с применением стабилитрона. Его вольтамперные характеристики выбирают таким образом, чтобы выходное напряжение сохраняло нужное значение при изменении входных параметров.
Величина напряжения, обеспеченная резисторным элементом
Идеальный элемент, который превращает электричество в другой вид энергии, называют резистивным. Электроэнергия может преобразовываться в световую, тепловую или механическую виды. Величина напряжения на таком элементе зависит от разности потенциалов на концах резистора. Это значит, чем больше значение его сопротивления, тем больше значение напряжения на нём.
Изменение такой характеристики резистора, как сопротивление, позволяет реализовывать схематические решения в разных отраслях радиотехники и электроники.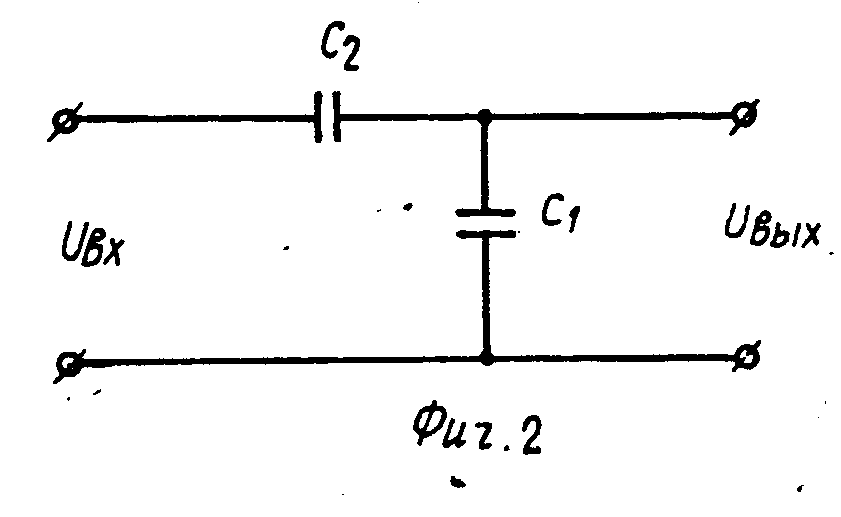 При выборе элементов следует учитывать удельное значение этой величины и изменение вольт-амперной характеристики при разных режимах работы.
При выборе элементов следует учитывать удельное значение этой величины и изменение вольт-амперной характеристики при разных режимах работы.
Резистивный делитель напряжения
В общем случае устройства этого типа выполняют преобразование по формуле Uвых=Uвх*К, где:
- Uвх (вых) – напряжения на входе и выходе, соответственно;
- К – корректирующий множитель, обозначающий передающие способности узла.
Если взять первый пример из рис. выше, для уточнения сути процессов подойдет второй закон Кирхгофа. В соответствии с этим правилом, общее значение напряжений на последовательно соединенных резисторах будет равно сумме ЭДС на каждом элементе. Так как ток не изменяется в замкнутом контуре, для расчета можно использовать закон Ома:
U (напряжение) = I (ток) * R (электрическое сопротивление)
Нижнюю часть схемы (плечо) используют для получения необходимого изменения входного параметра.
Удельное электрическое сопротивление
Удельное сопротивление представляет собой параметр, который определяет уровень препятствия движению электрического тока через проводник определенной длины. Зависит от параметра конкретного вещества, от длины. Для материала с однородными свойствами и известной величиной сопротивления и длиной проводника расчет удельного параметра идет по формуле ниже.
Зависит от параметра конкретного вещества, от длины. Для материала с однородными свойствами и известной величиной сопротивления и длиной проводника расчет удельного параметра идет по формуле ниже.
Расчет удельного объемного электрического сопротивления
Фактически смысл уравнение имеет следующий. Удельное сопротивление – величина сопротивления при прохождении через проводник определенной длины, с одинаковой площадью поперечного сечения на протяжении всего маршрута.
Параметр измеряется в Ом*метр. Таким образом, один Ом*метр равняется уровню препятствия направленному движению заряженных частиц через однородную проводящую среду с длиной в 100 см и площадью сечения в 1 квадратный метр.
Применение делителя для считывания показаний датчика
Другое применение делителя напряжения — это снятие показаний с датчиков. Существует множество
компонентов, которые меняют своё сопротивление в зависимости от внешних условий.
Так термисторы меняют сопротивление от нуля до определённого значения в зависимости
от температуры, фоторезисторы меняют сопротивление в зависимости от интенсивности попадающего
на них света и т.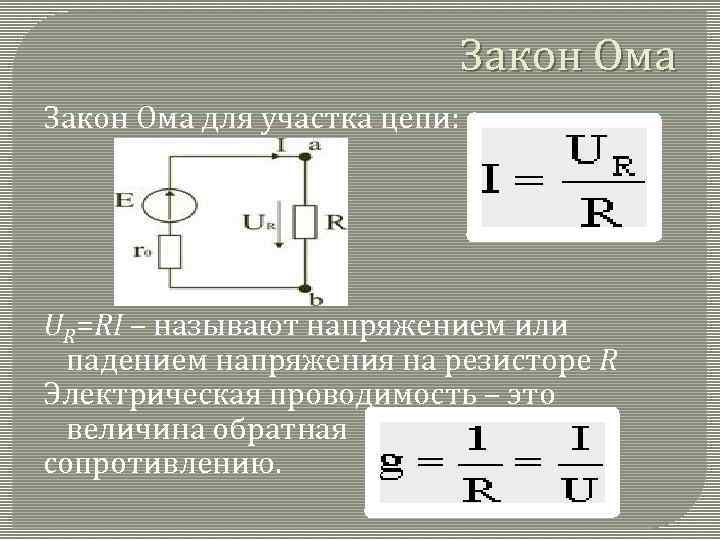 д.
д.
Если в приведённой выше схеме заменить R1 или R2 на один из таких
компонентов, Vout будет меняться в зависимости от внешних условий, влияющих
на датчик. Подключив это выходное напряжение к аналоговому входу Ардуино,
можно получать информацию о температуре, уровне освещённости и других параметрах среды.
Значение выходного напряжения при определённых параметрах среды можно расчитать, сопоставив документацию
на переменный компонент и общую формулу расчёта Vout.
Tags: автомат, ампер, бра, вид, вред, выбор, дом, е, как, конденсатор, контур, кт, монтаж, мощность, нагрузка, напряжение, номинал, переменный, потенциал, правило, принцип, провод, пуск, р, расчет, резистор, ряд, свет, светодиод, соединение, сопротивление, стабилизатор, стабилитрон, схема, тен, тип, ток, транзистор, ук, фильтр, фото, фоторезистор, эквивалентный, электричество, электронный
Калькулятор делителя напряжения на резисторах. Делитель напряжения на резисторах
Для того, чтобы получить из исходного напряжения лишь его часть используется делитель
напряжения (voltage divider). Это схема, строящаяся на основе пары резисторов .
Это схема, строящаяся на основе пары резисторов .
В примере, на вход подаются стандартные 9 В. Но какое напряжение получится на выходе V out ? Или эквивалентный вопрос: какое напряжение покажет вольтметр?
Ток, протекающий через R1 и R2 одинаков пока к выходу V out ничего не подключено. А суммарное сопротивление пары резисторов при последовательном соединении:
Таким образом, сила тока протекающая через резисторы
Теперь, когда нам известен ток в R2 , расчитаем напряжение вокруг него:
Или если отавить формулу в общем виде:
Так с помощью пары резисторов мы изменили значение входного напряжения с 9 до 5 В. Это простой способ получить несколько различных напряжений в одной схеме, оставив при этом только один источник питания.
Применение делителя для считывания показаний датчика
Другое применение делителя напряжения — это снятие показаний с датчиков. Существует множество
компонентов, которые меняют своё сопротивление в зависимости от внешних условий. Так термисторы меняют сопротивление от нуля до определённого значения в зависимости
от температуры, фоторезисторы меняют сопротивление в зависимости от интенсивности попадающего
на них света и т.д.
Так термисторы меняют сопротивление от нуля до определённого значения в зависимости
от температуры, фоторезисторы меняют сопротивление в зависимости от интенсивности попадающего
на них света и т.д.
Если в приведённой выше схеме заменить R1 или R2 на один из таких компонентов, V out будет меняться в зависимости от внешних условий, влияющих на датчик. Подключив это выходное напряжение к аналоговому входу Ардуино, можно получать информацию о температуре, уровне освещённости и других параметрах среды.
Значение выходного напряжения при определённых параметрах среды можно расчитать, сопоставив документацию на переменный компонент и общую формулу расчёта V out .
Подключение нагрузки
С делителем напряжения не всё так просто, когда к выходному подключения подключается какой-либо потребитель тока, который ещё называют нагрузкой (load):
В этом случае V out уже не может быть расчитано лишь на основе значений V in , R1 и R2 : сама нагрузка провоцирует дополнительное падение напряжения
(voltage drop). Пусть нагрузкой является нечто, что потребляет ток в 10 мА при предоставленных 5 В. Тогда
её сопротивление
Пусть нагрузкой является нечто, что потребляет ток в 10 мА при предоставленных 5 В. Тогда
её сопротивление
В случае с подключеной нагрузкой следует рассматривать нижнюю часть делителя, как два резистора соединённых параллельно:
Подставив значение в общую формулу расчёта V out , получим:
Как видно, мы потеряли более полутора вольт напряжения из-за подключения нагрузки. И тем ощутимее будут потери, чем больше номинал R2 по отношению к сопротивлению L . Чтобы нивелировать этот эффект мы могли бы использовать в качестве R1 и R2 резисторы, например, в 10 раз меньших номиналов.
Пропорция сохраняется, V out не меняется:
А потери уменьшатся:
Однако, у снижения сопротивления делящих резисторов есть обратная сторона медали. Большое количество энергии от
источника питания будет уходить в землю. В том числе при отсоединённой нагрузке. Это небольшая проблема, если
устройство питается от сети, но — нерациональное расточительство в случае питания от батарейки.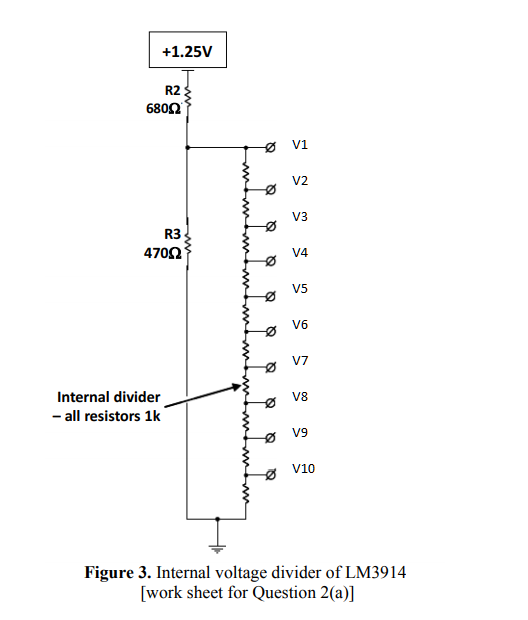
Кроме того, нужно помнить, что резисторы расчитаны на определённую предельную мощьность. В нашем случае нагрузка на R1 равна:
А это в 4-8 раз выше максимальной мощности самых распространённых резисторов! Попытка воспользоваться описанной схемой со сниженными номиналами и стандартными 0.25 или 0.5 Вт резисторами ничем хорошим не закончится. Очень вероятно, что результатом будет возгарание.
Применимость
Делитель напряжения подходит для получения необходимого заниженного напряжения в случаях, когда подключенная нагрузка потребляет небольшой ток (доли или единицы миллиампер). Примером подходящего использования является считывание напряжения аналоговым входом микроконтроллера, управление базой/затвором транзистора .
Делитель не подходит для подачи напряжения на мощных потребителей вроде моторов или светодиодных лент.
Чем меньшие номиналы выбраны для делящих резисторов, тем больше энергии расходуется впустую и тем выше нагрузка
на сами резисторы.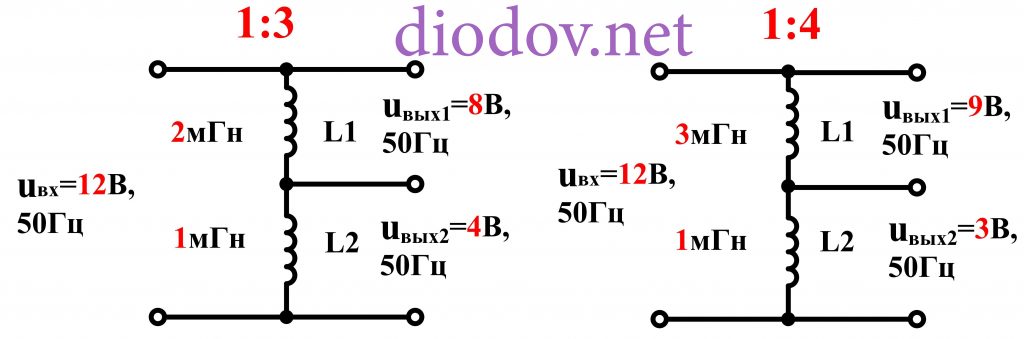 Чем номиналы больше, тем больше и дополнительное (нежелательное) падение напряжения, провоцируемое
самой нагрузкой.
Чем номиналы больше, тем больше и дополнительное (нежелательное) падение напряжения, провоцируемое
самой нагрузкой.
Если потребление тока нагрузкой неравномерно во времени, V out также будет неравномерным.
Как сделать делитель напряжения на резисторах? Часто в практике электронщика возникает необходимость снизить величину входного напряжения либо напряжение на отдельном участке цепи в строго определенной количество раз. Например, величина входного напряжения 50 В , а выходное напряжение нужно получить в 10 раз меньше, т. е. 5 В (рис. 1 ). Для этого используются делители напряжения.
Рис. 1 — Структурная схема делителя напряжения
Они бывают разных типов и выполняются на безе , катушек индуктивности (рис. 2 ). Однако мы рассмотрим только наиболее применяемые на практике делители напряжения.
Рис. 2 — Элементы, применяемые в качестве делителей напряжения
Наиболее простым делителем напряжения являются два последовательно соединенных резистора R1 и R2 , которые подключены к источнику напряжения U (рис. 3 ). Если сопротивление резисторов одинаковы R1 = R2 , то напряжение источника питания разделится поровну на них U1 = U2 = U/2 .
3 ). Если сопротивление резисторов одинаковы R1 = R2 , то напряжение источника питания разделится поровну на них U1 = U2 = U/2 .
Рис. 3 — Общая схема делителя напряжения на резисторах
Расчет делителя напряжения на резисторахДавайте разберемся как происходит деление напряжения. Для этого нам понадобится знание только закона Ома, который, если говорить очень обобщенно, звучит так: ток I , протекающий в цепи (или на ее участке), прямопропорционален приложенному напряжению U и обратнопропорционален сопротивлению цепи (или ее участка) R , т. е.
откуда
Также следует знать, что в последовательной цепи, т. е. в цепи, в которой все резисторы соединены последовательно, ток I протекает одной и той же величины через все резисторы, а общее сопротивление последовательно соединенных резисторов равно сумме сопротивлений всех резисторов Rобщ = R1+R2 .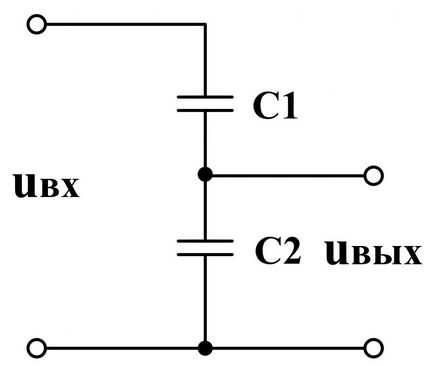
Теперь, на основании выше сказанного, давайте определим напряжения на резисторах в зависимости от величины их сопротивлений и напряжения источника питания.
Ток I , протекающий в цепи, равен отношению напряжения U к сумме сопротивлений R1+R2 , т. е.
Падение напряжения на первом резисторе равно
По аналогии находим падение напряжения на втором резисторе
Теперь в выражение (2) и (3) подставим значение тока из выражения (1), в результате получим
Делитель напряжения на резисторах. Различные номиналы резисторовС помощью полученных формул можно определить падение напряжения на резисторе, зная только величину входного напряжения и сопротивления самих резисторов. Однако такие формулы часто применимы лишь в теоретических расчётах. На практике же гораздо проще пользоваться основным свойством любого делителя напряжения, которое заключается в том, что при соответствующем подборе сопротивлений резисторов R1 и R2 выходное напряжение составляет часто входного (рис. 4 ).
4 ).
Рис. 4 — Схемы делителей напряжения на резисторах
Следует обратить внимание на то, что величина выходного напряжения зависит от относительного значения сопротивлений резисторов R1 и R2 , а не от абсолютного.
Рис. 5 — Схемы делителей напряжения с одинаковым коэффициентом деления при разных номиналах резисторов
Здесь возникает вопрос: какие же номиналы резисторов R1 и R2 применять, 3 кОм и 1 кОм или 30 кОм и 10 кОм ? Все зависит от конкретного случая. Однако есть рекомендация, которая исходит из закона Ома, чем меньше значение сопротивления R1 и R2 , тем больший ток будет протекать в цепи и тем большую мощность можно получить с выхода делителя напряжения, но нужно помнить, что эта мощность ограничивается мощностью источник питания и не может ее превысить.
Также делитель напряжения можно выполнять из нескольких последовательно соединенных резисторов (рис. 6 ).
Рис. 6 — Схема делителя напряжения с несколькими резисторами
И так, мы рассмотрели резисторный делитель напряжения с фиксированным значением выходного напряжения. Однако часто возникает необходимость в плавном изменении выходного напряжения. Например, при регулировании громкости звука мы плавно изменяем напряжение на усилителе.
Для плавного регулирования величины выходного напряжения применяются переменные и подстроечные резисторы (рис. 7 ).
Рис. 7 — Переменные и подстроечные резисторы
Переменный резистор еще называют потенциометром. Конструктивно он состоит из корпуса, имеющего три вывода, и рукоятки. При вращении ручки осуществляется скользящих контакт подвижной металлической пластины, которая замыкает две токопроводящие графитные дорожки, имеющие разную проводимость в зависимости от длины.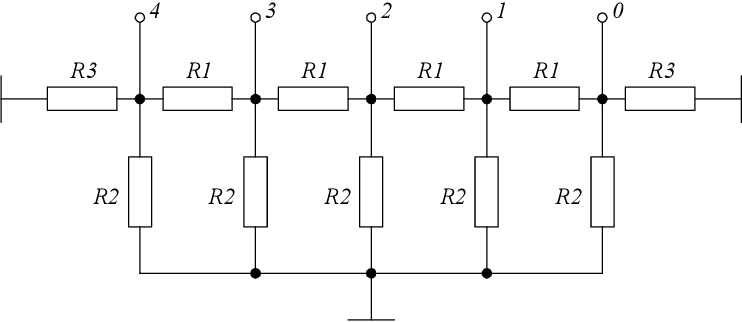 Благодаря этому изменяется сопротивление межу двумя, рядом расположенными, выводами. А сопротивление между двумя крайними выводами остается всегда неизменным.
Благодаря этому изменяется сопротивление межу двумя, рядом расположенными, выводами. А сопротивление между двумя крайними выводами остается всегда неизменным.
Схема подключения переменного резистора или же потенциометра приведена ниже (рис. 8 ). Два крайних вывода подключаются к источнику питания, а между средним и одним из крайних выводов снимается выходное напряжение, величину которого можно изменять от нуля до значения входного напряжения Uвых = 0…Uвх .
Рис. 8 — Схема включения переменного резистора для деления напряжения
Если, проворачивая ручку резистора, мы введем все сопротивление (как показано на схеме (рис. 9 )), то выходное напряжение будет равно входному Uвых = Uвх , так как подводимое напряжение будет полностью падать на сопротивлении резистора.
Если же вывести все сопротивление, то выходное напряжение будет равно нулю Uвых = 0 .
Рис. 9 — Схема плавного изменения напряжения
9 — Схема плавного изменения напряжения
В зависимости от степени относительного изменения сопротивления при вращении рукоятки переменного резистора их разделяют на три типа (рис. 10 ):
1) с линейной зависимостью;
2) с логарифмической зависимостью;
3) с экспоненциальной зависимостью.
Рис. 10 — Зависимости переменных резисторов
Переменные резисторы с логарифмической зависимостью часто используются для регулировки уровня звука, поскольку ухо человека воспринимает звук именно по такой зависимости.
Кроме того переменные резисторы бывают как одинарные, так и сдвоенные. Последние находят широкое применение в звуковой технике.
Делители напряжения на резисторах одинаково работают и рассчитываются как для постоянного, так и для переменного напряжения. Однако, в качестве делителей переменного напряжения также часто используются конденсаторы и реже – катушки индуктивности.
Делитель напряжения применяется, если нужно получить заданное напряжение при условии стабилизированного питания. Сейчас мы поговорим о постоянном токе и резисторных делителях. О делителях с использованием конденсаторов, диодов, стабилитронов, индуктивностей и других элементов будет отдельная статья. Подпишитесь на новости, чтобы ее не пропустить. В конце для примера расскажу, как сделать делитель напряжения для осциллографа, чтобы снимать осциллограммы высокого напряжения.
Резисторные делители также могут применяться для уменьшения в заданное количество раз сигналов сложной формы. На делителях напряжения с регулируемым коэффициентом ослабления строятся, например, регуляторы громкости.
Вашему вниманию подборка материалов: Схема традиционного резисторного делителя напряженияДля применения делителя напряжения нам надо уметь рассчитывать три величины: напряжение на выходе делителя, его эквивалентное выходное сопротивление, его входное сопротивление. Расчет резистивного делителя напряжения[Напряжение на выходе, В ] = [Напряжение питания, В ] * / ( + [Сопротивление резистора R2, Ом ]) Из этой формулы, в частности, видно, что резисторные (резистивные) делители выдают стабильное выходное напряжение, если напряжение питания фиксировано. = [Сопротивление резистора R1, Ом ] + [Сопротивление резистора R2, Ом ] Эта формула верна для ненагруженного делителя. Если делитель работает на нагрузку, то [Входное сопротивление делителя, Ом ] = [Сопротивление резистора R1, Ом ] + 1 / (1 / [Сопротивление резистора R2, Ом ] + 1 / [Сопротивление нагрузки, Ом ]) [Эквивалентное выходное сопротивление делителя, Ом ] = 1 / (1 / [Сопротивление резистора R1, Ом ] + 1 / [Сопротивление резистора R2, Ом ]) = [Сопротивление резистора R2, Ом ] / ([Сопротивление резистора R1, Ом ] + [Сопротивление резистора R2, Ом ]) [Действующее / мгновенное / амплитудное напряжение на выходе делителя, В ] = [Коэффициент ослабления сигнала ] * [Действующее / мгновенное / амплитудное напряжение на входе делителя, В ] Эта формула верна, если ток нагрузки делителя равен нулю. Пример — делитель для осциллографаЕсли мы хотим получить осциллограмму высокого напряжения, то сразу приходит в голову делитель напряжения. Изготавливаем делитель, подключаем его вход к источнику высоковольтного сигнала, а выход к входу осциллографа. Должны получить на входе осциллографа уменьшенную копию входного сигнала. Если наш сигнал имеет достаточно большую частоту или просто резкие фронты (например, меандр), то ничего не получится. Осциллограмма не будет похожа на изначальный сигнал. Причина в том, что осциллограф имеет некоторую входную емкость, которая образует с эквивалентным выходным сопротивлением делителя фильтр нижних частот. Все высшие гармоники сигнала подавляются. Кроме того этот фильтр формирует фазовый сдвиг. Это бывает существенным для многолучевых осциллографов, когда мы анализируем соотношения сигналов. Чтобы этого избежать, резистор R1 нужно зашунтировать конденсатором. Качество усилителей звуковой частоты. Обзор, схемы…. Как не спутать плюс и минус? Защита от переполярности. Описание… Бесперебойник своими руками. ИБП, UPS сделать самому. Синус, синусоида… Применение тиристоров (динисторов, тринисторов, симисторов). Схемы. Ис… Соединение светодиодов. Последовательное, параллельное включение оптоэ… Параллельное, последовательное соединение резисторов. Расчет сопротивл… |
Делитель напряжения на резисторах — это схема, позволяющая получить из высокого напряжения пониженное напряжение. Используя всего два резистора, мы можем создать любое выходное напряжение, составляющее меньшую часть от входного напряжения. Делитель напряжения является фундаментальной схемой в электронике и робототехнике. Для начала рассмотрим электрическую схему и формулу для расчета.
Используя всего два резистора, мы можем создать любое выходное напряжение, составляющее меньшую часть от входного напряжения. Делитель напряжения является фундаментальной схемой в электронике и робототехнике. Для начала рассмотрим электрическую схему и формулу для расчета.
Как работает делитель напряжения на резисторах
Для того, чтобы разобраться в принципе работы резисторного делителя напряжения и понять, как рассчитать делитель напряжения на резисторах, следует ознакомиться с его принципиальной схемой (см. картинку ниже — несколько вариантов изображения делителя). Схема включает в себя входное напряжение и два резистора.
Резистор, находящийся ближе к плюсу входного напряжения Vвх , обозначен R1 , резистор находящийся ближе к минусу обозначен R2 . Падение напряжения Vвых — это пониженное выходное напряжение, полученное в результате резисторного делителя напряжения. Для расчета выходного напряжения необходимо знать три величины из приведенной схемы — входное напряжение и сопротивление обоих резисторов.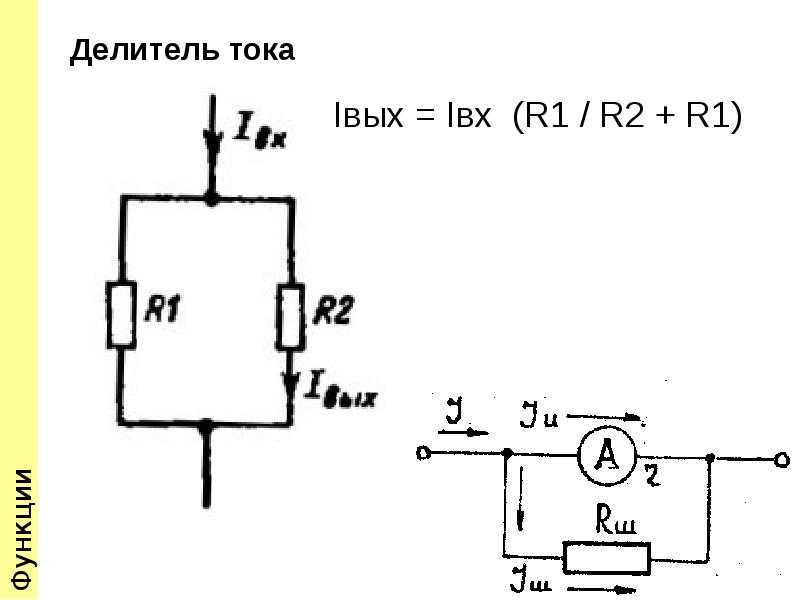
Расчет делителя напряжения на резисторах основан на законе Ома .
V вых = R2 х V вых / R1 + R2
Эта формула показывает, что выходное напряжение резисторного делителя прямо пропорционально входному напряжению и обратно пропорционально отношению сопротивлений R1 и R2. На этом принципе работают потенциометры (переменные резисторы) и многие резистивные датчики, например, датчик освещенности на фоторезисторе . Смотрите калькулятор делителя напряжения на резисторах онлайн.
КМБ: Делитель напряжения — Расчет делителя напряжения
Делитель напряжения позволяет получить меньшее напряжение из большего, напряжение может быть как постоянным, так и переменным.
Рис. 1. Схема простейшего делителя напряжения
Простейшая схема делителя напряжения содержит минимум два сопротивления. Если величины сопротивлений одинаковы, то согласно закону Ома, на выходе делителя будет получено напряжение, в два раза меньшее, чем на входе, так как падение напряжений на резисторах будет одинаковым. Для других случаев величина падения напряжений на резисторах делителя определяется по формулам
Для других случаев величина падения напряжений на резисторах делителя определяется по формулам
UR1 = I*R1; UR2 = I*R2 (1)
где UR1, UR2 — падения напряжения на резисторах R1 и R2 соответственно, I — ток в цепи. В схемах делителей выходное напряжение обычно снимают с нижнего по схеме резистора.
Сумма падений напряжений UR1, UR2 на резисторах равна напряжению источника питания. Ток в цепи будет равен напряжению источника питания, делённому на сумму сопротивлений резисторов R1 и R2:
I = Uпит / (R1 + R2) (2)
Рассмотрим практическую схему делителя постоянного напряжения (рис.2)
Рис. 2. Делитель постоянного напряжения.
Ток, протекающий в этой схеме, согласно формуле (2) будет равен
I = 10 / (10000+40000) = 0,0002 А = 0,2 мА.
Тогда согласно формуле (1) падение напряжения на резисторах делителя напряжения будет равно:
UR1 = 0,0002*10000 = 2 В;
UR2 = 0,0002*40000 = 8 В.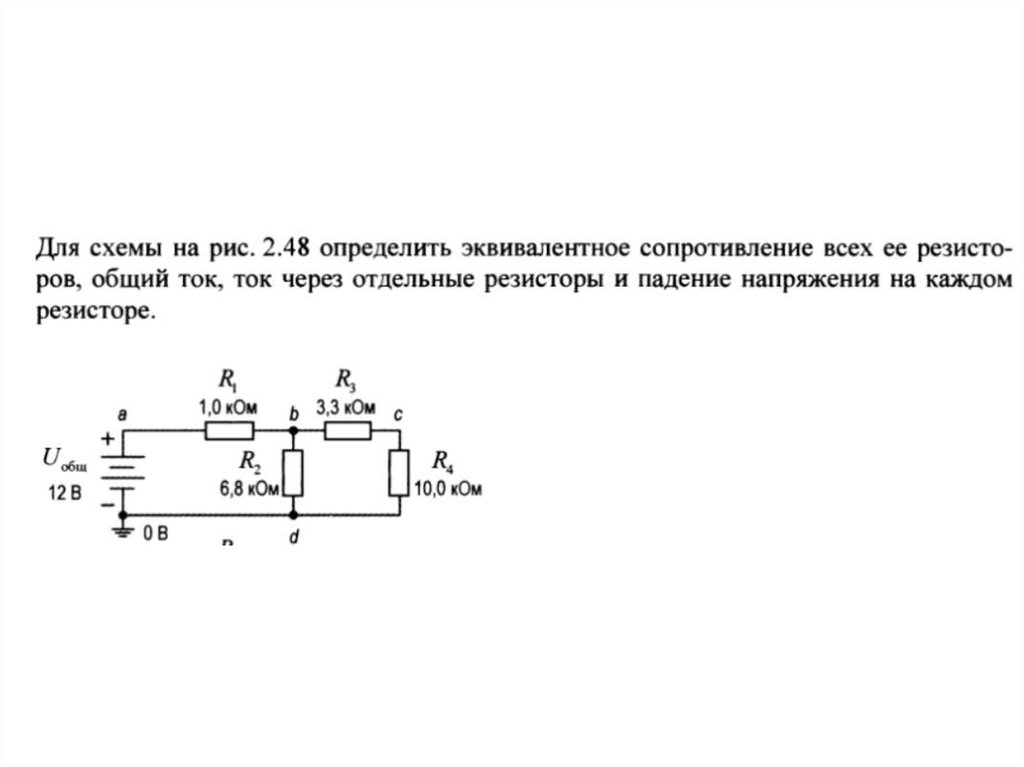
Если из формулы (1) вывести ток:
I = UR1 / R1 (3)
И подставить его значение в формулу (2), то получится универсальная формула для расчёта делителя напряжения:
UR1 / R1 = Uпит / (R1 + R2)
Откуда
UR1 = Uпит * R1 / (R1 + R2) (4)
Подставляя значения напряжения и сопротивлений в формулу (4), получим величину напряжения на резисторе R1:
UR1 = 10 * 10000 / (10000+40000) = 2 В,
и на резисторе R2:
UR2 = 10 * 40000 / (10000+40000) = 8 В.
В вышеприведённой схеме делителя напряжения (рис. 2) были использованы активные элементы — резисторы, и питание схемы осуществлялось постоянным напряжением (хотя схему можно питать и переменным током). Делитель напряжения может содержать так же и реактивные компоненты (конденсаторы, катушки индуктивности), но в этом случае для нормальной работы потребуется питание синусоидальным током (рис.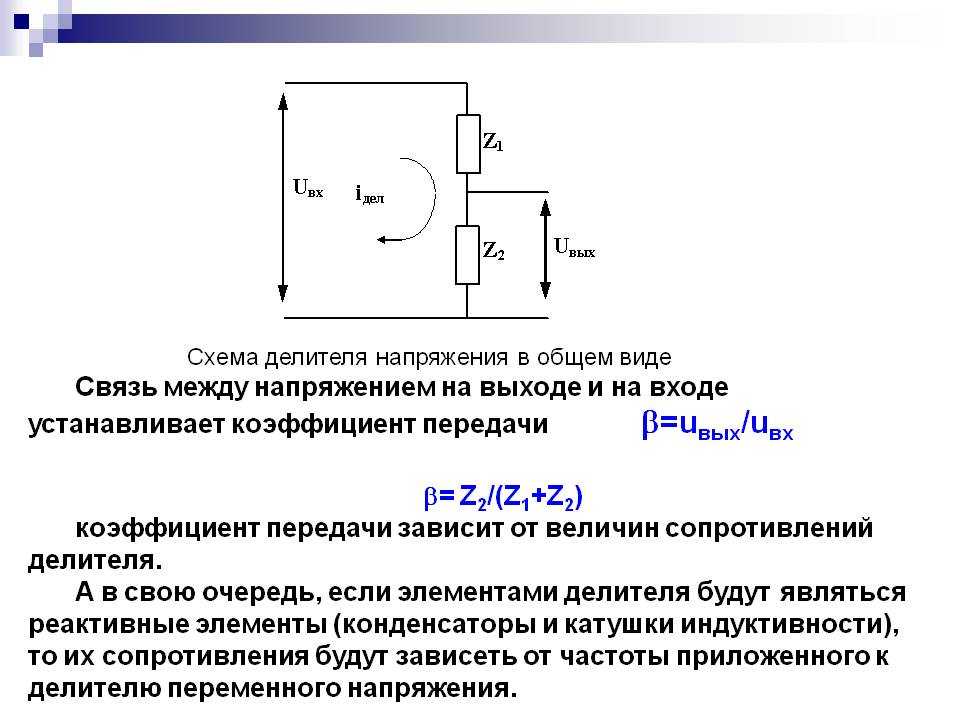 3).
3).
Рис. 3. Ёмкостный делитель напряжения в цепи переменного тока.
Изображённый на рисунке 3 ёмкостный делитель напряжения работает аналогично резистивному делителю, но рассчитывается несколько иначе, поскольку реактивное сопротивление конденсаторов обратно пропорционально их ёмкости:
Rc = 1/(2 * π * f * C)
Здесь Rc — реактивное сопротивление конденсатора;
π — число Пи = 3,14159…;
f — частота синусоидального напряжения, Гц;
C — ёмкость конденсатора, Фарад.
То есть чем больше ёмкость конденсатора, тем меньше его сопротивление, и следовательно в схеме делителя напряжения на конденсаторе с большей ёмкостью падение напряжения будет меньше, чем на конденсаторе с меньшей ёмкостью. Следовательно, формула (4) для ёмкостного делителя напряжения примет следующий вид:
UС1 = Uпит * С2 / (С1 + С2) (5)
UС1 = 10 * 40*10-9 / (10*10-9+40*10-9) = 8 В,
UС2 = 10 * 10*10-9 / (10*10-9+40*10-9) = 2 В.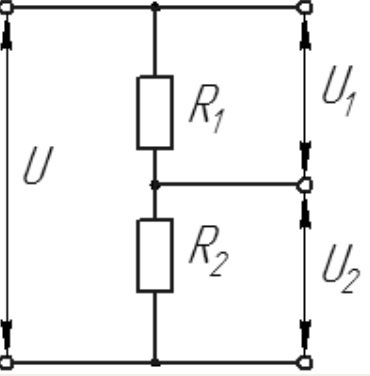
Индуктивный делитель напряжения (рис. 4.) так же как и ёмкостный требует для своей работы синусоидальное питающее напряжение.
Рис. 4. Индуктивный делитель напряжения в цепи переменного тока.
Поскольку реактивное сопротивление катушки индуктивности в цепи переменного тока пропорционально номиналу катушки:
RL = 2 * π * f * L
Здесь Rc — реактивное сопротивление катушки индуктивности;
π — число Пи = 3,14159…;
f — частота синусоидального напряжения, Гц;
L — индуктивность катушки, Генри.
То следовательно и формула для расчёта индуктивного делителя напряжения будет точно такой же, как и формула для расчёта резистивного делителя напряжения (4), где вместо сопротивлений будут использоваться индуктивности:
UL1 = Uпит * L1 / (L1 + L2) (6)
Подставив в эту формулу параметры элементов из рисунка 4, получим:
UL1 = 10 * 10*10-6 / (10*10-6+40*10-6) = 2 В,
UL2 = 10 * 40*10-6 / (10*10-6+40*10-6) = 8 В.
В заключении следует отметить, что во всех расчётах величина нагрузки была принята равной бесконечности, поэтому полученные значения верны при работе рассмотренных делителей на сопротивление нагрузки, во много раз большее, чем величина собственных сопротивлений.
Повышаем точность регулирования выходного напряжения источника питания с помощью инструмента для расчета резистивного делителя в программе LTpowerCAD
22 декабря 2021
универсальное применениеAnalog DevicesстатьяLDODC-DCСАПРрезистивный делитель
Хосе Рамон Сан Буэнавентура, Генри Чжан (Analog Devices)
Как выбрать компоненты для источника питания с правильными допусками? Для этого специалисты Analog Devices рекомендуют использовать инструмент для расчета резистивного делителя, интегрированный в программу LTpowerCAD. Он позволяет оценить ошибки в выходном напряжении при неверно выбранном допуске.
Блоки питания можно встретить практически в любой схеме.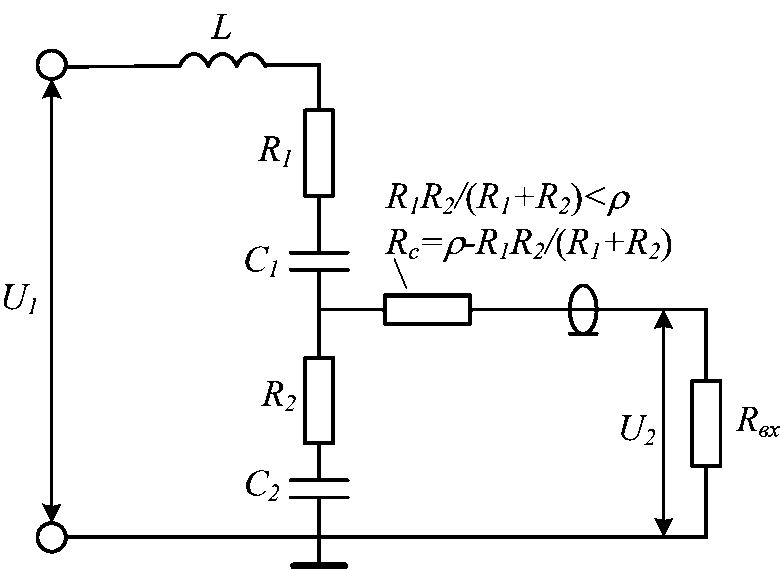 Наличие в схеме радиоприемопередатчиков, микропроцессоров, ПЛИС и усилителей – это гарантия того, что где-то есть блок питания. Он является важной частью любой аналоговой или цифровой схемы.
Наличие в схеме радиоприемопередатчиков, микропроцессоров, ПЛИС и усилителей – это гарантия того, что где-то есть блок питания. Он является важной частью любой аналоговой или цифровой схемы.
Как и любой другой компонент, преобразователи питания бывают разных размеров и форм. Различные архитектуры, такие как линейные регуляторы или импульсные DC/DC-преобразователи, имеют свои преимущества и недостатки в зависимости от применения. Но все эти архитектуры объединяет то, что выходной сигнал зачастую устанавливается комбинацией внешних компонентов, чаще всего – резистивным делителем.
С помощью инструментов моделирования источник питания может быть спроектирован в соответствии с необходимыми спецификациями и рассчитан с соответствующими им значениями компонентов. Несмотря на то, что результаты моделирования могут выглядеть многообещающе, в реальных условиях существуют некоторые ограничения. Одним из распространенных примеров таких ограничений может быть допуск компонентов. В действительности реальные значения таких компонентов, как резисторы или конденсаторы, могут отличаться от заявленных, и именно допуск описывает это отклонение.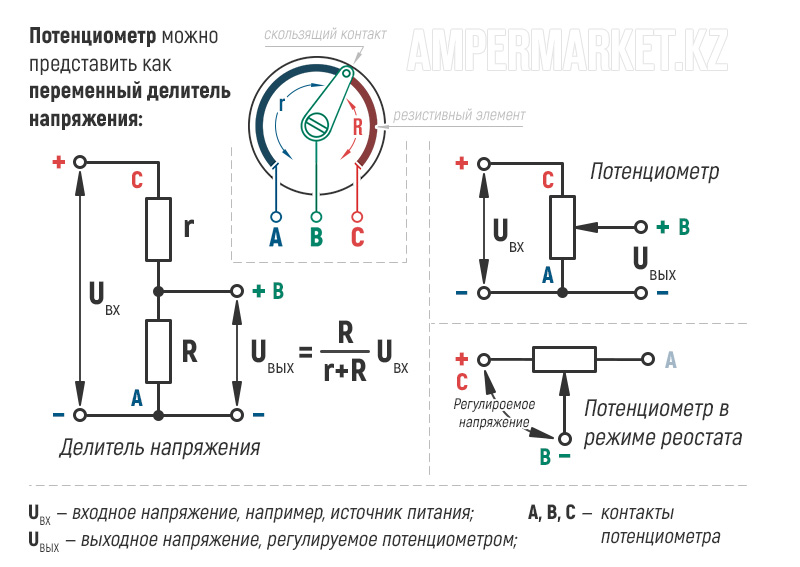 Смоделированная комбинация резисторов 57 кОм и 23 кОм для получения напряжения 5 В будет отличаться от реальной комбинации 57 кОм и 23 кОм, так как компоненты имеют допуск. Помимо погрешности самого преобразователя, точность выходного напряжения также зависит от этого допуска.
Смоделированная комбинация резисторов 57 кОм и 23 кОм для получения напряжения 5 В будет отличаться от реальной комбинации 57 кОм и 23 кОм, так как компоненты имеют допуск. Помимо погрешности самого преобразователя, точность выходного напряжения также зависит от этого допуска.
Расчет выходного напряжения преобразователя
Многие микросхемы преобразователей напряжения Analog Devices имеют вывод обратной связи (вывод FB или ADJ). Таким образом, выходное напряжение можно установить с помощью пары внешних резисторов RTOP и RBOT, где RTOP подключается к контактам VOUT и FB, а RBOT соединяет контакт FB с нулем.
Обычно стандартное уравнение (1) в даташите имеет вид:
$$V_{OUT}=V_{REF}\times \left(1+\frac{R_{TOP}}{R_{BOT}} \right),\qquad{\mathrm{(}}{1}{\mathrm{)}}$$
где VREF – внутреннее опорное напряжение. В качестве примера возьмем формулу выходного напряжения линейного регулятора LT3062.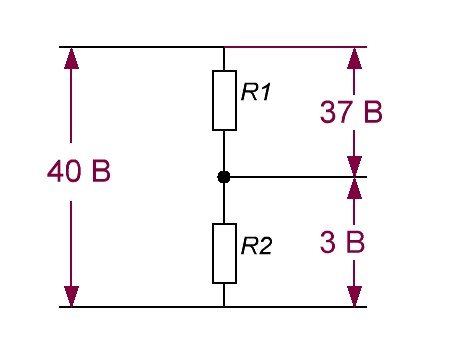 На рисунке 1 показано его расчетное выходное напряжение.
На рисунке 1 показано его расчетное выходное напряжение.
Рис. 1. Выходное напряжение для LT3062
При внутреннем, предполагаемо точном, генерируемом опорном напряжении (VREF = 0,6В LT3062) цень обратной связи делителя выходного напряжения (R1 и R2) определяет уровень напряжения, который регулирует микросхема (таблица 1). В уравнении для LT3062 есть дополнительный член IADJ, непреднамеренный ток смещения, протекающий из вывода ADJ. Его типовое значение составляет 15 нА, но может достигать 60 нА, как показано в таблице электрических параметров (ЕС), и это может вызвать дополнительную ошибку регулирования VOUT.
Таблица 1. LT3062: комбинации R1 и R2 для общих уровней выходного напряжения
| VOUT (В) | R1 (кОм) | R2 (кОм) |
|---|---|---|
| 1,2 | 118 | 118 |
| 1,5 | 121 | 182 |
| 1,8 | 124 | 249 |
| 2,5 | 115 | 365 |
| 3 | 124 | 499 |
| 3,3 | 124 | 562 |
| 5 | 115 | 845 |
| 12 | 124 | 2370 |
| 15 | 124 | 3010 |
Если используются резисторы R1 и R2 с допуском в 1%, то какова общая погрешность Vo, вызванная резистивным делителем – 1 или 2%? Следует ли использовать резисторы 0,5% или 0,1% для данного применения? Могут потребоваться определенные уровни точности выходного напряжения, и выбор правильных резисторов играет ключевую роль. Возможно, вы не захотите использовать резисторы с очень низким допуском (они могут стоить значительно дороже менее точных компонентов), если целевая ошибка может быть достигнута с помощью резистора с более высоким допуском.
Возможно, вы не захотите использовать резисторы с очень низким допуском (они могут стоить значительно дороже менее точных компонентов), если целевая ошибка может быть достигнута с помощью резистора с более высоким допуском.
Инструмент для расчета резистивного делителя в программе LTpowerCAD
Для облегчения проектирования можно использовать инструмент для расчета резистивного делителя в программе LTpowerCAD® (рисунок 2). LTpowerCAD – это программа проектирования источников питания, снабженная набором инструментов для проектирования, включая инструмент для проектирования резисторных делителей. Инструмент для расчета резисторного делителя учитывает такие входные данные, как желаемый уровень выходного напряжения VOUT и опорное напряжение регулятора VREF (напряжение на выводе ADJ или FB), а затем, в зависимости от выбранного допуска, рекомендует имеющиеся в стандартном ряду значения резисторов для достижения желаемого напряжения (рисунки 3…6).
С помощью этого инструмента оцениваются две ошибки:
1) Ошибка, вызванная стандартными дискретными значениями стандартного резистора.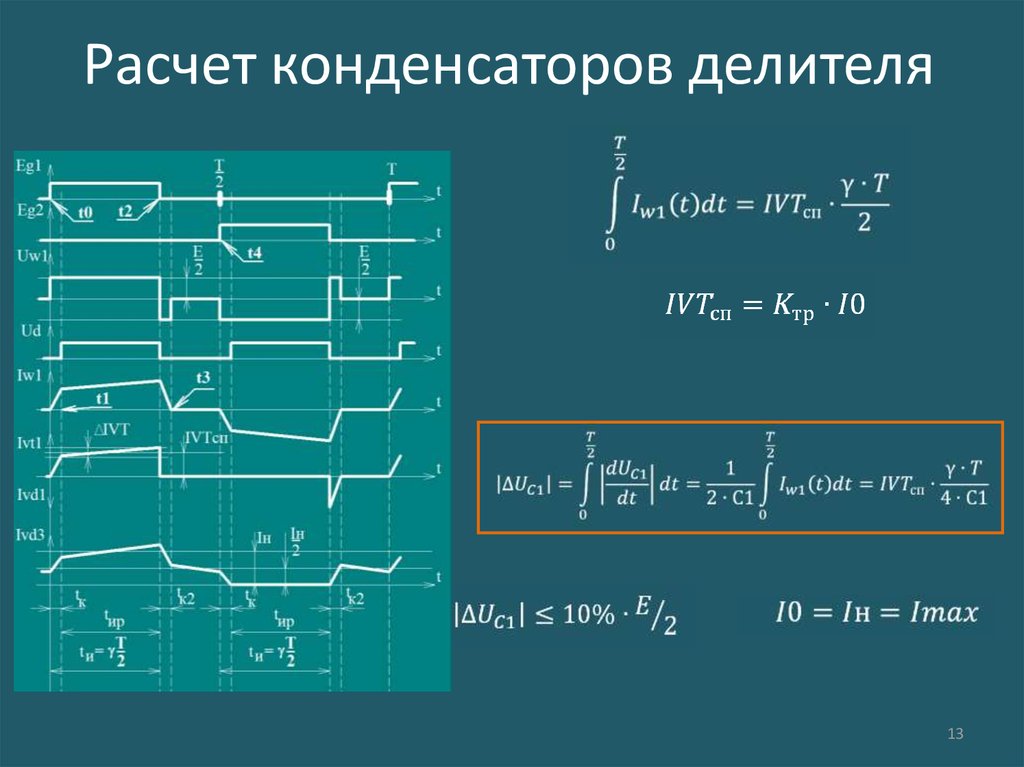 Примечание: для заданных значений VOUT и VREF инструмент автоматически выбирает наиболее подходящую пару значений стандартных резисторов, чтобы минимизировать эту ошибку, поэтому фактическое значение VOUT наиболее близко к целевому значению.
Примечание: для заданных значений VOUT и VREF инструмент автоматически выбирает наиболее подходящую пару значений стандартных резисторов, чтобы минимизировать эту ошибку, поэтому фактическое значение VOUT наиболее близко к целевому значению.
2) Ошибка, вызванная допуском резистора для данной комбинации VOUT и VREF. Фактически, с парой резисторов с точностью до 1% в делителе эффективный допуск делителя становится функцией коэффициента делителя в диапазоне от 1% до 2%. Инструмент для расчета резистивного делителя в программе LTpowerCAD суммирует эти две ошибки для получения общего допуска R-делителя. Это позволяет инженеру увидеть общую ошибку и решить, какой уровень допуска резистора (0,1%, 0,5%, 1% или 2%) будет необходим для достижения конечной цели.
Рис. 2. Откройте инструмент для расчета резистивного делителя на панели инструментов LTpowerCAD
Данный инструмент имеет дополнительную возможность ввода пользовательских значений верхнего или нижнего резистора, при этом также учитывая целевой или допустимый допуск компонентов.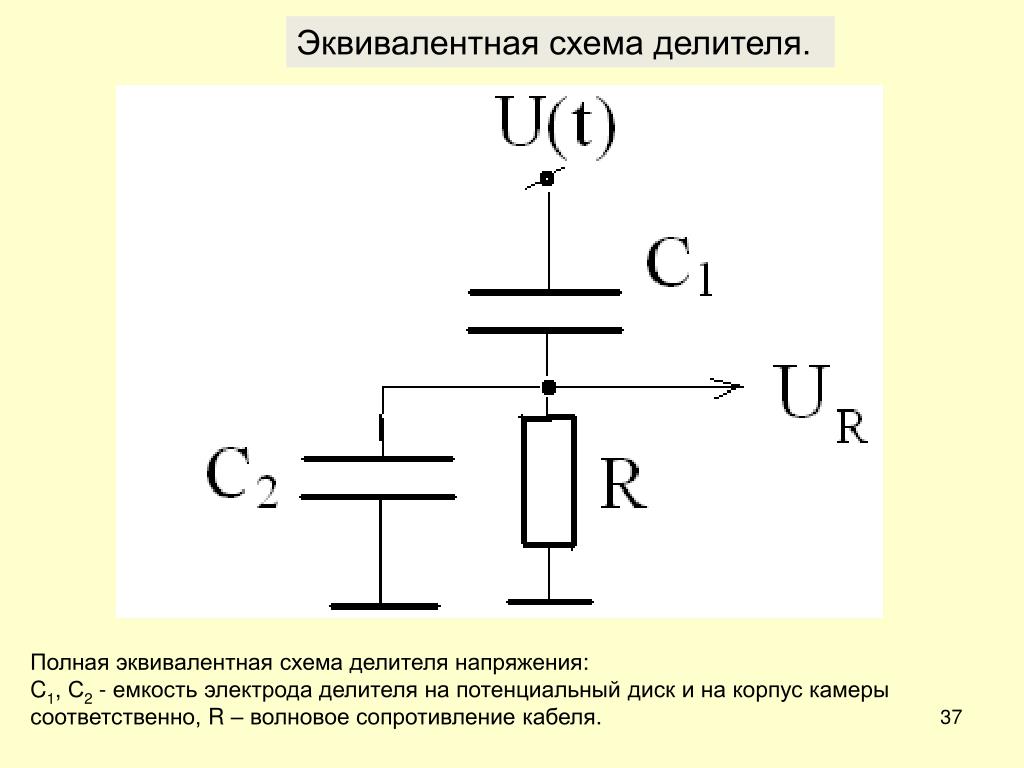 Помимо рекомендаций по номиналу резистора, данный инструмент также показывает расчеты ошибок, связанных с допуском компонентов по отношению к идеальному и фактическому VOUT. С помощью этих параметров разработчики могут получить представление об ожидаемом диапазоне напряжений с учетом выбранных допусков компонентов и оценить, подходит ли он для целевого приложения. И, наконец, этот инструмент также имеет функцию поиска резисторов стандартного номинала для любого заданного значения, что упрощает поиск компонентов.
Помимо рекомендаций по номиналу резистора, данный инструмент также показывает расчеты ошибок, связанных с допуском компонентов по отношению к идеальному и фактическому VOUT. С помощью этих параметров разработчики могут получить представление об ожидаемом диапазоне напряжений с учетом выбранных допусков компонентов и оценить, подходит ли он для целевого приложения. И, наконец, этот инструмент также имеет функцию поиска резисторов стандартного номинала для любого заданного значения, что упрощает поиск компонентов.
Дополнительные ошибки и компенсация
Следует отметить, что инструмент для расчета резистивного делителя оценивает только ошибку постоянного тока резисторного делителя. Он не включает другие ошибки постоянного тока, которые должны быть добавлены к ошибке резисторного делителя для общей точности регулирования VOUT источника питания.
Эти дополнительные ошибки включают:
1) ошибку VREF внутреннего опорного напряжения преобразователя, которая обычно находится в диапазоне от 0,5% до 1,5% и может быть найдена в таблице данных в даташите;
2) ошибки регулирования линии питания и нагрузки, которые также можно найти в даташите;
3) ошибку тока утечки вывода ADJ или FB, как в примере LT3062, при выборе более низкого значения RBOT из-за желания уменьшить значение этой ошибки;
4) дополнительные ошибки, вызванные сопротивлением проводников на печатной плате между преобразователем и удаленной нагрузкой и т.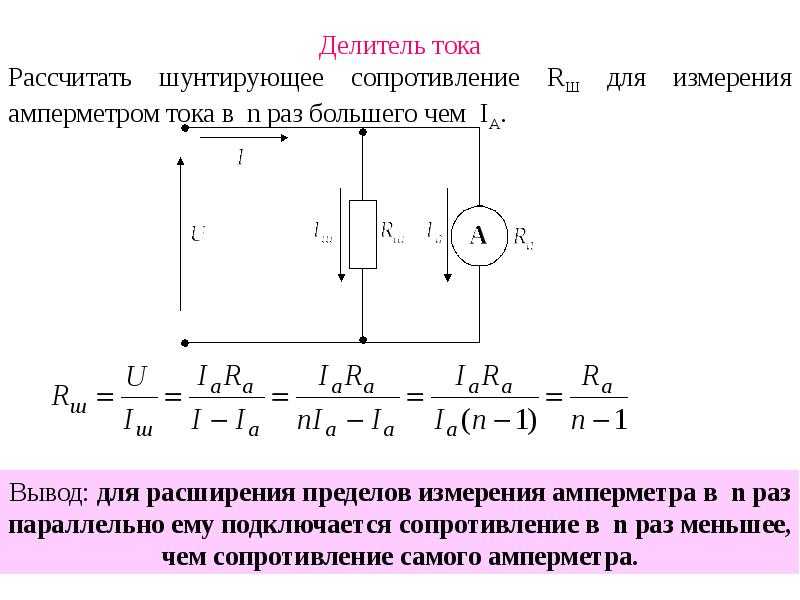 д. Все эти ошибки следует учитывать для оценки общей ошибки при проектировании источника питания.
д. Все эти ошибки следует учитывать для оценки общей ошибки при проектировании источника питания.
Кроме того, высокоточная электронная система может также иметь строгие требования к общему допуску выходного напряжения питания, включая ошибку постоянного тока и пульсации переменного тока. Например, для многих сильноточных ASIC и FPGA требуется окно общего допуска ± 2% или ± 3%, включая ошибку постоянного тока и пульсации переменного тока. Чтобы соответствовать этому строгому требованию, источник питания должен быть спроектирован с быстрой переходной характеристикой, а также иметь большие выходные конденсаторы, чтобы минимизировать пульсации VOUT во время быстрых переходных процессов при изменении нагрузки. В этом случае очень важно выбрать ИС с жестким допуском VREF. Для сильноточных шин желателен регулятор с дистанционным измерением напряжения. Кроме того, экономия места и стоимости выходных конденсаторов будет намного больше, чем небольшое увеличение стоимости при использовании резистора на 0,5% или даже 0,1%. Также полезно использовать высоко интегрированные модули, такие как μModule® серии ADI LTM, которые определяют общий допуск регулирования выходного напряжения (включая VREF, ошибки при изменении входного напряжения и нагрузки) для проектирования высокопроизводительных источников питания.
Также полезно использовать высоко интегрированные модули, такие как μModule® серии ADI LTM, которые определяют общий допуск регулирования выходного напряжения (включая VREF, ошибки при изменении входного напряжения и нагрузки) для проектирования высокопроизводительных источников питания.
Рис. 3. Инструмент для расчета резистивного делителя в программе LTpowerCAD: рекомендации по подбору резисторов
Рис. 4. Инструмент для расчета резистивного делителя в программе LTpowerCAD: выбор RTOP и RBOT
Рис. 5. Инструмент для расчета резистивного делителя в программе LTpowerCAD: расчет ошибки
Рис. 6. Инструмент для расчета резистивного делителя в программе LTpowerCAD: стандартный измеритель сопротивления
Заключение
В зависимости от целевого применения требуются определенные уровни допуска VOUT у источника питания. Погрешность в несколько милливольт может быть решающим аспектом в различных системах, поэтому необходимо учитывать соответствующие конструктивные особенности.
Одним из внешних и контролируемых факторов точности регулятора является допуск компонентов. Разница между резисторами с допуском 0,5% и допуском 2% может существенно повлиять на производительность вашей системы, а выбор правильных компонентов снижает вероятность ошибок. Выбор правильных компонентов также помогает минимизировать затраты и повысить надежность, поскольку необходимость в замене компонентов будет минимизирована или вовсе исключена.
Используя инструмент для расчета резистивного делителя программы LTpowerCAD, инженеры могут заметить влияние допусков компонентов на конструкцию своих источников питания. Первоначально выбирая целевое выходное напряжение и опорное напряжение на выводах, разработчики могут: (1) получить наиболее подходящую пару резисторов из стандартного ряда для заданного выходного напряжения, (2) получить значения верхнего и нижнего резисторов и (3) достичь желаемого диапазона погрешности напряжения, учитывая допуски компонентов в резистивном делителе.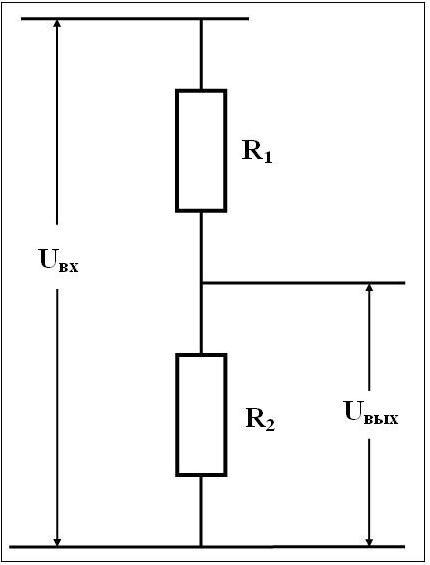
Благодаря данным возможностям, а также стандартному поиску резисторов, инструмент для расчета резистивного делителя является полезным при проектировании источников питания. особенно – начинающим инженерам, которые только осваивают проектирование блоков питания. Используя этот инструмент, инженер может спроектировать источники питания, соответствующие спецификациям, необходимым для предполагаемого применения, и обеспечить оптимальную производительность и мощность, подаваемую на различные системные блоки.
Оригинал статьи
Перевел Антон Хомяков по заказу АО Компэл
•••
Лабораторная на тему Исследование резистивного делителя напряжения
Цены в 2-3 раза ниже
Мы работаем
7 дней в неделю
Только проверенные эксперты
Готовые работы / Лабораторные работы / Электроника / Исследование резистивного делителя напряжения
Что найти?
Лабораторная работа №2
- Исследование резистивного делителя напряжения.

Произведем расчет тока и напряжений резистивного делителя рис 1. Полученные данные сведем в таблицу 1. Проведем моделирование схемы рис. 1, полученные данные сведем в таблицу 1.
Похожие работы
Разработка приложения калькулятор
Лабораторная, Электроника
Смотреть
Изучение ключевого режима работы биполярного транзистора
Лабораторная, Электроника
Смотреть
Реализовать заданную логическую функцию на трёх языках программирования
Лабораторная, Электроника
Смотреть
Исследование схемы регулирования напряжения фазовым способом, выполненной на триодном тиристоре
Лабораторная, Электроника
Смотреть
Исследование выпрямительного полупроводникового диода
Лабораторная, Электроника
Смотреть
Сделайте индивидуальный заказ на нашем сервисе. Там эксперты помогают с учебой без посредников Разместите задание – сайт бесплатно отправит его исполнителя, и они предложат цены.
Там эксперты помогают с учебой без посредников Разместите задание – сайт бесплатно отправит его исполнителя, и они предложат цены.
1 000 +
Новых работ ежедневно
Работы выполняют эксперты в своём деле. Они ценят свою репутацию, поэтому результат выполненной работы гарантирован
107034
рейтинг
2640
работ сдано
1205
отзывов
99331
рейтинг
5204
работ сдано
2334
отзывов
72211
рейтинг
1838
работ сдано
1158
отзывов
62710
рейтинг
1046
работ сдано
598
отзывов
Тип работыВыберите тип работыКонтрольнаяРешение задачКурсоваяРефератОнлайн-помощьТест дистанционноЛабораторнаяЧертежЭссеОтветы на билетыПеревод с ин. языкаДокладСтатьяБизнес-планПодбор литературыШпаргалкаПоиск информацииРецензияДругое
Владислав
Тюменский Индустриальный Университет
Всё отлично, исполнитель знает своё дело, выполнила лабораторную на 10 из 10, без замечани. ..
..
Александра
Финансовый университет при правительстве РФ
Хороший исполнитель, все детали задания были уточнены заранее, и все сделано в лучшем виде
Даниил
ПГГПУ
Второй раз обращался к данному исполнителю, был уверен, что мне смогут помочь вовремя и не…
Всё отлично, исполнитель знает своё дело, выполнила лабораторную на 10 из 10, без замечаний и досрочно, рекомендую!
Владислав
Тюменский Индустриальный Университет
Хороший исполнитель, все детали задания были уточнены заранее, и все сделано в лучшем виде
Александра
Финансовый университет при правительстве РФ
Второй раз обращался к данному исполнителю, был уверен, что мне смогут помочь вовремя и не ошибся. Если горят сроки сдачи, можете смело обращаться!
Даниил
ПГГПУ
Ежедневно эксперты готовы работать над 1000 заданиями. Контролируйте процесс написания работы в режиме онлайн
1 минуту назад
4 минуты назад
7 минут назад
8 минут назад
8 минут назад
9 минут назад
10 минут назад
11 минут назад
11 минут назад
11 минут назад
11 минут назад
11 минут назад
11 минут назад
11 минут назад
11 минут назад
11 минут назад
11 минут назад
11 минут назад
Закажи индивидуальную работу за 1 минуту!
Размещенные на сайт контрольные, курсовые и иные категории работ (далее — Работы) и их содержимое предназначены исключительно для ознакомления, без целей коммерческого использования.
 Все права в отношении Работ и их содержимого принадлежат их законным правообладателям. Любое их использование возможно лишь с согласия законных правообладателей. Администрация сайта не несет ответственности за возможный вред и/или убытки, возникшие в связи с использованием Работ и их содержимого.Основы схемы
Все права в отношении Работ и их содержимого принадлежат их законным правообладателям. Любое их использование возможно лишь с согласия законных правообладателей. Администрация сайта не несет ответственности за возможный вред и/или убытки, возникшие в связи с использованием Работ и их содержимого.Основы схемы— Цепь делителя напряжения — NightShade Electronics
NightShade Electronics будет ЗАКРЫТ с 21 по 27 сентября. Все заказы, размещенные в этот период, будут отправлены 28 числа.
ЗАКРЫТО 21–27 сентября: Заказы, размещенные в это время, будут отправлены 28 сентября.
перейти к содержаниюСоздано
Последнее обновление
АвторAaron Liebold
Печать
- Основная часть
- Учебники по электронике
- Основы схемотехники
- Основы схемотехники — схема делителя напряжения
< Все темы
Схема делителя напряжения — это пассивная схема, которая снижает напряжение до части исходного напряжения. Эта схема обычно используется в регуляторах напряжения и при считывании высокого напряжения с помощью низковольтных устройств (например, при измерении напряжения на солнечной панели с помощью микроконтроллера).
Эта схема обычно используется в регуляторах напряжения и при считывании высокого напряжения с помощью низковольтных устройств (например, при измерении напряжения на солнечной панели с помощью микроконтроллера).
Как использовать схему делителя напряжения?
При использовании схемы делителя напряжения необходимо обращать внимание на соотношение двух резисторов и величину тока, протекающего через цепь.
Отношение сопротивлений R1 и R2 определяет соотношение между Vin и Vout. Это соотношение определяется следующим уравнением:
\(\Large \frac{R_1}{R2} = \frac{V_{in}}{V_{out}} – 1 \)
Теперь, зная свой Vin и Vout, вы можете рассчитать коэффициент сопротивления, который вам нужен. Затем вы можете выбрать одно сопротивление произвольно и рассчитать другое, или вы можете использовать нашу страницу калькулятора резисторов, чтобы найти лучшую пару резисторов для создания вашего коэффициента.
При использовании схемы делителя напряжения необходимо обращать внимание на то, какой ток вытекает из Vout. Уравнение резисторного делителя предполагает, что через резисторы R1 и R2 протекает один и тот же ток. Любой ток, который покидает цепь через Vout, сделает соотношение менее точным. Общее эмпирическое правило, используемое для решения этой проблемы, заключается в том, что ток, протекающий через R1 и R2, должен как минимум в 100 раз превышать величину тока, протекающего через Vout. Мы можем найти ток, протекающий через R1 и R2, с помощью этого уравнения:
Уравнение резисторного делителя предполагает, что через резисторы R1 и R2 протекает один и тот же ток. Любой ток, который покидает цепь через Vout, сделает соотношение менее точным. Общее эмпирическое правило, используемое для решения этой проблемы, заключается в том, что ток, протекающий через R1 и R2, должен как минимум в 100 раз превышать величину тока, протекающего через Vout. Мы можем найти ток, протекающий через R1 и R2, с помощью этого уравнения:
\(\Large I = \frac{V_{in}}{R_1 + R_2} \)
Мы можем преобразовать это уравнение, чтобы вычислить максимальное полное сопротивление (R1 + R2) делителя напряжения, чтобы поддерживать минимальное необходимое Текущий.
\(\Large R_{total\_max} = R_1 + R_2 = \frac{V_{in}}{100 \cdot I_{V_{out}}}\)
Измерение напряжения солнечной панели с МК
Предположим, у вас есть солнечная панель на 12 В, и вы хотите измерить напряжение солнечной панели с помощью микроконтроллера (MCU) на 5 В, такого как плата Arduino.
Сначала мы должны рассмотреть максимальное напряжение солнечной панели и максимальный диапазон измерения MCU.
Несмотря на то, что номинальное напряжение солнечной панели составляет 12 В, напряжение солнечной панели чаще всего составляет 17,5 В и может достигать 22 В. Учитывая все это, мы увеличим читаемый диапазон напряжения солнечной панели до 25 В, чтобы убедиться, что напряжение панели никогда не выходит за пределы допустимого диапазона.
MCU 5V может измерять рабочее напряжение до 5V, но что действительно важно, так это положительное опорное напряжение модуля ADC MCU. Это может быть рабочее напряжение 5 В (которое может немного колебаться) или внутреннее опорное напряжение 1,1 В (в случае ATmega328P). В этом примере мы собираемся использовать внутреннее опорное напряжение 1,1 В, потому что оно будет стабильным независимо от того, как питается микроконтроллер.
Теперь мы знаем, что когда напряжение солнечных батарей равно 25 В, мы хотим, чтобы MCU видел 1,1 В.
\(\Large \frac{R_1}{R_2} = \frac{V_1}{V_2} – 1 = \frac{25V}{1.1V} – 1 = 21. \overline{7272} \)Мы можем использовать уравнение делителя напряжения, чтобы рассчитать требуемый коэффициент сопротивления.
Теперь, когда мы знаем отношение, мы можем произвольно выбрать R2 равным 1 кОм и умножить его на отношение, чтобы найти R1.
\(\Large R_1 = R_2 \cdot \frac{R_1}{R_2} = 1k \cdot 21.\overline{7272} = 21727\Omega \)Затем мы находим, что правильное значение R1 составляет 21727 Ом. Эти два резистора идеально уменьшат напряжение с 25 В до 1,1 В. Однако они не производят резисторы всех мыслимых номиналов. Ближайшее доступное значение (серия E12 или E24) — 22k. Если бы мы использовали резистор 22k с резистором 1k, это дало бы нам фактическое отношение резисторов 22 вместо нашего идеального 21,7272. В этом случае мы, вероятно, могли бы смириться с этим, потому что это означало бы только то, что верхняя часть нашего читаемого диапазона напряжения будет 25,3 В вместо 25 В.
\(\Large V_{in} = V_{out} (\frac{R_1}{R_2} + 1) = 1,1 В \cdot (\frac{22k}{1k} + 1) = 25,3 В \)Если мы хотим, чтобы соотношение было более точным, мы должны использовать Калькулятор резисторов NightShade, который находит пару реальных номиналов резисторов, которые лучше всего соответствуют желаемому значению. В калькуляторе выбираем серию резистора, которая у нас есть в наличии для макетирования (скорее всего Е12 или Е24). Затем мы вводим желаемое соотношение резисторов, и калькулятор находит комбинацию резисторов (R1 и R2), наиболее близкую к желаемому соотношению. Калькулятор соответствует нашему соотношению, используя 390k и резистор 18k для фактического коэффициента 21,67. Это соотношение имеет погрешность всего 0,28% от нашего идеального соотношения 21,73. Наша первая попытка с соотношением 22 имеет ошибку 1,26% от идеального соотношения, поэтому с помощью калькулятора мы смогли уменьшить ошибку на 78%!
Наконец, мы должны рассмотреть величину тока, которая должна протекать через наш делитель напряжения, чтобы перевесить ток, выходящий из цепи через Vout.
\(\Large I = \frac{V}{R} = \frac{25V}{390k\Omega + 18k \Omega} = 0,000061A = 61 \mu A \)Если микроконтроллер потребляет 1 мкА (0,000001 А) от Vout, то мы должны убедиться, что через делитель постоянно протекает в 100 раз больше тока. Сначала проверяем, какой ток сейчас будет протекать через наш делитель. Я просто посчитаю ток в нашей цепи при 25В, потому что нам действительно просто интересен порядок величины (10, 100, 1000 и т.д.).
Здесь мы рассчитали, что через наш резистивный делитель проходит только 61 мкА. Это меньше, чем минимальные 100 мкА (100*1 мкА), которые нам нужны. Итак, нам нужно уменьшить сопротивление нашего делителя напряжения, но мы не хотим испортить наш коэффициент. Что интересно в резисторах, так это то, что каждое значение резистора доступно в каждой декаде . Например, резистор 390k также доступен как 39.к, 3,9 к, 390, 39 и 3,9 Ом. Мы можем масштабировать верхний и нижний резисторы на одинаковую величину без изменения коэффициента делителя напряжения.
\(\Large I = \frac{V}{R} = \frac{25V}{39k\Omega + 1,8k \Omega} = 0,000613A = 613 \mu A \)Таким образом, вместо резисторов 390k и 18k мы будем использовать резисторы 39k и 1,8k. Уменьшив сопротивление в 10 раз, мы увеличили протекающий ток в 10 раз.
Это дает нам ток 610 мкА, протекающий через делитель, что намного превышает минимум 100 мкА, который нам нужен.
Попробуйте сами!
В этом примере первые две цепи представляют собой делители напряжения с коэффициентами 1 и 4. Они создают снижение напряжения на 1/2 и 1/5. Третья схема представляет собой очень простой регулируемый регулятор напряжения. Регулятор регулирует свой выход так, чтобы на выводе обратной связи было 0,5 В. Итак, мы регулируем напряжение, создавая делитель напряжения, который подает 0,5 В на вывод обратной связи (Vout), когда выходное напряжение соответствует желаемому. Здесь мы достигли выходного напряжения 12 В при снижении напряжения на 1/24. Теперь на контакте обратной связи есть 0,5 В, а выходное напряжение составляет 12 В.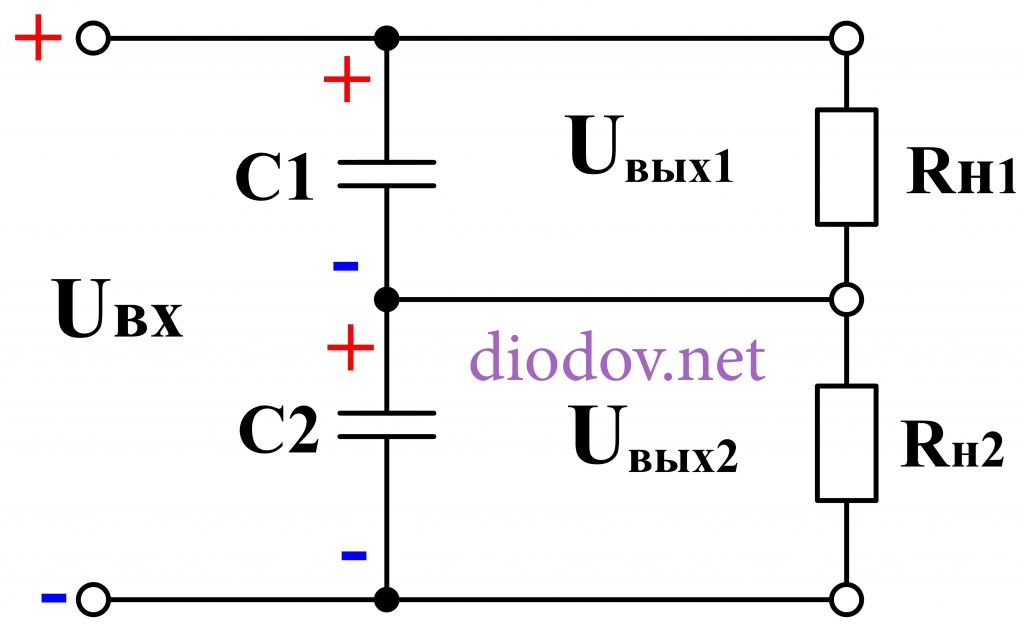
Содержание
Formula, Rule, Attenuator & Transistor
Делитель напряжения (также известный как делитель потенциала) представляет собой базовую, но очень важную электрическую схему , используемую для преобразования высокого напряжения в малое значение в электронике. Делители напряжения часто используются для уменьшения величины напряжения или обеспечения опорного напряжения. Их также можно использовать в качестве аттенюатора сигнала на низких частотах. Изучим это подробнее.
Что такое правило делителя напряжения?
В электрических цепях правило делителя напряжения используется для уменьшения или увеличения уровней напряжения источника. Это важная концепция, особенно при создании все более сложных схем. Инженеры используют это правило для анализа сопротивления и оптимизации электронного оборудования.
Пример схемы делителя напряжения, Oğulcan Tezcan – StudySmarter Originals
Формула делителя напряжения
Итак, как правило делителя напряжения применяется к электрическим цепям? Посмотрите на диаграмму выше: имеется n резисторов, и мы хотим получить выходное напряжение от R 1 , поэтому мы хотим рассчитать значение напряжения R 1 . Формула для нахождения значения напряжения R 1 (V R 1 ) равна
Формула для нахождения значения напряжения R 1 (V R 1 ) равна
. Давайте разберем это:
- Напомним, что ток резисторов, соединенных последовательно, одинаков.
- По закону Ома имеем В = I⋅R
- Таким образом, если I останется на том же уровне, то уровень напряжения V будет d прямо пропорционален значению сопротивления R.
- В приведенной выше формуле значение напряжения резистора равно значению сопротивления компонента, деленному на общее сопротивление и умноженному на значение напряжения источника (В).
В приведенной ниже схеме номиналы резисторов равны R 1 = 3 Ом, R 2 = 7 Ом и R 3 = 5 Ом. Найдите выходное напряжение (V o ).
An example diagram of a voltage divider circuit, Oğulcan Tezcan – StudySmarter Originals
Solution
We take the output voltage (V o ) from the R 3 полюсов резистора, что означает, что оно будет таким же значением, как R 3 значение напряжения напряжения сопротивления.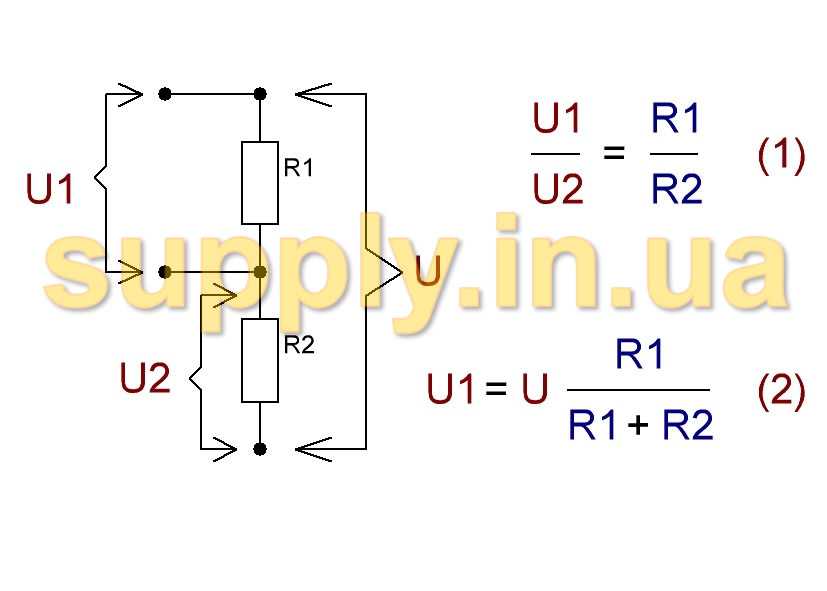 Для расчета значения напряжения R 3 , мы можем подставить данные значения в уравнение делителя напряжения:
Для расчета значения напряжения R 3 , мы можем подставить данные значения в уравнение делителя напряжения:
Из этого расчета мы можем найти выходное напряжение: Схема делителя немного упрощена. Чтобы помочь вам чувствовать себя комфортно с обоими типами диаграмм делителя напряжения, давайте рассмотрим еще один пример ниже.
В приведенной ниже схеме заданное значение входного напряжения (V в ) составляет 20 вольт, а заданные значения резисторов R 1 = 5 Ом и R 2 = 5 Ом. Найдите значение выходного напряжения (В o ).
Пример схемы делителя напряжения, Oğulcan Tezcan – StudySmarter Originals
Решение
Чтобы решить вопрос в этом стиле диаграммы, вы должны сначала понять, что он представляет. Это полная схема контура, и она показана ниже.
Пример схемы делителя напряжения, Oğulcan Tezcan – StudySmarter Originals
Точка, показанная как В в на первой диаграмме, показывает положительный полюс источника напряжения, а земля напоминает, что цепь представляет собой петлю, соединяющуюся с отрицательным полюсом источника В в .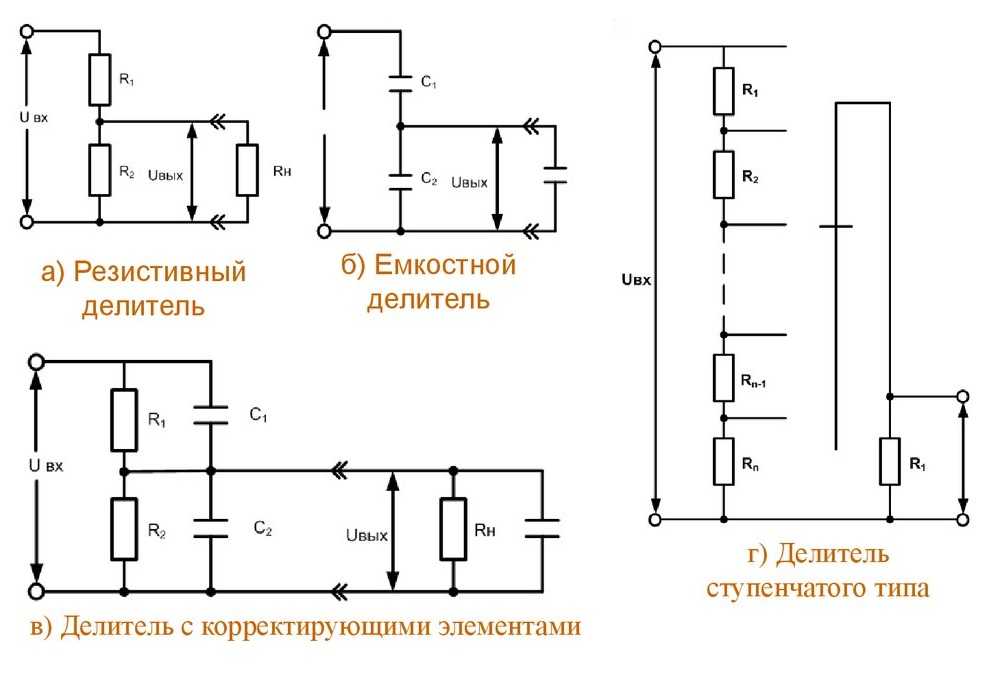 Теперь давайте применим уравнение делителя напряжения, чтобы найти выходное напряжение ( В o ), которое равно значению напряжения R 2 .
Теперь давайте применим уравнение делителя напряжения, чтобы найти выходное напряжение ( В o ), которое равно значению напряжения R 2 .
Поместим значения в правильное место в уравнении:
Где используются делители напряжения?
Делители напряжения используются для контроля уровня сигнала и проверки напряжения. Они также используются для смещения активных компонентов в усилителях. Делители напряжения есть и в мультиметрах .
Измерение высокого напряжения
Хотя существует множество типов вольтметров для различных уровней измерения напряжения, если измеряемое значение напряжения слишком велико, это невозможно сделать с помощью одного вольтметра. Здесь в игру вступают делители напряжения: напряжение подается на делитель напряжения, а затем на выход напряжения, то есть на пониженное количество напряжения , будет измеряться вольтметром. На последнем этапе измеренное напряжение умножается на коэффициент , на который было снижено входное напряжение.
На последнем этапе измеренное напряжение умножается на коэффициент , на который было снижено входное напряжение.
Измерение датчика
Микроконтроллер может считывать значение сопротивления датчика с помощью делителей напряжения. Делитель напряжения формируется последовательным подключением датчика с известным сопротивлением и подачей фиксированного напряжения на делитель. Аналого-цифровой преобразователь на микроконтроллере подключен к центральному отводу делителя. Это делается для того, чтобы он мог считывать напряжение ответвления и вычислять сопротивление датчика, используя наблюдаемое напряжение и определенное сопротивление и напряжение.
Сдвиг логического уровня
Делители напряжения также используются в качестве сдвига логического уровня. Сдвиги логического уровня соединяют две логические схемы последовательно друг с другом.
Некоторые логические схемы работают от 5В, и другие работают от 3,3В . Допустим, мы собираемся соединить две цепи последовательно друг с другом:
Допустим, мы собираемся соединить две цепи последовательно друг с другом:
- Первая работает на 5В. Это означает, что его входное и выходное напряжение будет 5V .
- Второй работает при напряжении 3,3 В, что означает, что его входное и выходное напряжение будет 3,3 В .
Если мы соединим эти две цепи напрямую, выходное напряжение 5 В первой цепи может со временем повредить вторую цепь, поскольку ее входное значение равно 3,3 В. Однако проблема будет решена, если между этими двумя цепями последовательно подключить схему делителя напряжения с выходным коэффициентом 3,3/5 .
Делитель напряжения — основные выводы
- В электронике делитель напряжения представляет собой фундаментальную и важную электрическую цепь, которая используется для преобразования большого напряжения в меньшее значение.
- Делители напряжения используются для контроля уровня сигнала и проверки напряжения.
 Они также используются для смещения активных компонентов в усилителях.
Они также используются для смещения активных компонентов в усилителях. - Делители напряжения используются для измерения датчиков, измерения высокого напряжения и смещения логического уровня.
- Выходное напряжение делителя напряжения можно определить путем деления значения сопротивления выходного компонента на общее последовательное сопротивление и умножения на значение напряжения источника.
Что, Почему, Работа, Применение, Подробные факты – Lambda Geeks
В этой статье мы узнаем о последовательном делителе напряжения. Делитель напряжения, как известно, представляет собой линейную электрическую схему, которая обеспечивает выходное напряжение относительно входного напряжения. Это последовательное соединение резисторов.
Делитель напряжения всегда представляет собой последовательную цепь. Простейший делитель напряжения состоит из двух последовательно соединенных сопротивлений. Деление напряжения необходимо для создания переменного напряжения, которое помогает в измерении напряжения, создавая сложную схему. Выходное напряжение, полученное делением напряжения, является частью входного напряжения.
Выходное напряжение, полученное делением напряжения, является частью входного напряжения.
Делитель напряжения представляет собой простую линейную схему с пассивными элементами. Он работает по принципу падения напряжения на резисторах при последовательном соединении. В то время как напряжение отличается в случае делителя напряжения, ток остается прежним.
Потенциометр является одним из наиболее часто используемых устройств, в которых используется делитель напряжения. Мы можем подать напряжение на клеммы потенциометра и сгенерировать выходное напряжение. Это напряжение пропорционально положению скользящего контакта. Перемещая этот контакт, мы можем изменить напряжение.
Делитель напряжения в последовательном соединении? Делитель напряжения в последовательном порядке дает нам представление о выходном напряжении в цепи, полученном с точки зрения входного напряжения и сопротивления, присутствующего в цепи. Делитель напряжения в последовательном соединении подчиняется закону Ома.
Делитель напряжения в последовательном соединении подчиняется закону Ома.
Падение напряжения является результатом прохождения тока через резистор. Это падение напряжения прямо пропорционально величине резистора. По правилу напряжение на любом резисторе делителя напряжения есть произведение напряжения сети на дробь. Эта доля представляет собой отношение этого сопротивления к эквивалентному сопротивлению.
Зачем использовать последовательный делитель напряжения?Разделение напряжения возможно только в последовательной цепи, так как напряжение на отдельных резисторах падает при протекании тока. В параллельной цепи напряжение остается неизменным, а ток — это величина, которая делится.
Как следует из названия, делитель напряжения последовательно делит общее напряжение на две равные или неравные части. Если бы нам пришлось рассматривать параллельную цепь, напряжение было бы одинаковым для каждой ветви. В серии разветвлений нет. Ток течет от одного резистора к другому и падает на некоторое значение.
Ток течет от одного резистора к другому и падает на некоторое значение.
Здесь, из закона Ома, мы получаем,
Напряжение через R 1 , [Латекс] V_{1}= iR_{1} [/Latex]
Напряжение через R 2 , [Латекс] V_{2}= iR_{2} [/Latex]
Применяя закон Кирхгофа, мы можем написать,
[Latex] -V_{in} + V_{1} + V_{2}= 0 [/Latex]
[Latex] V_{in} = V_{1} + V_{2}= iR_{1} + iR_{2} = i\left ( R_{1}+ R_{2} \right ) [/Latex]
Следовательно, [Latex] i = \frac{ V_{in}} {R_{1}+ R_{2}} [/Latex]
Снова применяя KVL, мы можем написать,
[Latex] V_{out} – iR_{2} = 0 [/Latex]
Или, [Latex] V_{out}= iR_{2 } = \frac{ V_{in}} {R_{1}+ R_{2}}\times R_{2} [/Latex]
Это требуемое разделенное выходное напряжение.
Делитель напряжения для последовательного соединения точно такой же, как резисторы. Здесь емкостное сопротивление аналогично сопротивлению. Способность конденсаторов противостоять протеканию тока известна как емкостное реактивное сопротивление.
Емкостной делитель напряжения последовательно; Кредиты изображения: SeekpngЕмкостное реактивное сопротивление, [Latex] X_{C} = \frac{1} {2\pi fC} [/Latex], где f — частота, а C — емкость.
Следовательно, если суммарное емкостное сопротивление равно X C’ последовательно, то [Latex] X_{C’} = \frac{1} {2\pi fC_{eq}} [/Latex]
Эквивалентная емкость последовательно [Latex] C_{eq} = \frac{C_{1}C_{2}} {C_{1}+C_{2}} [/Latex]
[Latex] X_{C ‘} = \frac{1} {2\pi f \times \frac{C_{1}C_{2}} {C_{1}+C_{2}}} [/Latex]
Итак, текущий [Латекс] i= \frac{V_{in}} {X_{C’}} [/Latex]
Теперь [Latex] V_{out}= iX_{C_{2 }}= \frac{V_{in}} {X_{C’}}\times \frac{1} {2\pi fC_{2}} [/Latex]
Как рассчитать напряжение в делителе напряжения? Делители напряжения являются очень важными компонентами усилителей и цепей управления. Мы можем рассчитать напряжения в цепи делителя напряжения, используя несколько простых формул, полученных из закона Ома и закона Кирхгофа.
Мы можем рассчитать напряжения в цепи делителя напряжения, используя несколько простых формул, полученных из закона Ома и закона Кирхгофа.
Для расчета напряжения на любом резисторе мы должны умножить ток на отношение значения этого сопротивления и эквивалентного последовательного сопротивления делителя напряжения. Если есть другие элементы, такие как конденсаторы, процедура будет такой же. В этом случае реактивным сопротивлением будет только сопротивление.
Нажмите, чтобы узнать больше о напряжении и падении напряжения: сравнительный анализ.
Выбор резистора делителя напряжения для светозависимого резистора – МО и статистика
Представьте, что вы планируете использовать светочувствительный резистор (LDR) для своего нового прототипа IoT, чтобы определить, включена ли лампа в (иначе темной) комнате. Распространенным способом решения этой проблемы является использование схемы делителя напряжения в следующем виде:
Рисунок 1: Схема делителя напряжения с LDR и резистором.
В этом сообщении блога мы обсудим, как правильно выбрать сопротивления для делителя напряжения.
На приведенной выше диаграмме LDR обозначен как и является другим сопротивлением, необходимым для деления напряжения соответствия. В зависимости от света, падающего на фоторезистор, сопротивление изменений, а также напряжение. Напряжение может быть преобразовано в дискретное значение с помощью аналого-цифрового преобразователя (АЦП), а полученное значение затем может быть оценено в программе микроконтроллера (μC) для определения текущих условий освещения в помещении. На приведенной выше диаграмме будет большим (близким к ), если свет очень яркий. Если на LDR не падает свет (в темной комнате), напряжение будет стремиться к небольшим значениям. Если вы хотите добиться прямо противоположного поведения (небольшое значение для яркого света), вы можете просто поменять местами резистор с LDR. Это показано на рисунке ниже:
Рис. 2: То же, что и на рис. 1, однако на этой диаграмме LDR заменен резистором.
Однако при использовании делителя напряжения возникает одна серьезная проблема: обычно требуется охватить широкий диапазон значений, в идеале от 0 В до (), независимо от диапазона . Это важно, например, при использовании АЦП, поскольку АЦП имеет только ограниченное разрешение. Если только изменения в небольшом диапазоне для разных условий освещения, то у нас не будет достаточного отношения сигнал/шум и отличить яркое от темного станет очень сложно. Предположим, например, что в нашей конфигурации (первая диаграмма = 5 В) напряжение изменяется от 3,5 В (очень темно) до 4,5 В (очень ярко). Если мы теперь используем 8-разрядный АЦП (при условии, что опорное напряжение АЦП также равно ), мы получим разрешение по напряжению, которое составляет ок. . Но поскольку входное напряжение перемещается только в интервале , АЦП будет генерировать только интервал примерно различимых значений, хотя теоретически возможно 256. С учетом слабо меняющихся условий освещения и других источников шума этот интервал, содержащий 50 дискретных значений, достаточно мал и, скорее всего, приведет к ложным утверждениям о состоянии лампы (вкл/выкл) в помещении.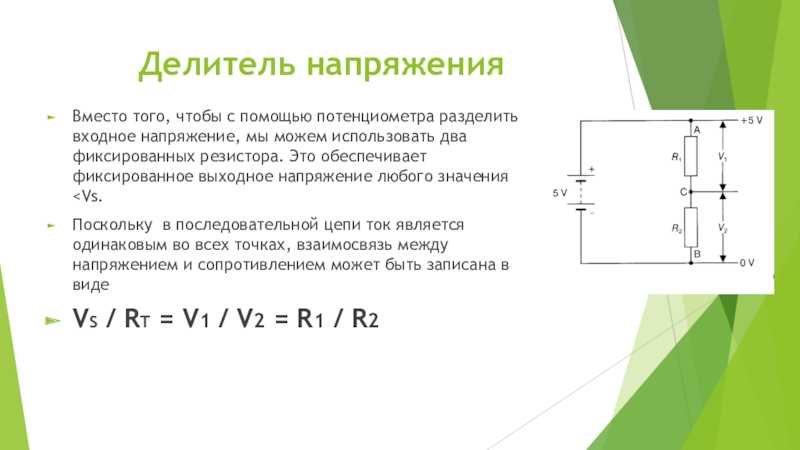 Даже если бы мы использовали АЦП с высоким разрешением в этой конфигурации, мы столкнулись бы с проблемами, если бы у нас было значительное количество шума в файлах . Следовательно, мы должны убедиться, что охватываемый интервал значений как можно больше, чтобы максимизировать отношение сигнал/шум.
Даже если бы мы использовали АЦП с высоким разрешением в этой конфигурации, мы столкнулись бы с проблемами, если бы у нас было значительное количество шума в файлах . Следовательно, мы должны убедиться, что охватываемый интервал значений как можно больше, чтобы максимизировать отношение сигнал/шум.
Хорошие новости: мы действительно можем максимизировать диапазон, выбирая соответствующим образом, если мы знаем наши экстремальные значения (например, для темного и светлого) . Плохая новость: если соотношение между этими экстремальными значениями, которые задаются физическими ограничениями LDR (или какого-либо другого компонента) и его окружения и которые мы не можем выбрать, слишком мало, то мы снова сталкиваемся с проблема, которая будет охватывать только небольшой интервал. По этой причине вы должны убедиться, что переменный резистор (LDR, чувствительный к усилию резистор и т. д.), который вы используете, имеет высокое соотношение между крайними значениями для тех условий, которые вы хотите различить.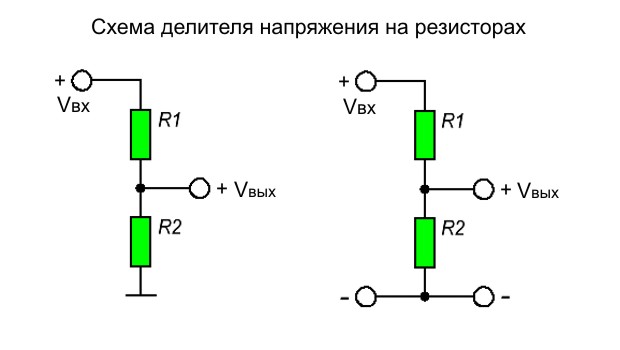 9* для экстремальных условий окружающей среды
9* для экстремальных условий окружающей среды
Максимизация запаса по напряжению для делителя напряжения
Мы предполагаем, что оба и известны.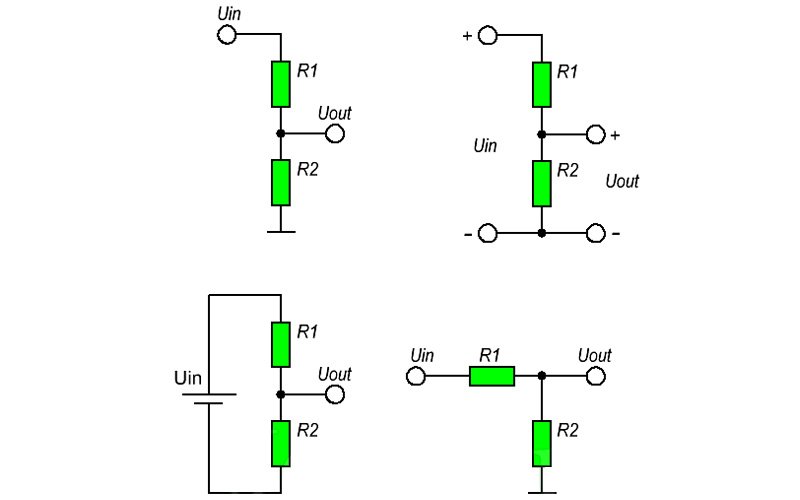 обычно также известен заранее, однако мы увидим, что он не играет роли при вычислении .
Для определенного сопротивления мы знаем, что (следуя рис. 1):
обычно также известен заранее, однако мы увидим, что он не играет роли при вычислении .
Для определенного сопротивления мы знаем, что (следуя рис. 1):
Поскольку мы хотим максимизировать запас по напряжению для , мы вводим новую величину , которая представляет собой просто разность напряжений для экстремальных значений :
Чтобы максимизировать вышеуказанную функцию, мы сначала вычисляем производную :
Затем мы решить , чтобы обнаружить экстремумы функции:
И, так как мы предполагаем, что строго больше, чем , следовательно , мы окончательно получаем:
Легко видеть, что приведенное выше решение для максимизирует запас напряжения.
Пример
На рисунке ниже показано поведение запаса по напряжению для различных пар минимальных и максимальных значений .
Рис. 3: График, показывающий кривые для различных пар минимальных и максимальных значений . Значения для отложены по оси абсцисс и пределу напряжения (в данном случае выраженному в напряжении соответствия ).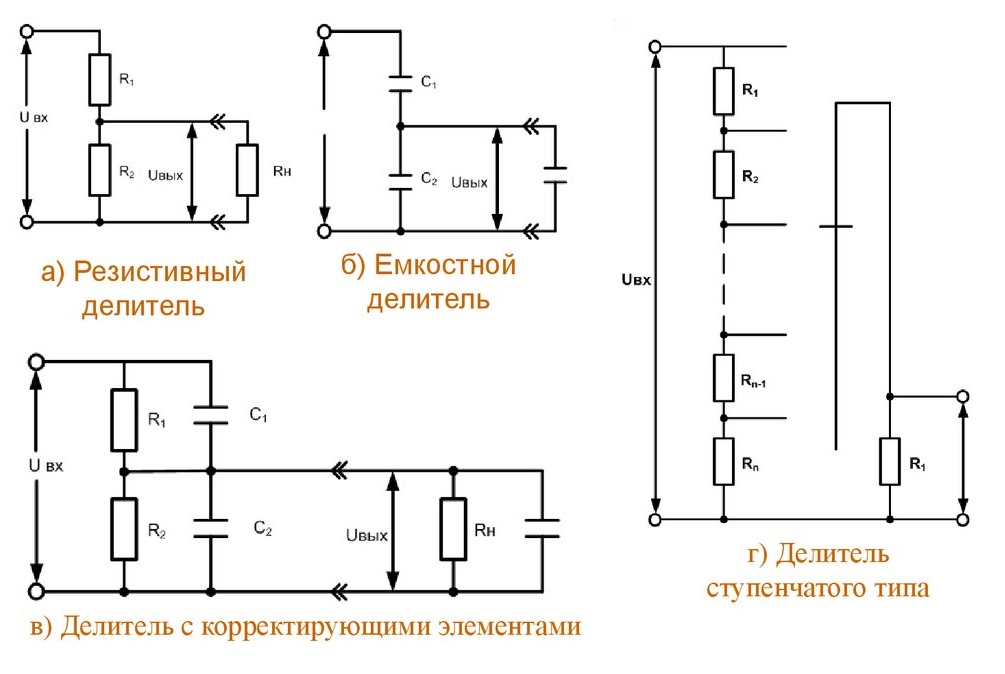 Метки кривых в скобках обозначают и соответственно. Перечеркнутыми кружками отмечены те точки, где запас по напряжению достигает наибольшего значения.
Метки кривых в скобках обозначают и соответственно. Перечеркнутыми кружками отмечены те точки, где запас по напряжению достигает наибольшего значения.
Как видно из диаграммы, при и в лучшем случае можно добиться запаса по напряжению, покрывающего около 38% исходного диапазона . Если мы отчитаем соответствующее значение от оси абсцисс, мы получим ок. . Истинное значение равно .
Как мы уже упоминали ранее, для макс. запас по напряжению, а скорее отношение . Например, значение пары имеет большую разницу, чем , однако макс. запас по напряжению значительно ниже для . Если имеем , то макс. запас по напряжению, которого мы можем достичь, точно такой же, как и для , так как отношение min-max эквивалентно, хотя обе кривые различаются. На практике предпочтительнее настройка , потому что она не такая крутая.
Если мы хотим увеличить запас по напряжению, мы должны найти настройку, которая допускает более высокое отношение мин./макс. На рисунке видно, что если мы, например, удвоим для , увеличится примерно на .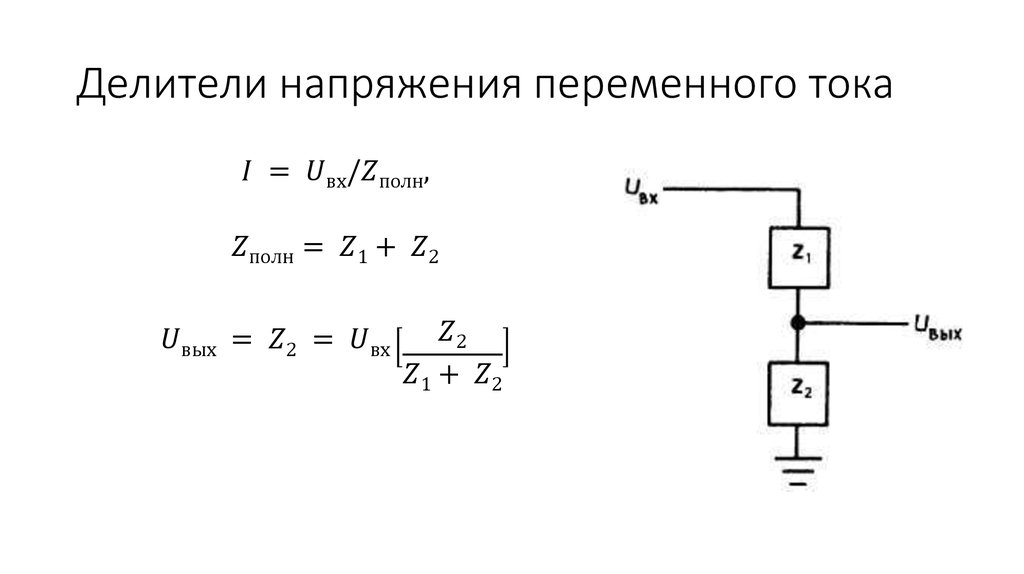 15%. Тем не менее, в этом случае покрывается только около 53% исходного диапазона.
15%. Тем не менее, в этом случае покрывается только около 53% исходного диапазона.
На практике, если нужно найти ближайший подходящий резистор для , обычно лучше двигаться в сторону немного больших значений. Это связано с тем, что наклон кривой запаса напряжения (как видно на рисунке выше) не такой высокий, когда мы выходим из оптимума в сторону более высоких значений, как если бы мы двигались в сторону меньших.
R-код для создания приведенного выше рисунка приведен ниже:
require(ggplot2)
требуют (изменить форму2)
требовать (ggrepel)
требуется (latex2exp)
RS <-список (c (2,10), c (20,100), c (2,20), c (10,20))
R3<-seq(1,100,.01)
и0<-100
myV<-функция (u0,r3,rs){(u0*r3)/(rs+r3)}
Vdiff<-функция(rs,u0,r3){
myV(u0,r3,rs[1])-myV(u0,r3,rs[2])
}
х<-R3
y<- lapply(RS, function(rs) sapply(x,FUN=Vdiff,u0=u0,rs=rs))
xs<-lapply(lapply(RS, prod),sqrt)
ys<-sapply(1:length(RS), function(i) Vdiff(rs=RS[[i]],u0=u0,r3=xs[[i]]))
переместить <- c(15,15,15,-5)
xsL<-sapply (1: длина (RS), функция (i) xs [[i]] + перемещение [i])
ysL<-sapply(1:length(RS), function(i) Vdiff(rs=RS[[i]],u0=u0,r3=xsL[[i]]))
df <- data.


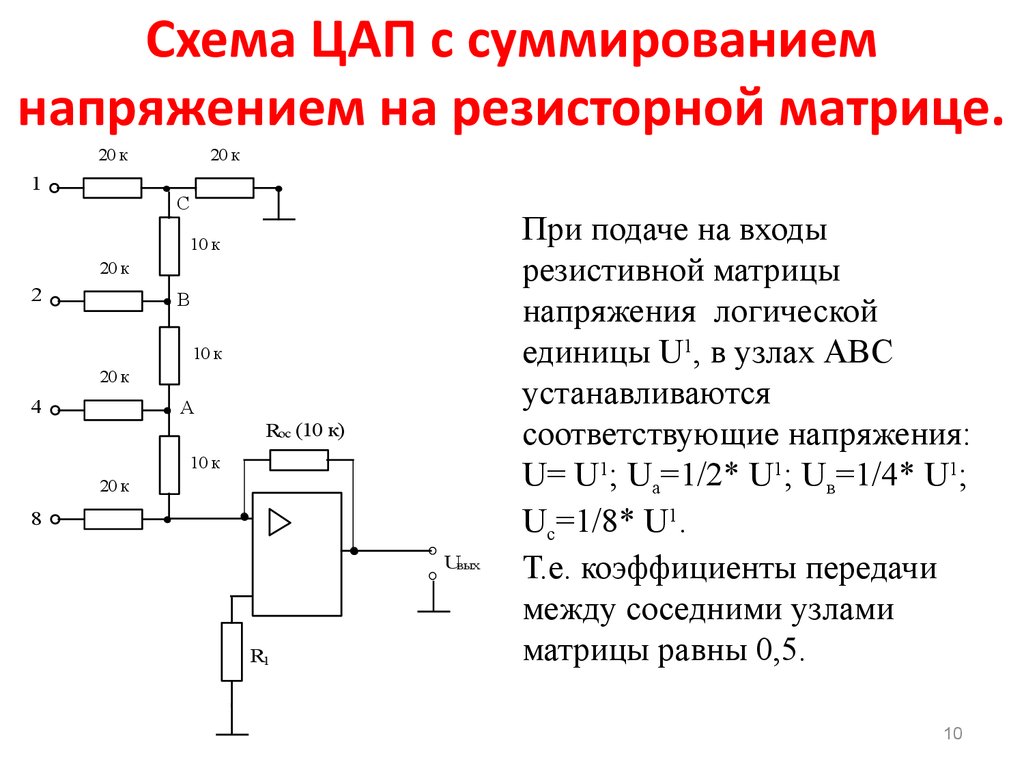
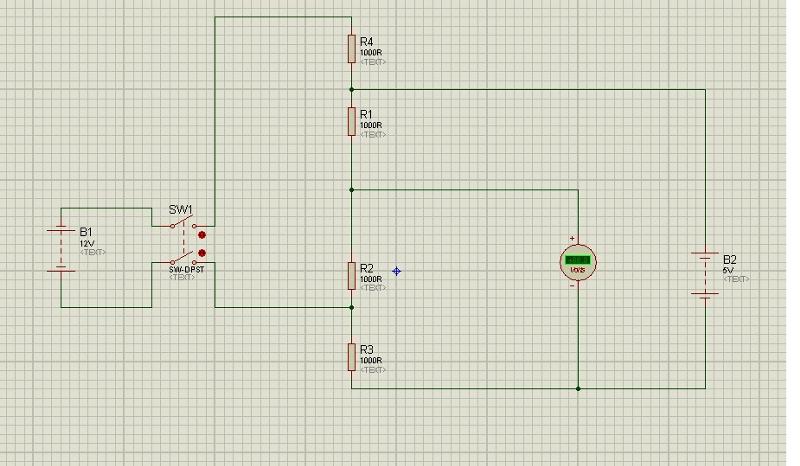
 С напряжением все понятно. Эквивалентное выходное сопротивление скажет нам, насколько изменится напряжение на выходе с изменением тока нагрузки делителя. Если эквивалентное выходное сопротивление равно 100 Ом, то изменение тока нагрузки на 10 мА приведет к изменению напряжения на выходе на 1 В. Входное сопротивление показывает, насколько делитель нагружает источник сигнала или источник питания. Дополнительно посчитаем коэффициент ослабления сигнала. Он может пригодиться при работе с сигналами сложной формы.
С напряжением все понятно. Эквивалентное выходное сопротивление скажет нам, насколько изменится напряжение на выходе с изменением тока нагрузки делителя. Если эквивалентное выходное сопротивление равно 100 Ом, то изменение тока нагрузки на 10 мА приведет к изменению напряжения на выходе на 1 В. Входное сопротивление показывает, насколько делитель нагружает источник сигнала или источник питания. Дополнительно посчитаем коэффициент ослабления сигнала. Он может пригодиться при работе с сигналами сложной формы.


 Сначала мы должны рассмотреть максимальное напряжение солнечной панели и максимальный диапазон измерения MCU.
Сначала мы должны рассмотреть максимальное напряжение солнечной панели и максимальный диапазон измерения MCU. Мы можем использовать уравнение делителя напряжения, чтобы рассчитать требуемый коэффициент сопротивления.
Мы можем использовать уравнение делителя напряжения, чтобы рассчитать требуемый коэффициент сопротивления.
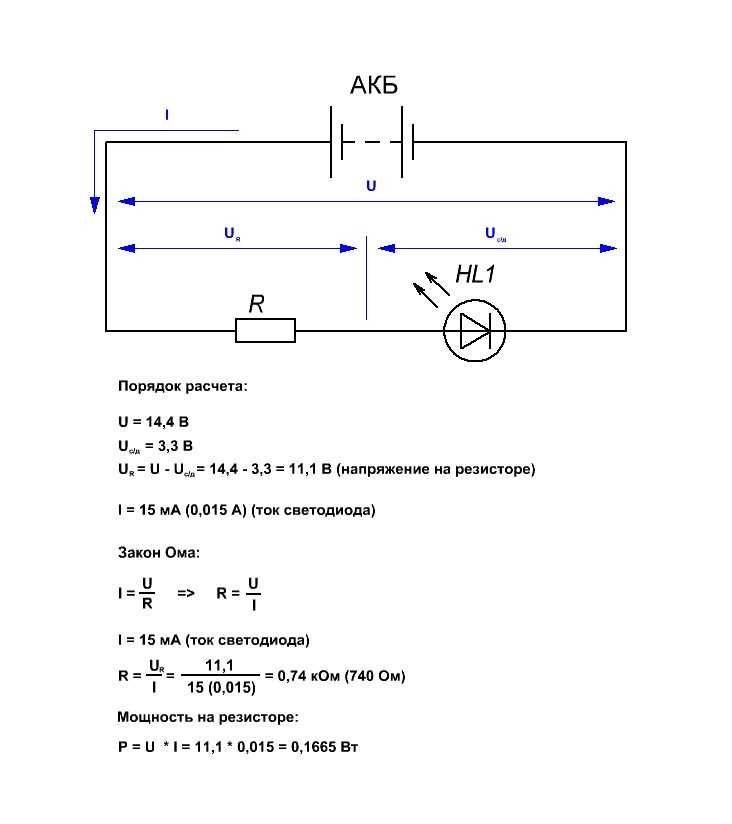 Если микроконтроллер потребляет 1 мкА (0,000001 А) от Vout, то мы должны убедиться, что через делитель постоянно протекает в 100 раз больше тока. Сначала проверяем, какой ток сейчас будет протекать через наш делитель. Я просто посчитаю ток в нашей цепи при 25В, потому что нам действительно просто интересен порядок величины (10, 100, 1000 и т.д.).
Если микроконтроллер потребляет 1 мкА (0,000001 А) от Vout, то мы должны убедиться, что через делитель постоянно протекает в 100 раз больше тока. Сначала проверяем, какой ток сейчас будет протекать через наш делитель. Я просто посчитаю ток в нашей цепи при 25В, потому что нам действительно просто интересен порядок величины (10, 100, 1000 и т.д.). Таким образом, вместо резисторов 390k и 18k мы будем использовать резисторы 39k и 1,8k. Уменьшив сопротивление в 10 раз, мы увеличили протекающий ток в 10 раз.
Таким образом, вместо резисторов 390k и 18k мы будем использовать резисторы 39k и 1,8k. Уменьшив сопротивление в 10 раз, мы увеличили протекающий ток в 10 раз.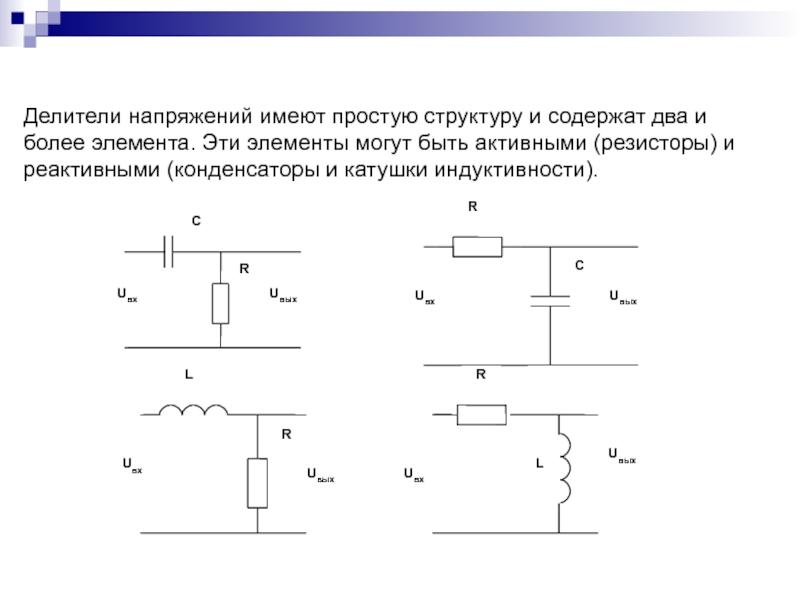 Они также используются для смещения активных компонентов в усилителях.
Они также используются для смещения активных компонентов в усилителях.