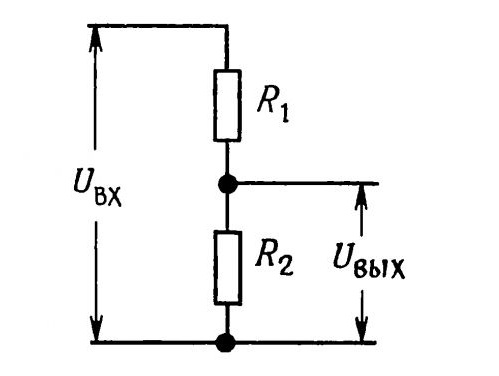
Расчет сопротивлений делителя напряжения. Делитель напряжения

Делитель тока – устройство позволяющее поделить ток в цепи на две составные части, с целью использования одной из них. Другими словами, делитель тока необходим в том случае, если устройство не рассчитано на большой ток, и нам необходима лишь некоторая часть этого тока.

Принцип действия делителя тока основан на первом законе Кирхгофа – сумма токов сходящихся в узле равна нулю. Если провести аналогию с водой, то его можно представить как русло реки, которое разветвляется на два более маленьких оттока.

Для нахождения токов I 1 и I 2 воспользуемся законом Ома , но для начала найдем эквивалентное сопротивление для параллельного соединения.

Делители тока применяются в измерительных устройствах, например при измерении больших токов. С помощью добавочного сопротивления – “шунта” расширяют предел измерения амперметра. Для этого, шунт подключается параллельно амперметру. В результате, через амперметр протекает ток, зная который, можно найти общий ток, протекающий в цепи.

Обычно шунт имеет сопротивление меньше, чем амперметр, для того чтобы значительная часть тока ушла через него.

Выведем коэффициент деления (шунтирования) n . Будем считать, что параметры с индексом 1 принадлежат амперметру (прибору), а параметры с индексом 2 – шунту. Параметры без индексов общие.

Рассмотрим пример.

Амперметром с пределом измерения 1 А и внутренним сопротивлением 12 Ом, необходимо измерить ток в 3 А. Каким должно быть сопротивление шунта?

Из формулы для коэффициента шунтирования, выразим R ш

Еще один пример

Каким станет новый предел измерения амперметра, после его шунтирования сопротивлением в 10 Ом, если старый предел был равен 0,5 А? Сопротивление измерительного механизма амперметра – 25 Ом.

Посчитаем коэффициент шунтирования

Тогда новый предел измерения амперметра

Дели́тель напряже́ния — устройство, в котором входное и выходное напряжение связаны коэффициентом передачи 0 ⩽ a ⩽ 1 {\displaystyle 0\leqslant a\leqslant 1} .

Энциклопедичный YouTube

• 1 / 5

  Простейший резистивный делитель напряжения представляет собой два последовательно включённых резистора и , подключённых к источнику напряжения U {\displaystyle U} . Поскольку резисторы соединены последовательно, то ток через них будет одинаков в соответствии с первым правилом Кирхгофа . Падение напряжения на каждом резисторе согласно закону Ома будет пропорционально сопротивлению (ток, как было установлено ранее, одинаков):

  U = I R {\displaystyle \ U=IR} .

  Для каждого резистора имеем:
  { U 1 = I R 1 U 2 = I R 2 {\displaystyle \left\{{\begin{array}{l l}U_{1}=IR_{1}\\U_{2}=IR_{2}\end{array}}\right.}
  Разделив выражение для на выражение для в итоге получаем:
  U 1 U 2 = R 1 R 2 {\displaystyle {\frac {U_{1}}{U_{2}}}={\frac {R_{1}}{R_{2}}}} Таким образом, отношение напряжений U 1 {\displaystyle U_{1}} и U 2 {\displaystyle U_{2}} в точности равно отношению сопротивлений R 1 {\displaystyle R_{1}} и R 2 {\displaystyle R_{2}} .

  
  Далее
  U 1 = R 1 R 2 U 2 {\displaystyle U_{1}={\frac {R_{1}}{R_{2}}}U_{2}}
  U 1 + U 2 = R 1 R 2 U 2 + U 2 {\displaystyle U_{1}+U_{2}={\frac {R_{1}}{R_{2}}}U_{2}+U_{2}}
  U = (R 1 R 2 + 1) U 2 {\displaystyle U=\left({\frac {R_{1}}{R_{2}}}+1\right)U_{2}}
  Т.е.
  U = (R 1 + R 2 R 2) U 2 {\displaystyle U=\left({\frac {R_{1}+R_{2}}{R_{2}}}\right)U_{2}}
  Откуда:
  U 2 = U R 2 R 1 + R 2 {\displaystyle U_{2}=U{\frac {R_{2}}{R_{1}+R_{2}}}}

  Следует обратить внимание, что сопротивление нагрузки делителя напряжения должно быть много больше собственного сопротивления делителя, так, чтобы в расчетах этим сопротивлением, включенным параллельно R 2 {\displaystyle R_{2}} можно было бы пренебречь. Для выбора конкретных значений сопротивлений на практике, как правило, достаточно следовать следующему алгоритму . Сначала необходимо определить величину тока делителя, работающего при отключенной нагрузке. Этот ток должен быть значительно больше тока (обычно принимают превышение от 10 раз по величине), потребляемого нагрузкой, но, однако, при этом указанный ток не должен создавать излишнюю нагрузку на источник напряжения U {\displaystyle U} .

  Исходя из величины тока, по закону Ома определяют значение суммарного сопротивления R = R 1 + R 2 {\displaystyle R=R_{1}+R_{2}} . Остается только взять конкретные значения сопротивлений из стандартного ряда , отношение величин которых близко́ требуемому отношению напряжений, а сумма величин близка расчетной. При расчете реального делителя необходимо учитывать температурный коэффициент сопротивления , допуски на номинальные значения сопротивлений, диапазон изменения входного напряжения и возможные изменения свойств нагрузки делителя, а также максимальную рассеиваемую мощность резисторов — она должна превышать выделяемую на них мощность.

  Делитель напряжения имеет важное значение в схемотехнике. В качестве реактивного делителя напряжения как пример можно привести простейший электрический фильтр , а в качестве нелинейного — параметрический стабилизатор напряжения .

  Делители напряжения использовались как электромеханическое запоминающее устройство в АВМ . В таких устройствах запоминаемым величинам соответствуют углы поворота реостатов. Подобные устройства могут неограниченное время хранить информацию.

  Цепи обратной связи в усилителях

  С помощью резистивного делителя напряжения в цепи обратной связи задаётся коэффициент усиления каскада на

  Представьте, что течёт река, и вдруг ширина её русла резко уменьшается, через некоторое расстояние ширина русла снова увеличивается. Что же происходит в том месте, где русло узкое? Скорость потока воды резко возрастает, вода пытается расширить русло реки, происходит разрушение берегов и углубление русла. Для того, чтобы скорость потока упала, достаточно прорыть дополнительный параллельный канал, по которому пустить часть потока. При этом, этот искусственный канал можно использовать в своих целях, например крутить водяное колесо (по современному — гидроэлектростанцию). Как правило, сначала делают «колесо», а потом перекрывают основное русло реки. Другими словами — поток воды делят на два потока, которые потом всё равно объединяются, но при этом один из потоков используют в своих определённых целях.

  В частности, на гидроэлектростанциях всегда имеется два потока — один используется для вращения турбин электростанции, а другой в зависимости от полноводности реки — «сброс», или дополнительный канал отвода воды — водосливную плотину, предназначенную для регулирования уровня воды перед плотиной ГЭС.

  Делитель тока на резисторах предназначен для того, чтобы, не изменяя общего тока протекающего через электрическую цепь, часть его направить в другое плечо делителя, а после выполнения определённой функции вернуть эту часть обратно.

  Где применяется делитель тока? Делитель тока применяется в измерительных приборах, когда необходимо измерить большой ток (единицы, или сотни Ампер) прибором, рассчитанным на маленький ток (миллиамперы или даже микроамперы). В этом случае, внутреннее сопротивление измерительного прибора выступает в качестве одного из резисторов, а второй резистор в таком случае называют «шунтом», так как он шунтирует проходящий ток (основная часть тока бежит через него).

  Шунт в схеме измерения имеет сопротивление, которое намного меньше внутреннего сопротивления измерительного прибора. Кроме того, делитель тока применяется в различных схемах автоматического регулирования, использующих в качестве контролируемого параметра — ток, проходящий через электрическую цепь. Делитель тока может применяться в различных каскадах передачи, или усиления тока, когда один пассивный, или усилительный элемент по своим электрическим параметрам не способен обеспечить прохождение через него большого тока. В этом случае их подключают параллельно, разделяя ток на равные доли (пополам). Наглядным примером использования делителя тока является его применение в цепи автоматического регулирования и измерения в , или в цепи контроля схемы защиты от перегрузки по току и удвоения мощности выходных транзисторов в .

  Изобразим цепь делителя тока:
  

  На рисунке видно, что общий входящий ток делится на два, и проходя цепь, снова объединяется в один.

  Расчёт делителя тока на резисторах основывается на законе Ома, правиле сложения токов (законе Кирхгофа) и формуле параллельного соединения резисторов:

  Выведем закон Ома для этой цепи. Его можно записать в следующем виде:

  Преобразовывая указанные формулы так, как нам удобно, мы можем определить:

  1. Определить ток I1 и I2 в плечах резисторов R1, R2 по известным значениям общего тока Iобщ и сопротивлений резисторов R1, R2 :

  Пример: Определить значения I1 и I1 делителя тока, если значение общего тока Iобщ = 0,6А, сопротивление R1 =100 Ом, а R2 = 20 Ом.

  I1 = 0,6 * 20 / (100 + 20) = 0,1 А; По формуле (18) вычисляем: I2 = 0,6 * 100 / (100 + 20) = 0,5 А; Не забывайте, что резисторы поглощают мощность, поэтому её необходимо рассчитать, (формула3):

  P = I * I * R

  Определим рассеиваемую мощность резисторов по формуле (3):

  Для резистора R1: P = 0,1 * 0,1 * 100 = 1 Вт; по правилу (1) выбираем резистор мощностью P = 2 Вт;

  Для резистора R2: P = 0,5 * 0,5 * 20 = 5 Вт; по правилу (1) выбираем резистор мощностью P = 10 Вт.

  2. Расчитать шунт R2 в цепи измерительного прибора, при известных: внутреннем сопротивлении R1 , максимальном токе обмотки катушки прибора I1 и максимальном значении общего тока Iобщ цепи делителя тока, представленного на схеме:
  

  Пример: Полное отклонение стрелки миллиамперметра при значении I1 = 1 мА, внутреннее сопротивление катушки прибора R1 = 200 Ом. Рассчитайте шунт R2 , чтобы стрелка прибора отклонялась на максимальное значение при общем токе Iобщ = 1 А.

  Решение: По формуле (17) вычисляем: R2 = 0,001 * 200 / (1 – 0,001) = 0,2 Ом; Рассчитаем поглощаемую (рассеиваемую) мощность R2 (формула 3): P = I2 * I2 * R2 , где I2 = Iобщ — I1 = 999 мА, P = 0,999 * 0,999 * 0,2 = 0,199 Вт; по правилу (1) выбираем резистор мощностью P = 0,25 Вт

  Для достижения точности в измерительных цепях, выбирают высокоточные резисторы, кроме того, используют их последовательное и параллельное соединение.

  Как и в случае с делителем напряжения, Вы спросите: Если это делитель, должен быть коэффициент деления? Да он есть, но в определении необходимых величин, пользоваться им крайне неудобно, поэтому не буду ломать голову ни себе, ни Вам.

резисторов — Как рассчитать необходимое сопротивление для делителя напряжения?

«Учитывая входное напряжение 15 В и требуемые выходные напряжения 10 В, 5 В и 0 В, как мне рассчитать необходимое для использования сопротивление?»

Я думаю, что хороший способ сделать это — просмотреть один набор за раз. Стандартное уравнение делителя напряжения достаточно простое: $$\text{Напряжение на интересующем резисторе} = \frac{(\text{Интересующий резистор})}{(\text{Интересующий резистор + Неинтересный резистор})} * V_{вход}$$

Когда есть несколько узлов, как в приведенном вами примере, просто упростите его до базового резисторного делителя и найдите первое напряжение. В качестве альтернативы, если нам заданы напряжения, мы можем изменить это уравнение, чтобы найти интересующий резистор в терминах неинтересного резистора.

$$\text{Исследуемый резистор} = \frac{1}{({V_{input}}\div{\text{Напряжение на интересующем резисторе}})-1}*\text{Сопротивление не представляет интереса }$$

Для упрощения в вашем примере для узла 10 В интересующий резистор представляет собой комбинацию R2 и R3, оставляя резистор не представляющим интереса как R1. Как только вы нашли соотношение между (R2+R3) и R1, вы можете перейти к поиску соотношения для R2 и R3. В этом случае вы можете просто смотреть на эти два как на еще один делитель, а входное напряжение — это напряжение первого узла, которое вы только что использовали в качестве выходного напряжения. Следуя этому методу, вы обнаружите, что R1 составляет одну треть (R2+R3), а R2 совпадает с R3. Имеет смысл, что при одинаковом протекании тока одинаковое падение на каждом резисторе означает и одинаковое сопротивление в соответствии с законом Ома V = IR.

«Можно ли создать делитель напряжения, который не имеет пропорционального падения (например, допустим, что из этой же схемы я хочу 14В, 12В, 5В и 0В)?»

Это будет тот же процесс, что и раньше, но с другим напряжением. Для первого узла:

$$\text{(R2+R3)} = (\frac{1}{(14V\div12V)-1})*\text{R1}=6*R1$$

Итак комбинация R2 и R3 в шесть раз больше, чем один R1. Для второго узла:

$$\text{(R2)} = (\frac{1}{(12V\div5V)-1})*\text{R3}=0,71*R3$$

Наконец, и это самая сложная часть для большинства учащихся, просто выберите номинал резистора. Это инженерная часть электротехники, вам предстоит принять решение. Это не так уж сложно, по большей части большее сопротивление лучше. Большее сопротивление уменьшит протекание тока, но при этом обеспечит необходимое напряжение.

При практическом использовании делителя напряжения необходимо учитывать еще несколько моментов. Они отлично подходят для базовых опорных напряжений или пропорционального снижения напряжения сигнала в одном направлении. Например, сигнал 5 В, понижаемый до 3,3 В для микроконтроллера, работает хорошо, потому что делитель напряжения действует как коэффициент ослабления сигнала, все уменьшается на одинаковую величину.

Если вы проверяете напряжение на каком-либо устройстве, вы можете иногда смоделировать потребление тока как сопротивление, предполагая, что оно всегда постоянное (R=V/I). Этот резистор устройства или нагрузка обычно представляет собой интересующий резистор или параллельный интересующему резистору. Однако я бы не рекомендовал это в любое время, поскольку напряжение узла будет меняться в зависимости от потребляемого тока нагрузки.

«И как работает эта математика?»

См. уравнения выше.

Как разделять и властвовать над разделителем: практические резистивные разделители, сделанные легко

Скачать PDF

Abstract

В этой статье представлена ​​простая таблица для проектирования резистивных делителей напряжения с использованием стандартных номиналов резисторов 1%. В примечаниях к применению описывается, как использовать электронную таблицу, и приводится ссылка для загрузки файла электронной таблицы.

Резистивный делитель напряжения — это базовая схема, которую изучают в каждом вводном курсе по электронике. Но выбрать значения из стандартных компонентов не так просто. Если вы когда-нибудь оказывались перед набором резисторов, вводя значения в свой калькулятор, то эта статья поможет вам.

Проблема в том, что типичные наборы резисторов не имеют всех номиналов. В этой статье демонстрируется небольшая электронная таблица, в которой представлена ​​таблица номиналов резисторов с точностью до 1%, что позволяет легко найти необходимое соотношение, используя два доступных резистора. 9((B$4+$A5)/96), который копируется в B5 через G20. Значения, выделенные желтым цветом, обычно доступны в наборах резисторов. Эти желтые блики с первого взгляда говорят вам, что типичный комплект содержит чуть больше четверти значений.

Рисунок 1. Эта таблица не только содержит список номиналов резисторов с шагом 1 %, но также позволяет легко определить отношение резисторов к делителю, используя два общедоступных значения (выделенные желтым цветом ячейки) из типичного набора резисторов.

На рис. 2 показано типичное применение резистивного делителя: внешняя обратная связь для регулятора напряжения, такого как понижающий преобразователь MAX8560 4 МГц. Соотношение делителя R2/(R1+R2) устанавливает выходное напряжение регулятора. MAX8560 имеет порог обратной связи 0,6 В на FB. В этом примере требуется выходное напряжение 1,5 В.

Рис. 2. Соотношение резистор-делитель R2/(R1+R2) задает выходное напряжение понижающего стабилизатора MAX8560 4 МГц. Электронная таблица на рис. 1 упрощает выбор R1 и R2 из общедоступных значений.

Чтобы вычислить значения для R1 и R2, введите требуемое выходное напряжение регулятора (напряжение на верхней части делителя) в ячейке B3 и порог обратной связи регулятора (напряжение в средней точке делителя) в ячейке C3.