Как изменится емкость сопротивления конденсатора

Конденсатор используется в схемах для разделения переменной и постоянной составляющей напряжения, при этом он хорошо проводит высокочастотный сигнал, и плохо — низкочастотный. Находясь в цепи постоянного тока, его импеданс принимается бесконечно большим. Для переменного тока ёмкостное сопротивление конденсатора не имеет постоянной величиной. Поэтому расчёт этого значения крайне важен при проектировании различных радиоэлектронных приборов. Физически электронное устройство — конденсатор — представляет собой две обкладки, выполненные из проводящего материала, между которыми находится диэлектрический слой. С поверхности пластин выводятся два электрода, предназначенные для подключения в электрическую цепь.

Поиск данных по Вашему запросу:

Схемы, справочники, даташиты:

Прайс-листы, цены:

Обсуждения, статьи, мануалы:

Дождитесь окончания поиска во всех базах.

По завершению появится ссылка для доступа к найденным материалам.

Содержание:

• Онлайн калькулятор расчета реактивного сопротивления
• Как найти сопротивление конденсатора формула. Активное и реактивное сопротивление
• Реактивное сопротивление
• Переменный ток и ёмкостное сопротивление конденсатора
• Емкостное сопротивление.
• уменьшится в 1,41 раза
• Переменный ток и ёмкостное сопротивление конденсатора
• Тест по теме: «Элетромагнитные колебания» .
• Конденсатор. Реактивное, емкостное сопротивление

ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: Параллельное и последовательное соединение конденсаторов

Онлайн калькулятор расчета реактивного сопротивления

Господа, сегодняшнюю статью можно считать в некотором роде продолжением предыдущей. Сначала я даже хотел поместить весь этот материал в одну статью. Но его получилось довольно много, на горизонте были новые проекты, и я в итоге разделил его на две. Итак, сегодня мы поговорим про сопротивление конденсатора переменному току. Мы получим выражение, по которому можно будет рассчитать, чему равно сопротивление любого конденсатора, включенного в цепь с переменным током, а в конце статьи рассмотрим несколько примеров такого расчета.

Сразу оговорюсь про одну важную вещь. Вообще говоря, реальный конденсатор обладает помимо емкостного сопротивления еще резистивным и индуктивным. На практике все это надо обязательно учитывать, потому что возможны ситуации обычно связанные с ростом частоты сигнала , когда конденсатор перестает быть конденсатором и превращается… в некое подобие катушки индуктивности.

При проектировании схем этот момент обязательно надо иметь в виду. Согласитесь, господа, крайне неприятно поставить в схему конденсатор и потом столкнуться с тем, что из-за высокой частоты он ведет себя и не как конденсатор вовсе, а как самый настоящий дроссель. Это, безусловно, очень важная тема, но сегодня речь пойдет не о ней. В сегодняшней статье мы будем говорить непосредственно про емкостное сопротивление конденсатора.

То есть мы будем считать его идеальным, без каких бы то ни было паразитных параметров вроде индуктивности или активного сопротивления. Давайте представим, что у нас есть конденсатор, который включен в цепь с переменным током. В цепи больше нет никаких компонентов, только один конденсатор и все рисунок 1. Рисунок 1 — Конденсатор в цепи переменного тока. К его обкладкам приложено некоторое переменное напряжение U t , и через него течет некоторый ток I t.

Зная одно, можно без проблем найти другое. Для этого надо всего лишь вспомнить прошлую статью про конденсатор в цепи переменного тока , там мы про все это довольно подробно говорили. Будем полагать, что ток через конденсатор изменяется по синусоидальному закону вот так.

В прошлой статье мы пришли к выводу, что если ток изменятся вот по такому закону, то напряжение на конденсаторе должно меняться следующим образом. Пока что ничего нового мы не записали, это все дословное повторение выкладок из предыдущей статьи. А сейчас самое время их немного преобразовать, придать им чуть другой облик. Если говорить конкретно, то нужно перейти к комплексному представлению сигналов!

Помните, на эту тему была отдельная статья? В ней я говорил, что она нужна для понимания некоторых моментов в дальнейших статьях. Вот как раз и наступил тот момент, когда пора вспомнить все эти хитрые мнимые единицы. Если говорить конкретно, то сейчас нам потребуется показательная запись комплексного числа.

Как мы помним из статьи про комплексные числа в электротехнике, если у нас есть синусоидальный сигнал вида. Почему это так, откуда взялось, что здесь какая буковка значит — обо всем уже подробно говорили. Для повторения можно перейти по ссылке и еще раз со всем ознакомиться.

Давайте-ка теперь применим это комплексное представление для нашей формулы напряжения на конденсаторе. Получим что-то типа такого. Теперь, господа, я хотел бы вам рассказать еще про один интересный момент, который, наверное, следовало бы описать в статье про комплексные числа в электротехнике.

Однако тогда я про него как-то позабыл, поэтому давайте рассмотрим его сейчас. Это приведет к исключению из расчетов времени и и частоты, и мы переходим к так называемым комплексным амплитудам сигнала. Безусловно, это не значит, что сигнал из переменного становится постоянным. Нет, он все так же продолжает изменяться по синусу с той же самой частотой.

Но бывают моменты, когда частота нам не очень важна, и тогда лучше от нее избавиться и работать только с амплитудой сигнала. Сейчас как раз такой момент. Давайте раскроем скобки в экспоненте и воспользуемся правилами работы с показательными функциями. Итак, у нас имеется три множителя.

Будем разбираться со всеми по порядку. Объединим первые два и запишем выражение следующего вида. Что мы вообще такое записали? Правильно, комплексную амплитуду тока через конденсатор.

Теперь выражение для комплексной амплитуды напряжения принимает вид. Результат, к которому мы стремимся, уже близок, но остается еще один не очень приятный множитель с экспонентой. Как с ним быть? А, оказывается, очень просто. И снова нам на помощь придет статья по комплексным числам в электротехнике , не зря ж я ее писал.

Давайте преобразуем этот множитель, воспользовавшись формулой Эйлера:. Да, вся эта хитрая экспонента с комплексными числами в показателе превращается всего лишь в мнимую единичку, перед которой стоит знак минус. Согласен, возможно, осознать это не так просто, но тем не менее математика говорит, что это так. Поэтому результирующая формула у нас принимает вид. Давайте выразим из этой формулы ток и приведем выражение к виду, соответствующему закону Ома.

Как мы помним из статьи про закон Ома , у нас ток равнялся напряжению, деленному на сопротивление. Так вот, здесь практически то же самое! Ну, за исключением того, что у нас ток и напряжение — переменные и представлены через комплексные амплитуды. Кроме того, не забываем, что ток течет у нас через конденсатор. Поэтому, выражение, которое стоит в знаменателе, можно рассматривать как емкостное сопротивление конденсатора переменному току :. Да, выражение для сопротивления конденсатора имеет вот такой вот вид.

Оно, как вы можете заметить, комплексное. Об этом свидетельствует буковка j в знаменателе дроби. А что значит эта комплексность? На что она влияет и что показывает? А показывает она, господа, исключительно сдвиг фаз в 90 градусов между током и напряжением на конденсаторе.

А именно, ток на 90 градусов опережает напряжение. Этот вывод не является для нас новостью, про все это было подробно рассказано в прошлой статье.

Чтобы это лучше осознать, надо теперь мысленно пройтись от полученной формулы вверх к тому моменту, где у нас это j возникло. В процессе подъема вы увидите, что мнимая единица j возникло из формулы Эйлера из-за того, что там был компонент.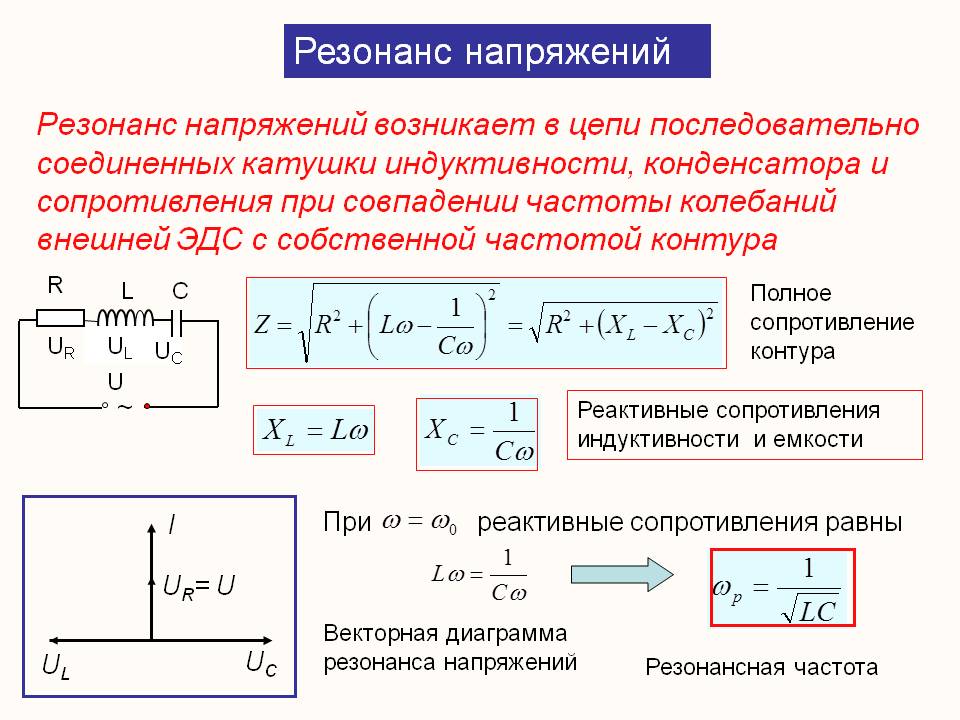

Формула Эйлера у нас возникла из комплексного представления синусоиды. А в исходной синусоиде как раз был заложен сдвиг фазы в 90 градусов тока относительно напряжения.

Как-то так. Вроде все логично и ничего лишнего не возникло. Теперь может возникнуть два совершенно логичных вопроса: как работать с таким представлением и в чем его выгода? Да и вообще, пока лишь какие-то дико абстрактные буковки и нифига не ясно, как взять и оценить сопротивление какого-нибудь конкретно конденсатора, который мы купили в магазине и воткнули в схему. Давайте разбираться постепенно. Как мы уже говорили, буковка j в знаменателе говорит нам лишь о сдвиге фаз тока и напряжения.

Но она не влияет на амплитуды тока и напряжения. Соответственно, если сдвиг фаз нас не интересует , то можно исключить эту буковку из рассмотрения и получить более простое выражение абсолютно без всяких комплексностей:. Согласитесь, жить стало чуточку легче. Это выражение позволяет рассчитать сопротивление конденсатора для конкретной емкость и частоты сигнала. Заметьте, господа, интересный факт. Сопротивление конденсатора, оказывается, зависит не только от самого конденсатора а именно его емкости , но и от частоты протекающего тока.

Если вспомнить обычные резисторы, то в них у нас сопротивление зависело только от самого резистора, материала, формы и всего такого прочего, но не зависело от частоты разумеется, мы говорим сейчас про идеальные резисторы, без всяких паразитных параметров.

Здесь все по-другому. Один и тот же конденсатор на разной частоте будет иметь разное сопротивление и через него будет течь ток разной амплитуды при одной и той же амплитуде напряжения. Что еще мы можем сказать, глядя на эту формулу? Например, то, что чем больше частота сигнала, тем меньше для него сопротивление конденсатора.

И чем больше емкость конденсатора, тем меньше его сопротивление переменному току. По аналогии с резисторами, сопротивление конденсаторов измеряется все так же в Омах. Однако всегда следует помнить, что это немного другое сопротивление, его называют реактивным.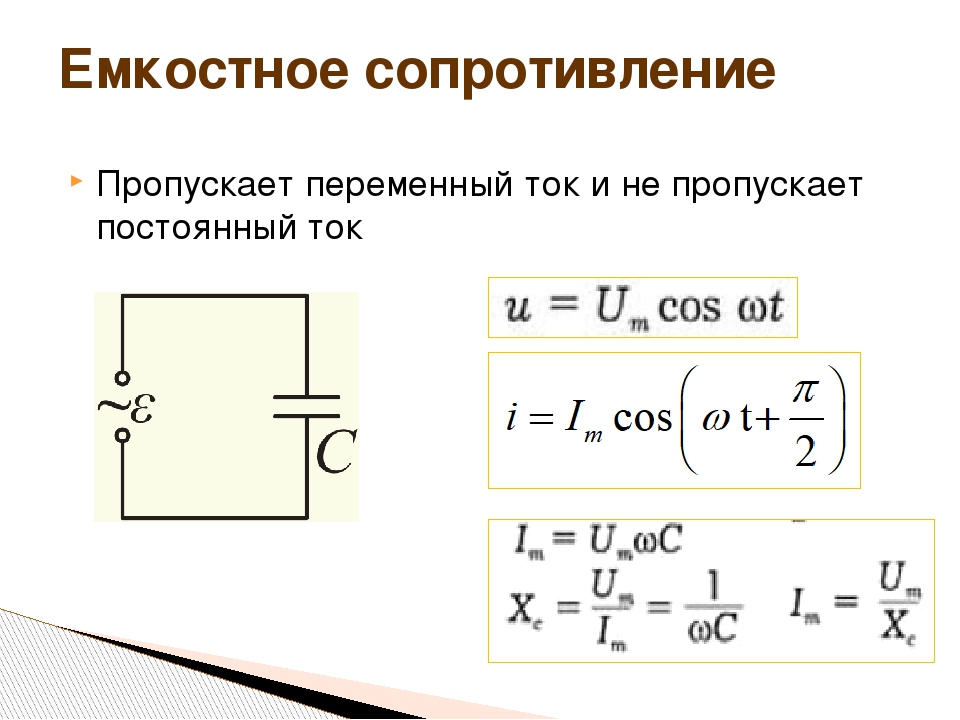 И другое оно в первую очередь из-за того самого пресловутого j в знаменателе, то есть из-за сдвига фазы. Давайте построим график зависимости сопротивления конденсатора от частоты.

Для определенности емкость конденсатора возьмем фиксированной, скажем, 1 мкФ. График представлен на рисунке 2. Рисунок 2 кликабельно — Зависимость сопротивления конденсатора от частоты. На рисунке 2 мы видим, что сопротивление конденсатора переменному току убывает по закону гиперболы.

Как найти сопротивление конденсатора формула. Активное и реактивное сопротивление

Импульсные блоки питания Линейные блоки питания Радиолюбителю конструктору Светодиоды, ламы и свет 3D печать и 3D модели Конденсаторы, как и резисторы, относятся к наиболее многочисленным элементам радиотехнических устройств. Тогда же говорил, что емкость конденсатора будет тем значительнее, чем больше площадь его обкладок и чем тоньше слой диэлектрика между ними. Основной единицей электрической емкости является фарада сокращенно Ф, названная так в честь английского физика М.

Емкостное сопротивление конденсатора Конденсатор используется в схемах для разделения переменной и постоянной составляющей напряжения.

Реактивное сопротивление

Соберем цепь с конденсатором , в которой генератор переменного тока создает синусоидальное напряжение. Разберем последовательно, что произойдет в цепи, когда мы замкнем ключ. Начальным будем считать тот момент, когда напряжение генератора равно нулю. Изменение тока и напряжения в цепи с емкостью. Таким образом, ток с наибольшей силой устремляется в свободный от заряда конденсатор, но тут же начинает убывать по мере заполнения зарядами пластин конденсатора и падает до нуля, полностью зарядив его. Сравним это явление с тем, что происходит с потоком воды в трубе, соединяющей два сообщающихся сосуда рис. Стоит только выдвинуть заслонку, преграждающую путь воде, как вода сразу же из левого сосуда под большим напором устремится по трубе в пустой правый сосуд. Однако тотчас же напор воды в трубе начнет постепенно ослабевать, вследствие выравнивания уровней в сосудах, и упадет до нуля. Течение воды прекратится.

Переменный ток и ёмкостное сопротивление конденсатора

В электрических и электронных системах реактивное сопротивление также реактанс — это сопротивление элемента схемы вызванное изменением тока или напряжения из-за индуктивности или емкости этого элемента. Понятие реактивного сопротивления аналогично электрическому сопротивлению , но оно несколько отличается в деталях. В векторном анализе реактивное сопротивление используется для вычисления амплитудных и фазовых изменений синусоидального переменного тока, проходящего через элемент цепи. Идеальный резистор имеет нулевое реактивное сопротивление, тогда как идеальные индуктивности и конденсаторы имеют нулевое сопротивление — то есть, реагируют на ток только по наличию реактивного сопротивления. Величина реактивного сопротивления индуктора увеличивается пропорционально увеличению частоты, в то время как величина реактивного сопротивления конденсатора уменьшается пропорционально увеличению частоты.

Быстрое изменение силы тока и его направления, характеризующее переменный ток, приводит к ряду важнейших особенностей, отличающих действие переменного тока от тока постоянного. Некоторые из этих особенностей отчетливо выступают при следующих опытах.

Емкостное сопротивление.

Предложить термин Сообщить об ошибке Отправить страницу Добавить в избранное. Емкостное сопротивление зависит от емкости конденсатора и частоты, причем с увеличением частоты емкостное сопротивление в отличие от индуктивного уменьшается. Емкостное сопротивление обратно пропорционально частоте. Емкостное сопротивление зависит не только от частоты переменного тока, но и от величины емкости, включенной в цепь. Емкостное сопротивление обратно пропорционально частоте приложенного напряжения.

уменьшится в 1,41 раза

Через какое минимальное время после замыкания конденсатора на катушку заряд на той же обкладке конденсатора станет равным — q , если период свободных колебаний в контуре Т? Какое уравнение выражает зависимость силы тока от времени? Период колебаний в колебательном контуре, состоящем из конденсатора ёмкостью мкФ и катушки индуктивностью 10 нГн, равен:. К ак изменится частота свободных колебаний в контуре, если ключ К перевести из положения 1 в положение 2. Какой будет энергия конденсатора и катушки в тот момент времени, когда сила тока в цепи 10 -4 А? Какое уравнение будет выражать зависимость ЭДС, возникающий в рамке, от времени?

Емкостное сопротивление конденсатора переменному току зависит от его емкости и частоты тока: чем больше емкость конденсатора и частота тока.

Переменный ток и ёмкостное сопротивление конденсатора

Здесь вы найдете подходящего репетитора быстро, удобно и бесплатно. Мы всегда рады проконсультировать Вас по вопросам образования. Задайте свои вопросы профессионалам.

Тест по теме: «Элетромагнитные колебания» .

Электрический ток в цепи возникает в результате изменения заряда конденсатора, поэтому колебания силы тока в цепи будут происходить по закону:. Произведение w CU m является амплитудой колебаний силы тока:. Аналогично тому, как было сделано с индуктивностью, введем понятие емкостного сопротивления конденсатора:. Рассмотрим электрическую схему на рис.

Для получения формулы емкостного сопротивления определим, как меняется сила тока в цепи , содержащей только конденсатор.

Конденсатор. Реактивное, емкостное сопротивление

Емкостное сопротивление в цепи переменного тока. Мгновенное значение напряжения равно. Мгновенное значение силы тока равно:. Емкостное сопротивление не является характеристикой проводника, так как зависит от параметров цепи частоты. Чем больше частота переменного тока, тем лучше пропускает конденсатор ток тем меньше сопротивление конденсатора переменному току. Такая нагрузка наз. Мгновенное значение силы тока:.

Компьютерные сети Системное программное обеспечение Информационные технологии Программирование. Все о программировании Обучение Linux Unix Алгоритмические языки Аналоговые и гибридные вычислительные устройства Архитектура микроконтроллеров Введение в разработку распределенных информационных систем Введение в численные методы Дискретная математика Информационное обслуживание пользователей Информация и моделирование в управлении производством Компьютерная графика Математическое и компьютерное моделирование Моделирование Нейрокомпьютеры Проектирование программ диагностики компьютерных систем и сетей Проектирование системных программ Системы счисления Теория статистики Теория оптимизации Уроки AutoCAD 3D Уроки базы данных Access Уроки Orcad Цифровые автоматы Шпаргалки по компьютеру Шпаргалки по программированию Экспертные системы Элементы теории информации Главная Тексты статей Добавить статьи Контакты уменьшится в 1,41 раза Дата добавления: ; просмотров: ; Нарушение авторских прав. Определите индуктивность катушки, сопротивление которой в цепи переменного тока частотой 50 Гц равна 20 Ом. Как изменится период колебаний в электрическом контуре, если емкость конденсатора увеличится в 2 раза, а индуктивность катушки уменьшится в 4 раза?

Пассивные электрические фильтры. фильтр низких частот

Автор: Рогожников Иван Павлович

Рубрика: Технические науки

Опубликовано в Молодой учёный №22 (417) июнь 2022 г.

Дата публикации: 04.06.2022 2022-06-04

Статья просмотрена: 15 раз

Скачать электронную версию

Скачать Часть 2 (pdf)

Библиографическое описание:

Рогожников, И. П. Пассивные электрические фильтры. фильтр низких частот / И. П. Рогожников. — Текст : непосредственный // Молодой ученый. — 2022. — № 22 (417). — С. 102-105. — URL: https://moluch.ru/archive/417/92636/ (дата обращения: 29.10.2022).



В настоящей статье затрагиваются Г-, Т-, П-образные пассивные k-фильтры низких частот (активные фильтры в настоящей статье не рассматриваются), рассматривается работа таких фильтров, приводятся графики амплитудно-частотных характеристик, показываются формулы характеристических сопротивлений для каждых фильтров.

Ключевые слова: электрические фильтры, АЧХ, ФНЧ, ФВЧ, индуктивность, емкость, ряд Фурье, гармонический сигнал.

В современном мире, при очень развитой полупроводниковой электронике, получили распространение так называемые электрические фильтры (далее — фильтры), построенные, в большинстве случаев, из пассивных реактивных компонентах — линейной катушки индуктивности и линейного конденсатора.

Работа фильтров основана на зависимости реактивного сопротивления элементов от частоты:

(1)

(2)

Фильтрами низких частот называют фильтры, пропускающие через себя, в общем случае, без изменений сигнал от 0 до , где — частота среза (частота, при которой наблюдается падение амплитуды выходного сигнала до амплитуды входного сигнала. В общем случае, фильтры являются симметричными — продольные сопротивления равны между собой, поперечные сопротивления равны между собой.

На рис. 1 приведены типичные конструкции фильтров низких частот.

Рис. 1. Конструкции фильтров нижних частот: а) Г-образный; б) Т-образный; в) П-образный

Рассмотрим на примере работу Т-образного фильтра нижних частот. (рис. 2)

Поскольку в составе фильтра имеются только реактивные элементы — фильтр относится к типу k-фильтров, так для таких фильтров выполняется условие симметричности: при изменении частоты характер продольного реактивного сопротивления обратен характеру поперечного реактивного сопротивления. Другими словами, например, при увеличении частоты индуктивное сопротивление увеличивается, а емкостное сопротивление — уменьшается.

Рис. 2. Испытательная схема

Пусть на входных зажимах имеется напряжение, изменяющееся по закону:

(3)

а параметры цепи будут равны: .

Исходя из данных условий, опуская весь математический аппарат, получим закон изменения во времени напряжения на нагрузки:

(4)

Составим график зависимости напряжения от времени для двух известных законов и получим следующую ситуацию:

Рис. 3. График напряжений на входе и на нагрузке

Из графика видно, что фильтр подавил токовые составляющие высших гармоник. Составим линейчатые спектры амплитуд входного напряжения и напряжения на нагрузки (рис. 4):

Рис. 4. Линейчатый спектр амплитуд напряжений

Для более глубокого анализа подобного фильтра, примем ФНЧ как четырехполюсник (рис. 5) и найдем его характеристическое сопротивление.

Рис. 5. Представление фильтра как четырехполюсника

Поскольку фильтр является симметричным — его продольные и поперечные сопротивления попарно равны — достаточным условием для поиска характеристического сопротивления (7) достаточно найти коэффициенты B, C по формулам четырехполюсника A-формы [1]:

(5)

(6)

(7)

Вариантов поиска коэффициентов четырехполюсника много, равно как и форм их записи, подробнее про формы записи можно ознакомится в авторитетных учебниках.

Найдя коэффициенты по формулам (6) и (7) и подставив в (5) получим:

Поскольку пассивные фильтры являются частотно-зависимыми (сопротивления их компонентов зависят от частоты), то при малейшем изменении частоты необходимо согласовывать нагрузку (в отличии m-фильтров, где существует небольшой диапазон частот, при котором согласование не требуется). Для симметричных k-фильтров нижних частот сопротивление нагрузки нужно выбирать в зависимости от характеристического сопротивления (далее — Zx) во избежание потерь фильтрующих свойств самого фильтра.

Построим график зависимости (рис. 6):

Рис. 6. График зависимости

Поскольку необходимо, чтобы фильтр работал до частоты среза ( ), то сопротивление нагрузки согласовывают с , т. е. выбирают примерно равным.

В данном примере видно, что фильтр подавляет токовые составляющие высших гармоник не сильно эффективно, т. е. наблюдается не крутой спад амплитудно-частотной характеристики. Для того, чтобы этого избежать, нужно либо увеличить емкость конденсатора, чтобы он зашунтировал нагрузку, что бывает неэффективно, либо заменить Т-образный фильтр на П-образный фильтр, получив уже крутость амплитудо-частотной характеристики, большую эффективность за счет создания дополнительных падений напряжений на элементах, не сильно увеличивая габариты и стоимость устройств.

Поскольку для современных задач в области обработки сигналов пассивные электрические фильтры были вытеснены активными, с применением операционных усилителей, пассивные фильтры очень широко применяются в силовой электронике, например, фильтрации блоков питания.

Литература:

1. Бессонов, Л. А. Теоретические основы электротехники. Электрические цепи / Л. А. Бессонов. — 11-е изд., переработанное и дополненное. — Москва: Юрайт, 2013. — 701 c. — Текст: непосредственный.

Основные термины (генерируются автоматически): фильтр, характеристическое сопротивление, частота, график зависимости, нагрузка, общий случай, сопротивление, сопротивление нагрузки, частота среза.

Ключевые слова

емкость, электрические фильтры, АЧХ, ФНЧ, ФВЧ, индуктивность, ряд Фурье, гармонический сигнал

электрические фильтры, АЧХ, ФНЧ, ФВЧ, индуктивность, емкость, ряд Фурье, гармонический сигнал

Похожие статьи

Метод расчета активного

сопротивления цилиндрического. ..

Проанализированы закономерности изменения активного сопротивления медных и алюминиевых проводов в зависимости от частоты и

 В данной статье рассматривается вопрос влияния высших гармоник тока на активное сопротивление цилиндрического провода в…

Управление

частотой среза конверторных фильтров

Требуемое изменение частоты среза можно провести не изменяя сопротивление резисторов , а только изменяя эквивалентное сопротивление ЧЗОС и нагрузки. Пусть исходная расчетная частота ФНЧ и требуется увеличить ее в 2 раза. Тогда, согласно (7), чтобы не менять…

Активные и пассивные электрические

фильтры | Молодой ученый

 Фильтр — устройство, которое передает сигналы в определенной области частот и препятствует прохождению сигналов вне этой области.

В идеальном случае разработчику хотелось бы получить

Управление частотой среза конверторных фильтров.

Применение пассивных

фильтров для компенсации высших…

В качестве спокойной нагрузки будет пониматься асинхронный двигатель (представлен

Рассмотрим для примера расчет фильтра для компенсации 5 гармоники тока в сети.

Емкостное сопротивление БСК на 5 гармонике равно Ом. Исходя из равенства емкостного и…

Эффективность работы активного

фильтра гармоник

Активные фильтры — это коммутируемые устройства, параметры которых создаются при помощи закона управления. Это адаптационные устройства, с величинами, которые меняются в соответствии с режимом работы сети и характеристик нагрузки.

Методики расчёта составляющих мощности при синусоидальных.

..

. Полная мощность определяется общепризнанной формулой в случае синусоидальной нагрузки: . Под полной мощностью понимают мощность, необходимую для обеспечения работы нагрузки, в случае неиспользования всей мощности при совершении полезной работы.

Исследование и разработка устройства для измерения больших…

Управление частотой среза конверторных фильтров. Для этого необходимо поделить сопротивления всех элементов LC-прототипа на на , где k – масштабный коэффициент, имеющий размерность времени; –текущая частота. В результате частотного преобразования…

Методы z-преобразования для расчета передаточной функции…

Заданный аналоговый прототип имеет следующие параметры: сопротивление R =10 Ом , ёмкость С = 10 пФ и индуктивность L =100 мГн. Прежде чем приступить к получению передаточной функции цифрового фильтра, необходимо посчитать операторную…

Методика расчета высотных зданий на воздействие ветровой…

В статье автор производит исследование методики расчета высотных зданий на воздействие ветровой нагрузки в программном комплексе Ansys.

Общая высота здания — 380м. Общий вид данного здания представлен ниже на Рис 2.

Похожие статьи

Метод расчета активного

сопротивления цилиндрического…

Проанализированы закономерности изменения активного сопротивления медных и алюминиевых проводов в зависимости от частоты и

 В данной статье рассматривается вопрос влияния высших гармоник тока на активное сопротивление цилиндрического провода в…

Управление

частотой среза конверторных фильтров

Требуемое изменение частоты среза можно провести не изменяя сопротивление резисторов , а только изменяя эквивалентное сопротивление ЧЗОС и нагрузки. Пусть исходная расчетная частота ФНЧ и требуется увеличить ее в 2 раза. Тогда, согласно (7), чтобы не менять…

Активные и пассивные электрические

фильтры | Молодой ученый

 Фильтр — устройство, которое передает сигналы в определенной области частот и препятствует прохождению сигналов вне этой области.

В идеальном случае разработчику хотелось бы получить

Управление частотой среза конверторных фильтров.

Применение пассивных

фильтров для компенсации высших…

В качестве спокойной нагрузки будет пониматься асинхронный двигатель (представлен

Рассмотрим для примера расчет фильтра для компенсации 5 гармоники тока в сети.

Емкостное сопротивление БСК на 5 гармонике равно Ом. Исходя из равенства емкостного и…

Эффективность работы активного

фильтра гармоник

Активные фильтры — это коммутируемые устройства, параметры которых создаются при помощи закона управления. Это адаптационные устройства, с величинами, которые меняются в соответствии с режимом работы сети и характеристик нагрузки.

Методики расчёта составляющих мощности при синусоидальных…

. Полная мощность определяется общепризнанной формулой в случае синусоидальной нагрузки: . Под полной мощностью понимают мощность, необходимую для обеспечения работы нагрузки, в случае неиспользования всей мощности при совершении полезной работы.

Исследование и разработка устройства для измерения больших…

Управление частотой среза конверторных фильтров. Для этого необходимо поделить сопротивления всех элементов LC-прототипа на на , где k – масштабный коэффициент, имеющий размерность времени; –текущая частота. В результате частотного преобразования…

Методы z-преобразования для расчета передаточной функции…

Заданный аналоговый прототип имеет следующие параметры: сопротивление R =10 Ом , ёмкость С = 10 пФ и индуктивность L =100 мГн. Прежде чем приступить к получению передаточной функции цифрового фильтра, необходимо посчитать операторную…

Методика расчета высотных зданий на воздействие ветровой…

В статье автор производит исследование методики расчета высотных зданий на воздействие ветровой нагрузки в программном комплексе Ansys.

Общая высота здания — 380м. Общий вид данного здания представлен ниже на Рис 2.

Калькулятор емкостного реактивного сопротивления и проводимости

Калькулятор емкостного реактивного сопротивления и проводимости: Используйте калькулятор емкостных реактивных сопротивлений и полной проводимости для определения реактивного сопротивления и проводимости любой цепи путем ввода соответствующих значений частоты и емкости. Обратное вычисление также возможно при использовании второй части калькулятора.

Калькулятор емкостного реактивного сопротивления и проводимости:

Этот онлайн-калькулятор емкостного реактивного сопротивления и проводимости помогает рассчитать значение реактивного сопротивления Xc (Ом) и активной проводимости Bc (м-мОм) конденсатора путем ввода значения емкости (пФ) и рабочая частота (ГГц).

Этот онлайн-калькулятор также предоставляет дополнительный калькулятор для расчета значения емкости (пФ) и активной проводимости Bc (м-мОм) путем ввода значения реактивного сопротивления Xc (Ом) и рабочей частоты (ГГц).

Что такое емкостное сопротивление?

Противодействие протеканию переменного тока за счет конденсатора называется емкостным реактивным сопротивлением. Поскольку он противодействует протеканию тока, подобно резистору, поэтому емкостное реактивное сопротивление измеряется в омах, Ω. Символом емкостного сопротивления является Xc.

Как рассчитать емкостное сопротивление?

Емкостное реактивное сопротивление Xc рассчитывается по следующей формуле в цепи переменного тока.

• Где:
• Xc = емкостное реактивное сопротивление в омах (Ом)
• C = Значение емкости в цепи переменного тока в пФ (пикофарад)
• f = Рабочая частота цепи переменного тока в ГГц

Что такое допуск?

В цепи переменного тока проводимость является мерой того, насколько легко цепь или устройство пропускают переменный ток. Адмиттанс является величиной, обратной импедансу Z. Адмиттанс обозначается буквой «Y», а единицей адмиттанса является сименс (S) или мхо (℧).

Полное сопротивление Z является мерой сопротивления прохождению электрического тока из-за цепи или устройства. Единицей импеданса Z является ом (Ом).

В цепи постоянного тока импеданс Z и сопротивление (R) одинаковы; таким образом, импеданс в цепи постоянного тока определяется как напряжение на элементе, деленное на ток (Z = R = V/I).

В цепи переменного тока «реактивное сопротивление (представленное буквой X)» входит в уравнение импеданса из-за частотно-зависимых вкладов емкости и индуктивности (если в цепи переменного тока присутствуют элементы конденсатора и катушки индуктивности). Символ емкостного сопротивления — Xc, а символ индуктивного сопротивления — XL.

Противодействие протеканию переменного тока из-за конденсатора называется емкостным реактивным сопротивлением (Xc), а противодействие протеканию переменного тока из-за катушки индуктивности называется индуктивным реактивным сопротивлением (XL). Как XL, так и Xc создают разность фаз между входным напряжением питания переменного тока и током, протекающим через цепь. Следовательно, импеданс (Z) цепи переменного тока представлен в комплексной форме Z=R+jX. Ниже приведены некоторые последовательные цепи, чтобы понять импеданс (Z) цепи.

Цепь постоянного тока (сопротивление Z=R1 Ом) Цепь переменного тока — присутствует только сопротивление (полное сопротивление Z = R Ω) Серия переменного тока RL – сопротивление цепи и катушка индуктивности присутствуют (импеданс Z = R+jXL Ω) Серия переменного тока RC-сопротивление цепи и наличие конденсатора (импеданс Z = R-jXc Ω) Серия переменного тока RLC-сопротивление цепи и наличие конденсатора (импеданс Z = R+j(XL — Xc Ω)

Адмиттивность обратно пропорциональна импедансу Z= R +jX.

т. е. Y = 1/Z = G+jB измеряется в сименсах

• Где:
• Y = проводимость цепи, измеренная в сименсах
• G = проводимость, измеренная в сименсах
• B = Сопротивление измерено в Siemens

Формула для расчета сопротивления следующей цепи: Bc = 1/Xc

Присутствует только конденсатор «C»

23.

11 Реактивное, индуктивное и емкостное сопротивление – College Physics

Глава 23 Электромагнитная индукция, цепи переменного тока и электрические технологии

Резюме

• Зарисовка зависимости напряжения и тока от времени в простых индуктивных, емкостных и резистивных цепях.
• Рассчитать индуктивное и емкостное сопротивление.
• Расчет тока и/или напряжения в простых индуктивных, емкостных и резистивных цепях.

Многие схемы также содержат конденсаторы и катушки индуктивности в дополнение к резисторам и источнику переменного напряжения. Мы видели, как конденсаторы и катушки индуктивности реагируют на постоянное напряжение при его включении и выключении. Теперь мы рассмотрим, как катушки индуктивности и конденсаторы реагируют на синусоидальное переменное напряжение.

Предположим, что катушка индуктивности подключена непосредственно к источнику переменного напряжения, как показано на рисунке 1. Разумно предположить пренебрежимо малое сопротивление, так как на практике мы можем сделать сопротивление катушки индуктивности настолько малым, что оно окажет незначительное влияние на цепь. Также показан график зависимости напряжения и тока от времени.

Рис. 1. (a) Источник переменного напряжения, включенный последовательно с катушкой индуктивности, имеющей незначительное сопротивление. (б) График тока и напряжения на катушке индуктивности в зависимости от времени.

График на рис. 2(b) начинается с максимального напряжения. Обратите внимание, что ток начинается с нуля и достигает своего пика после управляющего им напряжения, как это было в случае, когда в предыдущем разделе было включено постоянное напряжение. Когда напряжение в точке а становится отрицательным, ток начинает уменьшаться; он становится равным нулю в точке b, где напряжение является самым отрицательным. Затем ток становится отрицательным, снова следуя за напряжением. Напряжение становится положительным в точке с и начинает делать ток менее отрицательным. В точке d ток проходит через нуль как раз в тот момент, когда напряжение достигает своего положительного пика, чтобы начать новый цикл. Это поведение резюмируется следующим образом: 9{\circ}}[/latex] фазовый угол.

Ток отстает от напряжения, так как катушки индуктивности препятствуют изменению тока. Изменение тока индуцирует обратную ЭДС [латекс]{V= -L(\Delta I/ \Delta t)}[/латекс]. Это считается эффективным сопротивлением катушки индуктивности переменному току. Действующее значение тока [латекс]{I}[/латекс] через катушку индуктивности [латекс]{L}[/латекс] определяется версией закона Ома:

[латекс] {I =} [/ латекс] [латекс] {\ гидроразрыва {V} {X_L}}, [/ латекс]

, где [latex]{V}[/latex] — среднеквадратичное напряжение на катушке индуктивности, а [latex]{X_L}[/latex] определяется как 9.0003

[латекс]{X_L = 2 \pi fL},[/латекс]

с [latex]{f}[/latex] частотой источника переменного напряжения в герцах (анализ цепи с использованием правила цикла Кирхгофа и исчисления фактически дает это выражение). [латекс]{X_L}[/латекс] называется индуктивным реактивным сопротивлением, потому что индуктор препятствует протеканию тока. [latex]{X_L}[/latex] имеет единицы измерения омы ([latex]{1 \;\textbf{H}=1 \;\Omega \cdot \;\text{s}}[/latex], так что частота, умноженная на индуктивность, имеет единицы (циклы / с) ([латекс] {\ Omega \ cdot \; \ text {s}} [/ латекс]) = [латекс] {\ Omega} [/латекс]), что соответствует его роль эффективного сопротивления. Имеет смысл, что [латекс]{X_L}[/латекс] пропорционален [латексу]{L}[/латексу], поскольку чем больше индукция, тем больше его сопротивление изменению. Также разумно, что [латекс]{X_L}[/латекс] пропорционален частоте [латекс]{f}[/латекс], поскольку большая частота означает большее изменение тока. То есть [latex]{\Delta I/\Delta t}[/latex] велико для больших частот (большой [latex]{f}[/latex] , маленький [латекс] {\ Delta t} [/латекс]). Чем больше изменение, тем больше сопротивление индуктора.

Пример 1. Расчет индуктивного реактивного сопротивления, а затем тока

(a) Рассчитайте индуктивное реактивное сопротивление катушки индуктивности 3,00 мГн при подаче переменного напряжения частотой 60,0 Гц и 10,0 кГц. б) Чему равно среднеквадратичное значение тока на каждой частоте, если приложенное среднеквадратичное напряжение равно 120 В?

Стратегия

Индуктивное сопротивление находится непосредственно из выражения [латекс]{X_L = 2 \pi fL}[/латекс]. Как только [латекс]{X_L}[/латекс] найден на каждой частоте, можно использовать закон Ома, указанный в уравнении [латекс]{I=V/X_L}[/латекс], чтобы найти ток на каждой частоте. 94 \;\text{/s})(3,00 \;\text{мГн}) = 188 \;\Omega \;\text{at} 10 \;\text{кГц}}[/latex]

Решение для (b)

Среднеквадратичное значение тока теперь находится с использованием версии закона Ома в уравнении [latex]{I = V/X_L}[/latex], при условии, что приложенное среднеквадратичное напряжение составляет 120 В. Для первой частоты это дает

[латекс] {I =} [/латекс] [латекс] {\ гидроразрыва {V} {X_L}} [/ латекс] [латекс] {=} [/латекс] [латекс] {\ гидроразрыва {120 \;\text{V}}{1.13 \;\Omega}}[/latex] [латекс]{= 106 \;\text{A at} \; 60 \;\text{Гц}}. [/latex]

Аналогично, на частоте 10 кГц

[латекс] {I=}[/латекс] [латекс]{\ гидроразрыва {V} {X_L}}[/латекс] [латекс] {=}[/латекс] [латекс ] {\ frac {120 \; \ text {V}} {188 \; \ Omega}} [/latex] [латекс] {= 0,637 \; \ text {A at} \; 10 \;\text{кГц}}.[/latex]

Обсуждение

Катушка индуктивности очень по-разному реагирует на двух разных частотах. На более высокой частоте его реактивное сопротивление велико, а ток мал, что соответствует тому, как индуктор препятствует быстрому изменению. Таким образом, высокие частоты препятствуют больше всего. Индукторы можно использовать для фильтрации высоких частот; например, большой индуктор можно включить последовательно с системой воспроизведения звука или последовательно с вашим домашним компьютером, чтобы уменьшить высокочастотный звук, выходящий из ваших динамиков, или высокочастотные скачки мощности в вашем компьютере.

Обратите внимание, что хотя сопротивление в рассматриваемой цепи незначительно, переменный ток не очень велик, поскольку индуктивное сопротивление препятствует его протеканию. При переменном токе нет времени для того, чтобы ток стал чрезвычайно большим.

Рассмотрим конденсатор, подключенный непосредственно к источнику переменного напряжения, как показано на рис. 2. Сопротивление такой цепи можно сделать настолько малым, что оно оказывает незначительное влияние по сравнению с конденсатором, поэтому мы можем предположить пренебрежимо малое сопротивление. Напряжение на конденсаторе и ток представлены на рисунке как функции времени.

Рис. 2. (a) Источник переменного напряжения, включенный последовательно с конденсатором C , имеющим незначительное сопротивление. (б) График тока и напряжения на конденсаторе в зависимости от времени.

График на рис. 2 начинается с максимального напряжения на конденсаторе. В этот момент ток равен нулю, потому что конденсатор полностью заряжен и останавливает поток. Затем напряжение падает, а ток становится отрицательным по мере разряда конденсатора. В точке a конденсатор полностью разряжен ([латекс]{Q = 0}[/латекс] на нем), и напряжение на нем равно нулю. Ток между точками a и b остается отрицательным, что приводит к изменению напряжения на конденсаторе. Это завершается в точке b, где ток равен нулю, а напряжение имеет самое отрицательное значение. Ток становится положительным после точки b, нейтрализуя заряд конденсатора и сводя напряжение к нулю в точке c, что позволяет току достигать своего максимума. Между точками c и d ток падает до нуля, когда напряжение достигает своего пика, и процесс начинает повторяться. На протяжении всего цикла напряжение следует за током на одну четвертую цикла: 9{\circ}}[/latex] фазовый угол.

Конденсатор влияет на ток, имея возможность полностью остановить его при полной зарядке. Поскольку применяется переменное напряжение, существует среднеквадратичное значение тока, но оно ограничено конденсатором. Это считается эффективным сопротивлением конденсатора переменному току, поэтому среднеквадратичное значение тока [латекс]{I}[/латекс] в цепи, содержащей только конденсатор [латекс]{С}[/латекс], определяется другим выражением вариант закона Ома будет

[латекс] {I =} [/ латекс] [латекс] {\ гидроразрыва {V} {X_C}}, [/ латекс]

, где [латекс]{V}[/латекс] — среднеквадратичное значение напряжения, а [латекс]{X_C}[/латекс] определяется (как и в случае с [латекс]{X_L}[/латекс], это выражение для [латекс]{ X_C}[/latex] результат анализа схемы с использованием правил и исчисления Кирхгофа) равно

[латекс] {X_C =} [/латекс] [латекс] {\ гидроразрыва {1} {2 \ pi fC}}, [/латекс]

, где [латекс]{X_C}[/латекс] называется емкостным реактивным сопротивлением, потому что конденсатор препятствует протеканию тока. [latex]{X_C}[/latex] измеряется в омах (проверка оставлена ​​читателю в качестве упражнения). [латекс]{X_C}[/латекс] обратно пропорциональна емкости [латекс]{С}[/латекс]; чем больше конденсатор, тем больший заряд он может хранить и тем больший ток может протекать. Это также обратно пропорционально частоте [латекс]{ф}[/латекс]; чем больше частота, тем меньше времени остается для полной зарядки конденсатора, и поэтому он меньше препятствует току.

Пример 2. Расчет емкостного реактивного сопротивления, а затем тока

(a) Рассчитайте емкостное реактивное сопротивление конденсатора емкостью 5,00 мФ при подаче переменного напряжения частотой 60,0 Гц и 10,0 кГц. б) Чему равно среднеквадратичное значение тока, если приложенное среднеквадратичное напряжение равно 120 В?

Стратегия

Емкостное реактивное сопротивление находится непосредственно из выражения в [latex]{X_C = \frac{1}{2 \pi fC}}[/latex]. Как только [латекс]{X_C}[/латекс] найден на каждой частоте, можно использовать закон Ома, сформулированный как [латекс]{I = V/X_C}[/латекс], чтобы найти ток на каждой частоте. 4 \; \ text{/s}) (5,00 \; \ mu \ textbf {F} )}} \\[1em] & {3.18 \;\Omega \;\text{at} \; 10 \;\text{Гц}}. \end{массив}[/латекс]

Решение для (b)

Среднеквадратичное значение тока теперь находится с использованием версии закона Ома в [latex]{I = V/X_C}[/latex], при условии, что приложенное среднеквадратичное напряжение равно 120 В. Для первая частота, это дает

[латекс] {I =} [/латекс] [латекс] {\ гидроразрыва {V} {X_C}} [/латекс] [латекс] {=}[/латекс] [латекс] {\ frac{120 \;\text{V}}{531 \;\Omega}}[/latex] [латекс]{= 0,226 \;\text{A at} \; 60 \;\text{Гц}}.[/latex]

Аналогично, при 10 кГц

[латекс]{I =}[/латекс] [латекс]{\ гидроразрыва {V} {X_C}}[/ латекс] [латекс] {=}[/ латекс] [латекс] {\ гидроразрыва {120 \; \ текст {V}} {3,18 \; \ Omega}} [/ латекс] [латекс] {= 37,7 \; \ текст {А в} \; 10 \;\text{кГц}}.[/latex]

Обсуждение

Конденсатор очень по-разному реагирует на двух разных частотах, и совершенно противоположным образом реагирует индуктор. На более высокой частоте его реактивное сопротивление мало, а ток велик. Конденсаторы способствуют изменениям, тогда как индукторы сопротивляются изменениям. Конденсаторы больше всего препятствуют низким частотам, поскольку низкая частота дает им время зарядиться и остановить ток. Конденсаторы можно использовать для фильтрации низких частот. Например, конденсатор, включенный последовательно со звуковоспроизводящей системой, избавляет ее от гула частотой 60 Гц.

Хотя конденсатор в основном представляет собой разомкнутую цепь, в цепи с переменным напряжением, приложенным к конденсатору, существует среднеквадратичное значение тока. Это связано с тем, что напряжение постоянно меняется, заряжая и разряжая конденсатор. Если частота стремится к нулю (постоянный ток), [латекс]{X_C}[/латекс] стремится к бесконечности, а ток равен нулю после зарядки конденсатора. На очень высоких частотах реактивное сопротивление конденсатора стремится к нулю — он имеет пренебрежимо малое реактивное сопротивление и не препятствует протеканию тока (он действует как простой провод). Конденсаторы действуют на цепи переменного тока противоположно действию катушек индуктивности .

В качестве напоминания рассмотрите рисунок 3, на котором показано напряжение переменного тока, приложенное к резистору, и график зависимости напряжения и тока от времени. Напряжение и ток равны в фазе в резисторе. Поведение простого сопротивления в цепи не зависит от частоты:

Рис. 3. (a) Источник переменного напряжения последовательно с резистором. (b) График зависимости тока и напряжения на резисторе от времени, показывающий, что они точно совпадают по фазе. 9{\circ}}[/latex] фазовый угол.

Противодействие катушки индуктивности изменению тока выражается как вид сопротивления переменному току.

Закон Ома для катушки индуктивности

[латекс] {I =} [/ латекс] [латекс] {\ гидроразрыва {V} {X_L}}, [/ латекс]

, где [латекс]{В}[/латекс] — среднеквадратичное напряжение на катушке индуктивности.

[латекс]{X_L}[/латекс] определяется как индуктивное реактивное сопротивление, определяемое формулой

[латекс]{X_L = 2 \pi fL},[/латекс]

с [latex]{f}[/latex] частотой источника переменного напряжения в герцах. 9{\circ}}[/latex] фазовый угол.

Поскольку конденсатор может останавливать ток при полной зарядке, он ограничивает ток и предлагает другую форму сопротивления переменному току; Закон Ома для конденсатора

[латекс] {I =} [/латекс] [латекс] {\ гидроразрыва {V} {X_C}}, [/латекс]

, где [латекс]{В}[/латекс] — среднеквадратичное напряжение на конденсаторе.

[латекс]{X_C}[/латекс] определяется как емкостное реактивное сопротивление, определяемое формулой

[латекс] {X_C =} [/латекс] [латекс] {\ гидроразрыва {1} {2 \ pi fC}}. [/латекс]

[латекс]{X_C}[/латекс] измеряется в омах и максимален на низких частотах.

Задачи и упражнения

1: При какой частоте индуктор на 30,0 мГн будет иметь реактивное сопротивление [латекс]{100 \;\Омега}[/латекс]

2: Какое значение индуктивности следует использовать, если [латекс]{20,0 \;\text{k} \Omega}[/latex] реактивное сопротивление необходимо при частоте 500 Гц?

3: Какую емкость следует использовать для получения реактивного сопротивления [латекс]{2,00 \;\textbf{M} \Omega}[/latex] на частоте 60,0 Гц?

4: При какой частоте конденсатор емкостью 80,0 мФ будет иметь реактивное сопротивление [латекс]{0,250 \;\Омега}[/латекс]?

5: (a) Найдите ток через катушку индуктивности 0,500 Гн, подключенную к источнику переменного тока с частотой 60,0 Гц и напряжением 480 В. б) Какой будет сила тока на частоте 100 кГц?

6: (a) Какой ток протекает, когда источник переменного тока с частотой 60,0 Гц, 480 В подключен к [латексному] конденсатору {0,250 \;\мкФ}[/латекс]? б) Какой будет сила тока на частоте 25,0 кГц?

7: Источник 20,0 кГц, 16,0 В, подключенный к катушке индуктивности, производит ток силой 2,00 А. Индуктивность какая?

8: Источник 20,0 Гц, 16,0 В производит ток 2,00 мА при подключении к конденсатору. Какова емкость?

9: (a) Катушка индуктивности, предназначенная для фильтрации высокочастотных помех от питания, подаваемого на персональный компьютер, устанавливается последовательно с компьютером. Какой минимальной индуктивностью он должен обладать, чтобы создавать [латекс]{2,00 \;\текст{к} \Омега}[/латекс] реактивное сопротивление для шума 15,0 кГц? б) Каково его реактивное сопротивление при частоте 60,0 Гц?

10: Конденсатор на рис. 4(а) предназначен для фильтрации низкочастотных сигналов, препятствуя их передаче между цепями. а) Какая емкость необходима для получения реактивного сопротивления [латекс]{100 \;\text{k} \Омега}[/латекс] на частоте 120 Гц? б) Каким будет его реактивное сопротивление на частоте 1,00 МГц? (c) Обсудите последствия ваших ответов на вопросы (a) и (b).

11: Конденсатор на рис. 4(b) фильтрует высокочастотные сигналы, замыкая их на землю. (a) Какая емкость необходима для получения реактивного сопротивления [латекс]{10,0 \;\текст{м} \Омега}[/латекс] для сигнала 5,00 кГц? б) Каким будет его реактивное сопротивление при частоте 3,00 Гц? (c) Обсудите последствия ваших ответов на вопросы (a) и (b).

12: необоснованные результаты

При записи напряжений, вызванных активностью головного мозга (ЭЭГ), сигнал 10,0 мВ с частотой 0,500 Гц подается на конденсатор, производящий ток 100 мА. Сопротивление незначительно. а) Чему равна емкость? б) Что неразумного в этом результате? (c) Какое предположение или предпосылка являются ответственными?

13: Создайте свою собственную задачу

Рассмотрим использование катушки индуктивности последовательно с компьютером, работающим от электричества 60 Гц.